Describing strong correlation with fractional-spin correction in density functional theory

Significance

The static correlation error inherent in commonly used density functional approximations (DFAs) has seriously hindered the application of density functional theory (DFT) to strongly correlated systems. Here, an effective fractional-spin correction against the important issue of static/strong correlation in DFT is developed. With this, the flat-plane behavior of various DFAs is largely restored, and the potential energy curves of dissociation of ionic species, single bonds, and multiple bonds are properly described, which demonstrates great improvement in the treatment of strong correlation. This work should have a significant impact on the development and application of DFT.

Abstract

An effective fractional-spin correction is developed to describe static/strong correlation in density functional theory. Combined with the fractional-charge correction from recently developed localized orbital scaling correction (LOSC), a functional, the fractional-spin LOSC (FSLOSC), is proposed. FSLOSC, a correction to commonly used functional approximations, introduces the explicit derivative discontinuity and largely restores the flat-plane behavior of electronic energy at fractional charges and fractional spins. In addition to improving results from conventional functionals for the prediction of ionization potentials, electron affinities, quasiparticle spectra, and reaction barrier heights, FSLOSC properly describes the dissociation of ionic species, single bonds, and multiple bonds without breaking space or spin symmetry and corrects the spurious fractional-charge dissociation of heteroatom molecules of conventional functionals. Thus, FSLOSC demonstrates success in reducing delocalization error and including strong correlation, within low-cost density functional approximation.

Density functional theory (DFT) (1–3) is now the leading electronic structure method in chemistry, physics, and material science. This success should be attributed to the easily calculated energy functional of 3D electron density, which avoids solving the $3N$-dimensional Schrödinger equation ($N$ being the electron number). Being exact in principle, DFT has to rely on approximations to the unknown exchange-correlation (XC) functional in practical applications. Therefore, better density functional approximations (DFAs) have been the constant pursuit in DFT.

The incorrect treatment of static/strong correlation is among the most challenging problems in DFT (4–6). It is generally recognized that static correlation arises from the (near-)degeneracy of the reference Slater determinant with other low-energy configurations, while dynamic correlation is from the mixing of higher-energy excited configurations. Unlike the short-range feature of dynamic correlation, being multicenter in range (7) makes it difficult to model static correlation with (semi)local functionals.

To understand the systematic errors in existing DFAs and to guide the construction of better approximations, knowledge of the conditions satisfied by the exact functional is essential. Of particular interest here are the exact conditions of DFT on fractional charges and fractional spins. For fractional charges, the Perdew–Parr–Levy–Balduz (PPLB) condition (8–11) requires the total energy, as a function of electron number, to be piecewise straight lines interpolating between adjacent integers. Convex deviation from this piecewise linearity for fractional-charge (FC) systems has been defined as the delocalization error (4, 12, 13), which is related to the earlier concept of many-electron self-interaction error (14–17). For fractional spins, the constancy condition (4, 13, 18) requires the energy of a system with fractional-spin (FS) states to equate that of the comprising degenerate pure-spin states, which is a special case of the conditions for general degenerate states derived in ref. 9. Violation of this constancy requirement is the static correlation error inherent in approximate functionals (18). The FC and FS conditions were unified and extended to a more general and stringent condition, the flat-plane condition (19). The flat-plane condition requires the energy of systems with fractional charges and spins to be two flat planes intersecting in a seam defined by the line of integer electron number. It is this requirement that a discontinuous behavior comes out automatically when total electron number passes through an integer for any fractional spins, revealing the explicitly discontinuous nature of the derivative of the XC functional (19). Its satisfaction requires that the exact XC functional is not a continuously differentiable functional of either the electron density or the (generalized) Kohn–Sham [(G)KS] density matrix for strongly correlated systems (19). In comparison, the derivative discontinuity requirement derived from the PPLB condition for fractional charges is only a subset—it only requires that the exact XC functional is not a continuously differentiable functional of the electron density (20, 21).

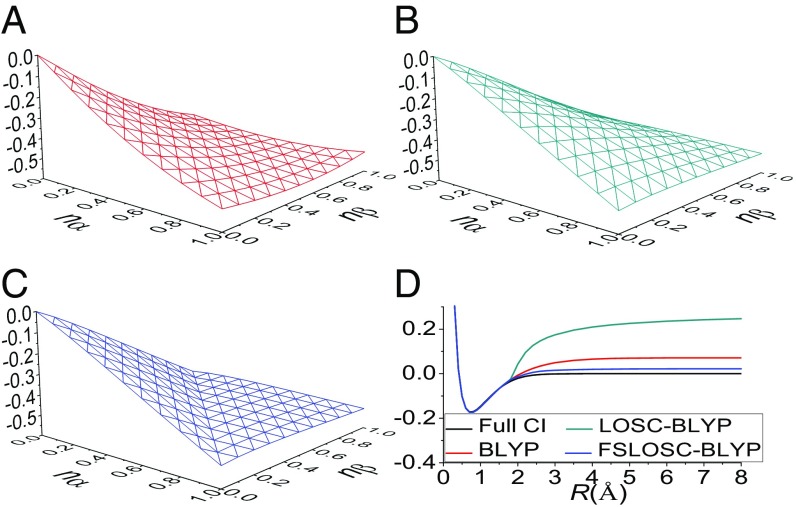
The behavior of semilocal functionals exemplified by BLYP (22, 23) is shown in Fig. 1A. As can be seen, the correct piecewise flat-plane behavior is erroneously smoothed out into a continuous shape. This poor performance indicates that severe delocalization and static correlation errors exist in the functional, which thus cause the spectacular failures in practical calculations (4, 11–19, 24). In particular, the erroneous dissociation limits of ${\mathrm{H}}_2^{+}$ and ${\mathrm{H}}_2$, resulting, respectively, from the large deviations of the FC point, H ($\frac{1}{2}$, 0), from linearity and the FS point, H ($\frac{1}{2}$, $\frac{1}{2}$), from constancy, are simple examples of the delocalization and static correlation errors (4, 13, 18).

Fig. 1.

Total energy of hydrogen atom with fractional charges and fractional spins, H ($n^{\alpha }$, $n^{\beta }$). (A–C) BLYP (A), LOSC-BLYP (B), and FSLOSC-BLYP (C) are examined. (D) Potential energy curve for H–H bond dissociation in ${\mathrm{H}}_2$. The total energy of two isolated doublet H atoms is set to zero in D. All energies are in a.u.

Intensive efforts have been made to eliminate the FC (14–17, 24–55) and FS (7, 18, 24, 26, 50–59) errors. In contrast to the great progresses made to improve the FC-error-related calculations, such as better prediction of ionization potentials and electron affinities (26–33, 46, 48, 52), and proper description of dissociation of cationic species (16, 17, 34, 47–52), etc., the FS error is still an outstanding issue. More precisely, to properly take into account the necessary static correlation without involving multideterminantal reference states remains a major challenge in DFT. Work from Becke showed some promise of describing static correlation with XC hole modeling (7, 60, 61), based on which Johnson and Contreras-García constructed strong-correlation models that improve the description of atoms with fractional charges and spins (58, 59). Recent works on recovering the flat-plane condition include the judiciously modified DFT approach (62) and the density matrix minimization model (63). We aim to develop general corrections to common DFAs by imposing the flat-plane condition on global and local regions, to systematically reduce the delocalization and static correlation errors for mainstream DFAs, all within the (G)KS single-determinant description of the electron density.

In this work, an effective FS correction is developed for the static correlation in DFT. Paired with the FC correction, i.e., the localized orbital scaling correction (LOSC) (48), our model of XC functional takes the form (see SI Appendix, section 1 for the expression of the total electronic energy):

$$E_{\mathrm{X}\mathrm{C}}\left[\rho \right]=E_{\mathrm{X}\mathrm{C}}^{\mathrm{D}\mathrm{F}\mathrm{A}}\left[\rho \right]+\mathrm{\Delta }{E}^{\mathrm{F}\mathrm{C}}\left[\rho \right]+\mathrm{\Delta }{E}^{\mathrm{F}\mathrm{S}}\left[\rho \right],$$ [1]

where $E_{\mathrm{X}\mathrm{C}}^{\mathrm{D}\mathrm{F}\mathrm{A}}\left[\rho \right]$ can be any functional of local density approximation (LDA), generalized gradient approximation (GGA), hybrid GGA, etc. Both spin-restricted and -unrestricted (G)KS methods are available (64, 65). Spin-restricted self-consistent field (SCF) (3, 66, 67) is used here to ensure that the systems possess the correct spin symmetry. In principle, the exact functional can give unrestricted solutions and degenerate restricted solutions which are with integer occupations in closed-shell systems and can be with fractional spins in open-shell systems (18, 19). A restricted solution with integer occupations for open-shell systems is a constrained solution (65) for correct spin symmetry. Before proceeding to derive the FS correction, the FC corrections will be first revisited below.

FC Correction Revisited

The scaling correction (SC) method (46) provides a simple and direct way to fix the incorrect FC behavior of mainstream DFAs. The correction is derived from the energy deviation of each component from linearity to second order, which leads to

$$\mathrm{\Delta }{E}_{\mathrm{C}\mathrm{O}}^{\mathrm{F}\mathrm{C}}=\sum _{\sigma }\frac{1}{2}{n}_f^{\sigma }\left(1-n_f^{\sigma }\right){\kappa }^{\mathrm{F}\mathrm{C}}\left[{\rho }_f,{\rho }_f\right].$$ [2]

Here, we assume all canonical orbitals (COs) are occupied by integer (0/1) $\alpha$ and $\beta$ electrons except orbital $f$ whose occupations are $n_f^{\alpha }$ and $n_f^{\beta }$. ${\rho }_f\left(\mathbf{r}\right)$ is orbital density $|{\phi }_f\left(\mathbf{r}\right){|}^2$; and ${\mathit{\kappa }}^{\mathrm{F}\mathrm{C}}$, here termed FC curvature matrix, takes the form of (with the extension from ref. 48)

$$\begin{array}{ll}\hfill {\kappa }^{\mathrm{F}\mathrm{C}}\left[{\rho }_p,{\rho }_q\right]=\left(1-d_{\mathrm{X}}^{\mathrm{H}\mathrm{F}}\right)& \left[\iint \frac{{\rho }_p\left(\mathbf{r}\right){\rho }_q\left(\mathbf{r}\prime \right)}{|\mathbf{r}-\mathbf{r}\prime |}d\mathbf{r}d\mathbf{r}\prime \right.\hfill \\ \hfill & -\left.\frac{2C_{\mathrm{X}}}{3}\int {\left[{\rho }_p\left(\mathbf{r}\right){\rho }_q\left(\mathbf{r}\right)\right]}^{2/3}d\mathbf{r}\right],\hfill \end{array}$$ [3]

where $C_{\mathrm{X}}=\frac{3}{4}{\left(\frac{6}{\pi }\right)}^{1/3}$, $d_{\mathrm{X}}^{\mathrm{H}\mathrm{F}}$ is the amount of HF exchange energy in the parent functional. As only the corrections to the Coulomb and exchange energies were treated in the SC method, Eq. 3 only encompasses curvatures for these two parts. With the integer points kept intact, Eq. 2 mainly restores the linear FC behavior; thus, it greatly improves the prediction of vertical ionization potentials ($I_{\mathrm{v}\mathrm{e}}$) and electron affinities ($A_{\mathrm{v}\mathrm{e}}$) from energies of the highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs) for small sized systems.

To bring in correction for systems with integer electrons in a size-consistent manner, the local SC (LSC) (47) was proposed by imposing the PPLB condition to local regions of a system. More recently, the LSC scheme was further generalized and LOSC was developed to use localized orbitals (LOs) and LO occupations to capture local FC information in the energy correction (48). LOSC is capable of correcting the total energy and orbital energies in a size-consistent manner; therefore, it improves the descriptions of dissociation of cationic species, the small-sized molecular and polymer band gaps. The LOSC correction to total energy is calculated via

$$\mathrm{\Delta }{E}_{\mathrm{L}\mathrm{O}}^{\mathrm{F}\mathrm{C}}=\sum _{pq}\sum _{\sigma }\frac{1}{2}{\lambda }_{pq}^{\sigma }\left({\delta }_{pq}-{\lambda }_{pq}^{\sigma }\right){\kappa }^{\mathrm{F}\mathrm{C}}\left[{\rho }_p,{\rho }_q\right].$$ [4]

Here, LOs are obtained by unitary transformation upon COs, ${\varphi }_p\left(\mathbf{r}\right)={\sum }_q{U}_{pq}{\phi }_q\left(\mathbf{r}\right)$, with $\mathit{U}$ defining the mixing of COs. The local occupation matrix ${\mathit{\lambda }}^{\sigma }$ is computed via ${\lambda }_{pq}^{\sigma }=⟨{\varphi }_p\left|{\rho }_s^{\sigma }\right|{\varphi }_q⟩$. Each diagonal element, ${\lambda }_{pp}^{\sigma }$, represents the occupation of an LO. Note that each off-diagonal element, ${\lambda }_{pq}^{\sigma }$, relates to an LO pair, with the magnitude indicating how much the pair of LOs formed from the mixing of the same occupied COs. ${\kappa }^{\mathrm{F}\mathrm{C}}\left[{\rho }_p,{\rho }_q\right]$ is the FC curvature associated with LOs, obtained by inserting LO densities, ${\rho }_p\left(\mathbf{r}\right)=|{\varphi }_p\left(\mathbf{r}\right){|}^2$, into Eq. 3.

The desired LOs are optimized through a special localization procedure (48), with the following objective function

$$F=\sum _p\left[⟨{\varphi }_p\left|{\mathbf{r}}^2\right|{\varphi }_p⟩-{⟨{\varphi }_p\left|\mathbf{r}\right|{\varphi }_p⟩}^2\right]+\sum _{pq}{\omega }_{pq}|⟨{\varphi }_p|{\phi }_q⟩{|}^2.$$ [5]

Here, the first term is the Foster–Boys objective function for physical space localization (68), while the second term is to restrict the mixing of COs with large energy difference. The LOs so obtained are called orbitalets, with localization in both physical and energy spaces (48). We would like to make comparison of LOSC with existing corrections using LOs, the generalized transition state (GTS) method (69), the LDA+U method (70, 71), and the Fermi–Lowdin orbital self-interaction correction (FLOSIC) (72, 73). GTS improves the LDA calculation for band gaps of solids, with an energy correction of $\mathrm{\Delta }{E}^{\mathrm{G}\mathrm{T}\mathrm{S}}={\sum }_i\frac{1}{2}{\kappa }_{ii}\left({\lambda }_{ii}-{\lambda }_{ii}^2\right)$, where each ${\kappa }_{ii}$ is determined by separate constrained LDA calculations. A scheme similar to GTS was recently constructed by Ma and Wang (74). In these works, the LOs come from mixing of only occupied or virtual COs; thus, they do not change the total energies for physical systems with integer number of electrons; hence, these energy functionals are not size consistent (48) and can only correct orbital energies (with failure, e.g., for ${\mathrm{H}}_2^{+}$ dissociation). In contrast, LOSC mixes occupied and virtual COs in the localization and offers an explicit form of Eq. 3 for the $\mathit{\kappa }$ matrix. It corrects the DFA energies at both integer and fractional electron numbers. Moreover, Eq. 4 involves off-diagonal ${\kappa }_{pq}$ and ${\lambda }_{pq}$ that are crucial to dispel the unwanted interaction between LO pairs for the dissociation of cationic species. In the case of ${\mathrm{H}}_2^{+}$ dissociation, it is only with these off-diagonal terms that the correct asymptotic behavior as $R\to \infty$ can be retrieved (SI Appendix, section 2.B). LDA+U uses a quadratic energy correction, uses transition metal d atomic orbitals as LOs, and determines the U parameters through linear response calculations or empirically. In contrast, LOSC uses the explicit functional form for the curvatures, and the orbitalets are dynamical because of energy localization, in that they can be just the COs as in ${\mathrm{H}}_2^{+}$ at equilibrium bond length and become localized like atomic orbitals at dissociation limit. The use of orbitalets allows a different and appropriate amount of corrections to the delocalization error in DFAs at different geometries, which cannot be achieved with a fixed set of atomic orbitals as in LDA+U. In a quite different manner, FLOSIC relies on the elimination of self-interaction for each LO, which spans the occupied space only.

To increase the ability of capturing the delocalization information of reaction transition states, in this work we use a modified ${\omega }_{pq}$ of the form

$${\omega }_{pq}=R_0^2\left\{\exp \left[{|\epsilon }_p{-\epsilon }_q|{/\epsilon }_0+\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\eta \sqrt{d_p{d}_q}\right)\right]-1\right\},$$ [6]

which depends not only on energy difference of COs, ${\epsilon }_p{-\epsilon }_q$, but also on the spatial delocalization of two COs, $d_p{d}_q$. Here, $d_p$ is called orbital delocalization factor, calculated via $d_p={\sum }_{A<B}{Q}_p\left(A\right)|{\mathbf{R}}_A-{\mathbf{R}}_B|Q_p\left(B\right)$, where $A$ and $B$ are atomic indices, ${\mathbf{R}}_A$ is the atomic position, and $Q_p\left(A\right)$ represents how much the $p$-th CO localized on atom $A$ (SI Appendix, section 2.A). Importantly, to capture the local FS information for FS correction, spin restriction is imposed during localization. The three parameters in Eq. 6 are: $R_0=4.2$, ${\epsilon }_0=20eV$, and $\eta =3.78^{-1}$. They are adjusted to obtain a balanced behavior between reaction barrier heights in HTBH38/08 and NHTBH38/08 (75) and the potential energy curve of ${\mathrm{H}}_2$.

With this choice for ${\omega }_{pq}$, the mixing between COs whose orbital energies are far apart is suppressed. Furthermore, spatially delocalized COs are more likely to mix with each other, which is conducive to the characterization of transition states, making use of the delocalized nature of these states.

FS Correction

The FC correction with LOSC only restores the linearity condition for fractional charges and largely eliminates the delocalization error in common DFAs. Here, we develop an FS correction to restore the flat-plane condition in DFAs and thus to properly describe the static correlation. We first consider the correction using COs. Based on the energy deviation of each component from the corresponding flat-plane condition, the mixed-spin terms form the CO-based FS correction (SI Appendix, section 1.D), taking the following quadratic form

$$\mathrm{\Delta }{E}_{\mathrm{C}\mathrm{O}}^{\mathrm{F}\mathrm{S}}=-\mathrm{\Lambda }\left(n_f^{\alpha },n_f^{\beta }\right){\kappa }^{\mathrm{F}\mathrm{S}}\left[{\rho }_f,{\rho }_f\right],$$ [7]

with $\mathrm{\Lambda }\left(n_f^{\alpha },n_f^{\beta }\right)$ defined as

$$\mathrm{\Lambda }\left(n_f^{\alpha },n_f^{\beta }\right)=\left\{\begin{array}{cc}{n}_f^{\alpha }{n}_f^{\beta },\hspace{1em}\hfill & n_f^{\alpha }+n_f^{\beta }\le 1\hfill \\ \left(1-n_f^{\alpha }\right)\left(1-n_f^{\beta }\right),\hspace{1em}\hfill & n_f^{\alpha }+n_f^{\beta }>1.\hfill \end{array}\right.$$ [8]

Here, the FS curvature matrix, ${\mathit{\kappa }}^{\mathrm{F}\mathrm{S}}$, is calculated by

$${\kappa }^{\mathrm{F}\mathrm{S}}\left[{\rho }_p,{\rho }_q\right]=\iint \frac{{\rho }_p\left(\mathbf{r}\right){\rho }_q\left(\mathbf{r}\prime \right)}{|\mathbf{r}-\mathbf{r}\prime |}d\mathbf{r}d\mathbf{r}\prime +{\kappa }_{\mathrm{C}}\left[\sqrt{{\rho }_p{\rho }_q}\right],$$ [9]

where the first term is obtained from the Coulomb energy as a quadratic function of $n_f^{\sigma }$. As the exchange energy is between same-spin electrons, it makes no contribution to the FS correction and curvature. Thus, the main problem is to derive the curvature from the correlation energy, ${\kappa }_{\mathrm{C}}$. Here, an approximate ${\kappa }_{\mathrm{C}}$ has been derived by imposing the constancy condition of fractional spins on the correlation energy (SI Appendix, section 1.D), it takes the following general form:

$${\kappa }_{\mathrm{C}}\left[{\rho }_f\right]=-4\int {\rho }_f\left(\mathbf{r}\right)\left({ϵ}_{\mathrm{C}}^1\left[{\rho }_f\right]-{ϵ}_{\mathrm{C}}^0\left[{\rho }_f\right]\right)d\mathbf{r}.$$ [10]

${ϵ}_{\mathrm{C}}^0$ and ${ϵ}_{\mathrm{C}}^1$ are the spin-compensated and fully spin-polarized correlation energy densities. While different kinds of functional approximations can be used in Eq. 10, the simple LDA forms of ${ϵ}_{\mathrm{C}}^0$ and ${ϵ}_{\mathrm{C}}^1$ developed recently (76) are used presently.

Eq. 7 provides the necessary correction for systems with fractional spins, combined with the FC correction of Eq. 2, a new functional, FS corrected SC (FSSC), can be constructed through Eq. 1. This functional can largely restore the flat-plane behavior, so that it improves the behavior of mainstream DFAs for small-sized systems with fractional charges and spins. However, this functional provides no correction for calculations in physical systems without fractionally occupied COs. To address the issue of static correlation in realistic systems with integer electrons and spins, an effective FS correction based on fractionally occupied LOs should be constructed, as was developed in LOSC (48) for the delocalization error correction.

Similar to the extension of FC correction from Eq. 2 to Eq. 4, the extension of the FS part can be performed by imposing a correction of Eq. 7 on each LO. The resulting FS correction works well for a system with well-separated fragments, but not for a system with overlapping LOs. Taking chemical-bond breaking as an example, as a bond is gradually stretched, the static correlation effect becomes increasingly pronounced. At the beginning of the dissociation, the bonding orbital (an occupied CO) will mix with the corresponding antibonding orbital (an unoccupied CO) into a pair of overlapping LOs; at this point, the positive correction provided by the FC correction is numerically much larger than the magnitude of the negative correction provided by the FS correction, resulting in a positive overall correction (SI Appendix, section 2.D). However, due to the lack of static correlation, the total energy calculated by commonly used DFAs is already too high; thus, the positive FC correction pushes the energy in the wrong direction. Therefore, proper treatment of the interaction between fragments with fractionally occupied LOs is essential for constructing LO-based FS correction. Considering all factors, the final FS correction takes the form

$$\begin{array}{ll}\hfill \mathrm{\Delta }{E}_{\mathrm{L}\mathrm{O}}^{\mathrm{F}\mathrm{S}}=& -\sum _p\left[\left(1-S_p\right)\mathrm{\Lambda }\left({\lambda }_{pp}^{\alpha },{\lambda }_{pp}^{\beta }\right)+S_p\mathrm{\Gamma }\left({\lambda }_{pp}^{\alpha },{\lambda }_{pp}^{\beta }\right)\right]{\kappa }^{\mathrm{F}\mathrm{S}}\left[{\rho }_p,{\rho }_p\right]\hfill \\ \hfill & +\sum _{p\ne q}{\lambda }_{pq}^{\alpha }{\lambda }_{pq}^{\beta }{\kappa }^{\mathrm{F}\mathrm{S}}\left[{\rho }_p,{\rho }_q\right],\hfill \end{array}$$ [11]

where ${\kappa }^{\mathrm{F}\mathrm{S}}\left[{\rho }_p,{\rho }_q\right]$ is the FS curvature matrix defined on LOs, calculated by inserting LO densities into Eq. 9. When a set of LOs is formed from the mixing of the same COs, $S_p$ defines how much the overlap between the $p$-th LO and other LOs in the set. $S_p$ approaches 0 when the $p$-th LO is well-separated from other LOs; otherwise, $S_p$ is large with a maximum of 1. The definition of $S_p$ will be given below.

We now discuss the form of Eq. 11. The first sum of Eq. 11 is about the correction for each lone LO with fractional spins. In this part, the two terms in brackets correspond to the corrections for well-separated and overlapping LOs, respectively. For a well-separated LO, i.e., $S_p=0$, only the first term is effective, and this part of correction reduces to a form similar to Eq. 7, thus providing a correct description for well-separated fragments; for a large $S_p$, as stated above, the FC correction from Eq. 4 causes a large positive correction that cannot be well neutralized by the first term. To fix this, the second term in the bracket is brought in, where $\mathrm{\Gamma }\left({\lambda }_{pp}^{\alpha },{\lambda }_{pp}^{\beta }\right)$ takes the form of

$$\mathrm{\Gamma }\left({\lambda }_{pp}^{\alpha },{\lambda }_{pp}^{\beta }\right)=\mathrm{m}\mathrm{i}\mathrm{n}\left({\lambda }_{pp}^{\alpha },{\lambda }_{pp}^{\beta }\right)\mathrm{m}\mathrm{i}\mathrm{n}\left(1-{\lambda }_{pp}^{\alpha },1-{\lambda }_{pp}^{\beta }\right),$$ [12]

which properly compensates for the positive correction from Eq. 4 when $S_p$ is large. Note that for any LO, $\mathrm{\Gamma }\left({\lambda }_{pp}^{\alpha },{\lambda }_{pp}^{\beta }\right)$ is nonzero only when both ${\lambda }_{pp}^{\alpha }$ and ${\lambda }_{pp}^{\beta }$ are fractional—thus, it takes effect only for FS cases. The second sum of Eq. 11 is the correction for each mixed-spin LO pair. Similar to the off-diagonal terms in Eq. 4 for correcting asymptotic behavior of the ionic molecule dissociation, this term further corrects the asymptotic behavior for the dissociation of covalent bonds in neutral molecules (SI Appendix, section 2).

The foregoing analysis thus suggests that $S_p$ in Eq. 11 should (i) allow the use of a set of LOs that are formed from the mixing of the same COs, and (ii) evaluate the degree of overlap between the $p$-th LO and other LOs in the set. As stated above, the off-diagonal element, ${\lambda }_{pq}^{\sigma }$, indicates how much a pair of LOs formed from the mixing of the same COs. Thus, the set of LOs (including the $p$-th LO) is formed by those LOs with large $\left[{\left({\lambda }_{pq}^{\alpha }\right)}^2+{\left({\lambda }_{pq}^{\beta }\right)}^2\right]$. Here, the degree of overlap between the $p$-th LO and other LOs in the set is evaluated by $S_p=\mathrm{e}\mathrm{r}\mathrm{f}\left(\gamma {\left(\int \sqrt{{\rho }_p\left(\mathbf{r}\right){\rho }_{q_{pmax}}\left(\mathbf{r}\right)}d\mathbf{r}\right)}^{\frac{1}{2}}\right)$, where $q_{pmax}$ = ${\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}_q\left[{\left({\lambda }_{pq}^{\alpha }\right)}^2+{\left({\lambda }_{pq}^{\beta }\right)}^2\right]$. $\gamma$, a parameter for controlling the change of $S_p$, is set at $\gamma =1.5$, which was optimized for a smooth dissociation curve for ${\mathrm{H}}_2$ (SI Appendix, Fig. S2).

With the FS correction described above, the new XC functional, the FS-corrected LOSC (FSLOSC), can be constructed. It should be noted that, because of the presence of $\mathrm{\Lambda }\left({\lambda }_{pp}^{\alpha },{\lambda }_{pp}^{\beta }\right)$ and $\mathrm{\Gamma }\left({\lambda }_{pp}^{\alpha },{\lambda }_{pp}^{\beta }\right)$ in the FS correction, the new functional is no longer a continuously differentiable functional of the (G)KS density matrix everywhere, but, rather, a functional encoding the derivative discontinuity, necessary for strongly correlated systems (19).

The orbital energies of FSLOSC can be obtained as

$${\epsilon }_s^{\mathrm{F}\mathrm{S}\mathrm{L}\mathrm{O}\mathrm{S}\mathrm{C},\sigma }=⟨{\phi }_s\left|h^{\mathrm{F}\mathrm{S}\mathrm{L}\mathrm{O}\mathrm{S}\mathrm{C},\sigma }\right|{\phi }_s⟩.$$ [13]

Here, the FSLOSC effective Hamiltonian $h^{\mathrm{F}\mathrm{S}\mathrm{L}\mathrm{O}\mathrm{S}\mathrm{C},\sigma }$ is calculated by $h^{\mathrm{F}\mathrm{S}\mathrm{L}\mathrm{O}\mathrm{S}\mathrm{C},\sigma }=h^{\mathrm{D}\mathrm{F}\mathrm{A},\sigma }+\mathrm{\Delta }{h}^{\mathrm{F}\mathrm{C},\sigma }+\mathrm{\Delta }{h}^{\mathrm{F}\mathrm{S},\sigma }$, with $h^{\mathrm{D}\mathrm{F}\mathrm{A},\sigma }$ from the parent DFA, $\mathrm{\Delta }{h}^{\mathrm{F}\mathrm{C},\sigma }$ from the FC correction (48), and $\mathrm{\Delta }{h}^{\mathrm{F}\mathrm{S},\sigma }$ from the FS correction (SI Appendix, section 2.F).

FSLOSC calculation can be performed in two ways. One is post-SCF, indicated as FSLOSC-DFA, in which FSLOSC corrections to the total energy and orbital energies are calculated after the SCF calculation of a parent DFA. The second is self-consistent calculation of FSLOSC, i.e., scFSLOSC-DFA. With the FSLOSC effective Hamiltonian, the routine SCF calculation or some gradient optimization algorithm can be applied to obtain a set of optimized orbitals, which improves the energy and density simultaneously. Since the effective Hamiltonian used here is derived based on the frozen-orbital assumption, we used the gradient-based optimization algorithm in combination with line search for better convergence.

Results and Conclusion

FSLOSC is examined on a variety of properties. The tests based on HTBH38/08, NHTBH38/08 (75), and G2-97 (77) test sets indicate that FSLOSC-DFAs show obvious improvement on reaction barrier heights while nearly keeping the thermochemistry unchanged (SI Appendix, Tables S1 and S2). In particular, dissociation of molecules without breaking space or spin symmetry is tested, which is one of the most demanding challenges in DFT since it requires a balanced treatment of dynamical and static correlation. In the following, the results of BLYP and (sc)FSLOSC-BLYP will be discussed; CCSD (86–88) results are also included for comparison. More calculation details and test results can be found in SI Appendix, section 3.

For the flat-plane test on the H atom, Fig. 1 shows that LOSC has corrected the convex FC behavior of BLYP, but enlarges the FS error. With FS correction, FSLOSC restores the flat-plane behavior, and consequently both dissociation limits of ${\mathrm{H}}_2^{+}$ and ${\mathrm{H}}_2$ are corrected.

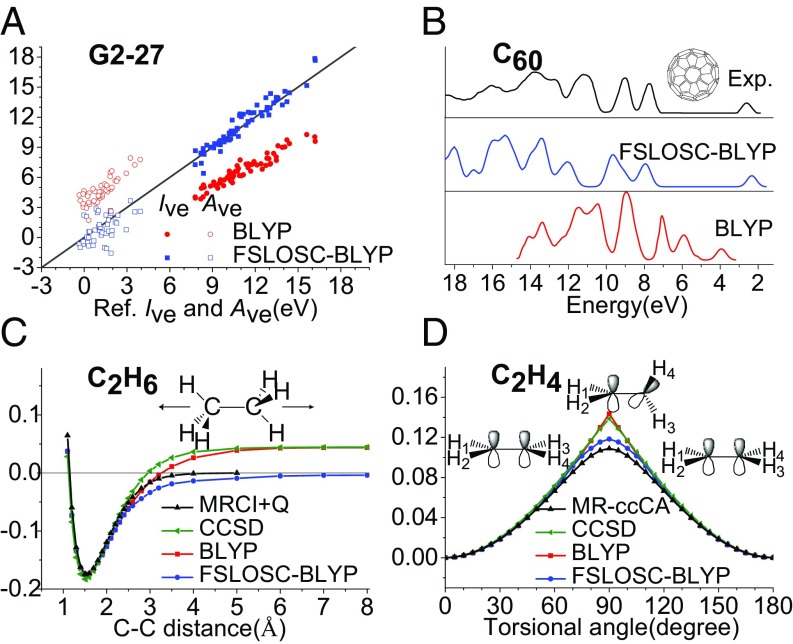
In addition to the simple H–H bond breaking in ${\mathrm{H}}_2$, the excellent description of potential energy curves of $\sigma$ bond breaking in ethane and $\pi$ bond breaking in twisted ethene again shows that FSLOSC is able to handle strongly correlated systems without involving multideterminantal reference states; Fig. 2 C and D. Furthermore, the improved prediction of $I_{\mathrm{v}\mathrm{e}}$, $A_{\mathrm{v}\mathrm{e}}$, and quasiparticle spectra by orbital energies of FSLOSC demonstrates that the delocalization error is greatly reduced, which is similar to LOSC (48); Fig. 2 A and B.

Fig. 2.

(A) Calculated ${-\epsilon }_{\mathrm{H}\mathrm{O}\mathrm{M}\mathrm{O}}$ (${-\epsilon }_{\mathrm{L}\mathrm{U}\mathrm{M}\mathrm{O}}$) vs. reference $I_{\mathrm{v}\mathrm{e}}$ ($A_{\mathrm{v}\mathrm{e}}$) for 64 (47) molecules from the G2-97 set (77). Reference data are obtained by CCSD(T) calculation and extrapolated to infinite basis limit. The solid line indicates $-{ϵ}_{\mathrm{H}\mathrm{O}\mathrm{M}\mathrm{O}}=I_{\mathrm{v}\mathrm{e}}$ or $-{ϵ}_{\mathrm{L}\mathrm{U}\mathrm{M}\mathrm{O}}=A_{\mathrm{v}\mathrm{e}}$. All data in A are in electronvolts. (B) Spectra of fullerene ${\mathrm{C}}_{60}$ obtained with BLYP and FSLOSC-BLYP, broadened by a 0.25-eV Gaussian, compared with experimental photoemission spectrum (78, 79). (C) Potential energy curve for C–C dissociation in ${\mathrm{C}}_2{\mathrm{H}}_6$. The total energy of two isolated doublet $\cdot {\mathrm{C}\mathrm{H}}_3$ is set to zero. MRCI+Q data (80) are used as reference. (D) Potential energy curve for twisted ethylene as a function of the HCCH torsion angle ($\theta$). The energy at $\theta =0$ is set to zero. MR-ccCA data (81) are used as reference. All energies in both C and D are in a.u.

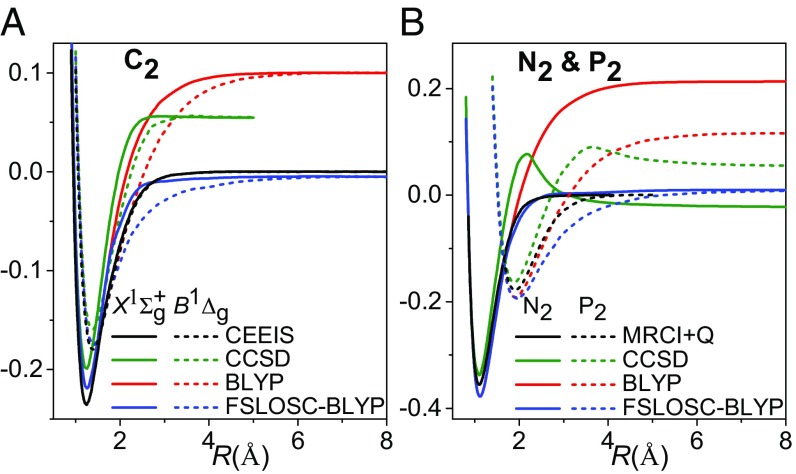
Moreover, FSLOSC can correctly dissociate multiple bonds. The dissociation curves of ${\mathrm{C}}_2$, ${\mathrm{N}}_2$, and ${\mathrm{P}}_2$ can be found in Fig. 3. These systems are not only a challenge to DFT, but also to wave-function methods. Because of the lack of static correlation, the CCSD level of correlation method is still insufficient to correctly describe multiple bond breaking. BLYP performs well at equilibrium distance, but its energies become too high as the bonds are stretched. FSLOSC, with the energies of BLYP around equilibrium kept unchanged, repairs the dissociation limits of BLYP, thus yielding good potential energy curves.

Fig. 3.

(A) Potential energy curves for C–C bond dissociation in ${\mathrm{C}}_2$. Two singlet states $X^1{\mathrm{\Sigma }}_{\mathrm{g}}^{+}$ and $B^1{\mathrm{\Delta }}_{\mathrm{g}}$ are plotted. Data of the correlation energy extrapolation by intrinsic scaling (CEEIS) method (82) are used as reference. The total energy of two triplet C atoms is set to zero. All of the methods show a crossing between $X^1{\mathrm{\Sigma }}_{\mathrm{g}}^{+}$ and $B^1{\mathrm{\Delta }}_{\mathrm{g}}$ at $\sim$1.6 Å. (B) Potential energy curves for N–N bond dissociation in ${\mathrm{N}}_2$ and P–P bond dissociation in ${\mathrm{P}}_2$. The total energies of two quartet N atoms and two quartet P atoms are set to zero for ${\mathrm{N}}_2$ and ${\mathrm{P}}_2$, respectively. MRCI+Q data (83) are used as reference. All energies are in a.u.

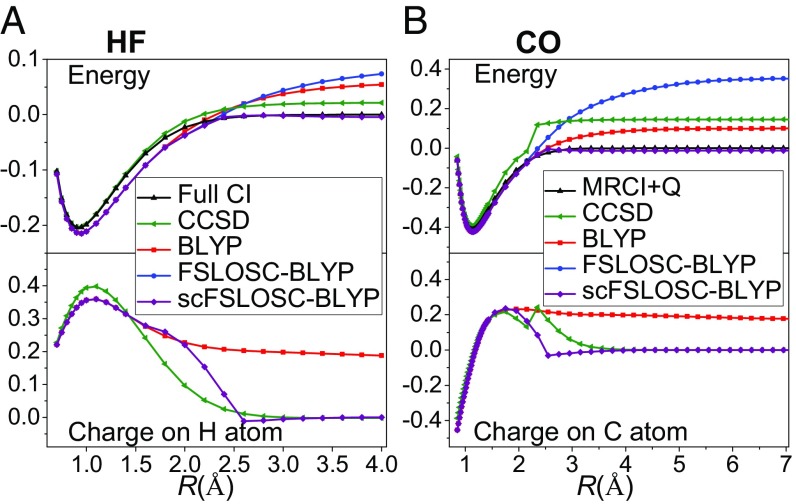
It has been found that semilocal DFAs can dramatically underestimate the energy of dissociating neutral heteroatom molecules into fractionally charged fragments in unrestricted (G)KS calculations with broken symmetry (14, 15, 89). The symmetry-preserved restricted calculations of such systems, however, lead to much too high energies at dissociation limits because of static correlation error as shown in FS behavior (18). Here, we test two molecules, single-bond HF and multiple-bond CO; Fig. 4. Restricted BLYP gives too high energies at dissociation limits and incorrectly predicts the charge distribution, showing fractional positive charge on H and C atoms at dissociation limits. Based on this erroneous charge distribution, FSLOSC in post-SCF application cannot improve the energies of BLYP. Through the self-consistent calculations, i.e., scFSLOSC, the charge distributions as well as the energies at dissociation limits are both improved. Therefore, scFSLOSC is necessary when the density of the parent DFA is incorrect.

Fig. 4.

(A) Potential energy curve and charge on H atom along H–F bond dissociation in HF. The total energy of a doublet H atom and a doublet F atom is set to zero. Full CI data (84) are used as reference. (B) Potential energy curve and charge on C atom along C–O bond dissociation in CO. The total energy of a triplet C atom and a triplet O atom is set to zero. MRCI+Q data (85) are used as reference. All energies and charges are in a.u.

To conclude, an effective FS correction has been developed to restore the flat-plane behavior and correct the static correlation error in existing DFAs. Based on this, the FSLOSC functional developed in this work shows significant improvement in the treatment of strongly correlated systems. All of the tests demonstrate that FSLOSC greatly reduces the delocalization and static correlation errors in mainstream DFAs.