A mean score method for sensitivity analysis to departures from the missing at random assumption in randomised trials

Abstract

Most analyses of randomised trials with incomplete outcomes make untestable assumptions and should therefore be subjected to sensitivity analyses. However, methods for sensitivity analyses are not widely used. We propose a mean score approach for exploring global sensitivity to departures from missing at random or other assumptions about incomplete outcome data in a randomised trial. We assume a single outcome analysed under a generalised linear model. One or more sensitivity parameters, specified by the user, measure the degree of departure from missing at random in a pattern mixture model. Advantages of our method are that its sensitivity parameters are relatively easy to interpret and so can be elicited from subject matter experts; it is fast and non-stochastic; and its point estimate, standard error and confidence interval agree perfectly with standard methods when particular values of the sensitivity parameters make those standard methods appropriate. We illustrate the method using data from a mental health trial.

1. Introduction

Missing outcome data are a threat to the validity of randomised controlled trials, and they usually require untestable assumptions to be made in the analysis. One common assumption is that data are missing at random (MAR) (Little and Rubin, 2002). Other possible assumptions may be less implausible in particular clinical settings. For example, in smoking cessation trials, the outcome is binary, indicating whether an individual quit over a given period, and it is common to assume that missing values are failures — “missing=failure” (West et al., 2005); while in weight loss trials, missing data is sometimes assumed to be unchanged since baseline — “baseline observation carried forward” (Ware, 2003).

The US National Research Council (2010) suggested measures that should be taken to minimise the amount of missing outcome data in randomised trials, and described analysis strategies based on various assumptions about the missing data. This report recommended that “Sensitivity analyses should be part of the primary reporting of finding from clinical trials. Examining sensitivity to the assumptions about the missing data mechanism should be a mandatory component of reporting.” However, among “several important areas where progress is particularly needed”, the first was “methods for sensitivity analysis and principled decision making based on the results from sensitivity analyses”. Sensitivity analysis is also an essential part of an intention-to-treat analysis strategy, which includes all randomised individuals in the analysis strategy (White et al., 2011a, 2012): even if the main analysis is performed under MAR and hence draws no information from individuals with no outcome data, such individuals are included in sensitivity analysis and hence in the analysis strategy.

Sensitivity analysis is often done by performing two different analyses, such as an analysis assuming MAR and an analysis by last observation carried forward, and concluding that inference is robust if the results are similar (Wood et al., 2004). Better is a principled sensitivity analysis, where the data analyst typically formulates a model including unidentified ‘sensitivity parameter(s)’ that govern the degree of departure from the main assumption (e.g. from MAR), and explores how the estimate of interest varies as the sensitivity parameter(s) are varied (Rotnitzky et al., 1998; Kenward et al., 2001). We consider global sensitivity analyses where the sensitivity parameter(s) are varied over a range of numerical values that subject-matter experts consider plausible.

Likelihood-based analyses assuming MAR can usually ignore the missing data mechanism and simply analyse the observed data (Little and Rubin, 2002). Under a missing not at random (MNAR) assumption, however, it is usually necessary to model the data of interest jointly with the assumed missing data mechanism. The joint model can be specified as a pattern-mixture model, which explicitly describes the differences between profiles of patients who complete and drop out (Little, 1993, 1994), or as a selection model, which relates the chance of drop-out to the (possibly missing) response values either directly (Diggle and Kenward, 1994; Kenward, 1998) or indirectly through a random effect (Follmann and Wu, 1995; Roy, 2003). Rotnitzky et al. (1998) proposed a selection model for incomplete repeated measures data and showed how to estimate it by inverse probability weighting, given values of the sensitivity parameters. Scharfstein et al. (2003) adopted a non-parametric Bayesian approach to analysing incomplete randomised trial data, and argued that sensitivity parameters are more plausibly a priori independent of other parameters of interest in a selection model than in a pattern-mixture model. Scharfstein et al. (2014) proposed a fully parametric approach based on a selection model. On the other hand, Daniels and Hogan (2000) advocated a pattern-mixture framework as “a convenient and intuitive framework for conducting sensitivity analyses”.

We use the pattern-mixture model in this paper because its sensitivity parameters are usually more easily interpreted (White et al., 2007, 2008). For a binary outcome, a convenient sensitivity parameter is the informative missing odds ratio (IMOR), defined, conditional on covariates, as the odds of positive outcome in missing values divided by the odds of positive outcome in observed values (Higgins et al., 2008; Kaciroti et al., 2009). For a continuous outcome, a convenient sensitivity parameter is the covariate-adjusted mean difference between missing and observed outcomes (Mavridis et al., 2015).

Most estimation procedures described for general pattern-mixture models are likelihood-based (Little, 1993, 1994; Little and Yau, 1996; Hedeker and Gibbons, 2006), while the National Research Council (2010) describes point estimation using sensitivity parameters with bootstrap standard errors. In this paper we propose instead using the mean score method, a computationally convenient method which was originally proposed under a MAR assumption for incomplete outcome data (Pepe et al., 1994) and for incomplete covariates (Reilly and Pepe, 1995). The method is particularly useful to allow for auxiliary variables, so that outcomes can be assumed MAR given model covariates and auxiliary variables but not necessarily MAR given model covariates alone (Pepe et al., 1994). We are not aware of the mean score method having been used for sensitivity analysis.

The aim of this paper is to propose methods for principled sensitivity analysis that are fast, non-stochastic, available in statistical software, and agree exactly with standard methods in the special cases where standard methods are appropriate. We focus on randomised trials with outcome measured at a single time, allowing for continuous or binary outcomes, or indeed any generalised linear model, and for covariate adjustment.

The paper is organised as follows. Section 2 describes our proposed method. Section 3 proposes small-sample corrections which yield exact equivalence to standard procedures in special cases. Section 4 illustrates our method in QUATRO, a mental health trial with outcome measured at a single time. Section 5 describes a simulation study. Section 6 discusses the implementation of our method, possible alternatives, limitations and extensions.

2. Mean score approach

Assume that for the ith individual (i = 1 to n) in an individually randomised trial, there is an outcome variable y_i, and let r_i be an indicator of y_i being observed. Let n_obs and n_mis = n − n_obs be the numbers of observed and missing values of y respectively. Let x_i be a vector of covariates including the p_S-dimensional fully-observed covariates x_Si in the substantive model, comprising an intercept, an indicator z_i for the randomised group, and (optionally) baseline covariates. x_i may also include fully-observed auxiliary covariates x_Ai that are not in the substantive model but that help to predict y_i, and/or covariates x_Ri that are only observed in individuals with missing y_i and describe the nature of the missing data: for example, the reason for missingness.

The aim of the analysis is to estimate the effect of randomised group, adjusting for the baseline covariates. We assume the substantive model is a generalised linear model (GLM) with canonical link,

$$\text{E}\left[y_i|{\mathbf{\text{x}}}_{Si};{\mathbf{\beta }}_S\right]=h\left({\mathbf{\beta }}_S^T{\mathbf{\text{x}}}_{Si}\right)$$ (1)

where h(.) is the inverse link function. We are interested in estimating β_Sz, the component of the p_S-dimensional vector β_S corresponding to z.

If we had complete data, we would estimate β_S by solving the estimating equation $U_S^{*}\left({\mathbf{\beta }}_S\right)=0$ where $U_S^{*}\left({\mathbf{\beta }}_S\right)={\Sigma }_i{U}_{Si}^{*}\left({\mathbf{\beta }}_S\right)$ and

$$U_{Si}^{*}\left({\mathbf{\beta }}_S\right)=\left\{y_i-h\left({\mathbf{\beta }}_S^T{\mathbf{\text{x}}}_{Si}\right)\right\}{\mathbf{\text{x}}}_{Si}.$$ (2)

The mean score approach (Pepe et al., 1994; Reilly and Pepe, 1995) handles missing data by replacing $U_S^{*}\left({\mathbf{\beta }}_S\right)$ with U_S(β_S), its expectation over the distribution of the missing data given the observed data. We write U_S(β_S) = ∑_i U_Si(β_S) and $U_{Si}\left({\mathbf{\beta }}_S\right)=\text{E}\left[U_{Si}^{*}\left({\mathbf{\beta }}_S\right)|{\mathbf{\text{x}}}_i,r_i,r_i{y}_i\right].$ Then by the repeated expectation rule, $\text{E}\left[U_{Si}\left({\mathbf{\beta }}_S\right)|{\mathbf{\text{x}}}_{Si}\right]=\text{E}\left[U_{Si}^{*}\left({\mathbf{\beta }}_S\right)|{\mathbf{\text{x}}}_{Si}\right]$ since x_i includes x_Si, so U_S(β_S) = 0 is an unbiased estimating equation if $U_S^{*}\left({\mathbf{\beta }}_S\right)=0$ is.

To compute U_Si(β_S), we need only E [y_i|x_i, r_i = 0], because (2) is linear in y_i. We estimate this using the pattern-mixture model

$$\text{E}\left[y_i|{\mathbf{\text{x}}}_i,r_i;{\mathbf{\beta }}_P\right]=h\left({\mathbf{\beta }}_P^T{\mathbf{\text{x}}}_{Pi}+\Delta ({\mathbf{\text{x}}}_i)(1-r_i)\right)$$ (3)

where x_Pi = (x_Si, x_Ai) of dimension p_P; the subscript P distinguishes the parameters β_P and covariates x_Pi of the pattern-mixture model from the parameters β_S and covariates x_Si of the substantive model. Models (1) and (3) are typically not both correctly specified: we return to this issue in the simulation study.

In equation (3), Δ(x_i) is a user-specified departure from MAR for individual i. MAR in this setting means that p(r_i = 1|x_i, y_i) = p(r_i = 1|x_i), which implies E [y_i|x_i, r_i] = E [y_i|x_i] and hence Δ(x_i) = 0 for all i. A simple choice of Δ(x_i) that expresses MNAR is Δ(x_i) = δ, where the departure from MAR is the same for all individuals. Differences in departure from MAR between randomised groups are often plausible and can have strong impact on the estimated treatment effect (White et al., 2007), so an alternative choice is Δ(x_i) = δ_zi . The departure Δ(x_i) could also depend on reasons for missingness coded in x_Ri: for example, it could be 0 for individuals lost to follow-up (if MAR seemed plausible for them), and δ_zi for individuals who refused follow-up.

Putting it all together, the mean score method solves

$${\displaystyle \sum _i\left\{{\tilde{y}}_i\left({\mathbf{\beta }}_P\right)-h\left({\mathbf{\beta }}_S^T{\mathbf{\text{x}}}_{Si}\right)\right\}{\mathbf{\text{x}}}_{Si}=\mathbf{0}}$$ (4)

where ỹ_i(β_P) is defined as y_i if r_i = 1 and $h\left({\mathbf{\beta }}_P^T{\mathbf{\text{x}}}_{Pi}+\Delta ({\mathbf{\text{x}}}_i)(1-r_i)\right)$ if r_i = 0.

2.1. Estimation using full sandwich variance

The parameter β_P in (3) is estimated by regressing y_i on x_Pi in the complete cases (r_i = 1). Once β_P is estimated, we calculate the ỹ_i(β̂_P) using the known values Δ(x_i) and solve (4) for β_S. The whole procedure amounts to solving the set of estimating equations U(β) = 0 where $\mathbf{\beta }={\left({\mathbf{\beta }}_S^T,{\mathbf{\beta }}_P^T\right)}^T,$ U(β) = (U_S(β)^T, U_P(β_P)^T)^T, U_S(β) = ∑_i U_Si(β), U_P(β_P) = ∑_i U_Pi(β_P),

$$\begin{array}{l}{\mathbf{\text{U}}}_{Si}\left(\mathbf{\beta }\right)=\{r_i{y}_i+(1-r_i)h({\mathbf{\beta }}_P^T{\mathbf{\text{x}}}_{Pi}+\Delta ({\mathbf{\text{x}}}_i))-h({\mathbf{\beta }}_S^T{\mathbf{\text{x}}}_{Si})\}{\mathbf{\text{x}}}_{Si},\\ {\mathbf{\text{U}}}_{Pi}\left({\mathbf{\beta }}_P\right)=r_i\left\{y_i–h\left({\mathbf{\beta }}_P^T{\mathbf{\text{x}}}_{Pi}\right)\right\}{\mathbf{\text{x}}}_{Pi}.\end{array}\}$$ (5)

Pepe et al. (1994) derived a variance expression for β_S assuming categorical x_Si. To accommodate any form of x_Si, we instead obtain standard errors by the sandwich method, based on both estimating equations. The sandwich estimator of var (β̂) is

$$\mathbf{\text{V}}={\mathbf{\text{B}}}^{-1}{\mathbf{\text{CB}}}^{-T}$$ (6)

where B = −dU/dβ evaluated at β = β̂, C = ∑_iU_i(β̂)U_i(β̂)^T and U_i(β) = (U_Si(β)^T, U_Pi(β_P)^T)^T. B and C are given in Section A of the Supplementary Materials.

2.2. Estimation using two linear regressions

A special case arises if there are no auxiliary variables, so x_Pi = x_Si for all i, and h(.) is the identity function, as in linear regression. Then we can rearrange (5) to give

$${\mathbf{\text{U}}}_{Si}\left(\mathbf{\beta }\right)-{\mathbf{\text{U}}}_{Pi}\left({\mathbf{\beta }}_P\right)=\left\{(1-r_i)\Delta \left({\mathbf{\text{x}}}_i\right)-{\left({\mathbf{\beta }}_S-{\mathbf{\beta }}_P\right)}^T{\mathbf{\text{x}}}_{Si}\right\}{\mathbf{\text{x}}}_{Si}.$$

Thus (β_S − β_P) may be estimated by linear regression of (1 − r_i)Δ(x_i) on x_Si. This estimate is uncorrelated with β̂_P because cov (U_Si(β) − U_Pi(β_P), U_Pi(β_P)) = 0. This gives a direct way to estimate β_S, and its variance var (β̂_P) + var (β̂_S − β̂_P), from standard linear regressions.

In particular, consider a two-arm trial with no covariates, and write the coefficients of z_i in (1) and (3) as β_Sz and β_Pz. Then β_Sz − β_Pz is estimated as the difference between arms in the mean of (1 − r_i)Δ(x_i), which is a₁δ₁ − a₀δ₀ where a_j is the proportion of missing data in arm j = 0, 1 and δ_j is the average of Δ(x_i) over individuals with missing data in arm j = 0, 1. Therefore the estimated parameter of interest is β̂_Sz = β̂_Pz + a₁δ₁ − a₀δ₀ as in White et al. (2007); the same result can be derived in other ways.

3. Equivalence to standard procedures

We now consider two special cases which can be fitted by standard procedures: (1) when MAR is assumed and there are no auxiliary variables, so incomplete cases contribute no information and the standard procedure is an analysis of complete cases, and (2) when ‘missing = failure’ is assumed for a binary outcome, so the standard procedure is to replace missing values with failures. Our aim is that point estimates, standard errors and confidence intervals produced by the mean score procedure should agree exactly with those produced by the standard procedures in these cases.

Equality of point estimates is easy to see. In case (1), we have Δ(x_i) = 0 and x_Pi = x_Si for all i, so if β_P solves U_P(β_P) = 0 then β = (β_P, β_P) solves U_S(β) = 0. In case (2), ‘missing = failure’ can be expressed as Δ(x_i) = −∞ for all i, so the mean score procedure gives $y_i^{*}=0$ whenever r_i = 0, and solving U_S(β_S, β_P) = 0 gives the same point estimate as replacing missing values with failures.

Exact equality of variances between mean score and standard procedures depends on which finite sample corrections (if any) are applied. Many such corrections have been proposed to reduce the small-sample bias of the sandwich variance estimator and to improve confidence interval coverage (Kauermann and Carroll, 2001; Lu et al., 2007). Here, we assume that the standard procedures use the commonly used small-sample correction factor for the sandwich variance $\widehat{\text{var}}\left({\widehat{\mathbf{\beta }}}_S\right)=f\mathbf{\text{V}}$ where f = n/(n − p*), n is the sample size and p* is the number of regression parameters (in linear regression) or 1 (in other GLMs): this is for example the default in Stata (StataCorp, 2011).

Exact equality of confidence intervals between mean score and standard procedures additionally depends on the distributional assumptions used to construct confidence intervals. Here, we assume that standard procedures for linear regression construct confidence intervals from the t distribution with n − p* degrees of freedom, and that standard procedures for other GLMs construct confidence intervals from the Normal distribution.

With missing data, we propose using the same small-sample correction factor, distributional assumptions and degrees of freedom, but replacing n by an effective sample size n_eff as shown below. Thus we propose forming confidence intervals for linear regression by assuming ${\widehat{\mathbf{\beta }}}_S\sim t_{n_{eff}-p^{*}}\left({\mathbf{\beta }}_S,\frac{n_{eff}}{n_{eff}-p^{*}}\mathbf{\text{V}}\right)$ and for other GLMs by assuming ${\widehat{\mathbf{\beta }}}_S\sim N\left({\mathbf{\beta }}_S,\frac{n_{eff}}{n_{eff}-p^{*}}\mathbf{\text{V}}\right).$

3.1. Full sandwich method

For the full sandwich method of Section 2.1, we propose computing n_eff as n_obs + (I_mis/I_mis*)n_mis where I_mis is the influence of the individuals with missing values, and I_mis* is the same individuals’ influence if the missing values had been observed. The comparison of the same individuals is crucial, because missing individuals, if observed, would have different influence from observed individuals.

To determine I_mis, we consider weighted estimating equations ∑_i w_iU_i(β) = 0 with solution β_w. Differentiating with respect to w = (w₁, . . . , w_n)^T at w = 1 gives ${\mathbf{\text{U}}}^T+\frac{d\mathbf{\text{U}}(\mathbf{\beta })}{d\mathbf{\beta }}\frac{d{\mathbf{\beta }}_{\mathbf{\text{w}}}}{d\mathbf{\text{w}}}=\mathbf{0}$ where U is a n × (p_S + p_P) matrix with ith row U_i(β). Since also $\frac{d\mathbf{\text{U}}(\mathbf{\beta })}{d\mathbf{\beta }}=-\mathbf{\text{B}},$ we get

$$\frac{d{\mathbf{\beta }}_{\mathbf{\text{w}}}}{d\mathbf{\text{w}}}=-{\mathbf{\text{B}}}^{-1}{\mathbf{\text{U}}}^T.$$ (7)

We now define the influence of observation i as

$$I_{mis,i}=\frac{{d{\mathbf{\beta }}_{\mathbf{\text{w}}S}}^T}{d{w}_i}{\mathbf{\text{V}}}_S^{-1}\frac{d{\mathbf{\beta }}_{\mathbf{\text{w}}S}}{d{w}_i}$$

where the S subscript denotes the elements corresponding to β_S. Hence we define the influence of the individuals with missing values as I_mis = ∑_i(1 − R_i)I_mis,i.

To determine I_mis* , we let ${\mathbf{\beta }}_{\mathbf{\text{w}}S}^{*}$ be the (unknown) parameter estimate that would be obtained if the complete data had been observed, following the pattern-mixture model (3). In this case the influence would be

$$I_{mis,i}^{*}=\frac{{d{\mathbf{\beta }}_{\mathbf{\text{w}}S}^{*}}^T}{d{w}_i}{\mathbf{\text{V}}}_S^{-1}\frac{d{\mathbf{\beta }}_{\mathbf{\text{w}}S}^{*}}{d{w}_i}.$$

We define the “full-data influence” as the expectation of ${{\displaystyle I}}_{mis,i}^{*}$ over the distribution of the complete data given the observed data, under the pattern-mixture model (3). From (7) we get $\frac{d{\mathbf{\beta }}_{\mathbf{\text{w}}}^{*}}{d{w}_i}={-{\mathbf{\text{B}}}^{-1}{\mathbf{\text{U}}}_i^{*}}^T$ and ${{\mathbf{\text{U}}}_i^{*}}^T=\left\{y_i^{*}-h\left({\mathbf{\beta }}_s^T{\mathbf{\text{x}}}_{Si}\right)\right\}{\mathbf{\text{x}}}_{Si},$ so that

$$\text{E}\left[{\mathit{I}}_{mis,i}^{*}\right]=\text{E}\left[{\left\{y_i^{*}-h({\mathbf{\beta }}_s^T{\mathbf{x}}_{Si})\right\}}^2\right]{\mathbf{x}}_{Si}^T{\mathbf{B}}_{SS}^{-T}{\mathbf{V}}_S^{-1}{\mathbf{B}}_{SS}^{-1}{\mathbf{x}}_{Si}$$ (8)

and $\text{E}\left[{\left\{y_i^{*}-h({\mathbf{\beta }}_s^T{\mathbf{x}}_S)\right\}}^2\right]$ is evaluated as the squared residual plus the residual variance from model (1) for individual i. Finally, $I_{mi{s}^{*}}={\sum }_i(1-r_i)\text{E}\left[I_{mis,i}^{*}\right].$ In case (1), I_mis = 0 so n_eff = n_obs, as in standard analysis. In case (2), I_mis* = I_mis so n_eff = n, again as in standard analysis.

3.2. Two linear regressions method

For the two linear regressions method of Section 2.2, the small-sample correction to the variance is naturally applied separately to each variance in $\widehat{\text{var}}\left({\widehat{\mathbf{\beta }}}_P\right)+\widehat{\text{var}}\left({\widehat{\mathbf{\beta }}}_S-{\widehat{\mathbf{\beta }}}_P\right)=V_{small}$ say. We can derive the corresponding variances without small-sample correction as $\frac{n_{obs}-p}{n_{obs}}\widehat{\text{var}}\left({\widehat{\mathbf{\beta }}}_P\right)+\frac{n-p}{n}\widehat{\text{var}}\left({\widehat{\mathbf{\beta }}}_S-{\widehat{\mathbf{\beta }}}_P\right)=V_{large}$ say. To compute n_eff, we use the heuristic $V_{small}\approx \frac{n_{eff}}{n_{ef{f}^{-p}}}{V}_{large}$ and hence we estimate n_eff by solving $\left|V_{small}\right|={\left(\frac{n_{eff}}{n_{ef{f}^{-p}}}\right)}^p\left|V_{large}\right|.$ In case (1), $\widehat{\text{var}}\left({\widehat{\mathbf{\beta }}}_S-{\widehat{\mathbf{\beta }}}_P\right)=0$ so n_eff = n_obs, as in standard analysis. Case (2) does not apply to linear regression.

4. Example: QUATRO trial

The QUATRO trial (Gray et al., 2006) was a randomised controlled trial in people with schizophrenia, to evaluate the effectiveness of a patient-centred intervention to improved adherence to prescribed antipsychotic medications. The trial included 409 participants in four European centres. The primary outcome, measured at baseline and 1 year, was participants’ quality of life, expressed as the mental health component score (MCS) of the SF-36 (Ware, 1993). The MCS is designed to have mean 50 and standard deviation 10 in a standard population, and a higher MCS score implies a better quality of life. The data are summarised in Table 1.

Table 1.

QUATRO trial: data summary.

		Intervention (n=204)	Control (n=205)
Centre	Amsterdam (%)	50 (25%)	50 (24%)
	Leipzig (%)	49 (24%)	48 (23%)
	London (%)	45 (22%)	47 (23%)
	Verona (%)	60 (29%)	60 (29%)
MCS at baseline	Mean (SD)	38.4 (11.2)	40.1 (12.1)
	Missing (%)	13 (6%)	10 (5%)
MCS at 1 year	Mean (SD)	40.2 (12.0)	41.3 (11.5)
	> 40 (%)	99 (57%)	104 (54%)
	Missing (%)	29 (14%)	13 (6%)

We first estimate the intervention effect on MCS, adjusted for baseline MCS and centre. Thus in the substantive model (1), h(.) is the identity link, y_i is MCS at 1 year for participant i, and x_Si is a vector containing 1, randomised group z_i (1 for the intervention group and 0 for the control group), baseline MCS and dummy variables for three centres. We have no x_Ai or x_Ri.

We also estimate the intervention effect on a binary variable, MCS dichotomised at an arbitrary value of 40, where for illustration we use baseline MCS and dummy variables for centre as auxiliary variables x_Ai. Thus in the substantive model (1), h(η) = 1/{1 + exp (−η)} is the inverse of the logit link, y_i is dichotomised MCS at 1 year for participant i, and x_Si is a vector containing 1 and z_i.

In both analyses, we replace the 23 missing values of baseline MCS with the mean baseline MCS: while such mean imputation is not valid in general, it is appropriate and efficient in the specific case of estimating intervention effects with missing baseline covariates in randomised trials (White and Thompson, 2005; Groenwold et al., 2012).

As expected (results not shown), the point estimate, standard error and confidence interval from the mean score method agree exactly with standard methods under MAR and under missing=failure, using the small-sample corrections of Section 3.

We consider three sets of sensitivity analyses using the mean score method around a MAR assumption, with departures from MAR (1) in the intervention arm only (Δ(x_i) = δz_i), (2) in both arms (Δ(x_i) = δ), or (3) in the control arm only (Δ(x_i) = δ(1 − z_i)) (White et al., 2012). For the quantitative outcome, the investigators suggested that the mean of the missing data could plausibly be lower than the mean of the observed data by up to 10 units (equal to nearly one standard deviation of the observed data), so we allow δ to range from 0 to -10 (Jackson et al., 2010). The investigators were not asked about missing values of the dichotomised outcome, so for illustrative purposes we allow δ to range from 0 to -6, which is close to “missing=failure”.

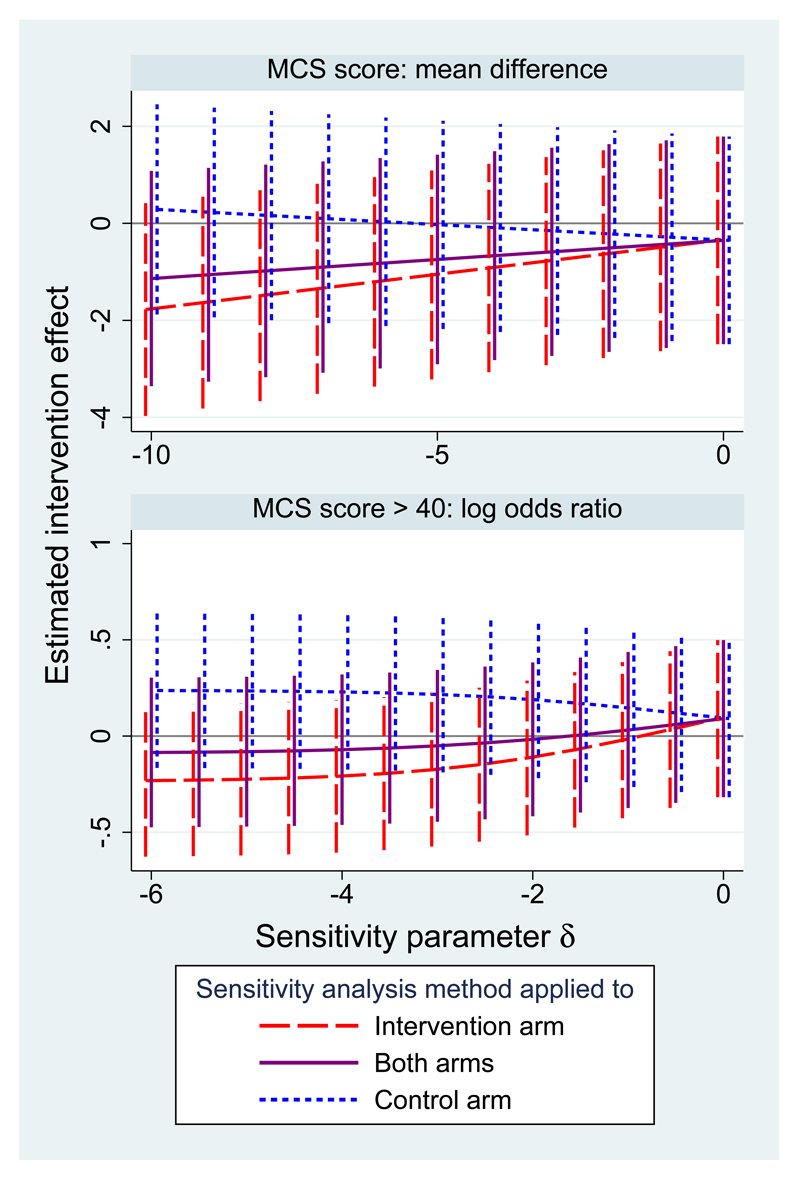
Figure 1 shows the results of these sensitivity analysis using the two linear regressions method for the quantitative outcome (upper panel) and using the full sandwich method for the dichotomised outcome (lower panel). Results are more sensitive to departures from MAR in the intervention arm because there are more missing data in this arm. However, the finding of a non-significant intervention effect is unchanged over these ranges of sensitivity analyses. This means that the main results of the trial are robust even to quite strong departures from MAR.

Figure 1.

QUATRO trial: sensitivity analysis for the estimated intervention effect on the MCS (with 95% confidence interval) over a range of departures from MAR.

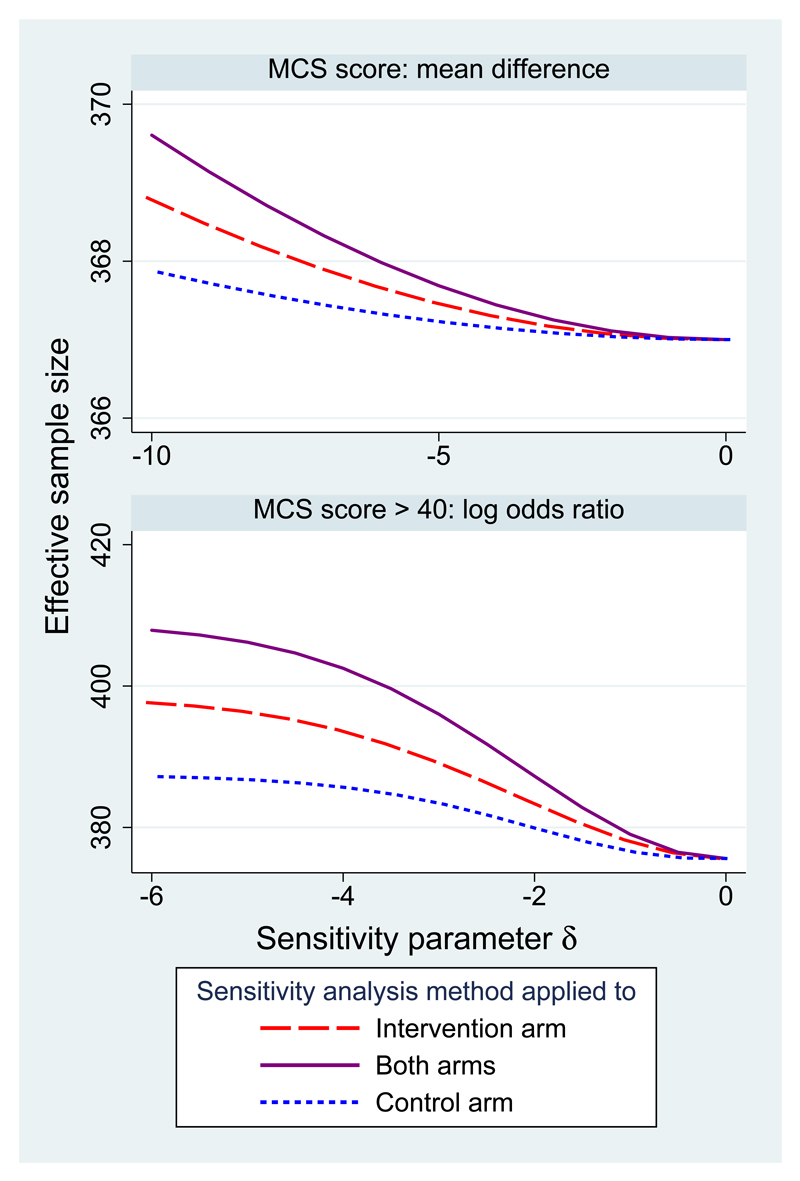
Figure 2 shows the effective sample size for these two analyses. Effective sample size increases from 367 at MAR for both analyses. For the dichotomised outcome it is near the total sample size of 409 when δ = −6 in both arms. For the quantitative outcome it does not pass 370 because the range of δ is more moderate.

Figure 2.

QUATRO data: effective sample size in sensitivity analysis.

5. Simulation study

We report a simulation study aiming (i) to evaluate the performance of the mean score method when it is correctly specified, (ii) to compare the mean score method with alternatives, and (iii) to explore the impact of the incompatibility of models (1) and (3). We assume the sensitivity parameters Δ(x_i) are correctly specified.

5.1. Data generating models

We generate data under four data generating models (DGMs), each with four choices of parameters. We focus on the case of a binary outcome. In DGMs 1-3, we generate data under a pattern-mixture model. In DGM 1, there are no baseline covariates, so x_i = x_Si = x_Pi = (1, z_i). We generate a treatment indicator z_i ∼ Bern(0.5); a missingness indicator r_i with logit P(r_i|z_i) = α₁ + α_zz_i; and a binary outcome y_i following model (3) with logit P(y_i|z_i, r_i) = β_P1 + β_Pzz_i + β_Pr(1 − r_i). The substantive model (1) is then logit P(y_i|z_i) = β_S1 + β_Szz_i. Because this substantive model contains only a single binary covariate, it is saturated and cannot be mis-specified. Therefore both substantive model and pattern-mixture model are correctly specified

DGM 2 extends DGM 1 by including x_i ∼ N(0, 1) as a single baseline covariate independent of z_i, so x_i = (1, x_i, z_i). The missingness indicator follows logit P(r_i|x_i, z_i) = α₁ + α_xx_i + α_zz_i and the binary outcome follows model (3) with logit P(y_i|x_i, z_i, r_i) = β_P1 + β_Pxx_i + β_Pzz_i + β_Pr(1 − r_i). The substantive model is as in DGM 1 with x_Si = (1, z_i), and x_Ai = (x_i) is an auxiliary variable in the analysis. Thus the substantive model and pattern-mixture model are again both correctly specified.

DGM 3 is identical to DGM 2, but now x_i is included in the substantive model, which is therefore logit P(y_i|x_i, z_i) = β_S1 + β_Sxx_i + β_Szz_i with x_Si = x_Pi = (1, x_i, z_i). Now the substantive model is incorrectly specified while the pattern-mixture model remains correctly specified.

DGM 4 is a selection model. Here z_i and x_i are generated as in DGM 2, then y_i is generated following the substantive model logit P(y_i|x_i, z_i) = β_S1 + β_Sxx_i + β_Szz_i and r_i is generated following logit P(r_i|x_i, z_i, y_i) = α₁ + α_xx_i + α_zz_i + α_yy_i. Here the substantive model is correctly specified while the pattern mixture model is mis-specified.

For the parameter values, we consider scenarios a-d for each DGM. In scenario a, the sample size is n_obs = 500; the missingness model has α_x = α_z = α_y = 1 and we choose α₁ to fix π_obs = P(r = 1) = 0.75; and the pattern mixture model has β_P1 = 0, β_Px = β_Pz = 1, β_Pr = −1. (α_x and β_Px are ignored in DGM 1, α_y is ignored in DGM 1-3 and β_Pr is ignored in DGM 4.) Scenarios b-d vary scenario a by setting n_obs = 2000, π_obs = 0.5, and β_Pr = −2 respectively. 1000 data sets were simulated in each case. Table 2 summarises the simulation design.

Table 2.

Simulation study: data generating models.

DGM	Type	PM correct?	SM correct?	Auxiliary variables?
1	Pattern-mixture	Yes	Yes	No
2	Pattern-mixture	Yes	Yes	Yes
3	Pattern-mixture	Yes	No	No
4	Selection	No	Yes	No
	Parameters	Description
	a	Base case
	b	Larger sample size
	c	More missing data
	d	Larger departure from MAR

5.2. Analysis methods

The mean score (MS) method is implemented as described in sections 2 and 3, with logit link. x_i is used as an auxiliary in DGM 2. In DGM 1-3, Δ(x_i) is taken to equal the known value −β_Pr for all individuals; in DGM 4, Δ(x_i) is not known but (for the purposes of the simulation study) is estimated by fitting the pattern-mixture model to a data set of size 1,000,000 before data deletion.

The MS method is compared with analysis of data before data deletion (Full); analysis of complete cases (CC), which wrongly assumes MAR; and two alternative methods that allow for MNAR, multiple imputation (MI) and selection model with inverse probability weighting (SM).

In the MI approach (Rubin, 1987; White et al., 2011b), the imputation model is equation (3), and data are imputed with an offset Δ(x_i) in the imputation model. The number of imputations is fixed at 30.

In the SM approach, we use the response model logit p(r_i = 1|y_i, x_i) = α^Tx_Pi+Δ*(x_i)y_i where the sensitivity parameter Δ*(x_i) expresses departure from MAR as the log odds ratio for response per 1-unit change in y_i. In DGM 4, Δ*(x_i) is taken to equal the known value α_y; in DGM 1-3, Δ*(x_i) is not known but (for the purposes of the simulation study) is estimated by fitting the selection model to a data set of size 1,000,000 before data deletion. The parameters α cannot be estimated by standard methods, since some y_i are missing, so we use a weighted estimating equation which does not involve the missing y_i’s (Rotnitzky et al., 1998; Dufouil et al., 2004; National Research Council, 2010):

$${\displaystyle \sum _i{\mathbf{x}}_{Pi}\left\{\frac{r_i}{h({\mathbf{\alpha }}^T{\mathbf{x}}_{Pi}+\text{Δ}*({\mathbf{x}}_i)y_i)}-1\right\}}=0.$$

The substantive model is then fitted to the complete cases with stabilised weights $\widehat{p}\left(r_i=1|{\mathbf{\text{x}}}_{Si}\right)/\widehat{p}\left(r_i=1|y_i,{\mathbf{\text{x}}}_i\right),$ where $\widehat{p}\left(r_i=1|{\mathbf{\text{x}}}_{Si}\right)$ is estimated by the same procedure as $\widehat{p}\left(r_i=1|y_i,{\mathbf{\text{x}}}_i\right)$ but with no Δ*(x_i)y_i or x_Ai terms (Robins et al., 2000). Variances are computed by the sandwich variance formula, ignoring uncertainty in α̂.

5.3. Estimand

The estimand of interest is the coefficient β_Sz in the substantive model. It is computed by fitting the substantive model to the data set of size 1,000,000 before data deletion. We explore bias, empirical and model-based standard errors, and coverage of estimates β̂_Sz.

5.4. Results

Results are shown in Table 3. CC is always biased, often inefficient, and poorly covering. Small bias (at most 3% of the true value) is observed in the “Full” analysis (i.e. before data deletion) in some settings: this is a small-sample effect (Nemes et al., 2009), since as noted above, the true value and “Full” are calculated in the same way with large and small samples respectively. Taking “Full” as a gold standard, MS, MI and SM methods all have minimal bias (at most 2% of true values). Precisions of MS and MI are similar, with SM slightly inferior in DGM 2. Coverages are near 95%, with some over-coverage for SM in some settings, as a consequence of slightly overestimated standard errors (results not shown) due to ignoring uncertainty in α̂ (Lunceford and Davidian, 2004). The performance of MS is not appreciably worse when the selection model is mis-specified (DGM 3) or when the pattern-mixture model is mis-specified (DGM 4). Computation times for MI are 15-18 times longer than for MS, which is 10-30% longer than SM.

Table 3.

Simulation results: bias, empirical standard error and coverage of nominal 95% confidence interval for methods Full (before data deletion), CC (complete cases analysis), MS (mean score), MI (multiple imputation), SM (selection model + IPW). Error denotes maximum Monte Carlo error.

DGM	Bias					Empirical SE					Coverage
	Full	CC	MS	MI	SM	Full	CC	MS	MI	SM	Full	CC	MS	MI	SM
1a	0.007	-0.128	0.010	0.010	0.009	0.191	0.223	0.218	0.219	0.218	95.0	90.6	95.1	95.3	95.8
1b	0.004	-0.130	0.007	0.006	0.006	0.095	0.113	0.111	0.112	0.111	94.3	76.7	93.8	93.4	94.6
1c	0.007	-0.167	0.018	0.018	0.018	0.183	0.267	0.258	0.259	0.258	96.5	91.9	95.9	95.4	96.6
1d	0.000	-0.177	0.003	0.004	0.004	0.187	0.223	0.203	0.204	0.203	95.1	88.3	95.6	95.5	97.1
2a	0.009	-0.151	0.010	0.010	0.005	0.178	0.219	0.203	0.203	0.209	96.3	90.1	95.4	95.4	97.0
2b	0.004	-0.157	0.003	0.003	-0.001	0.092	0.109	0.101	0.101	0.104	94.6	71.5	95.1	95.3	96.9
2c	0.005	-0.206	0.002	-0.001	-0.004	0.185	0.296	0.256	0.257	0.290	94.9	88.1	95.0	94.7	97.2
2d	0.011	-0.175	0.011	0.010	0.007	0.186	0.227	0.200	0.200	0.202	95.0	86.1	94.5	95.2	98.2
3a	0.016	-0.110	0.021	0.020	0.015	0.208	0.249	0.245	0.246	0.249	96.5	92.7	95.4	94.7	95.3
3b	0.003	-0.127	0.003	0.003	-0.003	0.106	0.122	0.120	0.120	0.121	94.8	81.8	95.3	95.2	95.3
3c	0.012	-0.160	0.015	0.012	0.018	0.217	0.327	0.316	0.318	0.323	95.1	90.3	95.0	95.1	95.4
3d	0.019	-0.163	0.020	0.020	0.020	0.216	0.254	0.238	0.239	0.249	94.2	88.6	94.5	94.6	95.3
4a	0.005	-0.148	0.014	0.012	0.006	0.218	0.255	0.251	0.252	0.253	94.2	90.0	94.8	94.5	95.0
4b	0.006	-0.147	0.015	0.015	0.008	0.107	0.124	0.122	0.122	0.123	94.0	77.1	94.0	94.1	94.6
4c	0.008	-0.203	0.004	0.002	0.011	0.213	0.345	0.336	0.337	0.343	94.2	90.8	94.2	94.3	95.0
4d	0.026	-0.118	0.045	0.045	0.036	0.211	0.250	0.246	0.248	0.249	94.2	91.2	94.3	94.5	94.8
Error	0.007	0.011	0.011	0.011	0.011	0.005	0.008	0.008	0.008	0.008	0.8	1.4	0.8	0.8	0.7

6. Discussion

We have proposed a mean score method which works well when the sensitivity parameters are known. In practice, of course, the sensitivity parameters are unknown, and a range of values will be used in a sensitivity analysis.

The main practical difficulty in implementing any principled sensitivity analysis is choosing the value(s) of the sensitivity parameters. This is a subjective process requiring subject-matter knowledge and is best done by discussion between statisticians and suitable ‘experts’, typically the trial investigators. By using the pattern-mixture model, we use a sensitivity parameter Δ(x_i) that is easier to communicate with ‘experts’ than the corresponding parameters in selection models or shared parameter models. The procedure has been successfully applied in several trials (White, 2015). Special attention is needed to the possibility that Δ(x_i) varies between randomised groups, because estimated treatment effects are highly sensitive to such variation (White et al., 2007). As with all aspects of trial analysis, plausible ranges of the Δ(x_i) parameters should be defined before the data are collected or before any analysis. An alternative approach would report the “tipping point”, the value of Δ(x_i) for which the main results are substantively affected, leaving the reader to make the subjective decisions about the plausibility of more extreme values (Liublinska and Rubin, 2014). Presenting this information could be complex without subjective decisions about the difference in Δ(x_i) between randomised groups. Effective methods are therefore needed for eliciting sensitivity parameters.

Our method does not incorporate data on discontinuation of treatment, unless this can be included as an auxiliary variable. Our method would however be a suitable adjunct to estimation of effectiveness in a trial with good follow-up after discontinuation of treatment. Further work is needed to combine our sensitivity analysis with models for outcome before and after discontinuation of treatment (Little and Yau, 1996). In a drug trial in which follow-up ends on discontinuation of treatment, we see our method as estimating efficacy or a de jure estimand; if effectiveness or a de facto estimand is required then post-discontinuation missing data in each arm may be imputed by the methods of Carpenter et al. (2013). Further work is needed to perform a full sensitivity analysis in this setting.

Our use of parametric models makes our results susceptible to model mis-specification, and indeed in many cases models (1) and (3) cannot both be correctly specified except under MAR. However, the simulation study shows that the impact of such model inconsistency is small relative to the impact of assumptions about the missing data and the difficulty of knowing the values of the sensitivity parameters.

We compared the mean score method with multiple imputation and inverse probability weighting. In the case of a quantitative outcome, MI can be simplified by imputing under MAR and then adding the offset to the imputed data before fitting the substantive model and applying Rubin’s rules. We could also impute under MAR and then use a weighted version of Rubin’s rules to allow for MNAR (Carpenter et al., 2007). Both MI methods are subject to Monte Carlo error and so seem inferior to the mean score method. A full likelihood-based analysis of the selection model would also be possible, and a Bayesian analysis could directly allow for uncertainty about Δ(x_i) in a single analysis (Mason et al., 2012). These alternative approaches are both more computationally complex.

The proposed mean score method can be extended in various ways. We have illustrated the method for departures from a MAR assumption, but it can equally be used if the primary analysis with a binary outcome assumed “missing = failure”, by varying Δ(x_i) from −∞ rather than from 0. The method is also appropriate in observational studies, except that mean imputation for missing covariates is not appropriate in this context. The method can be applied to a cluster-randomised trial as described in Section B of the Supplementary Materials. Further work could allow the imputation and substantive models to have different link functions, non-canonical links to be used with suitable modification to U_S, and extension to trials with more than two arms.

Sensitivity analysis should be more widely used to assess the importance of departures from assumptions about missing data. The proposed mean score approach provides data analysts with a fast and fully theoretically justified way to perform the sensitivity analyses. It is implemented in a Stata module rctmiss available from Statistical Software Components (SSC) at https://ideas.repec.org/s/boc/bocode.html.

Supplementary Materials

The supplementary materials give details of the sandwich variance in equation (6) and sketch an extension to clustered data.