Analysis of single, cisplatin-induced DNA bends by atomic force microscopy and simulations

Abstract

Bent DNA, or DNA that is locally more flexible, is a recognition motif for many DNA binding proteins. These DNA conformational properties can thus influence many cellular processes, such as replication, transcription and DNA repair. The importance of these DNA conformational properties is juxtaposed to the experimental difficulty to accurately determine small bends, locally more flexible DNA, or a combination of both (bends with increased flexibility). In essence, many current bulk methods use average quantities, such as the average end-to-end distance, to extract DNA conformational properties; they cannot access the additional information that is contained in the end-to-end distance distributions. We developed a method that exploits this additional information to determine DNA conformational parameters. The method is based on matching end-to-end distance distributions obtained experimentally by AFM imaging to distributions obtained from simulations. We applied this method to investigate cisplatin GG biadducts. We found that cisplatin induces a bend angle of 36º and softens the DNA locally around the bend.

Introduction

The average conformation of short (< 500 base pairs, (bp)), double-stranded DNA molecules, at low concentrations, is accurately described by the worm-like chain model ^1–2. In this model, DNA is treated as a semi-flexible polymer that deviates from its straight configuration due to thermal fluctuations. This deviation from linearity, θ, is determined by the stiffness, or persistence length, P, of the molecule; that is, the average deviation of two segments of a molecule separated by a distance, l, is given by <cosθ> = e ^−l/P. For double-stranded DNA, P is about 50 nm at physiological conditions; though it can vary depending on sequence and environmental conditions, such as cation concentration.

Atomic force microscopy (AFM) has been extensively utilized to image and analyze DNA molecules ^2–14. Much of this work is based on the finding that DNA retains its worm-like chain behavior and persistence length as it settles onto a mica surface from an aqueous solution under certain deposition conditions ². In other words, DNA molecules equilibrate in two dimensions on the substrate. This implies that a statistical analysis, based on the worm-like chain (WLC) model, can be used for AFM-imaged DNA molecules to determine their conformational and mechanical properties, such as contour length, L, end-to-end distance, R, persistence length, P, induced bend angle, β, and increased local flexibility ^2–4.

Many cancer drugs primarily target DNA and introduce structural changes like bending, kinking, crosslinking, and/or unwinding of the DNA molecule. These structural changes can alter signaling pathways, trap replication proteins and high mobility group (HMG) proteins, and ultimately lead to apoptosis ^15–18, which is the desired outcome for cancer treatment. Cisplatin (cisplatinum, or cis-diamminedichloroplatinum(II), (CDDP), trade names Platinol and Platinol-AQ) belongs to a family of inorganic metal drugs and has a success rate of more than 90% against testicular and ovarian cancer, but a much lower success rate for other cancers, such as lung cancer ^19–20. The underlying reason for these disparate success rates may be that DNA in different cancer cells respond differently to drug-induced DNA damage, such as DNA bends ^21–25. Cisplatin targets the major groove of DNA ^26–28 and forms intra-strand bi-adducts between purine bases ^29–30, thus bending the major groove and subsequently opening up the minor groove. The major adduct is a 1,2-intrastrand adduct between adjacent guanine bases ³¹. However, despite the fact that this drug has been used for several decades, the structural changes induced by cisplatin in a DNA molecule, especially the local changes due to its interaction with a single molecule of cisplatin (e.g. bend angle, bend flexibility, binding geometry) are still debated, even though these properties may play a key role in how cellular proteins process this damage ^{11, 31–32}. For example, the bend angle, β, of a GG adduct in cisplatinated DNA, as determined by bulk experimental techniques, such as gel electrophoresis and NMR, and X-ray crystallography ranges from 30° to 80° ^{28, 33–38}. Though, recent high resolution X-ray crystallography data (Figure 1A) point to a bend angle of 35° to 40°, local unwinding of the double helix by 25°, and mixed A-form/B-from DNA around the platination site ³⁷. Moreover, it is not known if the DNA becomes more, or less, flexible in the vicinity of the bend, though the partial unwinding may suggest increased flexibility around the bend. Thus, there is a need to develop methods that can determine the structural change induced by DNA ligands, such as cancer therapeutics, since these changes may be a key parameter determining the cellular response to, and ultimate outcome of, cancer treatment ^{11, 39–40}.

Figure 1.

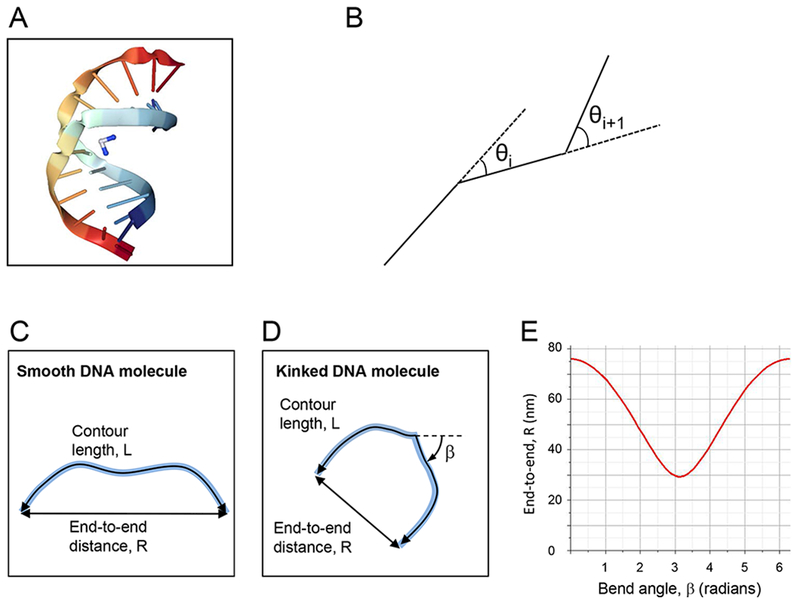
(A) Crystal structure of duplex DNA (rainbow color) containing a cisplatin 1,2-d(GpG) intrastrand cross-link (blue & white molecule), inducing a bend angle of 35° to 40° and local unwinding of the double helix by 25° ³⁷. (B) Schematic depiction of the DNA simulations. (C, D) Schematic depiction of an unbent DNA fragment (C) and a DNA fragment with a bend, β (D). (E) Plot of equation (2); end-to-end distance, R, as a function of the bend angle, β, for a 300 bp DNA fragment.

Imaging single DNA molecules is the most direct way to determine global DNA conformational changes, and AFM has been used to investigate the cisplatin–DNA interaction ^41–44 showing a significant change in the appearance and global persistence length of DNA upon massive cisplatination of the entire DNA molecule ⁴¹. However, since numerous sites on these molecules were subjected to cisplatin modification, it was not possible to determine β and the local flexibility of a single damage site. At first glance, it seems that simple visual inspection of DNA molecules in AFM images could be used to determine the bend angle, and, in fact, the ‘tangent method’ in which tangents are drawn along the DNA contour on either side of the bend works reasonably well for large bends ^{10, 45–47} . However, because of the DNA’s natural curvilinear shape due to thermal fluctuations, and because of the AFM tip-broadening effect, this method is associated with significant errors and user bias, especially for small bends of less than about 45° ^{3, 48}. Quantities that can be determined without user bias and very accurately by AFM are the contour length and end-to-end distance.

Here, we describe and apply an analysis method, based on the WLC model, to determine the bend angle and bend flexibility (local flexibility around a bend) of a DNA molecule due to its interaction with a ligand. A similar method has been applied to protein-induced bend angles ⁴⁸. In our method, the end-to-end distribution of simulated DNA molecules is compared with that of AFM-imaged DNA molecules. The end-to-end distance distributions change significantly for varying bend angles, persistence lengths and bend flexibilities. For example, we show that increasing the bend angle decreases the average end-to-end distance, shifts the peak of the end-to-end distance distribution to lower values and first widens, then narrows the distribution. Increasing the bend flexibility has a distinctly different effect, as it mostly widens the end-to-end distance distribution, but does not significantly shift the peak. Matching simulated and experimental data allows the extraction of the persistence length of the DNA arms, the bend angle, and bend flexibility. We used our method to study a 300 bp, double-stranded DNA molecule that is unmodified or contains a single cisplatin site in the middle. We were able to accurately determine the cisplatin-induced bend angle of GG- cisplatin adducts. We also extracted best-fit values for the bend flexibility. This method should be applicable to study the effect of many different ligands on DNA conformation. Elucidation of these parameters will enhance our understanding of how a ligand interacts with DNA and may, thus, enhance our understanding of the successes and limitations of chemotherapeutics and other DNA ligands.

Materials and Methods

Simulations.

300 bp long DNA molecules were generated computationally for a wide range of persistence lengths, P, bend angles, β, and bend flexibility, P’. Each simulation contained 10,000 molecules. The DNA was modeled as a semi-flexible chain consisting of 300 small segments of 0.32 nm length and negligible height ^{2, 49}, (Figure 1B). A length of 0.32 nm was chosen, since this number is most consistent with the length of one base pair in AFM images ⁵⁰. This value is 6% less than B-form DNA (0.34 nm rise per base pair) and 23% more than A-form DNA (0.26 nm rise per base pair). The angle, θ, between two adjacent segments was generated by Monte Carlo simulation selecting random angles, θ, from a Gaussian distribution with a zero mean and variance

$$<{\theta }^2(l){>}_{2D}=\frac{l}{P}$$ (1),

where l is the separation between segments. It should be noted that this is the variance for a worm-like chain in two dimensions (on the substrate surface); in three dimensions (in solution), the variance would be 2l/P. The surface interaction of the DNA and the excluded volume effect were assumed to be zero. The first assumption implies that DNA molecules can equilibrate in two dimensions on the surface, instead of being projected onto (trapped by) the surface. This is an excellent assumption for our deposition conditions, as was shown by Rivetti et al. ². These authors also showed that excluded volume effects can be neglected for 300 bp fragments, at the low DNA concentrations we used. For bent DNA molecules a specific bend angle, β, was introduced in the middle of the fragment. Bend flexibility, P’, was modeled as 5 links with lower persistence length, P’; two links on either side of the bent link, plus the bent link. This choice is based on the finding that a single GG-cisplatin adduct causes a global distortion extending over 4–5 DNA base pairs ^{35, 51–52}. We used 5 links in all simulations of P’ (number of links with increased flexibility was not varied). The magnitude of the end-to-end distance, $\text{R=}\left|\overrightarrow{R}\right|$, of each molecule was determined, and a histogram of the distribution of R/L values was then created from the simulated data (contour length L = 96 nm for simulated molecules). R/L, rather than just R, was plotted to normalize the distributions, and to eliminate the small variations in contour length, L, in the AFM measurements.

DNA fragments.

A custom plasmid, pIDT-SMART AFMGG, was synthesized by IDT (Coralville, IA) containing the following DNA sequence: 5’-CGATCGATCGATCGACGTGTCGCATTGATATCACGTCGATGATATCATGACGCGATCGTGATACATCGATCACACGATCGTGTGATGACGAATGACGAATCGAACGATACACGCGTGATGACATACATGCGATTCACGTATTCACATTCGGTCATCACACACGTAATCGTGCAATGCGAATCGTGTCATGCGCAACGTATCACATTGCGTACAACGTGCATATCGATCGAACGTGAATTCGTGATTTCGAATCGCGATCACGTGATCATGTCGTGCATCGCGTGTCGTGTCGATTTCACG flanked by unique XbaI and SacI restriction sites. This construct has a single GG site in its center (G₁₅₀G₁₅₁) that is susceptible to the formation of an intrastrand cross-link by cisplatin. The single GG sites in the DNA construct were selected because cisplatin has a high specificity of cross-linking GG sites in DNA ⁵³.

The DNA substrate was treated with a 500-fold excess of cisplatin for 6 hours. DNA was purified from unreacted cisplatin with a G-50 Sephadex spin column (GE Health Sciences). The treated DNA substrate was then quantified and the extent of cisplatin conjugation was determined by inductively coupled plasma-mass spectrometry (ICP-MS). The Pt/DNA ratio was found to be 0.95.

AFM imaging and analysis:

For AFM imaging, the DNA stock solution was diluted in DNA deposition buffer (4 mM HEPES, 2 mM MgCl₂, 10 mM NaCl, pH 7.4) to a final DNA concentration of 10 nM. 10 μL of this solution were deposited onto a ~ 1 cm², freshly cleaved muscovite mica disc (Paramount Corporation, NY), and was incubated on this mica surface for 1–2 minutes. The mica surface was then rinsed with de-ionized water, followed by drying in a gentle flow of nitrogen gas. The samples were imaged with stiff AFM probes (Nanosensors, spring constant, k = 21–98 N/m; resonance frequency, f = 146–236 kHz). Over 1000 molecules of non-cisplatinated (normal) and over 700 molecules of cisplatinated DNA were imaged. The contour length, L, and end-to-end distance, R, of each DNA molecule were measured by tracing the contour of the DNA molecules, and applying a polynomial fitting routine in the Matlab software program “Alex”². A histogram of the R/L values was then created from the AFM data.

Comparison between simulations and AFM data.

The comparisons of the R/L distributions of the AFM-imaged DNA molecules and the simulated DNA molecules were done using the χ²-test, the Ansari-Bradley (AB) test and the bootstrap method using MATLAB statistical subroutines. The χ²-test gives the probability that the R/L value of the simulated and the AFM imaged DNA molecule occur in the same bin. In addition to the χ²-test, the AB test and bootstrap sampling were done to determine if the experimental data and the simulation data belong to the same distribution. Both, the χ²-test and AB test were performed at a 5 % significance level. The Ansari-Bradley test ⁵⁴ is a non-parametric test which tests the null hypothesis, H₀, that the experimental and simulated data come from the same distribution function against the alternative (not the same distribution function) at a α = 5 % significance level. The Ansari-Bradley test combines and sorts the two data sets of interest followed by assigning a rank to each value in the data set. The ranks corresponding to one data set are added and its variance from the entire data set is calculated by finding the p value. If the two data sets are equally distributed in the ranking, indicating that they come from the same distribution, then the variance will be small resulting in a p > 0.05 ⁵⁵. p describes the probability of observing a sample at least as extreme as the one that was actually observed by chance, assuming H₀ is true. If we specify a value α such that H₀ is accepted at p > α and rejected at p < α, then α specifies the probability of falsely rejecting H₀ ⁵⁶. For p > 0.05 at 5 % significance level; the null hypothesis that the two data sets belong to the same distribution cannot be rejected; most important for our analysis, the higher the obtained p value, the higher the probability that the two distributions are similar. One advantage of using the Ansari Bradley test is that it does not require normal distributions. The accuracy of the fit determined using the χ²-test and AB test were verified by finding the confidence interval of the statistical location (mean and the median) of the data, and the confidence interval was calculated by bootstrapping the data at 95 % confidence interval. In addition to the χ²-test and AB test, the fits between the data sets were considered good if the confidence intervals of the mean and median from the two data overlapped significantly. To avoid any error in the statistical analysis, the medians were subtracted from the data set before the Ansari-Bradley test. To visualize the best fit between the experimental and simulated distributions, we plotted the absolute value of the logarithm of p as a function of the different parameters, namely the persistence length P, the bend angle β, and the bend flexibility P’.

Results

The overall goals of our paper are to develop a method to determine ligand-induced bend angles and bend flexibility, and to determine those quantities for a cisplatin-induced GG-adduct. Our DNA construct is 300 bp long and has a single GG target site for cisplatination in the center; the flanking sequences have a very low propensity for cisplatin-adduct formation. We chose a 300 bp fragment with a single cisplatination site in the middle for the following reasons. 1) A single, well-defined cisplatination site, as opposed to several random sites, allowed us to accurately study the effect of cisplatination on DNA conformation. 2) Having the site in the center divides the fragment into two 150 bp arms, which is about the persistence length of DNA. This makes the arms relatively stiff, resulting in a maximum reduction of the end-to-end distance upon bending the DNA. 3) On the other hand, the 300 bp fragment is long enough to be easily discernible and traceable in AFM images.

Figures 1C & D schematically depict the contour length and end-to-end distance of a DNA molecule without and with a central bend, β. Figure 1E shows how the end-to-end distance of a 300 bp fragment varies as a function of the bend angle β, according to equation

$${\langle R^2\rangle }_{2D}=4P\cdot L[1-\frac{2P}{L}(1-e^{-\frac{L}{4P}})(2-\cos \beta (1-e^{-\frac{L}{4p}}))]$$ (2),

which describes the mean squared end-to-end distance of a DNA fragment with a central bend, β ³. This equation reduces to

$${\langle R^2\rangle }_{2D}=4P\cdot L[1-\frac{2P}{L}(1-e^{-\frac{L}{P}})]$$ (3)

for β = 0°. Equations (2) and (3) are valid for DNA molecules that have equilibrated in two dimensions ².

We used equations (2) and (3) as a starting point to analyze our data, to get initial values for the bend angle and the persistence length of the DNA arms. However, these equations only use the average end-to-end distance, without exploiting the information contained in the end-to-end distance distribution, which is also available from AFM images. The distribution contains additional information. For example, by optimizing the match between the distribution of simulated molecules and experimental molecules, as done here, a more accurate, and reliable number for the bend angle can be obtained. Moreover, by analyzing the differences between experimental and simulated distributions (i.e. looking at the p-values of the Ansari-Bradley test), the most likely range of bend angles can be obtained. Analyzing the distribution may also reveal sub-populations, which are not seen when just considering the average end-to-end distance (this is also one of the disadvantages of bulk experiments). Finally, it is possible to extract information about the bend flexibility, i.e. the increased flexibility in the region immediately adjacent to the bend.

DNA molecules were simulated as outlined in Figure 1B. A DNA molecule is generated by linking N = 300 small segments of length l = 0.32 nm; each segment, i, deviates from the previous segment by an angle θ_i selected randomly from a Gaussian distribution $\wp {(\theta )}_{2D}=\sqrt{\frac{P}{2\pi l}}{e}^{-\frac{P\cdot {\theta }^2}{2l}}$ with zero mean and variance, l/P. To study bent DNA molecules, a specific bend angle, β, was introduced in the center of the fragment, i.e. after link 150. To simulate increased bend flexibility, the persistence length of the two segments on either side of the bend was changed to a smaller value, P’, i.e. the variance of the Gaussian distribution for the two links on either side of the bent link, and the variance of the bent link, was l/P’. 10,000 molecules were generated in each simulation.

Figures 2, 3 and 4 show sample images of simulated molecules and the normalized end-to-end distributions (R/L distributions) for a range of β, P and P’ values. Changing the bend angle, β, from 0 to 180° dramatically changes the distribution (Figure 2). As β changes from 0° to 180°, the peak (the most likely end-to-end distance) shifts from a value of R/L = 0.95 to R/L = 0.05. Additionally, the distribution broadens significantly as β increases to 120°, and then narrows again. Finally, the average end-to-end distance, shifts to lower values, though less pronounced than the shift of the peak, and the change in the width of the distribution. These observations indicate that the distributions contain more exploitable information than just the average end-to-end distance. Changing the persistence length, P, of the DNA arms also has a significant effect on the normalized end-to-end distance distribution (Figure 3). Increasing P from 20 nm to 70 nm narrows the width of the distribution, and the peak of the distribution shifts from a value of 0.84 to 0.98. Changing the bend flexibility, P’, also has a distinct and significant effect on the end-to-end distribution (Figure 4). A more flexible bend (small P’) results in a wider end-to-end distribution while not having a strong effect on the peak value of the distribution. As can be seen from these three figures, each of the three parameters, β, P and P’, has a different, distinct effect on the end-to-end distribution. In the following section we carefully match the end-to-end distance distributions of the simulated molecules to the experimentally obtained distributions to determinate values for β, P and P’.

Figure 2.

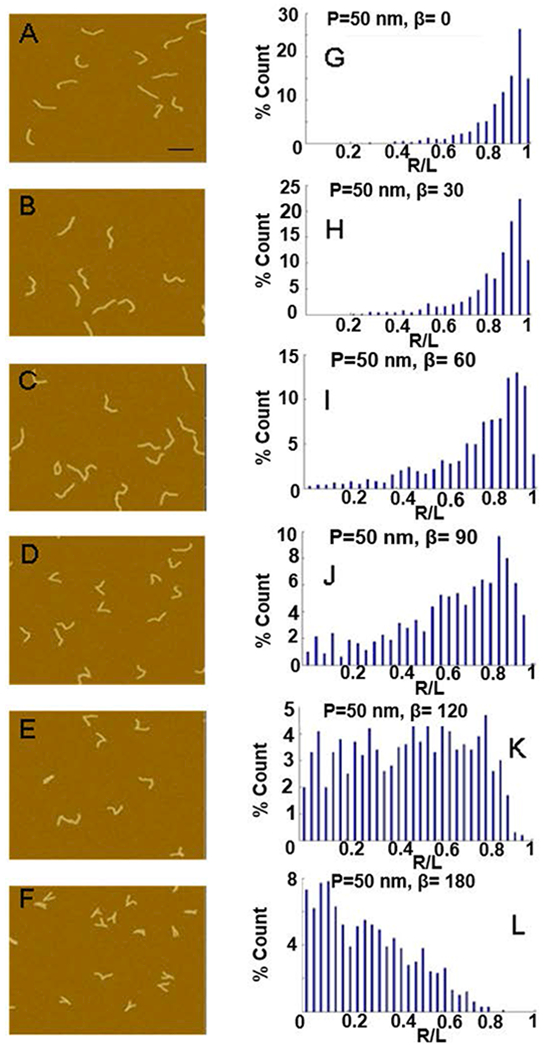
Effect of varying bend angle on end-to-end distance distributions. (A-F) Images of simulated DNA molecules for P = 50 nm and varying the bend angle, β, from 0 – 180°; scale bar is 100 nm. (G-L) The resulting R/L distribution for the molecules simulated in A-F.

Figure 3.

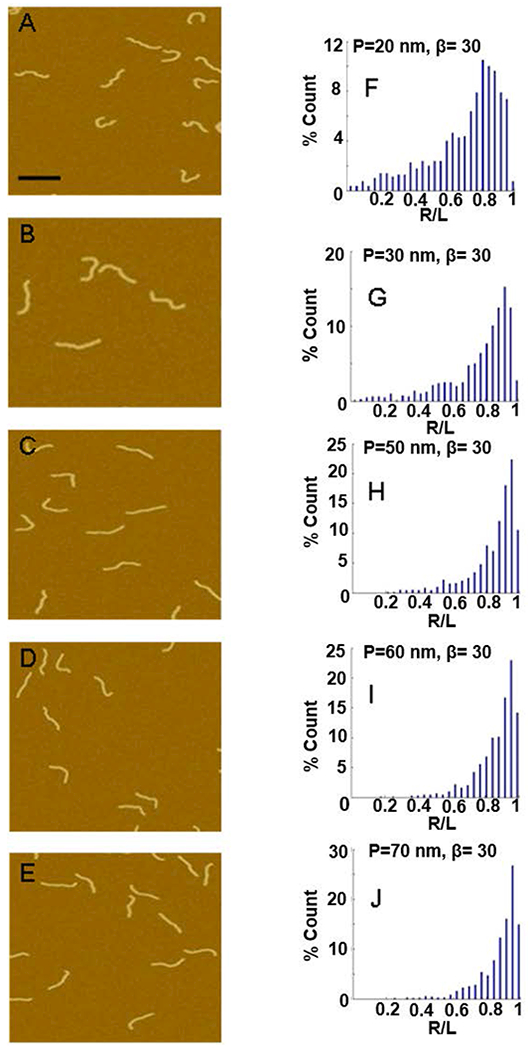
Effect of varying persistence length on end-to-end distance distributions. (A-E) Images of simulated DNA molecules for β = 30° and varying P from 20 nm to 70 nm; scale bar is 100 nm. (F-J) The resulting R/L distribution for the molecules simulated in A-E.

Figure 4.

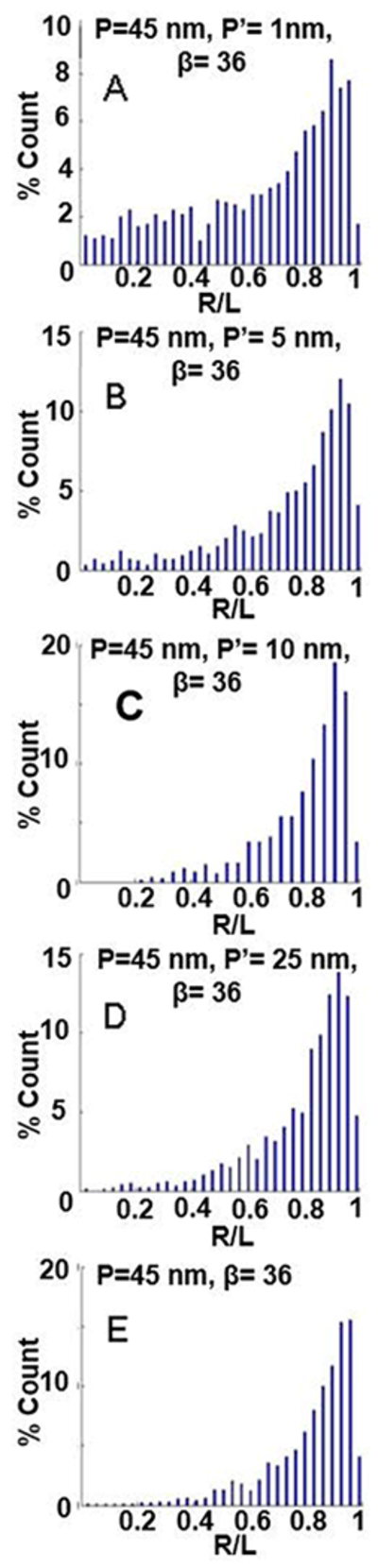
Effect of varying bend flexiblity on end-to-end distance distributions. (A-E) R/L distribution for simulated DNA molecules with β = 36° , P = 45 nm, and varying P’ from 1 nm to 45 nm.

We imaged about 1000 molecules of the untreated GG fragment and about 700 molecules of this fragment after it was treated with cisplatin (Figure 5, insets), and determined the corresponding R/L distributions. Such large numbers of imaged molecules result in smooth R/L distributions and increase the accuracy of our method. The average contour length of the untreated 300 bp DNA fragment was 92 ± 4 nm, and the average contour length of the cisplatin-treated 300 bp DNA fragment was also 92 ± 4 nm. These values corresponds to a rise of 0.31 nm/bp – close to the rise of 0.32 nm/bp that is typically observed for DNA molecules in AFM images taken in ambient conditions.⁵⁰ B-form DNA and A-form DNA have a rise of 0.34 nm/bp and 0.26 nm/bp, respectively.

Figure 5.

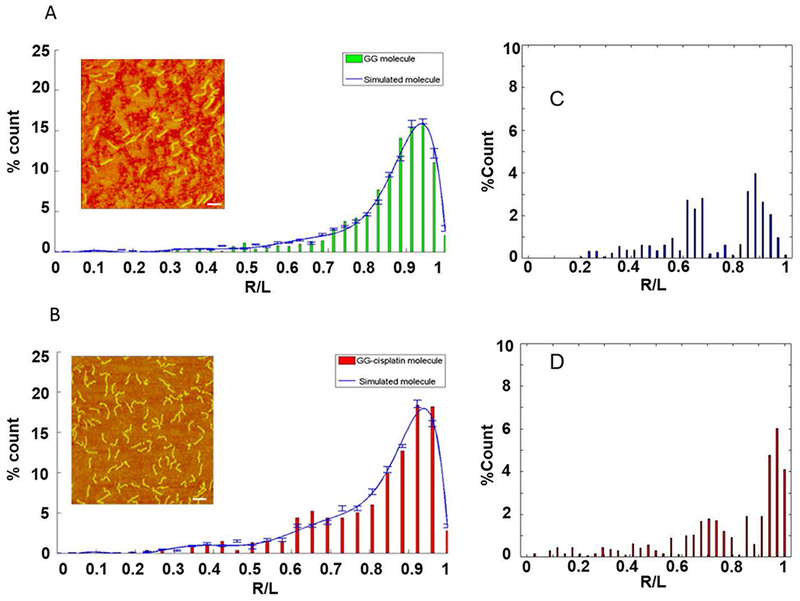
Matching simulated and experimental data. R/L distributions of experimental AFM data (bar chart) and simulated molecules (blue line). (A) Untreated DNA; (B) cisplatinated DNA with single GG-adduct in the middle of the strand. The error bars represent the percentage standard error of the mean (SEM) of the number of simulated DNA molecule in each bin. The error in the experimental data is estimated to be 10%, or less (see Discussion). (Insets) AFM images of untreated DNA and cisplatinated DNA; scale bar is 100 nm. (C) & (D) Differences in the R/L distributions between the untreated and cisplatinated DNA. (C) Difference between the measured distributions shown in (A) and (B). (D) Difference between the curve fits shown in (A) and (B). The distributions were first normalized and then subtracted from each other.

To obtain accurate values of P and β, we compared the R/L distributions of the various simulated DNA molecules with the distribution of the untreated and cisplatinated DNA molecules obtained from AFM images (Figure 5). We employed three comparison methods, the χ²-test, the Ansari-Bradley (AB) test and the boot strap method. The key point of comparing the R/L distributions is to find the simulations that best fit the experimental data. Figure 5A & B shows the best matches of the experimental distributions (green and red histograms) for the unmodified and modified DNA fragments and the simulated distributions (solid, blue line). Figure 5C &D show difference between the untreated and the cisplatinated DNA distributions.

Figure 6 shows the difference between the experimental and the simulated distributions as a function of the various tested parameters (persistence lengths, P, bend angle, β; and bend flexibility P’). The difference is plotted as the absolute value of the logarithm of the p-value (abs(log(p)); a smaller abs(log (p)) indicates a better fit between the experimental data and the data from the simulated molecules. The region of uncertainty (ROU) represents the range of persistence length, P, and bend angle, β, values over which the null hypothesis (distributions are the same) was accepted with p ≥ 0.05 and the confidence interval of the mean and the median of R/L values is within one another for the two data sets. This was considered a good fit.

Figure 6.

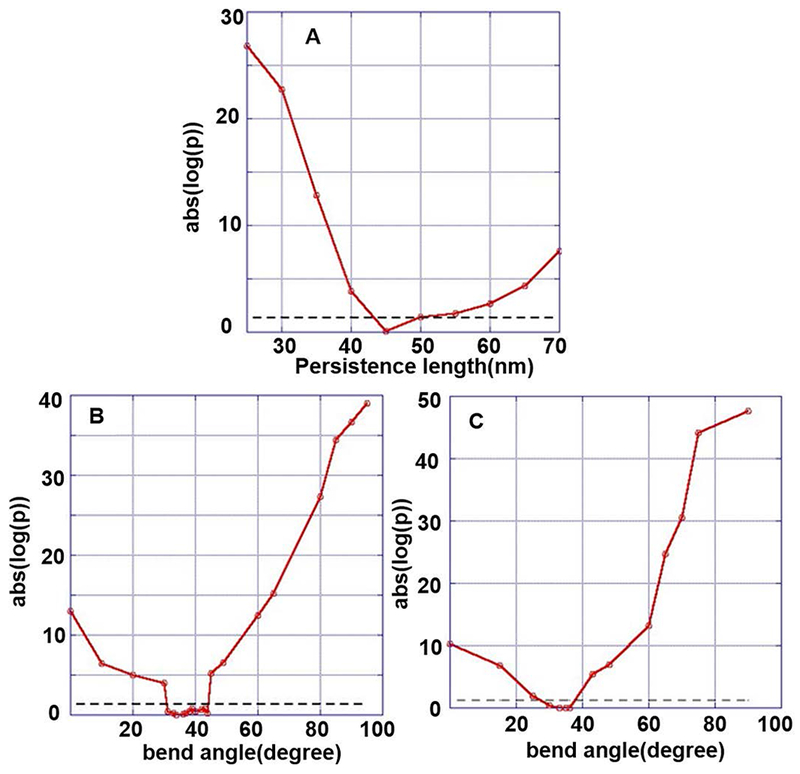
Plot of the p value showing the quality of the fit between the simulated and the experimental data and the acceptable fit region (region of uncertainty lying below dashed lines). (A) Normal DNA with P = 45 nm, β = 0°; (B) cisplatinated DNA with GG in the middle of the strand, P = 45 nm, acceptable fits are obtained for β = 30° – 44°; (C) cisplatinated DNA with GG in the middle of the strand, P = 45 nm, P’ = 20 nm, acceptable fits are obtained for β = 30° – 38°; best fit is obtained for β = 36°.

For the unmodified GG-DNA molecules, the best fit was obtained for β = 0°and P = 45 nm (Figure 5A, Figure 6A). Using equations (1), (2), and (3) the same values are obtained. A value of P = 45 nm is also consistent with published data for normal, unmodified DNA ^{2, 57}.

For the DNA construct with a single cisplatinated GG site, using a persistence length of P = 45 nm for the arms, a bend angle in the range of β = 34° – 44° resulted in a good fit of the experimental and simulated R/L distributions (0.39–0.84 p-value). The best fit was obtained for β = 36° with a p-value of 0.84 (Figure 5B, 6B).

The R/L distribution for the cisplatinated GG complex showed a slightly broader distribution than the other distributions (Figure 5 B). To further investigate this slight broadening, we included an additional parameter, bend flexibility, P’, in our simulations. A more flexible bend widens the end-to-end distance distribution (Figure 4). In the initial simulations (type I), we kept P of the entire molecule fixed at 45 nm and changed β. In the expanded simulations (type II), we reduced the persistence length of the 5 links around the damage site, while keeping P = 45 nm for the rest of the molecule, and then varied β. For the type I simulation, the ROU (good fit) was β = 30° – 44°. For the type II simulation we observed a narrowing of the ROU to β = 30° – 38°, and a better p-value, ranging from 0.37– 0.89. Figures 6B and C show the comparison of the distributions for the bend GG fragment without (Figure 6B) and with (Figure 6C) bend flexibility, P’. The best fit (best p-value) was obtained for P = 45 nm, β = 36° and P’ = 20 nm.

We also verified our approach by comparing the R/L distributions for the AFM imaged DNA molecules and simulated DNA molecules among each other. As expected, the comparison of R/L distributions for two different ensembles of DNA molecules was found dissimilar.

Discussion

We describe a method to determine the mechanical and conformational properties of DNA and ligand-DNA complexes. The method is based on matching the end-to-end distance distributions of simulated molecules and AFM-imaged molecules, and allows the extraction of such parameters as the persistence length, bend angle and bend flexibility. The advantage of this method over bulk methods is that it exploits the additional information that is contained in the end-to-end distance distributions, rather than just relying on the average end-to-end distance. This method provides for higher accuracy, especially for smaller bend angles, which escape detection by the tangent method. Moreover, our method may reveal sub populations, which are averaged out in bulk methods; and it can bring out additional features, such as bend flexibility, which is very difficult to determine with other methods.

We applied the method to analyze cisplatinated GG-bi-adducts. The persistence length of untreated DNA was 45 nm, in agreement with previously published values ². The bend angle β induced due to the cisplatin-GG adduct was determined to be in the range of 30° – 44°, with the best fit giving a value of 36°. This is in good agreement with the values obtained from gel electrophoresis and X-ray experiments ^{33, 35–37, 51}, but disagrees with other published values ^{34, 58}. Our data also indicate that the region around the bend softens, as we obtain the best fit with a P’ = 20 nm. This softening may be caused by the partial unwinding of the base pairs surrounding the GG-adduct ³⁷.

Because differences in distributions are subtle, especially for small bend angles, is critical to understand and reduce possible experimental error sources. Our experimental error in the contour length was 10%, taken as the difference between the average measured contour length (92 ± 4 nm) and the theoretical contour length (102 nm for B-form DNA). The error could be smaller if the DNA was partially converted to A-form DNA (a 300 bp A-form DNA would be 78 nm). A 300 bp fragment with 59% B-form and 41% A-form would be 92 nm long. Possible error sources include: 1) The accuracy of the length determination is limited by the pixel size, which was 2 nm in our images (image size 1000 nm, 512 pixels). When measuring R and L for N molecules, the associated error should approximately scale as $\sqrt{N,}$ and will, thus, be less than a nanometer (less than ~ 2%) for most bins of Figure 5. 2) The tip broadening effect overestimates lateral dimensions of an object by approximately the diameter of the tip (measured at the initial contact height of the tip and the object ⁵⁹. Depending on tip sharpness, this could result in an overestimation of 5–10 nm in DNA lateral dimensions (including DNA length); however, this overestimate in R and L can be effectively reduced by carefully defining the end points of the DNA contour length. The two terminal points in the contour length should be placed a bit short of the last pixel (by about half the measured width of the DNA strand). This practice may significantly reduce this error. 3) The polynomial fitting routine that traces the DNA contour may also introduce an error, as the fitted polynomial may not exactly follow the real DNA contour. This phenomenon was investigated by Rivetti & Codeluppi ⁵⁰, and it was found that this error can be reduced to 0.4% when using an ad hoc method that smoothes the DNA trace by a polynomial fitting of degree 3 over a moving window of 5 points. 4) The AFM piezoelectric transducers may not be perfectly calibrated and they can also show non-linear behavior.

The cisplatin-induced bend angle and bend flexibility may be features that are recognized by DNA repair proteins and other DNA binding proteins. For example, it was shown that the action of proteins involved in DNA repair (e.g. MutS) and transcription (e.g. phage phi 29 transcriptional regulator) is determined by DNA bends ^{11, 39–40}. Moreover, it has been proposed that DNA binding proteins, such as Cro protein, recognize pre-bent DNA and/or regions of increased DNA flexibility as they scan along DNA ¹⁰. DNA bending influences the binding of HMG proteins and other proteins, which regulate transcription, replication and DNA repair, and may, thus, have a significant influence on apoptosis ^{16, 19, 32, 60}. For signaling cascades, which start with bent DNA, it may also matter if the DNA is pre-bent or if the bend is induced by a ligand or a protein ¹⁰. A better, more accurate understanding of DNA conformational properties is thus important to better understand these cellular processes, and our analysis method can help to accurately extract these properties from AFM images of DNA molecules.

Conclusions

Many DNA-binding ligands, such as drugs or proteins, often induce DNA bends and/or increase local DNA flexibility. These changes in DNA conformation can have dramatic effects on the cellular and organismal level by altering signaling pathways, which can result in increased or decreased transcription, or failed or successful DNA repair. The ligand-induced bend angles are often small, and can be difficult to detect, because of the natural curvilinear structure of DNA. We developed a method to determine the ligand-induced DNA bend angle, β, global DNA flexibility, P, and local DNA flexibility, P’. The method is based on the fact that these quantities cause distinct changes in the end-to-end distribution of a DNA fragment. By AFM-imaging DNA molecules, determining their end-to-end distribution and matching the distribution to simulated molecules, accurate values for β, P and P’ can be extracted. We applied the method to cisplatinated DNA and found that cisplatin induces a bend angle of 36° and appears to make the DNA slightly more flexible around the bend. Our method should be applicable to many different ligand-DNA complexes.