Ryanodine Receptor Open Times Are Determined in the Closed State

Abstract

The ryanodine receptor (RyR) ion channel releases Ca²⁺ from intracellular stores by conducting Ca²⁺ but also by recruiting neighboring RyRs to open, as RyRs are activated by micromolar levels of cytosolic Ca²⁺. Using long single-RyR recordings of the cardiac isoform (RyR2), we conclude that Ca²⁺ binding to the cytosolic face of RyR while the channel is closed determines the distribution of open times. This mechanism explains previous findings that RyR is not activated by its own fluxed Ca²⁺. Our measurements also bolster previous findings that luminal [Ca²⁺] can affect both the cytosolic activation and inactivation sites and that RyR has different gating modes for the same ionic conditions.

Main Text

In cardiac myocytes, ryanodine receptors (RyRs) release Ca²⁺ from the sarcoplasmic reticulum to initiate muscle contraction. Because RyRs open in response to micromolar [Ca²⁺], the efflux of Ca²⁺ through one RyR is amplified by the recruitment of nearby RyRs. Although this inter-RyR Ca²⁺-induced Ca²⁺ release is largely understood, one open question is the extent to which the Ca²⁺ released by a RyR acts on itself (feedthrough activation).

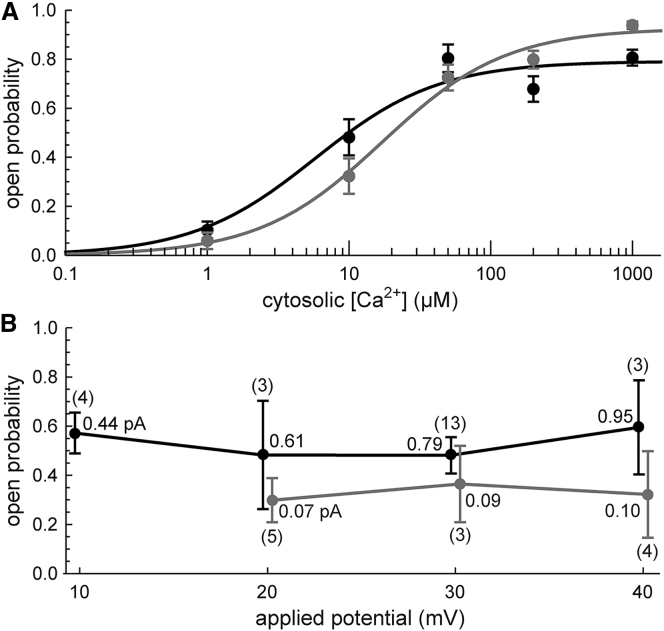
Previous studies showed that RyR generally does not react to its own fluxed Ca²⁺, with feedthrough activation only for superphysiological currents (>3 pA, compared to ∼0.4 pA under physiological conditions) (1, 2), or for RyRs that are hypersensitive to Ca²⁺ by the application of caffeine (2) or ATP (3), or in the absence of cytosolic Mg²⁺ (3, 4). ATP and Mg²⁺ potently modulate RyR Ca²⁺ sensitivity and are present at high concentrations in cells. Therefore, including these substances is vital when evaluating the physiological role of feedthrough activation. Our experiments with both ATP and Mg²⁺ at physiological cytosolic levels show that RyR does not see its own fluxed Ca²⁺; the open probability (P_o) (Fig. 1 A) is independent of Ca²⁺ flux <1 pA (Fig. 1 B).

Figure 1.

(A) P_o versus cytosolic [Ca²⁺] for high (black) and low (gray) luminal Ca²⁺. The lines are binding curves. (B) P_o versus applied voltage for high (black) and low (gray) luminal Ca²⁺. Parentheses: number of recordings. Also listed are calculated Ca²⁺ currents. Cytosolic [Ca²⁺] is 10 μM. Other [Ca²⁺] are also independent of potential (data not shown). Details of the P_o analysis, binding curves, and Ca²⁺ currents are in the Supporting Materials and Methods.

RyR not reacting to its own fluxed Ca²⁺ is difficult to reconcile with other data, namely that RyR open time increases with cytosolic [Ca²⁺] (1, 2, 5); mean open time (MOT) is shown in Fig. S5. Open channels are thought to close randomly. In that case, open times are defined while the channel is open. However, to be sensitive to cytosolic [Ca²⁺], the cytosolic Ca²⁺ binding sites would have to be accessible to Ca²⁺ during the open state and exposed to the fluxed Ca²⁺, which can raise Ca²⁺ concentration on the cytosolic face to >15 μM for physiological currents (6) and >50 μM in our experiments (Fig. S9). These are substantially larger than needed to activate RyR (Fig. 1 A), leading to feedthrough activation.

Here, we test a hypothesis that explains how RyR open times can depend on cytosolic [Ca²⁺] without having feedthrough activation: RyR open-time distributions are determined in the closed state, before the channel opens.

We do this by analyzing single-RyR2 recordings taken under conditions with high (1000 μM) and low (100 μM) luminal Ca²⁺ and with 1, 10, 50, 200, and 1000 μM cytosolic Ca²⁺. For each condition, we recorded 8–20 channels for a total time of 13–75 min. (Further details are in the Supporting Materials and Methods; Tables S1 and S2.) This was done to ensure that we understand RyR behavior with cell-like cytosolic Ca²⁺, Mg²⁺, and ATP levels, but also because there is variability between channels under identical conditions and within recordings. This variability is ubiquitous (Figs. S4 and S5), but subgroups of channels have identical open- and closed-time distributions, indicating a small number of gating modes for the same ionic condition (Fig. S6), a property that has been previously reported (7, 8, 9, 10). Importantly, however, all our analysis is largely independent of this variability, shown in the figures with 95% confidence intervals (see Supporting Material).

We include data with both high and low luminal Ca²⁺ because each is known to affect the channel differently (11, 12, 13, 14). RyR exposed to high luminal Ca²⁺ is more responsive to cytosolic Ca²⁺ (Fig. 1 A) and is also subject to inactivation at cytosolic [Ca²⁺] ≥200 μM (Fig. S7), whereas at low luminal Ca²⁺ it is not; the high luminal Ca²⁺ case has a marked drop in MOT between 50 and 200 μM that the low luminal Ca²⁺ case does not (Figs. S5 and S8). We will show that at both high and low luminal Ca²⁺, the open-time distributions are determined in the closed state.

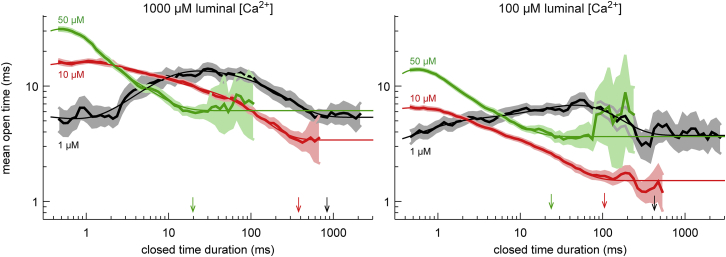
To start the analysis, we plot MOT versus closed-time duration in Figs. 2 and S10 A. This shows how open time correlates to the length of the previous closing. (Fig. S13 shows this in a different way.) The curves are not identical, so it is not merely the length of a closing that determines open time. However, the curves overlap significantly when the closures are longer than ∼3 ms, and this overlapping is consistent with our hypothesis that open-time distributions are determined in the closed state. We see from Fig. 2 that for each cytosolic [Ca²⁺], a final MOT is reached; for long enough closures, each curve becomes a constant. Moreover, the higher the cytosolic [Ca²⁺], the less time it takes to reach this steady state. Based on this, we hypothesize that there is an underlying Ca²⁺-dependent process that determines channel open-time distributions (and therefore MOT) and that this process is faster at higher cytosolic [Ca²⁺].

Figure 2.

MOT versus duration of the previous closed event for 1, 10, and 50 μM cytosolic [Ca²⁺] and for high (left) and low (right) luminal [Ca²⁺]. The thick lines are the mean times of the data, and the shaded areas are the 95% confidence intervals (see Supporting Materials and Methods). The thin lines are fits of a sum of three exponentials, and the arrows indicate when these fits approximately reach steady state (i.e., 4τ₃, as defined in Fig. 3). Fig. S10A shows the same for 200 and 1000 μM. Fig. S10B shows mean closed time versus open duration. To see this figure in color, go online.

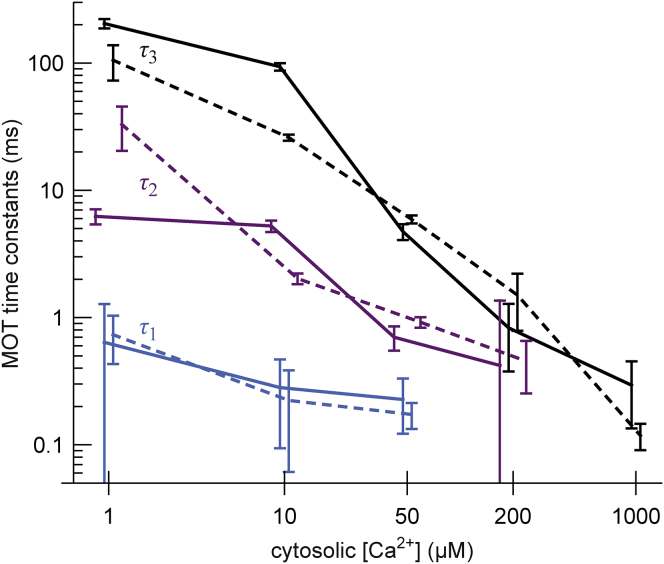
To identify this underlying process, we fit the curves in Figs. 2 and S10 A (thin lines) with a sum of up to three exponentials (see Supporting Materials and Methods). Fig. 3 shows the cytosolic [Ca²⁺] dependence of these time constants.

Figure 3.

The time constants from the exponential fits in Fig. 2 and Fig. S10A as a function of cytosolic [Ca²⁺] for both high (solid lines) and low (dashed lines) luminal [Ca²⁺]. To see this figure in color, go online.

If the time constants are from a single process, then the largest one (τ₃) defines the timescale it takes to reach steady state. Moreover, if this process defines RyR open-time distributions during the closed state, then the open-time distributions for each cytosolic [Ca²⁺] should be identical if the closed-time duration t is scaled by the τ₃ for each [Ca²⁺]; i.e., it is not the absolute closed times that determine the open-time distributions, but rather the fraction of time α through the process (α = t/τ₃ and steady state is reached for α > ∼4 (arrows in Fig. 2)). We show this in Fig. 4.

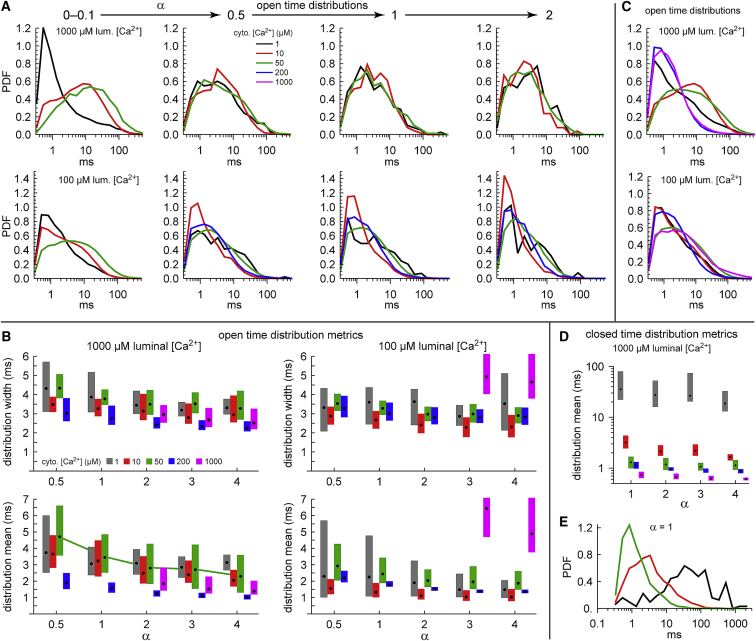
Figure 4.

(A) The probability distribution functions (PDFs) of the open times for different scaled times α. When a specific α is listed, all events with closed times t with 0.9ατ₃ ≤ t < 1.1ατ₃ are chosen and the distribution of the subsequent open times is shown. Top row, high luminal Ca²⁺; bottom row, low. (B) Metrics of the smoothed histograms described in the Supporting Materials and Methods, specifically the standard deviations (top row) and means (bottom row). (C) Open-time PDFs for all recorded openings are shown. (D) Distribution means are shown like in (B), but for closed-time distributions rather than open-time distributions. (E) PDFs are shown as in (A), but for closed-time distributions. To see this figure in color, go online.

Our goal is to show that the open-time distributions are identical for all cytosolic [Ca²⁺] after a sufficient amount of scaled time (α) has passed. We do this in several ways (with details described below): in Fig. 4 A, we show that the distributions look the same; in Fig. 4 B, we quantify distribution similarity using two metrics; in Fig. 4, C–E, we show negative controls; in Fig. S12, we show that the open-time distributions across cytosolic [Ca²⁺] are highly correlated.

Fig. 4 A shows how the open-time distributions change with α. The top row shows it for high luminal Ca²⁺, the bottom for low. Early in the process (0 < α < 0.1), the distributions are very different from each other but quickly become the same as α increases. Fig. 4 B shows metrics of the distributions with 95% confidence intervals (see Supporting Materials and Methods); the top row shows the widths of the distributions (standard deviations), the bottom row the means. The purpose of these metrics is to quantify the similarity between the distributions, which are shown in Figs. S1 and S2.

The distributions in Fig. 4 A and the metrics in Fig. 4 B are highly similar, with a few exceptions.

First, at high luminal Ca²⁺, the distribution means for 200 μM cytosolic Ca²⁺ are below those of the lower concentrations (blue boxes for all α in the lower left panel of Fig. 4 B). This is also true to a lesser extent for 1000 μM cytosolic Ca²⁺ (magenta boxes), whose metrics only appear for α ≥ 2 because its τ₃ is less than the shortest reliably measurable event time. We suspect that the reason for this is that at these high cytosolic Ca²⁺ concentrations, the Ca²⁺ is binding not only to the activation site of RyR but also to its inactivation site, which decreases MOT (Figs. S5 and S8). If this is the case, then the open-time distributions should be different. However, these distributions are still determined in the closed state, in line with our hypothesis.

Second, at low luminal Ca²⁺, the distributions for 10 μM cytosolic Ca²⁺ (Fig. 4 A, bottom row, red lines) appear shifted to shorter open times. This is reflected in the distribution means (Fig. 2; red boxes in the lower right panel of Fig. 4 B), but here, the confidence intervals are very close to the distribution means for the other cytosolic [Ca²⁺]; they are all within a fraction of a millisecond of each other. This case is different from the case above (high luminal and 200 μM cytosolic Ca²⁺) in which the confidence intervals are far from overlapping with other data intervals. Therefore, we believe that this is more a reflection of the variability among channels than a fundamental difference in the distribution shapes. Moreover, if it were significantly different, then this 10 μM cytosolic Ca²⁺ data point would be qualitatively different from surrounding data points at both lower (1 μM) and higher (50 and 200 μM) cytosolic [Ca²⁺].

Lastly, at low luminal Ca²⁺, the distribution for 1000 μM cytosolic Ca²⁺ is far different from all other open-time distributions (magenta boxes in the right panels of Fig. 4 B). Both its mean and its width are much larger, which can also be seen in Fig. S10 A (right panel). This is not due to inactivation; mean closed time is shorter than for smaller cytosolic [Ca²⁺], whereas MOT is longer (Fig. S5). In fact, its P_o is almost 1 (Fig. 1 A). At this point, it is not clear why this data point is so qualitatively different from all the others.

Except for this one outlier and when inactivation is present, we have now shown that open-time distributions of RyR are identical as long as sufficient time has passed in the closed state to be partly through a cytosolic Ca²⁺-dependent process. This similarity between the open-time distributions is not because the distributions are the same to begin with; early in the process, the distributions are quite different (Fig. 4 A, first column) and gating may be stochastic (Fig. S13), and the open-time distributions for all the data (i.e., for all opening events) are also very different (Fig. 4 C). Moreover, the similarity is not because the distributions do not change with α; their means change (Fig. 4 B, green line). Lastly, to show a counterexample in which distributions do not cluster, we consider closed- (rather than open-) time distributions and their time constants (Figs. S10 B and S11). Applying the same analysis, we find qualitatively different distributions (Fig. 4, D and E). The point of this is to show that the similarity of the open-time distributions is not expected and to show that closed-time distributions do not seem to be determined during the open state.

Finally, in Fig. S12, we show the Pearson correlation between open-time distributions for all pairs of cytosolic [Ca²⁺]. These high correlations, when combined with the analysis in Fig. 4 B, indicate each pair is the same (except cases noted above). Fig. S12 also shows that ∼30% through the process is sufficient to reach identical distributions.

We next focus on the nature of the cytosolic Ca²⁺-dependent process. Because RyR is activated by cytosolic Ca²⁺, we hypothesized that this process is Ca²⁺ binding to the activation site on the cytosolic face. A binding process has the necessary characteristics: it is [Ca²⁺] dependent and requires time to complete, which for simple models occurs through multiple, well-defined time constants. We first tried the simplest model, namely four independent binding sites, one on each of the four identical subunits of RyR. This has one time constant but failed to reproduce the [Ca²⁺] dependence of the τ₃ (data not shown). Next, we considered a model in which RyR can bind 0–3 Ca²⁺ ions (assuming three Ca²⁺ bound to any of the four subunits is enough to activate the channel) with on and off rates depending on how many are bound. This model describes the Ca²⁺ dependence (both cytosolic and luminal) of all three time constants (Fig. S3). (Details of the Ca²⁺ binding analysis are given in the Supporting Material.)

The model also provides an explanation of how high and low luminal Ca²⁺ differ in the binding of Ca²⁺ during the closed state. Specifically, we find significant overlap between the on and off rates that reproduce the measured time constants, indicating similarities in some Ca²⁺ binding steps. But, we find that the binding of the first Ca²⁺ is stabilized at low luminal Ca²⁺; the smaller time constants with low luminal Ca²⁺ come from preventing unbinding of the first Ca²⁺, with the other parameters unchanged (Fig. S3 C).

This very simple Ca²⁺ binding model provides a reasonable explanation of our data, but our analysis is by no means exhaustive; other Ca²⁺ binding models may explain the data. However, because the overarching goal of this study is to show that RyR open times are determined in the closed state, we limit our analysis to providing one possible explanation of what the cytosolic [Ca²⁺]-dependent process is that determines RyR open-time distributions.

The implications of our findings are far-ranging, both for RyR and ion channels in general.

With respect to RyR regulation by cytosolic Ca²⁺, influencing open time by what occurs during the closed state is probably the simplest way to keep a Ca²⁺-conducting, Ca²⁺-sensitive channel from activating itself. If RyR were activated by its own fluxed Ca²⁺, then some other mechanism would likely be necessary to control the closing of RyRs (e.g., some form of inactivation) lest all the RyRs in a cluster open (via inter-RyR Ca²⁺-induced Ca²⁺ release) and stay open (via feedthrough activation) until sarcoplasmic reticulum Ca²⁺ is depleted. Moreover, cytosolic Ca²⁺ binding in the closed state is probably the only way for RyR to be sensitive to 1 μM Ca²⁺. If RyR sensed cytosolic [Ca²⁺] in the open state, the sensor would have to have extraordinarily fine sensitivity, distinguishing, for example, 50 μM from 51 μM (Fig. S9).

In this picture, Ca²⁺ released during an opening diffuses away and does not appreciably increase the background cytosolic [Ca²⁺] seen by the RyR in the closed state. If this does not occur (e.g., in the tight geometry of the subsarcolemmal space), then the fluxed Ca²⁺ can reactivate RyR. Although more study is needed, we suspect that this is what occurs when we and other groups found feedthrough activation with Ca²⁺ fluxes ∼10 times larger than physiological (1, 2). Similarly, with caffeine, with ATP, or without cytosolic Mg²⁺, the activation site is more sensitive to Ca²⁺ and MOT is increased, and therefore residual Ca²⁺ is more likely to trigger a new opening.

Our analysis also has implications about RyR regulation by luminal Ca²⁺. It is already known that luminal Ca²⁺ affects RyR gating (11, 12, 13, 14), although this is phenomenon is not universal (e.g., the Ca²⁺ sensitivity shift in Fig. 1 A is not present in mouse RyR2 or with the addition of exogenous CSQ (11)) and more studies are necessary. Our study provides evidence that luminal Ca²⁺ can alter function of both the cytosolic activation and inactivation sites. With respect to the inactivation site, low luminal [Ca²⁺] seems to inhibit inactivation by preventing a drop in open times at high cytosolic [Ca²⁺] (Figs. S5 and S8). With respect to the activation site, the different time constants for high and low luminal Ca²⁺ in Fig. 3 are direct evidence that the luminal side changes the properties of the cytosolic site. Specifically, the shorter time constants with low luminal [Ca²⁺] indicate a faster setting of open times compared to high luminal [Ca²⁺], especially at low cytosolic [Ca²⁺]. Moreover, our modeling suggests that the affinity of the cytosolic Ca²⁺ binding site varies with luminal [Ca²⁺] (and probably mainly the affinity for the first Ca²⁺). Possible explanations include the occupancy state of the luminal Ca²⁺ binding site or a change in a luminal regulatory protein (e.g., unbinding) altering the cytosolic activation site architecture (11, 12, 13, 14).

Our results also have implications for understanding ion channels in general, not just RyR. For example, our work shows that channel gating is not always a random occurrence. For RyR, we showed that there is memory between the closed and open states through how much Ca²⁺ is bound during the closed state; if the binding process is >30% completed (Fig. S12), then the open-time distributions are the same. At shorter closed times, however, the openings do seem to be more stochastic (Fig. S13).

Overall, our analysis indicates that this memory is vital to physiological RyR2 function so it can sense micromolar cytosolic [Ca²⁺] and still mediate a large Ca²⁺ flux.

Author Contributions

The hypothesis was conceived by D.G. during discussions with M.F. M.F. provided the experimental data and contributed to the analyses and writing. D.G. conceived and performed the analyses and wrote the manuscript.

Editor: Eric Sobie.

Supporting Citations

References (15, 16, 17, 18, 19, 20, 21, 22, 23, 24) appear in the Supporting Material.