Quantifying Platelet Margination in Diabetic Blood Flow

Abstract

Patients with type 2 diabetes mellitus (T2DM) develop thrombotic abnormalities strongly associated with cardiovascular diseases. In addition to the changes of numerous coagulation factors such as elevated levels of thrombin and fibrinogen, the abnormal rheological effects of red blood cells (RBCs) and platelets flowing in blood are crucial in platelet adhesion and thrombus formation in T2DM. An important process contributing to the latter is the platelet margination. We employ the dissipative particle dynamics method to seamlessly model cells, plasma, and vessel walls. We perform a systematic study on RBC and platelet transport in cylindrical vessels by considering different cell shapes, sizes, and RBC deformabilities in healthy and T2DM blood, as well as variable flowrates and hematocrit. In particular, we use cellular-level RBC and platelet models with parameters derived from patient-specific data and present a sensitivity study. We find T2DM RBCs, which are less deformable compared to normal RBCs, lower the transport of platelets toward the vessel walls, whereas platelets with higher mean volume (often observed in T2DM) lead to enhanced margination. Furthermore, increasing the flowrate or hematocrit enhances platelet margination. We also investigated the effect of platelet shape and observed a nonmonotonic variation with the highest near-wall concentration corresponding to platelets with a moderate aspect ratio of 0.38. We examine the role of white blood cells (WBCs), whose count is increased notably in T2DM patients. We find that WBC rolling or WBC adhesion tends to decrease platelet margination due to hydrodynamic effects. To the best of our knowledge, such simulations of blood including all blood cells have not been performed before, and our quantitative findings can help separate the effects of hydrodynamic interactions from adhesive interactions and potentially shed light on the associated pathological processes in T2DM such as increased inflammatory response, platelet activation and adhesion, and ultimately thrombus formation.

Introduction

Patients with type 2 diabetes mellitus (T2DM) are at high risk of developing cardiovascular diseases because T2DM is clearly linked with the onset of a thrombotic event (1, 2). Several factors contribute to the prothrombotic status in T2DM, such as elevated coagulation, impaired fibrinolysis, endothelial dysfunction, and platelet hyperreactivity (3, 4, 5). Among them, the role of platelets in the formation and development of thrombi is of particular importance. Platelets in T2DM are characterized by dysregulation of several signaling pathways, and they can become hyperreactive and more prone to undesirable activation, adhesion, and aggregation (6, 7, 8, 9). Other abnormalities such as raised platelet count and high mean platelet volume (MPV) have also been observed in T2DM (10, 11). Shilpi et al. (12) showed that MPV (11.3 ± 1.0 fL) in diabetics is significantly higher than the MPV (9.0 ± 0.6 fL) in nondiabetics. For diabetic patients with micro- or macrovascular complications, MPV can be even higher (13, 14). Papanas et al. (13) found that T2DM patients without retinopathy have an MPV = 10.9 ± 1.1 fL, whereas those with retinopathy have an MPV = 15.8 ± 1.3 fL. It is reported that large platelets are more reactive than smaller platelets (15), produce more prothrombotic factors such as thromboxane A2, and express a greater number of adhesion receptors, such as P-selectin and GpIIb/IIIa (16).

The process of thrombus formation and development at an injured site on a blood vessel wall involves a number of simultaneous processes from flow dynamics, blood coagulation cascade, and transport of tissue factors to platelet adhesion, activation, and aggregation (17, 18, 19). Thrombosis can occur in the arterial or the venous circulation, and it is triggered by a disruption in endothelial cells and the exposure of tissue factors and collagen to blood. Accelerated atherosclerosis observed in T2DM would increase the risk of endothelial erosion of plaques, followed by thrombus formation (20). For efficient adhesion to an injured site, platelets must be sufficiently close to the site for platelet-subendothelium or platelet-platelet bonds to form. In a shear flow, red blood cells (RBCs) experience a wall-normal force that arises because of their deformation and propels them away from the vessel wall, leading to the formation of a cell-rich region in the core of the vessel and a cell-free layer (CFL) near the wall (21, 22, 23). This phenomenon was first quantified by Fahraeus and Lindqvist (24). Deformable RBCs, on the other hand, can expel platelets from the core of the stream toward the CFL region. Such transport and accumulation of platelets near the wall known as platelet margination occurs in the presence of RBCs at sufficient hematocrit (H_ct) and flowrate.

Significant progress has been made in understanding the platelet margination probability and dynamics, which characterize the physical contacts of platelet with the vessel wall and its direct or indirect effects on platelet adhesion. The first in vivo experiments of platelet distribution in venules and arterioles of rabbit mesentery were performed by the group of Reneman et al. (25, 26, 27). They found that the normalized platelet density is concentrated near the wall of arterioles, but the opposite platelet distribution is observed in venules. This discrepancy may be due to the rheological effects of RBCs, different position of a vessel in the vascular network, and also vessel wall properties. Numerous in vitro studies on the platelet margination and adhesion have also been reported (28, 29). Aarts et al. (30) examined the radial distribution of RBCs and platelets in 3-mm cylindrical vessels at various hematocrit and wall shear rates by the laser-Doppler technique. They found that near-wall concentration of platelets increases with increasing hematocrit and wall shear rates. Similar results of enhanced margination of platelet-sized spherical particles for H_ct = 20% compared to H_ct = 10% were found by Fitzgibbon et al. (31). In addition to the experiments, they conducted boundary integral simulations to confirm their experimental results and to track the trajectories of the particles with higher resolution. Eckstein and co-workers (32, 33) performed several studies on the lateral transport of platelet-sized latex beads in flows of blood suspensions. They found that the near-wall excess in concentrations of platelet-sized beads occurred when H_ct > 10% and the wall shear rate > 200 s⁻¹, whereas the largest amount of lateral transport of beads was observed at moderate shear rate ∼560 s⁻¹.

Along with the aforementioned experimental studies, recent advances in computational modeling and simulations enable us to investigate blood flow dynamics under physiological and pathological conditions (34, 35, 36, 37, 38). Crowl and Fogelson (39, 40) have performed blood flow simulations in a two-dimensional channel using a Lattice Boltzmann Method. They found that the lateral diffusivity of a platelet is correlated with its lateral position and platelet margination mostly occurs after the CFL has fully developed. The numerical studies from the group of Aidun et al. (41, 42, 43) demonstrated that, in addition to the hematocrit, the viscosity ratio of cytoplasm within the RBC to suspending fluid as well as the platelet shape play an important role in the margination process; less viscous cytoplasm of RBC than plasma or a more spherical shape of platelets can enhance the platelet margination rate. Vahidkhah et al. (44) have captured the three-dimensional nature of RBC-platelet collisions. For platelets approaching the wall, anisotropic platelet diffusion within CFL leads to the formation of platelet clusters, which might contribute to clot formation. Soares et al. (45) and Yazdani and Karniadakis (46) have performed simulations of platelet transport in complex geometries resembling arterial stenoses. They employed dissipative particle dynamics (DPD) to investigate the transport dynamics and self-orbiting motions of platelets when they flow through a constriction. Yazdani and Karniadakis (46) also found that higher levels of constriction and wall shear rates enhance platelet margination significantly, which may consequently lead to enhanced poststenosis platelet deposition onto the thrombus. In addition, the effects of microvessel tortuosity and the pathological alteration in the platelet size and density on the platelet activation and thrombus formation have been systematically investigated by Chesnutt and Han (47). In their study, however, they considered platelets as spherical particles and neglected the effects of RBCs for computational efficiency.

Following our previous work on modeling diabetic RBCs (48), here we extend our simulations to complex blood flow in microcirculation to study correlations between T2DM and increased platelet margination. We perform high-fidelity computational studies of blood flow through cylindrical vessels and focus on the radial distribution of diabetic RBCs and platelets under conditions resembling blood flow in an arteriole for T2DM subjects. In particular, we incorporate the properties of diabetic RBCs and platelets from available experiments and also a new data set collected from 64 diabetic patients. Several hemodynamic factors such as blood flowrate, hematocrit, and platelet shape are taken into account. In addition, there is growing evidence showing that white blood cells (WBCs) contribute to the disturbances of microcirculation in diabetes because of the promoted inflammatory cell recruitment (49, 50, 51). We further consider the influence of WBC dynamics on platelet transport in blood vessels by respectively incorporating leukocyte circulation, rolling along the vessel wall, and firm adhesion to the wall into our simulations. Such in silico hematologic studies involving large population of blood cells enables us to gain insights in the circulation and distribution of RBCs, platelets, and leukocytes in diabetic conditions, which in turn will help us understand the connection between enhanced thrombosis and inflammation in T2DM (52).

Methods

We employ DPD to model whole blood flow, i.e., plasma, RBCs, platelets, and WBCs, in 40-μm diameter vessels. DPD is a coarse-grained analog of molecular dynamics in which each particle represents a lump of molecules that interacts with other particles through soft pairwise forces. In addition to blood plasma modeled by collections of free DPD particles, the membrane of suspending cells including RBCs, platelets, and WBCs is constructed by a two-dimensional triangulated network with N_v vertices (DPD particles).These vertices are connected by N_s elastic bonds to impose proper membrane mechanics. More details of hydrodynamic interactions between DPD particles, and models for blood cells are presented in the Supporting Materials and Methods. We also validated systematically the DPD model by simulating the margination of spherical particles of different sizes in blood flow and compared against recent microfluidic measurements (53). The validation results are given in the Supporting Materials and Methods.

Parameter estimation

RBC models

Under physiological conditions, a healthy RBC has a large area/volume (S/V) ratio with a biconcave shape and a remarkable deformability and adaptability in mechanical behavior. In this study, we model an RBC at normal state (NRBC) with N_v = 500, shear modulus μ₀ = 4.73 μN/m, and bending rigidity k₀ = 2.4 × 10⁻¹⁹ J. An NRBC is set to have the cell surface area $A_0^{\text{tot}}$ = 132.9 μm² and cell volume $V_0^{\text{tot}}$ = 92.5 μm³, which give S/V = 1.44. All parameters used in our NRBC model are extracted from available measured data, and the representative RBC model has been extensively used from single-cell mechanics to blood flow dynamics (22, 23, 54, 55). Different from NRBCs, diabetic RBCs possess decreased cell deformability and are known to exhibit shape change from a normal biconcave shape to a near-oblate shape with a smaller S/V ratio (9, 56, 57). In addition, it was observed that the increase in mean corpuscular volume (MCV) is related to high blood glucose level (58, 59). Diabetic RBCs with high intracellular glucose will induce osmotic imbalance between RBCs and their surrounding plasma. Morse et al. have shown an increase in MCV from 93 to 114 μm³ by in vitro incubation of normal RBCs with glucose concentration of 20 mg/mL for an hour. A further increase in MCV (>120 μm³) can be achieved with increasing incubation temperature (59). This MCV change is reversible once the glucose concentration is diluted. Agrawal et al. also claimed that the swollen RBCs observed from the sample blood of T2DM patients can be associated with the possible metabolic disturbance (60).

In this work, we have performed an evaluation of several clinical characteristics in blood samples from 136 human subjects (see Table S4). The number of patients diagnosed with T2DM is 64 with a mean age of 61 ± 13.7 years, compared to 72 patients with a mean age of 52 ± 17.8 years in controls. The blood glucose parameters, hemoglobin A1c (HbA1c), and fasting blood glucose (FBG) are significantly higher in diabetics (HbA1c = 7.66 ± 1.41% and FBG = 144.5 ± 48.9 mg/dL) compared to the controls (HbA1c = 5.25 ± 0.29% and FBG = 99.0 ± 15.4 mg/dL). Details of the blood sample preparation and analysis procedures are included in the Supporting Materials and Methods. As shown in Fig. S3, a and b, diabetic RBCs exhibit no statistically different MCV compared to that of the normal RBCs. A recent study performed by Lee et al. (61) shows a reduction in the membrane fluctuation of diabetic red cells, but there was no statistical difference in volume and surface area distributions of nondiabetic and diabetic RBCs. Although the alteration in the size and shape of diabetic RBCs is still debatable and probably dependent on glycemic control of the study subjects, we considered extreme values for S/V that were reported by Jin et al. (57). We have recently proposed a T2DM RBC model (48), which has been validated with available experimental data. Following our previous study, here, we extend our T2DM RBC model (DRBC) to a suspension with cell properties similar to those of a NRBC except for a shear modulus μ_s = 2μ₀ (μ₀ is the shear modulus of healthy subjects) and a reduced S/V ratio, S/V = 1.04.

Platelet models

An inactivated platelet is an oblate spheroid that can be characterized by its aspect ratio (AR) defined as the ratio of the minor axis to major axis. The typical AR range for a normal platelet is 0.25–0.5, and the MPV is 6–10 fL (μm³) (62, 63). However, previous studies have revealed a higher MPV in diabetic patients than in nondiabetic controls, which is considered as a risk factor for vascular diseases (12). As shown in our statistical study in Fig. S3, c and d, the scattered data points and the number distribution of MPV are significantly higher in the diabetic group than in the control group. The average MPV in diabetic subjects is 10.0 ± 1.26 fL compared to 9.2 ± 1.70 fL in nondiabetics, with a p-value of 0.003. Such enhancement in the MPV of diabetic platelets may be due to osmotic swelling as a result of hyperglycemia. Patients with less well-controlled diabetes are the ones developing micro- and macrovascular complications such as retinopathy. In a previous study by Papanas et al. (13), diabetic patients with retinopathy had an MPV = 15.8 ± 1.3 fL, which corresponds to a ∼5 fL difference between the MPV (10.9 ± 1.1 fL) of diabetics without retinopathy. In addition to diabetic retinopathy, large databases with different categorizations (a wide range of HbA1c levels, other complications of diabetes, smoking history, age, gender, etc.) are needed to calibrate the current MPV values. Indeed, levels of glycemic control could have significant implications because the effect observed here could be much more pronounced in diabetics with poor glycemic control, who by definition are at much higher risk for developing cardiovascular disease (CVD) (1). Another potential factor is smoking, which has vasoconstrictive effects and is known to have multiplicative effects in terms of increasing CVD risk among diabetics (64).

Considering these facts, here, we started our efforts in this field by using the platelet model with cell volume based on patient-specific data and further conduct a sensitivity study. A normal platelet (PLT) has cell volume $V_0^{\text{tot}}$ = 6 μm³, whereas a diabetic platelet (PLT^∗) has $V_0^{\text{tot}}$ = 12 μm³. These extreme values are chosen to distinguish the platelet margination in diabetic blood from that in normal blood. In addition, we assume that the platelets are not activated, and they are modeled in an oblate-spheroid shape with the AR = 0.38. The major axis for PLT is 3.3 μm, whereas for PLT^∗, it is 4.1 μm. The number of vertices in membrane network N_v = 48 and elastic properties of platelets μ_s = 100 μ₀ and k_c = 16 k₀ are given to all platelet models. Note that platelets are considered nondeformable in their resting state; however, they exhibit mild deformation with no activation under moderate shear rates (65, 66). In this study, the elastic properties of platelets are given based on the fact that platelets are about one to two orders of magnitude stiffer than RBCs (65, 67, 68), and we keep μ_s and k_c parameters constant in all simulations. Platelet models with such high values of shear modulus and bending rigidity have also been extensively used to the study of platelet dynamics (39, 44, 46, 69, 70).

WBC model

A WBC is represented as a triangulated sphere with N_v = 2498 and a diameter of 10 μm, which is similar to the previous leukocyte model used by Lei and Karniadakis (71). Compared with healthy RBCs, a WBC is less deformable, with the estimated membrane stiffness 0.3–1.2 dyn/cm (72). It is also reported that impaired deformability has been observed in children with diabetes (73), but the changes in WBCs shape are unclear. In this study, we model a WBC with a membrane elasticity of μ_s = 22 μ₀ and k_c = k₀.

Fluid-cell, cell-cell, and fluid (cell)-wall interactions

Blood plasma is modeled by DPD fluid with viscosity η = 1.25 × 10⁻³ Pa ⋅ s. The fluid-cell interactions are accounted for through viscous friction using the dissipative and random DPD forces (see Supporting Materials and Methods for details). Cell-cell adhesive interactions exist among cells and may be amplified in several pathological conditions (e.g., sickle cell anemia, malaria, and diabetes) (74). In this study, we neglect the complex surface features of all blood cells and do not model cell-cell adhesive interactions to study systematically the hydrodynamic interactions that induce platelet margination. As two cells approach each other, strong repulsive lubrication forces develop preventing cells from overlap. We use DPD particles for both plasma and cell membranes for which the conservative repulsive forces (F^C) are not strong enough to prevent cells from contacting each other. Therefore, we adopt a Morse potential between cell membrane particles to ensure strong repulsive forces and prevent cell overlap. Only the repulsive part of the Morse potential is used for cell-cell interactions, for which the well depth parameter is adjusted appropriately to ensure enough clearance between the cells. Further, to simplify the representation of platelets and WBCs, we apply the same cell-cell interaction parameters for both platelets and WBCs. The parameters used for the fluid-cell and cell-cell interactions are given in Tables S1–S3 in the Supporting Materials and Methods. The adhesive interactions between different pairs of blood cells such as RBC-RBC and RBC-WBC can also be captured by proper tuning of a Morse potential model. Fedosov et al. (75) simulated RBCs aggregation and the formation of rouleaux structures by applying Morse potential interactions between RBCs. Similarly, Lei and Karniadakis (71) modeled the interactions between the adherent leukocytes and sickled RBCs by the Morse potential. Furthermore, the vessel wall is modeled by frozen DPD particles with the same radial distribution function as the fluid particles in combination with a specular reflection of the plasma and cell particles at the fluid-wall interface (22, 23). The scaling of model and physical units is also presented in the Supporting Materials and Methods. In all simulations, the length scale r^M = 1.0 × 10⁻⁶ m and the timescale τ = 1.8 × 10⁻⁴ s are adopted.

Simulation setup

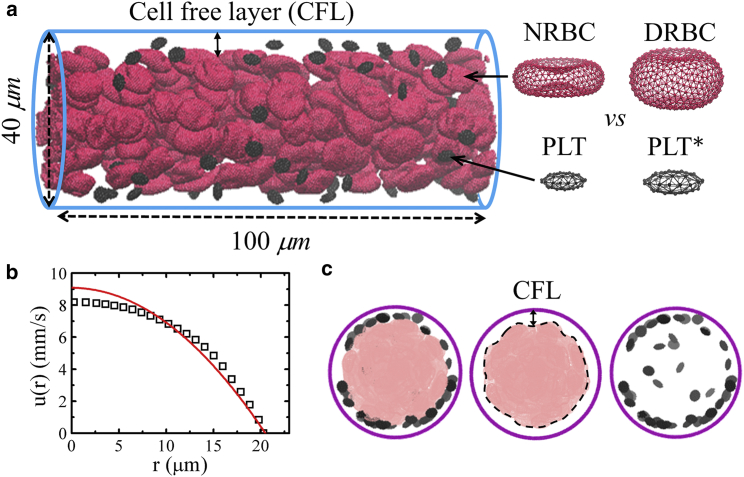
The blood flow domain is a cylindrical vessel with diameter D_t = 40 μm and periodic in the flow direction, as shown in Fig. 1 a. NRBCs in their resting form are biconcave in shape, whereas DRBCs are near oblate in shape. PLTs and PLT^∗s are both in oblate spheroid shape with AR = 0.38, but a PLT^∗ has a cell size twice the size of PLT. In this study, the volume fraction of RBCs, i.e., average hematocrit (H_ct), is varied, whereas the number of platelets in the blood is fixed at 437,000 platelets/mm³ (128,000–462,000 platelets/mm³ for normal blood (76)). All fluid particles and blood cells are randomly placed within the vessel for the initial condition. To drive the flow (simple fluid or blood) in the vessel, we apply a constant body force to each DPD particle in the flow direction. The simulations are performed for sufficient time to achieve steady state, which is characterized by a time-independent fully developed velocity profile, i.e., a plug-like profile for blood. In this study, the time to reach steady state is equal to approximately a half second in physical units. Fig. 1 b shows the time-averaged axial velocity distribution for the healthy blood at H_ct = 15%. The data is fitted with a parabolic curve (red line) that follows a plug-like characteristic. This plug-like velocity profile is due to the nonuniform distribution of RBCs in the vessel. RBCs in Poiseuille flow migrate to the vessel center forming a depleted region, the CFL, at the periphery of a vessel. A sample snapshot of NRBCs concentrated in the core region and PLTs marginated toward the wall is shown in Fig. 1 c. To vary the flowrate, we define a characteristic shear rate ${\dot{\gamma }}_w$ = 4$\overline{u}$/R_t, where $\overline{u}$ is the mean velocity and R_t is the vessel radius. ${\dot{\gamma }}_w$ corresponds to the wall shear rate of a parabolic Poiseuille flow with the same $\overline{u}$ and is varied in our simulations. In addition, the cell Reynolds number is defined based on ${\dot{\gamma }}_w$, RBC diameter (D_RBC), and the kinematic viscosity of plasma (ν), Re_cell = ${\dot{\gamma }}_w{D}_{RBC}^2$/ν ≈ 0.05, which renders the inertia effect negligible.

Figure 1.

A typical simulation setup. (a) Side view of the healthy blood flow in a vessel with diameter D_t = 40 μm and hematocrit = 15%. The cell-free layer (CFL) is evident at fully developed blood flow, red cells are deformable NRBCs with biconcave shape in their resting form, and small black cells are PLTs. Diabetic blood in a vessel is composed of DRBCs with near-oblate shape in their resting form and larger in size PLT^∗s. (b) A plug-like velocity profile is achieved, and a parabolic curve (red line) is superimposed for reference. (c) Front views of the vessel. Snapshots from left to right show the distributions of red cells and platelets at steady state. To see this figure in color, go online.

Our clinical data as well as previous studies have shown increased WBC recruitment and count in blood circulation in T2DM (49, 50, 51). In diabetics, P-selectin and intercellular adhesion molecule-1, which play important roles in the adhesion of leukocytes to endothelium, are significantly elevated in human retina and choroid (77). In addition, the rise in WBC count has been observed in our blood samples from diabetic patients (8.04 ± 2.16 k/μL) compared to control subjects (6.85 ± 1.96 k/μL) (see Table S4). We use our computational framework to investigate three different states of WBC dynamics in blood vessels: circulating in the blood stream, rolling on the wall, and adhered to the wall. For the last two states, we assume that WBCs and endothelial cells are activated and there are adhesive interactions between the receptors of WBCs and the associated ligands expressed on the endothelial surface. Depending on the type and strength of adhesive interactions, WBCs could roll or adhere on the endothelial surface. At physiological shear rates, rolling with selectin molecules (e.g., P- and E-selectins) is a prerequisite for chemoattractant-stimulated interaction of WBC integrins with endothelium intercellular adhesion molecule-1 that arrests rolling WBCs and strengthens adhesion (77, 78, 79). To simulate WBC rolling behavior, we initially place WBCs close to the wall and apply a weak conservative repulsive force between DPD particles of WBCs and the wall. To set up blood flow with adherent WBCs, we first run a short period of simulation with rolling WBCs, then freeze those DPD particles located at the interface between WBCs and the wall.

Results and Discussion

Having validated our cell transport model with in vitro experiments (53) in the Supporting Materials and Methods, here, we first present the results of healthy blood flow in a vessel and make comparisons with other numerical and experimental studies for further validation. We then study blood flow in diabetic conditions using a suspension of DRBCs and T2DM platelets with a higher MPV value (PLT^∗s). The time-averaged concentration profiles of modeled RBCs and platelets flowing through vessels are plotted for different flowrate and hematocrit values. In addition, we investigate the shape effects of platelets on their transport. Subsequently, we take into account the WBCs by including their different dynamics in our flow simulations and analyze their contributions to platelet dynamics and transport.

Flow of healthy and diabetic blood

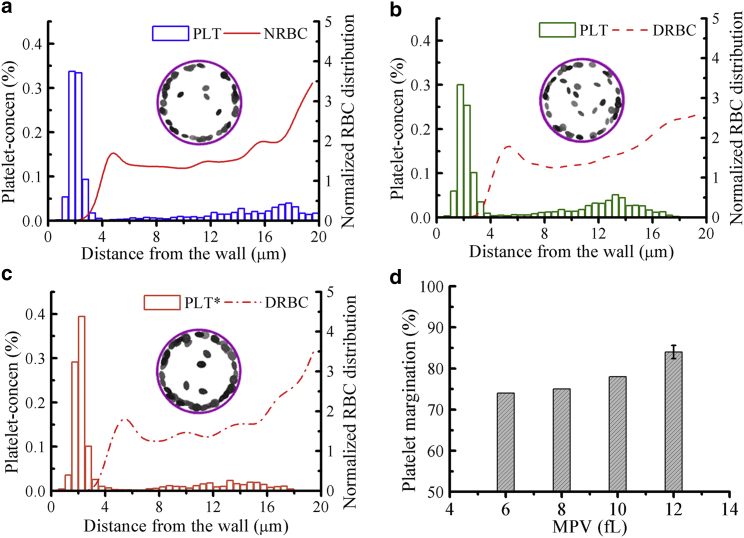
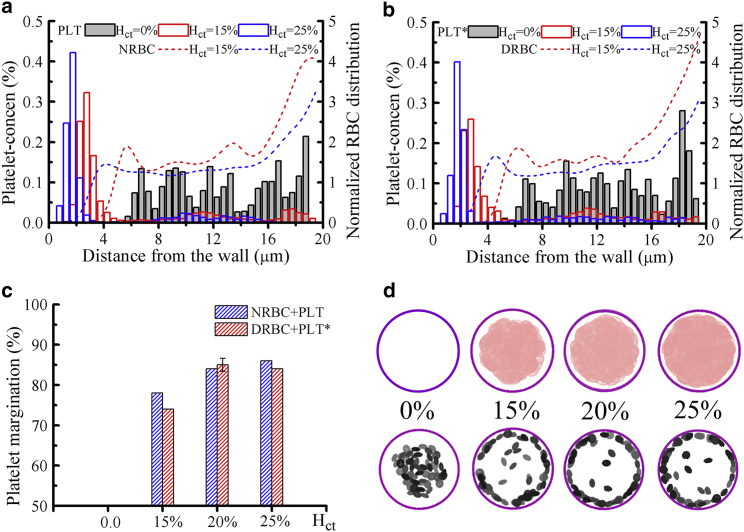
Fig. 2 shows the local concentration profiles of platelets and RBCs in the vessel (D_t = 40 μm). Here, blood is in two states, i.e., healthy or diabetic, while the wall shear rate and average hematocrit are kept fixed at ${\dot{\gamma }}_w$ = 1000 s⁻¹ and H_ct = 20%, respectively. Note that this flow condition is set based on the fact that platelets have higher near-wall presence in arterioles than in venules (27) and the mean hematocrit H_ct = 16–20% is a physiologically relevant value in small vessels (31, 80, 81). All simulations are performed for at least 3000 DPD time units (∼0.54 s) to achieve steady flow conditions, and the last 500 time units are used for the estimation of the time-averaged concentration of RBCs and platelets. These time-averaged concentration profiles are also spatially averaged along the flow direction and plotted against the radial distance from the wall. A histogram bin in the platelet concentration profile represents the number of platelets within a cylindrical shell with volume V_j (platelets/μm³) having a thickness of 0.5 μm. A cylindrical shell j has volume V_j = π(r_o² − r_i²) × L, where r_o is the outer radius, r_i is the inner radius, and L is the length of the shell, e.g., V_{j = 5} ≈ 5576 μm³ at r_o = 18.0 μm, r_i = 17.5 μm, and L = 100 μm. If the average number of platelets in the shell j = 5 is 20, then the cell-center density of platelets within the shell j = 5 is ∼0.36% (platelets/μm³). The local RBC concentration profile is the cell-center density distribution normalized with respect to the mean prescribed density in that shell (ρ_j). For example, we have 270 NRBCs, and hence ρ_j = 270 × V_j/V_t, where V_t is the total volume of the cylindrical vessel; similarly for DRBCs, for which we have 200 cells due to their larger size. Therefore, this normalized RBC distribution is adopted to eliminate the cell number difference between the modeled NRBCs and DRBCs.

Figure 2.

Difference in platelet margination between healthy and diabetic RBC + platelet suspensions. Concentration profiles of platelets and RBCs in the vessel for the cell suspensions of (a) NRBCs + PLTs, (b) DRBCs + PLTs, and (c) DRBCs + PLT^∗s. Snapshots showing the front views of vessels with platelets only at time = 0.54 s. (d) The percentage of platelet margination for platelets with different MPV values suspended in diabetic RBCs (DRBCs) and plasma. The vessel diameter D_t = 40 μm, average hematocrit H_ct = 20%, and wall shear rate ${\dot{\gamma }}_w$ = 1000 s⁻¹ remain the same for all cases. The error bar is obtained by performing three simulations with different random seeds to generate fluctuations in plasma and cell-cell interactions in the blood flow. To see this figure in color, go online.

In healthy blood flow, the distribution of NRBCs is increased around the center of the vessel, exhibiting a primary peak at the centerline and a secondary peak just outside the cell-free region (Fig. 2 a). Similar RBC distributions were found in previous studies (22, 23). A high cell density of NRBCs in the vessel center is due to the relatively small shear rate in that region, which allows a close packing of NRBCs. Away from the vessel center, the shear rate is increased, leading to the destruction of the close-packed structure of NRBCs. A peak in the distribution occurs next to the CFL, caused by the alignment of NRBCs and their cell centers that have similar radial positions. On the other hand, nondeformable PLTs are expelled by deformable NRBCs to the wall and dispersed in the CFL region. The formation of the CFL reduces the hydrodynamic resistance and also further promotes platelet margination. The CFL thickness can be determined by δ = R_t − R_core, where R_core is the average radius of the center-occupied RBC core (see also a snapshot of RBC core shown in Fig. 1 c); δ ≈ 2.75 μm is estimated for the healthy blood, with H_ct = 20% flowing through a vessel with diameter = 40 μm, which is close to that obtained by Mehrabadi et al. (42) (δ = 3 μm) for blood flowing in a channel of height = 40 μm and hematocrit = 20%. To quantify platelet margination, we define the percentage of platelet margination (ϕ_p) by the ratio of number of platelets in the cell-free region to the total number of platelets in the simulated blood. A value of ϕ_p = 84% is obtained for the NRBC and PLT suspensions flowing at ${\dot{\gamma }}_w$ = 1000 s⁻¹.

For diabetic blood flow simulation of DRBC suspensions, a relatively lower platelet concentration in the CFL and ϕ_p = 74% are observed (Fig. 2 b). The RBC deformability is crucial to the platelet transport, and the impaired deformability of DRBCs compared to NRBCs may cause weaker platelet margination toward the wall. There is in vitro evidence showing that the presence of rigid RBCs interferes with the WBC recruitment and platelet margination (82, 83). In addition, Kumar and Graham have presented a detailed analysis of the segregation mechanism incorporating binary mixtures of capsules with different rigidities by performing a computational study with the boundary integral method (84). They found that the degree of segregation increases with increasing rigidity difference between two types of capsules, which is also due to the increase in the heterogenous pair collisions between the stiff and floppy (deformable) capsules. In our study, platelet margination in T2DM RBC suspensions is found to increase when the platelet size is enlarged. As shown in the platelet concentration profiles in Fig. 2, b and c, the concentration of PLT^∗ in the CFL region is higher than that of PLT for both cases with identical hematocrit and flowrate. We also conducted a sensitivity study for the platelet transport with different MPV values (MPV = 6–12 fL) in the diabetic blood flow, confirming that the percentage of platelet margination increases monotonically with increasing MPV (Fig. 2 d). The size-dependent margination of particles in blood flow has been found in a number of experimental and computational studies (53, 85, 86, 87, 88, 89). For example, it is found that spherical microparticles (diameter > 0.5 μm) are marginated significantly more than nanoparticles (diameter < 0.5 μm), and those small-sized particles are easily trapped in the RBC core. Particle sizes close to the CFL thickness may have the optimized sizes for efficient margination and also for drug-delivery systems (90). Comparing the RBC distributions in the vessel, there is no distinct difference between the NRBC and DRBC suspensions as shown in Fig. 2, a–c. This result is also in agreement with the studies by Kumar and Graham, who showed that an alteration in the membrane rigidity of floppy capsules has minor impact on their distribution (84).

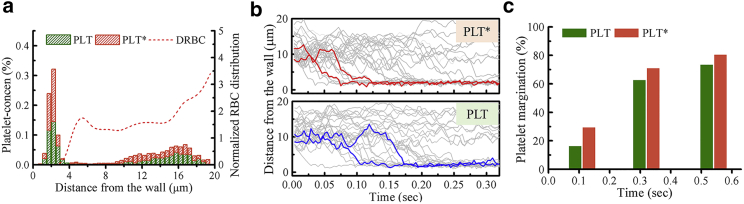
We have also performed simulations of blood flow with a binary mixture of 50% PLTs and 50% PLT^∗s suspended in DRBCs (Fig. 3). The normalized cell-center distribution of DRBCs is similar to the previous results, and the platelet concentration profile of the mixture (Fig. 3 a) exhibits a similar platelet distribution to that of Fig. 2 c, however, with relatively weaker platelet margination for which the values are somewhat in between those of Fig. 2, b and c. To compare the migration velocity of platelets, we plot the trajectories of all modeled PLTs and PLT^∗s with respect to time and highlight two representative trajectories. The blue trajectory represents the PLT, whereas the red one corresponds to the PLT^∗. Note that all platelets are initially placed away from the vessel wall with a minimal distance of 5 μm. As shown in Fig. 3 b, the larger PLT^∗s migrate to the wall faster than PLTs, and most marginated platelets show an abrupt lateral displacement once they reach closer to the edge of RBC core. This rapid margination, named “waterfall phenomenon,” was observed in other numerical simulations as well (44, 88). In addition, we estimate the transient percentage of platelet margination of two platelet sizes see (Fig. 3 c). Clearly, there is a higher tendency of margination for PLT^∗s than PLTs at the beginning ∼0.1 s, but the difference in the degree of margination becomes smaller at later times.

Figure 3.

DRBCs with a mixture of 50% PLTs and 50% PLT^∗s flowing in a vessel at ${\dot{\gamma }}_w$ = 1000 s⁻¹ and H_ct = 20%. (a) Concentration profiles of RBCs and platelets, in which the histogram plot is adopted for the platelet concentration profile. (b) The trajectories of PLTs and PLT^∗s with time. Two representative trajectories (the 4th and 10th marginated platelets) are shown in blue lines for PLT and in red lines for PLT^∗. (c) Temporal evolution of the percentage of PLT and PLT^∗ marginations based on their count. To see this figure in color, go online.

Effects of flowrate and blood hematocrit

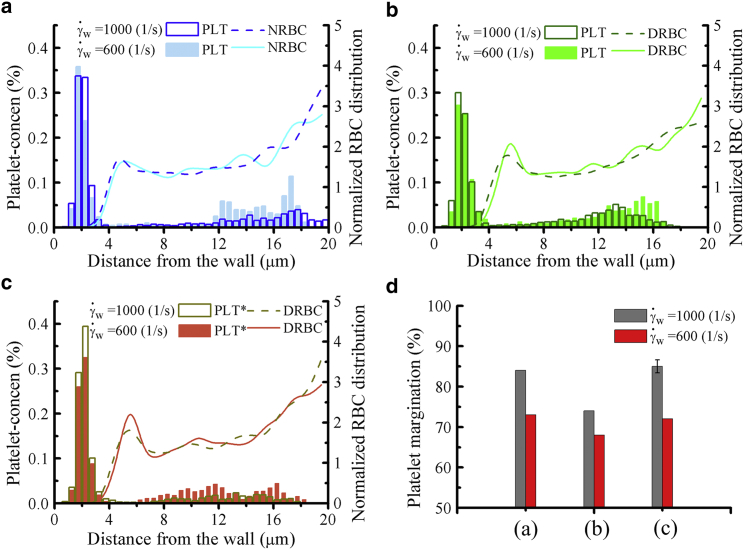
First, we investigate the effect of flowrate on RBC and platelet distributions in a vessel in which blood hematocrit H_ct = 20% is fixed for three different cell type suspensions: NRBCs+PLTs, DRBCs+PLTs and DRBCs+PLT^∗s. The RBC distribution and CFL thickness in Fig. 4, a–c seems to be independent of the variation of ${\dot{\gamma }}_w$ from 1000 s⁻¹ (previous case) to 600 s⁻¹. This is in agreement with the result of Freund et al. (80, 91) that showed the CFL thickness is independent of flowrate when the wall shear rate is high (>100 s⁻¹). Interestingly, although the normalized RBC distributions do not show significant difference at ${\dot{\gamma }}_w$ = 1000 and 600 s⁻¹, a decrease in the platelet concentration within the CFL region has been found in all blood cell suspensions. For a better comparison of the degree of platelet margination in all flow conditions, we estimate ϕ_p (see the values shown in Fig. 4 d). There is ∼6–10% decrease in ϕ_p when wall shear rate is reduced from ${\dot{\gamma }}_w$ = 1000 to 600 s⁻¹. The decrease in platelet margination with decreasing wall shear rate $\left({\dot{\gamma }}_w\right)$ is thought to be the result of reduction in the collision frequencies between RBCs and platelets. In addition, for the case of normal blood flow (NRBCs + PLTs), ϕ_p is close to the diabetic blood flow (DRBCs + PLT^∗s), and both are higher than the ϕ_p value for cell suspensions containing DRBCs and PLTs. In comparison with the normal platelets, our results indicate that the larger platelets (commonly observed in T2DM) have a stronger tendency to migrate toward the vessel wall. This observation, together with the platelets’ hyperreactivity in T2DM, could have significant contributions to increased thrombosis events in diabetic subjects.

Figure 4.

Effect of flowrate. Concentration profiles of platelets and RBCs in the vessel (D_t = 40 μm) are shown, in which cell suspensions of (a) NRBCs + PLTs, (b) DRBCs + PLTs, and (c) DRBCs + PLT^∗s with identical H_ct = 20% but at different wall shear rates ${\dot{\gamma }}_w$ = 600 and 1000 s⁻¹ are considered. (d) The percentage of marginated platelet ϕ_p is shown for all three cases. To see this figure in color, go online.

Fig. 5 shows RBC and platelet concentration profiles of normal and diabetic blood flow at different mean blood hematocrit (H_ct), where ${\dot{\gamma }}_w$ = 1000 s⁻¹. When there is no presence of RBCs (H_ct = 0%), platelets (either PLTs or PLT^∗s) are concentrated around the center of the vessel (see gray histograms in Fig. 5, a and b). This effect has also been observed in the experiments of particle transport in microchannels without RBCs (53, 92). When RBCs are introduced, the CFL is formed because of the wall-induced migration driving soft RBCs away from the wall, whereas platelets drift toward the wall because of the shear-induced diffusion caused by their heterogeneous collisions with the RBCs. The NRBC and DRBC concentration profiles in Fig. 5, a and b indicate that the RBC core is expanded and CFL thickness is decreased with increasing blood hematocrit H_ct. In addition, as H_ct increases, the near-wall peaks of platelet concentration shift toward the wall and the percentage of platelet margination (ϕ_p) increases and reaches ∼85% when H_ct ≥ 20% (see the platelet concentration profiles and ϕ_p estimated for different H_ct in Fig. 5, a–c). We also present the snapshots of diabetic blood flow with mean hematocrit from H_ct = 0 to 25% for a clear visualization of DRBCS and PLT^∗s distributions in the vessel at time = 0.54 s (Fig. 5 d).

Figure 5.

Effect of blood hematocrit at ${\dot{\gamma }}_w$ = 1000 s⁻¹. Concentration profiles of platelets and RBCs in the vessel (D_t = 40 μm) for (a) H_ct = 0% and NRBC + PLT for H_ct = 15 and 25% and (b) H_ct = 0% and DRBC + PLT^∗ for H_ct = 15 and 25%. (c) The percentage of marginated platelets ϕ_p for normal and diabetic cell suspensions at different H_ct. (d) Front views of the vessel to show the distributions of DRBCs (upper row) and PLT^∗s (lower row) are shown with H_ct = 0, 15, 20, and 25% at time = 0.54 s. To see this figure in color, go online.

Effects of platelet shape and WBC count

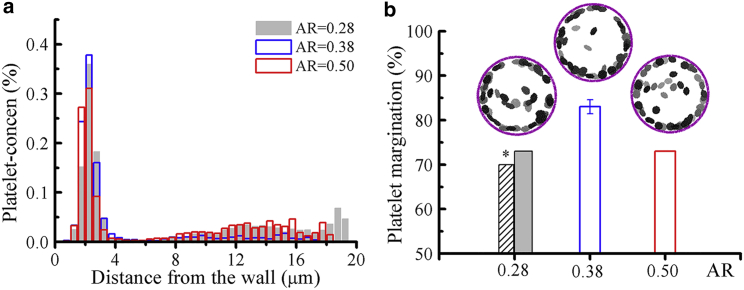
In general, an inactivated (resting) platelet has an oblate spheroid shape of AR = 0.25–0.5 (63). We further perform simulations to study the effects of platelet shape on its margination by varying the AR = 0.28, 0.38, and 0.5. Fig. 6 presents platelet concentration profiles and the percentage of platelet margination of PLT^∗ (MPV = 12 fL) for different AR values suspended in the DRBCs. It is clear that the highest near-wall concentration for PLT^∗ is achieved for AR = 0.38. The significantly flatter oblate shapes with AR = 0.28 and the tumid oblate shapes with AR = 0.5 for platelets show lower near-wall accumulations. This result has also been reported recently by Vahidkhah and Bagchi (93) for healthy blood, in which a higher margination rate was observed for moderately aspherical particles but not for the highly aspherical ones. In addition, we observe that platelets with AR = 0.28 have less margination propensity with decreasing blood hematocrit (see Fig. 6 b). Different from the hematocrit effect analysis on the margination of moderate-oblate-shaped PLT^∗s (see above), flat-oblate-shaped PLT^∗s are less sensitive to the change of blood hematocrit. Nevertheless, many studies have found higher margination and binding probabilities for particles with aspherical shape than those with spherical shape (94, 95, 96). Platelets with their naturally oblate spheroid shape are endowed with a larger contact area compared to the spherical particles of the same volume.

Figure 6.

Effect of platelet shape with ${\dot{\gamma }}_w$ = 1000 s⁻¹ and H_ct = 20%. (a) Concentration profiles of platelets in a vessel with DRBCs and PLT^∗ at different AR values. (b) The percentage of marginated platelets ϕ_p for each AR value. The histogram with ^∗ is the result for platelets with AR = 0.28 and blood hematocrit H_ct = 15%. Snapshots show the front views of vessel with different PLT^∗s suspended in DRBCs, for which H_ct = 20%. To see this figure in color, go online.

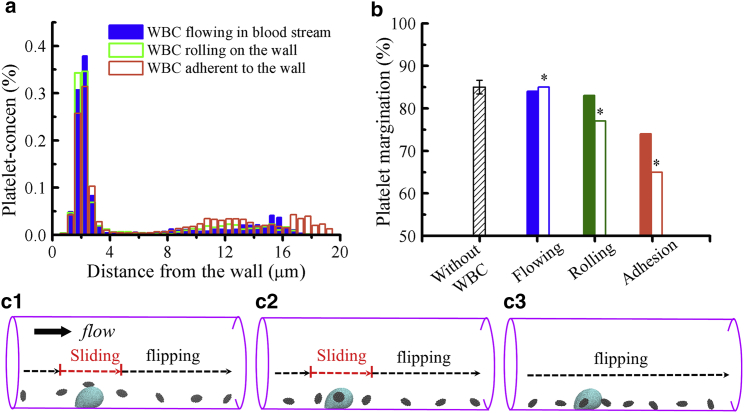
WBCs, as an important part of immune system, are subject to a recruitment process from the blood stream to a site of inflammation, followed by a number of interactions with endothelium via receptor-ligand bindings (77, 78, 79). For weak or few interactions, WBCs roll along the endothelium, whereas for strong interactions such as the integrin-mediated bonds, WBCs can be firmly attached on the endothelial surface (97). Similar to platelets, WBCs are substantially stiffer than RBCs, and their margination occurs because of the heterogeneous collisions with RBCs. WBCs margination is prominent in postcapillary venules with a characteristic of low blood flowrate in contrast to the massive number of marginated platelets extensively observed in arterioles (28). However, induced leukocyte-arterial endothelium interactions and the WBC recruitments into atherosclerotic lesions in arteries have been revealed by ex vivo experiments (98, 99).

Considering that the blood flow disturbance in small vessels may be caused by the presence of WBCs, we therefore include them into the simulations having three dynamic states often observed in blood vessels: circulating freely in the blood stream, rolling on the wall, and firm adhesion to the wall. The platelet concentration profiles and the percentage of platelet margination in Fig. 7, a and b show no clear difference in the near-wall concentration of PLT^∗s between the blood flows with freely flowing WBCs and without the presence of WBCs. However, we observe that platelet margination is impaired when WBCs emerge near the vessel wall, where more reduction in platelets margination is observed with more rolling or adherent WBCs close to the wall. The solid bars in Fig. 7 b correspond to a single WBC, whereas empty bars correspond to three WBCs in the domain. We also present three snapshots of near-wall platelet dynamics when platelets transport close to an adhered WBC (see Fig. 7 c and Videos S1, S2, and S3). The platelets that come in contact with an adhered WBC either slide from the top or on the side of the WBC, after which they undergo flipping motions (Videos S1 and S2). The platelets that move close to an adhered WBC only exhibit flipping motions in the direction of flow because of their discoid shapes (Video S3). In a flow system with adhered WBCs, platelet transport toward vessel walls is hindered because of the flow resistance induced by the adhered WBCs. However, the cell-cell contacts between platelets and WBCs might be enhanced because of the sliding motion of platelets on the surface of an adhered WBC. The sliding motion of platelets can facilitate the adhesive interactions between platelet CD62 and leukocyte P-selectin glycoprotein ligand-1, which further leads to platelet-WBC aggregations (100, 101). Here, we consider only hydrodynamic cell-cell interactions, and the effects of adhesive dynamics will be studied in our future work.

Figure 7.

Effect of WBC dynamics at ${\dot{\gamma }}_w$ = 1000 s⁻¹ and H_ct = 20%. (a) Concentration profiles of platelets in the vessel with a WBC flowing in the blood stream, rolling on the wall, and adhered to the wall are shown. (b) The percentage of marginated platelets ϕ_p in the blood flow without WBCs and with a WBC under different dynamical states, for which the ^∗ label on the histograms denotes the blood contains three WBCs. (c) Snapshots of near-wall platelet dynamics in a blood flow condition with an adhered WBC showing a representative platelet sliding on the top of the WBC (c1), sliding on the side of the WBC (c2), and flipping nearby the WBC (c3). DRBCs and PLT^∗s are used in these simulations. To see this figure in color, go online.

Conclusions

T2DM is strongly associated with the accelerated development of atherothrombosis and cardiovascular diseases (1). In this study, we perform high-fidelity blood flow simulations to investigate RBC and platelet transport in the cylindrical vessels resembling small arterioles under healthy and diabetic conditions. In particular, diabetic blood is composed of T2DM RBCs and T2DM platelets. We do not model cell-cell or cell-wall adhesive interactions to study systematically the hydrodynamic interactions that induce margination. We employ the DPD method to seamlessly model RBCs, platelets, WBCs, plasma, and the vessel wall. We first validate the DPD model using experimental data for margination of microbeads (three different sizes) in channel blood flow by Carboni et al. (53). We found that, in agreement with the experiments, margination of micro-beads increases with size and shear rate. We have introduced and validated a T2DM RBC model in our previous work (48). Here, we adopted the same red cell model for modeling the diabetic blood, whereas a T2DM platelet model is built based on the parameters informed by the clinical blood analysis of 64 diabetic patients. According to the statistical analysis for the blood characteristics, the average MPV in diabetics (10.0 ± 1.26 fL) is higher than the average MPV (9.2 ± 1.70 fL) in nondiabetics. To distinguish the platelet margination in diabetic blood from that in normal blood, we chose the extreme values of MPV = 6 fL for normal platelets and MPV = 12 fL for T2DM platelets. Similarly, for RBCs, we considered their volume (MCV) to have values close to mean value for normal blood and extreme value for diabetic blood. Our blood flow simulations show that platelet margination in whole blood is a very complex and multifactorial process, affected by the biomechanical properties of cells and their shape and size as well as blood flowrate and hematocrit. For diabetic blood flows, we found two competing effects on platelet margination: T2DM RBCs with less deformability compared to normal RBCs contribute to reduced heterogenous collisions, hence impairing platelet margination. On the other hand, T2DM platelets with higher MPV lead to increased margination. We also conducted sensitivity studies for the platelet transport with different MPV values in the diabetic blood flow and found that the percentage of platelet margination increases monotonically with increasing MPV. Similar to healthy blood flow, platelet margination in diabetic blood flow is increased with increasing flowrate and blood hematocrit. Considering the effect of platelet shape on its margination, we found that the highest near-wall accumulation of T2DM platelets are those with moderate AR. We further took into account the WBC dynamics in blood and found that WBC rolling and WBC adhesion tend to decrease platelet margination based on hydrodynamic interactions. In future work, we will include the effects of cell-cell adhesive interactions as well as cell-wall interactions, which could change some of the quantitative findings of this work. Elucidating the predictors of platelet margination and the highest near-wall accumulation of platelets in diabetics will not only allow for the creation of algorithms predicting CVD risk among diabetics but could also point to specific molecular pathways that could lend themselves to predictive or therapeutic interventions.

Author Contributions

H.-Y.C., A.Y., X.L., C.S.M., and G.E.K. conceived and designed the research. H.-Y.C. and A.Y. carried out all simulations. K.A.A.D. provided clinical data. H.-Y.C., A.Y., X.L., C.S.M., and G.E.K. analyzed the data. H.-Y.C., A.Y., X.L., C.S.M., and G.E.K. wrote the article.

Editor: Mark Alber.