Skip to main content
PMC home page
Journal of the Royal Society Interface logoLink to Journal of the Royal Society Interface
. 2018 Sep 26;15(146):20180486. doi: 10.1098/rsif.2018.0486

Accounting for residence-time in blood rheology models: do we really need non-Newtonian blood flow modelling in large arteries?

Amirhossein Arzani 1,✉
PMCID: PMC6170779  PMID: 30257924

Abstract

Patient-specific computational fluid dynamics (CFD) is a promising tool that provides highly resolved haemodynamics information. The choice of blood rheology is an assumption in CFD models that has been subject to extensive debate. Blood is known to exhibit shear-thinning behaviour, and non-Newtonian modelling has been recommended for aneurysmal flows. Current non-Newtonian models ignore rouleaux formation, which is the key player in blood's shear-thinning behaviour. Experimental data suggest that red blood cell aggregation and rouleaux formation require notable red blood cell residence-time (RT) in a low shear rate regime. This study proposes a novel hybrid Newtonian and non-Newtonian rheology model where the shear-thinning behaviour is activated in high RT regions based on experimental data. Image-based abdominal aortic and cerebral aneurysm models are considered and highly resolved CFD simulations are performed using a minimally dissipative solver. Lagrangian particle tracking is used to define a backward particle RT measure and detect stagnant regions with increased rouleaux formation likelihood. Our novel RT-based non-Newtonian model shows a significant reduction in shear-thinning effects and provides haemodynamic results qualitatively identical and quantitatively close to the Newtonian model. Our results have important implications in patient-specific CFD modelling and suggest that non-Newtonian models should be revisited in large artery flows.

Keywords: haemodynamics, computational fluid dynamics, aneurysm, wall shear stress, Lagrangian particle tracking, rouleaux formation

1. Introduction

Cardiovascular disease remains the leading cause of death in the USA [1]. Haemodynamics are believed to play a major role in cardiovascular disease progression. In the past two decades, patient-specific computational fluid dynamics (CFD) has grown to become a powerful tool in providing spatio-temporally resolved quantitative haemodynamics [2,3]. Like all physiological models, CFD models of blood flow employ several simplifying assumptions. The Newtonian blood rheology assumption is one of the popular assumptions, yet it has been subject to extensive debate and criticism in the literature. It is well known that blood exhibits shear-thinning behaviour where its viscosity increases in the low shear rate regime [4]. Shear-thinning generalized Newtonian models (commonly referred to as non-Newtonian models in the haemodynamics literature) have been proposed to model the non-Newtonian behaviour of blood [5]. At shear rates higher than 50 s−1, these models asymptote to the Newtonian limit, therefore justifying the popular Newtonian assumption in large arteries [6,7].

Although shear rate in large arteries is generally high, certain aortic conditions induce disturbance to blood flow and create recirculating and stagnant regions that are accompanied by significant reduction in shear rate. Aneurysms, localized enlargement of the vessels, represent a life threatening condition where significant disturbance is induced to the normal passage of blood. Recirculating flow, vortex structures, flow separation and flow stagnation are common features in aneurysmal flows [8–10], which enhance low shear rates and motivate non-Newtonian modelling. To this end, several studies have studied the effect of Newtonian assumption on haemodynamics in aneurysms [9,11–15] as well as other aortic flows [16–21]. These studies have often reached contradictory conclusions, and their judgement about the significance of the observed differences between the Newtonian and non-Newtonian models has sometimes been subjective. Particularly, it is not clear if these differences are significant compared to other inherent modelling errors [22].

The shear-thinning non-Newtonian models are often considered the true rheological behaviour in large arteries, yet they do not accurately model blood behaviour. These phenomenological models prescribe viscosity as a function of shear rate based on experimental results, which themselves have been obtained under certain assumptions [23]. More advanced blood rheology models have been proposed to model red blood cells (RBCs) and improve blood flow modelling. Multiphase models have been developed to model RBC and plasma transport separately where a shear-thinning viscosity is assumed for the mixture viscosity [24–26]. Other studies have used viscoelastic constitutive models to account for the elastic nature of blood [27–29].

Although these models offer an improvement over the traditional non-Newtonian models, they ignore the key player in blood shear-thinning behaviour, the ‘rouleaux’. The non-Newtonian behaviour of blood is due to RBC aggregates known as rouleaux. Interestingly, healthy RBCs in blood deprived of certain plasma proteins responsible for aggregation do not exhibit strong shear-thinning behaviour [30], even though the RBCs can deform and align. An accurate modelling of RBC aggregation requires cell-scale models such as coarse-grained molecular dynamics [31–33]. However, such models cannot be applied to large arteries due to scale disparities and the extensive computational power required. Experimental studies have shown that rouleaux formation requires a few seconds to minutes after the blood flow shear rate is abruptly dropped to zero [23,34,35]. Interestingly, rouleaux disaggregation occurs much faster once the shear rate is reapplied [23]. These experimental observations raise an important question: How likely and sustainable is rouleaux formation in large arterial flows? This immediately leads to a follow-up question: Do we really need non-Newtonian blood flow modelling in large arteries? In an intriguing article, Robertson et al. [23] have discouraged the application of current non-Newtonian blood flow models unless highly stagnant regions are observed. However, we do not yet understand the significance of non-Newtonian modelling in large diseased arteries prone to localized regions of elevated flow stagnation. This will require an appropriate definition of flow stagnation (residence-time, RT) that could be applied locally to estimate rouleaux formation time-scale, as well as a framework to develop a hybrid Newtonian and non-Newtonian model.

We hypothesize that accounting for rouleaux formation time-scale in a hybrid Newtonian and non-Newtonian model will significantly reduce the differences reported between Newtonian and traditional non-Newtonian models. To test this hypothesis, we consider one cerebral aneurysm and one abdominal aortic aneurysm (AAA) model. Aneurysms are known to promote flow stagnation, low shear rates and potentially non-Newtonian effects [9,11]. Lagrangian particle tracking is used to define a new backward particle RT measure to quantify rouleaux formation likelihood in space and time. Subsequently, a hybrid rheology model is developed where for each computational node a traditional Carreau–Yasuda (CY) non-Newtonian viscosity model is used in regions of high backward RT and a Newtonian viscosity is used in other regions. The results are compared between our novel RT based non-Newtonian model, the CY non-Newtonian model and the Newtonian model.

2. Methods

2.1. Computational fluid dynamics

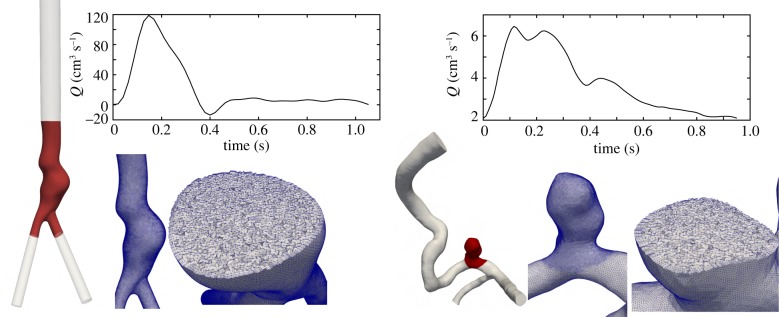
All simulations were done using Oasis [36], an open-source finite-element CFD solver developed using FEniCS [37]. FEniCS offers a flexible Python interface where the governing equations can be readily modified, which was used in the development of our novel RT-based rheology model. Oasis is a minimally dissipative, energy preserving, second-order accurate solver suitable for high-resolution transitional CFD simulations [38,39]. Oasis uses a fractional steps method using an incremental pressure correction scheme [40]. The convection term is discretized using a semi-implicit Adams–Bashforth scheme and Crank–Nicholson is used for the viscous term. Solver details are provided in [36]. Oasis solver has been validated [41] and has demonstrated superiority over normal resolution solvers used in the literature [38,42]. In this study, quadratic tetrahedral elements for velocity and linear elements for pressure (P2–P1 elements) are used to achieve high accuracy. Blood was assumed homogeneous and incompressible (ρ = 1.06 g cm−3), and rigid wall approximation was used. Pulsatile parabolic velocity profiles were prescribed at the inlet. One cerebral aneurysm and one AAA model were used as test cases (figure 1). The inlet and outlets were extended several diameters using the Vascular Modelling Toolkit (VMTK) [43] to reduce the effect of boundary conditions on the haemodynamics in the region of interest.

Figure 1.

Figure 1.

Open in a new tab

The three-dimensional computer models, corresponding computational mesh and the waveforms used as inlet boundary condition are shown (AAA model on the left and cerebral aneurysm model on the right). The highlighted red region shows the region of interest (aneurysmal region) where the RT calculation is done.

2.1.1. Cerebral aneurysm

An internal carotid artery (ICA) aneurysm model from the Aneurisk online database was selected (Aneurisk ID: C0005). A mesh was created with SimVascular [44] using tetrahedral elements with three layers of boundary layer meshing. A regional mesh refinement was used to achieve higher resolution in the aneurysmal region (figure 1). The final mesh had 3.53 M elements (second-order). In the context of typical linear elements used in most studies, our resolution corresponds to approximately 28 M elements (an order of magnitude higher than normal resolution studies in the literature [42]). A pulsatile waveform reported in a prior study [45] was scaled to match the mean flow rate reported for our selected Aneurisk ID model based on scaling laws [46]. Zero traction boundary conditions were applied at the outlets. This choice has been shown to have minimal influence on the aneurysm flow [47]. Simulation time step was selected such that the cardiac cycle was divided into 12 000 time steps. The first two cycles were ignored and the following six cycles were used for averaging the haemodynamics.

2.1.2. Abdominal aortic aneurysm

One AAA model constructed from magnetic resonance angiography and used in prior studies [10,48] was selected. The inlet of the model was set to the infrarenal level. SimVascular was used to create a computational mesh with 4.7 M tetrahedral elements and three layers of boundary layer meshing. Owing to the second-order tetrahedral elements used, our mesh corresponds to a standard linear tetrahedral mesh with approximately 37 M elements (an order of magnitude higher than most AAA studies [49,50]). Patient-specific flow rate measurements at the infrarenal artery were available [10,48] and used as inlet boundary condition. Resistance boundary conditions were imposed at the outlets to reach equal flow rate distribution at the common iliac arteries. The time step divided the cardiac cycle into 2000 time steps. The ICA time step was finer due to the Courant–Friedrichs–Lewy condition. The first two cycles were ignored and the final cardiac cycle was used in post-processing.

2.2. Residence-time based non-Newtonian model

Herein, the three rheology models are defined. First, a Newtonian rheology model is used with a constant dynamic viscosity of μN = 0.04 P. Next, the CY shear-thinning non-Newtonian model [51] is considered, which has been used in prior studies [52,53]. The CY model is defined as follows:

2.2. 2.1

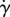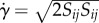where Inline graphic is an invariant of the strain rate tensor (Inline graphic).

Finally, our novel RT based non-Newtonian model is presented. The major motivation behind this model is the time-scale required for RBCs to form rouleaux structures, which are responsible for the shear-thinning behaviour of blood. According to experimental studies, once the blood shear rate is dropped from physiological shear rate to approximately zero, it requires a significant time to form aggregates [23,34,35]. The reported time-scale for normal blood is 3–5 s [34] and as high as one minute in some studies [35]. These experimental studies imply that blood not only needs low shear rate to demonstrate its strong shear-thinning behaviour, but it also needs to reside in a low shear rate region for a certain amount of time. In order to model such aggregation processes, one needs to model individual RBCs and account for their interaction with blood constituents. With the current computational power, this is not a feasible task for the spatial scale of large arteries. Therefore, it is assumed that these cells are passively advected by the flow, and we calculate RT using Lagrangian particle tracking of passive tracers. We assume that the clock for RBC aggregation starts once they enter the aneurysmal region (low shear rate region). That is, the aggregation process begins once the tracers are inside the aneurysm. This is a safe assumption since the above experimental studies measure the RBC aggregation time by setting the shear rate to approximately zero (much lower than the shear rate values inside an aneurysm). Our goal is to detect locations inside the aneurysmal region with the property that tracers entering these locations are tracers that have stayed inside the aneurysm for a long time prior to reaching that location. Such locations are likely to accompany RBCs that have spent enough time in a low shear rate region, and therefore may form rouleaux. Towards this goal, a backward particle RT is defined:

2.2. 2.2

where the initial tracer position is x(x0, t0), and the tracers are integrated backward in time to find backward trajectories x(x0, t0 − t). Γ is specified to be the aneurysmal region (red region in figure 1). We and others have used PRT in prior studies to quantify blood flow stagnation [54,55]; however, for our purpose, we need to modify this definition to backward time integration. Namely, we need to check for each spatial location at each intra-cardiac time-point to see if the tracer in that location is a tracer that has been inside the aneurysm for a long time. We use this definition as an indication of rouleaux formation likelihood. To calculate the spatio-temporal distribution of PRTbwd, tracers are seeded at each computational node at several intra-cardiac time-points (20 equally spaced intra-cardiac time-points). These tracers are integrated backward in time until they leave the pre-defined aneurysmal region where we record the integration time and map it to the initial location of tracer release. The tracers seeded on the surface nodes (no-slip wall) were perturbed in the wall normal direction to enable integration. Our calculation is based on the Newtonian model. The process is shown in figure 2.

Figure 2.

Figure 2.

Open in a new tab

Tracers are seeded on the computational nodes in the region of interest (aneurysmal region). The tracers are integrated backward in time until they leave the region of interest. Subsequently, backward RT is calculated and mapped to tracer initial location. The red dots demonstrate tracers that are initially densely seeded in the aneurysm and subsequently integrated backward in time.

To define our RT non-Newtonian model, first, we define a RT threshold required for rouleaux formation (RTth). Next, a hybrid viscosity model is defined where we assume that the viscosity is determined from the CY non-Newtonian model in high backward RT regions and from the Newtonian model in other regions:

2.2. 2.3

The time step used in CFD simulations is much smaller than the time interval for which PRTbwd is calculated. Therefore, linear interpolation is used to calculate PRTbwd at all time steps based on the pre-calculated 20 PRT time-points. Oasis was modified to model the above hybrid viscosity using pre-calculated PRTbwd values, which were computed using a customized version of an in-house code (FlowVC [56]). Different levels of RTth are prescribed on the order of reported experimental data to study the effect of this parameter.

2.3. Data post-processing

To compare the near-wall haemodynamics, we calculate time-average wall shear stress (TAWSS) and oscillatory shear index (OSI)

2.3. 2.4

and

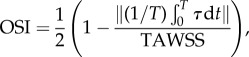2.3. 2.5

where τ is the wall shear stress vector. To quantify the variation between the non-Newtonian models and the Newtonian model, the relative point-wise difference is calculated between the haemodynamic values for all computational nodes in the region of interest.

3. Results

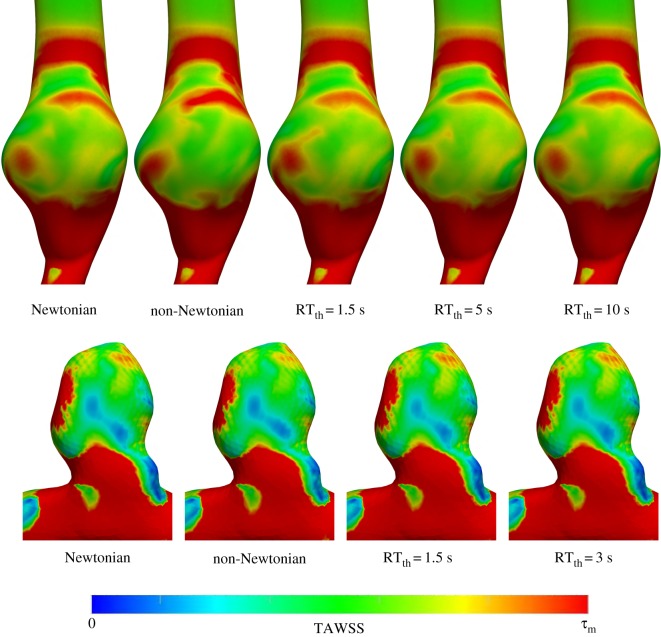
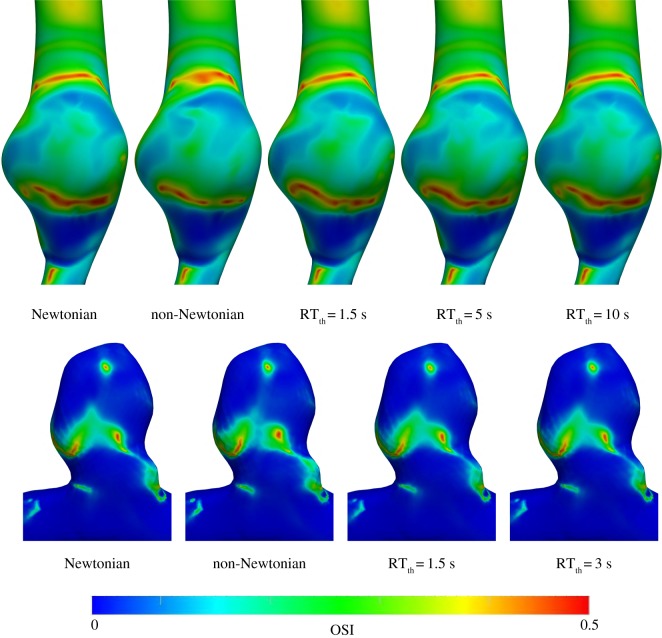
Based on reported rouleaux formation time-scales in the literature [23,34,35], RTth was varied between 1.5 s and 10 s. Namely, RT non-Newtonian simulations were carried out for RTth = 1.5, 3 s (ICA aneurysm model) and RTth = 1.5, 5, 10 s (AAA model). Lower values were used for the ICA model due to its lower RT. In this section, qualitative and quantitative comparisons between the Newtonian model and the other rheology models are presented. TAWSS and OSI results are shown in figures 3 and 4, respectively. The general qualitative features are similar in all models. As expected, with an increase in RTth, the RT non-Newtonian model becomes very similar to the Newtonian model. Differences in TAWSS qualitative patterns can hardly be detected between all of the RT non-Newtonian models and the Newtonian model. Qualitative differences in the OSI results are minor but higher than the TAWSS results.

Figure 3.

Figure 3.

Open in a new tab

TAWSS contours for the AAA (top row) and ICA aneurysm (bottom row) models. The τm value in the colour bar range is set to 0.7 and 20 Pa for the AAA and ICA aneurysm models, respectively. The different rheology models are shown in the figure.

Figure 4.

Figure 4.

Open in a new tab

OSI contours for the AAA (top row) and ICA aneurysm (bottom row) models. The different rheology models are shown in the figure.

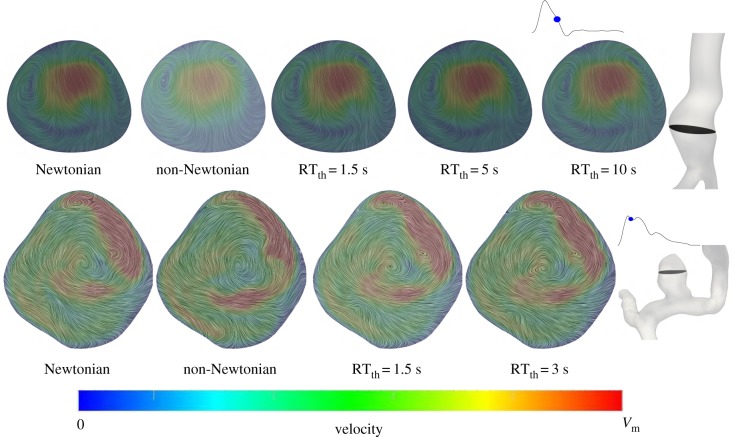
The velocity streamlines at a cross section inside the aneurysm sac are shown in figure 5. A similar observation is made where the distinctions in the velocity patterns between the RT non-Newtonian and Newtonian models are minor, and less than the differences in the CY non-Newtonian and Newtonian models. In short, the qualitative differences in haemodynamics between the Newtonian and non-Newtonian models are fairly minor and using a more realistic RT non-Newtonian model makes the qualitative patterns hardly distinguishable.

Figure 5.

Figure 5.

Open in a new tab

Velocity vectors for the AAA (top row) and ICA aneurysm (bottom row) models at the shown cross sections and intra-cardiac time-points. Surface streamlines of the velocity vectors projected to the cross section are shown. The streamlines are coloured based on the total velocity vector. The Vm value in the colour bar range is set to 4 and 10 m s−1 for the AAA and ICA aneurysm models, respectively. The different rheology models are shown in the figure.

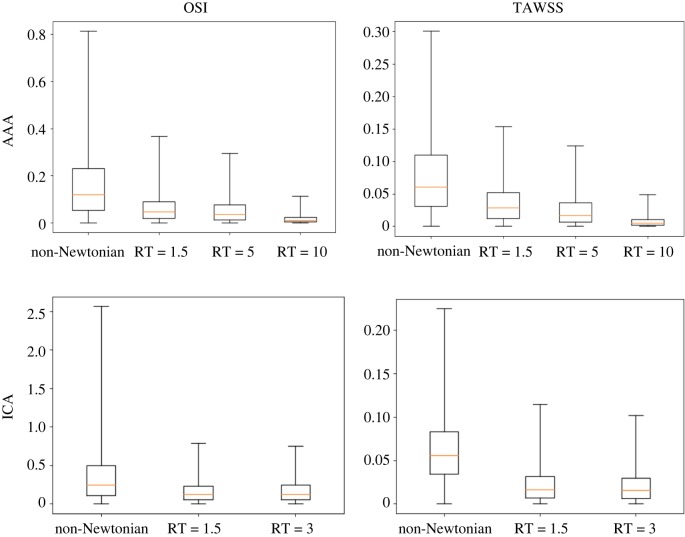
To study the quantitative difference between all of the non-Newtonian models and the Newtonian model, the point-wise relative difference was calculated for all of the computational nodes in the region of interest (red region in figure 1). That is, the Newtonian model is taken as reference, and the relative change in haemodynamics between this model and all of the other models is quantified. The results shown in figure 6 demonstrate a significant decrease in quantitative differences between the Newtonian and RT non-Newtonian models when compared with the differences between the Newtonian and CY non-Newtonian model. The variation in OSI is higher than TAWSS with the 99th percentile relative differences in the ICA aneurysm model reaching as high as 250% and 80% for the CY non-Newtonian and RT non-Newtonian models, respectively.

Figure 6.

Figure 6.

Open in a new tab

Box plots of the relative point-wise change (|τ1 − τ2|/τ2) between the Newtonian model (reference model) and the other rheological models for the OSI and TAWSS results in the AAA (top row) and ICA aneurysm (bottom row) models. The median, first and third quartiles are shown in the box plots. The whiskers correspond to the minimum and 99th percentile of the data. The plots are created based on all of the computational nodes in the aneurysmal region. (Online version in colour.)

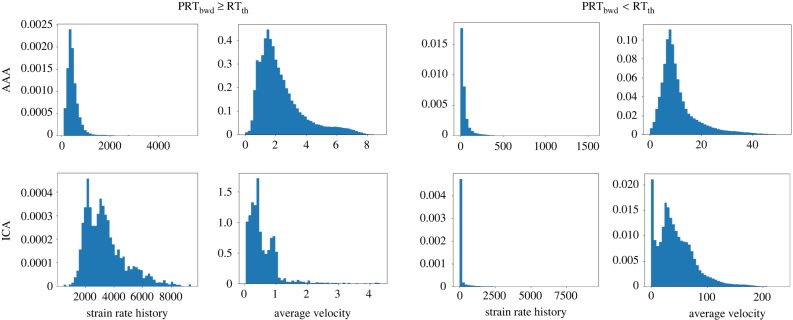
Probability density histograms of the strain rate history and average velocity experienced by tracers are shown in figure 7. To distinguish between the tracers that meet the RT threshold and tracers that do not meet the threshold, two sets of histograms are shown. Strain rate history is defined as the Lagrangian integral of Frobenius norm of the strain rate tensor (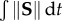Inline graphic). This definition is identical to the platelet activation potential measure used in prior studies [57]. Average velocity is defined as the average velocity that each tracer experiences along its path inside the region of interest. The histograms show that tracers meeting the RT threshold are more likely to experience higher accumulated strain rates and lower average velocities.

Figure 7.

Figure 7.

Open in a new tab

Probability density histograms of the strain rate history (integrated Frobenius norm of the strain rate tensor along each trajectory) and average velocity (average velocity experienced by each trajectory) for tracers that meet the RT threshold (left panels) and do not meet the RT threshold (right panels). The histograms are based on all of the tracers released at different time-points. The AAA (top row) and ICA aneurysm (bottom row) results are shown. The RT threshold used is RTth = 5 s for the AAA and RTth = 1.5 s for the ICA aneurysm model. Strain rate history (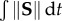Inline graphic) is dimensionless and the unit for velocity is cm s−1. (Online version in colour.)

4. Discussion

This study proposed a novel RT-based non-Newtonian model to account for the rouleaux formation time-scale in image-based CFD models. Our model is a significant improvement over traditional non-Newtonian models that assume a strong shear-thinning behaviour. Blood's strong shear-thinning behaviour is due to rouleaux formation, which requires significant flow stagnation [23]. To the best of our knowledge, our study is the first study to propose a hybrid rheology model where the strong shear-thinning behaviour is only activated in regions with considerably high flow stagnation. The important motivation behind our study is that regions of low shear rate do not necessarily imply high flow stagnation. Shear rate is an instantaneous Eulerian measure that cannot quantify transport properties [58]. A Lagrangian backward particle RT measure is proposed that identifies temporally varying points inside an aneurysm with the property that trajectories visiting these points have travelled for a long time inside the aneurysmal region (low shear rate region) before reaching that point. These high RT points are likely to accompany rouleaux structures because RBCs have had ample time to form aggregates.

The major finding from our study is that traditional shear-thinning non-Newtonian models used in the literature exaggerate the non-Newtonian behaviour of blood. Our RT non-Newtonian model reduced the strong non-Newtonian behaviour and produced results qualitatively indistinguishable and quantitatively closer to the Newtonian model. This has very important implications in patient-specific CFD simulations of blood flow and suggests that caution must be made when performing non-Newtonian blood flow modelling. Based on our new model, we suggest that researchers take the following steps:

  • (1) Check to ensure that their region of interest is accompanied by notable regions with low shear rate (lower than 50 s−1).

  • (2) Quantify the spatio-temporal distribution of backward RT to detect regions accompanied by RT higher than the experimentally reported values for rouleaux formation.

  • (3) If the majority of the domain is accompanied by high backward RT, then use a traditional non-Newtonian model. If a small to moderate percentage of the domain is accompanied by high backward RT, then use the proposed RT non-Newtonian model. Finally, if a minor portion of the domain (or none) is accompanied by high RT, then use a purely Newtonian model.

Another interesting finding from our study is the strong qualitative similarity between the CY non-Newtonian and Newtonian models. Quantitatively, the high differences were limited to the OSI measure and did not occur in the majority of the domain. Our study was based on a minimally dissipative code with a spatial and temporal resolution of an order of magnitude higher than what is traditionally used in the literature. These high-resolution solution strategies have recently been used in cerebral aneurysms using Oasis (the same CFD code used here) [15,38,42]. Interestingly, these high-resolution models have shown that the Newtonian rheology assumption has a much smaller effect on the haemodynamics compared to the solution strategy and boundary conditions [15]. It is likely that the normal-resolution solution strategies in the literature accompany artificial numerical diffusion that dissipates the flow, reduces shear rate, and therefore amplifies the non-Newtonian effects. Our high-resolution results support this but add rouleaux formation time-scale, the key player in blood's non-Newtonian behaviour, which has been overlooked in prior patient-specific CFD studies.

Regions of high particle RT typically occur near the vessel wall where the velocity is close to zero due to the no-slip condition. Interestingly, the near-wall regions usually have high shear rate, therefore reducing the shear-thinning effects, even though the flow stagnation can be high. To enable PRT calculation on surface nodes, these tracers were perturbed into the domain. It is noteworthy that accurate three-dimensional particle tracking immediately next to the vessel wall is a numerically challenging task [59]. A small inward wall-normal velocity needs to be prescribed on the vessel wall to avoid tracers sticking on the wall. Also, diffusion effects can become important next to the wall [59]. It is likely that our three-dimensional particle tracking method underestimates PRT immediately next to the vessel wall. It remains to be investigated how significant the non-Newtonian effects will be in this extremely thin region with potentially high shear rates.

It is important to note that even though our model shows a significant reduction in non-Newtonian effects, it may be perceived that our model still overestimates the non-Newtonian behaviour. We assumed that RBC aggregates start to form as soon as they are inside the aneurysmal region. In correspondence with the experimental studies discussed above, this implies that the aneurysmal region should have zero shear rate to make the correspondence accurate, but we know that the shear rates are not necessarily zero and sometimes even high shear rates emerge. Therefore, it is likely that we are underestimating the rouleaux formation time-scale, and therefore overestimating the non-Newtonian effects. The observation that RBC disaggregation occurs much faster than aggregation [23] further supports this conjecture. A more accurate model needs to track the shear rate history of advected tracers (similar to Lagrangian platelet activation potential measures [57,60,61]). The shear rate history for our data is reported in figure 7. However, for such models to become useful, experimental studies need to provide us with quantitative information about rouleaux formation time-scale when RBCs experience a certain shear rate history as opposed to suddenly being exposed to zero shear rate.

Our study is based on simplifying assumptions and modelling improvements are possible. Our model assumes that in the absence of rouleaux structures blood exhibits a purely Newtonian behaviour. This is not necessarily true and weak shear-thinning behaviour is possible due to RBC deformation [30]. However, 92% of blood shear-thinning behaviour requires aggregation, and the weak shear-thinning behaviour itself might also require a specific time-scale [23]. Nevertheless, assuming a weak shear-thinning model instead of constant viscosity might improve our rheology model. Polymer network theory has been used to develop advanced constitutive models for rouleaux formation and breakage [62,63]. Incorporation of such models into our framework can improve our purely phenomenological model. The PRT calculation in our study was based on the Newtonian model. A more accurate strategy is to modify the PRT results based on the RT non-Newtonian model in an iterative procedure. Additionally, our model activates non-Newtonian behaviour based on a hard PRT threshold. A probabilistic approach where non-Newtonian behaviour depends on PRT based on a stochastic model will likely offer improvements. Our study is based on two aneurysm models. Different aneurysm morphologies can create different flow patterns, and therefore our new model needs to be tested in more geometries. Nevertheless, the general conclusions are likely to remain unchanged. That is, accounting for rouleaux formation time-scale in non-Newtonian models reduces the non-Newtonian effects. The precise amount of this reduction will depend on patient-specific morphology and flow rates, and it is possible that some aneurysm models promote rouleaux formation and the non-Newtonian effects become more pronounced than the models studied here. Finally, our results need to be validated with carefully collected experimental data. This will likely be a challenging task. In vitro blood flow measurements in large arteries have been carried out using particle image velocimetry to study shear-thinning effects [64]. However, these studies use blood-analogue fluids that cannot model RBC aggregation and rouleaux formation. In vivo blood flow measurement techniques such as four-dimensional flow magnetic resonance imaging [65] offer an alternative strategy; however, it is not clear if the differences between our non-Newtonian and Newtonian models are meaningful when compared to inherent in vivo measurement errors.

5. Conclusion

We have developed a new non-Newtonian model to account for rouleaux formation time-scale in blood shear-thinning behaviour. It was demonstrated that current shear-thinning non-Newtonian models in the literature overestimate the non-Newtonian effects. Our highly resolved simulations using a minimally dissipative solver in one image-based cerebral aneurysm and one AAA model showed that activating shear-thinning behaviour only in regions of high flow stagnation produces haemodynamics qualitatively similar and quantitatively closer to the Newtonian model. In short, this study suggests that current non-Newtonian blood flow models in large arteries should be revisited, and the Newtonian model is likely appropriate for haemodynamics calculation in aneurysms unless significant regions of high backward RT coexisting with low shear rates are identified.

Supplementary Material

AAA STL file
rsif20180486supp1.zip (3.2MB, zip)

Acknowledgments

The author thanks Dr Shawn Shadden for a fruitful discussion related to this study. High-performance computing support from Northern Arizona University's high-performance computing staff and Monsoon cluster is acknowledged.

Data accessibility

All of the data and codes used to perform this study are publicly available. Oasis (CFD solver) is an open-source code that can be accessed (https://github.com/mikaem/Oasis). FlowVC (used for particle RT calculation) is also publicly available (http://shaddenlab.berkeley.edu/software.html). The cerebral aneurysm model used in this study was obtained from the publicly available AneuriskWeb database (http://ecm2.mathcs.emory.edu/aneuriskweb/index) with the Aneurisk ID of C0005. The AAA model is uploaded as part of the electronic supplementary material.

Competing interests

The author has no competing interests.

Funding

This work was supported by a startup fund from Northern Arizona University.

References

  • 1.Benjamin EJ. et al. 2018. Heart disease and stroke statistics 2018 update: a report from the American Heart Association. Circulation 137, e67–e492. ( 10.1161/CIR.0000000000000558) [DOI] [PubMed] [Google Scholar]
  • 2.Taylor CA, Figueroa CA. 2009. Patient-specific modeling of cardiovascular mechanics. Annu. Rev. Biomed. Eng. 11, 109–134. ( 10.1146/annurev.bioeng.10.061807.160521) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Taylor CA, Steinman DA. 2010. Image-based modeling of blood flow and vessel wall dynamics: applications, methods and future directions. Ann. Biomed. Eng. 38, 1188–1203. ( 10.1007/s10439-010-9901-0) [DOI] [PubMed] [Google Scholar]
  • 4.Fung YC. 2013. Biomechanics: mechanical properties of living tissues. Berlin, Germany: Springer Science & Business Media. [Google Scholar]
  • 5.Yilmaz F, Gundogdu MY. 2008. A critical review on blood flow in large arteries; relevance to blood rheology, viscosity models, and physiologic conditions. Korea-Australia Rheol. J. 20, 197–211. [Google Scholar]
  • 6.Stuart J, Kenny MW. 1980. Blood rheology. J. Clin. Pathol. 33, 417 ( 10.1136/jcp.33.5.417) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Long DS, Smith ML, Pries AR, Ley K, Damiano ER. 2004. Microviscometry reveals reduced blood viscosity and altered shear rate and shear stress profiles in microvessels after hemodilution. Proc. Natl Acad. Sci. USA 101, 10 060–10 065. ( 10.1073/pnas.0402937101) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Salsac AV, Sparks SR, Chomaz JM, Lasheras JC. 2006. Evolution of the wall shear stresses during the progressive enlargement of symmetric abdominal aortic aneurysms. J. Fluid Mech. 560, 19–52. ( 10.1017/s002211200600036x) [DOI] [Google Scholar]
  • 9.Rayz VL, Boussel L, Lawton MT, Acevedo-Bolton G, Ge L, Young WL, Higashida RT, Saloner D. 2008. Numerical modeling of the flow in intracranial aneurysms: prediction of regions prone to thrombus formation. Ann. Biomed. Eng. 36, 1793–1804. ( 10.1007/s10439-008-9561-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Arzani A, Shadden SC. 2012. Characterization of the transport topology in patient-specific abdominal aortic aneurysm models. Phys. Fluids 24, 081901 ( 10.1063/1.4744984) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Khanafer KM, Gadhoke P, Berguer R, Bull JL. 2006. Modeling pulsatile flow in aortic aneurysms: effect of non-Newtonian properties of blood. Biorheology 43, 661–679. [PubMed] [Google Scholar]
  • 12.Biasetti J, Hussain F, Gasser TC. 2011. Blood flow and coherent vortices in the normal and aneurysmatic aortas: a fluid dynamical approach to intra-luminal thrombus formation. J. R. Soc. Interface 8, 1449–1461. ( 10.1098/rsif.2011.0041) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Morales HG, Larrabide I, Geers AJ, Aguilar ML, Frangi AF. 2013. Newtonian and non-Newtonian blood flow in coiled cerebral aneurysms. J. Biomech. 46, 2158–2164. ( 10.1016/j.jbiomech.2013.06.034) [DOI] [PubMed] [Google Scholar]
  • 14.Marrero VL, Tichy JA, Sahni O, Jansen KE. 2014. Numerical study of purely viscous non-Newtonian flow in an abdominal aortic aneurysm. J. Biomech. Eng. 136, 101001 ( 10.1115/1.4027488) [DOI] [PubMed] [Google Scholar]
  • 15.Khan MO, Steinman DA, Valen-Sendstad K. 2017. Non-Newtonian versus numerical rheology: practical impact of shear-thinning on the prediction of stable and unstable flows in intracranial aneurysms. Int. J. Numer. Method. Biomed. Eng. 33, e2836 ( 10.1002/cnm.2836) [DOI] [PubMed] [Google Scholar]
  • 16.Gijsen FJH, van de Vosse FN, Janssen JD. 1999. The influence of the non-Newtonian properties of blood on the flow in large arteries: steady flow in a carotid bifurcation model. J. Biomech. 32, 601–608. ( 10.1016/s0021-9290(99)00015-9) [DOI] [PubMed] [Google Scholar]
  • 17.O'Callaghan S, Walsh M, McGloughlin T. 2006. Numerical modelling of Newtonian and non-Newtonian representation of blood in a distal end-to-side vascular bypass graft anastomosis. Med. Eng. Phys. 28, 70–74. ( 10.1016/j.medengphy.2005.04.001) [DOI] [PubMed] [Google Scholar]
  • 18.Razavi A, Shirani E, Sadeghi MR. 2011. Numerical simulation of blood pulsatile flow in a stenosed carotid artery using different rheological models. J. Biomech. 44, 2021–2030. ( 10.1016/j.jbiomech.2011.04.023) [DOI] [PubMed] [Google Scholar]
  • 19.Morbiducci U, Gallo D, Massai D, Ponzini R, Deriu MA, Antiga L, Redaelli A, Montevecchi FM. 2011. On the importance of blood rheology for bulk flow in hemodynamic models of the carotid bifurcation. J. Biomech. 44, 2427–2438. ( 10.1016/j.jbiomech.2011.06.028) [DOI] [PubMed] [Google Scholar]
  • 20.Molla MM, Paul MC. 2012. LES of non-Newtonian physiological blood flow in a model of arterial stenosis. Med. Eng. Phys. 34, 1079–1087. ( 10.1016/j.medengphy.2011.11.013) [DOI] [PubMed] [Google Scholar]
  • 21.Khan MO, Valen-Sendstad K, Steinman DA. In press Direct numerical simulation of laminar-turbulent transition in a non-axisymmetric stenosis model for Newtonian vs. shear-thinning non-Newtonian rheologies. Flow Turbul. Combust. ( 10.1007/s10494-018-9905-7) [DOI] [Google Scholar]
  • 22.Steinman DA. 2012. Assumptions in modelling of large artery hemodynamics. In Modeling of physiological flows, vol. 5 (eds Ambrosi D, Quarteroni A, Rozza G), pp. 1–18. Milan, Italy: Springer. [Google Scholar]
  • 23.Robertson AM, Sequeira A, Kameneva MV. 2008. Hemorheology. In Hemodynamical flows (eds Galdi GP, Robertson AM, Rannacher R, Turek S), pp. 63–120. Basel, Switzerland: Birkhauser. [Google Scholar]
  • 24.Jung J, Lyczkowski RW, Panchal CB, Hassanein A. 2006. Multiphase hemodynamic simulation of pulsatile flow in a coronary artery. J. Biomech. 39, 2064–2073. ( 10.1016/j.jbiomech.2005.06.023) [DOI] [PubMed] [Google Scholar]
  • 25.Wen J, Liu K, Khoshmanesh K, Jiang W, Zheng T. 2015. Numerical investigation of haemodynamics in a helical-type artery bypass graft using non-Newtonian multiphase model. Comput. Methods Biomech. Biomed. Eng. 18, 760–768. ( 10.1080/10255842.2013.845880) [DOI] [PubMed] [Google Scholar]
  • 26.Wu WT, Li Y, Aubry N, Massoudi M, Antaki JF. 2017. Numerical simulation of red blood cell-induced platelet transport in saccular aneurysms. Appl. Sci. 7, 484 ( 10.3390/app7050484) [DOI] [Google Scholar]
  • 27.Bodnár T, Sequeira A, Prosi M. 2011. On the shear-thinning and viscoelastic effects of blood flow under various flow rates. Appl. Math. Comput. 217, 5055–5067. ( 10.1016/j.amc.2010.07.054) [DOI] [Google Scholar]
  • 28.Good BC, Deutsch S, Manning KB. 2016. Hemodynamics in a pediatric ascending aorta using a viscoelastic pediatric blood model. Ann. Biomed. Eng. 44, 1019–1035. ( 10.1007/s10439-015-1370-z) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Menut M. et al. 2018. Comparison between a generalized Newtonian model and a network-type multiscale model for hemodynamic behavior in the aortic arch: validation with 4D MRI data for a case study. J. Biomech. 73, 119–126. ( 10.1016/j.jbiomech.2018.03.038) [DOI] [PubMed] [Google Scholar]
  • 30.Chien S. 1970. Shear dependence of effective cell volume as a determinant of blood viscosity. Science 168, 977–979. ( 10.1126/science.168.3934.977) [DOI] [PubMed] [Google Scholar]
  • 31.Li X, Vlahovska PM, Karniadakis GE. 2013. Continuum- and particle-based modeling of shapes and dynamics of red blood cells in health and disease. Soft Matter 9, 28–37. ( 10.1039/c2sm26891d) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Lei H, Fedosov DA, Caswell B, Karniadakis GE. 2013. Blood flow in small tubes: quantifying the transition to the non-continuum regime. J. Fluid Mech. 722, 214–239. ( 10.1017/jfm.2013.91) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Li X, Peng Z, Lei H, Dao M, Karniadakis GE. 2014. Probing red blood cell mechanics, rheology and dynamics with a two-component multi-scale model. Phil. Trans. R. Soc. A 372, 20130389 ( 10.1098/rsta.2013.0389) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Schmid-Schönbein H, Volger E, Klose HJ. 1972. Microrheology and light transmission of blood. Pflügers Archiv 333, 140–155. ( 10.1007/BF00586913) [DOI] [PubMed] [Google Scholar]
  • 35.Gaspar-Rosas A, Thurston GB. 1988. Erythrocyte aggregate rheology by transmitted and reflected light. Biorheology 25, 471–487. ( 10.3233/BIR-1988-25308) [DOI] [PubMed] [Google Scholar]
  • 36.Mortensen M, Valen-Sendstad K. 2015. Oasis: a high-level/high-performance open source Navier–Stokes solver. Comput. Phys. Commun. 188, 177–188. ( 10.1016/j.cpc.2014.10.026) [DOI] [Google Scholar]
  • 37.Logg A, Mardal KA, Wells G. 2012. Automated solution of differential equations by the finite element method, vol. 84 Berlin, Germany: Springer. [Google Scholar]
  • 38.Valen-Sendstad K, Steinman DA. 2014. Mind the gap: impact of computational fluid dynamics solution strategy on prediction of intracranial aneurysm hemodynamics and rupture status indicators. Am. J. Neuroradiol. 35, 536–543. ( 10.3174/ajnr.A3793) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Khan MO, Chnafa C, Gallo D, Molinari F, Morbiducci U, Steinman DA, Valen-Sendstad K. 2017. On the quantification and visualization of transient periodic instabilities in pulsatile flows. J. Biomech. 52, 179–182. ( 10.1016/j.jbiomech.2016.12.037) [DOI] [PubMed] [Google Scholar]
  • 40.Simo JC, Armero F. 1994. Unconditional stability and long-term behavior of transient algorithms for the incompressible Navier-Stokes and euler equations. Comput. Methods. Appl. Mech. Eng. 111, 111–154. ( 10.1016/0045-7825(94)90042-6) [DOI] [Google Scholar]
  • 41.Berg P. et al. 2015. The computational fluid dynamics rupture challenge 2013. Phase II: variability of hemodynamic simulations in two intracranial aneurysms. J. Biomech. Eng. 137, 121008 ( 10.1115/1.4031794) [DOI] [PubMed] [Google Scholar]
  • 42.Khan MO, Valen-Sendstad K, Steinman DA. 2015. Narrowing the expertise gap for predicting intracranial aneurysm hemodynamics: impact of solver numerics versus mesh and time-step resolution. Am. J. Neuroradiol. 36, 1310–1316. ( 10.3174/ajnr.A4263) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Antiga L, Piccinelli M, Botti L, Ene-Iordache B, Remuzzi A, Steinman DA. 2008. An image-based modeling framework for patient-specific computational hemodynamics. Med. Biol. Eng. Comput. 46, 1097–1112. ( 10.1007/s11517-008-0420-1) [DOI] [PubMed] [Google Scholar]
  • 44.Updegrove A, Wilson NM, Merkow J, Lan H, Marsden AL, Shadden SC. 2017. Simvascular: an open source pipeline for cardiovascular simulation. Ann. Biomed. Eng. 45, 525–541. ( 10.1007/s10439-016-1762-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Hoi Y, Wasserman BA, Xie YJ, Najjar SS, Ferruci L, Lakatta EG, Gerstenblith G, Steinman DA. 2010. Characterization of volumetric flow rate waveforms at the carotid bifurcations of older adults. Physiol. Meas. 31, 291–302. ( 10.1088/0967-3334/31/3/002) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Valen-Sendstad K, Piccinelli M, KrishnankuttyRema R, Steinman DA. 2015. Estimation of inlet flow rates for image-based aneurysm CFD models: where and how to begin? Ann. Biomed. Eng. 43, 1422–1431. ( 10.1007/s10439-015-1288-5) [DOI] [PubMed] [Google Scholar]
  • 47.Baek H, Jayaraman MV, Richardson PD, Karniadakis GE. 2009. Flow instability and wall shear stress variation in intracranial aneurysms. J. R. Soc. Interface 47, 967–988. ( 10.1098/rsif.2009.0476) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Les AS, Shadden SC, Figueroa CA, Park JM, Tedesco MM, Herfkens RJ, Dalman RL, Taylor CA. 2010. Quantification of hemodynamics in abdominal aortic aneurysms during rest and exercise using magnetic resonance imaging and computational fluid dynamics. Ann. Biomed. Eng. 38, 1288–1313. ( 10.1007/s10439-010-9949-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Arzani A, Suh GY, Dalman RL, Shadden SC. 2014. A longitudinal comparison of hemodynamics and intraluminal thrombus deposition in abdominal aortic aneurysms. Am. J. Physiol. Heart Circul. Physiol. 307, H1786–H1795. ( 10.1152/ajpheart.00461.2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Zambrano BA, Gharahi H, Lim C, Jaberi FA, Choi J, Lee W, Baek S. 2016. Association of intraluminal thrombus, hemodynamic forces, and abdominal aortic aneurysm expansion using longitudinal CT images. Ann. Biomed. Eng. 44, 1502–1514. ( 10.1007/s10439-015-1461-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Cho YI, Kensey KR. 1991. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1. Steady flows. Biorheology 28, 241–262. ( 10.3233/BIR-1991-283-415) [DOI] [PubMed] [Google Scholar]
  • 52.Fisher C, Rossmann JS. 2009. Effect of non-Newtonian behavior on hemodynamics of cerebral aneurysms. J. Biomech. Eng. 131, 091004 ( 10.1115/1.3148470) [DOI] [PubMed] [Google Scholar]
  • 53.Weddell JC, Kwack J, Imoukhuede PI, Masud A. 2015. Hemodynamic analysis in an idealized artery tree: differences in wall shear stress between Newtonian and non-Newtonian blood models. PLoS ONE 10, e0124575 ( 10.1371/journal.pone.0124575) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Suh GY, Les AS, Tenforde AS, Shadden SC, Spilker RL, Yeung JJ, Cheng CP, Herfkens RJ, Dalman RL, Taylor CA. 2011. Quantification of particle residence time in abdominal aortic aneurysms using magnetic resonance imaging and computational fluid dynamics. Ann. Biomed. Eng. 39, 864–883. ( 10.1007/s10439-010-0202-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Arzani A, Les AS, Dalman RL, Shadden SC. 2014. Effect of exercise on patient specific abdominal aortic aneurysm flow topology and mixing. Int. J. Numer. Methods Biomed. Eng. 30, 280–295. ( 10.1002/cnm.2601) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 56.Shadden SC. 2010. FlowVC. See http://shaddenlab.berkeley.edu/software/.
  • 57.Shadden SC, Hendabadi S. 2013. Potential fluid mechanic pathways of platelet activation. Biomech. Model. Mechanobiol. 12, 467–474. ( 10.1007/s10237-012-0417-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 58.Shadden SC, Arzani A. 2015. Lagrangian postprocessing of computational hemodynamics. Ann. Biomed. Eng. 43, 41–58. ( 10.1007/s10439-014-1070-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 59.Arzani A, Gambaruto AM, Chen G, Shadden SC. 2016. Lagrangian wall shear stress structures and near-wall transport in high-Schmidt-number aneurysmal flows. J. Fluid Mech. 790, 158–172. ( 10.1017/jfm.2016.6) [DOI] [Google Scholar]
  • 60.Alemu Y, Bluestein D. 2007. Flow-induced platelet activation and damage accumulation in a mechanical heart valve: numerical studies. Artif. Organs 31, 677–688. ( 10.1111/j.1525-1594.2007.00446.x) [DOI] [PubMed] [Google Scholar]
  • 61.Hansen KB, Arzani A, Shadden SC. 2015. Mechanical platelet activation potential in abdominal aortic aneurysms. J. Biomech. Eng. 137, 041005 ( 10.1115/1.4029580) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 62.Owens RG. 2006. A new microstructure-based constitutive model for human blood. J. Non-Newton. Fluid Mech. 140, 57–70. ( 10.1016/j.jnnfm.2006.01.015) [DOI] [Google Scholar]
  • 63.Tsimouri IC, Stephanou PS, Mavrantzas VG. 2018. A constitutive rheological model for agglomerating blood derived from nonequilibrium thermodynamics. Phys. Fluids 30, 030710 ( 10.1063/1.5016913) [DOI] [Google Scholar]
  • 64.Deplano V, Knapp YK, Bailly L, Bertrand E. 2014. Flow of a blood analogue fluid in a compliant abdominal aortic aneurysm model: experimental modelling. J. Biomech. 47, 1262–1269. ( 10.1016/j.jbiomech.2014.02.026) [DOI] [PubMed] [Google Scholar]
  • 65.Markl M, Frydrychowicz A, Kozerke S, Hope M, Wieben O. 2012. 4D flow MRI. J. Magn. Reson. Imaging 36, 1015–1036. ( 10.1002/jmri.23632) [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

AAA STL file
rsif20180486supp1.zip (3.2MB, zip)

Data Availability Statement

All of the data and codes used to perform this study are publicly available. Oasis (CFD solver) is an open-source code that can be accessed (https://github.com/mikaem/Oasis). FlowVC (used for particle RT calculation) is also publicly available (http://shaddenlab.berkeley.edu/software.html). The cerebral aneurysm model used in this study was obtained from the publicly available AneuriskWeb database (http://ecm2.mathcs.emory.edu/aneuriskweb/index) with the Aneurisk ID of C0005. The AAA model is uploaded as part of the electronic supplementary material.

Articles from Journal of the Royal Society Interface are provided here courtesy of The Royal Society

RESOURCES