Elucidating the Phosphate Binding Mode of PBP: The Critical Effect of Buffer Solution

Abstract

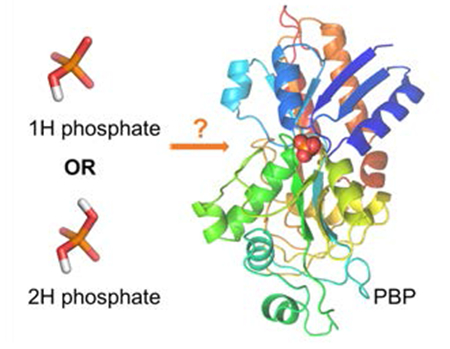
Phosphate is an essential component of cell functions and the specific transport of phosphorus into a cell is mediated by phosphate binding protein (PBP). The mechanism of PBP-phosphate recognition remains controversial: based on the similar binding affinities at acidic and basic pHs, it is believed that the hydrogen network in the binding site is flexible to adapt to different protonation states of phosphates. However, only hydrogen (1H) phosphate was observed in the sub-angstrom X-ray structures. To address this inconsistency, we performed molecular dynamics (MD) simulations using the AMOEBA polarizable force field. Structural and free energy data from simulations suggested that 1H phosphate was the preferred bound form at both pHs. The binding of dihydrogen (2H) phosphate disrupted the hydrogen-bond network in the PBP pocket and the computed affinity was much weaker than that of 1H phosphate. Furthermore, we showed that the discrepancy in the studies described above is resolved if the interaction between phosphate and the buffer agent is taken into account. The calculated apparent binding affinities are in excellent agreement with experimental measurements. Our results suggest the high specificity of PBP for 1H phosphate and highlight the importance of the buffer solution for the binding of highly charged ligands.

TOC Graphic:

INTRODUCTION

Inorganic phosphate (Pi) is one of the most important nutrients for organisms. It is not only used in the biosynthesis of cellular components, such as ATP, nucleic acids, phospholipids, and protein, but also an integral part of many biological processes, including metabolism, gene regulation, and muscle contraction.^1–6 Protein phosphorylation is a key mechanism for regulating transmembrane and intracellular signal transduction and affects every basic cellular process.^7–8 Due to the biological importance of Pi, the transport of Pi into cells and the maintenance of proper Pi homeostasis are critical. The phosphate binding protein (PBP), an initial receptor of the phosphate-specific transport systems (Pst),⁹–¹⁰ binds phosphate with high specificity against competing anions such as sulfate.^11–14 This high specificity is explained by a rich network of 12 hydrogen bonds (H-bonds) between phosphate and the binding site.^{9, 13, 15} Another distinct feature of the PBP binding site is a low-barrier hydrogen-bond (LBHB) between phosphate and the Asp side chain. While its effect on protein phosphate binding is not as significant as indicated by gas-phase calculations,¹⁶–¹⁷ the LBHB is responsible for discriminating arsenate and other similar tetrahedral oxyanions.^{9, 18}–¹⁹

Despite numerous studies on PBPs, questions remain about the binding mechanism. It is believed that PBP can bind to either 1H or 2H phosphate based on the observation that E. coli PBP has similar affinities for phosphate at pH 4.5 and 8.5.^{9, 15, 17}–^{18, 20}–²² It was suggested that the binding pocket is capable of binding to both 1H and 2H phosphate with reorientation of hydrogen atoms/H-bond network only.⁹ However, sub-angstrom X-ray crystallography studies of a topologically similar protein PfluDING (P. fluorescens PBP) showed that only 1H phosphate was present in the binding pocket at both pH 4.5 and 8.5, suggesting that PBP should follow a similar binding mechanism.¹⁸–^{19, 23} It seems that the conserved experimental affinities and the 1H-specific binding mode in sub-angstrom crystal structures cannot be reconciled with each other.

Molecular dynamics (MD) simulations based on classical force fields have been a valuable tool for the understanding of protein-ligand binding.²⁴–²⁷ The popular fixed-charge force fields have been applied to model neutral ligands and monovalent ions.^{24, 28}–³⁰ Highly charged species are more challenging in simulation and often treated by computationally demanding quantum mechanical (QM) methods.³¹–³³ Polarizable force fields offer an efficient way to model electrostatic interactions for highly charged species with high fidelity.³⁴–³⁶ Here, we carried out molecular dynamics simulations using the AMOEBA polarizable force field³⁷–³⁸ to investigate the phosphate binding mode of PBPs.

METHODS

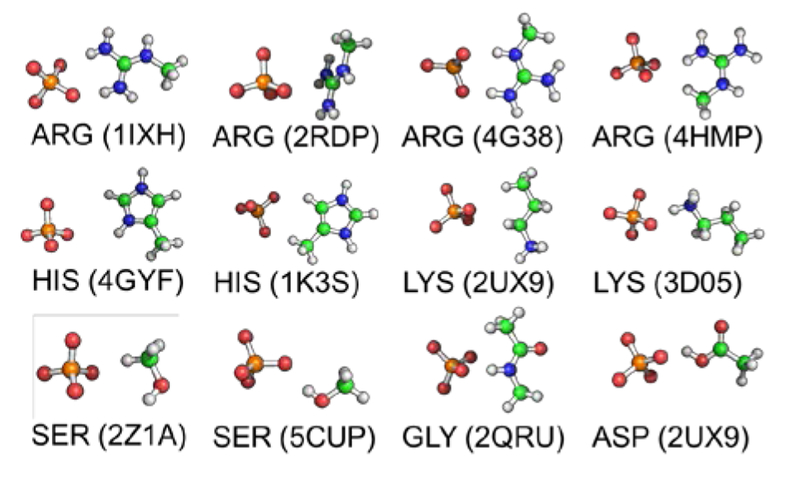
The AMOEBA force field was used for MD simulations. The electrostatic and polarization parameters were determined form the QM electrostatic potential and molecular polarizabilities at MP2/aug-cc-pVTZ and wB97X-D/6-311++G** level, respectively. The torsional parameters were derived to reproduce the QM conformational energy profile at MP2/6-311++G** level. The vdW parameters were optimized to capture the phosphate water interaction energy at different orientations calculated at the MP2/CBS level. 1H and 2H phosphate models share the same vdW parameters. To reproduce the interaction energy of the short H-bond between phosphate and carboxylate group, pairwise vdW parameters between the carboxylate O atom and phosphate H and O atoms were necessary. The pairwise vdW parameters were optimized by fitting to interaction energies calculated by MP2/CBS and PCM. Different pairwise vdW parameters were used among 1H and 2H models. As validation, the final force field parameters of phosphate were applied to compute the total interaction between phosphate and protein residue side chain models. The total interactions of residue-phosphate calculated using AMOEBA force field were compared to QM results at different levels including RIMP2/aug-cc-pVTZ, SAPT2+/aug-cc-pVDZ, and SAPT0/jun-cc-pVDZ. Good agreement between the AMOEBA and QM results was obtained with a correlation coefficient R² value of 0.99 across all dimers configurations and phosphate protonation states. The RMSE values are 3.4, 3.8, and 4.4 kcal/mol when comparing the total interaction energy calculated by AMOEBA and QM at RIMP2/aug-cc-pVTZ, SAPT2+/aug-cc-pVDZ, and SAPT0/jun-cc-pVDZ levels (Table 1, Figure 1). The parameters for Tris were derived by using POLTYPE.³⁹ Gaussian 09⁴⁰ and Psi4⁴¹ were used for the QM calculations.

Table 1.

Performance of AMOEBA interaction energies of 120 model compounds for amino acid-phosphate dimers compared to RIMP2/aug-cc-pVTZ, SAPT0/jun-ccpVDZ and SAPT2+/aug-cc-pVDZ results. MUE, MSE and RMSE stand for mean unsigned error, mean signed error and root mean squared error, respectively.

Statistics	RIMP2	SAPT2+	SAPT0
MUE (kcal/mol)	2.613	3.068	3.232
MSE (kcal/mol)	−0.528	0.110	−1.534
RMSE (kcal/mol)	3.404	3.816	4.411
R2	0.997	0.997	0.996

Figure 1.

Model compounds for amino acid-phosphate interactions extracted from PDB. All 10 possible protonation states for phosphate were considered.

The structures of the PBP-phosphate complexes for the wild type and the D56N mutant were taken from the PDB (PDB code: 1IXI and 1IXH). The structures were then solvated in periodic boxes of 73.27×73.27×91.59 ų with NaCl added to yield 0.15 M salt concentration. The systems were relaxed and heated before free energy simulations. The binding free energies were calculated by the double-decoupling scheme and the Bennet acceptance ratio (BAR) method.^{25, 42} Simulation details are provided in the SI. All molecular dynamics simulations were run with the Tinker-OpenMM program on GPU.⁴² The following equation was used to calculate the apparent K_D that takes into account the buffer effect at pH 8.5,

$$K_D^{\mathit{app}}=\frac{[\mathrm{PBP}]\times ([{\mathrm{HPO}}_4^{2-}]+[{\mathrm{H}}_2{\mathrm{PO}}_4^{-}]+[{\mathrm{HPO}}_4^{2-}:\mathrm{Tris}-{\mathrm{H}}^{+}]+[{\mathrm{H}}_2{\mathrm{PO}}_4^{-}:\mathrm{Tris}-{\mathrm{H}}^{+}])}{([{\mathrm{HPO}}_4^{2-}:\mathrm{PBP}]+[{\mathrm{H}}_2{\mathrm{PO}}_4^{-}:\mathrm{PBP}])}$$ (Eq. 1)

And similarly for pH 4.5 except Tris is replaced by Na+.

RESULTS AND DISCUSSIONS

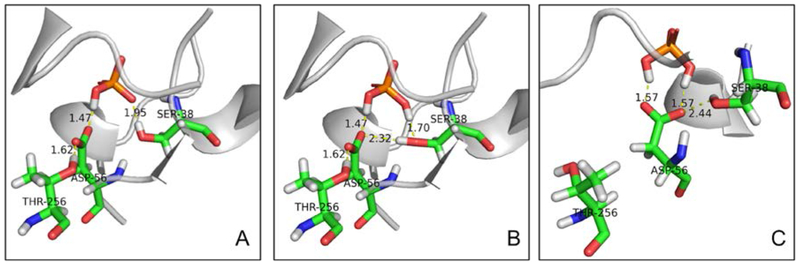
The molecular mechanism of phosphate-PBP binding in E.coli has been hypothesized based on X-ray structures without the protons on phosphate.^{9, 13, 17} The phosphate is bound through 12 H-bonds formed with 5 backbone NH groups, 4 hydroxyl groups of serine and threonine, 2 NH groups of the Arg135 sidechain, and one oxygen of the Asp56 sidechain. 1H phosphate was described as the acceptor for 11 H-bonds and the donor for one H-bond, in which 1H phosphate shared its proton with the carboxylate sidechain of Asp56 to form low-barrier hydrogen-bond (Figure 2A). In the 2H phosphate binding mode, Luecke et al.⁹ assumed that no drastic structural rearrangement of the binding pocket is needed. The only difference from 1H binding was that the hydroxyl group of Ser38, as the only one favorably positioned to have a proton bound to an O lone pairs, flipped to accept the second H on phosphate while donating its proton to Asp56 (Figure 2B). The binding pocket in the D56N mutant PBP is similar to the wild type, except for a normal hydrogen bond between Asn56 and phosphate.¹⁷

Figure 2.

Illustration of phosphate binding with Asp56 in wild-type PBPs. A. 1H phosphate binding mode in current simulation; B. Hypothesized 2H binding mode involves flipping of the hydroxyl group of Ser38 to Asp56 to accept the second proton on phosphate;⁹ C. 2H phosphate bidentate binding with Asp56 in current simulation. During the simulations, 1H phosphate kept the same binding mode as crystal structure while 2H phosphate preferred bidentate binding with Asp56, which is different from the monodentate binding hypothesized in literature.²³

To verify the experimentally hypothesized phosphate binding modes, we simulated the binding of 1H and 2H phosphates to both wild-type and the D56N mutant PBPs. The force field parameters for 1H and 2H phosphates were derived from QM data in this work (force field parameters are provided in the SI). Specific pairwise vdW interaction parameters were applied to represent the low-barrier hydrogen-bond between phosphate and carboxylate group. The force field was validated by comparing the calculated interaction energies between phosphate and model compounds for protein residues to QM results. Both the total interaction energies and the polarization energies from AMOEBA were in good agreement with QM results (Table 1).

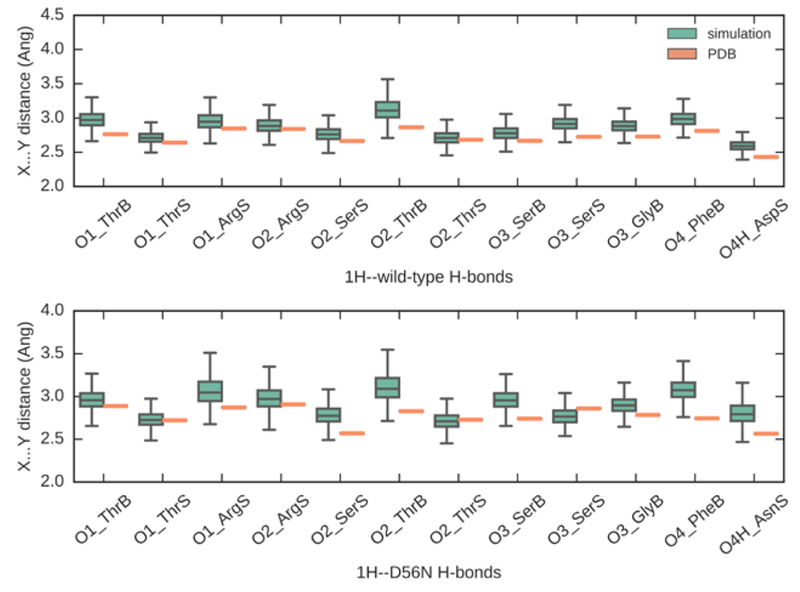
In the 1H phosphate binding simulations, 12 H-bonds for the wild type and the mutant were maintained over the entire 18-ns simulations (Figure 3). The mean distances are 2.87 ± 0.14 Å and 2.91 ± 0.14 Å for wild type and the mutant PBP binding pocket, respectively, compared to experimental H-bonds distances of 2.72 ± 0.11 Å and 2.77 ± 0.11 Å. The H-bond between Asp56 and 1H phosphate is the shortest among all H-bonds, which was captured by the simulation.

Figure 3.

Plot of 12 hydrogen bond distances (X…Y) between 1H phosphate and heavy atoms in wild type (top) and D56N mutant (bottom) PBP receptors. The orange symbols represent the distances in crystal structures and the green boxes represent the average distances in simulations with standard deviations. X axis lists all interacting residues in PBP. Suffix “S” stands for sidechain and “B” stands for backbone. In simulations, 1H phosphate reproduced and maintained 12 hydrogen bonds in both binding pockets and the H-bond distances are consistent with the experimental values

On the other hand, the binding of 2H phosphate led to significant rearrangement of the H-bond network and an unstable binding pocket. In the 2H phosphate-D56N mutant complex, the mean distances of all H-bond pairs increased to 3.23 ± 0.37 Å (Table S4). We observed relatively weak binding (discussed below) compared to 1H phosphate, with water molecules entering the binding pocket during the simulations. These water molecules replaced the binding with the Arg135 side chain and pushed Ser139, Ser 38, Gly 140, and Phe11 away from the phosphate.

It was found that the 2H phosphate preferred bidentate binding with Asp56 in wild-type protein, in contrast to the hypothesized monodentate binding mentioned above (Figure 2B and C). Asp56 rotated toward the phosphate and formed two stable hydrogen bonds with mean distances of 2.58 and 2.63 Å throughout the 18-ns simulation. The bidentate binding brings the negative-charge center closer to the phosphate, and disrupted the H-bonds between the phosphate and other residues, both of which would weaken the binding in the pocket. As for the 2H phosphate binding with the mutant protein, we observed water entering the pocket from the Arg135 side. As a result, the distances of all native H-bond pairs increased to 3.43± 0.42 Å.

Based on the simulations of phosphate binding with wild-type and mutant PBPs, the crystal structures for complexes could be well maintained when the PBPs were bound to 1H phosphate. However, 2H phosphate in the PBPs led to significant disruption of the H-bond network, and the hypothesized binding mode, which involves flipping of the hydroxyl group of Ser38 from phosphate to Asp56 (Figure 2B), is unlikely. This is consistent with the sub-angstrom X-ray structure analysis.^{18–19, 23} In the sub-angstrom X-ray crystallography studies of PfluDING, only one proton on oxygen atoms of the phosphate was observed at pH 4.5 and 8.5. PfluDING and E. coli PBP are topologically similar with a structural RMSD value of 1.34 Å over 228 Cα carbons and 0.23 Å over all heavy atoms in the binding pocket. Indeed, the residues in the binding pocket are conserved except that the Phe backbone is replaced by that with Leu, and the H-bond distances in the binding pocket are almost the same.²³ Thus, the phosphate-PBP binding should have the same mechanism i.e. 1H phosphate binds at both pHs. The result highlights the high specificity arising from the extensive network of H-bonds which can distinguish not only between 1H phosphate and sulfate, but also between 1H and 2H phosphates.

To determine the thermodynamic preference for 1H vs 2H phosphate, we calculated the free energy changes for transferring 1H/2H phosphate from water to PBPs using MD simulations (Table 2). The 1H phosphate binding free energies are 5-6 kcal/mol lower than those of 2H phosphate, suggesting that 1H is the dominant form bound to PBPs. This again agrees with sub-angstrom crystallography studies.^{18–19, 23} It should be noted that constant-pH MD is an alternative way to determine the protonation state of titratable groups.^43–44 In addition, the binding free energies of 1H phosphate are similar for the wild type and the mutant protein, consistent with experimental measurements. This similarity is a result of the compensation between the stabilization effect of the LBHB and the changes in total charge of the binding pocket. In the simulations, the stabilization of the LBHB was modeled by the special vdW interactions, which contributed −2.9 kcal/mol to the binding free energy between 1H phosphate and the wild-type PBP. In the mutant, the LBHB is replaced by a normal H-bond, while the replacement of Asp with Asn increases the electrostatic potential of the binding site and reinforce the interaction with the negatively charged phosphate ion. This explains why the D56N mutant with altered electrostatic potential can have a similar binding affinity to that of the wild type.

Table 2.

Calculated standard binding free energy (kcal/mol) of 1H/2H phosphate with PBPs or buffer ligands. The uncertainties are shown in parentheses.

	1H	2H
WT	−11.2 (0.4)	−6.4 (0.3)
D56N	−11.1 (0.4)	−5.1 (0.3)
Tris	−3.1 (0.3)	−1.1 (0.3)
Na+	−0.8 (0.3)	0.4 (0.3)

It remains unclear why the experimentally measured binding affinities are similar under acidic and basic conditions. The measured quantity is the apparent dissociation constant ($K_{\mathrm{D}}^{\mathrm{app}}$), which concerns the ratio between the total concentrations of phosphate in free and bound forms, $K_{\mathrm{D}}^{\mathrm{app}}=\frac{[\mathrm{PBP}]\times ([{\mathrm{HPO}}_4^{2-}]+[{\mathrm{H}}_2{\mathrm{PO}}_4^{-}])}{([{\mathrm{HPO}}_4^{2-}:\mathrm{PBP}]+[{\mathrm{H}}_2{\mathrm{PO}}_4^{-}:\mathrm{PBP}])}$. Because calculated binding free energy of 2H phosphate is ~5 kcal/mol smaller than that of 1H phosphate, [${\mathrm{H}}_2{\mathrm{PO}}_4^{-}:\mathrm{PBP}$] much smaller than [${\mathrm{HPO}}_4^{2-}:\mathrm{PBP}$] at pH 4.5 (see details in SI). As a result, $K_{\mathrm{D}}^{\mathrm{app}}$ depends on the ratio between 1H and 2H forms in solution, $K_{\mathrm{D}}^{\mathrm{app}}\approx K_{\mathrm{D},{\mathrm{HPO}}_4^{2-}:\mathrm{PBP}}∕\frac{[{\mathrm{HPO}}_4^{2-}]}{([{\mathrm{HPO}}_4^{2-}]+[{\mathrm{H}}_2{\mathrm{PO}}_4^{2-}])}$. The fraction of [${\mathrm{HPO}}_4^{2-}$] is close to 1 at pH 8.5, and reduces to ~1/500 at pH 4.5. Thus, the apparent $K_{\mathrm{D}}^{\mathrm{app}}$ will increase from 6 nM at pH 8.5 to 2.5 μM at pH 4.5, which corresponds to a change of +3.6 kcal/mol in binding free energy at 298 K. However, this is different from the experimental trend in binding free energy, which only increase by 1.5-1.7 kcal/mol when pH changes from 8.5 to 4.5. It is interesting to note that the calculated binding affinity at pH 4.5 is in excellent agreement with experimental measurement.

This discrepancy can be explained by the buffer solution, which has a significant effect on the binding free energy, especially for highly charged species.³² In previous experimental work, Tris acetate and sodium acetate buffer solutions were used to maintain the pH at 8.5 and 4.5, respectively.¹⁷ We calculated the binding free energy between 1H/2H phosphate and Tris-H+ or Na+ (Table 2). The calculated standard binding free energy between 1H phosphate and Tris-H+ is −3.1 kcal/mol and the corresponding K_D is 5.2 mM. At experimental Tris acetate concentrations of 50 mM, [${\mathrm{HPO}}_4^{2-}$] is ~10 times lower than [${\mathrm{HPO}}_4^{2-}$ : Tris-H⁺]. Therefore, at pH 8.5, this buffer agent will compete with PBP to bind the 1H phosphate and reduce the apparent binding affinity. This matches the observation that the binding affinity decreases with increasing ionic strength.²⁰ In acidic buffer solution, neither 1H nor 2H phosphate is bound to Na+, so the buffer solution does not affect $K_{\mathrm{D}}^{\mathrm{app}}$. Using the binding free energies of PBPs and buffer agents with phosphate and the concentration of the buffer solution, we computed the apparent binding free energies under the experimental conditions (Table 3, Eq. 1). For both wild-type and mutant PBPs, the binding free energy at pH 4.5 and 8.5 agrees with experimental data within ~1 kcal/mol.

Table 3.

Calculated apparent binding free energy (kcal/mol) of phosphate with PBP in wild type and D56N mutant protein at pH 8.5 and 4.5 and 50 mM sodium acetate/Tris acetate. The uncertainties are shown in parentheses.

		Expt.	Calc. without buffer effect		Calc. with buffer effect
pH	WT	D56N	WT	D56N	WT	D56N
8.5	−8.85	−8.76	−11.2 (0.5)	−11.1 (0.5)	−9.8 (0.5)	−9.7 (0.5)
4.5	−7.37	−7.05	−7.6 (0.4)	−7.5 (0.4)	−7.6 (0.4)	−7.5 (0.4)

Clearly, the interpretation that 1H and 2H phosphate should bind to PBP with similar affinities is due to neglecting the effect of buffer solution. The effect of buffer solution on the binding affinity measurement has been well recognized,⁴⁵ but not routinely incorporated in the experimental analyses. The current study demonstrates that molecular simulations can complement experimental measurement in delineating different contributions in the binding process.

In biology, pH is maintained at 7.4 by carbonic acid and bicarbonate, which are neutral or negatively charged and should not bind strongly to phosphates. Therefore, the biological buffer should not affect the specificity for 1H phosphate, i.e. 1H phosphate is the predominant bound state. This again points out the importance of considering the binding of buffer agents if the buffer used in biochemical experiment is different from the biological buffer.

CONCLUSION

In summary, we have resolved a long-standing controversy about the phosphate binding mode (1H vs. 2H) in PBPs through molecular dynamics simulations using the AMOEBA polarizable force field. We have shown that 1H phosphate is the energetically favorable species in the binding pocket at different pHs, and simulated H-bond network agrees well with the crystal structure. Based on our simulations, 2H phosphate binds much more weakly and disrupts the H-bond network observed in the crystal structure. After considering the interaction of phosphate with the agents in the buffer solution, for both WT and mutant PBP, the calculated binding free energies are in good agreement with experimental data, i.e. the binding affinity does not vary much with pH although only 1H phosphate is bound to PBPs. Our results highlight the importance of the buffer solution when interpreting the binding affinity data for highly charged species. In addition, we demonstrate that molecular simulations can bridge the gap between different experimental techniques and provide new insight for protein-ligand binding.

ABBREVIATIONS

1H phosphate

Hydrogen phosphate

2H phosphate

Dihydrogen phosphate

PBP

Phosphate binding protein

PfluDING

P. fluorescens PBP

MD

Molecular dynamics

Pi

Inorganic phosphate

QM

Quantum mechanics

MM

Molecular mechanics

Pst

phosphate-specific transport systems

LBHB

low-barrier hydrogen-bond