Nonadiabatic Excited-State Dynamics with Machine Learning

Abstract

We show that machine learning (ML) can be used to accurately reproduce nonadiabatic excited-state dynamics with decoherence-corrected fewest switches surface hopping in a 1-D model system. We propose to use ML to significantly reduce the simulation time of realistic, high-dimensional systems with good reproduction of observables obtained from reference simulations. Our approach is based on creating approximate ML potentials for each adiabatic state using a small number of training points. We investigate the feasibility of this approach by using adiabatic spin-boson Hamiltonian models of various dimensions as reference methods.

Excited-state dynamics simulations of molecules and molecular assemblies are as important as challenging. Some of the primary processes in nature (photosynthesis, light detection), medicine (phototherapy, DNA damage), and technology (photovoltaics, photonics) have at least one photoinduced reaction step occurring in the excited state.¹⁻³ The main difficulties in modeling these processes arise from the intricacies of excited-state electronic structure and from the intrinsic nonadiabaticity caused by the coupling between nuclear and electronic degrees of freedom driving the time evolution.

Significant advances in the simulation of nonadiabatic dynamics in excited states have been achieved in recent years.⁴ The development of on-the-fly nonadiabatic mixed quantum-classical (NA-MQC) strategies, in particular, has boosted the research field in the past decade, allowing full-dimensional simulations of systems with tens of atoms for several picoseconds. In these methods, nonadiabatic phenomena are introduced into a classical ensemble of trajectories through averaging, spawning, or hopping of quantum electronic information. At the same time, they rely on a local approximation, allowing for the computation of electronic properties only at the classical nuclear coordinates.

The on-the-fly strategy is a fundamental advantage because it avoids the costly calculation of multidimensional potential energy surfaces (PESs), a task that is the main bottleneck in full quantum approaches. However, the on-the-fly propagation of the dynamics is computationally demanding because expensive quantum mechanical (QM) quantities—energies, forces, and couplings between the electronic states—must be computed at each time step in the numerical integration of the equations of motion. Consequently, an on-the-fly NA-MQC simulation of a medium-sized molecule for several picoseconds may require hundreds of thousands of CPU hours when using first-principles QM methods.

The emergence of machine learning (ML) algorithms has the potential to change this scenario, ideally leading to situations where ML inexpensively predicts excited-state energies, forces, and couplings for on-the-fly NA-MQC dynamics. Encouragingly, ML has already been successfully applied in many atomistic simulations, for example, to represent PESs, to perform molecular dynamics in the ground state, and to predict excited-state properties.⁵⁻²² However, the application of ML to on-the-fly NA-MQC dynamics poses unique challenges. Among the most crucial problems is the higher complexity of the excited-state electronic structure, often leading to a high density of coupled states, with a strongly anharmonic dependence on nuclear coordinates. Moreover, in many cases, the nonadiabatic processes happen on time scales shorter than those of thermal equilibration, requiring the propagation of microcanonical rather than canonical ensembles, which are associated with much stricter conservation requirements.

Only few recent studies have attempted to use ML for such purposes. In a pilot study of ML-enhanced NA-MQC dynamics, ML was used only for the representation of the relevant PESs; however, the generation of training points was rather tedious and time-consuming, whereas the number of QM calculations performed during the training of the ML models and during the dynamics was close to the number of QM calculations typically required for a corresponding on-the-fly QM simulation.⁶ In another study, the accuracy of direct quantum wavepacket dynamics with ML PESs was shown to deteriorate quickly with increasing number of dimensions so that it became problematic to achieve good accuracy even for as few dimensions as six.¹⁷

The main aim of our work is to outline how ML can be used to achieve a significant reduction of the number of required QM calculations in practical on-the-fly NA-MQC simulations of high-dimensional systems. For this purpose, we use the popular decoherence-corrected fewest switches surface hopping (DC-FSSH; see the Supporting Information (SI)) approach in on-the-fly NA-MQC dynamics and an ML approach based on kernel ridge regression (KRR; see the SI for details). To avoid any bias associated with the choice of a specific QM method and a target molecule, we decided to use the two-state spin-boson Hamiltonian in the adiabatic representation (A-SBH; see the SI), which is easily adjustable in terms of the number of degrees of freedom and couplings. This choice of an analytical Hamiltonian allows for an extensive and general assessment of ML capabilities because we can compute many more trajectories and time steps than we would be able to do with any on-the-fly electronic structure method. Note, however, that the use of A-SBH does not lead to any loss of generality, as every element of an atomistic two-state simulation is present in this model, and the generalization to more states is straightforward. As discussed later, because of the strong coupling between different A-SBH dimensions, ML-based NA-MQC dynamics may in some aspects be even more challenging for A-SBH than for an atomistic model.

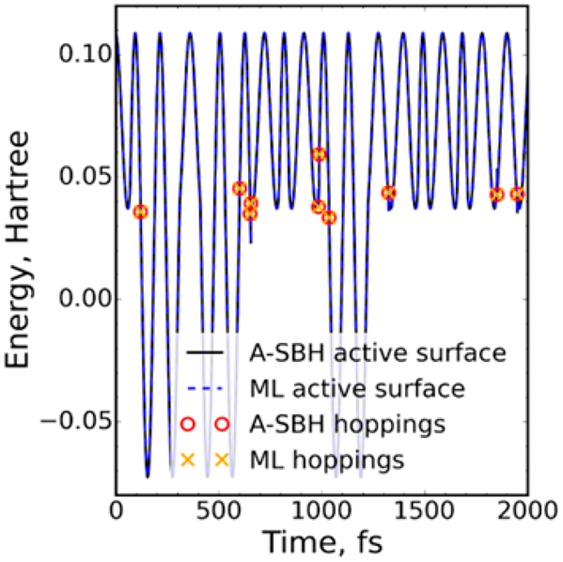
We start by demonstrating for the 1-D A-SBH model that it is possible, in principle, to create a complete ML model, which can accurately reproduce the reference A-SBH trajectory with all hopping events (Figure 1). This is achieved when using at least N_tr = 128 points in the training set (see the SI for further details).

Figure 1.

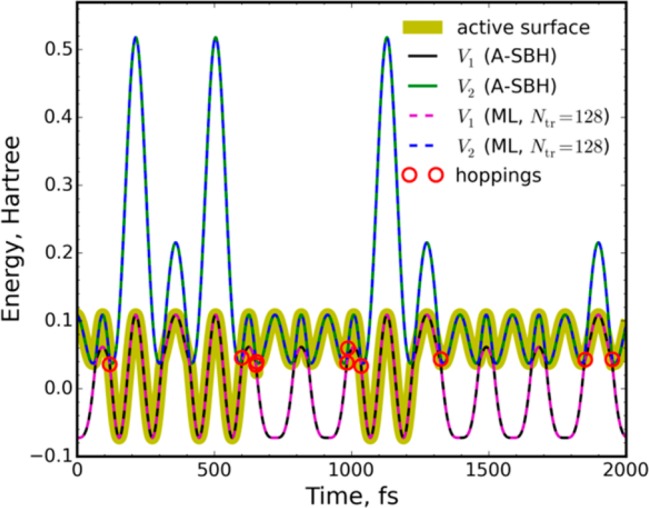
Comparison of A-SBH and complete ML surface hopping trajectories for the 1-D model. The simulations started from the same initial conditions and were run with the same random seed.

For high-dimensional systems, it is generally not feasible to build such complete ML models. First, generating a sufficient amount of accurate QM reference data quickly becomes too costly due to the curse of dimensionality. For a realistic 33-D model, it would be necessary to calculate reference values for 128³³ = 3.45 × 10⁶⁹ grid points to ensure sampling with the same density as for our complete 1-D ML model (Figure 1).²³ This is obviously impossible. Second, processing large amounts of reference data is also very challenging, in terms of both memory requirements and training time. Third, if the number of training points for ML becomes too large, then it may be more reasonable to run pure QM dynamics. Thus, for ML to significantly speed up nonadiabatic dynamics simulations, the training set has to be as small as possible and to be generated as quickly as possible.

In practical terms, our first aim is to keep the number of points in the training set preferably at most 10 000 points. For comparison, ground-state ML potentials have been trained on many fewer molecular geometries and used successfully for various purposes such as molecular dynamics, calculation of vibrational spectra, and geometry optimization.^7,14,15 From our experience with on-the-fly NA-MQC dynamics based on ab initio and semiempirical methods, we know that these simulations are typically run with about 100 trajectories with a time step of 0.5 fs for 1 ps; that is, they require 200 000 QM calculations. Therefore, 10 000 points represents merely 5% of a typical on-the-fly NA-MQC project. Moreover, the gains are potentially much larger. Although 100 trajectories are enough to reveal all main reaction pathways, their pathway yields are delivered with rather low precision. However, after training the machine, it can be used to run thousands of trajectories, producing highly precise results, which would simply be unaffordable with conventional QM approaches.

Proposed approaches for generating training sets are often iterative and rather time-consuming.¹⁵ Our second aim is to avoid such handicaps and keep the construction of the training set as simple and inexpensive as possible.

On the basis of these considerations, we target a relatively sparse grid of training points, sampled with a low discrepancy algorithm.^7,24 Inevitably, this will lead to some loss of accuracy. However, it is known that ML trained on points sampled along vibrational modes can describe larger molecules and also give rather accurate PESs.¹⁸ Furthermore, a very accurate ML PES can be obtained for small molecules.⁷

The most serious additional challenge in the case of DC-FSSH dynamics is that the nonadiabatic couplings feature sharp, narrow spikes around certain geometries (Figure 2). This necessitates very small time steps or special treatments even in the pure QM DC-FSSH dynamics.²⁵ Sparse sampling of ML training points will, in most cases, miss these spikes (Figure 2), and, consequently, no or too few hops will happen during ML dynamics.

Figure 2.

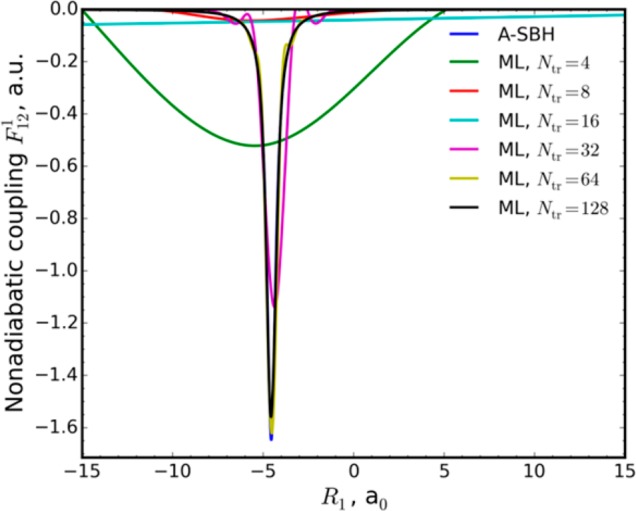
Comparison of nonadiabatic couplings calculated for the A-SBH and ML models trained on an increasing number of points for the 1-D model.

Indeed, we find no hops at all in the 2 ps trajectory produced with an ML model of the 1-D system trained on only 16 points (Figure S1) compared with four hops when we calculate nonadiabatic couplings with A-SBH throughout the trajectory (Figure S2). In previous work on ML for FSSH,⁶ the Zhu–Nakamura approach²⁶ was used to avoid the calculation of nonadiabatic couplings altogether. Here we solve this problem by performing QM (in this work A-SBH) calculations of nonadiabatic couplings instead of estimating them with ML when the band gap estimated with ML is small. A similar approach was tested for the Zhu–Nakamura dynamics for a different reason (to avoid errors of the ML potential in the vicinity of the conical intersections).⁶ In the case of our 1-D ML model trained on 16 points, five hops occur if we switch on A-SBH calculations for V₂^est – V₁ < 0.03 hartree (Figure S3). We use this cutoff in the following. Problems with sparse sampling concerning total energy conservation are discussed in the SI.

Next, we compare the performance of ML dynamics with A-SBH simulations for a realistic 33-D system. This system is rather challenging for ML, as exemplified by the fact that during a 50 ps A-SBH trajectory the smallest Euclidian distance between a point at a given time step to any point visited during the first 80% of previous time steps remained very large and did not decrease over time. This means that the same region in the high-dimensional space was not visited again during the 50 ps of nonadiabatic dynamics. Consequently, all of our attempts to use on-the-fly or adaptive learning strategies commonly employed in ground-state ML dynamics for atomistic systems^16,22 failed for our 33-D A-SBH system. This may be attributed to the strong coupling between different A-SBH dimensions, whereas in atomistic simulations it is often possible to partition the system into smaller, sufficiently independent substructures.^13,15,18,22

To collect enough data for statistical analysis, we ran 1000 trajectories with A-SBH and two different ML models, each starting on the S₁ surface. The ML models were trained on 1000 and on 10 000 points. The evolution of the S₁ state population during 2 ps dynamics is reproduced very well by both ML models (Figure 3) despite the relatively small training sets generated in a simple, noniterative manner. The excited-state lifetime is estimated (see the SI) to be 114 ± 1, 100 ± 1, and 105 ± 1 fs with A-SBH, ML trained on 1000 points, and ML trained on 10 000 points, respectively. The ML lifetimes are thus in reasonable agreement with the A-SBH lifetime. An additional comparative analysis is provided in the SI.

Figure 3.

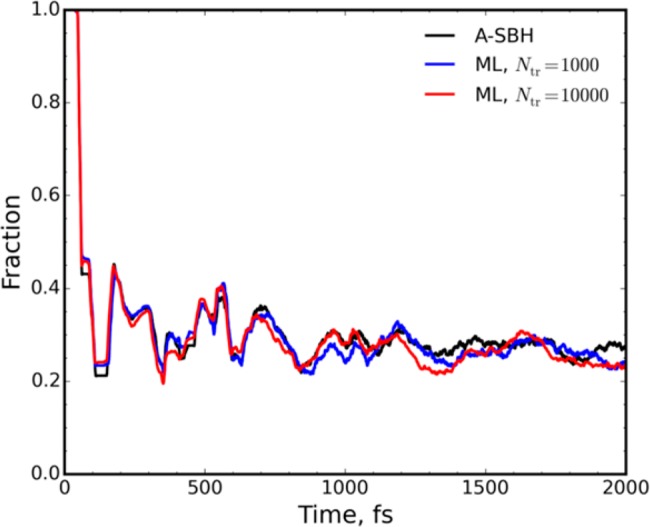
Evolution of the fraction of trajectories on state S₁ along A-SBH (black) and ML (blue, red) surface hopping trajectories for the 33-D model averaged for 1000 trajectories. The ML models were trained on 1000 and 10 000 points, respectively.

In our ML dynamics, A-SBH calculations during DC-FSSH dynamics were invoked only in 13–16% of time steps for V₂^est – V₁ < 0.03 hartree. Such QM calculations should be avoided in the future altogether by using local diabatization, which eliminates the problem with narrow couplings.²⁷ In this case, the cost of ML nonadiabatic dynamics will be essentially determined by the cost of training set generation.

In summary, we show that ML can be used to simulate accurate, multidimensional nonadiabatic dynamics with significant cost reduction. We suggest using fairly sparse small training sets sampled from the high-dimensional space to build approximate ML potentials for each adiabatic surface. We show that dynamics runs with these ML potentials well reproduce the time evolution of the adiabatic-state population and the excited-state lifetime obtained from the dynamics with the reference method.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.8b02469.

• Description of methods and additional technical details on nonadiabatic dynamics (PDF)

The authors declare no competing financial interest.