Abstract
Data of previous trials with a similar setting are often available in the analysis of clinical trials. Several Bayesian methods have been proposed for including historical data as prior information in the analysis of the current trial, such as the (modified) power prior, the (robust) meta-analytic-predictive prior, the commensurate prior and methods proposed by Pocock and Murray et al. We compared these methods and illustrated their use in a practical setting, including an assessment of the comparability of the current and the historical data. The motivating data set consists of randomised controlled trials for acute myeloid leukaemia. A simulation study was used to compare the methods in terms of bias, precision, power and type I error rate. Methods that estimate parameters for the between-trial heterogeneity generally offer the best trade-off of power, precision and type I error, with the meta-analytic-predictive prior being the most promising method. The results show that it can be feasible to include historical data in the analysis of clinical trials, if an appropriate method is used to estimate the heterogeneity between trials, and the historical data satisfy criteria for comparability.
Keywords: Bayesian statistics, commensurate prior, historical data, meta-analytic-predictive prior, power prior
1 Introduction
Clinical trials are seldom performed in isolation. In many cases, data of previous trials with a similar setting are available. Such historical data may provide information that is relevant to the research questions of the current trial.1 Including these historical data in the analysis of the current trial could improve the precision of the estimates, thereby increasing statistical power for hypothesis testing and reducing required sample sizes. The investigational treatment usually differs between trials, but the treatment in the control arm often remains stable over successive trials, so that only the control arms of previous trials are eligible for inclusion in the analysis of the current trial.
Differences in patient populations or other trial-specific circumstances can lead to heterogeneity among the historical trials and between the current trial and the historical trials. When including historical data in the analysis of a clinical trial, one should thus account for the possible heterogeneity between the trials. In case of large discrepancies between the historical trials and the current trial, the historical data should not influence the results of the analysis of the current trial.
In a seminal paper, Pocock1 proposed a statistical method that accounts for a difference in model parameters between the historical and the current data and treats this difference as a random variable. In recent years, there has been a renewed interest in methods for including historical data in the analysis of clinical trials. Ibrahim and Chen,2 Duan et al.3 and Neuenschwander et al.4 proposed the power prior and the modified power prior, i.e. Bayesian methods that use an informative prior based on the likelihood function of the historical data for the analysis of the current trial. These methods downweight the information in the historical data, to account for potential differences between historical and current data. Neuenschwander et al.5 described the use of meta-analytic methods to account for heterogeneity in model parameters between historical and current data and to determine the posterior distribution of the parameters for the current trial. Schmidli et al.6 extended these meta-analytic methods by adding a robust component, to account for the possibility of a conflict between historical and current data. Hobbs et al.7 developed the commensurate prior for various types of generalised linear mixed models, including models for time-to-event outcomes. In this method, the priors for the model parameters for the current data are centred at the corresponding parameters for the historical data, and a distribution is assumed for the difference in model parameters between the current and historical data. Murray et al.8 extended the commensurate prior to piecewise exponential survival distributions, using a flexible semi-parametric approach for combining historical and current data. All these methods are based on a Bayesian statistical framework, which seems natural when using historical data as prior information.
The historical trials used for these statistical methods should be chosen carefully, to ensure sufficient comparability with the current trial. The most commonly used criteria for assessing the comparability of the historical and the current trials are those proposed by Pocock.1 It is necessary to impose such comparability criteria, as the statistical methods for including historical data are based only on the results of the current and historical trials and do not take into account the context in which these trials were performed.
The inclusion of historical data in the analysis of clinical trials is not yet common in practice. One reason is that it is not yet clear which statistical method should be used, and practical experience with these methods is limited. In addition, it is not yet fully known in what kinds of settings the historical and current data are sufficiently comparable, and how strictly comparability criteria such as Pocock’s criteria should be upheld. Finally, although previous studies have assessed the type I error and power of some methods in relatively simple models,9,10 a comprehensive overview of the frequentist characteristics of the available methods, and how these outcomes depend on the between-trial heterogeneity, is not yet available. Therefore, regulatory authorities and other decision makers may not easily accept the inclusion of historical data into the planning and analysis of clinical trials.
In this paper, we give an overview of methods for including historical data in the analysis of clinical trials. We illustrate what kind of results these methods yield in a practical setting, and we assess the comparability of the current and the historical data. A simulation study is performed to compare the methods in terms of bias, precision, power and type I error rate.
This paper focuses on the analysis of survival data. The motivating data set consists of a number of randomised controlled trials for acute myeloid leukaemia (AML) that were conducted by the Dutch-Belgian Hemato-Oncology Cooperative Group (HOVON). The next section describes the HOVON data and evaluates to what extent these data satisfy comparability criteria. Section 3 gives an overview of methods for including historical data in the analysis of clinical trials. Section 4 describes the analysis and the results of the HOVON data. Section 5 presents the design and the results of the simulation study, and Section 6 concludes.
2 Motivating data set: HOVON data
AML is a cancer of the myeloid line of blood cells, with five-year survival rates in different patient populations ranging from 15% to 70%, depending on age and other factors. Despite a large amount of research, the available treatment options and the survival rate of AML have changed relatively slowly over time. Treatment of AML consists primarily of chemotherapy, which includes two phases: induction and consolidation therapy. Stem cell transplantation is usually considered if (a) the estimated risk of relapse is substantial after induction therapy, (b) induction chemotherapy fails, or (c) if the patient relapses.
HOVON has performed a number of randomised controlled trials on chemotherapy treatments for patients with AML since the 1980s.11–15 Each trial had its own control arm, but the control arm treatments were similar. Because AML is a relatively rare disease, it often takes several years of inclusion and large-scale international collaborations to recruit sufficient patients for a clinical trial. In this context, it is natural to consider previous HOVON AML trials for the analysis of a new trial. Ideally, this approach would enable researchers to design new AML trials with smaller control arms, thereby increasing the speed and the efficiency of the research. This prospect motivated the use of the HOVON data in this article. However, before including historical data in the analysis, the comparability of the historical trials and the current trial should be assessed.
2.1 Description of the data
We consider the analysis of the HOVON 42A trial, which investigated the effect of priming using a granulocyte colony-stimulating factor (G-CSF) in the remission induction chemotherapy course for treatment of AML. HOVON 42A is an extension of the HOVON 42 trial, which also considered the effect of G-CSF priming. However, HOVON 42 also included a randomisation for the dose of cytarabine (a chemotherapy agent) to either a conventional dose or an escalated dose, whereas all patients in HOVON 42A received the conventional cytarabine dose. An analysis of the effect of G-CSF using the combined data of HOVON 42 and HOVON 42A has been published,14 and no significant effect of G-CSF priming was found in the overall analysis.
In this paper, we treat HOVON 42A as the current trial and HOVON 42 as a separate study. We consider the inclusion of historical data of the trials HOVON 4,11 HOVON 4A, HOVON 2912 and HOVON 4213 to improve the analysis of HOVON 42A. Each trial used a 1:1 randomisation for the treatment in the induction phase, with the investigational treatment differing between trials. The control treatment in these trials consisted of one cycle of induction with an anthracycline (daunorubicin or idarubicin) in combination with cytarabine (200 for seven days) and a second cycle of amsacrine with intermediate-dose cytarabine (1000 every 12 h for six days). There were three types of post-remission therapy: (a) a continued third cycle of chemotherapy (so-called consolidation chemotherapy), (b) autologous stem cell transplantation (i.e. the patient’s own marrow or peripheral blood serves as the stem cell graft) or (c) allogeneic stem cell transplantation (i.e. a healthy donor’s marrow or peripheral blood serves as the stem cell graft). The choice of these post-remission therapies depended not only on the availability of a donor but also on the age of the patient and the prognostic risk features of the leukaemia. A second randomisation for the post-remission therapy treatment was used in HOVON 29 and HOVON 42, but only for a select subgroup of patients. In these two trials, the patients eligible for an autologous stem cell transplant were randomised between an autologous transplant and consolidation chemotherapy. Event-free survival and overall survival were important endpoints for each trial. The trials were approved by the ethics committees of the participating institutions and were conducted in accordance with the Declaration of Helsinki. All participants gave their informed consent.
We note that some of the historical HOVON trials used the same or a similar investigational treatment as the current trial. However, to obtain the usual setting where only the control arm treatments remain stable over successive trials, we excluded the patients treated with G-CSF in the historical trials from the analysis. We also excluded patients who received an escalated cytarabine dose in HOVON 42, as well as patients with AML subtype M3 according to the French-American-British classification. We only consider the outcome of overall survival. Table 1 presents descriptive statistics of the selected patients.
Table 1.
Descriptive statistics of selected patients in HOVON AML trials.
| Trial | HOVON 4 | HOVON 4A | HOVON 29 | HOVON 42 | HOVON 42A |
|---|---|---|---|---|---|
| Number of patients | 359 | 252 | 693 | 437 | 511 |
| Number of deaths | 277 (77.2%) | 181 (72.1%) | 474 (68.4%) | 293 (67.0%) | 294 (57.5%) |
| Age | 44 (34–53) | 43 (33–51) | 45 (35–54) | 49 (39–55) | 50 (39–56) |
| Gender (female) | 49.9% | 45.0% | 49.4% | 44.4% | 48.5% |
| Randomisation year | 1989 (1988–1992) | 1992 (1992–1993) | 1999 (1997–2000) | 2003 (2002–2004) | 2007 (2006–2008) |
| Complete response | 77.7% | 82.5% | 86.0% | 81.9% | 83.2% |
| White blood cell count | 14.7 (4.6–56.2) | 14.9 (4.3–48.8) | 13.6 (3.4–47.6) | 11.6 (3.5–46.0) | 11.2 (2.7–41.7) |
| Cytogenetic subgroup (karyotype) | |||||
| t(8;21) | 8.5% | 11.3% | 6.7% | 5.3% | 3.9% |
| inv(16) | 6.1% | 6.3% | 7.3% | 4.6% | 4.7% |
| t(15;17) | 0.3% | 0.5% | 0.3% | 0.0% | 0.0% |
| Cytogenetically normal | 48.8% | 49.1% | 51.9% | 47.5% | 47.5% |
| Cytogenetically abnormal | 25.6% | 24.8% | 24.9% | 32.1% | 29.0% |
| Monosomal karyotype | 10.6% | 8.1% | 8.9% | 10.6% | 14.8% |
Note: Continuous variables are described using medians and interquartile ranges, and categorical variables using percentages.
2.2 Evaluation of comparability criteria
For the selected HOVON trials, an evaluation of Pocock’s criteria for the comparability of historical and current controls is as follows:
P1: The historical controls must have received a precisely defined standard treatment which must be the same as the treatment for the randomised controls. In each trial, the initial treatment consisted of two cycles of chemotherapy for the induction treatment. The type of chemotherapy and the dose were the same in each control arm, but the consolidation phase treatment could differ. Some trials used an additional randomisation for the consolidation phase treatment. For these trials, the second randomisation concerned only the patients eligible for an autologous stem cell transplantation.
P2: The historical controls must have been part of a recent clinical study which contained the same requirements for patient eligibility. The HOVON trials have been performed over a considerable period of time. The first patient was registered in July 1987 for HOVON 4, in October 1990 for HOVON 4A, in March 1995 for HOVON 29, in January 2001 for HOVON 42 and in February 2006 for HOVON 42A. Although the available treatment options for AML have changed relatively slowly, the improvements in bone-marrow transplantation techniques and supportive care over a time span of 20 years can be substantial, such as new antibiotics, better antimicrobial prophylaxis and treatment, better blood transfusion support and other changes in medical care. Some of the historical trials used a slightly wider age range as inclusion criterion than HOVON 42A, which used an age range of 18–60 years.
P3: The methods of treatment evaluation must be the same. We use the endpoint of overall survival for all trials, and this outcome is measured in the same way in all trials.
P4: The distributions of important patient characteristics in the historical controls should be comparable with those in the new trial. There were statistically significant differences between trials in the distribution of age (Kruskal–Wallis test, p < 0.001) and the cytogenetic subgroup (chi-square test, p = 0.002), which are important prognostic factors for AML survival. There were no significant differences in the distribution of gender (chi-square test, p = 0.38) and the white blood cell count (Kruskal–Wallis test, p = 0.13).
P5: The previous studies must have been performed in the same organisation with largely the same clinical investigators. All trials were initiated and sponsored by HOVON. There have been relatively few changes in the organisation and structure of HOVON, though the number of associated treatment centres has increased over time.
P6: There must be no other indications leading one to expect differing results between the randomised and historical controls. Concomitant medications and overall quality of care may have improved over time. To our knowledge, there are no other indications for substantial differences between the trials.
This evaluation suggests that it is doubtful whether criteria P2 and P4 are satisfied, whereas the other Pocock criteria are satisfied to a large extent. We conclude that HOVON 4 and 4A are too old to be considered relevant for the analysis of HOVON 42A, and these trials are thus excluded from the analysis. The time gap among the three remaining trials (HOVON 29, 42 and 42A) is substantial with almost 11 years between the start dates of HOVON 29 and HOVON 42A. However, we do not consider this time gap to be too long, as modern antibiotics, antimicrobial prophylaxis and treatment and blood transfusion support were already available at the start of HOVON 29. To account for the differences in age range between trials, only patients with age between 18 and 60 years (i.e. the age range of HOVON 42A) were included in the analysis. Even after that correction, the age distribution differed significantly between trials, which was addressed by including age as a covariate in the analysis. Although there are some differences in the distribution of the cytogenetic subgroup between trials, we decided not to adjust for this variable in the analysis, as these differences are relatively small and partially explained by the differences in age distribution. Molecular biomarkers are also relevant predictors of survival among AML patients, but these were not available for the older trials, so that no comparison was possible.
As an alternative to using Pocock’s criteria, we could assume exchangeability of the historical trials and the current trial,16 which is a necessary assumption for several hierarchical methods (see the next section). Exchangeability implies that the parameters that generated the data of the different trials are drawn from the same (normal) distribution, and that there is no natural ordering of the trials. Of course, there is a natural ordering of the HOVON trials, namely the time period during which each trial was performed. This means that a time trend in the outcome (overall survival) would violate the assumption of exchangeability. Figure 1 shows the Kaplan–Meier estimates for overall survival in each control arm and in the investigational arm of HOVON 42A. The log-rank test revealed no significant differences in survival between the control arms of the included trials (p = 0.13); however, the differences were significant after adjusting for age using a Cox regression (p = 0.035). The difference in overall survival between the treatment arms of HOVON 42A was not significant (log-rank test, p = 0.29).
Figure 1.
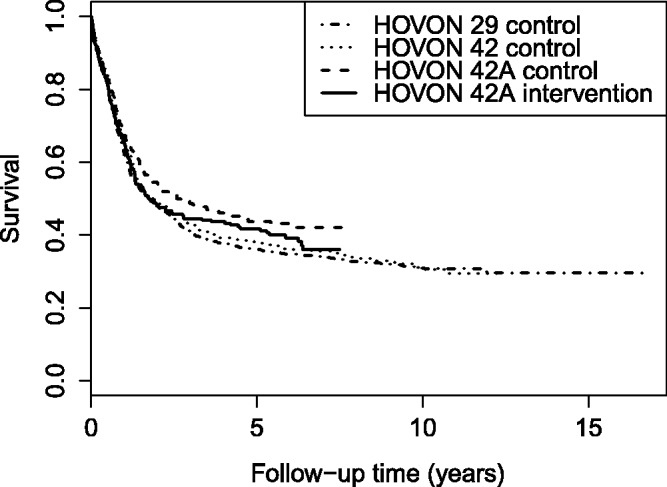
HOVON data: Kaplan–Meier curves of overall survival in the control arms of the HOVON trials, and the investigational arm of HOVON 42A.
3 Methods for including historical data
We assume that a current trial is available with likelihood function , and K historical trials with likelihood functions and pooled likelihood , where D represents the current data and represents the historical data. The current trial is assumed to consist of one investigational arm and one control arm, and for the historical trial(s), only the control arm data are used. The parameters θ can be decomposed as , where describes the intervention effect (i.e. the difference between the trial arms), and describes the distribution of the control arm data. In some methods, different model parameters are assumed for the historical and the current data. Below, we describe the methods for incorporating historical data using the likelihood functions of the trials, but ignoring the distributions of individual observations.
3.1 Pocock’s method
Pocock’s method assumes that the historical data are a potentially biased representation of the distribution of the data in the current trial.1 The bias is formally described as , where and describe the distribution (e.g. the mean outcome) of the current controls and the historical controls, respectively. The direction of the bias δ is typically unknown, and in Pocock’s method, this bias is assumed to be normally distributed with mean 0, so that . We use the term bias to describe the difference δ, as this term was also used by Pocock. However, the size of δ and thus the value of actually indicate the amount of between-trial heterogeneity. Pocock’s method only accounts for bias in a single parameter, though this method can be used in models with multiple parameters for the distribution of the control arm data.
It is difficult to estimate using the observed data if only a single or a small number of historical trials are available. Therefore, Pocock suggested that the researcher specify plausible values for instead of estimating it. The posterior distribution of the parameters using Pocock’s method is given by
| (1) |
where and are uninformative priors for the model parameters. In case of multiple historical trials, we assume that the bias varies randomly between trials, so that the posterior is then given by
| (2) |
3.2 Power prior and modified power prior
The idea of the power prior2,17 is to incorporate the historical data by using a downweighted version of the likelihood of the historical data as prior. This downweighting is achieved by raising the likelihood to a power α, with . Unlike Pocock’s method, the power prior assumes a common set of model parameters for the historical controls and the current controls. The power prior is defined as
| (3) |
and yields the posterior distribution
| (4) |
where and are uninformative priors. For the case of multiple historical trials, Chen et al.18 suggested to use a different weight parameter for each historical trial. However, as it is unclear how such differential weights should be chosen, we prefer to use the same weight for each trial.
Using the power prior, the weight parameter α must be chosen in advance. Setting α = 1 leads to a complete pooling of the data of the historical and current data, whereas setting α = 0 effectively discards the historical data. The parameter α can be interpreted as a precision parameter, as for many classes of models the power prior can asymptotically be approximated as , where is the mode of the power prior and .17 It is in general not clear how α should be chosen, though Ibrahim et al.17,19 have proposed to use the deviance information criterion or the logarithm of the pseudo marginal likelihood.
An alternative approach is to estimate α using the available data. This can be done with the modified power prior (MPP),3,4 which yields the posterior distribution
| (5) |
where is a scaling constant that depends only on α. The inclusion of this scaling constant ensures that the results satisfy the likelihood principle.3,20
A difficulty of the MPP is that the integral in the scaling constant must be calculated in every iteration of a Markov chain Monte Carlo (MCMC) sampler, which can be very time-consuming. This is especially problematic in case the number of parameters in θ is large, so that numerical or analytical integration becomes infeasible. To solve this problem, we developed a novel algorithm for calculating the scaling constant, based on an algorithm for calculating the marginal likelihood (i.e. with α = 1) using power posteriors that was proposed by Friel and Petitt.21 A simple adaptation of their algorithm enables the calculation of for . The steps of this algorithm are described in the supplementary material.
Furthermore, it is not yet clear how the MPP should be extended to the case of multiple historical data sets. Several formulations, with different definitions of the scaling constant, were proposed by Duan,22 but practical experience with these formulations is lacking.
3.3 Meta-analytic-predictive approach
Neuenschwander et al.5 proposed a method for including historical data based on meta-analytic techniques. This meta-analytic-predictive (MAP) approach assumes that the model parameters of all trials are exchangeable and are drawn from the same normal distribution. With a single outcome parameter that differs between trials, the study-specific parameters are given by
| (6) |
where and denote the outcome parameter for the k-th historical trial and the current control arm, respectively, is the population mean of these parameters and ηk is a normally distributed error term with . The MAP approach differs from conventional meta-analysis in that it aims to predict the outcome parameter for the current trial (i.e. ) instead of the overall mean outcome .
The implementation of this method requires the estimation of the between-study variance , for which several approaches were proposed by Neuenschwander et al.5 We estimate in a fully Bayesian way, which yields the following posterior:
| (7) |
Because the posterior results may be sensitive to , a sensitivity analysis is recommended, especially if the number of historical trials is low.
Schmidli et al.6 proposed a ‘robustification’ of the MAP approach to account for the possibility that the historical data and the current data are in conflict. In this robust MAP approach, the hierarchical model of the MAP approach is first estimated using only the historical data, yielding the posterior
| (8) |
Applying this posterior as prior distribution for an analysis of the current trial yields the same posterior for the MAP approach as in equation (7), see the proof given by Schmidli et al.
In the robust MAP approach, a robust (i.e. less informative) component is added to the prior for the analysis of the current data according to
| (9) |
where wr denotes the size of the robust component, πrobust is a vague prior for the model parameters and the model parameters have been omitted for brevity. The vague prior of the robust component serves to account for data in which the difference between historical and current data exceeds the heterogeneity among the historical trials. To implement this method, it is typically necessary to approximate πMAP with a parametric distribution, so that it can be used in the prior for the analysis of the current data.
3.4 Commensurate prior and method of Murray et al.
The commensurate prior model was developed by Hobbs et al.7,23 In this model, the distribution of the parameters for the current trial is centred on the corresponding parameters for the historical data, so that the prior is given by
where parameterizes the variance of given and thus specifies the amount of between-trial heterogeneity. The commensurate prior model accounts for between-trial heterogeneity in a single parameter.
Hobbs et al.7 described several ways to estimate the heterogeneity between historical and current data in the commensurate prior, including a fully Bayesian approach, which yields the following posterior:
| (10) |
where is the prior for .
Murray et al.8 proposed a fully Bayesian approach for incorporating data of historical trials with time-to-event outcomes. Their method can be seen as a specific implementation of the commensurate prior, with a flexible piecewise exponential specification for the baseline hazard and a correlated prior process. The parameters for the baseline hazard function and the covariate effects in the current trial are centred on the corresponding parameters for the historical data. Spike-and-slab prior distributions24 are used to model the variances of these parameters for the current data, conditional on the parameters of the historical data. The method of Murray et al. assumes that there is only a single historical data set.
3.5 Test-then-pool approach
Viele et al.10 describe a simple frequentist approach to determine how the historical data are included. This test-then-pool (TTP) approach consists of performing a frequentist test to determine whether there is a significant difference in distribution between the historical and the current controls. If the p-value of this test is lower than a prespecified cut-off value (e.g. 0.05), the analysis is done with only the current data, otherwise the historical data are fully included in the analysis.
3.6 Relationships between methods
Several of these methods are related to each other. Pocock’s method, the MAP approach and the commensurate prior are similar in that these methods assume or estimate a variance parameter for the between-trial heterogeneity. Pocock’s method is equivalent to the commensurate prior for a single historical trial, except that the between-study variance is not estimated but set in advance. Pocock’s method can also be seen as a special case of the MAP approach with a single historical trial, with the variance of the bias specified as , to account for the different parameterisations of the heterogeneity.
The power prior and the MPP constitute a different family of methods, due to the weight parameter for the historical data. However, even these methods are related to the other methods. Chen and Ibrahim25 showed that in linear and generalised linear models, the results of the power prior correspond with the results of hierarchical models (i.e. the MAP approach), provided that the weight parameter α equals a specific function of the parameters of the hierarchical model, and that certain types of priors are used.
4 Statistical analysis of the HOVON trials
Based on the evaluation of Pocock’s criteria, we used data of HOVON 29 and 42 as historical trials to help estimate the intervention effect in HOVON 42A with the methods described in Section 3. To compare these methods with standard approaches, we also performed a pooled Bayesian analysis that includes the data of all trials without accounting for between-trial heterogeneity, and a Bayesian analysis of only the current trial; these methods are referred to as ‘Pooled data’ and ‘Current data’, respectively.
All Bayesian methods were implemented using a proportional hazards survival model with overall survival (until the end of follow-up) as outcome and treatment (investigational or control) and age as independent variables. Vague normal priors (i.e. ) were used for the log-hazard ratios of treatment and age. To model the baseline hazard, we used the piecewise exponential specification given by Murray et al.8 (see the supplementary material). In all methods except the method of Murray et al., a proportional hazards specification was used to model the treatment effect and the differences between trials. Only the method of Murray et al. allowed for differences in the shape of the baseline hazard between the historical and the current data.
4.1 Method-specific settings
For the specific settings of each method, we followed as much as possible the recommendations in the papers that originally proposed the methods. In Pocock’s method, the variance of the bias in the log-hazard ratio between the historical controls and the current controls was set to 0.01, which yields a standard deviation of the hazard ratio of .1 In sensitivity analyses, the variance of the bias was varied to 0.0025 and 0.04. The power prior was applied using a weight of α = 0.5. For the MPP, a Beta(1,1) prior (i.e. a uniform distribution on [0,1]) was used for α. In sensitivity analyses, we varied this prior to Beta(0.5,0.5) (i.e. Jeffreys prior) and Beta(2,2). For the MAP approach, the data of all trials were combined in a single analysis; this approach is referred to as the meta-analytic-combined approach by Schmidli et al.6 A half-normal prior was used for the between-study standard deviation of the log-hazard ratio. Following Neuenschwander et al.,5 the standard deviation parameter of this half-normal distribution was set to 0.5 and was varied to 0.25 and 1 in sensitivity analyses. The standard deviations of 0.25, 0.5 and 1 are considered to represent a moderate, substantial and large amount of between-trial heterogeneity, respectively.26
To implement the robust MAP approach, the posterior of the historical data for the piecewise constant baseline log-hazard, the covariate effects on the log-hazard scale and the logarithm of was approximated with a multivariate normal distribution. This multivariate normal distribution was then used as prior πMAP in the analysis of the current data. The robust component πrobust was created by multiplying the variance of in πMAP by 10, and this component was given a weight of . We also implemented a version of the robust MAP approach where the variances and covariances of all parameters in πrobust were increased by a factor 10. However, the results were very similar to the version in which only was robustified, and we thus do not report the results of this alternative approach.
The TTP approach was implemented by testing the effect of trial in a Cox proportional hazards model for overall survival with trial, treatment and age as independent variables. In case of a significant effect (p < 0.05) of trial, we preferred the ‘Current data’ approach; otherwise, the ‘Pooled data’ approach would be used. The method of Murray et al. was run using the priors and settings proposed in their paper.8
4.2 Posterior sampling
For each Bayesian method, the posteriors were calculated using 500,000 iterations of MCMC sampling, after 100,000 burn-in iterations. This large number of iterations was necessary to ensure convergence in the algorithms for the power prior and the MPP. Convergence was assessed using Geweke’s diagnostic. The power prior, the MPP and the method of Murray et al. were applied to a situation with multiple historical trials by pooling the data of the historical trials, so that differences between these historical trials are not modelled explicitly.
All statistical analyses were done using R and JAGS. JAGS was used for posterior sampling for the (robust) MAP approach, the method of Murray et al., the pooled analysis of all trials and the analysis of the current data. For the method of Murray et al., we used the code that was made available by the authors of that paper.8 The MCMCpack package was used to perform posterior sampling and compute the scaling constant for the power prior and the MPP.
4.3 Results
Table 2 shows the posterior distribution of the hazard ratio of the investigational treatment (G-CSF priming) in HOVON 42A using different methods for including historical data. The 95% credible interval (CI) of the hazard ratio includes the value 1 for all methods, so that there is insufficient evidence to conclude that G-CSF priming affects survival. Nevertheless, the inclusion of historical data changes the results of the analysis considerably, as is demonstrated by the difference in estimated hazard ratio between the ‘Current data’ and ‘Pooled data’ results. Including historical data reduces the posterior standard deviation of the intervention effect.
Table 2.
HOVON data: Posterior distribution of the hazard ratio of the treatment effect in the HOVON 42A trial, using different methods for including historical data.
| Method | Mean | Standard deviation | 2.5% | 97.5% |
|---|---|---|---|---|
| Current data | 1.118 | 0.132 | 0.882 | 1.398 |
| Pooled data | 0.941 | 0.083 | 0.787 | 1.113 |
| Pocock’s method | 1.008 | 0.100 | 0.823 | 1.219 |
| Power prior with α = 0.5 | 0.971 | 0.090 | 0.805 | 1.156 |
| MPP | 0.979 | 0.095 | 0.809 | 1.178 |
| MAP approach | 1.066 | 0.127 | 0.843 | 1.338 |
| Robust MAP approach | 1.094 | 0.125 | 0.871 | 1.361 |
| Method of Murray et al. | 1.107 | 0.129 | 0.876 | 1.380 |
| TTP approach | 0.941 | 0.083 | 0.787 | 1.113 |
The results in Table 2 enable us to assess how much borrowing of information occurs with the different methods, based on how close the posterior results are to either the ‘Current data’ or the ‘Pooled data’ analysis. The power prior with α = 0.5 includes half of the historical data as prior information, but the posterior mean of the hazard ratio using the power prior lies closer to the posterior mean of the ‘Pooled data’ analysis. A similar amount of borrowing is found using the MPP, and less borrowing occurs using Pocock’s method. The MAP approach, the robust MAP approach and the method of Murray et al. lead to a relatively small amount of borrowing in the HOVON data. In the TTP approach, the effect of trial was not significant (p = 0.22), so that this approach uses the results of the ‘Pooled data’ analysis.
Table 3 shows, for each method, the posterior distributions of the parameters that represent the between-trial heterogeneity and the amount of borrowing from the historical data; see also Figures S1 and S2 in the supplementary material. In Pocock’s method, the main parameter for the between-trial heterogeneity (i.e. ) is not estimated but chosen in advance. However, it is useful to investigate the posterior distributions of the trial-specific biases δ. Because δ is modelled on a log-hazard scale, the associated hazard ratio is given by . The 95% CIs of include the value 1 for both HOVON 29 and HOVON 42, indicating that these trials do not differ from HOVON 42A. The posterior standard deviations of the hazard ratios are slightly lower than the prior standard deviation of 0.10.
Table 3.
HOVON data: Posterior distributions of parameters for the amount of borrowing from historical data, using different methods for including historical data.
| Method | Mean | Standard deviation | 2.5% | 97.5% |
|---|---|---|---|---|
| Pocock’s method | ||||
| for HOVON 29 | 1.117 | 0.070 | 0.985 | 1.261 |
| for HOVON 42 | 1.047 | 0.069 | 0.919 | 1.188 |
| MPP | ||||
| α | 0.527 | 0.240 | 0.120 | 0.968 |
| MAP approach | ||||
| 0.198 | 0.166 | 0.014 | 0.648 | |
| for HOVON 29 | 1.097 | 0.183 | 0.810 | 1.527 |
| for HOVON 42 | 1.031 | 0.168 | 0.749 | 1.419 |
| for HOVON 42A | 0.922 | 0.147 | 0.640 | 1.224 |
| Robust MAP approach | ||||
| 0.160 | 0.292 | 0.003 | 0.741 | |
| for HOVON 42A | 0.953 | 0.110 | 0.683 | 1.145 |
| Method of Murray et al. | ||||
| σAge | 0.442 | 0.590 | 0.071 | 1.749 |
| 0.071 | 0.000 | 0.071 | 0.071 |
Note: An explanation of the symbols can be found in the text.
The MAP approach estimates the between-trial heterogeneity, but the 95% CIs of the between-trial standard deviation (0.01–0.65, measured on the log-hazard scale) and the trial-specific hazard ratios (i.e. ) are wide. However, the posterior distribution in Figure S1 shows that the data provide evidence for at least some between-trial heterogeneity. This figure also includes the posterior of if only the historical data are included, which is used to construct the prior πMAP in the robust MAP approach. Due to the addition of the robust component, the posterior 95% CI of in the robust MAP approach is even wider than in the MAP approach without robustification. The 95% CI for the relative weight of the historical data (α) in the MPP is wide (0.12–0.97), but the posterior in Figure S2 shows that values of α between 0.2 and 0.8 are most likely given the observed data. The sensitivity analyses in Figures S1 and S2 show that the results of the MAP approach are somewhat sensitive to the prior . A relatively limited sensitivity to was observed for the MPP.
In the method of Murray et al., separate precision parameters are estimated for the between-trial heterogeneity regarding the covariate effects (i.e. age) and the baseline hazard. These parameters were denoted as and by Murray et al., respectively. Table 3 presents the posterior distributions of the associated standard deviations, i.e. and , which are the standard deviations of the parameters (on the log-hazard scale) for the current trial, conditional on the parameters for the historical trials. The prior consists of a ‘spike’ (i.e. a point mass representing near-homogeneity of historical and current data) at and a ‘slab’ (representing between-trial heterogeneity) between and , as was used by Murray et al. The posterior mass of the spike part of was 1, so that the possibility of substantial heterogeneity was rejected. Accordingly, the posterior standard deviation of was 0.
5 Simulation study
We evaluated all methods that were applied to the HOVON data using a simulation study. The purpose of this simulation study was (a) to assess the bias and precision of the estimates and the frequentist characteristics, (b) to determine if the methods produce biased results if there is a time trend in the outcome and (c) to assess the effects of the between-trial heterogeneity on the performance of these methods. The design of the simulation study was motivated by the HOVON data.
5.1 Design of the simulation study
Survival data were generated according to a Weibull distribution with density , with shape parameter a = 0.6 and scale parameter bi depending on the trial and the treatment arm. This scale parameter was defined such that there were proportional hazard effects of trial, intervention, and, in some scenarios, a time trend. The value of bi was chosen as , with , where Trial indicates the trial number with values 1, 2 or 3 for the historical trials and 4 for the current trial, Intervention is 0 for the control arm and 1 for the investigational arm, and is the variance of the trial-specific effect on the log-hazard scale. The baseline log-hazard was set to and the values of β1, β2 and were varied between the scenarios of the simulation study. Censoring dates were generated according to a uniform distribution between t = 36 and t = 84 months, based on the average duration of follow-up in the HOVON data.
We considered six scenarios with different settings for the level of heterogeneity and the time trend in the survival outcome. See Table 4 for an overview. The time trend in Scenarios 2 and 3 was simulated by letting the survival improve with a hazard ratio of 0.95 per trial, so that ; in the other scenarios, β1 was set to 0. In Scenario 3, the trial number was included as a covariate in the analysis model, to account for the time trend. In Scenarios 1, 2 and 3, the standard deviation of the trial-specific effect on the log-hazard scale was set to , leading to a standard deviation of the hazard ratio of 0.1. All scenarios were run with two settings for the intervention effect: (a) a hazard ratio of 0.7 (i.e. ) and (b) no intervention effect (). The hazard ratio of 0.7 was chosen so that the power of the analysis of the current trial would be approximately 70%.
Table 4.
Scenarios in simulation study.
| Scenario | Time trend | Heterogeneity | Trial number included as covariate |
|---|---|---|---|
| 1: Baseline scenario | No time trend | No | |
| 2: Time trend, no adjustment | No | ||
| 3: Time trend, with adjustment | Yes | ||
| 4: No heterogeneity | No time trend | No | |
| 5: Moderate heterogeneity | No time trend | No | |
| 6: Large heterogeneity | No time trend | No |
We simulated 500 data sets with K = 3 historical trials and 1 current trial for each scenario. The sample size was 150 patients per arm for each trial, so that a simulated data set included 750 patients in total. The effects of the settings of the simulation study are visualized in Figure 2, which shows the Kaplan–Meier curves for a simulated data set in Scenario 1, and in Figures S3 to S8, which present these curves for all scenarios. These figures include 95% confidence limits (with respect to the trial-specific effect) of the population survival curves. Because some methods evaluated in this study were not designed for data sets with multiple historical studies, we also ran the simulation study with K = 1 historical trial, and thus only 450 patients per data set.
Figure 2.
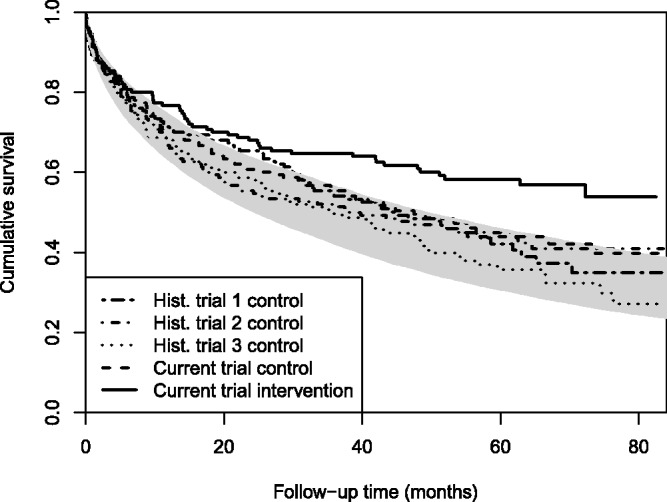
Simulation study: Kaplan–Meier curves of a simulated data set in Scenario 1, including the population survival curves (grey area) corresponding with the 2.5th and 97.5th percentile of the trial-specific effect.
To analyse the simulated data, we used the same methods and settings as for the HOVON data, including the piecewise-constant hazard function proposed by Murray et al., except that the number of intervals with piecewise-constant hazard was set to 5 (with the time axis partition chosen as the quintiles of the simulated event times), and only 150,000 MCMC iterations were used in each method. For all scenarios except Scenario 3, we adapted the code of the method of Murray et al. so that it could be run without covariates in the historical data; all parameters relating to these covariates were thus removed from the model for these scenarios. Outcome measures were the bias, posterior standard deviation and root mean square deviation (RMSD) of the log-hazard ratio of the intervention effect. For each simulated data set, these outcome measures were defined as
where is the posterior mean of β2 and is the intervention effect used to generate the data.
We also calculated the power (using ) and type I error rate (with no intervention effect) for rejecting the null hypothesis of no intervention effect, based on the 95% CI of the hazard ratio. All outcome measures were averaged over the 500 simulated data sets and calculated separately by method and scenario. The R codes of the simulation study are included in the online supplementary material.
5.2 Simulation results
Tables S1, S2 and S3 in the supplementary material present the average bias, standard deviation and RMSD of the methods in the simulation study, respectively, including 95% confidence intervals of these averages. Table S1 shows that all methods yield approximately unbiased results if there is no time trend in the outcome. In Scenario 2 (with a time trend in the survival), all borrowing methods, except the TTP approach, yield a biased estimate of the treatment effect. However, adjusting for this time trend (Scenario 3) eliminates most of this bias.
The average posterior SDs in Table S2 show the precision of the estimated treatment effect. These results can be used to determine how much information the different methods borrow from the historical data, as borrowing from the historical data increases the precision of the estimates. For all methods, the average standard deviation tends to lie between the ‘Current data’ and the ‘Pooled data’ analyses, indicating that some but not all of the historical data are used. Most borrowing of information occurs with Pocock’s method, the power prior, and the method of Murray et al., and the amount of borrowing in Pocock’s method and the power prior seems unaffected by the between-trial heterogeneity. For the other methods, the amount of borrowing is lower and depends strongly on the between-trial heterogeneity.
The average RMSDs in Table S3 show to what extent the estimation of the treatment effect is improved by the use of historical data. In Scenarios 1 to 4, all methods that use historical data perform well, with lower RMSDs than in the ‘Current data’ analysis. However, in Scenarios 5 and 6 (with a moderate or large heterogeneity), only the MAP approach and the robust MAP approach outperform the ‘Current data’ analysis.
The estimated power and type I error rates in Table 5 show that the ‘Pooled data’ analysis, Pocock’s method, the power prior and the method of Murray et al. lead to inflated type I error rates, especially in Scenarios 2, 5 and 6. The MAP approach, the robust MAP approach and the TTP approach have an estimated type I error rate close to the nominal rate of 5% in all scenarios, but these methods yield only a modest increase in power compared with the ‘Current data’ analysis, especially in Scenarios 5 and 6. Of these three methods, the MAP approach without robustification appears to yield the largest increase in power. The MPP offers a more substantial increase in power, but at the cost of an inflated (7.6% and 10.2%) type I error rate in Scenarios 5 and 6.
Table 5.
Simulation study: average power and type I error rate of the 95% credible interval of the treatment effect, based on 500 simulated data sets.
| Scenario | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Time trend | No | Yes | Yes | No | No | No |
| Heterogeneity | Small | Small | Small | None | Moderate | Large |
| Power | ||||||
| Current data | 0.690 | 0.692 | 0.690 | 0.662 | 0.668 | 0.670 |
| Pooled data | 0.842 | 0.946 | 0.728 | 0.876 | 0.734 | 0.650 |
| Pocock’s method | 0.842 | 0.930 | 0.708 | 0.854 | 0.750 | 0.660 |
| Power prior with α = 0.5 | 0.836 | 0.926 | 0.706 | 0.846 | 0.742 | 0.646 |
| MPP | 0.820 | 0.906 | 0.698 | 0.840 | 0.734 | 0.668 |
| MAP approach | 0.756 | 0.794 | 0.710 | 0.786 | 0.714 | 0.682 |
| Robust MAP approach | 0.744 | 0.772 | 0.686 | 0.738 | 0.700 | 0.682 |
| Method of Murray et al. | 0.826 | 0.924 | 0.722 | 0.858 | 0.728 | 0.672 |
| Test-then-pool method | 0.716 | 0.726 | 0.682 | 0.796 | 0.628 | 0.660 |
| Type I error rate | ||||||
| Current data | 0.042 | 0.040 | 0.040 | 0.046 | 0.040 | 0.048 |
| Pooled data | 0.096 | 0.162 | 0.064 | 0.052 | 0.254 | 0.542 |
| Pocock’s method | 0.068 | 0.118 | 0.038 | 0.040 | 0.152 | 0.428 |
| Power prior with α = 0.5 | 0.068 | 0.118 | 0.046 | 0.036 | 0.156 | 0.428 |
| MPP | 0.052 | 0.084 | 0.040 | 0.038 | 0.076 | 0.102 |
| MAP approach | 0.030 | 0.046 | 0.040 | 0.030 | 0.040 | 0.048 |
| Robust MAP approach | 0.030 | 0.040 | 0.040 | 0.034 | 0.036 | 0.048 |
| Method of Murray et al. | 0.086 | 0.138 | 0.062 | 0.044 | 0.144 | 0.172 |
| Test-then-pool method | 0.046 | 0.062 | 0.042 | 0.040 | 0.042 | 0.050 |
Note: The width of each side of the 95% binomial proportion confidence interval (not shown in the table) is approximately 2% to 3% for the type I error rate and 4% for the power.
The estimated power and type I error rates for the simulations with one historical trial (instead of three) are shown in Table S5. These results were generally similar to the results of the simulations with three historical trials, though the gain in power due to the inclusion of historical data was much lower. Surprisingly, the MAP approach and the robust MAP approach performed well in this setting, despite that there were only two trials in the meta-analysis model.
6 Discussion
Using the HOVON data, several methods for including historical data yielded substantial borrowing of information from the historical data, and thus greater precision (i.e. lower posterior SDs) of the estimated treatment effect. However, a prerequisite for including historical data in the analysis of clinical trials is that the trials are sufficiently comparable. The validity of the results using historical data may thus be questioned in this case, as not all of Pocock’s comparability criteria were satisfied. The greatest concern was the presence of a time trend in the survival over consecutive trials, which may be explained by improvements in supportive care and the consolidation phase treatment.
In the simulation study, the MAP approach yielded the best performance, with increased power and precision in every scenario (compared to an analysis without historical data), and a type I error rate close to 5%. The type I error rate was also well controlled in the robust MAP approach and the TTP approach, though the gain in power of these methods was slightly lower. The robust MAP approach provides additional safeguards for situations where the heterogeneity between the current trial and the historical trials exceeds the heterogeneity among the historical trials. Because this situation was not included in the design of the simulation study, one may prefer the robust MAP approach over the MAP approach without robustification for some applications. The MPP and the method of Murray et al. performed well in scenarios with a low between-trial heterogeneity, but had an inflated type I error rate in scenarios with a moderate or large heterogeneity. These methods all demonstrated adaptive borrowing of information: the amount of historical data used was lower in scenarios with higher between-trial heterogeneity. There is no adaptive borrowing in Pocock’s method and the power prior, because the parameters for the between-trial heterogeneity (i.e. α in the power prior and in Pocock’s method) are set in advance. We generally do not recommend to use these two methods, as they do not provide adequate safeguards against large differences between trials. Also, none of the methods showed adaptive borrowing in case of a time trend in the survival, suggesting that the methods are not robust to such biases in the historical data.
The simulation results may be used to determine which method for including historical data is most suitable for the HOVON data. The parameterisation of the heterogeneity in the MAP approach is the same as in the design of the simulation study, which means that the distribution of in the MAP approach can be linked to the values of in the scenarios of the simulation study. The values of and , which were considered to represent low, moderate and high levels of heterogeneity, correspond with the 31st, 64th and 90th percentiles of the posterior distribution of in the HOVON data, respectively. Therefore, it is not clear which scenario in the simulation study best represents the differences among the HOVON trials. We should thus adopt a method that performs well in all scenarios, such as the MAP approach or the robust MAP approach.
In the simulation study, all methods were compared using settings proposed in previous literature. However, the simulation results suggest that some of these settings may not be optimal. The MPP borrowed a relatively large amount of information from the historical data, both in the HOVON data and the simulation study, leading to inflated type I error rates. This may be due to the Beta(1,1) prior for α, which assigns little probability to values of α that lead to an exclusion of the historical data. A more sceptical prior, with more probability mass assigned to values close to 0, could lead to a better trade-off of power and type I error rate. Such overenthusiastic borrowing from the historical data was also observed for the method of Murray et al. Future simulation studies could investigate the optimal settings for the priors of these methods. The most appropriate implementation of the robust MAP approach for models with multiple parameters, including which parameters should be ‘robustified’, should also be further investigated.
Ideally, one would use the inclusion of historical data at the design stage of a new trial, so that fewer (control) patients have to be recruited. Using standard formulas for power analysis, the increase in power of the MAP approach versus the ‘Current data’ analysis from 0.69 to 0.76 in Scenario 1 and from 0.67 to 0.71 in Scenario 5 corresponds with approximate reductions of the sample size of 14% and 10%, respectively. See also Table S4 in the supplementary material and the results for the prior effective sample size reported by Neuenschwander et al.5 Although such sample size reductions are useful, they are not spectacular. Disadvantages of reducing the number of current controls are that (a) it becomes more difficult to detect whether the current data are in conflict with the historical data, and (b) in case of such a conflict, the methods with adaptive borrowing may discard the historical data, leaving insufficient power for the analysis of the current trial. This latter problem may be addressed by implementing adaptive randomisation designs.6
The HOVON data were chosen in this study because these data have characteristics that are advantageous for the use of historical data, as these are consecutive trials on the same disease and sponsored by the same organisation. Nevertheless, we found that not all of Pocock’s criteria were satisfied. The requirements that the historical trials (a) had the same control arm treatment, (b) were recent trials and (c) were conducted by the same organisation seem difficult to satisfy in general. There are not many research organisations that perform several trials on the same disease in a relatively short period of time, especially not in an academic setting, though this could be more common in industry-sponsored trials. Further research on how stringently such comparability criteria should be applied thus seems warranted.
The results of the HOVON data also illustrate the dangers of including older historical data in situations where the outcome improves over time. Such improvements in the outcome violate the exchangeability assumption underlying Pocock’s method and the MAP approach, because the between-trial differences do not have mean zero in that case. Borrowing of information from historical controls may then lead to an upward bias in the estimated treatment effect. We therefore recommend to carefully check the data for any time trends in the outcome, especially when the historical data are not recent.
Several limitations of the analyses in this article should be mentioned. We compared different methods using only a single application in which there was no significant effect of the investigational treatment; other data sets could potentially yield different results. However, we believe that the HOVON trials are representative for other clinical contexts where historical data are available. The amount of borrowing of information from the historical data would likely have been similar if there had been a significant treatment effect in the current trial, as in most methods the amount of borrowing is mainly determined by the differences among the control arms of all trials. In addition, we made no attempt to find the optimal settings and priors for the compared methods and instead relied on the values suggested in previous literature. It is possible that some methods would perform better with different priors, especially for the parameters that determine the amount of borrowing. The implementations of the power prior, the MPP and the method of Murray et al. did not take into account that there were multiple historical trials, and instead used the pooled data of the historical trials. Finally, we did not consider all available methods for including historical data, such as the commensurate power prior.23
7 Conclusions
It seems possible to improve the power and precision of the analysis of a clinical trial and simultaneously control the type I error rate, by including historical trials that are sufficiently comparable to the current trial. To do so, it is necessary to use a method that accounts for between-trial heterogeneity, such as the MAP approach or the robust MAP approach, so that the historical data are included adaptively. However, in many practical settings, historical data that satisfy the criteria for comparability may not be available. To ensure that these methods will be accepted by regulatory authorities and adopted by clinical researchers, further research is needed to determine in what situations the application of these methods is feasible.
Supplementary Material
Acknowledgements
The authors would like to thank two anonymous referees for useful comments that have helped to improve the quality of this article. In addition, the authors thank the Erasmus MC Cancer Computational Biology Center for giving access to their server, which was used for the computations of the simulation study.
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding
The author(s) received no financial support for the research, authorship, and/or publication of this article.
Supplementary material
Supplementary material is available for this article online.
References
- 1.Pocock SJ. The combination of randomized and historical controls in clinical trials. J Chron Dis 1976; 29: 175–188. [DOI] [PubMed] [Google Scholar]
- 2.Ibrahim JG, Chen MH. Power prior distributions for regression models. Stat Sci 2000; 15: 46–60. [Google Scholar]
- 3.Duan Y, Ye K, Smith EP. Evaluating water quality using power priors to incorporate historical information. Environmetrics 2006; 17: 95–106. [Google Scholar]
- 4.Neuenschwander B, Branson M, Spiegelhalter DJ. A note on the power prior. Stat Med 2009; 28: 3562–3566. [DOI] [PubMed] [Google Scholar]
- 5.Neuenschwander B, Capkun-Niggli G, Branson M, et al. Summarizing historical information on controls in clinical trials. Clin Trial 2010; 7: 5–18. [DOI] [PubMed] [Google Scholar]
- 6.Schmidli H, Gsteiger S, Roychoudhury S, et al. Robust meta-analytic-predictive priors in clinical trials with historical control information. Biometrics 2014; 70: 1023–1032. [DOI] [PubMed] [Google Scholar]
- 7.Hobbs BP, Sargent DJ, Carlin BP. Commensurate priors for incorporating historical information in clinical trials using general and generalized linear models. Bayesian Analy 2011; 7: 639–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Murray TA, Hobbs BP, Lystig TC, et al. Semiparametric Bayesian commensurate survival model for post-market medical device surveillance with non-exchangeable historical data. Biometrics 2014; 70: 185–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cuffe RL. The inclusion of historical control data may reduce the power of a confirmatory study. Stat Med 2011; 30: 1329–1338. [DOI] [PubMed] [Google Scholar]
- 10.Viele K, Berry S, Neuenschwander B, et al. Use of historical control data for assessing treatment effects in clinical trials. Pharm Stat 2014; 13: 41–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Löwenberg B, Boogaerts MA, Daenen SM, et al. Value of different modalities of granulocyte-macrophage colony-stimulating factor applied during or after induction therapy of acute myeloid leukemia. J Clin Oncol 1997; 15: 3496–3506. [DOI] [PubMed] [Google Scholar]
- 12.Löwenberg B, van Putten W, Theobald M, et al. Effect of priming with granulocyte colony-stimulating factor on the outcome of chemotherapy for acute myeloid leukemia. New Engl J Med 2003; 349: 743–752. [DOI] [PubMed] [Google Scholar]
- 13.Löwenberg B, Pabst T, Vellenga E, et al. Cytarabine dose for acute myeloid leukemia. New Engl J Med 2011; 364: 1027–1036. [DOI] [PubMed] [Google Scholar]
- 14.Pabst T, Vellenga E, van Putten W, et al. Favorable effect of priming with granulocyte colony-stimulating factor in remission induction of acute myeloid leukemia restricted to dose escalation of cytarabine. Blood 2012; 119: 5367–5373. [DOI] [PubMed] [Google Scholar]
- 15.Breems DA, Van Putten WL, Huijgens PC, et al. Prognostic index for adult patients with acute myeloid leukemia in first relapse. J Clin Oncol 2005; 23: 1969–1978. [DOI] [PubMed] [Google Scholar]
- 16.Bernardo JM. The concept of exchangeability and its applications. Far East J Math Sci 1996; 4: 111–122. [Google Scholar]
- 17.Ibrahim JG, Chen MH, Gwon Y, et al. The power prior: theory and applications. Stat Med 2015; 34: 3724–3749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chen MH, Ibrahim JG, Shao QM. Power prior distributions for generalized linear models. J Stat Plan Infer 2000; 84: 121–137. [Google Scholar]
- 19.Ibrahim JG, Chen MH, Chu H. Bayesian methods in clinical trials: a Bayesian analysis of ECOG trials E1684 and E1690. BMC Med Res Methodol 2012; 12: 183–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Birnbaum A. On the foundations of statistical inference. J Am Stat Assoc 1962; 57: 269–306. [Google Scholar]
- 21.Friel N, Pettitt AN. Marginal likelihood estimation via power posteriors. J R Stat Soc Ser B (Stat Methodol) 2008; 70: 589–607. [Google Scholar]
- 22.Duan Y. A modified Bayesian power prior approach with applications in water quality evaluation. PhD Thesis, Virginia Polytechnic Institute and State University, 2005.
- 23.Hobbs BP, Carlin BP, Mandrekar SJ, et al. Hierarchical commensurate and power prior models for adaptive incorporation of historical information in clinical trials. Biometrics 2011; 67: 1047–1056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.George EI, McCulloch RE. Variable selection via Gibbs sampling. J Am Stat Assoc 1993; 88: 881–889. [Google Scholar]
- 25.Chen MH, Ibrahim JG. The relationship between the power prior and hierarchical models. Bayesian Anal 2006; 1: 551–574. [Google Scholar]
- 26.Spiegelhalter DJ, Abrams KR, Myles JP. Prior distributions. In: Bayesian approaches to clinical trials and health-care evaluation, New York: Wiley, 2004. chapter 5, pp. 139–180. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


