Pressure-induced phase transitions and superconductivity in a black phosphorus single crystal

Significance

A high-pressure study of a black phosphorus crystal establishes a rich phase diagram, including Weyl semimetal and superconducting states, Lifshitz-type semiconductor–semimetal transitions, and two structural phase transitions. Transport properties and quantum oscillations under high pressure provide critically valuable information to understand the physics of these new phases. The pressure dependence of physical properties has been reliably measured under hydrostatic pressure and applied magnetic fields using a large-volume apparatus. Superconductivity in the A7 phase has been found to exhibit the largest magnetoresistance effect observed in its normal state so far. The Bardeen–Cooper–Schrieffer superconductivity in the A7 phase identified by the experiment can be accounted for by the phonon mechanism based on a first-principles calculation.

Abstract

We report a thorough study of the transport properties of the normal and superconducting states of black phosphorus (BP) under magnetic field and high pressure with a large-volume apparatus that provides hydrostatic pressure to induce transitions from the layered A17 phase to the layered A7 phase and to the cubic phase of BP. Quantum oscillations can be observed at P ≥ 1 GPa in both resistivity and Hall voltage, and their evolutions with pressure in the A17 phase imply a continuous enlargement of Fermi surface. A significantly large magnetoresistance (MR) at low temperatures is observed in the A7 phase that becomes superconducting below a superconducting transition temperature T_c ∼ 6–13 K. T_c increases continuously with pressure on crossing the A7 to the cubic phase boundary. The strong MR effect can be fit by a modified Kohler’s rule. A correlation between T_c and fitting parameters suggests that phonon-mediated interactions play dominant roles in driving the Cooper pairing, which is further supported by our density functional theory (DFT) calculations. The change of effective carrier mobility in the A17 phase under pressure derived from the MR effect is consistent with that obtained from the temperature dependence of the quantum oscillations. In situ single-crystal diffraction under high pressure indicates a total structural reconstruction instead of simple stretching of the A17 phase layers in the A17-to-A7-phase transition. This finding helps us to interpret transport properties on crossing the phase transition under high pressure.

Interest in black phosphorus (BP) as an emerging 2D material has been revived after exploring graphene and transition-metal dichacolgenides (1–6). In addition to the semiconducting A17 phase with the arm-chaired layer structure, BP has another two allotropic modifications under pressure, a layered A7 phase at 5 ≤ P < 10 GPa and a cubic (C) phase at P ≥ 10 GPa. Both high-pressure phases are superconducting. Recent high-pressure studies with a piston-cylinder cell have revealed an interesting transition from semiconductor to topological semimetal within the A17 phase at P ∼ 1 GPa (7). However, the transitions to those high-pressure phases occur at pressures out of the pressure range of the piston-cylinder devices (8); measurements of transport properties in the A7 and the C phases have been performed so far in a diamond anvil cell (DAC) and a multianvil device with a solid pressure-transmitting medium (9, 10). The importance of the choice of pressure medium and the construction of devices in the high-pressure study is never overexaggerated. The gas phase is ideal for the pressure medium, but it suffers a huge volume collapse under pressure and is not sustained at higher pressure. Shear stress is a major concern when a liquid phase is used, which varies among common fluids used as the pressure medium (11). The nonhydrostatic component in a fluid pressure medium is significantly reduced if the high-pressure chamber is compressed from multiple directions (12). The physical properties of most 2D materials are extremely sensitive to a nonhydrostatic pressure that can alter the physical properties dramatically in some cases (13, 14). Therefore, it is highly desired to perform a thorough study of BP with a liquid-filled, large-volume multianvil device to reveal the intrinsic physical properties of the A7 phase and the C phase.

In the A17 phase of BP, arm-chaired layers are held together by the van der Waals force (15). Under ambient conditions, bulk BP has a direct band gap of about 0.3 eV at the Z point of the Brillouin zone (16). Although the volume of BP decreases dramatically under pressure, a reduction of 26% at 10 GPa (9, 17, 18), physical properties change even more remarkably under pressure. Hydrostatic pressure induces a Lifshitz-like semiconductor–semimetal transition at P ∼ 1 GPa by closing up the direct gap (19). Increasing pressure slightly further in a narrow pressure near 1.0 GPa or applying surface charges induces a topological transition with band inversion, which results in two Dirac points near the Z point (7, 19, 20). The lack of inversion symmetry in the A17 phase converts the 2D Dirac semimetal into a Weyl semimetal (20). A negative magnetoresistance (MR) for B // I, consistent with the chiral anomaly characteristic of a Weyl semimetal, has indeed been reported in a high-pressure transport study (7). The Weyl semimetal phase of BP shows no sign of superconductivity down to 45 mK (21). Most previous studies were performed in the A17 phase and report an extremely large MR effect and quantum Shubnikov–de Haas (SdH) oscillations under high pressure (7, 10, 16, 19–26). Superconductivity in BP occurring right after the A7 phase is induced at P ≥ 5 GPa (27–29). Transport properties in the normal state of the A7 and the C phases and their relationship to superconductivity have been studied based mainly on measurements with a DAC and a multianvil device in which the solid pressure-transmitting medium used can exert a strong pressure inhomogeneity or uniaxial stress on the sample (10, 30). The most-cited high-pressure study (27) in the early days was actually made on a powder sample. It is unclear how the normal-state properties of BP are influenced by the uniaxial strains created in the devices with solid pressure media (31).

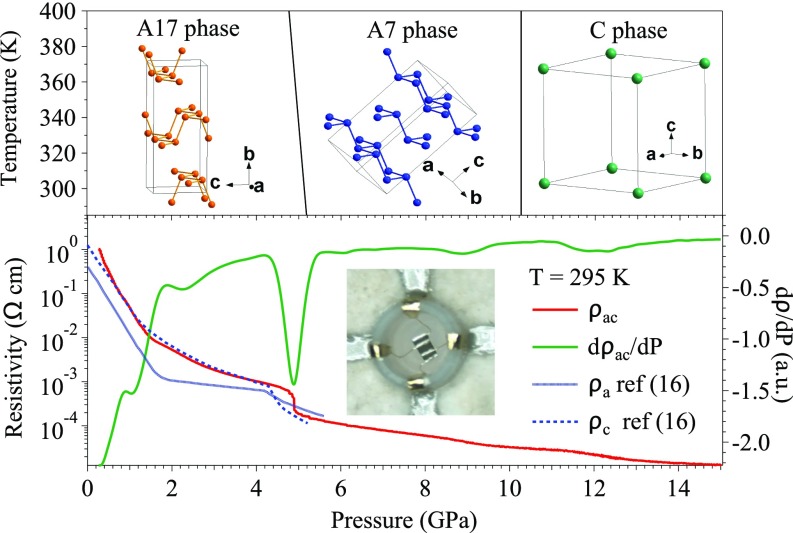
To unveil the intrinsic properties of the A7 and C phases under high pressures, we performed detailed measurements of magnetotransport properties with a large-volume cubic-anvil-cell apparatus that can maintain an excellent hydrostatic pressure condition (32–34) across the three phases of BP. In our measurements, a BP crystal grown under high pressure and temperature was cut into a rectangular bar (0.33 × 0.05 × 0.50 mm³) with the shortest dimension along the b axis. Fig. 1, Inset shows a picture of our sample assembly for the resistivity measurement with four-probe leads on the a–c plane crystal surface. The sample with leads is hung inside a Teflon capsule filled with glycerol as the pressure-transmitting medium. The magnetic field is applied along the b axis of the A17 phase. Detailed information about measurements with the cubic anvil cell can be found in SI Appendix. The sample thickness is important for measurements of transport properties in the A7 phase since the configuration can still pick up a significant contribution in the buckled layers if a layer is formed at 45° to the b–c plane of the A17 phase. In contrast, measurements on a flake sample with a DAC are dominated by the contribution normal to the layer in the A7 phase.

Fig. 1.

Pressure dependence of structural transition and zero-field resistivity. The top illustrates BP undergoes a reversible sequence of phase transitions under pressures from an orthorhombic A17 phase to a rhombohedral A7 phase at about 5 GPa and then to a simple-cubic C phase at about 10 GPa (17). The bottom shows the pressure dependence of resistivity at RT. (Inset ) The four-probe configuration for magnetoresistivity measurements in the cubic-anvil-cell apparatus.

Results and Discussion

Resistivity.

Fig. 1 shows the pressure dependence of resistivity at room temperature (RT). The pressure-induced A17-to-A7-phase transitions can be clearly discerned from the abrupt drop of ρ at 5 GPa, which is consistent with ρ(P) data in the literature (24) and also matches the critical pressure extracted from pressure-dependent structural studies (35). In contrast, there is only a weak kink in ρ(P) at ∼10 GPa where the A7-to-C-phase transition occurs in the structural study (17). In addition, a slope change is clearly visible at P ∼ 1–1.5 GPa, which is close to the reported critical pressure of 1.2 GPa for a pressure-induced Lifshitz transition obtained with a piston-cylinder cell (19).

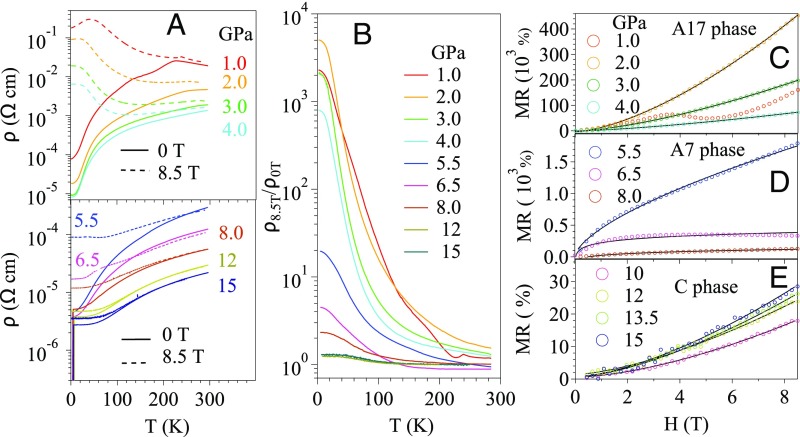
Reliable resistivity data carry information that is critically important to understand the electronic states in all three phases of BP. Specifically, the magnetic field dependence of resistivity sheds light on the charge carrier density, the mobility, and the ratio of electron–electron to electron–phonon interactions. The temperature dependence of resistivity ρ(T) under H = 0 and 8.5 T at various pressures is shown Fig. 2A. In zero field, the application of 1 GPa pressure closes up the direct band gap and results in a metallic behavior, as has also been reported previously (24). The anomalous hump around 220 K has been attributed to reduced thermal excitation of carriers during cooling at T > 220 K (21). This argument is not fully supported by the result of thermoelectric power measurement under the same pressure, in which no anomaly can be detected near 220 K (see the results in SI Appendix, Fig. S1). However, a clear anomaly does occur at 250 K in S(T) at the same pressure with a magnetic field H = 8 T. The anomaly of ρ(T) at 220 K disappears at P = 3 GPa. The resistivity at 1 GPa drops more than two orders in magnitude as the sample is cooled down from RT to 1.5 K, the largest drop ever reported for BP in the literature. The ratio ρ_300K/ρ_1.5K is normally used as a measurement of a metallic sample’s quality, the higher the better. In this case, hydrostatic pressure generated in the cubic anvil cell may also be a factor to differentiate our result from those in the literature. The evolution of the normal state ρ(T) shows no sign of structural transitions at 5 GPa and 10 GPa. Like other materials showing an extremely large MR (36, 37), ρ(T) at H = 8.5 T and P = 1 GPa increases dramatically relative to that of zero field by three orders of magnitude at low temperatures and shows a broad hump at low temperatures. This magnetic-field-induced upturn in ρ(T) moves progressively to lower temperatures upon increasing pressure within the A17 phase (P < 5.5 GPa), and completely disappears as BP enters the A7 phase (P > 5.5 GPa). However, a significant MR effect remains at low temperatures for the A7 and even the C phases, as is shown in Fig. 2B.

Fig. 2.

Temperature dependence of resistivity ρ(T) of BP (A) under 0 T and 8.5 T between 1 and 15 GPa and (B) normalized ρ_8.5T/ρ_0T. (C–E) Magnetic field dependence of MR at 1.5 K under various pressures up to 15 GPa: (C) A17 phase, (D) A7 phase, and (E) C phase. Open circles symbolize the experimental data and black solid lines denote the fitting curves with the modified Kohler’s model.

It is important to note that the Lifshitz transition at P ∼ 1 GPa changes the ρ(T) from activated to metallic with a power law (ρ ∼ Tⁿ) at low temperatures. A nearly temperature-independent ρ(T) at low temperatures can be accounted for by a two-carrier model without involving any effects due to electron–electron correlations. The behavior of the ρ(T) of BP on crossing the semiconductor–semimetal transition is in sharp contrast to that of a pressure-induced Mott insulator-to-metal transition where non-Fermi-liquid behavior with a power law exponent n ∼ 1–1.5 is normally observed at a quantum critical point as a long-range magnetic order is suppressed (38, 39).

Magnetoresistivity.

Fig. 2B shows the temperature dependence of the MR under different pressures. Within the A17 phase, the MR is dramatically enhanced as temperature decreases, saturating below 20 K. The MR value at 2 K and 2 GPa is similar to that at nearly the same pressure and temperature obtained with a piston-cylinder device (19). The MR remains significant even in the A7 and C phases in which superconductivity occurs at low temperatures. To our knowledge, the A7 phase of BP is the superconductor with the largest normal-state MR effect. This finding makes BP more interesting in a study of the relationship between normal-state properties and the superconducting transition. It is important to note that WTe₂ shows an extremely large MR effect only at low temperatures; at 100 K the MR effect is less than an order of magnitude (36). In contrast, the MR effect of BP at 1–2 GPa is still more than an order of magnitude at 100 K and it remains noticeable even at RT. In addition, the emergence of superconductivity in WTe₂ is accompanied by the suppression of a large MR (40).

In Boltzmann transport theory, MR in conductors arises from Lorentz-force deflection of electronic trajectories and is directly related to the electronic scattering path around the Fermi surface (FS). At a given charge carrier density $n_c$ and single relaxation time $\tau$ at all points on the FS, relative MR in a magnetic field H satisfies Kohler’s rule (41):

$$\text{MR}\equiv \frac{\rho \left(H\right)-\rho \left(0\right)}{\rho \left(0\right)}=F\left(H\tau \right).$$ [1]

By assuming that the mean mobility of carriers ${\mu }_m$ is proportional to $e\tau /m^{\ast }$, where $e$ and $m^{\ast }$ represent the electron charge and effective mass, respectively, and $m^{\ast }$ is weakly temperature-dependent. Kohler’s rule in an isotropic two-band model can be simplified to the approximate form (42)

$$\text{MR}={\left({\mu }_{m}H\right)}^2,$$ [2]

the same conclusion as inferred from the proposed compensative theory for the A17 phase (19). However, the isotropic assumption is apparently not applicable to highly anisotropic BP with orthorhombic symmetry (25). The anisotropic band structure near the Fermi level which is related to the effective mass and the variation of relaxation time $\tau$ with directions may result in a violation of the MR from the quadratic field dependence in Eq. 2. To verify this consideration, we measured the field dependence of MR at 1.5 K under various pressures, as summarized in the Fig. 2 C–E. At 1 GPa, an anomalous kink was observed that can be ascribed to the Adler–Bell–Jackiw anomaly in a Weyl semimetal (7); due to the large anisotropy discussed below or to a small tilt angle relative to the original sample’s position under high pressure, the chiral term $\left(e^3/4{\pi }^2{\hslash }^2\right)\mathit{E}\cdot \mathit{H}$ near the Lifshitz transition (43) can acquire a dipolar component that grows rapidly as H increases so as to result in a negative contribution to the MR. At 2 GPa, the positive MR reaches about 450,000% in a magnetic field of 8.5 T without any sign of saturation. With further pressure increase, the MR decreases dramatically, but it still remains significantly large in the A7 phase before it finally drops to a moderate value in the C phase. Apparently, the MR cannot be simply described by an $H^2$ power law in any of the three phases. Instead, we have to fit the MR data using a modified Kohler’s model (44):

$$\text{MR}={\left({\mu }_m{\gamma }_{m}H\right)}^2={{\mu }_m}^2{H}^{2-2\epsilon },$$ [3]

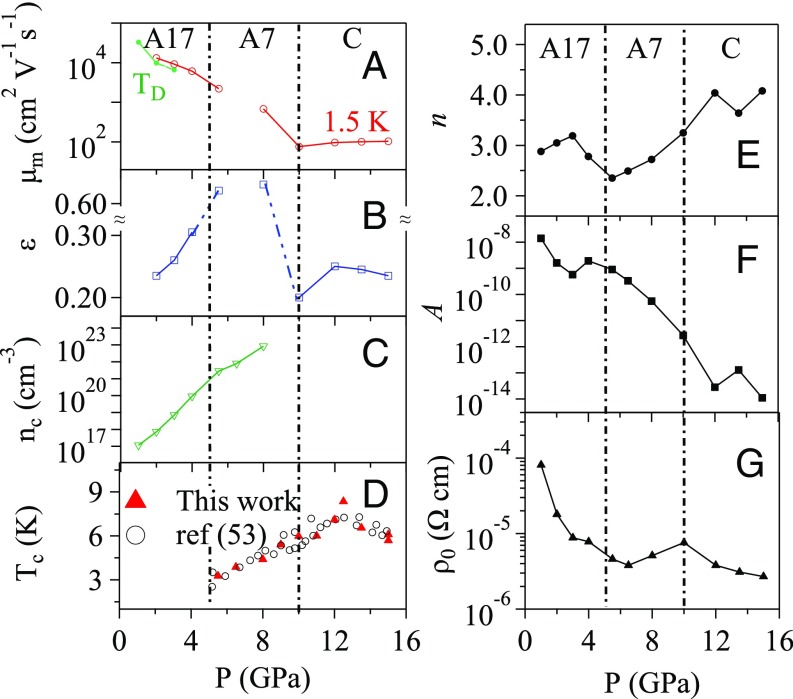
where the H-dependent anisotropic factor ${\gamma }_m\propto H^{-\epsilon }$ is intimately related to the field-induced changes to the FS and reflects an averaged anisotropic effect. The quality of the fit is clear in Fig. 2 C–E and the fitting parameters ${\mu }_m$ and $\epsilon$ as a function of pressure are plotted in Fig. 3 A and B, respectively. We have found that the mean carrier mobility ${\mu }_m$ is 1.3 × 10⁴ cm²⋅V⁻¹⋅s⁻¹ at 1.5 K for 2 GPa, which is the same order of magnitude as in a previous report (16). The value of ${\mu }_m$ rapidly decreases on crossing the A17-to-A7-phase boundary from 2 GPa to 10 GPa. ${\mu }_m$ again changes sharply across the boundary between the A7 and C phases and shows a slight increase with pressure in the C phase. An $\epsilon \approx 0.25$ in the A17 phase can be well-related to the highly anisotropic crystal structure (i.e., the arm-chaired layer and the weak coupling between layers by the van der Waals force). A similar $\epsilon$ found in the C phase cannot be attributed to the crystal structure, which is isotropic. Since the pressure-induced structural transitions among A17, A7, and C phases are reversible; no long-range atomic diffusion occurs in these phase transitions. The distribution of impurities residing in the A17 phase as the crystal is formed must follow a pattern compatible with the layered structure; the impurity distribution pattern is likely to be transferred in the C phase. We believe it is the origin why an anisotropic parameter similar to that in the A17 phase can be obtained in the C phase. Moreover, the slight variation with pressure of the anisotropic exponent $\epsilon$ in the A7 and C phases may be correlated to the mass renormalization effect or impurity scattering (45).

Fig. 3.

(A–G) The fitting parameters from the transport properties and superconducting transition temperature as a function of pressure across A17, A7, and C phases. Error bars are smaller than symbols.

In sharp contrast, the MR in the A7 phase shows a striking deviation from the MR found in either the A17 or the C phase; fitting the data with Eq. 3 gives an abrupt increase of $\epsilon \approx 0.70$ at 5.5 GPa and 8.0 GPa in the A7 phase. Moreover, fitting the data at 6.5 GPa to Eq. 3 failed. The MR at 6.5 GPa increases at low fields, but it decreases slightly as field further increases. This behavior is totally different from the prediction of Eq. 3, which gives a nonsaturated MR. An anomalously high $\epsilon$ obtained from fitting the data at 5.5 GPa and 8.0 GPa to Eq. 3 and a total failure for the fitting at 6.5 GPa call our attention to the mechanism of the A17-to-A7-phase transition and the experimental setup for measuring the MR effect in the A7 phase. There are two scenarios to explain the phase transition from A17 to A7: (i) The buckled layers in the A7 phase come directly from stretching the arm-chaired layers in the A17 phase (46) and (ii) P–P bonds form in some locations between the layers in the A17 phase and some bonds inside layers are broken, which give new layers of A7 phase along ∼45° projected on the b–c plane in the A17 phase (47, 48). In scenario ii, while H is still normal to the current direction as shown in Fig. 1, the current is no longer carried by electrons moving within layers and the field is not normal to layers in the A7 phase. To verify the mechanism of phase transition, we have carried out a single-crystal diffraction under pressure. The detailed information about this experiment is provided in SI Appendix. Based on Bragg’s law, $2d_{hkl}\text{sin}{\theta }_{hkl}=\lambda$, the X-ray diffraction pattern maps the crystal planes. Where the X-ray beam was normal to the arm-chaired layers of the A17 phase we observed only a single bright spot at the 2θ angle of ∼25° (d ∼ 1.65 Å), which is the (151) plane in the A17 phase. A diffraction spot at more or less the same location corresponding to the (110) plane of the A7 phase is expected (details provided in SI Appendix) if the layered structure is formed as described in scenario ii, which is indeed what we have observed. Therefore, the measurement configuration for the resistivity in Fig. 1 will pick up a combined response as the current flows within layers and between layers, whereas the field was applied along a direction about 45° normal to the buckled layers of the A7 phase. As a result, the MR effect highly depends on any subtle rotation of the sample in the cell under an assumption that the MR effect in the A7 phase is highly anisotropic. A strong angular dependence of MR has also been reported in a 3D Dirac semimetal Cd₃As₂, and actually an MR curve at a tilt angle of <5° is stunningly similar to that of BP at 6.5 GPa (49).

The metallic conductivity in all three phases with H = 0 has been fit to the power law, $\rho \left(T,0\right)={\rho }_0+A{T}^n$, where ${\rho }_0$ is the residual resistivity. The fitting has been carried out in ρ(T,0) at different pressures below 40 K. The fitting parameters are displayed in Fig. 3 E–G. Corresponding to the dramatic change of the MR effect on crossing the three phases, parameters of fitting to the power law also show anomalies at the phase boundaries. The n > 2 in the power law rules out the possibility of applying the Fermi liquid mode to describe the metallic phase in the A17 phase and the normal-state resistivity in the A7 and C phases. It is at the A17-to-A7-phase boundary that a minimum n close to 2 has been obtained. The residual resistivity ${\rho }_0$ reflects the scattering between electrons and impurities in a crystal, which normally shows a very small pressure dependence, especially in a single-crystal sample. A steeper decrease of ${\rho }_0$ by more than one order in magnitude in the metallic A17 phase as pressure increases is remarkable. Since ${\rho }_0$ is inversely proportional to the Fermi momentum k_F (50), the change of ${\rho }_0$ is caused by a substantial enlargement (by one order) of the FS over the same pressure range derived from our SdH study below. Similar results of the FS change under pressure have also been reported in the literature (19, 21). An increase of ${\rho }_0$ with pressure in the A7 phase is highly unusual; it must be correlated to a change of the conducting pathway through the layer and between the layers in the A7 phase under pressure. The phase boundary at 10 GPa marks an end of this unusual pressure dependence of ${\rho }_0$. The initial sharp drop of ${\rho }_0$ with increasing pressure may be caused by a two-phase (A7 and C) coexistence.

Hall Resistivity.

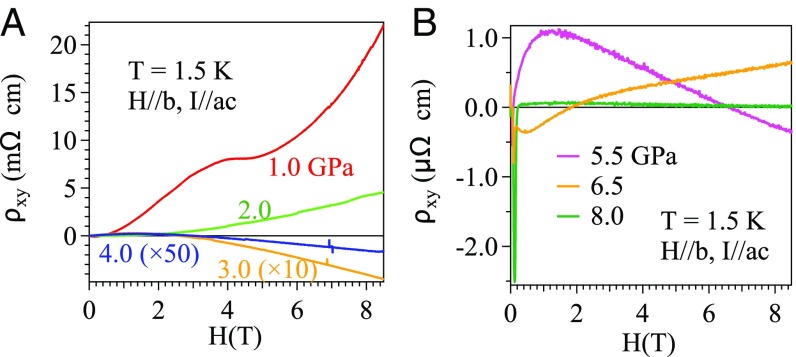
We have measured the Hall resistivity, which can probe the charge carrier density and mobility qualitatively. Fig. 4 shows the field dependence of Hall resistivity ρ_xy at 1.5 K, which changes remarkably with increasing pressure. It should be noticed that the results presented in Fig. 4 are significantly different from those in the literature (9). A discussion about the difference between these results is given in SI Appendix. Considering the case of two carriers, the Hall resistivity ρ_xy can be described as in ref. 21:

$${\rho }_{xy}=\frac{H}{e}\frac{\left(n_h{{\mu }_h}^2-n_e{{\mu }_e}^2\right)+(n_h-n_e){{\mu }_h}^2{{\mu }_e}^2{H}^2}{{\left(n_h{\mu }_h+n_e{\mu }_e\right)}^2+{(n_h-n_e)}^2{{\mu }_h}^2{{\mu }_e}^2{H}^2},$$ [4]

where $n_{h,\hspace{0.17em}e}$ and ${\mu }_{h,e}$ denote the carrier densities and mobilities of electron and hole, respectively. In the high-field limit ($H\gg {{\mu }_{h,e}}^{-1}$), the Hall coefficient $R_H\equiv d{\rho }_{xy}/dH=1/e\left(n_h-n_e\right)$ only depends on the difference in densities of hole and electron carriers ($n_h-n_e)$, but not on their mobility. Thus, the good linearity of ${\rho }_{xy}$ at high fields (SI Appendix) in both the A17 and A7 phases indicates the effective carrier density $n_c\equiv \left|\frac{1}{e{R}_H}\right|=\left|n_h-n_e\right|$ in the high-field region is a constant at each pressure, which justifies the assumption that the modified Kohler’s rule is applicable in our case. The calculated effective carrier density $n_c$ is plotted in Fig. 3C, which shows a great enhancement with increasing pressure. R_H in the A17 phase changes sign between 2 GPa and 3 GPa. The low-field behavior of ρ_xy could be influenced by the superconductivity in the A7 phase. The sign change of R_H at higher fields as a function of pressure appears not to follow a clear trend. This anomalous behavior may be related to the fact that the angle between the normal direction of layers in the A7 phase and the magnetic field direction is about 45°. In this situation, R_H is highly sensitive to any tilting on the sample caused by applying pressure. As summarized in Fig. 3, our study on a BP crystal with the multianvil device gives evidence that the pressure-induced structural transitions can be well distinguished by the transport properties. The Hall resistivity versus field at low fields is not linear due to the field-dependent balance between electrons and holes. This observation does not alter the discussion and the conclusion above since they are based on the data at the high-field limit where ${\rho }_{xy}\left(H\right)$ approaches a linear behavior.

Fig. 4.

Field dependence of Hall resistivity ρ_xy in a pressure range from (A) 1.0 GPa to 4.0 GPa and (B) 5.5 GPa to 8.0 GPa at 1.5 K.

SdH Oscillation.

SdH oscillations have been reported in the semimetal A17 phase at P ≥ 1 GPa, which reflects the change of FS at different pressures (7, 19, 21). SI Appendix, Fig. S5 shows the SdH oscillations (obtained from the second derivative of longitudinal magnetoresistivity ρ_xx) and the corresponding fast Fourier transform at different temperatures under three pressures. Our findings show that the major frequency component α moves substantially from ∼4.0 T (2) at 1 GPa to ∼28.0 T (5) at 2 GPa and to ∼67.0 T (9) at 3 GPa. The increase in the major frequency component with increasing pressure implies a change in dimensions of a single cyclotron orbit of a multisheeted FS. Accordingly, the cross-sectional area of FS is determined as 4.4 nm⁻² at 1 GPa, ∼26.8 nm⁻² at 2 GPa, and ∼65.8 nm⁻² at 3 GPa. SdH oscillations become indiscernible in the A17 phase for P > 3 GPa due to a much-enlarged FS. SI Appendix, Fig. S6, Inset displays the inverse fields corresponding to dips of oscillations as a function of the Landau index n_L. The intercepts at B⁻¹ = 0 of the linear extrapolations of B⁻¹ versus n_L axis yield the SdH phase value of −γ + δ as 0.15(1), 0.18(1), and 0.08(1) for 1, 2, and 3 GPa, respectively. Since the correction term δ varies within ±1/8 in the 3D limit (51), our results indicate a phase factor γ ≈ 0, which suggests a nontrivial Berry phase ϕ_B = π via the relationship γ = 1/2 − ϕ_B/2π. Our result agrees well with previous reports (7, 19). Moreover, by analyzing the temperature dependence of SdH oscillations in SI Appendix, Fig. S5, we can quantitatively obtain information about the mean mobility ${\mu }_m$. The amplitude of the oscillations ∆R is suppressed as temperature increases and can be described by the relation (52)

$$\mathrm{\Delta }R\propto \frac{\lambda T}{\sin h\left(\lambda T\right)}exp\left(-\lambda T_D\right),$$ [5]

where $\lambda =2{\pi }^2{k}_B/\hslash {\omega }_c$, ${\omega }_c=eB/m^{\ast }$, with Dingle temperature $T_D=\hslash /2\pi k_B\tau$. As shown in SI Appendix, Fig. S7, the best fit to Eq. 5. of our experimental data yields the effective mass $m^{\ast }$ of 0.041(1)m₀, 0.202(1)m₀, and 0.162(1)m₀ and a Dingle temperature $T_D$ of 15.3 K, 10.7 K, and 19.7 K for 1 GPa, 2 GPa, and 3 GPa, respectively. Such nonmonotonic trends of $m^{\ast }$ and $T_D$ reveal the changes of nonparabolic band dispersion under pressure. The corresponding effective mobility ${\mu }_m=e\tau /m^{\ast }$ can be calculated as 0.33 × 10⁴ cm²⋅V⁻¹⋅s⁻¹, 0.098 × 10⁴ cm²⋅V⁻¹⋅s⁻¹, and 0.066 × 10⁴ cm²⋅V⁻¹⋅s⁻¹ from 1 GPa to 3 GPa; the mobility is superimposed in Fig. 3A. The mobility derived from SdH oscillations is slightly smaller than that from the MR analysis since the former is based on data obtained at an average temperature of ∼10 K, whereas the latter is strictly at 1.5 K. The temperature dependence of ${\mu }_m$ is generally in line with that for a metal. The similar pressure dependence of ${\mu }_m$ from the two methods and the overall consistency in turn reinforce the validity of applying the modified Kohler’s model in analyzing the MR data.

The Lifshitz transition in BP leads to a Weyl semimetal based on an angle-resolved photoemission spectroscopy result (20). Electrons in the Weyl phase are Dirac fermions without inversion symmetry. The extremely small effective mass 0.041 m₀ derived from the temperature dependence of SdH at 1 GPa is related to the formation of massless Dirac fermions. The Dirac fermions should also exhibit a vanishing thermoelectric power. However, this expectation has not been fulfilled in BP under pressure (see the experimental result of thermoelectric power and the discussion in SI Appendix). The effective mass increases with pressure since the state of Dirac fermions is destroyed by further increasing pressure. Although SdH disappears in the A7 phase, it is likely that the trend of small effective mass goes into the A7 phase since several parameters of transport properties change smoothly on crossing the A17–A7 phase boundary.

Bardeen–Cooper–Schrieffer Superconductivity.

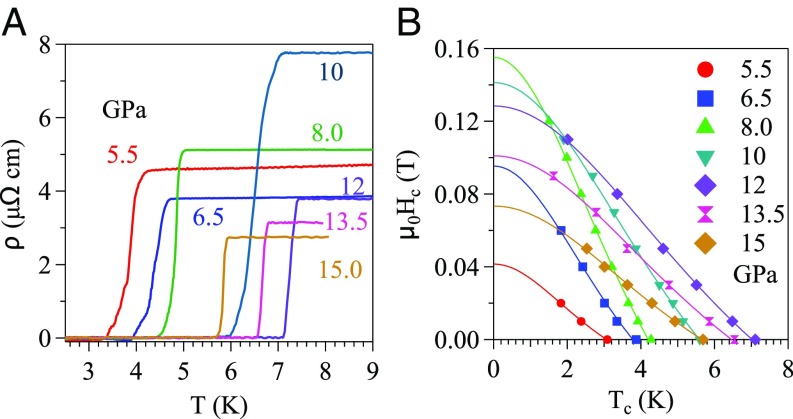
We now turn to discuss the pressure-induced superconductivity in BP. A zoom-in plot of ρ(T,0) in Fig. 2A at low temperatures is given in Fig. 5A; the superconducting transition temperature T_c versus pressure is summarized in Fig. 3D. As can be seen from Fig. 3D, superconductivity occurs right after pressure passes the A17-to-A7-phase boundary; the trend of monotonic increase of T_c with pressure in the A7 phase continues on crossing the A7–C phase boundary. T_c peaks out at 12.5 GPa within the C phase. These observations agree well with the results reported by Wittig et al. (53), although the pressure hydrostaticity at the sample in the latter is not clear. We have also examined the critical field H_c determined from the ρ(T) data under different magnetic fields; data are provided in SI Appendix, Fig. S9. The relationship of H_c versus T_c under different pressures is given in Fig. 5B. H(T_c) follows the Ginzburg–Landau relation, $H\left(T_c\right)=H_c\left(1-t^2\right)/\left(1+t^2\right)$, where $t=T⁄T_c$. It is interesting that the highest critical field does not occur in the C structure with the highest T_c at 12.5 GPa but in the A7 structure at 8 GPa (see SI Appendix, Fig. S10 for the data plot). A critical field of H_c < 0.15 T, which is a small fraction of the Pauli limit of 1.84 T_c (5.65–12.92 T) (54), and a very small coefficient $d{H}_c/dT$ ∼ 16 mT/K signal that the Bardeen–Cooper–Schrieffer (BCS) mechanism can be invoked to explain the observed superconductivity (55). Since H_c is related to the density of states N(ε_F) through the formula $H_C=2\mathrm{\Delta }{\left(\pi N\left({\epsilon }_F\right)\right)}^{1/2}$, where $\mathrm{\Delta }$ is the gap formed in a superconducting state, the small H_c observed can be accounted for by a small effective mass in the A7 phase as discussed above.

Fig. 5.

(A) Highlight of the low-temperature superconducting transition. (B) The superconducting critical field H_c versus T_c.

The critical pressures, P_c1 = 5 GPa and P_c2 = 10 GPa, for A17-to-A7- and A7-to-C-phase transitions in the literature are based on a structural study on the BP crystal grown under high pressure. Fitting parameters from transport properties of our single-crystal sample in Fig. 3 clearly indicate phase transitions at 5 GPa and 10 GPa. The peak of T_c appears to occur within the C phase. As shown in Fig. 3B, the anisotropic exponent ε does not vanish in the isotropic C phase. More interestingly, ε peaks out at the pressure corresponding to a maximum T_c. A full understanding of the behavior of ε in the C phase may provide an important clue to the anomalous pressure dependence of T_c.

Conclusions

In conclusion, we have studied the transport properties of a BP crystal with a large-volume multianvil apparatus filled with a liquid pressure medium. We have found that a nonsaturated, extremely large MR effect at 1.5 K in the A17 phase extends well into the A7 phase and it remains moderately large in the C phase under high pressure. Instead of the ordinary quadratic field dependence, the field dependence of the MR effect in the A17 and the C phase can be fit to a modified Kohler’s model in which an average anisotropic factor due to either anisotropic FS or scattering at impurities is introduced. The mobility obtained through the fitting is highly consistent with that derived from the temperature dependence of quantum oscillations. The anomalous field dependence of MR effect in the A7 phase can be accounted for by the structural reconstruction from the A17 to the A7 phase. Fitting the MR effect to a modified Kohler model and the normal-state resistivity to a power law give parameters that can clearly mark the phase transitions at the A17-to-A7- and A7-to-C-phase boundaries. The high-pressure study on BP leads to a rich phase diagram from the semiconductor–semimetal transition by closing up the gap between two Dirac cones, to a Weyl semimetal, and to a superconductor. To our best knowledge, the A7 phase shows the largest MR effect in its normal state while it exhibits superconductivity below T_c. Determination of the critical field for superconductors in the A7 and the C phase helps to identify that they are BCS superconductors. By applying the McMillian–Allen–Dynes formula and the electron and phonon structure from first-principles calculations, we are able to account for superconductivity in the A7 phase and partially the pressure dependence of T_c. Although it has an isotropic crystal structure, the C phase cannot be treated as an isotropic system from fitting the MR effect. It remains to be explained why the change of anisotropy is correlated to superconductivity in the C phase.

Materials and Methods

Single-crystal samples of BP were grown in a Walker-type multianvil module (Rockland Research Co.). Single-crystal X-ray diffraction under pressure was performed on a BP crystal with a DAC mounted on a Bruker P4 diffractometer with Mo K-alpha radiation (λ = 0.71069 Å) at RT. Hydrostatic high pressure was generated by a “Palm” cubic-anvil cell system (34). All details of these setups can be found in SI Appendix. First-principles calculation was performed within the generalized gradient approximation (GGA) with the Perdew–Burker–Ernzerhof (PBE) formula (see SI Appendix for detailed information).