Hippocampal CA1 gamma power predicts the precision of spatial memory judgments

Significance

Spatial memory is critical to every facet of our lives. The hippocampus is known to play a prominent role in the formation and retrieval of spatial memories; however, the exact mechanisms remain elusive. Using electrophysiology recordings from presurgical epilepsy patients implanted with depth electrodes, we measured high-frequency neural activity from the CA1 region of the hippocampus and the dorsolateral prefrontal cortex. We found associations between increased high-frequency activity and the precision of spatial memory retrieval. These data suggest that local processing within the CA1 subfield and the dorsolateral prefrontal cortex underlie the quality of retrieved spatial memories.

Abstract

The hippocampus plays a critical role in spatial memory. However, the exact neural mechanisms underlying high-fidelity spatial memory representations are unknown. We report findings from presurgical epilepsy patients with bilateral hippocampal depth electrodes performing an object-location memory task that provided a broad range of spatial memory precision. During encoding, patients were shown a series of objects along the circumference of an invisible circle. At test, the same objects were shown at the top of the circle (0°), and patients used a dial to move the object to its location shown during encoding. Angular error between the correct location and the indicated location was recorded as a continuous measure of performance. By registering pre- and postimplantation MRI scans, we were able to localize the electrodes to specific hippocampal subfields. We found a correlation between increased gamma power, thought to reflect local excitatory activity, and the precision of spatial memory retrieval in hippocampal CA1 electrodes. Additionally, we found a similar relationship between gamma power and memory precision in the dorsolateral prefrontal cortex and a directional relationship between activity in this region and in the CA1, suggesting that the dorsolateral prefrontal cortex is involved in postretrieval processing. These results indicate that local processing in hippocampal CA1 and dorsolateral prefrontal cortex supports high-fidelity spatial memory representations.

A critical feature of episodic memory is the ability to form associations between the elements of an experience. This ability is known to rely on the medial temporal lobe (MTL), consisting of the hippocampus (HC) and surrounding cortices. Neuroimaging and lesion studies have demonstrated that the HC plays a crucial role in tasks involving learned associations, such as between an object and a location (1). While the involvement of the HC in the successful encoding and storage of associative memories is well established, a major gap in our understanding stems from the use of binary (correct vs. incorrect) measures of performance, which do not allow a detailed examination of the factors underlying the precision of learned associations. For example, associative memory can be highly precise in some cases (e.g., “I parked my car in the far right corner of the parking lot”) or more general (e.g., “I parked my car in the parking lot”) (2). As such, the contributions of the HC to the precision of remembered associations remain poorly understood.

To address this gap, we developed an incidental object-location memory-encoding task designed to elicit a broad range of spatial memory precision. We used a mixture modeling approach to analyze performance on the task, which allowed us to estimate which trials were remembered with some degree of precision and which trials were likely guesses. Testing presurgical epilepsy patients with bilateral depth electrodes implanted in the HC and surrounding cortices, we used the objective, continuous measure of performance afforded by this task to examine the electrophysiological correlates of spatial memory precision. Previous studies using intracranial recordings in humans have shown that MTL gamma power (>40 Hz), which is thought to reflect local neural processing (3, 4), is associated with correct memory judgments (5–7). Here, we predicted that increases in hippocampal gamma power during retrieval would track increases in spatial memory precision. Furthermore, by coregistering pre- and postimplantation MRI scans, we were able to localize electrodes within hippocampal subfields. This approach allowed us to estimate subfield-level gamma power and to examine how this activity related to performance on the task. Additionally, as the prefrontal cortex has also been shown to be involved in associative memory, we tested the relationship between gamma power and precision in this region. Leveraging the high temporal resolution of intracranial recordings, we also examined the relative timing and directionality of the observed effects across regions.

Results

Task Performance.

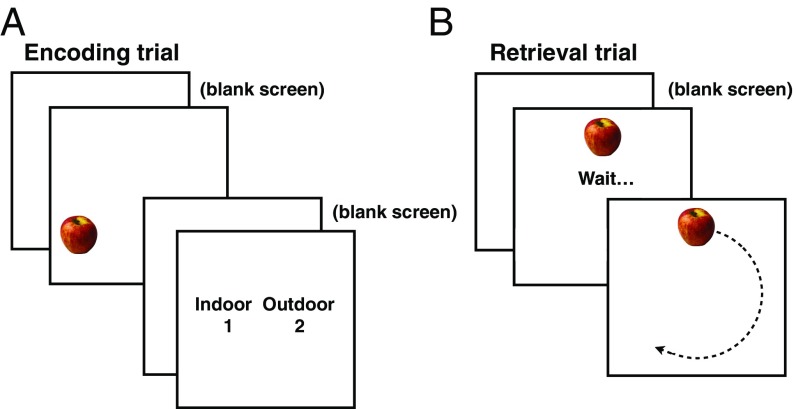
Subjects (seven sessions from four patients) performed an object-location memory task as we recorded an intracranial EEG. During the encoding phase, 100 objects were presented, one at a time, at random positions around the circumference of an invisible circle while subjects performed an incidental encoding task (Fig. 1). At test, the same objects were presented at the top of the circle, and subjects were instructed to use the mouse wheel to rotate the object to the location where it had appeared during encoding. Performance was measured as angular error, or the difference (in degrees) between the location where the subject placed the object and its correct initial location.

Fig. 1.

Spatial precision task. (A) During encoding, 100 objects were presented at random positions around the circumference of an invisible circle while subjects performed an incidental encoding task in which they were asked if each object was more likely to be found indoors or outdoors. Intertrial interval: 1.2 ± 0.2 s; interstimulus interval: 0.5 s. (B) At test, the same objects were presented at the top of the screen. After a 1-s wait period, subjects used the mouse wheel to rotate the object to the location where it appeared during encoding.

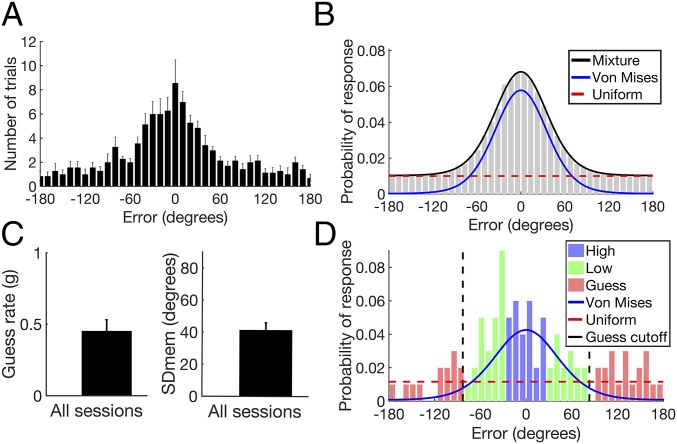
Across sessions, the distribution of angular error was centered around zero degrees (the correct location) and spanned the range of possible responses (−180° to 180°) (Fig. 2A). These error distributions can be modeled as a mixture of two distributions: a uniform distribution of errors and a von Mises distribution of errors (Fig. 2B) (8, 9). The uniform distribution reflects trials on which the subject had no memory for the location of the object and guessed randomly. The von Mises distribution, which is the circular analog of a Gaussian distribution, reflects trials on which the subject remembered the location of the object with some degree of precision.

Fig. 2.

Mixture model and performance. (A) Histogram of errors across all sessions. (B) Example of a mixture model fit to simulated data. (C) Mean guess rate and SDmem across all sessions. (D) Example of a mixture model fit to the data from subject 1. The cutoff for trials placed in the guess condition (±83; black dashed line) was derived from the cumulative distribution function of the von Mises distribution, i.e., 90% of trials that were remembered with some degree of precision fell within ±83 (see text). Error bars indicate SEM.

We used the MemFit function of MemToolbox in Matlab (10), to obtain an estimate of two parameters describing these distributions: the guess rate (g), which reflects the area under the uniform distribution, and the SD of the von Mises distribution (SDMem), which reflects the overall precision of responses that were not guesses. Fig. 2C shows the mean value of these parameters across sessions (see SI Appendix, Fig. S1 for parameter values for all sessions). The upper limit of the 95% credibility interval for each subject’s guess rate was less than one, indicating that performance was above chance for all subjects. An example of the mixture model fit of subject 1’s angular error is shown in Fig. 2D. In addition to using a continuous measure of error, in subsequent analyses we also divided trials into three conditions, high precision, low precision, and guess. We used the cumulative distribution function of the von Mises distribution estimated for each session to determine which trials to place in the guess condition. Trials that had less than a 10% chance of being remembered with some degree of precision were placed in the guess condition. For example, in subject 1, the middle 90% of the von Mises distribution spans ±83°, so trials with error greater/less than ±83° were placed in the guess condition (Fig. 2D). As such, across sessions most of the trials in the guess condition were likely guesses. The remaining trials were sorted by error and split evenly into the high- and low-precision conditions.

Electrode Localization.

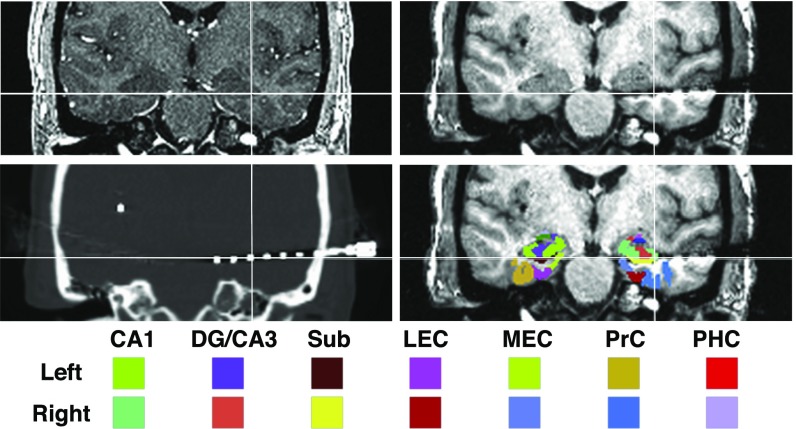
Depth electrodes were localized using coregistered pre- and postimplantation MRIs, as well as registration to a high-resolution anatomical atlas with manual tracings of hippocampal subfields and MTL subregions (Fig. 3) (11). Coregistered postimplantation computed tomography (CT) scans were also used to help determine the center of each electrode artifact. All subjects had electrodes localized to the HC and dorsolateral prefrontal cortex (dlPFC), and three of the four subjects had electrodes localized to the CA1 subfield. Only data from recordings contralateral to the seizure source or outside the seizure onset zone were used in subsequent analyses.

Fig. 3.

Examples of MRI, CT scan, and template for a single subject. Electrodes were localized in each subject using coregistered preimplantation (Upper Left), postimplantation MRI (Upper Right), and CT (Lower Left) scans. A high-resolution template labeled with medial temporal lobe (MTL) subregions was aligned to each subject’s preimplantation scan to guide electrode localization. Regions of interest in the MTL included the CA1, DG/CA3, subiculum (Sub), lateral and medial entorhinal cortex (LEC, MEC), and the PRC and PHC cortices. The template also provided labels for amygdala nuclei, which can be seen in the figure but were not included in the analysis.

CA1 Gamma Power Predicts Error Within Sessions.

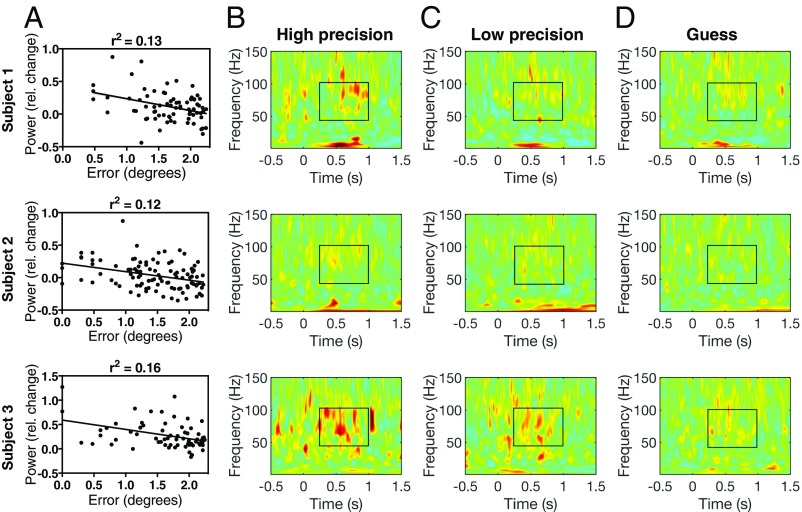
We first examined mean gamma power (40–100 Hz) over the retrieval window (0.25–1 s poststimulus onset) within each session. The start of the a priori retrieval window was based on the time at which stimulus-evoked activity has been shown to emerge in the HC following stimulus onset (12, 13), while the end of the retrieval window (1 s poststimulus onset) is the time at which subjects were able to start moving the object. The absolute value of the angular error was logged to account for the nonnormal distribution of error. We found a correlation between gamma power and logged error in all three subjects who had electrodes localized to the CA1 subfield (subject 1: P = 0.002, n = 74; subject 2: P = 0.0003, n = 98; subject 3: P = 0.0008, n = 63; all Ps < 0.05, Bonferroni corrected for number of MTL electrodes) (Fig. 4A; see Table 1 for the number of MTL electrodes tested). To better visualize the relationship between gamma power and error, spectrograms for high-precision, low-precision, and guess trials for the CA1 electrodes shown in Fig. 4A are included in Fig. 4 B–D. While there is a smaller increase in gamma power relative to baseline across trials in subject 2, a correlation between gamma power and error is observed in the trial-by-trial analysis. In the within-session analysis, the correlations in the CA1 subfield were the only ones that survived Bonferroni correction. However, the specificity of this effect should be interpreted with caution, as effects in other regions could be present but not strong enough to surpass the stringent statistical threshold for multiple-comparison correction.

Fig. 4.

Within-session CA1 gamma power predicts error. (A) Trial-by-trial Pearson correlation between mean gamma power and angular error. (B–D) Spectrograms showing mean power across high-precision (B), low-precision (C), and guess (D) trials for the CA1 electrodes shown in A. Stimulus onset is at time 0, and the frequency range (40–100 Hz) and time period (0.25–1 s poststimulus onset) of interest are indicated by the black rectangles.

Table 1.

Patient information, hemisphere included in the analyses, number of MTL contacts, and number of dlPFC contacts

Subject	Hand	Epileptogenic region	Coverage	Hemisphere analyzed	No. of sessions	MTL contacts	dlPFC contacts
1	R	Right TLE	Bilateral	L	1	7 (6 CA1)	7
2	L	Right medial frontal/supplementary motor area	Bilateral	Bilateral	3	9 (2 CA1)	6
3	R	Left TLE	Bilateral	R	1	5 (2 CA1)	10
4	R	Right TLE	Bilateral	L	2	11 (0 CA1)	8
Total						32	31

L, left; R, right; TLE, temporal lobe epilepsy.

Across Sessions, CA1 Gamma Power Predicts Spatial Memory Precision.

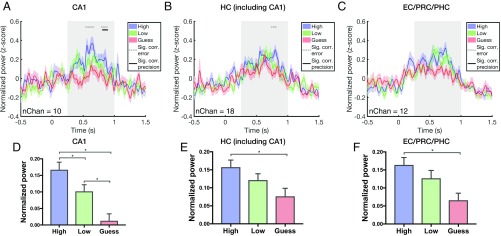
Fig. 5 A–C shows the time course of gamma power in the CA1 subfield, the HC, including CA1, dentate gyrus (DG)/CA3, and subiculum, and the entorhinal cortex (EC), perirhinal cortex (PRC), and parahippocampal cortex (PHC) for high-precision, low-precision, and guess trials. First, we pooled trials from all conditions across sessions and tested for a correlation between gamma power and error in each MTL region. Using a cluster-based permutation approach to correct for multiple comparisons across time points, we found significant negative correlations between gamma power and error during the retrieval window in the CA1 subfield and HC (Fig. 5 A–C). To address the concern that these correlations were driven by a binary effect of retrieval success vs. failure, we excluded trials that were likely guesses (i.e., the guess condition) and reran the analyses. In this, as well as in subsequent analyses, we refer to correlations with “precision” in analyses in which the guess condition was excluded. We found a significant correlation between gamma power and precision in the CA1 subfield beginning at 804 ms poststimulus onset (Fig. 5A). In a complementary analysis, we averaged gamma power over the retrieval window (0.25–1 s poststimulus onset) and ran a two-way ANOVA with error (high precision, low precision, and guess) and region (CA1, HC, and EC/PRC/PHC) as fixed factors. We found a significant effect of error [F(2, 1595) = 21.6; P = 5 × 10⁻¹⁰] but no significant effect of region [F(2, 1595) = 1.3; P = 0.28] and no interaction between region and error [F(4, 1595) = 0.81; P = 0.51]. Post hoc t tests revealed a significant difference between high-precision and guess conditions in all MTL regions (CA1 high vs. guess: mean difference = 0.15, P < 0.05, corrected; HC high vs. guess: mean difference = 0.08, P < 0.05, corrected; MTL high vs. guess: mean difference = 0.1, P < 0.05, corrected) (Fig. 5 D–F). We also found a significant difference between high and low precision as well as between low precision and guess in the CA1 subfield (high vs. low: mean difference = 0.07, P < 0.05, corrected; low vs. guess: mean difference = 0.09, P < 0.05, corrected). While the CA1 subfield was the only region to show significant correlations between gamma power and precision as well as a significant difference between high and low precision, we do not mean to imply that there are not similar effects in other MTL regions.

Fig. 5.

Across-session gamma power in the MTL. (A–C) Time course of gamma power in the CA1 subfield (A), HC, including CA1, CA3/DG, and subiculum (B), and EC, PRC, and PHC (C). Stimulus onset is at time 0, and the retrieval window (0.25–1 s poststimulus onset) is shaded in gray. Dotted gray horizontal lines indicate time points where there are significant correlations between gamma power and error (P < 0.05, cluster-corrected). Solid gray horizontal lines indicate time points where there are significant correlations between gamma power and precision (excluding the guess condition; P < 0.05, cluster-corrected). Colored shaded regions indicate SEM. (D–F) Mean gamma power over the retrieval window (0.25–1 s poststimulus onset) for high-precision, low-precision, and guess conditions in the indicated areas. Error bars indicate SEM; *P < 0.05.

PFC Gamma Power Lags CA1 in Predicting Spatial Memory Precision.

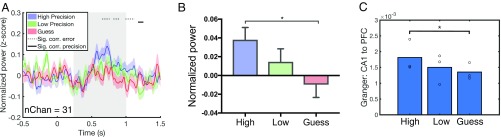
We also found a negative correlation between gamma power and error during the retrieval window in dlPFC contacts (P < 0.05 cluster-corrected) (Fig. 6A). There was no effect of error during the retrieval window or at any time period poststimulus onset in any of the other regions from which we recorded (SI Appendix, Fig. S3). Excluding the guess condition, we found a significant correlation between gamma power and precision starting at 1,175 ms poststimulus onset (Fig. 6A). Averaging power over the retrieval window, we found a main effect of error [F(2, 613) = 3.17, P = 0.04] and a significant difference between high-precision and guess conditions (mean difference = 0.05, P < 0.05, corrected) (Fig. 6B). Interestingly, we found that the significant correlations between gamma power and error as well as between gamma power and precision appeared later in the dlPFC than in the CA1 subfield (error effect: CA1 = 538 ms poststimulus onset, dlPFC = 652 ms; precision effect: CA1 = 804 ms, PFC = 1,175 ms). However, the timing of these effects should be interpreted with caution, as they might be subject to statistical thresholding effects resulting from the cluster-based correction over time points. For instance, while the dlPFC precision effect does not reach cluster-corrected significance until after the end of the retrieval period (i.e., after 1,000 ms), the effect is also present (P < 0.05, uncorrected) during the retrieval window. To further examine the relative timing and directionality of CA1 and dlPFC activity at retrieval, we performed a time-domain Granger prediction analysis using the gamma power time series for all sessions showing a significant correlation between gamma power and error (P < 0.05) in both CA1 and dlPFC electrodes (n = 3 subjects). Granger prediction provides a measure of directionality by testing if activity from region A (for example, the dlPFC) at one time point can be better predicted by knowing activity from region B (for example, the CA1) at past time points. We first calculated Granger prediction values for all CA1–dlPFC electrode pairs for high-precision, low-precision, and guess trials during the full retrieval period (0–1 s poststimulus onset) and then calculated the difference between conditions (e.g., high minus guess) for each electrode pair. We then averaged these Granger difference values first over electrode pairs within sessions and then across sessions (n = 3) and then compared this averaged difference value to a null distribution (Methods). We found greater CA1-to-dlPFC directionality for high-precision trials than for trials in the guess condition (P < 0.05, permutation test) (Methods), indicating that activity associated with high-precision spatial memory judgments starts earlier in the CA1 subfield (Fig. 6C). There was no significant difference between conditions (high vs. guess, high vs. low, low vs. guess) in dlPFC-to-CA1 Granger prediction values (P > 0.05, permutation test) (SI Appendix, Fig. S8).

Fig. 6.

dlPFC gamma power predicts the precision of spatial memory retrieval. (A) Time course of gamma power in the dlPFC. Stimulus onset is at time 0, and the retrieval window (0.25–1 s poststimulus onset) is shaded in gray. Dotted gray horizontal lines indicate time points where there are significant correlations between gamma power and error (P < 0.05, cluster-corrected). Solid gray horizontal lines indicate time points where there are significant correlations between gamma power and precision (excluding the guess condition; P < 0.05, cluster-corrected). Colored shaded regions indicate SEM. (B) Mean gamma power over the retrieval window for high-precision, low-precision, and guess conditions. (C) Mean CA1-to-dlPFC Granger prediction values for each condition. Asterisks indicate significantly greater CA1-to-dlPFC directionality for high-precision vs. guess trials as determined by permutation testing (P < 0.05).

Since the low-precision condition tended to cover a greater proportion of the estimated uniform distribution (Fig. 2D), the number of expected guesses in the low-precision condition was slightly higher than in the high-precision condition (on average, there were 2.8 more expected guesses per session in the low-precision condition than in the high-precision condition). As such, it is possible that the observed differences in CA1 gamma power across the high- and low-precision conditions were driven by a slightly higher number of guesses in the low-precision condition. However, balancing the number of expected guesses in the high- and low-precision conditions using simulated guesses derived from the mean power in the guess condition (SI Appendix, SI Materials and Methods) produced similar results [main effect of error: F(2, 462) = 12.5, P = 5 × 10⁻⁶; high vs. guess: mean difference = 0.14, P = 3 × 10⁻⁶; high vs. low: mean difference = 0.05, P = 0.06; low vs. guess: mean difference = 0.09, P = 0.004] (SI Appendix, Fig. S5). Since PFC activity is known to be modulated before the initiation of action, another possible confound is that the dlPFC gamma effect is due to differences in movement onset after the delay period (0–1 s poststimulus onset), as patients may start moving the object earlier for more precise trials (2, 14). However, we found no significant correlation between angular error and movement onset, indicating that this factor was not driving the effects (Kendall’s τ = −0.006; P = 0.86; the data from session 1 were not included in this analysis, as we did not record mouse movements for this session). We additionally performed control analyses to ascertain that the gamma effects in the CA1 and dlPFC were not associated with the distance the object was moved on the screen or trial order (SI Appendix, Figs. S6 and S7).

Discussion

Prior studies have shown that the HC and PFC are involved in associative memory retrieval. However, the contributions of these regions to the precision of remembered associations are poorly understood. One possibility is that activity within these regions reflects a binary signal of retrieval success vs. failure. Alternatively, activity within these regions could track the precision, or fidelity, of the retrieved memory. When we included guess trials in our analyses, we found increased hippocampal and prefrontal gamma power in highly precise trials vs. trials that were likely guesses (i.e., the guess condition). This is consistent with prior work showing increased activity in these regions associated with retrieval success (1, 6, 15). However, we additionally showed negative correlations between hippocampal and prefrontal gamma power and error magnitude, suggesting that increased activity in these regions tracks representational fidelity. Our additional analyses after excluding the guess condition further indicated that activity in these regions was associated with the precision of the spatial judgments. Overall, these results suggest that these regions are involved not only in retrieval success but also in indexing the precision of retrieved memories.

Across sessions, we found significant correlations between CA1 gamma power and precision and significant differences between the high- and low-precision conditions. The CA1 subfield has long been known to be involved in spatial processing and memory. For instance, CA1 “place cells” provide precise representations of specific locations in an environment and can code for associations between objects and locations (16, 17). While the current task does not involve subjects physically moving through space, studies in primates have shown that the CA1 also contains spatial “view cells” that respond whenever a monkey looks toward specific locations in the environment (18). More recently, studies in rats have found increased place-cell firing and gamma power (60–100 Hz) in the CA1 as animals explored familiar objects in novel locations (19, 20).

The neural mechanisms generating high-frequency gamma activity in humans remain a prominent question in the field. One possibility is that high-frequency gamma activity reflects gamma oscillations generated by local interactions between interneurons and pyramidal neurons (21). As gamma phase synchronization can enhance spike-timing–dependent plasticity, these oscillations are thought to play a mechanistic role in memory processing (21). Accumulating evidence from the rodent literature suggests that oscillatory gamma can be split into two types, slow gamma (25–55 Hz) and fast gamma (60–100 Hz), that play distinct roles in memory encoding and retrieval (22). As such, we examined the dominant frequency range influenced by task performance and found significant effects across our a priori frequency range (40–100 Hz) with peaks in the slow and fast gamma ranges (SI Appendix, Fig. S2). The significance of these peaks remains unclear, and whether two different neural mechanisms may give rise to these effects remains an outstanding question. Another possibility is that the high-frequency activity observed in humans does not reflect oscillatory activity but rather a broadband shift of the power spectrum stemming from increased neuronal spiking (21, 23). In this view, high-frequency activity is nonoscillatory and does not play a mechanistic role in memory processing but can be thought of as a biomarker for local activity (24, 25). Given that the frequency range of this broadband shift overlaps with that of oscillatory gamma activity, a third possibility is that high-frequency gamma power reflects a combination of these processes (3, 4). In each view, however, gamma power can be thought of as a spatially precise indicator of local excitatory activity. In light of our results, this suggests that increasing excitatory activity in the CA1 and dlPFC is associated with increasing memory precision.

A number of recent studies have implicated the extended hippocampal network in spatial memory precision (26–28). For example, Nilakantan et al. (26) found that stimulation of the posterior cortical–hippocampal network using transcranial magnetic stimulation in humans increased precision on an object-location memory task similar to the one used in the current study. In a case study that examined the performance of a patient with MTL damage on a virtual Morris water maze, Kolarik et al. (27) found that while the patient tended to search in the general vicinity of the correct location, the precision of her search path was significantly lower than that of controls. These findings provide convergent evidence that the HC facilitates the precise recall of learned associations. Our findings are consistent with these studies but further propose a role specifically for hippocampal CA1 and dlPFC as well as a temporal relationship between the two that may be an important facet of spatial memory retrieval.

Our results also are convergent with findings from studies that have shown that hippocampal activity tracks subjective measures of memory strength (e.g., confidence or vividness) (29–31). While subjective ratings are associated with performance accuracy (2), these measures could be influenced by a variety of factors including subject bias. Here, we fit a mixture model to an objective measure of precision to estimate the probability of guessing. This approach is less likely to be contaminated by subjective biases.

In addition to hippocampal CA1, we also observed that gamma power in the dlPFC at retrieval was associated with spatial memory precision. The dlPFC is reciprocally connected to the MTL and has been implicated in a wide variety of memory processes (15). For instance, fMRI studies have shown increased activity in the dlPFC when subjects retrieve contextual details about a cue, such as the location of a studied object (32). A common interpretation of these findings is that the dlPFC is involved in maintaining or monitoring information retrieved from episodic memory (32), which is consistent with the dlPFC’s well-recognized role in working memory (33). The precision effect observed in the CA1 region preceded the onset of the effect in dlPFC, which is consistent with this interpretation of the dlPFC’s role, as it involves postretrieval processes. The Granger prediction analysis further corroborated this finding, indicating that activity associated with highly precise spatial memory judgments appears earlier in the CA1 than in the dlPFC.

Overall, our results suggest a role for local processing within the HC and dlPFC in indexing the precision of spatial associative memory. The correlations between gamma power and the precision of spatial memory judgments raise the possibility that disrupting gamma activity in CA1 and/or dlPFC may reduce the precision of memory judgments, thereby establishing a causal link. Future studies using electrical disruption in humans or more invasive techniques in rodents can test these hypotheses directly.

Methods

Participants.

Subjects were four patients (three female, one male, age 32–58 y) who had stereotactically implanted intracranial depth electrodes (Integra or Ad-Tech, 5-mm interelectrode spacing) placed at the University of California Irvine Medical Center to localize the seizure onset zone for possible surgical resection. Informed consent was obtained from each subject before testing, and the research protocol was approved by the institutional review board of the University of California, Irvine. Electrode placement was guided exclusively by clinical needs.

Gamma Power Analyses.

Intracranial recordings were broken into event-related epochs and convolved with complex Morlet wavelets, implemented using the FieldTrip toolbox, to obtain a measure of instantaneous power (34). We used an a priori gamma frequency range of 40–100 Hz for our gamma power analyses. This frequency range was based on prior literature showing MTL gamma activity in this range (5, 7, 35) and reflected the dominant gamma frequency range that was influenced by task performance (SI Appendix, Fig. S2). For detailed information, see SI Appendix, SI Materials and Methods.

Granger Prediction Analysis.

The preprocessed local field potential was first downsampled to 250 Hz before obtaining the mean gamma power time series (40–100 Hz) during the full retrieval period (0–1 s post stimulus onset). Data were preprocessed to increase stationarity, and the Multivariate Granger Causality (MGVC) Matlab Toolbox was used to calculate the time-domain Granger prediction index for high-precision, low-precision, and guess trials for each CA1 and dlPFC electrode pair (see SI Appendix, SI Materials and Methods for details) (36, 37). The difference in Granger prediction values between conditions (e.g., high minus guess) was calculated for each electrode pair, averaged over electrode pairs within each session for each direction (CA1-to-dlPFC and dlPFC-to-CA1), and then averaged across sessions. A null average difference distribution was created by shuffling the trial labels 500 times before calculating the difference in Granger prediction values between conditions. These distributions of permuted difference values were then averaged first over electrode pairs and then across sessions, as described above (38). The observed average Granger difference value was compared with this null average Granger difference distribution. P values were calculated as the fraction of times the null average Granger difference values were equal to or more extreme than the observed average Granger difference value.

Task, Behavioral Analysis, Electrode Localization, Data Collection, and Preprocessing.

Detailed information can be found in SI Appendix, SI Materials and Methods.