Intrinsic spin of elastic waves

Significance

Spin unveils the fundamental geometrical and topological properties of waves. Massive studies have shown that the circularly polarized transverse wave can carry nontrivial spin density and thus possess quantum spin Hall effect. However, the spin nature of the longitudinal wave still lacks research. Here, based on the elastic wave platform, we show that the longitudinal wave can carry unique spin angular momentum due to its special spin–orbit coupling, and, importantly, the mixed longitudinal–transverse waves will induce an unusual spin form: hybrid spin. These spins in an elastic wave will be responsible for several spin-related phenomena beyond a pure transverse wave. Our work can advance physical understanding about spin properties of elastic waves.

Abstract

Unveiling spins of physical systems usually gives people a fundamental understanding of the geometrical properties of waves from classical to quantum aspects. A great variety of research has shown that transverse waves can possess nontrivial spins and spin-related properties naturally. However, until now, we still lack essential physical insights about the spin nature of longitudinal waves. Here, demonstrated by elastic waves, we uncover spins for longitudinal waves and the mixed longitudinal–transverse waves that play essential roles in spin–momentum locking. Based on this spin perspective, several abnormal phenomena beyond pure transverse waves are attributed to the hybrid spin induced by mixed longitudinal–transverse waves. The unique hybrid spin reveals the complex spin essence in elastic waves and advances our understanding about their fundamental geometrical properties. We also show that these spin-dependent phenomena can be exploited to control the wave propagation, such as nonsymmetric elastic wave excitation by spin pairs, a unidirectional Rayleigh wave, and spin-selected elastic wave routing. These findings are generally applicable for wave cases with longitudinal and transverse components.

Almost 150 years ago, Helmholtz’s theorem unveiled the fundamental geometry that any vector field can be decomposed into two parts $\mathit{u}={\mathit{u}}_L+{\mathit{u}}_T$ (1), a curl-free component and a divergence-free component, namely, a longitudinal wave and a transverse wave, respectively. Since then, several studies have shown that the transverse propagating waves, i.e., optical waves, carry their characteristic spin determined by the wave vector and polarization profile (2, 3). Due to the essential geometrical properties (4–6), nontrivial Berry phase and quantum spin Hall effect (QSHE) can be induced and possessed for transverse waves, even in a vacuum (7–13). Many experiments also have shown that the spin of transverse waves can supply a robust and powerful approach to control the wave flow (14–17). Nevertheless, despite distinct geometrical properties, no studies have yet been made to discuss the corresponding physical characteristics of longitudinal waves, especially their spin properties.

The elastic wave describes the basic dynamic principle of how solid objects deform and become internally stressed in a periodic form (18), which can reflect the properties from classical solid motion to lattice oscillation in a quantum field. Distinct from the transverse optical wave and longitudinal acoustic wave, the elastic wave can support both the longitudinal and transverse components simultaneously (18). Thus, the elastic wave serves as the ideal platform for exploring geometrical and spin properties of longitudinal waves, as well as the interaction between longitudinal and transverse ones. In this work, we find that the longitudinal component possesses its own unique spin density that plays an important role in geometrical and spin-related properties of elastic waves. The mixed longitudinal–transverse waves will carry an extra spin due to their hybridization, which will be responsible for abnormal phenomena beyond pure transverse waves. By analyzing the spin properties of elastic waves in detail, we identify that the total spin angular momentum density can be dissected into three contributions, as (see Materials and Methods)

$$\mathit{s}={\mathit{s}}_L+{\mathit{s}}_T+{\mathit{s}}_h$$ [1]

where ${\mathit{s}}_L=⟨{\mathit{u}}_L\left|\widehat{\mathit{S}}\right|{\mathit{u}}_L⟩$ is the spin contribution from longitudinal wave ${\mathit{u}}_L$, ${\mathit{s}}_T=⟨{\mathit{u}}_T\left|\widehat{\mathit{S}}\right|{\mathit{u}}_T⟩$ is from transverse wave ${\mathit{u}}_T$, and, specially, ${\mathit{s}}_h=⟨{\mathit{u}}_L\left|\widehat{\mathit{S}}\right|{\mathit{u}}_T⟩+⟨{\mathit{u}}_T\left|\widehat{\mathit{S}}\right|{\mathit{u}}_L⟩$ is the hybrid spin density due to nontrivial spin projections among these two states, where $\widehat{\mathit{S}}$ is the quantum spin operator for elastic waves. Spin is one of the most important physical properties in quantum mechanics and is a cornerstone for topological states, which can reveal the complex interactions among multiple physical mechanisms. It is worth emphasizing that the spin we discuss here is intrinsic in the sense that it is the real physical spin angular momentum of elastic waves, rather than the artificially constructed pseudospin degree of freedom in literature (19, 20). Except for the well-known spin ${\mathit{s}}_T$ (2, 3, 21), ${\mathit{s}}_L$ and ${\mathit{s}}_h$ are hidden and unobservable in a pure transverse wave. We will fill this gap and advance the understanding about the geometrical and spin properties of elastic waves in isotropic media.

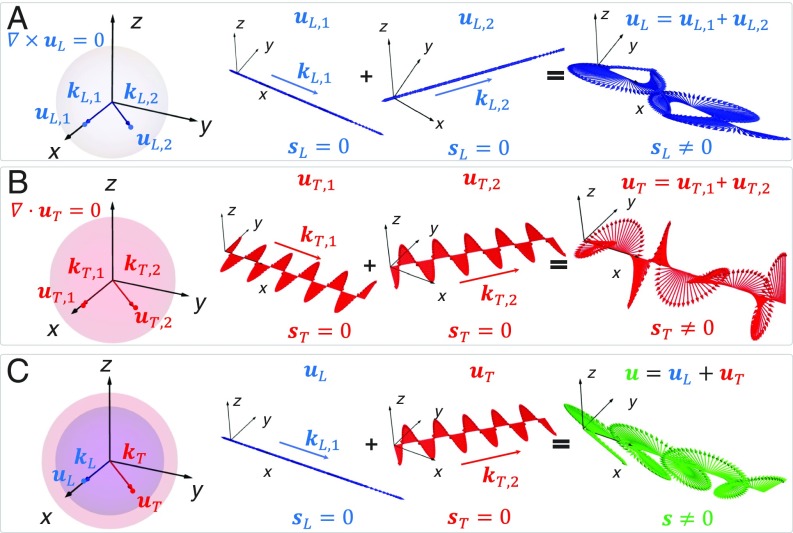
Considering the elastic waves in a homogeneous isotropic solid, the linear elastic equation can be decoupled into two independent forms: longitudinal wave ${\mathit{u}}_L$ and transverse wave ${\mathit{u}}_T$ (18). The propagating elastic waves in solid are polarized plane waves. With the basic geometrical conditions of longitudinal wave $\nabla \times {\mathit{u}}_L=0$ and transverse wave $\nabla \cdot {\mathit{u}}_T=0$, their polarization vectors will become momentum-dependent in plane wave form. The transverse wave can hold a circularly polarized propagating form and carry transverse wave spin density naturally ${\mathit{s}}_T\hspace{0.17em}\ne \hspace{0.17em}0$ (2, 21). For a pure longitudinal wave, there is no extra degree of freedom to constitute the nontrivial chirality so that ${\mathit{s}}_L=0$. However, geometrically, we can use two wave interferences (11) to induce an effective “circularly polarized” profile for the total wave field, as shown in Fig. 1. For the combination of two waves with different wave vectors, the total elastic wave will possess a similar property to the circularly polarized wave profile. In particular, the total elastic wave still keeps its original characteristic geometry relations, namely, $\nabla \times {\mathit{u}}_L=0$ in Fig. 1A and $\nabla \cdot {\mathit{u}}_T=0$ in Fig. 1B, but with nonzero spin ${\mathit{s}}_L\hspace{0.17em}\ne \hspace{0.17em}0$ and ${\mathit{s}}_T\hspace{0.17em}\ne \hspace{0.17em}0$, respectively. This is due to the fact that, despite $⟨{\mathit{u}}_i\left|\widehat{\mathit{S}}\right|{\mathit{u}}_i⟩=0$ for each single wave field ${\mathit{u}}_i,\left(i=\mathrm{1,2}\right)$, the wave interference within the total vector field $\mathit{u}={\mathit{u}}_1+{\mathit{u}}_2$ offers the nonzero cross terms $⟨\mathit{u}\left|\widehat{\mathit{S}}\right|\mathit{u}⟩=⟨{\mathit{u}}_1\left|\widehat{\mathit{S}}\right|{\mathit{u}}_2⟩+⟨{\mathit{u}}_2\left|\widehat{\mathit{S}}\right|{\mathit{u}}_1⟩\hspace{0.17em}\ne \hspace{0.17em}0$ that lead to the nonzero spin. Besides these conventional cases, there exists one special spin form ${\mathit{s}}_h$ in the mixed longitudinal–transverse wave in Fig. 1C. Although wave interference only occurs in waves of the same type conventionally, longitudinal–transverse wave mixing can be considered as generalized effective wave interference to produce the nontrivial hybrid spin: ${\mathit{s}}_h$.

Fig. 1.

Geometry and spin of arbitrary waves. The strong relations between polarization profile and wave vector reflect the spin–orbit couplings: ${\mathit{k}}_L\times {\mathit{u}}_L=0$ and ${\mathit{k}}_T\cdot {\mathit{u}}_T=0$, i.e., the spin–momentum lockings. (A) For the combinations of two longitudinal waves with different wave vectors ${\mathit{k}}_{L,1}\hspace{0.17em}\ne \hspace{0.17em}{\mathit{k}}_{L,2}$, ${\mathit{u}}_L={\mathit{u}}_{L,1}+{\mathit{u}}_{L,2}$, the total elastic field carries nontrivial spin angular momentum density ${\mathit{s}}_L\hspace{0.17em}\ne \hspace{0.17em}0$ due to the wave interference, $⟨{\mathit{u}}_{L,1}\left|\widehat{\mathit{S}}\right|{\mathit{u}}_{L,2}⟩$. (B) The transverse waves in the same settings, ${\mathit{u}}_T={\mathit{u}}_{T,1}+{\mathit{u}}_{T,2}$, also induce nontrivial spin density ${\mathit{s}}_T\hspace{0.17em}\ne \hspace{0.17em}0$. (C) For the total elastic waves that contain longitudinal and transverse plane waves simultaneously, $\mathit{u}={\mathit{u}}_L+{\mathit{u}}_T$, the total elastic spin density is attributed to the hybrid spin density $\mathit{s}={\mathit{s}}_h$, which reflects the major geometrical difference between longitudinal and transverse waves. The spheres in the figure are $\mathit{k}$ spheres, and the real parts of displacement fields are plotted.

Topological properties are associated with the momentum-dependent polarization profile, especially spin states (22, 23). Considering the basic momentum-dependent geometrical conditions of an elastic wave, we can see that the polarization profile of ${\mathit{u}}_L$ (${\mathit{u}}_T$) is normal (tangent) to the $\mathit{k}$ sphere. Actually, these essential geometrical relations underlie the spin–orbit coupling of elastic waves in an isotropic homogeneous solid, which is reminiscent of the spin–orbit coupling of light in a vacuum (4, 7). Generalizing the normalized longitudinal wave ${\mathit{u}}_L=\left(\mathrm{0,0,1}\right)e^{i{k}_{L}z}$ and the circularly polarized transverse wave ${\mathit{u}}_T=1/\sqrt{2}\hspace{0.17em}\left(1,i\sigma ,0\right)e^{i{k}_{T}z},\sigma =\pm 1$ into arbitrary direction ${\mathit{u}}_L\left({\mathit{k}}_L\right)$ and ${\mathit{u}}_T\left({\mathit{k}}_T\right)$, one can calculate their Berry connections ${\mathcal{A}}_T^{\sigma }=-i{\left({\mathit{u}}_T^{\sigma }\right)}^{*}\cdot \left({\nabla }_{\mathit{k}}\right){\mathit{u}}_T^{\sigma }$, ${\mathcal{A}}_L=-i{\left({\mathit{u}}_L\right)}^{*}\cdot \left({\nabla }_{\mathit{k}}\right){\mathit{u}}_L$ and obtain Berry curvatures, respectively, as

$${\mathcal{F}}_T^{\sigma }={\nabla }_{\mathit{k}}\times {\mathcal{A}}_T^{\sigma }=\sigma \frac{{\mathit{k}}_T}{k_T^3},{\mathcal{F}}_L={\nabla }_{\mathit{k}}\times {\mathcal{A}}_L=0.$$ [2]

The topological Chern numbers for the transverse wave $C_T^{\sigma }=\frac{1}{2\pi }\oint {\mathcal{F}}_T^{\sigma }{d}^2\mathit{k}$ and for the longitudinal wave $C_L=\frac{1}{2\pi }\oint {\mathcal{F}}_L{d}^2\mathit{k}$, where integrals are taken over the ${\mathit{k}}_T$ sphere and ${\mathit{k}}_L$ sphere, would be responsible for unveiling their topological nature. The circularly polarized transverse wave will yield $C_T^{\sigma }=2\sigma$, but, for the longitudinal wave, $C_L=0$ due to the zero Berry curvature. The total Chern numbers for the transverse wave and the longitudinal wave thus are trivial: $C_T={\sum }_{\sigma =\pm 1}{C}_T^{\sigma }=0$, $C_L=0$. However, for the spin Chern number $C_{spin}$, it would be nonzero for the transverse wave but vanishes for the longitudinal wave due to the lack of circularly polarized profile,

$$C_{spin}^T=\sum _{\sigma =\pm 1}\sigma C_T^{\sigma }=4,\hspace{1em}{C}_{spin}^L=0.$$ [3]

The nontrivial Berry curvature and nonzero spin Chern number $C_{spin}^T=4$ have been proposed theoretically (7, 12) in the circularly polarized electromagnetic wave and are verified experimentally (24, 25). Different from ${\mathit{k}}_T\cdot {\mathit{u}}_T=0$ for transverse wave, the geometric constrain ${\mathit{k}}_L\times {\mathit{u}}_L=0$ of the longitudinal wave gives a trivial Berry curvature and spin Chern number $C_{spin}^L=0$, implying its different topological nature. Their topological invariant difference can be defined by their distinct geometrical relations. To obtain nontrivial spin topology for longitudinal waves, one can exploit by constructing the circularly polarized profile or hybrid spin with the help of wave interference with others.

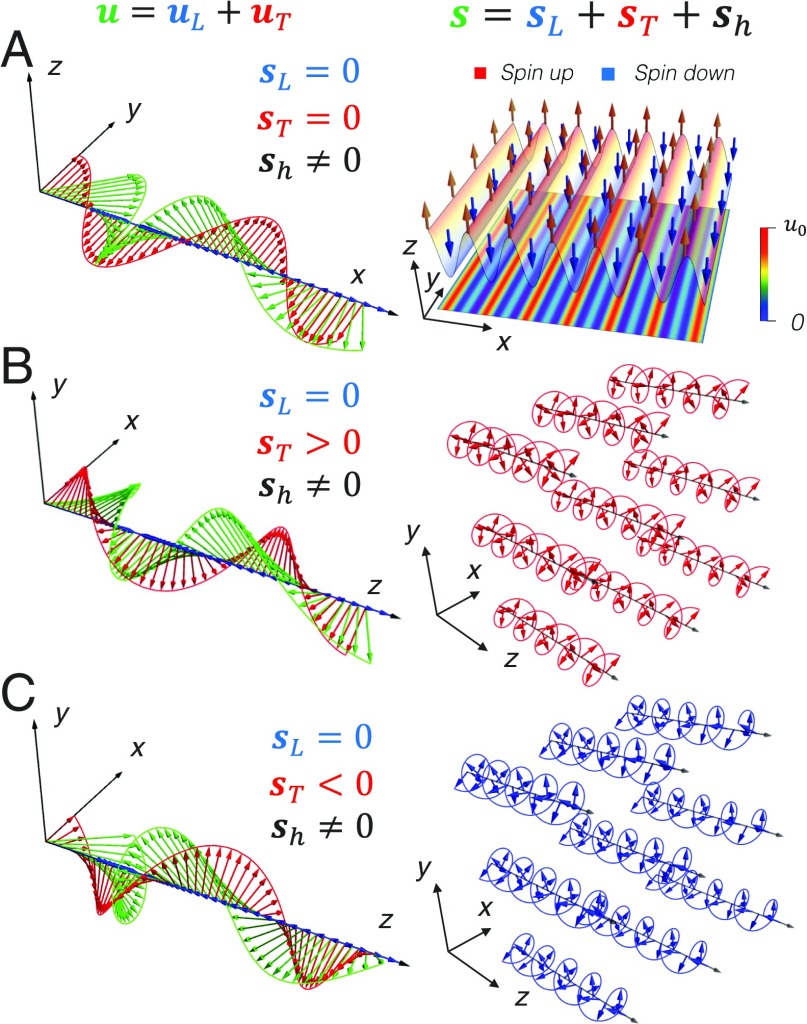
To exemplify the hybrid spin density ${\mathit{s}}_h$, we consider the simplest plane wave form in Fig. 2A. A longitudinal elastic wave and the other linear polarized transverse wave propagate in parallel. They both individually carry zero spin density, but the complex geometrical form of their total elastic field reflects the spin hybridization between them. This hybridization induces nonzero hybrid spin density ${\mathit{s}}_h\hspace{0.17em}\ne \hspace{0.17em}0$, which contributes to the total spin density $\mathit{s}={\mathit{s}}_h$. Importantly, this hybrid spin varies periodically along propagating direction ${\mathit{s}}_h\propto \sin \left(\left(k_L-k_T\right)x\right)$, and this oscillation induces nonzero Poynting vector contribution ${\mathit{p}}^s\propto \nabla \times \mathit{s}\hspace{0.17em}\ne \hspace{0.17em}0$, which is observable and detectable in experiments. The hybrid spin will introduce some interesting spin phenomena, such as wave spin lattice (see SI Appendix, Fig. S1) and rotating spin texture. Considering the combination of a longitudinal wave and a circularly polarized transverse wave with nontrivial spin density ${\mathit{s}}_T\hspace{0.17em}\ne \hspace{0.17em}0$ in Fig. 2 B and C, one can find that the total spin direction will rotate along the propagating direction. The rotating direction is associated with the spin profile of the transverse wave: clockwise for ${\mathit{s}}_T>0$ and anticlockwise for ${\mathit{s}}_T<0$. Conventionally, ${\mathit{p}}^s$ for the circularly polarized transverse wave vanishes due to the cancellation of neighbor spin currents (10). However, mixed with a longitudinal wave, the total elastic wave will carry detectable nonzero ${\mathit{p}}^s\hspace{0.17em}\ne \hspace{0.17em}0$ with the help of nonzero hybrid spin density ${\mathit{s}}_h$.

Fig. 2.

Spin hybridization of elastic waves. (Left) Plots showing real parts of displacement fields, and (Right) corresponding spin textures. (A) When two kinds of elastic waves propagate along same direction, longitudinal wave ${\mathit{u}}_L\propto \exp \left(i{k}_{L}x\right){\mathit{e}}_x$ and transverse wave ${\mathit{u}}_T\propto \exp \left(i{k}_{T}x\right){\mathit{e}}_y$ in plane wave form, the total elastic waves $\mathit{u}={\mathit{u}}_L+{\mathit{u}}_T$ reveal the spin hybridization raised from the geometrical differences. The total spin density varies periodically along the propagation direction $x$, $\mathit{s}={\mathit{s}}_h\propto \sin \left(\left(k_L-k_T\right)x\right){\mathit{e}}_z$. The $z$ component of $\mathit{s}$ is plotted beyond the total displacement field. Another intriguing case of elastic spin is rotating spin texture. (B) For the combination of longitudinal wave and circularly polarized transverse wave with nontrivial spin density ${\mathit{s}}_T>0$, the total elastic spin becomes clockwise rotating along the propagation direction. (C) When ${\mathit{s}}_T<0$, the total elastic spin density becomes anticlockwise rotating along the propagation direction; $\mathit{s}\propto \mp \cos \left(\left(k_L-k_T\right)x\right){\mathit{e}}_x-\sin \left(\left(k_L-k_T\right)x\right){\mathit{e}}_y\pm {\mathit{e}}_z$, positive for ${\mathit{s}}_T>0$ and negative for ${\mathit{s}}_T<0$, respectively.

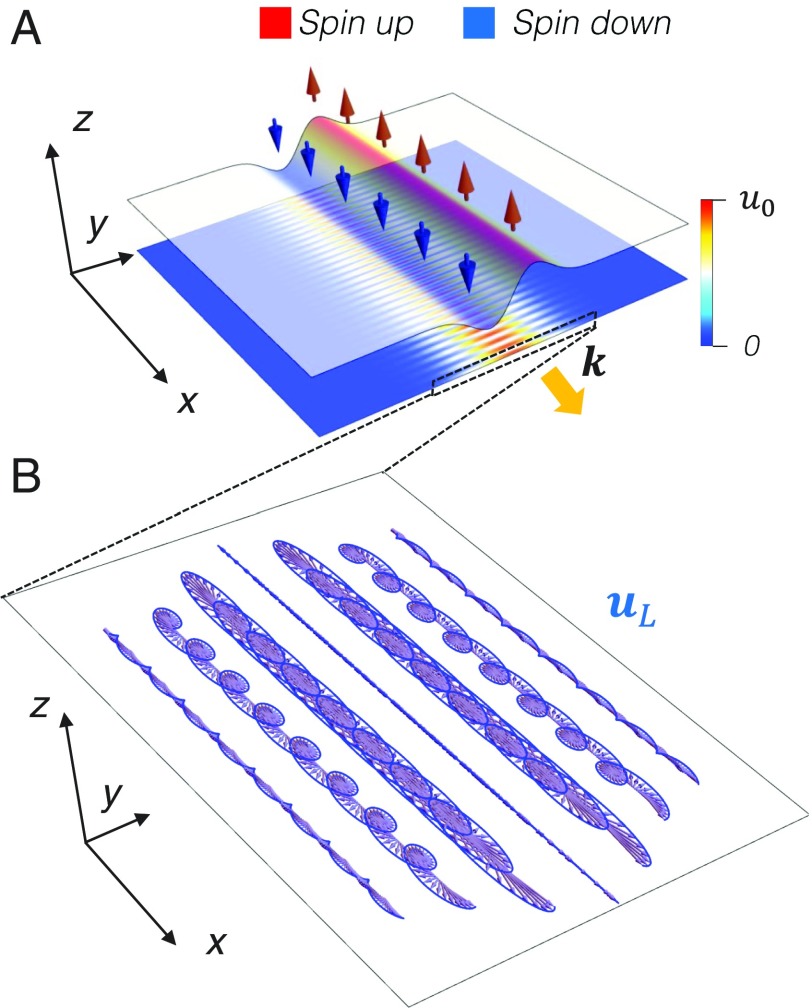
Besides two-wave interference, the pure longitudinal wave can also carry nontrivial spin density in spatial confined Gaussian waveform. We calculate the spin density of an elastic longitudinal wave in Fig. 3A (24). One can obtain that the two sides of the longitudinal wave beam have opposite spin distribution, which can be described by the nonzero spin density of a spatial Gaussian decay field $\mathit{s}\propto 4y/k_L{\delta }^2\exp \left(-2y^2/{\delta }^2\right){\mathit{e}}_z$, where $\delta$ is the width of Gaussian decay (detailed derivations can be found in SI Appendix, section 2). The nontrivial spin originates from the effective imaginary vector field along the Gaussian decay direction that induces the circularly polarized wave profile, with the geometrical constraint of longitudinal wave $\nabla \times {\mathit{u}}_L=0$. In Fig. 3B, we indeed see that the real part of displacement fields forms an opposite circularly polarized wave profile on both sides of the Gaussian beam, which can carry nontrivial spin along $z$ similar to the case of transverse waves (2, 24). This antisymmetric spin texture underlies the spin–orbit coupling in the Gaussian beam so that the waves over different sides possess different polarizations. Moreover, this spin texture is locked with the propagating direction of the Gaussian beam: opposite direction with opposite spin texture.

Fig. 3.

Nontrivial spin texture in an elastic longitudinal wave beam. Besides the wave interference approaches, the elastic Gaussian wave beam can also induce nontrivial spin density distribution. (A) The longitudinal wave Gaussian beam in the $xOy$ plane, $\left|{\mathit{u}}_L\right|\propto \exp \left(-y^2/{\delta }^2\right)$, will carry the antisymmetric spin density around the center of the beam, $\mathit{s}\propto \frac{4y}{k_L{\delta }^2}\exp \left(-2y^2/{\delta }^2\right){\mathit{e}}_z$. The $z$ component of $\mathit{s}$ is plotted above the displacement field of the longitudinal wave Gaussian beam. (B) The real part of the displacement field behaves effectively as a circularly polarized wave profile, whose rotation reflects the nontrivial transverse spin properties along both sides of the Gaussian beam.

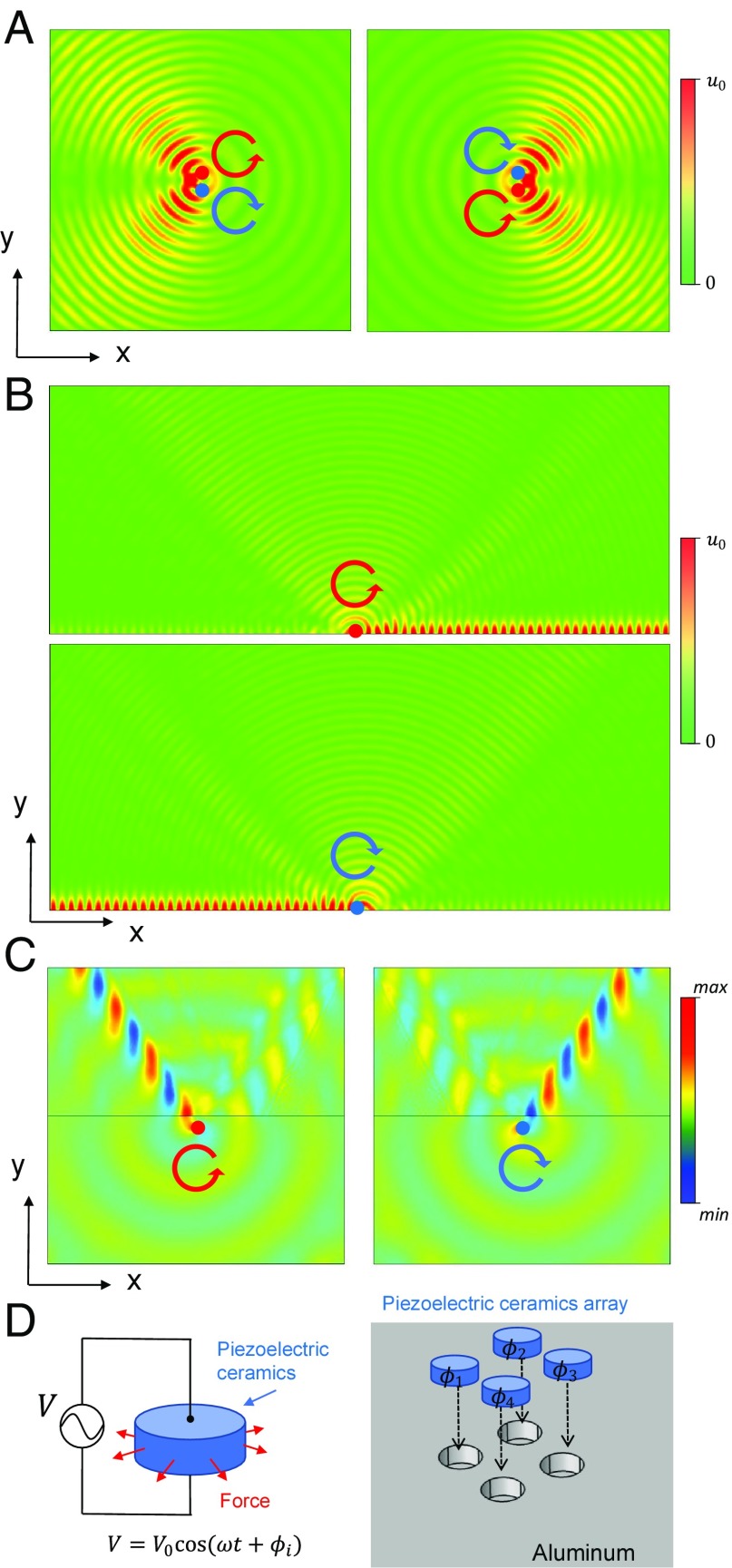
Strong spin texture momentum locking in an elastic wave inspires several schemes to excite a spatial nonsymmetric elastic wave with selective directionality. We exploit two different circularly polarized elastic loads to serve as the pair of spin sources to induce corresponding spin texture in Fig. 4A. We can see that the propagating direction of excited elastic waves shows strong dependence on the spin pair profile. Higher directionality can be excited by using more elastic wave sources with polarization gradients. Besides this scheme, we can excite the unidirectional Rayleigh wave and especially associate its propagation direction with spin profile, by using circularly elastic loads on the boundary of solids in Fig. 4B, reminiscent of the phononic QSHE (26) and photonic QSHE (7). However, the surface elastic modes are ${\mathbb{Z}}_2$ topologically trivial ($C_{spin}/2\mathrm{mod}2=0$, with $C_{spin}=C_{spin}^L+C_{spin}^T=4$); thus they have the usual scattering properties and are not robust against defects or disorders. Besides QSHE of elastic wave, in anisotropic material, we can realize spin-selected elastic routing, as shown in Fig. 4C, which can be regarded as SHE of the elastic wave, analogous to the optical case (27). It is achieved by placing the circularly elastic load in the isotropic side, in near-field proximity to the interface of the anisotropic elastic media with hyperbolic-like dispersion. The induced evanescent wave at interface possesses strong spin–momentum locked phenomena: different momentum directions with opposite spins. Thus, when the source excites the evanescent wave with a selected spin, the wave will choose the spin-locked momentum, and then it will selectively couple with the corresponding modes of high local density of states and excite unidirectional wave radiation propagating along a critical angle in the anisotropic elastic media. The spin of the elastic wave is defined in the isotropic side. The spin angular momentum of the elastic wave is responsible for all of these phenomena (details can be found in SI Appendix, section 3).

Fig. 4.

Spin-momentum locking in elastic waves. The strong directional excitation of a spin-selected elastic wave can be realized based on the spin–momentum locking. (A) Nonsymmetric elastic wave excitation in bulk can be achieved by exploiting two circularly polarized elastic loads to induce an effective opposite spin pair. The total displacement field is plotted. (B) Unidirectional elastic surface mode, Rayleigh wave, can be excited selectively by setting different circularly polarized elastic loads. The total displacement field is plotted. (C) The spin-controlled elastic wave routing in bulk can be achieved in anisotropic materials interfaced with isotropic media. The chiral elastic wave spins are excited and characterized in the isotropic side. Different spin excitation in the isotropic side selectively couples with the different directional wave routing in the anisotropic side through the selective local mode couplings of different spins at the interface. The area above the black line is anisotropic material, and the area below is isotropic material, with the black line as an interface. The divergence of the total displacement field that reflects the longitudinal component is plotted. (D) The experimental scheme to realize circularly polarized elastic loads. Four piezoelectric ceramics with different excitation phases are inserted into the surface of aluminum. By adjusting the excitation pattern $\left\{{\varphi }_1,{\varphi }_2,{\varphi }_3,{\varphi }_4\right\}$, we can excite the elastic wave with nontrivial spin density. After placing this array on the boundary of the aluminum block, we will observe spin–momentum locking phenomena: unidirectional excitations associated with their phase patterns. The spin–momentum locking analysis and experimental scheme details can be found in SI Appendix.

Finally, we discuss the experimental scheme to excite and observe elastic spin. To excite the elastic wave with nontrivial spin density, we consider four piezoelectric ceramics to induce effective circularly polarized elastic point loads shown in Fig. 4D. The spatial gradient of excitation phases $\left\{{\varphi }_1,{\varphi }_2,{\varphi }_3,{\varphi }_4\right\}$ will be responsible for reconstructing the circularly polarized profiles (i) ${\mathit{s}}_z>0$: ${\varphi }_1=0$, ${\varphi }_2=-\pi /2$, ${\varphi }_3=-\pi$, and ${\varphi }_4=-3\pi /2$; and (ii) ${\mathit{s}}_z<0$: ${\varphi }_1=0$, ${\varphi }_2=\pi /2$, ${\varphi }_3=\pi$, and ${\varphi }_4=3\pi /2$. Besides piezoelectric ceramics, the laser beam array with different phases can also induce the same spin excitation effect. To measure the elastic spin, we can focus on one of the spin-related physical phenomena: QSHE of elastic wave. After placing this excitation array on the boundary of elastic media, i.e., aluminum, one can observe the unidirectional excitation of the surface wave with different phase patterns: spin–momentum locking. The experimental proposal details and numerical verifications can be found in SI Appendix, sections 4 and 5.

Our work unveils the physical properties of the spin angular momentum in elastic waves of both longitudinal and transverse nature in isotropic media, which can be regarded as a generalization of the intimate relation between electron spin and angular momentum, revealed by Einstein and de Haas a century ago. Moreover, it gives us a perspective on the underlying relation between the spinful elementary excitations in condensed matter theory and polarized waves in classical fields. Potentially, our results about the elastic spin could be extended to connect other spin-related systems, (28) from conventional elastic wave devices (29) to nanoscale phononic materials (30, 31), e.g., the highly efficient spin-selected wave emitter, spin-sensitive detector, multichannel information transfer (32), or even spin conversions among different excitations (33, 34).

Materials and Methods

Here, we will show that the spin of an elastic wave is contained in the definition of angular momentum intrinsically, especially for the spin of a longitudinal wave and the hybrid spin in a mixed longitudinal–transverse wave. The total angular momentum density of an elastic wave in isotropic medium can be defined as $\mathit{R}\times \left(\rho \frac{d}{dt}\mathit{R}\right)$, where $\mathit{R}$ is the Lagrangian position vector $\mathit{R}=\mathit{r}-\mathit{u}$, $\mathit{r}$ is the Eulerian position vector after elastic deformation $\mathit{u}$, and $\rho$ is the mass density. For the velocity term $\frac{d}{dt}\mathit{u}$, we have

$$\begin{array}{cc}\hfill \frac{d\mathit{u}}{dt}& =\frac{d}{dt}\left(u_x{\mathit{e}}_x+u_y{\mathit{e}}_y+u_z{\mathit{e}}_z\right)\hfill \\ \hfill & ={\mathit{e}}_x\frac{d{u}_x}{dt}+{\mathit{e}}_y\frac{d{u}_y}{dt}+{\mathit{e}}_z\frac{d{u}_z}{dt}+u_x\frac{d{\mathit{e}}_x}{dt}+u_y\frac{d{\mathit{e}}_y}{dt}+u_z\frac{d{\mathit{e}}_z}{dt}\hfill \\ \hfill & =\frac{\partial \mathit{u}}{\partial t}+\left(\frac{\partial \mathit{u}}{\partial t}\cdot \nabla \right)\mathit{u}+\left(\frac{\partial }{\partial t}\nabla \times \mathit{u}\right)\times \mathit{u},\hfill \end{array}$$ [4]

where ${\mathit{e}}_x$, ${\mathit{e}}_y$, and ${\mathit{e}}_z$ are the unit vectors. From Eq. 4, we can see that the first part, $\partial \mathit{u}/\partial t+\left(\partial \mathit{u}/\partial t\cdot \nabla \right)\mathit{u}$, is a material derivate, which reflects the time evolution of the displacement field that is subjected to a space–time–dependent velocity field variations. The second part, $\partial /\partial t\left(\nabla \times \mathit{u}\right)\times \mathit{u}$, is raised from the rotating frame of reference with nonzero local vorticity, namely $\nabla \times \mathit{u}\hspace{0.17em}\ne \hspace{0.17em}0$.

Considering $\mathit{u}={\mathit{u}}_L+{\mathit{u}}_T$, the time-averaged angular momentum density $\mathit{j}$ can be written as

$$\begin{array}{cc}\hfill \mathit{j}& ={⟨\left(\mathit{r}-{\mathit{u}}_L-{\mathit{u}}_T\right)\times \left(\rho \frac{d}{dt}\left(\mathit{r}-{\mathit{u}}_L-{\mathit{u}}_T\right)\right)⟩}_t\hfill \\ \hfill & ={⟨\rho \left(\mathit{r}-{\mathit{u}}_L-{\mathit{u}}_T\right)\times \left(-\frac{\partial }{\partial t}{\mathit{u}}_L-\frac{\partial }{\partial t}{\mathit{u}}_T\right)⟩}_t\hfill \\ \hfill & +{⟨\rho \left(\mathit{r}-{\mathit{u}}_L-{\mathit{u}}_T\right)\times \left(-\frac{\partial }{\partial t}\left({\mathit{u}}_L+{\mathit{u}}_T\right)\cdot \nabla \right)\left({\mathit{u}}_L+{\mathit{u}}_T\right)⟩}_t\hfill \\ \hfill & +{⟨\rho \left(\mathit{r}-{\mathit{u}}_L-{\mathit{u}}_T\right)\times \left(-\left(\frac{\partial }{\partial t}\nabla \times {\mathit{u}}_T\right)\times \left({\mathit{u}}_L+{\mathit{u}}_T\right)\right)⟩}_t\hfill \\ \hfill & ={⟨-\rho \mathit{r}\times \frac{\partial }{\partial t}{\mathit{u}}_L⟩}_t+{⟨-\rho \mathit{r}\times \frac{\partial }{\partial t}{\mathit{u}}_T⟩}_t\hfill \\ \hfill & +{⟨\rho \left(\mathit{r}-{\mathit{u}}_L-{\mathit{u}}_T\right)\times \left(-\frac{\partial }{\partial t}\left({\mathit{u}}_L+{\mathit{u}}_T\right)\cdot \nabla \right)\left({\mathit{u}}_L+{\mathit{u}}_T\right)⟩}_t\hfill \\ \hfill & +{⟨\rho \left(\mathit{r}-{\mathit{u}}_L-{\mathit{u}}_T\right)\times \left(-\left(\frac{\partial }{\partial t}\nabla \times {\mathit{u}}_T\right)\times \left({\mathit{u}}_L+{\mathit{u}}_T\right)\right)⟩}_t\hfill \\ \hfill & +{⟨\rho \left({\mathit{u}}_L+{\mathit{u}}_T\right)\times \left(\frac{\partial }{\partial t}{\mathit{u}}_L+\frac{\partial }{\partial t}{\mathit{u}}_T\right)⟩}_t,\hfill \end{array}$$ [5]

where ${⟨\cdot ⟩}_t$ denotes the time-averaged operator. In our work, based on monochromatic elastic wave fields with frequency $\omega$ in a uniform nondispersive solid, the displacement field can be described by $\mathit{u}\left(\mathit{r},t\right)={\mathit{u}}_0\left(\mathit{r}\right)e^{-i\omega t}$; thus ${⟨\rho \mathit{r}\times \frac{\partial }{\partial t}{\mathit{u}}_L⟩}_t+{⟨\rho \mathit{r}\times \frac{\partial }{\partial t}{\mathit{u}}_T⟩}_t=0$. Considering $\left|\mathit{r}\right|\gg |{\mathit{u}}_L+{\mathit{u}}_T|$, $\mathit{R}\approx \mathit{r}$, we can decompose the time-averaged angular momentum density $\mathit{j}$ into two different parts,

$$\mathit{j}=\mathit{l}+\mathit{s}.$$ [6]

The first orbital angular momentum contribution $\mathit{l}=\rho \omega /2\mathit{r}\times \left(\mathrm{R}\mathrm{e}\left[-i{\mathit{u}}_L^{*}\cdot \left(\nabla \right){\mathit{u}}_L\right]+\mathrm{R}\mathrm{e}\left[-i{\mathit{u}}_T^{*}\cdot \left(\nabla \right){\mathit{u}}_T\right]+\mathrm{R}\mathrm{e}\left[-i{\mathit{u}}_L^{*}\cdot \left(\nabla \right){\mathit{u}}_T\right]+\mathrm{R}\mathrm{e}\left[-i{\mathit{u}}_T^{*}\cdot \left(\nabla \right){\mathit{u}}_L\right]\right)$, with $\mathit{u}*\cdot \left(\nabla \right)\mathit{u}=u_x^{*}\nabla u_x+u_y^{*}\nabla u_y+u_z^{*}\nabla u_z$, is an extrinsic origin-dependent quantity, which results from the third and fourth terms in Eq. 5. The second spin angular momentum contribution

$$\mathit{s}=\frac{\rho \omega }{2}\text{Im}\left[{\mathit{u}}_L^{*}\times {\mathit{u}}_L+{\mathit{u}}_T^{*}\times {\mathit{u}}_T+{\mathit{u}}_L^{*}\times {\mathit{u}}_T+{\mathit{u}}_T^{*}\times {\mathit{u}}_L\right]$$ [7]

represents the spin density of elastic waves, which is an intrinsic local property and is origin-independent, as a result of the last term in Eq. 5. Obviously, $\mathit{s}$ is strongly associated the polarization profile of the local elastic wave. In Eq. 7, the total spin density can be decomposed into three parts with different physical meanings,

$$\mathit{s}={\mathit{s}}_L+{\mathit{s}}_T+{\mathit{s}}_h,$$ [8]

where ${\mathit{s}}_L=\rho \omega /2\text{Im}\left[{\mathit{u}}_L^{*}\times {\mathit{u}}_L\right]$ is the spin density of longitudinal elastic wave, ${\mathit{s}}_T=\rho \omega /2\text{Im}\left[{\mathit{u}}_T^{*}\times {\mathit{u}}_T\right]$ is the spin density of transverse elastic wave, and ${\mathit{s}}_h=\rho \omega /2\text{Im}\left[{\mathit{u}}_L^{*}\times {\mathit{u}}_T+{\mathit{u}}_T^{*}\times {\mathit{u}}_L\right]$ is the hybrid spin density in a mixed longitudinal–transverse elastic wave.

It is interesting to point out that the spin density can be expressed as the quantum spin representation of the $SO\left(3\right)$ group. To represent the spin density in convenient quantum-like representation, we introduce the local state vector of the field,

$$\left|\mathit{u}\right.⟩=\left|{\mathit{u}}_L\right.⟩+\left|{\mathit{u}}_T\right.⟩,$$ [9]

where

$$\begin{array}{ccc}\hfill |{\mathit{u}}_L⟩& =\sqrt{\frac{\rho \omega }{2}}\left(\begin{array}{c}{u}_{L,x}\hfill \\ u_{L,y}\hfill \\ u_{L,z}\hfill \end{array}\right),\hspace{1em}|{\mathit{u}}_T⟩\hfill & \hfill =\sqrt{\frac{\rho \omega }{2}}\left(\begin{array}{c}{u}_{T,x}\hfill \\ u_{T,y}\hfill \\ u_{T,z}\hfill \end{array}\right).\end{array}$$ [10]

Using the state vector, spin and orbital angular momentum density can be written as “local expectation values” of the corresponding operators,

$$\begin{array}{cc}\hfill \mathit{l}& =\mathrm{R}\mathrm{e}\left[⟨\mathit{u}|-i\left(\mathit{r}\times \nabla \right)|\mathit{u}⟩\right]\hfill \\ \hfill {\mathit{s}}_L& =⟨{\mathit{u}}_L\left|\widehat{\mathit{S}}\right|{\mathit{u}}_L⟩\hfill \\ \hfill {\mathit{s}}_T& =⟨{\mathit{u}}_T\left|\widehat{\mathit{S}}\right|{\mathit{u}}_T⟩\hfill \\ \hfill {\mathit{s}}_h& =⟨{\mathit{u}}_T\left|\widehat{\mathit{S}}\right|{\mathit{u}}_L⟩+⟨{\mathit{u}}_L\left|\widehat{\mathit{S}}\right|{\mathit{u}}_T⟩,\hfill \end{array}$$ [11]

where $\widehat{\mathit{S}}$ is the spin angular momentum density operator for elastic wave, $\mathit{u}*\cdot \left(\widehat{\mathit{S}}\right)\mathit{u}=\text{Im}\left[\mathit{u}*\times \mathit{u}\right]$ (7, 10, 21, 35). From the results, we can find that the physical mechanism behind the nontrivial ${\mathit{s}}_h$ is the nonzero projection of spin from one kind of elastic wave to another kind.

Spin Operator

The spin angular momentum of an elastic wave can be described by the following spin-1 operator, which has the same form with light (7, 10) due to the similar geometry relation:

$$\begin{array}{ccc}\hfill {Ŝ}_x& =-i\left(\begin{array}{ccc}0\hspace{1em}\hfill & \hfill 0\hspace{1em}\hfill & \hfill 0\\ 0\hspace{1em}\hfill & \hfill 0\hspace{1em}\hfill & \hfill 1\\ 0\hspace{1em}\hfill & \hfill -1\hspace{1em}\hfill & \hfill 0\end{array}\right)\hspace{1em}{Ŝ}_y\hfill & \hfill =-i\left(\begin{array}{ccc}0\hspace{1em}\hfill & \hfill 0\hspace{1em}\hfill & \hfill -1\\ 0\hspace{1em}\hfill & \hfill 0\hspace{1em}\hfill & \hfill 0\\ 1\hspace{1em}\hfill & \hfill 0\hspace{1em}\hfill & \hfill 0\end{array}\right)\\ \hfill {Ŝ}_z& =-i\left(\begin{array}{ccc}0\hspace{1em}\hfill & \hfill 1\hspace{1em}\hfill & \hfill 0\\ -1\hspace{1em}\hfill & \hfill 0\hspace{1em}\hfill & \hfill 0\\ 0\hspace{1em}\hfill & \hfill 0\hspace{1em}\hfill & \hfill 0\end{array}\right).\hfill \end{array}$$ [12]

The spin operator $\widehat{\mathit{S}}$ satisfies the fundamental commutation relations of angular momentum: $\left[{Ŝ}_i,{Ŝ}_j\right]=i{ϵ}_{ijk}{Ŝ}_k$.