Tunable structure and dynamics of active liquid crystals

Activity tunes elastic properties and defect interactions in nematic liquid crystals.

Abstract

Active materials are capable of converting free energy into directional motion, giving rise to notable dynamical phenomena. Developing a general understanding of their structure in relation to the underlying nonequilibrium physics would provide a route toward control of their dynamic behavior and pave the way for potential applications. The active system considered here consists of a quasi–two-dimensional sheet of short (≈1 μm) actin filaments driven by myosin II motors. By adopting a concerted theoretical and experimental strategy, new insights are gained into the nonequilibrium properties of active nematics over a wide range of internal activity levels. In particular, it is shown that topological defect interactions can be led to transition from attractive to repulsive as a function of initial defect separation and relative orientation. Furthermore, by examining the +1/2 defect morphology as a function of activity, we found that the apparent elastic properties of the system (the ratio of bend-to-splay elastic moduli) are altered considerably by increased activity, leading to an effectively lower bend elasticity. At high levels of activity, the topological defects that decorate the material exhibit a liquid-like structure and adopt preferred orientations depending on their topological charge. Together, these results suggest that it should be possible to tune internal stresses in active nematic systems with the goal of designing out-of-equilibrium structures with engineered dynamic responses.

INTRODUCTION

Materials that contain mechanochemically active constituents are broadly referred to as active matter and are ubiquitous in natural (1, 2), biological (3), and physical (4–6) systems. The internal stresses that activity generates result in materials that can spontaneously flow and deform over macroscopic length scales (7). A fundamental question in active matter physics is how internal energy affects the structure, mechanics, and dynamics of a material that is out of thermodynamic equilibrium.

Structured fluids are a particularly rich system in which to explore these questions. On the one hand, nematic liquid crystals (LCs) can be used to manipulate active matter (8–10). On the other hand, activity may destroy orientational order of LCs and lead to generation of defect pairs and spontaneous flows (11). This behavior has been experimentally realized in vibrated granular matter (12), dense microtubule solutions driven by kinesin motors (13), bacterial suspensions (14), and cell colonies (15, 16). In the microtubule-kinesin active nematics of relevance to this work, recent efforts have sought to alter the defect structure using confinement (17) or surface fields (18) and have sought to characterize transport properties such as viscosity (19), elasticity, and active stresses (20). Despite this increased interest, foundational questions regarding the role of activity on characteristic length scales of active flows, or the nature of defect pair interactions far from equilibrium, remain unanswered. Addressing these questions might enable design and engineering of new classes of active and adaptive materials.

Here, we introduce a nematic LC composed of short actin filaments driven into an active state by myosin II motors. We first demonstrate that the long-time clustering dynamics of myosin motors can be exploited to probe the LC over a range of active stresses. We measure changes in the LC’s orientational and velocity correlation lengths as a function of motor density and find that these are consistent with theoretical calculations of nematic LCs with varying levels of internal stress. We then use the morphology of +1/2 defects to show, in both experiments and simulations, that increased activity reduces the LC’s bend elasticity relative to its splay elasticity. Thus, the degree to which an LC with known mechanics is driven out of equilibrium can be ascertained by the +1/2 defect morphology. We further demonstrate that varying internal activity can completely alter defect interaction, turning it from attractive to effectively repulsive. The activity at which this transition occurs is found to be a function of a defect pair’s initial separation and its relative orientation. To accurately capture these dynamics in simulations, contributions of both bend and splay elasticity in LC mechanics must be accounted for. We also analyze pair positional and orientational correlations of defects. Our calculations, which are confirmed by experimental observations and measurements, demonstrate that defects in active nematics exhibit liquid-like behavior. Last, we show that two preferable configurations for ±1/2 defect pairs exist, in contrast to like-charge defect pairs, which have single preferable configuration. These results demonstrate how internal stresses can be used to systematically change the mechanics and dynamics of LCs to enable structured liquids with tunable transport properties.

RESULTS

Actin-based active nematics with varying activity

We construct an active LC formed by the semiflexible biopolymer, F-actin, and the molecular motor, myosin II. A dilute suspension of monomeric actin (2 μM) is polymerized in the presence of a capping protein (CP) (21) to construct filaments with a mean length of l ≈ 1 μm. Filaments are crowded onto an oil-water interface by adding methylcellulose as a depletion agent (Fig. 1A), resulting in a dense film of filaments that form a two-dimensional (2D) nematic LC with an abundance of ±1/2 topological defects (movie S1) (22). Myosin II assembles into bipolar filaments of several hundred motor heads that appear as near diffraction–limited puncta in fluorescence microscopy (Fig. 1B and movie S2). Myosin II filaments generate stress on antiparallel actin filament pairs (Fig. 1C) to drive changes in the LC structure and dynamics, including the formation, transport, and annihilation of defect pairs (movies S2 to S4). Creation of new ±1/2 defects occurs over tens of seconds, with defects moving apart at a rate of ~0.8 μm/s (Fig. 1B). The direction of +1/2 defect motion indicates that the actomyosin generates extensile stresses (23), consistent with previous active nematics formed with microtubule-kinesin mixtures (13). This leads to the manifestation of active nematics, which, to the best of our knowledge, has not been reported in actin-based systems.

Fig. 1. F-actin–based active nematic LC driven by myosin II motors.

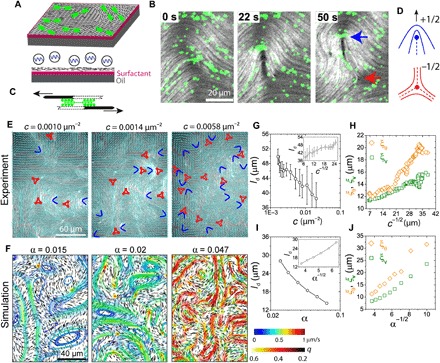
(A) Schematic of the experimental setup. Short actin filaments (black) are crowded to an oil-water interface supported by a layer of surfactant molecules (magenta) to form a 2D nematic LC. After formation of the passive LC, myosin motors (green) are added. (B) Time sequence of fluorescence images of actin filaments (gray scale) and myosin motors (green) showing the generation of a ±1/2 defect pair (blue and red arrows). Motor concentration, c = 0.019 μm⁻². Filament length, l = 1 μm. (C) Schematic of two actin filaments with antiparallel polarities sliding relative to each other due to the myosin II motor activity. (D) Schematic of ±1/2 defects. (E) Fluorescence images of actin LC (l = 1 μm) at different motor densities c. The director field (cyan lines) and ±1/2 defects (blue and red, respectively) are overlaid. (F) Simulation snapshots of LC at different activity levels α. Short black lines depict the local director field, and curves show streamlines (color indicates speed), with warmer colors indicating higher speeds. (G) Mean defect spacing l_d as a function of c. Inset: l_d plotted against c^−1/2. (H) Orientational and velocity-velocity correlation lengths (ξ_θ and ξ_v, respectively) plotted against c^−1/2. (I) l_d as a function of α in simulation. Inset: l_d plotted against α^−1/2. (J) ξ_θ and ξ_v plotted against α^−1/2 in simulation.

Over the course of 50 min, motors cluster into larger aggregates, resulting in a decrease in the myosin puncta number density (movie S2 and fig. S1). Motor clustering occurs concomitantly with a gradual decrease of the instantaneous velocity of the nematic (fig. S2), suggesting decreased active stress. We observe only a small, local distortion of the nematic field around large motor clusters. These clusters do not localize to the defects (fig. S3), indicating that motor clustering does not affect the LC structure. To explore the LC structure as the myosin puncta density, c, changes, we extract the nematic director field (24) and identify the ±1/2 defects over time as the puncta density decreases from 0.02 to 0.0016 μm⁻² (Fig. 1E). The fast relaxation time of the underlying actin LC relative to the rate of change of the motor density allows one to consider the system to be in a quasisteady state (see the “Analysis” section in Methods and fig. S4).

Effect of activity on correlation lengths: Myosin concentration acts as an activity parameter

To understand how internal stress drives nematic activity, we turn to a hydrodynamic model of active nematics (25). In the model, a phenomenological free energy is written in terms of a second-order, symmetric, and traceless Q-tensor: Q = q(nn − I/3) under uniaxial condition, where q is the nematic scalar order parameter, n is the director field, and I is the identity tensor (see supplementary text). The active stress Π^a caused by the presence of motors is written as

$${\mathbf{\Pi }}^{\mathit{a}}=-\mathrm{\alpha }\mathbf{Q}$$

where the activity parameter α has units of N/m² and is related to the magnitude of the force dipole that gives rise to local active, extensile stress. Physically, the competition of active stress and elastic stress leads to the generation of new defects, a feature that is characteristic of active nematics. If we introduce an elastic constant K for the nematic material, α/K bears the same units as c in the experiment. This is consistent with our intuition that motor number density is related to the activity of the system. One can therefore construct a natural length scale $\sqrt{\mathit{K}/\mathrm{\alpha }}$, and as discussed later, it should dictate the characteristic lengths that arise in our active nematics.

In Fig. 1F, we illustrate the hydrodynamic flows obtained from simulations with different levels of activity α. As α is increased, the average speed increases, indicated by the warmer color of the stream lines. The +1/2 defects are always associated with high-velocity regions, whereas the −1/2 defects are stagnation points. We also observe the formation of eddies, induced by the motion of defect pairs, and find that the average eddy size decreases with increased activity. The simulations also show that the distance between defect pairs in active nematics is susceptible to large fluctuations, caused by the competition between elastic forces and active stresses. The mean defect spacing decreases as a function of active stress (Fig. 1I) and agrees qualitatively with that observed experimentally (Fig. 1G). We observe that ${\mathit{l}}_{\mathrm{d}}\propto 1/\sqrt{\mathit{c}}\propto \sqrt{\mathit{K}/\mathrm{\alpha }}$ (Fig. 1, G and I, insets), consistent with theoretical expectations (26).

To further characterize the LC structure and dynamics, we measure the orientational and velocity-velocity correlation lengths, ξ_θ and ξ_v, respectively (see the “Analysis” section in Methods). These correlation lengths, along with l_d, have been shown to scale with activity ξ_θ ∝ ξ_v ∝ α^−1/2 (26), consistent with our simulation results (Fig. 1J). When these correlation lengths are extracted from the experimental data, we observe that they are proportional to c^−1/2 (Fig. 1H). These findings serve to establish that the number density of myosin puncta is a good measure of internal active stress in the actin-based nematic. Further, the time-dependent motor clustering provides a tool to directly observe the effects of varying activity on nematic structure and dynamics.

Change of the +1/2 defect morphology indicates lowering of effective bend-to-splay modulus ratio

Next, we explore how changes in active stresses affect the relative balance of bend and splay energies, which is manifested in the morphology of +1/2 defects (22). Figure 2A shows a fluorescence image of a passive (c = 0 μm⁻²) LC with average filament length, l = 2 μm. For clarity, the region around a +1/2 defect has been enlarged, and the corresponding director field is shown. In a 2D nematic system, the only relevant elastic modes are splay (K₁₁) and bend (K₃₃), and their ratio, κ = K₃₃/K₁₁, dictates the morphology of +1/2 defects (27, 28). Qualitatively, the “V-shaped” defect morphology can be understood by the relative dominance of the bend elasticity (K₃₃) to the splay elasticity (K₁₁). We quantify the defect morphology by circumnavigating the defect and plotting the angle the director field subtends with the tangent, θ, as a function of the angular coordinate φ (Fig. 2, A and B) averaged over a radial distance from the core where it remains relatively constant (22). These results are then fitted with a theoretical expression to extract a value of κ = 2.19 (22).

Fig. 2. Effect of activity on defect structure and effective elasticity.

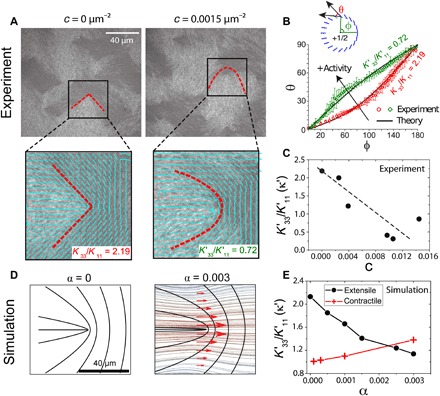
(A) Fluorescence actin images of a passive (c = 0 μm⁻²) and active (c = 0.0015 μm⁻²) LC (l = 2 μm). The region enclosed by the box is enlarged below, and the director field (cyan lines) and defect morphology (red dashed lines) are indicated. The ratio of bend (K₃₃) to splay (K₁₁) elasticity calculated from the defect morphology are indicated in the bottom right. (B) Plot of θ versus φ corresponding to experimental images of (A) for the passive (red circles) and active (green diamonds) LC. (C) Apparent elasticity $\mathrm{\kappa }\prime ={\mathit{K}}_{33}^{\prime }/{\mathit{K}}_{11}^{\prime }$ as a function of c for experimental data. Dashed line highlights the linear scaling. (D) Director field from the simulation for both passive (α = 0) and active (α = 0.003) LC. Red arrows around the defect represent the shear flow caused by the velocity field shown in the background. (E) Apparent elasticity κ′ as a function of α obtained from simulations for extensile (black circles) and contractile (red crosses) stresses.

In the presence of activity (c = 0.0015 μm⁻²), the defect morphology changes from V-shaped to “U-shaped” (Fig. 2A and movie S5). This is reflected in the θ(φ) plot, from which we calculate κ′ = 0.72 (Fig. 2B). By analyzing defects over a wide range of c, we find that κ decreases linearly with c (Fig. 2C). Thus, increased activity results in a lower value of effective bend modulus relative to the splay modulus, consistent with the fact that extensile active nematics are unstable to bend distortion (23, 29). That is, activity reduces the elastic penalty of nematic bend modes. The net effect is thus a reduction of the effective bend modulus of the LC as activity increases.

The change of the defect morphology induced by activity can also be explained in terms of hydrodynamic effects. We show in Fig. 2D the flow pattern obtained from our simulations that are associated with the motion of a +1/2 defect as α is increased from 0 (left) to 0.003 (right). There are shear flows on the two sides of the symmetry axis of the defect, with which the director field of a nematic LC tends to align, assuming a flow-aligning nematic (30). With this flow-aligning effect, the surrounding director field becomes more horizontal. This leads to the defect morphology becoming more U-shaped and a lower apparent bend modulus as the internal stress increases (Fig. 2E, circles). Further analysis, detailed in fig. S5, shows that although this effect is amplified by hydrodynamic flow alignment (31), activity-promoted bending is present even when the coupling to flow is turned off. In the simulations, we can change the sign of the active stress from extensile to contractile. These calculations predict that contractile stresses lower the effective splay elasticity, resulting in a tendency for the defect to become more V-shaped (Fig. 2E, crosses). These observations help establish that the defect morphology provides a direct reflection of the extent to which the LC is driven out of equilibrium. The nature of the defects’ morphological change also provides a simple visual marker to differentiate between the extensile or contractile nature of active stresses.

Activity as a means to switch the interaction between ±1/2 defects

Beyond the LC structure, activity also influences dynamics. In the absence of active stress (c = 0 μm⁻²), defects of opposite charge experience an attractive interaction, as the elastic energy is reduced through annihilation of +1/2 and −1/2 defects (Fig. 3A, top, and movie S6). We quantify defect annihilation by tracking the distance between defect pairs, Δr, over time (Fig. 3C). Defect annihilation occurs slowly, at a rate of 2 μm/min (Fig. 3C, green squares), a phenomenon that has been studied previously (22, 32). In contrast, at high motor density (c > 0.0015 μm⁻²), we observe that +1/2 and −1/2 defects effectively “repel” each other (Fig. 3A, bottom, and movie S7) such that the defect spacing increases at a rate of ≥10 μm/min (Fig. 3C, red triangles and blue circles). A similar phenomenon, namely, the “unbinding of defects,” has been reported in microtubule-kinesin–based systems (13) and 2D hydrodynamic simulations (33). Here, we examine this effect using our 3D simulations. Because of symmetry breaking in the surrounding director field, a +1/2 defect moves along its orientation (indicated by an arrow in Fig. 1D), activated by extensile stresses. In the absence of any far-field flows and elastic forces, simulations indicate that +1/2 defects are mobile, while −1/2 defects remain relatively immobile. The transition from attractive to repulsive interaction between defects of opposite topological charge is also observed in the simulations in the range from α = 0 to 0.001 (Fig. 3, B and D) and can be qualitatively understood as activity generating propulsive stresses within the nematic field that are sufficiently strong to overcome elastic stresses.

Fig. 3. Regulation of defect interactions by internal stress.

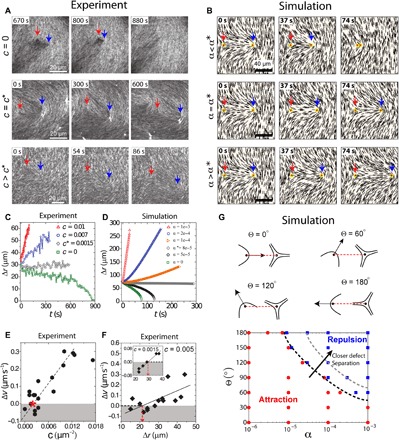
(A) Fluorescence images of actin LC showing dynamics of ±1/2 defect pair (blue and red arrows, respectively) for varying levels of c showing annihilation (top), stalling (middle), and repulsion (bottom). (B) Director field obtained around a ±1/2 defect pair from the simulations at varying levels of active stress showing annihilation (top), stalling (middle), and repulsion (bottom). (C) Defect separation, Δr, as a function of time at different values of c obtained from experimental data for defects with an initial separation of 30 μm. At c* = 0.0015 μm⁻², the defect spacing remains constant. (D) Defect separation, Δr, as a function of time as α is increased from 0 to 0.001 obtained from simulation data. (E) Relative velocity of defect separation, Δv, as a function of c obtained from experiments; the red asterisk corresponds to c*. Dashed line is the linear fit to the data. (F) Δv as a function of Δr for c = 0.005 and 0.0015 μm⁻² (inset). Solid black lines show linear fits. Red dashed lines indicate the length scale where Δv is zero. Data correspond to initial defect spacing, Δr = 30 μm. (G) Phase diagram of defect pair dynamics in terms of activity α and initial relative orientation Θ. Dashed lines indicate that phase boundary moves when the defect separation becomes smaller.

Our simulations also indicate that a critical activity (α*) exists for which the propulsive stresses are perfectly balanced by the elasticity of the LC, leading to the “stalling” of defect pairs where their separation stays constant for several hundred seconds (Fig. 3, B and D). We also observe this defect stalling experimentally at a critical motor density c* (Fig. 3, A and C, and movie S8). Both experiments and simulations show that although the interdefect distance remains constant over the course of several hundred seconds, their positions shift over time, possibly due to uncontrolled background flows. This demonstrates that propulsive stresses from activity can be used to qualitatively alter the defect dynamics.

To quantify the change from attractive to repulsive behavior, we plot the relative speeds between paired defects (Δv = v_+1/2 − v_−1/2) as a function of c for our experimental data (Fig. 3E). This shows that the transition from attractive to repulsive interactions for defects with an initial separation Δr = 30 μm occurs around c = 0.003 μm⁻², and the relative velocity is linearly controlled by motor concentration. Last, we find that, for a constant activity, Δv also scales linearly with the initial defect separation, Δr (Fig. 3F), such that we can define a length scale at which the transition between attractive and repulsive interactions occur. We see evidence that this length scale increases from 20 to 30 μm as the motor density decreases from 0.005 to 0.0015 μm⁻². Understanding how activity can alter the nature of defect interactions over varying length scales will be an exciting topic for future research.

To generalize the above findings, we also consider arbitrary relative orientations of a defect pair, as illustrated in Fig. 3G and fig. S6. The angle Θ between the +1/2 defect orientation and the line connecting the two defect cores has a profound effect on defect dynamics (34, 35). Using simulations (see supplementary text for details), we explore how defect pair interactions are affected by changes to Θ and activity α (Fig. 3G). When Θ is small, as the +1/2 defect faces the −1/2 defect, their interaction is always attractive; when Θ is large, as the +1/2 defect points away from the −1/2 defect, there is a transition activity α*(Θ) (as a function of Θ) above which defects become repulsive. Our simulations also show that when defect separation is closer, the phase boundary shifts to higher α, a feature consistent with experimental observations (Fig. 3, E and F). Thus, internal stresses can qualitatively change the interactions between defect pairs in LCs.

Defect density in an extensile active nematic is mainly determined by bend modulus

The inherent elasticity of a nematic LC can be viewed as a measure of the restoring force acting against spatial distortions (30). In two dimensions, a nematic LC opposes splay (K₁₁) and bend (K₃₃) deformations, but existing models of active nematics have been generally assumed K₁₁ = K₃₃ (7). Our results in Fig. 2 suggest that this may be insufficient to faithfully capture active LC mechanical response and, thus, their dynamics. To explore this, we construct an LC composed of actin filament length l = 1 μm and use the +1/2 defect morphology to calculate K₃₃/K₁₁ = 0.5 (22). As described earlier, the addition of motors drives LC dynamics, as shown in the series of optical images in Fig. 4A. We design two simulation systems, one with κ = 0.5 and another with κ = 1, for which the initial director field is directly taken from the experiments at time t = 0 s (see the “Numerical details” section in Methods). The dynamics obtained from these simulations are shown in Fig. 4 (B and C). We find that for κ = 0.5, locations and trajectories of defects in Fig. 4B exhibit good agreement with experiments, whereas agreement is poor for κ = 1. In particular, we find that the encircled defect pair undergoes annihilation for κ = 1, an event that is not observed in the experimental data or in the simulations with accurate mechanical properties. This shows that the defect dynamics at mesoscopic length and time scales strongly depends on the choice of splay and bend elasticity in the model. To isolate the roles of K₁₁ and K₃₃, we run simulations on a larger system size with variable elasticity. We find that the defect density, < n_defect >, defined as the total number of defects per unit area, decreases with κ with constant K₁₁ + K₃₃ at all activity values, as shown in Fig. 4D. Furthermore, by keeping K₃₃ constant and varying K₁₁ alone, we find that the defect density merely changes over a wide range of κ. Thus, for extensile active nematics, defect density in the active state is mainly controlled by K₃₃, by regulating the propensity of defect pairs to annihilate.

Fig. 4. LC mechanics is essential for predicting active-state dynamics and structure.

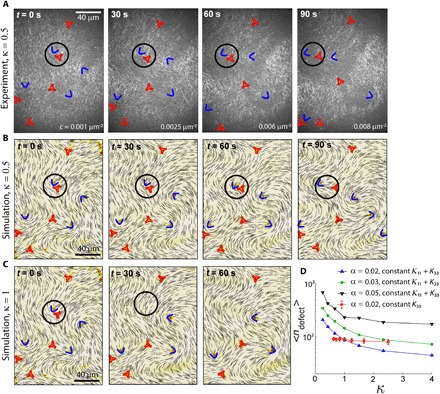
(A) Time-lapse fluorescence images of an active actin-based LC (κ = 0.5). ±1/2 defects are indicated by blue arcs and red triangles, respectively. The director field obtained from simulations of an active LC with the same instantaneous activity level as in the experiments evolved over time. Simulation is initiated with the director field from the experiments in (A) at t = 0. The mechanics of the LC are κ = 0.5 (K₃₃ = 0.5K, K₁₁ = K with K = 1 pN) in (B) and κ =1 (K₃₃ = K₁₁ = 0.75K) in (C). The black circle highlights a defect pair that undergoes an annihilation event in (C) but not in (A) or (B). (D) Defect density as a function of κ. < n_defect > decreases as a function of κ when K₃₃ decreases while keeping K₁₁ + K₃₃ constant for several different activity levels (black, green, and blue symbols). In contrast, it merely changes when K₁₁ is varied while keeping K₃₃ constant (red symbols).

Topological defects exhibit liquid-like structure and preferred orientations

To further understand the combined effects of activity and elasticity on the microstructure of active nematics, and gain insights into the seemingly chaotic behavior of topological defects, we rely on measures of order that have been particularly useful in the context of simple liquids, namely, radial distribution functions [g(r)]. Note that the correlation length calculations presented in Fig. 1 neglect the presence of defects. As a complimentary analysis tool, we introduce g(r) between defects and measure it as a function of activity. In this view, the active nematic system can be regarded as a binary system of positive and negative particles (defects; movie S9). In the first step, we ignore defect orientations and focus only on their spatial distribution. The radial distribution functions corresponding to defect cores in our active nematic system are akin to those observed in liquids, with a first peak corresponding to (+) and (−) defect pairs, and higher-order peaks arising from longer-range correlations. The predictions of simulations (Fig. 5A) are in semiquantitative agreement with our experimental observations (Fig. 5D). A shoulder is observed before the first peak of g(r); it can be explained by inspecting the radial distribution functions corresponding to like-charge defects.

Fig. 5. Radial distribution function of defect structure.

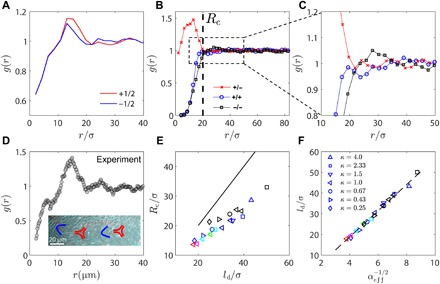
(A) Radial distribution function g(r) for +1/2 and −1/2 defects from simulations for ζ = 0.03 and κ = 1.0. (B) g(r) of defects of specific charge (+1/2 and −1/2) from simulation. (C) Zoom-in of (B) reveals higher-order peaks in g(r). (D) Radial distribution function g(r) of topological defects from experiments with activity c = 0.005 μm⁻². Inset shows experimental evidence of higher-order peaks in g(r). (E) A characteristic length scale R_c emerges from g(r) [illustrated in (B)], which is plotted against average defect spacing l_d. Black line corresponds to R_c = l_d. Warmer color of a marker indicates a higher activity. (F) Average defect spacing l_d is plotted against ${\mathrm{\alpha }}_{\text{eff}}^{-1/2}$, where the effective activity is defined as ${\mathrm{\alpha }}_{\text{eff}}=\mathrm{\alpha }/\sqrt{\mathrm{\kappa }}$.

In Fig. 5B, we differentiate + and − defects when calculating g(r) in simulation. We see that a length scale R_c exists below which the radial distribution of ± defects deviates considerably from unity. While +/− defect pairs exhibit a pronounced peak at distances below R_c, like-charge defects exhibit short-range repulsions. The repulsive core therefore shows up as the shoulder in the total g(r) seen in Fig. 5 (A and D). By closely examining g(r) at distances between 10 and 50 μm, we observe that g(r) for +/+ defect pairs reaches a plateau earlier than that for the −/− defect pair (Fig. 5C), implying that the average repulsive force between + defect pairs is weaker than that between − defect pairs. Higher-order peaks in g(r) at longer distances are clearly visible and can be explained by the fact that chains of alternating ±1/2 defects are occasionally formed in these systems (Fig. 5D, inset). In Fig. 5E, we find that the emerging length scale R_c exhibits a linear relation with the average defect spacing l_d. Thus, spatial inhomogeneity in defect charge becomes important when the defect separation is below the average spacing l_d.

These findings also imply that l_d is a fundamental length scale that sets the system’s defect structure. To examine the effect of elastic anisotropy, we plotted l_d against an effective activity α_eff, defined as ${\mathrm{\alpha }}_{\text{eff}}=\mathrm{\alpha }/\sqrt{\mathrm{\kappa }}$. Figure 5F shows that all data collapse onto a master curve. Because at rest (0 activity), systems of different κ are degenerate, bearing the same l_d = ∞ at equilibrium, we say that elastic anisotropy modifies the system’s activity rather than that activity modifies elastic anisotropy. Activity also breaks the symmetry of splay and bend. For the same activity level, extensile systems of lower κ engender more defects than those of higher κ with the same K₁₁ + K₃₃. This is consistent with the microscopic view that extensile systems are unstable to bend instability and low bend systems are prone to engender more defects.

We next consider defect orientation and study how it is coupled to defect separation. Figure 6 shows three types of defect pair, namely, +/− (Fig. 6A), +/+ (Fig. 6C), and −/− defects (Fig. 6D). By defining the angle between defect orientations, θ, one can prepare a probability heat map in terms of r and θ. The definition of +1/2 defect orientation is illustrated in the insets of Fig. 6. Because a −1/2 defect has threefold symmetry, one has to choose one of its three branches to define its orientation. For a +/− defect pair, we choose one branch as its orientation such that it is either parallel or antiparallel to the +1/2 defect’s orientation [a minimizer of cos(|θ|)]. For −/− defect pairs, we choose one such that it makes the smallest angle with the defect position vector r (always pointing away from the defect of interest). We observe that for opposite charge defect pairs, defects tend to align with each other when they are close (see Fig. 6B for experimental images and movie S10). There are two equally possible scenarios in a steady-state system; in one, the +1/2 defect points toward the −1/2 defect (pre-annihilation event), and in the other, the +1/2 defect points away from the −1/2 defect (post-proliferation event); similar scenarios are also reported in passive liquid crystals (22).

Fig. 6. Analysis of defect orientational structures.

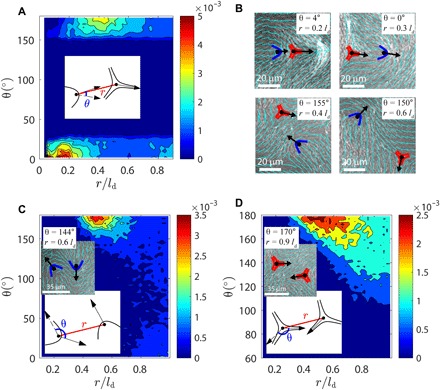
Probability distribution as function of defect distance r and defect angle θ (schematically defined in inset plots) for +/− (A), +/+ (C), and −/− (D) defect pair. Inset images in (C) and (D) show experimental observations of antiparallel like-charge defects (activity level c = 0.005 μm⁻² and l_d = 44 μm). (B) Typical structures of unlike-charge defect pairs observed in experiments. Top: Defect orientations tend to be parallel at short r. Bottom: Defect orientations tend to be antiparallel at intermediate r.

Unexpectedly, we find that there is a second stable regime for which ±1/2 defects are antiparallel at slightly longer separations r. This indicates that when defect spacing is in some intermediate range, the far field dictated by the −1/2 defect aligns the +1/2 defect in an antiparallel fashion. We have found abundant experimental evidences, some of which are shown in Fig. 6B and movie S10, in support of this prediction. For like-charge pairs (see Fig. 6, C and D), however, there is only one stable regime in which defects are antiparallel (face to face or back to back) to each other. Note that the above calculations are similar to Fig. 3G in terms of understanding defect orientations, but they are addressing different physics. In Fig. 3G, we examined the dynamics of an isolated defect pair at low activity, when the active stress is balanced by the elastic forces arising from existing defects. In contrast, in Fig. 6, we collected statistics for hundreds of interacting defect pairs in the high-activity regime, where activity is dissipated by generating new defects. Together, our findings indicate that defects in active systems can be described in terms of liquid state correlations, and that their interactions are anisotropic, with an interesting angular dependence that could potentially be used to engineer intricate transport mechanisms within these active materials.

DISCUSSION

Our work demonstrates the emergence of an active nematic in actin-based LC driven by myosin II motors. This system closely resembles the active nematics that are formed by microtubule filaments and kinesin motors (13). One notable finding is that active nematics can be realized with punctate myosin filaments, which contain ~100 s of motor heads and are sparsely distributed. While the kinesin tetramers used to realize active microtubule-based nematics have not been directly visualized, we presume that they would be more homogeneously distributed across the nematic. That stress inhomogeneities do not negatively affect the realization of active nematics underscores that these systems are dominated by long-range hydrodynamic and elastic effects. In both systems, motor-filament interactions give rise to uniaxial extensile stress. A previous work has shown that contractile stress dominates in actomyosin systems as filament length increases (36) or with the addition of cross-linking proteins (37). Further work will be needed to map out how the force generation by motor-filament interactions can be tuned by filament length, stiffness, and cross-linking (36).

The similarities between actin and microtubule systems notwithstanding, there are several quantitative differences that should be noted. First, activity-induced changes in defect shape have not been reported in microtubule-based nematics. We expect that higher levels of activity may be needed to overcome the higher rigidity of microtubules, which are 1000-fold stiffer than actin filaments. Furthermore, another notable difference between the two systems lies in the steady-state defect structure. In actin-myosin nematics, g(r) shows higher-order peaks, which indicate a strong interaction between defects; this more pronounced structure has not been reported in microtubule-kinesin experiments (38). A possible explanation for this difference might be the defect density, which is fivefold higher in actin than reported for microtubule-kinesin nematics.

In summary, we have performed experiments and simulations on a quasi-2D active nematic LC composed of short actin filaments driven by myosin motors. The clustering dynamics of myosin II motors have allowed us to investigate how the structure and dynamics of LCs vary as a function of internal activity. We characterize the motor-driven changes in structure and flows that arise in terms of the characteristic correlation lengths and defect density as a function of motor density, and find dependencies that are fully captured by nonequilibrium hydrodynamic simulations. Our combined theoretical and experimental approach has allowed us to use the change in the +1/2 defect morphology induced by activity to reveal the change in effective bend elasticity resulting from the microscopic stresses. We demonstrate that the activity can fundamentally change the nature of defect pair interactions, from attractive to effective repulsions, and we show that it is possible to control the relative defect speeds with motor concentration. The critical activity is shown to be a function of initial defect separation and relative orientation. Our further calculations of correlations of defects show that their configurations exhibit liquid-like structure and that the relative orientations of defect pairs become highly correlated when they are in close proximity.

METHODS

Experimental methods

Proteins

Monomeric actin was purified from rabbit skeletal muscle acetone powder (Pel-Freez Biologicals, Rogers, AR) (39) and stored at −80°C in G-buffer [2 mM tris-HCl (pH 8.0), 0.2 mM adenosine 5′-triphosphate (ATP), 0.2 mM CaCl₂, 0.2 mM dithiothreitol (DTT), and 0.005% NaN₃]. Tetramethylrhodamine-6-maleimide (TMR) dye (Life Technologies, Carlsbad, CA) was used to label actin. CP [mouse, with a HisTag, purified from bacteria (21); gift from the D. Kovar laboratory, The University of Chicago, Chicago, IL] was used to regulate actin polymerization and shorten the filament length. Skeletal muscle myosin II was purified from chicken breast (40) and labeled with Alexa-642 maleimide (Life Technologies, Carlsbad, CA) (41).

Experimental assay and microscopy

The actin is polymerized in 1× F-buffer [10 mM imidazole (pH 7.5), 50 mM KCl, 0.2 mM EGTA, 1 mM MgCl₂, and 1 mM ATP]. To avoid photobleaching, an oxygen-scavenging system [glucose (4.5 mg/ml), glucose oxidase (2.7 mg/ml; catalog no. 345486, Calbiochem, Billerica, MA), catalase (17,000 U/ml; catalog no. 02071, Sigma, St. Louis, MO), and 0.5 volume % β-mercaptoethanol] was added. Methylcellulose [15 centipoise; 0.3 weight % (wt %)] was used as the crowding agent. Actin from frozen stocks stored in G-buffer was added to a final concentration of 2 μM with a ratio of 1:5 TMR-maleimide labeled/unlabeled actin monomer. Frozen CP stocks were thawed on ice and added at the same time (6.7 and 3.3 nM for 1- and 2-μm long actin filaments). We call this assay “polymerization mixture” from henceforth. Myosin II was mixed with phalloidin-stabilized F-actin at a 1:4 myosin/actin molar ratio in spin-down buffer (20 mM MOPS, 500 mM KCl, 4 mM MgCl₂, 0.1 mM EGTA; pH 7.4) and centrifuged for 30 min at 100,000g. The supernatant containing myosin with low affinity to F-actin was used in experiments, whereas the high-affinity myosin was discarded.

The experiment was performed in a glass cylinder (catalog no. 09-552-22, Corning Inc.) glued to a coverslip (36). Coverslips were cleaned by sonicating in water and ethanol. The surface was treated with triethoxy(octyl)silane in isopropanol to produce a hydrophobic surface. To prepare a stable oil-water interface, PFPE-PEG-PFPE surfactant (catalog no. 008, RAN Biotechnologies, Beverly, MA) was dissolved in Novec 7500 Engineered Fluid (3M, St. Paul, MN) to a concentration of 2 wt %. To prevent flows at the surface, a small Teflon mask measuring 2 mm by 2 mm was placed on the treated coverslip before exposing it to ultraviolet-ozone for 10 min. The glass cylinder was thoroughly cleaned with water and ethanol before gluing it to the coverslip using instant epoxy. Then, 3 μl of oil-surfactant solution was added into the chamber and quickly pipetted out to leave a thin coating. The sample was always imaged in the middle of the film over the camera field of view, which was about 200 μm by 250 μm, to make sure that the sample remains in focus over this area, which is far away from the edges. Imaging close to the edges was avoided. The polymerization mixture was immediately added afterward. Thirty to 60 min later, a thin layer of actin LC was formed. Myosin II motors were added to the polymerization mixture at concentrations of 5 to 10 nM.

The sample was imaged using an inverted microscope (Eclipse Ti-E; Nikon, Melville, NY) with a spinning disc confocal head (CSU-X, Yokagawa Electric, Musashino, Tokyo, Japan), equipped with a CMOS camera (Zyla-4.2 USB 3; Andor, Belfast, UK). A 40× 1.15 numerical aperture water-immersion objective (Apo LWD, Nikon) was used for imaging. Images were collected using 568- and 642-nm excitation for actin and myosin, respectively. Image acquisition was controlled by MetaMorph (Molecular Devices, Sunnyvale, CA).

Image and data analysis

The nematic director field was extracted the same way as in (22), which used an algorithm that was described in detail in the methods section of Cetera et al. (24). The optical images were bandpass filtered and unsharp masked in ImageJ software (42) to remove noise and spatial irregularities in brightness. The image algorithm computes 2D fast Fourier transform of a small local square sections (of side ψ) of the image and uses an orthogonal vector to calculate the local actin orientation. The sections were overlapped over a distance ζ to improve statistics. ψ and ζ are varied over 15 to 30 μm and 1 to 3 μm, respectively, for different images to minimize errors in the local director without changing the final director field.

Myosin puncta density was calculated using ImageJ software. Toward the end of the experiment, large clusters of myosin were not counted. Because the number of myosin polymers remains at least 10-fold greater than that of myosin clusters, our results are insensitive to the choice of the cluster cutoff size. We calculated the mean l_d, ξ_θ, and ξ_v from overlapping 150-s intervals. We explored averaging over shorter time intervals and found that the trend in l_d was similar but, as expected, the SD increased (fig. S4). At the fastest rates of decrease, the myosin density does not decrease over this interval but is within the measurement error reported in Fig. 1C. The typical relaxation time of the actin nematic LC is given by τ_R = γl²/K, where γ, l, and K are the rotational viscosity, the filament length, and the LC elastic modulus, respectively. For γ ~ 0.1 Pa∙s, l = 1 μm, and K = 0.13 pN, we find that τ_R ~ 1 s. Thus, the LC structure achieves steady state on time scales much faster than the evolution of the myosin density.

The active flows were quantified using particle image velocimetry (available at www.oceanwave.jp/softwares/mpiv/) to extract local velocity field, v. The orientational correlation length, ξ_θ, was calculated by computing $\int \mathit{d}\mathit{r}\frac{{\mathit{g}}_2(\mathit{r})}{\mathit{g}(0)}$, where g₂(r) = 〈 cos[2(θ_i − θ_j)]〉, indicating spatial pairs i and j separated by a distance of r. Similarly, ${\mathrm{\xi }}_{\mathit{v}}=\int \mathit{d}\mathit{r}\frac{\langle {\mathbf{v}}_{\mathit{i}}(0)\cdot {\mathbf{v}}_{\mathit{j}}(\mathit{r})\rangle }{\langle {\mathit{v}}^2\rangle }$.

Theory and modeling

Theoretical model

The bulk free energy of the nematic LC, F, is defined as

$$\begin{array}{cc}\mathit{F}& ={\displaystyle {\int }_{\mathit{V}}}\mathit{d}\mathit{V}{\mathit{f}}_{\text{bulk}}+{\displaystyle {\int }_{\partial \mathit{V}}}\mathit{d}\mathit{S}{\mathit{f}}_{\text{surf}}\\ & ={\displaystyle {\int }_{\mathit{V}}}\mathit{d}\mathit{V}({\mathit{f}}_{\text{LdG}}+{\mathit{f}}_{\text{el}})+{\displaystyle {\int }_{\partial \mathit{V}}}\mathit{d}\mathit{S}{\mathit{f}}_{\text{surf}}\end{array}$$ (1)

where f_LdG is the short-range free energy, f_el is the long-range elastic energy, and f_surf is the surface free energy due to anchoring. f_LdG is given by a Landau–de Gennes expression of the form (30, 43)

$${\mathit{f}}_{\text{LdG}}=\frac{{\mathit{A}}_0}{2}(1-\frac{\mathit{U}}{3})\mathit{T}\mathit{r}({\mathbf{Q}}^2)-\frac{{\mathit{A}}_0\mathit{U}}{3}\mathit{T}\mathit{r}({\mathbf{Q}}^3)+\frac{{\mathit{A}}_0\mathit{U}}{4}{(\mathit{T}\mathit{r}({\mathbf{Q}}^2))}^2$$ (2)

Parameter U controls the magnitude of q₀, namely, the equilibrium scalar order parameter via ${\mathit{q}}_0=\frac{1}{4}+\frac{3}{4}\sqrt{1-\frac{8}{3\mathit{U}}}$. The elastic energy f_el is written as (Q_ij,k means ∂_kQ_ij)

$${\mathit{f}}_{\mathit{e}\mathit{l}}=\frac{1}{2}{\mathit{L}}_1{\mathit{Q}}_{\mathit{i}\mathit{j},\mathit{k}}{\mathit{Q}}_{\mathit{i}\mathit{j},\mathit{k}}+\frac{1}{2}{\mathit{L}}_2{\mathit{Q}}_{\mathit{j}\mathit{k},\mathit{k}}{\mathit{Q}}_{\mathit{j}\mathit{l},\mathit{l}}+\frac{1}{2}{\mathit{L}}_3{\mathit{Q}}_{\mathit{i}\mathit{j}}{\mathit{Q}}_{\mathit{k}\mathit{l},\mathit{i}}{\mathit{Q}}_{\mathit{k}\mathit{l},\mathit{j}}+\frac{1}{2}{\mathit{L}}_4{\mathit{Q}}_{\mathit{i}\mathit{k},\mathit{l}}{\mathit{Q}}_{\mathit{j}\mathit{l},\mathit{k}}$$ (3)

If the system is uniaxial, the above equation is equivalent to the Frank-Oseen expression

$$\begin{array}{c}{\mathit{f}}_{\mathrm{e}}=\frac{1}{2}{\mathit{K}}_{11}{(\nabla \cdot \mathbf{n})}^2+\frac{1}{2}{\mathit{K}}_{22}{(\mathbf{n}\cdot \nabla \times \mathbf{n})}^2+\frac{1}{2}{\mathit{K}}_{33}{(\mathbf{n}\times (\nabla \times \mathbf{n}))}^2\\ -\frac{1}{2}{\mathit{K}}_{24}\nabla \cdot [\mathbf{n}(\nabla \cdot \mathbf{n})+\mathbf{n}\times (\nabla \times \mathbf{n})]\end{array}$$ (4)

The L values in Eq. 3 can then be mapped to the K values in Eq. 4 via

$$\begin{array}{c}{\mathit{L}}_1=\frac{1}{2{\mathit{q}}_0^2}[{\mathit{K}}_{22}+\frac{1}{3}({\mathit{K}}_{33}-{\mathit{K}}_{11})]\\ {\mathit{L}}_2=\frac{1}{{\mathit{q}}_0^2}({\mathit{K}}_{11}-{\mathit{K}}_{24})\\ {\mathit{L}}_3=\frac{1}{2{\mathit{q}}_0^3}({\mathit{K}}_{33}-{\mathit{K}}_{11})\\ {\mathit{L}}_4=\frac{1}{{\mathit{q}}_0^2}({\mathit{K}}_{24}-{\mathit{K}}_{22})\end{array}$$ (5)

By assuming a one elastic constant K₁₁ = K₂₂ = K₃₃ = K₂₄ ≡ K, one has ${\mathit{L}}_1=\mathit{L}\equiv \mathit{K}/2{\mathit{q}}_0^2$ and L₂ = L₃ = L₄ = 0. Point-wise, n is the eigenvector associated with the greatest eigenvalue of the Q-tensor at each lattice point.

To simulate the LC’s nonequilibrium dynamics, a hybrid lattice Boltzmann method was used to simultaneously solve a Beris-Edwards equation and a momentum equation, which accounts for the hydrodynamic effects. By introducing a velocity gradient W_ij = ∂_ju_i, strain rate A = (W + W^T)/2, vorticity Ω = (W − W^T)/2, and a generalized advection term

$$\begin{array}{c}\mathbf{S}(\mathbf{W},\mathbf{Q})=(\mathrm{\xi }\mathbf{A}+\mathrm{\Omega })(\mathbf{Q}+\mathbf{I}/3)+(\mathbf{Q}+\mathbf{I}/3)(\mathrm{\xi }\mathbf{A}-\mathrm{\Omega })\\ -2\mathrm{\xi }(\mathbf{Q}+\mathbf{I}/3)\mathit{T}\mathit{r}(\mathbf{Q}\mathbf{W})\end{array}$$ (6)

one can write the Beris-Edwards equation (44) according to

$$({\partial }_{\mathit{t}}+\mathbf{u}\cdot \nabla )\mathbf{Q}-\mathbf{S}(\mathbf{W},\mathbf{Q})=\mathrm{\Gamma }\mathbf{H}$$ (7)

The constant ξ is related to the material’s aspect ratio, and Γ is related to the rotational viscosity γ₁ of the system by $\mathrm{\Gamma }=2{\mathit{q}}_0^2/{\mathrm{\gamma }}_1$(45). The molecular field H, which drives the system toward thermodynamic equilibrium, is given by

$$\mathbf{H}=-{\left[\frac{\mathrm{\delta }\mathit{F}}{\mathrm{\delta }\mathbf{Q}}\right]}^{\mathit{s}\mathit{t}}$$ (8)

where […]^st is a symmetric and traceless operator. When velocity is absent, that is, u(r) ≡ 0, Beris-Edwards equation (Eq. 7) reduces to Ginzburg-Landau equation

$${\partial }_{\mathit{t}}\mathbf{Q}=\mathrm{\Gamma }\mathbf{H}$$

To calculate the static structures of ±1/2 defects, we adopted the above equation to solve for the Q-tensor at equilibrium.

Degenerate planar anchoring is implemented through a Fournier-Galatola expression (46) that penalizes out-of-plane distortions of the Q tensor. The associated free energy expression is given by

$${\mathit{f}}_{\text{surf}}=\mathit{W}{(\tilde{\mathbf{Q}}-{\tilde{\mathbf{Q}}}^{\perp })}^2$$ (9)

where $\tilde{\mathbf{Q}}=\mathbf{Q}+({\mathit{q}}_0/3)\mathbf{I}$ and ${\tilde{\mathbf{Q}}}^{\perp }=\mathbf{P}\tilde{\mathbf{Q}}\mathbf{P}$. Here, P is the projection operator associated with the surface normal ν as P = I − νν. The evolution of the surface Q-field at one-constant approximation is governed by (47)

$$\frac{\partial \mathbf{Q}}{\partial \mathit{t}}=-{\mathrm{\Gamma }}_{\mathit{s}}(-{\mathit{L}}_1\mathrm{\nu }\cdot \nabla \mathbf{Q}+{\left[\frac{\partial {\mathit{f}}_{\text{surf}}}{\partial \mathbf{Q}}\right]}^{\text{st}})$$ (10)

where Γ_s = Γ/ξ_N with ${\mathrm{\xi }}_{\mathit{N}}=\sqrt{{\mathit{L}}_1/{\mathit{A}}_0}$, namely, nematic coherence length.

Using an Einstein summation rule, the momentum equation for the nematics can be written as (45, 48)

$$\begin{array}{cc}\mathrm{\rho }({\partial }_{\mathit{t}}+{\mathit{u}}_{\mathit{j}}{\partial }_{\mathit{j}}){\mathit{u}}_{\mathit{i}}=& {\partial }_{\mathit{j}}{\mathrm{\Pi }}_{\mathit{i}\mathit{j}}+\mathrm{\eta }{\partial }_{\mathit{j}}[{\partial }_{\mathit{i}}{\mathit{u}}_{\mathit{j}}+{\partial }_{\mathit{j}}{\mathit{u}}_{\mathit{i}}+(1-3{\partial }_{\mathrm{\rho }}{\mathit{P}}_0){\partial }_{\mathrm{\gamma }}{\mathit{u}}_{\mathrm{\gamma }}{\mathrm{\delta }}_{{\mathit{i}}_{\mathit{j}}}]\end{array}$$ (11)

The stress Π = Π^p + Π^a consists of a passive and an active part. The passive stress Π^p is defined as

$$\begin{array}{c}{\mathrm{\Pi }}_{\mathit{i}\mathit{j}}^{\mathit{p}}=-{\mathit{P}}_0{\mathrm{\delta }}_{\mathit{i}\mathit{j}}-\mathrm{\xi }{\mathit{H}}_{\mathit{i}\mathrm{\gamma }}({\mathit{Q}}_{\mathrm{\gamma }\mathit{j}}+\frac{1}{3}{\mathrm{\delta }}_{\mathrm{\gamma }\mathit{j}})-\mathrm{\xi }({\mathit{Q}}_{\mathit{i}\mathrm{\gamma }}+\frac{1}{3}{\mathrm{\delta }}_{\mathrm{\gamma }\mathit{j}}){\mathit{H}}_{\mathrm{\gamma }\mathit{j}}\\ +2\mathrm{\xi }({\mathit{Q}}_{\mathit{i}\mathit{j}}+\frac{1}{3}{\mathrm{\delta }}_{\mathit{i}\mathit{j}}){\mathit{Q}}_{\mathrm{\gamma }\mathrm{\epsilon }}{\mathit{H}}_{\mathrm{\gamma }\mathrm{\epsilon }}-{\partial }_{\mathit{j}}{\mathit{Q}}_{\mathrm{\gamma }\mathrm{\epsilon }}\frac{\mathrm{\delta }\mathrm{ℱ}}{\mathrm{\delta }{\partial }_{\mathit{i}}{\mathit{Q}}_{\mathrm{\gamma }\mathrm{\epsilon }}}+{\mathit{Q}}_{\mathit{i}\mathrm{\gamma }}{\mathit{H}}_{\mathrm{\gamma }\mathit{j}}-{\mathit{H}}_{\mathit{i}\mathrm{\gamma }}{\mathit{Q}}_{\mathrm{\gamma }\mathit{j}},\end{array}$$ (12)

where η is the isotropic viscosity, and the hydrostatic pressure P₀ is given by (49)

$${\mathit{P}}_0=\mathrm{\rho }\mathit{T}-{\mathit{f}}_{\text{bulk}}$$ (13)

The temperature T is related to the speed of sound c_s by $\mathit{T}={\mathit{c}}_{\mathit{s}}^2$. The active stress reads (50)

$${\mathrm{\Pi }}_{\mathit{i}\mathit{j}}^{\mathit{a}}=-\mathrm{\alpha }{\mathit{Q}}_{\mathit{i}\mathit{j}}$$ (14)

in which α is the activity in the simulation. The stress becomes extensile when α > 0 and contractile when α < 0.

Numerical details

We solve the evolution Eq. 7 using a finite difference method. The momentum Eq. 11 is solved simultaneously via a lattice Boltzmann method over a D3Q15 grid (51). The implementation of stress follows the approach proposed by Guo et al. (52). The units are chosen as follows: The unit length a is chosen to be a = ξ_N = 1 μm, characteristic of the filament length, the characteristic viscosity is set to γ₁ = 0.1 Pa∙s, and the force scale is made to be F₀ = 10⁻¹¹ N. Other parameters are chosen to be A₀ = 0.1, K = 0.1, ξ = 0.8, Γ = 0.13, η = 0.33, and U = 3.5, leading to q₀ ≈ 0.62. The simulation was performed in a rectangular box. The boundary conditions in the xy plane are periodic with size [N_x, N_y] = [250, 250]. Two confining walls were introduced in the z dimension, with strong degenerate planar anchoring, ensuring a quasi-2D system with z dimension 7 ≤ N_z ≤ 11. We refer the reader to (47) for additional details on the numerical methods used here.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/10/eaat7779/DC1

Fig. S1. Myosin motors cluster over time.

Fig. S2. Temporal behavior of root mean square velocity.

Fig. S3. Myosin motors do not localize to defect cores.

Fig. S4. Time averaging of defect spacing.

Fig. S5. Effect of flow alignment on the change of defect morphology.

Fig. S6. Director field associated with different defect orientations.

Supplementary Text

Movie S1. Crowding of actin filaments (mean length, l = 1 μm) on an oil-water interface forming a 2D nematic LC.

Movie S2. A dense film of actin filaments (red, l = 1 μm) and myosin II (green) form an active nematic.

Movie S3. Generation of topological defect pairs in actomyosin-based active nematic (l = 1 μm).

Movie S4. Persistent motion of a +1/2 defect (solid symbol) along its orientation in our actomyosin-based active nematics (l = 1 μm); −1/2 (open symbol) defect remains immobile.

Movie S5. Fluorescence images of actin (left) and myosin (right) in actin nematic (l = 2 μm).

Movie S6. Time-lapse imaging of fluorescent actin in a passive nematic LC (l = 1 μm, c = 0 μm⁻²) showing annihilation of defect pairs.

Movie S7. Time-lapse imaging of fluorescent actin in an active nematic LC (l = 1 μm, c = 0.01 μm⁻²) showing defect repulsion.

Movie S8. Time-lapse imaging of fluorescent actin in an active nematic LC (l = 1 μm, c = 0.0015 μm⁻²) showing defect stalling, where the defect pair separation (indicated by open symbols) does not change significantly over the course of 3 min.

Movie S9. Simulation movie of defect dynamics in a quasi-2D active nematic LC.

Movie S10. Time-lapse imaging of ± defect pair dynamics in active nematic LC (l = 1 μm, c = 0.0015 μm⁻²) showing that defect orientations change from roughly antiparallel at large separation to parallel when close, consistent with the structural analysis of defects in simulations.