Knowledge gaps in the early growth of semantic feature networks

Abstract

Understanding language learning, and more general knowledge acquisition, requires characterization of inherently qualitative structures. Recent work has applied network science to this task by creating semantic feature networks, in which words correspond to nodes and connections to shared features, then characterizing the structure of strongly inter-related groups of words. However, the importance of sparse portions of the semantic network - knowledge gaps - remains unexplored. Using applied topology we query the prevalence of knowledge gaps, which we propose manifest as cavities within the growing semantic feature network of toddlers. We detect topological cavities of multiple dimensions and find that despite word order variation, global organization remains similar. We also show that nodal network measures correlate with filling cavities better than basic lexical properties. Finally, we discuss the importance of semantic feature network topology in language learning and speculate that the progression through knowledge gaps may be a robust feature of knowledge acquisition.

Introduction

Formal understanding of the properties of knowledge acquisition remains a foundational area of research in cognitive science. In the domain of word learning, behavioral evidence suggests that this process is mediated in part by various properties of words at an individual level, such as the frequency of a given word or the extent to which it evokes a mental image.^1,2 Recently, tools from network science have offered a means of examining how lexical acquisition might also be mediated by higher-order relationships between many words, or the network topology underlying input that is available to the learner.³ In this theoretical framework, words are typically represented by the nodes of the network, while shared semantic or sound-based associations can be used to construct edges between nodes.^4–6 Broadly, evidence indicates that learners are particularly sensitive to how densely connected a given word is relative to others words in a network; specifically, see⁷ for networks defined by word co-occurrence,⁴ for networks formed from free associations, though this may be partially due to features of child-directed speech,⁸ and see⁹ for networks derived from multiple types of edges).

Because previous studies focus on the network properties of words that have already been learned by children, they have left open the question, “How do those words not yet known affect learning?” More precisely, as children produce new words does their resulting semantic feature network contain any knowledge gaps, or voids where a word is missing? Since edges correspond to at least one shared property (e.g., temporal co-occurrence or phonological similarity), a gap in the network suggests a unifying concept that is not yet understood. In the network science formalism, such knowledge gaps in a growing network correspond to topological cavities that are born, and then later filled in with the addition of new nodes and edges. We propose that characterizing the evolution patterns of these cavities in a semantic feature network built from any of multiple types of connections offers unique insight into lexical organization in children, and we investigate whether knowledge gaps might serve as a useful proxy for the difficulty associated with acquiring in particular feature-based concepts.

To answer these questions, we employ concepts and tools from applied topology that allow us to detect topological cavities within a growing network. The specific network that we study is a growing semantic feature network in which nouns correspond to nodes and edges are shared observable features or functions. For example, “cheese” and “bus” are both yellow, and thus the corresponding nodes are linked in the semantic feature network. In addition, words in this dataset are given a weight (inducing a word order) derived from the month that the word was produced by toddlers aged 16–30 months. Though such nodeweighted networks are commonly observed in biology, they are challenging to analyze because standard tools from network science, such as traditional graph metrics, can account for weighted edges, but not for weighted nodes. To address this challenge, we develop a formalism that transforms any node-weighted system into a sequence of binary graphs analyzable by both topological data analysis and standard tools of network science including graph metrics. Specifically, we encode the growing semantic feature network into a sequence of binary graphs called a filtration, with one new node (corresponding to one new word) added at each step. We call this sequence of graphs built from a node-ordered network a node-filtered order complex (hereafter referred to as the n-order complex for brevity), inspired by the order complex defined for edgeweighted networks¹⁰ and weight rank clique filtrations.^11,12 We can then compute persistent homology,^13,14 which tracks the formation and possible filling in of topological cavities of different dimensions throughout a filtration. This approach differs from many existing approaches by using information from node weights, encoding higher-order group relations, and identifying mesoscale topological features in the growing network.

By encoding the growing semantic feature network of children ages 16–30 months as a n-order complex, we use persistent homology to ask if topological cavities – corresponding to knowledge gaps – form and then fill in throughout the learning process. We find a collection of long-persisting cavities of varying dimensions do exist and interestingly, the pattern of cavity formation suggests that the semantic feature network is organized under external constraints. We adjudicate between conflicting hypotheses that topological cavities might either be robust to or vary systematically with the nature of input available to the learner, in this case indexed by the mother’s level of education. We observe at most minor differences in topological cavity existence despite variation in node order; on average, any ordering of learned words gives rise to a similar topological signature involving a regular birth and death of persistent cycles. Since the order of words learned can vary considerably, our results suggest that these topological cavities might be a conserved feature of the language learning process, and that semantic feature network growth is a robust phenomenon that can accommodate many local changes without abrupt restructuring of the network’s large-scale organization.

Results

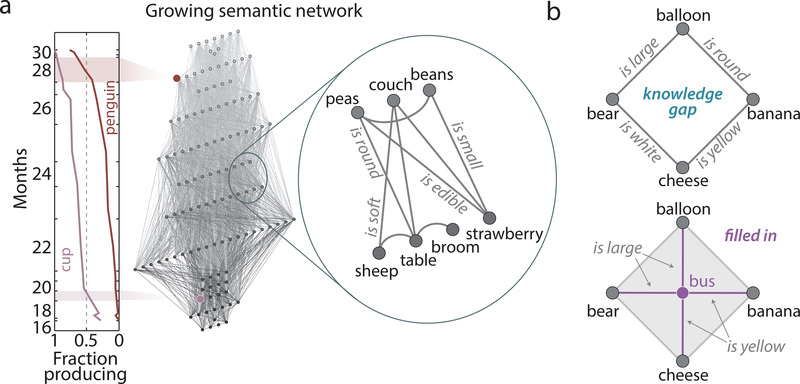
To begin, we construct an ordering on 120 nouns derived from the first month at which ≥50% of children between the ages of 16 and 30 months can produce each word (Fig. 1a, left).¹⁵ Multiple words could be first produced within one month, so we create a total ordering by sorting words learned within one month by descending percentage of children producing each word. We next form a binary semantic feature network with 120 nouns as nodes, and with edges connecting words that share a property or function (Fig. 1a, right).¹⁶ We note that these shared semantic features, for example ‘“yellow”, “has legs”, etc., can be observed by children before they can produce the feature words themselves. Together, the word ordering and binary network pair assemble into the growing semantic feature network,⁴ with the node added at step n connecting to all of its neighbors added at steps 1...,n − 1 (Fig. 1a, middle).

Figure 1: Knowledge gaps manifesting as topological cavities within the growing semantic feature network.

(a) (Left) Word ordering is given based on the month at which 50% of reported children produce each word. As an example, the word ‘spoon’ is first produced by ≥ 50% of children at 19 months, so it is placed at the appropriate location within the growing complex (purple node, towards the bottom). The word ‘moose’ is similarly placed at the 28 month mark (sienna node, towards the top). (Right) Semantic features connect nouns (corresponding to nodes), forming the semantic feature network. (Center) Combining the binary feature network and word production times creates a growing semantic feature network with nodes entering based on the first month at which ≥ 50% of children can produce the word. (b) A ‘knowledge gap’ could be seen as a topological void within the semantic feature network. The connection pattern between ‘balloon’, ‘bear’, ‘cheese’, and ‘banana’ leave a gap within the graph (top), but the addition of the node corresponding to ‘bus’ and its connections fills in the cavity (bottom).

We are interested in the presence of knowledge gaps, which we hypothesize manifest as voids within the growing semantic feature network that exist only for a finite number of months. For example, in Fig. 1b (top), the words ‘balloon’, ‘bear’, ‘cheese’, and ‘banana’ connect in a pattern that leaves a hole within the network. If the word ‘bus’ is learned later, this word connects to each of ‘balloon’, ‘bear’, ‘cheese’, and ‘banana’, so that there is no longer a void within the network. When a void in the network is extinguished, we say the knowledge gap is filled in (Fig. 1b, bottom). The features of interest in such a network are then the nodes responsible for filling in the cavity, which correspond to the temporarily missing words. Importantly, if a cavity is not filled by the end of the filtration, we cannot conclude that the cavity corresponds to a knowledge gap since it could be either surrounding a word that does not exist in our dataset or there simply exists a cavity in the network of the full English language.

To identify topological cavities within the growing semantic feature network, we will use a method from applied topology called persistent homology, which returns the (1) number, (2) dimension, and importantly (3) longevity of topological cavities within a growing network.

Topology of generative growing network models

Before approaching knowledge gaps in the semantic feature network, we first pause to ask if and how persistent homology can distinguish randomness from structure within artificial models of growing graphs (equivalently n-order complexes), which will additionally help us to gain an intuition for processes creating particular cavity existence patterns. Specifically, we test four growing graph models with varying degrees of predefined structure. Each model constructs a binary graph by assigning a probability to the existence of each edge as a function of one or both parent nodes. We call these generative models because they construct de novo both the binary graph and the node order. For the following models we let the node ordering s simply be 1 : N with N being the total number of nodes.

The most basic (and random) model that we tested assigns each edge entering the graph with the addition of node n a probability p(n) = c ∈ [0,1] of existing. We call this model the constant probability model, and we show its persistent homology in Fig. 2a with p(n) = 0.3. The next model, the proportional probability model, attaches edges from node n to all nodes 1,...,n − 1 with probability p(n) = n/N (Fig. 2b). Next, we generate a modular network composed of four equal-sized communities, and we refer to it as the modular growth model (Fig. 2c). We randomly assign nodes to communities; edges added with node n exist with probability p_in between node n and other nodes within its community, and with probability p_out between node n and other nodes in different communities. In our final generative model, each node n is assigned an affinity a_n that remains constant throughout the entire growth process. This temporal invariance ensures that after node n is added, any future node m will connect to node n with probability a_n. We require all a_n to be normalized so if $\overrightarrow{a}=\left(a_1,a_2,\dots ,a_N\right)$ is the vector of node affinities, $\max (\overrightarrow{a})=1$. We call this model the edge affinity model, and in Fig. 3d we show results for this model with node affinities drawn randomly without replacement from the vector $\overrightarrow{a}=\frac{\left(1,4,9,\dots ,{120}^2\right)}{{120}^2}$. For each of these models, we choose parameters so as to produce graphs whose edge density closely matches the edge density of the empirically measured semantic feature network, ∼ 0.3.

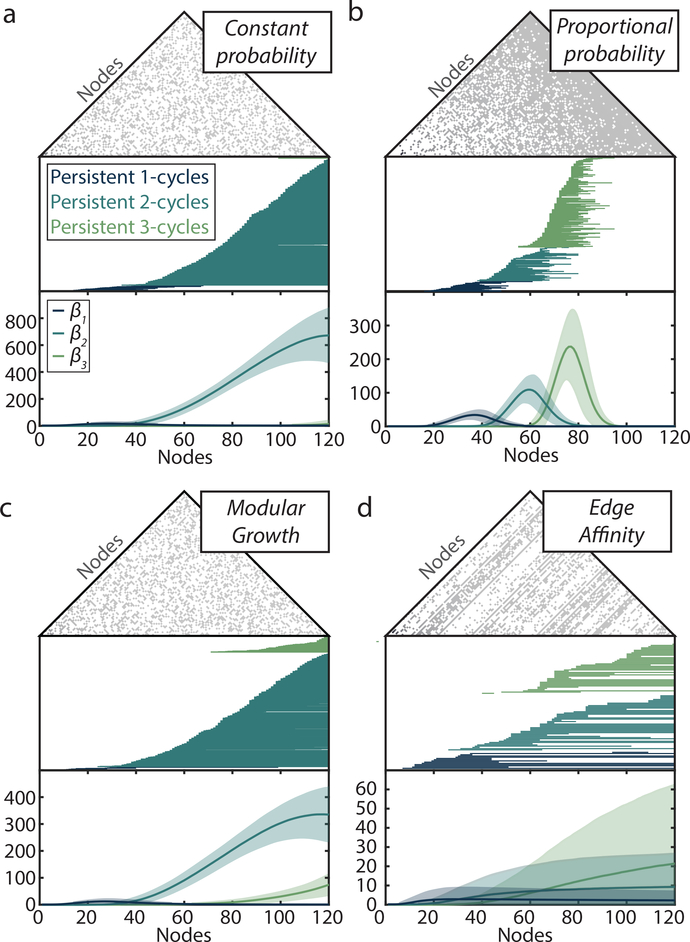
Figure 2: Persistent homology distinguishes random from structured generative models of nodefiltered order complexes.

Representative adjacency matrix (top), associated barcode plot (middle), and average Betti curves (bottom) for the (a) constant probability, (b) proportional probability, (c) modular growth, and (d) edge affinity models. Shaded regions in Betti curve plots indicate ±2 standard deviations.

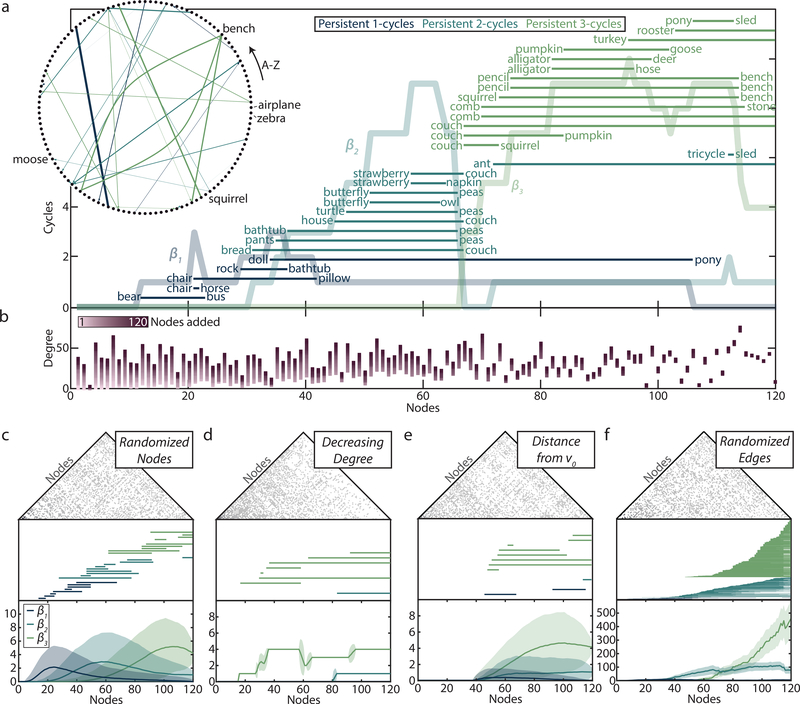
Figure 3: Topological cavities form and die within the semantic feature network with a pattern that is resistant to random node reordering.

(a) Barcode and Betti curves for the growing semantic feature network. The word added when the cavity is born (killed) is written on the left (right) of the corresponding bar. (Inset) Graph of persistent cycles with words as nodes in alphabetical order. An edge for each persistent cavity in (a) exists from the birth to the death node. Edges are weighted by the persistent cycle lifetime and colored according to the dimension. (b) The degree of each node throughout the growth process. Color indicates the number of nodes added. Representative adjacency matrix (top), associated barcode (middle), and average Betti curves (bottom) for the (c) randomized nodes, (d) decreasing degree, (e) distance from v₀, and (f) randomized edges models. Shaded areas of Betti curves indicate ±2 standard deviations.

The constant probability model generates growing graphs with the least amount of imposed structure, producing hundreds of persistent 2-cycles that never die. The β₂ curve on average dominates the Betti curves and we observe few if any persistent 1-cycles or 3-cycles. The proportional probability model generates a pattern of increasing Betti curve peaks with increasing dimension, contrary to the Betti curves of the constant probability model. The distinctive Betti curves between these two models implies that the underlying differences in growth rules are reflected in the global topology. Additionally, all persistent cycles of dimensions 1–3 die by around node 100, as later nodes are likely to tessellate cavities. Interestingly, the modular growth model produces Betti curves dominated by dimension 2, similar to the constant probability model. Though this model produces networks with high modularity throughout the node addition process, we see qualitatively similar properties between this and the constant probability model. Still, the density of within-community connections restricts the maximum height of the β₂ peak and drives the creation of persistent 3-cycles.

In contrast to these null models, we expect the growing semantic structure to be organized according to external constraints: there exist (external) properties of nodes that do not fluctuate based on the current state of the network. If a node (word) has some aptitude for connections (similar to many other words), such an aptitude should not change as the network grows. Such a constancy is unlike that observed in, for example, a preferential attachment process but is explicitly accounted for in our edge affinity model. Interestingly, we observe far fewer persistent cycles of each dimension in the edge affinity model than in the previous models. Furthermore, we observe a pattern of increasing peaks of persistent cycles as we move to higher dimensions. These results demonstrate that a growing process constrained by the external constraint of constant edge affinity will yield fewer topological cavities than that of a more random growth process.

Gaps in the growing semantic feature network

Now that we have developed some intuition for the structure detected by persistent homology, we ask if topological cavities exist within the growing semantic feature network and if so, what information such cavities might provide about the learning process. We observe multiple persistent cavities of dimensions 1–3, most of which die before the 30 month mark (Fig. 3a). The Betti curves show increasing peaks with larger dimensions as more nodes are added. Next, we ask which nodes (words) enter the growing graph when persistent cycles are born or killed. We list these words next to the corresponding bar, and we show persistent cycle birth and death nodes visually in the inset of Fig. 3a as a persistent cycle network, with words ordered alphabetically and an edge for each persistent cavity emanating from the birth node and terminating at the death node. The edge thickness is proportional to the corresponding cavity lifetime (index of death minus index of birth) and the edge color indicates cavity dimension. We observe nodes generally begin or kill one or no persistent cycles, with a few exceptions such as ‘bench’, ‘peas’, and ‘couch’. Persistent cavities that never die (have a death time of inf) are not shown in this inset. Note that those cavities that do not die are gaps in the semantic feature network created from the full dataset which contains only a subset of words in the entire language. This means that we should not classify infinitely persisting cavities as knowledge gaps since our data may simply not include words that do fill this gap, that is, using this data we cannot tell if there is a word in the English language to fill this gap or if there exists a true cavity within the complete semantic feature network. Indeed a child may even know more words than recorded in our dataset that prevent the formation of cavities we see here or form more cavities. We work under the assumption that this dataset, though limited, is topologically representative of the semantic feature network of the English language. Then the fact that we see cavities born and killed throughout development suggests that there are indeed knowledge gaps that not only form, but must also evolve and are extinguished during the learning process.

Next, we ask if there are simple rules by which cavities form and evolve in the growing semantic feature network. Due to the method of growth where the newly added node connects initially with only those added previously, we expect that the node degree at the time of node addition is positively correlated with node ordering. Thus, one might hypothesize that the empirically observed pattern of Betti curves follows simply from a pattern of higher-connectivity nodes added throughout the filtration. Contrary to this simplistic expectation, we observe instead that the degree of nodes varies considerably across time with no salient trend of either a decreasing or increasing node degree (Fig. 3b). The degree of a node when it is first added varies greatly along the filtration and indeed, when the final node is added there exists great variability in node degrees when plotted in the order of node addition. This complexity suggests a non-homogeneous connectivity pattern within the network, in turn motivating a more thorough effort to model the growth process and cavity evolution, which we turn to next.

The persistent homology of a growing network is classically used to infer global organizational properties, and we first use this tool to understand the growing semantic feature network from a global perspective. We begin by comparing the persistent homology of the growing semantic feature network to the generative models of Fig. 2. We observe that the edge affinity model generates n-order complexes with the most similar persistent homology to that of the growing semantic feature network. Upon closer inspection, we observe that the largest difference between the Betti curves of the edge affinity model and growing semantic feature network stems from the likelihood that cavities die. All but five persistent cavities in the growing semantic feature network die by node 120, while in the edge affinity model the barcodes show the majority of persistent cycles never die. Moreover the comparisons with models shown in Fig. 3 strongly imply that the evolving architecture of the growing semantic feature network is highly non-random, as the Betti curve peaks differ by an order of magnitude between the growing semantic feature network and the random n-order complex models. The growth rule for the constant probability model produces a random graph, where any subgraph will also be random, which would not be expected in the empirical data. The growth rule for the proportional probability and modular growth models both enforce higher structure on the network which at least from the applied topology perspective differ greatly from that of the empirical data. Taken together, these results suggest that the growing semantic feature network topology during learning is non-random and that node constraints such as a fixed affinity for connections might play a role in the evolving architecture.

To further probe processes guiding the evolution of the growing semantic structure, we construct derived n-order complex models that begin with the semantic feature network and alter either the node ordering or edge placement to determine which (if either) explains the observed evolving architecture. Beginning with the influence of node order, we compute the persistent homology of the randomized nodes n-order complex model, which retains the binary graph of semantic feature connections but randomly permutes the node order. We observe strikingly similar persistent homology between this model (Fig. 3c) and the growing semantic feature network, though note that any n-order complex built with the same binary graph G will necessarily have the same homology at G_N, which limits the variability in persistent homology. Next we ask if we can improve the model by ordering nodes by their degree or topological distance to the first node, both of which would capture the idea that a child learns highly connected nodes first or similar words to those already known. We see in Fig. 3d,e that both of these null models yield persistent homology that is distinctly unlike that observed in the original ordering. More specifically, both null models produce smaller Betti curves in all dimensions. Furthermore, we observed that the distance from v₀ model shows no persistent homology until nearly halfway through the filtration. These findings suggest that neither (i) first learning the most connected words, nor (ii) first learning words with the shortest semantic distance to the first word, can account for the evolution of the growing semantic feature network. These results are in line with prior work reporting that preferential attachment models are poor fits to the early learning of the semantic feature network.⁴ However, we find using distinctiveness¹⁷ or preferential acquisition¹⁸ to order nodes produces similar Betti curves to that of the semantic feature network (Supplementary Fig. 11). Finally, we keep the node ordering constant but now randomly rewire edges while preserving node degree; we call this the randomized edges model and note that it is similar in spirit to the configuration model.^19,20 We observe a highly random persistent homology signature as described by the Betti curves and barcodes (Fig. 3f) when we rewire edges randomly but keep the original node order. Together with Fig. 3c these results suggest that the pattern of semantic feature connections between words (i.e. edge linkage structure) is more important for the proper topological evolution of the network than the order in which those words are produced by children (i.e. node order).

Influence of or robustness to maternal education level

In the previous sections, we demonstrated that knowledge gaps not only exist but are created and filled in throughout early semantic learning, and that we can use the patterns of gap evolution to compare global structures of model learning processes. Knowledge gaps might correspond to learning relatively difficult concepts, and one could hypothesize that gaps would occur more frequently in the growing semantic feature networks of children with mothers having achieved a higher level of education, which – along with socioeconomic status^21,22 and structure built from co-occurrences in child-directed speech^23,24 – can significantly impact a childs linguistic input and output.²⁵ Yet, a contrary hypothesis is that the structure of language predisposes the growing semantic feature networks in children to be relatively robust to variations in the environment. To adjudicate between these two conflicting hypotheses, we create three distinct growing semantic feature networks from children with mothers whose highest education was some or all of secondary school (N = 146), some or all of college (N = 536), and some or all of graduate school (N = 338). Then we have the same binary network for each of the three networks, but the ordering of nodes has now changed (differences based on the maximum swap distance between two nodes in the ordering, see Supplementary Information). We label these networks the secondary, college, and graduate growing networks, respectively. We compute the persistent homology and find no trend of increasing topological cavity number or lifetimes (Fig. 4a-c), despite the differences in word ordering. This finding agrees with the earlier result in Fig. 3c. Furthermore, the lack of change in cavity number or lifetimes suggests that despite local scale differences in learning, children with mothers of varying education levels still experience a similar learning process at these meso- and global-scales. When drawing this conclusion, however, it is important to note that our dataset is limited to relatively common items whose frequency in the home environment is less likely to vary by maternal education.

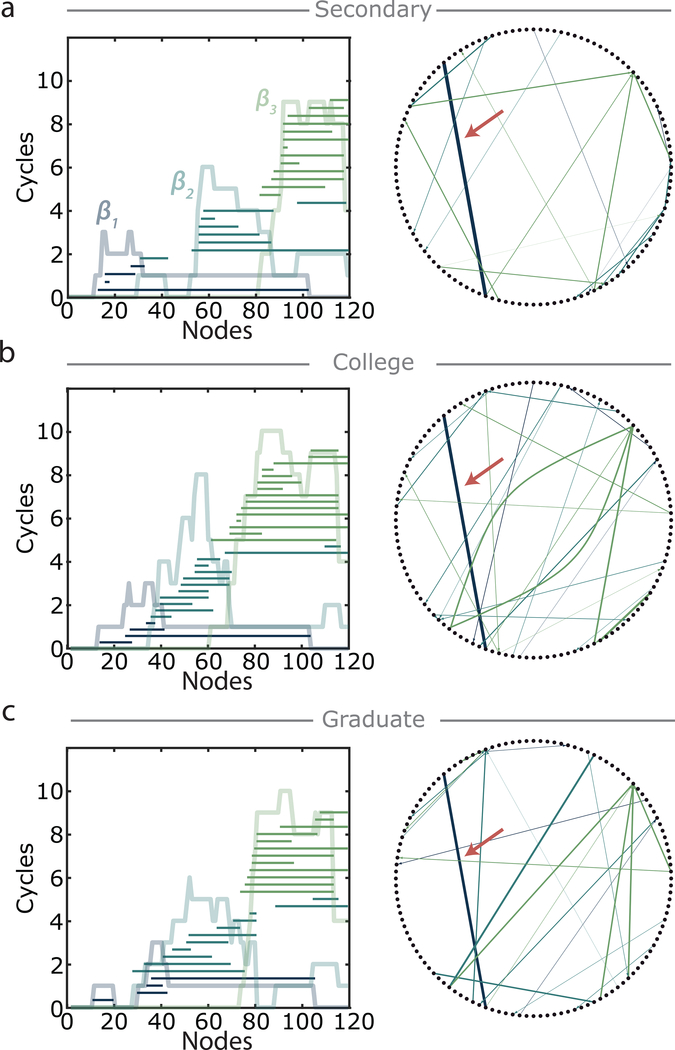
Figure 4: Global semantic feature network architecture is consistent across maternal education levels despite local variations.

(Left) Betti curves with barcodes overlaid and (right) persistent cycle networks for the (a) secondary, (b) college, and (c) graduate growing semantic feature networks. Red arrow in persistent cycle networks indicates a persistent cavity born and killed by the same word pair in each of the three education levels.

Since at a global level the persistent homology of the three growing networks varies little, we next ask if the same words correspond to nodes killing persistent cavities in each growing network. Figure 4 (also see Supplementary Fig. 9) shows persistent cycle networks for each of the three growing networks with nodes ordered and placed alphabetically as in Fig. 3a. This visualization allows for comparison of nodes that begin and kill persistent cavities across the three growing networks. For example, a persistent 1-cycle is seen beginning at ‘doll’ and ending at ‘pony’ in each of the secondary, college, and graduate growing networks (indicated by the red arrow). We observe that while a few node pairs begin and end persistent cycles in each of the secondary, college, and graduate growing networks, generally node pairs do not begin and end persistent cycles, or at least persistent cycles of the same dimension, across each of the education levels.

Characterizing the manner in which knowledge gaps are extinguished

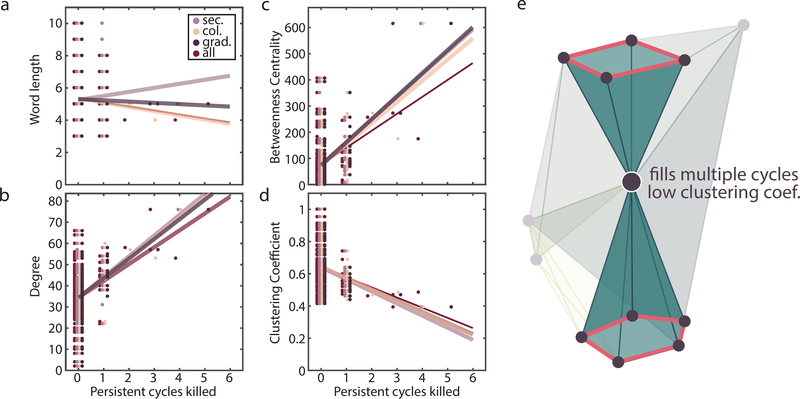
In the previous sections, we have shown that knowledge gaps are created and later filled in with similar rates despite differences in maternal education. These observations motivate our final effort to determine if particular properties of the nodes or their corresponding words increase the likelihood of a node tessellating cavities. For each of the secondary, college, graduate, and original all-inclusive growing semantic feature network barcodes, we count the number of persistent cavities killed by each node. Since these cavity-killing nodes correspond to temporarily missing words, one might hypothesize that these corresponding words are more difficult to learn. We use a simple proxy for word difficulty, given by the word length.²⁶ However we find no significant correlation between the number of cycles killed and the word length (Fig. 5a; Spearman correlation coefficient df = 118; all: r = −0.0661, p = 0.4734; secondary: r = 0.0998, p = 0.2781; college: r = −0.0881, p = 0.3386; graduate: r = 0.0023, p = 0.9799). Additionally, we ask whether the frequency with which caregivers use words when speaking to children could play a role in cavity filling, hypothesizing that lower-frequency words would be more difficult for children to learn. Previous work debates the role of word frequency in child-directed speech in early and late talkers^23,24,27 making this a particularly interesting measure. Another important property is the relative distinctiveness of a word in the network, shown in¹⁷ to predict word learning. Yet, again we observe no significant correlation between frequency and the number of persistent cycles killed (Supplementary Fig. 10; Spearman correlation coefficient df = 85; all: r = −0.2168, p = 0.0437; secondary: r = −0.2012, p = 0.0616; college: r = −0.1861, p = 0.0843; graduate: r = −0.0021, p = 0.9849) or between distinctiveness and the number of persistent cycles killed (Supplementary Fig. 11a; Spearman correlation coefficient df = 118; all: r = −0.1910, p = 0.0366; secondary: r = −0.2183, p = 0.0166; college: r = −0.1993, p = 0.0291; graduate: r = −0.0835, p = 0.3643). These results suggest that simple word descriptors such as length, frequency, and distinctiveness do not predict a word’s tendency to fill in knowledge gaps.

Figure 5: Number of persistent cycles killed correlates with topological properties instead of lexical features.

Scatter plots of the number of persistent cycles killed by each node against (a) corresponding word length (Spearman correlation coefficient df = 118; all: r = −0.0661, p = 0.4734; secondary: r = 0.0998, p = 0.2781; college: r = −0.0881, p = 0.3386; graduate: r = 0.0023, p = 0.9799), (b) node degree (Spearman correlation coefficient df = 118; all: r = 0.3027, p < 0.001; secondary: r = 0.2849, p = 0016; college: r = 0.3423, p < 0.001; graduate: r = 0.3730, p < 0.001), (c) betweenness centrality (Spearman correlation coefficient df = 118; all: r = 0.2972, p < 0.001; secondary: r = 0.2489, p = 0.0061; college: r = 0.2995, p < 0.001; graduate: r = 0.3492, p < 0.001), and (d) clustering coefficient (Spearman correlation coefficient df = 118; all: r = −0.2897, p = 0.0013; secondary: r = −0.2766, p = 0.0022; college: r = 0.3037, p < 0.001; graduate: r = −0.3626, p < 0.001). Lines of best fit overlaid. (e) Example node (outlined in white) that kills multiple cavities while retaining a low clustering coefficient. Triangles formed by the cavity-killed node highlighted, and cycles tessellated outlined in red.

Next we test if topological characteristics of nodes – rather than their non-topological statistics such as length and frequency – might better explain the number of persistent cycles killed. To address this question, we study the relation between the number of persistent cycles killed and the node degree, centrality, or clustering coefficient (Fig. 5b-d). A positive correlation between the number of persistent cycles killed and the node degree would indicate that knowledge gaps are extinguished by locally well-connected words. A positive correlation between the number of persistent cycles killed and the centrality would suggest that knowledge gaps form by a delay in learning words that are only a few features away from most other words. Finally, a positive correlation between the number of persistent cycles killed and the clustering coefficient would indicate that locally dense regions of the semantic feature network are likely to be involved in knowledge gaps. Nodes that kill cavities will likely have high degrees, unless their only neighbors are those involved in that cavity, which is unlikely. However it is less likely that betweenness centrality correlates with cavity-killing in general, since killing a cavity may only create a local star-like structure while betweenness centrality measures how a node acts globally in a network. Finally to kill a cavity a node must create many triangles, so we expect cavity-killing to be positively correlated with the clustering coefficient.

Shown in Fig. 5 we find that while node degree and betweenness centrality are often positively correlated with the number of persistent cycles killed (for node degree, Spearman correlation coefficient df = 118; all: r = 0.3027, p < 0.001; secondary: r = 0.2849, p = 0016; college: r = 0.3423, p < 0.001; graduate: r = 0.3730, p < 0.001; and for betweenness centrality, Spearman correlation coefficient df = 118; all: r = 0.2972, p < 0.001; secondary: r = 0.2489, p = 0.0061; college: r = 0.2995, p < 0.001; graduate: r = 0.3492, p < 0.001) as expected, the clustering coefficient shows a negative correlation (Spearman correlation coefficient df = 118; all: r = −0.2897, p = 0.0013; secondary: r = −0.2766, p = 0.0022; college: r = 0.3037, p < 0.001; graduate: r = −0.3626, p < 0.001). Initially, this result might appear counterintuitive because to cone (fill in) a cycle, a node must by definition create many triangles. Yet, if we combine this result with the positive correlations of persistent cycle killing to node degree and betweenness, we can construct a toy example of a possible cavity-killing node neighborhood. Shown in Fig. 5e, the central node outlined in white tessellates two cycles when added (cycles and coning triangles highlighted), but also has a low clustering coefficient. Taken together, we suggest that the connectivity pattern of words within the semantic feature network better predicts the tendency of that word to fill a knowledge gap than simple lexical features of the words themselves.

Discussion

In this study, we query the existence of knowledge gaps manifesting as topological cavities within the growing semantic feature network of toddlers. Using persistent homology and the formalism of node-filtered order complexes, we find that such knowledge gaps both form and are often later filled in throughout the learning process. We observe that the global architecture of the growing semantic feature network is similar to that of a constrained generative model. Furthermore we report similar persistent homology across growing semantic feature networks of children from mothers with differing education, and we find that this pattern of topological cavity existence remains present after node order randomization, but not after edge rewiring. Together these results suggest that knowledge gaps are robust features of word production order and that the global topology of the semantic feature network is resilient to local alterations induced by node reordering.

Understanding the growing semantic feature network through the lens of persistent homology offers a unique perspective on the nature of the learning process and features of language structure. Previous research has provided evidence supporting the influence of network topology on many types of language networks including those constructed from phonological^28,29 and syntactic relations.^30,31 Here we observe that the persistent homology of the growing semantic feature network follows a regular pattern throughout the majority of the learning process, indicating an organized and potentially predictable growth pattern – a global property of the network.

Yet when we consider the node (word) level, the fine-scale topology (node degree) varies considerably and does not suggest a predictable addition pattern. Furthermore if we permute the order of the nodes uniformly at random, we recover similar global topology to that observed in the unpermuted network, suggesting a topological homogeneity not found in n-order complex models, for example the edge affinity model. We describe the semantic feature network topology as accommodating, since its large-scale architecture changes little despite variations in small-scale inputs (specifically nodes with differing degrees). Previous studies show that the order in which words are learned by children depends on multiple variables including word frequency,^32,33 parental interaction,³⁴ small-worldness of co-occurrence networks,²³ word co-occurrence with associates,⁸ repetition,⁸ phonological patterns,^35,36 and communication quality.³⁷ We propose that the learning process might be supported by a global accommodating topology, which develops similarly in all typically developing children despite the natural variations in input (order of words learned) that occur due to differing environments. This claim is further supported by our observations that models ordering words by preferential acquisition or distinctiveness produce similar barcodes to those observed in the empirical data (Supplementary Fig. 7). Furthermore our results suggest that children who learn words in different orders (for example early versus late talkers²⁴) might experience the same patterns of knowledge gap formation and closure.

Though many possibilities for word production order yield similar persistent homology, we observe that the global structure disintegrates if we randomly rewire the network edges while preserving the degree of each node (Fig. 3). This finding – together with the results described in the previous paragraph – suggests that the higher order connectivity patterns between words, instead of individual word properties such as time of production, have a greater impact on the evolving global structure of the semantic feature network. This observation raises the important question of whether this resilience to node reordering and emphasis on fixing relations between words is restricted to the English language, or whether these phenomena are general properties of semantic feature networks. Previous research points to the similarity of word networks across languages³⁸ and supports the hypothesis that similar global patterns would be observed in languages other than English. Yet, the differences in node (word) connectivity patterns within this structure could offer insight into subtle distinguishing features between different languages.³⁹

The presence of persistent topological cavities of multiple dimensions in the growing semantic feature network offers insights into the learning process. One might expect that when a child grows his or her vocabulary, they tend to learn words that are similar to words already known. This is called the lure of the associates in⁴. Such a process would produce few if any knowledge gaps, corresponding to topological cavities, within the network, and should be well-modeled by a topological-distance-from-initial-node rule. Our results agree with those of⁴ indicating that the lure of the associates model does not provide a good fit to the growth of the semantic feature network. Furthermore we observe the salient presence of topological cavities in a growing semantic feature network that is best modeled by an edge-affinity rule. Yet, it is also important to acknowledge that the recovered gaps are not simply gaps in the final semantic feature network itself. Instead by the age of 30 months all but five gaps have been filled in by other words. Since we observed cavities in the growing semantic feature network irrespective of the mother’s education, we speculate that knowledge gaps that form and die may themselves be a feature of the semantic learning process. If indeed these knowledge gaps represent learning a more difficult word or concept, and filling in the created gap with intermediate concepts as they are later added, then these cavities may be a natural part of the learning process. As an application to more explicit learning in the classroom, one could ask if cavities exist as students learn other subjects as well, in particular math and science where reaching for an understanding of distant or difficult concepts may create higher numbers of cavities or longer-lived persistent cavities. In the laboratory, one could examine how knowledge gaps evolve in contexts where adult learners are exposed to new semantic relations between novel objects. Network gaps may be of interest in other domains as well, including business, where one wishes to assess a job candidate’s competence, identify open or underdeveloped areas of the market, or locate unreachable areas within a social system’s state space. Furthermore, previous studies have demonstrated the importance of global features such as small-worldness in early versus late talkers,²³ and one could therefore hypothesize that knowledge gaps might differ in children with disorders of language acquisition.

Many models exist for semantic networks in which edges are defined by word association such as can be estimated from a free association task or other metrics. Yet, the best models for the growing semantic feature network focus on node distinctiveness.¹⁷ Efforts to use preferential attachment or close variations have not been successful in capturing the feature network’s development⁴ while the lure of the associates and preferential acquisition models have been successful in semantics.^4,7 The difference between the previously defined preferential attachment model and the affinity model that we introduce here is that the likelihood of new connections for each node evolves based on how the network has already grown in the former, while the latter only relies on predefined nodal properties. These results suggest that the full semantic feature network matters instead of only what the child has learned up to a point, agreeing with the idea that learners are sensitive to the learning environment instead of only to their personal knowledge network.⁴ The semantic feature network lives within masters of the language and children are simply acquiring new words and connections of this pre-defined structure. As the semantic feature network a child is able to produce grows, the child is likely already sensitive to semantic relationships in their external world even before they acquire the label attached to a previously unnamed object. This sensitivity might explain why the affinity model better captures the topological properties of the growing semantic feature network.

One possible way that the above concept can manifest in our encoding is that labels for features are allowed to exist in the network before a child is able to produce this label. For example, if a child produces ‘cheese’ and ‘bus’ but not ‘yellow’ at a given time, the lack of the child’s ability to produce ‘yellow’ does not mean that ‘cheese’ and ‘bus’ are not still both yellow and thus are observed as similar to the child. Similarly, since each word exists and connects to other words in the external world, a word will always have the same affinity for others. For example, any new animal with legs will always be ready to connect to all other objects that have legs, regardless of which of these words is known to the child. Furthermore, we speculate that words corresponding to nodes with high affinity may generally be polysemous words, or those with multiple meanings, thus increasing the likelihood of connections to other words within the network.⁴⁰ Additionally these words may belong to larger or even multiple categories etched out by the shared feature network.⁴¹ Indeed such words may be crucial in upholding the small-world architecture of the early feature network,^23,41 or may promote category transition.^24,42 Overall our results are consistent with an externally constrained topology of the semantic feature network, as suggested in.^4,6

Growing networks are implemented in multiple systems including contagion propagation,⁴³ distribution networks in biological systems,⁴⁴ and social networks.⁴⁵ Consequentially, numerous methods exist for their analysis.⁴⁶ For example, representing a growing process as a dynamic network or directed graph (or directed dynamic graph) would allow for analyses with those corresponding sets of tools.^47,48 Though persistent homology for node-weighted systems is not a novel concept,^43,49,50 we suggest that the formalism presented here comprises a practical mode of encoding such systems, in which both graph metrics (for example k-clique community detection⁵¹) and topological data analysis can be applied simultaneously. Our approach may be valuable if one has weighted objects and links, if one can assume intimately pairwise-connected groups of objects act similarly (becomes a simplex in our encoding), and if cavities (or lack thereof) can be meaningfully interpreted in light of system function. On the theoretical side, the n-order complex models developed in this paper hearken back to previous studies of node-exchangeable graphs,^52,53 growing simplicial complexes,^50,54 and random clique complexes.⁵⁵

Furthermore, we propose that the persistent homology of a n-order complex at the level of persistent features (as opposed to the more commonly studied global structure) may be more easily interpretable than that of an edge-weighted network. In particular, here individual words initiate and terminate persistent cycles. In many biological contexts, nodes are objects with attached empirical observations and metadata. The analyses of such systems might include analyzing the number of persistent cycles a node begins or kills in relation to this metadata (though assigning full responsibility of persistent cycles to individual cliques of any size should always be done with care⁵⁶). Additionally the n-order complex is invariant under any monotonic (rank-preserving) transformation of the node weights, which is a noted benefit for applications to noisy experimental data.^10,11 Topics suitable for the node-filtered complex encoding and subsequent analyses include tracking information dissemination through brain networks,⁵⁷ signaling cascades in protein interaction networks,⁵⁸ sound propagation on force chains,⁵⁹ contagion spreading on social networks, and information transfer throughout enzyme architecture after allosteric effector binding.⁶⁰ Broadly, the formality presented in this study may be useful for “filling in” open questions from multiple areas of science.

In conclusion, we offer a unique perspective on the growing semantic feature network of toddlers that highlights the persistence of knowledge gaps in contrast to the formation of densely connected clusters. Using the node-filtered order complex formalism and persistent homology, we reveal the existence of such knowledge gaps and their persistence as children age. Furthermore we provide evidence supporting the notion that the gaps in the network will exist despite differences in word production times, and we propose that these gaps are an important and general component of the learning process.

Methods

Growing semantic feature network construction

We constructed a 120-node semantic feature network with node ordering following the procedure outlined in.⁴ Specifically, we extracted word production order from the MacArthur-Bates Communicative Development Inventory (MB-CDI).⁶¹ This database contains a record of which of 541 English words 2173 toddlers ages 16–30 months could produce, as determined via parental report. No statistical methods were used to predetermine sample sizes and we refer the reader to⁶¹ for more details. All genders were included and no data points were excluded. For each word we calculate the month at which ≥ 50% of children could produce the word.⁴ Within one month, words are ordered according to the percentage of children producing each word, resulting in a complete ordering of words.

To form a node-ordered network we represent words as nodes and connect two nodes (words) if they share a semantic feature within the McRae feature list.¹⁶ These semantic features were derived from adult norming data from 725 adults and are organized into categories based on feature type. When an individual generates features for a given concept, these features are interpretations of the abstract concept that are constructed for the sole purpose of description.⁶² Then feature norms offer a unique understanding of representation, which varies across and within individuals, and which often results in a collection of distinguishing features (as opposed to general features of many words),¹⁶ making them useful for modeling and theory testing.^63–66 We use all feature categories excluding encyclopedic and taxonomic, which are unlikely to be accessible to toddlers.⁴ Only the words included in both the McRae and Wordbankr databases were used in our final semantic feature network, thus refining our network to 120 nodes and 2163 edges.

Detecting cavities in node-ordered networks

Below we include a brief description of persistent homology. We refer the interested reader to^13,14,67 and the Supplementary Information for more details.

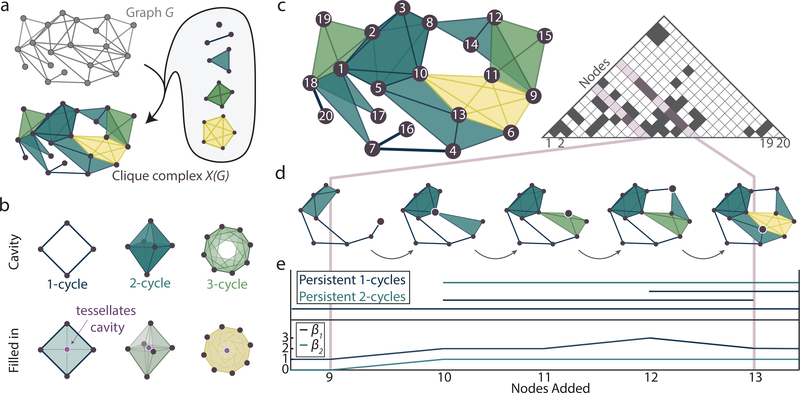
Before we discuss growing graphs, we outline the process of detecting cavities in a single binary network. Given a binary graph G, we first translate our graph into a combinatorial object on which we can perform the later computations. Instead of a simple graph described by nodes and edges, we allow all groups of completely connected nodes to define entities. Formally, we create the clique complex X(G), a collection of all the cliques, or all-to-all connected subgraphs, in the network. In Fig. 6a, we depict this process as ‘coloring in’ the graph G to build the clique complex X(G). For example, we color in 1-cliques (nodes), 2-cliques (edges), 3-cliques (triangles), and so on, giving us higher dimensional information about the structure (more precisely we assign a k-simplex to each (k + 1)-clique within G to create the clique complex. See Supplementary Information for definitions and details).

Figure 6: Persistent homology detects longevity of topological cavities within node-filtered order complexes.

(a) Example graph G (top) and its clique complex X(G) (bottom) created by filling in cliques, or all-to-all connected subgraphs of G. (b) Examples in dimensions 1–3 of cavities enclosed by cycles (closed paths of cliques) (top) and how an added node can tessellate a cycle thus filling in the cavity (bottom). (c) The clique complex from (a) with an ordering on the nodes (left), and the associated ordered adjacency matrix (right). (d) Steps 9–13 in the filtration created by taking the node-filtered order complex of the clique complex X(G) in (c) and the shown ordering. At each step a new node is added along with its connections to nodes already present in the complex. (e) Barcode (top) and Betti curves (bottom) for the example node-filtered order complex. The barcode shows the lifespan of a persistent cavity as a bar extending from [birth, death) node, and the Betti curves count the number of k-dimensional cavities as a function of nodes added. Lavender lines through (c), (d), and (e) connect the adjacency matrix row i to the clique complex at step i and to the persistent homology outputs.

Now with our graph encoded as a clique complex, we can use homology to detect cavity-surrounding motifs of edges, triangles, tetrahedra, and higher dimensional analogs (Fig. 6b). Loops of edges form 1-cycles, loops of triangles form 2-cycles, and loops of tetrahedra form 3-cycles. For example, Fig. 6b shows cavity-surrounding cycles of each dimension on the top row, while those on the bottom are tessellated by higher-dimensional cliques formed with the purple node. Homology distinguishes between cavity-surrounding loops and those tessellated by higher-dimensional cliques, thereby returning detailed information about the mesoscale architecture of the complex. In particular, homology detects equivalence classes of k-cycles, with two k-cycles being in the same equivalence class if their symmetric difference is a collection of higher dimensional cliques (see Supplementary Information for details). By abuse it is common to refer to an equivalence class of k-cycles as a k-cycle, and we will adopt this abbreviated description throughout the remainder of the paper. To summarize: homology counts the number of cavities in each dimension of a clique complex constructed from a binary graph.

While this approach is hypothetically useful, our data describes a growing network instead of a single binary graph, so we cannot simply compute its homology as above described. However, notice that we get a binary graph after the addition of each new node, and that the binary graph G_n created after the addition of node n is a subgraph of G_n+1 for all n. This sequence of objects (here, graphs) with G_n ⊆ G_n+1 is called a filtration (Supplementary Fig. 1, top and Supplementary Fig. 3b, top). If we construct a filtration of binary graphs G_n, we immediately gain a filtration of clique complexes X(G_n) with X(G_n) ⊆ X(G_n+1) necessarily true since G_n ⊆ G_n+1 (Supplementary Fig. 3b, middle). For example, using the ordering and clique complex in Fig. 6c, Fig. 6d illustrates the described filtration of clique complexes for steps 9–13 (addition of nodes 9–13), with new nodes (outlined in white) connecting to any neighbor already in the complex. We call the filtration of clique complexes created from a growing network the node-filtered order complex (see Supplementary Information for further details), inspired by the order complex in.¹⁰ The order complex creates a filtration of clique complexes from an edge-weighted network using the edge weights to induce an edge ordering. Here, the node filtered order complex (which we shorten to n-order complex for brevity) can be completely defined by the pair (G,s) with G a binary graph and s the ordering of vertices, possibly induced by a weighting on the nodes.

Finally, at each node addition we can map the clique complex X(G_n) into the next X(G_n+1), so that we can follow cycles, and consequentially cavities, throughout the filtration. We call these persistent cycles or persistent cavities. For example, the addition of node 10 creates a cavity surrounded by a 1-cycle, which persists in the complexes X(G₁₀), X(G₁₁), X(G₁₂) until it is tessellated with the addition of node 13. The barcode plot in the top of Fig. 6e records this persistent cavity as a horizontal line running throughout the duration of this persistent cavity, or its lifetime. We call the node at which the cavity begins the birth node, and we call the node at which the cavity is tessellated the death node. Thus, the lifetime is formally death−birth. The number of cavities of dimension k at each step (node addition) in the filtration is recorded in the Betti curves β_k(n) and shown in the bottom of Fig. 6e for the n-order complex of Fig. 6d. Tracking these persistent cycles throughout a filtration is called persistent homology,^13,14 which – in summary – allows us to extract the number and dimension along with the longevity of topological cavities throughout the growth process. We compute the persistent homology^13,14 in dimensions 1–3 using the Eirene software.⁶⁸

Models of n-order complexes

For each model n-order complex, we generate 1000 instances and provide MATLAB code and detailed descriptions at the Filtered Network Model Reference (filterednetworkmodelref.weebly.com).

Measures for correlation calculations

Since the addition of a node (and its connections) can kill persistent cavities, we can count the number of persistent cavities killed at each node. We can then calculate the Spearman correlation between the number of persistent cycles killed at each node and a graph statistic such as the node degree, clustering coefficient, and betweenness centrality calculated on the binary semantic feature network using.⁶⁹ The degree of a node is the number of edges incident to the node. The clustering coefficient measures the connectivity of a node’s neighbors, calculated by the ratio of existing triangles to the number of triangles possible. Precisely,

$$C_n=\frac{2t_n}{k_n\left(k_n-1\right)}$$ (1)

where t_n is the number of triangles formed by node n and its neighbors.⁷⁰

Additionally, we inquire whether the centrality – or the number of shortest paths passing through a node – might be correlated with the number of cycles killed. Though a cavity-killing node connects to a set of nodes in a star-like pattern, it is not necessarily the case that this node will act as a hub within the larger network. We calculate the betweenness centrality⁷¹ of a node as

$$B{C}_n={\displaystyle \sum _{s,t,n,s\ne t\ne n}\frac{{\lambda }_n(s,t)}{\lambda (s,t)}}$$ (2)

with λ(s,t) being the number of shortest paths between nodes s and t, and with λ_n(s,t) being the number of such paths passing through node n.