The Role of Network Science in the Study of Anesthetic State Transitions

Summary

The heterogeneity of molecular mechanisms, target neural circuits, and neurophysiological effects of general anesthetics makes it difficult to develop a reliable and drug-invariant index of general anesthesia. No single brain region or mechanism has been identified as the neural correlate of consciousness, suggesting that consciousness might emerge through complex interactions of spatially and temporally distributed brain functions. The goal of this review article is to introduce the basic concepts of networks and explain why the application of network science to general anesthesia could be a pathway to discover a fundamental mechanism of anesthetic-induced unconsciousness. We review data suggesting that reduced network efficiency, constrained network repertoires, and changes in cortical dynamics create inhospitable conditions for information processing and transfer, which lead to unconsciousness. We propose that network science is not just a useful tool but a necessary theoretical framework and method to uncover common principles of anesthetic-induced unconsciousness.

Why is it so difficult to develop a reliable and drug-invariant index of general anesthesia? Some obvious reasons include the heterogeneity of molecular mechanisms, target neural circuits, and neurophysiological effects of general anesthetics,^1–4 despite the common functional endpoint of hypnosis. One approach to the problem is to identify a fundamental mechanism of consciousness that is disrupted in association with particular physiologic, pharmacologic, or pathologic states. Since the early 1980s, there has been a search for the neural correlates of consciousness, defined by Crick and Koch as a minimal set of neuronal events and mechanisms sufficient for a specific conscious percept.^5,6 So far, however, no single brain region or mechanism has been identified as the neural correlate of consciousness, suggesting that consciousness might emerge through complex interactions of spatially and temporally distributed brain functions.^7,8 Thus, understanding how the brain integrates spatially distributed information and, conversely, how general anesthetics diminish or functionally isolate information in the brain might be a useful approach to uncovering common principles of diverse molecular anesthetic actions. The goal of this review article is to introduce the basic concepts of network science to the anesthesiologist and explain why the application of this science to general anesthesia could be a pathway to discover a fundamental mechanism of anesthetic-induced unconsciousness—not just as a useful tool, but as a necessary theoretical framework and method. We review the properties and organizational principles of networks; recent and relevant studies of information processing or transfer in large-scale brain networks; the pivotal role of hubs in information integration or disintegration; and anesthetic actions from a network perspective. We also introduce recent studies that potentially reveal a network-level mechanism for diverse emergence patterns from general anesthesia. Finally, we provide perspectives on future directions of network science in anesthesiology.

It is important to note that this review focuses primarily on corticocortical and thalamocortical networks. Although there is substantial evidence that subcortical nuclei in the brainstem and hypothalamus play critical roles in anesthetic-induced unconsciousness^9,10, the limited spatial resolution of most functional magnetic resonance imaging studies and the inability of electroencephalography to capture specific brainstem nuclei have excluded these regions from most graph-theoretical studies of general anesthesia. It has been argued that hypnotic effects of general anesthetics likely arise from a combination of bottom-up mechanisms (i.e., modulation of sleep or arousal pathways controlling level of consciousness) and top-down mechanisms (i.e., cortical or thalamocortical pathways controlling content of consciousness)¹¹. It is, however, likely that anesthetic actions in subcortical structures play a key role in the observed network effects in the cortex. We recognize the diversity of anesthetic actions at the molecular level as well as the key involvement of subcortical nuclei that govern sleep-wake physiology^12,13. However, this article does not focus on these diverse root causes that initiate mechanistic cascades but the ultimate network effects that might represent the proximate cause of losing consciousness.

Network science and complexity

Stephen Hawking suggested that the 21^st century would be the century of complexity. Studies of complex systems such as the stock market, social media, internet, traffic, genes or proteins, biological evolution, and the brain have achieved substantial progress and success in the last three decades.^14–17 The fundamental difficulty of studying these complex systems is that they are made up of many parts and complicated interactions, causing unpredictable collective behaviors. Herding behaviors in the stock market, political and social maps in the US presidential election, diverse higher-level functions of gene networks, and consciousness in the brain are examples. To study such collective behaviors, it is essential to understand how the parts are linked and how the dynamic interactions between these links generate emergent behaviors in the system. This study of collective behavior has important implications for how a complex system like the brain handles hierarchically distributed information at multiple scales (from neurotransmitters, to neural circuits, to function) without a single coordinator. Since the 1990s, with the development of technologies to store and measure big data, there have been new opportunities to construct structural and functional networks representing diverse systems. Combining big data and statistical physics revealed that most constructed networks are driven by a common set of fundamental laws and organizational principles, despite differences of form, size, nature, age, and scope of the actual networks from which they were derived.¹⁸ Once we set aside the specific material of the components (e.g., airport system vs. the brain) and the physical interactions between them, complex networks are more similar to one another than different. Therefore, abstracting key elements of networks enabled a common set of mathematical tools to explore dramatically different systems. This apparent universality allowed for the development of the recent discipline of network science,^18,19 and suggests that we can discover a common principle of brain network organization, function, growth, and evolution. Although the reconstruction of networks from structural or functional brain data can create abstraction and independence from the biological wiring of the brain, it also creates opportunities to study a variety of different data sources that might yield unique insight. Furthermore, although we discuss a variety of networks in this review, we do not mean to imply that any network is capable of generating conscious experience. Rather, we know that the brain generates conscious experience and network science enables us the opportunity to study the optimal conditions under which it does so.

Basic network properties

Graph theory provides the mathematical framework and principled method to study networked systems (see Glossary). The first use of a graph to understand a real-world system was performed by Leonhard Euler in 1736.²⁰ Euler lived in the Prussian town of Konigsberg (now the Russian city of Kaliningrad), which was built around seven bridges across the river Pregel, linking the two main riverbanks and two islands in the middle of the river (Figure 1A). An unresolved problem at that time was whether it was possible to walk around the town via a route that crossed each bridge only once. Euler solved this problem by representing the four land masses divided by the river as nodes, and the seven bridges as interconnecting edges. From this prototypical graph, he mathematically proved that, for such a walk to be possible, no more than two nodes should have an odd number of edges connecting them to the rest of the graph. In fact, all four nodes in the Konigsberg graph had an odd number of edges, meaning that it was impossible to find any route around the city that crossed each bridge only once. Euler’s topological analysis opened a new research field in mathematics, now known as graph theory, and became the foundation of network science. The importance of Euler’s analysis is not in the details of the geography of 18^th century Konigsberg; rather, what is important to consider is the topology of the graph that defines how the links are organized. Generally, the topological analysis is invariant under any continuous transformation of the system (Figure 1B) such as increasing, decreasing, rotating, reflecting, or stretching the physical scale of a system.^18,19 This topological invariance may be essential to study a commonality of brain structure and function across scales, individuals, and species. Topological principles may also help to dissociate what is changed and preserved after diverse pharmacologic and pathologic perturbations such as, respectively, general anesthesia and stroke.

Figure 1. The Konigsberg bridge puzzle and topological invariance.

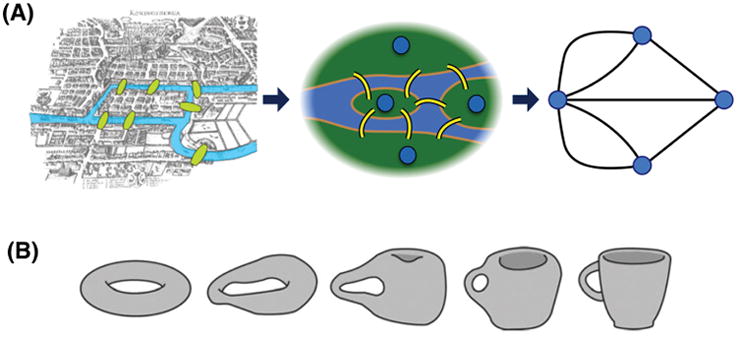
(A) This historical problem (circa 1736) in mathematics was to devise a walk through the Prussian city of Konigsberg that would cross each of the seven bridges once and only once. Famed mathematician Leonhard Euler reformulated the problem in abstract terms (laying the foundation of graph theory) by eliminating all detailed features and replacing each land mass with an abstract “node” and each bridge with an abstract connection or “edge.” The resulting mathematical structure is called a graph. Euler realized that the topology—or architecture—of the graph was of importance rather than the details of the geography. (B) A donut and a coffee cup have topological invariance, while a muffin and coffee cup do not, because both the donut and coffee cup have one hole. Continuous topological transformation can prove their equivalence. Topological properties—for instance, efficiency, clustering coefficient, and small-worldness—are invariant with continuous transformations such as increasing, decreasing, rotating, reflecting, and stretching. Topological invariance may help identify a fundamental network mechanism of anesthetic-induced unconsciousness across heterogeneous brain networks of different individuals and species.

If we want to understand a complex system like the brain, we first need to know how the components interact with each other, which can be achieved by generating a wiring diagram. Figure 2 illustrates how to reconstruct a structural and functional brain network. A network is a catalog of a system’s components, called nodes or vertices, and the direct interactions between them, called links or edges. The links of a network can be directed or undirected. For instance, phone calls are directed links in which one person calls the other person. By contrast, the transmission line on the power grid is an undirected link through which electric current can flow in both directions. However, some systems, like a metabolic network, have both directed and undirected links. Thus, when we apply network analysis to the brain under anesthesia, constructing the network (i.e., determining the nodes and edges) is the most important process in determining what kind of network we want to study.^21–24 The network topology (or architecture) is defined as the specific organization of nodes and edges, and the topological properties determine the functional aspects of the relationships. Here we explain the key network properties such as path length, efficiency, clustering coefficient, modularity, centrality, and small-worldness with three basic network models (Erdos-Reny, Watts-Strogatz, and Barabasi-Albert model). Figure 3 illustrates key network properties.

Figure 2. Reconstruction of a brain network.

Step 1: Define the network nodes. These could be defined as electroencephalography sources or multi-electrode-array electrodes as well as anatomically defined regions of histological, MRI or diffusion tensor imaging data.

Step 2: Define the network edges. Estimate a continuous measure of association between nodes. This could be the spectral coherence or Granger causality measures between two magnetoencephalography sensors, or the connection probability between two regions of an individual diffusion tensor imaging data set, or the inter-regional correlations in cortical thickness or volume MRI measurements estimated in groups of subjects.

Step 3: Define the network structure. Generate an association matrix by compiling all pairwise associations between nodes and apply a threshold to each element of this matrix to produce a binary or undirected or directed network.

Step 4: Calculate the network properties (path length, clustering coefficient, modularity, etc.) of interest in this graphical model of a brain network.

Figure 3. Basic network properties.

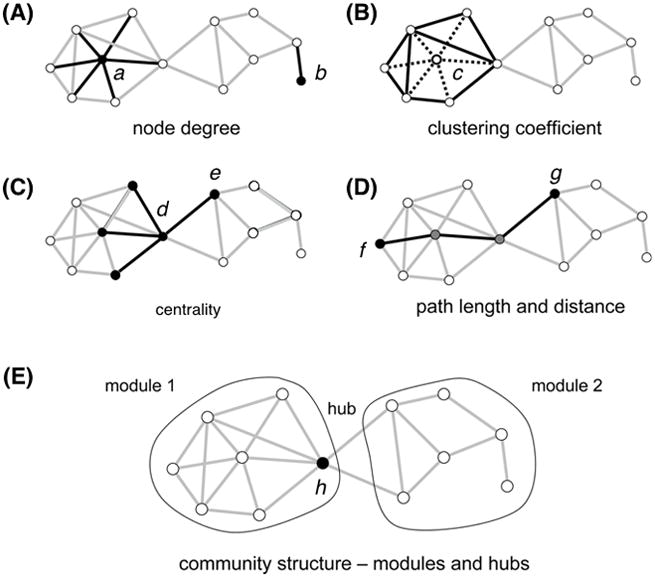
The measures are illustrated with a simple undirected graph with 12 nodes and 23 edges.

(A) Degree: the number of edges attached to a given node. The node a has a degree of 6 and the peripheral node b has the degree of 1.

(B) Clustering coefficient: the extent to which nodes tend to cluster together, measuring the segregation of a network. In this example, the central node c has 6 neighbors and 15 possible connections among the 6 neighbors. These neighbors maintain 8 out of 15 possible edges. Thus, the clustering coefficient is 0.53 (=8/15).

(C) Centrality: the indicators of centrality identify the most influential nodes within a network. In a social network, it is used to identify the most influential person. In this example, the node d contributes more to the centrality because all nodes on the right side pass through the node d to reach the other nodes in the left side.

(D) Path length: The average of the shortest distances for all node pairs in a network. The shortest path length between the nodes f and g is three steps that pass through two intermediate nodes.

(E) Modularity: one measure of the structure of networks that is designed to reflect the strength of a division of a network into modules (also called groups, clusters or communities). In the example, the network forms two modules interconnected by a single hub node h.

Small-world networks and random networks

The Watts-Strogatz model introduces clustering coefficient and characteristic path length.²⁵ The clustering coefficient provides an index of the “cliquishness” or clustering of connectivity in a graph. The characteristic path length is the minimum number of edges required to link any two nodes in the network on average, which is commonly used to index the integrative capacity of a network. A shorter average path length results in more rapid and efficient integration across a network (for instance, in the small-world network of Figure 4). In the brain, the shortest paths are like highly efficient highways of information transmission. These functional highways are disrupted during general anesthesia. Erdos and Renyi (1959) introduced the random network, in which the nodes of the graph are randomly connected with equal probability.²⁶ Random graphs have a short characteristic path length and low clustering. Thus, the random network has higher information integration capacity (short path length), but does not have the capacity to maintain functional specialization (lower clustering coefficient) in the network. At the other end of the extreme is the regular lattice with high clustering and long characteristic path length. This network has the capacity for functional specialization, but comes at the cost of lower integration. Importantly, however, by randomly rewiring just a few edges in the lattice, the characteristic path length of the graph dramatically decreases, but does not greatly reduce the high average clustering that characterizes the lattice. In other words, there is a range of rewiring probabilities that generates graphs with a hybrid combination of topological properties: short path length like a random graph and high-clustering like a lattice. Organizations in between the extremes of random and latticed represent a class of networks with a so-called small world topology. For instance, Facebook, the fastest growing social network, consists of about 1.59 billion connected people. However, despite the enormity of the network, each person in the world is connected to every other person by about 3.5 people.²⁷ In terms of efficiency, this outperforms the well-known “six degrees of separation” that was made famous by the work of psychologist Stanley Milgram at Harvard University in the late 1960s; Milgram demonstrated the idea that we are all connected to one another by just a few simple steps. Since then, global population has surged but the idea still holds true as social media like Facebook allow us to be more connected than ever before. The average path length of Facebook is getting shorter every year, enhancing its small-worldness. The healthy brain also demonstrates a small-world network property, which maintains the balance between global integration (short path length) and local segregation (large clustering coefficient).^28–30 A disrupted balance has been associated with various neurological disorders and psychiatric symptoms such as Alzheimer’s disease, dementia, and schizophrenia.³¹ Evidence suggests that the major action of anesthetics at the network level is also to disrupt the balance between functional integration and segregation, biasing the network toward excessive integration or segregation, and resulting in unconsciousness.^1,32–34

Figure 4. Network properties of normal and abnormal brain networks.

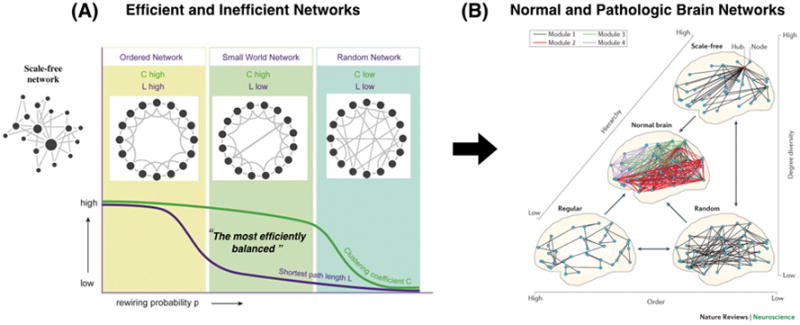
(A) Properties of basic network topologies. Random networks have a higher integration capacity (on average, a short path length from one node to another) and lower functional specialty (lower clustering coefficient). Conversely, regular networks have a lower integration capacity (long path length) and higher functional specialty (large clustering coefficient). In the middle of these two extreme networks is the so-called “small-world” network with both a large integration capacity (short path length) and a large functional specialization (large clustering coefficient), achieved after rewiring only a few of the edges in the lattice. A scale-free network is somewhere between a regular and random network, depending on the hub structure. (B) The organization of normal brain networks, interpreted as an intermediate structure between three extremes: a locally connected, highly ordered (or ‘regular’) network; a random network; and a scale-free network. The order component is reflected in the high clustering of regular brain networks. Randomness, or low order, is reflected in short path lengths. The scale-free component (high degree diversity and high hierarchy) is indicated by the presence of highly connected hubs. A normal brain network is a composite that contains these three elements. This results in a hierarchical, modular network (normal brain). The scale-free functional network structure of the human brain is preserved even during general anesthesia, whereas it is disrupted during the vegetative state and various neurologic diseases such as dementia and Alzheimer disease. (Figure source of 2B)

Scale-free network and power laws

Barabasi and Albert (1999) introduced another generative model that built a complex graph by adding nodes incrementally (the scale-free network in Figure 4).³⁵ New nodes connect preferentially to existing nodes that already have a large number of connections and thus represent putative network hubs. By this generative process of preferential attachment, the “rich get richer,” i.e., the nodes that have a high degree tend to have an even higher degree as the graph grows by the iterative addition of new nodes. As a result, the distribution of degree across network nodes has a characteristic fat-tailed distribution (like the US airport system in Figure 5), conforming to what is called scale-free or power-law distribution, which is distinct from a bell shape distribution of a random network (like the US highway system in Figure 5). Simply stated, it is likely that a scale-free network will contain at least a few highly connected hub nodes (like major hub airports in New York and Chicago). As the network grows, the size of the hubs increases exponentially in the scale-free network with infinite variance of power law distribution. By contrast, a bell shape distribution converges to an average node degree that serves as the “scale” of the system. These two systems (with scale-free and bell-shape distributions) have totally distinct organizations from one other.

Figure 5. Scale free network and power law distribution.

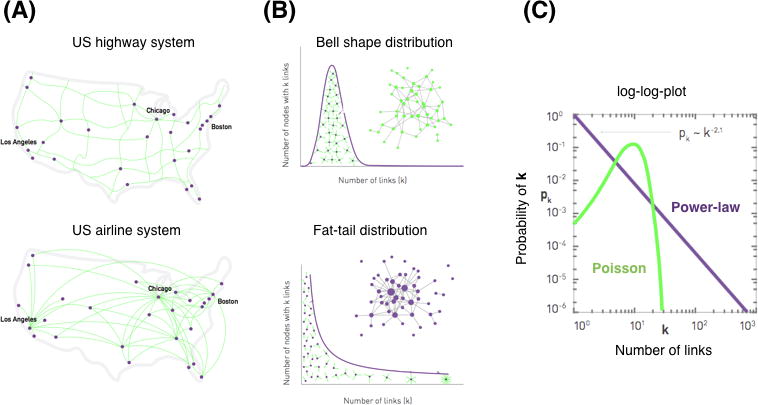
(A) and (B) The US highway system has a bell shape distribution of the number of links (highway connections among cities). By contrast, The US airline system has a fat tail distribution (air routes among airports). (B) For the bell shape distribution (Poisson), most nodes have comparable degrees and nodes with a large number of links absent. The average value of distribution represents the “scale” of the system. The fat tail distribution (Power law) consists of numerous low degree nodes that coexist with a few highly connected hubs. The size of each node is proportional to its degree. The system does not have a mean value and the variance becomes infinite as the system size grows, which is referred to as a “scale free” property. In the log-log plot, the slope of power law distribution categorizes the systems and determines the behavior of scale-free networks.

This scale-free property is ubiquitous in real life. In a scale-free network, the hubs play a central role in global information transfer, like a major international airport in an airline network. In addition, most scale-free networks are fairly resilient to a random attack on the nodes, but are much more vulnerable to a targeted attack that prioritizes the highest-degree hub nodes.³⁶ For instance, if the global airline network was attacked with nodes randomly targeted, the airports with just a few links would be attacked with high probability but without a significant effect on the overall efficiency of traffic. If, however, the attacks were specifically focused on a few major hub airports, like JFK or London Heathrow, it would be equivalent to disrupting most of the flights between the US and European modules. The result would be a dramatic increase in the number of flights required to transfer from one city to another city on different continents. The disrupted long-range connections between hub airports in two continents potentially fragments the network into two or more isolated modules. This mechanism of fragmentation in air traffic is also applicable to the enhanced fragmentation of functional brain networks when hub regions are preferentially disrupted by general anesthetics.^32,37 Understanding this network mechanism would be helpful to identify effective target sites of general anesthetics to maximize the drug effect on information transmission.

Describing general anesthesia in network terms

Before proceeding with a discussion of network-level mechanisms of general anesthesia, we would like to reiterate that the focus on cortical and thalamocortical networks in this article is not meant to imply that these networks are the exclusive or primary site of action of general anesthetics. Furthermore, we do not subscribe to a classical “unitary hypothesis” of anesthetic mechanism in which there is a single substrate for anesthetic action. We acknowledge the diversity of molecular actions and furthermore acknowledge the differing phenomenological aspects of different anesthetic experiences depending on dose or drug. For example, anesthetics such as ketamine induce a variety of subjective experiences despite the fact that connected consciousness appears lost during ketamine anesthesia, as evidenced by loss of responsiveness.^38,39,40

Theories of anesthetic-induced unconsciousness of relevance to network science

There is a multitude of theories related to conscious experience that have implications for anesthetic mechanism, including global neuronal workspace theory, higher-order thought theory, predictive coding, attention schema theory, and others.^41,42,43 Two theories have more explicitly attempted to explain how general anesthetics induce unconsciousness in terms of network science. The cognitive unbinding theory² proposes that anesthetic effects on regions important for the synthesis of information (the so-called process of “binding by convergence”) or effects that disrupt the communication between brain regions (the process of “binding by synchrony” or, more precisely, temporal coordination) would be sufficient conditions for unconsciousness⁴⁴. The theory predicts that the isolation, rather than the extinction, of neural activities is causally relevant to loss of consciousness. In network terms, functional disruption of hub structures or hub organization, increased modularity, increased path length, and decreased efficiency would create inhospitable conditions for the information transfer that is normally required to bind distinct perceptual features into one experience. This theory has been supported by empirical observations of preferential disruption of hubs during anesthetic-induced unconsciousness, altered network topology, and function disconnections that likely relate to temporal discoordination (discussed in detail below). Importantly, this was predicted to occur despite preserved mean neural firing rates, which has been empirically observed in the primate brain after induction doses of propofol³² and ketamine.^38,44 A related but more comprehensive network framework for consciousness is integrated information theory (IIT).^7,45–48 The central tenet of IIT is that consciousness arises from two central properties, information and integration. A system, such as a brain network, generates information if it is capable of being in many differentiated states. A system is said to be highly integrated if it cannot be reduced to independent parts. Any system that possesses both of these properties is deemed to be conscious.^45–50 IIT predicts theoretically that, during sleep and anesthesia, the repertoire of possible brain states is diminished (reduced information) and cortical communication is impaired (reduced integration). The combined loss of information and integration in the brain may result in unconsciousness.¹ The common argument shared by these two theories of anesthetic-induced unconsciousness is the disruption of network integration. Recently, Kim et al estimated a surrogate measure of integrated information (termed Φ) in relation to network modularity during conscious and anesthetized states using high-density electroencephalography in humans. They demonstrated a negative correlation between the number of modules and the measure of Φ (i.e., higher modularity, lower Φ) across various states (baseline, sedated, deep anesthetized, and recovery).⁵¹ This result supports the association of network integration with a surrogate of integrated information in the brain as well as its reduction during general anesthesia. It is therefore important to understand how the brain integrates and disintegrates globally distributed information in the resting state and how anesthetics disrupt information transmission at the whole brain network level.

Anesthetic effects on brain connectivity

Both surrogates of information transfer and the conditions for information transfer in large-scale brain networks have been assessed through measures of functional and effective connectivity between regional brain activities. Functional connectivity refers to the statistical similarity of two brain activities, which is measureable with correlation or coherence of two signals.^52–56 Effective connectivity infers a causal relationship between the activities of brain regions. This direct cause-effect measurement is often used in experimental paradigms using evoked neural responses. Another method to quantify connectivity of relevance to causal interaction is to estimate statistical inference between time series. Transfer entropy and Granger causality can measure how much the present of one signal A helps to predict the future of another signal B.^57–59 If the addition of information from A creates a better prediction than only using information from the past of signal B itself, A is considered to be causal to B. The opposite case also holds for evaluating the causal influence of B on A. These methods can be used to assess cause-effect relationship of spontaneous brain activities without a perturbation. It is critical to note that there are substantial theoretical and empirical limitations with any of these measures in terms of the accurate estimation of information, information transfer, or the capacity for information transfer.^55,60,61

It is now widely acknowledged that general anesthetics disrupt functional and effective connectivity between brain regions in the resting state; a full discussion of connectivity studies is beyond the scope of this review.^3,4,62,63,64 There appear to be characteristic disruptions of functional and effective connectivity in the cortex that have been observed across multiple anesthetics, multiple neuroimaging modalities, and multiple species (including human surgical patients). General anesthetics tend to (1) preferentially disrupt higher order information processing, with relative preservation of primary sensory networks and information processing,^65,66 (2) selectively inhibit effective connectivity from frontal to parietal regions ^67–70 and functional connectivity between frontal and parietal regions,^71,72 (3) selectively inhibit long-latency term evoked potentials, while preserving short-latency evoked responses,⁷³ (4) decrease spatiotemporal complexity,^74–78 and (5) constrain the repertoire of connectivity configurations.^79,80 There is supportive evidence of these network features derived from experiments performed with diverse species (mice, rat, ferret, monkey, and human)^{65,71,81–86} anesthetics (propofol, isoflurane, sevoflurane, barbiturates, midazolam, xenon, ketamine, and halothane)^{32,37,65,68,69,74,78,81–83,87–92} and modality (fMRI, electroencephalography, local field potentials, and single unit recordings).^{31,37,65,68,69,71,82–88,93} All of these empirical observations may reflect a reduction of information integration capacity in terms of both differentiated information and overall network integration, which is proposed to result in unconsciousness.

Anesthetic effects on efficiency of brain networks

Investigating the basic properties of functional brain networks reveals two common global network features across multiple anesthetics (dexmedetomidine, nitrous oxide, propofol, isoflurane, sevoflurane). The first is the reduction of global efficiency, which reflects the capacity of global information transmission in the brain network. The reduction of global efficiency results from the fragmentation of functional brain networks (with increasing clustering coefficient and modularity).^{33,87,94–98} The second is the reconfiguration of functional brain networks, mainly through the disruption of the posterior hub structure.^54,97–100 The fragmented and reconfigured hub structure is the functional substrate of the reduced information processing capacity that is consistently observed in the brain during general anesthesia, irrespective of the particular anesthetic. Anesthetics perturb the normal organization of functional brain networks, preferentially disrupting the hub activities and fragmenting the hierarchical network. Therefore, understanding the role of hub structure in information integration as well as how anesthetics disrupt the hub structure is essential to understand the network-level mechanisms of anesthetic-induced unconsciousness.

Hubs as a major determinant of global information processing

A systematic understanding of how anesthetics disrupt consciousness first requires an understanding of the relationship between brain network structure and information transmission. This is because brain network structure constrains the patterns of information flow much in the same way that the organization of an airport network across the continent constrains the patterns of airplane traffic. Like hub airports, hub nodes in the brain play a dominant role in enabling information transfer across the neural network.^60,101 Van den Huevel et al. introduced the concept of a “rich club” structure, a highly connected and highly central collection of connected hubs that occupy only 10% of the brain network but facilitate 70% of the communication pathways.¹⁰² The rich club (which includes, in descending order of hub status, the precuneus, superior frontal cortex, superior parietal cortex, hippocampus, thalamus, and putamen) acts as an attractor for signal traffic in the brain, receiving information that is integrated and then transmitted throughout the brain. The midline cortical rich club nodes (precuneus, superior frontal cortex, and superior parietal cortex) play an important role in between-module connectivity (called connector hubs), while subcortical rich-club regions (bilateral thalamus, putamen) play an important role in module structure (called provincial hubs). The frontoparietal control network plays a pivotal gate keeping role in goal directed cognition, mediating the dynamic balance between default and dorsal attention networks.¹⁰³ Rich club connections make up the majority of long-distance pathways that enable neurons to achieve efficient communication. However, such organization comes at a cost: the rich club connections make the brain network vulnerable to a targeted attack, such as a general anesthetic, that can disrupt global brain communication. This can be thought of as the neural equivalent of a snow storm in several major hub airports, which would cripple airplane travel. The hubs are also vulnerable to pathologic change.¹⁰⁴ The hyper- or hypo-activity of network hubs is one of the most consistent findings across all network studies of brain diseases, irrespective of the specific underlying pathology. Damage to hubs and a redistribution of hub nodes have been reported in neurological conditions such as Alzheimer’s disease, Parkinson’s disease, multiple sclerosis, traumatic brain injury, and epilepsy.³¹ Accounting for altered hub structure in various neurological diseases is critical to estimate altered patterns of information integration and disintegration. Furthermore, understanding the role of the hub structure in global information integration and disintegration may enable us to interpret the ostensibly different neurological and pharmacological perturbations in a unified framework.

Hubs as conductors of information traffic

Recent empirical observations suggest that network structure modulates the computation, dynamics, and causal interactions of regional brain areas.^105–112 In particular, hub structure plays a major role in modulating function. Empirical data analysis and computational models suggest that the relative location of neuronal populations in large-scale brain networks shapes directed interactions between brain regions.^113–118 Stam et al. showed in a brain network model that the phase lead/lag relationship between physically connected brain regions is correlated with the degree (i.e., number of connections) of the nodes.¹¹⁷ The phase lead/lag relationship of connected nodes was used instead of a measure of cause-effect relationship, an assumption that precludes a firm interpretation of how this affects information transfer. Angelini et al. demonstrated that the inflow/outflow ratio of Granger causality in human brain networks also depends on the degree of each node.¹¹⁹ Moon et al. identified a general relationship between the number of connections and the direction of information flow in large-scale brain networks.^60,101 Based on mathematical principles, Moon and colleagues estimated directional connectivity between dense and sparse brain regions with only a neuroanatomically-informed network scaffold. Theoretical predictions were confirmed with empirical neurophysiological data analysis in three species (human, monkey, and mouse). The model and analytic studies suggest that hub structure plays a critical role in directing information patterns in the brain. Specifically, higher degree nodes attract information flow from lower degree nodes. The outcomes from the model and empirical studies also explain the dominant directionality observed from frontal to posterior parietal region in the eyes-closed resting state, which naturally emerges from the asymmetric connections between frontal (relatively sparse connections) and posterior parietal regions (dense connections) in the human brain.^{68–70,101,120} However, only simple oscillatory models were used in these studies, so the relationship between the network structure and directionality holds only for coarse grained spatial and temporal brain activities, rather than the dynamic, short-term fluctuations of regional brain activities and connectivity. Other relevant studies investigated the role of hub structure on the modulation of amplitude, frequency, and variability of regional brain activities,^{60,107,109,110,121} which further elucidate how brain network topology shapes brain functions.

Scale-free networks and criticality

Brain states are not static, but reflect a dynamic process.^122–131 The brain forms and dissolves highly integrated functional ensembles of neuronal groups in a few hundreds of milliseconds, which corresponds to the temporal frame of conscious perceptions.¹²⁷ The dynamic evolution of the brain state with spatiotemporal neural coordination is the source of the wide neural repertoires and the prodigious information generation in the brain. Criticality, the state of a dynamical system at the boundary between order and disorder, has been proposed as the optimal brain state^132–137 and scale-free organization is one of the representative characteristics observed in a system existing in a critical state. The term “scale free” is rooted in a branch of statistical physics called the theory of phase transitions that extensively explored power laws in the 1960s and 1970s. The power law behavior (scale-free property) of a system is a phenomenon that can be observed at a critical state, that is, the transition point between phases (such as solid, liquid, and gaseous phases) in statistical physics. Criticality has long been considered as a potentially advantageous configuration of biological systems.^138,139 Criticality in the brain enhances information processing and memory capability of neural networks, optimizing the sensitivity and adaptability that are crucial for survival.^116,133,140 In contrast to the usual phase transitions, systems displaying self-organized criticality (Figure 6) do not require external tuning but rather drive their own critical behavior. Another important property of the brain in a critical state is metastability, which is associated with a large temporal repertoire of brain state transitions. The diversity of brain activity reflects the information capacity of the brain, which has been hypothesized to be essential to consciousness.^47,141 Metastability typically arises in a self-organized critical state and becomes a source of complex spatiotemporal fluctuations and continuous information generation in the brain.^{116,122,128,135,142,143}

Figure 6. Self-organized criticality.

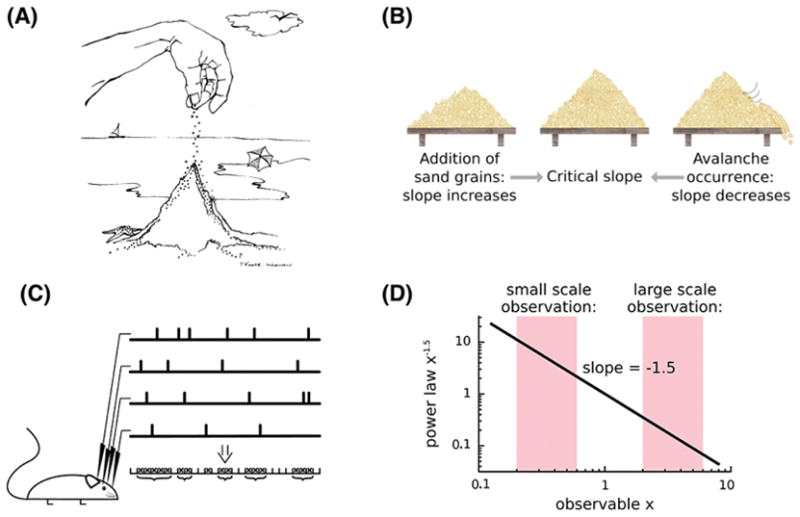
(A) The sand pile thought experiment explains the key concept of self-organized criticality (SOC). (B) Imagine dropping sands grain by grain. The sand grains accumulate but at some point the growing pile is so unstable that the next grain may cause it to collapse in an avalanche. When a collapse occurs, the sand starts to pile up again, until the mound hits the critical point once again. This series of avalanches, where smaller avalanches occur more frequently than larger ones, follows a power-law. The system does not require external tuning of the control parameters, i.e., the system organizes itself into the critical behavior. (C) The bursts of activities that spread through the network in the rat brain and the event trains recorded with the local field potentials are considered to be neuronal avalanches. (D) The avalanche size in the sand pile model and experiment, and the size distribution of neuronal avalanches in various animal brains in vitro and in vivo, follow a power law.

Over the past few years, anesthetics have been used as a tool to test the criticality hypothesis, which proposes that the brain operates in a critical state and deviation from criticality could be symptomatic or causative for certain pathologies.^137,144 Lee et al. (2010) demonstrated that anesthesia reduces the number of functional brain connections as well as the temporal complexity of the functional connection and disconnection patterns among EEG channels. However, scale-free organization was preserved across multiple subjects, anesthetic exposures, states of consciousness, and EEG frequencies.¹⁴⁵ The results implied that the state of general anesthesia does not seem to be a complete network failure but rather that the brain undergoes an adaptive reconfiguration to maintain an optimal (i.e., scale free) topology of global brain network organization. Liang et al. (2012) also demonstrated that the integrity of the whole brain network can be conserved for the anesthetized rat brain while local neural networks can flexibly adapt to new conditions.¹⁴⁶ Liu et al. (2014) compared the scale-free properties of fMRI brain networks from anesthetized healthy subjects and patients with unresponsive wakefulness syndrome (formerly known as the vegetative state).¹⁴⁷ They found that the scale-free distributions of node size and node degree were preserved across wakefulness, propofol sedation, and recovery, but absent in vegetative patients. The results suggested a fundamental difference in adaptive reconfiguration of the brain networks, potentially explaining why, despite certain shared neural features of the state, patients with pathologic disorders of consciousness do not recover with the same trajectory as healthy volunteers or patients after the discontinuation of the anesthetic. In line with these observations, Lee et al. (2013) presented evidence that bolus doses of propofol reconfigure dominant hubs from the parietal to frontal region, but do not eliminate the hierarchal hub structure entirely.³⁷ Hudetz et al. (2014) simulated the critical state of human brain networks with a modified spin glass model and human fMRI signals.¹⁴⁸ This computational model demonstrated that the diversity of brain states is maximum at the critical state and significantly reduced when the brain state moves away from the critical point. Moreover, Tagliazucchi et al. (2016) tested a theoretical prediction based on a robust feature of the critical state, called critical slowing down, which manifests as increased temporal autocorrelation of fluctuations through the system.¹³⁷ It was estimated that when a perturbation is given to a system with increased temporal correlation, the perturbational effect lasts longer and spreads farther, whereas the effect is limited locally when the system is far from a critical state. This characteristic feature of the critical state may explain why magnetic and electrical perturbations of the cortex during unconsciousness are characterized by a spatially localized response, whereas conscious wakefulness is characterized by a prolonged and spatiotemporally extended response.^74,75,149 The network effects of general anesthetics discussed thus far are summarized in Figure 7.

Figure 7. Summary of the anesthetic effects on the brain network.

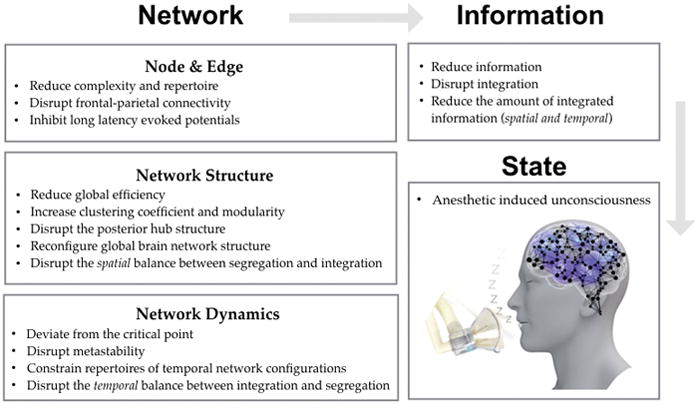
Anesthetic influences on the brain network at multiple scales: node, edge, structure, and dynamics. The altered brain network reduces the brain’s capacity to generate information and to integrate spatiotemporally distributed information, which consequently results in unconsciousness.

Diverse emergence patterns from general anesthesia

Anesthesiologists induce significant transitions between conscious and unconscious states as a part of routine clinical work. Studying the profound state transitions during loss and recovery of consciousness gives rise to important questions that may require novel theoretical approaches. How does the brain reconstitute consciousness and cognition after a major perturbation like general anesthesia? What determines reversibility in some states (e.g., sleep) and irreversibility in others (e.g., coma)? Despite the significant neuroscientific and clinical implications, the underlying mechanism of the reconstitution of brain function is poorly understood.

Recent empirical studies demonstrated that brain recovery from general anesthesia is not random, but ordered. Hudson et al. analyzed local field potential data in rat and found that when the anesthetic isoflurane is discontinued, brain activities recover through an ordered series of state transitions. Some transition paths were found to be more probable than other paths.¹⁵⁰ Hight et al. observed two distinct emergence patterns after general anesthesia.¹⁵¹ One pattern showed progressive spectral changes in the electroencephalogram before the response, while the other showed no explicit change of spectral properties before an abrupt return of responsiveness. A similar study was also carried out by Chander, Garcia et al. (2014) that classified the emergence patterns of 100 surgical patients as progressive (around 70% of the cohort) or abrupt (around 30% of the cohort) based on the power spectra of delta (0.5–4 Hz) and alpha/spindle (8–14 Hz) of frontal electroencephalogram.¹⁵² The emergence patterns can be qualitatively described as “progressive and earlier state transition” and “abrupt but delayed state transition.” Lee et al. (2011) applied a graph-theoretic network analysis that classified emergence patterns as progressive and abrupt, with accompanying network features.⁹⁷

A potential network mechanism of diverse state transitions

State transitions have been a focus of nonlinear dynamics and the physics of complex systems for the last three decades.¹⁵³ Taking into account the fact that some degree of neural synchronization is a condition for efficient neural information transmission across brain regions, the recovery of appropriately coordinated activities after anesthesia may be a mechanism of the recovery of normal neural communication. It can therefore be hypothesized that gradual and abrupt patterns of emergence from the anesthetized state are associated with, respectively, continuous and discontinuous synchronization transitions in functional brain networks. Recent empirical and computational studies support rapid or “explosive” synchronization as a mechanism for abrupt state transitions in the brain. This form of synchronization has long been studied in physics and network science, but only recently applied to biological systems. Variations in the network conditions that give rise to diverse synchronization pathways (gradual vs. explosive) might also give rise to diverse behavioral state transition patterns after general anesthesia. Kim et al. found that just over the threshold of unconsciousness induced by sevoflurane anesthesia, the brain develops the conditions for explosive synchronization, as represented by specific high-density electroencephalographic network configurations.⁹⁵ More recently, in another study, Kim et al. demonstrated that both gradual and abrupt transitions in a neuroanatomically informed model of human brain networks follow distinct synchronization processes at the individual node, cluster, and global levels.¹⁵⁴ The characteristic synchronization patterns of “gradual and earlier” and “abrupt but delayed” provides novel insights into how regional brain functions are reconstituted during gradual and abrupt emergence from the anesthetized state. Furthermore, a more precise understanding of network transitions might provide insight into altered states of consciousness or cognition in the post-anesthetic period. For example, emergence or postoperative delirium might represent partial network recovery that is amenable to graph theoretical analysis as a potential biomarker.

Convergence of anesthesiology and network science

How might the field of anesthesiology benefit from a greater integration of network science? Recently, major government-led brain projects have been launched in the US, EU, China, Japan, Korea, Canada, and Taiwan to uncover more precisely both brain structure and function. These massive endeavors and rapidly-evolving technology will create big data that can represent networks composed of interconnections linking the many elements of large-scale neurobiological systems. The data can span multiple levels of organization (neurons, circuits, systems, whole brain) and different domains of biology and data types. This integrative perspective of both brain function and structure will be especially pivotal for anesthesiology in order to understand multi-scale mechanisms of anesthetic actions from molecular and neuronal levels to behavior and cognition. Network science will bring new approaches and analytic methods that could transform the types of questions that can be asked and the hypotheses that can be tested. Another important frontier of network science is network dynamics, which can lead to greater understanding of state transitions due to diverse anesthetic perturbations. Network-based theories and analyses of big data in neuroscience might enable greater predictive power in the clinical realm as well. For example, it is conceivable that the loss of consciousness, recovery of consciousness, and specific altered cognitive functions could be predicted based on structural or functional network architectures and their dynamic response to anesthetic or sedative interventions. Such a framework could create new opportunities for clinical anesthesiologists to perturb consciousness and cognition or manipulate state transitions. In conclusion, network science has the potential to richly inform the scientific understanding of the interfaces between neuroscience and anesthesiology as well as contribute to new approaches to predicting and controlling neurologic function in the perioperative period and beyond.

Summary statement.

Network science is a necessary theoretical framework and method to understand multi-scale mechanisms of anesthetic actions from molecular and neuronal levels to behavior and cognition.

Glossary

Consciousness

Experience; the feeling of what it is like to be in a mental state.

Unconsciousness

A state devoid of experience, often operationally (and imperfectly) defined as a loss of responsiveness to command.

Levels vs. Contents of Consciousness

Levels of consciousness refer to the overall state of alertness, whereas contents of consciousness refer to the particular phenomenal aspects or qualities of conscious experience.

Network

A system of interconnected parts. Networks are defined by the nodes (or vertices) and the links (or edges) that connect them.

Degree

The number of links an individual node has to other nodes. The connections between nodes can be directed or undirected.

Path Length

The number of steps it takes to get from one node to another. Path length is inversely related to efficiency—the easier it is to get from one node to another, the more efficient the network is

Network Topology

The layout of a network; the way different nodes in a network are connected to each other.

Hub

A highly connected node in a network that creates ‘shortcuts’ across it, and (in the context of neural networks) plays a crucial role in communication and information transmission in the brain.

Information

In terms of Shannon entropy, reduced uncertainty defines the information created in a brain network. By contrast, the integrated information theory (IIT) approaches information more generally. According to IIT, information is defined as the cause-effect repertoires of a system.

Integration

According to IIT, integration is defined as an intrinsically irreducible cause-effect structure that specified by independent sub-systems. In plain words, it is defined as the extent to which a system generates more information than the sum of its parts.