Finite-difference time-domain analysis of increased penetration depth in optical coherence tomography by wavefront shaping

Abstract

Multiple scattering in turbid media inhibits optimal light focusing and thus limits the penetration depth in optical coherence tomography (OCT). However, the effects of multiple scattering in a turbid medium can be systematically controlled by shaping the incident wavefront. The authors utilize the reciprocity of Maxwell’s equations and finite-difference time-domain numerical analysis to investigate the ultimate performance bounds of wavefront shaping-OCT under ideal and realistic configurations and compare them with the conventional method. The results reveal that the optimized impinging wavefront significantly enhances the penetration depth of OCT.

1. Introduction

Scattering of waves due to inhomogeneous material compositions is a fundamental physical phenomenon on which most imaging methodologies, from seismology to medical imaging, are based. Among various three-dimensional imaging principles, coherence tomography, especially optical coherence tomography (OCT) has attracted much interest for its clinical and industrial applications [1, 2]. Based on low-coherence interferometry, an OCT system can reconstruct live three-dimensional images of sub-surface structures of a sample in a non-invasive manner by detecting back-scattered light.

Scattering, on the other hand, is also a limiting factor for imaging in general. While elastic scatterings do not necessarily result in loss of information in principle, the original information,encoded in the intensities, phases, and polarizations of each wavevector component, is perturbed each time a scattering event occurs [3–5]. Thus, from a practical point of view, it becomes increasingly more difficult to retrieve the original information faithfully as the number of scattering events increases, due to constraints such as the noise level of photodiodes or amount of post-processing required. Various solutions proposed so far, including optical clearing method [6–8], may be applicable in some situations, but a universal method that can fundamentally reduce multiple scattering-related decoherence without physically altering the sample has yet to be discovered. To remedy this situation, wavefront shaping, which has been successfully utilized for various other purposes [9–18], was recently applied for the first time to OCT [19, 20]. The experimental results suggested that the penetration depth can indeed be extended. However, only indirect evidence of distortion compensation was available because experimental measurement of the complete propagation pattern of a light beam inside a turbid medium is practically impossible.

In this paper, we utilize the reciprocity of Maxwell’s equations and a first-principle based numerical analysis method to investigate the theoretical performance bounds of wavefront shaping-OCT (WS-OCT). The exact spatial and spectral profiles of vectorial electromagnetic fields inside turbid media under non-trivial wavefront illumination conditions are obtained to verify the operation principle of WS-OCT; these profiles, however, were available neither from experiments nor from previously used numerical methods. For example, the extended Huygens-Fresnel principle is often used for OCT simulations [21, 22] but the adoption of a highly simplified model for scattering phenomena prevents it from obtaining intensity and phase distributions inside a specific sample. Monte Carlo simulations (MCS) have also been applied for analysis of the OCT system (Fig. 1(a)) [23–25]. The MCS is a stochastic ray-tracing method based on scattering phase function and, as such, is also not suitable for the exact calculation of electromagnetic vector fields necessary for analyzing the new OCT methodology [24]. Instead of these existing methods, we adopt finite-difference time-domain (FDTD) analysis [26–30], which is a first-principle based method with very general applicability. Based on FDTD analysis, and by applying the reciprocity principle, we design an ideal wavefront for the incident beam in WS-OCT and measure the intensity and phase profiles inside a turbid medium that approximates the scattering properties of actual human tissues. From the data, the performance of WS-OCT is calculated and compared to that of conventional OCT, including the effect of a finite numerical aperture of real OCT systems.

Fig. 1.

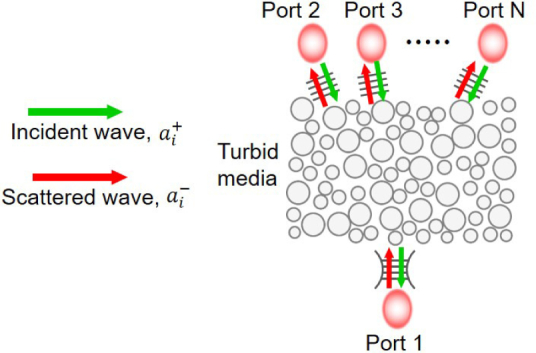
Schematic of reciprocal system coupled with multiple ports. The arrows indicate the scattered and incident wave amplitude.

2. First-principle analysis of WS-OCT

2.1. WS-OCT

Wavefront shaping-OCT can be regarded as an application of one of the well-known fundamental properties of Maxwell’s equations, Lorentz reciprocity, which applies to the propagation and scattering of electromagnetic waves in reciprocal media of arbitrary morphology [31],

$${\displaystyle \int ({\overrightarrow{E}}_2\cdot {\overrightarrow{J}}_1)dv=}{\displaystyle \int ({\overrightarrow{E}}_1\cdot {\overrightarrow{J}}_2)dv},$$ (1)

where ${\overrightarrow{J}}_1$ represents the phasor of an extrinsic current density vector field that is oscillating with a given angular frequency ω and ${\overrightarrow{E}}_1$ is the phasor of the total electric fields excited by this source taking into account the effect of the spatial composition of materials (including multiple scattering) inside the system. ${\overrightarrow{J}}_2$ and ${\overrightarrow{E}}_2$ are another independent set of source and fields. This equation is a special case of more general form of reciprocity, for which there is no source at infinity. There is no other restriction on the location of the source currents and they can be inside a turbid medium as well. Using this theorem, the optimal configuration of the input wave for WS-OCT can be easily derived. The time-reversal symmetry argument often found in previous literature on shaped-wavefront based focusing can be applied to lossless media with real-valued permittivity only [32–34]. Thus, researchers looked at alternative theoretical approaches with more relaxed constraints on the medium [35, 36]. Especially Tanter et al. used a reciprocity-based argument and the theoretical derivation below is close to their version but with the effect of loss on the transmittance efficiency explicitly shown.

Without losing generality, we assume that the system consists of N orthogonal ports, labeled 1 to N, as shown in Fig. 1. We denote the complex amplitudes of the incident and scattered wave at the i^th port by $a_i^{+}$ and $a_i^{-}$, respectively. The modes in the ports are normalized such that the incident and scattered powers through the i^th port are simply $|a_i^{+}{|}^2$ and $|a_i^{-}{|}^2$, respectively. The assumption of orthogonality allows a simple representation of the total incident (scattered) power through all ports of ${\displaystyle {\sum }_i|a_i^{+}{|}^2({\displaystyle {\sum }_i|a_i^{-}{|}^2})}$. The frequency-dependent port-to-port complex transmission coefficient is defined as $t_{ij}=a_i^{-}/a_j^{+}$ when the single-frequency wave is incident from the j^th port only and the system is in a steady-state. The reciprocity relation in Eq. (1), when applied to these discrete ports, dictates that t_ij = t_ji should be valid for all combinations of i and j [31]. Note that these ports are conceptual ports and need not be physical waveguides: any orthonormal basis for the Hilbert space of all propagating modes inside the surrounding material outside the turbid medium can constitute a set of orthonormal ports in this argument, including the set of linearly-polarized plane waves propagating in all possible directions. Linear combinations of such plane waves resulting from unitary transformation on the basis can be another example.

Now, we imagine that port 1 has a mode profile that is a focused Gaussian beam with a known waist located at the target depth of OCT. (For this argument, we ignore the scattering medium below the target depth. More rigorously, port 1 can be considered as a linear combination of plane wave ports located outside all scatterers including the scatters below the target depth, which generate such a Gaussian profile inside the turbid medium system.) If we conduct a conceptual experiment of launching a single-frequency incident wave through this port towards the scattering medium above and measure the scattered fields in a steady-state, the total scattered power is expressed as

$$P_{\text{total}}^{-}={\displaystyle \sum _{i=1}^N|a_i^{-}{|}^2={\displaystyle \sum _{i=1}^N|t_{i1}{a}_1^{+}{|}^2={\displaystyle \sum _{i=1}^N{(|t_{i1}||a_1^{+}|)}^2={\displaystyle \sum _{i=1}^N(|t_{i1}{|}^2|a_1^{+}{|}^2)=({\displaystyle \sum _{i=1}^N|t_{i1}{|}^2)|a_1^{+}{|}^2}}}}}.$$ (2)

On the other hand, $P_{\text{total}}^{-}=(1-A_1)|a_1^{+}{|}^2$, where A₁(0 ⩽ A₁ ⩽ 1) is the absorption factor of the system when excited by port 1, must be satisfied due to energy conservation because $|a_1^{+}{|}^2$ is the incident power. Hence, ${\displaystyle {\sum }_{i=1}^N|t_{i1}{|}^2=1-A_1⩽1}$ in general. (We note that clinically important human tissues such as the breast tissue, prostate tissue, and stomach mucous have high anisotropy factors, g ⩾ 0.9, for scattering and also that the magnitude of the scattering coefficient is two orders of magnitude higher than the absorption coefficient [37–39]. Hence, the forward scattering is the dominant factor affecting the signal attenuation in these cases, over the back-scattering and absorption.)

Now we consider a shaped wavefront for WS-OCT and, on the basis of aforementioned discrete ports, let $b_i^{+}$’s represent the decomposition of the incident wave with a complicated spatial profile. The resulting scattered wave at port i = 1 from the new source becomes

$$b_1^{-}={\displaystyle \sum _{i=1}^N{t}_{1i}{b}_i^{+}={\displaystyle \sum _{i=1}^N{t}_{i1}{b}_i^{+}}}.$$ (3)

The second equality sign in Eq. (3) is a direct consequence of reciprocity. The power of the scattered field coupled into port 1 is expressed as

$$P_1^{-}=|b_1^{-}{|}^2=|{\displaystyle \sum _{i=1}^N{t}_{i1}{b}_i^{+}{|}^2}.$$ (4)

Using the Cauchy-Schwarz inequality for complex variables in the last term of Eq. (4) yields

$$\begin{array}{c}|{\displaystyle \sum _{i=1}^N{t}_{i1}{b}_i^{+}{|}^2=({\displaystyle \sum _{i=1}^N{t}_{i1}{b}_i^{+})({\displaystyle \sum _{i=1}^N{t}_{i1}^{\ast }{b}_i^{+\ast })⩽({\displaystyle \sum _{i=1}^N{t}_{i1}{t}_{i1}^{\ast })({\displaystyle \sum _{i=1}^N{b}_i^{+}{b}_i^{+\ast })=}}}}}\\ {\displaystyle \sum _{i=1}^N|t_{i1}{|}^2{\displaystyle \sum _{i=1}^N|b_i^{+}{|}^2=(1-A_1)P^{+}}},\end{array}$$ (5)

where P⁺ is the incident power. As the right-most side of Eq. (5) is constant for a given incident power, the maximum excitation of the focused Gaussian profile (i.e., maximum $P_1^{-}$) can be achieved if and only if the equality condition for the above inequality holds true, which requires $b_i^{+}/t_{i1}^{\ast }=\kappa$ for some complex constant κ. Thus, the optimal incident source of power P⁺ for WS-OCT is $b_i^{+}=t_{i1}^{\ast }{(P^{+}/{\displaystyle \sum |t_{i1}{|}^2})}^{1/2}=t_{i1}^{\ast }{[P^{+}/(1-A_1)]}^{1/2}$, which is the main conclusion of this theoretical derivation. It is important to note that this is proportional to $a_i^{-\ast }$ excited through port 1, meaning that the optimal input beam for WS-OCT is the phase conjugated version of the recorded scattered wave when the system is excited by a Gaussian beam at the target depth. For optically lossless samples, this result is in agreement with the typical derivation based on time-reversal symmetry. However, this is more general as the results remain valid for lossy materials as well. Using this input beam, the amplitude of the fields at the target position is

$$b_1^{-}={\displaystyle \sum _{i=1}^N{t}_{i1}{b}_i^{+}={\displaystyle \sum _{i=1}^N{t}_{i1}{t}_{i1}^{\ast }\sqrt{\frac{P^{+}}{1-A_1}}=({\displaystyle \sum _{i=1}^N|t_{1i}{|}^2)\sqrt{\frac{P^{+}}{1-A_1}}=\sqrt{(1-A_1)P^{+}}}}}.$$ (6)

One can see that much of the input power can reach the focused target spot as long as the absorption is weak. In fact, this result, obtained from reciprocity and the Cauchy-Schwarz inequality, gives the fundamental upper bound for the maximum deliverable power fraction in WS-OCT and the necessary and sufficient conditions for the wavefronts to achieve such maximum power delivery.

In real OCT systems, it may be difficult to launch optimally-shaped wavefronts, for two reasons. First, the ports corresponding to waves propagating to and from the side or to the backside of the sample are normally inaccessible as input ports: i.e., there is no pratical way to launch waves into these ports from outside. Second, even among the top-side ports (plane waves entering and exiting through the sample surface), only those waves within the numerical aperture of the objective lens of the OCT system can be utilized. In other words, one cannot fully utilize all N ports required to generate the exact phase-conjugated beam. This may affect the amount of actual power transferred to the target spot in WS-OCT. We investigate this effect in the next section and show that good performance is still expected even when only the top-side ports with realistic numerical aperture values are considered, because the human tissues of interest are usually forward-scattering dominated with small scattering angles [37–39]. We also note that, while the process of finding the optimal wavefront based on reciprocity and an internal light source is a rigorous and simple theoretical process that can be easily adopted in numerical simulations, there are some pioneer unexperimental realization of the process could be challenge with a few novel schemes proposed only recently [17, 18]. Alternatively, actual implementations may use iterative optimization algorithms that aim to find an approximate wavefront with reasonable performances [10, 19]. Therefore, the reciprocal wavefront shaping operation we consider here is an ideal case serving as the ultimate benchmark for OCT based on shaped wavefronts, and can help verify the operation principles, identify possible challenges in practice, and evaluate the relative performance of actual beams obtained from optimization routines in experiments.

2.2. Finite difference time domain method

There are various numerical methods used to simulate light propagation in optical systems, such as ray-tracing, transfer-matrix method, rigorous coupled-wave analysis, the plane-wave expansion approach, the finite-difference frequency-domain method, and the finite-difference time-domain method [21–30]. These approaches use different degrees of approximation and assumptions. Among them, FDTD is a first-principle based simulation method, in which Maxwell’s equations are directly solved on a discretized grid. Its accuracy and versatility originate from its use of very few approximations, which include the substitution of differential equations with difference equations and fitting of the experimentally measured permittivities of materials with analytic expressions [26–29]. Due to the long history and wide acceptance of FDTD calculations, the accuracy and convergence of this method are now well understood [30].

For the particular problem of the WS-OCT, FDTD methods are well-suited, since both the amplitude and phase of the electric field can be mapped as a function of wavelength over the entire simulation region. Hence, the scattering and focusing behavior can be monitored quantitatively inside scattering samples as a function of scattering parameters or input beam conditions. One can also emulate the actual OCT process by placing a field monitor outside the scattering sample; this monitor captures back-scattered light within a finite numerical aperture. Details of the simulation setup are explained in the following section.

3. Simulation: modeling and signal retrieval

3.1. Modeling of turbid media

The turbid medium used in the OCT simulation is designed based on known optical properties of human tissue, which mainly consists of four components, two of which have lower refractive indices (interstitial tissue plasma, 1.33, and cell bodies, 1.36); the other two have larger indices (intracellular organelle and structural fibers, both with indices ranging from 1.40 to 1.45) [22, 40, 41]. In our model, the background index of the turbid medium is set at 1.35, close to the mean index of the cell bodies and interstitial tissue plasma, while the refractive index of randomly distributed scatterers are set as 1.40, which is similar to the indices of intracellular organelles and structural fibers. The diameters of the scatterers are chosen to be a uniformly distributed random variables ranging from 1 to 2 µm, which gives the scattering anisotropy factor in the range of 0.9–0.95. The particles are randomly placed without overlap with density of 0.1 particle/µm², resulting in a calculated scattering coefficient of 22 mm⁻¹ [42, 43]. Similar conditions for the scattering coefficient and anisotropy were used in other numerical studies of human tissue OCT as well as experimental works [37–40]. Additionally, unity-index particles with 4 µm width and 1.4 µm height are periodically inserted to provide reference signals at predefined depths in the OCT A-line scan profiles. These particles (located between 50 and 490 µm with an interval of 40 µm) serve as quantitative markers to help evaluate the performance of the WS-OCT method compared to the standard OCT measurement method. For lossy turbid media, the imaginary part of refractive index is adjusted to obtain a desired absorption coefficient. We further note that, even though the turbid medium parameters are chosen to simulate human tissue-like samples in this work, the method is general and can be applied to vastly different situations such as micro-crack detection or defect analysis in industry.

3.2. Construction of an optimal wavefront and set up of numerical simulations

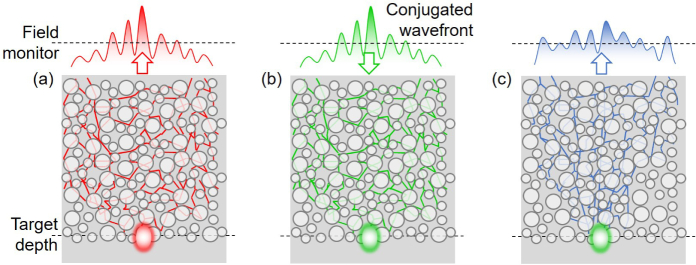
Figure 2 shows a schematic diagram for finding the optimal wavefront by reciprocity. First, a Gaussian beam is launched at the target depth toward the surface through the turbid medium, as shown in Fig. 2(a). Outside the turbid medium, the complex wavefront resulting from multiple scattering events is recorded by a field monitor (the dashed line in Fig. 2(a)). The optimal wavefront for WS-OCT is obtained by taking the complex conjugate of the recorded electric and magnetic fields and flipping the direction of the magnetic fields. To account for the effect of a finite numerical aperture, the optimal wavefront is Fourier-transformed into its spatial frequency components, onto which a top-hat filter is applied to cut off high spatial frequency components outside the numerical aperture, and then Fourier-transformed back to the real domain. The actual WS-OCT system can be emulated by launching this complex wavefront towards the turbid medium by placing a source plane outside the turbid medium (Figs. 2(b)). According to the surface equivalence theorem [44], this source plane can emulate any actual incident beam configuration through the objective lens system in OCT. While it is possible to find and utilize the optimal phase-conjugated wavefront for individual wavelengths simultaneously in one numerical simulation using a broadband source, this is a difficult task in experiments. Hence, we retained the phase of the center wavelength only in the phase conjugation process, and set the phases of all other wavelengths according to this value, more in line with a realistic phase conjugation mirror. The resulting field profile inside and outside the medium is recorded to analyze the OCT performance (Fig. 2(c)). The simulations are performed using a commercially available FDTD solver (Lumerical FDTD solutions) with custom-made scripts for the phase conjugated input beam.

Fig. 2.

Schematic illustrations of conceptual experiments that find and utilize the optimal wavefronts for WS-OCT. (a) A focused Gaussian beam is launched toward the surface from the target depth. The beam propagates through the turbid medium and is collected outside the sample surface. (b) Optimal wavefronts for WS-OCT, obtained by conjugating the phase of the collected beam, is launched into the turbid medium and form a desired focused spot at the target location. (c) The back-scattered light is collected outside the sample to be used for coherence tomography. This becomes the model case against which realistic WS-OCTs can be compared.

The field monitor and simulation domain width are set at least two times larger than the target depth to ensure that most of the scattered beam is captured and perfect matched layers (PML) are used for all boundaries to emulate open boundary conditions. We used a light source with a center wavelength of 1000 nm and a full-width half-maximum bandwidth of 40 nm. The Gaussian beams used in the conventional OCT simulations have a waist size of 8 µm.

3.3. Obtaining the depth profile

In OCT systems, the “A-line signal” (depth profile) is typically extracted by moving the reference mirror (time-domain OCT) or by performing a Fourier transform on the frequency-resolved measurements (frequency-domain OCT). The frequency-domain method is employed in our numerical simulations. The frequency-resolved back-scattered spatial electric field, ${\overrightarrow{E}}_{scat}$, is collected at the field monitor above the sample surface, as depicted in Fig. 2(c), and the electric field of the reference beam is calculated as ${\overrightarrow{E}}_{ref}=R(\lambda )e^{-i(2k_{0}d)}$, where R(λ) is the reflection amplitude at wavelength λ, d is one-way path-length up to a virtual mirror, and k₀ is the wavenumber. Before calculating the OCT signal, ${\overrightarrow{E}}_{scat}$ is spatially Fourier-transformed and only those spatial frequency components that fall inside the numerical aperture of the virtual OCT lens system are retained and focused on to a virtual detector together with the reference beam. The intensity is expressed as,

$$I(\lambda )=|{\overrightarrow{E}}_{\text{scat}}(\lambda )+{\overrightarrow{E}}_{\text{ref}}(\lambda ){|}^2=|{\overrightarrow{E}}_{\text{scat}}(\lambda ){|}^2+|{\overrightarrow{E}}_{\text{ref}}(\lambda ){|}^2+2Re({\overrightarrow{E}}_{\text{scat}}(\lambda ){\overrightarrow{E}}_{\text{ref}}^{\ast }(\lambda )),$$ (7)

We assume that the reference beam is perfectly reflected, R ~ 1, and then Eq. (7) is rewritten as $I(\lambda )=|{\overrightarrow{E}}_{\text{scat}}(\lambda )+e^{-i(2k_{0}d)}{|}^2$. The A-line signal yields to superposition of intensity at all wavelengths;

$$I_{OCT}={\displaystyle \int |{\overrightarrow{E}}_{\text{scat}}(\lambda )+e^{-2ikd}{|}^{2}d\lambda }.$$ (8)

4. Results and discussion

4.1. Reciprocal beam focusing

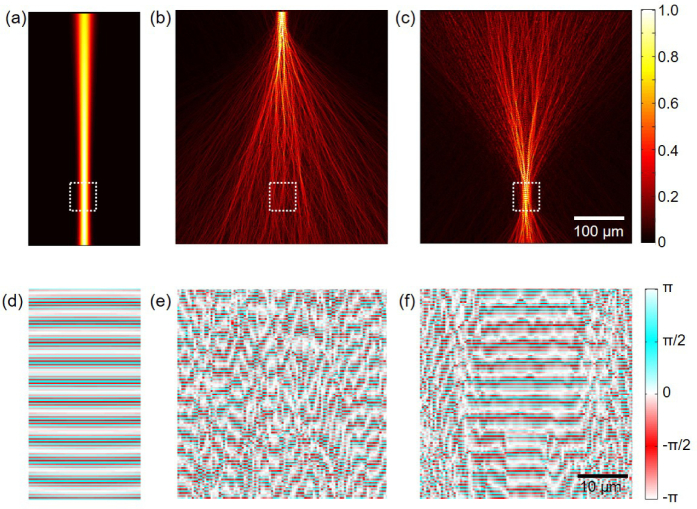
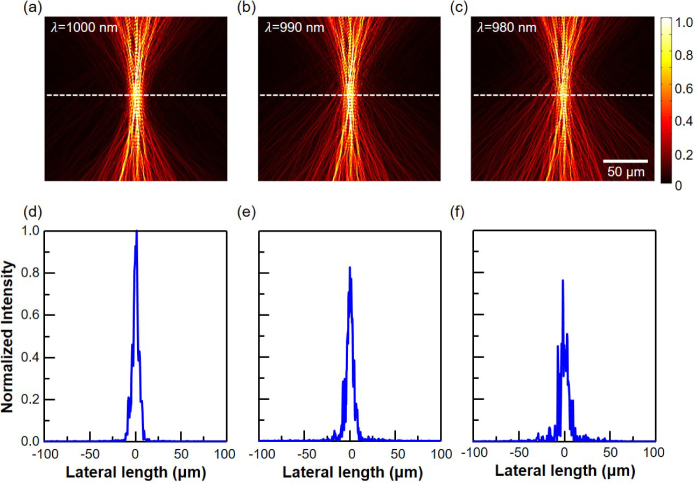
When a Gaussian beam is used as the illumination source in OCT, the beam undergoes multiple scatterings until it reaches the target depth. Thus, even when the objective lens is set to produce a focused Gaussian beam with a desired width at the target depth (Fig. 3(a)), the actual beam profile becomes distorted and much wider than the intended Gaussian beam after only a few tens of micrometers of propagation in typical human tissues phantoms, as shown in Fig. 3(b). This results in loss of lateral resolution, a lower signal-to-noise ratio, and decreased penetration depth. On the other hand, when the optimal wavefront obtained from the aforementioned procedure with a unity numerical aperture is used, a numerical simulation confirms that this beam indeed forms a near-perfect Gaussian spot at the target depth, which is set to 400 µm in this example (Fig. 3(c)). The figure reveals that at depths between 350 and 450 µm, the beam is tightly focused, as expected, and the maximum field intensity is attained at the target depth. For quantitative comparison, electric field intensities are averaged over an 8 µm-wide focus region and the optimal beam shows 47.3 times higher average intensity compared to the conventional Gaussian beam. The phase profiles shown in Figs. 3(d–f) further illustrate the performance of the optimal beam compared to that of the Gaussian beam. The phase of the Gaussian beam is highly perturbed, while a locally uniform phase profile distribution is observed around the 400 µm target depth for the WS beam. The uniform phase distribution region closely corresponds to the tightly focused region in the amplitude profile and this provides concrete evidence that the wavefront shaping successfully compensates for the multiple-scattering based decoherence. While the phase conjugation is performed based on the phase of the center wavelength (λ= 1000 nm) only, Fig. 4 confirms that the optimal beam is well-focused at the target depth for other wavelengths up to 40 nm bandwidth around the center wavelength as well. This is in agreement with the theoretical spectral correlation bandwidth, Δλ = (λ²l^∗)/L² =60 nm, where l^∗ and L are the transport length and thickness of the turbid medium, respectively. The peak intensities of those off-center wavelengths shown in Fig. 4(e) and (f) are slightly lower than the center wavelength case (Fig. 4(d)), and a few small side peaks are observed. Nonetheless, the Gaussian-like center peak shape and its width are well maintained. These results indicate that near-optimal light focusing is possible for a reasonably broad wavelength range, even though only the center wavelength is used for the phase conjugation operation.

Fig. 3.

Simulated electric field amplitude profile at 1000 nm wavelength, when an optical beam is launched from the top side. (a) A Gaussian beam is launched into a uniform medium with a refractive index of 1.35, showing a well-focused spot at the target depth. (b) A Gaussian beam is launched into a turbid medium, showing the effect of multiple scattering. (c) The optimal beam is launched into the same turbid medium, showing a well-focused spot at the target depth. (d–f) Magnified phase profiles of the white dashed region in (a–c), respectively.

Fig. 4.

Simulated electric field amplitude profiles of a shaped-wavefront beam, phase-conjugated at 1000 nm, at various wavelength of (a) 1000 nm, (b) 990 nm, and (c) 980 nm. (d–f) Corresponding lateral electric field intensity along the white dashed line, respectively.

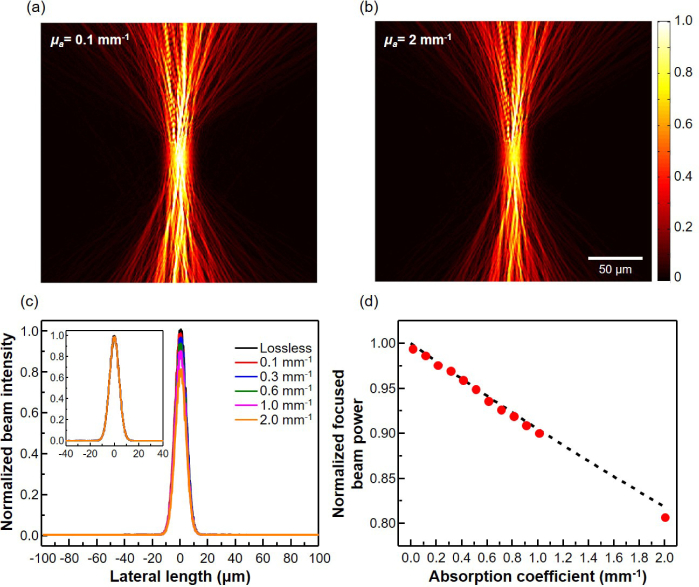
Actual biological tissues are optically lossy, and the power reaching the focusing spot at the target depth will be smaller than the lossless case, as predicted by Eq. (6). Nonetheless, the wavefront shaping can still produce a well-focused beam at the target depth as evidenced by the simulated amplitude profiles of the optimal shaped-wavefront beam in turbid medium with the absorption coefficient of 0.1 and 2 mm⁻¹, respectively, in Figs. 5(a–b). The lateral beam profiles at the target depth, shown in Fig. 5(c) for biologically important range of absorption coefficients from 0.1 to 2 mm⁻¹, further confirm that the Gaussian-like beam profiles are well maintained, albeit with progressively reduced intensities as the absorption increases. The normalized lateral beam profiles in the inset of Fig. 5(c) overlap with one another almost completely for all the absorption coefficients considered. Figure 5(d) compares quantitatively the theoretically and numerically calculated fractional beam power reaching the target focal spot as a function of the absorption coefficients. The fractional beam power is calculated by integrating the Poynting vector over a 30 µm focal spot at the target depth and normalizing it by the incident beam power. As the absorption coefficient is increased, the fractional beam power at the target focal spot decreases from unity. However, the value obtained by the optimal shaped-wavefront beam (red dots in Fig. 5(d)) is very close to the theoretically predicted maximum value of 1 − e^−αL, where α is the absorption coefficient and L is the target depth (black dashed line in Fig. 5(d)). From the above observations, it is expected that the measured OCT signal based on the optimal beam will have substantially enhanced signal-to-noise ratio, lateral resolution, and penetration depth, compared to those of the conventional OCT.

Fig. 5.

Simulated electric field amplitude profiles of a shaped-wavefront beam inside the turbid medium with absorption coefficient of (a) 0.1, and (b) 2 mm⁻¹. (c) Lateral profile of the electric field intensity at the target depth for various absorption coefficients of the turbid medium. (d) Optical power reaching the focusing spot at the target depth, normalized by the input beam power. The dashed line and red dots correspond to the theoretically derived and simulated values, respectively.

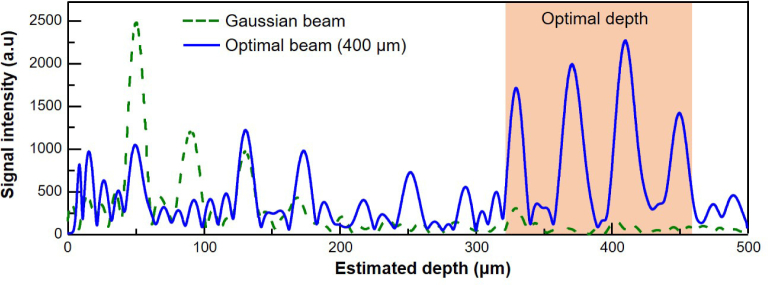
For quantitative comparison of the conventional OCT and the WS-OCT, we obtain the depth profiles from both methods. The results for the conventional OCT and the WS-OCT optimized at a target depth of 400 µm are shown in Fig. 6, denoted as a dashed green line and a solid blue line, respectively. For the conventional OCT, the signal level is gradually reduced as the depth increases; its rate is in agreement with actual experimental results [20]. On the other hand, the signal levels of the WS-OCT show enhancements at depths near the target depth of 400 µm (red-shaded area in Fig. 6). Signal from the marker particles at 370 and 410 µm in the WS-OCT case are enhanced 31.1 and 36.7 times, respectively, in comparison to those of the conventional method. For other particles, the signal levels of WS-OCT are lower, indicating that WS-OCT has clear depth selectivity and is optimized to investigate features near the target depth. We note that, in an experimental investigation of WS-OCT using tissue phantoms with similar scattering parameters as ours, significantly enhanced signals near the target depth was observed as well. The exact level of enhancement was not as high as this numerically predicted value, which is due to the fact that the wavefront used in the experiment was not the ideal wavefront obtained by reciprocity but an approximate one that was found by optimizations [19].

Fig. 6.

OCT signal intensity for the WS-OCT at the target depth of 400 µm; the dashed green line and solid blue line represent the signal levels of the conventional OCT and the WS-OCT, respectively. The red shaded area indicates the depth range over which a significant enhancement of the signal intensity occurs.

4.2. Enhanced penetration depth of the WS-OCT

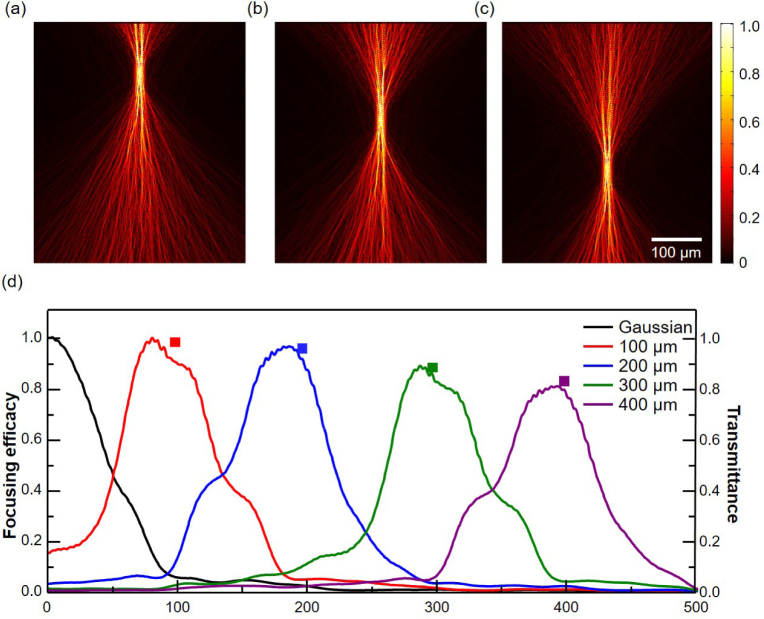
The depth selectivity of WS-OCT also means that a composite of several independent WS-OCTs may be required if one wants to obtain a full-depth profile with a total depth span more than a couple of hundred microns. The electric field amplitude profiles, shown in Figs. 7(a–c), illustrate that the optimal wavefront can be found for different target depths, in addition to 400 µm, as can be seen in Fig. 3(c). The focusing efficacy of each beam is quantified by averaging the electric field intensity over an 8 µm-wide center region and plotted as a function of depth (Fig. 7(d)). While the Gaussian beam, which can be considered as an optimal beam with zero target depth, has the maximum intensity near the surface, the maximum intensities of the shaped-wavefront beams are achieved at the corresponding depths, as expected. Moreover, the intensity difference between the Gaussian beam and the shaped-wavefront beams becomes greater for larger depths. The gradual decrease of the focusing efficacy with the increasing target depth is also evident. It is noteworthy that this monotonically decreasing peak value of the focusing efficacy near each target depth is very close to the value predicted by the reciprocity (square markers in Fig. 7(d)). As the target depth is increased, more beams are scattered to the side and backward directions during the WS beam generation step (Fig. 2(b)). Hence, the transmittance to the top surface, i.e., into the ports accessible from outside, decreases and, by reciprocity, the shaped-wavefront beam injected from those ports (Fig. 2(c)) has decreased transmittance to the focal spot at the target depth.

Fig. 7.

Simulated electric field amplitude profiles of optimal beams at different target depths of (a) 100, (b) 200, and (c) 300 µm. (d) Longitudinal profiles of the focusing efficacy of the optimal beams and a Gaussian beam. Square markers represent the transmittance of optical power from a virtual Gaussian source at the target depth to the field monitors near the sample surface.

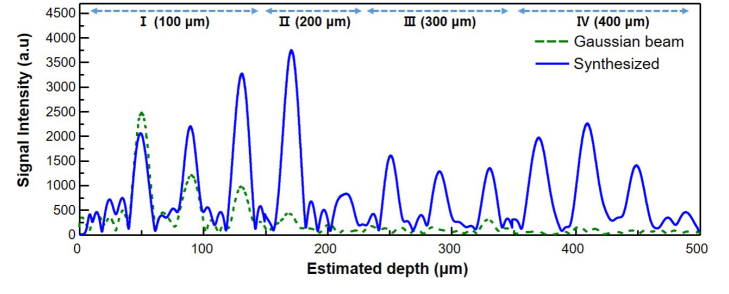
The composite A-line scan profile in Fig. 8 is from four WS-OCTs optimized at progressively deeper target depths: I (100 µm), II(200 µm), III(300 µm), and IV(400 µm). Away from the surface, WS-OCT shows consistently higher intensity than that of conventional OCT. The highest signal enhancement is 40.2 times by the particle located at 450 µm. Since the penetration depth is limited by the signal-to-noise ratio, these results based on human-tissue emulating phantoms suggest that WS-OCT can allow significantly enhanced penetration depths in clinical situations.

Fig. 8.

Composite OCT A-line signal from four WS-OCTs with individual target depths of 100, 200, 300, and 400 µm (solid blue line) is compared to that of a conventional OCT using a Gaussian beam (dashed green line). Significant signal enhancement is observed at all depths except at 50 µm, at which the conventional OCT also performs well.

4.3. Effect of a finite numerical aperture

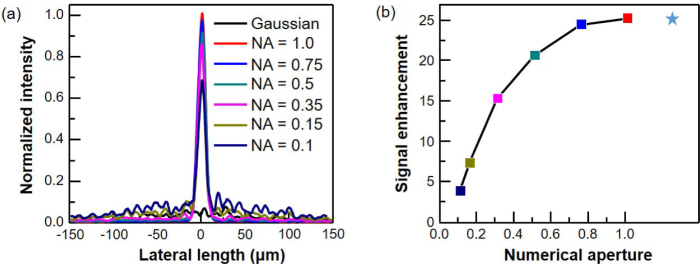
The lens systems used in actual OCT setups have a finite numerical aperture (NA) with a limited range of angles within which the incident wavefront can be injected and the scattered light from the sample can be collected. With a limited NA, the optimal beam found from reciprocity cannot be realized exactly and the signal performance is expected to be lower than the ideal case. Hence, it is practically important to know how large an NA is required for the WS-OCT to be meaningful. Figure 9(a) shows the electric field intensity of the shaped-wavefront beams at a target depth of 300 µm under varying assumptions on NA. The intensity of a Gaussian beam at 300 µm depth is also plotted for comparison. This clearly shows that, even with a small NA of 0.1, the wavefront shaping is effective. As NA decreases from 1.0 to 0.1, the intensity becomes progressively lower but the Gaussian-like main intensity profile is well maintained. Though this study mainly addresses OCT, the principle can be transferred to high-resolution reflection in-vivo imaging technologies that use high-NA optical systems.

Fig. 9.

(a) Electric field intensity of Gaussian beam and of shaped-wavefront beam with NA of 0.1, 0.15, 0.35, 0.5, 0.75, and 1 at depth of 300 µm. (b) Signal enhancement of WS-OCT modeled with corresponding NA. Star mark represents signal enhancement for ideal case, for which full spatial information is used.

5. Conclusion

We have quantitatively investigated the performance of the proposed WS-OCT through FDTD simulations, demonstrating the exact amplitude and phase profiles of the injected beam within a turbid medium whose scattering properties are similar to those of clinically important human tissues. The profiles exhibited tight focusing and high intensity at the target depth, as predicted. In the quantitative analysis, the numerically extracted OCT depth-scan results revealed that, in comparison to the conventional OCT system, the WS-OCT has a signal level that is significantly enhanced near the target depth. Also, the depth selectivity and the performance under small numerical aperture found in actual OCT lens systems are investigated. These outcomes provide concrete evidence and physical explanation for the performance of the WS-OCT, and have potential applications in the field of deep-tissue biomedical imaging. Moreover, this work also illustrates that FDTD analysis can provide exact profile information that can be obtained neither by experiments nor other simulation methods developed so far, and can become a useful platform for quantitatively examination of the principles and performance of new imaging schemes to be proposed.

Appendix

More detailed explanation of orthonormal ports in the theory section is provided here. A set of all possible plane waves in the air can become a set of orthonormal ports, with each port indexed by a directional vector indicating the direction of propagation for an outgoing wave through the port and a Boolean variable indicating whether wave is s-polarized or p-polarized. While the number of possible propagation directions is infinite, one can first assume a finite universe with size D and work with discrete wavenumbers in each direction in the multiples of 2π/D bounded by the vacuum wavenumber. This assumption allows the number of modes as well as the total power in a port for a finite electric field to remain finite, until we let D approach infinity. For these finite ports, we can use a single, integer-valued index m, which simplifies the notation. Inspection of the mode profiles for these ports reveals their orthogonality. The complex electric and magnetic field profiles for a plane wave can be expressed as $\overrightarrow{E}(r)=a_m{\overrightarrow{E}}_{mo}(r)$ and $\overrightarrow{H}(r)=a_m{\overrightarrow{H}}_{mo}(r)$ where a_m is the complex amplitude of the wave and ${\overrightarrow{E}}_{mo}$ and ${\overrightarrow{H}}_{mo}$ represent the electric and magnetic field distribution at the m^th port, respectively, with explicit forms of ${\overrightarrow{E}}_{mo}=({\overrightarrow{e}}_m/D)\exp (i{\overrightarrow{k}}_m\cdot \overrightarrow{r})$ and ${\overrightarrow{H}}_{mo}=({\overrightarrow{h}}_m/D)\exp (i{\overrightarrow{k}}_m\cdot \overrightarrow{r})$, where ${\overrightarrow{k}}_m$ is the wavevector for the m^th port, and ${\overrightarrow{e}}_m$(${\overrightarrow{h}}_m$ is an electric (magnetic) field vector in one of the two ortogonal polarization configurations allowed for given ${\overrightarrow{k}}_m$, satisfying ${\overrightarrow{h}}_m=|{\eta }_0{\overrightarrow{k}}_m{|}^{-1}{\overrightarrow{k}}_m\times {\overrightarrow{e}}_m$ and $0.5\mathrm{Re}({\overrightarrow{e}}_m\times {\overrightarrow{h}}_m^{\ast })\cdot {\overrightarrow{k}}_m/|{\overrightarrow{k}}_m|=1\mathrm{W}/{\mathrm{m}}^2$ (η₀ is the vacuum impedance) [45]. Now, for any two mode indices m and n, it follows that ${\displaystyle {\int }_{S}1/D^2\exp (i{\overrightarrow{k}}_m\cdot \overrightarrow{r})\exp (i{\overrightarrow{k}}_n\cdot \overrightarrow{r})d^{2}r=0}$if ${\overrightarrow{k}}_m\ne {\overrightarrow{k}}_n$ and ${\displaystyle {\int }_{S}1/D^2\exp (i{\overrightarrow{k}}_m\cdot \overrightarrow{r})\exp (i{\overrightarrow{k}}_n\cdot \overrightarrow{r})d^{2}r=1}$ and $0.5\mathrm{Re}({\overrightarrow{e}}_m\times {\overrightarrow{h}}_n^{\ast })\cdot {\overrightarrow{k}}_m/|{\overrightarrow{k}}_m|={\delta }_{mn}$ if ${\overrightarrow{k}}_m={\overrightarrow{k}}_n$. Hence, ${\displaystyle {\int }_{S}0.5\mathrm{Re}({\overrightarrow{e}}_m\times {\overrightarrow{h}}_n^{\ast })\cdot {\overrightarrow{k}}_m/|{\overrightarrow{k}}_m|d^{2}r={\delta }_{mn}}$ is satisfied for any m and n, which proves the orthonormality of the modes. It it known in linear algebra that the result of any unitary transformation on an orthonormal basis is another orthonormal basis. As such, a Gaussian port can be one of the orthonormal ports.

Funding

Samsung Advanced Institute of Technology; National Research Foundation of Korea (NRF-2013M3C1A3063598, NRF-2014M3A6B3063708).

Disclosures

The authors declare that there are no conflicts of interest related to this article.