Analysis of RNA nearest neighbor parameters reveals interdependencies and quantifies the uncertainty in RNA secondary structure prediction

Abstract

RNA secondary structure prediction is often used to develop hypotheses about structure-function relationships for newly discovered RNA sequences, to identify unknown functional RNAs, and to design sequences. Secondary structure prediction methods typically use a thermodynamic model that estimates the free energy change of possible structures based on a set of nearest neighbor parameters. These parameters were derived from optical melting experiments of small model oligonucleotides. This work aims to better understand the precision of structure prediction. Here, the experimental errors in optical melting experiments were propagated to errors in the derived nearest neighbor parameter values and then to errors in RNA secondary structure prediction. To perform this analysis, the optical melting experimental values were systematically perturbed within the estimates of experimental error and alternative sets of nearest neighbor parameters were then derived from these error-bounded values. Secondary structure predictions using either the perturbed or reference parameter sets were then compared. This work demonstrated that the precision of RNA secondary structure prediction is more robust than suggested by previous work based on perturbation of the nearest neighbor parameters. This robustness is due to correlations between parameters. Additionally, this work identified weaknesses in the parameter derivation that makes accurate assessment of parameter uncertainty difficult. Considerations for experimental design are provided to mitigate these weaknesses are provided.

INTRODUCTION

Noncoding RNAs (ncRNA) are RNAs that function by means other than being translated into protein. These functions for ncRNAs include enzymatic catalysis (ribozymes) (Doudna and Cech 2002), regulation of gene expression (siRNA, miRNA, and riboswitches) (Wu and Belasco 2008; Serganov and Nudler 2013), and target identification (guide RNAs) (Yu and Meier 2014). These diverse functions are often the result of specific structures.

RNA structure can be characterized at both the secondary and tertiary levels. Secondary structure is defined as the set of canonical base pairs (including Watson–Crick and GU pairs), whereas tertiary structure is classified as the set of additional contacts that determine the full three-dimensional structure. The secondary structure, in addition to sequence, provides enough information to identify a functional RNA (Nawrocki and Eddy 2013) and develop hypotheses about function (Seetin and Mathews 2012). Compared to tertiary structure, secondary structure tends to be more thermally stable and tends to form faster (Tinoco and Bustamante 1999). This allows RNA secondary structure to be predicted independently of tertiary structure (Tinoco and Bustamante 1999).

The Turner nearest neighbor rules and their associated parameters can be used to estimate the folding energy of an RNA secondary structure. The stability of a given motif, such as a stack of a base pair on an adjacent pair or a set of unpaired nucleotides and its closing base pairs, called a loop, is assumed to be determined by the sequence of the motif and the adjacent base pairs. The thermodynamic parameters were determined using linear regression on a database of small RNA sequences with stabilities measured by optical melting experiments (Andronescu et al. 2014). The most recent complete set of Turner rules was assembled in 2004 (Mathews et al. 2004; Turner and Mathews 2010) and includes the Watson–Crick terms determined in 1998 (Xia et al. 1998).

The nearest neighbor parameters are widely used in software for RNA secondary structure prediction (Andronescu et al. 2003; Zuker 2003; Reuter and Mathews 2010; Lorenz et al. 2011). A popular approach to structure prediction is to use a dynamic programing algorithm to predict a lowest free energy structure (Seetin and Mathews 2012; Hofacker 2014) or base-pairing probabilities across an ensemble of structures for a given sequence (McCaskill 1990; Mathews 2004). Additionally, methods that infer folding parameters from the set of sequences with known structure generally use the same functional form (Do et al. 2006; Andronescu et al. 2010; Rivas et al. 2012). The current set of RNA folding parameters are enumerated in the nearest neighbor database (NNDB), along with examples of their use (Turner and Mathews 2010). Subsequent to the determination of the latest set of Turner rules, a number of optical melting experiments have demonstrated that improvements in the nearest neighbor parameter models and values are possible (Huynen et al. 1997; Znosko et al. 2002; Chen et al. 2004, 2005, 2006, 2009, 2012; Vecenie and Serra 2004; Bourdelat-Parks and Wartell 2005; O'Toole et al. 2005, 2006; Chen and Turner 2006; Vecenie et al. 2006; Wilkinson et al. 2006; Badhwar et al. 2007; Blose et al. 2007; Davis and Znosko 2007, 2008, 2010; Shankar et al. 2007; Carter-O'Connell et al. 2008; Christiansen and Znosko 2008, 2009; Clanton-Arrowood et al. 2008; Miller et al. 2008; Nguyen and Schroeder 2010; Sheehy et al. 2010; Thulasi et al. 2010; Liu et al. 2011; McCann et al. 2011; Hausmann and Znosko 2012; Lim et al. 2012; Vanegas et al. 2012; Kent et al. 2014; Murray et al. 2014; Kwok et al. 2015; Strom et al. 2015; Tomcho et al. 2015; Crowther et al. 2017; Phan et al. 2017).

This study focuses on how uncertainty in parameter values can result in uncertainty in structure prediction. It has been established that free energy minimization is ill-conditioned. In other words, changes in the nearest neighbor parameter values, within experimental errors, can change the resultant predicted structure (Layton and Bundschuh 2005). Moreover, it has been established that base-pairing probabilities and centroid structures are more robust to these changes in nearest neighbor parameter values (Layton and Bundschuh 2005; Rogers et al. 2017). To provide these insights, previous studies treated each parameter as independent of the other parameters (Layton and Bundschuh 2005; Rogers et al. 2017). However, because the parameters are not independent from each other, there is more to learn about parameter uncertainty. Parameters can be correlated within a regression. For example, in the regression for estimating stacking values for adjacent Watson–Crick pairs, stacks that can share a base pair are more likely to appear adjacent to each other in the set of helices that were experimentally studied, resulting in a correlation between the stacking parameters. Additionally, there are complex interdependent relationships across regressions. For example, the Watson–Crick stacking terms are used in the derivation of the terms that estimate hairpin loop and internal loop folding stabilities.

In this work, the experimental uncertainties in the optical melting experiments are mapped to uncertainties in the nearest neighbor parameters, and their impact on RNA secondary structure prediction is quantified. It shows that the uncertainties in the parameter values have a smaller effect on uncertainty in secondary structure prediction than previously estimated. This study reveals previously undocumented correlations between the nearest neighbor parameters, and provides guidance about the design of future optical melting experiments.

RESULTS

Overview

In this study, the nearest neighbor parameters are perturbed to estimate the uncertainty in secondary structure prediction. The nearest neighbor parameters are perturbed either indirectly, by perturbing the values of the underlying optical melting values within the bounds of experimental error, or directly, by perturbing the values of the nearest neighbor parameters (Fig. 1). When perturbing the experimental values, changes in the underlying optical melting experimental data are propagated through the regression procedures to derive new values for the nearest neighbor parameters. When these perturbations are randomly sampled within the error of the original experiments, the resulting set of perturbed nearest neighbor parameter values are necessarily as equally valid as the current set of nearest neighbor parameter values, called the reference values. Secondary structure predictions using the perturbed and reference nearest neighbor parameter sets can then be compared. In contrast, perturbing the parameters directly treats the parameter values and errors as though they are uncorrelated.

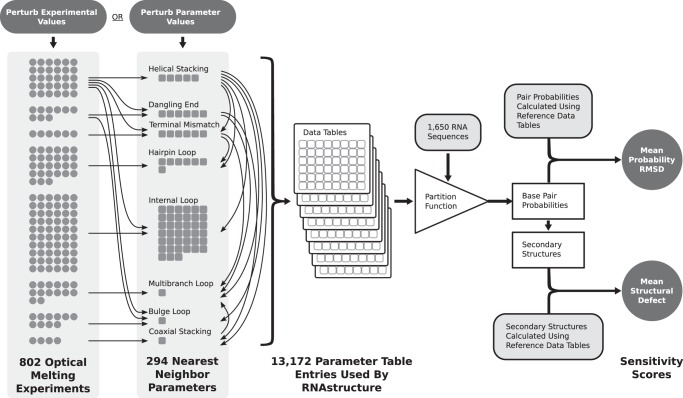
FIGURE 1.

Experimental outline. The nearest neighbor parameters are derived from 802 optical melting experiments on small model systems, as illustrated in the first column, where each circle represents approximately five experiments. A total of 294 independent nearest neighbor parameters are fit, as illustrated in the second column, where each square stands for approximately five nearest neighbor parameters. The arrows show how nearest neighbor parameters depend on the experiments and also on each other. The third column illustrates the total number of parameter table entries that are used by the RNAstructure software package. In this work, perturbed thermodynamic data tables are generated by either perturbing the experimental values used to generate the nearest neighbor parameters based on the experimental uncertainty, or by directly perturbing the nearest neighbor parameters based on the standard error of the regression (for parameters determined by linear regression) or uncertainty values calculated by the propagation of error from the underlying experiments (Zuber et al. 2017). Parameter tables using these perturbed nearest neighbor parameter sets are then used to predict base-pairing probabilities and secondary structures for an archive of 1650 sequences. The pair probabilities and structures are then compared to those obtained using the reference parameter set.

This study focuses on the Turner 2004 parameter set, which is composed of 294 parameters (Mathews et al. 2004), and uses the nearest neighbor models from that work. Those parameters were derived from a set of 802 optical melting experiments, with 109 Watson–Crick helices, 39 helices including G-U base pairs, 136 hairpin stem-loop structures, 304 internal loops, 49 bulge loops, 18 coaxial stacks, 45 helices with dangling ends, 33 helices with terminal mismatches, and 69 multibranch loops. The sequences and the experimentally determined folding free energy changes are provided in Supplemental Tables 1–8.

In this work, base pair probabilities are estimated using a partition function calculation (McCaskill 1990; Mathews 2004), which uses thermodynamics to estimate the Boltzmann ensemble of secondary structures. Subsequently, secondary structures are predicted using ProbKnot prediction from the estimated base pair probabilities (Bellaousov and Mathews 2010). ProbKnot assembles a structure composed of base pairs between nucleotides that are mutually maximal base-pairing partners. Compared to minimum free energy structure prediction, pairs predicted by ProbKnot can include pseudoknots.

Review of nearest neighbor parameter derivation

To generate the 294 nearest neighbor parameters from optical melting experiments, a series of linear fits are performed (Xia et al. 1998; Mathews et al. 1999, 2004). The parameters for Watson–Crick stacks are fit by linear regression to the 109 stabilities for duplexes composed of only Watson–Crick helices. Then, parameters for stacks including G-U base pairs are fit by linear regression to a set of duplexes composed of both Watson–Crick pairs and G-U pairs. In this regression, the values for the folding free energy change of stacks composed of only Watson–Crick pairs are taken from the first regression. These first two regressions provide the set of nearest neighbor parameters needed to estimate the stabilities of helices.

The parameters for dangling ends, unpaired nucleotides at the end of a helix on either the 5′ end or 3′ end of a strand, are determined as the difference in stability for duplex that forms a helix with a dangling end and a duplex that only forms the helix. These parameters are sequence dependent, but not all dangling end sequences were measured. No dangling end measurements were made for nucleotides dangling from a G-U or U-G closing base pair. In those cases, the parameter was assumed to be equal to the same dangling nucleotide off of an A-U or U-A closing base pair. For example, $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{GA}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{U}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ is assumed to be equal to $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{A}\mathrm{A}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{U}\text{-}{5}^{\mathrm{\prime }}\end{array}]$. Additionally, neither $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{A}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{UG}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ nor $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{A}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{U}\mathrm{U}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ were measured. Those dangling end parameters were both estimated as the average of $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{A}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{U}\mathrm{C}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ and $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{A}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{U}\mathrm{A}\text{-}{5}^{\mathrm{\prime }}\end{array}]$.

Terminal mismatches occur when there are unpaired nucleotides at the end of a helix at both the 5′ end and 3′ end of the two strands that compose the helix end. These are also determined by the difference in stability of a duplex with a helix and terminal mismatch and a duplex with only the helix. These are sequence dependent, and 33 of 60 terminal mismatches were measured. When a mismatch sequence was not measured, its stability is estimated as the sum of the 5′ and 3′ dangling ends plus a 0.2 kcal/mol penalty for purine–purine mismatches, except for mismatches with a G-U or U-G base pair. For those cases, the parameter was assumed to be equal to the corresponding mismatch on an A-U or U-A base pair. Because the partition function samples all possible secondary structures, including structures with a terminal mismatch that can base pair, folding free energies of pairing capable mismatches need to be defined. In those cases, the folding free energy change of a A-C or C-A mismatch on the same closing base pair is used, depending on the purine–pyrimidine orientation. For example, the $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{GU}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{CG}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ mismatch is given the energy from the $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{GC}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{CA}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ mismatch.

Next the loop parameters are determined. Loop stabilities are determined from optical melting experiments on small model systems by subtracting the stability of helices from the stabilities determined for systems with one loop and helices. Parameters for hairpin loops, internal loops, bulge loops, and multibranch loops parameters are fit in six separate linear regressions. Hairpin loops with 3, 4, or 6 unpaired nucleotides whose measured folding free energy changes differ by more than 1 kcal/mol from predicted folding free energy changes are included in separate data tables. These nearest neighbor parameters have dependencies on the optical melting experiments, on the helical nearest neighbor parameters, and on each other. These dependencies are illustrated by the arrows to nearest neighbor parameters in Figure 1.

From the 294 parameters, a set of tables is generated for use in secondary structure prediction. These tables are composed of 13,172 total parameters, where the extra entries are used to accelerate secondary structure prediction. A total of 4095 parameters are repeated in the reverse orientation. For example, the Watson–Crick stack of $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{UG}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{AC}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ also appears as $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{CA}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{GU}\text{-}{5}^{\mathrm{\prime }}\end{array}]$. The independent nearest neighbor parameters are also used to generate tables that contain the free energy changes for all internal loop sequences of sizes 1 × 1, 1 × 2, and 2 × 2. In this way, these can be looked up during calculations rather than being calculated.

Comparison between structure prediction using reference and perturbed parameter sets

To quantify the differences in predicted secondary structures between the reference and a perturbed parameter set, four scores are used. The first is a root mean squared deviation (RMSD) calculation of the differences in the base-pairing probabilities when using perturbed data tables versus reference data tables for a sequence. To compare the secondary structures between the reference and perturbed parameter sets, the differences are quantified as sensitivity and positive predictive value (PPV). The sensitivity (also known as recall) is the percent of pairs predicted using the reference parameters that are also predicted using the perturbed parameters. The PPV (also known as precision) is the percent of pairs predicted using the perturbed parameter set that are also predicted using the reference parameter set. A sensitivity and PPV of 100% would indicate that the structures predicted using perturbed parameters are identical to those predicted using the reference parameter set. Conversely, a sensitivity and PPV of 0% would indicate that the structures predicted using perturbed parameters share no pairs with those predicted using the reference parameter set.

Single experiment sensitivity analysis

To assess the impact of uncertainty in single experimental values on the nearest neighbor parameter values, each experimental value was individually perturbed by both +3 σ and −3 σ, where σ is the experimental uncertainty for that experiment. A set of perturbed nearest neighbor parameter values were calculated using the procedure reviewed above. The perturbed parameter sets were used to estimate base pair probabilities and predict secondary structures for each sequence in a database. The sequence database includes 1650 RNA sequences, with both structured RNAs (detailed in the Materials and Methods) and unstructured RNAs (mRNAs and shuffled RNAs).

The base pair probabilities were compared to those predicted using the reference parameter set to determine base pair probability RMSDs. The mean RMSD value for each parameter set is shown in Figure 2. A summary of the experiments and their impacts is available in an interactive Excel spreadsheet provided in the Supplemental Materials.

FIGURE 2.

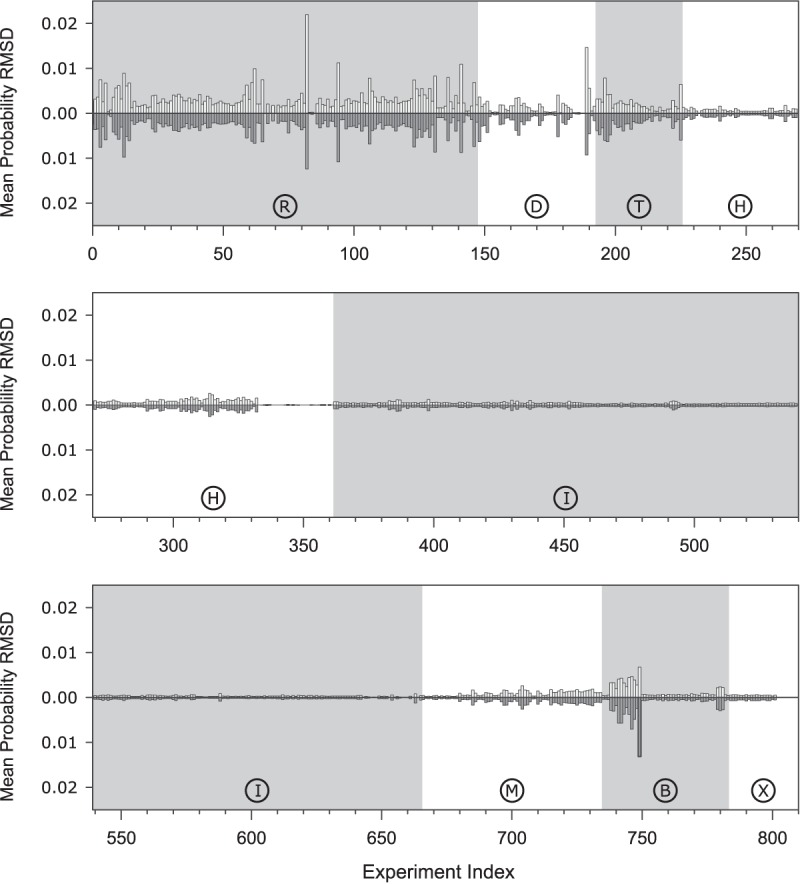
Sensitivity analysis by perturbing single optical melting experiments. Experiment indices are along the x-axis, organized by the type of RNA motif, denoted by the letters in the circles that correspond to the experiment codes in Supplemental Tables 1–8. Mean base pair probability RMSD for the entire sequence archive (except randomized sequences) is shown for the perturbation of ±3 σ. Randomly shuffled sequences were excluded so that the sensitivity scores would more accurately reflect the uncertainty in the structure predictions of natural ncRNAs. The RMSDs for +3 σ are shown above the x-axis, while the RMSDs for −3 σ are shown below the x-axis. The details of each experiment are available in Supplemental Tables 1–8.

The effect of perturbing single optical melting experiments by +3 σ was also mapped onto the parameter space. Each perturbed parameter set was compared to the reference parameter set to generate a difference map to illustrate how individual experiment values impact the nearest neighbor parameters (Fig. 3). Mapping experimental values to parameter values illustrates the interrelationship of the nearest neighbor parameters and the underlying optical melting experiments. For example, the effects of perturbing the folding free energies of Watson–Crick duplexes can be seen on the values of nearest neighbor parameters across many parameter classes (including hairpin loop parameters, bulge loop initiation terms, internal loop parameters, and multibranch loop terms). Additional experiments were performed by perturbing single experimental values by −3 σ. The results were highly symmetric to those in which the values were perturbed by +3 σ (Supplemental Fig. S1). On average, each experimental measurement impacts the values of 38 of 294 parameters in the nearest neighbor rules, though individual optical melting experiments can impact as few as one or as many as 243 nearest neighbor parameters.

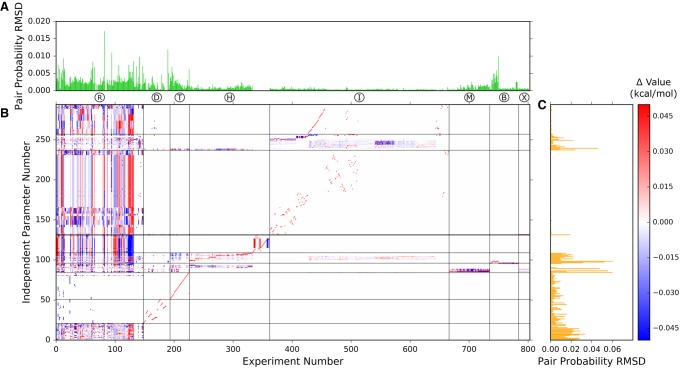
FIGURE 3.

Experiment mapping. This figure shows the effect of perturbing each single experiment based on the experimental error. (A) Mean base pair probability RMSD, averaged between ±3 σ perturbations of the experimental values. The x-axis, which is shared with subplot B, shows the experiment number. This shows how perturbing a single experiment and then propagating the perturbation through the nearest neighbor parameters values alters the predicted base-pairing probabilities. The experiment codes are shown below the x-axis and correspond to the experiment labels in Supplemental Tables 1–8. (B) The impact of changing an individual experimental value by +3 σ on the parameter values. Independent parameters are along the y-axis, organized by motif type, and the experiment number is shown on the x-axis. This shows how perturbing each experiment perturbs the nearest neighbor parameters. Note that the scale is clipped at ±0.05 kcal/mol to highlight some of the weaker interactions. A list of the independent parameters and their values is available in the Supplemental Excel file. (C) Mean base pair probability RMSD, averaged between ±3 σ perturbations of the parameter values. Parameter indices are along the y-axis, grouped by parameter type and shared with subplot B. A list of the parameters and their impact on secondary structure prediction can be found in the interactive tables in the Supplemental Files. An interactive version of this figure is available at http://rna.urmc.rochester.edu/publications.html.

Covariance of parameter values

To measure parameter covariation, 100,000 perturbed parameter sets were generated by simultaneously perturbing every experimental value within its experimental uncertainty, assuming a Gaussian distribution of errors. The perturbed experimental values were then propagated through the procedure reviewed above to generate nearest neighbor parameters with perturbed values. This method accounts for the inherent relationships between the nearest neighbor parameters. Each of these parameter sets could reasonably be the true values of the nearest neighbor parameters. A covariance matrix and Pearson correlation matrix were then calculated from the 100,000 parameter sets (Fig. 4). Average parameter values were also calculated from the set of parameter values and the observed variance in parameter values could be extracted from the diagonal of the covariance matrix.

FIGURE 4.

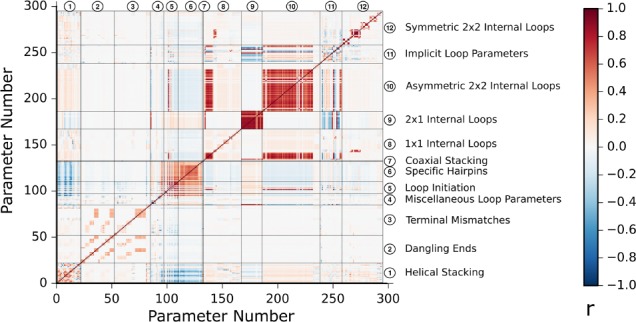
Observed Pearson correlation coefficients (r) across perturbed sets of nearest neighbor parameter values. A total of 100,000 parameter sets were randomly generated by simultaneously perturbing all experiment values within their uncertainty and then using those experiment values to derive new parameter sets. On the x- and y-axes are the independent parameter indices for the 294 independent parameters in the nearest neighbor rules (Zuber et al. 2017). The positive correlations between parameters are shown in red and negative correlations between parameters are shown in blue. An interactive version of this figure is available at http://rna.urmc.rochester.edu/publications.html.

Computing the covariance matrix with 10% of the perturbed parameter sets, i.e. 10,000 sets, resulted in a mean absolute value difference of less than 0.01 for the computed Pearson correlation value (the values range from +1.0 to −0.86) as compared to 100,000 sets, indicating a reasonable level of convergence within the 100,000 sets.

Generally, there was agreement between the parameter uncertainty values estimated by propagation of error (as done previously Zuber et al. 2017) and values determined from observed parameter standard deviations. Over 75% of the estimates agreed within 0.05 kcal/mol, compared to an average observed parameter standard deviation of 0.31 kcal/mol (Supplemental Fig. S2). Of those parameter uncertainties that differed by more than 0.05 kcal/mol, most had an observed standard deviation that was smaller in magnitude than predicted using propagation of uncertainty (52 of 65). Significantly, this means that the previous study, which used error estimates from the propagation of uncertainty, tended to overestimate rather than underestimate the uncertainty (Zuber et al. 2017).

The covariation between parameters is largely due to the use of reference duplexes. Parameters that rely on the same reference duplex will have a positive correlation with each other (shown as red cross-peaks among dangling end, terminal mismatch, and specific internal loop parameters in Fig. 4). Hairpin loop parameters use the stacking parameters to estimate the folding free energy change contribution of the hairpin stem, resulting in a negative correlation between the hairpin parameters and the stacking parameters (shown as blue cross-peaks in Fig. 4).

Structure prediction effects of simultaneous perturbation of experiment values

Using 1000 of the perturbed nearest neighbor parameter sets generated by randomly perturbing every optical experiment value, base pair probabilities and secondary structures were predicted for the set of 1650 RNA sequences. These structure prediction calculations, when compared to a calculation using the reference parameter set, provide estimates for the uncertainties in RNA secondary structure prediction due to uncertainties in the experimental optical melting data.

Additionally, 1000 perturbed parameter value sets were generated by directly perturbing the nearest neighbor parameters within their errors, randomly sampling from a Gaussian distribution. In these parameter sets, the parameters are treated as though they are independent as a contrast to calculations where the experimental values are perturbed. Base-pairing probabilities and secondary structures were predicted using these parameter sets for each of the sequences in the archive.

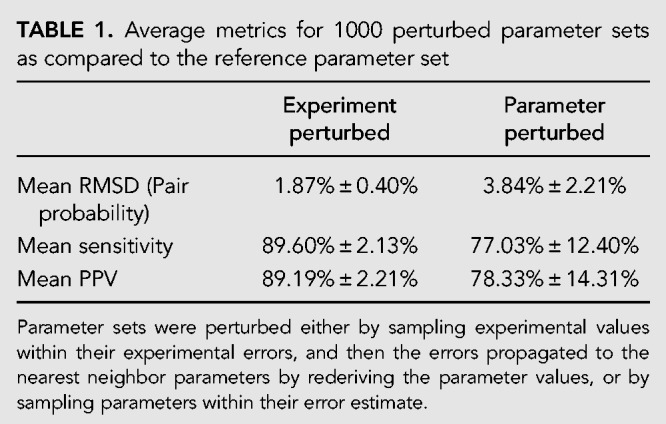
Table 1 shows the mean change in predictions using perturbed parameter sets from both of these approaches versus the reference parameter sets, characterized as RMSD of base-pairing probabilities, sensitivity, and PPV. Structure predictions using parameter sets generated by perturbing experimental values had an average agreement of ∼90% to the structures predicted using reference data tables (Score distributions are shown in Supplemental Fig. S3 and RMSD distributions are shown in Supplemental Fig. S4). Generally, perturbing parameter values has a larger impact on predicted base pair probabilities and secondary structures than perturbing experiment values. Plots of cumulative RMSD values indicate that sufficient sampling was achieved (Supplemental Fig. S5).

TABLE 1.

Average metrics for 1000 perturbed parameter sets as compared to the reference parameter set

Estimated base-pairing probabilities correlate with the frequency with which pairs are observed in perturbed parameter sets

To assess which pairs were most likely to be predicted using multiple perturbed parameter sets, the frequency at which each possible base pair appeared in secondary structures predicted using 1000 parameter sets generated from randomly perturbed experiment sets was calculated. The frequency distributions for base pair probability bins were then determined (Fig. 5). As expected, the frequency at which a base pair is observed in the secondary structures predicted using the perturbed parameter sets is directly related to the base pair probability predicted using the reference parameter set.

FIGURE 5.

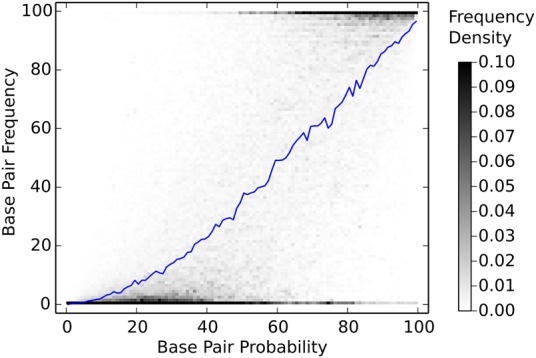
Base pair frequency is correlated with predicted base pair probability. The secondary structure for each sequence in the archive was determined using 1000 parameter sets that were generated by randomly perturbing experimental values within experimental uncertainty. The frequency of prediction was calculated for each possible base pair and plotted against the base pair probability predicted using an unperturbed (reference) parameter set. The shades of gray indicate the proportion of the base pairs in the pair probability bin that are observed with that frequency. The blue line plots the average pair frequency for that pair probability bin. Bins have a width of 1% in the probability and frequency dimensions. Note that scale has been clipped to highlight detail.

Influence of precision on the accuracy of RNA secondary structure prediction

To assess the extent to which the uncertainties in nearest neighbor parameters influence the accuracy of RNA secondary structure prediction, we calculated the mean accuracy of RNA secondary structure prediction using the 1000 perturbed parameter sets used to generate Table 1. Supplemental Figure S6 shows the distribution of sensitivity and PPV across nearest neighbor parameters sets. The reference parameter set results in a mean sensitivity and PPV of 65.5% and 58.6%, respectively. The perturbed sets have a range of sensitivity from 60.9% to 67.7%, with a mode of 66.7%. The range of PPV is from 53.9% to 60.0%, with a mode of 58.4%. One interesting observation is that the sensitivities and PPVs are positively correlated with each other (Supplemental Fig. S7), contrasting with most modifications to structure prediction algorithms, which usually involve a trade-off between sensitivity and PPV. The reference parameter set outperforms 78.2% of the perturbed parameter sets in PPV, but only 38.6% of the perturbed parameter sets in sensitivity.

Top experiments with largest impact on parameters

The effect of the perturbation of a single experimental value is not uniform across the optical melting experiments. A subset of experiments has a larger impact, and these are generally experiments that are used to determine multiple parameters. As expected, the class of experiments with the greatest impact on the RNA structure predictions are the optical melts of canonical helices because these parameters are used most frequently in structure prediction (Zuber et al. 2017). The five optical melting experiments with the greatest impact remained consistent regardless of the metric used, whether base pair probability RMSD, sensitivity, or PPV.

The experimental value with the most impact on the precision of secondary structure prediction is for a Watson–Crick duplex (experiment ID# R95 $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{U}\mathrm{GACCUC}\mathrm{A}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{ACUGGAGU}\text{-}{5}^{\mathrm{\prime }}\end{array}]$, Peritz et al. 1991). This experimental value was used to determine the stabilities of 42 internal loops for which it was the reference duplex, out of set of 304 total internal loop measurements, including 21 that were explicitly entered into the 1 × 1, 1 × 2, or 2 × 2 internal loop data tables (Peritz et al. 1991; Schroeder et al. 1996). In determining internal loop stabilities, the free energy change of the reference duplex without the loop is subtracted from the free energy change of the duplex with the internal loop, and then the stability of the base pair stack that is present in the reference and absent in the loop duplex is added. It is common practice to use the same reference duplex for more than one loop experiment. Additionally, this R95 duplex was used in four regressions, including the Watson–Crick stack parameter regression and all three internal loop regressions used to determine internal loop nearest neighbor parameters. Significantly, for one of the internal loop regression tables, this particular experimental value was used in the determination of 17 of 20 regressands (the values that are fit by the linear regression). At the same time, the free energy change of this experiment has a relatively large uncertainty of 0.58 kcal/mol (ranked 18th highest out of 802).

The second most impactful experimental value is for a duplex with a 3′ dangling nucleotide on each end (experiment ID# D42 $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{GCGGCGA}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{A}\mathrm{CGCC}\mathrm{GC}\text{-}{5}^{\mathrm{\prime }}\end{array}]$, Longfellow et al. 1990). This duplex was not used in the determination of dangling end parameters, but was used as a reference duplex for four bulge loop structures (Longfellow et al. 1990). As with internal loops, the free energy change of a bulge loop was determined by using the free energies for two duplexes, one with a bulge loop and another reference duplex without the bulge loop. The experiment D42 served as the reference for four bulge loop measurements that contributed to the values of bulge loop initiation parameters for bulge loops of sizes two (two of six total measurements) and three unpaired nucleotides (two of six total measurements) (experiment ID#’s B12-B15, Longfellow et al. 1990). Previous work had identified the uncertainty in those two parameters as having a large impact on the precision of secondary structure prediction (Zuber et al. 2017). Combined with the relatively large uncertainty for this experiment (5th highest at 0.76 kcal/mol), this explains the large impact of this experiment despite the relatively few parameters influenced by it.

The experiment with the third largest impact on secondary structure prediction is a Watson–Crick duplex (experiment ID# R109 $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{GAGGAG}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{C}\mathrm{U}\mathrm{C}\mathrm{C}\mathrm{UC}\text{-}{5}^{\mathrm{\prime }}\end{array}]$, Xia et al. 1997). This experimental value is used similarly to experiment R95, the experiment with the greatest impact. It was used as a reference helix in the determination of 52 internal loop folding free energies, including 50 that are directly included in the parameter tables for 1 × 1 and 2 × 2 internal loops used by RNAstructure. This value is used in two regressions, one used to determine base pair stacking parameters and another that determined multiple internal loop parameters. The lower impact of this experimental value compared to R95 is likely due to the smaller uncertainty associated with this experiment (0.36 kcal/mol versus 0.58 kcal/mol).

In agreement with the impact that bulge loop initiation parameters have on the precision of secondary structure prediction, many of the experiments that were used to determine those parameters were also found to be individually impactful. Of the 16 experiments used to determine the bulge loop initiation parameters for loop sizes two and three, 13 of them ranked in the top 100 experiments for impact and four in the top 20 most impactful experiments, including the experiment with the fourth greatest impact (experiment ID# B19 $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{GCGaaaGUCA}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{ACGC\_}\mathrm{\_}\mathrm{\_CAG}\text{-}{5}^{\mathrm{\prime }}\end{array}]$, Longfellow et al. 1990).

The experimental value with the fifth greatest impact is another Watson–Crick duplex (experiment ID# R162 $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{GAGCCGAC}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{CUCGGCUG}\text{-}{5}^{\mathrm{\prime }}\end{array}]$, Schroeder and Turner 2000). It was used as a reference helix for 30 internal loop energies, eight 2 × 3 internal loops and twenty-two 3 × 3 internal loops. Although these energies for these sizes of internal loops are not enumerated in the parameter tables, they affect the values of 17 nearest neighbor parameters that are determined by linear regression, including internal loop initiation energies for loops of 4, 5, and 6 unpaired nucleotides. The initiation term for loops of six unpaired nucleotides is important because the initiation free energy changes for all larger loops are extrapolated from that term using polymer theory (Jacobson and Stockmayer 1950).

Additional interesting experiments are two dangling end duplexes (experiment ID# D15 and D16, Freier et al. 1983, 1986), which were used to determine the value of the $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{CA}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{G}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ dangling end parameter. This particular dangle also appears in the possible multibranch loop configurations for 56 out of 69 measured multibranch loop systems, possibly appearing multiple times within a single system (Diamond et al. 2001; Mathews and Turner 2002). Therefore, changes to this dangling end stability affect the values of the multibranch loop parameters, which have previously been shown to have a large impact on RNA secondary structure predictions (Zuber et al. 2017), contributing to their relatively high ranking (38th and 56th when using the RMSD metric).

Some of the most impactful experiments were used to determine the values of many different nearest neighbor parameters while others only impacted one or two parameters. Eleven experiments in the top 50 most impactful experiments only affected two or fewer parameters, nine of which were those used to determine the bulge loop initiation parameters for loops of size two and three unpaired nucleotides. The two that were not involved in bulge loop parameters were a helical duplex (experiment ID# R87 $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{GAGUUGAG}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{CUCGGCUC}\text{-}{5}^{\mathrm{\prime }}\end{array}]$, He et al. 1991) and a dangling end duplex (experiment ID# D1 $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{UGCGCAA}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{AACGCGU}\text{-}{5}^{\mathrm{\prime }}\end{array}]$, Sugimoto et al. 1987). The helical duplex R87 was used in the linear regressions that determined the values of the stacking parameters with GU base pairs. The helical duplex is notable in that it is the only duplex in the regression with the $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{GG}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{UU}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ nearest neighbor. Hence, any variation in this experiment value is directly reflected in the $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{GG}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{UU}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ nearest neighbor. The dangling end duplex was used to determine the value for the parameter for a $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{AA}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{U}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ dangling end. Due to a lack of experimental data, this parameter was also used to estimate a $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{GA}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{U}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ dangling end and several terminal mismatch parameters that did not have experimental data.

Other experiments achieve high impact by affecting many parameter values. For example, the most impactful experimental value (experiment ID# R95) affected the values of 232 of 294 parameters. Of the top 50 most impactful experiments, half affected the values of 230 or more parameters.

There are some optical melting experiments that were asymmetric in their effect, where making the experimental value more stable had a different magnitude of effect than making the experimental value more unstable (Supplemental Fig. S8). The most asymmetric melting experiment was for the helical duplex R95, where increasing the folding free energy had a greater effect than decreasing the folding free energy. Increasing this experimental value decreased the folding free energy of those parameters that used this duplex as a reference duplex. This is in agreement with a previous analysis that found, in general, decreasing the folding free energy contribution of a nearest neighbor parameter generally had a greater impact than increasing them (Zuber et al. 2017). The next most asymmetric experiment was the melt of duplex B19 (a bulge loop with three unpaired nucleotides), which had a greater impact when the folding free energy was decreased. This direction of perturbation results in reducing the energetic penalty for initializing larger bulge loops, which had already been shown to have a greater impact than increasing the energetic cost of large bulge loops.

The results from this analysis are largely consistent with the sensitivity analysis that studied the impact of each of the single parameters (Zuber et al. 2017) and identified the bulge loop initiation parameters and the stacking parameters as being among the most impactful. However, this analysis also highlighted the impact that the reference duplexes have on the precision of RNA structure prediction. Many of the most impactful experiments are reference duplexes that were repeatedly used to determine multiple nearest neighbor parameters.

DISCUSSION

Parameters are not independent of each other

One assumption that has been made in previous assessments of the impact of parameter uncertainty on RNA secondary structure predictions is that each parameter is independent of all others (Layton and Bundschuh 2005; Stern and Mathews 2013; Rogers et al. 2017). However, this does not account for the correlations between parameters due to the functional forms used and the exact sequences used in the parameter derivations.

There are eight linear regressions that are used in the determination of the nearest neighbor thermodynamic parameters. Of those regressions, most have regressands that are correlated with each other because of the practice of using the same reference helices in hairpin loops, internal loops, bulge loops, and multibranch loop stems in multiple measured sequences. One consequence of the correlation of the nearest neighbor parameters is that the observed standard deviations in the values for 22 of the parameters differ by more than 0.1 kcal/mol from the standard errors returned by their linear regression fit. The GU base pair stacks demonstrate this effect, with an average 0.17 kcal/mol lower standard deviation than standard error of the regression (Supplemental Fig. S1).

Another striking example is the initiation energy of 1 × 2 internal loops, which has an observed standard deviation that is 0.44 kcal/mol larger than the standard error of the regression. This term is determined from a linear regression using 20 internal loop melting experiments. However, 17 of the 20 experiments use the same reference helix, meaning the experimental value for that helix has a strong effect on the initiation term in the regression. Indeed, the observed variance for that initiation term is closer to the variance of the reference experiment than the standard error of the regression. Here, the standard error of the regression fails to accurately describe the uncertainty in the parameter because the observations are not independent, breaking one of the underlying assumptions of linear regression.

Additionally, there are inherent correlations in the predictor variables used in the stacking regressions because any given base pair will appear in two different base pair stacks (with the exception of terminal base pairs).

Comparison of parameter perturbation versus experiment perturbation

Comparing the effects of perturbing the nearest neighbor parameters directly versus perturbing the experimental data and rederiving the parameters on RNA secondary structure prediction revealed several differences. These differences show that the nearest neighbor parameters are more robust for RNA secondary structure prediction than suggested by previous studies that treated each parameter as independent. On average, perturbing every parameter independently results in greater differences in predicted secondary structures than perturbing every experimental value and then recalculating the nearest neighbor parameters (Table 1). Additionally, the distribution of the average scores for the parameter sets differed between the two groups. Perturbing independent parameters resulted in a much greater range of observed scores, with a minimum mean similarity in predicted secondary structures of nearly 20% from those structures predicted using the unperturbed parameter set, compared to a minimum mean similarity of more than 70% using parameter sets derived from perturbed experimental values (Supplemental Fig. S3).

When perturbing experimental values, the resulting predicted secondary structures had on average an agreement of 90% with those structures predicted using reference parameter sets. Because the experimental values were perturbed using the experimental errors to determine the distribution of each experimental value, this agreement represents the estimated precision in secondary structure prediction using the nearest neighbor thermodynamic rules. Further analysis showed that the frequency at which each base pair is predicted by the ensemble of parameter sets can be reasonably approximated by the predicted probability of the base pair (Fig. 5).

Analysis of observed parameter variance

In addition to parameter correlations, average parameter values and observed parameter variance from the data set of 100,000 parameter sets derived from randomly perturbed experimental values were calculated. Surprisingly, there were 10 parameters whose mean value differed by more than 0.01 kcal/mol from the value calculated with unperturbed experimental values (Supplemental Fig. S2). Most strikingly, the multibranch loop offset parameter had an average value that was 0.12 kcal/mol more unstable than the reference value. Other notable parameters in this analysis are the $[\begin{array}{c}{5}^{\mathrm{\prime }}\text{-}\mathrm{U}\mathrm{A}\text{-}{3}^{\mathrm{\prime }}\\ 3^{\mathrm{\prime }}\text{-}\mathrm{GA}\text{-}{5}^{\mathrm{\prime }}\end{array}]$ terminal mismatch, multibranch loop strain, and GGG hairpin bonus.

There are 64 parameters whose observed variances differed by more than 0.05 kcal/mol than those predicted using propagation of errors or using standard error of the coefficient from linear regression, and 53 parameters that differ by more than 0.10 kcal/mol (Supplemental Fig. S2). There were two underlying causes for the differences in observed versus predicted variances. First, the propagation of errors method treats each input value as independent. Therefore, those nearest neighbor parameters that depended on correlated nearest neighbor parameters to determine their values inaccurately estimated their variances. The most common case is when the energy of the reference helix was calculated using the nearest neighbor rules (as in the case for one terminal mismatch and a number of internal loops). In that case, the strong negative covariance between the intermolecular initiation term and the other stacking terms resulted in a lower observed variance than predicted when treating each parameter as independent.

Another case is when an experimental value and a parameter correlated with that experiment are used in the determination of another parameter. For example, as noted above, the folding free energy change for all measured internal loops is calculated using the folding free energies of a reference duplex and a Watson–Crick stacking parameter (Wu et al. 1995). Often, the reference duplex is also used in the regression that calculated the value of the stacking parameter, resulting in a correlation between the two terms, making the error estimation by propagation of uncertainty inaccurate when assuming independent values.

Another underlying cause for a difference between calculated and observed variance is if the regressands in a linear regression are not independent of each other. The most striking example is the regression for 1 × 2 internal loop parameters, which has already been discussed. Another example is the intercept parameter for hairpin loops composed of all cytidines. The value for this parameter is determined from four hairpin melts that are added to the hairpin loop regression tables. However, all four of these hairpins share the same hairpin stem and first mismatch. As a result, the observed variance in this parameter value is approximately 0.7 kcal/mol lower than the regression calculates.

Recommendations for future optical melting experiments

One of the striking observations from this study is that the unintended correlations in the input experiments have had a greater impact on parameter estimation than previously expected. Most notably, the effect of reusing reference helices breaks the underlying assumption of linear regression that the errors in the dependent values are uncorrelated. In many cases, this results in inaccurate standard error of the coefficients.

Previously, the time and expense that was involved with synthesizing the oligonucleotides used in the optical melting experiments meant that reusing reference duplexes was a practical necessity. However, advances in oligonucleotide synthesis mean that it is now feasible and, as this study suggests, desirable to use a wider array of reference duplexes in future studies to minimize correlations.

Additionally, many parameters are being used in general situations where the experimental data is either from a single context or biased toward a single context. For example, only eight hairpin stems account for 84% of the hairpin loops used in the hairpin regression tables. Additionally, all the oligo-cytidine loops share the same hairpin stems. Another example is the optical melting experiments of multibranch loops. Those experiments were conducted by synthesizing multiple oligonucleotides that could be mixed in different combinations to produce different potential multibranch loops. One effect of this combinatorial approach is that the possible configurations of dangling ends, terminal mismatches, and coaxial stacks in the multibranch loop are severely constrained. For example, of 48 possible dangling ends, four dangling ends (a 5′ or 3′ A on a GC or CG base pair) account for 256 of 278 dangling ends in the sampled multibranch loop measurements. Possible terminal mismatch and coaxial stacking configurations are similarly undersampled. These biased input data sets are then used to generate parameters that might not accurately reflect the energies of the general ensemble of secondary structures.

Application to RNA structure prediction

Predicted secondary structures are commonly annotated by base-pairing probability or Shannon entropy, to provide information about reliability of individual base pair predictions (Huynen et al. 1997; Mathews 2004). Previously, the reliability estimations were intuitive, but were only supported empirically, where predicted base pairs with higher predicted probabilities are observed to be more accurate than predicted base pairs with lower predicted probabilities. Figure 5 shows the base pair frequency in structures predicted using the 1000 sets of equivalent nearest neighbor parameters derived from perturbing all experiments as a function of estimated base-pairing probability using the reference nearest neighbor parameter values. It shows that highly probable base pairs are also more reliably predicted across the equivalent nearest neighbor parameter sets. This supports the use of base-pairing probability as a proxy for estimating reliability.

Although the frequency at which a base pair appears in predicted secondary structures is correlated with the base pair probability calculated by the partition function, the relationship is not absolute. There are substantial populations of high probability base pairs that are infrequently predicted and low probability base pairs that are frequently predicted (Fig. 5). Algorithms that can identify base pairs whose frequencies are poorly predicted by their calculated probability and can then incorporate that information into RNA structure prediction may be able to increase the accuracy of secondary structure prediction by identifying structures that are representative of the ensemble of potential parameter sets.

Summary

This work developed several new insights into the prediction of RNA secondary structure. First, the identity of the specific optical melting experiments with the greatest impact on RNA secondary structure predictions were determined. Secondly, the correlation between nearest neighbor parameters has been empirically calculated for the first time to the authors’ knowledge. Additionally, the relationship between base pair probabilities calculated by the partition function and the frequency at which the base pair is observed in predicted secondary structures was determined. Finally, a measure for the precision of the RNA secondary structure predictions was estimated.

MATERIALS AND METHODS

Software

Calculations were performed using the RNAstructure package (Reuter and Mathews 2010), specifically a CUDA-enabled partition function (program partition-cuda) (Mathews 2004; Stern and Mathews 2013). partition-cuda predicts both the base pair probabilities using a partition function and secondary structures using the ProbKnot algorithm (Mathews 2004; Bellaousov and Mathews 2010). Exact pairing probabilities are calculated. The ProbKnot algorithm includes all base pairs (i–j) such that the highest probability pairing partner for nucleotide i is j and likewise the highest probability pairing partner of j is i (Bellaousov and Mathews 2010).

Sequence archive

There were 1650 sequences used in this analysis. The sequence families in this collection include 5S rRNA (309 sequences; 119.5 nt mean length), 16S rRNA (21 sequences, 1512.7 nt mean length), 23S rRNA (4 sequences, 2577.5 nt mean length), tRNA (484 sequences, 77.5 nt mean length), tmRNA (462 sequences, 366.0 nt mean length), Group I Introns (25 sequences 343.0 nt mean length), Group II Introns (3 sequences, 668.7 nt mean length), RNase P RNA (15 sequences, 378.7 nt mean length), SRP RNA (91 sequences, 267.9 nt mean length), mRNAs (100 sequences, 1078.3 nt mean length), telomerase RNA (37 sequences, 444.5 nt mean length), and shuffled sequences (100 sequences, 241.5 nt mean length). The structural RNA sequences were previously assembled for structure prediction accuracy benchmarks (Bellaousov and Mathews 2010). The mRNAs were from the RefSeq database and included 5′- and 3′-UTRs (Pruitt et al. 2007). The mRNAs were randomly selected from approximately 90,000 human mRNA sequences, limited to those that were less than 1.5 kb in length. The shuffled RNA sequences were randomly selected from the 1650 sequences and shuffled such that the dinucleotide frequency was maintained, using the Python module uShuffle. This module implements the Euler algorithm to randomly permute a sequence while maintaining k-let frequencies for an arbitrary k (Jiang et al. 2008).

Parameter tables

To generate thermodynamic parameter tables from sets of experimental values, a new data table format was implemented. The tables are similar in structure to those used by the software RNAstructure. However, the tables do not contain any explicit parameter values. Instead each parameter is defined in terms of experiment values and other parameter values. Additionally regression tables were created for those parameters defined through linear regression. The free energy values that are fit by the linear regression are similarly defined in terms of experiment and parameter values. For example, the values in the internal loop regression tables are defined in terms of values from internal loop optical melts, reference helix optical melts, and stacking nearest neighbor parameters.

To determine the multibranch loop parameters, functions were written to determine the optimal configuration of dangling ends, terminal mismatches, and coaxial stacks for each multibranch loop, because the optimal configuration depends on the specific parameter values for those secondary structure motifs.

With these data tables and regression tables, a set of experiment values can be used to generate new thermodynamic tables through automated linear regressions and by propagating experiment and parameter values. The uncertainty for the ΔG values for each optical melting experiment were determined by propagating the errors from the experimentally determined ΔH and ΔS values using:

$${\sigma }_{\mathrm{\Delta }\mathrm{G}}^2={\sigma }_{\mathrm{\Delta }\mathrm{H}}^2+\text{T}\times {\sigma }_{\mathrm{\Delta }\mathrm{S}}^2-2\times \text{r}\times {\sigma }_{\mathrm{\Delta }\mathrm{H}}\times \text{T}\times {\sigma }_{\mathrm{\Delta }\mathrm{S}},$$

using 0.9996 for the correlation coefficient (r) between ΔH and ΔS (Xia et al. 1998).

Covariance analysis

For each parameter set used to calculate the covariance matrix, all experimental values were simultaneously perturbed within the experimental uncertainty. An inverse cumulative distribution function was used to map a random probability between 0 and 1 to a perturbation value, in terms of σ, assuming a normal distribution. 100,000 parameter sets were calculated from randomly perturbed sets of experiment values. The covariance matrix and Pearson correlation matrix were then calculated using the NumPy Python module. Observed parameter value variances were extracted from the diagonal of the covariation matrix.

Sensitivity analysis

Three types of sensitivity analyses were performed by perturbing single experiment values, all experiment values simultaneously, or all parameter values simultaneously (Fig. 1). For the single experiment value sensitivity analysis, data tables were generated by perturbing each experiment value individually by −3 or 3σ, where σ is the experimentally determined standard error for the experiment.

For the sensitivity analysis where every experimental value is perturbed simultaneously, experimental value sets were generated by perturbing each experiment value using a percent point function (an inverse of the cumulative density function) to assign a random normally distributed z-value to each experiment value. The z-value is then multiplied by σ, where σ is the standard error for the experiment, to determine the perturbation to the experimental value. The new experimental values were then used to generate new data tables of thermodynamic parameters for use in RNAstructure.

For the parameter value sensitivity analysis, the values of the 294 independent nearest neighbor parameters (Mathews et al. 2004; Zuber et al. 2017) were directly perturbed. New parameter sets were generated by assigning a random normally-distributed z-value to each independent parameter value. The z-value is then multiplied by σ, where σ is the standard error for the parameter, determined either by the linear regression or by the propagation of uncertainty through the equations used to calculate the parameter values. The new independent parameter values were then used to populate the entirety of the data tables.

For each sensitivity analysis, the new data tables were used to calculate the partition function for an archive of 1650 sequences using the program partition-cuda, resulting in base-pairing probabilities and secondary structures calculated using the ProbKnot algorithm. These base pair probabilities were compared to those predicted using reference data tables to generate pair probability root mean squared deviations (RMSDs). The secondary structures were compared to those predicted using reference data tables to measure the similarity of the secondary structures, reflected in the metrics sensitivity and PPV.

The root mean squared deviations (RMSDs) were calculated using:

$$\text{RMSD}=\sqrt{\frac{{\sum }_{\mathrm{All}\mathrm{BP}}{({\text{P}}_{\mathrm{N}}-{\text{P}}_{\mathrm{R}})}^2}{{\text{N}}_{\mathrm{BP}}}},$$

where P_N is the probability of a base pair calculated using the perturbed data tables, P_R is the probability of a base pair calculated using the reference data tables and N_BP refers to the number of base pairs. Additionally, a corrected RMSD (cRMSD), which corrects for the effect of sequence length on base pair RMSD was calculated for each sequence using the following equation (Zuber et al. 2017):

$$\text{cRMSD}=\sqrt{\frac{{\sum }_{\mathrm{All}\mathrm{BP}}{({\text{P}}_{\mathrm{N}}-{\text{P}}_{\mathrm{R}})}^2}{\sqrt{{\text{N}}_{\mathrm{BP}}}}}.$$

This equation corrects for the fact that the number of possible base pairs scales with the square of the number of bases in the sequence but the number of probable base pairs scales linearly with the sequence length.

To compare predicted secondary structures, sensitivity defect and PPV defect are calculated using the following equations:

$$\mathrm{Sensitivity}=100\mathrm{\%}\times \left(\frac{{\mathrm{N}}_{\mathrm{BP}\mathrm{with}\mathrm{both}\mathrm{tables}}}{{\mathrm{N}}_{\mathrm{BP}\mathrm{with}\mathrm{reference}\mathrm{tables}}}\right),$$

$$\mathrm{PPV}=100\mathrm{\%}\times \left(\frac{{\mathrm{N}}_{\mathrm{BP}\mathrm{with}\mathrm{both}\mathrm{tables}}}{{\mathrm{N}}_{\mathrm{BP}\mathrm{with}\mathrm{perturbed}\mathrm{tables}}}\right).$$

When scoring, a base pair between nucleotides i and j in one structure was considered to be present in the other structure if one of the following pairs exist: i − j, (i ± 1)−j, i−(j ± 1). This is done to reflect the perturbations to the secondary structure due to thermal fluctuations as well as the difficulty in discriminating between these base pairs via comparative sequence analysis, used to determine the set of known structures (Mathews et al. 1999).

When calculating the accuracy benchmarks, average sensitivity and PPV were calculated for each RNA family, where the predicted secondary structures are compared against known secondary structures. The scores for each family were then averaged to generate the scores for the parameter set.

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.