Chained Regularization for Identifying Brain Patterns Specific to HIV Infection

Abstract

Human Immunodeficiency Virus (HIV) infection continues to have major adverse public health and clinical consequences despite the effectiveness of combination Antiretroviral Therapy (cART) in reducing HIV viral load and improving immune function. As successfully treated individuals with HIV infection age, their cognition declines faster than reported for normal aging. This phenomenon underlines the importance of improving long-term care, which requires better understanding of the impact of HIV on the brain. In this paper, automated identification of patients and brain regions affected by HIV infection are modeled as a classification problem, whose solution is determined in two steps within our proposed Chained-Regularization framework. The first step focuses on selecting the HIV pattern (i.e., the most informative constellation of brain region measurements for distinguishing HIV infected subjects from healthy controls) by constraining the search for the optimal parameter setting of the classifier via group sparsity (ℓ_2,1-norm). The second step improves classification accuracy by constraining the parameterization with respect to the selected measurements and the Euclidean regularization (ℓ₂-norm). When applied to the cortical and subcortical structural Magnetic Resonance Images (MRI) measurements of 65 controls and 65 HIV infected individuals, this approach is more accurate in distinguishing the two cohorts than more common models. Finally, the brain regions of the identified HIV pattern concur with the HIV literature that uses traditional group analysis models.

1. Introduction

Despite the success of highly active antiretroviral therapy (HAART) and combination antiretroviral therapy (cART) in extending longevity of individuals infected with the Human Immunodeficiency Virus (HIV), neurocognitive impairments still commonly occur [1, 2, 3]. Structural Magnetic Resonance Imaging (MRI) has often been used to determine the neural correlates of cognitive and motor deficits in HIV infection, indicating, for example, specific relationships between regional brain volume deficits [4, 5], memory compromise [6], and accelerated brain aging in HIV infected adults [7]. Neurocognitive and motor impairments in HIV infection, however, are similar to those reported in other age-related diagnoses [8]. To improve diagnostic specificity of MRI in HIV, this manuscript proposes a novel machine learning method and applies it to the morphometric measurements extracted from structural MRI scans collected from HIV infected and healthy control (CTRL) participants.

Conventional HIV MRI studies typically test for group differences (with respect to the CTRL cohort) by separately analyzing each image measurement for the impact of HIV [4, 9, 6, 10, 2, 1]. Separate analysis of measurements may lead to contradicting or inconclusive findings [11]. By contrast, our proposed analysis is a type of machine learning framework that considers all image measurements together to identify the subset of measurements (called patterns) specific to HIV and then relates the significance of the pattern to its accuracy in distinguishing individuals with HIV from CTRLs. A popular approach for identifying patterns uses sparse classifiers [12, 13, 14, 15, 16, 8], which assume that only a few measurements are informative for distinguishing cohorts. After identifying a pattern, the corresponding measures are often applied to a second (non-sparse) approach, which focuses only on improving classification accuracy [17, 18, 19, 20, 21, 22]. This two-step regularization procedure assumes that measurements selected by the sparse classifier define the unique, optimal pattern for distinguishing the two cohorts [23, 24, 17, 25]. This assumption, however, is generally not true because the redundancy in information across image measurements allows for multiple solutions [19]. As the two steps are based on different classification approaches, the pattern identified by the sparse classifier of the first step are generally not optimal for the non-sparse approach of the second step.

Herein, we propose an approach (denoted as Chained-Regularization) that uses the same classifier first to identify a pattern and then, using the pattern, to distinguish individuals; however, different constraints guide the parameterization of the classifier in each step. Our proposed algorithm models the selection of the most informative image measurements in the first step by confining parameterization of the classifier through group sparsity (ℓ_2,1-norm) regularization [26, 8]. Group sparsity extends the concept of the ℓ₁-norm [27, 28, 16] of identifying a few informative measurements for combining measurements into groups and then identifying a small number of groups [27]. The grouping can be used for explicit modeling of relationships between measurements [29]. In this work, each measurement from the regions of interest (ROIs) is grouped with its counterpart in the other brain hemisphere given our assumption that HIV infection affects the brain bilaterally. In the second step of Chained-Regularization, the classifier is trained on just the selected individual measurements with the search for the optimal parameter setting being constrained via Euclidean (ℓ₂-norm) regularization. The logic of this approach is that the ℓ_2,1 regularization generally improves the accuracy of classifiers in the presence of a large number of uninformative or redundant image measurements (as it is often the case of neuroimaging studies), while the ℓ₂ regularization improves the accuracy of classifiers in the event that all provided image measurements are informative [17, 18]. Our chained-regularization scheme, which uses a sequential dependency approach to identify a pattern to be applied for determining group membership of individuals, is different from chain-regularization [30], a concept used in physics to describe group of objects interacting with each other in a chain.

We implement Chained-Regularization within a multiple kernel learning (MKL) framework [31, 18]. MKL is based on the assumption that samples (i.e., individual participants) that are similar to each other should be assigned to the same cohort (e.g., HIV). Similarity between two samples is measured through a pairwise comparison of the corresponding image measurements. This comparison is defined by a set of metrics (i.e., linear and nonlinear kernel functions), each capturing a unique characteristic across image measurements. The MKL algorithm now determines the combination of metrics and image measurements [18] that lead to the highest classification accuracy (see Figure 1). It thus omits the simplifying assumption of most other classifiers that the discriminating characteristics of all image measurements are best captured by a single metric (as in [18, 32, 33, 31, 34]).

Figure 1:

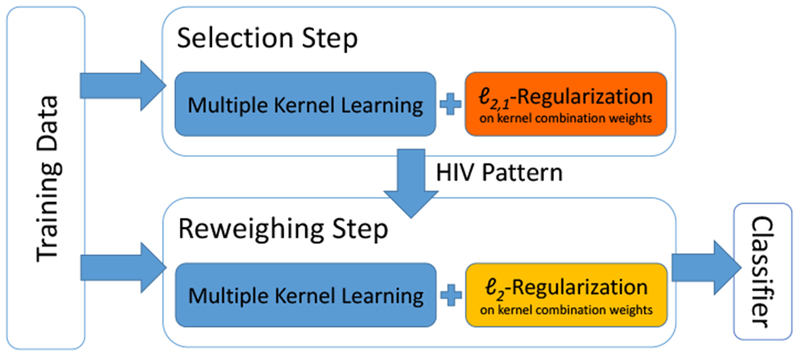
Training of the Chained-Regularization approach: The first step (top, denoted as Selection Step) selects the image measurements informative for distinguishing HIV from controls, while the second step (bottom, denoted as Reweighing Step) focuses on improving the accuracy by reweighing the selected measures for classifying the samples. Note, both steps are based on the same classifier but differ in regularizing (or constraining) its parameterization.

In summary, our analysis makes two novel contributions: (1) We propose Chained-Regularization within the MKL framework, which, in our experiments, is significantly more accurate than single-step and other two-step approaches. (2) To the best of our knowledge, this is the first study to examine both linear and non-linear supervised learning approaches to identify patterns that discriminate HIV infected from healthy control brains.

The rest of the paper is organized as follows: Section 2 introduces the materials (the data set), preprocessing, the proposed chained regularization and the experimental setup. Appendix A provides additional technical details of the proposed method. Section 3 compares our approach to other implementations on the HIV data set and reports on its identified pattern specific to HIV. Section 4 provides an in depth discussion about the findings of the previous section and their relevance with respect to the HIV literature. The paper concludes with Section 5.

2. Materials and Methods

2.1. Participant Information

Data used in this study are from 65 HIV infected individuals and 245 CTRL subjects. For classification, we match 65 CTRLs to the 65 HIV cohort. Specifically, for each HIV subject, one subject is selected from the CTRL cohort, such that they have the same sex and a minimal difference in their ages. We refer to the matched samples as ‘matched CTRL group’. The remaining 180 CTRL subjects, referred to as Confounding Factors CTRL group (CF CTRL group), are used for analysis of the confounding factors and minimizing their effects. Table 1 shows the demographic information of participants in all groups, and Figure 2 plots their age distributions. All 310 participants are tested for HIV, viral load, and CD4 T-cell count. HIV infected individuals had a CD4 count $>100\frac{\text{cells}}{\mu L}$ and a Karnofsky score > 70 [35]. Data from these subjects were used in previous studies [10, 4, 9].

Table 1:

Demographic information (‘svol’ = supratentorial volume).

	Total	sex		Age (years)	svol(×106)
		F	M
HIV	65	20	45	51.81 ± 8.44	1.26 ± 0.12
Matched CTRL	65	20	45	51.76 ± 8.44	1.26 ± 0.13
CF CTRL	180	102	78	43.36 ± 18.92	1.26 ± 0.13

Figure 2:

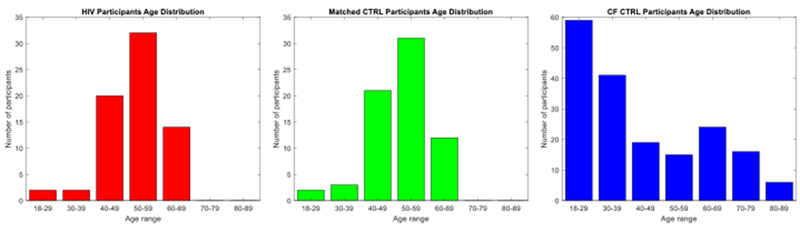
Age distribution of the participants: HIV (left), Matched CTRL (middle), and CF CTRL (right).

2.2. Structural MRI Data Acquisition

Imaging data are acquired from each participant on a 3T General Electric (GE) SIGNA HDx system using an 8-channel Array Spatial Sensitivity Encoding Technique (ASSET) coil for parallel and accelerated imaging. Furthermore, Inversion Recovery-SPoiled Gradient Recalled (IR-SPGR) echo sequence (TR=7.068ms, TI=300ms, TE = 2.208ms, flip angle=15°, matrix=256 × 256, slice dimensions=1.2 × 0.9375 × 0.9375mm, 124 slices) are collected in the sagittal plane.

2.3. MRI Data Preprocessing and Feature Extraction

Preprocessing of the T1-weighted (T1w) MR images involves noise removal [36], computing signal-to-noise ratio (SNR) [37] and correcting field inhomogeneity via N4ITK (Version 2.1.0) [38]. Next, the brain mask is segmented by majority voting [39] across maps extracted by FSL BET (Version 5.0.6) [40], AFNI 3dSkullStrip (Version AFNI_011_12_21_1014) [41], FreeSurfer mri-gcut (Version 5.3.0) [42], and the Robust Brain Extraction (ROBEX) method (Version 1.2) [43], applied to bias and non-bias corrected T1w images. The refined mask is then used to repeat image inhomogeneity correction.

We further apply the cross-sectional approach of FreeSurfer (Version 5.3.0) [44, 45] to the skull-stripped T1w MRI of each subject in order to measure the mean curvature (MeanCurv), surface area (SurfArea), gray matter volume (GrayVol), and average thickness (ThickAvg) of 34 bilateral cortical Regions Of Interest (ROIs) [2 hemispheres × 4 measurement types × 34 ROIs = 272], the volumes of 8 bilateral sub-cortical ROIs (i.e., thalamus, caudate, putamen, pallidum, hippocampus, amygdala, accumbens, cerebellar cortex) [2 × 8 = 16], the volumes of 5 subregions of the corpus callosum (posterior, mid-posterior, central, mid-central and anterior), and the combined volume of all white matter hypointensities [5 + 1 = 6]. White matter hypointensities are defined according to Freesurfer as voxels inside the white matter with signal intensities lower than a threshold level [46]. Finally, volumes of the left and right lateral and third ventricles [2 × 2 = 4] are measured by non-rigidly aligning the SRI24 atlas [47] to the T1w MRI of the subject via ANTS (Version: 2.1.0) [48]. This procedure thus extracts 298 measures from each brain MRI.

For the entire matched data set, each of these 298 brain measures are normalized using their z-scores [49]. To avoid using any data for testing the model, the z-scores are parameterized by computing the mean and standard deviations of measurements across the CF CTRL cohort. Based on this distribution, the z-scores are then computed for each subject of the matched CTRL and HIV groups. Furthermore, the segmentations are used to compute the supratentorial volume (svol) for each subject. As in [50], svol is used to approximate brain size.

2.4. Confounding Factors

For each of the 298 measures, we compute the Pearson correlation between the corresponding z-scores of the 180 subjects of the CF CTRL group and the factors, i.e., age, sex, svol, race, and SNR. Some of the measures are significantly correlated with age, sex, and svol (p-value < 0.05). For each measurement, a general linear model (GLM) [51] is parameterized with respect to corresponding z-scores to omit the effect of the confounding factors. Specifically, for each image measure m ∈ {1,…, 298}, the following GLM is fit across the subjects i ∈ {1,…, 180} of the CF CTRL group with the corresponding z-score $v_i^m$ as the observation and age ($f_i^{\text{age}}$), sex ($f_i^{\text{age}}$), and svol ($f_i^{\text{svol}}$) as the confounding factors:

$$v_i^m~{\beta }_{m,0}+{\beta }_{m,1}{f}_i^{\text{age}}+{\beta }_{m,2}{f}_i^{\text{sex}}+{\beta }_{m,3}{f}_i^{\text{svol}}.$$ (1)

After obtaining the optimal regression coefficients (${\widehat{\beta }}_{m,0},{\widehat{\beta }}_{m,1},{\widehat{\beta }}_{m,2},{\widehat{\beta }}_{m,3}$) across all subjects, the model is applied to the HIV and matched CTRL dataset. Specifically, the residual explained by each subject’s individual confounding factors multiplied by the regression coefficients is removed from the initial observation, i.e., the residual scores $x_i^m$ defined as

$$x_i^m≔v_i^m-({\widehat{\beta }}_{m,0}+{\widehat{\beta }}_{m,1}{f}_i^{\text{age}}+{\widehat{\beta }}_{m,2}{f}_i^{\text{sex}}+{\widehat{\beta }}_{m,3}{f}_i^{\text{svol}}).$$ (2)

2.5. Pattern Extraction and Classification

In this section, the proposed Chained-Regularization technique is outlined. For the interested reader, Appendix A derives the Chained-Regularization approach in detail. Based on the residual scores of the matched data set, the accuracy of the proposed Chained-Regularization framework (denoted as ℓ_2,1-ℓ₂-reg; see also Figure 1) in correctly labeling HIV infected and health control subjects is measured via 10-fold (nested) cross-validation (see Figure 4). With respect to each (testing) fold, the training of ℓ_2,1-ℓ₂-reg on the remaining data starts with the Selection Step, i.e., extract the informative pattern for classifying samples. The training then proceeds with the Reweighing Step, i.e., finding the optimal parameterization of the classifier based on that pattern. On the testing fold, we record the labeling of subjects according to the trained ℓ_2,1-ℓ₂-reg. This procedure between training and testing is repeated until the labeling across all 10 testing folds are generated. Based on those labelings, we compute the Accuracy of prediction (i.e., the percentage of the testing subjects that are classified correctly into their respective classes), specificity (SPE), sensitivity (SEN) and area under the receiver operating characteristic (ROC) curve (AUC). Note, our MKL-based mapping function outputs a continuous value (more details in Appendix A) from which a binary class label is derived via thresholding. By changing the threshold, we can create the ROC curve and hence calculate the AUCs. In addition, we apply the Fisher’s exact test [52] to ensure that implementation is significantly better than chance (p-value < 0.01). The remainder of this section provides further details about training of ℓ_2,1-ℓ₂-reg.

Figure 4:

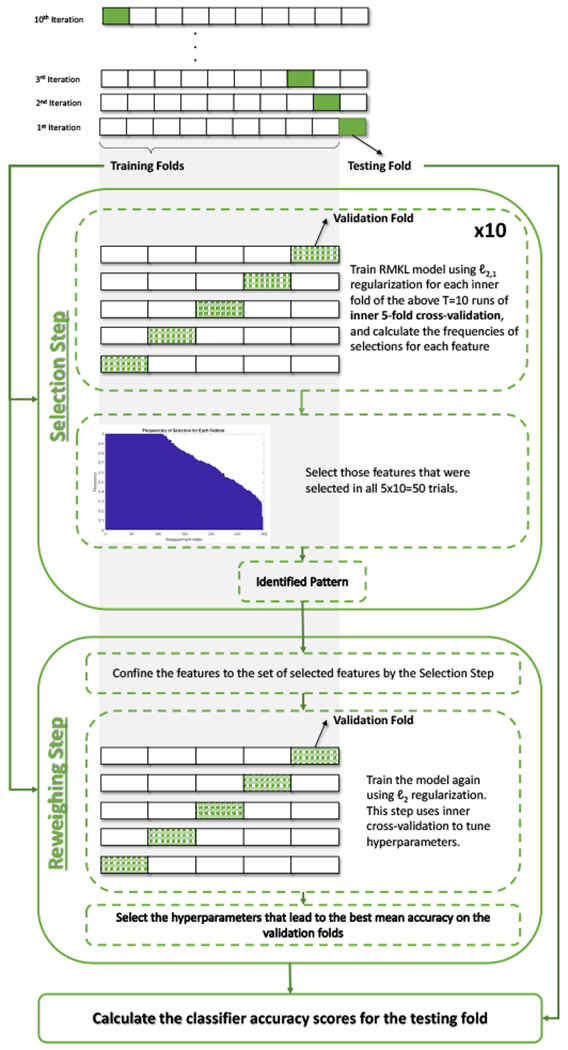
Illustration of the nested cross-validation strategy used in Chained-Regularization (ℓ_2,1-ℓ₂-reg). On the i^th training iteration, the Selection Step selects the most informative measurements(i.e., the pattern) using ℓ_2,1-regularization, and then the Reweighing Step uses that pattern to build the classifier with ℓ₂-regularization. In the second step, inner cross-validation is used to choose the model hyperparameters. Next, the built classifier is used to calculate the accuracy scores on the corresponding testing fold (say Acci). The average accuracy for all folds is then reported (i.e., $\mathrm{Acc}=\frac{1}{10}{\sum }_{i=1}^{10}{\mathrm{Acc}}_i$).

Inspired by [18, 13], the HIV specific pattern, identified in the Selection Step during training, is defined by the optimal ‘weight’ vector specifying a linear multivariate model defined by image measurements that correctly label subjects according to the MKL model. MKL classifies samples by learning the optimal pairings between kernels and image measurements. Finding the optimal pairing is described as a minimization problem with respect to a weight vector, sparsity of which specifies the importance of pairings for class separation. We use 7 different kernels to build our multiple kernel learning model, including 3 kernel types [linear, histogram intersection kernel (HIK), and redial basis function kernel (RBF)] with different settings of their hyperparameters. These 7 kernels are defined in detail in Appendix A. Specific to our implementation, the optimal weight vector minimizes a cost function measuring classification accuracy and ‘group-sparsity’ associated with those weights. As also shown in Figure 3, group-sparsity is measured by first transforming the weight vector into a matrix so that each column represents a group and each group combines the weights associated with measurements from the same type and region (regardless of hemisphere). ℓ_2,1-norm is then applied to the matrix, i.e., the ℓ₂-norm is applied to each column resulting in the column being reduced to a scalar value and then the ℓ₁-norm is applied to the vector of those scalar values resulting in the entire matrix being reduced to a scalar value. Note, this computation generally penalizes weight vectors that select a larger number of groups, i.e., are not sparse on a group level.

Figure 3:

Illustration of feature grouping for group sparsity. (a) Regular sparsity (ℓ₁-norm) operates on a vector that concatenates the measurements from the left and right hemispheres. (b) Group sparsity operates on the matrix formed by putting the features from the same ROIs of the left and right hemispheres in its columns.

The optimal ‘weight’ vector now depends on the weight C of the term measuring classification accuracy and the weight λ of the term measuring group sparsity within the MKL cost function (refer to Appendix A for more details). As in [13, 53], the search space for those two hyperparameters is {10⁻³, 10⁻², 10⁻¹, 1, 10¹, 10², 10³}. To identify the best hyperparameter setting, we perform 5-fold inner cross-validation 10 times. Each time, we randomly divide the training data into 5 validation folds. For each validation fold, we first train our implementation of MKL with respect to a specific hyperparameter setting on the remaining training data. For that setting, we then record the accuracy of the implementation on the validation fold and the identified pattern, i.e., regional scores associated with non-zero weights. We repeat this process for each hyperparameter setting and then only keep the pattern that is associated with the highest validation accuracy across all parameter settings. Repeating this process for the remaining 4 validation folds and 9 more inner-cross validations then results in a total of 50 ‘trials’. The Selection Step then defines the HIV specific pattern as the set of residual scores that were part of all 50 trial patterns. This multi-trial selection process is considered more robust than only relying on single run of a sparse classifier [18, 23].

The Reweighing Step focuses on improving MKL’s classification accuracy when only relying on the residual scores of the HIV specific pattern. As training of the classifier is now confined to only informative image measurements, classification accuracy is generally improved by replacing the ℓ_2,1-norm with the ℓ₂-norm in the cost function of the MKL implementation. The Reweighing Step then performs parameter exploration of this MKL implementation via 5 fold inner cross-validation, i.e., it records the hyperparameter setting that leads to the highest average validation accuracy across the 5 inner folds. The training of ℓ_2,1-ℓ₂-reg is completed by training MKL with the selected hyperparameter setting on the complete training data. Note, choosing the optimal hyperparameters without including any data from the testing fold yields more reliable and reproducible results [54] than tuning the hyperparameters without any inner validation folds.

The group sparsity (in the Selection Step) guarantees ‘bilateral selection’ of each type of ROI-specific measurement (i.e., measurements on both left and right hemispheres are selected or neither one of them). The Reweighing Step then builds the final classifier relying on all selected individual measurements and the ℓ₂-norm, which generates non-sparse classifiers that generalize well to unseen testing data [17, 55]. For the interested reader, Appendix A derives the Chained-Regularization approach in detail. Specifically, we first generalize the MKL approach of [13], which was specific to ℓ₁-norm regularization, to regularizers that are convex and differentiable in ${ℝ}_{\ge 0}$. We then embed that approach into the proposed Chained-Regularization framework.

2.6. Alternative Implementations

To motivate the specific implementation of the Chained-Regularization approach, the nested cross-validation of Chained-Regularization is repeated with different combinations of regularizers, i.e., using ℓ₁-norm in the Selection Step and ℓ₂-norm in the Reweighing Step (denoted by ℓ₁-ℓ₂-reg), using ℓ_2,1-norm in the Selection Step and ℓ₁-norm in the Reweighing Step (denoted by ℓ_2,1-ℓ₁-reg), and using ℓ₂-norm in both steps (denoted by ℓ₂-ℓ₂-reg). In addition, the comparison includes an implicit model for the grouping of the ROI measurements by computing the average value of each group and then using the ℓ₁-norm in the Selection Step and ℓ₂-norm in the Reweighing Step (denoted as Avg ℓ₁-ℓ₂-reg). To demonstrate the advantages of Chained-Regularization, only the MKL approach is cross-validated, i.e., omitting the Reweighing Step as well as the repeated selection procedure. The corresponding Single-Step Regularization approaches are denoted as ℓ₁-reg, ℓ₂-reg and ℓ_2,1-reg. Note, we omitted certain alternative implementations from the experimental setup to keep the comparison concise and informative. For example, one could implement Chained-Regularization using the ℓ₁-norm in both steps. While this implementation produces similar accuracy score as ℓ_2,1-ℓ₁-reg, the approach most likely underestimates the impact of the disease on a small number of brain regions; a risk generally associated with sparse classifiers based on the ℓ₁-norm [56]. Furthermore, note that training a MKL without regularization, constraint or a penalty term (in the reweighing step) is not feasible as the underlying minimization problem is then underdetermined [18], i.e., results in an unstable classifier.

In addition to variations of Chained-Regularization, the comparison includes conventional support vector machine (SVM) classifiers widely used in neuroimaging applications to highlight the benefits of Chained-Regularization in the context of MKL. The class of alternative SVM classifiers include linear SVM, SparseSVM [57], and sparse feature selection [20] followed by a linear SVM (SFS+SVM). In addition, t-test [20], elastic-net [24], and the mutual information based feature selector minimum-redundancy maximum-relevancy (mRMR) [58] are coupled with a linear SVM classifier to further evaluate the performance of the proposed feature selection technique.

For each implementation, the accuracy scores of the previous section are computed. We also apply the DeLong test [59] to mark implementations that are significantly worse (p-value < 0.01) than the proposed ℓ_2,1-ℓ₁-reg.

3. Results

3.1. Comparison

Classification results of the proposed and alternative methods are summarized in Table 2. The proposed Chained-Regularization technique (ℓ_2,1-ℓ₂-reg) achieves the highest Accuracy (82.3%), SEN (0.84), and AUC (0.87). The SPE (0.82) is equivalent to ‘ℓ₁-ℓ₂-reg’ and ‘Avg ℓ₁-ℓ₂-reg’. All other implementations of the comparison (including ℓ₂-ℓ₂-reg and ℓ_2,1-ℓ₁-reg) not only received lower scores, but were also significantly worse than the proposed chained ℓ_2,1-ℓ₂ regularization. The single step regularizers received higher scores in all four performance measures than the conventional approaches with the exception of SFS+SVM. The performance scores of SFS+SVM (Accuracy: 0.69%, SPE: 0.69, SEN: 0.70 and AUC: 0.73) were higher than those of ℓ₂-reg and ℓ_2,1-reg but lower than ℓ₁-reg (Accuracy: 70.3%, SPE: 0.70, SEN: 0.70, AUC: 0.73), the single step regularization with the highest Accuracy and AUC. Finally, only conventional methods (i.e., t-test+SVM, mRMR+SVM, SparseSVM and SVM) produced classification results that were not significantly better than chance.

Table 2:

Classification results of different approaches summarized by Accuracy, specificity (SPE), sensitivity (SEN) and area under the ROC curve (AUC). The best score in each category is in bold. Methods are marked with †, if they were significantly worse than the proposed approach (p < 0.01 according to Delong’s Test [59]). Methods marked with ‡ are significantly better than chance (p < 0.01 according to the Fisher exact test [52]).

	Method	Accuracy (%)	SPE	SEN	AUC
Proposed	ℓ2,1-ℓ2-reg‡	82.3	0.82	0.84	0.87
Chained (Baseline)	ℓ1-ℓ2-reg‡	81.9	0.82	0.79	0.86
	Avg ℓ1-ℓ2-reg‡	79.7	0.82	0.77	0.85
	ℓ2-ℓ2-reg†‡	73.1	0.74	0.73	0.76
	ℓ2,1ℓ1-reg†‡	72.5	0.72	0.73	0.76
Single Step Regularization	ℓ1-reg†‡	70.3	0.70	0.70	0.75
	ℓ2,1-reg†‡	69.7	0.70	0.68	0.73
	ℓ2-reg†‡	68.7	0.64	0.70	0.71
Conventional Methods	SFS [20]+SVM†‡	69.9	0.69	0.70	0.73
	elastic-net [24]+SVM†‡	65.1	0.64	0.64	0.69
	t-test [20]+SVM†	59.1	0.61	0.56	0.65
	mRMR [58]+SVM†	59.6	0.56	0.61	0.64
	SparseSVM [57]†	57.9	0.55	0.60	0.64
	SVM†	56.7	0.57	0.56	0.60

3.2. The HIV Pattern

For ℓ_2,1-ℓ₂-reg (the most accurate approach in the comparison), Figure 5 shows the frequencies (normalized in the range [1]) of the 298 image measurements selected by the Selection Step across the 10 runs of cross-validation on the whole matched data set considered for identifying the pattern. This figure shows the measurements with a selection frequency of 1 (selected all times), i.e., those that are actually used in the Reweighing Step of our method, with colors based on their measurement types. Note, the ordering of measurement types is arbitrary. We refer to this set of measurements as the HIV pattern. The remaining measurements are displayed in gray regardless of the type of measurement. Approximately 39% of all image measurements are selected in all runs. These measures define the HIV pattern.

Figure 5:

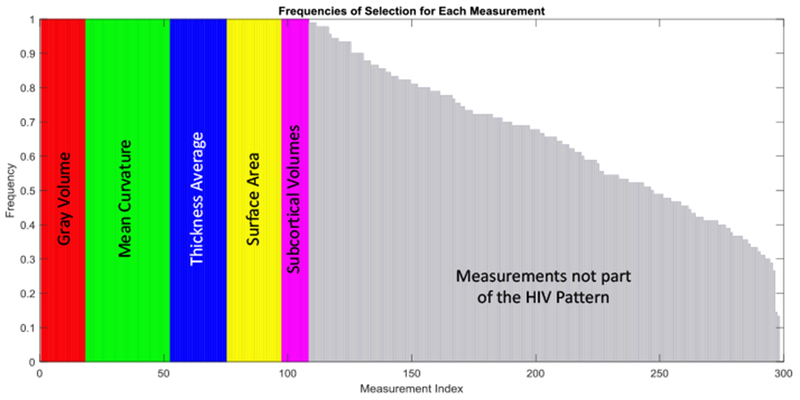
Frequencies of selection for each of the 298 features. Colors encode measurement types. The measurements in gray are those ignored in the Reweighing step.

To analyze the significance of each type of measurement (Mean Curvature, Surface Area, Gray Matter Volume, Average Thickness, and Subcortical ROI Volumes), we first create a baseline for comparison by performing 10-fold cross validation just on the Reweighing Step with the scores being confined to the HIV pattern, recording the testing accuracy for each fold, and then computing the mean and standard deviation in the accuracy score across all 10 folds. The results in an accuracy of 87.69% ± 1.69 (mean ± standard deviation), which we refer to as ‘All Measurements’ in Table 3. For each measurement type, we then omit the corresponding measures from the data, perform 10-fold cross-validation of the Selection Step on this subset of data, record the pattern, and repeat the previous cross-validation of the Reweighing Step with respect to that pattern.

Table 3:

The mean±standard of the classification Accuracy and area under the ROC curve (AUC) of the proposed method with different subsets of the 298 measurements. Entries marked with f are significantly worse (p < 0.01; Delong’s Test) compared to ‘All Measurements’.

Method	Accuracy (%)	AUC
All Measurements	87.7 ± 1.69	0.87 ± 0.03
No Average Thickness	79.6 ± 1.96	0.78 ± 0.07
No Mean Curvature†	77.2 ± 1.92	0.84 ± 0.05
No Surface Area†	73.9 ± 1.77	0.79 ± 0.03
No Gray Matter Volume†	66.8 ± 1.49	0.74 ± 0.06
Only Cortical Measurements†	69.2 ± 2.10	0.75 ± 0.02

With respect to using subsets of the measurements, omitting Average Thickness from the data resulted in the pattern with the highest mean accuracy score (79.6% ± 1.96). Omitting Mean Curvature, Surface Area, or Volume from the HIV pattern resulted in accuracy scores that were significantly lower than those produced by All Measurements (or the HIV pattern). The same was true when confining classification to cortical gray matter volumes.

Beyond the type of measurements, Table 4 lists and Figure 6 visualizes the selected cortical regions. 35% of all cortical measurements are selected by our method. Furthermore, a total of 52% of the subcortical measurements are selected. Figure 7 shows the selected subcortical regions (i.e., hippocampus, amygdala, accumbens and cerebellar cortex) along with the white matter structures (i.e., corpus callosum posterior and mid-posterior) selected by our approach. In addition to these ROIs, hypointensity lesion volumes are also selected. Note, as also argued in [8], the coefficients computed by sparse classifiers simply parameterize a linear multivariate model (explained in detail in Appendix A), which predicts the class labels. Thus, coefficients are informative with respect to feature selection but are not good indicators for differentiating the importance among the selected features with respect to identifying cohorts.

Table 4:

Cortical surface ROIs and their measurement types selected by our method.

ROI	GrayVol	MeanCurv	ThickAvg	SurfArea
Bankssts		✓	✓
Caudalanteriorcingulate	✓	✓	✓
Caudalmiddlefrontal		✓	✓	✓
Cuneus
Entorhinal	✓
Fusiform	✓	✓	✓
Inferiorparietal	✓
Inferiortemporal		✓
Isthmuscingulate		✓	✓	✓
Lateraloccipital	✓
Lateralorbitofrontal			✓	✓
Lingual
Medialorbitofrontal
Middletemporal		✓		✓
Parahippocampal	✓	✓		✓
Paracentral	✓	✓	✓	✓
Parsopercularis			✓	✓
Parsorbitalis			✓
Parstriangularis		✓
Pericalcarine		✓		✓
Postcentral	✓
Posteriorcingulate		✓	✓	✓
Precentral	✓	✓		✓
Precuneus		✓	✓
Rostralanteriorcingulate		✓		✓
Rostralmiddlefrontal	✓	✓	✓
Superiorfrontal	✓	✓
Superiorparietal		✓	✓	✓
Superiortemporal		✓
Supramarginal
Frontalpole		✓
Temporalpole				✓
Transversetemporal	✓	✓		✓
Insula	✓	✓	✓

Figure 6:

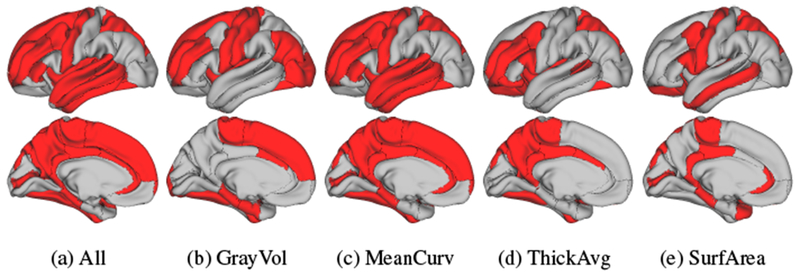
cortical ROIs selected by our proposed approach. (b-e) show the selected ROIs for each measurement type separately, while (a) visualizes the union of the four types.

Figure 7:

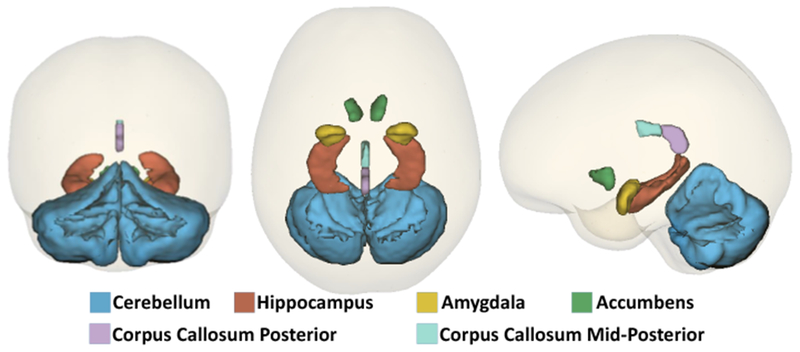
Subcortical ROIs and white matter structures selected by our method.

The comparison of different approaches (see Table 2) revealed that our Chained-Regularization approach was significantly better than confining analysis to any one single step (i.e., ℓ_2,1-reg or ℓ₂-reg). Our approach was also significantly better than alternative implementations of the Chained-Regularization that used the same type of regularizer for both steps (i.e., sparse regularizer (ℓ_2,1-ℓ₁-reg) or Euclidean regularizer (ℓ₂-ℓ₂-reg)). This finding underlines the importance of selecting two regularizers that complement each other for our approach, i.e., the first regularizer models the selection of the measurements, while the second one reweighs the influence of the selected measurements in order to improve the classification accuracy.

Choosing alternative complementary regularizers by replacing the ℓ_2,1-norm in the Selection Step with other sparse regularizers (while leaving the Reweighing Step unchanged) results in non-significantly lower accuracy scores compared with the proposed approach. Unlike other implementations of the Chained-Regularization, our proposed ℓ_2,1 regularizer was the only one that explicitly modeled the bilateral effect of HIV on the brain by grouping measurements across hemispheres. This additional modelling constraint simplifies the classification task and results in higher performance scores.

With the exception of SFS+SVM (which is also significantly less accurate than our proposed method), the worst performing methods are common (two-step) approaches that used different methods for feature selection and classification. Such approaches view pattern identification and classification as two disconnected machine learning tasks [20, 60, 61]. Thus, the optimal pattern identified in the first step is generally not optimal for the classifier in the second step, which would explain the low accuracy scores.

All implementations led to SPE, SEN, and AUC values similar to their Accuracy score (which is being maximized). This concurrence emerged because our data set is well balanced between the two cohorts. The residual scores of the imaging measures further minimizes the risk of biasing analysis towards one cohort.

Note that ℓ_2,1-ℓ₂-reg iteratively runs several trials of nested cross-validation in the Selection Step for reliable selection of the relevant features (i.e., the HIV pattern). However, training based on this procedure is computational expensive, the training time is insignificant in comparison with the years it took to acquire the data. With the implementations done only on a single computing core of a machine with an Intel® Core™ i7-4712HQ CPU @ 2.30 GHz with 16 Gigabytes of memory, using Matlab R2017a, it took approximately 6 hours to train the model and search all possible settings for the hyperparameters and tune them. Note, our implementation was not optimized and therefore computation times may be improved. Furthermore, the training is done only once, after which the model parameters are saved and run on test data. The testing time of ℓ_2,1-ℓ₂-reg is less than 0.01 second, which is similar to the other implementations of this comparison. Note that the increase in the running time of our method (compared to single-step methods) is mainly due to the constant number of trials that we repeat the method to get a more robust pattern selected, i.e., the increase in the running time is not exponential to the number of subjects or measurements. Therefore, the method is scalable for larger number of inputs. However, if the number of measurements dramatically increases, the approach faces the so-called ‘Small-Sample-Size’ problem, a common issue in machine learning [62]. This problem arises when the number available samples (N) is far fewer than the number of features (d) extracted from them (i.e., N << d). Under these settings, all machine learning and pattern recognition methods fail to identify the intrinsic space of the samples.

The HIV pattern identified by the proposed Chained-Regularization technique composes of approximately 39% of the 298 measurements that were selected in all 50 training runs (see Figure 5). This frequent selection of such a large number of measurements does not contradict the sparsity constraint of MKL but rather is due to grouping of measurement and the accounting done by the Chained-Regularization approach. Classifiers relying on group sparsity (ℓ_2,1) tend to select more measurements than those relying solely on sparsity (ℓ₁ [27]). Furthermore, our method marks a measurement as informative if it is selected by MKL at least once in connection with one of the 7 kernels (i.e., Linear, HIK, and RBF with 5 instances of its hyperparamter setting). That those kernel-measurement pairs are actually sparsely selected by MKL is shown in Figure 8, which lists each pair separately. By doing so, our Chained-Regularization approach avoids underestimating the impact of the disease to a small region of the brain as commonly done by sparse classifiers [56].

Figure 8:

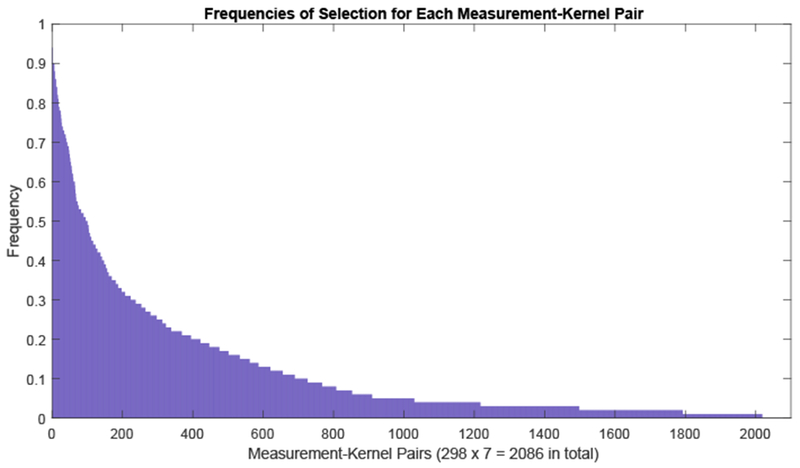
Frequencies of selection for each of the measurement-subkernel pair. Note that 298 brain measurements are used, together with 7 different subkernels resulting in 2098 total pairs.

As indicated by Table 4, combining the four different types of measurements used in our analysis is essential for creating a highly accurate HIV pattern. Of all measurement types, the Mean Curvature is the most frequent measurement type present in the pattern. However, when performing classification without the Mean Curvature (see Table 3), the drop in accuracy is less then when omitting Surface Area and Gray Matter Volume scores. The opposite is true for the regional gray matter volumes, which are least often selected, but whose omission from the pattern results in the largest drop in accuracy. This observation acknowledges that the number of times any type of measurement is part of a selected pattern does not necessarily indicate how important that type is for characterizing the disease.

4. Discussion

The measurements composing the HIV pattern identified by the most accurate approach, the proposed Chained-Regularization, are in agreement with the literature, which suggests that HIV infection is associated with volume deficits in cortical, subcortical, and white matter regions [63, 64, 65, 66, 67, 68, 69, 70, 71, 72]. As identified using our automated, machine learning method (Table 4), the literature indicates that cortical areas affected in HIV relative to healthy controls include frontal, cingulate, sensorimotor, and parietal regions [9, 73, 74, 75, 76, 77]. For other cortical regions identified herein, reports on the effects of HIV are relatively less common: [9] lists temporoparietal regions; [71, 78] include effects of HIV on thinning of the temporal cortices; [72] describes effects on insula; [79] lists parahippocampal cortex. That our methods identified regions not commonly reported in the HIV literature (e.g., Caudalanteriorcingulate, Isthmuscingulate, Lateralorbitalfrontal, Parsopercularis, and Frontalpole) may be due to our inclusion of cortical measures such as mean curvature, thickness, and surface area, which are not typical metrics used in the HIV literature. Instead, the imaging literature usually focuses on the effects of HIV on gray matter volume (see the following for exceptions [80, 81, 82]). Indeed, in studies that assess cortical thickness rather than cortical volume, HIV effects are evident in areas such as the insula, orbitofrontal, temporal, and cingulate cortices [78, 83], similar to the ones identified here.

As also confirmed by our results, white matter is notably affected by HIV infection. Damage to myelin sheathes may be reflected in lower than normal white matter volume and greater prevalence of white matter hyperintensities [84] (deemed “hypointensities” by FreeSurfer [44]). Indeed, examination of brain microstructural integrity using DTI has detected subtle HIV-related differences from controls (e.g., lower fractional anisotropy and higher mean diffusivity) in myelin and axonal integrity [85, 86, 87, 88, 89, 90], even in normal-appearing white matter [91, 92, 93].

Subcortical regions frequently reported in the literature to have significantly smaller volumes in HIV subjects relative to healthy controls include hippocampus and basal ganglia structures [64, 94, 95, 96, 4]. Regarding the basal ganglia and limbic structures, our results specifically identify the accumbens and amygdala, whereas the literature more frequently cites the caudate, putamen, and pallidum (e.g., [65, 94, 95, 96]).

Although our approach does not identify the thalamus, a structure as particularly susceptible to HIV despite other reports (e.g., [9, 83, 4, 6]), our scheme does note cerebellum as a significant contributor to diagnosis differences. This inclusion is consistent with several other studies report HIV-related gray matter volume deficits in the cerebellum [68, 69, 97]. The functional consequences of HIV effects on the cerebellum have been reported [98]; yet the cerebellum is generally underappreciated in the imaging literature as common analysis methods are designed with the neocortex in mind and may be suboptimal for the analysis of the cerebellum.

One of the main limitations of the proposed study is the large imbalance between the number of HIV patients and CTRL subjects. We addressed this issue by matching (and hence balancing) a subset of the CTRLs to the HIV group. However, this greatly reduced the number of samples used for extracting the pattern and testing, and thus the power of the analysis. To preserve the power of the provided data, expanding Chained-Regularization for explicit modeling of the imbalance between the cohorts can be a direction for future work.

5. Conclusion

We presented Chained-Regularization, a two-step-approach to identifying disease-specific patterns and performing pattern-based classification that, unlike the state-of the art, uses the same classification model for first identifying informative measures and then improving the accuracy of the classification based on the selected measures. Our choice of classification approach was a generalized version of the MKL method proposed by [13]. In the Selection Step, parameterization of MKL was confined by groups sparsity (ℓ_2,1-norm) and in the Reweighing Step, the parameterization was penalized by the Euclidean (ℓ₂-norm) regularization. This implementation was more accurate than alternative implementations and significantly better than common (two-step) approaches using different methods for feature selection and classification.

The Chained-Regularization approach identified a number of brain regions comporting with the literature and designated a few novel regions that (to our knowledge) have not been previously described in the HIV literature. These regions would benefit from further investigation as an improved understanding of the diseases remains critical for advancing the long-term care for the large number of HIV infected patients, who (even with suppressed viral loads) can suffer from cognitive disorders associated with HIV. Our current contribution in improving this understanding is in providing an automated, impartial approach for identifying key brain regions implicated in HIV infection.

Appendix A. Multiple Kernel Learning for Feature Selection and Classification

Table A.5:

Notations: Note that throughout this paper, we refer to matrices with bold capital letters (e.g., A), vectors with small bold letters (e.g., a), and scalars or functions with all non-bold letters. $a_j^i$ is the scalar in row i and column j of A, while aⁱ the i^th row and a_j the j^th column of A.

Notation	Description
N	Number of training samples
d	Dimensionality of the feature vectors
d′	The dimensionality of the selected features set
$\mathbf{X}\in {ℝ}^{d\times N}$	Feature matrix of all samples
$\mathbf{y}\in {ℝ}^{1\times N}$	The class labels for each of the samples
${\mathbf{X}}^{\prime }\in {ℝ}^{d^{\prime }\times N}$	The new reduced feature matrix, after feature selection
k(x, xn)	Subkernel function between the two samples x and xn
α	Weights vector learned to aggregate subkernels into a kernel
k(x, xn, α)	Aggregate kernel of the two samples x and xn, using weights α
∥a∥1	The ℓ1 norm of vector a (i.e., ${\parallel \mathbf{a}\parallel }_1={\sum }_i\mid a_i\mid$)
∥a∥2	The ℓ2 norm of vector a (i.e., ${\parallel \mathbf{a}\parallel }_2={({\sum }_i{a}_i^2)}^{\frac{1}{2}}$)
∥A∥2,1	The ℓ2,1 norm of the matrix A (i.e., ${\parallel \mathbf{A}\parallel }_{2,1}≔{\sum }_j({\sum }_i{\mid a_j^i\mid }^2{)}^{\frac{1}{2}}$)
${ℝ}_{\ge 0}$	The set of non-negative real numbers

The MKL of [13, 18] classifies samples by learning the optimal pairings between kernels and image measurements. Finding the optimal paring is described as a minimization problem with respect to a weight vector (denoted α), sparsity of which specifies the importance of pairings for class separation. To make the minimization problem tractable, the search for the optimal weight vector is constrained by a regularization term $\mathcal{R}(\alpha )$. The minimization problem is furthermore characterized by a prediction function f (x, α) that maps the image measurements x of a sample to a label or cohort (i.e., y). The max-margin term ${\parallel f(.,.)\parallel }_{\mathcal{H}}^2$ (or ${\parallel f\parallel }_{\mathcal{H}}^2$ for short) then measures the distance between the ‘support vectors’ of the classes (i.e., HIV and CTRL) as defined by f(·, ·) (see [53, 99] for detailed definition and see Table A.5 for the notations). Introducing the loss function L(y, f(x, α)) for measuring the difference between the predicted and actual label of a sample, the final term of the minimization problem computes that difference across all training samples, i.e., $\mathcal{L}(\mathbf{y},\mathbf{X},f,\alpha )≔{\sum }_{m=1}^{N}L(y_m,f({\mathbf{x}}_m,\alpha ))$. Thus, the regularized MKL approach is completely defined by

$$\begin{array}{cc}\hfill \underset{f\in \mathcal{H},\alpha }{\min }& \frac{1}{2}\parallel f{\parallel }_{\mathcal{H}}^2+C\cdot \mathcal{L}(\mathbf{y},\mathbf{X},f,\alpha )+\lambda \mathcal{R}(\alpha ),\hfill \\ \hfill s.t.& \alpha \ge 0,\hfill \end{array}$$ (A.1)

where C and λ are trade-off hyperparameters, the constraint α ≥ 0 is needed to efficiently solve the minimization problem (similar to [13, 18]), and $\mathcal{H}$ is a Reproducing Kernel Hilbert Space (RKHS) [100]. Note that α ≥ 0 guarantees that the search for the optimal parameters is done in the space of non-negative values, in which we can define flexible (convex and smooth) regularization functions. The regularizers ℓ_2,1 and ℓ₁ are only smooth in the domain of non-negative values [18, 27]. For more details, refer to Section Appendix A.1.

In the above objective, function f is expressed in terms of the aggregated kernel function k(·, ·, α), the weight w_n of a training samples ‘n’ in the decision process, and bias parameter b [101, 53]¹:

$$f(\mathbf{X},\alpha )≔\underset{n=1}{\overset{N}{\Sigma }}{w}_n\cdot y_n\cdot k({\mathbf{X}}_n,\mathbf{X},\alpha )+b.$$ (A.2)

As shown in Figure A.9 (and [13]), the aggregated kernel function k(·,·, α) applies a set of subkernels {k₁ (·, ·),…, k_κ(·, ·)} to each single residual score and then computes a weighted average across all subkernels and residual scores with the weight defined by α, i.e.,

$$k(\mathbf{X},{\mathbf{X}}_n,\alpha )≔\underset{q=1}{\overset{k}{\Sigma }}\underset{i=1}{\overset{d}{\Sigma }}{\alpha }_{(i-1)\cdot k+q}{k}_q(x^i,x_n^i).$$ (A.3)

An efficient solution to Eq. (A.1) requires the subkernels to be positive semidefinite (PSD), which is a common constraint for kernel methods [101]. Note, that any linear combination (with non-negative coefficients) of PSD subkernels also results in PSD kernel (as in Eq. (A.3)). For our specific application, we choose three types of subkernels. The first one is a Linear (LIN) kernel, which is one of the simplest and most widely used kernels in machine learning:

$$k_{\mathrm{LIN}}(\mathbf{X},{\mathbf{X}}_n)≔{\mathbf{X}}^{⊺}\cdot {\mathbf{X}}_n.$$ (A.4)

As an alternative to the linear kernel, k(·, ·, ·) also includes the histogram intersection kernel (HIK) [102], a non-linear kernel popular for non-negative features. This kernel is applied to the absolute values of the residuals in X (as in Eq. (2)), i.e.,

$$k_{\mathrm{HIK}}(\mathbf{X},{\mathbf{X}}_n)≔\underset{i=1}{\overset{d}{\Sigma }}\min (\mid x^i\mid ,\mid x_n^i\mid ).$$ (A.5)

Finally, the implementation includes several instances of the Radial Basis Function (RBF) or the Gaussian kernel [103], a popular, non-linear kernel that depends on the kernel hyperparameter σ:

$$k_{\mathrm{RBF}}(\mathbf{X},{\mathbf{X}}_n)≔\exp \left(\frac{\parallel \mathbf{X}-{\mathbf{X}}_n{\parallel }_2^2}{2{\sigma }^2}\right).$$ (A.6)

This kernel can be built by different values of its hyperparameter, σ. We build several instances of the RBF subkernel with respect to σ ∈ {10⁻², 10⁻¹, 1, 10, 10²}. Doing so avoids hyperparameter tuning for this kernel, as MKL solves Eq. (A.1) with respect to α to select the pairs of subkernels and residual scores that best fit the data.

Assuming that $\mathcal{R}(\alpha )$ (which is explicitly defined later) is convex and differentiable for non-negative input values (i.e., α ≥ 0), the solution to Eq. (A.1) can be efficiently determined via Optimize-RMKL(·) (see Algorithm 1). Inspired by [13], “Optimize-RMKL(·)”, iteratively solves the equation based on Block Coordinate Descent [104], i.e., by alternating between optimizing for f and α until convergence. When optimizing for f (with α being fixed), Eq. (A.1) reduces to a SVM that can be solved

Algorithm 1.

“Regularized multiple kernel learning” (RMKL), as in Eq. (A.1).

	Optimize-RMKL (y, X, $\mathcal{R}(.)$, C, λ)
	Input: Training features X, labels y, the regularization function $\mathcal{R}(.)$, and hyperparamters C and λ.
1:	t ←, α0 = 1
2:	repeat
3:	ft+1 ← SVMSolver(yk(.,., αt)).
4:	αt+1 ← Solve (A.1) by using f* = ft+1 and regularization $\mathcal{R}(.)$, using PGD.
5:	αt+1 ← max(0, α), t ← t + 1.
6:	$\mathcal{M}\leftarrow \mid \frac{1}{2}{\parallel f^t\parallel }_{\mathcal{H}}^2+C\mathcal{L}(\mathbf{y},\mathbf{X},f^t,{\alpha }^t)+\lambda \mathcal{R}({\alpha }^t)\mid$.
7:	until $\frac{{\parallel {\alpha }^{t-1}-{\alpha }^t\parallel }_2}{({\parallel {\alpha }^{t-1}\parallel }_2\times {\parallel {\alpha }^t\parallel }_2)}<{10}^{-3}$, or $\mathcal{M}<{10}^{-6}$, or t > 100
	Output: f*, αt.

with standard approaches (e.g., LIBSVM [105]). To determine the optimal feature-kernel weights α (with f being fixed), projected gradient decent (PDG) [106] is applied to Eq. (A.1).

Appendix A.1. Chained ℓ_2,1,-ℓ₂ Regularization

Given the training data as well as the search space {10⁻³, 10⁻², 10⁻¹, 1, 10¹, 10², 10³} for both hyperparameters λ and C of Optimize-RMKL(·), our Chained-Regularization approach (called Chained-Reg; see also Algorithm 2) now makes use of Optimize-RMKL(·) in the Selection Step and the Reweighing Step. In the Selection Step, the regularizer $\mathcal{R}(\cdot )$ of Eq. (A.1) is defined by group sparsity (i.e., ℓ_2,1 norm) so that Optimize-RMKL(·) identifies the kernel-measurement pairs that best distinguish the two cohorts. To explicitly define $\mathcal{R}(\cdot )$, we introduce the group matrix $\mathcal{G}(\alpha )$, in which each column represents a group according to bilateral dependencies of ROI measurements and the entries of the rows are the elements of α corresponding to those measurements. Then, the first step of the Chained-Regularization defines $\mathcal{R}(\cdot )$ as

$${\mathcal{R}}_{2,1}({\alpha }_1)=\parallel \mathcal{G}({\alpha }_1){\parallel }_{2,1}.$$ (A.7)

Algorithm 2.

Chained ℓ_2,1-ℓ₂ regularization for joint feature selection & classification.

As mentioned, for the selection process to be reliable, we compute a distribution over the selected features by repeatedly solving Eq. (A.1) and then select residual scores based on that distribution. Specifically, the training data is split into 5 (inner)

Figure A.9:

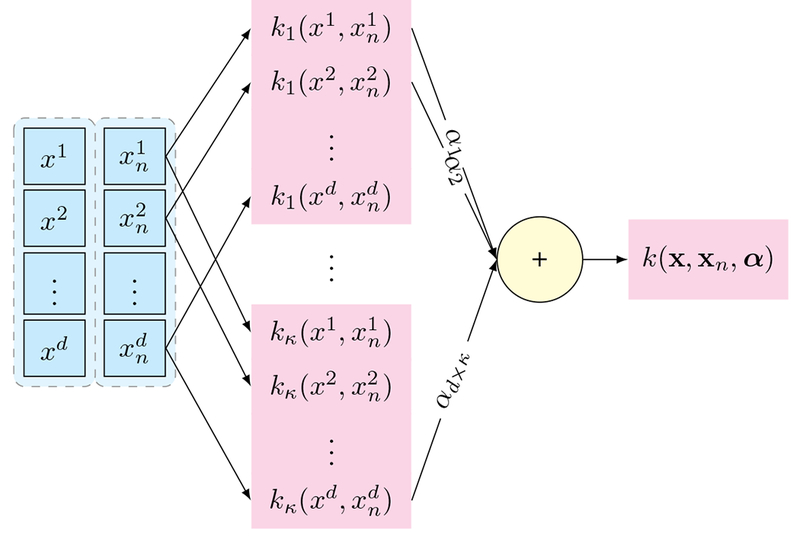
An illustration of computing the kernel for each pair of samples (x and x_n), similar to what is presented in Eq. (A.3). The final kernel is computed by a weighted aggregation of κ different kernels applied on each single feature.

folds based on random sampling. For each fold, the approach records the set of selected kernel-feature pairs associated with the most accurate (hyperparameter) setting of Optimize-RMKL(·). The accuracy of a setting is determined by parameterizing Optimize-RMKL(·) accordingly, training the approach on the remaining training data, and applying the resulting implementation to the inner fold. The entire process of splitting the training data and recording the set of selected kernel-feature pairs is repeated 9 more times to produce a total of 50 sets. The features selected in all trials then define the ‘selected measurement matrix’ X’. Note, this conservative threshold minimizes the chance to introduce another hyperparameter that requires tuning. However, one can implement other selection criteria if required by the application.

Given the selected measurements, the Reweighing Step of the Chained-Regularization again applies Optimize-RMKL(·) to solve Eq. (A.1), but now with respect to X’ and the regularizer defined by the Euclidean norm, i.e.,

$${\mathcal{R}}_2({\alpha }_2)=\parallel {\alpha }_2{\parallel }_2.$$ (A.8)

To find the most accurate reweighing α₂ of the selected measurements, 5-fold (inner) cross-validation coupled with hyperparameter exploration is performed. The accuracy of each hyperparameter setting is computed by first recording the classification results on the fold not used for training Optimize-RMKL(·) and then averaging those results across all folds. With respect to the most accurate setting of Optimize-RMKL(·), Chained-Regularization returns the kernel function f and corresponding weight vector α₂ to define the classifier for the testing data.

We end the description of Chained-Regularization by noting that the proposed approach is not specific to the two norms discussed here. As mentioned, Optimize-RMKL(·) only requires that the chosen norms are convex and differentiable in ${ℝ}_{\ge 0}^{d\times k}$, which, for example, ℓ₁ and ℓ_2,1 norms are.