Abstract
In the field of cardiac modelling, the mechanical action of the heart is often simulated using finite element methods. These simulations are becoming increasingly challenging as the computational domain is customized to a patient’s anatomy, within which large heterogeneous tension gradients are generated via biophysical cell models which drive simulations of the cardiac pump cycle. The convergence of nonlinear solvers in simulations of large deformation mechanics depends on many factors. When extreme stress or irregular deformations are modelled, commonly used numerical methods can often fail to find a solution, which can prevent investigation of interesting parameter variations or use of models in a clinical context with high standards for robustness. This article outlines a novel numerical method that is straightforward to implement and which significantly improves the stability of these simulations. The method involves adding a compressibility penalty to the standard incompressible formulation of large deformation mechanics. We compare the method’s performance when used with both a direct discretization of the equations for incompressible solid mechanics, as well as the formulation based on an isochoric/deviatoric split of the deformation gradient. The addition of this penalty decreases the tendency for solutions to deviate from the incompressibility constraint, and significantly improves the ability of the Newton solver to find a solution. Additionally our method maintains the expected order of convergence under mesh refinement, has nearly identical solutions for the pressure-volume relations, and stabilizes the solver to allow challenging simulations of both diastolic and systolic function on personalized patient geometries.
Index Terms: solid mechanics, incompressibility, nonlinear solvers, cardiac mechanics
I. Introduction
Finite element methods are increasingly used to study the mechanics of the heart. Studies in this area range from detailed electromechanical simulations with the goal of improving our understanding of physiology [1], [2], [3], genetically modified animals [4], [5], disease [6], [7], [8], and clinical intervention [9]. As the range of applications for these models is expanding, robustness of simulations over a large number of different cardiac geometries and physiological perturbations is becoming increasingly important.
A problem that frequently arises in solving these large deformation mechanics problems is that the nonlinear solution processes do not guarantee convergence to a solution of the set of governing equations [10]. As the number of degrees of freedom in these problems is typically in the tens to hundreds of thousands, it is difficult to uniquely identify the cause of such solver nonconvergence in a given context. These convergence problems can prevent researchers from investigating the effect of a large range of perturbations to the heart, as the more extreme (and often more interesting) variations are less likely to be solved. Furthermore, the convergence behavior of a solver for a biophysically detailed simulation of cardiac mechanics is sensitive to many other factors, including the computational mesh, choice of spatial or temporal numerical discretization, model parameters, boundary conditions, and many aspects of the numerical solver such as the matrix solver and line search algorithm.
Solver convergence issues have become even more relevant in the context of personalizing cardiac geometries for mechanical simulations [6], [11], where image processing and mesh fitting procedures now significantly influence the ability of a nonlinear solver to find a solution to the computational model. In particular, matching the patient’s anatomy more accurately has been shown to result in a more challenging computational problem, and achieving a good balance between accuracy and solver stability is a difficult problem. Furthermore, although mesh quality metrics can be maximized during mesh generation, they can not be robustly used to determine the solver performance [10]. Robust solver convergence when using these models is also important in the context of the parameter estimation required to further personalize these cardiac models [12], as the methods used to run the estimation procedures assume the simulations can be evaluated for a wide range of parameters.
There are a large number of numerical schemes that have been proposed for the numerical solution of the solid mechanics equations in the past fifty years. Many of these schemes are designed to overcome the difficulties of modelling incompressible materials. Two common approaches are the use of penalty methods and Lagrange multiplier methods. Penalty methods approximate fully incompressible materials as nearly incompressible, penalizing changes in volume causing with a large increase in strain energy. The compressibility of the material decreases as the penalty term is increased, but the resulting system of equations becomes numerically more difficult to solve. Several numerical schemes have been devised to alleviate these problems, including updating schemes based on augmented Lagrangians. For more information on these schemes and other method based on specific finite element implementations see e.g. [13], [14], [15] and references therein. A technique which can be applied in both nearly- and fully incompressible modelling, are schemes based on a multiplicative split of the deformation gradient into isochoric and deviatoric components, which can be traced back to early work of Flory [16]. Within these schemes, and indeed for the material itself, the stress response is assumed to depend only on the isochoric (i.e. volume-preserving) part of the deformation. Although in the formulation of fully incompressible solid mechanics, there is no volume change in the exact solution, this assumption affects the numerical solution process, making it generally more likely to converge to a solution [17]. These methods have also been used in cardiac modelling, primarily in the context of simulating diastolic inflation of the ventricles [18], [19], For a more detailed review of these methods and their theoretical foundation based on the Hu-Washizu principle, see e.g. [20], [21], [17]. Although this isochoric/deviatoric formulation is known to be particularly robust [17], a direct discretization of the equations for solid mechanics, without using an alternative stabilizing formulation, remains the most common approach in cardiac modelling [22], [23], [24], [25], [26], [27], [28], [29]. The fact that with very few exceptions [30], this includes nearly all detailed whole-cycle electromechanical models suggests that the implementation challenge of using these schemes, combined with the uncertainties of their effectiveness in solving whole-cycle cardiac simulations, may represent a significant hurdle to their adoption.
Given the lack of application of these more advanced schemes to complex cardiac simulation, and the apparent implementation barriers, the objectives of this paper are twofold. Firstly, we investigate the performance of the direct and isochoric/deviatoric formulations of the solid mechanics equations for a range of problems in cardiac mechanics, including both extreme inflation and simulations of the cardiac cycle. Secondly, we present an alternative scheme which is both simple and practical, and which significantly improves the stability and accuracy of cardiac simulations. This adjustment is straightforward to implement in a code using the direct finite element discretization of the solid mechanics equations, and calculation of the term has a negligible additional computational cost. The scheme can be applied to both the direct and isochoric/deviatoric formulations, and we compare the effect of this scheme on both methods. Below we present the mathematical background of our proposed novel numerical scheme. We then perform a detailed analysis on a simple test problem, to show the convergence under mesh refinement of the different numerical schemes. Finally, we analyze the stability and computational performance of the different methods on a range of practical problems of personalized cardiac models of human patients.
II. Methods and Results
Cardiac tissue is typically modelled as an incompressible material [22], [24], [9], [26]. Although cardiac cells do not change volume over the course of a beat, estimates of tissue volume change during the cardiac cycle range from 2 – 15% [31]. As these volume changes are driven by changes in perfusion, we approximate cardiac tissue as a fully incompressible material, in the absence of a perfusion component in our model. In large deformation mechanics, the governing equations are given by:
| (1) |
Where F is the deformation gradient and coordinates in the undeformed and deformed configuration are denoted by X and x respectively. In equation 1, T is the second Piola-Kirchhoff stress, given by the derivative of the strain energy function W:
| (2) |
Where are the Lagrangian and right Cauchy-Green strain tensors respectively. For the purpose of demonstration we will use the exponential strain-energy function proposed by Guccione et al. [32] throughout this manuscript:
| (3) |
Where f, s, n have the conventional definition of ‘fiber direction’, ‘sheet direction’ and ‘normal direction’ in local tissue microstructure coordinates for cardiac simulations [33].
There are two main approaches to incompressibility in cardiac mechanics: the Lagrange multiplier method, and the penalty method. These are given by the strain energy functions:
| (4) |
| (5) |
Where p is the hydrostatic pressure and J = det F. In addition, we investigate an alternative discretization, as used by Göktepe et al. and Wang et al. among others [34], [18], [19]. This scheme defines the isochoric component of the deformation gradient as along with isochoric strain tensors and uses these to define a strain energy function independent of changes in volume:
| (6) |
Analogous variations of penalty methods (equation 5) also exists, but are susceptible to non-physical behaviour [35] and will not be considered here. We focus on the often adopted choice in cardiac mechanics where equation 1 is solved using tricubic Lagrange elements and the constraint J = 1 is solved using trilinear elements where applicable [22], [4]. Specifically, the weak form of the incompressibility constraint J = 1 in terms of basis functions ϕj is:
| (7) |
In analyzing situations where the Newton solver does not converge to a solution, we observed that the local change in volume J can be significantly different from unity while still obeying equation 7, and observed non-physical trial solutions where J < 0. Based on this observation, we introduce two novel schemes, based on adding a compressibility penalty (as in equation 5) to the Lagrange multiplier schemes.
| (8) |
| (9) |
Where the incompressibility constraint J = 1 applies in both schemes. The deformation (and thus J) is represented by higher order finite elements, while p is represented by trilinear elements. Thus, the addition of a higher order incompressibility penalty term means that the deformation is expected to more accurately obey the incompressibility constraint. In addition, the strain energy in equation 8 is similar to that used in augmented Lagrange schemes [15], which iteratively update p at each Gauss point and use sub-iterations to achieve incompressibility. However, these schemes do not solve the incompressibility constraint J = 1 directly, but instead represent a variation of the strain energy in equation 5. The electronic supplement includes derivations of the Piola-Kirchhoff stress tensors for the schemes we compare, as well as mathematical details.
As discussed in the introduction, there are many other numerical schemes for solid mechanics. In this paper, we limit our investigation to methods that are commonly used in cardiac mechanics and our proposed novel variations on them, i.e. the five strain energy functions given in this section. We also limit the investigation of the penalty method to κ = 1000 kPa, which limits the difference in volume to approximately 10% compared to fully incompressible schemes in the physiological range of pressure and stiffness. The following sections show the effect of these different numerical methods on the convergence under mesh refinement and solver stability of mechanical simulations.
A. Tests on a cylinder problem
In this section we present an analysis of the convergence behaviour under mesh refinement of the five different schemes described in the previous section (the direct and isochoric/deviatoric schemes, both with and without the additional stabilizing term, and a penalty method). For this purpose, we consider a simple test problem by inflating a thin cylinder of radius 30 mm and thickness 3 mm to typical end diastolic pressure of Pcav = 1 kPa. This test problem allows us to unambiguously analyze differences between the various computational schemes, without the complicating factors inherited from methods used in fitting the computational domain to physiological data, while still retaining some of the properties of the deformations seen in simulations of cardiac mechanics. The symmetry of the problem also makes it more tractable, as mesh refinement in two dimensions is sufficient to study convergence. For simplicity we define the material to be isotropic by using C2 = C3 = C4 to eliminate the dependence on the fiber direction, specifically we use C1 = 1 kPa, C2 = C3 = C4 = 5 to approximately double volume at the inflation pressure. We use a small load increment to maximize the change of convergence for the first solver steps, incrementing pressure by 0.01 kPa each step.
For this problem we consider the following three error metrics. Firstly, we consider the mean error in the deformation in Cartesian coordinates:
| (10) |
Where x is the node position, and the set of points A to be compared are all the nodes in the least refined mesh, including nodes internal to elements. We use a further refined solution with 128 × 8 elements to determine the converged solution xconv. Secondly, we consider the error as measured by the total strain energy (in Joules):
| (11) |
Thirdly, we consider the error in solving the incompressibility constraint, per unit volume, which measures how well the solution found obeys the incompressibility constraint:
| (12) |
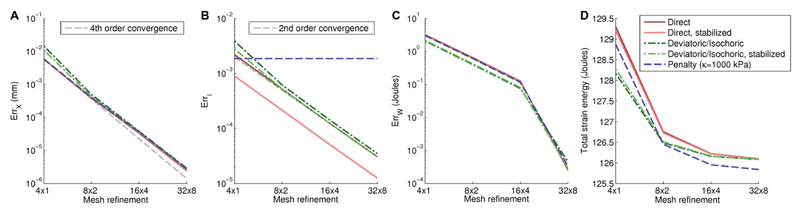
For the stabilization terms we initially set the compressibility penalty parameter to κ = 5 Pcav. The dependence of κ on cavity pressure compensates well for the tendency for the solution to show greater deviation from the theoretically incompressible cases in larger deformations due to greater cavity pressures being applied. We will consider the choice of κ in more detail later in this paper. Figure 2 shows convergence under mesh refinement for all four numerical schemes on the meshes shown in Figure 1. These plots show that the proposed stabilization preserves the solution in terms of pressure-volume relationship and has identical convergence behaviour compared to standard methods, while giving a more accurate solution for the incompressibility constraint. Table I shows differences between the methods are on the order of 10−6 mm, with similar differences resulting from using the isochoric/deviatoric discretization over the direct discretization, as resulting from the introduction of a stabilizing term. Additional benchmark problems confirming the lack of locking across different schemes are shown in the electronic supplement.
Fig. 2. Convergence results for the cylinder problem.
Our refinement study shows fourth-order convergence for deformation (Panel A, Equation 10), and shows second-order convergence for the incompressibility constraint (Panel B, Equation 12). Panel B also shows that our proposed method can significantly reduce error in solving this equation. Results for all methods are compared to a refined solution computed with the same method, while table I shows differences between methods for these refined solutions. Panels C shows error in total strain energy convergence, while Panel D confirms convergence to identical total strain energy for all fully incompressible schemes.
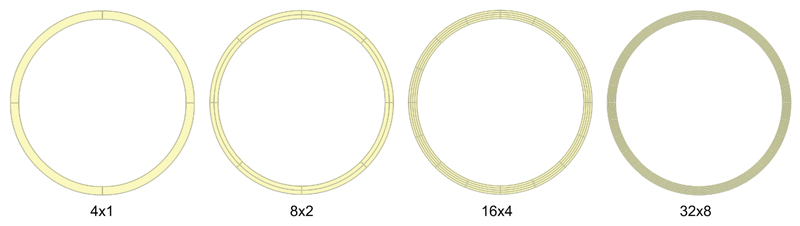
Fig. 1. Meshes used for the cylinder problem.
Since the problem is perfectly symmetric, we only refine the mesh circumferentially and radially as shown in panel (a), indicating the level of refinement as ‘number of elements circumferentially × number of elements radially’.
Table I. Differences in deformation for the different numerical method.
Results show mean differences in deformation between the different methods, as measured by the mean difference between nodes in the most highly refined mesh (128 circumferential elements), measured in mm. Table entries at the top are abbreviations for the different numerical methods as indicated in parenthesis at the start of each row. As the penalty method has a different exact solution, differences with this scheme are significantly larger, leading to identical entries in the last column at this level of precision.
| Method | D | DS | I | IS | P |
|---|---|---|---|---|---|
| Direct discretization (D) | - | 6.8 · 10−7 | 1.9 · 10−6 | 1.8 · 10−6 | 5.4 · 10−3 |
| … with stabilization (DS) | - | 1.4 · 10−6 | 1.3 · 10−6 | 5.4 · 10−3 | |
| Isochoric/deviatoric discretization (I) | - | 1.4 · 10−7 | 5.4 · 10−3 | ||
| … with stabilization (IS) | - | 5.4 · 10−3 | |||
| Penalty (P) | - | ||||
B. Investigating nonconvergence of the Newton solver
As outlined in the methods section, the addition of a compressibility penalty to the stress tensor was motivated by the observation of a negative det F in the Newton iteration process. However, we have found that mesh refinement can result in a the incompressibility equation being solved more accurately, yet still resulting in a negative det F in the Newton search direction and non-convergence of the solver, at nearly identical pressures. In this section we investigate a number of alternative explanations for solver non-convergence, including numerical roundoff, the choice of initial solution, and the properties of the Jacobian at the point of solver non-convergence. We use the 4 × 1 mesh for efficiency reasons, as all problems show similar behaviour. We define the vector of unknowns as x in solving the system of equations ‖r(x)‖ < Nrreltol where N is the number of nodes and our default rreltol = 10−9. For this choice of tolerance, inflation pressure is 48 kPa for the direct discretization, increasing to > 100 kPa when adding a stabilization term.
Firstly, we test whether loss of numerical precision may prevent the residual r from decreasing sufficiently. Increasing rreltol also results in non-convergence of the Newton solver, with an identical inflation pressure for rreltol = 10−6 and surprisingly a lower inflation pressure of 35 kPa for rreltol = 10−3. However, decreasing rreltol to e.g. 10−12 results in earlier failure (< 2 kPa) in both the non-stabilized and stabilized method. This shows that the solver convergence problems are not caused purely by numerical roundoff for our typical choice of rreltol = 10−9, but reflect a more fundamental problem. More detailed results for the dependence of solver convergence on this tolerance as well as mesh refinement and discretization method are shown in the electronic supplement.
Secondly, we tested the hypothesis that the choice of initial solution is the typical cause of solver non-convergence. Running with the direct discretization to the point of non-convergence, and using the last iteration as a starting point for the stabilized method (κ = 1 kPa) results in convergence for that load increment. Trying to re-solve the same load increment without stabilization, using the solution found with the stabilized method, once again results in non-convergence, even though the initial guess for the solution is close to the one being sought. Similarly, switching back at a later load increment results in non-convergence. Thus, it appears unlikely that finding a better initial solution is a practical solution for solver nonconvergence.
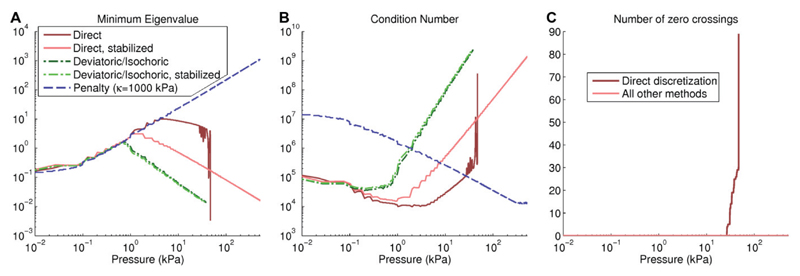
Finally, we have tested the properties of the nonlinear system throughout the simulation by analyzing the eigenvalues of the Jacobian matrix. The Jacobian matrix is typically positive definite, i.e. all eigenvalues are positive, and a loss of this property is associated with instability, as the Jacobian matrix becomes (nearly) singular every time an eigenvalue crosses from positive to negative. This presence of a near-zero eigenvalue in the Jacobian matrix A leads a large solver step Δx = A−1r, with trial solutions that are generally non-physical. Small eigenvalues can also also lead to a large condition number (largest eigenvalue/smallest eigenvalue) which is associated with loss of numerical precision. To test the connection between the eigenvalues and solver stability in practice, we have explicitly determined the eigenvalues of the Jacobian matrix each time the Jacobian matrix is calculated, to investigate which discretization schemes show negative eigenvalues. Figure II-B shows the minimal eigenvalues throughout the solution process for the different discretization schemes. These results show that for the direct discretization, zero crossings appear after 26.5 kPa inflation, with a risk for eigenvalues close to zero and subsequent solver nonconvergence. These zero crossings also explain the irregular dependence on load increment and convergence tolerance resulting in inflation pressures between 35-48 kPa, and the fact that use of a smaller load increment can result in a lower inflation pressure. For the stabilized method, as well as the isochoric/deviatoric approach and the penalty method, no zero crossings appear, and solver performance is more consistent. However, for higher pressures the Newton solver eventually fails, possibly due to the high condition number (≈ 109), which is associated with loss of numerical precision. The isochoric/deviatoric discretization shows especially high condition numbers, resulting in earlier failure for this particular problem. The penalty method shows increased stability at higher pressures, with the first load increments being most difficult to solve in practice, but eventually fails at 790 kPa inflation.
Testing the dependence of solver convergence on the load increment (from 0.01 to 1 kPa) and choice of Newton solver (modified or not) confirms these observations. The direct discretization shows less predictable results, as explained by the chance of solver failure at each zero crossing of an eigenvalue, whereas the other methods are far more consistent. Furthermore, increasing the load increment makes the penalty method fail more often. Detailed results for these simulations are presented in the electronic supplement.
In conclusion, solver non-convergence when using the direct discretization appears to be related to a nearly singular Jacobian, which is associated with local extrema, saddle points, and bifurcations. The extra compressibility penalty term tends to prevent the Jacobian from becoming singular, thus improving convergence of the nonlinear solver. The improvement we are reporting may be related to improving the ellipticity and convexity of the strain energy function, conditions which are important for preventing unnatural deformations. Specifically, the deformation block of the Jacobian being positive definite is implied by the ‘strong ellipticity’ condition. Although the Guccione law has been shown to be locally convex for any positive parameters [36], it is not strongly elliptic for anisotropic three-dimensional problems. Specifically, this important property can be violated under certain types of deformations involving fiber compression in exponential strain energy laws [37] and when active contraction is added [25].
C. Personalized biventricular simulations
Our second test case relates to one of the primary motivation for the stability improvement: allowing researchers to more robustly simulate mechanics on personalized patient geometries. For this purpose, we have created twenty personalized biventricular cardiac meshes (shown in Figure 4) which represent an accurate fit to a varied set of patient anatomies. The meshes were generated using our mesh personalization tool [38] which was recently made available as a web service [39].
Fig. 4. Biventricular meshes used for our test case.
Twenty 144 element personalized geometries generated from MRI data of patients.
As a test for numerical stability, each of these twenty ventricles is inflated to a left-ventricular pressure of Pcav = 100 kPa, while maintaining right-ventricular pressure at of the left ventricular pressure. For comparison, typical left-ventricular end-diastolic pressures are around 1 kPa [40]. As in the previous section, we initially test three different settings for κ for the stabilized method, as in the cylinder problem. We use the constitutive parameters C1 = 4 kPa, C2 = 10, C3 = 5, C4 = 2.5 based on typical volume changes at end-diastolic pressures. We set the fiber direction ranging from −60 degrees at the epicardium to +80 degrees at the endocardium.
Table II shows the results for these test runs, indicating the number of simulations which inflate to typical end-diastolic pressure, and those that succeed to extreme inflation of 100 kPa. As in the cylinder test, we use κ = 5 Pcav. Using the direct method, none of the meshes reach extreme inflation. After adding the stabilization term with κ = 5 Pcav, 18/20 cases reach 100 kPa, while the other two meshes still fail to reach 1 kPa inflation. Using the isochoric/deviatoric discretization, solver convergence is much improved, and only one case remains problematic. This is the same case that shows worst-case behaviour in all methods, which suggests that generation of the computational mesh is still an important factor regardless of the numerical scheme used. Nevertheless, the addition of the stabilization term in the isochoric/deviatoric discretization roughly triples the inflation pressure for this case.
Table II. Summary of results for inflation of biventricular meshes.
Results show key metrics of stability for the direct discretization compared with our stabilized method, discretization using the isochoric/deviatoric split, and a penalty method. For each setting, we show the number of cases that succeed up to typical end-diastolic pressure (1 kPa), and the number of cases that reach extreme inflation (100 kPa), as well as the mean pressure reached when averaging results over all 20 cases, and the worst case pressure reached over all cases. For the stabilization we use κ = 5 Pcav, while the penalty method uses κ = 1000 kPa.
| Method | Mean inflation pressure | Worst-case pressure | Typical EDP | Extreme inflation |
|---|---|---|---|---|
| Direct discretization | 4.25 kPa | 0.11 kPa | 18/20 | 0/20 |
| … with stabilization | 90.1 kPa | 0.12 kPa | 18/20 | 18/20 |
| Isochoric/deviatoric discretization | 95.1 kPa | 1.3 kPa | 20/20 | 19/20 |
| … with stabilization | 95.2 kPa | 3.8 kPa | 20/20 | 19/20 |
| Penalty method | 85.2 kPa | 0.01 kPa | 18/20 | 17/20 |
Comparing the solutions for the incompressible schemes reveals that differences are small. The left-ventricular cavity volume when adding the stabilization term is approximately 0.02% lower compared to the direct method without stabilization. Differences with the isochoric/deviatoric discretization are larger, with volume almost 0.2% higher without a stabilization term, and 0.13% higher with this term included. The penalty method shows larger differences in volume which are very load dependent. Although small at < 5 kPa, solutions diverge to a volume of approximately 50% higher than fully incompressible schemes at 100 kPa.
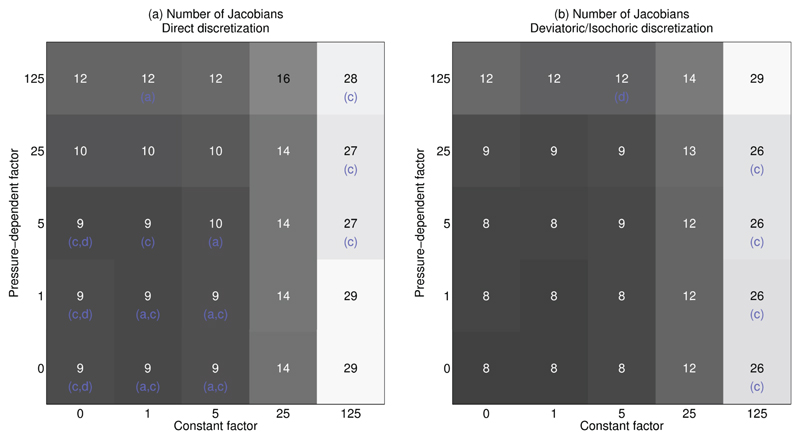
Finally, these twenty cases also give us the opportunity to look at the effects of the free parameter κ in more detail. So far we have only used the setting κ = 5 Pcav, which was found to work well in practice. To explore the choice of stabilization parameter in more detail and determine its effects on stability and computational cost, we run all 20 biventricular cases with κ = κc + κp Pcav. Variations in both the constant factor κc and the pressure-dependent factor κp are tested, using the values 0, 1, 5, 25, 125 for a total of 1000 simulations. Results for inflation to 1 kPa are shown in Figure 5. Most cases show a similar pattern, where the computational cost increases significantly for higher κc, and less so for increasing values of κp. A few especially challenging cases fail to solve except when using a large stabilization term or using the deviatoric/isochoric formulation.
Fig. 5. Influence of the penalty term on stability and computational cost.
These plots show average performance over 20 cases for varying constant factor κc and pressure dependent factor κp, where κ = κc + κp Pcav. The number in the middle of the squares shows the average number of Jacobians required in successful simulations only. Letters in parenthesis indicate the meshes which failed to reach 1 kPa in these settings, and only include a,b,d as all other cases succeeded in all settings. Panel (a) shows these results for the direct discretization, and panel (b) for the deviatoric/isochoric formulation. Note that the choice of 1 kPa pressure implies solutions to the deformation on top-left to bottom-right diagonals of identical κc + κp are completely identical, while total computational cost shown here can differ significantly.
D. Whole-cycle biventricular simulations
In this section we present simulations of the full cardiac cycle on the same twenty biventricular patient geometries. Simulating a contracting heart adds a wider range of deformations to our tests, and thus will better distinguish the practical performance of the different numerical methods. The whole-cycle model with phase transitions is solved monolithically with the solid mechanics equations, as in our previous work [3]. Three-element windkessel parameters for the ejection phase were prescribed as R = 1.06 mmHg s/ml, C = 1.9 mmHg s/ml, Z = 0.062 ml/mmHg based on Westerhof et al. [41], with right-ventricular parameters set to R′ = R/3, Z′ = Z/3, C′ = 3C based on typical pressure differences between the ventricles. For active tension Ta we use the model from Niederer et al. [8] based on work by Kerckhoffs et al. [42], given by
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
Where tr0 = 80 ms, a4 = 650 ms, td = 90 ms, b = 1 ms, ld = −500, a6 = 6, a7 = 0.7, T0 = 180 kPa, and f is a unit vector in the fibre direction. The stress tensor T′ including active tension is used instead of T in Equation 1. As is usual, λ represents the local change in length in the fibre direction, given by
We tested two different electrical activation patterns: firstly, a more physiological homogeneous activation, and secondly, a heterogeneous activation pattern which starts at the basal part of the septum and spreads homogeneously with a conduction velocity of 0.75 mm/ms, representative of pathological cases such as left bundle branch block. Results are shown in Table III. Notably, unlike in passive inflation tests, the isochoric/deviatoric formulation performs much worse than the direct discretization in these cases without additional stabilization. The ejection and isovolumetric relaxation phase appears especially difficult to solve using this numerical method. For both formulations, the pressure-dependent penalty, although shown to be effective for achieving high computational performance, shows its limitations in this challenging test case. Specifically, in isovolumetric relaxation, the decreasing pressure will result in a decreasing penalty, which we hypothesised is the cause for their large number of failed simulations in IVR. This inspired a further test in which the parameter κ can not decrease, resulting in a total of 95% of successful simulations for both activation patterns.
Table III. Results for whole cycle simulations.
The left-most column indicates the number of simulations that complete successfully to end isovolumetric relaxation. Letters in the other columns indicate the number of meshes for which the simulation failed to converge in a certain cardiac phase, and match those from Figure 5. For the stabilization we use κ = 5 PCav, and for ‘Non-Decreasing’ entries we do not allow κ to decrease during the simulation.
| Homogeneous activation | |||||
| Method | Succeed | Fail in inflation | Fail in IVC | Fail in ejection | Fail in IVR |
| Direct discretization | 16 | 2 | 1 | 1 | |
| … with stabilization | 17 | 2 | 1 | ||
| … with stabilization, non-decreasing | 17 | 2 | 1 | ||
| Isochoric/deviatoric discretization | 5 | 1 | 11 | 3 | |
| … with stabilization | 16 | 1 | 3 | ||
| … with stabilization, non-decreasing | 19 | 1 | |||
| Septal activation | |||||
| Method | Succeed | Fail in inflation | Fail in IVC | Fail in ejection | Fail in IVR |
| Direct discretization | 0 | 2 | 1 | 11 | 6 |
| … with stabilization | 1 | 2 | 1 | 16 | |
| … with stabilization, non-decreasing | 17 | 2 | 1 | ||
| Isochoric/deviatoric discretization | 0 | 1 | 10 | 9 | |
| … with stabilization | 0 | 1 | 19 | ||
| … with stabilization, non-decreasing | 19 | 1 | |||
III. Discussion
In this paper we have presented, to our knowledge, the first report of the performance of the different available numerical schemes on detailed simulations of the entire cardiac cycle. This analysis revealed the limited performance of several existing numerical methods for the simulation of more challenging heterogeneous cardiac simulations. In addition, we have proposed alternative ‘stabilized’ schemes which are straightforward to implement and significantly increases the stability of simulations during extreme inflation, ejection, and isovolumetric relaxation in personalized cardiac geometries.
When analyzing the effects of the proposed methods using an idealized cylinder inflation test, we showed that our stabilized method improves the accuracy of solving the incompressibility constraint while converging as expected for deformation and volume measurements. In our test of biventricular mesh inflation, maximal inflation pressure was 6.6 kPa across all meshes when applying the commonly used direct discretization, When adding the stabilization term or using the deviatoric/isochoric formulation, at least 90% of the cases inflate to extreme pressures of 100 kPa. This is a significant improvement over the previous results reported by Lamata et al. [10] using the same kind of cardiac meshes, and shows the complex interaction between mesh quality and the choice of numerical methods.
Unlike its good performance in diastolic inflation, the isochoric/deviatoric formulation shows relatively poor performance in running whole-cycle models on personalized patient geometries. As our proposed stabilized method performs better on these simulations, and is competitive with the isochoric/deviatoric formulation for extreme inflation, it may be a good choice with a lower implementation barrier for modifying an existing finite element implementation to be more stable. However, the proposed stabilization can also be easily added to an implementation using the isochoric/deviatoric discretization, and this combination gives the best results in both diastolic inflation tests, and completing whole cycles.
From the range of tests shown for the effects of the extra parameter κ we can derive some practical guidelines for the choice of stabilization term. Although the stabilization term does not add significant computational cost by itself, a high penalty term can in practice lead to slower convergence of the nonlinear solver. To limit this effect, we recommend using a penalty with a constant factor of 1-5 kPa and a pressure-dependent factor of 1-25.
As mentioned previously, although the observation of negative det F in the Newton iteration process was the main inspiration for the stabilized method, the connection between this problem and solver stability remains to be fully elucidated. We identified the main cause of solver non-convergence to be a near-singular Jacobian leading to exploration of nonphysical and self-intersecting trial solutions, and numerical overflow of the stress tensor. The contribution of the cubic order deformation to the incompressibility constraint is likely to regularize the deformation, and may help to prevent local extremes in stress and strain. Underlying these erratic failure of the Newton solver for more extreme deformations is the loss of ellipticity for the direct discretization, while more consistent failure at extreme deformations is correlated with loss of numerical precision due to high condition numbers.
In this study we focussed our attention on our preferred application of cardiac mechanics. Our focus on this particular application may have introduced a number of limitations. Firstly, we have used the Guccione constitutive law in our test problems as it is relevant to our research and is similar to most other constitutive laws used in cardiac mechanics [43], as they have similar exponential strain energy functions. If the nonconvergence is indeed related to a loss of ellipticity, different types of constitutive laws may not require the stabilized method. This makes our method more suitable for biological materials with complex anisotropic properties. Indeed, limited tests using a Neo-Hookean law showed that very extreme and non-physical deformations are required before the solver fails. However, as shown by Pathmanathan et al. [25], any strain energy function will lose strong ellipticity when sufficient active tension is added. The results shown in this paper when solving a full cardiac cycle with the isochoric/deviatoric formulation, shows that although this method has been analyzed in detail for passive mechanics, the addition of active tension introduces unique challenges which have not been sufficiently investigated. Another aspect of stability is the possibility for snap-through solutions, in which one pressure yields multiple possible solutions for the deformation. These issues can be addressed by the use of arc-length methods [20]. However, for our constitutive laws such phenomena are not expected because total strain energy grows exponentially in strain while external work grows proportional to surface area. Indeed, our solutions show no indication of sudden jumps in volume or solver-independent points of failure.
In conclusion, in this study we have proposed a new formulation of incompressible large deformation mechanics. The method can improve the stability of simulations while maintaining computational efficiency.
Fig. 3. Eigenvalue analysis on the cylinder problem.
Panel A shows the minimum absolute eigenvalue decreasing for higher pressures, leading to very high condition numbers (Panel B). For the direct discretization without stabilization, the erratic values are caused by eigenvalues crossing zero (Panel C), which does not happen in the stabilized methods or isochoric/deviatoric approach.
Acknowledgments
This work was supported by the BBSRC (BB/J017272/1) and the EPSRC (EP/F043929/1 and EP/G007527/2). P. Lamata holds a Sir Henry Dale Fellowship jointly funded by the Wellcome Trust and the Royal Society (099973/Z/12/Z). The authors acknowledge financial support from the Department of Health via the National Institute for Health Research (NIHR) comprehensive Biomedical Research Centre award to Guy’s & St Thomas’ NHS Foundation Trust in partnership with King’s College London and King’s College Hospital NHS Foundation Trust
Contributor Information
Pablo Lamata, Biomedical Engineering Department, King’s College London, London SE17EH, UK; Department of Computer Science, University of Oxford, Oxford OX13QD, UK.
Nicolas P. Smith, Biomedical Engineering Department, King’s College London, London SE17EH, UK; Department of Engineering, The University of Auckland, Auckland, New Zealand
References
- [1].Nash MP, Panfilov AV. Electromechanical model of excitable tissue to study reentrant cardiac arrhythmias. Prog Biophys Mol Biol. 2004;85(2–3):501–522. doi: 10.1016/j.pbiomolbio.2004.01.016. [DOI] [PubMed] [Google Scholar]
- [2].Sermesant M, Rhode K, Sanchez-Ortiz GI, Camara O, An-driantsimiavona R, Hegde S, Rueckert D, Lambiase P, Bucknall C, Rosenthal E, Delingette H, et al. Simulation of cardiac pathologies using an electromechanical biventricular model and XMR interventional imaging. Med Image Anal. 2005 Oct;9(5):467–480. doi: 10.1016/j.media.2005.05.003. [DOI] [PubMed] [Google Scholar]
- [3].Land S, Niederer SA, Aronsen JM, Espe EKS, Zhang L, Louch WE, Sjaastad I, Sejersted OM, Smith NP. An analysis of deformation-dependent electromechanical coupling in the mouse heart. J Physiol. 2012 Sep;590(18):4553–4569. doi: 10.1113/jphysiol.2012.231928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Sheikh F, Ouyang K, Campbell SG, Lyon RC, Chuang J, Fitzsimons D, Tangney J, Hidalgo CG, Chung CS, Cheng H, Dalton ND, et al. Mouse and computational models link mlc2v dephosphorylation to altered myosin kinetics in early cardiac disease. J Clin Invest. 2012 Apr;122(4):1209–1221. doi: 10.1172/JCI61134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Land S, Louch WE, Niederer SA, Aronsen JM, Christensen GA, Sjaastad I, Sejersted OM, Smith NP. Beta-adrenergic stimulation maintains cardiac function in serca2 knockout mice. Biophys J. 2013 Mar;104(6):1349–1356. doi: 10.1016/j.bpj.2013.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Krishnamurthy A, Villongco CT, Chuang J, Frank LR, Nigam V, Belezzuoli E, Stark P, Krummen DE, Narayan S, Omens JH, McCulloch AD, et al. Patient-specific models of cardiac biomechanics. J Comput Phys. 2013 Jul;244:4–21. doi: 10.1016/j.jcp.2012.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Usyk TP, McCulloch AD. Electromechanical model of cardiac resynchronization in the dilated failing heart with left bundle branch block. J Electrocardiol. 2003;36:57–61. doi: 10.1016/j.jelectrocard.2003.09.015. [DOI] [PubMed] [Google Scholar]
- [8].Niederer SA, Plank G, Chinchapatnam P, Ginks M, Lamata P, Rhode KS, Rinaldi CA, Razavi R, Smith NP. Length-dependent tension in the failing heart and the efficacy of cardiac resynchronization therapy. Cardiovascular Research. 2011;89(2):336. doi: 10.1093/cvr/cvq318. [DOI] [PubMed] [Google Scholar]
- [9].Niederer S, Lamata P, Plank G, Chinchapatnam P, Ginks M, Rhode K, Rinaldi C, Razavi R, Smith N. Analyses of the redistribution of work following cardiac resynchronisation therapy in a patient specific model. PLoS ONE. 2012;7(8) doi: 10.1371/journal.pone.0043504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Lamata P, Roy I, Blazevic B, Crozier A, Land S, Niederer SA, Hose DR, Smith NP. Quality metrics for high order meshes: analysis of the mechanical simulation of the heart beat. IEEE Trans Med Imag. 2013 Jan;32(1):130–138. doi: 10.1109/TMI.2012.2231094. [DOI] [PubMed] [Google Scholar]
- [11].Lamata P, Niederer S, Nordsletten D, Barber DC, Roy I, Hose DR, Smith N. An accurate, fast and robust method to generate patient-specific cubic hermite meshes. Med Image Anal. 2011 Dec;15(6):801–813. doi: 10.1016/j.media.2011.06.010. [DOI] [PubMed] [Google Scholar]
- [12].Xi J, Lamata P, Niederer S, Land S, Shi W, Zhuang X, Ourselin S, Duckett SG, Shetty AK, Rinaldi CA, Rueckert D, et al. The estimation of patient-specific cardiac diastolic functions from clinical measurements. Med Image Anal. 2013 Feb;17(2):133–146. doi: 10.1016/j.media.2012.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Simo JC, Taylor RL, Pister KS. Variational and projection methods for the volume constraint in finite deformation elasto-plasticity. Comput Methods Appl Mech Eng. 1985;51(1):177–208. [Google Scholar]
- [14].Simo JC, Taylor RL. Quasi-incompressible finite elasticity in principal stretches. continuum basis and numerical algorithms. Comput Methods Appl Mech Eng. 1991 Feb;85(3):273–310. [Google Scholar]
- [15].Miehe C. Aspects of the formulation and finite element implementation of large strain isotropic elasticity. Int J Numer Methods Eng. 1994;37(12):1981–2004. [Google Scholar]
- [16].Flory PJ. Thermodynamic relations for high elastic materials. Transactions of the Faraday Society. 1961 Jan;57(0):829–838. [Google Scholar]
- [17].Wriggers P. Nonlinear finite element methods. Springer; 2008. [Google Scholar]
- [18].Göktepe S, Acharya SNS, Wong J, Kuhl E. Computational modeling of passive myocardium. Int J Numer Method Biomed Eng. 2011;27(1):1–12. [Google Scholar]
- [19].Wang HM, Gao H, Luo XY, Berry C, Griffith BE, Ogden RW, Wang TJ. Structure-based finite strain modelling of the human left ventricle in diastole. Int J Numer Method Biomed Eng. 2013;29(1):83–103. doi: 10.1002/cnm.2497. [DOI] [PubMed] [Google Scholar]
- [20].Holzapfel GA. Nonlinear solid mechanics: a continuum approach for engineering. Wiley-Blackwell; 2000. [Google Scholar]
- [21].Bonet J, Wood RD. Nonlinear Continuum Mechanics for Finite Element Analysis. 2nd ed. Cambridge University Press; 2008. Mar, [Google Scholar]
- [22].Nash MP, Hunter PJ. Computational mechanics of the heart. Journal of elasticity. 2000;61(1):113–141. [Google Scholar]
- [23].Usyk TP, LeGrice IJ, McCulloch AD. Computational model of three-dimensional cardiac electromechanics. Comput Vis Sci. 2002;4(4):249–257. [Google Scholar]
- [24].Watanabe H, Sugiura S, Kafuku H, Hisada T. Multiphysics simulation of left ventricular filling dynamics using fluid-structure interaction finite element method. Biophys J. 2004;87(3):2074–2085. doi: 10.1529/biophysj.103.035840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Pathmanathan P, Chapman SJ, Gavaghan DJ, Whiteley JP. Cardiac electromechanics: the effect of contraction model on the mathematical problem and accuracy of the numerical scheme. Q J Mech Appl Math. 2010;63(3):375–399. [Google Scholar]
- [26].Nordsletten D, Niederer S, Nash M, Hunter P, Smith N. Coupling multi-physics models to cardiac mechanics. Prog Biophys Mol Biol. 2011 Jan;104(13):77–88. doi: 10.1016/j.pbiomolbio.2009.11.001. [DOI] [PubMed] [Google Scholar]
- [27].Land S, Niederer SA, Smith NP. Efficient computational methods for strongly coupled cardiac electromechanics. IEEE Trans Biomed Eng. 2012 May;59(5):1219–1228. doi: 10.1109/TBME.2011.2112359. [DOI] [PubMed] [Google Scholar]
- [28].Xia H, Wong K, Zhao X. A fully coupled model for electromechanics of the heart. Comput Math Methods Med. 2012 Oct;2012 doi: 10.1155/2012/927279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Kerckhoffs RCP, Omens JH, McCulloch AD. A single strain-based growth law predicts concentric and eccentric cardiac growth during pressure and volume overload. Mechanics Research Communications. 2012 Jun;42:40–50. doi: 10.1016/j.mechrescom.2011.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Dal H, Göktepe S, Kaliske M, Kuhl E. A fully implicit finite element method for bidomain models of cardiac electromechanics. Comput Methods Appl Mech Eng. 2013 Jan;253:323–336. doi: 10.1016/j.cma.2012.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Cheng A, Langer F, Rodriguez F, Criscione JC, Daughters GT, Miller DC, Ingels NB., Jr Transmural cardiac strains in the lateral wall of the ovine left ventricle. Amer J Physiol Heart Circ Physiol. 2005 Apr;288(4):H1546–1556. doi: 10.1152/ajpheart.00716.2004. [DOI] [PubMed] [Google Scholar]
- [32].Guccione JM, McCulloch AD, Waldman LK. Passive material properties of intact ventricular myocardium determined from a cylindrical model. J Biomech Eng. 1991 Feb;113(1):42–55. doi: 10.1115/1.2894084. [DOI] [PubMed] [Google Scholar]
- [33].Legrice IJ, Hunter PJ, Smaill BH. Laminar structure of the heart: a mathematical model. Amer J Physiol Heart Circ Physiol. 1997 May;272(5):H2466–2476. doi: 10.1152/ajpheart.1997.272.5.H2466. [DOI] [PubMed] [Google Scholar]
- [34].Weiss JA, Maker BN, Govindjee S. Finite element implementation of incompressible, transversely isotropic hyperelasticity. Comput Methods Appl Mech Eng. 1996 Aug;135(12):107–128. [Google Scholar]
- [35].Helfenstein J, Jabareen M, Mazza E, Govindjee S. On non-physical response in models for fiber-reinforced hyperelastic materials. Int J Solids Struct. 2010 Aug;47(16):2056–2061. [Google Scholar]
- [36].Federico S, Grillo A, Giaquinta G, Herzog W. Convex fung-type potentials for biological tissues. Meccanica. 2008 Jun;43(3):279–288. [Google Scholar]
- [37].Holzapfel GA, Ogden RW. Constitutive modelling of passive myocardium: a structurally based framework for material characterization. Phil Trans R Soc A. 2009;367(1902):3445. doi: 10.1098/rsta.2009.0091. [DOI] [PubMed] [Google Scholar]
- [38].Lamata P, Sinclair M, Kerfoot E, Lee A, Crozier A, Blazevic B, Land S, Lewandowski AJ, Barber D, Niederer S, Smith N. An automatic service for the personalization of ventricular cardiac meshes. J R Soc Interface. 2014 Feb;11(91) doi: 10.1098/rsif.2013.1023. p. 20131023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Kerfoot E, Lamata P, Niederer S, Hose R, Spaan J, Smith N. Share and enjoy: anatomical models database - generating and sharing cardiovascular model data using web services. Medical & Biological Engineering & Computing. 2013:1–10. doi: 10.1007/s11517-012-1023-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Kass DA, Midei M, Brinker J, Maughan WL. Influence of coronary occlusion during PTCA on end-systolic and end-diastolic pressure-volume relations in humans. Circulation. 1990 Jan;81(2):447–460. doi: 10.1161/01.cir.81.2.447. [DOI] [PubMed] [Google Scholar]
- [41].Westerhof N, Elzinga G. Normalized input impedance and arterial decay time over heart period are independent of animal size. Am J Physiol Regul Integr Comp Physiol. 1991 Jul;261(1):R126–133. doi: 10.1152/ajpregu.1991.261.1.R126. [DOI] [PubMed] [Google Scholar]
- [42].Kerckhoffs RCP, Bovendeerd PHM, Prinzen FW, Smits K, Arts T. Intra- and interventricular asynchrony of electromechanics in the ventricularly paced heart. J Eng Math. 2003 Dec;47(3/4):201–216. [Google Scholar]
- [43].Schmid H, Nash MP, Young AA, Hunter PJ. Myocardial material parameter estimationa comparative study for simple shear. J Biomech Eng. 2006;128:742. doi: 10.1115/1.2244576. [DOI] [PubMed] [Google Scholar]