Abstract
Transcription is an episodic process characterized by probabilistic bursts; but how the transcriptional noise from these bursts is modulated by cellular physiology remains unclear. Using simulations and single-molecule RNA counting, we examined how cellular processes influence cell-to-cell variability (noise). The results show that RNA noise is higher in the cytoplasm compared to the nucleus in ~85% of genes across diverse promoters, genomic loci, and cell types (human and mouse). Measurements show further amplification of RNA noise in the cytoplasm, fitting a model of biphasic mRNA conversion between translation- and degradation-competent states. This multi-state translation-degradation of mRNA also causes substantial noise amplification in protein levels, ultimately accounting for ~74% of intrinsic protein variability in cell populations. Overall, the results demonstrate how noise from transcriptional bursts is intrinsically amplified by mRNA processing leading to large, super-Poissonian variability in protein levels.
Keywords: stochastic noise, bursting, mathematical modeling, noise-amplification, noise-attenuation
eTOC:
Transcription is a noisy process characterized by probabilistic bursts; but how fluctuations (noise) propagate from transcription though translation in eukaryotic cells remains unclear. Hansen et al. discover that the processes of mRNA export, translation and degradation, in general amplify transcriptional noise generating large variability in cell-to-cell protein levels.
INTRODUCTION
Intracellular biological reactions can exhibit large intrinsic fluctuations (i.e., stochastic ‘noise’) that manifest as cell-to-cell variability, even in isogenic populations of cells (Blake et al., 2003; Elowitz et al., 2002; Kaern et al., 2005; Kepler and Elston, 2001). These intrinsic, stochastic fluctuations partly originate during transcription (Golding et al., 2005; Raj et al., 2006), are subject to strong evolutionary selection pressures (Fraser et al., 2004; Metzger et al., 2015) and drive cell-fate decisions (Balázsi et al., 2011; Suel et al., 2007; Weinberger et al., 2005).
Transcriptional fluctuations can be largely due to the episodic nature of transcription, commonly called ‘bursting’, in which short periods of productive promoter activity are interspersed between long periods of promoter inactivity (Chong et al., 2014; Coulon et al., 2013; Dar et al., 2012; Golding et al., 2005; Raj et al., 2006; Sanchez and Golding, 2013; Singh et al., 2010; Suter et al., 2011; Zenklusen et al., 2008). These episodic transcriptional bursts appear to be predominant in mammalian cells, especially at low transcript abundance (Dar et al., 2012; Raj et al., 2006). In the common transcriptional bursting model, the ‘two-state random-telegraph’ model, a promoter toggles between a transcriptionally inactive OFF state and an active ON state (Kepler and Elston, 2001). While more than two promoter states may exist, all multistate transcription models generate super-Poissonian cell-to-cell distributions (high noise) in mRNA and protein, especially for the relatively slow toggling rates measured for many promoters (Harper et al., 2011; Zenklusen et al., 2008). These transcriptional bursting models contrast with minimally stochastic, single-state (i.e., constitutive) transcription models, which are Poisson processes and generate Poisson distributions for cell-to-cell variability in gene products. These Poisson distributions represent the theoretical low-noise limit for gene expression (Kaern et al., 2005), but the more complex multi-state models (e.g. random-telegraph models) are required to fit the vast majority of measured cell-to-cell expression distributions, which are super-Poissonian (Sanchez and Golding, 2013). Variability in the abundance of nascent transcripts—those still tethered to DNA at the transcriptional center—can fall under the Poisson limit (Choubey et al., 2015), because this scenario is not a Poisson process but a special case of an age-structured process described by a particular form of the gamma distribution called an Erlang distribution (Mittler et al., 1998). Nevertheless, once transcripts are released from the DNA, the process returns to a Poisson process and can no longer be considered age structured. Thus, after nascent transcripts are released from the DNA the distributions are, at best, Poisson limited.
Noise that originates during transcription can be modulated by various cellular mechanisms. For example, translation often amplifies transcriptional bursting noise (Ozbudak et al., 2002) and auto-regulatory gene circuits can, depending upon their architecture, either amplify or attenuate noise for their specific target genes (Arias and Hayward, 2006; Austin et al., 2006; Barkai and Leibler, 2000; Isaacs et al., 2003). However, recent studies have suggested that transcriptional noise is efficiently and non-specifically buffered to minimal Poisson levels by ‘passive’ cellular compartmentalization, specifically nuclear export (Battich et al., 2015; Stoeger et al., 2016). The resulting conundrum is, if compartmentalization broadly buffers noise to minimal levels, how can noise drive cell fate decisions? Moreover, how are transcriptional regulatory circuits able to modulate noise—i.e., attenuate (Arias and Hayward, 2006) or amplify (Weinberger et al., 2005) noise—when nuclear export acts as a strong downstream filter reducing noise to the theoretical limit?
Given the literature reporting super-Poissonian cytoplasmic mRNA and protein noise in nucleated eukaryotic cells, we sought to reconcile how evidence of super-Poissonian noise could co-exist with nuclear export passively and broadly buffering noise to minimal levels. Since we are specifically concerned with understanding how transcriptional fluctuations (i.e., bursts) are influenced by downstream processing (i.e. nuclear export), we examine the normalized variance of mRNA counts (a.k.a. Fano factor), the typical measure of transcriptional bursting (Blake et al., 2003; Munsky et al., 2012; Ozbudak et al., 2002; Sanchez and Golding, 2013). Using computational modeling and single-molecule quantitation by RNA Fluorescence in situ Hybridization (FISH), we predict and then experimentally measure mRNA noise in the nucleus and cytoplasm. We model across the known physiological parameter range and find that in the vast majority of cases (~85%), mRNA noise is amplified by export from the nucleus and is super-Poissonian in the cytoplasm. smFISH measurements corroborate this finding for diverse promoters (LTR, UBC, Ef1-1α, SV40, c-Jun, c-Fos, COX-2, FoxO, Per1, NR4A2 and NANOG) in different cell types. As predicted by modeling, modulation of nuclear export has little effect in changing this amplification. The smFISH measurements and perturbation experiments indicate a further post-export step of noise-amplification for cytoplasmic mRNA, which supports mRNA translation and degradation being mutually exclusive and is characterized by biphasic mRNA degradation. Finally, we present a model that quantifies how mRNA fluctuations originating at the promoter are amplified in the cytoplasm compared to the nucleus and predicts super-Poissonian protein noise from transcriptional measures. Overall, the findings demonstrate that transcriptional noise is intrinsically amplified in cells, showing how noise can act as a driving force in cell-fate decisions.
RESULTS
The standard model of gene expression predicts that—in the physiological parameter regime—transcriptional bursts are often amplified in the cytoplasm compared to the nucleus
To explore how cellular physiology influences gene expression noise, we used Gillespie’s method (Gillespie, 1977) to perform stochastic numeric simulations of a conventional model of eukaryotic mRNA transcription (Dar et al., 2014; Raj et al., 2006; Raser and O'Shea, 2004; Suter et al., 2011), expanded to include both the nuclear and cytoplasmic compartments (Figure 1A). Since most genes are co-transcriptionally spliced (Tilgner et al., 2012), splicing was incorporated into the transcription rate. A total of 7776 (65) parameter combinations were examined—with 1000 simulations run per parameter combination (i.e., over 7 million simulation runs)—allowing us to vary the rate of each cellular process (e.g., transcription, export, decay) over several orders of magnitude based on literature estimates (Bahar Halpern et al., 2015a; Bahar Halpern et al., 2015b; Battich et al., 2015; Dar et al., 2012; Harper et al., 2011; Suter et al., 2011). Mean (μ) and variance (σ2) in mRNA counts were determined for both nuclear and cytoplasmic compartments (Figure S1A-B), allowing for subsequent noise quantification.
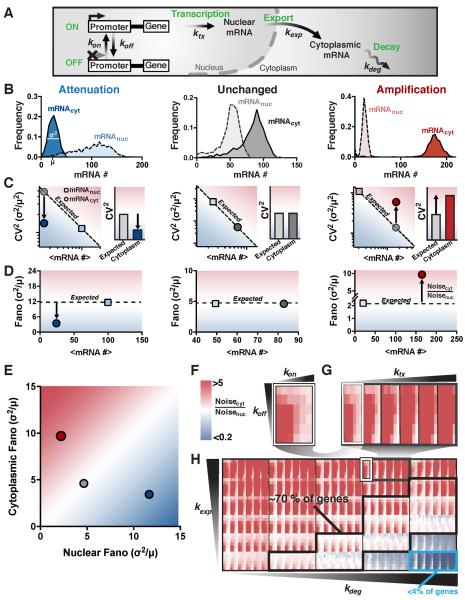
Figure 1: The random-telegraph model of gene expression predicts that mRNA noise is amplified by nuclear-to-cytoplasmic export. See also Figure S1 and Figure S2.
(A) Schematic representation of the conventional model of eukaryotic mRNA transcription expanded to include both nuclear and cytoplasmic compartments.
(B) Representative distributions of nuclear (dashed lines) and cytoplasmic (solid lines) mRNA for parameter combinations yielding noise attenuation (blue), unchanged noise (black), and noise amplification (red). Distributions are from 1000 simulations per parameter condition.
(C) Mean versus CV2 for nuclear (squares), expected cytoplasmic (grey circles) and cytoplasmic (colored circles) mRNAs, corresponding to each distribution in B. Bar graphs show the expected cytoplasmic CV2 due to Poisson scaling and the actual cytoplasmic CV2.
(D) Mean versus σ2/μ (Fano factor) for both nuclear (squares) and cytoplasmic (circles) mRNAs, corresponding to each distribution in B.
(E) Comparison of nuclear versus cytoplasmic mRNA noise (σ2/μ).
(F-H) Nuclear-to-cytoplasmic noise ratio (Noisecyt /Noisenuc) simulated for the physiologically possible parameter space, as calculated by varying each parameter from its highest-reported to its lowest-reported value (1000 simulations run per parameter combination; > 7 million runs). Increasing red represents increasing noise amplification while increasing blue represents increasing noise attenuation, white represents no change in noise from nucleus to cytoplasm. Panel F (a subpanel of G) shows how varying kon and koff across the full range of reported values, affects the noise ratio (all other parameters are kept fixed). Panel G (a subpanel of H) shows how varying ktx across its full range of reported values affects the noise ratio for the array of kon koff simulations. Panel H represents the full set of simulation results where the array of kon koff ktx simulations is varied over the full reported range of kexp and kdeg values. The probable parameter space (70% of measurements) is marked by the black box, whereas the cyan box (< 4% of measurements) represents the regime of efficient buffering.
When comparing mRNA noise in the nucleus and cytoplasm, three scenarios are possible: (i) Noise can be lower in the cytoplasm than in the nucleus (i.e. attenuated) (Figure 1B, blue); (ii) noise can be the same in both compartments (i.e. unchanged) (Figure 1B, grey); or (iii), noise can be higher in the cytoplasm than the nucleus (i.e. amplified) (Figure 1B, red).
Importantly, there are subtle but critical differences between the possible measures for noise, with the ideal quantification method depending on the question being addressed. For example, if the underlying distribution is of importance, then statistics such as the KS test could be used. On the other hand, if the frequency of the fluctuations is important then autocorrelation functions should be quantified. The coefficient of variation (CV2 = σ2/μ2) is an intuitive measure of fluctuation size with respect to the mean. However, its main drawback is that both mean and CV2 need to be taken into consideration for any comparative analysis. Therefore, a decrease in CV2 when comparing cytoplasmic to nuclear mRNA distributions does not necessarily translate to attenuation of promoter toggling noise because CV2 scales inversely with the mean. To correctly interpret decreased CV2 as an attenuation of transcriptional bursting, a scaling factor for the change in mean must be taken into account (Figure 1C, dashed “expected” line). In other words, a decrease in CV2 is only an effective attenuation of transcriptional bursts if the decrease is greater than would be obtained by a simple scaling of the mean such that CV2cytoplasm < CV2expected (i.e., attenuated noise only occurs when the CV2 falls below the “expected” dashed diagonal in Figure 1C, left). In contrast, a direct measure of changes in transcriptional bursting is typically calculated by variance over the mean (σ2/μ; a.k.a,, the Fano factor) (Blake et al., 2003; Munsky et al., 2012; Ozbudak et al., 2002; Sanchez and Golding, 2013; Thattai and van Oudenaarden, 2001), which omits the somewhat complex scaling properties of CV2 (see Star Methods: Analytical arguments for protein noise dependence on Fano factor versus CV2, for an in depth mathematical explanation). Consequently, the Fano factor automatically provides a measure of both the magnitude of fluctuations and deviation from a Poisson process (where σ2/μ = 1), and arguably provides a more direct and concise measure of noise propagation during mRNA processing. For example, attenuation of transcriptional noise from downstream mRNA processing corresponds to σ2/μ approaching a Poisson process (where σ2/μ = 1) while amplification of transcriptional noise corresponds to σ2/μ increasing and diverging from a Poisson process (Figure 1D–E). Hence, to understand how the downstream propagation of transcriptional noise is modulated, we focus on changes in the Fano factor, the typical measure of transcriptional bursting (Blake et al., 2003; Munsky et al., 2012; Ozbudak et al., 2002; Sanchez and Golding, 2013; Thattai and van Oudenaarden, 2001).
We examined the noise ratio—Noisecytoplasm / Noisenucleus (i.e. Fanocytoplasm / Fanonucleus, which is equivalent to CV2cytoplasm /CV2expected)—for all 7776 parameter combinations (Figure 1F-H). Remarkably, the results show that for most combinations of physiologically relevant parameters, mRNA noise is largely amplified in the cytoplasm compared to the nucleus (Figure 1F–H, red rectangles). Moreover, the possible physiological parameter space can be further limited to a probable regime using previously reported genome-wide mRNA counts (Bahar Halpern et al., 2015a). Namely, the reported nuclear and cytoplasmic mRNA counts were used to estimate likely ratios of mRNA export-to-degradation rates (Figure S1C, and Star Methods Equations 1–5), which largely determine whether noise is amplified, unchanged, or attenuated. This data constraint is applied to generate a probable physiological parameter regime in which amplification becomes even more prevalent (Figure 1H and Figure S1D, black box). Specifically, about 15% of genes across the genome show >20-fold higher export rates than degradation rates, thus falling within the parameter regime of highly amplified cytoplasmic noise. Another 70% of genes across the genome have significantly faster rates of export than degradation, also falling in the parameter regime of amplification. Finally, only ~15% of genes across the genome fall in the parameter regime in which the rate of export is slower than cytoplasmic mRNA degradation, of which less than 4% have rates where substantial noise attenuation (>5-fold) is even possible (Figure 1H, light blue box). Thus, the data constraints show that ~85% of genes fall in the parameter regime in which noise is amplified in the cytoplasm and only about 2.5% of genes fall in the parameter regime where noise is attenuated down to minimally stochastic Poisson levels—substantially less than previously implied (Battich et al., 2015). A discrete-diffusion model of nuclear export does not alter these results (Figure S1E-G and Figure S2A-D).
Analytically, a fairly simple expression for the Fano factor ratio between cytoplasm and nucleus can be obtained (see Star Methods: Analytical derivation):
| Eq.(1) |
Where ⟨N⟩ and ⟨C⟩ are the mean mRNA abundances in the nucleus and cytoplasm, respectively, while ξcyt and ξnuc are the noise bandwidths (Simpson et al., 2003) in the cytoplasm and nucleus, respectively. In both cases, the noise bandwidth is dominated by the lowest critical frequency it is associated with (i.e. either the critical frequency of promoter toggling or mRNA export for ξnuc, and either the critical frequency of promoter toggling, mRNA export or degradation for ξcyt). Intuitively, this means that ξnuc ≥ ξcyt, since ξcyt can be dominated by the additional critical frequency associated with degradation, which has no impact on ξnuc. Therefore, for all cases Eq. [1] reduces to , and when ⟨C⟩ > ⟨N⟩, only for a small parameter regime where the noise bandwidth in the cytoplasm is sufficiently smaller than it is in the nucleus. As a result, there is a strong tendency for Noisecyt > Noisenuc when ⟨C⟩ > ⟨N⟩ (Bahar Halpern et al., 2015a). Given previous reports that most genes exhibit ⟨C⟩ > ⟨N⟩, most genes are expected to fall in the amplification regime as the numerical simulations show (Figure 1H).
Single-molecule mRNA quantification shows generalized amplification of noise in the cytoplasm
To experimentally test the model predictions that noise is generally amplified in the cytoplasm, we used single-molecule RNA Fluorescence in situ Hybridization (smFISH) to quantify individual mRNA transcripts in both the nucleus and cytoplasm. To span across the physiological parameter regime, we examined both a panel of GFP-expressing reporter constructs which exhibit widely different transcriptional bursting and expression rates (Figure 2), as well as endogenous genes c-Jun, c-Fos, COX-2, PER1, FoxO, NR4A2 and NANOG (Figure 3).
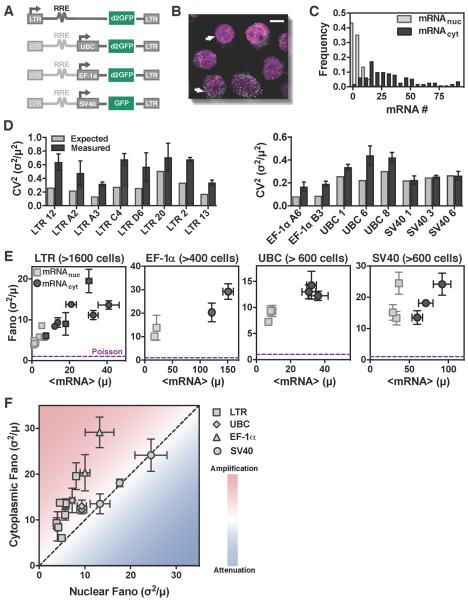
Figure 2: Single-molecule mRNA counting shows amplification of noise in the cytoplasm, independent of promoter type and genomic locus. See also Figure S3.
(A) Schematic of reporter constructs used to express mRNAs from the HIV-1 LTR promoter in isoclonal populations of human T lymphocytes (Jurkat) and from the UBC, SV40, and EF-1α promoters in isoclonal populations of human myeloid leukemia cells (K562).
(B) Representative smRNA FISH micrograph of an isoclonal T-lymphocyte population (maximum intensity projection of 15 optical sections, each spaced 0.4 μm apart) where DNA has been DAPI stained (purple) and mRNAs (white dots) are GFP mRNAs expressed from a single lentiviral-vector integration of a GFP-reporter cassette. Scale bar represents 5 μm, and arrows point towards two similarly sized cells that show high variability in mRNA levels.
(C) Typical probability distribution of cytoplasmic and nuclear mRNA numbers for a single mRNA reporter species (e.g. GFP mRNA) in an isoclonal population of T cells, after extrinsic noise filtering.
(D) Expected (grey) versus measured (from smFISH, black) cytoplasmic CV2 of mRNAs expressed from all four promoters.
(E) Mean mRNA expression (μ) versus noise (σ2/μ) for both nuclear (squares) and cytoplasmic (circles) mRNAs. Data points are biological replicates, and error bars represent SEM. The minimal noise defined by a Poisson process is shown as a purple line (σ2/μ = 1).
(F) Comparison of nuclear versus cytoplasmic mRNA noise (from smFISH) for all promoters (LTR, UBC, EF-1α, and SV40) shows that noise is primarily amplified from nucleus to cytoplasm. Data points are mean of two biological replicates, and error bars represent SEM.
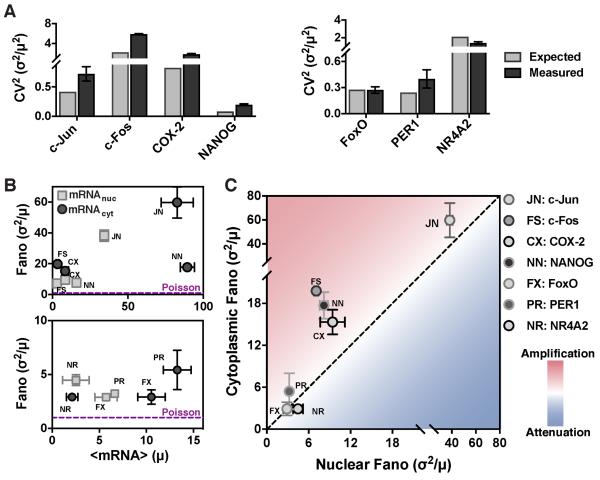
Figure 3: Endogenous genes exhibit amplification of mRNA noise from nucleus to cytoplasm.
(A-B) smFISH analysis, post extrinsic-noise filtering, for Per1, NR4A2, FoxO, c-Jun, c-Fos, and COX-2 mRNAs in human embryonic kidney cells (293) and for NANOG mRNA in mouse embryonic stem cells. Data points are biological replicates, and error bars represent SEM. (A) Expected versus measured cytoplasmic CV2 of expressed mRNAs. (B) Mean mRNA expression (μ) versus noise (σ2/μ) for both nuclear (squares) and cytoplasmic (circles) mRNAs.
(C) Comparison of nuclear versus cytoplasmic noise, (from smFISH) for Per1, NR4A2, FoxO, c-Jun, c-Fos, COX-2, and NANOG shows that cytoplasmic mRNA noise is primarily amplified.
For the reporter constructs, lentiviral vectors were used to semi-randomly integrate the reporters into the genome and isoclonal populations were generated from individual transduced cells such that each isoclone carried a single promoter integrated at a unique genomic locus. This approach controls for the effect of a specific genomic locus on both noise levels (Becskei et al., 2005) and the localization of nuclear transport machinery (Casolari et al., 2004) by allowing for analysis of the same promoter at multiple genomic loci. The reporter constructs (Figure 2A) used a range of both human and viral promoters, including: the human ubiquitin C (UBC) promoter, which drives an essential cellular housekeeping gene and results in abundant protein expression across integration sites and cell types (Kim et al., 1990); the human elongation factor 1α (EF-1α) promoter, a stronger constitutive promoter also expressing an essential cellular housekeeping gene; the HIV-1 long terminal repeat (LTR) promoter, an inducible and exceptionally bursty viral promoter; and, the Simian virus 40 (SV40) promoter, a viral promoter that is far less bursty than the LTR promoter (Dar et al., 2012; Gilbert et al., 2013).
Isoclonal populations were imaged using three-dimensional (3D) confocal microscopy (Figure 2B and S3A–B), and individual mRNA molecules were quantified to give the number of mRNAs per cell, which in turn allowed quantification of the Fano factor. Cells were then analyzed with a series of extrinsic-noise filtering steps that eliminate contributions to the Fano factor arising from external stimuli (Raj et al., 2006). Consistent with previous observations (Padovan-Merhar et al., 2015), analysis of correlation strength between cellular volume, shape, and DNA-stain intensity with mRNA count indicated that cell size was the strongest measure of extrinsic noise (i.e., mRNA copy number scales most tightly with cell size) (Figure S3C–F). Consequently, our analysis focused primarily on size-dependent extrinsic-noise filtering, as done in similar genome-wide analyses in yeast (Newman et al., 2006). To confirm that the extrinsic-noise filtering efficiently removes predictable (extrinsic) noise, we identified 10 cell components from our imaging and performed multi linear regression (MLR) on both nuclear and cytoplasmic mean mRNA counts (Figure S3G). We then performed MLR-filtering (see Star Methods for specifics) so that the prediction strength (i.e. R2) of our MLR model drops below 0.1 (Figure S3H-I). Comparing noise values of MLR-filtering and our extrinsic noise filtering (Figure S3J) shows that, as expected, we efficiently filter out predictable noise. Nuclear and cytoplasmic mRNA counts were measured through 3D image analysis and DAPI staining of nuclear DNA. Frequency distributions (Figure 2C) were obtained for each isoclonal population of cells (minimum of ~100 cells, as much lower cell counts significantly increased the calculated Fano factors by increasing the effect of outliers) (1Figure S3E).
As predicted by the simulations (Figure 1) and analytic arguments (Eq. [1]), smFISH mRNA quantifications largely show amplification of mRNA noise in the cytoplasm relative to the noise in the nucleus; in virtually all cases, the CV2 of cytoplasmic mRNA is significantly higher than expected from Poisson scaling (Figure 2D), with all data falling far above the minimally stochastic Poisson noise (Fano factor = 1) for all promoters (Figures 2E). The SV40 promoter was the only promoter with comparable mRNA noise in the nucleus and cytoplasm, although it still generated mRNA noise far from Poissonian in both the nucleus and cytoplasm. Directly comparing cytoplasmic versus nuclear noise for all four promoters (16 genomic loci), shows that, in most cases, cytoplasmic noise was significantly amplified relative to nuclear noise (Figure 2F), with the data falling within the parameter space that most genes were predicted to fall (Figure S1D). This generalized amplification of mRNA noise in the cytoplasm occurs despite very different mRNA mean and noise levels.
To further validate these results, smRNA FISH was performed on seven endogenous genes in adherent cell lines (mouse embryonic stem cells and human embryonic kidney cells). These measurements encompass a circadian clock gene (PER1), a gene constitutively expressed in the pluripotent state (NANOG), and five signal-responsive genes (three immediate-early response genes c-Jun, c-Fos, and NR4A2; the forkhead transcription factor, FoxO1; and, a late-response gene COX-2). Consistent with data from non-adherent cell lines (Figure 2), the majority of these genes exhibit cytoplasmic mRNA noise that is amplified relative to nuclear noise (i.e., CV2 larger than expected from Poisson scaling) and is far above the minimally stochastic Poisson limit (Figure 3A-B). While NR4A2, COX-2 and c-Fos have a similar number of mRNAs in the nucleus and cytoplasm, NANOG, PER1, FoxO and c-Jun have higher cytoplasmic than nuclear means (Figure 3B). Five of the genes show higher cytoplasmic than nuclear noise and fall in the amplification regime, FoxO falls in the unchanged regime, and NR4A2 is the only gene which shows slight attenuation of cytoplasmic mRNA noise compared to nuclear mRNA noise (Figure 3C). Thus, in agreement with theoretical predictions (Figure 1 and Eq. [1]), experimental observations show that the majority of genes exhibit amplification of mRNA noise in the cytoplasm compared to the nucleus, especially when the mean cytoplasmic abundance is greater than the mean nuclear abundance.
As predicted, cytoplasmic mRNA and protein noise are largely insensitive to changes in nuclear export
To test model predictions of the effects of nuclear export on cytoplasmic noise, we computationally and experimentally perturbed nuclear export. Numerical simulations and analytical arguments (Eq. [1]) predicted that slowed nuclear export should only impact nuclear noise, without affecting cytoplasmic noise (Figure 4A, Figure S4A), because most genes fall in a regime in which nuclear export is much faster than cytoplasmic mRNA degradation (kexp >> kdeg). An important assumption of the model is that nuclear-export rate is not operating in the saturated regime, which could lead to nuclear pileup of mRNA, manifesting as reduced net export, and alter these predictions (Xiong et al., 2010). To verify that nuclear export is not saturated, transcriptional center (TC) intensity and frequency were measured by smFISH, and then used together with nuclear mRNA means to quantify the export rate (see Star Methods: Rate calculations) after transcriptional activation with tumor necrosis factor (TNF) (Duh et al., 1989) for 24 hours. We did not observe altered nuclear-export kinetics compared to the untreated control, indicating that export is operating far from saturation (Figure S4F). Overall, simulations predict that export rates can be the cause of altered nuclear-to-cytoplasmic noise ratio (Figure 4A); however, the export rate does not impact cytoplasmic mRNA noise and, consequently, is predicted to have no impact on protein noise.
Figure 4: Slowed nuclear export can cause apparent attenuation of nuclear-vs-cytoplasmic RNA noise by amplifying nuclear RNA noise and not decreasing cytoplasmic RNA noise. See also Figure S4.
(A) Simulations predict that slowing the nuclear export rate shifts the nuclear-to-cytoplasmic noise ratio by affecting nuclear noise.
(B–C) smFISH analysis of HIV LTR–expressed mRNA in isoclonal cells treated with the nuclear-export inhibitor leptomycin B (green). Nuclear mean and noise increase whereas cytoplasmic mean or noise remain unchanged (grey).
(D) Comparison of nuclear versus cytoplasmic mRNA noise by smFISH analysis before and after leptomycin B treatment. All isoclonal populations remain in the amplification regime.
(E) Protein (d2GFP) noise of the same isoclones measured by flow cytometry before and after 5 hours of leptomycin B treatment. As predicted, no change in noise is observed. Inset: cytoplasmic mRNA noise from (C) for comparison. All data points represent means of two biological replicates, and error bars represent SEM.
To experimentally perturb nuclear-export rates, we took advantage of the fact that HIV and lentiviral reporter constructs (e.g., the LTR-GFP construct, Figure 2A) can utilize the cellular chromosome region maintenance 1 (CRM1) pathway for nuclear export (Felber et al., 1989; Malim et al., 1988; Ossareh-Nazari et al., 1997) even in the absence of Rev (Urcuqui-Inchima et al., 2011). Cells were treated with leptomycin B, a small-molecule inhibitor of CRM1-mediated nuclear export, (Watanabe et al., 1999) and imaged by smRNA FISH. Both dose and duration of leptomycin B were titrated to determine the maximum tolerable concentration (Figure S4C-D) (i.e., 0.6 ng/mL for 2.5 hours gave minimal cytotoxicity while still giving significantly increased mean nuclear mRNA). As above, extrinsic-noise filtering (i.e., cell size and DNA content) was employed, which further controls for cytotoxic effects, because dying and dead cells tend to be smaller. To validate that the nuclear-export rate was specifically decreased, without affecting other rates (Figure S4E-F), we measured TC intensity and frequency by smFISH, and then used mRNA distributions to calculate rates for each individual biochemical step in mRNA biogenesis as previously done (Bahar Halpern et al., 2015a; Munsky et al., 2012).
As predicted, the data shows that both the mean and noise of nuclear mRNA increased significantly (paired t test: p=0.012 and p=0.007) when nuclear export is diminished approximately 2-fold (Figure 4B). In contrast, neither mean nor noise of cytoplasmic mRNA change significantly when nuclear export is diminished (paired t test: p = 0.374 and p = 0.06, respectively) (Figure 4C-D). Protein noise did not change significantly (paired t test: p = 0.162) (Figure 4E) despite use of a short-lived GFP reporter that is particularly sensitive to changes in transcriptional noise (Dar et al., 2012). This result is expected given the lack of change in cytoplasmic mRNA noise. To test that these results were not caused by an off-target effect of leptomycin B (i.e. observed effects were specific to inhibition of CRM1 export pathway), we treated the SV40 and UBC promoters with leptomycin B. Transcripts expressed from either promoter lack an RRE (Figure 2A) and are presumably not exported via the CRM1 dependent pathway. Therefore, mRNA expressed from either SV40 or UBC should be insensitive to leptomycin B treatment. As expected, we found no significant difference in nuclear mRNA distributions (KS test p > 0.1 compared to p <0.0001 for LTR isoclone A3, Figure S4G).
In extreme cases when export rates fall below the mRNA-degradation rates—as occurs for a small fraction of genes (Bahar Halpern et al., 2015a)—the situation is slightly different. In this regime, cytoplasmic noise can be affected by decreases in export rate (Figure S4A). However, even for a conservatively low protein half-life of two hours, simulations show that this decrease in cytoplasmic mRNA noise cannot propagate to protein noise (Figure S4B). Consequently, for most physiologically relevant parameters, nuclear export is predicted to cause noise amplification rather than attenuation.
Cytoplasmic mRNA noise is further amplified by super-Poissonian mRNA decay and translation processes caused by mRNA switching between alternate states
Based on previous reports (Battich et al., 2015), we next explored whether there might be noise-attenuation processes concealed within the data. Briefly, we used a common model-validation approach (Munsky et al., 2012) to determine whether cytoplasmic mRNA distributions could be predicted from measured nuclear mRNA distributions using the existing model parameter estimates (Figure S4E). If nuclear mRNA distributions predicted broader cytoplasmic mRNA noise distributions than experimentally measured, it could indicate hidden noise-attenuation processes. The goal of this analysis is distinct from the analysis above (Figure 2), which shows that cytoplasmic noise is higher than predicted from the cytoplasmic mean level. Instead, the goal of this analysis was to test if measured cytoplasmic noise levels are different than predicted from nuclear parameters (i.e., transcriptional burst frequency, transcriptional burst size, mean, and noise).
The data show precisely the opposite of attenuation: the experimentally measured cytoplasmic RNA distributions are significantly broader than predicted from nuclear distributions [KS test: p = 0.0002 (Figure 5A, right panel, grey bar chart versus green dashed line)]. To fit both nuclear and cytoplasmic mRNA distributions, we then analyzed a series of models of increasing complexity in order to arrive at a best-fit model of lowest complexity (Figure S5). We examined eight models consisting of: (Models i-ii) single to multiple mRNA states followed by first order mRNA degradation; (Models iii-iv) single to multiple mRNA states with zero-order mRNA degradation; (Models v-vii) multiple mRNA states with the rate of mRNA entering the degradation-competent state exhibiting zero-order kinetics, followed by first order mRNA degradation; (Model viii) one mRNA state with ribosomes switching from a translationally active to inactive state, followed by first order mRNA degradation only occurring in the translationally inactive state. While nuclear mRNA distributions could be fit by all models examined, the amplified mRNA noise in the cytoplasm could only be fit when mRNA degradation was modeled in a biphasic manner (Model vii or viii) rather than as a simple Poisson process (i.e., exponential waiting times).
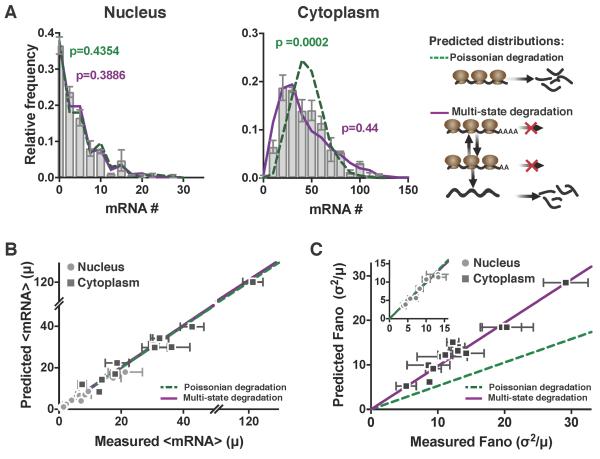
Figure 5: Cytoplasmic mRNA noise is further amplified by multi-state mRNA decay. See also Figure S5 and Figure S6.
(A) Representative smFISH probability distributions of nuclear and cytoplasmic HIV LTR–expressed mRNA in an isoclonal population of human T lymphocytes. Both the single-state Poissonian degradation model (dashed green line) and multi-state degradation model (solid purple line) fit the experimental probability distribution (bar graph) of nuclear mRNA levels (left column), but the mRNA distribution in the cytoplasm (middle column) is significantly wider than predicted from Poissonian degradation (dashed green line) and fits a multi-state super-Poissonian degradation model (solid purple line). Schematics of each degradation model are shown on the right. P values are from KS test to the experimental data.
(B) Both the super-Poissonian and Poissonian degradation models accurately predict nuclear (circles) and cytoplasmic (squares) mean mRNA levels – paired t-test p = 0.1623 and 0.3737 respectively.
(C) The Poissonian degradation model (dashed line) does not accurately predict the cytoplasmic mRNA noise – paired t-test p=0.0002. Only the super-Poissonian degradation model (solid line) accurately predicts both nuclear (circles–inset) and cytoplasmic (squares) mRNA noise – paired t-test p=0.1411 and 0.1623 respectively. Inset: both models accurately predict nuclear mRNA noise.
(B–C) All data points are mean of two biological replicates, and error bars represent SEM. Lines are linear regressions.
Notably, we were unable to determine which of the two models (either vii or viii) is responsible for the observed cytoplasmic mRNA noise amplification. However, both resulting best-fit models [Model vii and viii; KS test: p > 0.42 (Figure 5A, right panel, grey bar chart versus purple full line)] incorporate two previously documented phenomena: (1) biphasic mRNA degradation in mammalian cells (Yamashita et al., 2005); and (2) the well-documented inverse relationship between translation rates and rates of mRNA degradation (LaGrandeur and Parker, 1999; Parker, 2012; Presnyak et al., 2015), which posits that translational machinery protects mRNA from degradation or, vice versa, that the presence of mRNA degradation machinery inhibits translation.
To further validate these multi-state degradation (super-Poissonian) models, we analyzed the panel of clones from above (Figure 2). We first double-checked that the measured TC frequency and size could accurately predict mRNA distributions in the nucleus and, consistent with the computational predictions, measured TC size and frequency indeed accurately predicted nuclear mRNA distributions using either a Poisson or the non-Poisson models for all clones (Figures 5A, left panel, and 5B-C circles). However, consistent with the results above (Figure S5), for all clones examined, cytoplasmic mRNA distributions had substantially higher noise than predicted by Poisson degradation and these super-Poissonian distributions could be fit by the multi-state mRNA degradation models (Figures 5A, right panel, and 5C squares). Overall, these data confirm a further amplification of cytoplasmic mRNA noise relative to the nucleus, consistent with multi-state (super-Poissonian) mRNA degradation.
To experimentally test the multi-state translation-degradation models, we next analyzed the effects of two small-molecule inhibitors (cyclohexamide and lactimidomycin) that block mRNA translation through alternate mechanisms of action (Figure S6A-C) and that numerical simulations predicted would have inverse effects on mRNA half-life in the translation-degradation model (Figure S6D, dashed lines). Specifically, cyclohexamide (CHX) inhibits the elongation of ribosomes, causing ribosomes to accumulate on the mRNA (Lee et al., 2012), whereas lactimidomycin (LTM) inhibits the final step of translational initiation (Lee et al., 2012). If mRNAs undergo multi-state degradation-translation with ribosomes protecting mRNAs from degradation, the model predicts that CHX would prevent transcripts from entering the degradation-competent state, resulting in a lower kon_deg (or lower koff_rib) and longer mRNA half-life (predictions shown in Figure S6D, left – dashed blue line). In contrast, in the presence of LTM, the mRNA is free of ribosomes—except for the initiating ribosome which is frozen in place—and more susceptible to exosomal decay (Garneau et al., 2007). Consequently, the model predicts that LTM should push transcripts into the degradation-competent state, resulting in a higher kon_deg (or lower kon_rib) and a decrease in mean cytoplasmic mRNA per cell (Figure S6D, right – dashed red line). Despite both CHX and LTM inhibiting protein translation to the same extent (Figure S6A), CHX causes an accumulation of cytoplasmic mRNA over time while LTM treatment shows a decrease in cytoplasmic mRNA (Figure S6D), as predicted. We did observe LTM inducing an initial 1-hr transient increase in cytoplasmic mRNA preceding the decrease, and, as previously reported, this transient increase could be due to the cell globally decreasing degradation rates as a response to stress (Horvathova et al., 2017). These changes in cytoplasmic mRNA levels are not due to changes in transcription rate, since the nuclear mean (Figure S6D, black data points) and respective distributions (Figure S6B) show no significant differences. Overall, a multi-state mRNA translation-degradation model appears to be the most parsimonious with the cytoplasmic RNA data.
Multi-state mRNA translation-degradation amplifies protein noise, accounting for up to 74% of intrinsic cell-to-cell variability in protein levels
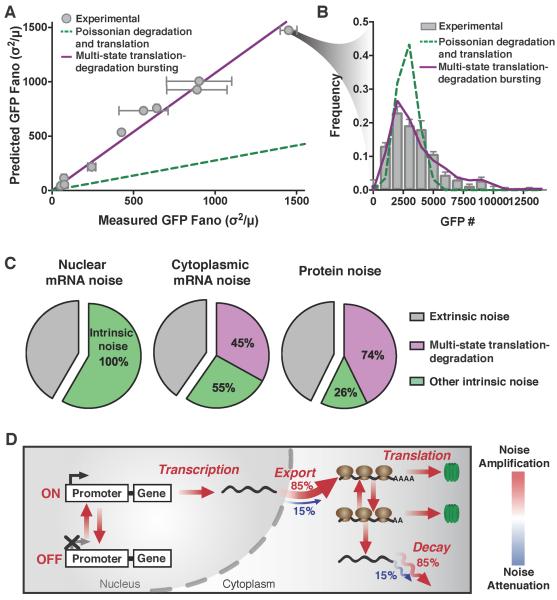
To examine how mRNA noise propagates to protein levels, we combined quantitative protein imaging with cytoplasmic smRNA FISH. GFP levels were quantified in individual isoclonal LTR-GFP reporter cells by confocal microscopy (Figure 6A-B, grey circles and bars), and molecular concentrations were calculated by calibration against purified, soluble GFP standards (Figure S7A). Using the measured mean GFP level and half-life (Dar et al., 2012) in combination with previously established parameters (Figures S4E), simulations were used to identify which of the previously developed models could best fit the protein data (Figure S5). As above, the protein distributions can only be fit using the seventh or eighth model where both degradation and translation are multi-state (i.e., super-Poissonian) processes (KS test p > 0.45). Notably, these multi-state processes are fundamentally different from previously reported translational “bursting” (Thattai and van Oudenaarden, 2001) (Figure S7C, green line), as they generate a significantly higher degree of noise amplification in a translation-competent mRNA species and hence in protein (Figure S7C, purple line). These multi-state degradation and translation models—where translation and degradation are mutually exclusive—are necessary and sufficient to explain the amplified mRNA noise in the cytoplasm, as well as the measured protein noise for the various promoters and integration sites examined (Figure 6A-B and S7B).
Figure 6: Protein noise is linked to cytoplasmic mRNA noise, indicating an overall model for amplification of transcriptional noise. See also Figure S7.
(A) Measured versus predicted noise (σ2/μ) of d2GFP levels expressed from the HIV LTR promoter in isoclonal population of human T lymphocytes, and from the UBC, and EF-1α promoters (grey squares) in isoclonal populations of human myeloid leukemia cells, determined by microscopy. The single-state Poissonian translation-degradation model (dashed line) poorly predicts the measured d2GFP expression noise (grey circles). While the super-Poissonian translation-degradation model (solid line) can accurately predict protein noise. Data points are the mean of two biological replicates, and error bars represent SEM.
(B) Representative probability distribution of experimental data (bar graph) is significantly wider than the distribution predicted from Poissonian degradation and translation (dashed line), but is fit by a multi-state degradation and translation model (solid line). P values are from KS test to the experimental data.
(C) Contributions from extrinsic noise (grey), multi-state translation-degradation (purple) and all other intrinsic noise (green) to total nuclear mRNA, cytoplasmic mRNA or protein noise.
(D) Schematic of cumulative model showing steps that amplify (red) or attenuate (blue) expression noise.
Next, to determine the contribution of multi-state translation-degradation to overall cellular noise, and specifically intrinsic noise, we analyzed flow cytometry data and microscopy measurements against predictions from numerical simulations. First, using an established size-gating approach (Blake et al., 2003; Newman et al., 2006; Singh et al., 2010) that isolates cells with similar sizes (correlates to cells synchronized by cell-cycle state) we separated intrinsic and extrinsic noise (Figure S7D and S3C-G). While this size-gating approach may slightly under-estimate extrinsic factors (Newman et al., 2006), it excludes the majority of extrinsic cellular variability especially for low expressing genes, which is an expression regime where other methods (e.g., two-color analysis) are technically difficult to employ. Consistent with previous large-scale analysis of low abundance genes in eukaryotes (Bar-Even et al., 2006; Dar et al., 2012; Newman et al., 2006), we find that intrinsic factors appear to account for a large portion of total protein noise in flow cytometry data—the intrinsic contribution ranged from 59–76% for the LTR promoter (Figure S7F and S7H), to 41-61% for more highly expressing promoters (EF-1α, SV40 and UBC, Figure S7E and S7H) and ~37% for constitutively expressed NANOG (Figure S7G and S7H). Then, to determine how translation-degradation bursting quantitatively contributes to this intrinsic noise, we calculated the expected protein noise for all clones (LTR, EF-1α and UBC) under two alternate scenarios: (i) a scenario where noise is generated only from previously characterized sources (i.e., transcriptional bursting, nuclear export, and Poissonian mRNA degradation and translation); or, (ii) the scenario where multi-state translation and degradation is included as a potential noise source. This analysis indicates that for the LTR, UBC and EF-1α promoters in both human T lymphocytes and immortalized myelogenous leukemia cells, multi-state translation-degradation bursting accounts for ~74% of intrinsic cell-to-cell variability (Figure 6C) making it the dominant source of intrinsic cellular variability (other processes account for ~26% of intrinsic noise).
DISCUSSION
How cellular processes amplify or attenuate gene-expression fluctuations (noise) is crucial to designing synthetic gene-regulatory circuits (Hasty et al., 2002) and for efforts to efficiently specify cell fate (Blake et al., 2006; Dar et al., 2014). Here, we analyzed how transcriptional fluctuations are modulated by cellular processes as mRNAs proceed through translation. Since we are concerned with quantifying transcriptional fluctuations (i.e., bursts) and how they influence protein noise, we examined the normalized variance (a.k.a. Fano factor), the typical measure of transcriptional bursting (Blake et al., 2003; Munsky et al., 2012; Ozbudak et al., 2002; Sanchez and Golding, 2013; Thattai and van Oudenaarden, 2001).
Computational results (Figure 1) show that in the majority of physiologically relevant scenarios (approximately 85%), nuclear export of mRNA amplifies mRNA fluctuations generated by transcriptional bursts, and single-molecule RNA counting corroborates this prediction for several viral and mammalian promoters (LTR, UBC, EF-1α, SV40, c-Jun, c-Fos, COX-2, FoxO, Per1, NR4A2 and NANOG) in different mammalian cell types (Figure 2–3). The results also show that cytoplasmic mRNA noise is robust to changes in nuclear export (Figure 4), but can be substantially amplified by super-Poissonian mRNA decay (Figure 5) and translation processes (Figures 6). Cumulatively, the resulting models can predict protein noise from transcriptional measures and shows that the effects of nuclear export, mRNA degradation, and translation amplify gene-expression noise, resulting in cytoplasmic mRNA and protein distributions that are super-Poissonian (i.e., far from minimal Poisson noise). These results, which show that transcriptional noise propagates to the protein level, are consistent with findings that noise can drive diversifying (positive) selection for bet-hedging phenotypes (Balázsi et al., 2011; Beaumont et al., 2009; Raj and van Oudenaarden, 2008; Rouzine et al., 2015).
Relationship to previous findings
These results build on previous findings that translation can proportionally amplify transcriptional fluctuations (Thattai and van Oudenaarden, 2001) since a single RNA typically produces hundreds to thousands of protein molecules (Bar-Even et al., 2006; Blake et al., 2003)—i.e., fluctuations of a single mRNA molecule can generate large fluctuations in protein numbers. However, the multi-state translation-degradation models presented here are fundamentally different from previously reported translational “bursting” (Thattai and van Oudenaarden, 2001), which is not sufficient to fit measured noise levels. We also note that the findings herein are consistent with two computational studies showing that passive noise attenuation can only occur when nuclear mRNA export is very slow or in a saturation regime (Singh and Bokes, 2012; Xiong et al., 2010).
This study does not dispute that passive noise attenuation is possible, as it can occur when kexp < kdeg. Therefore, our data are also in agreement with a recent study showing that in ~15% of cases nuclear export is slower than cytoplasmic mRNA degradation, and that passive attenuation of mRNA noise can occur in this regime (Bahar Halpern et al., 2015a); whereas cytoplasmic mRNA noise is larger in magnitude than nuclear mRNA noise (i.e., amplification) when kexp > kdeg. An accompanying study reported that noise attenuation was more widespread (Battich et al., 2015) when quantifying noise for specific genes by CV2 (which scales with the mean). However, even when noise is quantified in terms of Fano factor (which is independent of mean scaling), our data (Figure 3) show different noise properties for a number of the same genes (i.e., COX-2, c-Fos, Per1, and FoxO). The HeLa cells and primary human keratinocytes examined in that study could exhibit significantly slower nuclear export and faster mRNA degradation than the lymphocytes, embryonic murine cells, and kidney cells examined here. However, a potentially more important difference is that Battich et al. analyze nuclear versus cytoplasmic noise for these genes in the pre-steady-state regime after perturbation (serum starvation), while gene expression was still in the process of re-establishing steady state (Battich et al., 2015). Consequently, during pre-steady-state (i.e. after transcription is initiated and before mRNA is exported to the cytoplasm), the nuclear mean mRNA and noise are likely to be higher than cytoplasmic mean and noise. How noise propagates during non-steady state kinetics is in itself an interesting question, however such pre-steady state analysis may not accurately predict the impact of nuclear export on noise in the steady state regime. Our data on the other hand are collected from cells expressing genes at a steady-state level.
Nevertheless, the results herein demonstrate that any potential attenuation of mRNA noise is unlikely to cause decreased protein noise, due to longer protein versus mRNA half-lives [in line with previous predictions (Singh and Bokes, 2012)], and possibly due to multi-state degradation and translation (Figure 5–6). A recent study also found higher-than-predicted cytoplasmic noise for transcripts expressed from 12 yeast genes, which was attributed to mRNA processing downstream of transcription (Choubey et al., 2015). Overall, amplification appears to be the most common form of noise modulation in the absence of specific gene-regulatory circuits. Intuitively, the widespread nature of noise amplification makes sense because of the inefficient and costly nature of noise attenuation. However, it is feasible that for certain genes where robust expression is important, the benefit of low noise outweighs the cost of noise attenuation.
Appropriateness of the Fano factor for comparing nuclear vs. cytoplasmic noise
Both the CV2 and Fano factor are typically used to quantify noise in biological systems and some may ask why an increase in mean—which naturally results in a reduction of CV2 (e.g. for a Poisson process)—is not a "legitimate" reduction of noise. We note that a reduction in CV2 from increasing the mean may indeed be ‘noise attenuation’ but, if the magnitude of the CV2 reduction differs from what would be obtained simply by increasing the mean (Poisson scaling), the discrepancy needs to be explained as we have done in this study (e.g., what mechanisms account for the discrepancy and why isn’t the noise change scaling with the mean as a Poisson?). Such discrepancies from Poisson scaling are in fact an established method used to characterize transcriptional bursting (Ozbudak et al., 2002) and also feedback regulation and malfunctions in circuits (Simpson et al., 2003). Thus, the use of CV2 is appropriate, but if Poisson scaling is not taken into account, underlying regulatory mechanisms will be missed; examining the Fano factor helps avoid this mistake. In essence, this is the reason that the conventional experiment is to alter noise independent of the mean (Dar et al., 2014; Maamar et al., 2007).
Another potential argument could be that in contrast to comparing nuclear-versus-cytoplasmic noise levels, the appropriate comparison is to compare noise with versus without nuclear export (i.e., in the regime of an infinite export rate). However, we are aware of no technique to eliminate the nucleus or generate an infinite export rate, whereas nuclear-versus-cytoplasmic noise can be empirically measured. This empirical definition also enables testing by perturbation experiments (Figure 4) and as Figure 4 shows, when nuclear export rate is pharmacologically decreased in cells, the results are in agreement with the model predictions.
Potential mechanisms of noise amplification
The data herein support a model for cytoplasmic mRNA degradation occurring in a bi-phasic manner (Yamashita et al., 2005), with translational initiation and mRNA degradation being inversely proportional and mutually exclusive processes (LaGrandeur and Parker, 1999; Parker, 2012; Pelechano et al., 2015; Schwartz and Parker, 1999). However, our data cannot distinguish between two competing models of bi-phasic degradation (Figure S5vii and S5viii). These models do not contradict recent data obtained from yeast demonstrating that some mRNAs undergo co-translational mRNA degradation (Pelechano et al., 2015). Since, both models require that translational initiation and degradation be mutually exclusive, elongation could still occur during 5’ to 3’ degradation. Hence, cytoplasmic mRNA is subject to another, multi-state process, which adds a significant noise-amplification step to gene expression. Several mechanisms could explain the multi-state degradation and translation including the association of non-translating mRNAs into P-bodies or stress granules, as P-bodies and stress granules are enriched with mRNA degradation and translational initiation machinery respectively (Decker and Parker, 2012). However, our smFISH data do not show evidence of mRNA aggregates in the cytoplasm. Therefore, the data appear more parsimonious with two other mechanistic models: (i) spatial heterogeneity in mRNA degradation and translation machinery, due to translational “hot-spots” (Katz et al., 2016), or heterogeneity in the amount of actively translating mRNA per cell (Pichon et al., 2016; Yan et al., 2016); or (ii) multi-state pseudo-zero order (or Michaelis-Menten-like) mRNA decay along with mutually exclusive degradation and translation.
Model limitations and caveats
While the computational model we employed was admittedly simplified—it considered only two transcriptional states without important processes such as splicing—the smFISH measurements show that amplification of noise occurs primarily via post-transcriptional processes in the cytoplasm (e.g., export, degradation and translation; see Figure 6D). If splicing were included as a rate-limiting step (Hao and Baltimore, 2013), it would add an extra noise source and most likely further amplify noise. Moreover, the results do not depend on the strict two-state random-telegraph transcription model, because noise amplification is primarily post-transcriptional—i.e., the noise amplification result would hold for other transcription models with greater than two transcriptional states (Corrigan et al., 2016; Neuert et al., 2013; Zoller et al., 2015). Finally, though a discrete diffusion model does not alter our results, if nuclear pores were saturated (i.e. nuclear export were pseudo-zero order) then attenuation may become more prevalent (Singh and Bokes, 2012; Xiong et al., 2010). Yet, our data show no evidence of nuclear export operating close to saturation.
It is not clear how widespread biphasic mRNA decay is across the mammalian genome or even across different mammalian cell types, and mRNAs that exhibit Poisson-like mRNA decay (Horvathova et al., 2017) would not be subject to this additional noise amplification step. From an evolutionary perspective it is conceivable that the ~15% of mRNA species that are subject to passive attenuation of mRNA noise (Bahar Halpern et al., 2015a) could also exhibit Poisson-like mRNA decay, allowing for a low-noise gene expression pathway. It is also possible that untranslated mRNAs, such as miRNAs or shRNAs, are not subject to multi-state degradation and accompanying noise amplification, due to the lack of protecting ribosomes; However, Dicer and other processing machinery could serve an equivalent protection role. Since miRNAs modulate protein levels via mRNA degradation and translational repression (Bartel, 2004), miRNAs could influence multi-state degradation and translation rates to modulate noise (Garg and Sharp, 2016; Schmiedel et al., 2015).
In summary, the results show that in the majority of scenarios, transcriptional noise is amplified by nuclear export and then further amplified by mRNAs switching between translation- and degradation-competent states. The results indicate that intrinsic cellular processes, amplify noise originating from transcriptional bursts and ultimately account for ~74% of the intrinsic noise. These amplification processes provide a foundational basis for how noise may have acted as a driving force in cell-fate decisions, and explains why transcriptional regulatory circuits are required to modulate noise.
STAR METHODS
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and reagents should be directed to and will be fulfilled by Leor S. Weinberger (leor.weinberger@gladstone.ucsf.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Cell lines
Mouse E14 embryonic stem cells (male) were cultured in feeder-free conditions on gelatin-coated, 10cm Corning plates (Sokolik et al., 2015). ESGRO 2i + LIF media (SF016-200) was used for cell culture. Jurkat T Lymphocytes (male) were cultured in RPMI-1640 medium (supplemented with L-glutamine, 10% fetal bovine serum, and 1% penicillin-streptomycin), at 37°C, 5% CO2, in humidified conditions at b 0.05 × 105 to 1 × 106 cells/mL. Human immortalized myelogenous leukemia (K652, female) cells were cultured in RPMI-1640 medium (supplemented with L-glutamine, 10% fetal bovine serum, and 1% penicillin-streptomycin), at 37°C, 5% CO2, in humidified conditions at 2 × 105 to 2 × 106 cells/mL. Human embryonic kidney (HEK293, female) cells were cultured in DMEM (supplemented with 10% fetal bovine serum and 1% penicillin-streptomycin) at 37°C, 5% CO2, in humidified conditions at 10 to 90% confluency. All cell lines were passaged at least three times prior to smRNA FISH imaging.
Approximating mRNA diffusion out of the nucleus using a lumped export rate parameter
Diffusion of the mRNA out of the nucleus may be modeled using the diffusion equation with an absorbing boundary that represents the transition from the nucleus to the cytoplasm. An approximation to diffusion that is amenable to Gillespie simulation is a multistep random walk (Figure S2a, left) with an absorbing state that models the transition from the nucleus to the cytoplasm. The mRNA molecules synthesized in the nucleus begin in state N0 and then follow random walk rules until captured in the absorbed (C) state. Left and right transitions have equal probabilities (p(left) = p(right) = 0.5) for each step in the walk. (Note that p(N0 → N1) = 1). The final step in the walk (N3 → C) is irreversible and could be modeled with a different probability than the reversible steps. However, for convenience p(N3 → C) is also set to be 0.5.
The distribution of mRNA lifetime in the nucleus is easily found by setting the initial condition (t=0) of the system as
and using a recursive application of the random walk rules (Figure S2b) to map out the probability of the molecule being found in a particular state. The probability of the mRNA molecule remaining in the nucleus at step number s (P(s)) is
The distribution of mRNA lifetime in the nucleus is the plot of P(s) vs s (Figure S2c). The random walk produces two distinct phases of the mRNA lifetime in the nucleus. First, there is the delay phase, which represents the minimum time needed for the mRNA molecule to travel from the point of synthesis to the nuclear boundary. Next is a nearly exponential decay that represents the stochastic export of mRNA molecules at the boundary into the cytoplasm.
A simpler model would consider only the transition from the nuclear boundary into the cytoplasm using one irreversible step (Figure S2a, right). This model has the virtue of allowing easy noise filtering analysis using the frequency domain formalism described in the main text, and is computationally faster for the Gillespie simulation. Although this simplified model reproduces the exponential decay feature of the random walk, it cannot generate the initial delay phase. However, as seen above, the delay phase of the mRNA nuclear retention time is short compared to the exponential decay phase and very little loss of accuracy is introduced by the simplified model (Figure S2d).
Computational modeling
Stochastic simulations
A simplified two-state transcription model incorporating two compartments (nucleus and cytoplasm) was constructed and simulated using the Gillespie algorithm (Gillespie, 1977), with reaction scheme and parameters as defined in Table S1. Stochastic simulations were run in MATLAB. Initial conditions for all species were set to 0, except for PromoterOFF which was set to 1. Simulations were run to time = 25 (arbitrary time units) and 1000 simulations were run for each parameter set. For the final “time-point” of simulations, nuclear and cytoplasmic mean and Fano factor were calculated. The discrete diffusion model was constructed as described above, with two additional nuclear mRNA species (3 total). The transition between all three nuclear mRNA species is reversible with both forward and backwards rate constants set to 1.6 and the irreversible export rate constant set to 25.
Ordinary differential equations for probable parameter regime calculations
Assuming a simplified mathematical model where mRNAs are transcribed at rate α, nuclear and cytoplasmic mRNA means can be approximated by the following equations:
| (Equation S1) |
| (Equation S2) |
At steady state the mean amount of nuclear and cytoplasmic mRNA is therefore:
| (Equation S3) |
| (Equation S4) |
And the ratio of nuclear to cytoplasmic mRNA is:
| (Equation S5) |
From previously reported genome-wide mRNA counts of nuclear versus cytoplasmic mRNA, the ratio between the degradation and export rate (kdeg/kexp) per gene can be estimated (Figure S1C) (Bahar Halpern et al., 2015a), and the possible parameter space can be further limited to a probable regime. From the probable parameter regime, we could determine how many scenarios resulted in true attenuation of mRNA noise (i.e. cytoplasmic noise was attenuated down to minimal Poissonian levels). To remain on the conservative side, a given parameter combination was labeled true attenuation, when cytoplasmic noise was lower than nuclear noise, and cytoplasmic Fano factor was < 2. Next, the percentage of scenarios resulting in true attenuation was calculated, resulting in only ~2.5%.
Analytical arguments for protein noise dependence on Fano factor versus CV2
The variance () in the protein population may be calculated as follows:
where
=variance in the cyto mRNA
⟨P⟩ =steady-state protein population
⟨C⟩ = steady-state cyto mRNA population
NBWp = noise bandwidth of the protein
NBWc = noise bandwidth of the cyto mRNA
From this we can calculate the CV2 of the protein () as follows:
Where FFc = the Fano factor of cyto mRNA. The noise bandwidth of the protein is usually set by the protein decay/dilution rate (γp) as (Simpson et al. 2003)
and
where is the average transcription rate and γr is the decay rate of the cyto mRNA. This leaves
where only the noise bandwidth of the mRNA cyto remains undefined as it will depend on both γr and the mRNA export rate (kexp). However, the upper limit on NBWc is
If mRNA export is slower than cytoplasmic mRNA degradation, then the low export rate can decrease NBWc below the value set by mRNA decay, but it cannot increase NBWc. As a result, we obtain
This equation indicates that the Fano factor of the cytoplasmic mRNA sets the minimum obtainable protein CV2 regardless of the mRNA export rate.
The above equation can also be written in terms of cytoplasmic mRNA CV2
However, the critical point is that this CV2 version of the equation does not reflect the noise caused by promoter architecture represented by . In other words, using this equation to determine the minimum obtainable protein CV2, means that the protein CV2 will be obscured by both protein and mRNA half-life. In order to use the CV2 of the cytoplasmic mRNA to accurately determine the minimum obtainable protein CV2, while still maintaining the underlying promoter architecture (), the following equation must be used:
Where there is an unavoidable scaling of the mean ⟨C⟩.
Analytical derivation of the relationship between the nuclear and cytoplasmic Fano factor
The power spectral density (PSD) of the noise in the Nuc mRNA populations (SNUC (f) is (see Simpson et al. 2003; Simpson et al. 2004; Cox et al Chaos 2006)
| (Equation S6) |
Where
f=frequency in Hz
SNUC(0)= PSD of NUC mRNA population noise at f=0
= critical frequency associated with promoter toggling
= critical frequency associated with export of mRNA
The variance of the noise in the Nuc mRNA populations () is (Simpson et al. PNAS 2003)
Where NBWNUC is known as the noise bandwidth and is a function of the two critical frequencies described above (Simpson at al. PNAS 2003).
The Fano factor of the noise in the nuclear mRNA population (FFNUC) is
Where ⟨N⟩ is the steady-state value of the Nuc mRNA population.
The PSD of the noise in the Cyto mRNA population (SCYTO(f) is
where is the “gain” between Cyto and Nuc mRNA populations.
<C> is the Cyto mRNA population
kdeg is the rate of mRNA degradation in the cyto
is the critical frequency associated with mRNA degradation in the cytoplasm.
The variance () and Fano factors (FFCYTO) for the cytoplasmic mRNA population are
The ratio of the Fano factors is
| (Equation S7) |
The two noise bandwidths are controlled by the three critical frequencies associated with (i) Promoter toggling; (ii) mRNA export; and for the cytoplasm (iii) mRNA degradation. In both cases, the noise bandwidth is dominated by the lowest of the critical frequencies that are associated with it. As a result,
and therefore,
and
Equation S7 shows that there is a strong tendency for FFCYTO> FFNUC for cases where <C> > <N>. Only in the special case where the cytoplasm has a much lower noise bandwidth than the nucleus is it possible to have both <C> > <N> and FFNUC> FFCYTO. These relationships can clarified by examining the following limiting cases:
| Parameter relationship |
Noise bandwidth relationship | Steady-state population relationship |
Fano factor relationship |
|---|---|---|---|
| kdeg>>kexp | |||
| kdeg < kexp >> kON+ kOFF | |||
| kdeg << kexp << kON+ kOFF | |||
| kdeg << kexp ≈ kON+ kOFF | |||
| kdeg ≈< kexp << kON+ kOFF | |||
| kexp >> kON+ kOFF ≈ kdeg |
Rate calculations
The number of mRNAs at the transcriptional center (TCmRNA) can be calculated from the transcriptional center intensity (TCint):
| (Equation S8) |
where Spotint is the median single mRNA intensity. From this the transcription rate (ktx) was calculated (Bahar Halpern et al., 2015b):
| (Equation S9) |
where kelongation (1.9 kb/min) is the elongation rate of RNAPII (Boireau et al., 2007) and L is the length of the gene. The TC frequency is an approximation for the frequency that the respective promoter is on (fon). Assuming gene expression is at steady-state, then export (kexp) and degradation (kdeg) rates were calculated from nuclear (meannuc) and cytoplasmic (meancyt) mean mRNA count respectively (Munsky et al., 2012):
| (Equation S10) |
| (Equation S11) |
To verify the accuracy of these rate calculations, we also determined export and degradation rates by fitting nuclear and cytoplasmic decay curves. smRNA FISH was performed at 15-minute time intervals after treatment with an orthogonal transcriptional inhibitor Actinomycin D (Bensaude, 2011), and the experimental data was then fit with an exponential decay curve to determine the rate constants. For both export and degradation, similar rate constants were obtained (Figure S4F).
Prediction of cytoplasmic noise
From the frequency that the respective promoter is on (fon):
| (Equation S12) |
and the nuclear noise (Fanonuc):
| (Equation S13) |
the promoter ON (kon) and promoter OFF (koff) rates were calculated (Munsky et al., 2012), given that all other parameters are known. These parameters were then used to predict cytoplasmic noise, using both Poissonian and multi-state cytoplasmic mRNA degradation models. The additional rates involved in multi-state degradation (Table S1) were determined by manual screening of parameter ranges.
Single molecule RNA FISH
Sample preparation
Probes were developed using the designer tool from Stellaris (LGC Biosearch Technologies, Novato, CA) (http://www.singlemoleculefish.com/) to detect d2GFP, GFP, c-Jun, c-Fos, COX-2, FoxO, NR4A2, Per1, c-Fos. Because NANOG had a GFP tag, it could be detected using the GFP probes. Probes were designed using a masking level of 5, and at least 2 base pair spacing between single probes. Each probe set contained 29-48 probes, with each probe being 18-20 nt long and conjugated with TAMRA (see Tables S3).
Approximately 6×105 isoclonal cells were washed with 2 mL of PBS solution and then immobilized on a Cell-Tak (Corning, Bedford, MA) coated 8-well chambered image dish. Human embryonic kidney (293F) cells were trypsinized with 0.05% Trypsin EDTA (Mediatech, MT 25-052-C1) for 1 minute followed by neutralization with DMEM prior to PBS washing step. If applicable, cells were then treated with leptomycin B (Sigma Aldrich, Darmstadt, Germany). Prior to fixing, mouse E14 embryonic stem cells (mESCs) were cultured on a 35mm MatTek dish (P35G-1.5-14C, MatTek, Ashland, MA). Cells were then fixed with PBS in 3.4% paraformaldehyde for 10 minutes. Fixed cells were washed with PBS and stored in 70% EtOH at 4 °C for a minimum of one hour to permeabilize the cell membranes. Probes were diluted 200-fold and allowed to hybridize at 37 °C overnight. Wash steps and DAPI (Thermo Fisher Scientific, Waltham, MA) staining were performed as described (https://www.biosearchtech.com/support/applications/stellaris-rna-fish).
Imaging
To minimize photo bleaching, cells were imaged in a photo-protective buffer containing 50% glycerol (Thermo Fisher Scientific, Waltham, MA), 75 μg/mL glucose oxidase (Sigma Aldrich, Darmstadt, Germany), 520 μg/mL catalase (Sigma Aldrich, Darmstadt, Germany), and 0.5 mg/mL Trolox (Sigma Aldrich, Darmstadt, Germany). Images were taken on a Nikon Ti-E microscope equipped with a W1 Spinning Disk unit, an Andor iXon Ultra DU888 1k x 1k EMCCD camera and a Plan Apo VC 100x/1.4 oil objective in the UCSF Nikon Imaging Center. Approximately 10 xy locations were randomly selected for each isoclonal population. For each xy location, Nyquist sampling was performed by taking ~30, 0.4 um steps along the z-plane. The exposure times for TAMRA (100% laser power), and DAPI (50 % laser power) channels were 500 ms, and 50 ms for single mRNA analysis and 50 ms, and for transcriptional center (TC) analysis. For each z-plane in a 3-D stack images for both single mRNA analysis and TC analysis were taken.
Image analysis
mESCs were segmented manually and all other cells were segmented using a short in-house Fiji (Schindelin et al., 2012) script (available upon request), which relied on the auto fluorescence visible in the RFP channel. Spot/TC identification and counting was then performed using in-house MATLAB programs (available upon request). In short, the user enters a cellular size and eccentricity range, DAPI intensity threshold, FISH intensity threshold and TC intensity threshold. The MATLAB program then uses the central z-slice DAPI image to create a general nuclear mask. Together with the cellular mask established in ImageJ this nuclear mask is used to exclude cells outside a given size range, nuclear DAPI intensity range or eccentricity range (see extrinsic noise section below). Cells which contained more than one nuclei were also excluded to eliminate multiple cells which were segmented as one. Notably, these steps automatically exclude unhealthy cells, since the cells tend to shrink and/or DAPI intensity becomes much brighter. Next, the DAPI and FISH images of each individual z-slice are sequentially analyzed. After background subtraction, a Gaussian filter was applied to reduce the amount of local maxima caused by pixel-to-pixel noise. Individual spots and TC’s are then segmented using the predefined thresholds to determine possible spot/TC areas. For each z-slice the local maxima of the segmented spot areas are detected. Local maxima which show up within the possible spot areas of multiple sequential images were only counted as one local maxima. Each DAPI image was used to create a nuclear mask for that specific z-slice, which in turn was used together with the cellular mask to allocate a specific spot to either the nucleus or the cytoplasm of each individual cell. TC’s were defined as such, if their local maxima’s were at least double as bright as the median single mRNA local maxima intensity. The number of mRNAs at the transcriptional center were quantified as the intensity of the transcriptional center divided by the median single mRNA intensity.
Extrinsic noise filtering
Cellular properties were measured using the MATLAB program mentioned above, but the respective ranges for extrinsic noise-filtering were determined manually. For the extrinsic noise filtering three parameters were quantified: cellular size; DAPI intensity; and cellular eccentricity (Figure S3C-D). For each parameter the Pearson’s correlation between the total mRNAs per cell and the respective parameter was quantified. The extrinsic noise filtering steps were applied such that the analyzed range of cells was within the respective noise filtering boundaries (see Table S2 for an example). For two extrinsic noise filtering boundaries to be accepted, the Pearson’s correlation must not be statistically significant (i.e. p>0.05). The final extrinsic noise filtering boundaries were manually chosen in order to include as many cells as possible while maintaining a Pearson’s correlation p>0.05 for all three measured parameters.
Multi linear regression (MLR)
10 cellular properties were measured using a MATLAB program modified from the one mentioned above: (1) cellular area of central z-plane; (2) cellular eccentricity of central z-plane; (3) nuclear area of central z-plane; (4) average DAPI intensity of central z-plane; (5) maximum DAPI intensity of central z-plane; (6) nuclear eccentricity of central z-plane; (7) average nuclear area across all z-planes; (8) average DAPI intensity across all z-planes; (9) maximum DAPI across all z-planes; (10) average nuclear eccentricity across all z-planes. These features were used to perform MLR using the regress function in MATLAB on nuclear and cytoplasmic cellular mRNA. The prediction strength (i.e. pS = R2) of the MLR model was then calculated before and after MLR-filtering. The MLR-filtering performed was as follows: For each parameter the Pearson’s correlation between the total mRNAs per cell and the respective parameter was quantified. The MLR- filtering steps were applied such that the analyzed range of cells was within their respective boundaries. These boundaries were manually chosen in order to include as many cells as possible while maintaining a pS <0.1. Once the pS dropped below 0.1 for both nuclear and cytoplasmic mrNA, the Fano factor was calculated and compared to the Fano factor of the same samples with the more coarse-grained extrinsic noise-filtering described above.
GFP expression analysis
Microscopy
Isoclonal populations were washed with 10 mL PBS solution and then immobilized on Cell-Tak coated 8-well chambered image dish. For the GFP standard curve, soluble eGFP (Cell Biolabs, San Diego, CA) standards (in PBS) of known concentration were imaged under the same conditions as cellular GFP. Both GFP standards, and cellular GFP were imaged on a Nikon Ti-E microscope equipped with a W1 Spinning Disk unit, an Andor iXon Ultra DU888 1k x 1k EMCCD camera and a Plan Apo VC 100x/1.4 oil objective in the UCSF Nikon Imaging Center, exposure time was 200 ms with 20% laser power. Approximately 10 xy locations were randomly selected for each isoclonal population. After background and auto-fluorescence subtraction from cellular GFP images, the cellular GFP concentration was calculated from the GFP standard curve (Figure S7A). Using the measured cellular volume and cellular GFP concentration, the absolute number of GFP molecules per cell was calculated. For a review on molecular counting see (Coffman and Wu, 2014).
Flow cytometry
Flow cytometry data was collected on an LSRII cytometer (BD Biosciences) with a 488-nm laser used to detect GFP. The cytometry data was analyzed using FlowJo (http://www.flowjo.com/).
QUANTIFICATION AND STATISTICAL ANALYSIS
Statistical analysis was performed by Pearson correlation analysis, Kolmogorov–Smirnov test or paired t test. All data are presented as mean ± SEM or SD. Significance levels were set at P < 0.05. For statistical analysis GraphPad™ Prism was used, unless otherwise specified.
Supplementary Material
Sequences for smFISH probes, related to Star Methods
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| N/A | ||
| Bacterial and Virus Strains | ||
| N/A | ||
| Biological Samples | ||
| N/A | ||
| Chemicals, Peptides, and Recombinant Proteins | ||
| TNF-alpha | Sigma | cat # T0157 |
| Leptomycin B | Sigma | cat # L2913 |
| Cell-Tak Cell and Tissue Adhesive | Corning | cat # CB-40240 |
| actinomycin D | Sigma | cat # A9415 |
| dextran sulfate | Sigma | cat # 42867 |
| formamide | ThermoFisher | cat # AM9342 |
| formaldehyde | Tousimis | cat # 1008A |
| Cycloheximide | Sigma | cat # 239763 |
| Lactimidomycin | EMD Millipore | cat # 5.06291.0001 |
| soluble eGFP | Cell Biolabs | cat # 4999 |
| Critical Commercial Assays | ||
| NA | ||
| Deposited Data | ||
| N/A | ||
| Experimental Models: Cell Lines | ||
| HEK 239T | American Type Culture Collection | CRL-3216 |
| Jurkat | American Type Culture Collection | TIB-152 |
| Mouse E14 embryonic stem cells | Dr. Matt Thomson (Sokolik et al., 2015) | N/A |
| K-562 | American Type Culture Collection | CCL-243 |
| Experimental Models: Organisms/Strains | ||
| N/A | ||
| Oligonucleotides | ||
| Please see Table S3 | This paper | N/A |
| Recombinant DNA | ||
| N/A | ||
| Software and Algorithms | ||
| FlowJo | FlowJo, LLC | http://www.flowjo.com/ |
| Stellaris® Probe Designer version 4.2 | LGC Biosearch Technologies | http://www.singlemoleculefish.com/ |
| Fiji | (Schindelin et al., 2012) | https://imagej.net/Fiji/Downloads |
| MATLAB | MathWorks | https://www.mathworks.com/products/matlab.html |
| Other | ||
HIGHLIGHTS:
Transcriptional fluctuations are typically amplified during mRNA nuclear export
Cytoplasmic mRNA fluctuations are further amplified by super-Poissonian mRNA decay
Translation processes amplify and propagate mRNA fluctuations to protein levels
ACKNOWLEDGEMENTS
We are grateful to Brandon Razooky, Noam Vardi and members of the Weinberger Lab for extensive discussions, as well as Kurt Thorn and DeLaine Larsen (Nikon Imaging Center, UCSF, NIH S10 1S10OD017993-01A1) and the Gladstone Flow Cytometry Core (NIH P30 AI027763, NIH S10 RR028962 and the James B. Pendleton Charitable Trust) for invaluable technical expertise. We would like to thank Elizabeth Tanner for the LTR d2GFP isoclones 2, 12, and 13, and Noam Vardi for the LTR d2GFP isoclones A3, C4 and D6, the EF-1α d2GFP isoclones, and the UBC d2GFP isoclones. The K562 cell line, along with the SV40 GFP isoclones, were a kind donation from Jonathan Weissman. M.M.K.H is supported by the Netherlands Organization of Scientific Research (NWO) through a Rubicon fellowship (No. 019.153LW.028). MLS acknowledges support from the Center for Nanophase Materials Sciences, which is a DOE Office of Science User Facility. L.S.W. acknowledges support from the Alfred P. Sloan Research Fellowship, NIH awards R01AI109593, P01AI090935, and the NIH Director’s New Innovator Award (OD006677) and Pioneer Award (OD17181) programs.
Abbreviations
- smFISH
(single-molecule fluorescence in situ hybridization)
- TNF-α
(Tumor Necrosis Factor alpha)
- UBC
(ubiquitin C)
- EF-1α
(elongation factor 1 alpha)
- LTR
(long terminal repeat)
- Simian virus 40
(SV40)
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
DECLARATION OF INTERESTS
Leor Weinberger serves as chair of the Scientific Advisory Board of Autonomous Therapeutics Inc.
Patent application PCT/US2014/058687 is related to this work.
REFERENCES
- Arias AM, and Hayward P (2006). Filtering transcriptional noise during development: concepts and mechanisms. Nat Rev Genet 7, 34–44. [DOI] [PubMed] [Google Scholar]
- Bahar Halpern K, Caspi I, Lemze D, Levy M, Landen S, Elinav E, Ulitsky I, and Itzkovitz S (2015a). Nuclear Retention of mRNA in Mammalian Tissues. Cell Reports 13, 2653–2662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bahar Halpern K, Tanami S, Landen S, Chapal M, Szlak L, Hutzler A, Nizhberg A, and Itzkovitz S (2015b). Bursty Gene Expression in the Intact Mammalian Liver. Molecular Cell 58, 147–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balázsi G, van Oudenaarden A, and Collins James J. (2011). Cellular Decision Making and Biological Noise: From Microbes to Mammals. Cell 144, 910–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bar-Even A, Paulsson J, Maheshri N, Carmi M, O'Shea E, Pilpel Y, and Barkai N (2006). Noise in protein expression scales with natural protein abundance. Nat Genet 38, 636–643. [DOI] [PubMed] [Google Scholar]
- Bartel DP (2004). MicroRNAs: Genomics, Biogenesis, Mechanism, and Function. Cell 116, 281–297. [DOI] [PubMed] [Google Scholar]
- Battich N, Stoeger T, and Pelkmans L (2015). Control of Transcript Variability in Single Mammalian Cells. Cell 163, 1596–1610. [DOI] [PubMed] [Google Scholar]
- Beaumont HJE, Gallie J, Kost C, Ferguson GC, and Rainey PB (2009). Experimental evolution of bet hedging. Nature 462, 90–93. [DOI] [PubMed] [Google Scholar]
- Becskei A, Kaufmann BB, and van Oudenaarden A (2005). Contributions of low molecule number and chromosomal positioning to stochastic gene expression. Nat Genet 37, 937–944. [DOI] [PubMed] [Google Scholar]
- Bensaude O (2011). Inhibiting eukaryotic transcription: Which compound to choose? How to evaluate its activity? Transcription 2, 103–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blake WJ, Balázsi G, Kohanski MA, Isaacs FJ, Murphy KF, Kuang Y, Cantor CR, Walt DR, and Collins JJ (2006). Phenotypic Consequences of Promoter-Mediated Transcriptional Noise. Molecular Cell 24, 853–865. [DOI] [PubMed] [Google Scholar]
- Blake WJ, Kaern M, Cantor CR, and Collins JJ (2003). Noise in eukaryotic gene expression. Nature 422, 633–637. [DOI] [PubMed] [Google Scholar]
- Boireau S, Maiuri P, Basyuk E, de la Mata M, Knezevich A, Pradet-Balade B, Bäcker V, Kornblihtt A, Marcello A, and Bertrand E (2007). The transcriptional cycle of HIV-1 in real-time and live cells. J Cell Biol 179, 291–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casolari JM, Brown CR, Komili S, West J, Hieronymus H, and Silver PA (2004). Genome-Wide Localization of the Nuclear Transport Machinery Couples Transcriptional Status and Nuclear Organization. Cell 117, 427–439. [DOI] [PubMed] [Google Scholar]
- Choubey S, Kondev J, and Sanchez A (2015). Deciphering Transcriptional Dynamics In Vivo by Counting Nascent RNA Molecules. PLOS Computational Biology 11, e1004345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coffman VC, and Wu J-Q (2014). Every laboratory with a fluorescence microscope should consider counting molecules. Molecular Biology of the Cell 25, 1545–1548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dar RD, Hosmane NN, Arkin MR, Siliciano RF, and Weinberger LS (2014). Screening for noise in gene expression identifies drug synergies. Science 344, 1392–1396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dar RD, Razooky BS, Singh A, Trimeloni TV, McCollum JM, Cox CD, Simpson ML, and Weinberger LS (2012). Transcriptional burst frequency and burst size are equally modulated across the human genome. Proceedings of the National Academy of Sciences 109, 17454–17459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Decker CJ, and Parker R (2012). P-Bodies and Stress Granules: Possible Roles in the Control of Translation and mRNA Degradation. Cold Spring Harbor Perspectives in Biology 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duh EJ, Maury WJ, Folks TM, Fauci AS, and Rabson AB (1989). Tumor necrosis factor alpha activates human immunodeficiency virus type 1 through induction of nuclear factor binding to the NF-kappa B sites in the long terminal repeat. Proceedings of the National Academy of Sciences 86, 5974–5978. [Google Scholar]
- Felber BK, Hadzopoulou-Cladaras M, Cladaras C, Copeland T, and Pavlakis GN (1989). rev protein of human immunodeficiency virus type 1 affects the stability and transport of the viral mRNA. Proc Natl Acad Sci U S A 86, 1495–1499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garg S, and Sharp PA (2016). Single-cell variability guided by microRNAs. Science 352, 1390. [DOI] [PubMed] [Google Scholar]
- Garneau NL, Wilusz J, and Wilusz CJ (2007). The highways and byways of mRNA decay. Nat Rev Mol Cell Biol 8, 113–126. [DOI] [PubMed] [Google Scholar]
- Gilbert Luke A., Larson Matthew H., Morsut L, Liu Z, Brar Gloria A., Torres Sandra E., Stern-Ginossar N, Brandman O, Whitehead Evan H., Doudna Jennifer A., et al. (2013). CRISPR-Mediated Modular RNA-Guided Regulation of Transcription in Eukaryotes. Cell 154, 442–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie DT (1977). Exact stochastic simulation of coupled chemical reactions. The Journal of Physical Chemistry 81, 2340–2361. [Google Scholar]
- Hasty J, McMillen D, and Collins JJ (2002). Engineered gene circuits. Nature 420, 224–230. [DOI] [PubMed] [Google Scholar]
- Horvathova I, Voigt F, Kotrys AV, Zhan Y, Artus-Revel CG, Eglinger J, Stadler MB, Giorgetti L, and Chao JA (2017). The Dynamics of mRNA Turnover Revealed by Single- Molecule Imaging in Single Cells. Molecular Cell 68, 615–625.e619. [DOI] [PubMed] [Google Scholar]
- Kaern M, Elston TC, Blake WJ, and Collins JJ (2005). Stochasticity in gene expression: from theories to phenotypes. Nat Rev Genet 6, 451–464. [DOI] [PubMed] [Google Scholar]
- Katz ZB, English BP, Lionnet T, Yoon YJ, Monnier N, Ovryn B, Bathe M, and Singer RH (2016). Mapping translation 'hot-spots' in live cells by tracking single molecules of mRNA and ribosomes. eLife 5, e10415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepler TB, and Elston TC (2001). Stochasticity in transcriptional regulation: origins, consequences, and mathematical representations. Biophys J 81, 3116–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim DW, Uetsuki T, Kaziro Y, Yamaguchi N, and Sugano S (1990). Use of the Human Elongation Factor-1-Alpha Promoter as a Versatile and Efficient Expression System. Gene 91, 217–223. [DOI] [PubMed] [Google Scholar]
- LaGrandeur T, and Parker R (1999). The cis acting sequences responsible for the differential decay of the unstable MFA2 and stable PGK1 transcripts in yeast include the context of the translational start codon. RNA 5, 420–433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S, Liu B, Lee S, Huang S-X, Shen B, and Qian S-B (2012). Global mapping of translation initiation sites in mammalian cells at single-nucleotide resolution. Proceedings of the National Academy of Sciences 109, E2424–E2432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maamar H, Raj A, and Dubnau D (2007). Noise in Gene Expression Determines Cell Fate in Bacillus subtilis. Science 317, 526–529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malim MH, Hauber J, Fenrick R, and Cullen BR (1988). Immunodeficiency virus rev trans-activator modulates the expression of the viral regulatory genes. Nature 335, 181–183. [DOI] [PubMed] [Google Scholar]
- Mittler JE, Sulzer B, Neumann AU, and Perelson AS (1998). Influence of delayed viral production on viral dynamics in HIV-1 infected patients. Mathematical Biosciences 152, 143–163. [DOI] [PubMed] [Google Scholar]
- Munsky B, Neuert G, and van Oudenaarden A (2012). Using Gene Expression Noise to Understand Gene Regulation. Science 336, 183–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman JRS, Ghaemmaghami S, Ihmels J, Breslow DK, Noble M, DeRisi JL, and Weissman JS (2006). Single-cell proteomic analysis of S. cerevisiae reveals the architecture of biological noise. Nature 441, 840–846. [DOI] [PubMed] [Google Scholar]
- Ossareh-Nazari B, Bachelerie F, and Dargemont C (1997). Evidence for a role of CRM1 in signal-mediated nuclear protein export. Science 278, 141–144. [DOI] [PubMed] [Google Scholar]
- Ozbudak EM, Thattai M, Kurtser I, Grossman AD, and van Oudenaarden A (2002). Regulation of noise in the expression of a single gene. Nat Genet 31, 69–73. [DOI] [PubMed] [Google Scholar]
- Padovan-Merhar O, Nair PG, Biaesch GA, Mayer A, Scarfone S, Foley WS, Wu RA, Churchman LS, Singh A, and Raj A (2015). Single Mammalian Cells Compensate for Differences in Cellular Volume and DNA Copy Number through Independent Global Transcriptional Mechanisms. Molecular Cell 58, 339–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker R (2012). RNA Degradation in Saccharomyces cerevisae. Genetics 191, 671–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelechano V, Wei W, and Steinmetz Lars M. (2015). Widespread Co-translational RNA Decay Reveals Ribosome Dynamics. Cell 161, 1400–1412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pichon X, Bastide A, Safieddine A, Chouaib R, Samacoits A, Basyuk E, Peter M, Mueller F, and Bertrand E (2016). Visualization of single endogenous polysomes reveals the dynamics of translation in live human cells. The Journal of Cell Biology 214, 769–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Presnyak V, Alhusaini N, Chen Y-H, Martin S, Morris N, Kline N, Olson S, Weinberg D, Baker Kristian E., Graveley Brenton R., et al. (2015). Codon Optimality Is a Major Determinant of mRNA Stability. Cell 160, 1111–1124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj A, Peskin CS, Tranchina D, Vargas DY, and Tyagi S (2006). Stochastic mRNA Synthesis in Mammalian Cells. PLOS Biology 4, e309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj A, and van Oudenaarden A (2008). Nature, Nurture, or Chance: Stochastic Gene Expression and Its Consequences. Cell 135, 216–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzine IM, Weinberger AD, and Weinberger LS (2015). An evolutionary role for HIV latency in enhancing viral transmission. Cell 160, 1002–1012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez A, and Golding I (2013). Genetic Determinants and Cellular Constraints in Noisy Gene Expression. Science 342, 1188–1193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, et al. (2012). Fiji: an open-source platform for biological-image analysis. Nature Methods 9, 676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmiedel JM, Klemm SL, Zheng Y, Sahay A, Blüthgen N, Marks DS, and van Oudenaarden A (2015). MicroRNA control of protein expression noise. Science 348, 128. [DOI] [PubMed] [Google Scholar]
- Simpson ML, Cox CD, and Sayler GS (2003). Frequency domain analysis of noise in autoregulated gene circuits. Proceedings of the National Academy of Sciences 100, 4551–4556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh A, and Bokes P (2012). Consequences of mRNA Transport on Stochastic Variability in Protein Levels. Biophysical Journal 103, 1087–1096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh A, Razooky B, Cox CD, Simpson ML, and Weinberger LS (2010). Transcriptional Bursting from the HIV-1 Promoter Is a Significant Source of Stochastic Noise in HIV-1 Gene Expression. Biophysical Journal 98, L32–L34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokolik C, Liu Y, Bauer D, McPherson J, Broeker M, Heimberg G, Qi Lei S., Sivak David A., and Thomson M (2015). Transcription Factor Competition Allows Embryonic Stem Cells to Distinguish Authentic Signals from Noise. Cell Systems 1, 117–129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoeger T, Battich N, and Pelkmans L (2016). Passive Noise Filtering by Cellular Compartmentalization. Cell 164, 1151–1161. [DOI] [PubMed] [Google Scholar]
- Thattai M, and van Oudenaarden A (2001). Intrinsic noise in gene regulatory networks. Proceedings of the National Academy of Sciences 98, 8614–8619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tilgner H, Knowles DG, Johnson R, Davis CA, Chakrabortty S, Djebali S, Curado J, Snyder M, Gingeras TR, and Guigó R (2012). Deep sequencing of subcellular RNA fractions shows splicing to be predominantly co-transcriptional in the human genome but inefficient for lncRNAs. Genome Research 22, 1616–1625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urcuqui-Inchima S, Patiño C, Zapata X, García MP, Arteaga J, Chamot C, Kumar A, and Hernandez-Verdun D (2011). Production of HIV Particles Is Regulated by Altering Sub- Cellular Localization and Dynamics of Rev Induced by Double-Strand RNA Binding Protein. PLOS ONE 6, e16686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe M, Fukuda M, Yoshida M, Yanagida M, and Nishida E (1999). Involvement of CRM1, a nuclear export receptor, in mRNA export in mammalian cells and fission yeast. Genes to Cells 4, 291–297. [DOI] [PubMed] [Google Scholar]
- Weinberger LS, Burnett JC, Toettcher JE, Arkin AP, and Schaffer DV (2005). Stochastic gene expression in a lentiviral positive-feedback loop: HIV-1 Tat fluctuations drive phenotypic diversity. Cell 122, 169–182. [DOI] [PubMed] [Google Scholar]
- Xiong L.-p., Ma Y.-q., and Tang L.-h. (2010). Attenuation of transcriptional bursting in mRNA transport. Physical Biology 7, 016005. [DOI] [PubMed] [Google Scholar]
- Yamashita A, Chang T-C, Yamashita Y, Zhu W, Zhong Z, Chen C-YA, and Shyu A-B (2005). Concerted action of poly(A) nucleases and decapping enzyme in mammalian mRNA turnover. Nature Structural &Amp; Molecular Biology 12, 1054. [DOI] [PubMed] [Google Scholar]
- Yan X, Hoek Tim A., Vale Ronald D., and Tanenbaum Marvin E. (2016). Dynamics of Translation of Single mRNA Molecules In Vivo. Cell 165, 976–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Sequences for smFISH probes, related to Star Methods