Geometry dependent arrhythmias in electrically excitable tissues

Summary

Little is known about how individual cells sense the macroscopic geometry of their tissue environment. Here we explore whether long-range electrical signaling can convey information on tissue geometry to individual cells. First, we studied an engineered electrically excitable cell line. Cells grown in patterned islands of different shapes showed remarkably diverse firing patterns under otherwise identical conditions, including regular spiking, period-doubling alternans, and arrhythmic firing. A Hodgkin-Huxley numerical model quantitatively reproduced these effects, showing how the macroscopic geometry affected the single-cell electrophysiology via the influence of gap junction-mediated electrical coupling. Qualitatively similar geometry dependent dynamics were observed in human induced pluripotent stem cell (iPSC)-derived cardiomyocytes. The cardiac results urge caution in translating observations of arrhythmia in vitro to predictions in vivo where the tissue geometry is very different. We study how to extrapolate electrophysiological measurements between tissues with different geometries and different gap junction couplings.

Graphical Abstract

eTOC:

McNamara et al. show that the electrical spiking of an engineered cell line, and its susceptibility to arrhythmia, depend on its tissue geometry.

Introduction

Cells in multicellular organisms sense their location within tissues via diffusible molecules, contact interactions, and mechanical signals.(Warmflash et al., 2014) Gap junction-mediated electrical signals can also, in principle, provide long-range positional cues (Sundelacruz, Levin & Kaplan, 2009), though mechanistic details have been difficult to determine due to simultaneous interactions between all of the above signaling modalities. Here we use a simple genetically engineered excitable tissue to ask how the electrical dynamics of a cell inside the tissue are affected by remote boundaries.

The electrophysiological properties of many types of isolated cells have been probed in detail via patch clamp electrophysiology.(Hille, 2001) For isolated cells or small clusters, spiking dynamics can often be described by simple autoregressive models.(Nolasco, Dahlen, 1968, Kaplan et al., 1996, Clay, Shrier, 1999) In extended tissues, cells form electrical connections with their neighbors via gap junction channels. One can then ask whether this coupling is a minor perturbation on the individual cells, or whether it fundamentally changes the dynamics. In condensed matter physics, the properties of a bulk solid can differ dramatically from those of its constituent atoms. Similarly, the emergent electrical properties of bulk tissue might differ dramatically from those of individual cells. Indeed, recent theoretical work showed that electrical conduction could shift the transitions between stability and arrhythmia in excitable tissues.(Cherry, Fenton, 2004, Cytrynbaum, Keener, 2002)

Much of the interest in long-range electrical coupling has focused on the heart, where transitions between regular and irregular beating can be a matter of life or death. Rearrangements of electrical gap junctions have been implicated in the onset of arrhythmia(Jongsma, Wilders, 2000), and structural defects can also act as nuclei for arrhythmias (Roes et al., 2009). In both cases, establishing the causal roles of electrical coupling is difficult due to the simultaneous occurrence of mechano-electrical feedbacks (Bers, 2002, Nitsan et al., 2016) and changes in single-cell properties.(Ng, Wong & Tsang, 2010, Amin, Tan & Wilde, 2010, Hume, Uehara, 1985, Werley, Brookings et al., 2017) Furthermore, the wide diversity of cardiac models, combined with uncertainty in model parameters, presents a challenge for comparison to experiments.(Clayton et al., 2011, Cytrynbaum, Keener, 2002) Only a few experiments have explicitly probed the roles of intercellular coupling in cardiac dynamics.(Bub, Shrier & Glass, 2002, Bub, Shrier & Glass, 2005, Rohr et al., 1997)

Uncertainties regarding the role of geometry in cardiac stability have an important practical implication: it has been widely claimed that if human induced pluripotent stem cell (iPSC)-derived cardiomyocytes (hiPSC-CM) can be made to show mature patterns of ion channel expression,(Du et al., 2015, Denning et al., 2016, Yang, Pabon & Murry, 2014, Protze et al., 2017) then in vitro cultures will be a useful substrate for studying arrhythmias.(Hoekstra et al., 2012, Colatsky et al., 2016, Sharma, Wu & Wu, 2013, Birket et al., 2015) This belief underpins a large-scale effort, called the Comprehensive in-vitro Proarrhythmia Assay (CiPA), sponsored by the U.S. Food and Drug Administration (FDA) to use hiPSC-CM as a substrate for evaluating pro-arrhythmia risks in candidate therapeutics. However, this approach would need to be reconsidered if one found fundamental geometry-driven differences in stability between cultured cells and intact tissue, even when all voltage-dependent conductances were identical.

To explore the role of geometry under controlled conditions, we engineered a synthetic excitable tissue where all elements were well understood. We previously introduced Optopatch Spiking Human Embryonic Kidney (OS-HEK) cells (McNamara et al., 2016) as an engineered excitable cell type with an all-optical electrophysiological interface. HEK293 cells present a clean electrophysiological background, in that their membranes pass little current between −80 and +30 mV (Varghese et al., 2006), while an endogenous Na⁺/K⁺ ATPase maintains steady cardiac-like transmembrane concentration gradients for these two cations (Sultan et al., 2008). The cells were engineered to express just two voltage-dependent channels, the voltage-gated cardiac sodium channel, Na_V 1.5, and the inward rectifier potassium channel, K_ir2.1. Expression of a channelrhodopsin, CheRiff, permitted optogenetic stimulation. Membrane voltage was recorded optically, via either a far-red voltage-sensitive protein (QuasAr2 (Hochbaum et al., 2014)) or dye (BeRST1 (Huang, Walker & Miller, 2015)). Endogenous gap junction proteins introduced nearest-neighbor electrical coupling. (McNamara et al., 2016) The individual components of the OS-HEK cells have previously been characterized in detail by manual patch clamp recordings (Hochbaum et al., 2014, Zhang, Reichert & Cohen, 2016).

When optogenetically stimulated, these OS-HEK cells produced single action potentials. When grown into a confluent syncytium, the endogenous gap junctions mediated bulk propagation of electrical waves.(McNamara et al., 2016) The OS-HEK cells previously demonstrated many interesting attributes of excitable tissues, including wave conduction, curvature-dependent wavefront velocity, and re-entrant spiral waves,(McNamara et al., 2016) but we did not observe arrhythmias, suggesting that a necessary ingredient was missing from this model system.

Here we describe isradipine-OS-HEK (iOS-HEK, where the ‘i’ stands for isradipine) cells as a model for studying the impacts of geometry on arrhythmia. This synthetic bioelectric system showed dynamical transitions between regimes of regular pacing, complex but repeating patterns, and irregular (nonrepeating) dynamics as the pace frequency was increased. We explored in detail how these stability regimes were influenced by the macroscopic tissue geometry. Transitions to complex and irregular patterns depended sensitively on the culture geometry. At a single pacing frequency, we simultaneously observed regular rhythms, alternating patterns, irregular dynamics, or depolarization block in islands that were identical in all respects except for their geometry. A biophysically detailed Hodgkin Huxley-style model captured these geometric effects. The iOS-HEK cells further showed second-degree conduction block in regions of high wavefront curvature, demonstrating sensitivity to two-dimensional geometric features. Finally, we show that similar geometry-dependent transitions occur in cultured human iPSC-derived cardiomyocytes. Together our findings show that macroscopic tissue geometry is a fundamental determinant of bioelectrical dynamics, and not just a perturbation on the cell-autonomous behavior. We discuss which parameters are sensitive or insensitive to tissue geometry, and propose scaling relations that can be used to extrapolate across tissue geometries and across intercellular coupling strengths.

Results

iOS-HEK cells show alternans and arrhythmias

We hypothesized that our previous failure to observe arrhythmia in the OS-HEK system was due to the absence of slowly recovering conductances. In cardiomyocytes, delayed rectifier potassium channels gradually restore excitability after repolarization, so that the waveform of each beat depends on the interval since its predecessor. This beat-to-beat memory can lead to instabilities under periodic pacing. The drug isradipine causes state-dependent block in the Na_V1.7 and Na_V1.5 sodium channels, with a with a recovery time of ~200 ms at −100 mV.(Zhang et al., 2016) We reasoned that isradipine would cause a slow recovery of the Na_V1.5 channels in OS-HEK cells after a beat, mimicking via a different ionic mechanism the slow recovery of cardiomyocytes after repolarization. We hypothesized that this slow recovery would be sufficient to support arrhythmic dynamics.

In a confluent monolayer of OS-HEK cells, we observed regular spiking when the cells were optogenetically paced at 4 Hz (10 ms pulses, 100 mW/cm²). Addition of isradipine (10 μM) converted the spiking to an alternating rhythm between large and small spikes (Fig. 1), consistent with a previous report.(Zhang et al., 2016) We refer to the OS-HEK cells with 10 μM isradipine as iOS-HEK cells. This dynamical transition qualitatively resembles the ‘alternans’ instability in cardiac tissue, in which rapid pacing causes an alternating series of large and small excitations.

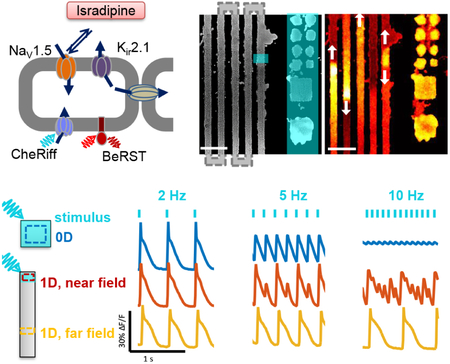
Figure 1. Isradipine renders Optopatch-Spiking HEK cells susceptible to arrhythmia.

A) Molecular components of the synthetic excitable tissue. The voltage-gated sodium channel Na_V1.5 and inward-rectifying potassium channel K_ir2.1 are together sufficient to produce action potentials in response to a depolarizing stimulus. CheRiff is a blue-shifted channelrhodopsin which depolarizes the cells in response to blue light, and BeRST1 is a dye which reports voltage through changes in red fluorescence. Connexin channels (Cxn) introduce electrical coupling between neighboring cells. B) Left: microcontact printing defines patterns of cell growth. The vertical stripes connect in a serpentine pattern outside the field of view. Blue overlay shows regions of optogenetic stimulation. Zero-dimensional “islands” are tested alongside one-dimensional “tracks”. Right: single frame from a movie of BeRST1 fluorescence showing traveling waves in the track region. See Supplementary Movie 1. Scale bars 500 mm. C) Fluorescence recordings of membrane voltage showing that isradipine (10 μM) induces alternans in OS-HEK cells paced at 4 Hz. D) At low pace frequency isradipine OS-HEK (iOS-HEK) cells beat periodically in synchrony with the pacing, but at high pace frequency the cells produce an irregular rhythm.

Using microcontact printing,(Qin, Xia & Whitesides, 2010) we patterned cell-adhesive fibronectin features onto cytophobic polyacrylamide surfaces. Features comprised square islands of linear size 100 μm, 200 μm and 500 μm, as well as serpentine tracks of width 100, 200, 500 μm and edge length of 1 mm and 5 mm. Overall track lengths were as long as 7 cm. Cell growth followed the printed patterns (Fig. 1b). We used a digital micromirror device (DMD) to target blue light stimulation to specific regions of the sample. In a change from previous studies on OS-HEK cells, we used the far-red dye BeRST1 (Huang et al., 2015) to report membrane voltage. This dye had superior brightness to the protein-based reporter, QuasAr2, had low toxicity and showed similar sensitivity to voltage. We recorded the voltage dynamics using a custom ultrawide-field ‘Firefly’ microscope.(Werley, Nagle et al., 2017) Once on the microscope, cell cultures showed stable behavior for typically ~90 min. All data presented here were acquired in < 60 min.

Localized stimulation of the serpentine tracks induced propagating electrical waves (Supplementary Movie 1). Optogenetically induced waves propagated with a typical conduction velocity of 3.3 cm/s, had an AP width at 50% repolarization of 110 ms, and thus had a depolarized action potential length, λ, of λ = 3.6 mm. The fluorescence in the paced region of the track showed complex beat rate-dependent dynamics. At 2 Hz pacing, the cells spiked regularly and in phase with the drive (Fig. 1d, left). At 8.5 Hz pacing, the cells showed a complex and irregular fluorescence pattern, indicative of arrhythmia (Fig. 1d, right).

Geometry dependent instabilities in iOS-HEK cells

We characterized in detail the dependence of the electrical dynamics on local geometry. Cells were grown either in small square ‘islands’ or on adjacent linear ‘tracks’, and paced simultaneously in both geometries at frequencies between 2 and 11 Hz. The islands were paced with spatially homogeneous illumination, so cells across each island spiked synchronously and gap junction-mediated conduction did not contribute to the dynamics. We refer to these as zero-dimensional (0D) dynamics.

Tracks were stimulated in small regions (200 μm wide, 100 μm long) to induce 1D propagating waves. We observed the response in both the directly stimulated region (near field) and in the conductively stimulated region (far field; Fig. 2a). Electrical waveforms stabilized to their far-field dynamics within a distance d ≈ 0.05 λ from the stimulus (d = 180 μm in our experiments), so we characterized the far-field dynamics at a distance 750 μm from the stimulus. In the far-field, the waves propagated stably, reaching > 1 cm from the stimulated zone. Island and track features were intermixed within each dish, were seeded with the same stock of OS-HEK cells, and were measured simultaneously. Thus any differences in dynamics between regions could be ascribed to the island geometry.

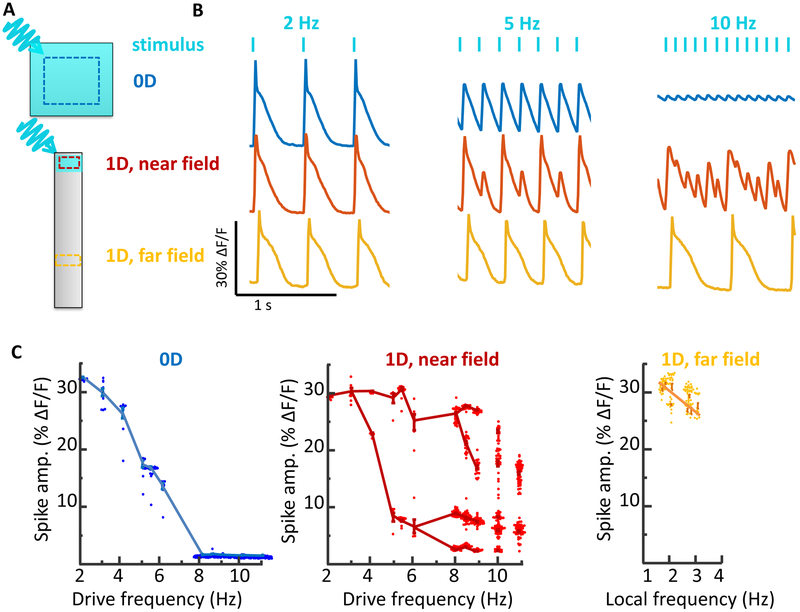
Figure 2. Stability of spiking in iOS-HEKs cells depends on sample geometry and location of pacing.

A) Cell culture geometries, with locations of optogenetic stimulus shown in blue and regions of fluorescence voltage imaging shown with dotted lines. See Supplementary Movie 2. B) Simultaneously recorded electrical dynamics in 0D, 1D near field, and 1D far field. At pacing frequencies of 5 and 10 Hz the cells showed different dynamics in the three regions. C) Geometry-dependent spike amplitude as a function of beat frequency. The plots for 0D and 1D near field show spike amplitude as a function of pacing frequency. The plot for 1D far field shows spike amplitude as a function of local frequency, which can be a sub-harmonic of the pacing frequency. Fluorescence dynamics were recorded from regions of interest typically 100 μm on a side, containing ~100 cells. Due to the strong gap junction coupling between cells, the fluorescence waveforms of individual cells closely matched the local population average. For each stimulus frequency, the amplitudes of up to 100 spikes were displayed in a beeswarm plot. The lines are a guide to the eye connecting clusters of spikes with similar amplitudes. The data for all plots were recorded simultaneously from adjacent features in the same dish. Each plot represents a recording from a single feature. Similar dynamics were observed in n = 4 0D features and n = 3 1D features.

At low pace frequencies (≤ 3 Hz), all three regions spiked with a stable rhythm in synchrony with the pacing (Fig. 2b). To our surprise, at higher pace frequencies we observed dramatically different dynamics in the three regions (Supplementary Movie 2). The 0D islands always produced regular electrical oscillations at the pace frequency. As the pace frequency increased, the amplitude of these oscillations diminished, up to 8 Hz, beyond which the responses were undetectable (Fig. 2c).

The 1D near-field response developed a 1:1 alternans pattern at frequencies > 3 Hz. Additional bifurcations arose at 6 Hz and 8 Hz. At 10 Hz the dynamics no longer showed any repeating pattern, suggesting a transition to irregular dynamics (Fig. 2c).

Remarkably, the 1D far-field showed no transitions to alternans or irregular dynamics (Fig. 2b). All spikes in the far-field had nearly equal amplitude and waveform. At pace frequencies between 3 and 6 Hz, only every other spike propagated to the far field, i.e. the local beat frequency was half the pace frequency. At higher pace frequencies, a smaller portion of spikes reached the far field. These spikes had irregular timing in the near-field but conducted at velocities which gradually evened out timing variations, such that the spiking appeared regular in the far-field, always at a frequency < 3 Hz. The 1D track acted as a filter which converted high-frequency arrhythmic spiking in the near-field into lower frequency rhythmic spiking in the far field. Together these experiments gave the unanticipated result that under regular pacing, iOS-HEK cells showed irregular dynamics only in the 1D near-field, not in the 0D or 1D far-field regions.

A Hodgkin-Huxley model captures iOS-HEK dynamics

We developed a conductance-based Hodgkin Huxley-type model to simulate the dynamics of iOS-HEK cells. The properties of Na_V1.5, K_ir2.1, and channelrhodopsin CheRiff are all well known, so we were able to constrain the model with a small number of free parameters (Fig. 3a). The sodium channel model comprised Hodgkin-Huxley activation and inactivation gates m and h with dynamics taken from the literature.(ten Tusscher et al., 2004, ten Tusscher, Panfilov, 2006) To capture the use-dependent block by isradipine, we introduced an additional slowly activating and slowly recovering gate, j (Methods). The K_ir2.1 conductance was modeled as an instantaneous function of voltage, inferred from the shape of the action potential repolarization (Methods). The channelrhodopsin was modeled as a linear conductance with a 0 mV reversal potential, modulated in space and time by the blue light illumination. A diffusive term captured the nearest-neighbor gap junction coupling. The governing equation is:

$$C_m\frac{\partial V}{\partial t}=G_{\mathit{Cxn}}{\nabla }^{2}V-g_{\mathit{NaV}}{m}^{3}h(1-j)(V-E_{\mathit{Na}})-g_{\mathit{Kir}}(V)(V-E_k)-g_{\mathit{ChR}}(x,t)(V-E_{\mathit{ChR}}),$$ [Eq.1]

where C_m is the membrane capacitance of a cell, and G_Cxn = g_Cxn×l² where g_Cxn is the gap junction conductance between cells, and l is the linear dimension of a cell. The electrical diffusion coefficient is given by G_Cxn /C_m. To simulate 0D dynamics, g_Cxn was set to zero. Eq. 1 represents a continuum model, which treats the domain as homogeneous tissue. In simulations, the cell discreteness is recovered by setting the spatial discretization equal to cell length.

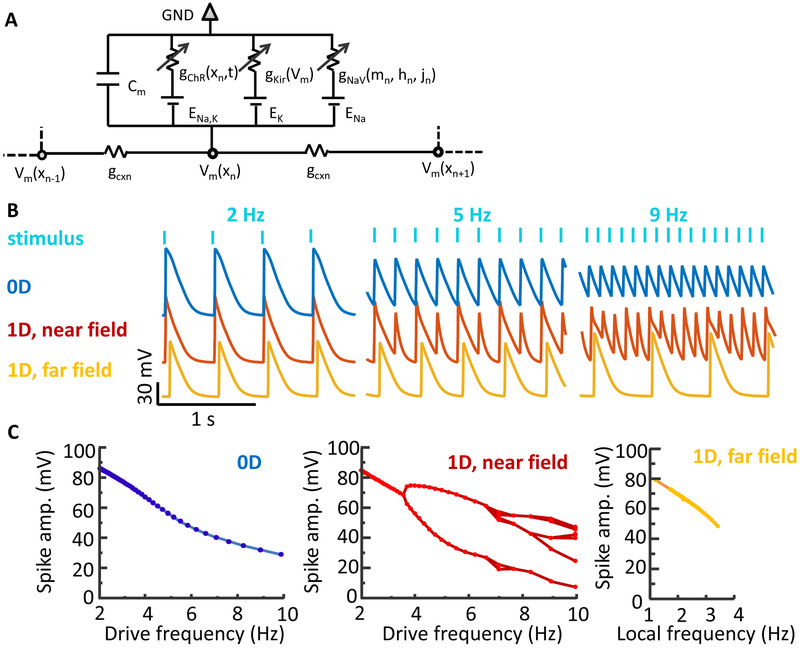
Figure 3: A Hodgkin-Huxley model recapitulates the effect of geometry on spike dynamics.

A) Model schematic. Each cell has a channelrhodopsin (ChR), an inward-rectifier potassium channel (K_ir 2.1) and a voltage-gated sodium channel (Na_V 1.5). The Na_V is further gated by a state-dependent isradipine block. Neighboring cells are coupled via gap junctions. B) Simulated action potential waveforms in different geometries and pace frequencies (analogous to data in Fig. 2b). C) Simulated spike amplitude as a function of frequency for three geometries (analogous to data in Fig. 2c). See also Figure S1.

The unknown parameters (C_m, g_Cxn, g_Kir, g_ChR) were determined by fitting to observed fluorescence waveforms, conduction velocities, and patch clamp measurements (Methods). The free parameters in the model enter in the dynamics of the isradipine variable, j, which was assumed to bind sodium channels in their open state with rate α and unbind with rate μ:

$$\frac{\mathit{dj}}{\mathit{dt}}=\alpha m_{\infty }(1-j)-\mu j,$$ [Eq.2]

where m_∞ is the steady state value of the m gate. The kinetic parameters in Eq. 2 were chosen to fit the experimentally observed dynamical transitions.

Action potential waveforms were simulated in a 0D geometry and in a linear 1D track comprising 2000 cells, with pacing delivered to 40 cells on one end. The near-field response was monitored in the paced zone, and the far-field response was monitored at a distance of 3 mm from the stimulus.

Simulated electrical waveforms (Fig. 3b) captured the main geometry and frequency-dependent features of the data. Specifically, the simulations in 0D showed a smooth and monotonic decrease in spike amplitude with increasing pace frequency. At high pace frequencies, the baseline potential increased in both simulation and experiment, reflecting simultaneous Na_V channel inactivation and stimulus-driven depolarization relative to the k_ir reversal potential (i.e. depolarization block).

Simulations in the 1D near-field showed a series of frequency-dependent bifurcations that became increasingly irregular at high pace frequency. In the 1D far-field, these bifurcations were suppressed: spikes that propagated to the far-field had full amplitude, regular spacing, and were within the narrow band of frequencies that supported far-field propagation.

The simulated 0D waveforms had greater amplitude than the experimental waves at high stimulus frequencies. This minor discrepancy traces to an overestimate of the strength of the channelrhodopsin drive. In all other circumstances, the strength of channelrhodopsin stimulation was not a critical parameter because the channelrhodopsin only served to raise the membrane voltage above threshold. But in the 0D, high frequency case, the other ion channels were largely inactive, so the amplitude of the residual voltage fluctuations depended on the strength of the channelrhodopsin drive. Overall, these simulations confirmed that cells with identical conductances, paced at the same frequency, can show widely divergent behavior depending upon the geometry of the surrounding excitable tissue.

Mapping the transition between the near field and far field response

We next investigated the transition from near-field to far-field behavior. How does alternans, or even irregular spiking, in the near-field lead to regular spiking in the far-field? We mapped the fluorescence dynamics of 1D tracks as a function of distance from the stimulated zone, across a range of stimulus frequencies (Fig. 4a,b). There was a clear bifurcation in the ability of spikes to propagate into the far-field. Near-field spikes with amplitude lower than a critical threshold decayed as a function of distance, while spikes above this threshold grew to become propagating far-field spikes. Once in the far-field, spikes propagated stably for several cm, until reaching a break in the track (see e.g. Movie S1). Spatially resolved simulations yielded similar results (Fig. 4d). The simulations showed that the conduction velocity of each far-field spike decreased as it approached the preceding spike such that irregularities spike spacing gradually evened out. The small dip in the amplitude of propagating spikes near the stimulated zone (Fig. 4c,d) was traced to a buildup of bound isradipine in cells subjected to rapid optogenetic stimulation.

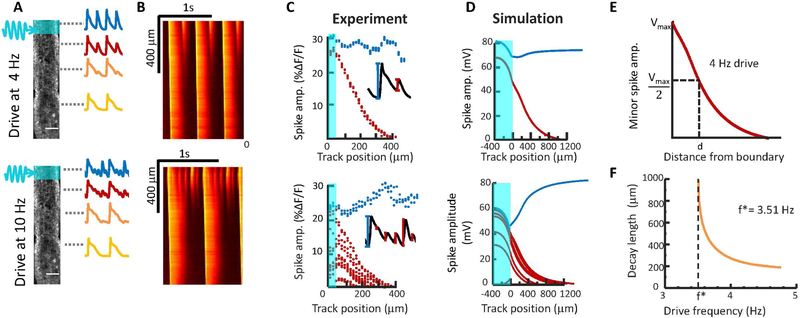
Figure 4. Mapping the transition from near field to far field dynamics.

A) 1D tracks were stimulated at one end and action potential waveforms were recorded as a function of distance from the pacing stimulus. B) Kymographs showing electrical dynamics as a function of distance from the pacing stimulus. Some spikes decay in amplitude, while others grow in amplitude. C) Quantification of spike amplitude as a function of distance from the stimulus (shown in cyan). Spikes that reach the far field are shown in blue and spikes that decay are shown in red. D) Numerical simulations under conditions matched to the experiments. E) Definition of the spike decay length, corresponding to 50% loss of amplitude. F) Simulated decay length for near-field spikes as a function of pacing frequency. Below a critical frequency, f*, all spikes reach the far field.

At pace frequencies just above the transition to near-field alternans (experimentally observed between 3 and 4 Hz), one might expect period-doubling deviations from a regular spike train to arise slowly. We defined an alternans decay length, d, as the distance over which a near-field alternans beat decayed to 50% of its initial height (Fig. 4e). Simulations near the alternans transition indeed revealed a divergence in d near the critical frequency. At pace frequencies far above the critical frequency, the alternans decay length became a small fraction of the far-field action potential length, d ≈ 0.04 λ (Fig. 4f), consistent with experimental results (Fig. 4c).

Second-degree conduction block in iOS-HEK cells

Conduction block and consequent arrhythmias can arise when a region of the heart acts as a partial barrier to conduction.(Shrier et al., 1987) This effect can arise from spatial variations in either ion channel expression (Kruse et al., 2009), or gap junctional coupling.(Donoghue et al., , Temple et al., 2013) We thus explored the effect of local defects on spike propagation in iOS-HEK cell tracks. In a serpentine track with sharp turns, we observed that stably propagating far-field waves sometimes failed at the turns (Fig. 5a, Supplementary Movie 3). Furthermore, failures occurred in a regular temporal sequence, e.g. Fig. 5a shows a pattern that after the first few beats stabilized into a 3:2 block (3 upstream spikes triggered 2 downstream spikes). The waves developed a curved wavefront and slowed repolarization at the turns, a purely geometrical consequence of the increased electrotonic loading associated with bending a wavefront around a corner. Thus geometrical effects alone are sufficient to cause conduction block, even in a background of homogeneous ion channel levels and gap junction strengths. A related effect has been reported in cultured cardiomyocytes, where a junction of a thin strand of cells to a large island showed unidirectional conduction block due to the inability of the thin strand to drive the large island.(Fast, Kléber, 1995)

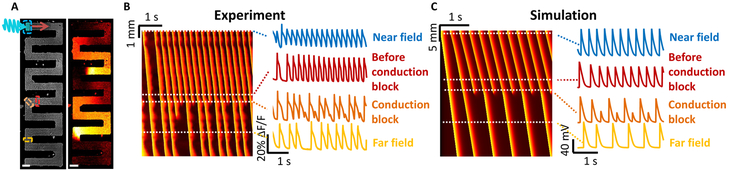
Figure 5. Curvature-induced second-degree conduction block in iOS-HEK cell tracks.

A) Left: image of an iOS-HEK cell track showing stimulus region highlighted in cyan and regions of fluorescence monitoring shown with dashed rectangles. Right: single frame from an optical voltage recording showing two action potentials propagating through the track. See Supplementary Movie 3. Scale bars 200 μm. B) Left: kymograph showing action potential propagation with a 4 Hz pacing frequency. The vertical axis represents contour coordinate along the track. All spikes conducted into the far-field, but conduction showed second-degree block at a corner where there was a slight defect in the pattern, corresponding to the red and orange rectangles. C) Numerical simulations of second-degree conduction block in a 1D track with a 10 cell zone of 3-fold reduced gap junctional coupling.

In our experiments, the conduction block was attributable to a 2D wavefront curvature effect. To capture this effect in computationally tractable 1D simulations, we simulated linear tracks in which a small region (10 cells) had a reduced gap junctional coupling $\left(G_{\mathit{Cxn}}^{\prime }=G_{\mathit{cxn}}∕3\right)$. The simulated waves showed a 1:1 conduction block (Fig. 5c), qualitatively similar to that observed experimentally. These experiments and simulations show that local perturbations in the electrotonic coupling, are sufficient to lead to second-degree conduction block.

Geometry dependent instabilities in human iPSC cardiomyocytes

Finally, we explored whether the geometry-dependent effects observed in iOS-HEK cells also occurred in human iPSC-derived cardiomyocytes (hiPSC-CM). (Yamamoto et al., 2016) Due to the significant commercial interest in using these cells as an in vitro model for cardiotoxicity testing (Karakikes et al., 2015, Burridge et al., 2012, Hoekstra et al., 2012, Colatsky et al., 2016, Mordwinkin, Burridge & Wu, 2013), the correspondence (or lack of) between in vitro and in vivo arrhythmias has some practical importance.

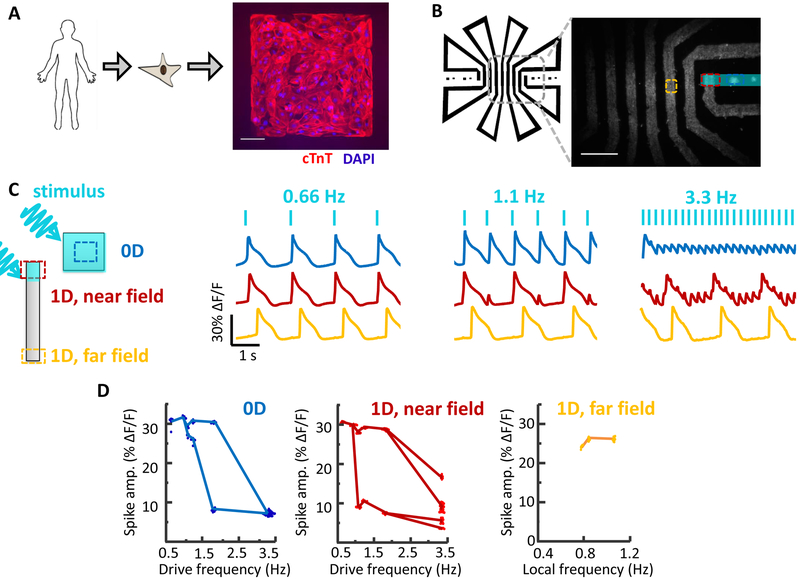
We used microcontact printing to define side-by-side patterns of 0D islands and 1D tracks and then plated hiPSC-CM onto these patterns (Fig. 6). CheRiff was expressed using a lentiviral vector to allow patterned blue light stimulation(Werley, Chien et al., 2017), and BeRST1 was used to image changes in membrane potential. We optogenetically paced 0D islands and 1D tracks simultaneously across a range of frequencies with pulses of 50 ms duration. In the 1D tracks, waves propagated with a conduction velocity of 7.2 cm/s and had an AP duration of 360 ms, corresponding to a depolarized action potential length of 2.6 cm.

Figure 6. Geometry-dependent arrhythmias in cultured human iPSC-derived cardiomyocytes (hiPSC-CM).

A) Image of hiPSC-CM grown on a patterned square island. Scale bar 100 μm. B) Patterned hiPSC-CM cell growth in a set of 0D islands and a long 1D track. The track geometry was designed to interpose long path lengths between returns to the field of view (2 cm between red and yellow regions of interest), to account for the high propagation speed of action potentials in hiPSC-CM compared to iOS-HEK cells. Scale bar 1 mm. C) Simultaneously recorded electrical dynamics in 0D, 1D near field, and 1D far field. At elevated pacing frequencies the cells showed different dynamics in the three geometrical regimes.

As with the iOS-HEK cells, we observed that the dynamics depended strongly on the geometry (Fig. 6c, Supplementary Movie 4). At high pace frequency (3.3 Hz), the 0D islands showed small regular oscillations, the 1D near-field showed an erratic pattern of large beats with small oscillations superposed, and the 1D far-field only showed the large beats at a sub-harmonic of the pace frequency. As in the iOS-HEK cultures, the alternans beats decayed over a distance much less than the action potential length (decay length d = 535 μm, corresponding to d = 0.2 λ). Thus the qualitative geometry-dependent behavior of the hiPSC-CM largely mirrored the behavior of the iOS-HEK cells.

The hiPSC-CM cells differed from the iOS-HEK cells in several important regards. First, the hiPSC-CM were spontaneously active, imposing a minimum on the optogenetic pace frequency. Second, the 0D hiPSC-CM islands showed a transition to alternans (Fig. 6c,d) which disappeared at high drive frequencies (3 Hz). Third, the 1D bifurcation to alternans was continuous in the iOS-HEK cells but discontinuous in the hiPSC-CM. In iOS-HEK simulations, these last two differences can be captured simply by tuning the isradipine unbinding rate (Fig. S1). We also simulated the Noble model, a more realistic cardiac model based on recordings from Purkinje fibers.(Noble, 1962) As in the simplified Hodgkin-Huxley model, we observed clear geometry-dependent differences in the onset of instabilities (Fig. S1c). Finally, real cardiac tissue can support alternans in far-field traveling waves (Mines, 1914), while both the iOS-HEK cells and the hiPSC-CM seemed only to support this phenomenon in the near field. Thus there remain important dynamical features of real cardiac tissue which appear not to be captured by either the iOS-HEk cells or the hiPSC-CM.

Scaling properties of electrical instabilities

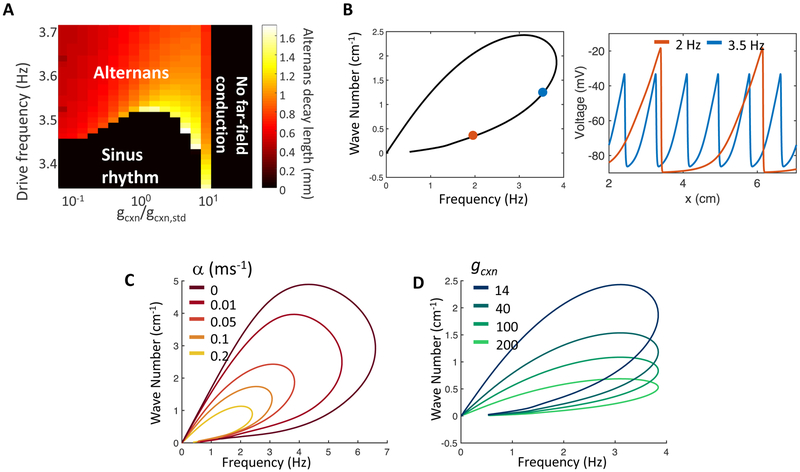
Given the importance of gap junction strength and sample geometry, it is interesting to ask whether one can scale both parameters to preserve the overall dynamics. Such scaling could be useful, for instance, in modeling in vivo cardiac dynamics in a cell culture system. We explored this question by systematically varying the gap junction strength in iOS-HEK simulations of a 1-D track (Fig. 7a). As anticipated from dimensional analysis, the far-field conduction velocity scaled as $\mathit{CV}\propto \sqrt{g_{\mathit{cxn}}}$ (Fig. S2a). The action potential duration (APD) was largely insensitive to g_cxn, so the action potential length λ scaled as $\lambda \propto \sqrt{g_{\mathit{cxn}}}$ (Fig. S2b). Together these results imply that scaling the size of a system by some factor k and the gap junction strength by $\sqrt{k}$ will preserve the overall dynamics.

Figure 7. Scaling properties of instabilities in iOS-HEK cells.

A)Frequency of near-field alternans onset as a function of gap junction coupling strength. The onset frequency varies by < 2% over a 100-fold variation in g_cxn. Pseudocolor shows the spatial extent of alternans, measured as the distance over which alternans beats decay to half of their value in the stimulus region. B-D) Nonlinear dispersion relations show which frequencies are stable in far-field and the corresponding wave numbers (inverse of peak-to-peak wavelength) selected by each frequency. In panels B-D, bottom branches of nonlinear dispersion relations are stable and the top branches are unstable. B) Left: nonlinear dispersion relation under conditions corresponding to experimental data. Right: spatial structure of voltage waves in the far-field with frequencies 2 and 3.5 Hz. Position on nonlinear dispersion relation indicated by correspondingly colored dots. C) Effect of varying the isradipine binding rate, α, on the nonlinear dispersion relation. Increasing α decreases the maximum frequency that propagates to the far field. D) Changes in the connexin strength, g_cxn, affect the wavelength but have little effect on the maximum stably propagating frequency. Thus the maximum frequency prior to alternans onset is a parameter that is largely independent of gap junction strength, and by extension, tissue geometry. See also Fig. S2.

The propagation of spikes in the far-field is governed by the nonlinear dispersion relation, which defines the relationship between wavenumber and frequency (Fig. 7). The numerically simulated dispersion relation indicated that the far-field dynamics only supported frequencies up to f_max = 3.85 Hz. Waves of greater frequency could not propagate into the far field.

The transition frequency for alternans, f* was largely insensitive to g_cxn, varying by < 2% over a 100-fold change in g_cxn (Fig. 7a), but f* depended sensitively on the dynamics of the slow recovery variable (Fig. 7c). This effect can be understood from the dispersion relation of the iOS-HEK system (Fig. 7b). Without isradipine (α = 0), the far field can support drive frequencies of up to f* = 6.5 Hz (set by the action potential width). As the slow recovery variable j is turned on (α > 0), the transition frequency f* is reduced dramatically. Thus, the maximum stable frequency is a parameter that should be largely independent of gap junction strength, and by extension, tissue geometry—provided that the cells are paced via gap junction-mediated conduction rather than by direct pacing.

Can one extrapolate from in vitro measurements of small samples with relatively weak gap junction coupling to larger tissues with stronger gap junctional coupling? In iOS-HEK simulations, the alternans decay length, d, scaled almost linearly with λ (Fig. S2c). These simulations suggest that the action potential length, λ, sets a natural length scale for a bioelectric tissue. Moreover, using λ as a scaling parameter is advantageous since this parameter can be experimentally measured without knowledge of gap junction conductance or other system parameters.

The conduction velocity in the atria and ventricles of the human heart in vivo is approximately 50 cm/s (Draper, Mya-Tu, 1959, Hoffman et al., 1959), and action potential durations are typically 350 ms, implying an action potential length of λ = 18 cm. An adult human heart is approximately L = 12 cm long, so L ≈ 0.7 λ. Pacemaker-triggered action potentials in vivo are thus primarily in the near-field and close far-field regimes. Remarkably, the near-field is the only regime in which we observed arrhythmias in either the iOS-HEK cells or in the hiPSC-CMs, either in experiment or in simulation.

In the cultured hiPSC-CM the action potential length was λ = 2.6 cm, so to best match the geometrical regime of the heart, the culture should have size L ≈ 0.7 λ, or ~1.7 cm. Others have reported conduction velocities in vitro ranging from 3.5 to 20 cm/s,(Werley et al., 2017, Denning et al., 2016, Zhu et al., 2017) corresponding to λ = 1.2 to 7 cm (assuming a 350 ms AP width). While cultures of size L ≈ 0.7 λ are easily accessible on the smaller end of the λ range, 5 cm-wide hiPSC-CM cultures are impractical. This challenge can be addressed either by cell patterning to produce serpentine tracks, or by adding gap junction blockers such as 2-APB to diminish the strength of the gap junction coupling and thereby to slow the conduction velocity.

In vivo, the heart is paced by autonomous cells in the sinoatrial node, which initiate waves that propagate across the myocardium. To best mimic wave conduction in the heart, cultures of hiPSC-CM should be stimulated locally to launch propagating waves. Whole-field stimuli, e.g. as delivered by field stimulation electrodes or wide-area optogenetic stimulation, will induce synchronous depolarization of all cells, mimicking the 0D case and missing possibly important gap junction-mediated dynamical instabilities. One should ideally perform spatially-resolved voltage measurements to reveal the distinct dynamics in the near- and far-field regimes. While it is not possible to recapitulate the full spatial structure of connectivity of the adult myocardium in vitro, one can use the in vitro measurements to benchmark dynamical regimes according to biophysical parameters (e.g. λ and L) which can be measured in vivo. We expect that these considerations will be important for ongoing efforts to develop in vitro models of cardiac dynamics.

Discussion

Gap junction-mediated currents convey the effects of boundaries to all cells in the tissue. In the highly simplified iOS-HEK ‘toy’ model, the qualitative spiking dynamics depended in a sensitive way on the overall geometry. Islands of composed of identical cells and differing only in geometry showed vastly different dynamics under identical pacing frequencies, including regular spiking, complex but repeating multi-spike patterns, and irregular spiking. This work further highlighted the importance of a slowly recovering conductance (in our case state-dependent isradipine block) to support transitions to alternans and arrhythmia.

Our experimental and theoretical approach was guided by the aim to make the simplest possible models that captured key aspects of excitable dynamics. The iOS-HEK system was simple enough to model with biophysically realistic numerical simulations, which confirmed that the observations could be explained by geometry alone. The iOS-HEK cells bore little resemblance to cardiomyocytes from a molecular perspective, lacking, for instance, voltage-gated Ca²⁺ channels, calcium-induced calcium release, delayed rectifier potassium channels, and mechano-electrical feedbacks. The observation of similar geometry-dependent bifurcations in hiPSC-CM cultures suggests that similar principles apply to physiological tissues, despite the myriad differences in channel expression and electrophysiological details between the iOS-HEK cells and cardiomyocytes. Indeed, several distinct numerical models of excitable dynamics all showed geometry dependent bifurcations and transitions to irregular dynamics (Fig. S1). Based on these observations, we propose that long-range electrical signaling may be a generic mechanism for conveying information on tissue geometry to cells interior to a tissue.(Pietak, Levin, 2017).

A cardiomyocyte in isolation would behave very differently from one embedded in a two-dimensional culture or one embedded in a real heart—even if the ion channels were identical in all three cases. This fact suggests caution regarding the CiPA initiative to extrapolate from in vitro measurements of arrhythmia to in vivo predictions. One should not naively infer that a pro-arrhythmic compound in vitro will be pro-arrhythmic in vivo. Indeed, different cell culture geometries and different mechanisms of pacing can produce dramatically different results in vitro. By analyzing the scaling properties of waves in excitable tissues, we propose that to best mimic conditions in vivo, hiPSC-CM should (a) be stimulated via gap junction-mediated conduction, and not by direct electrical or optogenetic stimulation, and (b) that the ratio of culture size to action potential length should approximately mimic the corresponding ratio in vivo.

STAR Methods

Contact: Adam Cohen, cohen@chemistry.harvard.edu

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Adam Cohen (cohen@chemistry.harvard.edu).

Experimental Model and Subject Details

iOS-HEK cell line generation and culture

Clonal OS-HEK cell lines were generated as described previously (see Method Details)(Zhang et al., 2016) and maintained in DMEM-10 supplemented with antibiotics to maintain transgene expression. For functional imaging experiments, cells were first incubated for 30 minutes in Tyrode’s solution (containing 125 mM NaCl, 2 mM KCl, 2 mM CaCl₂, 1 mM MgCl₂, 10 mM HEPES, 30 mM glucose; pH 7.3, osmolality 305-310 mOsm) supplemented with 10 μM isradipine and 1 μM BeRST1 voltage-sensitive dye.

hiPSC-CM cell culture

Cultures of hiPSC-CM cells were procured from Cellular Dynamics International (iCell Cardiomyocytes) and maintained according to vendor protocols. Briefly, iCell Cardiomyocytes were thawed from frozen stocks and plated on gelatin coated plastic tissue culture tissues in plating medium for 48 hours.. While in plating medium, hiPSC-CMs were incubated with lentivirus containing a coding sequence for CheRiff-CFP. Cardiomyocytes were then passaged and re-plated onto fibronectin-patterned dishes (see Method Details) in maintenance medium at sufficiently high density as to completely cover dish patterns. hiPSC-CM cultures were imaged between 24 and 72 hours after re-plating in Tyrode’s solution with 1 μM BeRST1, and without including isradipine.

Method Details

iOS-HEK cell line generation

All HEK cells were maintained in Dulbecco’s modified Eagle medium with 10% fetal bovine serum (DMEM-10), penicillin (100 U/mL), and streptomycin (100 μg/mL). OS-HEK cells were generated as described previously.(McNamara et al., 2016) Briefly, a Na_V1.5 plasmid (Johns Hopkins University ChemCORE) containing a puromycin selection marker was transfected into HEK cells using TransIT-293 transfection reagent (Mirus Bio). 48 hours after transfection, 2 μg/mL puromycin was introduced into the culture medium for 14 days to select for stably expressing Na_V1.5 cells. Following this selection, an Optopatch construct containing coding sequences of CheRiff-eGFP and QuasAr2-mOrange (separated by a self-cleaving P2A peptide sequence) was introduced using a lentiviral construct.(Hochbaum et al., 2014) GFP-expressing cells were enriched 10 days after infection via fluorescence-activated cell sorting (FACS). Finally, a K_ir2.1 lentiviral construct containing a blasticidin selection marker was introduced. After 2 days, cell culture media was supplemented with 5 μg/mL blasticidin (to select for K_ir2.1-expressing cells) and 2 μg/mL puromycin (to ensure continued Na_V1.5 expression). After 14 days, cells were dispersed as single cells into a 48 well plate, and clonal populations were selected on their ability to spike robustly in response to a blue light stimulus.

Clonal cell lines were maintained in DMEM-10 supplemented with 5 μg/mL blasticidin and 2 μg/mL puromycin in 10 cm tissue culture dishes up until 80% confluence, after which they were trypsinized and cryopreserved at 500,000 cells/vial in 90% DMEM-10, 10% dimethylsulfoxide (DMSO). Cryopreserved vials were then thawed and subcultured in antibiotic-supplemented DMEM-10 in 10 cm tissue culture dishes, and were passaged via trypsinization at 80% confluence at a 1:3 ratio. A given subculture typically maintained robust blue-light induced spiking for approximately seven passages, or 2 weeks, after which cells become less excitable (presumably due to decreased K_ir2.1 expression over time).

To prepare OS-HEK cells as iOS-HEK cells for functional experiments, cells were incubated in Tyrode’s solution (containing 125 mM NaCl, 2 mM KCl, 2 mM CaCl₂, 1 mM MgCl₂, 10 mM HEPES, 30 mM glucose; pH 7.3, osmolality 305-310 mOsm) further supplemented with 10 μM isradipine and 1 μM BeRST1 voltage-sensitive dye for 30 minutes in a mammalian tissue-culture incubator prior to imaging.

Cell patterning

Patterned cell growth was achieved using previously described methods(Qin et al., 2010, McNamara et al., 2016). Cytophilic fibronectin patterns were defined on a functionalized cyotophobic polyacrylamide gel using microcontact printing with patterned PDMS stamps. Patterns were first designed in silico (Inkscape) and printed onto a Mylar transparency mask (CAD Art Services). Pattern negatives were then transferred onto silicon wafers coated in SU-8 3025 via contact photolithography and subsequent development of unexposed photoresist. PDMS stamps were then cast from the silicon wafer template.

Functionalized polyacrylamide dishes were prepared from MatTek 35 mm-glass bottom dishes. Glass coverslips were chemically activated by plasma cleaning and then incubated for 30 min in a nitrogen-purged glovebox with silane solution (v/v: 0.5% 3-methacryloxypropyltrimethoxysilane, 2% acetic acid, 97.5% anhydrous EtOH). A 40:1 acrylamide:bisacrylamide gel doped with 4.2 mg/mL acryl-NHS (to allow for covalent bonding of fibronectic matrix) was then gelled for 2-3 minutes in ambient air under siliconized coverslips (to ensure smooth gel surfaces). Functionalized acryl-NHS dishes were then sealed in nitrogen and drierite and transferred to −80 C for long-term storage.

To complete dish preparation, patterned PDMS stamps were first coated in fibronectin protein (Yo Proteins no. 663) dissolved in PBS (0.05 mg/mL fibronectin final concentration) in a sterile tissue culture hood. Coating was allowed to settle for 30 minutes, after which excess fibronectin-PBS solution was carefully removed via aspiration. Stamps were further air-dried for 10 minutes to remove excess moisture that could blur pattern transfer. Functionalized dishes were then printed with fibronectin-coated stamps for 1 hour in a tissue-culture incubator, after which stamps were gently removed and dishes re-sterilized for 10 minutes with UV illumination. Cells were deposited by gently pipetting 500 μL DMEM-10 droplet containing the desired cell density (typically between 500,000 and 1M cells/mL). Cells were allowed to adhere for 30 minutes in a tissue culture laminar hood before an additional 2 mL of DMEM-10 was added and cells were transferred to an incubator.

Wide-field all-optical electrophysiology

All-optical electrophysiology of iOS-HEK and hiPSC-CM cells was performed using an adapted ‘Firefly’ ultrawidefield inverted microscope.(Werley et al., 2017) Spatially patterned blue excitation for optogenetic stimulation was achieved using digital micromirror device (DMD) module with an onboard 460 nm LED (Wintech DLP Lightcrafter 4500). Pixels of linear dimension 7.637 μm were demagnified 2x for optical pattern resolution of approximately 3.8 μm. Action potentials in iOS-HEK cells were triggered with 10 ms pulses at 100 mW/cm² ; action potentials in hiPSC cardiomyocytes were triggered with 50 ms stimuli. Patterns were defined using custom software (MATLAB). DMD pixels were mapped to sample pixels by calibrating a linear transformation to a test pattern on a fluorescent target.

Near-infrared voltage sensors were excited using widefield 635 nm illumination (DILAS 8 W diode laser, M1B-638.3-8C-SS4.3-T3) configured in a near-TIRF configuration (to reduce background autofluorescence). Robust signals from BeRST1 were obtained at an illumination intensity of 2 W/cm². Near-infrared fluorescence emission was filtered using emission filters (Chroma ET665lp and Semrock quadband 336/510/581/703) and reimaged onto a sCMOS camera (Hamamatsu Orca Flash 4.2). Movies were acquired at 100 Hz over a 5 mm × 5 mm field of view.

Custom LabView software allowed for synchronization of time-modulated signals controlling blue and red light excitation, DMD patterns, and camera acquisitions over experimental runs. All data were processed and analyzed using custom software (Quantification and Statistical Analysis). To investigate geometry-dependent dynamical regimes, spatial regions of interest (ROIs) were defined and averaged across pixels to give fluorescence time-traces. A single set of ROIs was defined for a given sample dish and was applied uniformly across movies at different drive frequencies to systematically investigate dynamical responses (Figs. 2B and6C). Using these spatially resolved measurements, we extract information from multiple replicates of 0D, 1D near-field, and 1D far-field responses all in a single dish.

Quantification and Statistical Analysis

Image processing and experimental data analysis

All data were processed and analyzed using custom software (MATLAB). For each pixel, a baseline fluorescence, F, was calculated from the first percentile of the values in the recorded time-trace. The movie was then converted into units of ΔF/F. Pixels that did not contain cells were set to zero (using a criterion that the 99^th percentile of a time trace must be over a user-specified threshold). A spatial median filter (5×5 pixel filter) was further applied to account for measurement noise. At the illumination intensities used, BeRST1 photobleaching was negligible.

To investigate geometry-dependent dynamical regimes, spatial regions of interest (ROIs) were defined and averaged across pixels to give fluorescence time-traces. A single set of ROIs was defined for a given sample dish and was applied uniformly across movies at different drive frequencies to systematically investigate dynamical responses (Figs. 2B and 6C). Using these spatially resolved measurements, we extract information from multiple replicates of 0D, 1D near-field, and 1D far-field responses all in a single dish.

We extracted action potential amplitudes for each spike detected in each feature across movies taken at different pacing frequencies. Spike upstrokes were detected via a threshold on the time derivative. Spike amplitudes (in units ΔF/F) were defined as the difference between the maximum value after a given upstroke and the minimum value preceding the upstroke. Between 10 and 300 spikes per feature were collected in a given movie, depending on drive frequency and acquisition time. Beeswarm plots of spike amplitudes at each pacing frequency were used to visualize the dynamical patterns of activity (Figs. 2c, 6d). Only spikes taken from the second half of movies are visualized to avoid early transients which decay as patterns converges to a stable cycle. The drive frequency in 0D and 1D near field measurements was set by the frequency of the blue light-gated CheRiff activation; in 1D far-field measurements, the pacing frequency is defined as the local frequency (i.e., the reciprocal of the interval between successive spikes).

The transition between the near-field and far-field region was mapped using kymographs (Figures 4B and 5B). Kymographs were generated by spatially averaging ΔF/F movies across the short dimension of a linear track. For serpentine tracks (Figure 5), tracks segments were first computationally aligned into a single long track, and then spatially averaged along the short dimension. Alternans transitions were spatially mapped by performing spike detection (as described above) across linear windows of 8 pixels (Fig. 4C).

Numerical modeling of iOS-HEK cells

In the conductance-based model, the voltage dynamics are governed by the equation

$$C_m\frac{\partial V}{\partial t}=G_{\mathit{Cxn}}{\nabla }^{2}V-(I_{\mathit{NaV}}+I_{\mathit{Kir}}+I_{\mathit{ChR}})$$

where V is the voltage in mV. Recall G_Cxn = g_Cxn × l², where g_Cxn is the gap junction conductance between cells, and l is the linear dimension of a cell. The ionic currents drive local dynamics, while the diffusion term couples neighboring regions. Units of space are 10⁻⁵ m (corresponding to linear size of one cell), and time is in ms. Conductances are measured in nS/pF and ionic currents in pA/pF. The currents are:

$$\begin{array}{c}\hfill I_{\mathit{NaV}}=g_{\mathit{NaV}}{m}_{\infty }^3(V)h(1-j)(V-E_{\mathit{Na}})\hfill \\ \hfill I_{\mathit{Kir}}=g_{\mathit{Kir}}(V)(V-E_k)\hfill \\ \hfill I_{\mathit{ChR}}=g_{\mathit{ChR}}(\overrightarrow{x},t)(V-E_{\mathit{ChR}}).\hfill \end{array}$$

The gating variables for the sodium activation and inactivation gates, m and h respectively, and for the effect of isradipine, j, are dimensionless variables which take values between 0 and 1. The inactivation gate evolves following

$$\frac{\partial h}{\partial t}=\frac{1}{{\tau }_h(V)}(h_{\infty }(V)-h).$$

To capture the use-dependent sodium block by isradipine, we introduced a slowly activating and recovering gate, j, with behavior governed by

$$\frac{\partial j}{\partial t}=\alpha m_{\infty }(V)(1-j)-\mu j.$$

That is, the drug binds sodium channels in its open state with rate α, and unbinds with rate μ. These kinetic parameters were chosen to fit the experimentally observed dynamical transitions.

Since the time constant of the sodium activation gate, m, is orders of magnitude faster than the other gates, the gate was replaced with the asymptotic limit, m_∞(V). This standard approximation allowed for more efficient computations without impacting the simulation results.

The gating variables approach steady-state asymptotic values, which are functions of the voltage.

$$\begin{array}{c}\hfill h_{\infty }(V)={\left(1+\text{exp}\left(\frac{V+71.55}{7.43}\right)\right)}^{-2},\hfill \\ \hfill j_{\infty }(V)=\frac{\alpha m_{\infty }(V)}{\alpha m_{\infty }(V)+\mu }\hfill \\ \hfill m_{\infty }(V)={\left(1+\text{exp}\left(\frac{-56.86-V}{9.03}\right)\right)}^{-2}.\hfill \end{array}$$

Time constants for each gate tell how quickly the behaviors approach the asymptotic values, and are given by

$$\begin{array}{c}\hfill {\tau }_h(V)=\frac{1}{2}\left(1-\tanh \left(\frac{V+40}{10}\right)\right){\tau }_{h1}(V)+\frac{1}{2}\left(1+\tanh \left(\frac{V+40}{10}\right)\right){\tau }_{h2}(V)\hfill \\ \hfill {\tau }_{h1}(V)={\left(0.057\text{exp}\left(\frac{-V-80}{6.8}\right)+2.7\text{exp}(0.079V)+(3.1\times {10}^5)\text{exp}(0.3485V)\right)}^{-1}\hfill \\ \hfill {\tau }_{h2}(V)=\frac{0.13\left(1+\text{exp}\left(\frac{-V-10.66}{11.1}\right)\right)}{0.77}\hfill \\ \hfill {\tau }_j(V)={(\alpha m_{\infty }(V)+\mu )}^{-1}.\hfill \end{array}$$

The equations governing the sodium channel activation, m, and inactivation, h, gates were set following literature values.(ten Tusscher et al., 2004, ten Tusscher, Panfilov, 2006) Minor modifications were made to the h time constant, τ_h (V), to smooth the discontinuous function. The channelrhodopsin was modeled as a linear conductance, modulated in space, ×, and time, t, by the blue light illumination. The repolarization conductance g_Kir was modeled as an instantaneous function of voltage derived from a smoothing spline fit to the action potential waveform at low drive frequency (f = 2 Hz).

Numerical simulations were run on single-cells for the 0D case, and 2 cm 1D tracks with Neumann (noflux) boundary conditions at each end. The 1D tracks were discretized with a spatial step size, dx, equal to 10 μm, the length of one OS-HEK cell. With this discretization size, each grid point represented one cell, allowing the simulations to have similar spatial resolution as the experiments.

The Laplacian was modelled with a fourth-order centered finite difference scheme. Boundary conditions were implemented using the standard ghost-point method. A combination IMEX scheme was used for the time evolution, with implicit Crank-Nicholson applied to the diffusion terms and explicit Adams-Bashforth applied to the remaining nonlinear terms (ion currents and gating dynamics). A time step of 0.1 dx ms (10⁻⁶ ms in the case of 10 μm spatial step) was used, which is well within the accuracies of the numerical scheme and is significantly smaller than any time scales in the model. Single cell, 0D dynamics were modelled by setting g_cxn to zero, and time evolution was performed with the same Adams-Bashforth scheme. All computations were performed using MATLAB.

Initial model parameters were experimentally constrained and fit using a combination of patch clamp measurements and fluorescent voltage recordings. Reversal potentials of E_Na = 75 mV, E_K = −107 mV, and E_ChR = 0 mV were determined according to Nernst equation for the corresponding intracellular and extracellular ionic concentrations. All conductances were expressed as specific conductances per unit capacitance, allowing us to set C_m = 1. The sodium conductance g_NaV was set to 1.5 nS/pF, corresponding to a maximum transient current of 3 nA at −25 mV (V − E_Na = −100 mV) measured in a 20 pF patch clamp recording. The channelrhodopsin conductance was determined to be 15 pS/pF following similar methodology. The inward rectifying potassium current g_Kir was represented as an instantaneous function of voltage, determined by fitting to the experimentally observed fluorescence repolarization waveform at low drive frequency (2 Hz). Because fluorescence traces do not report absolute voltage, we assumed a resting potential of −90 mV and peak voltage of + 30 mV, in accordance with patch clamp recordings. The diffusion coefficient G_Cxn is given by G_Cxn = g_Cxn × l², where l = 1 cell. The connexin conductance g_Cxn was estimated according to measurements of the static electronic coupling length (McNamara et al., 2016) as 40 nS/pF.

The parameters α and μ were chosen to match experimentally determined dynamical regimes. Setting α = 0.5 ms⁻¹ and μ = 0.015 ms⁻¹ gave close agreement with the complex landscape of dynamical transitions observed experimentally (Fig. 3c) as well as simulated voltage traces which closely resembled experimental observations (Fig. 3b). Sensitivity analysis was performed to validate these parameter choices (Supplementary Methods).

Model dynamics were characterized using analogous parameters as for experimental results. Simulations were conducted for both an isolated cell which was directly paced (‘0D’) as well as for linear tracks of 2000 cells (i.e. L = 2 cm) in which 40 cells were paced on one end. Simulations were run across a range of stimulus intervals between 500 ms (2 Hz) and 100 ms (10 Hz), sampled at 10 ms intervals. For each numerical experiment, we detected spike upstrokes as upward deflections of the derivative of the simulated

Sensitivity analysis of model parameters

Parameter values for α,μ,g_NaV, and g_cxn were selected to match as closely as possible the experimental results in both the 0D and 1D settings. The model was simulated for 1,500 ms with a given set of parameters under 2 Hz stimuli, and the resulting voltage at times t_k, V(X, t_k), was compared to analogous experimental results, W (X, t_k), using the ordinary least squares (OLS) objective function

$${\mathit{OLS}}_{\mathit{Obj}}=\sum _k{\mid W(x,t_k)-V(x,t_k)\mid }^2.$$

Simulated and experimental voltage values were scaled to be between 0 and 1 to allow for direct comparison. An optimal set of parameters minimizes the objective function; minimization was performed with the MATLAB constrained optimization function fmincon. Realistic parameter constraints were chosen from the patch clamp data.

Sensitivity of model parameters was tested using Latin Hypercube Sampling (LHS).(Marino et al., 2008) The LHS results identified α,μ, and, g_NaV as the most sensitive parameters, with g_Cxn as the least. That is, small changes in the connexin strength, g_Cxn, had negligible impact on the simulated voltages. Regardless, changing any model parameters over a modest regime maintained the main geometry-dependent differences in stability, giving confidence in the appropriateness of the model.

Nonlinear dispersion analysis of far-field dynamics

In the far-field, the waves become spatially periodic structures of constant shape and velocity, both of which are uniquely determined by the frequency. The nonlinear dispersion relation of the far-field equation indicates which wave number (inverse of peak-to-peak wavelength) is selected by each frequency (Fig. 7b). The nonlinear dispersion relation is computed by considering the far-field traveling waves as periodic stationary solutions in a moving frame, which allows for the traveling wave and wave number to be solved for as a function of frequency. The full dispersion relation curve is traced out with pseudo-arclength numerical continuation implemented in MATLAB, and using the spatial discretization scheme as in the numerical simulations.

Each frequency has two associated wave numbers, with the bottom branch stable and top branch unstable. Two examples of the spatial structure of the far-field waves are given, and their positions along the dispersion relation marked. The curve does not extend past 3.85 Hz, indicating the far-field equation does not support waves of higher frequencies. Therefore, for drive frequencies above 3.85 Hz, each stimulus will not propagate into the far-field, leading to the appearance of near-field alternans, and aligning with the experimentally and numerically observed behavior.

Changing the drug binding rate, α, and connexin strength, g_cxn, have different impacts on the nonlinear dispersion relation (Fig. 7c and 7d). Small changes in α lead to large shifts in the transition frequency, indicating that faster binding rates will induce near-field alternans at lower drive frequencies. However, large changes to the coupling strength change properties of the traveling waves, such as wave number, wave length, and speed, but do not appreciably change the range of allowed frequencies or transition frequency. Changes to model parameters μ (drug unbinding rate) and g_Na (sodium conductance) are not shown, but have a similar effect as changing α.

The 2:1 conduction block observed from local changes in the connexin strength (Fig. 5) is also explained from the nonlinear dispersion relation. As the spike propagates through the small region of lower connexin strength, the wavenumber and frequency are adjusted to values that are no longer stable when the wave reenters the region of higher connexin strength (observe the differences in the curves with g_cxn values of 40 and 14 in Fig. 7d). The modification of wavenumber and frequency upon the reentry results in the observed 2:1 conduction block.

Noble model of cardiomyocyte dynamics

To demonstrate that the observed geometry effects are not unique to the OS-HEK cell model and are of importance in cardiac dynamics, we performed 0D and 1D simulations in the Noble model. The Noble model is an ionic channel model for Purkinje fibers and the voltage dynamics are governed by sodium, potassium, and background chloride currents (I_Na, I_K, and I_cl, respectively). Spatial coupling between cells was again incorporated through a Laplacian.

$$\begin{array}{c}\hfill C_m\frac{\partial V}{\partial t}=\delta {\nabla }^{2}V-(I_{\mathit{Na}}+I_{K1}+I_{K2}+I_{\mathit{cl}}+I_{\mathit{ext}})\hfill \\ \hfill I_{\mathit{Na}}=({\overline{g}}_{\mathit{Na}}{m}^{3}h+g_{\mathit{Na}})(V-E_{\mathit{Na}})\hfill \\ \hfill I_{K1}=\left[g_K\text{exp}\left(\frac{-V-90}{50}\right)+0.015\text{exp}\left(\frac{V+90}{60}\right)\right](V-E_K)\hfill \\ \hfill I_{K2}=g_K{n}^4(V-E_K)\hfill \\ \hfill I_{\mathit{cl}}=g_{\mathit{cl}}(V-E_{\mathit{cl}})\hfill \\ \hfill I_{\mathit{ext}}=g_{\mathit{stim}}(V-E_{\mathit{ChR}})\hfill \end{array}$$

The dynamics of the dimensionless ionic gates for sodium activation, m, sodium deactivation, h, and potassium, n, take the form

$$\frac{d{z}_i}{\mathit{dt}}={\alpha }_i(V)(1-z_i)-{\beta }_i(V)z_i$$

where z_i stands for m, h, and n and α_i and β_i similarly correspond to opening and closing rates of the m, h, and n channels. The rates are given by

$$\begin{array}{c}\hfill {\alpha }_m(V)=0.1(V+48){\left(1-\text{exp}\left(\frac{-V-48}{15}\right)\right)}^{-1},{\beta }_m(V)=0.12(V+8){\left(\text{exp}\left(\frac{V+8}{5}\right)-1\right)}^{-1}\hfill \\ \hfill {\alpha }_h(V)=0.17\text{exp}\left(\frac{-V-90}{20}\right),{\beta }_h(V)=\text{exp}{\left(\frac{-V-42}{10}\right)}^{-1}\hfill \\ \hfill {\alpha }_n(V)=-0.0001(V+50){\left(\text{exp}\left(\frac{-V-50}{10}\right)-1\right)}^{-1},{\beta }_n(V)=0.002{\left(\text{exp}\left(\frac{-V-90}{80}\right)\right)}^{-1}.\hfill \end{array}$$

All ionic currents, dynamic gating variables, and parameter values were set from literature. Membrane capacitance, conductances, and Nernst potentials are given in Table 1.(Clayton, Panfilov, 2008, Noble, 1962) The form of the applied current, I_ext, was set to mimic the channelrhodopsin stimulus. The Noble model was chosen for its ability to reproduce realistic behaviors observed in cardiac cells and the relatively low number of ionic currents allowed for efficient simulation.

Table 1:

Values of membrane conductance, conductances, and Nernst potentials used in simulations of the Noble model.

Cm = 12 μF/cm2	g̅Na = 400 mS/cm2
ENa = 40 mV	gK = 1.2 mS/cm2
EK = −100 mV	gcl = 0.075 mS/cm2
ECl = −60 mV	gstim = 0.5 mS/cm2
δ = 0.001 cm2/ms

Numerical simulations in 0D and 1D geometries used the same centered finite-difference Laplacian and IMEX time evolution schemes described above. Simulations were run on 1D tracks of up to 6 cm in length with spatial grid spacing set to 0.1 mm and time step of 0.01 ms. Due to the higher cell coupling and conduction values, the stimulus duration was increased to 50 ms. Simulations were run for at least two forcing cycles before recording results to remove any transient effects caused by the self-spiking behavior of the Noble model. Model output was analyzed in a similar fashion to the OS-HEK model results.

The Noble model simulations also exhibit geometry-dependent changes in stability (Fig. S1c). The 1D near-field results show a dramatic transition first to alternans at 4.5 Hz, and then to irregular dynamics at 8 Hz. Similar transitions are not observed in the 0D or far-field results, which instead display monotonically decreasing spike amplitude for higher frequencies. As before, the model selects a narrow range of wave frequencies which propagate into the far-field.

Supplementary Material

Movie S1. Electrical waves propagating through patterned iOS-HEK cells, Related to Figure 1.

Optical recordings of optogenetically triggered action potentials propagating through confluent monolayers of patterned electrically excitable iOS-HEK cells. See Fig. 1 for details.

Movie S2. Geometry dependent action potential dynamics in iOS-HEK cells, Related to Figure 2.

The square islands on the right produced spikes in response to each stimulus. The 1D tracks on the left produced an alternans pattern in the near-field and conducting waves only on alternating stimuli.

Movie S3. Second degree conduction block near sharp turns in an iOS-HEK serpentine track, Related to Figure 5.

The first four action potentials conducted into the far-field, but the fifth failed to conduct at a defect in the middle of the track. Thereafter the waves showed a 3:2 conduction block at the defect in the track.

Movie S4. Geometry dependent action potential dynamics in hiPSC-CM, Related to Figure 6.

The square islands on the right produced spikes in response to each stimulus. The 1D tracks on the left produced an alternans pattern in the near-field and conducting waves only on alternating stimuli.

Key Resources Table.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Isradipine	Tocris Bioscience	2004
Puromycin	ThermoFisher	A1113802
Blasticidin	ThermoFisher	A1113902
Fibronectin	Yo Proteins	Cat #663
Acrylic acid N-hydroxysuccinimide ester	Sigma	A8060
Acrylamide solution (40%)	Sigma	A4058-100ML
Acrylamide/Bisacrylamide, (40% solution, 19:1)	Sigma	A9926-100ML
SU-8 3025 Photoresist	Microchem	SU-8 3025
SU-8 Developer	Microchem	N/A
3-(Trimethoxysilyl)propyl methacrylate	Sigma	2530-85-0
Anhydrous ethanol	Sigma	277649-100ML
Glacial acetic acid	Sigma	A6283-100ML
Potassium persulfate	Sigma	7727-21-1
Experimental Models: Cell Lines
Optopatch-Spiking HEK Cells	This paper, McNamara et al 201632	N/A
iCell Cardiomyocytes	Cellular Dynamics	Kit 01434
Recombinant DNA
pENTR-L5-Kir2.1-mCherry-L2	Addgene	32,669
pIRESpuro3-NaV1.5	Johns Hopkins University ChemCORE	N/A
FCK-Optopatch1	Hochbaum et al 201435, Addgene	51695
FCK-CMV-CheRiff-CFP	N/A
psPAX2	Addgene	12260
VsVg	Addgene	12259
Software and Algorithms
MATLAB code for image processing and data analysis	This paper	Supplement
MATLAB code for iOS-HEK model simulation and dispersion analysis	This paper	Supplement
MATLAB code for Noble model simulation	This paper	Supplement
Other
Firefly Widefield Microscope	This paper, Werley et al 201739	N/A
Silicon Wafers	University Wafers	58.52-1
Lithography transparency mask	CADArt Services	N/A (custom order)

Highlights:

• An engineered excitable cell line becomes arrhythmic when rapidly paced.

• The transition to arrhythmia depends on the geometry of the culture.

• Numerical Hodgkin-Huxley models reproduce these effects.

• Human stem cell-derived cardiomyocytes also show geometry-dependent arrhythmias.