Topological quantum computation based on chiral Majorana fermions

Significance

We propose a platform of quantum computation using the chiral Majorana fermions on the edges of topological materials. The quantum gates are naturally accomplished by the propagation of chiral Majorana fermions. If realized, its computation speed can be $10^3$ faster than the currently existing quantum computation schemes.

Abstract

The chiral Majorana fermion is a massless self-conjugate fermion which can arise as the edge state of certain 2D topological matters. It has been theoretically predicted and experimentally observed in a hybrid device of a quantum anomalous Hall insulator and a conventional superconductor. Its closely related cousin, the Majorana zero mode in the bulk of the corresponding topological matter, is known to be applicable in topological quantum computations. Here we show that the propagation of chiral Majorana fermions leads to the same unitary transformation as that in the braiding of Majorana zero modes and propose a platform to perform quantum computation with chiral Majorana fermions. A Corbino ring junction of the hybrid device can use quantum coherent chiral Majorana fermions to implement the Hadamard gate and the phase gate, and the junction conductance yields a natural readout for the qubit state.

The chiral Majorana fermion, also known as the Majorana–Weyl fermion, is a massless fermionic particle being its own antiparticle proposed long ago in theoretical physics. The simplest chiral Majorana fermion is predicted in 1D space, where it propagates unidirectionally. In condensed-matter physics, 1D chiral Majorana fermions can be realized as quasiparticle edge states of a 2D topological state of matter (1). A celebrated example is the $p+ip$ chiral topological superconductor (TSC), which carries a Bogoliubov–de Gennes (BdG) Chern number $\mathcal{N}=1$ and can be realized from a quantum anomalous Hall insulator (QAHI) with Chern number $\mathcal{C}=1$ in proximity with an $s$-wave superconductor (2–5). A QAHI–TSC–QAHI junction implemented this way is predicted to exhibit a half-quantized conductance plateau induced by chiral Majorana fermions (3, 4), which has been recently observed in the Cr-doped (Bi,Sb)₂Te₃ thin-film QAHI system in proximity with the Nb superconductor (6). The chiral Majorana fermion could also arise in the Moore–Read state of the fractional quantum Hall effect (7) and topologically ordered states of spin systems (8).

A closely related concept, Majorana zero modes (MZMs), which emerge in the bulk vortices of a $p+ip$ TSC (9) or at the endpoints of a 1D $p$-wave TSC (10, 11), are known to obey non-Abelian braiding statistics and can be used in fault-tolerant topological quantum computations (12–17). Despite the theoretical progress made during the past decade on using MZMs in universal quantum computation (14–17), due to the localized and point-like nature of MZMs, all existing proposed architectures inevitably require nanoscale design and control of the coupling among MZMs. As an essential step toward topological quantum computing, the braiding of MZMs has not yet been experimentally demonstrated.

In this paper, we propose a platform to implement topologically protected quantum gates at mesoscopic scales, which uses propagation of chiral Majorana fermions with purely electrical manipulations instead of MZMs.

Chiral Majorana Fermion Qubits

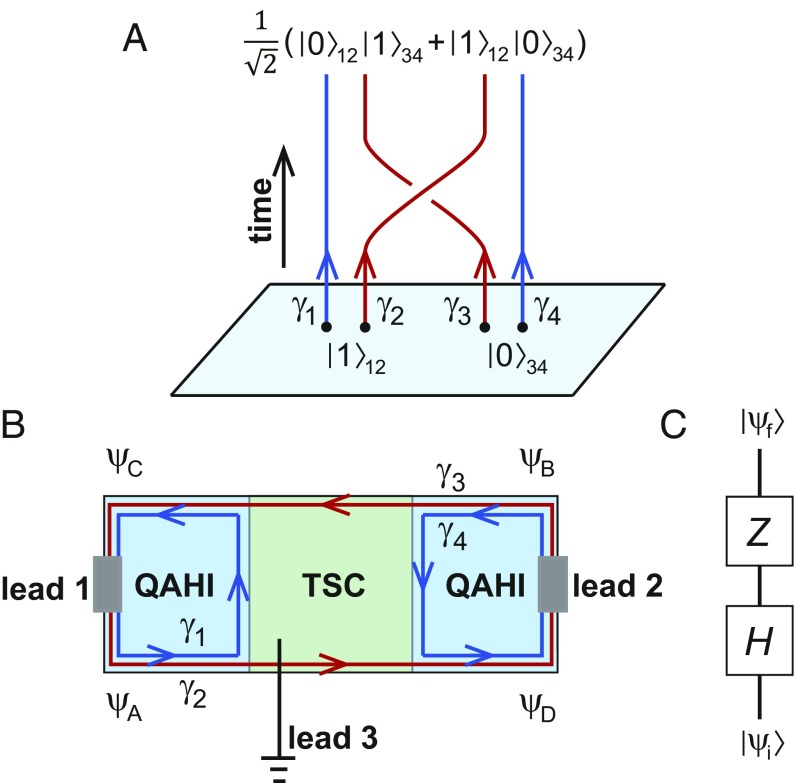
The main goal of our proposal is to show that the chiral Majorana fermion edge state of the TSC can be used to realize non-Abelian quantum gate operations on electron states, even if there is no non-Abelian anyon traveling along the edge. Since our proposal is closely related to the braiding of MZMs in vortices of the $p+ip$ TSC, we begin by reviewing this process, as illustrated in Fig. 1A. Each vortex supports a single MZM ${\gamma }_i$, and thus two vortices together define two quantum states of a fermion degree of freedom. The MZM operators satisfy the anticommutation relation $\left\{{\gamma }_i,{\gamma }_j\right\}={\delta }_{ij}$. If we define $f_{12}=\frac{1}{2}\left({\gamma }_1+i{\gamma }_2\right)$ as a complex fermion number, the two states are labeled by $f_{12}^{†}{f}_{12}=\mathrm{0,1}$, which corresponds to $i{\gamma }_1{\gamma }_2=-1,+1$, respectively. When two vortices are exchanged, the corresponding MZMs also are exchanged. In the process in Fig. 1A, we have ${\gamma }_2\to {\gamma }_3,{\gamma }_3\to -{\gamma }_2$. The relative minus sign is necessary to preserve the fermion number parity $i{\gamma }_2{\gamma }_3$ of this pair. As a consequence, the eigenstates of $i{\gamma }_1{\gamma }_2$ and $i{\gamma }_3{\gamma }_4$ evolve to eigenstates of $i{\gamma }_1{\gamma }_3$ and $-i{\gamma }_2{\gamma }_4$, which are entangled states when written in the original basis of $i{\gamma }_1{\gamma }_2$ and $i{\gamma }_3{\gamma }_4$. For example, the state ${\left|1\right.⟩}_{12}{\left|0\right.⟩}_{34}$ evolves into $\frac{1}{\sqrt{2}}\left({\left|0\right.⟩}_{12}{\left|1\right.⟩}_{34}+{\left|1\right.⟩}_{12}{\left|0\right.⟩}_{34}\right)$. Since the vortices have long-range interaction, the Abelian phase during the braiding may not be well defined, but the non-Abelian unitary operation is robust (12). From the reasoning presented above, one can see that the non-Abelian gate during MZM braiding is a direct consequence of exchanging MZMs ${\gamma }_2,{\gamma }_3$. The resulting gate must be non-Abelian because $i{\gamma }_1{\gamma }_2$ anticommutes with $i{\gamma }_1{\gamma }_3$. Therefore, the same non-Abelian gate can be realized by another physical process that exchanges Majorana fermions, even if no braiding of the non-Abelian anyon is involved. In the following, we show how to obtain a realization of the same gate by making use of chiral Majorana fermion edge states of the TSC and complex chiral fermion edge states of the QAHI.

Fig. 1.

(A) The braiding of vortices in the $p+ip$ TSC. Each pair of vortices supports two states of a single fermion, and the braiding leads to a non-Abelian operation and maps a product state of vortices 12 and 34 into an entangled state, as a consequence of exchanging MZMs ${\gamma }_2,{\gamma }_3$. (B) Our proposed device of QAHI–TSC–QAHI junction. The same partner switch as in A occurs between incoming electrons from leads A and B and outgoing electrons in leads C and D. (C) Such an exchange leads to a non-Abelian gate that is equivalent to a Hadamard gate $H$ followed by a Pauli-Z gate $Z$.

The device we propose to study is a 2D QAHI–TSC–QAHI junction predicted in refs. 3 and 4. As shown in Fig. 1B, the junction consists of two QAHIs (18–20) of Chern number $\mathcal{C}=1$ and a chiral TSC of BdG Chern number $\mathcal{N}=1$. The conductance ${\sigma }_{12}$ is measured between metallic leads 1 and 2 by driving a current $I$, where no current flows through lead 3 which grounds the TSC. Each edge between the chiral TSC and the vacuum or a QAHI hosts a chiral Majorana fermion edge mode governed by a Hamiltonian $H_M\left(x\right)=-i\hslash v_F\gamma \left(x\right){\partial }_x\gamma \left(x\right)$, where $\gamma \left(x\right)$ is the Majorana operator satisfying $\gamma \left(x\right)={\gamma }^{†}\left(x\right)$ and the anticommutation relation $\left\{\gamma \left(x\right),\gamma \left(x\prime \right)\right\}=\delta \left(x-x\prime \right)/2$, $v_F$ is the Fermi velocity, and $x$ is the coordinate of the 1D edge. In contrast, each edge between a QAHI and the vacuum hosts a charged chiral fermion (electron) edge mode with a Hamiltonian $H_F\left(x\right)=-i\hslash v_F{\psi }^{†}\left(x\right){\partial }_x\psi \left(x\right)$, where $\psi \left(x\right)$ and ${\psi }^{†}\left(x\right)$ are the annihilation and creation operators of the edge fermion, and we have assumed chemical potential $\mu =0$ for the moment. By defining two Majorana operators ${\gamma }_1=\left(\psi +{\psi }^{†}\right)/2$ and ${\gamma }_2=\left(\psi -{\psi }^{†}\right)/2i$ [hereafter ${\gamma }_i={\gamma }_i\left(x\right)$ is short for chiral Majorana fermion], one can rewrite $H_F\left(x\right)$ as $H_F\left(x\right)=-i\hslash v_F\left({\gamma }_1{\partial }_x{\gamma }_1+{\gamma }_2{\partial }_x{\gamma }_2\right)$, which implies a charged chiral fermion mode is equivalent to two chiral Majorana fermion modes. As a result, the edge states of the junction consist of four chiral Majorana fermion modes ${\gamma }_i$ ($1\le i\le 4$) as shown in Fig. 1B, which are related to the charged chiral fermion modes on the QAHI edges as ${\psi }_A={\gamma }_1+i{\gamma }_2$, ${\psi }_B={\gamma }_4+i{\gamma }_3$, ${\psi }_C={\gamma }_1-i{\gamma }_3$, and ${\psi }_D={\gamma }_4+i{\gamma }_2$ (3).

Our key observation is that the same kind of partner switch of Majorana fermions as that of the vortex braiding occurs in this device between incoming and outgoing electrons. An incoming electron from lead $A$ becomes a nonlocal fermion simultaneously on the two edges of the TSC described by ${\gamma }_1$ and ${\gamma }_2$. If we measure the number of outgoing electrons in leads $C$ and $D$, we find that the outgoing states in the two leads are entangled, because the number operators in these leads do not commute with those of incoming electrons.

To be more specific and to make a connection with quantum computation, consider the low-current limit $I\to 0$ where electrons are injected from lead 1 one by one, each of which occupies a traveling-wave packet state of ${\psi }_A$. The occupation number 0 or 1 of such a fermion wave packet state then defines a qubit $A$ with basis $\left|0_A\right.⟩$ and $\left|1_A\right.⟩$. Similarly, we can define the qubits $B$, $C$, and $D$ for ${\psi }_B$, ${\psi }_C$, and ${\psi }_D$, respectively. At each moment of time, the real and imaginary parts of the fermionic annihilation operator of each wave packet state define two self-conjugate Majorana operators localized at the wave packet. When the wave packets move out the superconducting region, they merge with a different partner and form states of the outgoing qubits. In the evolution of the incident electrons, qubits $A$ and $B$ span the Hilbert space of the initial state $\left|{\psi }_i\right.⟩$, while qubits $C$ and $D$ form the Hilbert space of the final state $\left|{\psi }_f\right.⟩$. In the same way as the MZM braiding case, the exchange of ${\gamma }_2$ with ${\gamma }_3$ then leads to a unitary evolution

$$\left(\begin{array}{c}\left|0_C{0}_D\right.⟩\hfill \\ \left|0_C{1}_D\right.⟩\hfill \\ \left|1_C{0}_D\right.⟩\hfill \\ \left|1_C{1}_D\right.⟩\hfill \end{array}\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{cccc}1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\\ 0\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 0\\ 0\hfill & \hfill -1\hfill & \hfill 1\hfill & \hfill 0\\ -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\end{array}\right)\left(\begin{array}{c}\left|0_A{0}_B\right.⟩\hfill \\ \left|0_A{1}_B\right.⟩\hfill \\ \left|1_A{0}_B\right.⟩\hfill \\ \left|1_A{1}_B\right.⟩\hfill \end{array}\right).$$ [1]

This transformation should be viewed as an S matrix between incoming and outgoing electron states. Note that the fermion parity is conserved in the unitary evolution. If we define a new qubit $\left(\left|0\right.⟩,\left|1\right.⟩\right)$ in the odd fermion parity subspace as $\left(\left|0_A{1}_B\right.⟩,\left|1_A{0}_B\right.⟩\right)$ initially and $\left(\left|0_C{1}_D\right.⟩,\left|1_C{0}_D\right.⟩\right)$ at the final time, the above unitary evolution is exactly a topologically protected Hadamard gate $H$ followed by a Pauli-Z gate $Z$ as shown in Fig. 1C; namely, $\left|{\psi }_f\right.⟩=ZH\left|{\psi }_i\right.⟩$, where

$$H=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1\hfill & \hfill 1\\ 1\hfill & \hfill -1\end{array}\right),\hspace{1em}Z=\left(\begin{array}{cc}1\hfill & \hfill 0\\ 0\hfill & \hfill -1\end{array}\right).$$ [2]

The same conclusion holds for the even fermion parity subspace. Therefore, the two qubits A and B (C and D) behave effectively as a single qubit, and we can regard qubit A (C) as the data qubit, while qubit B (D) is a correlated ancilla qubit.

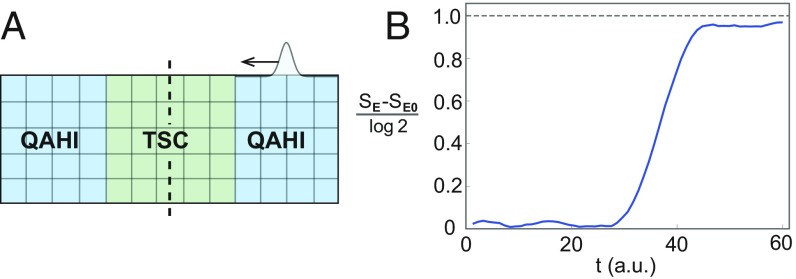
For an electron incident from lead 1 represented by initial state $\left|{\psi }_i\right.⟩=\left|1_A{0}_B\right.⟩$, the junction turns it into a final state $\left|{\psi }_f\right.⟩=\left(\left|0_C{1}_D\right.⟩+\left|1_C{0}_D\right.⟩\right)/\sqrt{2}$. This implies (SI Appendix) that the entanglement entropy between left and right halves of the junction divided by the dashed line in Fig. 2A increases by $\log 2$. Indeed, this is verified by our numerical calculation in a lattice model of the junction (Fig. 2A), where the entanglement entropy $S_E$ increases with time $t$ as shown in Fig. 2B, after an electron is injected from lead 1 above the Fermi sea. More details of this calculation are provided in SI Appendix. Since ${\psi }_C$ and ${\psi }_D$ propagate into leads 1 and 2, respectively, the electron has $r=1/2$ probability to return to lead 1 and $t=1/2$ probability to tunnel into lead 2. This yields (3) a half-quantized two-terminal conductance ${\sigma }_{12}=t{e}^2/h=e^2/2h$. Since lead 1 (lead 2) connects ${\psi }_A$ (${\psi }_B$) with ${\psi }_C$ (${\psi }_D$) (Fig. 1B), we are in fact identifying the charge basis of final qubit $C$ ($D$) with that of initial qubit $A$ ($B$). Accordingly, the conductance ${\sigma }_{12}$ provides a natural measurement of the overlap probability between $\left|{\psi }_i\right.⟩$ and $\left|{\psi }_f\right.⟩$ under this common basis; namely, ${\sigma }_{12}=\left(1-{\left|⟨{\psi }_f|{\psi }_i⟩\right|}^2\right)e^2/h$.

Fig. 2.

(A) The setup for numerical computation of entanglement entropy. We use a lattice model of QAHI–TSC–QAHI junction, add an initial edge wave packet on a QAHI edge, and then examine the time evolution of the state and the entanglement entropy between the left and the right part of the lattice separated by the dashed line. (B) Evolution of entanglement entropy $S_E$ between left and right halves of the junction (divided by dashed line in A) with time $t$ (arbitrary unit) after an electron above the Fermi sea is injected from lead 1, where $S_{E0}$ is the entanglement entropy of the Fermi sea.

As we have discussed, the above process is topologically equivalent to fusion and braiding of four vortex operators in the TSC bulk (SI Appendix) (21, 22). More concretely, when the electron of an incident state $\left|1_A{0}_B\right.⟩$ reaches the boundary of the TSC, one can imagine an operation of dragging the electron (fermion) into the Hilbert space of two nearby vortices ${\sigma }_1$ and ${\sigma }_2$ in the TSC bulk, after which ${\sigma }_1$ and ${\sigma }_2$ are in the fermionic fusion channel. Meanwhile, one can create two more vortices ${\sigma }_3$ and ${\sigma }_4$ in the bulk of the TSC in the vacuum fusion channel. Next, one can braid the vortices, fuse ${\sigma }_1$ with ${\sigma }_3$, and fuse ${\sigma }_2$ with ${\sigma }_4$. Finally, one can drag the state in the Hilbert space of ${\sigma }_1$ and ${\sigma }_3$ onto the QAH edge of ${\psi }_C$ and that of ${\sigma }_2$ and ${\sigma }_4$ onto the QAH edge of ${\psi }_D$. During such a vortex braiding and fusing process, there is no Majorana fermion propagating on the TSC edge. However, the initial state and the final state in this case are the same as the above process of chiral Majorana fermion propagation (SI Appendix), so the two processes are topologically equivalent.

A Testable Quantum Gate

The conductance ${\sigma }_{12}$ of the above junction, however, cannot confirm whether chiral Majorana fermions ${\gamma }_i$ are coherent or not during the propagation and thus whether the process is a coherent quantum gate. For instance, if a random phase factor is introduced in the propagation of ${\psi }_C$ and ${\psi }_D$, a pure initial state $\left|{\psi }_i\right.⟩=\left|1_A{0}_B\right.⟩$ will evolve into a mixed final state with a density matrix ${\rho }_f=\left(\left|0_C{1}_D\right.⟩\left.⟨0_C{1}_D\right|+\left|1_C{0}_D\right.⟩\left.⟨1_C{0}_D\right|\right)/2$, while the conductance remains ${\sigma }_{12}=\left[1-\text{tr}\left({\rho }_f\left|{\psi }_i\right.⟩\left.⟨{\psi }_i\right|\right)\right]e^2/h=e^2/2h$.

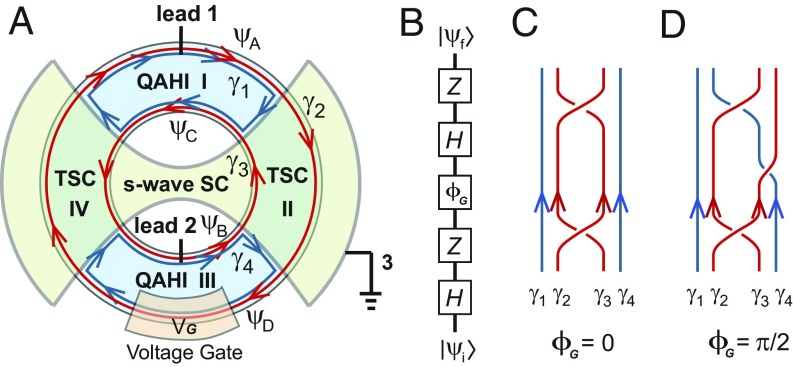
To confirm whether the system as a quantum gate is coherent, we propose to implement a Corbino geometry QAHI–TSC–QAHI–TSC junction as shown in Fig. 3A and measure the conductance ${\sigma }_{12}$ between lead 1 and lead 2. The junction can be realized by attaching a fan-shaped $s$-wave superconductor on top of a $\mathcal{C}=1$ QAHI Corbino ring, with a proper out-of-plane magnetic field driving the two regions II and IV into the $\mathcal{N}=1$ TSC phase (4, 6). A voltage gate $V_G$ is added on the bottom edge of QAHI region III covering a length $l_G$ of the edge. Lead 3 grounds the superconductor and has no current passing through. At zero gate voltage, the edge states of the Corbino junction are four chiral Majorana edge states ${\gamma }_i$ ($1\le i\le 4$) as shown in Fig. 3A.

Fig. 3.

Quantum interference in the QAHI–TSC–QAHI–TSC Corbino junction. (A) The Corbino junction consists of a Corbino QAHI ring with a fan-shaped $s$-wave superconductor on top of it which drives regions II and IV into the TSC, and a voltage gate $V_G$ is added at the bottom edge. (B) Such a junction is equivalent to a series of single-qubit quantum gates $ZH{R}_{{\varphi }_G}ZH$, where $R_{{\varphi }_G}$ is a phase gate controlled by $V_G$. (C and D) The MZM braiding process that gives the same gates as the Corbino device with ${\varphi }_G=0$ and ${\varphi }_G=\pi /2$, respectively.

The gate voltage $V_G$ on the bottom edge of region III behaves as a chemical potential term $H_G=e{V}_G{\psi }_D^{†}{\psi }_D$ for ${\psi }_D={\gamma }_4+i{\gamma }_2$ in a length $l_G$. In the language of quantum computation, this induces a phase gate

$$R_{{\varphi }_G}=\left(\begin{array}{cc}{e}^{-i{\varphi }_G}\hfill & \hfill 0\\ 0\hfill & \hfill 1\end{array}\right)$$ [3]

acting on the corresponding qubit $D$, where the phase shift ${\varphi }_G=e{V}_G{l}_G/\hslash v_F$ is tunable via $V_G$. Accordingly, the fermion operator ${\psi }_D$ undergoes a unitary evolution ${\psi }_D\to e^{i{\varphi }_G}{\psi }_D$. In particular, when ${\varphi }_G=\pi /2$, this is equivalent to an exchange of Majorana modes ${\gamma }_2$ and ${\gamma }_4$; namely, ${\gamma }_4\to {\gamma }_2$, and ${\gamma }_2\to -{\gamma }_4$.

If we regard the charged chiral edge modes of QAHI region I (${\psi }_A$ and ${\psi }_C$) as the data qubit and those of QAHI region III (${\psi }_B$ and ${\psi }_D$) as the ancilla qubit, the junction can be viewed as a series of quantum gates as shown in Fig. 3B, with a total unitary evolution $\left|{\psi }_f\right.⟩=ZH{R}_{{\varphi }_G}ZH\left|{\psi }_i\right.⟩$. Fig. 3 C and D shows the MZM braiding process that results in the same non-Abelian gate as the ${\varphi }_G=0$ case and the $\pi /2$ case, respectively. For an electron incident from lead 1 represented by the initial state $\left|{\psi }_i\right.⟩=\left|1_A{0}_B\right.⟩$, the finial state is

$$\left|{\psi }_f\right.⟩=e^{-i{\varphi }_G/2}\left(\cos \frac{{\varphi }_G}{2}\left|0_A{1}_B\right.⟩+i\sin \frac{{\varphi }_G}{2}\left|1_A{0}_B\right.⟩\right).$$ [4]

Therefore, the two-terminal conductance of this Corbino junction is

$${\sigma }_{12}=\left(1-|⟨{\psi }_f|{\psi }_i⟩{|}^2\right)\frac{e^2}{h}=\frac{1+\cos {\varphi }_G}{2}\frac{e^2}{h},$$ [5]

which oscillates as a function of $V_G$ with a peak-to-valley amplitude $e^2/h$. In contrast, if the system loses coherence completely, the final state will be the maximally mixed state described by density matrix ${\rho }_f=\left(\left|0_A{1}_B\right.⟩\left.⟨0_A{1}_B\right|+\left|1_A{0}_B\right.⟩\left.⟨1_A{0}_B\right|\right)/2$, and the conductance will constantly be ${\sigma }_{12}=e^2/2h$. Therefore, the oscillation amplitude of ${\sigma }_{12}$ measures the coherence of the chiral Majorana fermions in the junction.

So far we have assumed chemical potential $\mu =0$ on all QAHI edges except the interval covered by voltage gate. In general, $\mu$ is nonzero and is nonuniform along the QAHI edges when there are disorders. Such a nonzero landscape of $\mu$ contributes an additional phase gate, which leads to a phase shift ${\varphi }_G\to {\varphi }_G+{\varphi }_0$, with ${\varphi }_0$ being a fixed phase (SI Appendix). Experimentally, the gate voltage $V_G$ and thus ${\varphi }_G$ can be well controlled by current techniques at a high precision level (23).

Decoherence

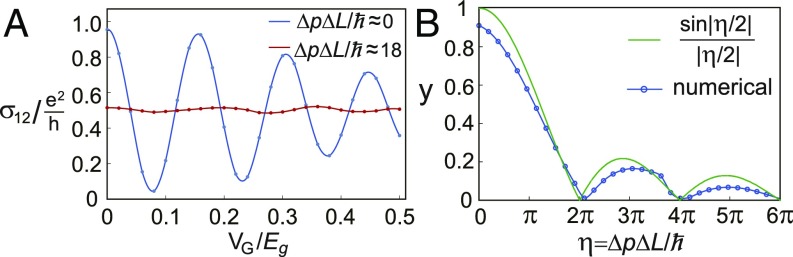
There are mainly two effects contributing to the decoherence of chiral Majorana fermions. The first one is the nonmonochromaticity of the incident electron wave packet, which is characterized by a momentum uncertainty $\mathrm{\Delta }p\approx 2\pi \hslash /l_W$ for a wave packet of width $l_W$. In general, the (effective) path lengths of the four chiral Majorana modes ${\gamma }_i\left(1\le i\le 4\right)$ in Fig. 3A may differ by a length scale $\mathrm{\Delta }L$, and the ${\sigma }_{12}$ oscillation is sharp only if $\mathrm{\Delta }p\mathrm{\Delta }L<2\pi \hslash$. As a demonstration, we numerically examine the time evolution of an electron wave packet from lead 1 within an energy window $v_F\left[-\mathrm{\Delta }p/2,\mathrm{\Delta }p/2\right]$ on a lattice model of the Corbino junction and calculate ${\sigma }_{12}$ (SI Appendix). Fig. 4A shows ${\sigma }_{12}$ as a function of $V_G/E_g$ for $\mathrm{\Delta }p\mathrm{\Delta }L/\hslash \approx 0$ and 18, respectively, where $E_g$ is the QAHI bulk gap. The modulation of the ${\sigma }_{12}$ amplitude by $V_G$ is due to the effective change of $\mathrm{\Delta }L$ as a result of the change in $v_F$ on the edge covered by voltage gate $V_G$. Fig. 4B shows the peak-to-valley amplitude $y=\mathrm{\Delta }{\sigma }_{12}/\left(e^2/h\right)$ as a function of $\eta =\mathrm{\Delta }p\mathrm{\Delta }L/\hslash$, where we find the amplitude roughly decays as $y=|\sin \left(\eta /2\right)/\left(\eta /2\right)|$. In the experiments, the temperature $T$ yields a momentum uncertainty $\mathrm{\Delta }p\approx k_{B}T/v_F$, where $k_B$ is the Boltzmann constant. For the Cr-doped (Bi,Sb)₂Te₃ thin-film QAHI with superconducting proximity studied in ref. 6, the Fermi velocity is of order $\hslash v_F\sim 3$ eV$\cdot$Å (24), and the temperature $T$ reaches as low as 20 mK. This requires a path-length difference $\mathrm{\Delta }L\sim 100\hspace{0.17em}\mathrm{\mu }\text{m}$ or smaller, which is experimentally feasible (6, 25).

Fig. 4.

Numerically calculated ${\sigma }_{12}$ oscillation for the Corbino junction. (A) ${\sigma }_{12}$ calculated for $\mathrm{\Delta }p\mathrm{\Delta }L/\hslash \approx 0$ and 18 as a function of $V_G$, respectively. (B) The peak-to-valley amplitude $y$ of ${\sigma }_{12}$ in units of $e^2/h$ with respect to $\eta =\mathrm{\Delta }p\mathrm{\Delta }L/\hslash$, which is roughly given by $y=\sin |\eta /2|/|\eta /2|$.

The second effect causing decoherence is the inelastic scattering. The inelastic scattering of charged chiral fermions ${\psi }_i$ mainly originates from the electron–phonon coupling, which yields an inelastic scattering length $l_{in}\propto T^{-p/2}$ at temperature $T$ (26–28). For integer quantum Hall systems, $l_{in}$ exceeds $10^2\mathrm{\mu }$m at $T\sim 20$ mK (29), while $l_{in}$ is expected to be smaller for QAHI (20). In contrast, since the electron–phonon coupling is odd under charge conjugation, the neutral chiral Majorana fermions ${\gamma }_i$ are immune to phonon coupling. Instead, their lowest-order local interaction is of the form ${\gamma }_i{\partial }_x{\gamma }_i{\partial }_x^2{\gamma }_i{\partial }_x^3{\gamma }_i$ (30), which is highly irrelevant. Therefore, $l_{in}$ of ${\gamma }_i$ in TSCs should be much longer than that of ${\psi }_i$ in QAHIs. If the ${\sigma }_{12}$ interference is to be observed, the sizes of the QAHI and TSC regions in the junction have to be within their inelastic scattering lengths $l_{in}$, respectively.

Conclusion

In summary, we have introduced the appealing possibility of performing topological quantum computations via propagations of 1D chiral Majorana fermion wave packets, which are physically equivalent to the braiding of MZMs. The Corbino junction above gives a minimal demonstration of single-qubit quantum-gate operations with chiral Majorana fermions, and the conductance of the junction provides a natural readout for the final qubit states. Most importantly, this circumvents two main experimental difficulties in quantum computations with MZMs: the braiding operation of MZMs and the readout of the qubit states. The high velocity of chiral Majorana edge modes also makes the quantum gates $10^3$ times faster than those of other quantum computation schemes (31, 32). Furthermore, the development of a single-electron source (33) makes the injection and detection of a single-electron wave packet qubit on edges possible. Yet in the current stage we still face difficulties which are also encountered by the MZM quantum computation scheme: the error correction of the phase gate $R_{{\varphi }_G}$ (34, 35) and nondemolitional four-Majorana implementation of the controlled not gate (14, 35, 36). If one could overcome these difficulties, one may in principle achieve universal quantum computation using chiral Majorana fermion devices, which would have a high computation speed. Finally, we remark that the conductance oscillation in the Corbino junction, if observed, will also unambiguously prove the existence of quantum coherent chiral Majorana fermions in the experiment (6, 22, 30, 37–39).