On the Null Distribution of Bayes Factors in Linear Regression

Abstract

We show that under the null, the 2 log(Bayes factor) is asymptotically distributed as a weighted sum of chi-squared random variables with a shifted mean. This claim holds for Bayesian multi-linear regression with a family of conjugate priors, namely, the normal-inverse-gamma prior, the g-prior, and the normal prior. Our results have three immediate impacts. First, we can compute analytically a p-value associated with a Bayes factor without the need of permutation. We provide a software package that can evaluate the p-value associated with Bayes factor efficiently and accurately. Second, the null distribution is illuminating to some intrinsic properties of Bayes factor, namely, how Bayes factor quantitatively depends on prior and the genesis of Bartlett's paradox. Third, enlightened by the null distribution of Bayes factor, we formulate a novel scaled Bayes factor that depends less on the prior and is immune to Bartlett's paradox. When two tests have an identical p-value, the test with a larger power tends to have a larger scaled Bayes factor, a desirable property that is missing for the (unscaled) Bayes factor.

1 Introduction

Bayesian methods have been sidelined by most practitioners in genetic association studies. The main reason is that p-value, although often misinterpreted, is entrenched among practitioners [Sellke et al., 2001, Nuzzo, 2014]. A Bayesian method that performs genetic association tests, such as that of Guan and Stephens [2008], often faces an inconvenient demand to produce a p-value associated with an extraordinarily large Bayes factor. Because the null distribution of Bayes factor is unknown, a previous solution has been to obtain the p-value through permutation [Servin and Stephens, 2007]. In genome-wide association studies, however, the significance threshold for p-values is exceedingly small, owing to the burden of multiple testing; thus, the number of permutations required is often prohibitively large and hence impractical. This motivates us to quantify the null distribution of Bayes factors, from which we can compute a p-value associated with Bayes factor analytically, without the need of permutation.

Our second motivation is to understand Bayes factor itself, first and foremost to understand, quantitatively, the prior-dependence nature of Bayes factors. Such prior-dependency often turns away naive practitioners. The second is to investigate the root of inconsistency of Bayes factor, namely, Bartlett’s paradox [Bartlett, 1957]. Bartlett discovered that a diffusive prior tends to favor, unintentionally, the null model. In other words, if one were uncertain about the prior effects, one would automatically favor the null. (On the other hand, if one were too certain about the prior effects, one would risk prior-misspecification, which also unintentionally favors the null.) We identified the dominant term in Bayes factor that is affected by the prior, which motivates us to systematically scale Bayes factor. The scaled Bayes factor depends weakly on the prior and no longer suffers from the Barlett’s paradox.

Our third motivation is to emphasize the necessity of taking into account power to interpret p-values. The probability that a positive report is false depends on both the p-value and the power of a test [Wacholder et al., 2004]. A plainer reiteration of this insightful observation is that a small p-value alone cannot provide a strong evidence for a true association, and it has to be interpreted in light of the statistical power [Burton et al., 2007]. A large Bayes factor, however, by itself provides a strong evidence for a true association [Stephens and Balding, 2009]. And Sawcer [2010] related Bayes factor to the ratio between the power and the p-value. It is therefore beneficial for a study to report both Bayes factors and their associated p-values. The idea of computing a p-value associated with Bayes factor dates back to Good [1957], as a symbol of “Bayes/non-Bayes compromise” [Good, 1992]. The p-values will satisfy the practical mandate imposed by the research community, and the companion Bayes factors will remind one to account for power when interpreting p-values. For example, tests may be ranked differently by their p-values than by their Bayes factors, and two identical p-values may associate with different Bayes factors. Both examples highlight the necessity of taking into account the statistical power to interpret p-values. To this end, our scaled Bayes factor becomes more appealing. When two tests produce identical p-values, the scaled Bayes factor tends to assign a larger value to the test with a larger power, while the (unscaled) Bayes factor does not.

Our main result states that, under the null, the logarithm of Bayes factor has the same distribution as a weighted sum of chi-squared random variables with a shifted mean. The results hold asymptotically for Bayesian multi-linear regression. For simple linear regression, we have $2\text{ log}(\text{Bayes factor})=\mathrm{\lambda }{\chi }_1^2+\text{log}(1-\mathrm{\lambda })$, where λ is a quantity related to the prior and the data, and ${\chi }_1^2$ denotes a chi-squared random variable of one degree of freedom (denoted by d.f.). The undesirable properties of Bayes factor, namely, its over-dependence on the prior and Bartlett’s paradox, find their roots in the shift term log(1 − λ). Our scaled Bayes factor effectively substitutes this term with −λ to achieve $2\text{ log}(\text{scaled Bayes factor})=\mathrm{\lambda }({\chi }_1^2-1)$. For simple linear regression, the p-value associated with a Bayes factor is the same as the p-value of the likelihood ratio test. For multi-linear regression, computing the p-value associated with a Bayes factor requires evaluation of the distribution function of a weighted sum of chi-squared random variables. Based on a recently published polynomial algorithm [Bausch, 2013], we developed a software package to evaluate the p-values analytically, which can efficiently achieve an arbitrary precision.

The paper is structured as follows. In Section 2 we formulate the model and the priors, and provide our main result on the null distribution of Bayes factors. In Section 3 we demonstrate how to compute a p-value associated with a Bayes factor. In Section 4 we introduce the scaled Bayes factor and demonstrate its benefits. In Section 5 we analyze a real dataset to compute and compare Bayes factor, the scaled Bayes factor, and the p-values associated with Bayes factors. In the last section we summarize our findings and discuss relevant (future) topics. All proofs are in the Supplementary online.

2 The Null Distribution of Bayes factor

We consider the standard hypothesis testing problem in linear regression with independent normal errors.

$$H_0:\mathit{y}|\mathit{a},\tau ~\text{MVN}(\mathit{\text{Wa}},{\tau }^{-1}{\mathit{I}}_n),H_1:\mathit{y}|\mathit{a},\mathit{b},\tau ~\text{MVN}(\mathit{\text{Wa}}+\mathit{\text{Lb}},{\tau }^{-1}{\mathit{I}}_n),$$ (1)

where MVN stands for the multivariate normal distribution, I_n is an n × n identity matrix, W is a full-rank n × q matrix representing the nuisance covariates, including a column of 1, a is a q-vector, L is an n × p matrix representing the covariates of interest, b is a p-vector, and τ⁻¹ is the error variance. The two models H₀ and H₁ are nested and the null model H₀ represents no effect of L.

The Bayesian linear regression comes with three forms of conjugate priors in the literature. The first is the normal-inverse-gamma (NIG) prior [O’Hagan and Forster, 2004, Chap. 9], detailed below:

$$\mathit{a}|\tau ~\text{MVN}(\mathbf{0},{\tau }^{-1}{\mathit{V}}_a),\mathit{b}|\tau ~\text{MVN}(\mathbf{0},{\tau }^{-1}{\mathit{V}}_b),\tau ~\text{Gamma}({\kappa }_1/2,{\kappa }_2/2),$$ (2)

where V_a and V_b are some positive definite matrices, and the gamma distribution is in the shape-rate parameterization. Following the standard treatment [c.f., Servin and Stephens, 2007] to let ${\mathit{V}}_a^{-1}\to \mathit{0}$ and κ₁, κ₂ → 0, we can compute Bayes factor in the closed form

$$\text{BF}={|{\mathit{V}}_b|}^{-1/2}{|{\mathit{X}}^t\mathit{X}+{\mathit{V}}_b^{-1}|}^{-1/2}{\{1-\frac{{\mathit{y}}^t\mathit{X}{({\mathit{X}}^t\mathit{X}+{\mathit{V}}_b^{-1})}^{-1}{\mathit{X}}^t\mathit{y}}{{\mathit{y}}^t\mathit{y}-{\mathit{y}}^t\mathit{W}{({\mathit{W}}^t\mathit{W})}^{-1}{\mathit{W}}^t\mathit{y}}\}}^{-n/2}$$ (3)

where

$$\mathit{X}=({\mathit{I}}_n-\mathit{W}{({\mathit{W}}^t\mathit{W})}^{-1}{\mathit{W}}^t)\mathit{L}$$ (4)

is the residuals of L after regressing out W, and |·| denotes the determinant. Since W is assumed to contain a column of 1, each column in X is therefore centered.

Bayes factor in (3) uses the null as the base model and is thus called the null-based Bayes factor [c.f., Liang et al., 2008], which has been widely used in genetic association studies [Balding, 2006, Marchini et al., 2007, Guan and Stephens, 2008, Xu and Guan, 2014].

The use of the improper prior ${\mathit{V}}_a^{-1}\to 0$, κ₁, κ₂ → 0 has two merits. First, the limiting prior distributions for a and τ is equivalent to Jeffreys’ prior [Ibrahim and Laud, 1991, O’Hagan and Forster, 2004], p(a, τ ) ∝ τ^{(q−2)/ 2}, which is the standard choice of the non-informative prior for the nuisance parameters in the literature. Moreover, the posterior distributions for a and τ are proper. Second, Bayes factor in (3), which can be written as the limit of a sequence of Bayes factors with proper priors (see proof in Supplementary), is invariant to the shifting and scaling of y (or independent of a and τ). To see this, replace y with the standardized random variable

$$z\stackrel{\text{def}}{=}{\tau }^{1/2}(\mathit{y}-\mathit{\text{Wa}}).$$ (5)

and one can check (3) still holds.

We assume a priori that the expectation of b is zero so that the direction of the effect has no influence on Bayes factor. This prior for b is commonly adopted in practice [c.f., Jeffreys, 1961, Chap. 5]. For the NIG prior, we further assume independence between the effects and the covariates. Henceforth when we refer to the NIG prior we mean

$${\mathit{V}}_b={\sigma }_b^2{\mathit{I}}_p,$$ (6)

unless otherwise stated. The NIG prior and the corresponding Bayes factor will be the primary focus of this paper.

The second conjugate prior is Zellner’s g-prior [Zellner, 1986, Liang et al., 2008]:

$$p(\mathit{a},\tau )\propto 1/\tau ,\mathit{b}|\tau ~\text{MVN}(\mathbf{0},\frac{g}{\tau }({\mathit{X}}^t\mathit{X})-1).$$ (7)

This can be seen as a special case of the NIG prior with V_b = g(X^tX)⁻¹ and thus Bayes factor under the g-prior can be derived straightforwardly from (3).

The third conjugate prior, the normal prior, can also be viewed as a special case of the NIG prior, when the error variance τ⁻¹ is assumed known:

$$\mathit{a}|\tau ~\text{MVN}(\mathbf{0},{\tau }^{-1}{\mathit{V}}_a),\mathit{b}|\tau ~\text{MVN}(\mathbf{0},{\tau }^{-1}{\mathit{V}}_b).$$ (8)

Under this prior, and letting ${\mathit{V}}_a^{-1}\to \mathit{0}$, Bayes factor can also be computed analytically

$$\text{BF}={|{\mathit{V}}_b|}^{-1/2}{|{\mathit{X}}^t\mathit{X}+{\mathit{V}}_b^{-1}|}^{-1/2}\text{exp}\left\{\frac{1}{2}{z}^t\mathit{X}{({\mathit{X}}^t\mathit{X}+{\mathit{V}}_b^{-1})}^{-1}{\mathit{X}}^{t}z\right\},$$ (9)

where X is defined in (4) and z is defined in (5). Because the error variance in most applications is unknown, the normal prior is more of theoretical interest. But, as we will see shortly, Bayes factor with the normal prior is approximately equal to that with the NIG prior. This is not too surprising because the data are very informative on the error variance.

Theorem 1. For multi-linear regression (1) with the NIG prior (2), the g-prior (7), and the normal prior (8), under the null Bayes factors (BF) given in (3) and (9) follow

$$2\text{log}(\text{BF})=\sum _{i=1}^p[{\lambda }_i{Q}_i+\text{log}(1-{\lambda }_i)]+\epsilon ,$$ (10)

where $Q_i={({\mathit{u}}_i^t\mathit{z})}^2\underset{~}{\mathit{\text{i.i.d}}}{\chi }_1^2$ with z defined in (5), and (λ_i, u_i) is the ith eigenvalue-eigenvector pair of $\mathit{X}{({\mathit{X}}^t\mathit{X}+{\mathit{V}}_b^{-1})}^{-1}{\mathit{X}}^t$ with X defined in (4). For the NIG prior and the g-prior, ε = o_P (1) vanishes in probability when the sample size n → ∞. For the normal prior ε = 0.

Theorem 1 states that under the null 2 log BF is distributed as a weighted sum of chi-squared random variables with a shifted mean, and the weights and the mean-shift can be computed. By evaluating the distribution function, we can obtain a p-value associated with Bayes factor. For simple linear regression, Q₁ is asymptotically equal to the test statistic of the likelihood ratio test. Thus, the p-value associated with Bayes factor is the same as the p-value of the likelihood ratio test.

It is easy to see that λ_i ∈ [0, 1). When the leading eigenvalue approaches 1, ${\sum }_{i=1}^p\text{log}(1-{\lambda }_i)$ goes to negative infinity, and so does the 2 log BF. Under two scenarios the leading eigenvalue does approach 1: the sample size goes to infinity or the prior diffuses indefinitely. Thus the prior-dependence nature of Bayesfactor and the Barlett’s paradox both find their roots in the term ${\sum }_{i=1}^p\text{log}(1-{\lambda }_i)$. Moreover, when the sample size gets extraordinarily large, every λ_i approaches 1 and ${\sum }_{i=1}^p{\lambda }_i{Q}_i$ behaves like the likelihood ratio test statistic, which is distributed as a chi-squared random variable with p degrees of freedom, a special case of Wilks’s [1938] theorem.

3 The P-value Associated with Bayes factor

Using Theorem 1 we can compute a p-value associated with Bayes factor given in (3), which henceforth is denoted by p_B. Since Bayes factor is a test statistic, p_B is naturally a Frequentist p-value. We point out p_B is also a Bayesian p-value. The p-values, or tail probabilities, are frequently computed in Bayesian context to check whether the model provides a good fit to the data. Bayesians p-values can be computed by comparing the observed test statistic to a predictive distribution obtained by integrating out the nuisance parameters over a reference distribution. Different Bayesian p-values can be computed using different reference distributions [Robins et al., 2000, Table 1]. Two well-known examples are the prior predictive p-values [Box, 1980] and the posterior predictive p-values [Rubin, 1984, Meng, 1994], which use the prior and the posterior as the reference distributions respectively. In our case, Bayes factors in (3) and (9) are independent of the nuisance parameters; thus, p_B can be viewed as a posterior predictive p-value. This convenience can be viewed as a bonus from the improper prior we used.

Table 1.

Top 20 single SNP associations.

SNP	Chr	Pos	MAF	bf(y)	bf(ỹ)	sbf(y)	sbf(ỹ)	p(y)	p(ỹ)
rs12120962	1	10.53	0.384	3.88 (5)	−0.90	4.56 (4)	−0.21	5.63 (5)	0.01
rs12127400	1	10.54	0.384	3.61 (9)	−0.90	4.29 (8)	−0.21	5.34 (9)	0.01
rs4656461	1	163.95	0.140	5.71 (2)	−0.57	6.26 (2)	−0.03	7.51 (2)	0.46
rs7411708	1	163.99	0.428	3.69 (8)	−0.68	4.38 (7)	0.01	5.43 (8)	0.52
rs10918276	1	163.99	0.427	3.59 (10)	−0.66	4.28 (9)	0.03	5.33 (10)	0.54
rs7518099	1	164.00	0.140	6.04 (1)	−0.61	6.58 (1)	−0.07	7.85 (1)	0.38
rs972237	2	125.89	0.119	3.05 (15)	−0.62	3.56 (17)	−0.11	4.65 (18)	0.31
rs2728034	3	2.72	0.090	3.80 (6)	−0.62	4.27 (10)	−0.15	5.45 (7)	0.22
rs7645716	3	46.31	0.254	3.34 (11)	−0.88	3.98 (11)	−0.16	5.03 (11)	0.21
rs7696626	4	8.73	0.023	2.96 (18)	−0.33	3.20 (42)	−0.01	4.70 (16)	0.31
rs301088	4	53.53	0.473	2.95 (20)	−0.81	3.64 (16)	−0.11	4.65 (17)	0.31
rs2025751	6	51.73	0.466	3.78 (7)	−0.75	4.47 (6)	−0.06	5.53 (6)	0.41
rs10757601	9	26.18	0.443	3.09 (13)	−0.79	3.78 (12)	−0.10	4.80 (13)	0.33
rs10506464	12	62.50	0.164	2.97 (17)	−0.75	3.54 (18)	−0.18	4.59 (19)	0.15
rs10778292	12	102.78	0.140	4.00 (4)	−0.75	4.54 (5)	−0.21	5.68 (4)	0.02
rs2576969	12	102.80	0.271	3.07 (14)	−0.85	3.71 (14)	−0.20	4.75 (14)	0.08
rs17034938	12	102.85	0.127	3.23 (12)	−0.71	3.75 (13)	−0.19	4.85 (12)	0.13
rs1288861	15	43.50	0.120	2.95 (19)	−0.45	3.46 (20)	0.06	4.54 (21)	0.59
rs4984577	15	93.76	0.367	3.02 (16)	−0.64	3.69 (15)	0.04	4.71 (15)	0.56
rs12150284	17	9.97	0.353	4.95 (3)	−0.75	5.63 (3)	−0.07	6.75 (3)	0.38

The SNPs chosen have top 20 BF values using σ_b = 0.2. The rankings by three test statistics are given in the parentheses. ỹ is obtained by permuting y once. SNP IDs are in bold if they are mentioned specifically in the main text. The column names are explained as following. Pos: genomic position in megabase pair according to HG18; bf(y): log₁₀ BF(y); bf(ỹ): log₁₀ BF(ỹ); sbf(y): log₁₀ sBF(y); sbf(ỹ): log₁₀ sBF(ỹ); p(y): −log₁₀ p_B(y); and p(ỹ): −log₁₀ p_B(ỹ).

Corollary 1. Denote by p_F the p-value from the likelihood ratio test, then for simple linear regression, we have asymptotically p_B = p_F.

When p = 1, the right-hand side of (10) contains a single chi-squared random variable Q₁, which is asymptotically equal to the likelihood ratio test statistic, and therefore the two p-values are equal. In addition, for simple linear regression (10) explains the linear relationship between log BF and the likelihood ratio test statistic observed in Wakefield [2008] and Guan and Stephens [2008].

3.1 Weighted Sum of ${\chi }_1^2$

For multi-linear regression, the right hand side of (10) contains a weighted sum of chi-squared variables. The weights λ₁, ..., λ_p are functions of the prior effect size σ_b and the eigenvalues of the matrix X defined in (4). In contrast, the likelihood ratio test statistic is asymptotically equal to ${\sum }_{i=1}^p{Q}_i$ and distributed as ${\chi }_p^2$, which does not take into account the eigenvalues of X. Consequently, p_B no longer equals to p_F in general. One exception, however, is Bayes factor under the g-prior, where we have λ_i = g/(g + 1) for every i.

To compute p_B for multi-linear regression requires evaluating the distribution function of a weighted sum of chi-squared random variables, a challenging problem. Fortunately, a recent polynomial method by Bausch [2013] provides an efficient solution. Our contribution here is its implementation. We have implemented Bausch’s method in C++, which allows one to compute p-values (tail probabilities) to an arbitrary precision efficiently.

First we briefly summarize Bausch’s method and then provide more details of our implementation. Bausch pairs the chi-squared variables to take advantage of the identity

$$f_{{\mathrm{\lambda }}_1{Q}_1+{\mathrm{\lambda }}_2{Q}_2}(x)={(4{\mathrm{\lambda }}_1{\mathrm{\lambda }}_2)}^{-1/2}\text{exp}(-\frac{{\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2}{4{\mathrm{\lambda }}_1{\mathrm{\lambda }}_2}x)I_0(\frac{{\mathrm{\lambda }}_2-{\mathrm{\lambda }}_1}{4{\mathrm{\lambda }}_1{\mathrm{\lambda }}_2}x),$$

where Q₁ and Q₂ are independent ${\chi }_1^2$ random variables and I₀ is the modified Bessel function of the first kind. I₀ can be approximated, to an arbitrary precision, by its Taylor expansion, and the series obtained can be integrated algebraically in the subsequent convolutions. The error of this algorithm only depends on the remainder terms of the Taylor expansions and thus can be quantified. Bausch showed that the complexity of this algorithm is polynomial in p.

In our implementation, the weights (λ₁, ..., λ_p) are sorted in a descending order and the chi-squared variables are then paired consecutively. If p is odd, the term with the smallest weight is retained for a numerical convolution in the last step. This pairing strategy aims to minimize the number of terms needed in Taylor expansions for a pre-specified precision. After Taylor expansion, we are faced with convolving gamma density functions (up to a normalizing constant). The order of the convolutions is determined by a single-linkage hierarchical clustering [Murtagh and Contreras, 2012] on the rate parameters of the gamma densities. Convolving two gamma densities of similar rates is computationally more efficient.

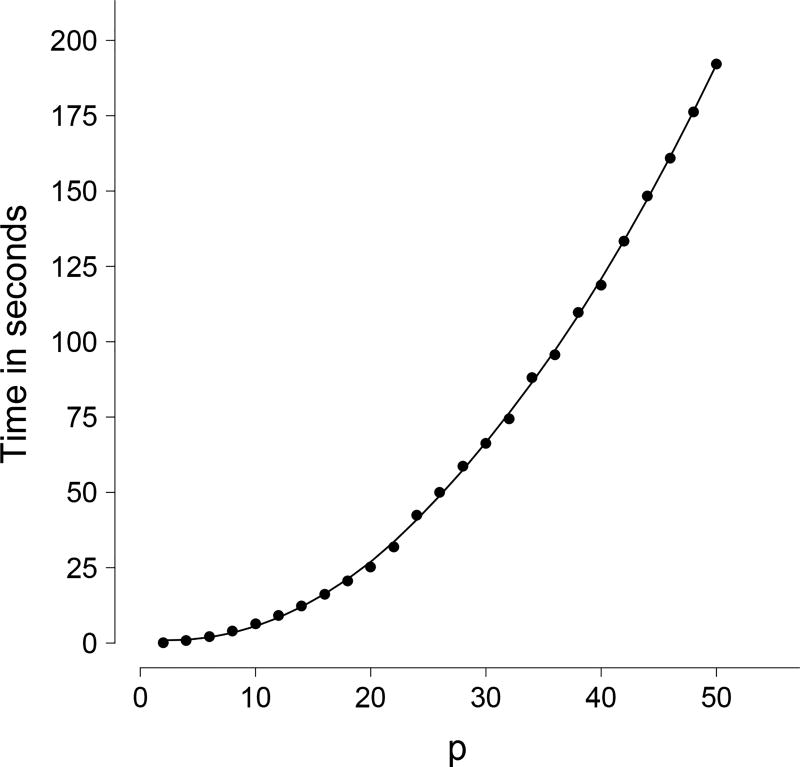
Our program has four features outstanding. First, we adopted GNU Multi-Precision Library so that our program can produce an arbitrarily small p-value without suffering underflow or overflow. Second, for an even number of chi-squared variables, p_B can be computed at an arbitrary precision; for an odd number of chi-squared variables, the error introduced at the last step of numerical convolution can be made arbitrarily small. Third, the terms of Taylor expansion are determined by a pre-specified precision and a strict error bound is provided. Last, since the program is written in C++, it is fast and suitable for studies that evaluate millions of tests, such as genetic association studies. Figure 1 demonstrates the efficiency of our program, for example, when p = 10 our program can evaluate ≈ 150 p-values per second. The speed appears to be quadratic in p. The weighted sum of chi-squared variables occurs frequently in statistical applications, such as the ridge regression, the variance component model, and recently the association testing for rare variants [Wu et al., 2011, Epstein et al., 2015]. We believe our program has a wide range of applications. The source code and executables of our program BACH (Bausch’s Algorithm for CHi-square weighted sum) are freely available at http://haplotype.org.

Figure 1.

Speed of evaluating p_B. The plot shows the time spent (y-axis) evaluating 1, 000 density functions to obtain 1, 000 p-values for different number of ${\chi }_1^2$ components (2–50 on x-axis). The p-values were evaluated with relative error < 10⁻⁵.

3.2 Accuracy and Calibration of p_B for Finite Sample Sizes

Using Theorem 1, we can evaluate extremely small p-values, an important advantage in applications such as genome-wide association studies (GWAS) compared to the permutation method described in [Servin and Stephens, 2007]. Since p_B is quantified asymptotically, we are compelled to evaluate the accuracy and calibration of p_B for small sample sizes. We also computed the likelihood ratio test p-value p_F as a comparison because of its intrinsic connection to Bayes factor (and hence p_B) shown in Theorem 1.

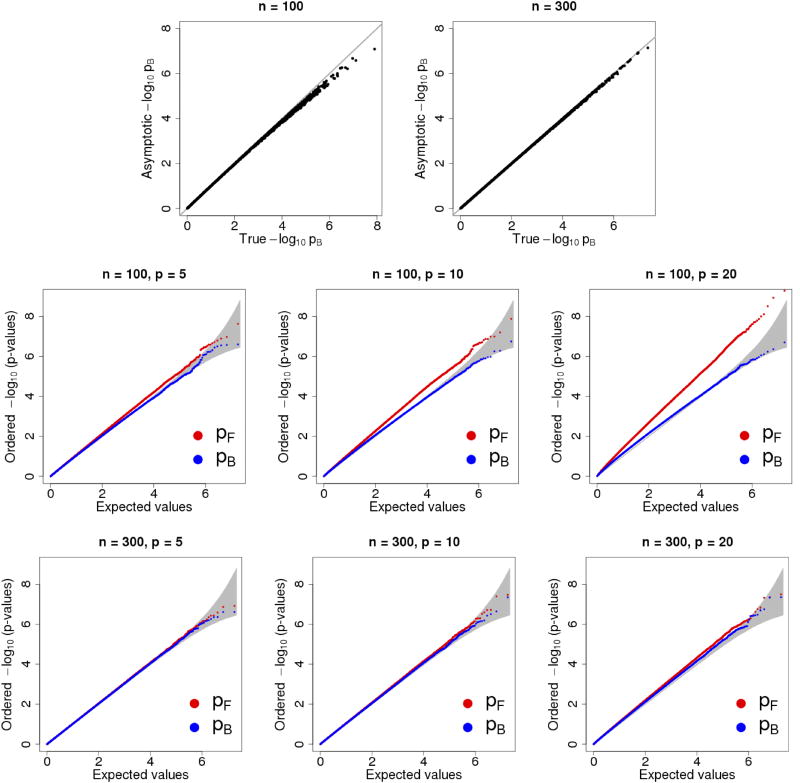
We used a GWAS dataset to perform our simulation studies. The details of the dataset are provided in Section 5. For given n and p, we randomly sampled a subset of genotypes of n individuals and p SNPs. Then we simulated y under the null, that is, y ~ MVN(0, I_n). For each pair of sampled genotypes and simulated phenotypes, we computed p_B, using σ_b = 0.2, and p_F. We chose n = 100, 300 and p = 1, 5, 10, 20. For every combination of n and p we repeated the simulations 10⁷ times. For p = 1, we can compute the exact p-value associated with Bayes factor using the F test (see proof in Supplementary). The comparison between exact values of p_B and p_B obtained from asymptotic approximation is shown in the top row of Figure 2. For p > 1, true values of p_B cannot be obtained analytically, we thus compared our asymptotic results against the theoretical uniform distribution. The two bottom rows show that for n = 100, the asymptotic results are conservative for small p-values; but for n = 300, the asymptotic results appear to be well-aligned with the theoretical prediction. Overall, Fig. 2 demonstrates that p_B is well calibrated, and the calibration is better than the p_F at the tail. We thus conclude that our asymptotic method for obtaining p_B is accurate and well-calibrated when the sample size is more than a few hundred.

Figure 2.

Accuracy and calibration of p_B. The top row is for simple linear regression. The “true values” for p_B are obtained from F-tests. The y-axis is the asymptotic p_B. Line y = x is marked in grey. Two bottom rows are for multi-linear regression. Red dots represent p_F (from likelihood ratio tests) and blue p_B. The grey region represents a 95% prediction intervals for uniformly distributed p-values.

4 Scaled Bayes Factors

Bayes factors are sensitive to the specification of priors. Let’s consider the NIG prior with ${\mathit{V}}_b={\sigma }_b^2{\mathit{I}}_p$ and denote the singular values of X by δ_i for i = 1, …, p. Then λ_i in (10) becomes ${\mathrm{\lambda }}_i={\delta }_i^2/({\delta }_i^2+1/{\sigma }_b^2)$, and thus

$$2\text{log BF}=\sum _{i=1}^p\{\frac{{\delta }_i^2{Q}_i}{{\delta }_i^2+1/{\sigma }_b^2}-\text{log}(1+{\delta }_i^2{\sigma }_b^2\}.$$ (11)

Here we assume the sample size is sufficiently large such that the o_P(1) error term can be safely omitted. The term λ_iQ_i is bounded by Q_i (because λ_i < 1), but the term $\text{log}(1/{\delta }_i^2{\sigma }_b^2)$ is monotonically increasing with respect to both δ_i and σ_b. When the sample size goes to infinity, δ_i goes to infinity; when the prior becomes more diffusive, σ_b goes to infinity. These properties give rise to the prior-dependence nature of Bayes factor and Bartlett’s paradox.

By (10), ${𝔼}_0[2\text{log BF}]={\sum }_{i=1}^p({\mathrm{\lambda }}_i+\text{log}(1-{\mathrm{\lambda }}_i))$, where 𝔼₀ is the expectation evaluated under the null. Centering 2 log BF to obtain

$$2\text{log sBF}\stackrel{\text{def}}{=}2\text{log BF}-{𝔼}_0[2\text{log BF}]=\sum _{i=1}^p{\lambda }_i(Q_i-1).$$ (12)

We call the quantity log BF − 𝔼₀[log BF] the logarithm of the scaled Bayes factor (sBF). By definition, evaluating sBF requires computing 𝔼₀[2 log BF]. In addition to direct computation, 𝔼₀[2 log BF] can also be evaluated by simulating y under the null. A valid and convenient approach to simulating under the null was proposed by Kennedy [1995]. The approach is to permute y_W, the residuals of y regressing out covariates W. Since 2 log BF is a weighted sum of chi-squared random variables, a modest number of permutations of y_W provide an accurate estimation of its mean under the null. The permutation might be advantageous over the analytical computation when the model is mis-specified.

Proposition 2. The scaled Bayes factor has the following properties.

1. ${𝔼}_0[2\text{log sBF}]=0;\text{sBF/BF}={\prod }_{i=1}^p\{\text{exp}(-{\mathrm{\lambda }}_i/2)/\sqrt{(1-{\mathrm{\lambda }}_i)}\}>1$.

2. sBF and BF have the same (Bayesian) p-value p_B.

3. Let ỹ be a permutation of y. Then $\text{BF}(\mathit{y})/\text{BF}(\mathit{ỹ})=\text{sBF}(\mathit{y})/\text{sBF}(\mathit{ỹ})\stackrel{\text{def}}{=}D(\mathit{ỹ})$, and 𝔼_P[log D (ỹ)] = log sBF(y), and sBF(y) < 𝔼_P[D(ỹ)].

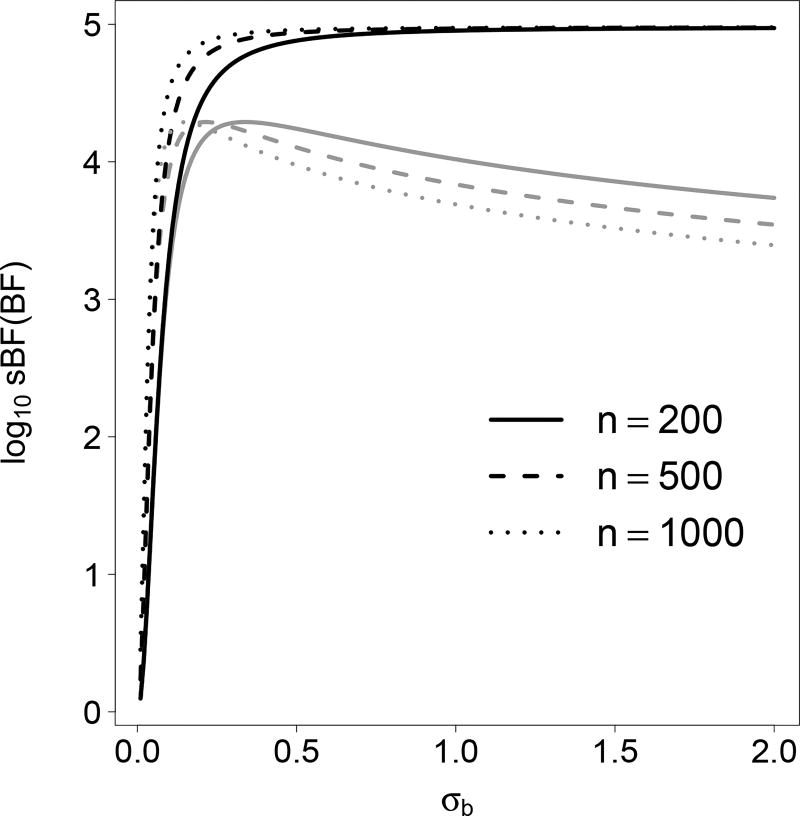
Comparing (11) and (12), the scaling removes from sBF the over-dependence on prior and Bartlett’s paradox observed in BF (Fig. 3). The scaling is a function of λ which takes value in [0, 1)^p. If there is a gap between λ_i and 1, then the i-th component contributes modestly to the scaling. For example, when p = 1 the scaling is 1:5 when λ₁ = 0.8 and 2.0 when λ₁ = 0.9. When all λ_i → 0, the scaling approaches 1 and meanwhile sBF → 1, as expected; when all λ_i → 1, although the scaling factor blows up (sBF=BF → ∞), 2 log sBF is stable and $2\text{log sBF}\to {\chi }_p^2-p.$

Figure 3.

BF and sBF as functions of σ_b. The plot is for simple linear regression of various sample sizes. BF is in gray and sBF black. BF and sBF are computed assuming the covariate has unit variance.

Consider a multiple testing problem that tests H₁, H₂, … against H₀. Each alternative model is concerned with testing a single covariate in association with the response variable, and each covariate has the same λ₁. Then sBF and BF produce the same ranking for alltests, because the scaling coefficient is determined solely by λ₁. In light of the connection between BF and p_F [Wakefield, 2008, Guan and Stephens, 2008], we have that, asymptotically, sBF and p_F produce the same ranking for all tests that have the same λ₁. However, when λ₁ differs, the three statistics BF, sBF, and p_F (or p_B) produce different rankings.

4.1 sBF disregards informativeness of covariates under the null

Let us focus on simple linear regression. The treatment of multi-linear regression can be found in Supplementary. Let ${\mathit{V}}_b={\sigma }_b^2\text{and}{\mathit{X}}^t\mathit{X}={\delta }_1^2$. Then we have ${\mathrm{\lambda }}_1={\delta }_1^2/({\delta }_1^2+1/{\delta }_b^2)$. So λ₁ can be taken as a measurement of the informativeness of a covariate. In genetic association studies, a SNP’s λ₁ is determined by the minor allele frequency and the prior effect size, and for a fixed prior effect size, the larger the minor allele frequency, the larger the λ₁.

Proposition 3. Suppose two models H₁ and H₂ are each concerned with a single but different covariate, and H₁ associates with a larger λ₁. Denote BF_j and sBF_j of BF and sBF for model H_j (j = 1, 2). We have

$${𝔼}_0[{\text{log BF}}_1-{\text{log BF}}_2]<0,{𝔼}_o[{\text{log sBF}}_1-{\text{log sBF}}_2]=0.$$ (13)

Although it is rudimentary to prove Proposition 3 (see Supplementary), the result is illuminating with respect to the difference between BF and sBF. Under the null, BF has the propensity to assign a larger value to a less informative covariate. In other words, BF penalizes more heavily to a more informative covariate. On the other hand, sBF disregards the informativeness of a covariate under the null. This indifference to the informativeness of sBF is advantageous under the alternative model (next section), because, loosely speaking, the over-penalty of BF on more informative covariates applies not just under the null, but also under the alternative.

4.2 BF and sBF under the local alternatives

The local alternatives are a sequence of alternatives that scale down the effect size when sample size increases so that the test statistic converges for large samples [c.f. Ferguson, 1996, Chap. 22]. The following theorem quantifies BF (and hence sBF) under the local alternatives.

Theorem 4. For multi-linear regression (1) with the NIG prior (2), the g-prior (7), and the normal prior (8), under the local alternatives $\mathit{b}=\mathit{\beta }/\sqrt{n\tau }$ and assuming either L^tL/nconverges or L is entry-wise bounded, Bayes factors given in (3) and (9) follow

$$2\text{log BF}=\sum _{i=1}^p{\lambda }_i{Q}_i+\text{log}(1-{\lambda }_i)+\mathrm{\epsilon },Q_i\sim X_1^2({\rho }_i),$$ (14)

where ε ~ o_P (1), Qi is a noncentral chi-squared random variable with d.f. = 1 and thenoncentrality parameter ${\rho }_i={({\mathit{u}}_i^t\mathit{L}\mathit{\beta })}^2/n$, and (λ_i, u_i) is the ith eigenvalue-eigenvector pair of $\mathit{X}{({\mathit{X}}^t\mathit{X}+{\mathit{V}}_b^{-1})}^{-1}{\mathit{X}}^t$. For the normal prior ε = 0.

Note in the above theorem 2 log BF has the same form as in (10). The only difference is that under the local alternatives Q₁, …, Q_p become noncentral chi-squared random variables instead of central chi-squared under the null. The assumptions on L guarantees the stochastic boundedness of ρ_i, permitting a Taylor expansion that leads to the linear approximation. These two assumptions are usually satisfied in practice, particularly in genetic association studies, where each entry of L is the allele counts of an individual at a marker and thus bounded by two.

Let’s assume that the sample size is large enough so that the error term ε in Theorem 4 can be safely ignored. For simple linear regression, we have 2 log BF = λ₁Q₁ + log(1−λ₁) and 2 log sBF = λ₁(Q₁−1), where $Q_1~{\chi }_1^2({\rho }_1)$ is a noncentral chi-squared random variable. Because 𝔼[Q₁] = ρ₁ + 1, we have 𝔼[2 log sBF] = λ₁ρ₁, which is proportional to λ₁ for a fixed ρ₁. In other words, under the local alternatives, sBF tends to assign larger values to more informative covariates. On the other hand, 𝔼[2 log BF] = λ₁(ρ₁ + 1) + log(1−λ₁) is not a monotonic function of λ₁ for a fixed ρ₁. Thus, the (unscaled) Bayes factor does not respect the informativeness of covariates under the alternative model.

Proposition 5. Consider simple linear regression in the context of Theorem 4,

1. Given $b={\sigma }_b/\sqrt{\tau },Q_1~{\chi }_1^2({\rho }_1)$.

2. Let $b~N(0,{\sigma }_b^2/\tau )$, the marginal distribution (over b) of Q₁ is ${(1-{\mathrm{\lambda }}_1)}^{-1}{\chi }_1^2$, a scaled central chi-squared distribution.

The above proposition says that under the local alternatives the distribution of Q₁ (and hence BF and sBF) is determined by λ₁. In (a), the alternative is evaluated at a fixed point, while in (b) it is averaged over the prior distribution of b. Because the power of a test is determined by the alternative distribution of Q₁ (for a fixed null), Proposition 5 suggests that the statistical power is positively correlated with λ₁. This result is simple yet profound. Suppose we are faced with two tests with equal p-values that suggest the null should be rejected. Without knowing the powers of the tests, we cannot decide which rejection is more reliable or carries more evidence [Stephens and Balding, 2009]. Suppose two tests have different λ₁’s but the same Q₁’s, then the two tests have the same p-value. From 2 log sBF = λ₁(Q₁−1), the scaled Bayes factor has a propensity to assign a largervalue to the test that has a larger power (or a larger λ₁), a desirable property. On the other hand, this desirable property is missing for the unscaled Bayes factor.

5 Applying to Ocular Hypertension GWAS Datasets

To illustrate how the scaled Bayes factor performs in real data analysis, we applied for access and downloaded two GWAS datasets from the database of Genotypes and Phentoypes (dbGaP). Both studies were funded by the National Eye Institute: one is the Ocular Hypertension Treatment Study [Kass et al., 2002] (henceforth OHTS, dbGaP accession number: phs000240.v1.p1), the other is National Eye Institute Human Genetics Collaboration Consortium Glaucoma Genome-Wide Association Study [Ulmer et al., 2012] (henceforth NEIGHBOR, dbGaP accession number: phs000238.v1.p1).

The phenotype of interest is the intraocular pressure (IOP). The OHTS dataset only contains individuals of high IOP (> 21). The NEIGHBOR dataset is a case-control design for glaucoma [Ulmer et al., 2012, Weinreb et al., 2014], in which many samples have IOP measurements because a high IOP is considered a major risk factor and a precursor phenotype for glaucoma. The NEIGHBOR dataset, however, contains case samples with small IOP and control samples with large IOP. Since IOP and glaucoma evidently have different genetic basis, though many are overlapping, we removed those samples. We also removed samples whose IOP measurements differ by more than 10 between the two eyes since such a large difference is likely to be caused by a different mechanism, e.g., physical accidents. The average IOP of the two eyes was used as the raw phentoype. We then performed the routine quality control for the genotypes using the same procedure described in Xu and Guan [2014]. OHTS and NEIGHBOR were genotyped on different SNP arrays, and there remained 301, 143 autosome SNPs genotyped in both datasets that passed QC. We then performed principal component analysis to remove the outliers and extracted 3,226 subjects (740 from OHTS and 2486 from NEIGHBOR) that clustered around the European samples in HapMap3 [The International HapMap Consortium, 2010]. We regressed out age, sex, and 6 leading principal components from the raw phenotypes, quantile normalized the residuals and used them as the phenotypes for single SNP analysis. We computed BF, sBF and p_B using prior σ_b = 0.2.

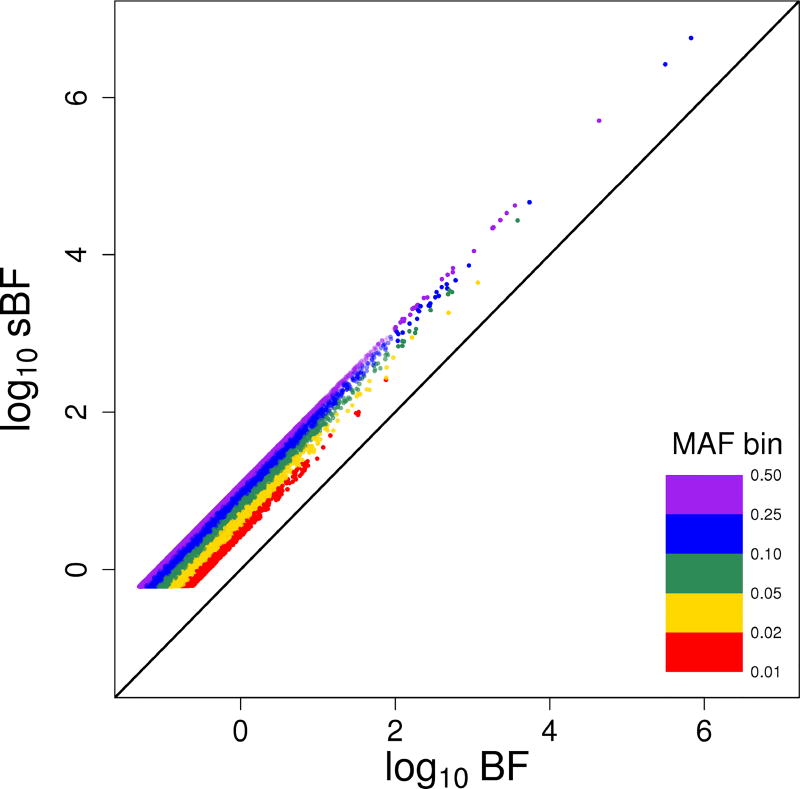
We first compared BF and sBF in different minor allele frequency (MAF) bins. Different MAF bins correspond to different bins of the informativeness (λ₁) of SNPs. Figure 4 shows that in each bin log₁₀ sBF ~ log₁₀ BF is roughly parallel to the line y = x, and more importantly the larger the MAF, the further are the points away from y = x, or in other words, log₁₀ sBF − log₁₀ BF is larger, which agrees well with the definition of sBF (Fig. 3), and fits the theoretical predictions (Propositions 3 and 5). Another noticeable feature in Fig. 4 is that the minimum value of sBF is larger than that of BF, which is consistent with the Proposition 2(a).

Figure 4.

The distributions of log₁₀ BF and log₁₀ sBF by different bins of minor allele frequency (MAF). The bins are marked by color and the diagonal line is y = x.

Next we examined the ranking of SNPs by different test statistics. Table 1 contains the top 20 SNPs in the ranking by BF. Rows were then sorted according to SNP’s chromosome and position. Incidentally, the top 2 hits (rs7518099 and rs4656461) are the same for all the three test statistics. The rankings are largely similar to one another among the three test statistics: BF, sBF, and p_B, particularly so between BF and p_B. There is, however, the noticeable exception of SNP rs7696626; with a ranking by sBF that is much worse than its rankings by BF and p_B. Not surprisingly, this SNP has the smallest MAF (0.023) among the 20 SNPs included in Table 1. This example fits the theoretical observations made in Proposition 3. We permuted the phenotypes once, and recomputed the test statistics. The permutation is to simulate under the null to confirm that 𝔼₀[log sBF] = 0. Apparently sBF is more invariant against permutation compared to BF in the sense that log(sBF(y)/sBF(ỹ)) ≈ log sBF(y).

Our choice of the σ_b = 0.2 represents the prior belief of small but noticeable effect size in the context of GWAS [c.f. Burton et al., 2007]. To check how sensitive our results with respect to the choice of σ_b = 0.2, we redid the analysis using σ_b = 0.5. As predicted by our theory (Fig. 3), we observed that with σ_b = 0.5 BF tends to be smaller and sBF tends to be larger, and p_B remains unchanged. Moreover, the rankings of the SNPs remained mostly unchanged between the two choices of σ_b (Table S1 in Supplementary).

Lastly, although it was not our main objective, we examined the top hits in the association result. Our analysis reproduced three known genetic associations for IOP. Namely, the TMCO1 gene on chromosome 1 (163.9M-164.0M) which was reported in [van Koolwijk et al., 2012]; a single hit rs2025751 in the PKHD1 gene on chromosome 6 [Hysi et al., 2014]; and a single hit rs12150284 in the GAS7 gene on chromosom 17 [Ozel et al., 2014]. A noticeable potentially novel finding is the gene PEX14 on chrosome 1. Two SNPs, rs12120962 and rs12127400, have modest association signals from BF and p_B, but their scaled Bayes factors are noteworthy. PEX14 encodes an essential component of the peroxisomal import machinery. The protein interacts with the cytosolic receptor for proteins containing a PTS1 peroxisomal targeting signal. Incidentally, PTS1 is known to elevate the intraocular pressure [Shepard et al., 2007]. In addition, a mutation in PEX14 results in one form of Zellweger syndrome, and for children who suffer from Zellweger syndrome, congenital glaucoma is a typical neonatal-infantile presentation [Klouwer et al., 2015].

6 Discussion

In this paper, we quantify the null distribution of Bayes factors in the context of multilinear regression. We showed that under the null, 2 log BF is distributed as a weighted sum of chi-squared random variables. The null distribution allows us to compute the p-value associated with Bayes factor analytically, and we have developed a software package to do so efficiently. The software package can be used in a wide range of applications such as ridge regression, variance component model, and genetic association studies. The null distribution of Bayes factors also allows us to study the properties of Bayes factors, and we identified the dominant term in Bayes factor that leads to its excessive prior-dependence and Bartlett’s paradox. We proposed the scaled Bayes factor, which depends less on the prior and is immune to Bartlett’s paradox. We then studied the properties of the sBF under the null and the local alternatives. Compared to BF, sBF respects more to the informativeness of data.

Very often the covariates L are inferred from a statistical model, for example, imputed allele dosages in Guan and Stephens [2008] and the haplotype loading matrix in Xu and Guan [2014]. One would like to take into account the uncertainty of the inferred L. In imputation-based association studies, one may compute the posterior mean of L and then perform the test. But in haplotype association analysis [Xu and Guan, 2014], using the posterior mean of L is impractical as one realization of L may be a column switching of the other, to say the least. A natural solution is to compute a Bayes factor for each realization of L and use the averaged Bayes factor as the test statistic. Then how to evaluate the associated p-value for the averaged Bayes factor? The same question also arises after obtaining an averaged Bayes factor from multiple choices of σ_b’s. Two commonly used methods to combine p-values are Fisher’s [1948] method and Stouffer et al.’s [1949] method. Fisher’s method uses $-2{\sum }_{i=1}^k\text{log}(p_i)~{\chi }_{2k}^2$; and Stouffer’s method first obtains a Z-score for each p-value and then uses ${\sum }_{i=1}^k{Z}_i/\sqrt{k}~N(0,1)$. Both methods assume the p-values to be combined are independent, while in our situations the p-values are obviously dependent. Motivated by Theorem 1, we propose to combine p-values using $2\text{ log}({\sum }_{i=1}^k\text{exp}(W_i/2)/k)~{\chi }_1^2$, where W_i = Ψ⁻¹ (1−p_i) and Ψ is the cumulative distribution function of ${\chi }_1^2$. In essence, we converted each p-value to its associated Bayes factor, averaged Bayes factors, and computed p_B of the average Bayes factor. Since averaging over Bayes factors is always valid and Theorem 1 provides the necessary connection between p-values and Bayes factors, our approach to combining the correlated p-values appears to work well, at least for the afore-mentioned two examples, where the existing methods surely fail.

By definition, 𝔼₀[BF] = 1 which is a nice property because it suggests that BF does not favor either the null or the alternative when the data are simulated under the null. A careful investigation into Proposition 3, however, revealed that this seemingly nice property effectively results in a greater penalty on more informative covariates. The scaled Bayes factor, on the other hand, satisfies 𝔼₀[log sBF] = 0, trading the property 𝔼₀[BF] = 1 of the (unscaled) Bayes factor. Immediately, this trade suggests that sBF favors the alternative over the null (by Jensen’s inequality or simply Proposition 2(a)). We argue that this trade brings several benefits to sBF: it depends less on prior; it becomes immune to Bartlett’s paradox; and, more importantly, sBF becomes well calibrated with respect to permutation. Suppose we permute the response variable y once to obtain ỹ and compute the test statistic (either BF or sBF) with ỹ, treating it as the test statistic under the null. Obviously, 2 log(sBF(y)/sBF(ỹ)) is expected to have the same mean as that of 2 log sBF(y) (Proposition 2(c)). On the other hand 2 log(BF(y)/BF(ỹ)) is expected to have a different (shifted) mean from 2 log BF(y). We believe this better calibration of sBF with respect to permutation will make it a better test statistic for Bayesian variable selection regression [Guan and Stephens, 2011].

In genetic association studies one routinely performs millions of simple linear regression to test for the association between each genetic variant and the phenotype. In general, sBF and p_B would produce different rankings for the variants, because their corresponding λ₁’s differ. When a special prior, σ_b ∝ 1/δ₁, is used, however, sBF (and BF) will produce the same ranking as p_B [Wakefield, 2008, Guan and Stephens, 2008]. This prior, which produces the same λ₁ for all covariates, somewhat defeats the purpose of specifying a prior, because it practically eliminates the effect of a variant’s variance to its test statistic. In multi-linear regression, such a special prior is the g-prior which sets every λ_i to g/(g + 1). At some sense ranking variants using sBF is more “informative” than using p_B, and we would like to control false discovery rate (FDR) for sBF. One approach is specifying the prior odds, multiplying the prior odds with BF or sBF to obtain the posterior odds, and then the posterior probability of association (PPA) for each variant. But specifying the prior odds is somewhat arbitrary, which unfortunately has a strong influence on PPA. An alternative approach is perhaps to develop a procedure that is similar to that of Benjamini and Hochberg [1995]. The Benjamini-Hochberg procedure relies on the null distribution of the p-values (which is uniform) to control FDR, but it is noted that the p-value may not be the optimal statistic for controlling FDR [Sun and Cai, 2009]. Since now we know the null distribution of sBF (and BF), we can estimate the expected FDR for sBF (and BF). Such a FDR controlling procedure will provide an alternative solution to “calibrating” Bayes factors (either scaled or unscaled), and it will strengthen the “Bayes/non-Bayes compromise,” which is likely to attract more practitioners to apply Bayesian methods in their studies.