Methodological variations in lagged regression for detecting physiologic drug effects in EHR data

Abstract

We studied how lagged linear regression can be used to detect the physiologic effects of drugs from data in the electronic health record (EHR). We systematically examined the effect of methodological variations ((i) time series construction, (ii) temporal parameterization, (iii) intra-subject normalization, (iv) differencing (lagged rates of change achieved by taking differences between consecutive measurements), (v) explanatory variables, and (vi) regression models) on performance of lagged linear methods in this context. We generated two gold standards (one knowledge-base derived, one expert-curated) for expected pairwise relationships between 7 drugs and 4 labs, and evaluated how the 64 unique combinations of methodological perturbations reproduce the gold standards. Our 28 cohorts included patients in the Columbia University Medical Center/NewYork-Presbyterian Hospital clinical database, and ranged from 2,820 to 79,514 patients with between 8 and 209 average time points per patient. The most accurate methods achieved AUROC of 0.794 for knowledge-base derived gold standard (95%CI [0.741, 0.847]) and 0.705 for expert-curated gold standard (95% CI [0.629, 0.781]). We observed a mean AUROC of 0.633 (95%CI [0.610, 0.657], expert-curated gold standard) across all methods that re-parameterize time according to sequence and use either a joint autoregressive model with time-series differencing or an independent lag model without differencing. The complement of this set of methods achieved a mean AUROC close to 0.5, indicating the importance of these choices. We conclude that time-series analysis of EHR data will likely rely on some of the beneficial pre-processing and modeling methodologies identified, and will certainly benefit from continued careful analysis of methodological perturbations. This study found that methodological variations, such as pre-processing and representations, have a large effect on results, exposing the importance of thoroughly evaluating these components when comparing machine-learning methods.

Graphical abstract

INTRODUCTION

Widespread adoption of electronic health records (EHRs) over the past 30 years has created a rich resource of observational health data, and research communities continue to dedicate themselves to leveraging these data to improve clinical care and knowledge [1] EHR-based observational research enables new discoveries that are nearly impossible to achieve using traditional experimental methods, and encourages collaborative, open science [2]. However, in order to properly leverage EHR data in observational studies, we must address the special properties of EHR data by adapting and re-inventing existing statistical methods. Here we formulate how to use lagged linear vector regression with EHR data, using interactions between medication administration and laboratory measurements as our clinical context.

Using EHR data to tackle the identification and characterization of the physiologic effects of drugs is a substantial challenge. Although most drugs have known mechanisms of intended action, the full diversity of their myriad effects on biological function is poorly understood and impractical to study experimentally. Such an understanding is important in the context of adverse effects, where drugs induce unexpectedly harmful consequences, as well as for uncovering beneficial effects not detected in small, controlled clinical trials.

There exist data-driven solutions for studying drugs and their physiologic effects, but challenges remain for uncovering their true complexity. Traditional epidemiological approaches are most successful for identifying relatively simple trends (e.g. does condition X occur after the first administration of drug Y), and progress has been made in automatically detecting adverse drug effects [3] using structured clinical databases [4], clinical notes [5], [6], and online health forums [7]. Recent work has focused on scaling these methods to massive data sets [8] and incorporating all available drug and outcome data [9]. Yet finer temporal structure is often desired in order to better understand and predict physiologic treatment responses.

Computational methods exist for uncovering detailed temporal relationships between drugs and outcomes in EHR data, and recent advances have been made in machine-learning approaches to phenotyping [10]–[12], pattern discovery [13]–[15], temporal abstraction over intervals [16], [17], and dynamic Bayesian networks [18]. However, these advances typically highlight one or two approaches at a time, and do not rigorously justify or study methodological decisions that may be inconsequential or vital to a method’s success. In addition, many of these approaches rely on assumptions of stationarity that are frequently broken by clinical data [19], [20], or do not account for health care process effects.

Hripcsak et al. [21], [22] have demonstrated that time-series methods applied to EHR data can identify meaningful, high-fidelity [23] trends that relate drugs and physiologic processes. However, standard time-series analysis tools rely on assumptions like stationarity and, to a lesser extent, regular sampling frequencies, which are generally absent from EHR. We have shown that temporal re-parameterizations (e.g. indexing events by their sequence, rather than their clock-time) can overcome non-stationarity in some clinical contexts, likely because physicians sample at frequencies proportional to a patient’s variance [24]. We have also demonstrated efficacy of various other pre-processing and modeling approaches improving time series analysis results in EHR studies: for example, intra-patient normalization can filter out inter-patient effects [25], [26], and adding contextual variables (e.g. inpatient admission events) can address health care process effects [26]. We nevertheless lack an understanding of how such specific modeling choices—performed alone or in combination—impact inference quality and predictive performance within a lagged linear paradigm for analyzing EHR data.

We apply two specific perturbations to each of the following six important steps in time-series modeling of EHR data: (i) time series construction (i.e. the process for converting raw data into a numerical time series representation) [25], [27], comparing with and without a binning window; (ii) temporal parameterization [24] comparing parameterizing by measurement sequence and by clock-time; (iii) intra-subject normalization [25], [27], comparing with and without; (iv) differencing (lagged rates of change achieved by taking differences between consecutive measurements) [26], comparing with and without; (v) explanatory variables [26], comparing with and without an inpatient admission variable; and (vi) regression models, comparing joint autoregressive and independent lag models.

Here, we systematically evaluate these methodological perturbations for their efficacy in uncovering known physiologic effects of each of 7 drugs. We do this by considering a combinatorial set of 7 drug and 4 laboratory measurement conditions, and compute a bootstrapped estimate of predictive performance with respect to gold standard expectations for each of the 28 pair-wise relationships under each of 64 (2⁶) methodological variations. In this way, we probe for modeling choices that provide statistically meaningful improvements to detecting physiologic drug effects. Furthermore, we obtain a more reliable estimate for the ability of well-tuned lagged linear methods to predict physiologic drug effects.

MATERIALS AND METHODS

Cohort Criteria

The 30-year-old clinical data warehouse at NewYork-Presbyterian Hospital, which contains electronic health records for over 5 million patients, was used to examine pairwise relationships between drug order records and laboratory measurements. Our clinical expert identified seven commonly administered drugs with at least one known physiologic effect that can be captured by commonly administered blood laboratory measurements. In particular, they were initially interested in observing: 1) simvastatin causing rhabdomyolysis (with total creatine kinase as a proxy), 2) amphotericin B causing acute renal failure (with potassium and creatinine as proxies), 3) warfarin causing gastrointestinal bleeding (with hemoglobin as a proxy), 4) ibuprofen causing gastrointestinal bleeding and renal failure (with hemoglobin and creatinine as proxies, respectively), 5) spironolactone causing hyperkalemia (high potassium), 6) furosemide causing electrolyte and volume changes via potassium, hemoglobin, and creatinine, and 7) allopurinol causing anemia (with hemoglobin as a proxy).

In order to broaden our set of hypotheses, we created cohorts for all 28 pairwise combinations of the 7 drugs (amphotericin B, simvastatin, warfarin, spironolactone, ibuprofen, furosemide, allopurinol) and the 4 laboratory measurements (total creatine kinase, creatinine, potassium, hemoglobin) (descriptions are listed in Supplementary Table 2). For each drug-lab pair we identified a cohort of patients that met the following criteria: 1) at least 2 of the laboratory measurements of interest on record, 2) at least 1 order for the drug of interest, and 3) more than 30 combined data points between laboratory measurements of interest and total drug orders for any drug. We collected the entire drug-order history, the entire history of laboratory measurements of interest, and entire history of inpatient admissions for each included patient (for use as optional contextual variables). These selection criteria returned between 2,820 and 79,514 patients for the 28 cohorts, with between 8 and 209 average time points per patient, and between 78,624 and 6,107,601 total time points overall.

Building a time series with clinical data

We convert binary inputs to continuous values as follows. We constructed a time series of drug values by setting all drug-orders of interest to 1, and all orders of other drugs to 0 [25], and constructed a time series for contextual variables (in this case, inpatient admission) by setting the event to 1, and setting a 0 at 24 hours before and after that event [26]. To simplify our analysis, we treated all drug orders identically, without regard to repeated administrations or dosage quantities.

Since measurements were sparse and rarely aligned, we interpolated each time series (see Figure 1 for a graphical depiction). For every time point where there was a concept (lab, drug, or inpatient admission), the values of each other variable at that time point were interpolated. This interpolation was computed as the clock-time weighted mean of the preceding and succeeding value of each respective variable. Weighting our interpolation by clock-time allows an estimated lab value at the time of a drug order to be closest to the nearest lab value, and takes into account the trend of the lab near that time. This was performed at each time-point by weighting the nearest two bordering concept values according to their temporal distance from the interpolated time-point. For example, at the time of an ibuprofen administration, we may wish to compute an interpolated creatinine level. To do this, we use the most recent and next upcoming lab measurements, and average the two of them, weighted by their temporal distance from the ibuprofen administration time. Ultimately, all concepts, whether from categorical or real-valued sources, took on continuous values that were paired at each time point. For a more complete description of how we construct a multivariate time series from clinical data, see our previous work [25], [26].

Fig 1. Timeline Construction.

We performed a linear temporal interpolation in order to align sparse, asynchronous measurements and events. For every time point where there was a value (lab, drug concept, or context (i.e. inpatient admission)), the values of each other variable at that time point were interpolated as the clock-time weighted mean of the preceding and succeeding value of each respective variable.

Methodological variations for lagged linear regression with clinical data

In order to evaluate time series methods for uncovering physiologic drug effects, we focused on lagged linear regression and performed 64 (2⁶) perturbations of the standard methodology. The data we use are nonstandard, biased by the health care process, non-stationary, irregularly measured, and missing not at random, requiring methodological explorations to understand how to cope with irregularities of EHR data [24], [28]–[32]. We consider temporal parameterization, time series window construction, intra-subject normalization, differencing, inclusion of other variables (e.g. related to health care process), and choices in how regression models are computed.

Temporal parameterization

Previous studies have shown that, in some clinical settings, indexing a clinical time series by its sequence order can have significant advantages over traditional clock-time [24]; note that this is not likely the case in settings with random or uniform sampling, such as intensive care unit monitoring. To test this, we indexed our lagged analysis with respect to both real-time and sequence-time. Clock-time was converted to sequence-time by setting all time intervals between interpolated, pre-processed values to unit 1 length, making all times ordered integers with no missing times. For further details on their implementation, see our previous descriptions [24], [26].

Binning and windowing

In signal processing, window functions are often used to extract a smoothed or filtered segment of a time series near a particular time point. They are typically non-negative and smooth over a finite interval; examples include a constant over a rectangle, a triangle, and a Gaussian window. The right choice of window function can remove bias from a signal, and can improve results of cross-correlation analysis. However, choosing appropriate windows is challenging and problem-dependent, and improper choices can lead to spurious signals, aliasing, and other spectral leakage pathologies [33]–[36].

We hypothesize a particular type of bias that we introduce in our timeline construction methodology, and attempt to remove it with a simple window function, a maximum function over a 24hr width on the drug time series, which we refer to as “binning”. The heuristics we have used previously [25] cause drug signals to diminish when a drug of interest is consistently ordered between two other drugs. Ideally, the drug timeline should retain mass for as long as a patient is consistently taking a drug. We attempted to remove this bias by setting all drugs within 12 hours of the drug of interest to 1. It should be clear that this process is equivalent to applying a fixed-width window equipped with the max-function.

Regression Models

We considered lags from 1–30 days when using real-time, and 1–30 indices when using sequence time. We studied two variations of lagged linear regression—univariate (i.e. lags estimated one at a time, independently) and multivariable (i.e. lags estimated jointly). Independent, univariate estimation provides a simple model similar to lagged correlation that separately relates each lagged time-point of each lagged variable to the target response variable; joint, multivariable estimation is an autoregression (specifically, an ARX model) and computes each lagged coefficient conditional on the other estimates, balancing the shared information across lags and thus bringing out more subtle details of each lag. First, we considered independent estimation of lagged drug coefficients, β_τ, from the following model, where y_t is the lab value (i.e., the outcome of interest) at time t, x_t is the drug value at time t, and τ is the lag time (for τ=1:30):

$$y_t=c_{\tau }+{\beta }_{\tau }{x}_{t-\tau }+{\epsilon }_{\tau }$$

Second, we considered joint autoregressive estimation of lagged drug coefficients,β_τ, by the following form (L=30):

$$y_t=c+{\displaystyle \sum _{\tau =1}^L{\beta }_{\tau }{x}_{t-\tau }}+{\displaystyle \sum _{\tau =1}^L{\alpha }_{\tau }{y}_{t-\tau }+\epsilon }$$

This form generalizes to an arbitrary number of other lagged explanatory variables, uⁱ (which can include y), as:

$$y_t=c+{\displaystyle \sum _{\tau =1}^L{\beta }_{\tau }{x}_{t-\tau }}+{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{\tau =1}^L{\omega }_{\tau }^i{u}_{t-\tau }^i+\epsilon }}$$

Differencing

In time series analysis, pre-processing steps, like taking differences between consecutive measurements, are often performed to de-correlate lagged variables [37]. More formally, a differencing operator can be applied to resolve non-stationarity that results from a unit root in the characteristic equation of an autoregressive stochastic process—the presence of a unit root can be identified with statistical tests, like Dickey-Fuller [38], and removed by iterative differencing [39]. When unit roots remain, ordinary least squares estimation of autoregression coefficients has been shown to fail [40] and non-stationarity persists. The simplest example is the case of a random walk, in which each position is highly correlated with the previous positions. By taking the differences between consecutive steps of a random walk, these correlations are removed and the statistics of the signal can be more easily recovered. Similar effects can be seen in clinical data, where treatments often drive physiologic change. Levine et al. [26] demonstrated that taking differences is an important step in multivariable lagged regression with clinical data; here, we tested the value of differencing in additional clinical and methodological contexts.

Intra-patient normalization

Previous work demonstrated that intra-patient normalization is an important step when extracting correct physiologic drug effects using lagged correlation [25]. In order to investigate the importance of removing inter-patient effects in different methodological contexts, we included the option to normalize each patient’s time series by subtracting their mean and dividing by their standard deviation. More sophisticated schemes for approaching this problem exist (e.g. Box Cox transform [41] or other power transforms), but we wished to first examine a simpler method. It is also important to note that the univariate lagged regression coefficient (i.e. AR-1) on normalized (zero mean, unit variance) time series is identical to the coefficient from lagged correlation. Thus, as various pre-processing and analytic steps are combined, the resulting method often devolves into a specially named sub-class of methods.

Including context variables

In order to account for health care process effects and biases, we often wish to include potential confounding variables in the model. Levine et al. [26] found that including inpatient admission events as autoregressive variables in a multivariable multi-lag model (i.e. vector autoregression [37], [42]) attenuated some confounded physiologic signals. We evaluated the same approach here, and introduced the context variable z to correct lagged drug coefficients, β_τ:

$$y_t=c+{\displaystyle \sum _{\tau =1}^L{\beta }_{\tau }{x}_{t-\tau }}+{\displaystyle \sum _{\tau =1}^L{\alpha }_{\tau }{y}_{t-\tau }+}{\displaystyle \sum _{\tau =1}^L{\gamma }_{\tau }{z}_{t-\tau }+\epsilon }$$

Gold Standard Creation

In order to evaluate computationally determined interactions between each drug-lab pair, we created two separate, but related gold standards for whether a given drug is expected to increase, decrease, or have no effect on a given lab: 1) a knowledge-base derived gold standard that was created by synthesizing existing medical literature and knowledge bases—this represents information that could, in theory, be obtained automatically, and 2) a clinical expert curated gold standard, for which the knowledge-base derived gold standard was reviewed and edited by a clinical expert. In table 1, we indicate whether a given drug is expected to increase, decrease, or have no effect on a given lab (denoted as 1, −1, 0, respectively), according to the two gold standards (68% total agreement, Cohen’s Kappa=0.53, 95% CI [0.27–0.78]). We recognize that a perfect gold standard does not exist; in order to better demonstrate the robustness of our findings, we evaluate our results separately with respect to the two gold standards.

Table 1.

Clinical gold standards for expected drug effects.

Drug	Laboratory Measurement	Knowledge- base derived gold standard	Expert-curated gold standard
Allopurinol	Total Creatine Kinase	1	0
Allopurinol	Creatinine	1	1
Allopurinol	Potassium	0	0
Allopurinol	Hemoglobin	-1	0
Amphotericin B	Total Creatine Kinase	0	0
Amphotericin B	Creatinine	1	1
Amphotericin B	Potassium	-1	-1
Amphotericin B	Hemoglobin	-1	-1
Furosemide	Total Creatine Kinase	0	0
Furosemide	Creatinine	1	1
Furosemide	Potassium	-1	-1
Furosemide	Hemoglobin	-1	1
Ibuprofen	Total Creatine Kinase	0	0
Ibuprofen	Creatinine	1	0
Ibuprofen	Potassium	1	0
Ibuprofen	Hemoglobin	-1	-1
Simvastatin	Total Creatine Kinase	1	1
Simvastatin	Creatinine	1	0
Simvastatin	Potassium	1	0
Simvastatin	Hemoglobin	-1	0
Spironolactone	Total Creatine Kinase	0	0
Spironolactone	Creatinine	1	1
Spironolactone	Potassium	1	1
Spironolactone	Hemoglobin	-1	1
Warfarin	Total Creatine Kinase	0	0
Warfarin	Creatinine	0	0
Warfarin	Potassium	0	0
Warfarin	Hemoglobin	-1	-1

Literature search for expected physiologic drug effects

For each drug-lab pair, an author (ML) searched PubMed for articles using the drug and lab as keywords, along with terms “increase”, “decrease”, and “association”. The authors selected articles that reported quantitative information about associations and causations between the two entities within their abstracts. The author then read these articles and determined whether their reported associations between the drug and lab of interest should be expected to generalize to a large EHR database (e.g., a study of cancer patients would not be included). Contradictory literature results were considered as inconclusive.

LAERTES knowledge base queries for expected physiologic drug effects

The LAERTES (Large-scale Adverse Effects Related to Treatment Evidence Standardization) [43] knowledge-base was developed as part of the Observational Health Data Sciences and Informatics initiative to record existing pharmacosurveillance knowledge that could be compared to new empirical evidence. It draws from package inserts, Food and Drug Administration databases, and also the literature. LAERTES was queried for associations between side effects associated with the 4 lab measurements (muscle weakness and rhabdomyolysis for creatine kinase, renal impairment for creatinine, hyperkalemia and hypokalemia for potassium, and anemia for hemoglobin) and each of the 7 drugs.

Knowledge-base derived gold standard—combining results from literature search and knowledge base

Resulting directional associations from LAERTES were taken in union with the directional associations from our literature search. When one search method yielded no associations, and the other did, we took the association, rather than the null result (except in the case of ibuprofen and total creatine kinase, for which we rejected LAERTES’s positive result). When multiple results were present in the LAERTES results, we selected those that matched results in the literature—this occurred twice, for spironolactone’s effect on potassium and ibuprofen’s effect on potassium. Together, these data formed the knowledge-base derived gold standard.

Expert-curated gold standard

A clinical expert (GH) subsequently curated the knowledge-base derived gold standard, and modified 9 of its 28 expected associations. The expert modified the directionality only twice (i.e. −1 to +1), where he believed that diuretic-induced anemia was less likely to be present than rises in hemoglobin due to diuretic-induced fluid loss. The other seven modifications removed expected effects in the knowledge-base derived gold standard (i.e. changed +1 or −1 to 0), which the expert judged sufficiently rare to be missing from a database of the size of ours. The expert-curated gold standard allows us to probe the robustness of conclusions made from the knowledge-base derived gold standard. We note that comparison with this second expert-curated gold standard may be a weaker indicator of stability than comparison with an independently generated gold standard (e.g. compiled solely by expert clinicians); however, we expect that the two are sufficiently different to provide a reasonable check on each other.

Evaluating accuracy of lagged regressions

We evaluated the predictive accuracy of each tested method and the associated uncertainty by performing a layered bootstrap resampling over patient cohorts [44]. Figure 2 provides a schematic for the experimental protocol. Figure 2 presents the experiment in a “top-down” approach, whereas the subsequent text presents the design “bottom-up.” Because we are interested in uncovering physiologic drug effects across people, rather than predicting specific laboratory measurements, we focus on comparing the computed lagged drug coefficients from each method with gold standards for known physiologic phenomena. The forecasting error of these models (i.e. their ability to predict individual laboratory measurements) is not of direct interest and does not affect the models’ ability to correctly recover the overall signal of the process (e.g. coefficients can be fully recovered from a densely sampled autoregressive process with large, uncorrelated, zero-mean noise, and the forecasting error would take the size of the process’s noise).

Figure 2.

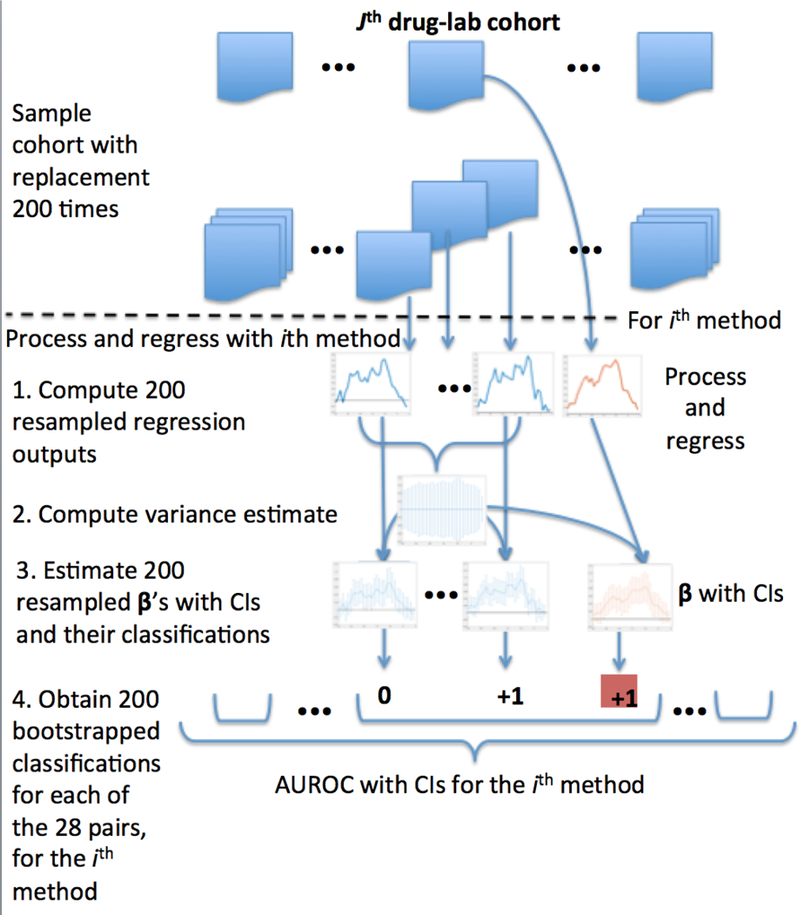
Experimental Design Overview

Estimating variance of lagged drug coefficients

For a given drug-lab pair and methodological variation, we empirically computed estimates of variance for the lagged drug coefficients, β_τ, using a bootstrap estimate of variance. For each drug-lab cohort, we sampled patients with replacement to create 200 bootstrapped samples, and ran all 64 regressions for each of these 200 samples from the drug-lab cohort. We sampled over all patients in a given cohort—for each drug-lab pair, the number of patients differed. We estimated the variance of β_τ for a given drug-lab pair and particular methodological variation using the variance of the samples generated for that particular drug-lab-method combination, and subsequently determined empirical 95% confidence intervals of β_τ ([ β_τ – 1.96σ, β_τ – 1.96σ], where σ is the standard deviation of the samples of β_τ).

Classifying lagged drug coefficient profiles

We are ultimately interested in the trajectory of β_τ as they vary over τ, and write $\beta ={\left\{{\beta }_{\tau }\right\}}_{\tau =1}^{30}$ . Other model parameters were not examined because only β directly encodes the inferred relationship between a drug and lab. Note that output from methods that used sequence or real-time can be directly compared, as they result in identical models, where one has time units “days” and the other “index”. In order to perform a first-order evaluation of lagged drug coefficients trajectories, we first converted them to the format of the gold standards (increase, decrease, or no effect). We classified β as increasing (+1) if at least 15 consecutive coefficients were all greater than zero within 95% confidence interval, decreasing (−1) if at least 15 consecutive coefficients were all less than zero within 95% confidence interval, and neither (0) otherwise. We selected 15 as the threshold because it is half-the number of total estimated coefficients, making it the smallest threshold that can ensure there will be only one directional designation (we did not want a trajectory of to be β classified as both increasing and decreasing).

Computing predictive performance of lagged regressions with respect to gold standards

For each of the 64 method combinations, we evaluated classifications of the 28 gold standard drug-lab effects by estimating a Receiver Operating Characteristic (ROC) curve, and reported the area under ROC (AUROC) separately for the two gold standards. Recall that AUROC is a common evaluation metric for binary classification models, and is equal to the expected probability that the model will rank a randomly chosen positive event above a randomly chosen negative one. Given our ranked classifications (−1,0,1), we evaluated sensitivity and specificity of each method’s ability to perform binary discrimination across two thresholds, −0.5 and 0.5, which provided two points for an ROC curve. Discrimination across a threshold of 0.5 asks the classifier to discriminate between sets {+1} and {0, −1} (e.g. in addition to rewarding exact equality, it also considers 0 and −1); similarly, a threshold of −0.5 evaluates discrimination between {0, +1 and {−1}. We computed AUROC using simple trapezoidal integration.

Estimating variance of AUROC for each methodological variation

In order to estimate the variance of each method’s AUROC, we leveraged the previously performed bootstrapped regressions. For each of the 200 previously computed estimates of β for each drug-lab pair, we created a new classification using a confidence interval with fixed variance (previously computed) that was centered at that particular bootstrapped estimate of β.

We thus obtained 200 independent samples of β We classified these, and subsequently arrived at 200 independent, identically applied samples of AUROC for each methodological variation, which were used to statistically compare performance of different methods.

Comparing predictive performance of lagged regression methods

We want to compare disjoint classes of methods; for example, we want to compare all methods that use sequence time against all methods that use real time, and ask whether sequence time or real time offers an average performance benefit. In order to perform such comparisons, we report the average difference between AUROCs and the 95% Confidence Intervals (CIs) of this difference for both gold standards. Concretely, we compared two disjoint groups of methods by computing the difference between each group’s mean AUROC. We then estimated the 95% CI of this difference using the variance of the pairwise differences between each group’s 200 mean sampled AUROCs. This results in a determination of whether one disjoint group of methods is better or worse than another, within a 95% CI, and enables queries like “overall, is it better to use sequence time or real time?” or “overall, is it better to use sequence time with or without normalization?”.

We performed these comparisons systematically to arrive at a final set of statistically significant methodological variations. First, we evaluated the impact of each variation across all other variations, i.e. marginal impact; for example, we compared all methods that use normalization against all methods that do not. Then we evaluated the impact of each variation given a variation of another variable; for example, we compared all methods that use normalization and sequence time against all methods that use normalization and real time. We also compared sequences of 3 variations. This allowed us to evaluate the impact of methods, both alone and in combination. We report methodological variations that are influential alone and in combination with others, along with the magnitude of their marginal impact on AUROC.

Summary

In order to evaluate and compare methodological variations of lagged linear regressions for determining physiologic drug effects from clinical time series, we 1) identify patient cohorts for each drug-lab pair of interest, 2) report the predictive performance of each method with respect to two gold standards, and 3) draw statistically meaningful comparisons between classes of methods to demonstrate important modeling steps that ought to be taken either alone or in combination to achieve desired results.

RESULTS

Illustrating example of importance of methodological variations of lagged linear regression for assessing physiologic drug effects

In order to illustrate the importance of variations in methodology for analysis of clinical time series, we examined some possible inferences of the relationships between amphotericin B and levels of potassium and creatinine. Our knowledge-base derived gold standard and clinical expert agreed that amphotericin B should be expected to raise creatinine levels and lower potassium levels.

Figure 3 shows the resulting inferences when varying three aspects of the computation (temporal parameterization, differencing, and regression models) and fixing the other three aspects (normalization, no additional context variable, and no binning). Figure 3a shows that the expected trends are accurately reconstructed with statistical significance when using sequence time, differences, and a joint AR model. Figures 3b and 3c show that no significant association can be found when switching to real-time or not using differences. However, Fig 3d shows that multiple changes to the successful method in Fig 3a (using an independent lag model and not using differences) can obtain expected trends, albeit with less significance for creatinine (blue). Results from these methodological combinations for all 28 drug-lab pairs are shown in Supplementary Figures 1–7.

Figure 3.

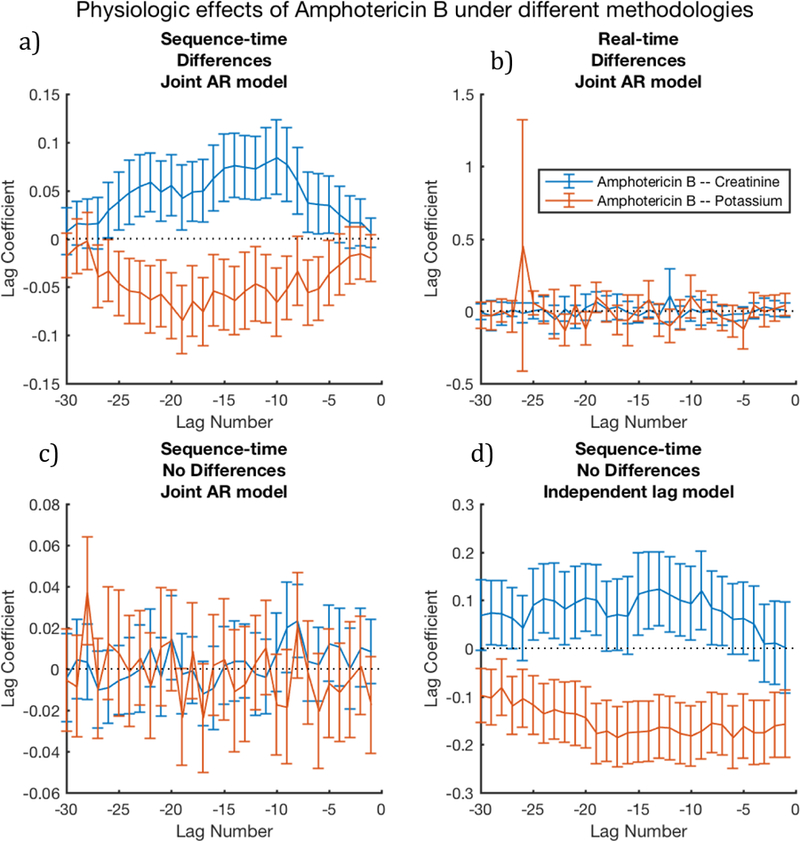
Signal quality is noticeably affected by combinations of methodological choices, especially temporal parameterizations, differencing, and lag model type; here we vary these 3 dimensions, and fix the remaining 3 using intra-patient normalization, no binning, and no additional context variables. Here, we expect Amphotericin B to increase Creatinine (hence, blue should be significantly above zero) and Amphotericin B to decrease Potassium (hence, red should be significantly below zero). The figures demonstrate that sequence-time is often a necessary, singular choice: figure 3a, which uses sequence time, produces the expected result, whereas figure 3b shows a non-significant noise pattern; the methods used in these figures differ only by their treatment of temporal parameterization. The figures also demonstrate that methods must be combined carefully—figure 3a combines differencing with the joint AR model, and produces expected patterns, whereas figure 3c uses an identical method, but omits differencing, and produces a non-significant noise pattern. However, pairing the independent lag model without differencing appears to reconstruct the signal, albeit with less significance than fig 3a.

Combinatorial evaluation of lagged regression assessments of physiologic drug effects under methodological variations

In order to thoroughly understand the impact of methodological choices in this context, we evaluated all 64 combinations of methods with respect to the two gold standards (knowledge-base derived, and expert-curated).

Our main results are shown in Figure 4. We report each method’s AUROC and an estimate of the AUROC variance for both gold standards; we rank the results by descending expert-curated AUROC, and indicate the vector of method pairings for each row in the plot. These results are also enumerated explicitly in Supplementary Table 1.

Figure 4.

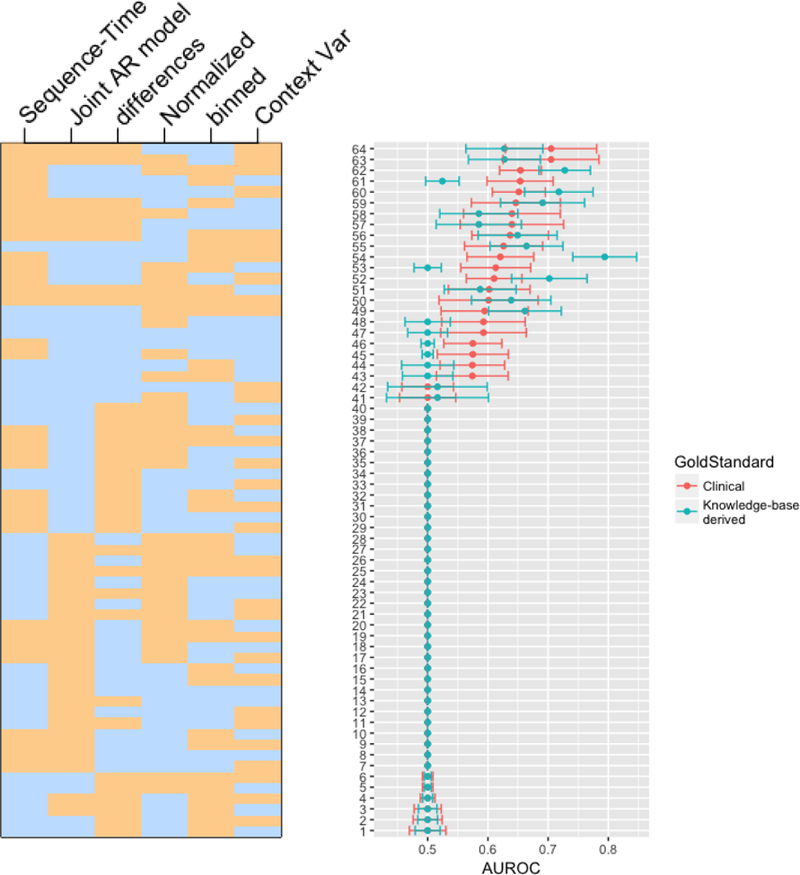
This figure displays AUROC confidence intervals for each of 2⁶ methodological combinations. AUROCs are ordered from top-to-bottom in descending order of AUROC from the expert-curated gold standard. The heatmap on the left indicates the presence (tan) or absence (blue) of each of the 6 method variables for each plotted AUROC. For example, the top AUROC method (according to the clinically-curated gold standard) used sequence-time, no binning, intra-patient normalization, differencing, no additional context variable, and a joint AR model. Note that these results are enumerated explicitly in Supplementary Table 1.

We first point out that, surprisingly, the majority of method combinations had AUROC of 0.5, indicating performance no better than chance. This implies that the choice of methods, combinations of methods, and even the data representation—differences versus raw values—is very important. Furthermore, while the two gold standards differed significantly according to Table 1, they agreed fairly well on which combinations were better than chance. The superior performance of some combinations does not appear to be artifact.

We observe that there is a concentration of methods using sequence time at the top of the plot, suggesting that sequence time is a beneficial choice independent of other methods. We can also observe patterns that relate differencing with model choice—in particular, we note that of our four possible combinations of differencing and model, only two of these (differences with joint estimation and no differences with independent estimation) ever yield AUROC above 0.5. This suggests an interaction between these two choices, which we subsequently interrogate quantitatively.

The best method, according to the expert-curated gold standard used sequence time, normalization, differencing, a joint AR model, no binning, and no additional context variable (AUROC = 0.705, 95%CI [0.629, 0.781]). According to the knowledge-base derived gold standard, the best method also used sequence time, normalization, and no additional context variable, but did not use differencing, used an independent lag model, and used binning (AUROC = 0.794, 95%CI [0.741, 0.847]).

Comparing predictive performance between lagged regression methods

We test for statistically significant differences between marginal effects of different method variations. We observe that choosing sequence time instead of real time is the only single methodological choice that both gold standards agree has a statistically significant effect. For the knowledge-base derived gold standard, sequence time yields a 0.049 (95%CI [0.035, 0.063]) marginal AUROC improvement over real time; for the expert-curated gold standard, the marginal improvement is 0.050 (95%CI [0.038, 0.062]).

In addition, we examined combinations of method choices, and found a consistent, statistically significant indication that a joint AR model is better with differences than without (0.062 marginal AUROC improvement with 95%CI [0.045, 0.079] for knowledge-base derived gold standard, 0.074 marginal AUROC improvement with 95%CI [0.053, 0.094] for expert-curated gold standard), and that an independent lagged model is worse with differences than without (0.083 marginal AUROC reduction with 95%CI [−0.100, −0.065] for knowledge-base derived gold standard, 0.094 marginal AUROC reduction with 95%CI [−0.114, −0.075] for expert-curated gold standard). We also evaluated the converse statements (e.g. when using differences, is joint AR or independent lag model significantly better), and found similar associations.

We further compared the two preferred pairs, and found that while the independent lag model without differences slightly outperformed the joint AR model with differences overall (0.021 marginal AUROC improvement for both gold standards), these changes were not statistically significant (95%CI [−0.046,0.004] for knowledge-base derived gold standard, 95% CI [−0.049,0.008] for expert-curated gold standard). However, the opposite, albeit statistically insignificant, effect was observed when comparing these methods only in the context of the clearly preferred sequence time.

We ultimately found that once a choice of sequence time and either of the preferred pairs of differencing and modeling (i.e. no differences with independent lag model or differences with joint AR model) was made, no additional choices (binning, context variables, normalization) provided marginal improvement to AUROC with statistical significance. We observe a mean AUROC of 0.633 (95%CI [0.610, 0.657]) for expert-curated gold standard (and 0.622 mean AUROC with 95%CI [0.603, 0.641] for knowledge-base derived gold standard) across methods that use sequence time and one of the preferred difference-model pairs, whereas the complement of this set of methods achieves a mean AUROC close to 0.5 (0.512 with 95%CI [0.506, 0.517] for clinically curated-gold standard; 0.507 with 95%CI [0.503, 0.512] for knowledge-base derived gold standard). In this way, we demonstrate that temporal parameterization, time series differencing, and regression-type are important choices that must be selected in concert to achieve optimal predictive performance.

Comparing evaluations from two gold standards

The gold standards differed on 32% of cases (Cohen’s Unweighted Kappa=0.53, 95% CI [0.27–0.78]; Cohen’s Linear Weighted (ordinal) Kappa=0.54, 95% CI [0.11–0.97]). In two cases, the knowledge-base derived gold standard reported diuretics as possibly causing anemia, thus lowering hemoglobin, without accounting for potential diuretic fluid loss and resultant rise in hemoglobin. This represents a disconnect between the condition (anemia) and the observed entity (hemoglobin), which was noted by the expert. In other cases, a potential side effect was judged to be sufficiently rare that it should be missing from a database of the size of ours.

The effect of the difference in gold standards can be seen in Figure 4 and Figure 5. Figure 5 shows that the AUROCs for each methodological variation are correlated across the two gold standards (Pearson correlation coefficient 0.759, 95%CI [0.631, 0.847), but that substantial differences exist. Figure 4 shows that each gold standard would rank individual methods differently; nevertheless, major conclusions of the study, such as the superiority of using sequence time and the dependencies between differencing and regression-type, are upheld by both gold standards.

Figure 5.

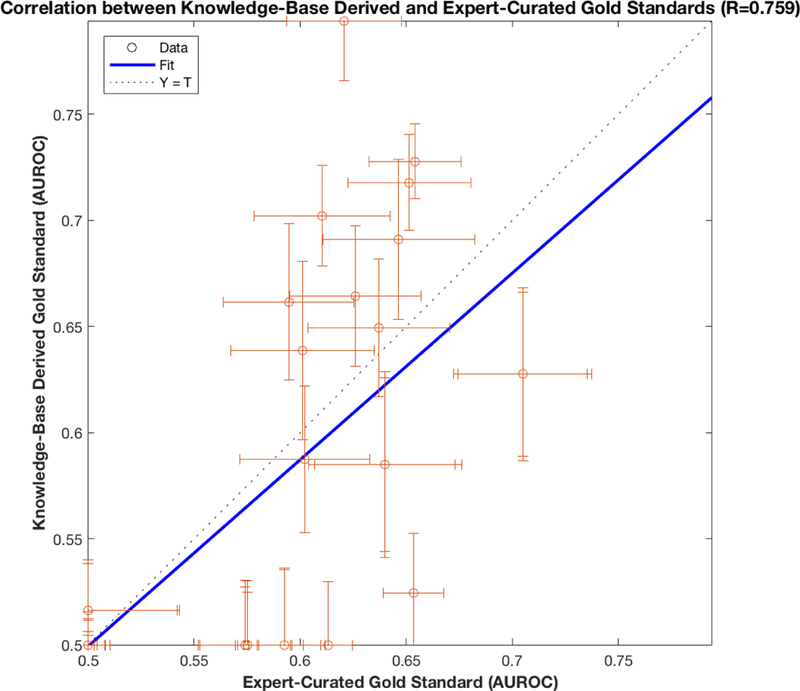
Here we plot the correlation (Pearson correlation coefficient 0.759, p=3.7e-13) between AUROCs computed using clinically curated and knowledge-base derived gold standards. Error bars for each AUROC couple are 95% Confidence Intervals computed using a bootstrap resampling. We observe that the two gold standards, despite significant disagreements (Table 1), ultimately provide evaluations with reasonable similarity. This result instills a confidence in both gold standards that could not be achieved with a single gold standard.

DISCUSSION

Here we study how lagged linear regressions, a simple, robust, commonly used class of methods, can be tuned to efficiently extract drugs’ temporal effects on patient physiology from EHR data. Data in the EHR present a variety of challenges (low, erratic measurement frequency, high noise, and non-stationarity), making time-series analysis highly non-trivial and requiring careful pre-processing and re-parameterization. We evaluated combinations of pre-processing, modeling, and temporal parameterization steps in order to understand how to better cope with challenges in extracting temporal information from EHR data. We used 64 of these methodological perturbations to analyze 28 drug-lab pairs, and evaluated the results against two gold standards.

We found that the correct combination of regression type (independent lag or joint autoregressive) and differencing was essential—independent lag models cannot be used with differencing, whereas the joint AR model must be used with differencing. Furthermore, we found a large significant improvement (for expert-curated gold standard, 0.05 average AUROC increase, 95%CI [0.038, 0.062]) when re-indexing time according to the sequence of events. These selections created high-performing methods, and the top methods achieved AUROC of over 0.7 (for knowledge-base derived gold standard, best AUROC = 0.794, 95%CI [0.741, 0.847]; for expert-curated gold standard, best AUROC = 0.705, 95% CI [0.629, 0.781]).

We also found that the regressions were robust to our choices of normalization, binning, and context variable inclusions. While these choices were statistically unimportant, in aggregate, among our cohorts, their impact could become more noticeable when testing different hypotheses or when using different data. Moreover, we selected one simple form for each of these variations, and it is likely that more targeted formulations will have greater effects.

Benefits of multiple gold standards

Gold standards often vary, but by using several gold standards, researchers can— formally or informally—assess their evaluations’ sensitivities to the gold standard. If only one gold standard is used, then there is no way to characterize the dependency of conclusions on that particular gold standard. In our case, results were similar but not identical for the two gold standards, indicating that our findings are not mere artifacts of the gold standard. It is important to note that our gold standards were not completely independent, as one author created the knowledge-base derived gold standard, and the clinical expert modified it according to clinical and informatics knowledge. Gold standards that are completely independent (e.g. created by separate panels of clinical experts) would likely provide more potent verification of robustness. However, the approach of having a clinician curate an automatically generated gold standard can be especially relevant in high-throughput analysis approaches, like OHDSI [9].

Reflections on important methodological steps

We found that decomposing the overall modeling process into smaller, discrete methods allowed us to systematically interrogate the effect of each choice. However, it is also instructive to note that many of the combinations of methods are in fact equivalent to established methodologies. For example, the joint autoregressive model is very similar to Granger causality, and the independent lag model is analogous to lagged correlation analysis up to normalization. Both of these modeling methods, combined with any windowing function, fall under similar classes of statistical spectral analysis methods and econometrics [37], [39], [45]–[47].

Our previous studies have reported improved performance of lagged methods on EHR data when using sequence time [24], [26], and have investigated the mechanics of these phenomena [19], [20], [24]. We maintain the hypothesis that sequence time removes non-stationarity by leveraging the fact that clinicians sample at rates proportional to patient variability [24], [48], but feel that this hypothesis, while implied, has yet to have been explicitly proven. Lagged regression methods rely on assumptions of weak stationarity, and their performance improves when data are pre-processed to remove temporal swings in mean and variance. There exist methods like autoregressive moving average models that can cope with certain relatively benign non-stationarity effects, such as a slowly and continuously varying mean, but these models are likely unable to resolve clinical non-stationarity effects that are combined with data missing non-randomly (e.g., correlated with health). Such EHR-data-specific pathologies were the original motivation for even attempting sequence time-based methods.

Non-stationarity in EHR data may partly manifest in unit roots of the characteristic equation of the autoregressive stochastic process, causing failure of ordinary least squares estimation, and ought to be explicitly tested in the future using the augmented Dickey-Fuller test [37], [38]. While we optionally applied a differencing operator once to our clinical time series, we did not test for the presence of unit roots. Future work may benefit from iteratively applying a difference operator and re-testing with a statistical test, like augmented Dickey-Fuller, until unit roots are removed, as is the strategy of the Box-Jenkins modeling approach [39].

Differencing is a well-known method [37] for reducing correlation between lagged variables in time-series analysis, and Levine et al. [26] provided anecdotal evidence of its benefit for lagged linear analysis of drug and lab data from the EHR. For this reason, we expected it to improve results across all methods. We were surprised to learn that differencing corrupted the performance of the independent lag model. We recognize, however, that there is a tradeoff between sharing uncorrelated information across variables and adding noise to any particular variable. In the case of the independent lag model, we correlate with one variable at a time, effectively losing all of the upside of differencing. Because the joint autoregressive model holds some advantages over the independent lag model (it is easier and more intuitive to add additional explanatory variables to the joint model), differencing clearly has an important role to play in temporal analysis of EHR data. Incorporating rates of change must typically be done intentionally within any machine learning framework, including deep learning, either by pre-processing the features or by choosing model structures that learn temporal feature representations as linear combinations of neighboring sequential elements.

Opportunities for revealing finer temporal structure in EHR data

It is also important to note that lagged coefficients from these analyses contain information far richer than the evaluated classifications (increasing, none, or decreasing physiologic responses). The trajectories of lagged coefficients (as seen in Figure 2, c.f. Figures 6–8 in [27], c.f. Figure 2 in [25]) can shed light on temporal dynamics and important time scales of the physiologic and/or health care process, rather than merely indicate the presence of an effect. We originally wanted to also evaluate these methods for their ability to detect finer temporal associations, but challenges remain for creating a reliable gold standard upon which to base validations of more complex insights, such as the rate or magnitude of a drug’s physiologic effect (trustworthy quantitative information of this type does not exist for most cases). With sufficient validation, properly tuned lagged linear methods may eventually become useful for discovering novel associations in EHR data.

Implications for comparing machine learning methods

Most of the tested method combinations failed (AUROC=0.5), indicating that these choices are critically important. We observe that, for the same machine-learning algorithm, differences in preprocessing and experimental setup result in a range of AUROC from 0.5 to 0.8. Therefore, the choice of an overall algorithm (regression, support vector machines, neural networks, decision trees, etc.) is just one factor that could affect results, and researchers need to be mindful of this not only when performing experimental comparisons of algorithms, but also when presenting the results of these comparisons. While sophisticated machine-learning techniques aid learning of data representation, the structure for these models is still often selected based on certain hypotheses about how the data might be best represented. Our results suggest that data representations, either pre-processed or learned, should look like sequence time, and, most likely, contain information about the differences between successive measurements and normalize values across patients in the data set. Preprocessing conditions may have different effects on different methods, so a variety of these conditions ought to be rigorously tested, compared, and reported. The combination of pre-processing methodology and choice of gold standards could have large effects on machine learning evaluations, and it is likely that confidence intervals normally reported in machine learning studies fail to include the uncertainty related to these choices.

Implications for reproducibility of observational studies

Our evaluation pipeline is an important part of reproducible observational research, allowing researchers to quantify the impact of the various modeling choices made throughout the research process. Thorough comparisons across wider ranges of methods and source data are critical for advancing our ability to trust what we can learn from the EHR. The Observational Health Data Science and Informatics (OHDSI) consortium provides a common data model and a research community dedicated to such reproducible and generalizable advancements, and we aim to expand our pipeline into an OHDSI-compatible, open-source repository.

How to choose the right method

We have demonstrated the value of rigorous, systematic perturbations to chosen methods, and we encourage readers to perform similar evaluations in their own research contexts. However, we also hope that our results are somewhat generalizable to time-series analyses of medical data. We have found sequence time to provide a large, significant performance boon, and strongly recommend that researchers in similar domains consider re-indexing their time-series according to sequences. We do not know in which contexts the superiority of sequence time holds—contexts with random sampling would still likely benefit from clock-time indexing. For example, many measurements in the intensive care unit are taken at regular intervals, but are missing at random; however other measurements, like troponin, are only ordered when physicians suspect additional trauma, and may be benefit from being re-parameterized by sequence [49]. For lagged linear analysis, we recommend using either a simple independent lag model (without differencing) or a joint autoregressive model with differencing (recall that differencing corrupted the signals from the independent lag model). In general, we recommend performing differencing in accordance with results from statistical tests of unit root presence, like augmented Dickey-Fuller [37]. While we identified no statistical difference between the joint AR model with differencing and the independent lag model without differencing, qualitative assessment (e.g. see supplementary figures 1–7) suggests that the joint AR model provides finer resolution of temporal dynamics of physiologic process. In addition, even when the joint AR and independent lag models return the same drug-effect classifications, the joint AR model appears to be more robustly representative of the classification (e.g. supplementary figure 1, where it more clearly depicts that amphotericin B has no effect on total creatine kinase). These qualitative inspections cause us to favor the joint autoregressive model with differencing. Intra-patient normalization had no statistically significant effect in our cohort, but we recommend its continued usage, because a) it has been shown to improve performance in similar studies [25], and b) it did not create any disadvantage in our current study. We did not observe any useful effect from our experimental choice of windowing, and recommend readers select none or constant window functions as opposed our experimental choice. However, we encourage researchers to more thoroughly investigate appropriate windowing functions for EHR data, and insist that this be done in combination with other potential methodological choices, as there may be unexpected method-dependent dependencies. By studying the impact of methodological variations alone and in concert with each other, we can improve model performance and help make research results more generalizable and implementable for researchers.

LIMITATIONS

This study was performed at a single academic medical center, and its findings may not generalize to different sources of medical record data. The gold standards are subject to existing, accessible knowledge—neither gold standard is perfect and they are correlated, but evaluating with respect to both is more informative than comparing to only one. Associations between drugs and lab measurements were studied pairwise—confounding effects of other drugs and drug-drug interactions were not considered. The selected method for classifying lagged coefficients was not studied rigorously, and may possess unforeseen biases.

CONCLUSIONS

We used lagged linear methods to detect physiologic drug effects in EHR data. We used two clinical gold standards and a bootstrap methodology to evaluate the reliance of lagged methods on combinations of methodological perturbations. We observed important statistically significant improvements from particular combinations of temporal re-parameterization, time-series differencing, and regression model choice. We expect that these steps will play an important role in revealing fine temporal structure from EHR data, and we recognize the overarching importance of systematic comparison of machine learning methods under a broad range of pre-processing scenarios.

Highlights.

• Standard timeseries methods accurately detected physiologic drug effects in EHR data

• Systematic evaluation revealed important interactions of methodological choices

• Indexing timeseries by sequence consistently improved drug-effect detection