Signal percolation within a bacterial community

SUMMARY

Signal transmission among cells enables long-range coordination in biological systems. However, the scarcity of quantitative measurements hinders the development of theories that relate signal propagation to cellular heterogeneity and spatial organization. We address this problem in a bacterial community that employs electrochemical cell-to-cell communication. We developed a model based on percolation theory, which describes how signals propagate through a heterogeneous medium. Our model predicts that signal transmission becomes possible when the community is organized near a critical phase transition between a disconnected and a fully connected conduit of signaling cells. By measuring population-level signal transmission with single-cell resolution in wild-type and genetically modified communities, we confirm that the spatial distribution of signaling cells is organized at the predicted phase transition. Our findings suggest that at this critical point, the population-level benefit of signal transmission outweighs the single-cell level cost. The bacterial community thus appears to be organized according to a theoretically predicted spatial heterogeneity that promotes efficient signal transmission.

eTOC blurb:

Long-range electrical signal transmission allows dense bacterial communities known as biofilms to coordinate their actions and collectively enhance their fitness. However, it remains unclear how the community is organized to enable efficient long-range signal transmission, especially given that the community-level benefit comes at a cost to individual cells that relay the signal. Here we find that the biofilm copes with this cost-benefit problem by self-organizing at a theoretically defined tipping point (critical phase transition). At this critical point, the system transitions from having only short-range connectivity among a few cells to a fully connected conduit of signaling cells that span the entire community. Using mutant biofilms, we show that this regime optimally balances the cost and benefit of electrical signal transmission. The opposing constraints of performing a function that inherently carries a cost thus appear to drive a biological system to self-organize its heterogeneity at a critical phase transition.

Graphical Abstract

We report the use of a chip-based system for combinatorial high-throughput differentiation screening of microscale 3D human neural progenitor cells.

INTRODUCTION

Biological systems such as tissues or bacterial communities often require reliable signal transmission among cells to coordinate actions at a distance (Debanne et al., 2011; Notaguchi and Okamoto, 2015). In metazoans, highly specialized and sophisticated structures are dedicated to signal transmission, such as axons that relay electrical signals in the nervous system. Densely packed bacterial communities have also been shown to benefit from coordinating their metabolic activities over long distances (exceeding hundreds of cell lengths) to cope with nutrient competition (Liu et al., 2015; Waters and Bassler, 2005). However, these bacterial communities face at least two main challenges to coordinate cellular actions at long distances. First, it is unclear how bacterial communities can achieve reliable signal propagation to desired target sites without specialized structures that direct the signals. Second, bacterial communities exhibit significant cell-to-cell heterogeneity that can constitute a key obstacle for long-range signal propagation (Li and You, 2013; Raj and van Oudenaarden, 2008; Symmons and Raj, 2016). For example, if only a fraction of cells contributes to signal transmission, the resulting cell-to-cell heterogeneity could cause the propagating signal to die out before reaching its desired target (Alonso and Bär, 2016; Cao et al., 1999; Steinberg et al., 2006; Waxman, 2006). It is thus important to establish the relevance of heterogeneity in bacterial communities in the context of long-range signal transmission (Figure 1A).

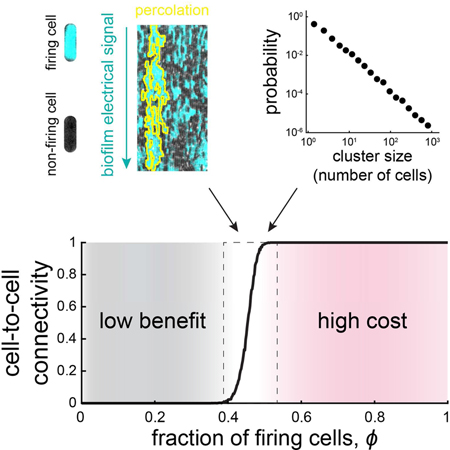
Figure 1. A percolation theory-based model for electrochemical signaling in biofilms.

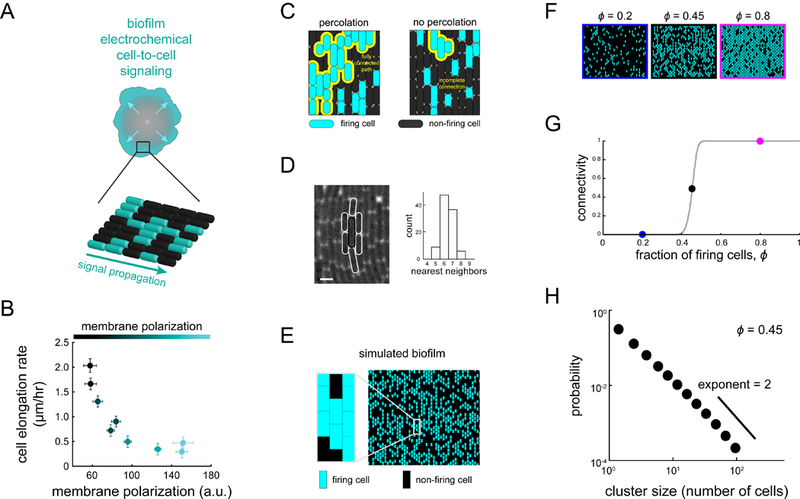
(A)Biofilms undergo electrochemical signaling where the stressed biofilm interior periodically signals cells at the biofilm edge (arrows). Bottom cartoon depicts heterogeneous signaling where some cells participate in signaling (cyan), becoming hyperpolarized, while many cells do not participate (black). (B) Cell elongation rate is inversely correlated with membrane polarization, indicating a cost of electrical signaling activity to individual cells (N = 35 cells, error bars indicate ± SEM). (C) Percolation theory predicts the emergence of a connected path of firing cells (yellow line) when the fraction of firing cells exceeds a critical value (left) but not below this critical value (right). (D) Image illustrating a method for counting the number of neighbors for a given cell, highlighted in white (left). Scale bar, 2 μm. Histogram (right) indicates the modal number of nearest neighbors is 6 (N = 100 cells). (E) Using the experimentally constrained nearest neighbor value of 6 (see also Figure S1), firing and non-firing cells are randomly positioned on a two-dimensional lattice with probability ϕ (0.5 in this image). (F) Representative snapshots showing lattice simulations at various values of ϕ (see also Figure S2). (G) Onset of connectivity (percolation) is predicted when ϕ exceeds 0.45. The ϕ values for the representative images in (F) are indicated on the graph by their respective colored circles. (H) Model-generated cluster size distribution at the percolation threshold (ϕ = 0.45), where clusters are distributed according to a power-law.

The molecular mechanism that underlies signal propagation from the interior of the B. subtilis community towards its edge is based on ion channel-mediated electrochemical cell-to- cell signaling (Figure 1A). Specifically, electrochemical signaling is initiated by cells in the biofilm interior when they experience glutamate starvation during biofilm expansion. This nutrient starvation leads to the opening of the metabolically-gated YugO potassium ion channel and subsequent release of intracellular potassium. The resulting local increase in extracellular potassium causes immediately adjacent cells to depolarize, which interferes with their uptake of glutamate, a charged amino acid. Consequently, the depolarized neighboring cell also experiences glutamate limitation and opens its potassium ion channels, releasing its own potassium ions (Prindle et al., 2015). This cell-to-cell relay mechanism gives rise to a chain- reaction that propagates the signal to the biofilm periphery. When the electrochemical signal reaches the biofilm edge, it halts growth of peripheral cells and thereby reduces their nutrient consumption. This reduction in nutrient consumption allows higher nutrient availability to the stressed cells in the biofilm interior. When nutrient stress in the interior is alleviated, signaling ceases. Now the biofilm resumes growth, which again results in a renewed starvation of interior cells and initiation of the electrochemical signal. This signaling process thus increases the overall fitness of the biofilm against chemical attack by maintaining a viable population of sheltered interior cells.

In addition to the population-level benefit, electrochemical signaling carries a measurable cost to individual cells, in the form of a reduction in growth rate (Figure 1B) (Liu et al., 2015). This trade-off between single-cell level cost and population-level benefit suggests that it might be advantageous for the biofilm that not all cells carry the burden of relaying the signal for long-range transmission to succeed. But it is unclear what fraction of signaling cells is needed and how these cells would be organized in space to transmit the signal. Notably, signal propagation through such inhomogeneous populations is not a problem exclusive to biological systems, but a general question that has been deeply explored in fields such as physics, chemistry and materials science (Bär et al., 1996; Sendiña-Nadal et al., 1998; Steinbock et al., 1995). Percolation theory has emerged as the simplest statistical physics approach that directly addresses this problem. This theory has been commonly applied to study signal propagation through various spatially extended heterogeneous systems (Bak et al., 1990; Zhou et al., 2015). In particular, it describes the emergence of a connected path (connected cluster of cells) that spans the entire size of a spatially extended system, providing a conduit for signal transmission.

Here, we apply the framework of percolation theory to understand how electrochemical signals are propagated across a heterogeneous B. subtilis biofilm community. By incorporating excitable dynamics into a percolation model, we predict the ability of a biofilm to transmit a signal given different fractions of cells participating in signaling, as well as different signaling dynamics. We define cost and benefit for each set of signaling parameters and predict a region in parameter space, determined by the critical percolation point, where the signaling benefit outweighs the associated cost. Integration of mathematical predictions with quantitative experimental data from wild-type and mutant biofilms suggests that wild-type biofilms operate near this region. Our findings are likely to apply to other percolation systems where the benefit exhibits a sharp sigmoidal shape due to its population-level character, while the cost is associated with the individual units that comprise the system and thus increases linearly with the fraction of signaling units. We argue that in such systems, the benefit will outweigh the cost near the percolation threshold.

RESULTS

To address the problem of long-range signal transmission in biofilms, we began by constructing a percolation-theory-based model to investigate how a population of cells with heterogeneous electrical activity can reliably propagate signals (Figure 1A, STAR Methods). Percolation theory predicts the transition of a network from having only localized short-range connections to the emergence of a fully connected path that spans the entire system (Figure 1C). Specifically, for a defined two-dimensional lattice, the onset of percolation occurs when the fraction of randomly positioned firing cells, ϕ, reaches a critical value, ϕ_c (Stauffer and Aharony, 1994). At this point, the system undergoes a sharp phase transition in its connectivity, giving rise to a connected cluster of firing cells with a size close to that of the entire system. Below the critical ϕ, too few cells are firing to have sufficient adjacent cells to comprise a fully connected cluster that can span the entire size of the system. Therefore, the probability of having a fully connected conduit for signal transmission across the system remains zero below the critical fraction, but then suddenly jumps to 1 (complete connectivity) as ϕ reaches the critical value. In other words, only when ϕ has reached the critical fraction of firing cells can there be clusters of firing cells that are large enough to span the system. This gives rise to the characteristic sudden phase transitions associated with criticality (Figure 1G) (Stauffer and Aharony, 1994).

Given the experimentally constrained size of the system and a modal value of six neighbors for the biofilm cells (Figure 1D), the model predicts an onset of signaling connectivity (percolation) when the fraction of firing cells in the biofilm reaches 0.45 (Figure 1E-G, see Figure S1C for lattices with different numbers of nearest neighbors). At this critical fraction, a firing cell is likely to have at least one immediately adjacent neighbor that is also a firing cell. Consequently, the cluster size distribution of firing cells will have a long tail. In other words, there is always a finite probability of finding a very large, system-spanning cluster of firing cells. Specifically, theory predicts that near this critical percolation threshold, and only near this point, the distribution of cluster sizes formed by signaling cells follows a power-law decay with an exponent of 2.05 (Stauffer and Aharony, 1994) (Figures 1H, S2). While the critical value for the fraction of firing cells depends on the specifics of the lattice, such as the number of neighboring cells, the exponent is universal (Figure S1D). This means that the exponent value is the same for any two-dimensional lattice and thus a very stringent and general prediction (Aharony, 1980).

To reiterate, percolation theory thus makes two precise predictions required for signal transmission to become possible in bacterial communities: 1) The fraction of firing cells in the biofilm should be at, or above, the critical percolation threshold of 0.45, and 2) near the percolation threshold, the distribution of cluster sizes formed by firing cells should follow a power-law decay with a slope of 2.05.

To test these theoretical predictions, we determined the spatial arrangement of signaling cells within biofilms. We utilized a microfluidic platform to grow B. subtilis biofilm communities (Liu et al., 2015) and image them with single-cell resolution (Figure S3). The microfluidic growth chamber contained designated regions where the biofilm was constrained in height to a twodimensional mono-layer. This allowed us to accurately quantify the spatial organization and dynamics of electrochemical signaling at the single cell-level. Furthermore, the two-dimensional geometry allowed us to directly investigate signal transmission in a geometry where the number of neighboring cells is limited, compared to three-dimensional regions of the biofilm where each cell has more than 6 neighbors on average. The ability of the biofilm to transmit signals even in a monolayer is crucial, since the leading edge of the biofilm is predominantly a monolayer (Seminara et al., 2012) and constitutes the destination for electrochemical signaling (Figures 2A, S3).

Figure 2. Electrochemical signaling within biofilms is heterogeneous at the single cell- level.

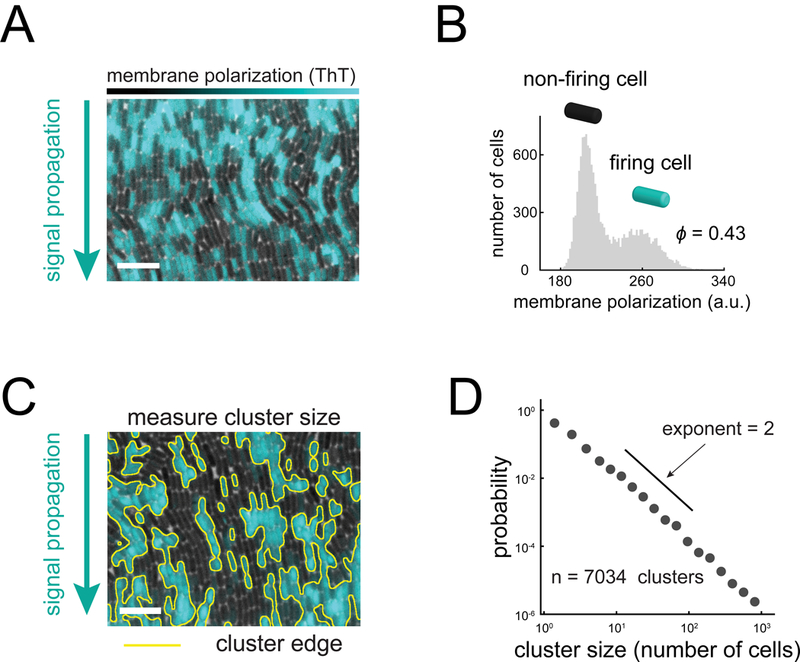
(A) Membrane polarization is heterogeneous at the single cell level within signaling biofilms. Cyan overlay indicates fluorescence of Thioflavin T (ThT), a cationic membrane polarization reporter. Scale bar, 10 μm (see also Figure S3). (B) Histogram of individual cell ThT intensity (N = 14,936 cells) during a signal pulse. The bimodal shape of the histogram indicates that only a fraction of firing cells (cyan) participate in signaling (0.43±0.02, mean+/−SEM). (C) Firing cells are spatially clustered within biofilms. Yellow lines indicate cluster edges identified by image analysis based on ThT fluorescence. Scale bar, 10 μm. (D) Cluster sizes (N = 7,034 clusters) are distributed according to a power-law decay across 3 decades with an approximate exponent of 2. These properties indicate that the arrangement of firing cell clusters within the biofilm can be described by percolation theory.

To measure membrane potential of individual bacteria within biofilms during electrochemical signaling, we used the previously characterized fluorescent reporter thioflavin-T (ThT), which acts as a Nernstian membrane potential indicator (Prindle et al., 2015). Specifically, the higher the membrane potential of the cell, the larger the amplitude of the fluorescent ThT signal. Single-cell resolution measurements of the biofilm show that only some cells exhibit pulses in electrical activity, while others do not appear to participate in signaling (Figures 2A, 2B, and S4). Analysis of all cells reveals a bimodal distribution of membrane potential amplitudes during signal propagation, with the fraction of signaling cells being ϕ = 0.43±0.02 (Figure 2B, STAR Methods), in agreement with the theoretically predicted percolation threshold. We then measured the spatial distribution of signaling (firing) cells and determined that they were clustered in space (Figure 2C). Moreover, the distribution of cluster sizes follows a power-law decay that extends across three decades and has an exponent of approximately 2 (Figure 2D). Both the fraction of firing cells and the distribution of firing cell cluster sizes are thus consistent with percolation theory predictions. These results suggest that the spatial organization of signaling cell within the bacterial community may be organized near the percolation threshold.

Signal transmission is inherently a dynamic process that unfolds over time. In our system, the signal propagates from one cell to the next, where each cell undergoes an excitable pulse (firing) in its membrane potential. The amplitude of the pulse must be sufficiently high to trigger a response in the neighboring cell. It is also important that the cell does not spend excessive time in the firing (and thus non-growing) state, as this would result in unnecessary cost (Figure 1B). In its simplest form, percolation theory is a statistical framework that does not account for such pulse durations and signaling dynamics of cells. Therefore, we created a model that takes into account both the spatial arrangement of firing cells and the single cell dynamics during signal transmission.

We described the single cell-level electrochemical signals in the biofilm with the FitzHugh-Nagumo (FN) model of excitable dynamics (Figure 3A) (Tuckwell, 1988). This simple model, commonly used for studying action potential dynamics in neurons, accounts here for excitable dynamics in individual cells as well as for the transmission of signals between neighboring cells (Figure 3B, 3C). It contains three parameters: the first is the activation or firing threshold, u₀, which defines the amplitude that an external signal has to exceed in order to trigger a response in the form of a pulse. The second parameter is the recovery time, T, which sets the pulse duration of a given response and thus governs the signaling dynamics. The third parameter is the ratio Ɛ of excitation to cell-to-cell coupling strength, which when sufficiently high supports pulse-coupled wave propagation (see STAR Methods) (Mirollo and Strogatz, 1990). To account for heterogeneity in signaling, different fractions of cells can be assigned as firing cells by giving them a higher value for Ɛ than the other cells (Figure 3D). We integrated the FN model with percolation theory by evolving the dynamics on a two-dimensional lattice of excitable cells (Figure 3F). Simulations show that successful signal propagation through the lattice of cells depends on both the firing duration and the fraction of firing cells. Importantly, for the same dynamic parameters, a fraction of firing cells near or above the percolation threshold enables successful signal transmission, while a fraction below the threshold fails to propagate the signal (Figure 3D, 3E).

Figure 3. An excitable model for signal propagation in biofilms.

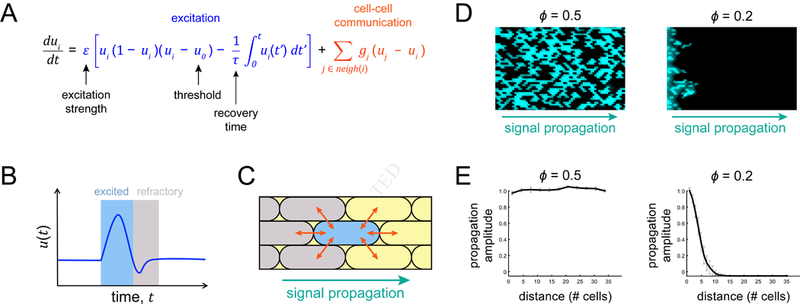
(A) Model equation combines excitation (blue) and cell-cell communication (orange) to give rise to excitable propagation. The geometric factor g_j is 1/4 at the cell poles and 1/2 otherwise. (B) A cartoon trace illustrates firing (blue-shading) followed by a refractory period (gray-shading) for a given excitable cell. (C) Cell-cell communication (arrows) allows directional signal propagation from one cell to another. Refractory cells are gray and excited cells are blue. (D) Example model snapshots depict complete signal propagation (direction indicated by arrow, Ɛ = 10 for active cells) in the regime above the percolation threshold (left, ϕ = 0.5) and incomplete signal propagation below the percolation threshold (right, ϕ = 0.2). Both cases have the same values for the dynamic parameters, u_o = 0.01, τ = 300. (E) Example amplitude profiles for the images shown in (D).

To experimentally investigate how biofilm dynamics and spatial structure jointly determine signal transmission and to integrate our findings with mathematical predictions, we utilized three gene-deletion strains that generate biofilms with altered structure and dynamics (Figure 4A, STAR Methods). We first focused on structural differences among biofilms and began by investigating the ΔtrkA strain, which lacks the gating domain of the YugO potassium ion channel and is known to be deficient in electrochemical signaling (Humphries et al., 2017; Liu et al., 2017; Prindle et al., 2015). Indeed, biofilms formed by the ΔtrkA strain contain a low fraction of firing cells, 0.13±0.04 (mean±SEM), compared to 0.43±0.02 observed in wild-type biofilms (Figure 4B, 4D). We also utilized a strain that lacks the KtrA potassium pump (ΔktrA) and generates biofilms with a fraction of firing cells similar to wild-type biofilms (0.48±0.11). In contrast, deletion of SinR (ΔsinR), a transcription factor that represses expression of the YugO ion channel (Lundberg et al., 2013), results in biofilms with a higher fraction of firing cells, 0.74±0.04 (Figure 4B, 4D). Biofilms formed by these strains thus contain structural differences as defined by differences in the fraction of firing cells.

Figure 4. Experimental tuning of firing cell fraction and pulse duration with mutant biofilms.

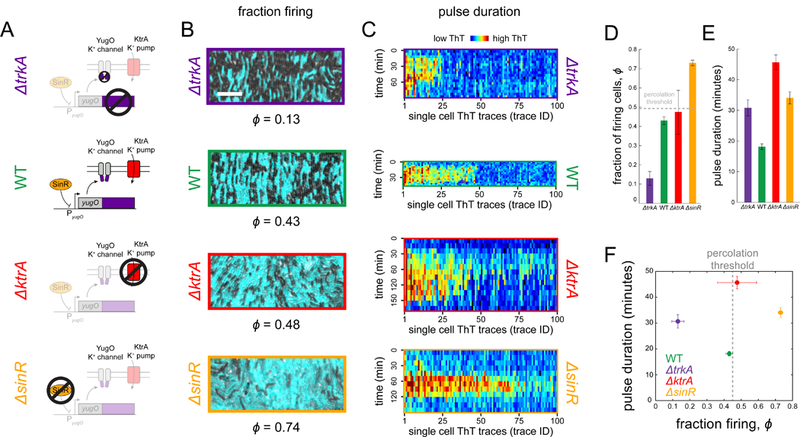
(A) A series of cartoons illustrates the function of genes deleted in the mutant strains. (B) Representative images from time points of peak signaling activity depicting the fraction of firing cells for each strain (cyan ThT fluorescence). Scale bar, 10 μm. (C) Heatmaps depict single cell ThT trajectories (N = 100) for all strains. Each column is one cell trace, with time progressing downwards. The color-scale varies across strains due to baseline fluorescence differences among experiments (see also Figure S5). (D) Mutant strains exhibit decreased (ΔtrkA, 0.13±0.04, N = 7, mean ± SEM) or increased (ΔsinR, 0.74±0.04, N = 4 and ΔktrA 0.48±0,11, N = 4) fraction of firing cells relative to wild-type (0.43±0.02, N = 12). Wild-type is near, but slightly below, the percolation threshold, ϕ_c = 0.45. The ΔtrkA strain (purple), which lacks the gating domain of the potassium channel YugO, is expected to exhibit reduced signaling activity. The ΔktrA strain (red) lacks a potassium uptake pump and is expected to remain hyperpolarized for longer than wild-type. The ΔsinR mutant (orange) lacks a transcription factor (SinR) that represses expression of YugO, resulting in higher signaling activity. (E) Pulse duration measurements, where pulse duration is defined as the amount of time membrane polarization remains above baseline level. All mutant strains (ΔtrkA 30.6±2.6, 124 cells, 3 biofilms, and ΔktrA 45.7±2.4, 204 cells, 3 biofilms, and ΔsinR 34.1±2.0, 165 cells, 3 biofilms, mean ± SEM) have larger pulse durations than wild-type (18.1±1.0, 383 cells, 3 biofilms). (F) A phase plot of pulse duration and fraction firing for each strain. ΔtrkA lies below the percolation threshold (dotted line) and ΔsinR above, both with longer pulse duration than wild-type. Wild-type and ΔktrA lie near the threshold, but with different pulse times.

To characterize the signaling dynamics of each strain, we tracked hundreds of individual cells within the wild-type and genetically modified biofilms and measured their electrical activity during signal transmission (Figure 4C). We found that the wild-type biofilm has the shortest pulse duration, followed by ΔsinR and ΔtrkA biofilms (Figure 4E). The absence of the KtrA potassium uptake pump extends the pulse duration, presumably by delaying the recovery of intracellular potassium stores. Notably, wild-type and ΔktrA biofilms have a similar fraction of firing cells, despite their difference in average pulse durations. In contrast, ΔtrkA and ΔsinR biofilms have similar pulse durations, even though DtrkA biofilms contain the lowest and DsinR biofilms the highest fraction of firing cells (see Figure S5 for single cell traces from the model). Together, these strains show that the fraction of firing cells and average pulse durations can be separately modulated, allowing us to experimentally explore the phase space defined by the structure and dynamics of biofilms during signal transmission (Figure 4F).

The different combinations of biofilm structure and dynamics that are accessible through genetic perturbations provide an opportunity to investigate why the wild-type cell-to-cell heterogeneity is organized near the critical percolation threshold. Motivated by the notion that biological processes carry not only a benefit, but also a cost, we asked whether the observed spatial organization of wild-type biofilms could be explained by the balance between the benefit and cost of signal transmission. The benefit is defined by the ability to successfully transmit the signal within the biofilm, since such signaling has been previously shown to increase the population-level fitness against chemical attack (Liu et al., 2015). Therefore, we can experimentally define the population-level benefit of signaling based on the fidelity of signal transmission. Specifically, we measure the relative fraction of cells that relay the signal at the two most distant locations within the field of view of our experimental set up (approximately 25 cell lengths in Figure 5B). We find that the wild-type and mutant biofilms that contain a fraction of firing cells that is near or above the critical percolation threshold can successfully transmit the signal without a decay in its amplitude (Figure 5A, 5B). In contrast, the ΔtrkA strain, which has a fraction of firing cells well below the percolation threshold (Figure 4D, 4F), fails to transmit the signal (Figure 5A, 5B). We can now relate this experimentally determined benefit to the mathematical model based on the fidelity of signal transmission. In particular, the model predicts that as a function of ϕ, the benefit will sharply rise in a sigmoidal manner (Figure 5C). This sudden rise in the population-level benefit is due to the sudden transition in connectivity at the percolation threshold that enables signal transmission through the system. Beyond the percolation threshold, the benefit is predicted to saturate, since a fully connected conduit for singling has already been formed, and a further increase in the fraction of firing cells does not qualitatively alter signal transmission (Figure 5C). Our experimental data are consistent with the mathematically predicted benefit function (Figure 5C).

Figure 5. Signal transmission occurs above the percolation threshold.

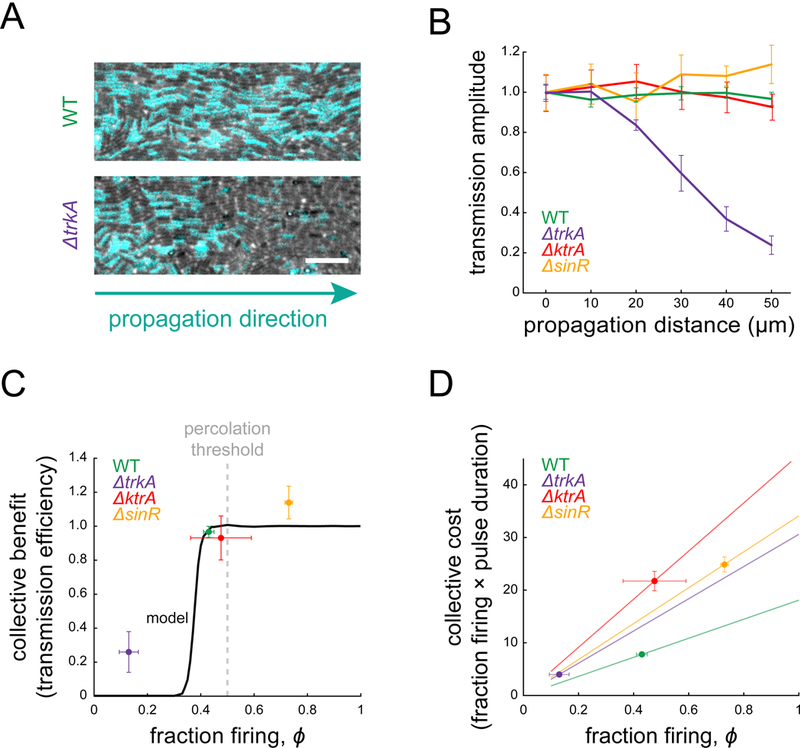
(A) Phase images with overlaid ThT intensity (cyan) during peak signaling show steady propagation in wild-type (top) and spatial signal decay in ΔtrkA (bottom). Scale bar, 10 μm. (B) Transmission amplitude measurements show that wild-type (N = 7), ΔktrA (N =4), and ΔsinR (N = 4) propagate the signal at a constant amplitude, while ΔtrkA (N = 5) does not. Transmission amplitude is defined as the fraction of firing cells at a given position divided by the firing fraction at the beginning of the field of view (error bars, ± SEM). (C) Collective benefit of signaling is defined as the ratio of transmission amplitudes at the biofilm edge and at the beginning of the field of view. Experimental data are shown by points. The model output for wild-type parameters (black curve) illustrates the non-linear nature of collective benefit. (D) Collective cost of signaling is defined as the product of the firing cell fraction, ϕ, and mean pulse time. Experimental data are shown as points. Lines represent the cost that would be incurred for each strain given its mean pulse time.

On the other hand, community-level benefit is also associated with a single-cell-level cost. Specifically, firing cells incur a metabolic burden during their electrical activity, as evidenced by the experimentally observed reduction in their cell elongation rate (Figure 1B). Therefore, we define population-level cost as the fraction of firing cells multiplied by their mean signaling duration (Figure 5D). The biofilm incurs greater cost with an increasing number of firing cells, or longer firing durations per cell. Consequently, the cost function increases gradually with the increase in the fraction of firing cells. While both the cost and benefit increase as a function of the fraction of firing cells, the gradual rise of the cost function and the sharp sigmoidal shape of the benefit function imply an intriguing cost-benefit relationship (Figure 5C, 5D).

We find that the intersection of a nonlinear benefit function and a linear cost function gives rise to a non-monotonic benefit-to-cost relationship. Specifically, the cost rises at a constant rate independent of different dynamic parameter values (firing durations) (Figures 6A, 6B). In contrast, the benefit jumps at the percolation threshold and then saturates (Figure 6A). This suggests that the benefit-to-cost ratio would be highest near the percolation threshold. Indeed, when we plot the benefit-to-cost ratio from the model as a function of the fraction of firing cells, we find a well-defined peak near the percolation threshold (Figure 6D). The result does not depend on the specific way in which benefit and cost are compared: subtracting the cost from the benefit, for instance, also yields a peak near the percolation threshold (Figure S6). The experimentally determined values place the wild-type biofilm near this region defined by the peak, while the mutant biofilms are located away from this region (Figure 6D). These results indicate that the spatial organization of heterogeneity in the wild-type biofilm promotes efficient signal transmission by residing near the percolation threshold.

Figure 6. Cost-benefit negotiation in signal transmission.

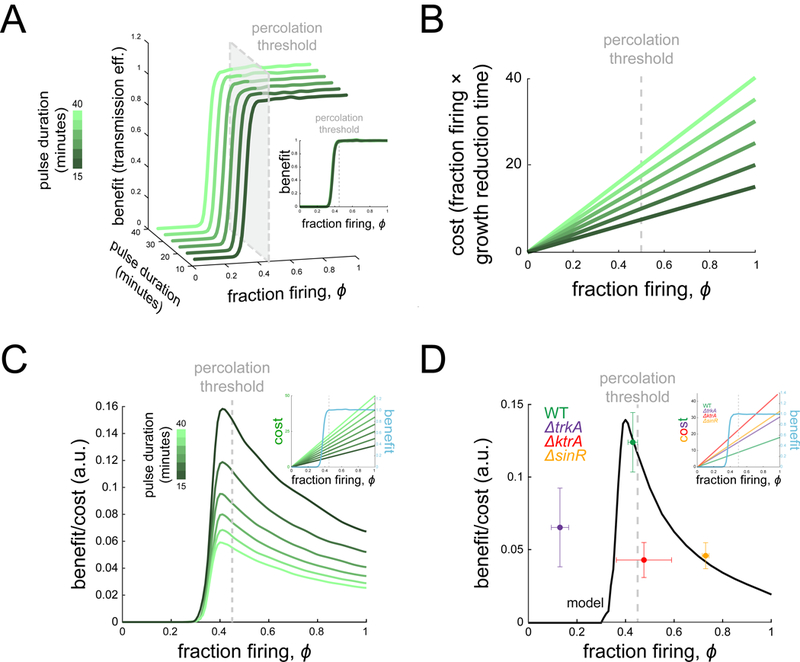
(A) The benefit (transmission efficiency) is plotted for different dynamic parameters as a function of ϕ and resulting pulse time (green color scale). When plotted as a function of ϕ only, the curves line up with benefit rising near the threshold (inset). (B) The cost function is plotted for the corresponding benefit curves from (A). (C) Benefit/cost ratio is plotted as a function of ϕ for the different model curves in (A) and (B), illustrating that, no matter the dynamic model parameters, benefit/cost ratio has a peak near the percolation threshold. This comes from the fact that benefit is highly non-linear in ϕ while cost increases smoothly for any set of dynamic parameters (inset). (D) Measured benefit/cost ratio is plotted for each strain (dots), along with the model output given wild-type parameters (curve). The ratio exhibits a peak due to the linear cost but highly non-linear benefit, with wild-type near the maximum (see also Figure S6). Inset plot overlays cost and benefit on separate y axes.

We note that given a sharp rise in the benefit due to the critical phase transition, the benefit will outweigh the cost near the percolation threshold for a broad range of slopes of the cost function (Figures 6C, 6D inset). We also note that linearity is not required, for as long as the cost function increases gradually, the benefit-to-cost function will always be dominated by the jump in the benefit.

DISCUSSION

It has been suggested that biological systems across different scales exhibit properties consistent with critical phase transitions. This claim is often justified by the observation of scalefree behaviors such as power-law dependencies (Bialek et al., 2014; Dai et al., 2013; Steiner et al., 2016). However, two common concerns are that many biological systems lack an underlying theoretical justification of a critical phase transition, and that the biological purpose of operating near a phase transition is unclear (Mora and Bialek, 2011). Here we demonstrate that the spatial organization of a bacterial biofilm is consistent with percolation theory, which is well- known to exhibit a critical phase transition. Specifically, we observe a power law that arises at the predicted value (percolation threshold) and with the predicted exponent. Furthermore, we offer a biological rationale for why the system would be at criticality, by showing that the benefit outweighs the cost near the critical point. It is thus intriguing to speculate that a cost-benefit negotiation may be an organizing principle that drives the biofilm structure to the critical percolation threshold. Our findings suggest that the cost and benefit of signal transmission may thus play a role in promoting spatial heterogeneity that is organized near criticality. Consequently, the theory developed in statistical physics to describe criticality may also describe the spatiotemporal organization of diverse biological systems and provide a conceptual framework to uncover the functional pressures that drive these systems to phase transition points.

STAR METHODS

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
B. subtilis NCIB 3610	Bacillus Genetic Stock Center, (Irnov and Winkler, 2010)	BGSCID. 3A1
sacA::Pcitz-yfp (CmR)	This study	N/A
trkA ::NeoR	(Prindle et al., 2015)	N/A
sinR: :NeoR	(Asally et al., 2012)	N/A
ktrA::ErmR	(Humphries et al., 2017)	N/A
Software and Algorithms
Custom MATLAB and Fiji scripts	This study
mT rackJ	(Meijering et al., 2012)

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Gürol M. Süel (gsuel@ucsd.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Table of strains
Strain	Genotype	Source
Wild type	B. subtilis NCIB 3610	(Irnov and Winkler, 2010)
Pctz-YFP	sacA::PCitZ-yfp (CmR)	this study
ΔtrkA	trkA::NeoR	(Prindle et al., 2015)
ΔsinR	sinR..NeoR	(Asally et al., 2012)
ΔktrA	ktrA::ErmR	(Humphries et al., 2017)

Bacillus subtilis strains

We conducted all experiments with B. subtilis NCIB 3610. Wild-type 3610 was a gift from W. Winkler (University of Maryland) (Irnov and Winkler, 2010). All other strains were derived from it and verified by sequencing.

Biofilm growth conditions

We grew biofilms in MSgg medium containing 5 mM potassium phosphate buffer (pH 7.0), 100 mM MOPS buffer (pH 7.0, adjusted using NaOH), 2 mM MgCl₂, 700 μM CaCl₂, 50 μM MnCl₂, 100 μM FeCl₃, 1 μM ZnCl₂, 2 μM thiamine HCl, 2 mM sodium citrate, 0.5% (v/v) glycerol and 0.4% (w/v) monosodium glutamate. Media were made from stock solutions immediately before experiments, and the stock solution of glutamate made fresh every two days.

Microfluidics and Experimental Conditions

24 hours before experiments, we streaked strains from −80 C glycerol stocks onto LB agar platers and grew overnight at 37 C. The day of experiments, we inoculated single colonies from LB plates into 5 ml of liquid LB media and grew in a 37 C shaker for ~2.5–3 hours. We centrifuged LB-grown cultures at 4800 rpm for 2 minutes and resuspended cell pellets in MSgg medium. We then immediately loaded cells into a Y04D microfluidic plate using the CellASIC ONIX microfluidic system (EMD Millipore) (Liu et al., 2015). After loading, we grew cells in the microfluidics at 37 C and 0.5 psi (~8 μm/s) flow for ~2 hours before changing temperature to 30 C and growing overnight under 1.5 psi flow (~24 μm/s). After 12 hours of growth in plain MSgg, ThT dye was flowed in at a concentration of 10 μM. Experiments were conducted under these conditions.

METHOD DETAILS

Percolation Theory

To describe the connectivity and clustering statistics of firing cells in the biofilm, we simulate cells on a regular triangular two-dimensional lattice. Because cells in the experimental biofilms have a modal value of six neighbors (Figure 1D), we use a triangular lattice, in which cells have six nearest neighbors to which they connect forming triangles (Stauffer and Aharony, 1994). Other lattices that would be good approximations of the biofilm predict similar results to those of the triangular lattice (Figure S1). Percolation theory describes the statistics of lattices in which a fraction ϕ of cells are firing. Firing cells are positioned uniform randomly within the lattice.

Percolation theory predicts that for sufficiently large lattices there is a critical threshold ϕ_c at which several key features occur (Stauffer and Aharony, 1994). First, the probability of a connected path (a contiguous path of firing cells that spans from one side of the lattice to the other) transitions from 0 to 1 at ϕ_c (Figure 1G). Second, at ϕ_c the distribution of cluster sizes becomes a power law, p(n) a n^-α (Figure S1), where a cluster is defined as a group of contiguous firing cells, and n is the number of cells in the cluster. For two-dimensional infinite lattices, the exponent is α = 187/91 ≈ 2.05 (Stauffer and Aharony, 1994). Below ϕ_c the distribution falls off exponentially (Figure S1), and above ϕ_c the distribution acquires weight near the lattice size due to the emergence of a giant cluster (Figure S1).

In all simulations we use a lattice size that corresponds to the approximate observation window in the experiments, L = 35 cell heights by W = 200 cell widths. Connectivity is determined along the shorter direction L, since this is the direction of signal propagation in the biofilm. The asymmetric geometry (L ≠ W) is responsible for the deviation of the percolation threshold (ϕ_c = 0.45) seen in the main figures from the predicted value for a symmetric triangular lattice (ϕ_c = 0.5) (Stauffer and Aharony, 1994). Figures 1G, 1H, and S2 were generated using 2000 realizations of the lattice.

Dynamical Model

To model the single-cell dynamics of electrical pulses in the biofilm, we utilized the FitzHugh- Nagumo (FN) model (Figure 3A) (Tuckwell, 1988). The FN model is a minimal model of excitable dynamics and is commonly utilized for studying action potential dynamics in neurons. Here we use it to model the bucket-brigade mechanism of effective electrical activation of neighboring cells reported previously (Prindle et al., 2015). Specifically, we use a discretized Laplacian term to account for the cell-cell communication (Figure 3A, 3C). In general, the parameters of this phenomenological model do not have a precise mechanistic interpretation, but rather are calibrated from the experiments as described below.

In all dynamical simulations, cells in the first row are initialized with u = 1 to trigger the excitable wave; all other cells are initialized with u = 0. We use a lattice of L’ = 100 rows by W = 200 and record from a window of L = 35 by W = 200 that is positioned just after the first row. Choosing L̓ > L avoids boundary effects at the last row. We use an absorbing boundary at the last row and reflecting boundaries on the other three sides. To evolve the dynamics, we discretize the FN model in time using the fourth-order Runge-Kutta method with time step Δt = 0.02. For the cell-cell coupling we use g_j = 1/2 and 1/4 (Figure 3A) for the two short-edge and four long-edge neighbors, respectively, corresponding to a rectangular cell with a 2-to-1 aspect ratio on a triangular lattice.

A fraction ϕ of cells are firing and are positioned randomly in accordance with percolation theory as described above. All firing cells have the same FN parameters, given below. Non-firing cells have the same parameters as firing cells, except that we reduce the recovery time τ by a factor of 60, which we find strongly reduces the firing propensity of these cells (Figures 3D, 3E).

Model Calibration

We calibrate the parameters of the model (Figure 3A) from the wild type (WT) data in the following way. The fraction of firing cells ϕ = 0.43 is obtained directly from the experiments (Figure 4D). The excitation strength Ɛ must be larger than 1 because otherwise diffusion outpaces excitation and the wave does not propagate; therefore we set Ɛ = 10 (note that because the model is phenomenological, the diffusion we describe here is effective and does not correspond to the diffusion of, say, the potassium ions between cells). The threshold uo must be significantly less than 1 because otherwise signal from a neighboring cell is insufficient to trigger an excitation and the wave does not propagate; we find that u_o = 0.02 suffices (Figure 3D). The recovery time of firing cells τ = 300 is set such that the mean wavelength over 10 simulations is equal to the approximate experimental wavelength of 35 cells. Finally, we convert from dimensionless time t to minutes by equating the mean pulse duration in the simulations to the experimental value (Figure 4E). Pulse duration is averaged over all firing cells and defined as the time over which u > 0.6. See Figure S5 for single-cell time traces from model biofilms with parameters corresponding to each experimental strain.

Model Validation

We validate the model using one of the mutant strains, ΔsinR. This strain has a higher fraction ϕ = 0.74 of firing cells than WT. We anticipate that because structure and dynamics are connected in the integrated model, changing the fraction of firing cells will also change the mean pulse duration. We test this expectation in the model, setting ϕ = 0.74 and keeping all other parameters the same as WT. We observe in the simulations that the mean pulse duration rises from 18.1 min (WT) to 33.2 min (ΔsinR). In the experiments, we measure the mean pulse duration for ΔsinR to be 34.1 min, which agrees very closely with the value from the simulations. This validates the model and demonstrates that structure and dynamics are tightly connected in the integrated model.

Cost-Benefit Curves

To determine the cost and benefit curves in Figures 5 and 6, we use the following procedure. In Figures 5C, we vary ϕ while keeping all other parameters as calibrated above. For each ϕ value, we calculate the benefit as the average over 100 simulations of the ratio of the number of firing cells in the final five rows to that in the initial five rows. In Figure 6D, we calculate the cost as the average over 100 simulations of the product of the fraction of firing cells and the mean pulse duration. In Figure 6D, for each ϕ value, we vary τ in the range 5 to 1000 and measure the mean duration and benefit-to-cost ratio over 30 simulations for each τ value. Then we use linear interpolation to find the benefit-to-cost ratio corresponding to a particular duration. This produces curves of benefit-to-cost ratio vs. ϕ at fixed duration. Finally, we smooth these curves using a Gaussian filter of width 0.01, producing the result in Figure 6D.

Time-lapse Microscopy

We recorded phase-contrast and fluorescence images of biofilms at regular time intervals (between 3 and 10 minutes across experiments). For most experiments, we recorded phase, ThT fluorescence (for electrical signaling), and YFP fluorescence (for other analysis, see below). We used an Olympus IX83 inverted epifluorescence microscope with autofocus and a 40X, 0.6 NA or 100X, 1.4 NA objective, depending on the experiment. For each image, we used the minimum fluorescence exposure time that yielded good signal. For ThT images, exposure time was 17 ms and for YFP, exposure time was 150 ms.

QUANTIFICATION AND STATISTICAL ANALYSIS

Image Analysis

In order to segment single cells in each field of view, we took both ThT and YFP images with a 40X, 0.6 NA objective at the peak of each signal pulse as determined by the highest average ThT intensity of each field of view during signaling. Each field of view contained roughly 8000 bacteria. Cells expressed YFP from the citZ promoter, which gave a strong constitutive signal in each cell. From YFP images, we created thresholded binary images, from which we could identify the position and outline of each cell. We then thresholded ThT images at a fluorescence intensity value directly between the two peak peaks of the bimodal ThT intensity distribution (Figure 2B) to create a binary image with contiguous high ThT regions corresponding to clusters of firing cells (Figure 2C). Cluster sizes were measured by superimposing the high ThT cluster outlines on the binarized YFP image and counting the number of cells with a majority of their area inside each high ThT contour. The fraction of firing cells, ϕ, was computed by dividing the number of firing cells (high ThT) by the total number of cells in the field of view. All processing was performed with custom Fiji macros.

Dynamic Analysis

Pulse durations come from single-cell tracking measurements, where a cell was considered to be pulsing if its ThT level was above the threshold described above. Tracking was performed with the mTrackJ Fiji plugin by manually clicking on cells in each frame of a time lapse movie (Meijering et al., 2012). To measure single cell cost (Figure 1B) we measured elongation rate and ThT signal of single cells during a signal pulse with custom software written in MATLAB.

Highlights:

• Biofilm cells exhibit heterogeneity (firing/non-firing) in electrical signaling

• Firing cells arrange themselves into a theoretically predicted percolated network

• Percolation model accounts for signal transmission in wild-type and mutant biofilms

• Cost-benefit balance can organize the community at the critical percolation point