Comparing continual task learning in minds and machines

Significance

Humans learn to perform many different tasks over the lifespan, such as speaking both French and Spanish. The brain has to represent task information without mutual interference. In machine learning, this “continual learning” is a major unsolved challenge. Here, we studied the patterns of errors made by humans and state-of-the-art neural networks while they learned new tasks from scratch and without instruction. Humans, but not machines, seem to benefit from training regimes that blocked one task at a time, especially when they had a prior bias to represent stimuli in a way that encouraged task separation. Machines trained to exhibit the same prior bias suffered less interference between tasks, suggesting new avenues for solving continual learning in artificial systems.

Abstract

Humans can learn to perform multiple tasks in succession over the lifespan (“continual” learning), whereas current machine learning systems fail. Here, we investigated the cognitive mechanisms that permit successful continual learning in humans and harnessed our behavioral findings for neural network design. Humans categorized naturalistic images of trees according to one of two orthogonal task rules that were learned by trial and error. Training regimes that focused on individual rules for prolonged periods (blocked training) improved human performance on a later test involving randomly interleaved rules, compared with control regimes that trained in an interleaved fashion. Analysis of human error patterns suggested that blocked training encouraged humans to form “factorized” representation that optimally segregated the tasks, especially for those individuals with a strong prior bias to represent the stimulus space in a well-structured way. By contrast, standard supervised deep neural networks trained on the same tasks suffered catastrophic forgetting under blocked training, due to representational interference in the deeper layers. However, augmenting deep networks with an unsupervised generative model that allowed it to first learn a good embedding of the stimulus space (similar to that observed in humans) reduced catastrophic forgetting under blocked training. Building artificial agents that first learn a model of the world may be one promising route to solving continual task performance in artificial intelligence research.

Intelligent systems must learn to perform multiple distinct tasks over their lifetimes while avoiding mutual interference among them (1). Building artificial systems that can exhibit this “continual” learning is currently an unsolved problem in machine learning (2, 3). Despite achieving high levels of performance when training samples are drawn at random (“interleaved” training), standard supervised neural networks fail to learn continually in settings characteristic of the natural world, where one objective is pursued for an extended time before switching to another (“blocked” training). After first learning task A, relevant knowledge is overwritten as network parameters are optimized to meet the objectives of a second task B, so that the agent “catastrophically” forgets how to perform task A (4). For example, state-of-the-art deep reinforcement learning systems can learn to play several individual Atari 2600 games at superhuman levels, but fail over successive games unless their network weights are randomly reinitialized before attempting each new problem (5, 6).

Human evolution, however, appears to have largely solved this problem. Healthy humans have little difficulty learning to classify a fixed stimulus set along multiple novel dimensions encountered in series. For example, during development, children learn to categorize animals flexibly according to dimensions such as size or ferocity, and the subsequent introduction of a conceptually novel axis of classification (e.g., species) rarely corrupts or distorts past category knowledge. In other words, humans can learn multiple potentially orthogonal rules for classifying the same stimulus set without mutual interference among them. One theory explains continual learning by combining insights from neural network research and systems neurobiology, arguing that hippocampal-dependent mechanisms intersperse ongoing experiences with recalled memories of past training samples, allowing replay of remembered states among real ones (7, 8). This process serves to decorrelate inputs in time and avoids catastrophic interference in neural networks by preventing successive overfitting to each task in turn. Indeed, allowing neural networks to store and “replay” memories from an episodic buffer can accelerate training in temporally autocorrelated environments, such as in video games, where one objective is pursued for a prolonged period before the task changes (5, 9).

However, in human psychology, evidence for the relative benefits of blocked and interleaved training has been mixed. Several studies have reported an advantage for interleaved training, for example during skilled motor performance, such as in sports (10) or language translation (11), and even in the acquisition of abstract knowledge, such as mathematical concepts (12). Similar results have been reported in human category learning, with several studies reporting an advantage for mixing exemplars from different categories, rather than blocking one category at a time (13, 14). Interleaving might allow task sets to be constantly reinstantiated from memory, conferring robustness on the relevant representations (15), or amplify category-salient dimensions, by contrasting items from different categories against each other on consecutive trials (16). Taken in isolation, these findings support a single, general theory that emphasizes the benefits of interleaved training for continual task performance in humans and neural networks. Interestingly however, in other settings, blocked training has been found to facilitate performance. For example, blocked skill practice enhances performance for complex, but not simple motor tasks (15), and, in category learning, clearly verbalizable categories are better learned in a blocked fashion, whereas interleaving boosts learning of categories that require integration of different feature dimensions (17). In other words, blocking may help learn dimensions where the exemplars are characterized by higher between-category variability, whereas interleaving helps when exemplars differ between categories (16). However, these insights from category learning have yet to be harnessed to address the challenge of continual learning in neural networks that learn tabula rasa via parameter optimization, without handcrafting of the model state space.

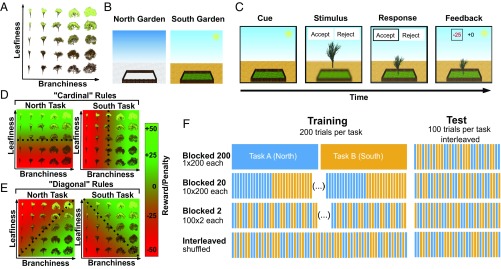
Here, our goal was to compare the mechanisms that promote continual task performance in humans and neural networks. We employed a canonical cognitive paradigm that involves switching between classification tasks with orthogonal rules. While much is known about the factors that limit task switching performance in explicitly instructed, rule-based paradigms with simple stimuli (18), here we explored how humans learned to switch between classification tasks involving naturalistic, high-dimensional stimuli from scratch and without prior instruction. In other words, rather than studying the control processes that permit task switching, we investigated how a general problem composed of two orthogonal task rules is learned by trial and error alone. We taught human and artificial agents to classify naturalistic images of trees according to whether they were more or less leafy (task A) or more or less branchy (task B), drawing trial-unique exemplars from a uniform bidimensional space of leafiness and branchiness (Fig. 1A).

Fig. 1.

Task design, experiment 1. (A) Naturalistic tree stimuli were parametrically varied along two dimensions (leafiness and branchiness). (B) All participants engaged in a virtual gardening task with two different gardens (north and south). Via trial and error, they had to learn which type of tree grows best in each garden. (C) Each training trial consisted of a cue, stimulus, response, and feedback period. At the beginning of each trial, an image of one of the two gardens served as contextual cue. Next, the context was blurred (to direct the attention toward the task-relevant stimulus while still providing information about the contextual cue), and the stimulus (tree) appeared together with a reminder of the key mapping (“accept” vs. “reject,” corresponding to “plant” vs. “don’t plant”) in the center of the screen. Once the participant had communicated her decision via button press (left or right arrow key), the tree would either be planted inside the garden (“accept”) or disappear (“reject”). In the feedback period, the received and counterfactual rewards were displayed above the tree, with the received one being highlighted, and the tree would either grow or shrink, proportionally to the received reward. Test trials had the same structure, but no feedback was provided. Key mappings were counterbalanced across participants. (D) Unbeknownst to the participants a priori, there were clear mappings of feature dimensions onto rewards. In experiment 1a (cardinal group), each of the two feature dimensions (branchiness or leafiness) was mapped onto one task rule (north or south). The sign of the rewards was counterbalanced across participants (see Methods). (E) In experiment 1b (diagonal group), feature combinations were mapped onto rewards, yielding nonverbalizable rules. Once again, we counterbalanced the sign of the rewards across participants. (F) Experiments 1a and 1b were between-group designs. All four groups were trained on 400 trials (200 per task) and evaluated on 200 trials (100 per task). The groups differed in the temporal autocorrelation of the tasks during training, ranging from “blocked 200” (200 trials of one task, thus only one switch) to “interleaved” (randomly shuffled and thus unpredictable task switches). Importantly, all four groups were evaluated on interleaved test trials. The order of tasks for the blocked groups was counterbalanced across participants.

To preview our findings, we observed that, relative to interleaved training, providing humans (but not neural networks) with blocked, and therefore temporally autocorrelated, objectives promoted learning of mutually exclusive rules. Blocked training successfully prevented interference between tasks, even on a later generalization test involving a set of previously unseen tree stimuli and random interleaving over trials. This occurred even though interleaved testing should pose a particular challenge to the blocked training group, as they did not practice random and rapid task switches during training. Fitting a psychophysical model to the data, we found that blocked training promoted accurate representations of two orthogonal decision boundaries required to perform the task (i.e., to “factorize” the problem according to the two rules), whereas interleaved training encouraged humans to form a single linear boundary that failed to properly disentangle the two tasks. This benefit was greatest for those individuals whose prior representation of the stimulus space (as measured by preexperimental similarity judgments among exemplars) organized the stimuli along the cardinal task axes of leafiness and branchiness. Surprisingly, we even found evidence for the protective effect of blocked learning after rotating the category boundaries such that rules were no longer verbalizable. These findings suggest that temporally autocorrelated training objectives encourage humans to factorize complex tasks into orthogonal subcomponents that can be represented without mutual interference.

Subsequently, we trained a deep neural network to solve the same problem, learning by trial and error from image pixels alone. As expected, a standard supervised deep network exhibited catastrophic forgetting under blocked training, and we used multivariate analysis of network activations to pinpoint the source of interference to the deeper network layer. However, building on the insights from human learning, we show that pretraining the network in an unsupervised way to represent the stimulus space according to the major axes of leafiness and branchiness ameliorated (but did not eliminate) catastrophic forgetting during subsequent supervised training.

Results

In experiment 1a, adult humans (n ≈ 200) performed a “virtual gardening task” that required them to learn to plant naturalistic tree stimuli in different gardens (north vs. south, denoted by different images) (Fig. 1 B and C). Unbeknownst to participants, different features of the trees (leafiness vs. branchiness) predicted growth success (and thus reward) in either garden (Fig. 1D). Different cohorts learned to plant (classify) trees under training regimes in which gardens (tasks) switched randomly from trial to trial (Interleaved group) or remained constant over sequences of 200 trials (B200 group), 20 trials (B20 group), or 2 trials (B2 group) (Fig. 1F). All learning was guided by trialwise feedback alone; we were careful not to alert participants either to the rules or to the cardinal dimensions of the tree space (leafiness, branchiness). Our critical dependent measure was performance on a final generalization test session involving novel tree exemplars in which leafy and branchy tasks were interleaved but no feedback was provided.

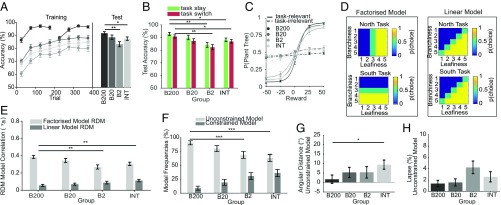
We first describe three observations that we found surprising. Firstly, the B200 group (which received the most blocked training) performed overall best during interleaved test (ANOVA: F_3,172 = 5.06, P < 0.05; B200 > Interleaved: t₉₃ = 2.32, P < 0.05, d = 0.47; B200 > B2: t₈₆ = 3.81, P < 0.001, d = 0.80) (Fig. 2A). This is striking, given the encoding specificity benefit that the rival Interleaved group should have received from the shared context during learning and evaluation (19). Secondly, the benefits of blocked training were observed even when analysis was limited to switch trials at test (ANOVA: F_3,172 = 4.59, P < 0.01; B200 > Interleaved: t₉₃ = 2.06, P < 0.05, d = 0.43; B200 > B2: t₈₆ = 3.59, P < 0.01, d = 0.76), despite the fact that participants in the B200 group had only experienced a single switch during training (Fig. 2B). We found this remarkable, given that training on task switching has previously been shown to reduce switch costs (20); our data suggest that task switching can be paradoxically facilitated without any switch practice.

Fig. 2.

Results of experiment 1a. All error bars depict SEM. (A) Training curves of mean accuracy, averaged over 50 trials, and averaged test-phase accuracy. Performance of all groups plateaued by the end of training. At test, the B200 group performed significantly better than the B2 and Interleaved groups. (B) Mean test performance on task switch and task stay trials. Even on switch trials, the B200 group outperformed the Interleaved and B2 groups, despite having experienced only one task switch during training. (C) Sigmoid fits to the test-phase choice proportions of the task-relevant (solid lines) and task-irrelevant dimensions (dashed lines). Higher sensitivity (i.e., steeper slope) to the task-relevant dimension was observed for the B200, compared with the Interleaved group. There was stronger intrusion from the task-irrelevant dimension in Interleaved compared with B200. (D) Conceptual choice models. The factorized model (Left) predicted that participants learned two separate boundaries for each task, corresponding to the rewards that were assigned to each dimension in trees space. The linear model (Right) simulated that participants had learned the same, linear boundary for both tasks, separating the trees space roughly into two halves that yielded equal rewards and penalties in both tasks. (E) Results of RDM model correlations on test-phase data. While the factorized model provided a better fit to the data for all groups, its benefit over the linear model was greater for the B200 than for the B2 and Interleaved groups. (F) Bayesian model selection for the unconstrained and constrained psychophysical models. The estimated model frequencies support the RSA findings, as we observed an interaction of group with model type. (G) Mean angular distances between true and subjective boundary, estimated by the 2-boundary model. A significantly stronger bias for Interleaved compared with B200 suggests that blocked training optimizes boundary estimation. (H) Mean lapse rates, obtained from the same 2-boundary model. There were no significant differences between groups. *P < 0.05; **P < 0.01; ***P < 0.001.

We next explored how blocked training promoted task performance in humans, using three more detailed analysis strategies. First, we plotted psychometric curves showing choice probabilities (at test) as a function of the feature values along the relevant dimension (e.g., leafiness in the leafiness task) and the irrelevant dimension (e.g., branchiness in the leafiness task). A nonzero slope along the task-irrelevant dimensions signals interference between the two categorization rules. Comparing the slopes of these fitted curves revealed that blocked learning reduced the impact of the irrelevant dimension on choice, as if B200 training prevented intrusions from the rival task (B200 < Interleaved: Z = 2.99, P < 0.01 r = 0.31; Fig. 2C). This interference might reasonably occur because participants learned an inaccurate bound, or because they were confused about which rule to use. However, a model in which participants confused the two rules with a given probability failed to explain the data (SI Appendix, Fig. S4).

Secondly, we plotted choice probabilities p(plant) at test for each level of the relevant and irrelevant dimension, to visualize the decision boundary learned in each training regime. Visual inspection suggested that, whereas B200 training allowed participants to learn two orthogonal decision boundaries that cleanly segregated trees in leafiness and branchiness conditions, after interleaved training, participants were more prone to use a single, diagonal boundary through 2D tree space that failed to disentangle the two tasks (SI Appendix, Fig. S1A). Using an approach related to representational similarity analysis (RSA) (21, 22), we correlated human choices matrices for each of the two tasks with those predicted by two different models (Fig. 2D). The first used the single best possible linear boundary in tree space (linear model), and the second used two boundaries that cleaved different compressions of the tree space optimally according to the relevant dimension (factorized model). Although the factorized model fit human data better than the linear model in all conditions, its advantage was greatest in the B200 condition (group*model interaction: B200_{tau_diff} > Interleaved_{tau_diff}: Z = 3.59, P < 0.01, r = 0.37; B200_{tau_diff} > B2_{tau_diff}: Z = 3.70, P < 0.01, r = 0.39; Fig. 2E).

Thirdly, we combined elements of these analysis approaches, fitting a family of less constrained psychophysical models (to the test data) that allowed the decision boundary angle to vary parametrically through 2D tree space, and compared model variants with either a single boundary or with one boundary for each task (2-boundary model). Each model also featured policy parameters that allowed the slopes, offset, and termination (e.g., lapse rate) of a logistic choice function to vary freely for each participant (SI Appendix, Fig. S3). After appropriately penalizing for model complexity, we subjected model fits to Bayesian model selection at the random effects level (23–25). This more principled modeling exercise confirmed the results of the RSA analysis above. Although all groups were overall better fit by the 2-boundary model variant (protected exceedance probabilities, 2-boundary vs. 1-boundary: B200: 1.0 vs. 0.0; B20: 1.0 vs. 0.0; B2: 0.69 vs. 0.31; Interleaved: 0.65 vs. 0.35), the estimated model frequencies were significantly greater for the 2-boundary over the 1-boundary model in the B200 relative to Interleaved group (group × model interaction: B200_{ef_diff} > Interleaved_{ef_diff}: Z = 4.28, P < 0.001, r = 0.44; B200_{ef_diff} > B2_{ef_diff}: Z = 4.52, P < 0.001, r = 0.48; Fig. 2F). Examining the resulting parameters from the 2-boundary model, we found that participants in the B200 condition exhibited sharper and more accurate boundaries in tree space (boundary deviance: B200 < Int: Z = 2.36, P < 0.05, r = 0.24; slope: B200 > B2: Z = 3.18, P < 0.01, r = 0.34; B200 > Interleaved: Z = 2.43, P < 0.05, r = 0.25; Fig. 2G), but not a different lapse rate (Kruskal−Wallis H_3,172 = 4.98, P = 0.17; Fig. 2H). Together, these findings suggest that blocked training helps promote two separate representations of the two rules from which the problem was composed, in a way that is robust to mutual interference. Strikingly, this protective effect of blocked training persisted under test conditions in which tasks were encountered in random succession.

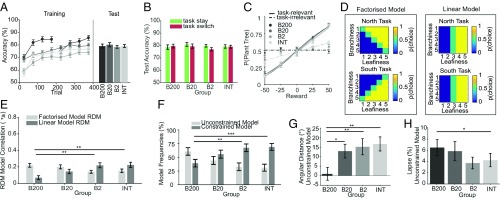
Categorization can rely on explicit rule discovery or more implicit learning of stimulus−response associations (26). Previous studies on category learning have provided evidence for an interaction of training regime (blocked vs. interleaved) and the type of categorization problem (rule-based vs. information integration) (17). To test whether the benefit of blocked training depended on the use of rule-based strategies, next we rotated the category boundaries for tasks A and B by 45° in tree space such that they lay along a nonverbalizable leafy/branchy axis (“diagonal boundary” condition) and repeated our experiment in a new cohort of participants (experiment 1b; n ≈ 200). Partially consistent with a previous report (17), we observed no significant differences in test performance among the different training groups for this “information integration” task (ANOVA on accuracy: F_3,162 = 0.25, P = 0.86; stay trials only: F_3,162 = 0.37, P = 0.78; switch trials only: F_3,162 = 0.63, P = 0.60) (Fig. 3 A and B). Interestingly, however, we still saw evidence of factorized learning in the B200 condition. This was revealed by shallower psychometric slopes for the irrelevant dimension at test (B200 < Interleaved: Z = 3.11, P < 0.01, r = 0.34; B200 < B2 Z = 2.91, P < 0.01, r = 0.32; Fig. 3C), and a better fit to representational dissimilarity matrices (RDMs) for the factorized task model in the B200 condition, both relative to Interleaved (Z = 3.10, P < 0.01, r = 0.33) and B2 (Z = 3.45, P < 0.01, r = 0.38) training conditions (Fig. 3E). Moreover, as revealed by Bayesian model comparison, the 2-boundary model fit the data best in the B200 condition, but the more constrained 1-boundary model explains the data best in the interleaved condition (protected exceedance probabilities 2-boundary vs. 1-boundary: B200: 0.59 vs. 0.41, B20: 0.47 vs. 0.53, B2: 0.25 vs. 0.75, Interleaved: 0.17 vs. 0.83; group × model interaction of estimated frequencies: B200_{ef_diff} > Interleaved_{ef_diff}: Z = 3.55, P < 0.001, r = 0.38; B200_{ef_diff} > B2_{ef_diff}: Z = 3.01, P < 0.01, r = 0.33; Fig. 3F). Once again, using the unconstrained (2-boundary) psychophysical model (as for the “cardinal” condition above), we observed lower estimates of boundary error in the B200 condition (B200 < Interleaved Z = 2.86, P < 0.01, r = 0.31; B200 < B2 Z = 2.63, P < 0.01, r = 0.29; Fig. 3G), but higher lapse rates (B200 > Interleaved Z = 2.01, P < 0.05, r = 0.22; Fig. 3H). Thus, it seems that, under nonverbalizable boundaries, blocked training promotes learning of the effective boundary, but this benefit only offsets (but does not reverse) a nonspecific cost incurred by random task lapses. The reason for these lapses is unclear. Reasoning that participants might forget the task trained first to a greater extent in the diagonal condition, we plotted performance separately for task 1 (i.e., that experienced first) and task 2 (second) in the cardinal and diagonal cases. However, forgetting did not differ (SI Appendix, Fig. S2). It may be that the limited experience with task switching during training is more detrimental to performance when rules are nonverbalizable (26).

Fig. 3.

Results of experiment 1b. All error bars depict SEM. (A) Training curves and averaged test-phase performance. At the end of the training, performance plateaued for all groups. At test, in contrast to experiment 1a, there was no significant difference in performance between groups. (B) No performance difference between task switch and stay trials. (C) Sigmoid fits to the test-phase choice proportions of the task-relevant (solid lines) and task-irrelevant dimensions (dashed lines). No sensitivity differences were observed along the relevant dimension. However, once again, there was stronger intrusion from the task-irrelevant dimension for Interleaved compared with B200. (D) Conceptual model RDMs. The same reasoning applies as described in Fig. 2D. (E) RDM model correlations at test. Despite equal test performance, the relative advantage of the factorized over the linear model is stronger for B200 than for B2 or Interleaved, suggesting that blocked training did result in better task separation, despite equal performance. (F) Bayesian model comparison between unconstrained and constrained models supports the RSA findings. The unconstrained model fits best in the B200 group, but the constrained model fits best to the Interleaved group. (G) Mean bias of the decision boundary obtained by the unconstrained model. The bias was smallest for B200, indicating that this group estimated the boundaries with high precision. (H) Mean lapse rates. The B200 group made a higher number of unspecific random errors during the test phase, compared with the Interleaved group, which explains equal test performance despite evidence for successful task factorization. We suspect that limited experience with task switches is more detrimental when rules are nonverbalizable. Asterisks denote significance: *P < 0.05; **P < 0.01; ***P < 0.001.

Our favored explanation for these findings is that blocked training allows humans to compress the high-dimensional image onto distinct, rule-specific discrimination axes (see Discussion). In other words, blocked training promotes an understanding of the structure of the task space as being primarily dictated by the leafiness and branchiness of the trees. If so, then it follows that participants who are a priori predisposed to represent the trees according to orthogonal axes of leafiness vs. branchiness might be most able to benefit most from such a strategy. We might thus expect these participants to learn disproportionately faster under blocked training, especially when the task-specific category boundaries lie on the cardinal axes of the stimulus feature space.

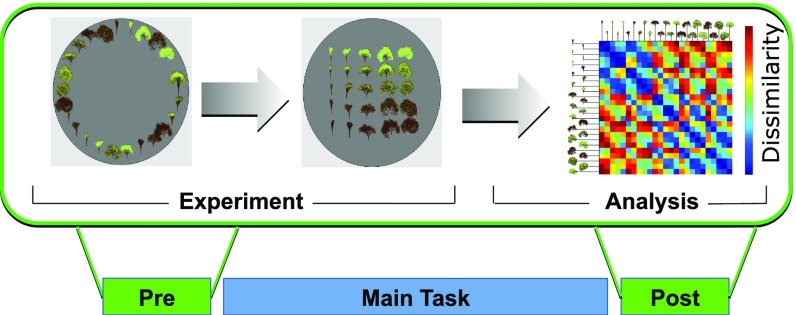
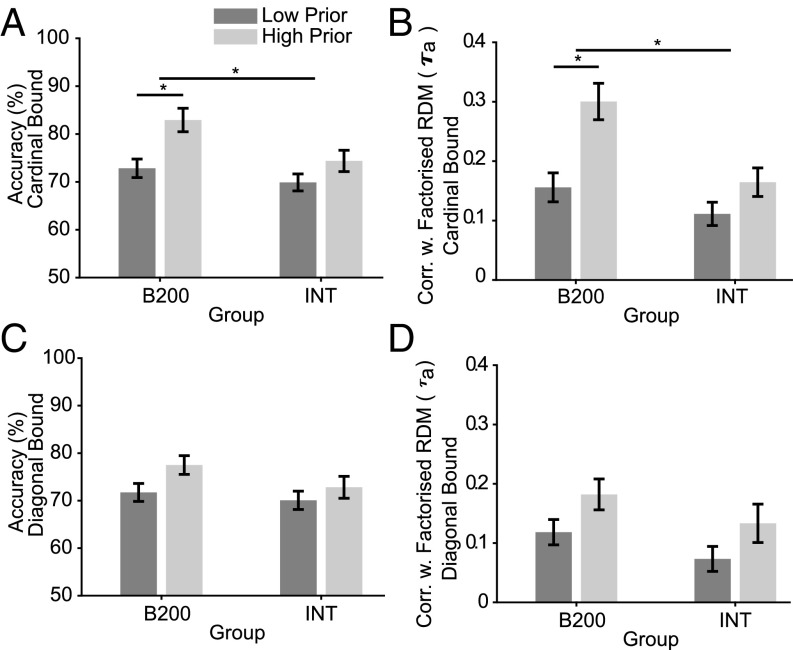
Next, thus, we repeated our experiments on a new participant cohort who classified the stimuli once again according to cardinal (experiment 2a) and diagonal (experiment 2b) boundaries, but this time we measured participants’ representation of tree space using a preexperimental and postexperimental “arena” task, in which trees were manually arranged according to their similarity or dissimilarity within a circular aperture (27, 28). This allowed us to estimate the extent to which the a priori prestimulus arrangement matched the 2D leafy vs. branchy grid encountered in the subsequent classification task(s), and to quantify participants’ prior sensitivity to stimulus variations along the two major feature axes of leafiness and branchiness (Fig. 4). We computed a single quantity, that we refer to as a “grid prior,” that captured the extent to which the reported pairwise dissimilarities align with those predicted by a 2D grid-like arrangement of the stimuli on the screen (although our metric did not require participants to align the trees precisely in a grid, but merely to organize the trees along orthogonal axes of leafiness and branchiness). We then tested how this grid prior (measured from preexperimental data alone) interacted with training regime to predict subsequent test performance.

Fig. 4.

Task design, experiment 2. Before and after the main experiment (identical to experiment 1), participants engaged in a dissimilarity rating arena task, in which they had to rearrange trees via mouse drag and drop inside a circular aperture to communicate subjective dissimilarity (see Methods). We obtained one RDM per subject and phase, depicting how dissimilarly the trees were perceived. Correlation of the RDMs from the “Pre” with a model RDM that assumed perfect grid-like arrangement (branchiness × leafiness) yielded a grid prior (Kendall tau) for each participant.

Although performance was overall poorer in this cohort, the results of the main task were similar to those of experiments 1a and 1b, with stronger evidence for factorized learning under B200 than interleaved training from the RSA analysis, as indicated by fits to choice matrices (experiment 2a: B200 > Interleaved: Z = 3.21, P < 0.001, r = 0.27; experiment 2b: B200 > Interleaved Z = 2.31, P < 0.05, r = 0.23), a significant interaction effect of group and model on the estimated model frequencies (experiment 2a: B200_{ef_diff} > Interleaved_{ef_diff}: Z = 4.77, P < 0.0001, r = 0.41; experiment 2b: B200_{ef_diff} > Interleaved_{ef_diff}: Z = 2.82, P < 0.01, r = 0.28) and estimates of boundary error of the 2-boundary model for cardinal boundaries (experiment 2a: B200 < Interleaved: Z = 2.56, P < 0.05, r = 0.22; experiment 2b: B200 < Interleaved Z = 1.97, P < 0.05, r = 0.19) from the psychophysical model (SI Appendix, Fig. S5). However, of primary interest for this experiment was how participants’ prior representation of the stimulus space interacted with training regime to promote learning. Splitting participants according to the median grid prior, in experiment 2a (cardinal boundaries), we found that those participants who tended to a priori represent leafiness and branchiness orthogonally exhibited more benefit from B200 training than those who did not (B200_highPrior > B200_lowPrior: Z = 2.871, P < 0.005, r = 0.35; Int_highPrior = Int_lowPrior: Z = 1.692, P = 0.09; Fig. 5A). The finding remained significant when we used an analysis of covariance (ANCOVA) to estimate interactions between grid prior and training on performance (grid prior: F_1,134 = 13.54, P < 0.001; group: F_1,134 = 6.6, P < 0.05; grid prior*group: F_1,134 = 6.28, P < 0.05). Moreover, signatures of factorized learning, including the fits of the factorized model to human choice matrices, were more pronounced for the high grid prior group under B200 but not interleaved training (B200_highPrior > B200_lowPrior: Z = 3.12, P < 0.01, r = 0.38; Int_highPrior = Int_lowPrior: Z = 1.55, P = 0.06; ANCOVA: Grid prior: F_1,134 = 22.36, P < 0.0001; Group: F_1,134 = 12.18, P < 0.001; grid prior*group: F_1,134 = 8.16, P < 0.01; Fig. 5B). By contrast, in the diagonal boundary case (experiment 2b), we observed generally higher performance and task factorization for those participants who had a higher grid prior, but no interaction with training regime (accuracy: highPrior_pooled > lowPrior_pooled, Z = 2.052, P < 0.05, r = 0.20; factorization: highPrior_pooled > lowPrior_pooled, Z = 1.97, P < 0.05, r = 0.194; ANCOVA on accuracy: grid prior: F_1,99 = 5.96, P < 0.02, group: F_1,99 = 1.5, P = 0.223, grid prior*group: F_1,99 = 0.31, P = 0.579; ANCOVA on correlations with factorized model: grid prior: F_1,99 = 9.15, P < 0.01; group: F_1,99 = 2.07, P = 0.15; grid prior*group: F_1,99 = 0.01, P = 0.91; Fig. 5 C and D).

Fig. 5.

Results of experiment 2. All error bars depict SEM. (A) Experiment 2a (cardinal boundary): median split of test performance. The benefit of blocked training was significantly stronger for participants with a higher prior on the structure of the trees space. (B) Experiment 2a: median split of correlations between choice probabilities and factorized model (Fig. 1D). Under blocked training, participants with a strong prior showed significantly stronger evidence of task factorization. (C) Experiment 2b (diagonal boundary). There was no difference between low and high grid priors on mean test accuracy. (D) Experiment 2b. The correlation coefficients of the factorized model did not differ between groups. An ANCOVA (see Results) revealed a main effect of the prior on task factorization, but no interaction with group. *P < 0.05.

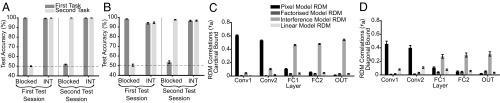
Next, for comparison with humans, we trained deep artificial neural networks to perform the task. In experiment 3, convolutional neural networks (CNNs) were separately trained on the cardinal and diagonal tasks under either blocked or interleaved training conditions, and classification performance was periodically evaluated with a held-out test set for which no supervision was administered. On each “trial,” the networks received images of task-specific gardens onto which trees were superimposed as input (analogous to the content of the stimulus presentation period in the human experiments) and were optimized (during training) with a supervision signal designed to match the reward given to humans (SI Appendix, Fig. S6A). As expected, under interleaved training, the network rapidly achieved ceiling performance at test on both tasks. However, under blocked training, network performance dropped to chance after each task switch (Fig. 6 A and B), in line with an extensive literature indicating that such networks suffer catastrophic interference in temporally autocorrelated environments (4, 29). Using an RSA approach, we correlated the layer-wise activity patterns with model RDMs that either assumed pixel value encoding (pixel model), category encoding of both tasks (factorized model), category encoding of the most recent task only (interference model), or a linear boundary through feature space (linear model; see Methods for details). Unit activation similarity patterns in the early layers reflected the pixelwise similarity among input images, whereas deeper layers exhibited a representational geometry that flipped with each new task, as predicted by the interference model, and indicative of catastrophic forgetting (Fig. 6 C and D).

Fig. 6.

Results of experiment 3. All error bars depict SEM across independent runs. (A) Experiment 3a (cardinal boundary): mean performance of the CNN on independent test data, calculated after the first and second half of training, separately for the first and second task and blocked vs. interleaved training. Interleaved training resulted quickly in ceiling performance. In contrast, the network trained with a blocked regime performed at ceiling for the first task, but dropped back to chance level after it had been trained on the second task, on which it did also achieve ceiling performance. (B) Experiment 3b (diagonal boundary): mean test performance. Similar patterns as for the cardinal boundary were found: Blocked training resulted in catastrophic interference, whereas interleaved training allowed the network to learn both tasks equally well. Interestingly, the CNNs performed slightly worse on the diagonal boundary, as did our human participants. (C) Experiment 2a, blocked training. Layer-wise RDM correlations between RDMs were obtained from activity patterns and model RDMs. The correlation with the pixel dissimilarity model decreases with depth, whereas the correlation with the catastrophic interference model increases. Neither the factorized nor the linear model explain the data well, indicating that blocked training did not result in task factorization or convergence toward a single linear boundary. (D) Experiment 2b, blocked training. Again, correlations with the pixel model decrease and correlations with the interference model increase with network depth.

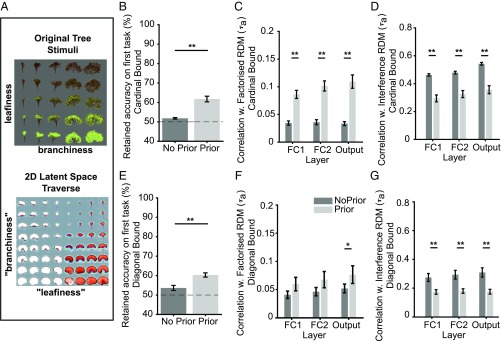
Our investigations of human task learning suggested that prior knowledge of the structure of the stimulus space allows humans to learn factorized task representations that are protected from mutual interference. We thus wondered whether pretraining the CNN to factorize the task space appropriately would mitigate the effect of catastrophic interference. To achieve this, we trained a deep generative model [a beta variational autoencoder or β-VAE (30)] on a large dataset of trees drawn from the 2D leafy × branchy space (experiment 4a), but without the gardens as contextual cues. The autoencoder learned to reconstruct its inputs after passing signals through two “bottleneck” nodes, which encourages the network to form a compressed (2D) representation of the latent stimulus space (SI Appendix, Fig. S6B). Unlike a standard VAE, which typically learns an unstructured latent representation, the β-VAE can learn disentangled and interpretable data generating factors, similar to a child who acquires structured visual concepts through passive observation of its surroundings (30). To verify that the network had learned appropriately, we traversed the latent space of activations in the two bottleneck units and visualized the resulting tree reconstructions, revealing a 2D embedding space that was organized by leafiness × branchiness (Fig. 7A).

Fig. 7.

Results of experiment 4. (A) Experiment 4a. (Top) Example of tree images used for training the autoencoder. (Bottom) The 2D latent space traversal of trained autoencoder (see Methods). For each x,y coordinate pair, we plot a tree image sampled from the generative model, revealing that the autoencoder learned a disentangled low-dimensional representation of branchiness and leafiness. (B) Experiment 4b (cardinal), blocked training: comparison of performance on the first task after training on the second task, between the model from experiment 3 (“vanilla” CNN, without priors) and the model from experiment 4 (“pretrained” CNN, with priors from VAE encoder). Unsupervised pretraining partially mitigated catastrophic interference. (C) Experiment 4b (cardinal), blocked training: comparison of layer-wise RDM correlations with factorized model for CNN, between networks without and with unsupervised pretraining. Pretraining yielded stronger correlations with the factorized model in each layer. (D) Experiment 4b (cardinal), blocked training: comparison of layer-wise RDM correlations with interference model. Likewise, pretraining significantly reduced correlations with the catastrophic interference model in each layer. (E) Experiment 4b (diagonal), blocked training: mean accuracy on the first task after training on the second task, for vanilla and pretrained CNN. Again, pretraining mitigated catastrophic interference. (F) Experiment 4b (diagonal), blocked training. RDM correlations with factorized model only increased in the output layer. (G) Experiment 4b (diagonal), blocked training. RDM correlations with the interference model increased significantly in each layer. All error bars indicate SEM across independent runs. *P < 0.05; **P < 0.01.

Next, thus, in experiment 4b, we retrained the CNN of experiment 3, again on blocked and interleaved curricula, but using the trained β-VAE encoder from experiment 4a as a feature extractor for the main task. We provided the output of the encoder from the β-VAE an input to the first fully connected layer in the CNN, thereby allowing it to utilize similar prior knowledge about the structure of the inputs, as our human participants seemed to do (SI Appendix, Fig. S6C). This approach mirrors that which occurs during human development, in which rich knowledge of the statistical structure of the world is learned before the rules guiding behavior are explicitly taught (31). The effect of catastrophic interference in the CNN, although still present, was reduced by this intervention. More precisely, the network retained some knowledge of previous tasks it had experienced during blocked training (Fig. 7 B and E), leading to overall improved performance in this condition relative to the vanilla CNN for the cardinal as well as the diagonal group (test accuracy, blocked training: cardinal prior CNN > vanilla CNN Z = 5.50, P < 0.001, r = 0.66, diagonal priorCNN > vanilla CNN Z = 2.83, P < 0.01, r = 0.34). Using RSA to investigate representational geometry in the network, we found that using the autoencoder as a feature extractor encouraged the network to represent the task in a factorized manner, with RDMs showing reduced correlations with the interference model and increased correlations with the factorized model in both fully connected layers [correlation with factorized model for prior CNN > vanilla CNN, all P values < 0.01 for both FC layers (r = 0.66) and output layer (r_fc1 = 0.66, r_fc2 = 0.66, r_out = 0.54); correlation with interference model for vanilla CNN > prior CNN, all P values < 0.001 (r_fc1 = 0.68, r_fc2 = 0.53, r_out = 0.56); Fig. 7 C and D]. Interestingly, in the diagonal boundary case, the advantage for the factorized model was only significant in the output layer (Z = 2.2, P < 0.05, r = 0.26; Fig. 7F), but we observed reduced correlations with the interference model in all three earlier layers (all P values < 0.01, r_fc1 = 0.41, r_fc2 = 0.41, r_out = 0.40; Fig. 7G). We take these data as a proof-of-concept that unsupervised learning of the statistical structure of the world may be one important factor for promoting continual task performance in both humans and neural networks.

Discussion

Humans can continually learn to perform new tasks across the lifespan, but the computational mechanisms that permit continual learning are unknown. Here, we tackled the problem of understanding how humans learn to classify high-dimensional stimuli according to two orthogonal rules, from scratch and without instruction. We first show that humans benefit from blocked training conditions, in which task objectives are presented in a temporally autocorrelated fashion, even when later test stimuli are interleaved between trials, a scenario that was not experienced during initial training. This result poses a challenge for standard computational models of learning, including current neural network accounts, where test performance is typically heavily determined by the level of exposure to equivalent training examples (19, 32). Our detailed behavioral analysis offers some insight into how blocked training promotes continual task performance in humans. Under blocked training, participants learned the two category boundaries more accurately and with reduced mutual interference, as revealed by a psychophysical model which separately modeled errors arising from boundary inaccuracy and those incurred by generalized forms of forgetting. Secondly, those participants with a prior bias to represent the trees according to their orthogonal leafiness and branchiness enjoyed greatest benefit from blocked training, but only when the rules mapped onto the cardinal axes of the branch × leaf space, and not in the diagonal case. This benefit exceeded that conferred during interleaved training, ruling out generalized explanations for this phenomenon. Our favored interpretation is that continual learning is facilitated when participants have learned a low-dimensional embedding of the stimulus space that maps cleanly onto the rules which could plausibly be useful for behavior (in this case, leafy vs. branchy classification), and that blocked training promotes such a representation in a way that interacts with prior knowledge.

A rich literature has sought to understand how visual representations are formed and sculpted during category learning. One prominent theme is that, during training, expertise emerges as high-dimensional (or “integral”) representations of a stimulus are disentangled into more separable neural codes (33–35). However, the precise computational mechanisms by which this occurs remain unresolved. Several models have assumed that unsupervised processes allow decision-relevant features to be appropriately clustered into categories, explaining why feedback-driven category learning is easier when stimuli already differ on fewer dimensions (as in “rule-based” tasks), or exhibit decision-relevant features that are a priori salient (36). However, most previous models have been applied to tasks involving clearly instructed rules, or artificial stimuli in which dimensions were clearly segregable, and thus involve limited state spaces which are prepopulated by the features or dimensions manipulated by the researchers. Our modeling approach is different. We tackled a problem related to that faced by the mammalian visual system, i.e., how to learn compressed representations from atomistic features (e.g., image pixels) in a way that enhanced continual category learning in a network of neurons. Nevertheless, our work draws on extant themes in the past literature. For example, our use of a variational autoencoder as a feature extractor builds on the appeal to unsupervised methods but extends these approaches to the more biologically plausible case where features are image pixels and clusters are extracted through multiple hierarchically ordered layers in a densely parameterized neural network.

However, our main finding, namely the representational robustness conferred by a blocked curriculum, remains unexplained by existing category learning models. One existing suggestion is that attentional mechanisms are central to this process. Blocked training may allow participants to orient attention more effectively to the relevant dimension(s), or to actively filter or suppress the irrelevant dimension, facilitating dimension segregation for leafiness/branchiness. Indeed, previous work has suggested that the performance benefits of blocked training are limited to rule-based categorization, perhaps because it is easier to orient attention to dimensions that are a priori separable according to a verbalizable rule (17). Had we examined percent test accuracy alone, we might have drawn similar conclusions from our data, because there was no overall test benefit for blocked regimes under the diagonal (i.e., information integration) condition. However, a model-based analysis disclosed that humans nevertheless tended to factorize the relevant boundaries more cleanly after blocked training on diagonal as well as cardinal boundaries (Fig. 3G). Thus, any mechanistic account that appeals to attention will need to explain why task factorization occurs for both verbalizable and nonverbalizable rules. For example, it is possible that switching between two reward functions in the interleaved learning provokes a generic processing cost in humans that is lower or absent in the blocked condition (37). Another possibility is that effects of blocking vs. interleaving are related to the spacing of conditions in time (11), which, in turn, may be due to the relative attentional salience of items experienced at longer lags. More generally, attention mechanisms are widely thought to play a prominent role in controlling the allocation of neural resources (or gain) in a way that allows task sets to be effectively segregated (35), and yet are notably absent from our neural network account. Understanding how the executive processes that characterize human learning may be effectively incorporated into deep learning models is a frontier topic in machine learning and may be an important future approach to bridging the performance gap in continual learning between humans and machines.

Our work is related to previous suggestions that temporally structured contextual information (e.g., that available in our blocked north or south gardens) is clustered into “parcels” that are tagged by their temporal context (38). Indeed, studies of expert knowledge (39) and laboratory-based categorization (40, 41) show that the task context is an excessively salient cue for retrieval, as if participants partitioned their knowledge between tasks even when it was unnecessary or detrimental to do so (42). Moreover, humans have a strong tendency to infer contextual structure in an otherwise unstructured task, pointing to the existence of a mechanism that structures knowledge strongly according to local context (43). Lastly, previous work on concept learning suggests that blocking such that instances of concepts occur in close proximity aids learning of these concepts and even outperforms blocking based on perceptual similarity (44).

These findings, and ours, raise the critical question of how knowledge is partitioned among tasks in cortical areas, such as the prefrontal cortex, that subserve executive control. We did not investigate neural signals, and so it is challenging to draw strong inferences about how the task representations formed by blocked and interleaved learning may differ. However, single-cell recordings in the macaque have suggested that after extensive (interleaved) training, neurons in prefrontal cortex form high-dimensional representations of task variables that are mixed across the neuronal population (dimension expansion), allowing efficient decoding of relevant actions via appropriate linear readout (45, 46). Mixed selectivity for distinct tasks will naturally similarly emerge in supervised neural networks after training on randomly intermixed examples, but not after blocked training, where, instead, representations oscillate periodically in line with the slowly changing objectives (4). One possibility is that previously observed dimension expansion occurs only after extensive interleaved training (e.g., over months or years) that is a hallmark of animal training regimes and human development, but not most laboratory-based studies involving humans. We think it is likely that blocked training in humans will facilitate the emergence of compressive representations formed by our unsupervised network, and these may be visible in human neuroimaging data. Indeed, there are recent hints that category learning reduces the dimensionality of blood oxygenation level-dependent (BOLD) signals in decision-related regions (47). However, this remains to be fully tested by future studies.

Our work uses insights from human psychology to enhance the performance of artificial neural networks. Our goal here was not to achieve state-of-the-art performance in machine learning classification using the tree dataset. Indeed, as we show, ceiling performance on our task can easily be achieved with a standard CNN via interleaved training. Rather, we were interested in understanding the representations formed by the network during blocked training, which exhibits the temporal autocorrelation typical of naturalistic environments, and examining how these might be altered by exposure to unsupervised pretraining that encouraged the network to form appropriate embeddings of the 2D tree space—the same grid prior that allowed humans to benefit most from blocked training. We found that using a deep generative model as a feature extractor for the CNN partially guarded against catastrophic interference, and encouraged the preservation of representations of task A when later performing task B. One interpretation of this finding is that human continual learning is scaffolded by extensive unsupervised training that confers an understanding of the statistics of the world before any rule learning. However, we note several caveats to this finding. Firstly, comparing the performance of adult humans—who bring a lifetime of visual experience and rich conceptual knowledge to the laboratory—with neural networks that learn tabula rasa is always a challenge. For example, by necessity, our neural networks were trained with many more examples than the humans, because they began the task with weights initialized to random. Secondly, we are conscious that our experiment tested only conditions in which a single stimulus set is categorized according to two orthogonal rules; further work will be required to see whether the findings reported here from humans and neural networks generalize to different experimental settings, for example where there are multiple stimulus sets, or a symmetric categorization rule (rather than “plant vs. no plant”) is employed (14). Finally, we acknowledge that our pretraining intervention only mitigated, but did not remove, the effect of catastrophic interference. Indeed, it is very likely that other mechanisms, including weight protection schemes that allow new learning to be allocated to synapses according to their importance for past learning, will also play a key role (3, 48). A promising avenue for future research may be to understand how structure learning and resource allocation schemes interact.

Methods

An expanded version is presented in SI Appendix.

Participants.

We recruited a large cohort (n = 768) of adult participants via Amazon Mechanical Turk. We set a criterion of >55% accuracy at test for inclusion in the analysis and continued to recruit participants until we reached at least n = 40 in each training group; In total, we included 352 male and 231 female participants (SI Appendix, Table S1), with a mean age of 33.33 y (range 19 y to 55 y); ages did not differ reliably between groups (SI Appendix, Table S2).

All participants provided consent before taking part, and the studies were approved by the University of Oxford Central University Research Ethics Committee (approval R50750/RE001).

Stimuli.

Trees were generated by a custom fractal tree generator and varied parametrically in five discrete steps along two feature dimensions, spanning a 2D space of leafiness × branchiness. For human studies and neural network simulations, we created independent training and test sets of trees for each level of branchiness and leafiness (5 × 5 levels). The same trees were shown for both tasks. Different trees were used for training and test to prevent rote learning.

Task and Procedure.

Experiments 1 and 2 were run online in forced fullscreen mode. All experiments began with written instructions and consisted of a training phase (400 trials) and a test phase (200 trials). In both phases, participants viewed a tree in one of two contexts (north and south gardens) and decided whether to plant it or not. They received feedback (points) according to how well it grew. During both training and test for experiments 1a and 2a, the tree’s leafiness determined how well it grew in one context, and branchiness determined its growth in the other (cardinal boundary). In experiments 1b and 2b, the decision boundary was rotated by 45°, to align with the diagonal axes of the branch × leaf stimulus space, so that growth success depended jointly on leafiness and branchiness (diagonal boundary). We equated the number of presentations of each condition (leafy level [5] × branchy level [5] × context [2]). In experiment 2, a further task that involved rearranging trees in a circular arena according to their similarity was added before and after the main task.

In experiment 1, we trained participants in four conditions, each involving 200 north and 200 south gardens in different order. In the interleaved condition, gardens were randomly interleaved over trials. In the B2, B20, and B200 conditions, gardens remained constant over 2, 20, or 200 trials. In experiment 2, we included only the B200 and interleaved training conditions. All groups were evaluated with a randomly interleaved test session (100 instances of each).

RSA.

We calculated p(plant) as a function of every level of leafiness × branchiness, and then computed an RDM expressing the dissimilarity (in average accuracy) between each pair of leaf × branch level. We compared these to model-predicted RDMs that were generated to match a theoretically perfect observer (model 1) or an observer who learned the best possible single linear boundary through the 2D space and applied it to both tasks (model 2).

Psychophysical Model.

Each stimulus was represented in terms of its distance to a decision boundary with an angle φ. This value was converted to a choice probability via a logistic function with slope s, bias b, and lapse parameter ε (SI Appendix, Fig. S3). We compared two variants of this model. An unconstrained model, which had two boundaries and two logistic functions with different slope, one for each task (eight parameters), and a constrained model with only one boundary and one slope (four parameters). The two models were fit to the human data via maximum likelihood estimation. We compared the best-fitting parameters across groups using nonparametric statistics. Model comparisons were conducted with random effects Bayesian model selection.

Neural Network Simulations.

All networks consisted of several convolutional and fully connected layers arranged in a feed-forward architecture. They received RGB images as input. In experiment 3, the network was trained in online mode (one sample per time) on 10,000 trials per task, which were randomly sampled from the training data and superimposed onto the contextual cues (gardens). We trained the networks on blocked and interleaved curricula. Test performance on both tasks was assessed on independent data (10,000 trees) after the first and second half of the training session. We collected 20 independent runs for each group. In experiment 4a, the β-VAE was trained until convergence on the training data. We then replaced the convolutional layers of the experiment 3 network with the trained encoder and froze the weights, such that training on the task took only place in the two fully connected layers.

Statistical Tests.

We tested for significance at the group level using standard (non) parametric tests. We calculated Cohen’s d and z/sqrt(N) as measures of effect size for parametric and nonparametric post hoc tests, respectively.