Advancing front of old-age human survival

Significance

Old-age mortality decline has driven recent lifespan increases, but there is no agreement about the age pattern of old-age deaths. For example, some argue that old-age deaths should become compressed at advanced ages, and others argue that old-age deaths should become more dispersed with age. Here we show, for five decades in 20 developed countries, that old-age survival follows an advancing front, like a traveling wave. We make and test several predictions that support the existence of this front. Our unexpected result underscores the plasticity of old-age human mortality, with deaths steadily delayed as societies develop, and supports an ongoing increase in the age of transition to disability. We find no evidence of an impending limit to human lifespan.

Abstract

Old-age mortality decline has driven recent increases in lifespans, but there is no agreement about trends in the age pattern of old-age deaths. Some argue that old-age deaths should become compressed at advanced ages, others argue that old-age deaths should become more dispersed with age, and yet others argue that old-age deaths are consistent with little change in dispersion. However, direct analysis of old-age deaths presents unusual challenges: Death rates at the oldest ages are always noisy, published life tables must assume an asymptotic age pattern of deaths, and the definition of “old-age” changes as lives lengthen. Here we use robust percentile-based methods to overcome some of these challenges and show, for five decades in 20 developed countries, that old-age survival follows an advancing front, like a traveling wave. The front lies between the 25th and 90th percentiles of old-age deaths, advancing with nearly constant long-term shape but annual fluctuations in speed. The existence of this front leads to several predictions that we verify, e.g., that advances in life expectancy at age 65 y are highly correlated with the advance of the 25th percentile, but not with distances between higher percentiles. Our unexpected result has implications for biological hypotheses about human aging and for future mortality change.

Longer lives are an achievement (1) but also pose individual and social challenges (2, 3). In the last few decades, increases in human longevity have been driven by reductions in mortality at older ages (4) in contrast to the earlier importance of declining infant and child mortality (5). Thus, mortality at older ages, here treated as synonymous with postretirement ages (ages 65+ y), is increasingly important, but the age pattern of old-age deaths remains hotly debated. If lifespans are approaching a limit [based on biological hypotheses (6) or on analyses of the oldest ages at death (7)], death should gradually become compressed toward the most advanced ages near the limit. If long life depends on endowments [e.g., economic (8) or genetic (9)], the oldest deaths should represent the “best” endowments and over time become distanced from earlier deaths. But if long life is driven by decreases in old-age disability (10) and by medical advances (11) that are widely available, there may be little or no change in the age pattern of old-age deaths.

However, direct analyses of old-age deaths face unusual challenges. First, in any year the oldest ages are always reached by the fewest survivors so corresponding death rates are noisy. That stochastic noise remains even when data are collected to minimize or eliminate any systematic error (12). Second, published life tables assume a maximum age and an age pattern of oldest deaths, even though neither is known (13). Third, the definition of “old age” is changing: e.g., Japanese females had an $\sim$80% probability of living past age 60 y in 1960, past age 70 y by 1977, and past age 80 y by 2011 (13). Partly as a result, previous work has focused on the compression of adult deaths (14), on deaths near a modal adult age (15, 16), or on oldest death records (12, 17). Here we use percentiles [extending their demographic use (14)] to overcome many of these problems and robustly examine the age pattern of old-age mortality.

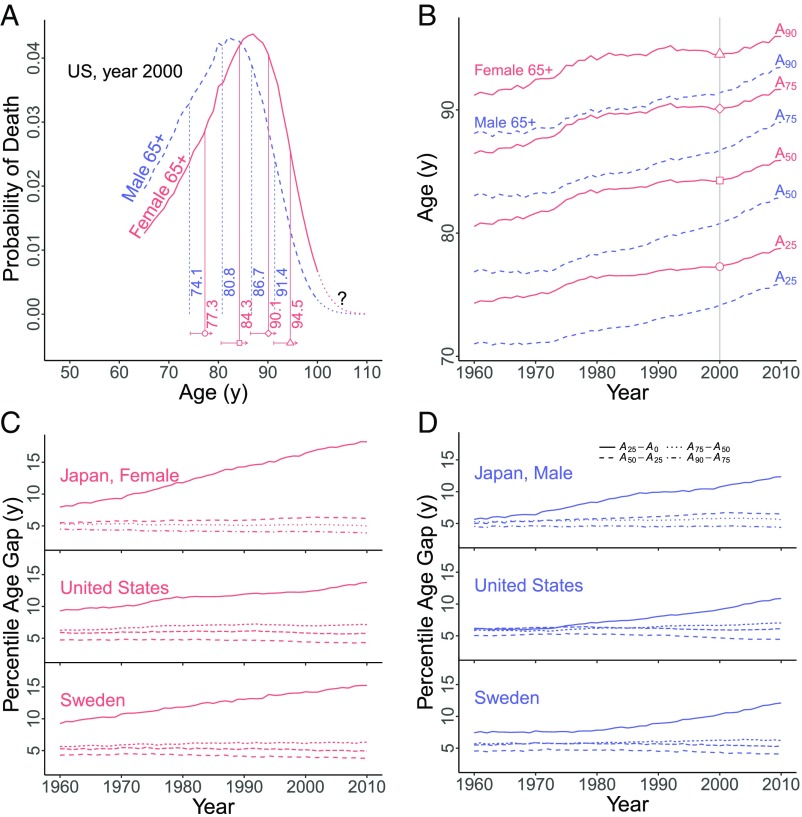
Annual life tables [female and male, 1960–2010 (13)] (Materials and Methods) provide age-specific death rates for each sex and year. To focus on old-age deaths we consider individuals in each year who are alive at age 65 y and thereafter experience death rates for that year: The age by which $q$% of such individuals would die is called $A_q$ (Materials and Methods). Thus, we use period death rates and not cohort death rates. The ages $A_q$ are percentiles of the period death distribution (with $A_0=65$), as illustrated in Fig. 1A for US males (blue) and females (red) using period death rates in the year 2000. Fig. 1A shows that males would die at younger ages: e.g., at 2000 death rates, the 25th percentile $A_{25}$ is 74.1 y for males but 77.3 y for females, while the 90th percentile $A_{90}$ is 91.4 y for males but 94.5 y for females. Over calendar time, all percentiles are expected to move to older ages as lives lengthen, but their relative locations depend on the shape of old-age deaths. For a simple example, percentiles for a narrow distribution have to be closer together than for a wider distribution. For another example, if the difference $\left(A_{90}-A_{75}\right)$ increases faster than $\left(A_{75}-A_{50}\right)$, we expect a selective advantage enjoyed by only the longest lived.

Fig. 1.

(A) Probabilities of death at ages past 65 y for US females, red solid lines, and males, blue dashed lines, using death rates in year 2000. Question mark indicates oldest ages with uncertain death rates. Vertical (solid, dashed) lines mark corresponding 25th, 50th, 75th, and 90th percentiles of death. Horizontal solid arrows show movements from 1960 to 2010 of the $A_q$; symbols on arrows mark year 2000. (B) Changes in $A_{25},A_{50},A_{75},A_{90}$ for US females, red solid lines, and males, blue dashed lines; symbols mark year 2000. (C and D) Interval $\left(A_{25}-65\right)$ and between consecutive percentiles $A_q$ (for $q=$ 25, 50, 75, 90) for Japan, the United States, and Sweden (Top, Middle, and Bottom). (C) Females (red). (D) Males (blue). Only $\left(A_{25}-65\right)$ rises steadily. All other intervals show little long-term trend and small annual fluctuations.

Percentiles have another virtue: Given $q$, the corresponding $A_q$ is computed forward from age 65 y and so is unaffected by later deaths. The question mark in Fig. 1A indicates that, for each year, uncertainty about the location of percentiles beyond the 90th increases as one probes older ages. For this reason, much of our analysis stops at the 90th percentile, although we do provide information for higher percentiles. Note from our example (Fig. 1A) that stopping at the 90th percentile does not mean that we stop at age 90 y.

Results

Percentiles increased for US females over five decades, as shown in Fig. 1B for the 25th, 50th, 75th, and 90th percentiles ($A_{25}$, $A_{50}$, $A_{75}$, and $A_{90}$), albeit with annual fluctuations. But surprisingly, the age intervals between adjacent percentiles appear nearly constant, suggesting that the period distribution of old-age female deaths had nearly the same shape for five decades. Compared with US females, age percentiles for US males changed at different rates (Fig. 1B), but here too age intervals between adjacent percentiles appear nearly constant for five decades. These observations led to a comparison of Japan, Sweden, and the United States (Fig. 1 C and D). For each country and sex, the age percentile $A_{25}$ moves steadily away from age 65 y (i.e., the age $A_0$), but the age intervals between adjacent higher percentiles change little and have only small annual fluctuations, again suggesting a stable shape for old-age deaths.

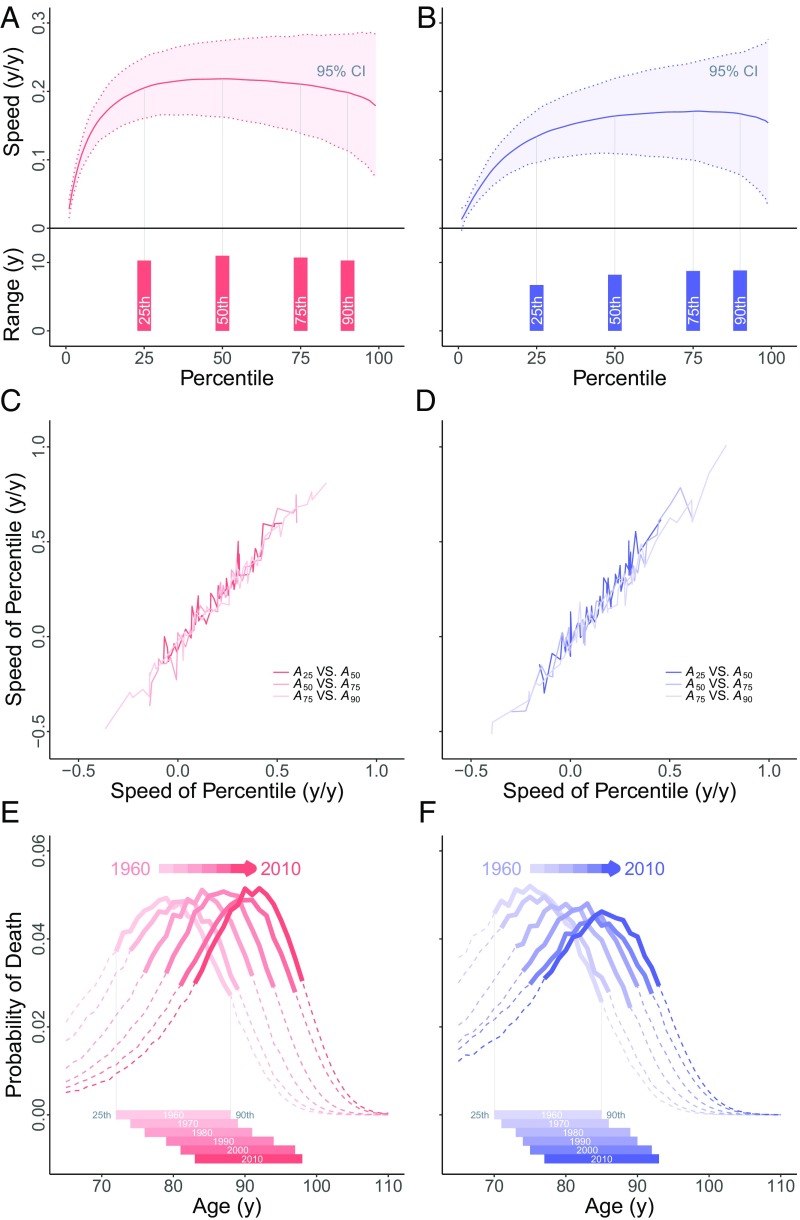
Next, we examined annual speeds (change over a year) and long-term speeds (the average of the annual speeds from 1960 to 2010) for age percentiles at 1% intervals, i.e., $A_1,A_2,\dots ,A_{99}$. The location of percentiles above $A_{90}$ was computed using the actual (raw) age at death data reported in ref. 13. Fig. 2 A and B shows the speeds of all percentiles for Japanese females (red, left) and males (blue, right). The solid lines shown are long-term speeds, while the bands indicate the range of annual speeds (shown as 95% confidence intervals; Materials and Methods). All percentiles between $A_{25}$ and $A_{90}$ have similar positive long-term speeds. But annual speeds are highly variable, especially at older ages (note the width of the bands in Fig. 2 A and B). That variability should imply a high annual variability of the intervals between consecutive percentiles. However, the latter intervals display only small annual fluctuations (Fig. 1 C and D). Therefore, even when adjacent percentiles each move by a large amount in 1 y, the distance between them stays nearly constant—implying a survival front with nearly constant shape. Thus, we predict a strong positive correlation between annual changes in consecutive percentiles, which we indeed find in Japan (Fig. 2 C and D).

Fig. 2.

An example from Japan. (A and B) Speeds (rates of movement) for percentiles $A_q$ at every 1% (using raw data on death ages above $A_{90}$). (A and B, Top) Speeds for percentiles for females (A) and males (B). Solid line (red, respectively blue) indicates long-term speed. Percentiles from the 25th to the 90th show similar long-term speeds (note the vertical scale). Long-term speeds 0.2 y/y are shown for females. Also shown is the 95% confidence interval (1.96 × SD, distributions symmetric and approximately normal) for annual speeds: dotted lines and bands (pink, respectively blue). Annual variability is high (compare modest annual variability for intervals between percentiles, Fig. 1 C and D). (A and B, Bottom) Solid bars (red, females; blue, males) show ranges. (C and D) For each ending year, annual speeds of percentiles: (C) females in red and (D) males in blue. Shown is annual change in $A_{50}$ on the vertical vs. annual change in $A_{25}$ on the horizontal and correspondingly for the pairs $A_{75},A_{50}$ and $A_{90},A_{75}$. (E and F) Probability distributions of deaths at 65+ y. Solid lines show advancing front of old-age survival (between $A_{25}$ and $A_{90}$, dashes outside that range) for decades 1960–2010. (E) Females in red. (F) Males in blue. For each year, solid bars (E and F, Bottom) show distance between $A_{25}$ and $A_{90}$.

All 19 other countries showed similar patterns: nearly equal long-term speeds for every single percentile between $A_{25}$ and $A_{90}$, but high variability in annual speeds especially at the oldest ages (SI Appendix, Figs. S1–S4). In every country, we also found strong positive correlations between annual changes in consecutive percentiles (SI Appendix, Figs. S5–S8).

We linearly regressed the intervals $\left(A_{90}-A_{25}\right)$ and $\left(A_{75}-A_{25}\right)$ against elapsed time for each country. All slopes were significantly different from zero. For females, for the first interval, 8 slopes are negative and 12 positive, while for the second interval 2 slopes are negative and 18 positive. All male slopes were slightly positive. Letting $\beta$ be the slope for such a regression, and ignoring volatility, the relevant interval between percentiles would change by 1 y over an elapsed time of $\left(1/\beta \right)$ y. In 19 countries, the front $\left(A_{90}-A_{25}\right)$ would expand or narrow by about 6% in one to two human generations. And over the same long time, the interquartile range $\left(A_{75}-A_{25}\right)$ would expand or narrow by about 10%. The only exceptions are Denmark for females and Japan for males, where both intervals have expanded more rapidly (SI Appendix, Fig. S9). Ignoring noise at advanced ages, the interval $\left(A_{99}-A_{90}\right)$ (as in Fig. 2 A and B) expands slowly in some countries, contracts slowly in some countries, and has little trend in others (SI Appendix, Figs. S1–S4).

These results support the existence of an advancing old-age survival front with a nearly stable shape between the 25th and (at least) the 90th death percentiles (Fig. 2 E and F for Japan; SI Appendix, Fig. S10). The shape fluctuates modestly over time but with little long-term change from 1960 to 2010. The male front has lower long-term speed and is more dispersed than the female front. We found similar old-age survival fronts over these five decades for females and males in all of the industrialized countries studied.

The existence of an old-age survival front with nearly constant shape yields four testable predictions that can be examined separately. First, annual changes in the locations of consecutive $A_q$ (i.e., their annual speeds) should be strongly positively correlated across successive percentiles—this has been verified, as described above (Fig. 2 C and D and SI Appendix, Figs. S5–S8).

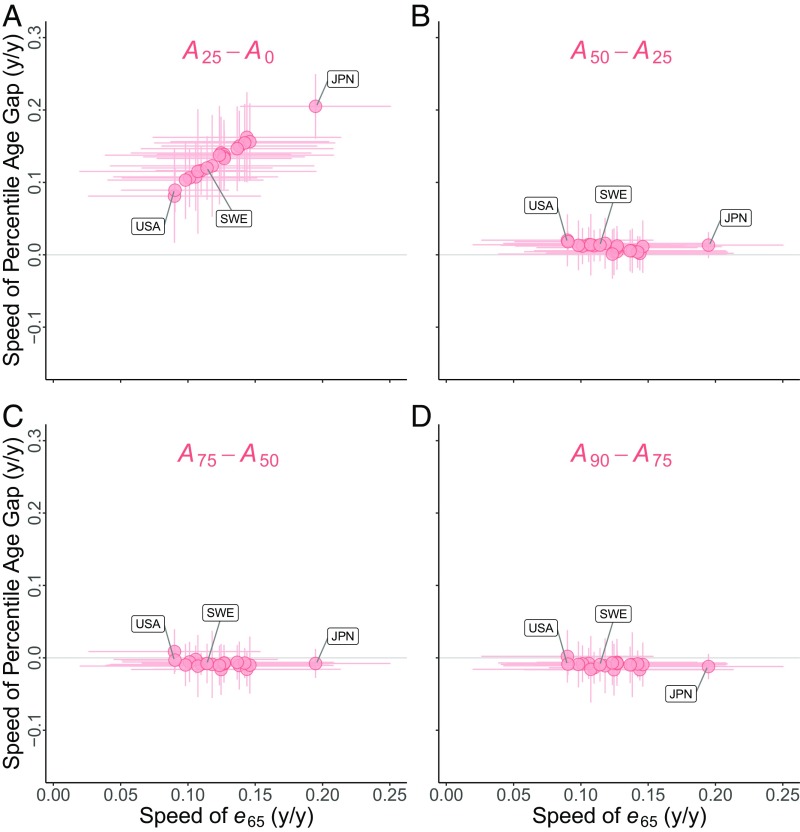
Second, the increase of life expectancy $e_{65}$ at age 65 y should depend on the movement of the trailing edge of the survival front, i.e., on the increasing distance of $A_{25}$ from age 65 y (as in Fig. 1 C and D), but not on the higher percentiles that define the front. The prediction here is that, across countries, the long-term speed of $e_{65}$ should be positively correlated with the long-term speed of $\left(A_{25}-65\right)$, but uncorrelated with the long-term speeds of intervals between higher percentiles, such as $\left(A_{75}-A_{50}\right)$. We find that these predictions hold for both sexes: A scatter plot for females is shown in Fig. 3 (countries are identified in SI Appendix, Fig. S11), and a similar result holds for males (SI Appendix, Fig. S12).

Fig. 3.

(A) Vertical axis, long-term speed of $\left(A_{25}-65\right)$; horizontal axis, long-term speed of $e_{65}$ (life expectancy at age 65 y). Each circle is a country; for each circle, the vertical and horizontal lines show 95% confidence intervals for annual speeds. There is a strong positive correlation. (B) Vertical axis, long-term speed of $\left(A_{50}-A_{25}\right)$; horizontal axis, long-term speed of $e_{65}$. Each circle is a country. There is nearly zero correlation. (C) Long-term speed of $\left(A_{75}-A_{50}\right)$ (vertical axis) uncorrelated with long-term speed of $e_{65}$ (horizontal axis). (D) Long-term speed of $\left(A_{90}-A_{75}\right)$ (vertical axis) uncorrelated with long-term speed of $e_{65}$ (horizontal axis).

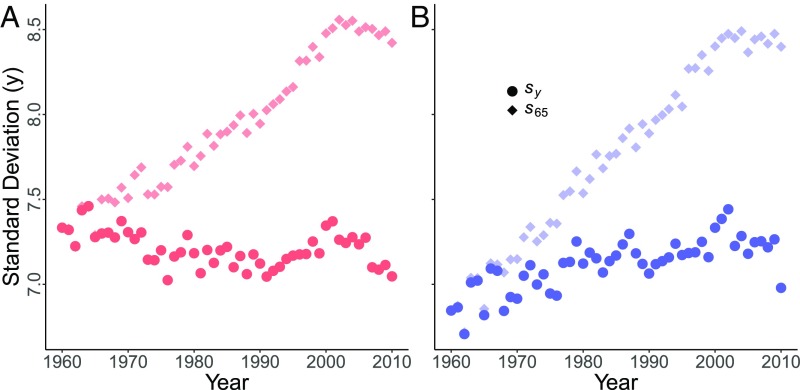
Third, the variability of deaths after age 65 y should increase over time as the survival front moves to older ages. For any age $a$, variability among older deaths (i.e., deaths at ages $>a$) is here measured by the SD $s_a$ of the corresponding ages of death [determined by the period life table (15)]. The prediction is that $s_{65}$ should increase with time. The prediction is supported by data for Japanese males and females, as shown by the diamonds (males in blue, females in red; SI Appendix, Figs. S13 and S14). Similar increases are observed in all countries (SI Appendix, Figs. S13 and S14). This increase in variability was shown, but not explained, in ref. 18.

Fourth, since the advance of the survival front produces most of the increase in $s_{65}$, we should see little or no increase in the variability of deaths past an age that moves along with the survival front. For each year $t$ from 1960 to 2010, define an age $y=65+v\hspace{0.17em}\left(t-1960\right)$, where $v$ is the long-term speed of $e_{65}$. We predict that deaths after age $y$ ($>65$) have a near-constant dispersion $s_y$, in sharp contrast to the increasing trend in $s_{65}$. We find such a contrast for Japan, shown by comparing the circles (values of $s_y$) and the diamonds (values of $s_{65}$) in Fig. 4 A (males) and B (females). Similar differences between $s_y$ and $s_{65}$ occur in all countries (SI Appendix, Figs. S14 and S15). In some countries, $s_y$ actually declines modestly with time. Small increases or decreases in $s_y$ can occur, depending on the distribution of deaths between the moving age $y$ and the percentile $A_{25}$ (the long-term speed of $A_{25}$ is similar to but not exactly equal to $v$) (Fig. 3).

Fig. 4.

(A and B) Vertical axis: variability (measured by SD of age at death) for deaths past age 65 y (diamonds) or a moving age $y$ (circles). Horizontal axis: year from 1960 to 2010. (A) Japanese females, red. (B) Japanese males, blue. Diamonds show rapid increase of $s_{65}$. For each year $t$, moving age $y=65+v\left(t-1960\right)$, with $v$ the long-term speed of the survival front. Circles show variability $s_y$.

Discussion

We conclude that an advancing old-age front characterizes old-age human survival in 20 developed countries. Note that the location of the survival front (i.e., of the percentile $A_{25}$) in any year may be affected by earlier death, e.g., due to opioids (19), as reflected in the annual volatility of changes in the percentiles (Fig. 2 A and B). The long-term speed of the advancing front is $\simeq$0.12 y per calendar year, about 3 y per human generation. Thus, the front implies that, e.g., age 68 y today is equivalent, in terms of mortality, to age 65 y a generation ago.

Our findings echo aspects of an earlier proposal that mortality hazards have, over the years, shifted rigidly to older ages (20). That proposal used all ages $\ge 25$ y and assumed a logistic age pattern of mortality at the oldest ages. Our analysis of percentiles makes no assumptions about the pattern of mortality at young or old ages and focuses on older deaths. However, our finding of a shifting front in the percentiles of death at old age is consistent with some patterns of shifts in old-age mortality hazards.

Our findings provide no support for an impending limit to human lifespan, certainly not at an age that affects the movement of the survival front (between the 25th and 90th percentiles). To the extent that we can rely on the long-term speeds of percentiles above the 90th, the oldest deaths are being compressed in some countries but definitely not in others (Fig. 2 and SI Appendix, Figs. S1–S4). Here again we find no support for an approaching limit to human lifespan.

Nor do our results suggest that endowments, biological or other, are a principal determinant of old-age survival. The advancing survival front that we find suggests that the effects of inequality on mortality (21, 22) may be much smaller among old-aged adults than among younger adults.

Our analyses use period life tables, not cohorts, and suggest that continued mortality improvement depends largely on period processes such as economic growth, investment and advances in health science research and practice, and increases in the age of transition to disability. Our results also constrain biological arguments about the causes of death (23), especially the plasticity of death rates in response to environmental factors. Our moving survival front is consistent with a plateau in mortality rates (12), but implies that the location and possibly the level of the plateau change over time.

Our results can be used to bound the parameters of mortality models such as the Gompertz (not necessarily consistent with our results; Materials and Methods), but do not explain differences in the location and speed of the front between sexes or countries. The surprising regularity we report should be used to improve mortality forecasts, such as the well-known Lee–Carter method (24, 25), especially at older ages. Our findings imply that we must welcome continued aging despite its challenges.

Materials and Methods

Data.

We use annual life tables (female and male) from the Human Mortality Database (HMD) (13) for 20 countries, for national populations covered over 1960–2010. We exclude countries whose populations were under 4 million. We exclude 14 countries of the former Soviet Bloc because mortality there went through a crisis in the 1990s (26).

Percentiles and Speeds.

For any year, write $\mu \left(x\right)$ for the period mortality rate at age $x$ and $l\left(x\right)$ for the corresponding survivorship to age $x$. The probability of dying at age $x$ is

$$\varphi \left(x\right)=\mu \left(x\right)l\left(x\right),\text{and}\hspace{0.17em}l\left(y\right)={\int }_0^y\hspace{0.17em}ds\hspace{0.17em}\varphi \hspace{0.17em}\left(s\right).$$

Given that an individual is alive at age $B\ge 0$ the probability of surviving to age $x\ge B$ is

$$l_1\left(x\right)=\frac{1}{l\left(B\right)}\exp \left[-{\int }_0^x\hspace{0.17em}ds\hspace{0.17em}\mu \left(s\right)\right].$$

Take $B=65$ and a percentage $q$. Then $A_q\ge 65$ is the age at which $q$% of individuals alive at age 65 y would be dead, and

$$1-l_1\left(A_q\right)=\left(q/100\right).$$

To compute percentiles, we used splines in R (27) to interpolate the $l_1\left(x\right)$.

For old-age deaths, $A_0=65$ and $A_q$ is the age at which $q$% of a synthetic cohort (assembled from the period life table) would die. Clearly the $A_q$ are ages as well as percentiles. For the United States in year 2000, the age $A_{90}$ is high, but, e.g., for a synthetic cohort based on the United States in year 2000, 8.7% of newborn females and 7.8% of newborn males live past that age.

Given years $t,t+1$ the data yield corresponding probabilities of death, say $\varphi$ and ${\varphi }_1$. These in turn yield age percentiles: For a given $q$ we call these $A_q\left(t\right)$ and $A_q\left(t+1\right)$. The annual speed of the $q$th percentile in year $t+1$ is the difference

$$\left(A_q\left(t+1\right)-A_q\left(t\right)\right).$$

We describe the variation in annual speeds by a 95% confidence interval, computed as 1.96 times the SE of the annual speeds; we find that the distributions of all speeds are symmetric and approximately normal. The average of these annual speeds over the entire five decades is the long-term speed. Speeds for intervals such as

$$\mathrm{\Delta }\left(t\right)=\left(A_{75}\left(t\right)-A_{50}\left(t\right)\right)$$

are defined similarly.

Percentiles for the Gompertz Model.

Above some age $C$ assume period mortality is given by the Gompertz model,

$$\mu \left(x\right)={\mu }_C\hspace{0.17em}{e}^{b\hspace{0.17em}x},x\ge C.$$

Denote by $y_q$ the $q$th percentile of deaths past $C$. Then

$$\left(\log \left(1-p/100\right)-\log \left(1-q/100\right)\right)=\frac{{\mu }_C\left(e^{b{y}_q}-e^{b{y}_p}\right)}{b}.$$

It is straightforward to show that changes in the parameters of the model can lead to declining, expanding, or contracting distances between percentiles.