Giant anomalous Hall effect in a ferromagnetic Kagomé-lattice semimetal

Abstract

Magnetic Weyl semimetals with broken time-reversal symmetry are expected to generate strong intrinsic anomalous Hall effects, due to their large Berry curvature. Here, we report a magnetic Weyl semimetal candidate, Co₃Sn₂S₂, with a quasi-two-dimensional crystal structure consisting of stacked Kagomé lattices. This lattice provides an excellent platform for hosting exotic topological quantum states. We observe a negative magnetoresistance that is consistent with the chiral anomaly expected from the presence of Weyl nodes close to the Fermi level. The anomalous Hall conductivity is robust against both increased temperature and charge conductivity, which corroborates the intrinsic Berry-curvature mechanism in momentum space. Owing to the low carrier density in this material and the significantly enhanced Berry curvature from its band structure, the anomalous Hall conductivity and the anomalous Hall angle simultaneously reach 1130 Ω⁻¹ cm⁻¹ and 20%, respectively, an order of magnitude larger than typical magnetic systems. Combining the Kagomé-lattice structure and the out-of-plane ferromagnetic order of Co₃Sn₂S₂, we expect that this material is an excellent candidate for observation of the quantum anomalous Hall state in the two-dimensional limit.

The anomalous Hall effect (AHE) is an important electronic transport phenomenon¹. It can arise because of two qualitatively different microscopic mechanisms: Extrinsic processes due to scattering effects, and an intrinsic mechanism connected to the Berry curvature^1–5. The large Berry curvature comes from the entangled Bloch electronic bands with spin-orbit coupling when the spatial-inversion or time-reversal symmetry of the material is broken^6,7. The quantum AHE in two-dimensional (2D) systems is determined solely by this intrinsic contribution^8,9. It manifests itself as a quantized anomalous Hall conductance due to the presence of a bulk gap in combination with dissipationless edge states^10–13. A magnetic Weyl semimetal with broken time-reversal symmetry can be interpreted as a stacked heterostructure of such quantum anomalous Hall insulator layers^14,15, where the coupling between the layers closes the bulk band gap at isolated Weyl nodes. At these Weyl nodes, the Berry curvature is enhanced while the carrier density vanishes^2–4,16,17. This suggests that an intrinsic large anomalous Hall conductivity and a large anomalous Hall angle can be expected in such systems.

To date, a number of promising candidates for magnetic Weyl semimetals have been proposed, including Y₂Ir₂O₇ (18), HgCr₂Se₄ (19), and certain Co₂-based Heusler compounds^20–22. Indeed, an anomalous Hall angle of ~16% was recently observed at low temperatures in the magnetic-field induced Weyl semimetal GdPtBi (23). However, a finite external magnetic field is mandatory to make GdPtBi a Weyl semimetal. Therefore, the search for intrinsic magnetic Weyl semimetals with Weyl nodes close to the Fermi level is not only an efficient strategy to obtain materials exhibiting both a high anomalous Hall conductivity and large anomalous Hall angle, but also important for a comprehensive understanding of the Weyl topological effects on the AHE in real materials.

The Kagomé lattice has become one of the most fundamental models for exotic topological states in condensed matter physics. In particular, the Kagomé lattice with out-of-plane magnetization is an excellent platform for quantum anomalous Hall effect^24,25. Thus, it provides an effective guiding principle for realizing magnetic Weyl semimetals via stacking^14,15. Although a Dirac dispersion with a finite spin-orbit-coupling induced gap has recently been observed in a Kagomé-lattice metal²⁶, the Weyl phase in a magnetic Kagomé material still remains elusive. Here, we report a time-reversal-symmetry-breaking Weyl semimetal in the magnetic Kagomé-lattice compound Co₃Sn₂S₂ with out-of-plane ferromagnetic order, and demonstrate both a large intrinsic anomalous Hall conductivity (1130 Ω^-1 cm^-1) and giant anomalous Hall angle (20%).

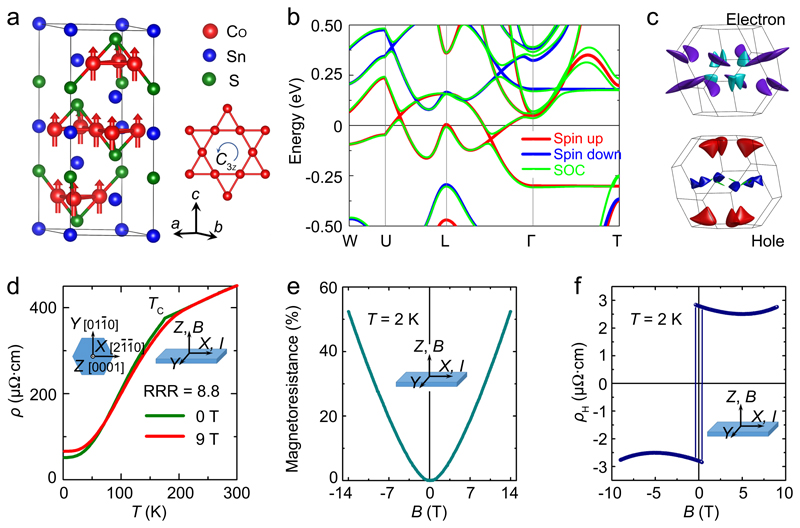
Co₃Sn₂S₂, a Shandite compound, is known to be a ferromagnet with a Curie temperature (T_C) of 177 K and a magnetic moment of 0.29 μ_B/Co (27–29). Magnetization measurements have shown that the easy axis of the magnetization lies along the c-axis³⁰, while photoemission measurements and band structure calculations revealed that below T_C, Co₃Sn₂S₂ exhibits Type-IA half-metallic ferromagnetism in which spin-minority states are gapped^31,32. Figure 1 summarizes the structural and electronic properties of Co₃Sn₂S₂. As shown in Fig. 1a, Co₃Sn₂S₂ crystallizes in a rhombohedral structure of the space group, R-3m (no. 166) (27). The crystal possesses a quasi-2D Co₃Sn layer sandwiched between sulphur atoms, with the magnetic cobalt atoms arranged on a Kagomé lattice in the a-b plane in the hexagonal representation of the space group. Owing to the strong magnetic anisotropy, this material shows a quasi-2D nature of magnetism³⁰. Our magnetization measurements revealed a quite low saturation field (~ 0.05 T) along the c-axis and an extremely high one (> 9 T) in the a-b plane, confirming a dominantly out-of-plane magnetization in Co₃Sn₂S₂ (see Supplementary Information). By itself, the dimensional restriction of the out-of-plane magnetization may be responsible for some of the interesting electronic and magnetic properties of this compound. We discuss band structure calculations of Co₃Sn₂S₂ with spin polarization along the c-axis. The calculated magnetic moments without and with spin-orbit coupling are 0.33 and 0.30 μ_B/Co, respectively, which are very close to the experimental values of 0.29 μ_B/Co obtained from neutron diffraction²⁹, 0.31 μ_B/Co from magnetization measurement³⁰, and 0.30 μ_B/Co from our measurement (see Supplementary Information). As expected, the calculation including spin-orbit coupling yields a more accurate result.

Figure 1. Crystal and electronic structures of Co₃Sn₂S₂ and the measured electric resistivity.

a, Unit cell in a hexagonal setting. The cobalt atoms form a ferromagnetic Kagomé lattice with a C_3z-rotation. The magnetic moments are shown along the c-axis. b, Energy dispersion of electronic bands along high-symmetry paths without and with spin-orbit coupling, respectively. "SOC" denotes "Spin-orbit coupling". c, Fermi surfaces of two bands (upper: electron; lower: hole) under spin-orbit coupling calculations. Different colors indicate different parts of the Fermi surface in the Brillouin zone. d, Temperature dependences of the longitudinal electric resistivity (ρ) in zero and 9-T fields. In zero field, a residual resistance ratio (RRR, ρ_300K/ρ_2K) value of 8.8 and a residual resistivity of ρ_2K ~ 50 μΩ cm is observed. e, Magnetoresistance measured in fields up to 14 T at 2 K, showing a non-saturated positive magnetoresistance. f, Hall data with a non-linear behaviour at high fields, indicating the coexistence of electron and hole carriers at 2 K. All transport measurements depicted here were performed in out−of−plane configuration with I // x // [21̄1̄0] and B // z // [0001]. The x and z axes, respectively, are thus parallel to the a and c ones shown in a.

The band structures of Co₃Sn₂S₂ calculated without and with spin-orbit coupling are shown in Fig. 1b. The bands corresponding to the spin-down channel are insulating in character with a gap of 0.35 eV, while the spin-up channel crosses the Fermi level and thus has metallic character. This half-metallic behaviour is consistent with the results of previous studies on this compound^30–32. Furthermore, for the spin-up states, we observe linear band crossings along the Γ–L and L–U paths, just slightly above and below the Fermi energy, respectively. For finite spin-orbit coupling, these linear crossings open small gaps with band anti-crossings, and make this compound semimetal-like. The relatively small Fermi surfaces (Fig. 1c), showing the coexistence of holes and electrons, further corroborate the semi-metallic character in this compound. This calculated band structure is in good agreement with our angle-resolved photoemission spectroscopy (ARPES) measurements (see Supplementary Information). When these results are considered in connection with the ferromagnetism of Co₃Sn₂S₂ (27–30), they suggest that a time-reversal symmetry broken Weyl semimetal phase might be hidden in this compound.

In order to confirm this prediction, single crystals of Co₃Sn₂S₂ were grown for further experimental investigations (see Methods and Supplementary Information). The high quality of the crystals was confirmed by structure refinements based on single-crystal X-ray diffraction and topographic images of the hexagonal lattice array obtained using scanning tunneling microscopy (see Supplementary Information). As shown in Fig. 1d, the longitudinal electric resistivity (ρ) decreases with decreasing temperature, showing a kink at T_C = 175 K and a moderate residual resistivity of ~50 μΩ cm at 2 K. In a high field of 9 T, a negative magnetoresistance appears around the Curie temperature owing to the spin-dependent scattering in magnetic systems. At low temperatures, the MR increases and becomes positive (Fig. 1d). This behaviour is further demonstrated by the field dependent resistance (Fig. 1e). Importantly, the positive magnetoresistance shows no signature of saturation even up to 14 T, which is typical of a semi-metal^33,34. The notable non-linear field dependence of the Hall resistivity (ρ_H) (Fig. 1f) further indicates the coexistence of hole and electron carriers at 2 K, which is in good agreement with our band structure calculations (Figs. 1b and 1c). By using the semiclassical two-band model³⁵, we extract the carrier densities of holes (n_h ~ 9.3 × 10¹⁹ cm^-3) and electrons (n_e ~ 7.5 × 10¹⁹ cm^-3) of our Co₃Sn₂S₂ samples. These relatively low carrier densities and a near compensation of charge carriers further confirm the semi-metallicity of Co₃Sn₂S₂.

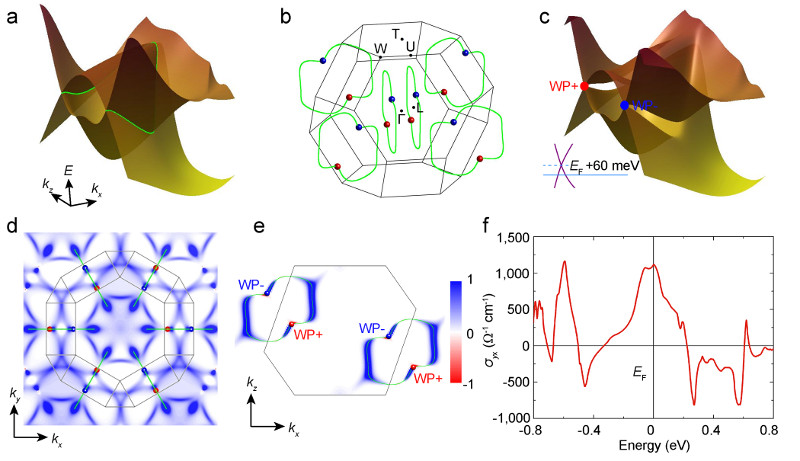
In order to further analyze the topological character of Co₃Sn₂S₂ suggested by Fig. 1b, we now consider the linear band crossings in more detail. The space group R-3m of Co₃Sn₂S₂ has one mirror plane M₀₁₀. Without spin-orbit coupling, the interaction between spin-up and spin-down states is ignored and the mirror plane is a high symmetry plane of the Hamiltonian. Thus, as they are protected by this mirror symmetry, the linear band crossing identified in Fig. 1b form a nodal ring in the mirror plane based on the band inversion, as shown in Fig. 2a. Moreover, the linear crossings between the L–Γ and L–U paths are just single points on the ring. When the C_3z-rotation and inversion symmetries of the material are considered, one finds a total of six nodal rings in the Brillouin zone, as shown schematically in Fig. 2b.

Figure 2. Theoretical calculations of the Berry curvature and anomalous Hall conductivity.

a, Linear band crossings form a nodal ring in the mirror plane. b, The nodal rings and distribution of the Weyl points in the Brillouin zone. c, Spin-orbit coupling breaks the nodal ring band structure into opened gaps and Weyl nodes. The Weyl nodes are located just 60 meV above the Fermi level, and the gapped nodal lines are distributed around the Fermi level. d, Berry curvature distribution projected to the k_x–k_y plane. e, Berry curvature distribution in the k_y = 0 plane. The color bar for d and e are in arbitrary units. f, Energy dependence of the anomalous Hall conductivity in terms of the components of ${\Omega }_{yx}^z(k).$

Upon taking spin-orbit coupling into account, the spin s_z is no longer a good quantum number and the mirror symmetry of the Hamiltonian is broken, which causes the linear crossings of the nodal lines to split, as presented in Fig. 2c. Interestingly, one pair of linear crossing points remains in the form of Weyl nodes along the former nodal line. These two Weyl nodes act as a monopole sink and source of Berry curvature (see Supplementary Information) and possess opposite topological charges of +1 and −1, respectively. In total, there are three such pairs of Weyl nodes in the first Brillouin zone due to the inversion and C_3z-rotation symmetries of the crystal, and their distribution is presented in Fig. 2b. It is important to emphasize that the Weyl nodes in Co₃Sn₂S₂ are only 60 meV above the charge neutrality point, which is much closer to the Fermi energy than previously proposed magnetic Weyl semimetals. These Weyl nodes and non-trivial Weyl nodal rings together make this material exhibit a simple topological band structure around the E_F. It is thus easy to further observe the surface Fermi arcs³⁶. As a result, the Weyl node-dominated physics in Co₃Sn₂S₂ should be prominent and easy to detect in experiments.

We now address the AHE response of Co₃Sn₂S₂ that can be expected from the particular band structure properties outlined above. In order to obtain a complete topological character, we integrated the Berry curvature ${\Omega }_{yx}^z(k)$ along k_z in the Brillouin zone. Our results reveal two main types of hot spots for the integrated Berry curvature: One that is located around the Weyl nodes, and the other near the edge of the nodal lines (see Fig. 2d). To investigate the origin of the hot spot of the Berry curvature distribution, we choose the k_y = 0 plane, which includes two nodal rings and two pairs of Weyl nodes, as shown in Fig. 2e. We note that hot spots of the integrated Berry curvature are primarily determined by the shape of the nodal lines, and both types of hot spots observed here originate from the nodal-line-like band anti-crossing behaviour. Along the nodal ring, the component of the Berry curvature parallel to k_z leads to the larger hot spot we observe, while a different part around the Weyl node contributes to the smaller hot spot. Owing to the band anti-crossing behaviour and the position of the six Weyl nodal rings around the Fermi level, the calculated Berry curvature is clean and large, which should yield fascinating spin-electronic transport behaviours including a large intrinsic AHE³.

The energy dependent anomalous Hall conductivity (σ_yx) calculated from the Berry curvature is shown in Fig. 2f. As one can see from the figure, a large peak in σ_yx appears around E_F with a maximum of 1100 Ω⁻¹ cm⁻¹. Since the σ_yx depends on the location of the Fermi level (see Eq. (1), Methods), it usually changes sharply as a function of energy. However, the peak in σ_yx in Fig. 2f stays above 1000 Ω⁻¹ cm⁻¹ within an energy window of 100 meV below E_F. Therefore, we expect to observe a high σ_yx in experiments for charge neutral or slightly p-doped Co₃Sn₂S₂ samples. We also consider the non-collinear magnetic structures on the Kagomé lattice in Co₃Sn₂S₂. During the spin tilting from c-axis, the calculated σ_yx always keeps above 1000 Ω⁻¹ cm⁻¹. The existence of Weyl nodes and large anomalous Hall conductivity are robust against the change of magnetic structure in Co₃Sn₂S₂ (see Supplementary Information).

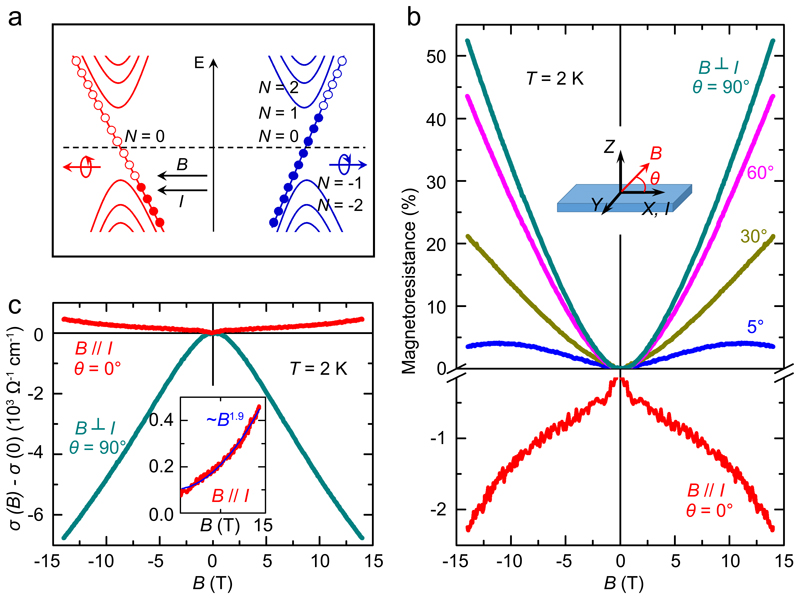
A Weyl semimetal is expected to exhibit the so-called chiral anomaly³⁷ in transport, when the conservation of chiral charges is violated in case of a parallel magnetic and electric field, as shown in Fig. 3a. We measured the impact of magnetic field orientation on transverse resistivity at 2 K (Fig. 3b). For B ⊥ I (θ = 90°), the positive unsaturated magnetoresistance (see Fig. 1e) is observed. The magnetoresistance decreases rapidly with decreasing θ. A clear negative magnetoresistance appears when B // I (θ = 0°) which again does not saturate up to 14 T. As an equivalent description of the magnetoresistance, the magnetoconductance is shown in Fig. 3c. In the parallel case (B // I), the positive magnetoconductance can be well described by a near parabolic field dependence³⁸, ~ B^1.9, up to 14 T (Inset of Fig. 3c). In this case, the charge carriers are pumped from one Weyl point to the other one with opposite chirality, which leads to an additional contribution to the conductance, resulting in a negative magnetoresistance^37,38. The chiral anomaly evident from Fig. 3 represents an important signature of the Weyl fermions in Co₃Sn₂S₂.

Figure 3. Chiral anomaly induced negative magnetoresistance.

a, Schematic of chiral anomaly. When electron current I and magnetic field B are not perpendicular, the charge carriers pump from one Weyl point to the other one with opposite chirality, which leads to an additional contribution to the conductivity and negative magnetoresistance. b, Angle dependence of magnetoresistance at 2 K. For B ⊥ I // x // [21̄1̄0] (θ = 90°), the magnetoresistance curve shows a positive, non-saturated behaviour up to 14 T. The MR decreases rapidly with decreasing angle. A negative magnetoresistance appears when B // I // x // [21̄1̄0] (θ = 0°). c, Magnetoconductance at 2 K in both cases of B ⊥ I and B // I. The magnetoconductance is an equivalent description for the magnetoresistance. The positive magnetoconductance is observed in Co₃Sn₂S₂ when B // I. The fitting of the positive magnetoconductance in Inset shows a ~B^1.9 dependence, which is very close to the parabolic (~B²) field dependence.

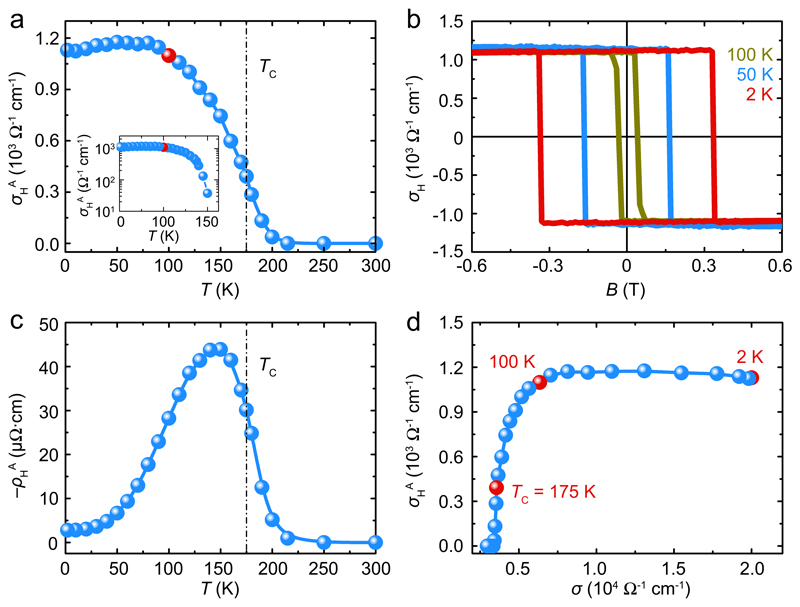
Our transport measurements further verify the strong AHE induced by the Weyl band topology. An out–of–plane configuration of I // x //[21̄1̄0] and B // z // [0001] was applied in these measurements (see Fig. 1d and Methods). As we observe in Fig. 4a, the anomalous Hall conductivity (σ_H^A) (see Methods) shows a high value of 1130 Ω⁻¹ cm⁻¹ at 2 K, which is in very good agreement with our predicted theoretical value (σ_yx, Fig. 2f). We also studied the in–plane case (I // x // [21̄1̄0] and B // y // [011̄0]), for which the AHE disappears (not shown), due to strong magnetic and Berry-curvature anisotropies. Moreover, at temperatures below 100 K (T < T_C), for the out–of–plane case σ_H^A ~ 1000 Ω⁻¹ cm⁻¹ is revealed to be independent of temperature (see also the inset of Fig. 4a, and note the logarithmic vertical axis). This robust behaviour against temperature indicates that the AHE is not governed by scattering events in the system. In addition, σ_H shows rectangular hysteresis loops with very sharp switching (Fig. 4b), and the coercive field is seen to increase with decreasing temperature, resulting in a value of 0.33 T at 2 K (also see Supplementary Information). As is evident from the figure, a large remanent Hall effect at zero field is observed in this material.

Figure 4. Transport measurements of the AHE.

a, Temperature dependence of the anomalous Hall conductivity (σ_H^A) at zero magnetic field. The inset shows the logarithmic temperature dependence of σ_H^A. b, Field dependence of the Hall conductivity σ_H at 100, 50, and 2 K with I // x // [21̄1̄0] and B // z // [0001]. Hysteretic behaviour and the sharp switching appears at temperatures below 100 K. c, Temperature dependence of the anomalous Hall resistivity (ρ_H^A). A peak appears around 150 K. Since ρ_H^A was derived by extrapolating the high-field part of ρ_H to zero field, non-zero values can be observed just above T_C due to the short-range magnetic exchange interactions enhanced by high fields. d, σ dependence of σ_H^A. The σ-independent σ_H^A (i.e., σ_H^A ~ (σ)⁰ = constant), below 100 K, puts this system into the intrinsic regime according to the unified model of AHE physics (for more details see Supplementary Information)³⁹,⁴⁰.

We plot ρ_H^A as a function of temperature in Fig. 4c. A large peak in ρ_H^A with a maximum of 44 μΩ cm appears at 150 K. When σ_H^A is plotted against σ, as presented in Fig. 4d, we also find that σ_H^A is nearly independent of σ (i.e., σ_H^A ~ (σ)⁰ = constant) for temperatures below 100 K, as is expected for an intrinsic AHE in the framework of the unified model for AHE physics^39,40 (see Supplementary Information for more details). This independence of ρ_H^A with respect to both T and ρ indicates that the AHE only originates from the intrinsic scattering-independent mechanism, and is thus dominated by the Berry curvature in momentum space¹. This present scaling behaviour is well consistent with our first-principles calculations and also provides another important signature for the magnetic Weyl fermions in Co₃Sn₂S₂.

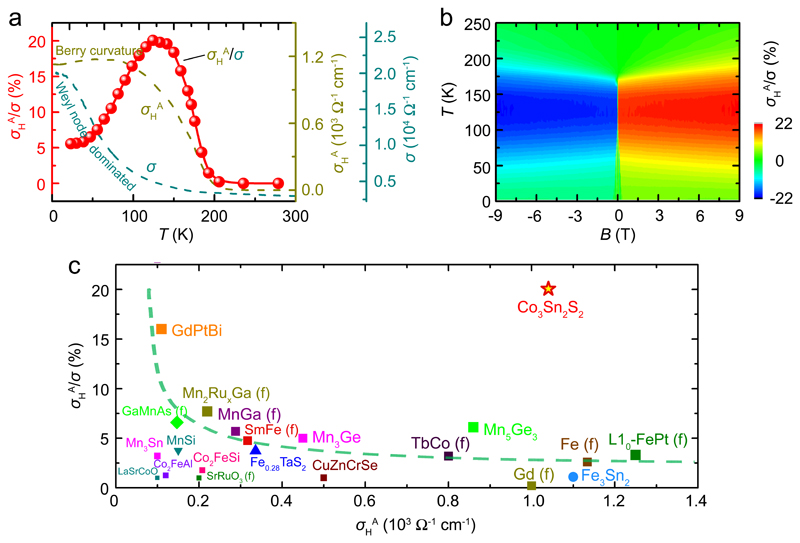
In addition to a large σ_H^A, and arguably more importantly, the magnetic Weyl semimetal Co₃Sn₂S₂ also features a giant anomalous Hall angle that can be characterized by the ratio of σ_H^A/σ. The temperature dependence of the σ_H^A/σ is shown in Fig. 5a. With increasing temperature, the σ_H^A/σ first increases from 5.6% at 2 K, reaching a maximum of ~ 20% around 120 K, before decreasing again as the temperature increases above T_C. The contour plot of σ_H/σ with respect to B and T is depicted in Fig. 5b, and makes it intuitively clear that a giant Hall angle appears between 75 – 175 K irrespective of the magnetic field magnitude. This can be straightforwardly understood by considering that the σ_H^A arises from the Berry curvature of the occupied states. The band topology of these states is basically unaffected by the small energy scale of thermal excitations up to room temperature⁴¹. In other words, the topologically protected σ_H^A is relatively robust against temperature. In contrast, the Weyl-node-related charge conductivity (σ) is sensitive to temperature due to electron–phonon scattering⁴². These behaviours are also shown in Fig. 5a. Therefore, the σ_H^A/σ is expected to increase with increasing temperature in a wide temperature range below T_C. The semi-metallicity (low carrier density and low charge conductivity) largely improves the value of σ_H^A/σ in this system.

Figure 5. Transport measurements of the anomalous Hall angle.

a, Temperature dependences of the anomalous Hall conductivity (σ_H^A), the charge conductivity (σ), and the anomalous Hall angle (σ_H^A/σ) at zero magnetic field. Since the ordinary Hall effect vanishes at zero field, only the anomalous Hall contribution prevails (see Supplementary Information). b, Contour plots of the Hall angle in the B–T space. c, Comparison of our σ_H^A-dependent anomalous Hall angle results and previously reported data for other AHE materials. "(f)" denotes thin-film materials. The dashed line is a guide to the eye. The reported data were taken from references that can be found in the Supplementary Information.

When compared to previously reported results for other AHE materials (see Fig. 5c), the value of anomalous Hall angle in Co₃Sn₂S₂ observed in this work is seen to be the largest by quite a prominent margin. For most of these materials — formed mainly of ferromagnetic transition metals and alloys — the anomalous Hall conductivities originate from topologically trivial electronic bands. A typical feature of these materials is that both the σ_H^A and the σ are either large or small and therefore the σ_H^A/σ of these materials typically cannot be large. While the magnetic-field-induced Weyl semimetal GdPtBi has a large σ_H^A/σ of 16%, its σ_H^A is very small, and moreover, it requires an external field to induce the Weyl phase²³. In contrast, owing to the non-trivial Berry curvature and the Weyl semi-metallic character, the Kagomé-lattice Co₃Sn₂S₂ possesses both a large σ_H^A and giant σ_H^A/σ simultaneously and at zero magnetic field, which promotes this system to quite a different position among the known AHE materials. As a consequence, a large anomalous Hall current can be expected in thin films of this material that may even reach the limit of a quantized AHE with dissipationless quantum Hall edge states^13,24,43,44. In more general terms, a clean topological band structure induces both a large anomalous Hall conductivity and giant anomalous Hall angle (as demonstrated here for the Weyl semimetal Co₃Sn₂S₂), and so can be seen as a guide for the realization of strong AHE in magnetic half-metallic topological semimetals.

In summary, Co₃Sn₂S₂ is a Weyl semimetal candidate derived from a ferromagnetic Kagomé lattice. It is the first material that hosts both a large anomalous Hall conductivity and a giant anomalous Hall angle that originate from Berry curvature. This compound is an ideal candidate for developing a quantum anomalous Hall state due to its distinctive quasi-2D out-of-plane ferromagnetic order and simple electronic structure near the Fermi energy. Moreover, it is straightforward to grow large, high-quality, single crystals, which makes Co₃Sn₂S₂ and the Shandite family an excellent platform for comprehensive studies on topological electron behaviour. Our work motivates the study of the strong anomalous Hall effect based on magnetic Weyl semimetals, and establishes the ferromagnetic Kagomé-lattice Weyl semimetals as a key class of materials for fundamental research and applications connecting topological physics^45–48 and spintronics^49,50.

Methods

Single-crystal growth

The single crystals of Co₃Sn₂S₂ were grown by self-flux methods with Sn as flux or with the congruent composition in a graphite crucible sealed in a quartz tube (see Supplementary Information). The stoichiometric samples (Co : Sn : S = 3 : 2 : 2) were heated to 1000°C over 48 hours and kept there for 24 hours before being slowly cooled to 600 °C over 7 days. The samples were kept at 600 °C for 24 hours to obtain the homogeneous and ordered crystals. The compositions of crystals were checked by energy dispersive X-ray spectroscopy. The crystals were characterized by powder X-ray diffraction as single phase with a Shandite-type structure. The lattice parameters at room temperature are a = 5.3689 Å and c = 13.176 Å. The single crystals and orientations were confirmed by single-crystal X-ray diffraction technique.

Scanning tunneling microscopy (STM)

Topographic images of the crystal surface were characterized by a cryogenic STM, taken at conditions of T = 2.5 K, a bias voltage of V_b = 100 mV, and a tunnel current of I_t = 500 pA. The sample was cleaved in situ (p ≤ 2 × 10^-9 Pa) at 20 K. The high quality of the single crystals was confirmed by STM (see Supplementary Information).

Magnetization measurements

Magnetization measurements were carried out on oriented crystals with the magnetic field applied along both the a and c axes using a vibrating sample magnetometer (MPMS 3, Quantum Design). The results show an extremely strong magnetic anisotropy in Co₃Sn₂S₂ (see Supplementary Information).

Out-of-plane transport measurements

The out-of-plane transport measurements on longitudinal charge and Hall resistivities, with B // z //[0001] and I // x //[21̄1̄0], were performed on a PPMS 9 (Quantum Design) using the low-frequency alternating current (ACT) option. The standard four-probe method was used to measure the longitudinal electrical resistivity, while for the Hall resistivity measurements, the five-probe method was used with a balance protection meter to eliminate possible magnetoresistance signals. The charge and Hall resistivities were measured alternatively at each temperature.

Angle dependent longitudinal electric resistivity

The angle dependence of longitudinal electric resistivity was measured on PPMS DynaCool (Quantum Design) using the DC Resistivity Option. For the angle-dependent measurements, B // θ and I // x //[21̄1̄0], while θ is the angle with respect to x //[21̄1̄0]. The currents were always applied along the a-axis, e.g. I // x // [21̄1̄0] (a axis = x axis). Different crystals, grown by two self-flux methods and with different RRR (ρ_300K/ρ_2K) values, were used in this study.

Analysis of Hall effect and semi-metallicity

At high temperatures (50 K < T < T_C), the Hall signal shows a linear field-dependent behaviour after saturation. At low temperatures (T < 50 K), a notable non-linear field dependence of the Hall resistivity is observed, indicating the existence of two types of carriers (electrons and holes). This indicates the coexistence of hole and electron carriers. The electron carriers appear at low temperatures. The single-band and two-band models were thus applied to extract the pure anomalous Hall resistivity, carrier densities and mobilities, for high-temperature and low-temperature cases, respectively.

The anomalous Hall conductivity was calculated by

$${{\sigma }_{\text{H}}}^{\text{A}}=-{{\rho }_{\text{H}}}^{\text{A}}/({({{\rho }_{\text{H}}}^{\text{A}})}^2+{\rho }^2).$$

Here ρ_H^A is the anomalous Hall resistivity at zero field; ρ is the longitudinal resistivity at zero field.

The two-band model³⁵ was applied to extract the densities of both carriers at low temperatures.

$$\sigma (B)=\frac{n_{h}e{\mu }_h}{1+{\mu }_h^2{B}^2}+\frac{n_{e}e{\mu }_e}{1+{\mu }_e^2{B}^2}$$

$${\sigma }_{\text{H}}(B)=\frac{n_{h}e{\mu }_h^{2}B}{1+{\mu }_h^2{B}^2}+\frac{n_{e}e{\mu }_e^{2}B}{1+{\mu }_e^2{B}^2}$$

Here B is applied magnetic field, σ(B) is longitudinal charge conductivity, σ_H(B) is anomalous Hall effect, n_h is carrier concentration of holes and μ_h is carrier mobility of holes, n_e is carrier concentration of electrons and μ_e is carrier mobility of electrons.

Longitudinal magnetoresistance in static high magnetic fields

The field-dependent longitudinal magnetoresistance was measured in static high magnetic fields up to 37 T, by a standard four-probe method in a 3He cryostat with B // c-axis, using a hybrid magnet at the High Magnetic Field Laboratory, Chinese Academy of Sciences. The current was 5 mA at a frequency of 13.7 Hz applied by a Keithley 6221. The voltage was measured by a SR830 Lock-In Amplifier. The Shubnikov-de Haas (SdH) quantum oscillations of magnetoresistivity was observed above 17 T in the present crystal. A cubic polynomial background was subtracted from the resistivity data. For the fast Fourier transform, Hanning window was applied in the Origin software.

Density functional theory (DFT) calculations

The electronic structure calculations were performed based on the DFT using the Vienna ab-initio simulation package (VASP)⁵¹. The exchange and correlation energies were considered in the generalized gradient approximation (GGA), following the Perdew–Burke–Ernzerhof parametrization scheme⁵². We have projected the Bloch wave functions into Wannier functions⁵³, and constructed the tight binding model Hamiltonian based on the Wannier functions. The anomalous Hall conductivity and Berry curvature was calculated by the Kubo formula approach in the linear response and clean limit⁴:

$${\sigma }_{yx}^z(E_F)=e^2ħ{(\frac{1}{2\pi })}^3{\displaystyle \underset{\overrightarrow{k}}{\int }d\overrightarrow{k}}{\displaystyle \sum _{E(n,\overrightarrow{k})<E_F}f(n,\overrightarrow{k})}{\Omega }_{n,yx}^z(\overrightarrow{k})$$

$${\Omega }_{n,yx}^z(\overrightarrow{k})=\mathrm{Im}{\displaystyle \sum _{n^{\prime }\ne n}\frac{<u(n,\overrightarrow{k})\left|{\widehat{v}}_y\right|u(n^{\prime },\overrightarrow{k})><u(n^{\prime },\overrightarrow{k})\left|{\widehat{v}}_x\right|u(n,\overrightarrow{k})>-(x\leftrightarrow y)}{{(E(n,\overrightarrow{k})-E(n^{\prime },\overrightarrow{k}))}^2}}$$ (1)

where f(n, k⃗) is the Fermi-Dirac distribution, E(n, k⃗) is the eigen-value of the n-th eigen-state of | u(n, k⃗) > at k⃗ point, and ${\widehat{v}}_{x(y)}=\frac{1}{ħ}\frac{\partial H(\overrightarrow{k})}{\partial k_{x(y)}}$ is the velocity operator. The numerical integration was performed using a 501 × 501 × 501 k-grid. The Fermi surfaces were calculated by a k-grid of 120×120×120 from the tight binding model Hamiltonian, and the frequencies of electron oscillations were calculated from the extremal cross-section areas of the Fermi surface perpendicular to the applied magnetic field.

Angle-resolved photoemission spectroscopy (ARPES)

ARPES measurements on single crystals were performed at beamline BL5-2 of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, and the beamline BL10.0.1 of the Advanced Light Source (ALS). The data were recorded by a Scienta R4000 analyzer at p = 4×10^-9 Pa at 20 K in both facilities. The total convolved energy and angle resolutions were E = 10 to 20 meV and θ = 0.2°, respectively. Good agreements of the Fermi surfaces and energy dispersions from ARPES measurements and DFT calculations are also obtained (see Supplementary Information).