Estimates of the Heritability of Human Longevity Are Substantially Inflated due to Assortative Mating

Here, Ruby et al. analyze an unprecedented amount of public family tree data from Ancestry and determine that the heritability of human longevity was well below 10%, lower than the widely-held belief that lifespan...

Abstract

Human life span is a phenotype that integrates many aspects of health and environment into a single ultimate quantity: the elapsed time between birth and death. Though it is widely believed that long life runs in families for genetic reasons, estimates of life span “heritability” are consistently low (∼15–30%). Here, we used pedigree data from Ancestry public trees, including hundreds of millions of historical persons, to estimate the heritability of human longevity. Although “nominal heritability” estimates based on correlations among genetic relatives agreed with prior literature, the majority of that correlation was also captured by correlations among nongenetic (in-law) relatives, suggestive of highly assortative mating around life span-influencing factors (genetic and/or environmental). We used structural equation modeling to account for assortative mating, and concluded that the true heritability of human longevity for birth cohorts across the 1800s and early 1900s was well below 10%, and that it has been generally overestimated due to the effect of assortative mating.

MORTALITY is an umbrella metric for the health of human populations, covering the endpoints of a plethora of human diseases, accidents, wars, and other human tragedies, as well as the biology of the “aging” process itself. A strong connection between genetics and human life span is generally acknowledged. Many human diseases are known to be genetic in nature (McClellan and King 2010), and alleles affecting the aging process itself are speculated to exist, though are not as firmly established (Brooks-Wilson 2013). But genes are far from the only factors that contribute to human life span. Over the past two centuries, massive progress has been made extending human longevity, mostly through improvements to sanitation and the fight against infectious disease (Cutler et al. 2006). Understanding the overall impact of genetics, or heritability, can provide a crucial context for broadly scoped genetic studies of human mortality and aging.

Heritability (h²), defined as the fraction of phenotypic variance that is due to genetic variance, is traditionally measured using phenotypic correlation between relatives and assumes that the correlation arises due to the sharing of genetic alleles (Falconer 1967). In practice, household environments are also shared between close family members, and “sociocultural” factors that affect the phenotype can be inherited and transferred through families in a manner similar to genetics (Rao et al. 1976; Cloninger et al. 1979). These multiple sources of phenotypic correlation can be cohesively modeled using structural equations based on pathway diagrams, as pioneered by Wright (1921).

The contributions by each of the two types of inherited factors, genetic (i.e., the heritability, h²) or sociocultural (whose analogous term to heritability is b²), can be simultaneously modeled in the structural equation framework. However, their individual contributions to phenotypic variance may be indistinguishable. Very few relationship-types give the power to resolve between these two types of inheritance, and those that do represent rare and difficult-to-identify family histories (e.g., Heath et al. 1985). But their combined effects can be captured by a single variable, t², representing the total transferrable phenotypic variance (Cloninger et al. 1979). The transferrable variance therefore represents the effect of all inherited factors, be they genetic or otherwise, on the phenotype (see Supplemental Material, Supplemental Text, section 1.2 for further discussion).

The heritability of human longevity has been estimated many times before (in some cases, more properly: the transferrable variance) using a variety of populations and methods. The reported values vary ∼20%: 16–22% from six family pedigrees, b1650–1874 (Mayer 1991); 26% for males and 23% for females, using Danish twins b1870–1900 (Herskind et al. 1996); 33% for Swedish twins b1886–1900 (Ljungquist et al. 1998); 18% for males and 20% for females, from European royalty and nobility (Gavrilova et al. 1998); 25% for an Amish community (Mitchell et al. 2001); 15% from Utah genealogies b1870–1907 (Kerber et al. 2001); 15% from historic Alpine communities (Gögele et al. 2011); and ∼15% from analysis of crowd-sourced web pedigrees including millions of individuals (Kaplanis et al. 2018). These estimates consider the correlations of life spans between blood (genetic) relatives. However, spouse life spans correlate as much or more than those of genetic relatives (Philippe 1978; Jarry et al. 2012), raising the possibility that correlated environments and/or assortative mating have confounded those estimates.

Here, we estimated the transferable variance of human life span, an upper-bound of genetic heritability, using the collapsed pedigrees from Ancestry. This massive resource included records for hundreds of millions of historical persons, facilitating a multitude of independent analyses across a plethora of relative-types and historical cohorts. While the phenotypic correlations between blood relatives matched those reported elsewhere in the literature, we also observed considerable correlation between in-law relatives, suggesting a substantial amount of assortative mating of relevance to life span. We developed and applied a simple structural equation model to quantify assortative mating and account for it when calculating transferrable variance. Across a variety of relative-types, consistently high values of assortment were measured, and the consequent values for transferable variance (t²) were consistently < 10%. Given that t² encompasses both the contributions of genetics and inherited sociocultural factors, a yet-lower value for heritability (h²) is implied.

Methods

Pedigree aggregation and deduplication

Our data set was a nonredundant set of aggregated and anonymized pedigrees (referred to as SAP) generated by collapsing Ancestry subscriber-generated family trees based on shared data and source references. To protect subscriber privacy, only relevant data were used, often at reduced resolution (e.g., only the year was provided for dates of birth and death, and for birth and death locations, and only the country outside the U.S.A. or state inside the U.S.A. were represented). Furthermore, the nonredundant aggregated pedigree set constructed for this study was limited in its source data to those Ancestry subscriber-generated family trees that were designated as “public.” There were 54 million such family trees containing more than six billion ancestors and relatives. Below, we describe the methods for performing entity resolution, comparing nodes between user-generated family trees, and the aggregation process used to create the nonredundant set used for the study.

Ancestry website users can generate personal pedigree by adding ancestor and relative nodes to a tree structure. For each pedigree node representing a single individual, consumers can record the following pieces of information: name, gender, birth date/place, marriage dates/locations, residences, death date/place, and links to parents/spouses/children. Ancestry subscribers can also link digital records to specific nodes in a pedigree as supporting evidence for the information recorded (e.g., a birth certificate as evidence of a birth date or parents’ names). Subscribers construct their own account-specific pedigrees, so multiple pedigrees often contain the same ancestors due to shared ancestry. To remove this redundancy, we aggregated 54.43 million publicly visible consumer pedigrees, containing a total of 6.44 billion nodes, through a multistep process.

Initially, nodes were clustered using a proprietary vector space model to block similar pairwise comparison candidates to reduce redundancy of nodes (persons) and begin building the consensus SAP. Each block of the pairwise candidates was then classified and placed into independent clusters using a proprietary comparator algorithm. The comparator algorithm determined cluster classifications based on several hundred pairwise features that measured node value similarities. The algorithm was developed in conjunction with a team of professional genealogists. The consensus SAP processing was considered complete once each node had been compared to its respective block.

Further, a proprietary algorithm was used to evaluate attributes of the cluster for quality and historical veracity, using the genealogical proof standards (Ancestry.com and Board for Certification of Genealogists, 2014). Attributes we evaluated included names, relationships, dates, and places contained in the nodes for each cluster.

Lastly, relationship edges were generated by retaining all such edges from source pedigrees linking the high-quality node relationship attributes of one cluster to any node in any other cluster. In this way, the data for a persona in the aggregated pedigree set came exclusively from a single, high-quality subscriber node’s relationship attributes, but the relationship connections were drawn from the high-quality data of multiple subscriber pedigrees.

The consensus SAP generated, as described above, contained several artifacts of specific relevance to heritability; therefore, the following three changes were made to the SAP prior to analysis. First: self-edges (a person being listed as their own spouse, parent, or child) were removed; only 16 such edges existed in the SAP (∼0.000002% of edges; see below). Second: 4,212,779 spousal edges were added connecting the mother and father of a given child (∼3% of spousal edges). Our data says little about the nature of people’s relationships. For this analysis, the social concept of a nuclear family was not rigidly defined and the spectrum of lifestyles covered by annotated spouse-pairs most likely spanned a variety of cohabitation paradigms (Rubin 2001). We saw missing data to be common in the SAP (Figure 1) and saw no reason to afford special status to parents for whom a spousal edge had been drawn by a user. Third: 3588 parent–child edges (∼0.0005% of edges) were severed if the assigned gender of the parent contradicted that expected for the parent-type (male for “father” and female for “mother”). Our analyses of heritability assumed biological parentage, in contrast with the sociological definitions of family (Stolley 1993) that were likely employed by Ancestry users when creating their family trees. These gender-incongruous edges represented visible instances of either adoption or mislabeling, and were therefore severed.

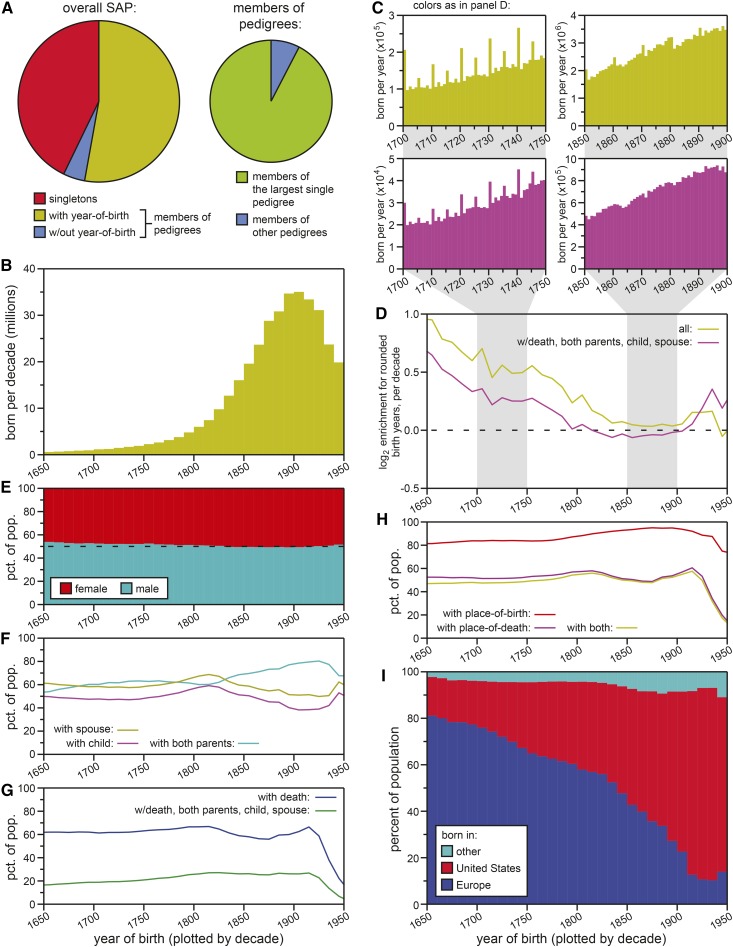
Figure 1.

Properties of the Ancestry data set. (A) An overview of the SAP, showing the fraction of the data meeting the most basic requirements for this analysis (pedigree membership and assignment to a birth cohort: left) and the composition of the SAP in terms of subtrees (almost the entire pedigree-linked population being members of a single tree: right). (B) The number of individuals born per decade. Limited to nonsingleton individuals with known year-of-birth. (C) The number of individuals born per year. All nonsingleton individuals with known year-of-birth (yellow), and individuals who additionally have year-of-death data and have tree connections to both parents, to a child, and to a spouse (purple). The panels on the left depict birth years 1700–1749; the panels on the right depict birth years 1850–1899. (D) Enrichment for “rounded” years-of-birth: for each decade, the log₂ of the ratio between mean number of births for years ending in “0” or “5,” and the mean number of births for other years is plotted on the y-axis. Colors as in (C). (E) Male-to-female gender ratio for nonsingleton individuals with known year-of-birth, plotted by decade-of-birth. (F) Percentages of the nonsingleton, known-year-of-birth population with spouses (yellow), with at least one child (purple), and with both parents (cyan), per birth-decade. (G) Percentages of the nonsingleton, known-year-of-birth population with known year-of-death (blue), or additionally with tree connections to both parents, to a child, and to a spouse (purple), per birth-decade. (H) Percentages of the nonsingleton, known-year-of-birth population with geographical data at any resolution for birth (red), for death (also requiring a known year-of-death; purple), and for both birth and death (yellow). (I) Percentages of the nonsingleton, known-year-and-geography-of-birth population born in the contiguous U.S.A. (red), Europe (blue), or elsewhere (cyan), per birth-decade. pct. of pop., percent of population; SAP, set of aggregated and anonymized pedigrees.

Properties of the SAP

The SAP contained 831,666,654 nodes (i.e., nonredundant representations of historical persons) connected by 852,321,294 edges (708,879,422 parent–child edges and 143,441,872 spousal edges). Of those nodes, 43% were singletons (had no edges connecting them to relatives; Figure 1A): singletons were excluded from these analyses. Of the remaining 475,489,572 individuals, 439,323,145 (> 92%) were connected as a single pedigree (i.e., linked by continuous paths of parent–child and/or spousal edges). The second-biggest single pedigree included only 8800 individuals. If only genetic edges (i.e., parent–child) were considered, 406,428,234 individuals (> 85% of nonsingletons) were connected as a single pedigree, illustrating a highly comprehensive family structure for the represented population.

Data fields were not universally populated across the analyzed (nonsingleton) population. However, the majority (439,361,203; > 92%; Figure 1A) carried year-of-birth data, allowing our analyses to be performed with birth cohort specificity. Population sizes were in the millions for every birth-decade after 1700 (Figure 1B). However, the quality of year-of-birth data were not consistent through history. The rounding of years-of-birth to years ending with a zero or a five (“rounded-years”) has been noted for other analyses of large pedigree databases (Kaplanis et al. 2018), and was seen in the Ancestry data set as well (Figure 1C). While still apparent across the latter half of the 19th century, rounding diminished in later birth-decades, and births in rounded-years were only slightly more abundant than in nonrounded-years by ∼1830 (Figure 1, C and D; yellow).

The quality of year-of-birth data also improved for individuals for whom other data fields were populated (Figure 1, C and D; purple). Additional fields were broadly required, in addition to year-of-birth, across most of the analyses presented here: year-of-death, satisfied by 212,586,785 persons; connection to a parent, satisfied by 377,746,933 persons (331,132,493 with both parents); connection to a child (i.e., parenthood), satisfied by 202,435,285 persons; and connection to a spouse, satisfied by 249,547,670). Figure 1, C and D, combined with our broad application of additional data and pedigree requirements in the course of our analyses, suggested the rounding-of-birth-years to be a nonconfounder for our analyses from ∼1800 to 1920 (i.e., the interval to which we limited our analyses).

Throughout the historical span of the SAP, gender was highly reported (always at > 99% for decades beyond 1650), with consistently balanced representations of males and females (Figure 1E). Other fields were sparser: edges to children, spouses, and both parents were historically variable, and were typically ∼50–70% (Figure 1F). Year-of-death representation declined rapidly after 1920 (presumably due to individuals either still living or a lag in their deaths being updated by Ancestry users). But even for much older birth cohorts, year-of-death-reporting never exceeded ∼two-thirds of individuals (Figure 1G; blue). Therefore, it would have been inappropriate to consider missing year-of-death as an indication that an individual was still living. This caveat prevented us from considering any life span data as legitimately right-censored, thereby precluding any longevity analysis based on the Cox proportional hazards model (Cox 1972). For life span analysis, years of birth and death were required as gating criteria, limiting our analysis to those birth cohorts for which the vast majority of the population would already be dead.

The highly connected single pedigree that dominated our data set indicated a highly comprehensive family structure for the represented population. Geographic data provided further insight into the make-up of that population. Place-of-birth records were available for the large majority of the population across birth cohorts (Figure 1H; red). Place-of-death records were less common, available for only ∼half of the population, but almost always provided in addition to, rather than independently of, place-of-birth (Figure 1H; violet and yellow). The place-of-birth distribution revealed a clear trend: the large majority of births in the 20th century were within North America—specifically, in the contiguous United States—while the large majority of births in and prior to the 18th century were in Europe. The population-in-question was therefore determined to be primarily Americans of European descent.

Identity-by-descent analysis of SAP accuracy

We used identity-by-descent analysis of genotyped individuals in the SAP for pedigree validation. These analyses are described in the Supplemental Text, section 4 and Figure S1.

Institutional review board review regarding the use of genotype data

The Quorum Review institutional review board (IRB) determined that this research project does not constitute research involving human subjects, and does not require IRB review and approval due to the investigators only obtaining deidentified and aggregated data for use in the research project.

Calculation of life span correlations and nominal heritabilities

Our focal phenotype was life span, i.e., years elapsed between birth and death. Values were limited to 0–120 years, with nonconforming values treated as missing data. Even though values as low as zero were allowed, we comprehensively applied a filter to the individuals whose phenotypes were analyzed, requiring them to have children represented in the SAP. That requirement resulted in few data for life spans < 20. Counts for unrealistically short life spans given parenthood were not excluded, but such presumably erroneous data were negligibly rare (all data for ages < 10 comprised ∼0.1% of life spans). This method of focusing the analyses on adult life spans also enriched the quality of the life span data (see above; Figure 1, C and D).

Correlation values were calculated using linear regression (Falconer 1967). Each pair of life spans for an appropriate (proband, relative) pair was treated as an (x,y) coordinate (x = proband life span, y = relative life span). Each such datum was weighted as described below, and the best-fit slope (θ) calculated by weighted-least-squares:

$$\theta =\frac{{{\displaystyle \sum }}^{\text{}}(w_i)*{{\displaystyle \sum }}^{\text{}}(w_i*x_i*y_i)-{{\displaystyle \sum }}^{\text{}}(w_i*x_i)*{{\displaystyle \sum }}^{\text{}}(w_i*y_i)}{{{\displaystyle \sum }}^{\text{}}(w_i)*{{\displaystyle \sum }}^{\text{}}(x_i^2)-{{\displaystyle \sum }}^{\text{}}{(w_i*x_i)}^2}$$

Standard error (SE) for θ was computed under the normality assumption:

$$\text{SE}(\theta )=\sqrt{\frac{{{\displaystyle \sum }}^{\text{}}(R_i^2*w_i)}{{{\displaystyle \sum }}^{\text{}}(w_i*S_i^2)*(N_{eff}-2)}}$$

where w_i is the weight of datum i (described below), x_i is the x-coordinate of datum i, R_i is the y-axis residual of datum i from the linear regression, x_mean is the weighted mean of all x-axis values, and S_i = x_i – x_mean. As highlighted by the weighting scheme below, not all (x,y) pairs are independent. For the purpose of calculating the effective number of independent data for the SE estimate (N_eff), we applied the following formula:

$$N_{eff}=\frac{N_{pro}+N_{rel}}{2}$$

where N_pro equals the number of unique persons used as probands and N_rel equals the number of unique persons used as relatives.

Standard practice is to directly apply the SE of the regression to the derivative heritability estimate (Falconer and Mackay 1996, p. 177). Nonetheless, correlations between relative pairs that exist within the context of a larger family could have reduced the independence of the data points, thereby causing overestimation of the estimate’s accuracy. We explored this potential issue empirically in the SAP (see Supplemental Text, section 5) and observed the true errors to be highly consistent with our expectations based on sample size from the equation above (see Figure S2). Therefore, we continued to report errors according to the above method throughout the manuscript.

The linear regression approach to heritability estimation, as traditionally applied (Falconer 1967), assumes that relative pairs are drawn from the same population, and therefore that the means and variances along the two axes are equal (Falconer 1967). Here, all regressions were performed on nonreciprocal proband–relative pairs, with nonreciprocity always achieved by plotting the older of each pair on one axis and the younger on the other, so the assumption of equal means and variance did not hold. Differences in mean do not affect the slope that is used to calculate heritability, so no compensatory action was needed to address mean differences. However, variance differences were addressed. To compensate for differences in the life span variance between x- and y-axis populations, θ was multiplied by the ratio of standard deviations (SD’s) for the nonredundant populations corresponding to each axis to arrive at the correlation value (ρ):

$$\rho =\theta *\frac{SD(proband)}{SD\left(relative\right)}$$

This equation is simply the well-known relationship between regression slope and correlation coefficient, restated in terms of the specific data from our analyses. SE were multiplied by the same quotient to arrive at the SE for the correlation.

Nominally, heritability can be calculated through division of ρ by the additive relatedness for the relative-pair (Falconer 1967). When we did that, we referred to the value as nominal heritability. SE were again divided by the same factor.

Datum weights (each datum being an x,y pair of proband–relative phenotypes) were calculated using the number of times each half-datum was used in the analysis (n_x,n_y) by the following equation:

$$w= \frac{1/n_x+1/n_y}{2}$$

For a unique pair, w = 1; for a pair where one half-datum is used once and the other is used twice, w = 0.75; and for a pair where each half-datum is used twice, w = 0.5. Use of the same half-datum as both a proband (x-axis) and as a relative (y-axis) was not considered to be redundant in this normalization scheme.

A structural equation model for parsing the contributions to life span correlations

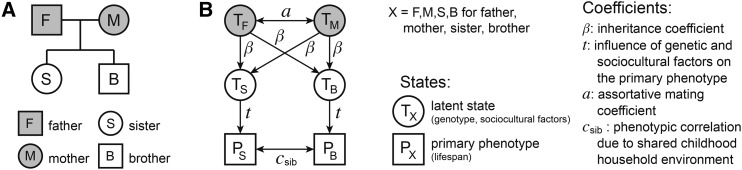
We developed a structural equation model to describe the phenotypic (life span) correlations between relatives of various types. The full development and mathematical description of the model and its applications can be found in the Supplemental Text (sections 1–3). Here, we give a brief overview, using a small nuclear family (depicted in the pedigree of Figure 2A) as an exemplar.

Figure 2.

A summary of our structural equation model. (A) A traditionally drawn pedigree of a nuclear family, with two parents (father: F and mother: M) and two children (sister: S and brother: B). As per convention, squares represent males and circles represent females. (B) The pathway diagram for our structural equation model’s description of the phenotypic correlation between the two siblings from the family depicted in (A). Please note the different convention for node shapes in pathway diagrams for structural equation models: here, squares represent observable states (phenotypes), while circles represent latent states. See Supplemental Text, section 1 for more discussion of these diagrams and a full explanation of the model.

Our structural equation model was built on the foundations of Rice et al. (1978) and Cloninger et al. (1979), and included three core variables. The first, transferable variance (t²), is the phenotypic variance attributable to transferable factors (genotype and sociocultural factors). It is akin to, and includes, heritability (h²), but it also encompasses the variance due to inherited sociocultural factors (b²) as well as covariance between the two. The second core variable is the inheritance coefficient (β), which describes the extent to which genetic and sociocultural factors are transferred from one parent to one child. In traditional genetics, this variable has a fixed value of one-half, but the transference of sociocultural factors could theoretically happen at a much wider range of efficiencies. The third core variable is the assortative mating coefficient (a), which describes the correlation between the latent genetic and sociocultural states of spouses. This term is meant to encompass all mechanisms of assortative mating (primary assortment on the phenotype, secondary assortment on other phenotypes, inbreeding, and social homogamy, etc.), though we note that primary assortment is limited for life span because the phenotype cannot be observed until death, at which point the opportunity to mate has ended. See Supplemental Text (section 1.3) for more details.

In Figure 2B, the pathway diagram for our structural model is applied to the nuclear family from Figure 2A, showing the terms necessary to describe the phenotypic correlation between the two siblings (S and B). In these pathway diagrams (Figure 2B), circles and squares represent latent and observable states, respectively (as opposed to female and male, as in traditional pedigrees and Figure 2A). The observable states here are the phenotypes of the siblings (life spans: P_S and P_B). The latent states are the genotypes and sociocultural equivalents for each individual (T_S and T_B for the siblings; T_F and T_M for the parents). Arrows connecting the latent and observable states represent correlations, with the coefficient of each correlation indicated next to the arrow.

Siblings share a correlation term in addition to the three core variables of our model: c_sib. This coefficient describes the contribution of nontransferable aspects of the siblings’ shared environment (presumably, childhood household). Such additional variables are only added in cases of such extensive sharing of environment (e.g., c_sp is added for spouses). This approximation matches the rarity of extended-family household-sharing for extended families in contemporary American society (consistently < 6% of children sharing with a grandparent between 1970 and 2003; U.S. Census Bureau 2004). However, more extensive household/community-sharing between extended relatives is not omitted from the model: sociocultural transference is inclusive of such practices across extended-family networks. Phrased differently, if the frequency of household-sharing or geographic proximity are greater between relatives than between randomly selected individuals, and that frequency/proximity decreases as relatives become more remote, then the definition of sociocultural transference applies. Under those circumstances, household and geography would qualify as nongenetic factors that are inherited through families, whose probability of being shared is diluted through each generation of outcrossing (just like alleles).

Data availability

Raw values for all population-level statistics presented in this manuscript, including sample sizes and estimate errors where appropriate, are provided as Supplemental Data File 1 (Excel spreadsheet), organized by figure. A far more comprehensive set of regression-based heritability estimates, along with cohort statistics and estimate errors, are provided as Supplemental Data File 2 (tab-delimited text). In both cases, population sizes are rounded to 1000-person resolution (or < 1000 indicated when relevant), and calculated values are limited to five significant figures or decimal places, whichever is fewer. Supplemental material available at Figshare: https://doi.org/10.25386/genetics.7108637. Although we cannot make the genealogical and genotype data widely available to the academic community, due to customer privacy commitments and the terms of consent, specific requests for deidentified data access will be considered on a case-by-case basis. Readers are welcome to comment on the online version of the paper. Correspondence and requests for materials should be addressed to Catherine Ball (cball@ancestry.com).

Results

The nominal heritability of human life span was accompanied by substantial assortative mating

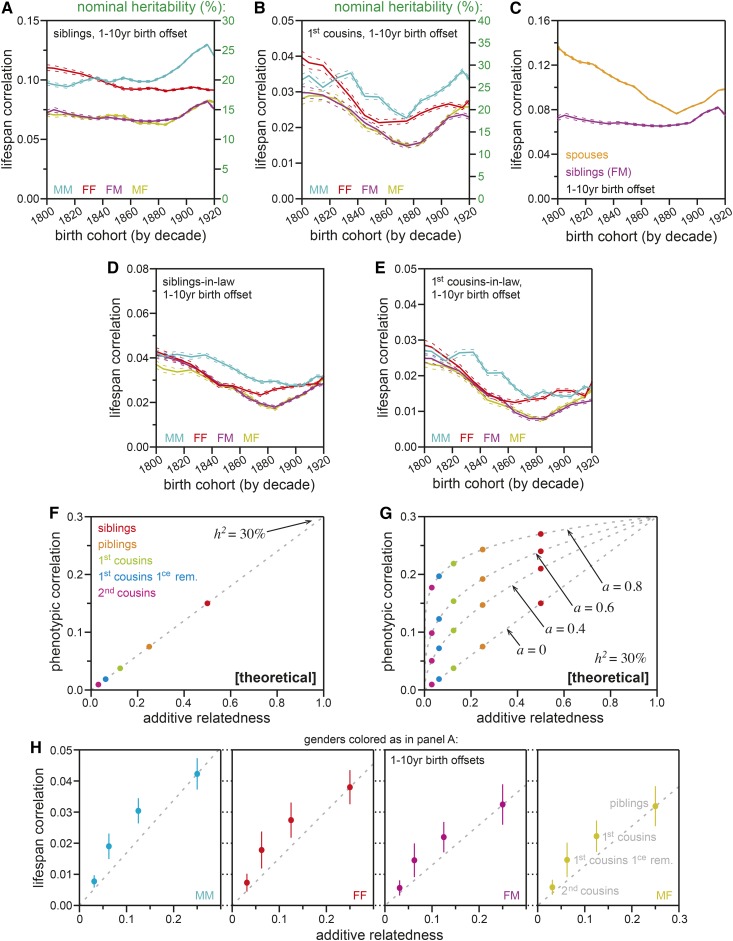
Phenotypic correlations were measured between relatives for birth cohorts across the 19th and early 20th centuries, beginning with contemporary relative-types (i.e., relative-pairs born within 10 years of one another): siblings (Figure 3A) and first cousins (Figure 3B). For both relative-types, and across the 120-year span of birth cohorts, the nominal estimates of heritability (calculated by division of the correlation by the additive relatedness of the relative-type) agreed with estimates from the existing literature, with most estimates between 20 and 30%, and with across-gender comparisons sometimes dropping below 15% (Figure 3, A and B).

Figure 3.

Life span correlations with in-law relatives and patterns of remote relative correlations reveal substantial assortative mating for factors affecting longevity. (A) Life span correlations for siblings (y-axis); x-axis: the birth-decade of the proband. The sibling of each proband was required to be born 1–10 years prior to that proband. Gender-specific correlations between male–male (MM; cyan), female–female (FF; red), female–male (FM; magenta), and male–female (MF; yellow) sibling-pairs were calculated separately. Dotted lines indicate estimate SE. The nominally estimated heritability values are shown on the right-hand y-axis. (B) Life span correlations for first cousins, calculated and plotted as in (A). (C) Life span correlations for female–male sibling-pairs [FM; magenta; reproduced from (A)] and spouse-pairs (orange), calculated and plotted as in (A). (D) Life span correlations for siblings-in-law, calculated and plotted as in (A). (E) Life span correlations for first-cousins-in-law, calculated and plotted as in (A). (F) A theoretical plot illustrating the linearity between additive relatedness (x-axis) vs. phenotypic correlation (y-axis) that is assumed across relative types by the nominal heritability model (see Supplemental Text, section 2). Dots indicate particular relationship types; the dashed gray line indicates the continuous function. (G) A theoretical plot illustrating the amplifying effects of assortative mating (a) on phenotypic correlations. Axes as in (F). For various values of a, dots indicate particular relationship types [colored as in (F)]; dashed gray lines indicate the continuous functions (see Supplemental Text, section 2). (H) The observed relationships between additive relatedness (x-axis) and life span correlations (y-axis) for four remote relative types, all relatives born 1–10 years prior to the proband. Dots indicate the mean value for decade birth cohorts, 1800–1920. Vertical lines indicate the SD of correlation values across those decades. Each panel displays estimates for a particular gender pair, colored as in (A). Dashed gray lines indicated a nominal (linear) extrapolation through piblings. Siblings are omitted from this plot due to the confounding effects of shared-household environment (see Supplemental Text, sections 1.4 and 2.2).

Considerable correlation was also observed between spousal life spans, consistently in excess of that observed between opposite-gendered siblings (Figure 3C). Spousal correlation is expected on two grounds: shared-household environment during adulthood and/or assortative mating. The two can be distinguished by definition: the effects of shared-household environment are nontransferable through inheritance, whereas the factors correlated by assortative mating are transferable, allowing them to also generate correlations with family members of the spouse (see Supplemental Text, Diagram S4). To test whether spousal correlation was due to shared-household environment or assortative mating, we measured the phenotypic correlations across two classes of contemporary in-law relatives that do not typically share household environment: siblings-in-law (Figure 3D) and first-cousins-in-law (Figure 3E). In both cases, considerable correlation was observed: in the case of first cousins, the correlation of in-laws was within twofold that of blood relatives (Figure 3B vs. Figure 3E). These observations were consistent with a substantial role for assortative mating with respect to the life span phenotype.

Assortative mating increased the phenotypic correlations of extended relatives above the expectations of linearly additive genetics

The framework for nominal heritability analysis is a linear increase of relatives’ phenotypic correlation with their additive relatedness (Falconer 1967), theoretically illustrated in Figure 3F. In this framework, higher-than-expected correlations (upward deviations from the line in Figure 3F) are expected on a case-by-case basis, due to shared environment for close relatives (generally considered in terms of shared household), and/or the additional genetic variance from shared dominance and epistasis properties between siblings. The otherwise strictly linear expectation of additive relatedness vs. phenotypic correlation derives from the genetic inheritance model, which itself derives from the rules of meiosis: one-half of genetics are shared between a parent and a child (in the context of our structural equation model from Figure 2B: β = 1/2). Two modifications to the nominal heritability framework can create general deviation from that linear expectation. The first is population-wide deviation from the β = 1/2 assumption. Although unrealistic for genetics, the inheritance of sociocultural factors could be governed by a wider range of values. The second possible modification is the addition of an assortative mating term, discussed below.

The contribution of assortative mating to phenotypic correlations between relatives has been explored using structural equation models (e.g., Rao et al. 1976; Rice et al. 1978, 1980; Cloninger et al. 1979; Cloninger 1980; Heath and Eaves 1985; Russell et al. 1985). Building on the frameworks of Rice et al. (1978) and Cloninger et al. (1979), we developed a simplified structural equation model to theoretically explore the impact of assortative mating (see Supplemental Text, section 1 for full details). Our model included a single variable a to describe the correlation between the latent states of spouses (i.e., genotypes and sociocultural factors) due to assortative mating of any variety (Figure 2B; see Supplemental Text, section 1.3 for discussion of the varieties of assortative mating). In this model (or any that includes assortative mating), the correlations between relatives deviate from their nominally expected values, becoming greater as a increases (illustrated in Figure 3G). In our data, we observed such an elevation of correlations between relatives vs. the linear expectation extrapolated from closer relatives (Figure 3H). This arched pattern was consistent with substantial assortative mating for the transferable factors that affect longevity.

An alternative explanation for the arched pattern in Figure 3H would have been an elevated value for the inheritance term (β) above the expectation of one-half from genetics. When sociocultural factors are considered, this is a realistic possibility. Nonetheless, this alternative hypothesis was inconsistent with our data: although it would predict the behavior seen in Figure 3H, it would not contribute to any correlation between in-law relatives, as was observed in Figure 3, D and E (see Supplemental Text, equation 32: nonzero a is required for in-law correlations to themselves be nonzero). Therefore, we attributed the bulk of the behavior observed in Figure 3H to assortative mating.

The nonlinear relationship between life span correlations and additive relatedness (Figure 3H), combined with the substantial life span correlations between in-law relatives (Figure 3, D and E), confirmed substantial assortative mating for factors of relevance to life span. Consequentially, any linear extrapolation of transferrable variance (t²) would be expected to be inflated, potentially to a massive degree (see Supplemental Text, section 2 for further exploration of this phenomenon). Therefore, we sought other means to calculate the value of t².

Structural equation modeling of (co)siblings-in-law suggested an upper-bound heritability estimate of 7%

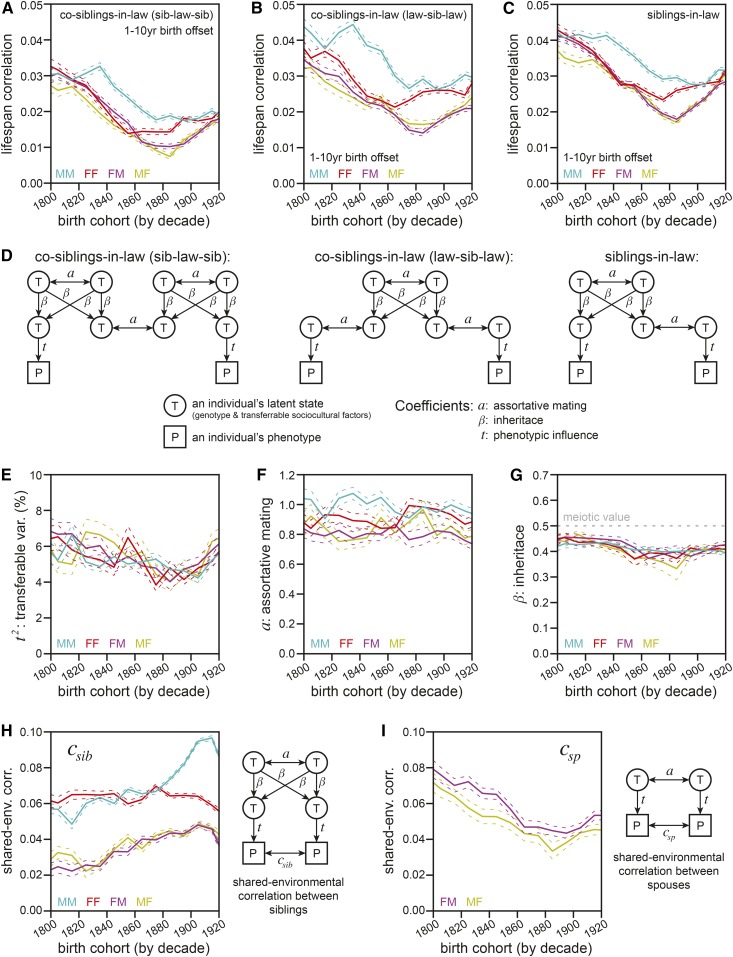
To assign values to the various sources of phenotypic correlation between family members, we applied our structural equation model to the correlations observed between additional relative types. Despite its size, the SAP was composed of deidentified data, and it therefore lacked specific information about household status or, for the deceased subjects of our analyses (who were therefore nongenotyped), zygosity status for twins. Most of the relative types considered to be the most informative in structural equation modeling (Heath et al. 1985) were therefore absent in our anonymized data set. Nonetheless, the parameters of our simplified structural equation model were solvable with the use of cosiblings-in-law (see Supplemental Text, section 3 for details).

Correlations between two types of cosiblings-in-law were measured: the sibling of a sibling’s spouse (sib-law-sib; Figure 4A) and the spouse of a spouse’s sibling (law-sib-law; Figure 4B; pathway diagrams shown in Figure 4D). Correlations were additionally measured between siblings-in-law (Figure 4C). The phenotypic correlations across both varieties of cosibling-in-law were close to those of siblings-in-law, with the drop in covariance due to an additional spouse edge (law-sib-law; Figure 4B) being less than the drop due to an additional sibling edge (sib-law-sib; Figure 4B). Like the results in Figure 3, this again suggested a considerable quantity of assortative mating.

Figure 4.

Structural equation modeling of sibling-in-law networks reveals a substantial role for assortative mating and a diminished role for transferable variance (t²) in human life span. (A) Life span correlations for cosiblings-in-law of the sib-law-sib variety (see Results), calculated and plotted as in Figure 3A. (B) Life span correlations for cosiblings-in-law of the law-sib-law variety (the sibling of a sibling’s spouse, see Results), calculated and plotted as in Figure 3A. (C) Life span correlations for siblings-in-law (reproduced from Figure 3D; shown for direct comparison to (A and B). (D) Pathway diagrams for the application of our structural equation model to the three relative types in (A–C) (see Supplemental Text, section 1 for details). (E). Transferable variance (t²), calculated from the data in (A–C) (see Supplemental Text, section 3.3 for solving method). Colored as in Figure 3A. (F) The assortative mating coefficient (a), calculated from the data in (A–C) (see Supplemental Text, section 3.4 equation 43 for solving method). Colored as in Figure 3A. (G) The inheritance coefficient (β), calculated from the data in (A–C) (see Supplemental Text, section 3.5 for solving method). Colored as in Figure 5A. (H) The correlative effect of nontransferable shared childhood environment (shared-env. corr.) on sibling life spans (c_sib; y-axis), along with the relevant pathway diagram. See Supplemental Text, section 3.6 for solving method. Colored as in Figure 3A. (I) The correlative effect of nontransferable shared adult environment on spouses’ life spans (c_sp; y-axis), along with the relevant pathway diagram. See Supplemental Text, section 3.6 for solving method. Female–male (FM; magenta) and male–female (MF; yellow) spouse-pairs are plotted, with the first-listed gender of each pair being the proband (younger individual).

As illustrated in their pathway diagrams (Figure 4D), the correlations for these three relative-types share unequal dependencies on the core model parameters describing assortative mating (a), inheritance (β), and the influence of transferable factors on the phenotype (t), which when squared equals the transferrable variance (t²). Therefore, we were able to solve for each parameter (see Supplemental Text, section 3 for mathematical details). For all gender combinations and birth cohorts across the 19th and early 20th centuries, t² was < 7% (Figure 4E). Because t² represents the combined effects of transferred genetic (h²) and sociocultural (b²) factors, it can be considered as an upper-bound estimate of heritability. So even if transferred sociocultural factors had no effect whatsoever on life span, heritability would still only be 7% according to these estimates.

We additionally solved for the assortative mating and inheritance coefficients (a and β, respectively; Figure 4, F and G). Across all comparisons, we estimated a to be > 0.8 (Figure 4F). This unexpectedly high value implied that the large majority of the factors affecting life span that can be transferred through inheritance are also matched between spouses. At the same time, we estimated β to be only ∼0.40–0.45 (Figure 4G), lower than the value of 0.5 expected for genetics. These two estimates were not statistically independent: both are base terms raised to exponents whose values increase with the degree of relative, so overestimation of one would result in underestimation of the other (see Supplemental Text, section 1.6 for mathematical details). Nonetheless, the observed values were both theoretically reasonable and in accord with other observations. As discussed in the Methods and in the Supplemental Text, section 3.7, β is traditionally assigned a value of one-half for genetic factors due to the rules of meiosis; in this case, β represented the inheritance term for both genetic and sociocultural factors, so there was no such expectation for its value. Further, the high correlations for relatives in-law (Figure 3, D and E) and curvature of additive relatedness vs. phenotypic correlation for blood relatives (Figure 3H) both supported the conclusion of there being substantial assortative mating. Below, we will further describe independent estimates of a to evaluate the robustness of this result.

The solutions for the terms above, gathered from the three (co)sibling-in-law correlations, allowed us to revisit the correlations between siblings (Figure 3A) and spouses (Figure 3C), and to parse out the correlative effects of shared-household environments for each (Figure 4, H and I). In each case, the contribution of household environment was substantial, equaling or exceeding that of transferrable factors (independent of assortative mating, i.e., t²) in all cases except siblings of opposite gender.

Reestimation of assortment and transferable variance across multiple remote relative types consistently suggested life span heritability to be well below 10%

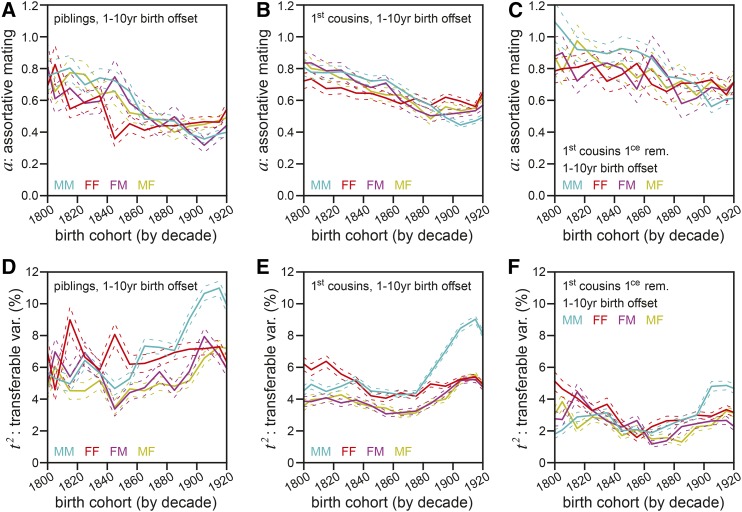
To test the robustness of our model’s estimates of a and t², we applied an alternative method, the assortment-correction method (see Supplemental Text, section 3.7 for details), to estimate a and t² using data from across a wider variety of relationship types. This method is built upon independent measurements of the assortative mating coefficient a from arbitrary pairs of blood and equivalent in-law relatives. We measured a repeatedly, comparing the correlations of piblings (parents’ siblings; avuncular relatives) with those of piblings-in-law (Figure 5A); first cousins with first-cousins-in-law (Figure 5B); and first-cousins-once-removed with first-cousins-once-removed-in-law (Figure 5C). These separate estimates yielded values that were statistically distinct from one another, suggesting some limitations to our simplified model. Nonetheless, the values were always substantial, closer to 1.0 than to zero, consistent with the high estimates derived from siblings-in-law (Figure 4F).

Figure 5.

Correlations between remote in-law relatives confirm a substantial role for assortative mating and a diminished role for transferable variance (t²) in human life span. (A) The assortative mating coefficient (a), calculated via division of pibling-in-law life span correlation by pibling life span correlation (see Supplemental Text, section 3.4 equation 44 for solving method). (B) The assortative mating coefficient (a), calculated via division of first-cousin-in-law life span correlation by first cousin life span correlation. (C) The assortative mating coefficient (a), calculated via division of first-cousin-once-removed-in-law life span correlation by first-cousin-once-removed life span correlation. (D) Transferable variance (var.) (t²), calculated by the assortment-correction method (see Supplemental Text, section 3.7 for solving method) using pibling correlations and a estimates from (A). (E) Transferable variance (t²), calculated by the assortment-correction method using first-cousin correlations and a estimates from (B). (F) Transferable variance (t²), calculated by the assortment-correction method using first-cousin-once-removed correlations and a estimates from (C). (A–F) Colored as in Figure 3A.

Using each of our independently ascertained values for a from Figure 5, A–C, we estimated t² for the corresponding blood relative type using the assortment-correction method (see Supplemental Text, section 3.7). Like the estimates for a, those for t² varied between piblings (Figure 5D), first cousins (Figure 5E), and first-cousins-once-removed (Figure 5F). However, in no case was the estimate of t² from these extended-relative analyses (Figure 5, D–F) substantially greater than the value derived in the siblings-in-law analysis (Figure 4E). Even in the case of the highest estimates, those of contemporary piblings, t² was consistently ∼6–7%, occasionally spiking to 10% (Figure 5D). Considered together with the sibling-in-law results, these analyses consistently and independently indicated t² for human longevity to be well under 10% across the birth cohorts examined.

The transferable variance of life span decreased as the disparity between relatives’ birth cohorts increased

The major threats to human health and life have changed dramatically across the time periods explored in our analyses. Therefore, it cannot be taken for granted that the factors that are transferred and inherited between relatives, and upon which assortative mating occurs, would have equal impacts on life span across different historical contexts. All of our analyses up to this point have evaluated the correlations between contemporary relatives, born within a decade of one another. To evaluate the consistency of phenotypic correlation as birth cohort disparity grew, we examined piblings, whose birth offsets were more variable (0–60 year range) than for most relative-types.

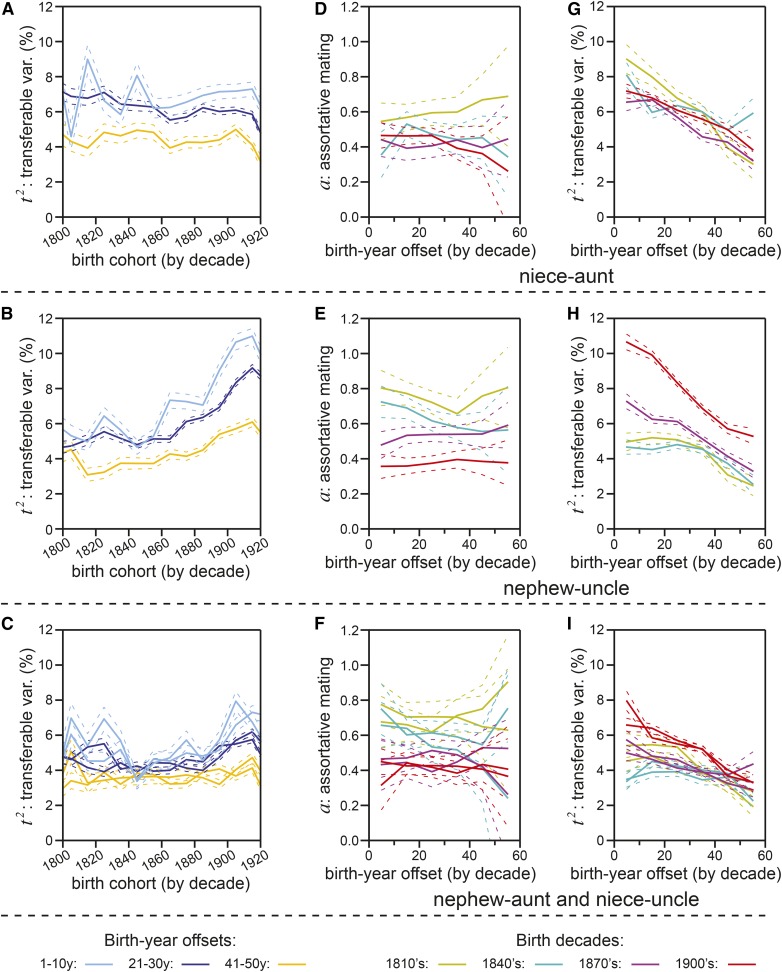
We estimated t², correcting for assortative mating (using the assortment-correction method described in the Supplemental Text, section 3.7), for niece–aunt (Figure 6A), nephew–uncle (Figure 6B), and niece–uncle/nephew–aunt (Figure 6C) pairs, across the 19th and early 20th century birth cohorts. These analyses revealed that relatives born within a decade of one another (light blue) had higher t² values than those born two-to-three decades apart (dark blue) or four-to-five decades apart (yellow). Plots of the pibling vs. pibling-in-law estimates for a as a function of birth-year offsets revealed no upward or downward trends across any gender combinations (Figure 6, D–F). In contrast, t² estimates dropped clearly, significantly, and consistently as birth cohort offsets increased, across all gender combinations (Figure 6, G–I).

Figure 6.

Assortment-corrected estimates of transferable variance (var.) (t²) diminish as relatives’ birth cohorts diverge. (A) Niece–aunt transferable variance (t²) (solid lines) calculated by the assortment-correction method (see Supplemental Text, section 3.7 for solving method) for each decade-long niece birth cohort, for aunts whose birth years were offset from their nieces by 1–10 years (cyan), 21–30 years (blue), or 41–50 years (yellow). SE of estimates are shown as dotted lines. (B) Nephew–uncle transferable variance (t²), calculated and plotted as in (A). (C) Nephew–aunt and niece–uncle transferable variances (t²), each calculated and plotted together as in (A). (D) The assortative mating coefficient (a; y-axis), calculated via division of niece–aunt-in-law life span correlation by niece–aunt life span correlation (see Supplemental Text, section 3.4 equation 44 for solving method), plotted for niece–aunt pairs of varying birth-year offsets (x-axis indicates the number of years prior to the niece’s birth the aunt was born) for four decade-long niece birth cohorts: 1810s (yellow), 1840s (cyan), 1870s (magenta), and 1900s (red). Dotted lines show SE. (E) The assortative mating coefficient (a) vs. birth-year offsets for nephew–uncle and nephew–uncle-in-law pairs, calculated and plotted as in (D). (F) The assortative mating coefficient (a) vs. birth-year offsets for niece–uncle and niece–uncle-in-law pairs, or nephew–aunt and nephew–aunt-in-law pairs, calculated for each and plotted together as in (D). (G) Niece–aunt transferable variance (t²) calculated as in (A), plotted by birth-year offset as in (D). (H) Nephew–uncle transferable variance (t²) calculated as in (B), plotted by birth-year offset as in (E). (I) Niece–uncle and nephew–aunt transferable variances (t²) calculated as in (C), plotted by birth-year offset as in (F).

Discussion

The heritability of human longevity is far less than previously estimated

Our analyses began with measurements of the correlations of human life span across a massive pedigree, the SAP, and extrapolation of the nominal heritability of that trait using the known additive genetic relatedness of the relative-types. These values were in the same range as the plurality of life span heritability estimates already to be found in the literature: ∼15–30% (Figure 3, A and B) (Mayer 1991; Herskind et al. 1996; Gavrilova et al. 1998; Ljungquist et al. 1998; Kerber et al. 2001; Mitchell et al. 2001; Gögele et al. 2011; Kaplanis et al. 2018). We also reproduced a less-abundantly reported but nonetheless important feature of the literature, that the correlations between spouses are also high (Philippe 1978; Jarry et al. 2012), and we extended that observation of substantial correlation between spouses to remote in-law relatives, suggesting the inherited factors driving life span correlations between blood relatives to also be transferable between spouses.

While ambiguity remained around the relative contributions of genetic vs. nongenetic inherited factors, the implication of in-law correlations was clear: assortative mating for life span has occurred. We modeled the effects of assortative mating on familial correlations using the established framework of structural equations (Rice et al. 1978; Cloninger et al. 1979), and showed clear and profound inflation of nominal heritability estimates when assortment is anything other than negligible (Figure 3G; see Supplemental Text, section 2). We further demonstrated assortative mating using the pattern of correlations vs. additive relatedness across remote blood relatives (Figure 3H), and measured its coefficient a repeatedly using siblings-in-law with cosiblings-in-law (Figure 4F), piblings with piblings-in-law (Figure 5A), first cousins with first-cousins-in-law (Figure 5B), and first-cousins-once-removed with first-cousins-once-removed-in-law (Figure 5C), always getting substantial values, generally much greater than 0.5. For each measurement of a, we also measured the transferable variance t² that was implied by the value of a. And in all cases, the value was considerably lower than what is generally ascribed to just its genetic component (heritability, h²): well under 10% (Figure 4E, Figure 5, D–F, and Figure 6, G–I). These results are summarized in Table 1.

Table 1. Average estimates of structural equation model parameters from various data sources.

Birth cohort range	Model Parameter	(Co)siblings-in-law	Piblings	First cousins	First-cousins-once-removed	Households
1800s–1830s	t2	5.86% (± 0.68%)	5.85% (± 1.52%)	4.63% (± 0.91%)	3.21% (± 0.95%)	–
	a	0.883 (± 0.096)	0.681 (± 0.123)	0.750 (± 0.061)	0.852 (± 0.103)	–
	β	0.440 (± 0.013)	(1/2)	(1/2)	(1/2)	–
	csib	–	–	–	–	0.0433 (± 0.0179)
	csp	–	–	–	–	0.0659 (± 0.0083)
1840s–1870s	t2	5.19% (± 0.66%)	5.47% (± 1.20%)	3.79% (± 0.64%)	1.96% (± 0.61%)	–
	a	0.881 (± 0.092)	0.527 (± 0.114)	0.637 (± 0.058)	0.785 (± 0.080)	–
	β	0.395 (± 0.025)	(1/2)	(1/2)	(1/2)	–
	csib	–	–	–	–	0.0510 (± 0.0155)
	csp	–	–	–	–	0.0504 (± 0.0079)
1880s–1910s	t2	4.79% (± 0.59%)	7.19% (± 1.68%)	5.47% (± 1.50%)	2.90% (± 0.89%)	–
	a	0.888 (± 0.084)	0.425 (± 0.044)	0.532 (± 0.047)	0.667 (± 0.055)	–
	β	0.398 (± 0.020)	(1/2)	(1/2)	(1/2)	–
	csib	–	–	–	–	0.0600 (± 0.0172)
	csp	–	–	–	–	0.0436 (± 0.0050)

The mean (± SD) of estimates across all gender combinations and across the indicated birth-decade cohorts were averaged. SD is for those estimates; per-estimate SEs were not considered here. “(1/2)” indicates a value imposed by the estimation technique. Source data for these calculations are plotted in Figure 4 and Figure 5, and are provided in Supplemental Data File 1.

While novel, our low estimate of heritability was easy to reconcile with the higher estimates of previous literature. Many of the previous estimates derive from a nominal heritability estimate, which involves a straightforward multiplication of the correlation by the additive relatedness (see Methods and Supplemental Text, section 1.1). As we note above, when we failed to take assortative mating into account (Figure 3, A and B), our own nominal estimates were similar to those of the literature (see the Introduction).

In comparison to twin studies, which take shared and transferred environment largely into account, and in which assortative mating has less of an impact, our estimates were still lower than the literature consensus. We rationalize those discrepancies by invoking the definition of heritability, as described by Falconer (1967): “heritability is a property not only of a character but also of the population and of the environmental circumstance to which the individuals are subjected. Since the value of heritability depends on the magnitude of all the components of variance, a change in any one of these will affect it.” (p. 166). The twin studies to which we compare our results include a Danish twin cohort (Herskind et al. 1996) and a Swedish twin cohort (Ljungquist et al. 1998). In addition to their limited geographic scope, the recruitment biases into such cohorts are more severe than for inclusion in the SAP. It is reasonable to assume that the geographic and socioeconomic scopes of such studies were more limited than our study. To the extent that any aspects of geography or socioeconomic status are not transferrable but do affect life span, their limitation is expected to increase the heritability value for the population: if h² = V_G/(V_G + V_E), then decreasing the environmental variance V_E through limitation of geographic and socioeconomic diversity would increase the value of h² (see Supplemental Text, section 1.1). A similar argument about limited environmental diversity can be made about studies of European royalty and nobility (Gavrilova et al. 1998), an Amish community (Mitchell et al. 2001), Utah genealogies (Kerber et al. 2001), or Alpine communities (Gögele et al. 2011).

The only other life span heritability study of sufficiently global scope for the results to be comparable to ours is that of the analysis of Kaplanis et al. (2018), which analyzes crowd-sourced web pedigrees including millions of individuals. Like our study, theirs presents an estimate of heritability below the consensus of the literature (∼15%). But it is still far above our upper-bound estimate of < 10%. The estimates provided by Kaplanis et al. are based on a maximum-likelihood fit to the nominal estimation model: correlations vs. a matrix of inferred genome sharing (their Supplemental Text, p21–23), with inbreeding observed in their pedigree taken into account. However, assortative mating can take many forms beyond inbreeding (e.g., social homogamy or primary assortment on related secondary phenotypes; see Supplemental Text, section 1.3), and we have shown inbreeding to be at most a minor contributor to the observed assortative mating around life span (see our Supplemental Text, section 4 and Figure S1). Accordingly, we note the close similarity between figure 3D of Kaplanis et al. (IBD vs. longevity correlation) and our Diagram S12 (see Supplemental Text), which illustrates the ability of linear extrapolation through data with both assortative mating and household-environmental sharing to erase the effects of both, and produce an inflated estimate of heritability.

On the relative impact of genetic vs. sociocultural transferrable factors on life span

Our analysis of transferrable variance (t²) did not distinguish between the contributions of genetic (h²) vs. sociocultural (b²) factors. Since t² is the sum of those two components, it follows that neither value can individually exceed the value of t², implying an at least twofold reduction in the estimate of genetic contribution to human longevity based on our results. That would be if t² were entirely comprised of h², with no additional contribution by b². Nonetheless, as we argue below, there is ample evidence from the sociology and economics literature that sociocultural factors of relevance to human life span are indeed inherited through families.

The concept of socioeconomic status is broad and complex, encompassing or directly connected to many diverse factors: wealth, geography, education, occupational prestige, race/ethnicity, cultural affiliations, neighborhood environment (built, social, and service), and even diet (Braveman et al. 2005). It therefore encompasses many, if not all, of the factors described by Cloninger et al. as “sociocultural” (1979). Despite the complexity of its definition and its diverse forms of measurement, socioeconomic status is well established as a major driver of variance in human health and longevity (Marmot 2005). For instance, the strong link between income (a component of socioeconomic status) and longevity manifests on both the macro scale—national GDP per capita vs. national life expectancy, first noted by Preston (1975) and reproduced numerous times since (e.g., Pritchett and Summers 1996; Deaton 2003)—and on the micro scale, with year-specific income predicting age-specific mortality within the U.S.A. (Chetty et al. 2016).

Socioeconomic status is known to be transferred in families. The study of adoptees has further demonstrated that educational and income status can be transferred between generations independently of genetics (Sacerdote 2002). Such human capital transfers within families are sometimes reinforced by explicit nepotism, furthering the correlations of scholastic and employment status (Lentz and Laband 1988). These transfers of socioeconomic status are sufficiently established for economists to use sibling correlation as a measurement tool for the importance of family and community on status (Björklund et al. 2002), and attempts have been made to measure the dilution factor for human capital as it is transferred through families (i.e., the β that would apply to b²) (Becker and Tomes 1986). Beyond the vertical inheritance (β) of socioeconomic status, its horizontal transfer through assortative mating (a) is also well established, with multiple aspects—e.g., education and occupational prestige—known to align between spouses prior to marriage (Watkins and Meredith 1981; Kalmijn 1994).

To summarize: there are a multitude of ways in which socioeconomic status is known to be transferred within families, and socioeconomic status is known to affect human life span. Our own analyses did not parse apart the relative contributions of genetic (h²) vs. sociocultural (b²) factors from the total transferrable variance (t²). Nonetheless, the literature outlined above provides evidence that the contribution of transferred sociocultural factors (b²) to human life span must be far from zero, suggesting that heritability (h²) of life span is likely much lower than our estimate of transferrable variance.

Lower heritability for more-disparate birth cohorts may reflect cause-of-death dynamics through history

The decrease of transferable variance t² as piblings’ birth cohorts became increasingly disparate (Figure 6, G–I) was not expected. Our null assumption was that alleles and sociocultural factors would influence the phenotype in a consistent manner though history, albeit with perhaps a different balance between the relative contributions of those factors vs. environmental noise. Instead, we observed that even when transferable variance (t²) was high within each of a broad range of cohorts, the transferable variance between those cohorts was low. This was observed across all gender combinations (Figure 6, G–I), but was especially clear for female–female comparisons (Figure 6G). Therefore, we speculated that the genetic and sociocultural factors of greatest importance to life span may have changed across historical eras. If that were true, then the life span-affecting factors would be unlikely to act through fundamental drivers of life span (such as the aging process itself), which have been consistent through human history.

The term aging itself broadly describes the erosion of physiological maintenance through time (López-Otín et al. 2013). Since that decline ultimately leads to death, mortality is frequently used as the experimental endpoint, but risks for many nonmortal pathologies also increase with age (Selman and Withers 2011; Kirkland 2013). The fundamental connection between all of those pathologies and death is not understood, but the rate of increase of mortal susceptibility to the decline of aging is exponential, as first noted by Gompertz (1825). There is much debate about how consistent this rate of mortality hazard increase is across human populations, so it was noteworthy to see that, in the SAP, the rate of hazard doubling was highly consistent across the full span of birth cohorts we examined, as well as across both genders (see Supplemental Text, section 6 and Figure S3). The implication was that despite shifting environmental hazards and causes of death, the rate of age-related decline has been a consistent feature of human biology through these cohorts.

In contrast to the rate of aging, as defined above, the major threats to human health and life have changed dramatically across the focal time periods and geography of our analyses: the U.S.A. over the 19th and 20th centuries. Mortality rates plummeted during that time for several environmental reasons, including improved nutrition and water sanitation, antibiotics, vaccinations, and demographic trends in smoking rates. (Pierce and Gilpin 1995; Cutler and Miller 2005). But some of these only emerged as substantial hazards within the same time period: the growth of U.S. cities in the late 1800s strained existing sewage and fresh-water infrastructure, and the cigarette epidemic was driven by aggressive marketing that was accelerated in the 1910s. Therefore, we expected that if any of the transferrable factors were modifying life span through sensitivity or resilience to these emerging and declining hazards, they would lose their effect on life span in historically-distant cohorts.

Under the above assumptions, genetic or sociocultural factors that modify a fundamental aging process would be expected to continue to drive correlation of life span phenotypes, even as birth cohorts (i.e., environmental contexts) became increasingly distinct. Conversely, factors modifying the susceptibility to historically transient hazards would be expected to lose their ability to generate life span correlations across distinct historical eras. Therefore, the observed decrease of transferable variance t² as piblings’ birth cohorts became increasingly disparate (Figure 6, G–I) suggested that the transferable genetic and sociocultural factors affected survival in specific historical environments, rather than something as fundamental as the rate of human aging.