Abstract
We investigate the fate of de novo mutations that occur during the in-host replication of a pathogenic virus, predicting the probability that such mutations are passed on during disease transmission to a new host. Using influenza A virus as a model organism, we develop a life-history model of the within-host dynamics of the infection, deriving a multitype branching process with a coupled deterministic model to capture the population of available target cells. We quantify the fate of neutral mutations and mutations affecting five life-history traits: clearance, attachment, budding, cell death, and eclipse phase timing. Despite the severity of disease transmission bottlenecks, our results suggest that in a single transmission event, several mutations that appeared de novo in the donor are likely to be transmitted to the recipient. Even in the absence of a selective advantage for these mutations, the sustained growth phase inherent in each disease transmission cycle generates genetic diversity that is not eliminated during the transmission bottleneck.
Keywords: mutation, disease transmission, adaptation, influenza, life history
MANY pathogens experience population dynamics characterized by periods of rapid expansion, while a host is colonized, interleaved with extreme bottlenecks during transmission to new hosts. The effect of these transmission cycles on pathogen evolution has been well studied, with particular focus on long-standing predictions regarding the evolution of virulence [reviewed in Alizon et al. (2009)], conflicting pressures of within- and between-host fitness [Gilchrist and Sasaki 2002; Coombs et al. 2007; Day et al. 2011; see Mideo et al. (2008) for review], or broader factors affecting the evolutionary emergence of pathogenic strains [Antia et al. 2003; Iwasa et al. 2003; Reluga et al. 2007; Alexander and Day 2010; see Gandon et al. (2012) for review].
In the experimental evolution of microbial populations, the impact of population bottlenecks has also been studied in some depth, both theoretically (Bergstrom et al. 1999; Wahl and Gerrish 2001; Wahl et al. 2002) and experimentally (Burch and Chao 1999; Elena et al. 2001; Raynes et al. 2014; Lachapelle et al. 2015; Vogwill et al. 2016). While severe population bottlenecks clearly reduce genetic diversity, the period of growth between bottlenecks can have the reverse effect, generating substantial de novo adaptive mutations and promoting their survival (Wahl et al. 2002). The survival of a novel adaptive lineage is predicted to depend not only to the timing and severity of bottlenecks, but on the details of the microbial life history and the trait affected by the mutation (Alexander and Wahl 2008; Patwa and Wahl 2008; Wahl and Zhu 2015).
The effects of transmission bottlenecks on the evolution of an RNA virus have been explicitly studied in a series of experimental papers, demonstrating that severe bottlenecks (one surviving individual) reduced fitness (Duarte et al. 1992) despite rapid population expansion between transmission events (Duarte et al. 1993). The magnitude of this effect depends on both the initial fitness of the lineage (Novella et al. 1995) and on bottleneck severity (Novella et al. 1996). In theoretical work, a model of a viral quasispecies undergoing periodic transmission events predicts that pathogens should maintain a mutation–selection balance with high virulence if the pathogen is horizontally transferred, if the bottleneck size is not too small, and if the number of generations between bottlenecks is large (Bergstrom et al. 1999).
Unlike the bottlenecks imposed in serial passaging, transmission bottlenecks in nature are not constrained by experimental control. Thus, key parameters such as the bottleneck size, i.e., the number of microbes initiating an infection, have proven difficult to estimate. Nonetheless, experimental models [see Abel et al. (2015) for review], as well as recent techniques such as DNA barcoding (Varble et al. 2014) and sequencing of donor–recipient pairs in humans (Poon et al. 2016) have shed new light on this issue. In addition, we note that many human viruses—including human immunodeficiency virus, hepatitis B virus, and influenza A virus (IAV)—reproduce by viral budding in the context of a potentially limited target cell population (Garoff et al. 1998); the survival of de novo mutations has not yet been predicted for this microbial life history. Thus, the effects of transmission bottlenecks on the genetic diversity of viral pathogens, that is, on the fate of de novo mutations, are as yet unknown.
In this contribution, we first develop a deterministic model of the within-host dynamics of early infection by a viral pathogen. We couple this to a detailed life-history model, using a branching process approach to follow the fate of specific de novo mutations that are either phenotypically neutral or affect various life-history traits. These techniques allow us to predict which adaptive changes in virus life history are most likely to persist, and how the diversity of the viral sequence is predicted to change between donor and recipient. We can thus predict, for example, the rate at which de novo single-nucleotide polymorphisms arise during the course of a single infection and are transmitted to a subsequent host.
Throughout the paper, we will illustrate our results with parameters that have been chosen to model the life history and transmission dynamics of IAV. IAV is an orthomyxovirus (Bouvier and Palese 2008) that imposes a significant burden on global health, causing seasonal epidemics, sporadic pandemics, morbidity, and mortality (Carrat and Flahault 2007). It is estimated that infection with seasonal strains of influenza results in ∼36,000 deaths per year in the U.S., although exact numbers are difficult to determine (Chowell et al. 2008).
Mathematical modeling is a well-established tool for predicting the evolution of influenza (Larson et al. 1976; Bocharov and Romanyukha 1994). Because of the critical importance of immune evasion in influenza, interest has focused on the adaptation of the virus in response to immune pressure, focusing on antigenic drift (Boianelli et al. 2015) and antigenic shift (Feng et al. 2011) in the global influenza pandemic (van de Sandt et al. 2012). However, recent models have specifically addressed the within-host dynamics of IAV (Beauchemin et al. 2005; Baccam et al. 2006; Beauchemin and Handel 2011; Smith and Perelson 2011; Dobrovolny et al. 2013; Boianelli et al. 2015). In concert with these contributions, recent empirical work has elucidated the life history of the IAV, providing quantitative estimates of parameters such as the minimum infectious dose (Varble et al. 2014; Poon et al. 2016), the size of the target cell population, and the kinetics of viral budding (Baccam et al. 2006; Beauchemin and Handel 2011; Pinilla et al. 2012). Although we now have an increasingly clear picture of the within-host life history of this important pathogen (Beauchemin and Handel 2011; Biggerstaff et al. 2014), estimates of the rate at which de novo mutations arise and are transmitted have not yet been available. Our approach allows direct access to this question.
Methods
Life-history and transmission model
Deterministic model:
We use a system of ordinary differential equations (ODEs) to approximate the within-host dynamics during the early stages of infection by a pathogenic virus, assuming a life history that involves infection of a target cell, an eclipse phase, and finally an infectious stage. Specifically, we propose:
| (1) |
Here, represents susceptible target cells (in the case of IAV we consider epithelial cells of the upper respiratory tract), represents cells that are infected by the virus but not yet in the budding stage, represents mature infected cells (infected cells that are budding), and v represents the free virus, that is, virions not attached to target cells (Baccam et al. 2006). Parameter B gives the rate at which budding cells produce infectious free virus and C gives the clearance rate for free virus. Infected cells die at constant rate D, while E represents the rate at which infected cells mature, leaving the eclipse phase and becoming budding cells. The parameter α gives the rate of attachment per available target cell. Thus, the overall attachment rate for a virion is a function of the time-varying target cell population, and can be written with the corresponding mean attachment time,
A limitation of ODE approaches is that all transitions are described by exponential distributions. To relax this assumption, we introduce a sequence of k infected stages through which infected cells pass before reaching the budding stage. This “chain of independent exponentials” allows for more realistic gamma distributions of eclipse times (Wahl and Zhu 2015). Specifically, we replace Equation (1) with:
| (2) |
When this model reduces to Equation (1); for gives the population of initially infected cells, which pass through k eclipse stages at rate before budding. The transition rate is set such that the expected time in the eclipse phase, in total, is fixed at for any value of k. In the Supplemental Material, we also investigate a model in which the death term, D, is set to zero during the eclipse stages and only acts during the budding stage. This likewise gives a more realistic distribution for the lifetime of infected cells.
The founding virus begins as an initial population of free virus (the initial infectious dose, ) at time We do not assume that all viral particles in the founding dose are genetically identical, but we do assume that they are phenotypically identical, that is, they are described by the same parameter values in the deterministic model. As described further in the stochastic model below, we assume that disease transmission occurs at time τ during the peak viral shedding period (when the free virus population, v, reaches its peak value; see Figure 1). For the transmission event to a new susceptible individual, a new founding population is sampled from the total viral load. In particular, each free viral particle becomes part of the infectious dose transmitted to the next individual with probability F. The value of F is computed such that for the founding virus, the expected size of the transmitted sample is that is, Note that only free virions (those not yet attached to a target cell) are transferred to the next individual during transmission.
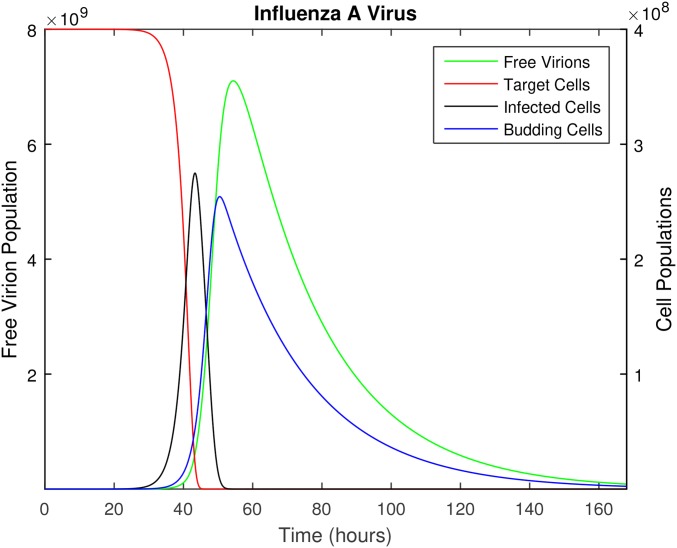
Figure 1.
The time course of influenza A infection over the span of 1 week (168 hr). Parameter values are provided in Table 1, with the following initial conditions: epithelial cells (target cells), 100 virions (initial infection dose), and all other populations initially zero.
Immune responses clearly play a critical role in the within-host dynamics of viral infections, as is well documented for models of IAV (Beauchemin and Handel 2011; Smith and Perelson 2011; Dobrovolny et al. 2013). In the model proposed above, innate immune mechanisms are included in the clearance rate of free virus and the death rate of infected cells; these constant rates are used as an approximation since the innate immune response will vary over the infection time course. Because we use this model only until the time of peak viral shedding, which occurs 54.5-hr post infection (see parameter values, below) and before the adaptive immune response is activated (Tamura and Kurata 2004), we do not include the adaptive immune response. We address this issue further in the Discussion. Likewise, we do not include replenishment of the susceptible target cell population over the initial 54.5 hr of the infection. This is consistent with complete desquamation of the epithelium (loss of all ciliated cells) within 3 days postinfection in murine influenza, followed by regeneration of the epithelial cells beginning 5 days postinfection (Ramphal et al. 1979).
Stochastic life-history model:
To describe the lineage associated with a rare de novo mutation, a stochastic model is required. To gain tractability, we assume that the mutant lineage propagates in an environment for which the overall dynamics of the target cell population are driven by the deterministic Equation (2). Thus, we treat the free virus, eclipse-phase cells, and budding cells in the mutant lineage stochastically, but use the deterministic system to predict the susceptible target cell population at any time.
As in the deterministic model, free virions clear at a constant rate C or adsorb to susceptible host cells at rate Note that the attachment rate of a free virion is not constant; it depends on target cell availability, such that where is the target cell population predicted by Equation (2). Host cells enter the eclipse phase when a virion adsorbs, and exit the eclipse phase at rate E. After the eclipse phase, mature infected cells bud virions at rate B. Since budding itself does not immediately kill the host cells (Garoff et al. 1998), after infection the cell is subject to a constant death rate D, or in other words the cell remains alive for an average time
This stochastic growth process can be described as a branching process, using a multitype probability generating function (pgf) to describe a single lineage of free virions. As described in the Appendix, this approach allows us to estimate the probability, that a lineage initiated by a de novo mutation at time is not transmitted to the next host. The rate at which mutations arise that will be transmitted, is then given by
| (3) |
where is the rate at which new virions are produced at time μ is the probability that the mutation of interest occurs per new virion produced, and is the probability that the lineage is transmitted.
We use this result to compute the expected number of times that the mutation of interest occurs de novo, over the course of the infection, and survives to be transmitted to the next host:
where τ is the time of disease transmission. Finally, consider dividing the time interval such that and In this case for small the quantity approximates the probability that a surviving mutation occurs during time interval This allows us to compute the probability that at least one copy of the mutation of interest arises de novo during the course of the infection, survives the bottleneck, and is transmitted to the new host:
which by product integration can be succinctly expressed as:
| (4) |
Beneficial mutations
Our goal is to predict the fate of mutations that may arise de novo in the viral population. Although most mutations will be deleterious, we note that the virus population grows by several orders of magnitude (possibly up to seven) during a single infection, and thus deleterious mutations should be effectively outcompeted, consistent with significant purifying selection reported in sequencing studies of IAV in humans (Poon et al. 2016; Debbink et al. 2017; McCrone et al. 2018). Therefore, in this contribution, we focus on neutral mutations (no phenotypic effect) or rare mutations that confer an adaptive advantage to the virus. For a budding virus, changes in five life-history traits can confer a selective advantage: a reduction in either the cell death rate, or clearance rate, an increase in the attachment rate, or budding rate, or an increase in the rate at which cells mature and begin budding,
To estimate the probability that a beneficial mutation ultimately survives, we substitute the parameters above for the analogous parameters in the pgf and numerically evaluate which describes the distribution of free virions in the mutant lineage at time τ, as described in the Appendix. We then compose this function with the pgf describing disease transmission. The accuracy of these numerical solutions was verified using an individual-based Monte Carlo simulation, developed for a reduced model without target cell limitation, similar to the approach described by Patwa and Wahl (2009).
Selective advantage
Finally, to compare the fitness of mutations affecting different traits, we calculate the selective advantage of each mutation. Following common experimental practice, we define fitness in terms of the doubling time, that is, we assume that in the time required for the founding population to double, the mutant lineage grows by a factor of Given the founding growth rate g, we substitute the founding doubling into to find the selective advantage of the mutant, where For the relatively small s values presented here, this definition of the selective advantage differs from the more appropriate but less commonly used by a constant factor of
To estimate the average growth rates, g and we consider a single cycle of growth, starting from a single free virus at time 0. In this case, the partial derivative of G with respect to defined as gives the expected number of free virions at time τ, illustrated here for the case (Grimmett and Welsh 2014). The derivative was calculated numerically and the average growth rate of the free virus population is then calculated as Thus, although growth is not exponential due to target cell limitation, g estimates the exponential growth rate that would achieve the same number of free virions at time τ.
Parameter values for IAV
Parameter values were estimated where possible from the empirical and clinical literature for IAV, and are displayed in Table 1. Beauchemin and Handel (2011) give a range of values for several relevant parameters, from which parameter estimates for C, D, and E were chosen. Specifically, we take the clearance time to be 3 hr, the cell death time 25 hr, and the eclipse time 6 hr (Baccam et al. 2006; Beauchemin and Handel 2011).
Table 1. Parameter estimates for influenza A virus.
| Parameter | Definition | Estimate |
|---|---|---|
| α | Per target cell attachment rate | |
| Mean time between each budding event | ||
| Mean clearance time | 3 hr | |
| Mean cell death time | 25 hr | |
| Mean eclipse time | 6 hr | |
| Initial number of target cells | ||
| Number of virions to initiate infection | 100 | |
| k | Stages in eclipse phase | 30 |
| μ | Mutation rate (per site per replication) |
To estimate the time between each budding event, we first consider the total number of virions produced per cell, the “burst size.” For IAV, the burst size has been estimated to be between 1000 and 10,000 virions (Stray and Air 2001). However, not all virions produced are infectious and in fact a large fraction are unable to infect a host cell; the particle-to-infectivity ratio for IAV is ∼50:1 (Martin and Helenius 1991; Roy et al. 2000). Taking the upper bound of the range for burst size, of the 10,000 virions produced, only 200 are predicted to be infectious. Recall that budding does not kill the host cell, therefore budding time depends on the eclipse and cell death times. An eclipse time of 6 hr and a cell death time of 25 hr gives a budding time of 19 hr. Therefore, the time between each infectious budding event, is assumed to be hr per infectious virion.
The number of upper respiratory epithelial cells in a healthy adult is estimated to be (Baccam et al. 2006). Consistent with the complete desquamation of the epithelium observed in murine influenza (Ramphal et al. 1979), we therefore take In the supplemental material, we investigate the sensitivity of our main results to this value. Similarly, as a default value we assume that an infection is founded by virions, consistent with recent sequencing studies (Poon et al. 2016; Sobel Leonard et al. 2017). However, we note that average values of 10–200 have been previously suggested in the literature (McCaw et al. 2011; Varble et al. 2014; Peck et al. 2015), with substantial variability observed across donor–recipient pairs (Sobel Leonard et al. 2017). Finally, the most recent estimate from donor–recipient pairs suggests that a typical bottleneck size during seasonal influenza in a temperate climate may be as small as one or two viral genomes (McCrone et al. 2018). Therefore, we will demonstrate results over a range of values and address the implications of these varying estimates in the Discussion.
To allow for realistically distributed eclipse times, we assume a gamma-distributed eclipse phase by including a sequence of k infected stages before the budding stage. As described above, the mean eclipse time, is set to 6 hr. The variance of the eclipse period of IAV can then be used to estimate k. Pinilla et al. (2012) used a best-fit analysis for kinetic parameters of IAV to predict a mean eclipse time of 6.6 hr, with an eclipse period SD, σ, of 1.2 hr. Since the SD for a gamma distribution with mean m is given by these values suggest that a realistic value of k is ∼30.
We fix the attachment rate, α, such that the peak of the free viral load occurs within the reported range for IAV of 48–72 hr postinfection (Wright and Webster 2001; Lau et al. 2010). The attachment rate /hr/cell provided in Table 1 yields a peak time of hr, and implies a mean attachment time, of just over 1 hr when target cells are plentiful. We assume that disease transmission is most likely at the peak viral shedding time, and thus study a transmission event that occurs at this peak time, τ. Note that when we examine the sensitivity of the model, for example when changing we leave the attachment rate α fixed. We recompute the time course and assume that the transmission event occurs at the peak value of The transmission time, τ, then differs slightly between cases. In no case was τ outside the empirically estimated range of 48–72 hr.
The probability that a free virion survives the bottleneck and is transmitted to the next susceptible individual is defined as F. This probability is calculated by using the peak number of free virions, found by numerically solving model 2. As only free virions contribute to the infectious dose, the fraction of free virions surviving the bottleneck is where again is the founding population size for the next infected individual.
The mutation rate for IAV, per nucleotide per replication, has been estimated as (Nobusawa and Sato 2006). This estimate was obtained for the IAV nonstructural (NS) gene during plaque growth and thus does not include lethal mutations. Neglecting differences in transition and transversion rates, we divide this value by three to estimate the rate at which a specific, nonlethal nucleotide substitution occurs. We investigate the sensitivity of our results to this parameter as well.
Data availability
The authors affirm that all data necessary for confirming the conclusions of this article are represented fully within the article and its tables and figures. Supplemental material available at Figshare: https://doi.org/10.25386/genetics.6430487.
Results
Figure 1 illustrates the deterministic dynamics of Equation (2), showing the time course of the in-host IAV infection. The free virus peaks at 54.5 hr, just after the peak in the mature (budding) cell population. Note that in this simplified model, the availability of target cells limits the infection. As described earlier, this model is only accurate while the adaptive immune response remains negligible; although we illustrate the full 7 days of infection, we use only the first 54.5 hr in the subsequent analysis.
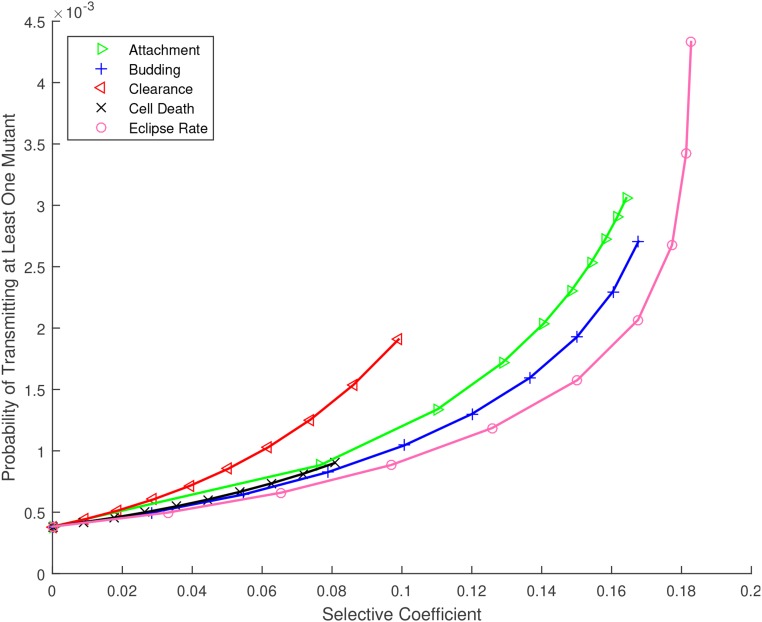
Figure 2 shows what we will refer to as the “mutation transmission probability,” that is, the probability that at least one copy of a specific mutation arises de novo during an infection time course, survives genetic drift, and is successfully transmitted to the subsequent host ( Equation (4)). Model predictions for beneficial mutations affecting each life-history trait are shown vs. the selective coefficient, s, while the intercept at shows the prediction for neutral mutations. Here, we have assumed for comparison that the baseline mutation rate is equal for all types of mutation; however, the y-axis in Figure 2 scales approximately linearly with μ. In the supplemental material, we illustrate results for a wide range of mutation rates.
Figure 2.
Probability that at least one copy of a specific de novo mutation arises during the infection time course and is passed to the next host, for mutations affecting the life history of influenza A virus, vs. their selective coefficient. Numerical results [ Equation (4)] are plotted as symbols (per substitution, per site); lines are provided to guide the eye. Parameters as given in Table 1.
To interpret these results, the empirical mutation rate must be carefully considered. The rate estimate we use reflects the probability, per replication, that a specific substitution occurs at a specific nucleotide in the IAV sequence, given that the substitution is nonlethal. Thus for example if the substitution of interest is neutral or effectively neutral, the model predicts that this substitution would occur de novo in the donor and be transmitted to a recipient about once in every 2000 transmission events. If the substitution of interest confers a selective advantage, the mutation transmission probability would be higher. Clearly, a large fraction of viable mutations will be deleterious and would be outcompeted before transmission; this would correspond to a lower overall mutation rate, as examined in the supplemental material and outlined further in the Discussion.
The most striking result of Figure 2 is the predicted evolvability of IAV during a single transmission cycle. The mutation transmission probability of 1 in 2000, per substitution per site, may contribute substantial diversity since the IAV genome is a sequence of over 13,000 nucleotides with three possible substitutions per site. We will return to the interpretation and implications of this prediction in the Discussion.
The near-overlapping lines in Figure 2 indicate that the mutation transmission probability does not vary widely across life-history traits, and also illustrates the maximum selective advantage made possible by improvements to each trait. For example, clearance and cell death rates can only be reduced to zero, limiting the range of s for these traits. Although there is no upper bound on the rates of attachment or maturation to budding (eclipse rate), once these rates are effectively instantaneous, further increases do not appreciably change the growth rate, and so higher s values are also inaccessible for these traits. Similarly, increases to the budding rate cannot improve the growth rate without bound, due to target cell limitation.
Results in Figure 2 assume the default parameter set (Table 1); in particular, 100 virions are chosen at random from the free virus population and transmitted to the new host. In Figure 3, we fix the selective coefficient but vary the size of this transmission bottleneck. We find that the mutation transmission probability increases roughly linearly with bottleneck size.
Figure 3.
Probability that at least one copy of a de novo mutation arises during the infection time course and is passed to the next host, for mutations affecting the life history of influenza A virus, vs. the number of virions in the transmission bottleneck. All mutations have a selective advantage of except for the line marked neutral, for which Other parameters as provided in Table 1. The inset shows the same results for small bottleneck sizes. Numerical results [ Equation (4)] are plotted as symbols (per substitution, per site); lines are provided to guide the eye.
The results above compare mutations that have equivalent effects on the overall growth rate of the virus, assuming that the underlying mutation rate is the same for all mutations. Although the question of mutational accessibility is beyond our focus, some sense of the degree to which these mutations might be physiologically achievable can be obtained by considering the relative changes required to the trait value. To this end, Figure 4 shows the relative change in each life-history parameter necessary to achieve a specific increase in growth rate (selective coefficient). To incur an advantage of for example, requires less than a 10% change in the rate at which cells leave the eclipse phase and begin budding; in contrast, the attachment rate would need to double (change by over 100%) to achieve the same selective advantage. Note again that clearance and cell death rates can only be reduced by at most 100%, limiting the range of their possible effects. For the other three traits, as described previously, beneficial mutations can produce selection coefficients in the approximate range but further rate increases produce diminishing returns and fitness saturates.
Figure 4.
The change in selective coefficient achieved by a given absolute percent change in trait value for mutations affecting the five life-history traits. For example, large changes in attachment rate would be required to achieve the same advantage as relatively small changes in eclipse timing. Numerical results plotted as symbols; lines provided to guide the eye.
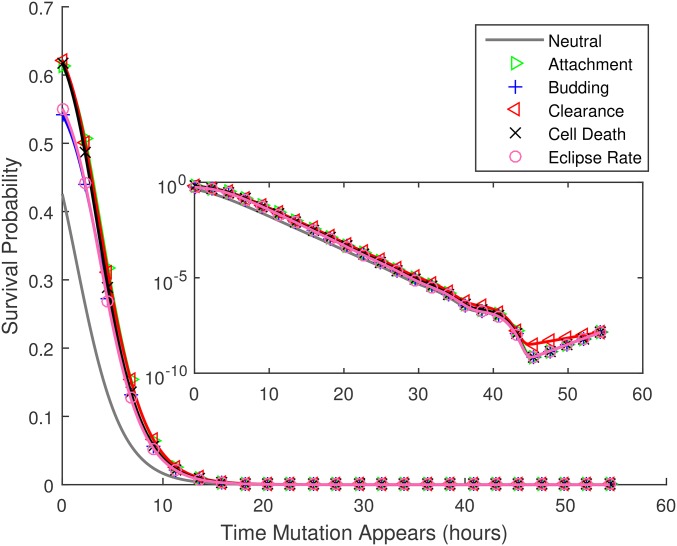
Figure 2 gives the overall probability that a de novo mutation is generated and passed on. As described in the Methods, this value reflects the integrated probability of occurrence and survival for mutations that could first occur at any time during the infection time course. To better understand the dynamics of this process, in Figure 5 we show the predicted survival probability, the probability that the mutation survives and is transmitted to the next host, for mutations that arise at time during the infection time course; survival is typically reduced for lineages that arise later in the infection. However, for mutations that first occur immediately previous to the bottleneck, this trend is briefly reversed (see inset), presumably because newly released virions have a lower chance of being attached to a host cell at the transmission time. Overall, Figure 5 gives the impression that mutations that arise after about the first 10 hr of infection have little chance of survival.
Figure 5.
Given that a de novo mutation first occurs at time after the start of the infection, the probability that at least one copy of it is transmitted to the next host, vs. All mutations have a selective advantage of except for the curve marked neutral, for which Parameters as provided in Table 1. The inset shows the same results in a semilog plot, illustrating that the survival probability increases slightly for mutations that first occur just before the bottleneck (see text). Note that in this figure numerical results are plotted by both lines and symbols.
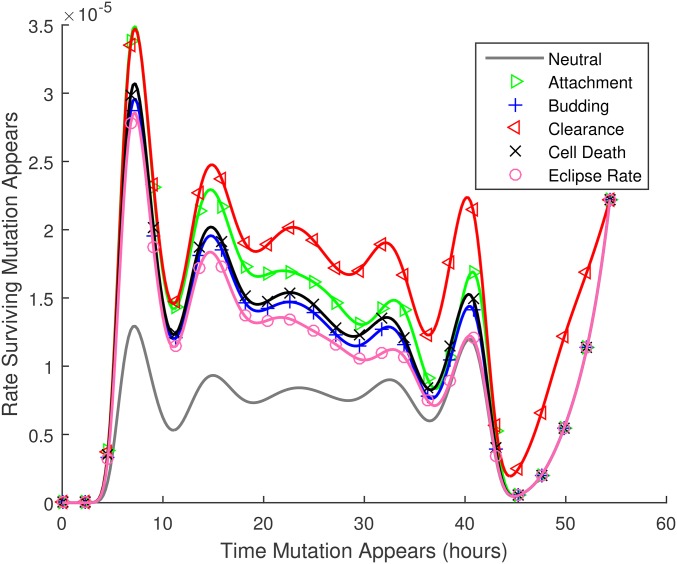
The results in Figure 5 are mitigated by the fact that many more replication events occur later during the growth phase. To investigate the rate at which surviving mutations (mutations that are transferred to the next host) first occur, we consider the product of the transmission probability for mutations that arise at each time and the number of new virions produced at that time, Figure 6 shows these results. The model predicts that transmitted mutations occur throughout the infection time course, except during the first few hours of infection, when very few new virions are produced, and for a brief window ∼10 hr before the transmission event. The latter effect presumably occurs because virions produced in this window are unlikely to be free at the time of transmission (infected cells are not transmitted). The oscillations in these curves occur because the founder virions start synchronously at as free virions, and must attach and complete the eclipse phase before new virions can be produced.
Figure 6.
The rate at which transmitted mutations appear [ν, Equation (3)] vs. the time at which they first appear, For this figure, the probabilities of being passed on to the next host illustrated in Figure 5 are multiplied by the number of new virions produced at each time. Thus the figure illustrates the relative numbers of ultimately transmitted mutations that occur at each time during the infection time course, per substitution, per site. Note that in this figure numerical results are plotted by both lines and symbols.
Discussion
We develop a model of within-host pathogen evolution and use this to predict the fate of de novo mutations that occur during disease transmission cycles. Using parameter values for IAV and estimating the founding inoculum size as 100 viral particles, our results predict that the probability that at least one copy of a de novo nucleotide substitution is transmitted to the subsequent host is ∼ per substitution per site. Multiplying by three possible nucleotide changes and the 13,600 sites in the IAV genome yields an estimate that as many as 20 sites in the founding dose for the recipient may contain substitutions that occurred de novo in the donor. However, this upper bound must be corrected by two factors: the fraction of nonlethal mutations that are either neutral or beneficial, and the inoculum size. If approximately half of all nonlethal mutations are neutral or beneficial, consistent with estimates in both influenza and in another single-stranded RNA virus with a similar genome length (Sanjuán et al. 2004; Visher et al. 2016), we predict each recipient founding dose will contain ∼10 de novo substitutions. If the fraction of neutral or beneficial mutations, among nonlethal mutations, is closer to 10% [see Eyre-Walker and Keightley (2007) for review], we predict around two new substitutions in each founding dose.
As demonstrated in Figure 3, these estimates scale linearly with the size of the transmission bottleneck. Thus, if a single virion founds the infection (Debbink et al. 2017; McCrone et al. 2018), rather than 2–10 new substitutions per transmission, we predict around one new substitution in the IAV genome every 10–50 transmission events. The longer-term fate of these new substitutions also critically depends on the size of the founding virus population. Clearly, if only a single viral particle founds the new infection, transmission implies fixation; genetic heterogeneity that arises during the infection will be lost, consistent with the extinction or fixation of minor variants observed during seasonal influenza in a temperate climate (Debbink et al. 2017; McCrone et al. 2018). In contrast, if the founding inoculum contains ≥ 100 viral particles, the long-term picture is more complex. Our assumption that the founding infectious dose in the donor is phenotypically uniform only holds as an approximation, and the predicted de novo mutations may occur on different genetic backgrounds circulating within the donor. Recent evidence from IAV transmissions in Hong Kong suggests that multiple lineages can be transmitted, including minor variants that are shared between donor and recipient (Poon et al. 2016; Sobel Leonard et al. 2017). Thus, a clear direction for future work would be to expand our approach to track multiple distinct lineages within the host and predict the longer-term fates of mutations occurring on these backgrounds.
We can also take our estimate of ( nonlethal substitutions per site per transmission event) × (10–50% neutral or beneficial) to predict substitutions per site per transmission event. These values are consistent with the observed evolutionary rate of IAV throughout a seasonal epidemic, substitutions per site per year in the NS gene (Kawaoka et al. 1998; Rambaut et al. 2008), if the chain of influenza transmission involves 3–30 transmission events per season.
Although transmission bottlenecks in IAV, as in many other pathogens, can be extremely severe, our results are consistent with previous work demonstrating that the period of growth between population bottlenecks can have a greater impact on diversity than the bottlenecks themselves (Wahl et al. 2002); this period of sustained population expansion promotes the survival of new mutations, as seen more generally in any growing population (Otto and Whitlock 1997). The rapid growth of influenza during early infection, from a relatively small infectious dose to peak viral loads many orders of magnitude larger, implies that neutral substitutions, or mutations conferring even a small benefit, will have ample opportunity to compete with founder strains. This further implies that the life history of IAV should be well adapted to the disease transmission cycle in humans; in other words, selection has the opportunity to rapidly fine-tune the life histories of pathogens experiencing extreme transmission bottlenecks.
This result is consistent with previous theoretical (Bergstrom et al. 1999) and experimental work on viral evolution (Duarte et al. 1993; Novella et al. 1995, 1996). The latter work focused on the loss of fitness due to population bottlenecks, but fitness could be maintained or improved when the bottleneck size was as large as 5 or 10 individuals (Novella et al. 1996). Similarly, Bergstrom et al. (1999) predicted that viral pathogens would be well adapted if the bottleneck size is large (or order 5 or 10), and the number of generations between bottlenecks is large (of order 25 or 50). The parameter values we explored for IAV correspond to over 25 population doublings between transmission events. With bottleneck sizes of 10–200, our model is consistent with a parameter regime in which the pathogen is able to improve or maintain fitness. However, if only one or two virions found each infection (McCrone et al. 2018), the theoretical expectation would be that viral fitness should decline due to the accumulation of deleterious mutations [see LeClair and Wahl (2017) for review]. An interesting speculation is that the founding dose may in fact be one-to-two virions during seasonal IAV epidemics in temperate zones, but could be two orders of magnitude larger in tropical regions (Xue et al. 2018). Our model would then predict multiple de novo substitutions arising per transmission event in the tropics, whereas in temperate climates substitutions are relatively rare (but tend to fix when they occur). This would also be consistent with the source-sink hypothesis for the global evolution of influenza (Rambaut et al. 2008).
The use of a specific life-history model imposes natural limits on the growth rate and thus the selective advantage that can be achieved by budding viruses. For the parameters specific to IAV, changes to the clearance rate of the free virus or death rate of infected cells could only achieve a selective advantage of This occurs mathematically because these rates cannot be reduced below zero; it follows intuitively because even if infected cells or virus never die or lose infectivity, growth remains limited by other processes. Mutations with larger beneficial effects, in the range are accessible only by reducing the eclipse phase, or through very large-magnitude changes to the attachment or budding rates. Given that predicted differences in survival probability for the different traits are rather modest (Figure 5), these results suggest that small magnitude changes in the eclipse timing of IAV will be subject to selective pressure. The limits we observe in the achievable growth rate suggest that larger effect beneficial mutations in IAV are not only unlikely, they may not be physically possible given the life history of this virus.
We have focused this study on the in-host life history of the virus. However, in principle, a beneficial mutation could also affect the transmissibility of the lineage (parameter F), producing virions that are preferentially transferred to a new host (Handel and Bennett 2008). This would be distinct from mutations that increase viral load; mutations affecting F would increase the probability that an individual viral particle is transmitted, for example by prolonging the stability of the virion in the external environment. In addition, viral life-history traits that are important for establishing a new infection may differ from those that maximize growth once established, such that the transmission bottleneck itself is highly selective, as evidence suggests for human immunodeficiency virus (Joseph et al. 2015; Kariuki et al. 2017). Understanding the effects of selective transmission on de novo diversity remains an open question.
These results explore mutations affecting a single trait in isolation. Clearly, higher fitness could be achieved by mutations that affect several traits if beneficial pleiotropic mutations are available. Previous work suggests that the survival probability of pleiotropic mutations typically falls between the predictions obtained for single-trait mutations of equivalent selective effect (Wahl and Zhu 2015). In addition, we have investigated the transmission of de novo mutations when rare. Given the magnitude of the viral loads measured in IAV, it is clear that multiple beneficial mutations could emerge and compete before the virus is transmitted to a new host. Thus, we would expect that clonal interference and multiple mutation dynamics might come into play in describing the adaptive trajectory more fully (Desai and Fisher 2007; Desai et al. 2007).
A limitation of the model is that the immune response is not explicitly included as a dynamic variable. Innate immunity is activated when an infection is detected, which is usually within the first few hours of infection. However, adaptive immunity is activated, at the earliest, 3 days postinfection (Tamura and Kurata 2004). Since our model addresses early infection (up to 54.5-hr postinfection), adaptive immune effects are assumed negligible. However, the innate immune response cannot be neglected, as its main purpose is to limit viral replication (van de Sandt et al. 2012). In our approach, innate immune mechanisms are included in the viral clearance and infected cell death rates, but are assumed to be constant throughout this early stage of the infection. This phenomenon has been reviewed in some detail in previous work (Baccam et al. 2006; Beauchemin and Handel 2011; Smith and Perelson 2011; Boianelli et al. 2015), from which it is clear that directly incorporating the immune response is necessary for an accurate representation of the full time course of infection (Boianelli et al. 2015). Even when limiting our attention to early infection only, interferon-I and natural killer cells could be included to more accurately model innate immunity (Boianelli et al. 2015). However, the complexity of the immune system creates a significant challenge in accurately modeling IAV dynamics, even during this initial time period (Boianelli et al. 2015). In particular, many key parameters of immune kinetics remain unquantified, creating additional uncertainty (Dobrovolny et al. 2013).
Finally, it is well understood that antigenic drift is associated with the evolution of IAV (Carrat and Flahault 2007). Antigenic drift would be formalized in our model as a reduction in the death rate of infected cells or the clearance rate of free virions, as these life-history parameters would be improved by any immune evasion. In fact, Figure 2 predicts that for mutations with small selective effects of all possible mutations with the same selective effect, clearance mutations are the most likely to survive when rare. Thus, mutations affecting the viral clearance rate are most likely to adapt. This could shed light on the mechanisms underlying the maintenance of antigenic drift; however, much remains to be understood about the complex transmission and evolutionary dynamics of IAV. It is our hope that predicting the fate of de novo mutations affecting IAV life history is an important piece of this interesting puzzle.
Acknowledgments
We thank Catherine Beauchemin for insightful and helpful comments. J.N.S.R. was funded by the Ontario Graduate Scholarship (OGS). L.M.W. is funded by the Natural Sciences and Engineering Research Council of Canada (NSERC).
Appendix
Let be the probability that l free virions, m infected cells, and n mature cells exist in the focal lineage at time t, and let denote the time-dependent per virion attachment rate, which depends on the available target cells, as predicted in the deterministic model 1. Parameters B, C, and D represent the budding, clearance, and cell death rates, while E denotes the rate at which cells exit the eclipse phase and begin budding. Although the stochastic model follows the mutant lineage, for simplicity we will use A as opposed to etc., throughout the Appendix. Also, for notational clarity, we illustrate the case Taking into account the stochastic events of attachment, budding, clearance, cell death, and cell maturation, it is straightforward to demonstrate that the pgf describing the time evolution of the lineage must satisfy:
| (5) |
Taking the limit as Equation (5) yields the following linear partial differential equation:
| (6) |
Equation (6) can be converted to a system of ODEs using the standard method of characteristics, which yields the following system of ODEs
The value of G is constant along any trajectory in the system above, and thus the system can be solved numerically to determine the value of G at time τ, given an appropriate initial condition. To study the fate of a de novo mutation that first occurs at time we use the initial condition corresponding to a single free virus existing in the lineage, with probability one, at
For notational convenience, we define as shorthand for when evaluated with this initial condition. The function thus gives the distribution of free virions at time τ, just before disease transmission, given that the lineage began with a single virion at time Composing this with the pgf of the bottleneck process, we obtain as the pgf describing the distribution of free virions transmitted to a new host (given that one new host is infected). The probability that a given lineage, that arose at time is not transmitted to the new host is obtained by evaluating at
As described in the main text, we then use this to compute the expected rate at which surviving mutant lineages (lineages that will eventually be transmitted to the next host) appear during the infection time course.
For the supplemental figures, we also compute the expected number of mutant virions transmitted to the recipient host, We do this by first computing which gives the expected number of mutant virions at time τ, given that a mutant virion was produced at time We multiply this value by the number of mutant virions being produced at time and integrate from 0 to τ, to get the total expected number of mutant virions at time τ. Multiplying by the bottleneck fraction, F, gives the expected number of mutant virions transmitted to the recipient host:
Note that (defined in the main text) and differ because each de novo mutation produces a lineage that could in principle contribute more than one virion to the recipient.
Footnotes
Supplemental material available at Figshare: https://doi.org/10.25386/genetics.6430487.
Communicating editor: D. Weinreich
Literature Cited
- Abel S., zur Wiesch P. A., Davis B., Waldor M., 2015. Analysis of bottlenecks in experimental models of infection. PLoS Pathog. 11: e1004823 10.1371/journal.ppat.1004823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander H., Day T., 2010. Risk factors for the evolutionary emergence of pathogens. J. R. Soc. Interface 7: 1455–1474 [corrigenda: J. R. Soc. Interface 8: 1064 (2011)] 10.1098/rsif.2010.0123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander H., Wahl L., 2008. Fixation probabilities depend on life history: fecundity, generation time and survival in a burst-death model. Evolution 62: 1600–1609. 10.1111/j.1558-5646.2008.00396.x [DOI] [PubMed] [Google Scholar]
- Alizon S., Hurfurd A., Mideo N., Van Baalen M., 2009. Virulence evolution and the trade-off hypothesis: history, current state of affairs and the future. J. Evol. Biol. 22: 245–259. 10.1111/j.1420-9101.2008.01658.x [DOI] [PubMed] [Google Scholar]
- Antia R., Regoes R., Koella J., Bergstrom C., 2003. The role of evolution in the emergence of infectious diseases. Nature 426: 658–661. 10.1038/nature02104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baccam P., Beauchemin C., Macken C. A., Hayden F. G., Perelson A. S., 2006. Kinetics of influenza A virus infection in humans. J. Virol. 80: 7590–7599. 10.1128/JVI.01623-05 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beauchemin C., Handel A., 2011. A review of mathematical models of influenza A infections within a host or cell culture: lessons learned and challenges ahead. BMC Public Health 11: S7 10.1186/1471-2458-11-S1-S7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beauchemin C., Samuel J., Tuszynski J., 2005. A simple cellular automaton model for influenza A viral infections. J. Theor. Biol. 232: 223–234. 10.1016/j.jtbi.2004.08.001 [DOI] [PubMed] [Google Scholar]
- Bergstrom C. T., McElhany P., Real L. A., 1999. Transmission bottlenecks as determinants of virulence in rapidly evolving pathogens. Proc. Natl. Acad. Sci. USA 96: 5095–5100. 10.1073/pnas.96.9.5095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biggerstaff M., Cauchemez S., Reed C., Gambhir M., Finelli L., 2014. Estimates of the reproduction number for seasonal, pandemic, and zoonotic influenza: a systematic review of the literature. BMC Infect. Dis. 14: 480 10.1186/1471-2334-14-480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bocharov G., Romanyukha A., 1994. Mathematical model of antiviral immune response III. Influenza A virus infection. J. Theor. Biol. 167: 323–360. 10.1006/jtbi.1994.1074 [DOI] [PubMed] [Google Scholar]
- Boianelli A., Nguyen V. K., Ebensen T., Schulze K., Wilk E., et al. , 2015. Modeling influenza virus infection: a roadmap for influenza research. Viruses 7: 5274–5304. 10.3390/v7102875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouvier N. M., Palese P., 2008. The biology of influenza viruses. Vaccine 26: D49–D53. 10.1016/j.vaccine.2008.07.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burch C. L., Chao L., 1999. Evolution by small steps and rugged landscapes in the RNA virus phi6. Genetics 151: 921–927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrat F., Flahault A., 2007. Influenza vaccine: the challenge of antigenic drift. Vaccine 25: 6852–6862. 10.1016/j.vaccine.2007.07.027 [DOI] [PubMed] [Google Scholar]
- Chowell G., Miller M., Viboud C., 2008. Seasonal influenza in the United States, France, and Australia: transmission and prospects for control. Epidemiol. Infect. 136: 852–864. 10.1017/S0950268807009144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coombs D., Gilchrist M., Ball C., 2007. Evaluating the importance of within- and between-host selection pressures on the evolution of chronic pathogens. Theor. Popul. Biol. 72: 576–591. 10.1016/j.tpb.2007.08.005 [DOI] [PubMed] [Google Scholar]
- Day T., Alizon S., Mideo N., 2011. Bridging scales in the evolution of infectious disease life histories: theory. Evolution 65: 3448–3461. 10.1111/j.1558-5646.2011.01394.x [DOI] [PubMed] [Google Scholar]
- Debbink K., McCrone J. T., Petrie J. G., Truscon R., Johnson E., et al. , 2017. Vaccination has minimal impact on the intrahost diversity of H3N2 influenza viruses. PLoS Pathog. 13: e1006194 10.1371/journal.ppat.1006194 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desai M. M., Fisher D. S., 2007. Beneficial mutation–selection balance and the effect of linkage on positive selection. Genetics 176: 1759–1798. 10.1534/genetics.106.067678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desai M. M., Fisher D. S., Murray A. W., 2007. The speed of evolution and maintenance of variation in asexual populations. Curr. Biol. 17: 385–394. 10.1016/j.cub.2007.01.072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobrovolny H. M., Reddy M. B., Kamal M. A., Rayner C. R., Beauchemin C. A., 2013. Assessing mathematical models of influenza infections using features of the immune response. PLoS One 8: e57088 10.1371/journal.pone.0057088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duarte E., Clarke D., Moya A., Domingo E., Holland J., 1992. Rapid fitness losses in mammalian RNA virus clones due to Muller’s ratchet. Proc. Natl. Acad. Sci. USA 89: 6015–6019. 10.1073/pnas.89.13.6015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duarte E. A., Clarke D. K., Moya A., Elena S. F., Domingo E., et al. , 1993. Many-trillionfold amplification of single RNA virus particles fails to overcome the Muller’s ratchet effect. J. Virol. 67: 3620–3623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elena S. F., Sanjuán R., Bordería A. V., Turner P. E., 2001. Transmission bottlenecks and the evolution of fitness in rapidly evolving RNA viruses. Infect. Genet. Evol. 1: 41–48. 10.1016/S1567-1348(01)00006-5 [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A., Keightley P. D., 2007. The distribution of fitness effects of new mutations. Nat. Rev. Genet. 8: 610–618. 10.1038/nrg2146 [DOI] [PubMed] [Google Scholar]
- Feng Z., Towers S., Yang Y., 2011. Modeling the effects of vaccination and treatment on pandemic influenza. AAPS J. 13: 427–437. 10.1208/s12248-011-9284-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gandon S., Hochberg M. E., Holt R. D., Day T., 2012. What limits the evolutionary emergence of pathogens? Philos. Trans. R. Soc. Lond. B Biol. Sci. 368: 20120086 10.1098/rstb.2012.0086 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garoff H., Hewson R., Opstelten D.-J. E., 1998. Virus maturation by budding. Microbiol. Mol. Biol. Rev. 62: 1171–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilchrist M., Sasaki A., 2002. Modeling host-parasite coevolution: a nested approach based on mechanistic models. J. Theor. Biol. 218: 289–308. 10.1006/jtbi.2002.3076 [DOI] [PubMed] [Google Scholar]
- Grimmett G., Welsh D., 2014. Probability: An Introduction. Oxford University Press, New York. [Google Scholar]
- Handel A., Bennett M. R., 2008. Surviving the bottleneck: transmission mutants and of microbial populations. Genetics 180: 2193–2200. 10.1534/genetics.108.093013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwasa Y., Michor F., Nowak M., 2003. Evolutionary dynamics of escape from biomedical intervention. Proc. Biol. Sci. 270: 2573–2578. 10.1098/rspb.2003.2539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joseph S. B., Swanstrom R., Kashuba A. D. M., Cohen M. S., 2015. Bottlenecks in HIV-1 transmission: insights from the study of founder viruses. Nat. Rev. Microbiol. 13: 414–425. 10.1038/nrmicro3471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kariuki S. M., Selhorst P., Ariën K. K., Dorfman J. R., 2017. The HIV-1 transmission bottleneck. Retrovirology 14: 22 10.1186/s12977-017-0343-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawaoka Y., Gorman O. T., Ito T., Wells K., Donis R. O., et al. , 1998. Influence of host species on the evolution of the nonstructural (NS) gene of influenza A viruses. Virus Res. 55: 143–156. 10.1016/S0168-1702(98)00038-0 [DOI] [PubMed] [Google Scholar]
- Lachapelle J., Reid J., Colegrave N., 2015. Repeatability of adaptation in experimental populations of different sizes. Proc. Biol. Sci. 282: 20143033 10.1098/rspb.2014.3033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson E. W., Dominik J. W., Rowberg A. H., Higbee G. A., 1976. Influenza virus population dynamics in the respiratory tract of experimentally infected mice. Infect. Immun. 13: 438–447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau L. L., Cowling B. J., Fang V. J., Chan K.-H., Lau E. H., et al. , 2010. Viral shedding and clinical illness in naturally acquired influenza virus infections. J. Infect. Dis. 201: 1509–1516. 10.1086/652241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeClair J. S., Wahl L. M., 2017. The impact of population bottlenecks on microbial adaptation. J. Stat. Phys. 172: 114–125. 10.1007/s10955-017-1924-6 [DOI] [Google Scholar]
- Martin K., Helenius A., 1991. Transport of incoming influenza virus nucleocapsids into the nucleus. J. Virol. 65: 232–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCaw J. M., Arinaminpathy N., Hurt A. C., McVernon J., McLean A. R., 2011. A mathematical framework for estimating pathogen transmission fitness and inoculum size using data from a competitive mixtures animal model. PLOS Comput. Biol. 7: e1002026 10.1371/journal.pcbi.1002026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCrone J. T., Woods R. J., Martin E. T., Malosh R. E., Monto A. S., et al. , 2018. Stochastic processes constrain the within and between host evolution of influenza virus. Elife 7: e35962 10.7554/eLife.35962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mideo N., Alizon S., Day T., 2008. Linking within- and between-host dynamics in the evolutionary epidemiology of infectious diseases. Trends Ecol. Evol. 23: 511–517. 10.1016/j.tree.2008.05.009 [DOI] [PubMed] [Google Scholar]
- Nobusawa E., Sato K., 2006. Comparison of the mutation rates of human influenza A and B viruses. J. Virol. 80: 3675–3678. 10.1128/JVI.80.7.3675-3678.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novella I. S., Elena S. F., Moya A., Domingo E., Holland J. J., 1995. Size of genetic bottlenecks leading to virus fitness loss is determined by mean initial population fitness. J. Virol. 69: 2869–2872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novella I. S., Elena S. F., Moya A., Domingo E., Holland J. J., 1996. Repeated transfer of small RNA virus populations leading to balanced fitness with infrequent stochastic drift. Mol. Gen. Genet. 252: 733–738. 10.1007/BF02173980 [DOI] [PubMed] [Google Scholar]
- Otto S. P., Whitlock M. C., 1997. The probability of fixation in populations of changing size. Genetics 146: 723–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patwa Z., Wahl L., 2008. Fixation probabilities for lytic viruses: the attachment-lysis model. Genetics 180: 459–470. 10.1534/genetics.108.090555 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patwa Z., Wahl L., 2009. The impact of host-cell dynamics on the fixation probability for lytic viruses. J. Theor. Biol. 259: 799–810. 10.1016/j.jtbi.2009.05.008 [DOI] [PubMed] [Google Scholar]
- Peck K. M., Chan C. H., Tanaka M. M., 2015. Connecting within-host dynamics to the rate of viral molecular evolution. Virus Evol. 1: vev013 10.1093/ve/vev013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinilla L. T., Holder B. P., Abed Y., Boivin G., Beauchemin C. A., 2012. The H275Y neuraminidase mutation of the pandemic A/H1N1 influenza virus lengthens the eclipse phase and reduces viral output of infected cells, potentially compromising fitness in ferrets. J. Virol. 86: 10651–10660. 10.1128/JVI.07244-11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poon L. L., Song T., Rosenfeld R., Lin X., Rogers M. B., et al. , 2016. Quantifying influenza virus diversity and transmission in humans. Nat. Genet. 48: 195–200. 10.1038/ng.3479 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rambaut A., Pybus O. G., Nelson M. I., Viboud C., Taubenberger J. K., et al. , 2008. The genomic and epidemiological dynamics of human influenza A virus. Nature 453: 615–619. 10.1038/nature06945 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramphal R., Fischlschweiger W., Shands J. W., Jr., Small P. A., Jr., 1979. Murine influenzal tracheitis: a model for the study of influenza and tracheal epithelial repair. Am. Rev. Respir. Dis. 120: 1313–1324. [DOI] [PubMed] [Google Scholar]
- Raynes Y., Halstead A., Sniegowski P., 2014. The effect of population bottlenecks on mutation rate evolution in asexual populations. J. Evol. Biol. 27: 161–169. 10.1111/2jeb.12284 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reluga T., Meza R., Walton D., Galvani A., 2007. Reservoir interactions and disease emergence. Theor. Popul. Biol. 72: 400–408. 10.1016/j.tpb.2007.07.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy A.-M. M., Parker J. S., Parrish C. R., Whittaker G. R., 2000. Early stages of influenza virus entry into Mv-1 lung cells: involvement of dynamin. Virology 267: 17–28. 10.1006/viro.1999.0109 [DOI] [PubMed] [Google Scholar]
- Sanjuán R., Moya A., Elena S. F., 2004. The distribution of fitness effects caused by single-nucleotide substitutions in an RNA virus. Proc. Natl. Acad. Sci. USA 101: 8396–8401. 10.1073/pnas.0400146101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith A., Perelson A. S., 2011. Influenza A virus infection kinetics: quantitative data and models. Wiley Interdiscip. Rev. Syst. Biol. Med. 3: 429–445. 10.1002/wsbm.129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobel Leonard A., Weissman D. B., Greenbaum B., Ghedin E., Koelle K., 2017. Transmission bottleneck size estimation from pathogen deep-sequencing data, with an application to human influenza A virus. J. Virol. 91: e00171–00187 10.1128/JVI.00171-17 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stray S. J., Air G. M., 2001. Apoptosis by influenza viruses correlates with efficiency of viral mRNA synthesis. Virus Res. 77: 3–17. 10.1016/S0168-1702(01)00260-X [DOI] [PubMed] [Google Scholar]
- Tamura S.-I., Kurata T., 2004. Defense mechanisms against influenza virus infection in the respiratory tract mucosa. Jpn. J. Infect. Dis. 57: 236–247. [PubMed] [Google Scholar]
- van de Sandt C. E., Kreijtz J. H., Rimmelzwaan G. F., 2012. Evasion of influenza A viruses from innate and adaptive immune responses. Viruses 4: 1438–1476. 10.3390/v4091438 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varble A., Albrecht R. A., Backes S., Crumiller M., Bouvier N. M., et al. , 2014. Influenza A virus transmission bottlenecks are defined by infection route and recipient host. Cell Host Microbe 16: 691–700. 10.1016/j.chom.2014.09.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visher E., Whitefield S. E., McCrone J. T., Fitzsimmons W., Lauring A. S., 2016. The mutational robustness of influenza A virus. PLoS Pathog. 12: e1005856 10.1371/journal.ppat.1005856 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogwill T., Phillips R. L., Gifford D. R., MacLean R. C., 2016. Divergent evolution peaks under intermediate population bottlenecks during bacterial experimental evolution. Proc. Biol. Sci. 283: 20160749 10.1098/rspb.2016.0749 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wahl L., Gerrish P. J., 2001. The probability that beneficial mutations are lost in populations with periodic bottlenecks. Evolution 55: 2606–2610. 10.1111/j.0014-3820.2001.tb00772.x [DOI] [PubMed] [Google Scholar]
- Wahl L., Zhu A. D., 2015. Survival probability of beneficial mutations in bacterial batch culture. Genetics 200: 309–320. 10.1534/genetics.114.172890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wahl L., Gerrish P. J., Saika-Voivod I., 2002. Evaluating the impact of population bottlenecks in experimental evolution. Genetics 162: 961–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright P. F., Webster R. G., 2001. Orthomyxoviruses, pp. 1533–1579 in Fields Virology, edited by Fields B. N., Knipe D. M. Lippincott Williams & Wilkins, Philadelphia. [Google Scholar]
- Xue K. S., Moncla L. H., Bedford T., Bloom J. D., 2018. Within-host evolution of human influenza virus. Trends Microbiol. 26: 781–793. 10.1016/j.tim.2018.02.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors affirm that all data necessary for confirming the conclusions of this article are represented fully within the article and its tables and figures. Supplemental material available at Figshare: https://doi.org/10.25386/genetics.6430487.