Molecular dynamics simulations of lipid nanodiscs

Abstract

A lipid nanodisc is a discoidal lipid bilayer stabilized by proteins, peptides, or polymers on its edge. Nanodiscs have two important connections to structural biology. The first is associated with high-density lipoprotein (HDL), a particle with a variety of functionalities including lipid transport. Nascent HDL (nHDL) is a nanodisc stabilized by Apolipoprotein A-I (APOA1). Determining the structure of APOA1 and its mimetic peptides in nanodiscs is crucial to understanding pathologies related to HDL maturation and designing effective therapies. Secondly, nanodiscs offer non-detergent membrane-mimicking environments and greatly facilitate structural studies of membrane proteins. Although seemingly similar, natural and synthetic nanodiscs are different in that nHDL is heterogeneous in size, due to APOA1 elasticity, and gradually matures to become spherical. Synthetic nanodiscs, in contrast, should be homogenous, stable, and size-tunable. This report reviews previous molecular dynamics (MD) simulation studies of nanodiscs and illustrates convergence and accuracy issues using results from new multi-microsecond atomistic MD simulations. These new simulations reveal that APOA1 helices take 10–20 μs to rearrange on the nanodisc, while peptides take 2 μs to migrate from the disc surfaces to the edge. These systems can also become kinetically trapped depending on the initial conditions. For example, APOA1 was trapped in a biologically irrelevant conformation for the duration of a 10 μs trajectory; the peptides were similarly trapped for 5 μs. It therefore remains essential to validate MD simulations of these systems with experiments due to convergence and accuracy issues.

1. Introduction

Lipid nanodiscs are planar assemblies consisting of a lipid bilayer stabilized by protein or peptide scaffolds. Naturally occurring nanodiscs such as nascent high-density lipoprotein are cardio-protective and play a critical role in reverse cholesterol transport (RCT) [1, 2]. RCT begins when APOA1 interacts with the ATP-binding cassette sub-family A member 1 (ABCA1), which transports lipids and cholesterols from macrophages, a process called cholesterol efflux. This yields nHDL, a discoidal bilayer stabilized by two molecules of APOA1. nHDL then interacts with lecithin–cholesterol acyltransferase (LCAT) [3], which converts unesterified cholesterol (UC) to cholesteryl ester (CE), resulting in mature (spherical) HDL (sHDL). In direct RCT, scavenger receptor class B member 1 (SR-BI) mediates the absorption of sHDL to the liver [4]. Indirect RCT involves the transfer of CE in exchange for triglycerides to very low-density lipoprotein (VLDL) and low-density lipoprotein (LDL) by CE transfer protein (CETP), and the delivery of LDL to the liver by the LDL receptor.

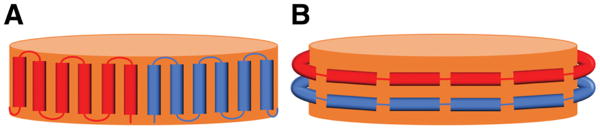
APOA1 mimetic peptides [5, 6] have biological properties similar to full-length APOA1, such as the ability to promote cholesterol efflux from cells [7] and to stabilize nanodiscs [8]. Despite functional similarities, APOA1 and mimetic peptides may stabilize nanodiscs differently. For example, it is possible that a “picket fence” arrangement of peptides is preferable to the belt-like one found for APOA1. A picket fence motif was in fact proposed for APOA1 [9, 10] but later disproven [11]. Figure 1 is a schematic of the picket fence and belt configurations of APOA1 on a lipid nanodisc.

Fig. 1.

Schematic representation of picket fence (A) and belt (B) configurations of APOA1 around a nanodisc.

Synthetic nanodiscs are composed of a bilayer patch encircled by membrane scaffold proteins (MSPs) [12–19] or polymers [20] similar to Fig. 1B. MSPs include truncated apolipoproteins, and can be linked at the termini to form rings. These nanodiscs provide detergent-free lipid bilayer models for biochemical and biophysical characterization of membrane proteins in a physiologically relevant environment [21–25].

Detailed knowledge of the structure of nanodiscs is crucial to understanding HDL functions, designing more effective mimetic peptides, and accurate characterization of membrane proteins. Early work established the association of low plasma HDL cholesterol (HDL-C) with an elevated risk of cardiovascular diseases [26], but did not indicate which of the HDL particles (nascent or mature) is more important. More recent studies have shown that low cholesterol efflux capacity of serum is a better predictor of cardiovascular diseases than HDL-C levels [27]; i.e., measurement of only HDL-C is insufficient [2, 28]. nHDL excels in mobilizing cellular cholesterol via cell surface transporters in the cholesterol efflux process, thereby supporting an important atheroprotective role. Understanding and enhancing this process paves the way for controlling cardiovascular diseases. nHDL is also related to the diseases associated with LCAT. Fish eye disease [29] arises from the loss of LCAT activity towards nHDL. A detailed model for LCAT–nHDL interaction, which depends on the atomistic structure of both APOA1 and LCAT, potentially leads to effective therapeutics for this disease. HDL functions are not limited to lipid transport. HDL has roles in inflammation, innate immunity, and glucose control [30]. Determining the structure of APOA1 in nHDL and sHDL will aid in identifying these functions. Structural studies of APOA1 mimetic peptides are also crucial to the rational design of these peptides to enhance cholesterol efflux. It remains unclear what arrangement—picket fence or belt (Fig. 1)—these peptides take on the nanodisc edge, and how they can be controlled. It was recently shown [31] that an ELK peptide (comprised solely of Glu (E), Leu (L), and Lys (K)) takes a tilted picket fence configuration. The tilted configuration exposes parts of lipid acyl chains to water, and it is possible that slight modifications of the amino acid sequence could promote a vertical picket fence configuration, more effectively stabilize the nanodisc, and thereby enhance cholesterol efflux. Finally, as the synthetic nanodiscs are primarily used for studying membrane proteins, detailed knowledge of their lipids and MSPs is crucial to correctly interpreting structural data of the embedded proteins and tuning nanodisc sizes, respectively.

As would be expected given their different functions, there are critical differences between nHDL, formed by APOA1 or mimetic peptides, and synthetic nanodiscs. nHDL adjusts its diameter along the RCT pathway and gradually transforms to sHDL. Hence, APOA1 must be sufficiently adaptable to stabilize the assorted sizes and shapes of HDL. This is possible due to the relatively low stability of APOA1 helices, which are in the range of 3–5 kcal/mol, indicating high flexibility and dynamic unfolding and refolding in seconds or less [32]. This dynamic behavior makes the classification and orientation determination of structures challenging when using techniques such as cryo-electron tomography. Hence, there has been no high-resolution experimental structure of full-length lipid-bound or lipid-free APOA1; there have been only models [33–35] in which the arrangement of the N- and C-terminals are substantially different. See Fig. 2 for the most recent model of APOA1 determined by a 20 μs-long MD simulation, a technique that does not have the above-mentioned experimental difficulty. As a common feature of almost all lipid-bound APOA1 models, the two APOA1 monomers stack in an antiparallel belt-like fashion with pairwise overlapping of residues 121–142 (Helix 5) producing a registry called LL5/5 [36–38]. Synthetic nanodiscs, in contrast, can be reconstituted using truncated MSPs to completely encircle a nanodisc with minimal displaced and fluctuating terminal domains, and this can greatly facilitate high-resolution studies [39]. The circularization of MSPs by covalently bonding the N- and C-terminals also enhances the thermal and proteolytic stabilities and yields more homogeneous and size-tunable nanodiscs [19].

Fig. 2.

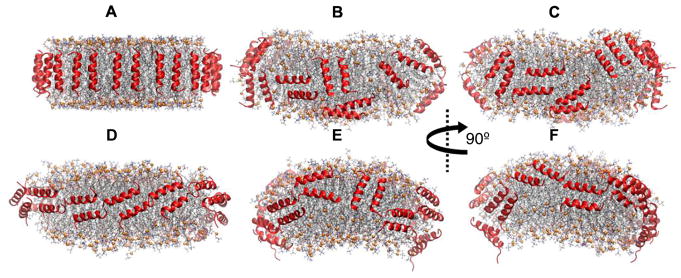
Structure of APOA1 in 160:24:2 POPC:UC:APOA1 [35]. (A) Side view at t = 0 μs facing terminals. (B) Side view at t = 20μs facing terminals. (C) Side view at t = 20 μs facing residue 121–142 (helix 5). (D) Top-down view at t = 20 μs. Proteins are shown as blue or red ribbons, and phosphorus atoms of lipids in orange spheres. Other lipid atoms are in stick representation (oxygen, red; nitrogen, blue; carbon of POPC, sliver; carbon of UC, black).

This paper provides an overview of MD simulations of lipid nanodiscs. Technically, many of the requirements for simulating lipid bilayers and lipid nanodiscs are the same: an accurate potential energy function (or force field), suitable simulation software, and a sufficiently fast computer. However, as explained in detail in Section 2, an effectively infinite planar bilayer at full hydration can be modeled reasonably well with systems of 20,000 particles in all-atom representations, while optimal modeling of nHDL requires over 250,000 particles. This increase in size makes it qualitatively more challenging to simulate a lipid nanodisc than a planar lipid bilayer.

By way of outline, Section 2, Review of simulation methodology, discusses system sizes and geometries (2.1), all-atom (AA) and coarse-grained (CG) representations (2.2), and enhanced sampling methods and accuracy issues (2.3); these considerations are also relevant for simulations of similar lipid assemblies including LDL, VLDL, and lipid droplets. This section is primarily aimed at the nonexpert and includes descriptions of some techniques that have been applied to bilayers but not yet to nanodiscs. Section 3, Review of previous simulations of nanodiscs, discusses papers from 1997 to 2017. Section 4, Sampling and convergence, presents selected technical results from our own MD simulations of APOA1 and mimetic peptides stabilizing nHDL; both conventional MD and enhanced sampling are considered. Section 5, Conclusions and future studies, summarizes the results, and considers targets related to HDL structure, fusion, and maturation, and the properties of embedded proteins in synthetic nanodiscs.

2. Review of simulation methodology

2.1 System Size and Geometry

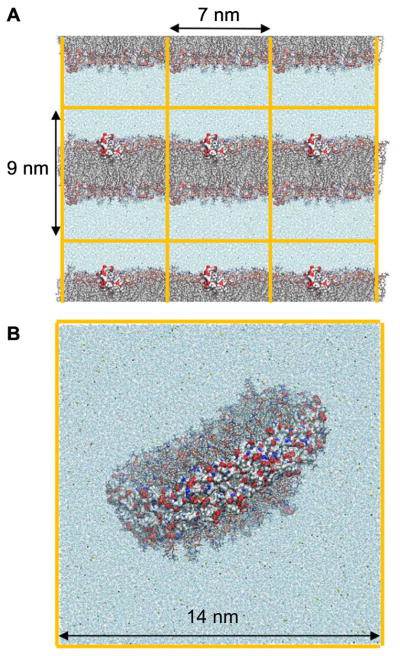
Essentially all MD simulations are carried out with periodic boundary conditions (PBC), wherein the primary cell of a system is replicated and a particle can pass though one side of the cell to an image and emerges from the image on the other side of the cell (Fig. 3). This avoids artifacts arising from using a hard wall to maintain the volume. For planar bilayers, PBC allow the modeling of an effectively infinite sheet using as few as 72 lipids (box length and height of approximately 5 and 7 nm, respectively) and a total number of atoms (including water) of less than 20,000. Systems of this size are sufficient for reproducing many experimental properties of single lipids [40], with the notable exception of lateral diffusion [41–43]. Larger boxes are required when peptides are added to the lipid system, because the peptide termini should not interact with each other through periodic images. This increases the number of lipids to 60,000 for a 40-mer peptide (box length and height of approximately 7 and 9 nm, respectively) (Fig. 3A). Not surprisingly, properties related to undulatory motions such as bending moduli also require larger systems [40]. For optimal realism, the nanodisc must be simulated in its entirety, though PBC are still required to avoid a hard wall around waters far from the disc surface (Fig. 3B). Even physically small lipid nanodiscs are large by simulation standards. For example, reconstituted nHDLs range in size from 50 to 200 lipids and contain 2 APOA1 (243 amino acids each); the diameters are between 8 and 11 nm. Simulations of these systems, including waters, require between 200,000–300,000 atoms. This number of atoms is presently difficult to simulate for more than several hundred nanoseconds on most laboratory-based computer clusters, a length far too short to allow for rearrangements of the APOA1 [35]. As shown in Section 4, even tens of microseconds might not be sufficient to assure convergence of simulations.

Fig. 3.

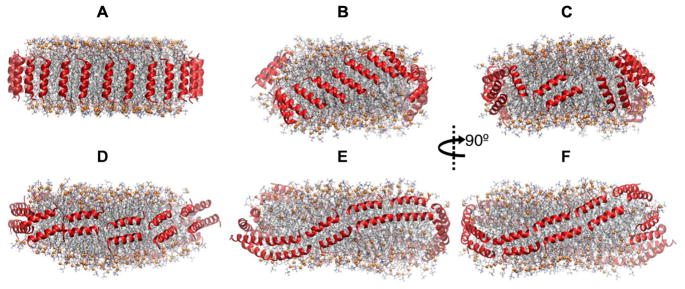
Simulation boxes are repeated in all directions by periodic images. (A) Lipid bilayer interacting with apolipoprotein CII mimetic peptides, one on each leaflet. (B) Nanodisc stabilized by a double belt of APOA1. Both systems are surrounded by water and ions. Orange lines show box boundaries. Only one simulation box is shown in (B). Representation codes: Lipids, sticks; proteins and peptides, surface; water and ions, beads (Oxygen of water, blue; Na⁺, yellow; CI⁻, green).

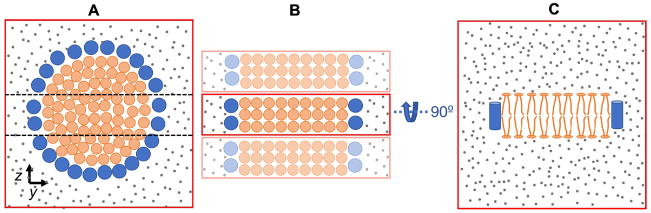
It is possible to simulate a discoidal HDL, especially one which is generated by short APOA1 mimetic peptides, using only part of the disc. Consider a disc in a simulation box with its top and bottom surfaces parallel to the yz plane (Fig. 4A). The disc is covered by peptides on the lateral surface and surrounded by water and ions. Cutting the box by two planes perpendicular to the yz plane yields a smaller box that is computationally less expensive to simulate. The bilayer in the smaller box is a rectangular cuboid that interacts with the surrounding environment through four faces and with its periodic images along the z axis through the other two faces (Fig. 4B,C). This allows the modeling of a nanodisc patch using as few as 60 lipids (box length and height of approximately 9 and 4.5 nm, respectively) and a total number of atoms (including water) of less than 40,000. Such a setup was previously used for the study of four APOA1 mimetic peptides, and correctly contrasted the experimentally observed abilities of peptides to stabilize nanodiscs [31]. It also yielded interpeptide and peptide-lipid salt bridges comparable to those obtained from an entire nanodisc simulation. As a caveat, the setup is best suited for the picket fence arrangement of peptides because it models the curved edge of a nanodisc by a flat edge of a bilayer slab. A belt configuration spans a larger arc on the bilayer edge, and curvature effects may become important. It is, however, not known a priori whether a peptide adopts a picket fence or belt configuration on the disc edge. Therefore, before using this setup, the picket fence configuration of peptides in a whole nanodisc should be explored by less expensive methods, such CG MD. AA MD with this setup can then be used to study the peptide–peptide and peptide–lipid interactions in more detail.

Fig. 4.

Reducing the number of particles for simulations of peptides on the edge of a nanodisc. (A) Top-down view; an entire nanodisc is cut through by two planes (dashed lines) yielding an approximately rectangular bilayer. (B) Top-down view; a rectangular bilayer models the nanodisc patch. The bilayer is surrounded by peptides and water and is periodic along the z axis. Periodic boxes are shown in lighter colors. (C) Side view of the bilayer in (B). Lipids, peptides, and water are shown as orange, blue, and gray circles, respectively. Simulation boxes are shown in red.

The diameter of spherical HDL is approximately 10 nm; therefore, it can be simulated in the same box size as one of the larger discoidal HDLs [44–51]. In contrast, the diameters of LDL and VLDL are approximately 20 and 30 nm, respectively. An AA simulation of an entire LDL would require a system size of about 700,000 particles, and VLDL more than 2,000,000 particles. These are at, or beyond, the current limits of appropriately long MD simulations. Large spherical lipoproteins are presently better explored using a “trilayer” geometry in which a layer of cholesteryl ester (for LDL) or triglyceride (for VLDL) is surrounded by two layers of phospholipids (Fig. 5). Such a system of 128 lipids, 64 triglycerides, and 2 peptides in a box with 10 nm height modeled a segment of apolipoprotein B-100 on VLDL [52]. It contained only 50,000 atoms and was simulated for 120 ns on a standard laboratory computer cluster. CG simulations by Ollila et al. [47] showed that, for a fixed area per lipid, the interfacial tension of a trilayer is higher than that of HDL-size droplets, and the difference was larger when lipids were more packed. The interfacial tensions of LDL and VLDL are likely more comparable to that of a flat trilayer because of weaker curvature effects. Ideally, the validity of this setup should be confirmed by simulations of the whole LDL or VLDL particles, which currently do not exist due to the large system size and the lack of precise structure of relevant apolipoproteins, such as apolipoprotein B-100.

Fig. 5.

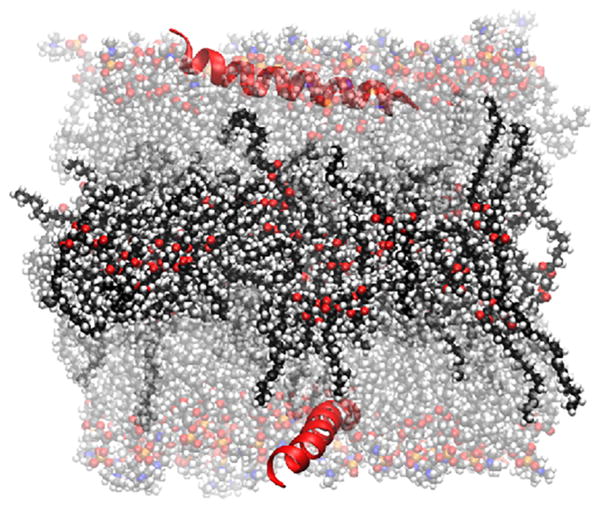
A trilayer comprised of a layer of triolein surrounded by two POPC monolayers, interacting with a peptide (B38, a segment of apoB-100) [52]. Water molecules are not shown for clarity. Representation codes: Peptide, red ribbon; lipids, CPK; POPC, transparent; triolein carbon, black; POPC carbon, gray; oxygen, red; nitrogen, blue; phosphorus, orange; hydrogen, white.

Similarly, a tetra-layer was used to study the passage of CE from HDL to LDL through CETP [53]. The model consisted of two opposing double layers. One double layer had palmitoyl-oleoyl-phosphatidylcholine (POPC) and CE and the other had POPC and triglyceride (TG). The drawback of this geometry is that the fatty acids can exchange through the periodic boundary, thus care must be taken in interpreting the results.

2.2 All-atom and coarse-grained representations

The forces between particles in a molecular dynamics simulation are determined based on mathematical functions and parameters that are derived empirically; the combination of functions and parameters is called the force field (FF). Trajectories are propagated according to Newton’s law of motion; i.e., the treatment is classical, even though quantum mechanics is used in the development of parts of the more detailed FF [54–56]. Most classical FF are additive, which signifies that the partial charges on each particle are fixed throughout the trajectory. The charges in polarizable FF can vary in response to the environment. This is a relatively recent development, and none of the simulations described here were carried out with a polarizable FF.

The representations of particles range from AA (each atom, including hydrogens, is treated separately), united atom (UA) (hydrogens and heavy atoms are merged), and CG. The CG FF themselves vary in resolution [57, 58]. A widely used CG FF is Martini [59, 60], wherein each fundamental particle consists of 3–4 heavy atoms and their hydrogens. The more coarse-grained Cooke model [61] represents individual lipids by only 3 particles (1 hydrophilic and 2 hydrophobic). AA and UA lipid FF typically include explicit water, although water was implicit in the model developed by De Loof et al. [62] The original Martini contains explicit water (the CG water represents 4 AA waters); water molecules are implicit in the more recent “Dry Martini” [63]. A variant of Dry Martini uses stochastic rotational dynamics (STRD) to include the hydrodynamic effects of the water [64]. The Cooke model and similar aggressively CG representations do not include explicit water. The following example shows the speed-up obtained by the reduction in the number of particles. Dipalmitoyl-phosphatidylcholine (DPPC) contains 130 atoms (including hydrogens), and DPPC bilayers are hydrated with approximately 30 waters/lipid at full hydration. There are 12 atoms/DPPC in Martini, and full hydration adds 8 water particles. Hence 20,000 particles are sufficient to model a bilayer with 91 lipids in an all-atom representation, 1000 lipids in Martini, nearly 1700 in Dry Martini, and 6700 in the Cooke model. The advantages of each representation must therefore be considered carefully. The speed-up in CG FF is not only due to the reduction in the number of particles but also due to the softening of the particle–particle potentials. This softening allows a larger time step; for example, the time step, which is limited by the frequency of bond stretching, is typically 1–2 fs in AA simulations, and 20–40 fs in Martini. The number of local energy minima is also lower in CG representations. The preceding two factors lead to substantially better sampling of the energy landscape for the same computer time for the CG simulation. As a technical note, trajectory lengths for CG simulations are sometimes scaled up to account for the lower viscosity of bilayers in the representation. Unless noted as “scaled time,” the times reported here are simply a product of the number of steps and the time step.

AA MD allows detailed investigations of phenomena that evolve on nanometer length scales and microsecond time scales. System sizes and simulation lengths for CG models can be three to four orders of magnitude larger than AA, but the results are less accurate due to the reduced detail. For example, the secondary structure transformations are not modeled in the CG Martini force field [59]. Processes in which folding and unfolding are playing a substantial role are therefore not suitable for such a model description. There are numerous other issues: the simple water models (the water in Martini is a single Lennard-Jones sphere with no partial charges); electrostatics (insufficient screening); and entropy (far fewer degrees of freedom). These issues reduce the accuracy of CG with respect to AA models, and highlight the importance of critical benchmarking. See Refs. [59], [60], and [63] for further discussion. However, the value of CG simulations should not be discounted. CG simulations characterized the disassembly of nanodiscs by cholate [65], self-assembly and fusion of nanodiscs [66], and a pathway for the formation of nHDL from lipid and cholesterol domains [67]. Simulations of LDL and lipid droplets have also been carried out with CG models [47, 49, 68]. These simulations are computationally challenging with AA force fields because they require large boxes to accommodate such lipoproteins and long simulation times to fold the relevant apolipoproteins, such as apolipoprotein B-100, for which there is no high-resolution structure or low-resolution model.

2.3 Enhanced sampling methods and accuracy issues

Despite recent advances in computational hardware, lengths of conventional AA MD simulations on typical laboratory clusters are still only several hundred of nanoseconds to a microsecond. Even on specialized supercomputers, such as Anton-2 [69], trajectories are limited to tens of microseconds for most users. Such simulations are usually too short to observe processes involving the large-scale rearrangements of proteins or peptides as required to properly model nanodiscs. Enhanced sampling techniques can be used to overcome the time scale limitations of conventional MD. These techniques range from ad hoc to rigorous. The former group includes applying high temperatures or guiding forces, both of which enable passage over kinetic barriers. For example, recent simulations of the antimicrobial peptide (AMP) PGLa in lipid bilayers at 140–180° C showed numerous translocation events [70]. The translocation of AMPs can also be effected by steered molecular dynamics (SMD) [71, 72], where external forces are applied to molecules during the dynamics run to accelerate processes that are otherwise too slow to model or to probe mechanical functions. As described below, the difficulty of ad hoc methods is that the results are not necessarily representative at biological temperatures. More rigorous methods, which in principle generate results consistent with an ensemble at an appropriate target temperature are preferable. These include replica exchange MD [73–75], accelerated MD [76], adaptively biased MD [77], and self-guided Langevin dynamics (SGLD) based on the generalized Langevin equation (SGLD-GLE) [78]. The remainder of this subsection focuses on HDL- or LDL-related simulations.

MD simulated annealing (MDSA) [79, 80] has been used to sample configurations of APOA1 on a nanodisc [34, 81, 82]. Here the temperature of the system is rapidly (e.g., in 20 ps) increased to 500–1000 K to overcome the energy barriers, and then slowly (e.g., in 10 ns) decreased to physiological temperature (~310 K) for a transition to a local or global free energy minimum. The danger in MDSA is that high temperature can distort the structure unless specific parts of the system are restrained [83].

Temperature replica exchange (TREX) [73–75] may be considered a rigorous version of MDSA. In replica exchange (REX, sometimes called REMD for replica exchange molecular dynamics) a system is simulated with multiple baths at different temperatures or a relevant term in the Hamilton, and exchanges are allowed between baths using a Monte Carlo acceptance criterion. Consequently, a configuration that migrates to the target bath (usually room temperature) is representative of the correct equilibrium ensemble and is unlikely to be an artifact.

In analogy to TREX and MDSA, umbrella sampling [84, 85] is a rigorous version of SMD. This method combines the results of a series of simulations to calculate the free energy change along a pathway (reaction coordinate). Each simulation (window) restrains certain configurational parameters along the pathway. A drawback is that individual simulations may suffer from poor sampling of the other degrees of freedom. The convergence of free energy profiles can be accelerated by combining umbrella sampling with Hamiltonian REX, whereby windows are allowed to exchange along the reaction coordinate [86, 87]. This technique was used by Karilainen et al. [51] to estimate the free energy of uptake of cholesterol and 7-ketocholesterol into α-HDL.

SGLD [88] enhances sampling through acceleration of low frequency motions. A low frequency motion represents the slow conformational change that contributes the most in the conformational search and is determined based on a local average of momenta. Enhancement is achieved by introducing a guiding force that resonates with the low frequency motion. There are numerous variants [89], including SGLD-GLE [78], which rigorously conserves the ensemble. A less rigorous, but more efficient, version [88] is tested on nanodiscs in Section 4.3.

3. Review of previous simulations of nanodiscs

The first AA MD simulations of planar lipid bilayers were published in the early 1990s [90], and those of nanodiscs were not far behind [91]. However, computer power was limited and trajectory lengths with conventional MD simulations did not reach the ns time scale until the early 2000s. Hence, many of the early simulations described below should be considered exploratory. There is a place for such work in nearly every field. The following summary follows chronological order.

3.1 1997–2000

The first MD simulation of a nanodisc was carried out in 1997 and employed MDSA to compare the stability of two possible picket fence configurations of APOA1 dimer, namely head-to-tail and head-to-head [91]. Each configuration was heated up to 500 K, and then cooled down either in 35 ps or in 70 ps; both cooling schemes (or replicas) yielded a similar structure for each configuration. The simulation length did not allow for discrimination between the two configurations. Subsequently, an AA simulation of a nanodisc of 20 POPC and 12 APOA1 mimetic peptides—called 18A—highlighted the importance of inter- and intrapeptide salt bridges in the stability of a picket fence peptide scaffold [92]. The peptides were initially oriented antiparallel to each other on the disc edge to create favorable helix–dipole interactions. The system was heated from 10 K to 300 K in 30 ps and remained at 300 K for 703 ps. Although only one replica was simulated, 12 peptides allowed for the analysis of 12 interhelix interactions. The salt bridges were found to dominate the interhelix energies, and the mean lifetime for salt bridges was estimated to be in the range of 1–10 ns.

3.2 2001–2010

Upon the proposal of the double belt model of APOA1 [93], three nHDL models with different registries of APOA1 molecules were each simulated for 1 ns [94]. The short simulations did not allow the three replicas to yield a single structure with an optimal registry. Nevertheless, they revealed salt bridging triads; e.g., between an acidic residue in one monomer and two basic residues in the other. Moreover, the distribution of charged amino acids along the α11/3-helices of APOA1 suggested a mechanism for the rotation of APOA1 monomers relative to one another. An acidic residue that forms an interhelical salt bridge with a basic residue would be able to form a second salt bridge with another basic residue 11 residues down in the sequence and would then be free to disassociate from its initial salt bridging partner. Two factors were postulated to hinder the sliding of monomers once the optimal registry is reached: 1) the kinks created by proline residues, which punctuate the APOA1 helices and should overlap to minimize the hydrophobic energy cost, and 2) the presence of two 11-mer helices, which disrupt the periodic 22-mer helices and guarantee a preferred rotational alignment.

Shih et al. [14] carried out four AA simulations of four double belt configurations of MSP variants each encircling nanodiscs of 160 DPPC lipids for 4.2 ns–6.9 ns. Moreover, a 4.5 ns-long AA simulation investigated the stability of bacteriorhodopsin, an integral membrane protein that contains seven transmembrane helices, embedded in a nanodisc stabilized by a double belt of MSP.

Particles with 160:2, 120:2, 100:2, and 50:2 POPC:Δ40APOA1 were simulated for 10 ns, 5 ns, 7 ns, and 5 ns, respectively, using an AA force field [95]. Starting from the particle with 160 lipids, the lipids were removed incrementally to generate the initial configurations of the smaller particles. The tertiary structure of proteins in 120:2 POPC:Δ40APOA1 resembled the crystal structure of the lipid-free Δ43APOA1 [96]. This particle was simulated with three more initial configurations for up to 4 ns, obtained from different lipid reduction methods, all of which yielded similar protein structures.

The first CG simulation of a nanodisc was carried out by Shih et al. [97] The nanodisc was composed of 160 DPPC lipids and a double belt of MSP, and was simulated for 62.5 ns at 300 K, for 100 ns at 323 K, and for 285 ns at 353 K. The simulations confirmed the reliability of the CG model in maintaining the shape of particles and in reproducing the overall structural features of discoidal HDL. The self-assembly of nanodisc was also investigated in three simulations at 323 K with three different initial configurations for 1 μs, 1.5 μs, and 1.5 μs. The proteins covered the lipid assembly in all three simulations, but no protein–protein interaction was observed to initiate the formation of a double belt. The structures slightly resembled a picket fence arrangement. The protein–lipid–water CG model in this study [97] was an extension of a previous [98] lipid–water CG model. Shih et al. [99] improved the CG model and used it in three series of simulations. 1) Three double belt configurations of MSP variants each encircling a nanodisc of 160 DPPC lipids were simulated for 500 ns. MSP1 was shown to be too large to fit around such a nanodisc, and as a result its terminal ends overlapped. MSP1 Δ(1–22), in contrast, showed a gap between the terminal ends. MSP1 Δ(1–11) showed no mismatch between its length and the circumference of the nanodisc. 2) A head-to-tail picket fence initial configuration of MSP1 evolved to a belt-like structure in 1 μs. 3) Self-assembly simulations with two replicas suggested that lipids and proteins aggregate in about 1 μs, but a longer time is required for optimization of protein structure. A 2 μs-long CG simulation lent further insight to the role of cholate molecules in disassembling of nanodiscs that were initially stabilized by MSPs [65]. The molecules migrate to the disc edge, insert between the proteins and the lateral surface of the disc, and disrupt the protein-lipid assembly.

Hydrogen-deuterium exchange mass spectrometry combined with homology modelling (but no dynamics) yielded the solar flare model, wherein residues 159–180 of each APOA1 form a protruding solvent-exposed (akin to solar flare) loop [100]. This configuration generated interest because it was suggested to activate LCAT. However, the solar flare regions collapsed onto the disc in 10 ns AA and 700 ns CG simulations [101], raising concerns with the model. A subsequent study [3] also questioned the significance of this region as LCAT activator, although the debate still continues [102].

The stability of discoidal HDL was studied by six 20 ns-long AA simulations of 100:2 POPC:Δ40APOA1 at 500 K [83]. The high temperature caused the bilayer to expand by 40% and the helicity of proteins to decrease from 95% to 72%. The helicity and stability of salt bridges in the central region of proteins (helices 4–6) were unaffected, whereas the terminal ends (helices 1 and 10) were mobile, giving rise to different tertiary structures.

Four 20 ns-long AA MDSA followed by a 20 μs-long (scaled time) CG simulation had major implications for mechanisms of LCAT activation [103]. The two overlapped helices in the double belt, i.e. residues 121–142, present a hydrophobic tunnel at the juxtaposed residues G129. The sn-2 methyl ends of POPC lipids were exposed to the surrounding solvent through the tunnel in three out of four MDSA replicas. The CG simulation showed that the hydroxyl group of UC can also contact the solvent through the tunnel. These observations lead to the hypothesis that the tunnel facilitates the esterification of UC by LCAT.

Small angle neutron scattering (SANS) combined with an 80 ns-long MD simulation with a UA force field [104, 105] yielded the double super helix (DSH) model; i.e., an antiparallel double super helix wrapped around a prolate ellipsoidal lipid assembly of 200:20 POPC:UC. The simulation was performed at constant volume, rather than constant pressure, resulting in a separation of the two lipid leaflets and a hole in the ellipsoid. There is a wide separation (77 Å) between the termini of each APOA1 in this model. Jones et al. [106] carried out the following series of simulations at constant pressure to assess the validity of the DSH model. The model was first used as the initial point for a 5-ns AA simulation. The empty space in the ellipsoid disappeared in 2 ns, although the resultant tertiary structure of proteins did not change significantly. This configuration was then subjected to two successive MDSA for a total time of 60 ns, followed by a 60 μs-long CG simulation. The wide separation between the terminal ends of proteins persisted, exposing a large patch of hydrophobic acyl chains (~ 65 Å) to water. This implies that both MDSA and CG simulations were not converged to the global free energy minimum. Moreover, the discoidal lipid assembly resulting from the constant pressure simulations showed that the ellipsoidal lipid assembly in the DSH model is thermodynamically unstable.

3.3 2011–2018

The mobility of the terminal domains of APOA1 was investigated using a series of MDSA simulations of nanodiscs of 160:24:2, 100:15:2, and 50:8:2 POPC:UC:APOA1 and a simulation of 240:36:2 POPC:UC:APOA1 at 500 K [34]. The N-terminals of the two proteins were associated via salt bridges in all except the largest particle, whereas the C-terminals were always mobile and distant. The N-terminals were thus proposed to act as a molecular latch that holds the dimer together and breaks at a critical threshold of particle size.

The self-assembly and structure of nanodiscs were studied in a 2 ms-long (scaled time) CG simulation with implicit solvent [66]. The system contained 60 18A peptides and 960 dimyristoyl-phosphatidylcholine (DMPC). Starting from a random gas-like configuration, small peptide–lipid aggregates quickly formed, which over time fused into progressively larger aggregates of varying sizes. Therefore, the simulation revealed polydispersity of aggregate sizes and the evolution of the size distribution over time.

The self-assembly and physical properties of 160 phospholipids and a double belt of MSP were investigated using two 42 μs-long self-assembly CG simulations followed by a 50 ns-long AA simulation [107]. All lipids were incorporated into the confined space encircled by the MSPs in 7.5 μs of the self-assembly simulation. Lipids at the center of the nanodisc in the AA simulation were highly ordered, whereas annular lipids that were in contact with the proteins were disordered due to perturbed packing. Comparison with an infinite (periodic) bilayer showed that lipids in the nanodisc have in average lower configurational entropy and higher acyl tail order than in a lamellar bilayer phase. This is consistent with SANS and fluorescence measurements of nanodiscs comprised of DMPC and APOA1 [108].

The pleating of lipid domains was simulated using a CG force field to study the formation of nHDL [67]. The study was based on the hypothesis that ABCA1 creates domains that have a larger lipid density in the outer monolayer than in the inner monolayer. The transbilayer density gradient in the CG simulations was created by membrane insertion of amphipathic helices and/or excess phospholipids (ABCA1 was not simulated). Simulations resulted in the pleating of the outer monolayer and formation of membrane-attached discs stabilized by APOA1 or mimetic peptides, and vesicles in the absence of APOA1 or mimetic peptides (see Fig. 3 of Ref. [67]).

As a follow-up to the study of the 18A peptide [66], the self-assembly of DMPC nanodiscs stabilized by three dimeric 18A peptides was studied in three 2 ms-long (scaled time) CG simulations with implicit water [109]. The two copies of 18A were either directly connected (without a linker), or were linked with Pro or with Gly–Gly. The smaller particles merged by collisions to form larger particles. The sizes of the largest particles in the simulations were consistent with those obtained from the small-angle scattering models. The number of lipids in the largest particles converged after approximately 1.1 ms; hence, the time scale for the formation of full-sized peptide nanodiscs is milliseconds. The simulations converged to different total energies and these energies correlated well with the stability of the systems, as determined by static light scattering. For example, the nanodisc reconstituted by the dimer with Pro linker was the most unstable and converged to the highest energy, and the nanodisc reconstituted by the dimer without any linker was the most stable and reached the lowest energy.

CG simulations with Martini force field shed light on the encapsulation of gold nanoparticles (AuNPs) by lipid nanodiscs, composed of 3:1 DPPC and dihexanoyl-phosphatidylcholine (DHPC) [110]. The systems did not include any stabilizing MSPs or peptides. Simulations with two initial configurations, one with AuNPs close to the nanodisc surfaces and the other with AuNPs close to the edge, suggested that the particles are encapsulated predominantly from the edge, where the lipids are more disordered. The AuNPs were localized near the tails of the edge lipids forming a ring within the nanodisc. A temperature increase from 288 K to 310 K in about 1.5 μs transformed an AuNP-free nanodisc into a vesicle. In contrast, the same temperature increase over 10.5 μs of an AuNP-included nanodisc caused the AuNPs to cluster into a close-packed ring, thereby stalling the vesiculation process at a “round vase” stage.

The stabilization of nanodiscs by four ELK peptides were studied by AA MD simulations, and the results were compared with the experimentally-measured cholesterol efflux ability of the peptides [31]. One peptide was positive in charge (pos), one negative (neg), and two were neutral with different hydrophobicities (hyd and neu). First, the geometry in Fig. 4 was used in four 500 ns-long simulations. The peptides initially arranged in antiparallel picket fence configurations. Hyd and neu remained on the edge by forming favorable salt bridges, whereas pos and neg repelled each other and migrated to the disc surface (neg formed dimers but the dimers repelled each other). These behaviors correlated with the cholesterol efflux abilities of peptides. Second, neu was simulated in an entire nanodisc, wherein the peptides migrated from the disc surface to the edge and formed a picket fence arrangement.

The structures of APOA1 in two nHDLs comprised of 160:24:2 and 200:20:2 POPC:UC:APOA1 were studied using 20 μs and 10 μs AA MD simulations, respectively [35]. The double belt model of APOA1 [93] was used as the initial configurations. The first 21 residues of the two proteins overlapped and formed similar salt bridges in both particles on the disc edge. In the smaller particle, residues 26–43 of one protein formed a condensed region, which ejected the C-terminal domain of the other protein to the disc surface (Fig. 2). These rearrangements were absent in the larger particle (details in Section 4.3). Therefore, the simulations provided a mechanistic understanding of how nHDL matures. The protein structure in the smaller particle was validated by cross-linking data. Technical details from the nanodisc simulations in this and the preceding paragraph are discussed further in the following section.

4. Sampling and convergence

4.1. The Systems

This section describes results from our own new and recently published [31,35] simulations illustrating some of the pitfalls of conventional MD simulations as long as 20 μs for nanodisc systems, and from SGLD, the enhanced sampling method introduced in Section 2.3. The systems are listed in Table 1 and described in more detail below.

Table 1.

All-atom simulations of APOA1 (A1) and mimetic peptides in nanodiscs with different initial configurations. The two peptides discussed here are neu: NH₃⁺-EKLKELLEKLLEKLKELL-COO⁻; and neg: NH₃⁺-EELKEKLEELKEKLEEKL-COO⁻.

#	Stoichiometry		Initial Condition	Time
1a	200:20:2	POPC:UC:A1	planar double belt	10 μs
2	200:20:2	POPC:UC:A1	uneven double	10 μs
3	200:20:26		picket fence	5 μs
4	200:20:26		belt	5 μs
5b	150:15:24		surface	3 μs
6	150:15:18		surface	3 μs
7	200:20:26		picket fence	2 μs
8	200:20:26		belt	2 μs
9SGLD	150:15:24		surface	40 ns
10SGLD	200:20:26		belt	40 ns
11SGLDc	80:1	DOPC:WALP	periodic bilayer	20 ns

^aReported in Ref. [35].

^bFirst 2 μs reported in Ref. [31].

^cIncludes 7 simulations; see Table 2.

4.2. Simulation Details

4.2.1 Development of initial conditions

All nanodiscs were solvated with water molecules and 0.15 M NaCl in cubic boxes 15–16 nm side length using the CHARMM-GUI [111] web interface.

The initial condition of Simulation 1 was developed by building a nanodisc of 200 POPC, 20 UC, and 2 MSPs in CHARMM-GUI. MSPs were replaced by the planar double belt of APOA1 [93]. All histidine residues were protonated, as they are in the same position as basic residues on helical repeats [112].

The initial configuration of proteins and lipids in Simulation 2 was obtained from an AA MD simulation on the planar double belt of APOA1 [93] for 5 ns at 310 K. The coordinates were provided by Martin Jones (Vanderbilt University Medical Center).

The initial condition of Simulation 3 was developed by building a nanodisc of 200 POPC, 20 UC, and 2 MSPs in CHARMM-GUI [111], followed by the removal of MSPs from the assembly. The coordinates of neu (see Table 1 for the sequence) were obtained from a previous study [31]. Twenty-six peptides were arranged on the lateral surface of the disc in an antiparallel picket fence configuration.

The initial configuration of peptides and lipids in Simulation 4 was developed by considering the initial configuration of proteins and lipids in Simulation 2 as the reference. C_α atoms of 13 identical dimers of neu, obtained from a previous study [31], were mapped onto the C_α atoms of APOA1 dimer in the reference structure. Hence, the peptides were oriented along the APOA1 molecules.

The initial configuration of lipids in Simulation 5 was obtained by randomly deleting 50 POPC and 5 UC from a disc of 200:20 POPC:UC, which was already simulated for 128 ns. The nanodisc was centered so that its normal vector was along the z axis. Twenty-four peptides were randomly placed close to the head groups of POPCs, 12 per leaflet. Previous study showed that neu resides 1.57 nm away from the middle of a 90:10 POPC:UC bilayer [31]. Hence, the peptides were restrained at z = ±1.57 nm with a force constant of 0.1 kcal/mol for 6.6 ns to associate with the POPC head groups. The φ and ψ angles of residues 4 to 16 were restrained at −57° and −47°, respectively, to preserve the helicity.

The initial condition of Simulation 6 was developed by removing 6 out of 24 peptides from the initial condition of Simulation 5.

The development of initial conditions of Simulations 7 and 8 followed the same procedures as for Simulations 3 and 4, respectively.

The initial condition of Simulation 9_SGLD was the same as Simulation 5. The 4-μs frame of Simulation 4 was used as the initial condition of Simulation 10_SGLD.

The simulation boxes for Simulations 11_SGLD were similar to Fig. 3A. They contained dioleoyl-phosphatidylcholine (DOPC), WALP19 (a 19-mer peptide comprised of Trp (W), Ala (A), and Leu (L)), water, and ions.

4.2.2 Simulation parameters and methods

CHARMM 36 [113, 114] was used for lipid and protein parameters. The TIP3P water model [115] as modified for CHARMM [116] was used to describe water molecules. Lennard-Jones (LJ) parameters of Na⁺ and Cl⁻ as well as Na⁺ and selected oxygens of lipids and proteins were taken from the CHARMM 36 ion parameters (NBFIX) [117–119].

Conventional MD simulations were prepared using the CHARMM program [120] and run on the Anton-2 supercomputer [69]. Trajectories were generated with a multigrator [121] and a time step of 2 fs. Temperature and pressure were kept constant at 310 K and 1 bar, respectively, using a variant [121] of the Nosé–Hoover [122, 123] and the Martyna–Tobias–Klein algorithm [124]. Electrostatic forces were calculated using the u-series method [69]. Water molecules and all bond lengths to hydrogen atoms were constrained using the M-SHAKE algorithm [125].

SGLD [88] simulations were performed using the CHARMM program [120] with the following parameters: TSGAVG = 0.2 ps (local average time; all motions with periods larger than TSGAVG were enhanced); SGFT = 1.0 (momentum guiding factor; λ in the SGLD equation of motion); FBETA = 1.0 (friction constant). Trajectories were generated with a leapfrog Verlet algorithm and a time step of 2 fs. Electrostatics were evaluated using particle-mesh Ewald [126]. All bonds to hydrogen atoms were constrained using the SHAKE algorithm [127].

4.3. Results

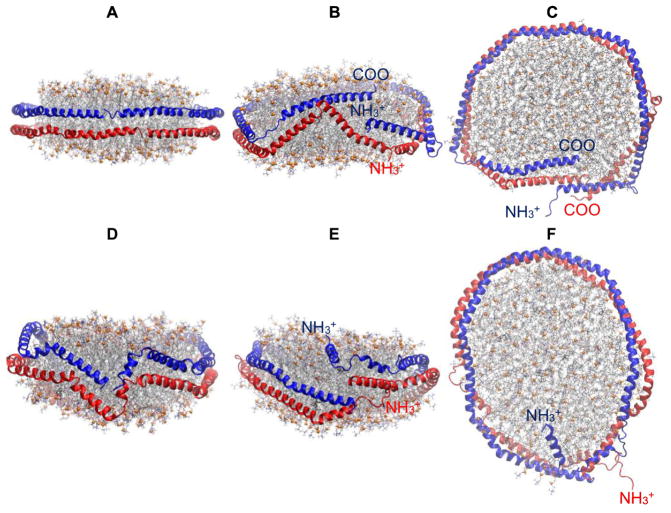
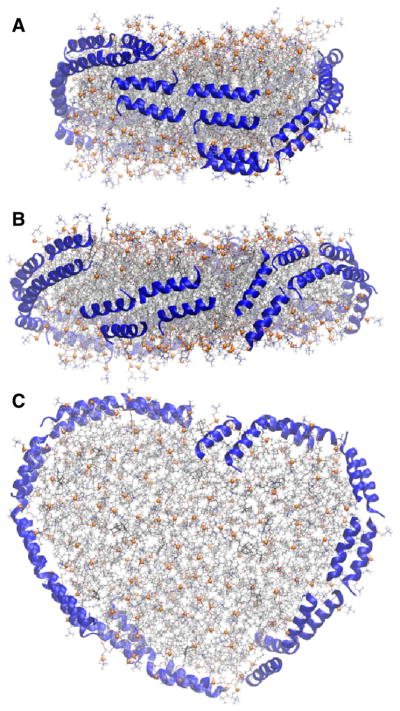
Two 10 μs-long AA simulations on a discoidal HDL with 200:20:2 POPC:UC:APOA1 demonstrate the convergence issue of these systems. The initial configuration of APOA1 in Simulation 1 [35] was the “planar double belt” in which α-helical pairs of APOA1 form a smooth double-ring around the lipid disc in an antiparallel fashion where the N-terminals of the two APOA1 (residues 1 to 12) overlap (Fig. 6A). This simulation is described in more detail elsewhere [35]. The planar double belt was slightly distorted and the overlap between N-terminals was not optimal in the initial configuration of Simulation 2 (Fig. 6D). This slight difference in the initial configurations resulted in dramatically different final configurations at 10 μs. The N-terminal overlap increased in the first simulation to tighten the proteins around the nanodisc (Fig. 6B,C) [35]. In contrast, the N-terminals completely dissociated in the second simulation in 30 ns; one migrated to the disc surface and the other became a random coil in water (Fig. 6E,F). This arrangement remained unchanged for the entire 10 μs trajectory. These results show that the final tertiary structure of APOA1 in currently accessible simulation times largely depends on the initial configuration. It is tempting to conclude that the structure in Simulation 2 resides on an elongated nanodisc (Fig. 6F) in contrast to the more circular shape of Fig. 6C. However, these are both snapshots and, on average, their shapes are statistically equivalent. Much longer simulations may reveal a relation between disc shape and protein conformation, but that does not appear possible at present.

Fig. 6.

10 μs-long simulations of HDL nanodiscs with 200:20:2 POPC:UC:APOA1 showing the convergence issue. (A) Simulation 1[35]; initial configuration (t = 0 μs); side view. (B) Simulation 1; t = 10 μs; side view. (C) Simulation 1; t = 10 μs; top-down view. (D) Simulation 2; initial configuration (t = 0 μs); side view. (E) Simulation 2; t = 10 μs side view. (F) Simulation 2; t = 10 μs top-down view. Representation codes are the same as in Fig. 2.

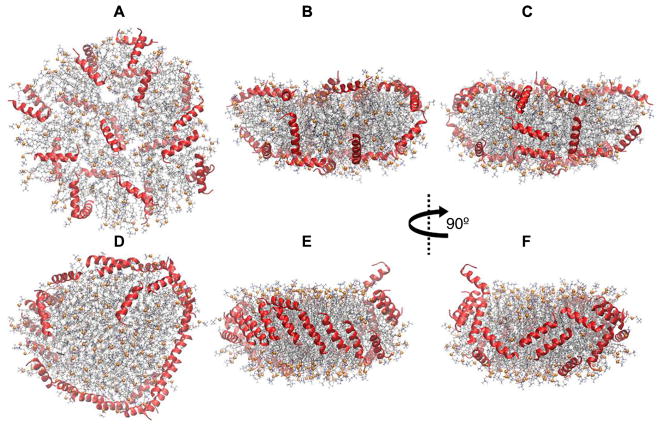
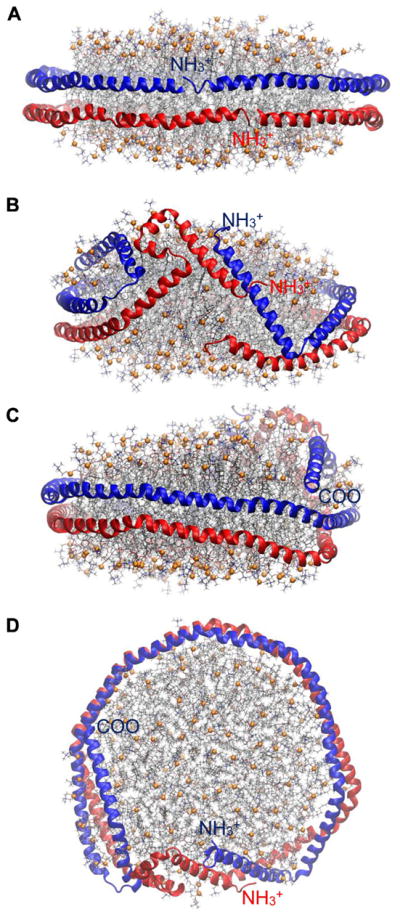
APOA1 mimetic peptides in nanodiscs can also be kinetically trapped depending on the initial configuration. This issue is best exemplified in the following series of simulations on neu (Table 1), which is an amphipathic α-helix ELK peptide having a net charge of zero. Two 5 μs-long AA simulations were carried out on a disc of 200 POPC, 20 UC, and 26 neu. The initial configurations were developed by arranging the peptides around the disc along its normal vector as a picket fence (Simulation 3) and perpendicular to it as a double belt (Simulation 4) (Figs. 7A and D, respectively). Adjacent peptides were antiparallel to each other. Geometrically, 26 picket fence peptides are less than sufficient to optimally cover the edge of such a disc, and the picket fence in the initial configuration of Simulation 3 tilted in 3 μs to cover the edge more effectively and optimize inter-helical salt bridges. The structure remained stable for the last 2 μs (Fig. 7B,C). In contrast to the picket fence geometry, 26 peptides in a double belt arrangement are too crowded when placed on the edge, and the peptides in Simulation 4 changed the disc shape from planar to saddle-shaped to create more edge (Fig. 7E,F). The peptides remained stable for the last 2 μs in the double belt configuration. Neither of the configurations in Simulations 3 or 4 transitioned to the other in 5 μs. Hence, either longer simulations are required to reveal the global free energy minimum or the initial configuration should change to avoid kinetically trapped structures.

Fig. 7.

Side views of HDL nanodiscs with 200:20:26 POPC:UC:neu showing the convergence issue. (A) Simulation 3; picket fence initial configuration (t = 0 μs). (B,C) Simulation 3; t = 5 μs. (D) Simulation 4; belt initial configuration (t = 0 μs). (E,F) Simulation 4; t = 5 μs. Peptides are shown in red ribbons. Lipid representation codes follow Fig. 2.

Simulation 5 was carried out to resolve the convergence issue described above. The initial configuration was developed by randomly covering the top and bottom surfaces of the disc with peptides to allow for an unbiased evolution of the peptide assembly (Figs. 8A–C). The simulation time was 3 μs and the stoichiometry was chosen based on experimental data as 150:15:24 POPC:UC:neu [31]. Figures 8D–F show the snapshots at 3 μs. The peptides predominantly take a picket fence configuration on the side of the nanodisc that is more crowded (Fig. 8E). They are less ordered on the other side (Fig. 8F); nevertheless, the picket fence configuration is more favored. All but two peptides (one of which left the disc and entered the water phase) migrated to the edge by 2 μs. The arrangement of peptides with respect to each other remained unchanged on the crowded side between 2–3 μs, but continued to evolve on the other side (a few of them migrated from the edge to the surface and returned to the edge).

Fig. 8.

First and last configurations of Simulation 5 on 150:15:24 POPC:UC:neu. (A–C) Initial configuration (t = 0 μs); peptides are on disc surfaces. (D–F) t = 3 μs. (A) and (D) are top-down views, and the rest of the panels are side views. Peptides are shown in red ribbons. Lipid representation codes follow Fig. 2.

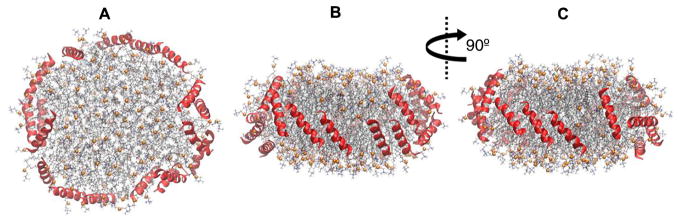
The purpose of Simulation 6 was to test the hypothesis that the configuration of peptides depends on the stoichiometry. It was similar to Simulation 5 but with 18 peptides. Eighteen peptides can geometrically take an ideal double belt on a disc of 150:15 POPC:UC. Figure 9 shows the final configuration at 3 μs which does not support the above hypothesis. Fourteen picket fence and 4 belt peptides were formed. Hence, neu tends to arrange as a picket fence irrespective of the stoichiometry.

Fig. 9.

3-μs snapshots of Simulation 6 on 150:15:18 POPC:UC:neu showing the preferred picket fence configuration of peptides. (A) Top-down view. (B,C) Side views. Peptides were on disc surfaces in the initial configuration. Peptides are shown in red ribbons. Lipid representation codes follow Fig. 2.

In contrast to neu that is effective in cholesterol efflux, neg (Table 1), which has a net charge of -3 e, is ineffective. Simulations 7 and 8 tested the hypothesis that the inactivity of neg stems from its inability to stabilize a nanodisc. The initial conditions were developed by arranging 26 peptides in ideal picket fence and double belt configurations on the edge of discs of 200 POPC and 20 UC (Figs. 10A,D). Although neg readily dimerized, the dimers became disordered on the disc edge, and some migrated to the disc surface and exposed hydrophobic acyl chains to water (Figs. 10B,C,E,F). This was because not only were the side chains of adjacent dimers unable to form salt bridges but they also repelled each other.

Fig. 10.

Side views of nanodiscs with 200:20:26 POPC:UC:neg showing the disordered configuration of peptides. (A) Simulation 7; picket fence initial configuration (t = 0 μs). (B,C) Simulation 7; t = 2 μs. (D) Simulation 8; belt initial configuration (t = 0 μs). (E,F) Simulation 8; t = 2 μs. Peptides are shown in red ribbons. Lipid representation codes follow Fig. 2.

Simulation 9 tested SGLD on a nanodisc with neu peptides. The initial configuration was the same as Simulation 5 (conventional MD) in which 24 peptides covered the phospholipid head groups (Fig. 11A). As the snapshots in Figs. 11B and C show, a number of peptides migrated to the disc edge to shield the lipid acyl chains from water during the 40 ns-long simulation; the time series is plotted in Fig. 11D. The number of peptides on the edge for Simulation 5 is also presented for comparison. Thirteen and 8 peptides were on the disc edge at 40 ns in the SGLD and conventional MD simulations, respectively, demonstrating the remarkable enhanced sampling power of SGLD. However, a top-down view of the SGLD structure at 40 ns in Fig. 11C shows that the disc is elongated; in the conventional MD it remained circular throughout the 3 μs-long simulation (Fig. 8F). In a subsequent study, Simulation 10 employed SGLD for 40 ns starting from the 4-μs frame of Simulation 4 (a double belt of peptides) (Fig. 12A). The purpose of this simulation was to accelerate the transition of peptides from the kinetically trapped belt (in Simulation 4) to picket fence and to examine the disc shape. Indeed, SGLD broke the double belt of peptides to initiate the picket fence configuration (Figs. 12B,C). However, the breakage of the belts was due to the disc elongation; the peptides inevitably separated in the expanded disc.

Fig. 11.

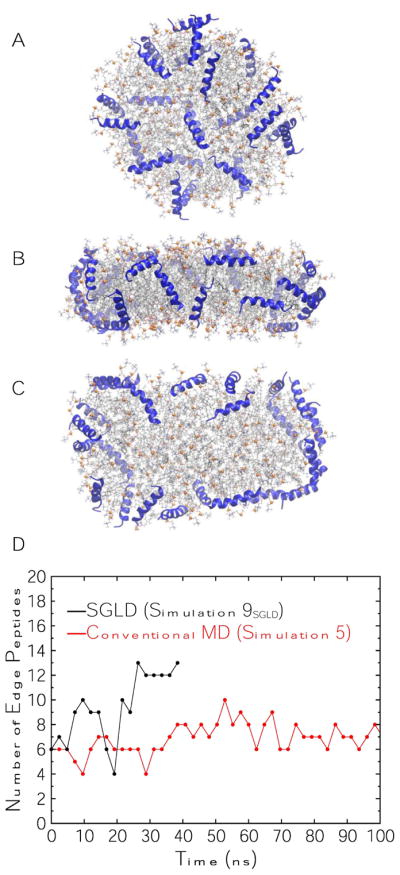
Simulation 9_SGLD on 150:15:24 POPC:UC:neu. (A) Top-down view of initial configuration (t = 0 μs); peptides are on disc surfaces identical to initial configuration of Simulation 5. (B) Side view at t = 40 ns. (C) Top-down view at t = 40 ns. Peptides are shown in blue ribbons. Lipid representation codes follow Fig. 2. (D) Time series of the number of peptides on disc edges in Simulation 9_SGLD and Simulation 5 (time series of Simulation 5 is truncated at 100 ns for clarity).

Fig. 12.

Simulation 10_SGLD on 200:20:26 POPC:UC:neu. (A) Side view of the initial configuration (t = 0 μs), which is the 4-μs frame of Simulation 4. (B) Side view at t = 40 ns. (C) Top-down view at t = 40 ns. Peptides are shown in blue ribbons. Lipid representation codes follow Fig. 2.

Simulations 11_SGLD were carried out to investigate whether SGLD expands a periodic (infinite) bilayer similar to nanodiscs. The simulations were performed using conventional MD (control) and SGLD with different guiding factors ranging from 0 (no SGLD) to 1 (full strength). As Table 2 shows, the area per lipid does not change when the guiding factors are small, but it starts to increase with guiding factors larger than 0.4. These results demonstrate that the area increase by SGLD is not limited to nanodiscs. Disc expansion cautions against SGLD usage for nHDL, because APOA1 readily responds to the particle shape and size. These results highlight the difficulty of enhanced methods. Though SGLD is well-tested for proteins, the application to lipid assemblies requires additional refinement.

Table 2.

Area per DOPC for a system of 80:1 DOPC:WALP19 at 313 K. SGLD and conventional MD simulations are compared.

Simulation Method	Area per Lipid
Conventional MD	74.0 ± 0.3
SGLD, guiding factor =	73.4 ± 0.5
SGLD, guiding factor =	74.3 ± 0.3
SGLD, guiding factor =	76.2 ± 0.4
SGLD, guiding factor =	79.6 ± 0.3
SGLD, guiding factor =	82.5 ± 0.4
SGLD, guiding factor =	86.9 ± 0.2

5. Conclusions and future studies

A system containing high-density lipoprotein (HDL) in solution as illustrated in Fig. 3B contains approximately 250,000 atoms. As reviewed in Section 3, until recently it was not possible to generate trajectories longer than approximately 100 ns for such systems with all-atom models. Given the significantly longer times required for lipid and protein rearrangements, molecular dynamics simulations were mostly carried out using coarse-grained models or with aggressive enhanced sampling methods (summarized in Section 2). The multi-microsecond simulations described in Section 4 allow a critical evaluation of some of the important time scales in lipid nanodiscs stabilized by proteins or peptides.

Rearrangement of terminal domains of APOA1 in nanodiscs takes 10–20 μs (Figs. 2 and 6) [35]. AOPA1 in Simulation 2, however, was trapped for the entire 10 μs trajectory due to the distorted initial condition (Figs. 6D,E,F). Peptides in nanodiscs are also prone to be kinetically trapped for 5 μs (Simulation 4) or more when on the edge in the initial configuration. When on the top and bottom surfaces, they migrate to the edge in 3 μs, but may take longer time in the crowded environment of the edge to reach an optimal configuration, e.g., parallel or antiparallel orientation in either picket fence or belt arrangement. These results highlight both the importance of multi μs-long simulations of nanodiscs to obtain valid results, and the necessity of confirming the results with experiments. Enhanced sampling methods potentially overcome the above issues, although careful tuning is required otherwise the results are difficult to interpret (Simulations 9_SGLD,10_SGLD, and 11_SGLD).

Simulations 5 and 6 showed that neu adapts a picket fence configuration on the nanodisc edge. Future studies should investigate whether this holds true for other peptides, as it can change the rationale for the design of such therapeutics. A peptide belonging to a picket fence configuration interacts with two neighbors, whereas the peptide in a belt configuration interacts strongly with only one neighbor. A stable picket fence scaffold requires the residues in both hydrophobic–hydrophilic boundaries of an amphipathic peptide to form salt bridges with those of their neighboring peptides. This imposes additional constraints when designing the sequence of effective APOA1 mimetic peptides. One can use the affordable simulation setup illustrated in Fig. 4 to study the stability of several peptides on the disc edge, and then simulate the optimal ones in entire nanodiscs for more accuracy. Other relevant questions concern the maximal length of peptides that is consistent with a picket fence arrangement, and the fundamental factor that determines the disc size for any peptide. CG force fields, such as Martini, are feasible for studying peptide systems, because conformations are restrained in Martini and the AA simulations in the present study did not show any change in the helicity of peptides.

Time-resolved SANS determined that lipid exchange in APOA1 nanodiscs is mediated by diffusion of lipids in an aqueous medium, not by a mechanism involving collisions between the discs [108]. In contrast, nanodiscs reconstituted by mimetic peptides repeatedly exchange lipids during collision between particles [8]. This likely stems from the cleavage between the peptides, which results in a lower energy of lipid transfer. Studying the details of fusion of nanodiscs stabilized with peptides should lead to the design of peptides with better functional mimicry and more success in clinical trials.

Understanding the maturation of nHDL is the most challenging of future studies, because not only does it require huge computational resources, but also depends on high-resolution structures of other involved proteins. APOA1 first interacts with ABCA1 to acquire lipids. Little is known about the details of this first stage. Single-molecule imaging revealed that a dimeric form of ABCA1 interacts with APOA1 [128]. CG simulations by Segrest et al. [67] showed that a dimeric form of APOA1 can promote the formation of nanodiscs from lipid bilayers with transbilayer lipid density gradient. Recently, a consensus model for monomeric and lipid-free APOA1 was proposed [129], and the structure of ABCA1 was resolved with 4.1 Å resolution with cryo-electron microscopy [130], paving the way for studying the interaction of APOA1 with ABCA1. Furthermore, the subsequent interactions of nHDL with ABCA1 and LCAT are not well characterized. MD simulations should ultimately be useful for sampling protein–protein interactions on a nanodisc.

While the simulations reported here pertained to HDL nanodiscs and related biological assemblies, many of the considerations are relevant to simulations of synthetic nanodiscs. For example, lipids are more packed in nanodiscs than in lamellar bilayers [8, 107]. This implies that lateral pressure profiles are different in the two systems. Such pressure differences could lead to structural differences in the embedded proteins. It is now feasible to simulate the same protein in planar bilayers and nanodiscs, and such simulations can be used for validation and refinement of potential scaffolds.

Highlights.

• Review of molecular dynamics simulations of lipid nanodiscs from 1997 to 2018.

• Pedagogical review of simulation methods related to nanodiscs.

• New atomistic simulations of nascent HDL show that the N- and C- terminal helices of APOA1 can be kinetically trapped on the 10 microsecond timescale.

• Mimetic peptides of APOA1 can diffuse from the nanodisc surface to the edge within 2 microseconds, appear to favor “picket fence” arrangement on the nanodisc edge as opposed to a double belt, but can also be kinetically trapped for multiple microseconds.