Abstract
Many membrane remodeling events rely on the ability of curvature-generating N-BAR membrane proteins to organize into distinctive supramolecular configurations. Experiments have revealed a conformational switch in N-BAR proteins resulting in vesicular or tubular membrane shapes, with shallow membrane immersion of the H0 amphipathic helices of N-BAR proteins on vesicles but deep H0 immersion on tubes. We develop here a minimal elastic model of the local thinning of the lipid bilayer resulting from H0 immersion. Our model predicts that the observed conformational switch in N-BAR proteins produces a corresponding switch in the bilayer-mediated N-BAR interactions due to the H0 helices. In agreement with experiments, we find that bilayer-mediated H0 interactions oppose N-BAR multimerization for the shallow H0 membrane immersion depths measured on vesicles, but promote self-assembly of supramolecular N-BAR chains for the increased H0 membrane immersion depths measured on tubes. Finally, we consider the possibility that bilayer-mediated H0 interactions might contribute to the concerted structural reorganization of N-BAR proteins suggested by experiments. Our results indicate that the membrane immersion depth of amphipathic protein helices may provide a general molecular control parameter for membrane organization.
Introduction
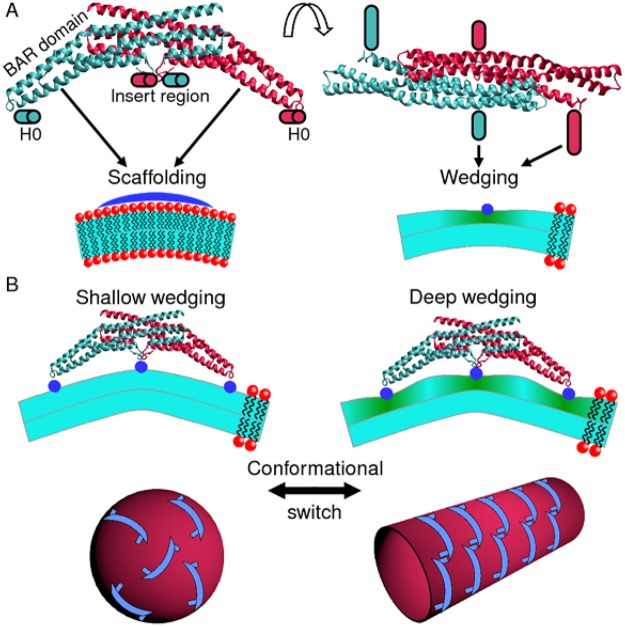
The remodeling of cellular membrane shape is often regulated1–5 by curvature-generating membrane proteins adsorbing onto one lipid bilayer leaflet. Biologically important examples of membrane remodeling are provided by synaptic endocytosis and T-tubule formation5–9, where N-BAR proteins such as amphiphysin and endophilin deform the cell membrane to generate highly curved cylindrical tubes and spherical vesicles. The ability of N-BAR proteins to induce tubular and spherical membrane shapes has been confirmed through in vitro experiments, which have shown10–15 that amphiphysin and endophilin can generate highly curved lipid bilayer tubes and vesicles with diameter ≈15–50 nm from large vesicles with diameter >100 nm. N-BAR proteins are homo- or heterodimers with a highly homologous structure consisting of the crescent-shaped BIN/amphiphysin/Rvs (BAR) domain and the N-terminal amphipathic H0 helices located close to the tips of the BAR domain10,11,15–18 (see Fig. 1A). The structure of N-BAR proteins10,11,15–18 suggests two key molecular mechanisms1–5,19–21 for generation of membrane curvature by N-BAR proteins: scaffolding and wedging (Fig. 1A). In the scaffolding mechanism, curved proteins deform the membrane by binding to one of the two lipid bilayer leaflets. In the wedging mechanism, proteins partially insert amphipathic helices into one lipid bilayer leaflet, making it favorable for the lipid bilayer to be curved. N-BAR proteins induce1–5,10,11,15–18 scaffolding via their BAR domains and wedging via their H0 helices (Fig. 1A). Some N-BAR proteins such as endophilin, but not amphiphysin, also interact with the membrane through wedging of additional amphipathic helices (Fig. 1A).
Figure 1.
Illustration of membrane curvature generation by N-BAR proteins. (A) Molecular structure of the N-BAR protein endophilin (PDB ID code 2C08) viewed perpendicular (upper left panel) and parallel (upper right panel) to the plane of the membrane. Endophilin employs the scaffolding (lower left panel) and wedging (lower right panel) mechanisms for membrane curvature generation through its BAR domain and through its N-terminal H0 helices and insert region, respectively. The molecular structure of amphiphysin is highly homologous to that of endophilin but lacks the insert region10,11,15. (B) A conformational switch controls generation of isotropic (vesicular) and anisotropic (tubular) membrane curvatures by N-BAR proteins22–24, with shallow wedging and little scaffolding on vesicles (left panel) but deep wedging and pronounced scaffolding on tubes (right panel). In the membrane cross sections, green shading indicates membrane regions in which deep membrane immersion of amphipathic helices22,23 induces compression of the lipid bilayer hydrophobic thickness42–50.
A remarkable feature of membrane remodeling by N-BAR proteins is that a single protein species can induce distinct types of membrane curvature, such as the isotropic and anisotropic curvatures associated with lipid bilayer vesicles and tubes, respectively. Electron paramagnetic resonance (EPR) experiments22–24 have revealed that a conformational switch in the molecular structure of the membrane-bound protein controls the competition between generation of highly curved isotropic (vesicular) and anisotropic (tubular) membrane shapes by amphiphysin and endophilin (see Fig. 1B). In particular, vesicle-bound N-BAR proteins interact with the lipid bilayer through shallow wedging of the H0 helices with little or no scaffolding (left panel of Fig. 1B), while tube-bound N-BAR proteins show a combination of scaffolding and increased wedging depths of the H0 helices (right panel of Fig. 1B). However, it is unknown how the observed conformational switch in N-BAR proteins22–24 generates the observed isotropic and anisotropic membrane curvatures1–5,10,11,15,25. A key challenge is that membrane remodeling by N-BAR proteins is a collective phenomenon requiring a threshold N-BAR concentration and distinctive supramolecular arrangements of N-BAR proteins5,10–14,22–24,26–33, and therefore results from many interacting proteins rather than individual, isolated proteins. In particular, generation of vesicles by N-BAR proteins is thought to rely on membrane-bound N-BAR proteins being oriented in a range of different directions (left panel of Fig. 1B) while, on tubes, N-BAR proteins form supramolecular, locally ordered tip-to-tail chains with antiparallel alignment and dimerization of the H0 helices of neighboring N-BAR proteins5,12,22–24,26–28,31–33 (right panel of Fig. 1B).
How does the observed conformational switch in N-BAR proteins control the supramolecular organization of N-BAR proteins? Experiments have suggested5,26,27,33 that nonspecific interactions between the H0 helices of neighboring N-BAR proteins are essential for the self-assembly, local ordering, and stability of supramolecular chains of N-BAR proteins. Indeed, BAR proteins lacking the H0 helices are also able to generate tubes, but show supramolecular configurations distinct from those of N-BAR proteins2,5. In the case of integral membrane proteins spanning the lipid bilayer, bilayer-thickness-mediated protein interactions originating from a bilayer-protein hydrophobic thickness mismatch have been found34–41 to provide a general physical mechanism underlying protein organization. A wide range of experiments42–47 and molecular dynamics (MD) simulations42–44,48–50 have shown that membrane immersion of amphipathic protein wedges can substantially decrease the lipid bilayer thickness. Unlike integral membrane proteins, however, amphipathic protein wedges only insert partially into one lipid bilayer leaflet (Fig. 1). We show here how the classic elastic model describing bilayer-thickness-mediated interactions between integral membrane proteins34–41 can be generalized to obtain a minimal elastic model of lipid bilayer-mediated wedge interactions. Our model provides a quantitative link between the observed structures of N-BAR proteins10,11,15–18,22,23 and the distinctive supramolecular arrangements of N-BAR proteins yielding isotropic and anisotropic membrane curvatures5,12,22–24,26–28,31–33. With the key model parameters estimated directly from experiments, our model predicts that the shallow H0 membrane immersion depths measured on vesicles22,23 result in bilayer-mediated H0 interactions between N-BAR proteins that oppose the self-assembly of N-BAR chains through H0 dimerization5,26–28, thus allowing a variety of different N-BAR orientations on vesicles (left panel of Fig. 1B). In contrast, our model predicts that the increased H0 membrane immersion depths measured on tubes22,23 result in bilayer-mediated H0 interactions between N-BAR proteins that promote the self-assembly of locally ordered tip-to-tail N-BAR chains5,12,26–28,33 via the observed antiparallel alignment and dimerization of the H0 helices of neighboring N-BAR proteins (right panel of Fig. 1B). Finally, we consider the possibility that bilayer-mediated H0 interactions might contribute to the concerted structural reorganization of N-BAR proteins suggested by experiments13,14,22–24, and may thus help to initiate membrane remodeling. Our results only rely on generic features of bilayer-wedge interactions and therefore suggest that, in analogy to the sorting of integral membrane proteins through bilayer-protein hydrophobic thickness mismatch34–41, the membrane immersion depth of amphipathic helices1–5 may provide a general molecular control parameter for the supramolecular organization of membrane proteins with amphipathic protein wedges.
Elastic model of bilayer-mediated wedge interactions
We develop in this section a minimal elastic model of wedge-induced lipid bilayer thickness deformations in which, akin to the classic Helfrich-Canham-Evans model of bilayer-scaffold interactions19–21,51–54, the key model parameters can be directly estimated from experiments. Key structural parameters characterizing bilayer-wedge interactions are the wedge immersion depth and the wedge size10,19,22,23,51,55–58. Protein wedges only directly interact with one leaflet of the lipid bilayer, which we take to correspond to the upper leaflet, with the wedge-induced deformation of the other leaflet being determined by the coupling between upper and lower leaflets (Fig. 1). Contrary to the classic elastic model describing bilayer-protein interactions for integral membrane proteins34–41, protein wedges are expected to induce distinct, asymmetric deformations in the two bilayer leaflets. Following recent generalizations of the continuum elasticity theory of lipid bilayers59–62, we separately account for wedge-induced deformations in each bilayer leaflet through the fields h± (x, y) and u± (x, y) capturing the height and thickness deformations in the upper and lower lipid bilayer leaflets (see Fig. 2). Expansion of the leaflet elastic energies in terms of the lipid area deformation and the leaflet curvatures up to second order61 yields the following energy cost of wedge-induced lipid bilayer deformations (see Supplementary Information Sec. S1):
| 1 |
where Kb is the lipid bilayer bending rigidity, Kt is the lipid bilayer thickness deformation modulus, a is the thickness of the unperturbed monolayer hydrophobic core, and τ is the membrane tension. To ensure that no overlaps and voids occur within the lipid bilayer, the deformation fields in equation (1) are required to satisfy a bilayer continuity constraint61 (Fig. 2) which, to leading order, is given by
| 2 |
Figure 2.
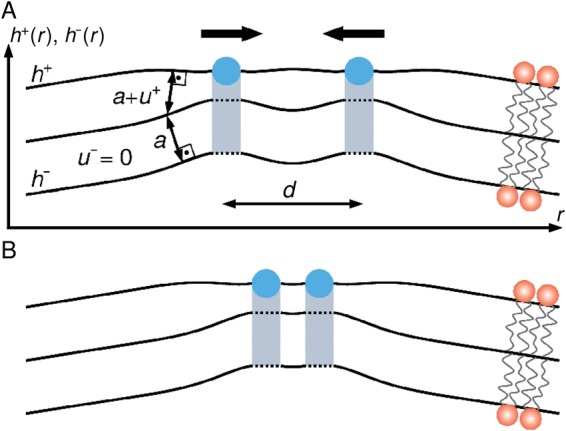
Schematic of bilayer-mediated interactions between protein wedges. (A) Amphipathic helices (viewed parallel to the helix axes and indicated in blue) deform the shape h+ and hydrophobic thickness u+ +a of the upper lipid bilayer leaflet, and may indirectly perturb h− and u− in the lower leaflet via the coupling between upper and lower leaflets. We set here u− = 0 (see main text). For simplicity, we assume in this schematic that the H0 helices are in the face-on orientation, and that the H0-induced membrane deformations are only a function of the spatial coordinate r measured perpendicular to the helix axes. Equation (3) predicts that, for large enough helix immersion depths, two protein wedges can be attracted to each other by bilayer-mediated wedge interactions (black arrows). (B) Our elastic model of bilayer-mediated wedge interactions predicts that, for large enough helix immersion depths, the distance d separating the axes of two neighboring amphipathic helices can take an optimal value set by the key lipid and protein properties captured by equation (3).
The effective parameters Kb, Kt, and a in equations (1) and (2) characterize the mechanical properties of lipid bilayers and can be directly estimated from, for instance, micropipette aspiration and x-ray diffraction experiments. Typical values of these parameters for phospholipid bilayers are Kb ≈ 20 kBT, Kt ≈ 60 kBT/nm2, and a ≈ 2.0 nm36,63, which we used for all the numerical results obtained here. The terms with coefficient Kb in equation (1) describe the energy cost of wedge-induced leaflet bending deformations, and generalize the standard elastic model of protein-induced bilayer bending deformations34–36,40,64–66 to scenarios in which the two bilayer leaflets do not necessarily show identical bending deformations. Similarly, the Kt- and τ-terms in equation (1) generalize the standard elastic models of bilayer thickness deformations and membrane tension34–36,40,64–66 to allow for asymmetric deformations of the bilayer leaflets. In the special case of symmetric bilayer thickness deformations, u+ = u−, equation (1) with equation (2) reduces to the classic elastic model of bilayer-protein interactions for integral membrane proteins34–41,64–66.
A variety of experiments42–47 and MD simulations42–44,48–50 have shown that insertion of amphipathic protein wedges into the membrane can substantially decrease the lipid bilayer thickness. Following this previous work, we assume here that the H0 helices of N-BAR proteins can locally compress the bilayer leaflet into which they are inserted. For simplicity, we further assume that, in the vicinity of the H0 helices, the magnitude of the H0-induced leaflet compression approximately matches the membrane immersion depth of the H0 helices so as to optimize the electrostatic and hydrophobic interactions between the H0 helices and the membrane. In particular, previous studies22,23,45,46 indicate that, if a protein wedge is inserted into the membrane, the lipids surrounding the protein wedge tend to compress so that the negatively charged moieties of the lipid head groups are in contact with the hydrophilic, positively charged portion of the wedge surface, and the lipid tails shield the hydrophobic portion of the wedge surface. This suggests that the observed membrane immersion depths of the H0 helices of N-BAR proteins22,23, which are measured with respect to the unperturbed lipid bilayer thickness, take a similar magnitude as the compression of the lipids surrounding the H0 helices (Fig. 2). However, this assumption is not essential for our model of bilayer-mediated wedge interactions, and we study here the dependence of bilayer-mediated H0 interactions on the magnitude of H0-induced leaflet compression. This allows us to arrive at a general understanding of how H0-induced leaflet compression affects N-BAR organization—even if the assumption that the magnitude of H0-induced local leaflet compression matches the H0 membrane immersion depth is not entirely accurate—and, more generally, permits us to estimate the overall trends by which wedge-induced alterations in lipid bilayer thickness affect proximity between wedges in other protein systems. We note that the large membrane immersion depths of the H0 helices observed in experiments on N-BAR proteins may, at least in part, be stabilized by favorable interactions between the lipid bilayer and the BAR domains22–24.
The above picture of bilayer-wedge interactions suggests that, for large enough wedge immersion depths, an amphipathic protein wedge induces substantial local compression of the bilayer leaflet into which the protein wedge is inserted, with only minor thickness deformations in the opposite leaflet not directly interacting with the protein wedge22,23,35,45,46. We therefore simplify equation (1) by setting u− = 0 which, together with equation (2), yields
| 3 |
Note that the above elastic model of bilayer-wedge interactions involves, in addition to the bending, thickness deformation, and tension terms associated with h+ and u+ in equation (1)34–36,40,64–66, bending and tension terms penalizing leaflet deformations that induce opposite signs in the curvatures and gradients of h+ and u+, respectively. As a result, h+ and u+ are coupled to each other. Also, since we set u− = 0 but allow for deformations of h− (Fig. 2), the bending and tension terms associated with u+ in equation (3) are reduced by a factor of 1/2 with respect to the corresponding terms for h+, which effectively also involve contributions due to h−. Protein wedges may, in addition to the bilayer thickness deformations found previously42–50, also induce lipid tilt deformations. Our aim here is to explore the role of bilayer-mediated H0 interactions due to bilayer thickness deformations42–50 in N-BAR organization, and we therefore do not include lipid tilt deformations in equation (3).
In analogy to bilayer-mediated interactions between integral membrane proteins34–41,64–66, overlapping wedge-induced lipid bilayer deformations are expected to give rise to bilayer-mediated interactions between protein wedges (Fig. 2). To calculate these interactions for Figs. 3–6, we proceed similarly as in the classic elastic model of bilayer-protein interactions for integral membrane proteins34–41,64–66 and minimize equation (3) with respect to h+ and u+ subject to suitable boundary conditions at the bilayer-wedge interface (see the Methods section). We use here the wedge length L ≈ 3 nm and the wedge radius r0 ≈ 0.6 nm associated with the H0 helices of endophilin10,67. As suggested by experiments and MD simulations5,27, we take the bilayer-H0 interactions to be uniform along the H0 helix axes. The most pronounced bilayer-mediated wedge interactions are expected to occur for wedges in the face-on orientation, for which the wedge interaction surface is maximized. Neglecting boundary effects due to the H0 tips, the energy density of bilayer-mediated wedge interactions can then be estimated from a one-dimensional representation of equation (3) with a single spatial coordinate r measured perpendicular to the helix axes (Fig. 2). We scale this energy density by L to obtain the total interaction energy (see the Methods section). With the exception of Fig. 4, where we test these assumptions and allow for arbitrary wedge orientations, we focus, throughout this Article, on wedges in the face-on orientation and neglect boundary effects due to the wedge tips. We have obtained, for wedges in the face-on orientation with negligible boundary effects, the exact analytic solution of the bilayer-mediated wedge interaction potential implied by equation (3) (see the Methods section), which we employ, with the exception of Fig. 4, throughout this Article. For Fig. 4, we resort to numerical methods to calculate the bilayer-mediated wedge interactions.
Figure 3.
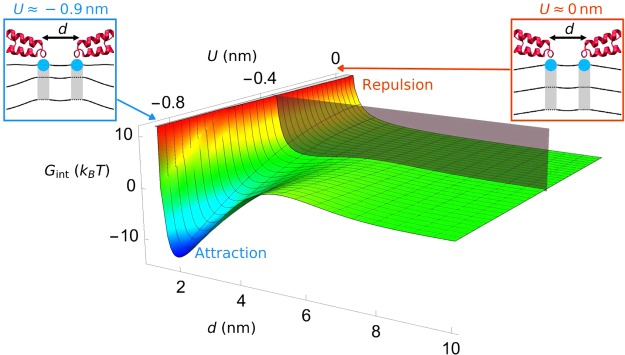
Bilayer-mediated interactions between H0 helices. Interaction potential Gint between two parallel H0 helices of neighboring N-BAR proteins versus the immersion depth of the two helices, U, and the distance separating the two H0 axes, d, for τ = 0. We obtained Gint from the exact analytic solution minimizing the energy cost of H0-induced lipid bilayer deformations in equation (3) (see the Methods section), which neglects boundary effects due to the H0 tips. Gint < 0 corresponds to favorable bilayer-mediated interactions between H0 helices, and Gint > 0 corresponds to unfavorable interactions. EPR experiments suggest U ≈ 0 nm and U ≈ −0.9 nm for vesicle- and tube-bound N-BAR proteins22,23 (see schematics in insets).
Figure 6.
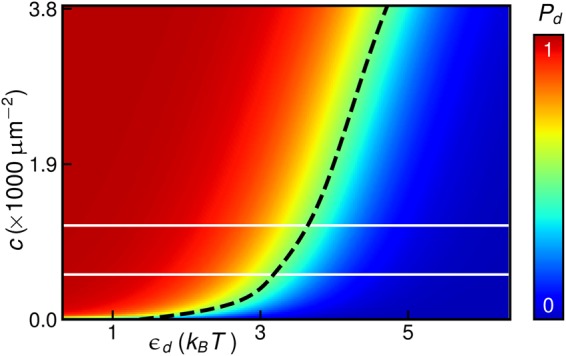
Concerted structural reorganization of N-BAR proteins through bilayer-mediated interactions between H0 helices. Probability of a pair of N-BAR proteins to be collectively in the observed conformational state with deep immersion of the H0 helices22,23, Pd, obtained from equation (8) versus concentration of membrane-bound N-BAR proteins, c, and the energy difference between the observed N-BAR conformational states with deep and shallow immersion of the H0 helices22,23 in the absence of any interactions between N-BAR proteins, εd. We analytically calculated the H0-induced N-BAR interactions following similar steps as for Fig. 3 (see the Methods section) and set τ = 0. The dashed black curve corresponds to Pd = 1/2 and, for reference, the solid white lines delineate the approximate range of N-BAR concentrations found to tubulate large vesicles in vitro30.
Figure 4.
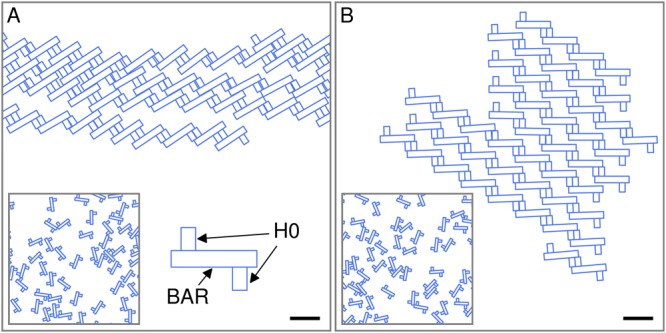
Multimerization of N-BAR proteins through bilayer-mediated interactions. Energetically favorable N-BAR arrangements obtained, for U ≈ −0.9 nm22,23 and τ = 0, from simulated annealing Monte Carlo simulations using (A) the N-BAR pair potential implied by the H0-induced leaflet thickness deformations in equation (3) with h+ = 0 and (B) a total N-BAR pair potential that is the sum of the potential used in (A) and a BAR pair potential based on previous calculations53 (see the Methods section). The left insets in (A) and (B) show the random initial N-BAR configurations employed for (A) and (B). We used the N-BAR shape shown in the right inset in (A), which we modeled after the N-BAR structures described previously5, with hardcore steric constraints (see Supplementary Information Sec. S6). We employed periodic boundary conditions, with the N-BAR proteins in (A) forming a single chain. Scale bars, 10 nm.
A key parameter in our model of bilayer-mediated wedge interactions is the wedge immersion depth U, where we set u+ = U at the bilayer-wedge interface. We thereby assume that the thickness of the lipid bilayer leaflet decreases in the vicinity of amphipathic protein wedges so as to match the wedge immersion depth. Based on EPR experiments on amphiphysin and endophilin22,23, we have the wedge immersion depths U ≈ 0 nm and U ≈ −0.9 nm for the shallow and deep immersion states of the H0 helices of N-BAR proteins. While, as discussed above, it is known that protein wedges can substantially decrease the lipid bilayer thickness42–50, the precise relation between helix immersion depth and local leaflet thickness deformations remains to be elucidated. Previous work on integral membrane proteins68 suggests that, for substantial protein-induced lipid bilayer thickness deformations, insertion of amphipathic helices may be alleviated by a combination of bilayer thickness deformations42–50 and (unfavorable) interactions between hydrophobic and hydrophilic surfaces. As a result, the value nm estimated from EPR experiments for the deep H0 immersion state22,23 may be effectively reduced. We show, below, that the strength of favorable bilayer-mediated interactions between two H0 helices with membrane immersion depth U decreases with the value of . However, we also find that there is a whole range of U yielding unfavorable and favorable bilayer-mediated H0 interactions, with unfavorable interactions for and favorable interactions for , where Uc is the critical membrane immersion depth of the H0 helices governing the crossover from unfavorable to favorable bilayer-mediated H0 interactions. For the scenarios considered here we have Uc ≈ −0.4 nm at zero membrane tension, but the numerical value of Uc depends on the specific lipid and wedge properties under consideration (see Supplementary Information Table S1). We follow here previous theoretical and computational studies of protein-induced lipid bilayer deformations31,32,34–36,40,53,54,64–66 and assume that the unperturbed reference state of the lipid bilayer corresponds to a flat surface with h+ = u+ = 0, but have confirmed that similar results for H0-induced N-BAR interactions are obtained if the reference state of the bilayer is highly curved (see Supplementary Information Sec. S5).
Results
Helix immersion depth is crucial for bilayer-mediated H0 interactions
Equation (3) allows prediction of the contributions to bilayer-mediated N-BAR interactions due to the H0 helices. Other contributions to N-BAR interactions can arise, for instance, through bilayer-mediated interactions between the BAR domains19–21,51–54, which we return to in the next section. We focus, for now, on neighboring N-BAR proteins with H0 helices that face each other, which is expected to yield particularly pronounced bilayer-mediated H0 interactions, and neglect any boundary effects on the wedge-induced membrane deformations due to the H0 tips. We test these assumptions in the next section. The only relevant spatial dimension for H0-induced bilayer-mediated interactions between N-BAR proteins is then the distance d separating the axes of the neighboring H0 helices of the two N-BAR proteins, which we measure perpendicular to the H0 helix axes (Fig. 2). We have obtained the general analytic solution of the resulting H0-induced interaction potential between N-BAR proteins (see the Methods section), which is plotted in Fig. 3 for membranes with vanishing tension. With the key model parameters estimated directly from experiments, our model predicts that bilayer-mediated N-BAR interactions due to the H0 helices depend critically on the membrane immersion depth of the H0 helices. For shallow immersion depths U > −0.4 nm, we find that the H0 helices of neighboring N-BAR proteins repel each other. This can be understood by noting that, in this regime, the leaflet curvature deformations induced by the H0 helices dominate over leaflet thickness deformations, resulting in unfavorable bilayer-mediated protein interactions36,40,52–54,65,66. EPR experiments have shown22,23 that the H0 helices of vesicle-bound N-BAR proteins are at a similar height as the lipid phosphate headgroups in the unperturbed lipid bilayer, suggesting that U ≈ 0 nm. Our model therefore predicts that, on vesicles, bilayer-H0 interactions oppose the self-assembly of supramolecular N-BAR chains through H0 dimerization5,26–28, with an energy cost >10 kBT for each H0 dimer, thus allowing a variety of different N-BAR orientations on vesicles22–24.
For immersion depths U < −0.4 nm, in contrast, the interplay between protein-induced leaflet curvature and thickness deformations yields non-monotonic interactions between the H0 helices of neighboring N-BAR proteins. We find that, in this regime, H0-induced leaflet thickness deformations produce favorable lipid bilayer-mediated interactions between H0 helices at intermediate helix separations , with unfavorable interactions at small and large helix separations, thus making it energetically favorable for H0 helices to reduce their bilayer deformation footprint by forming dimers. EPR measurements suggest that U ≈ −0.9 nm for tube-bound N-BAR proteins22,23, for which our model predicts that bilayer-H0 interactions strongly promote the self-assembly of supramolecular, locally ordered tip-to-tail N-BAR chains5,12,26–28,33 via the observed dimerization of the H0 helices of neighboring N-BAR proteins, with an energy gain >10 kBT for each H0 dimer. We find H0 dimerization energies >1 kBT for U < −0.5 nm. Figure 3 thus predicts that the observed conformational switch from shallow to deep wedging of the H0 helices22,23 yields a corresponding switch from unfavorable to favorable bilayer-mediated N-BAR interactions due to the H0 helices, thereby allowing a variety of different orientations of neighboring N-BAR proteins on vesicles but not on tubes. Furthermore, our model predicts that, for deep immersion of the H0 helices, the interplay between H0-induced leaflet curvature and thickness deformations yields an optimal H0 separation. In particular, for the parameter values used for Fig. 3 we find an optimal H0 separation d ≈ 2 nm for U ≈ −0.9 nm. While available experimental data does not allow a precise estimate of the separation of neighboring H0 helices in supramolecular N-BAR chains, such a characteristic H0 separation is consistent with EPR experiments on tube-bound N-BAR proteins22,23. Finally, Fig. 3 also predicts that a transition from deep to shallow wedging of the H0 helices in N-BAR chains yields a transition from favorable to unfavorable H0-induced N-BAR interactions, which may assist in the disassembly of N-BAR chains27. Such a change in H0 membrane immersion depth could potentially be accomplished through phosphorylation of N-BAR proteins22. In agreement with electron cryo-tomography experiments5,27,33, the predicted bilayer-mediated N-BAR interactions due to the H0 helices are highly pliable, nonspecific, and can stabilize loose assemblies of N-BAR proteins without requiring direct protein-protein contacts between N-BAR proteins, which could potentially allow the formation of mixed N-BAR chains consisting of, for instance, amphiphysin and endophilin5.
Bilayer-thickness-mediated H0 interactions facilitate self-assembly of N-BAR chains
To test whether, if one allows for arbitrary configurations of neighboring N-BAR proteins and boundary effects arising from the H0 tips, lipid bilayer-mediated interactions between N-BAR proteins due to H0-induced leaflet thickness deformations can yield self-assembly of extended tip-to-tail N-BAR chains5,12,26–28,33, we performed Monte Carlo simulations with simulated annealing of N-BAR pair potentials. We note that simulated annealing Monte Carlo simulations are an approach for finding low-energy configurations of a system, and hence do not capture thermal effects or effects depending on the concentration of N-BAR proteins. We modeled N-BAR proteins as rigid molecules formed by two H0 helices joined together by a protein backbone representing the BAR domain (see Fig. 4A), with arbitrary separations and orientations of N-BAR proteins. We consider, for now, interactions between N-BAR proteins arising solely from leaflet thickness deformations induced by the H0 helices with U ≈ −0.9 nm22,23, which we computed from equation (3) with h+ = 0 using finite elements40 and which are approximately pairwise additive (see Supplementary Information Sec. S6). In agreement with experiments5,12,26–28,33, and as expected from Fig. 3, we find that, starting from a random initial distribution of N-BAR proteins, N-BAR interactions due to H0-induced leaflet thickness deformations yield self-assembly of extended tip-to-tail N-BAR chains via formation of antiparallel dimers of the H0 helices of neighboring N-BAR proteins (Fig. 4A). The nonspecificity of H0-induced N-BAR interactions implied by our model, and also suggested by experiments5,27,33, thereby results in a degenerate architecture of antiparallel H0 dimers in N-BAR chains, with favorable links in N-BAR chains along either one of the two elongated sides of the H0 helices of neighboring N-BAR proteins (Fig. 4A).
EPR experiments22,23 have shown that, for N-BAR proteins with the H0 helices in the deep immersion state U ≈ −0.9 nm, the BAR scaffolding domain is in contact with the lipid bilayer. The resulting BAR-induced membrane curvature deformations have been studied extensively within the Helfrich-Canham-Evans framework of membrane elasticity19–21,51. In particular, the contributions to bilayer-mediated N-BAR interactions due to the BAR domain have been found to favor the face-on orientation of neighboring N-BAR proteins52–54. In contrast, we find here that the N-BAR interactions due to the H0 helices yield the observed tip-to-tail arrangement of neighboring N-BAR proteins5,12,26–28,33. To test whether contributions to N-BAR interactions due to the BAR domain may disrupt the tip-to-tail N-BAR chains favored by bilayer-thickness-mediated H0 interactions, we allowed for contributions to N-BAR interactions due to the BAR domain as well as H0-induced leaflet thickness deformations (see Fig. 4B). We thereby employed a BAR pair interaction potential based on previous calculations53 of bilayer-mediated interactions between endophilin BAR domains (see the Methods section). While the contributions to bilayer-mediated N-BAR interactions due to the BAR domain are not expected to be pairwise additive69, it has been found52–54 that BAR pair potentials can still provide useful insights into self-assembly of protein clusters via bilayer-mediated BAR interactions. The total pair interaction potential employed for Fig. 4B is given by the sum of the BAR interactions53 and the N-BAR interactions due to H0-induced bilayer thickness deformations also used for Fig. 4A. We note that membrane curvature only indirectly enters Fig. 4B through the effective BAR pair interactions53, and that the generic properties of bilayer-mediated H0 interactions are not sensitive to membrane curvature (see Supplementary Information Sec. S5). Figure 4B shows that, if one allows for N-BAR interactions due to the BAR domains as well as the H0 helices, bilayer-thickness-mediated H0 interactions still yield self-assembly of tip-to-tail N-BAR chains, but that the degeneracy in the architecture of antiparallel H0 dimers is lifted. Consistent with experimental observations5,26,27, our simulations suggest that N-BAR configurations with the “outer” elongated sides of the H0 helices of neighboring N-BAR proteins facing each other provide the most favorable links in supramolecular N-BAR chains. Furthermore, our results suggest that the interplay of H0-induced leaflet thickness deformations and bilayer-BAR interactions52–54 can yield self-assembly of supramolecular N-BAR chains into extended two-dimensional lattices.
Membrane tension weakens bilayer-thickness-mediated H0 interactions
In vitro experiments30 have shown that a finite membrane tension decreases the propensity of endophilin to tubulate large vesicles. While the observed effect of membrane tension on curvature generation by endophilin may have a variety of different origins30,32, MD simulations32 have suggested that membrane tension inhibits self-assembly of supramolecular endophilin chains. Proceeding as for Fig. 3, we used equation (3) to explore how membrane tension modifies bilayer-mediated N-BAR interactions due to the H0 helices (see Fig. 5). In particular, we focus in Fig. 5 on H0 helices in the face-on orientation and neglect boundary effects due to the H0 tips. We find that, for the deep H0 immersion state U ≈ −0.9 nm22,23, an increased membrane tension makes self-assembly of supramolecular N-BAR chains via dimerization of neighboring H0 helices5,12,26–28 less favorable. This result can be understood by noting that a finite membrane tension tends to reduce the preferred thickness of the lipid bilayer, thus diminishing the effect of H0-induced leaflet thickness deformations. Consistent with this picture, we find that membrane tension only has a minor effect on H0-induced N-BAR interactions for the shallow H0 immersion state U ≈ 0 nm22,23, for which the leaflet curvature deformations induced by the H0 helices dominate over leaflet thickness deformations. However, equation (3) implies that, compared to changes in H0 immersion depth (Fig. 3), the H0 dimerization energy does not have a pronounced dependence on membrane tension, with shifts in dimerization energy <1 kBT for the typical membrane tensions encountered in experiments30.
Figure 5.
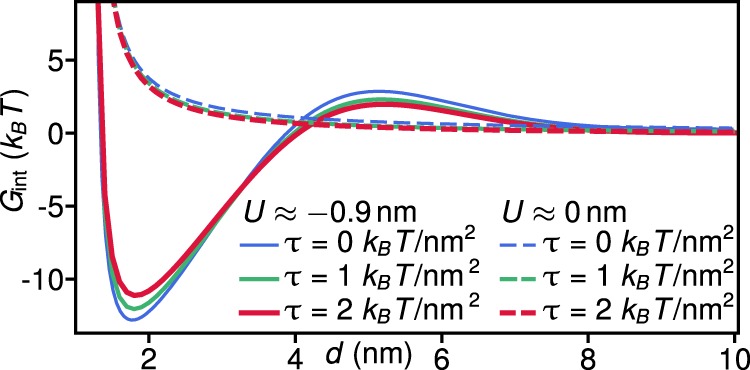
Effect of membrane tension on bilayer-mediated interactions between H0 helices. Interaction potential Gint between two parallel H0 helices of neighboring N-BAR proteins obtained from equation (3) as in Fig. 3 versus the distance separating the two H0 axes, d, for the deep (U ≈ −0.9 nm) and shallow (U ≈ 0 nm) immersion states of the H0 helices of N-BAR proteins22,23 at the indicated values of the membrane tension τ.
Concerted structural reorganization of N-BAR proteins
Equation (3) predicts that bilayer-mediated H0 interactions depend strongly on the separation of the H0 helices of neighboring N-BAR proteins as well as on the H0 membrane immersion depth (Fig. 3). This implies that, for large enough concentrations of membrane-bound N-BAR proteins, the energy difference between the observed N-BAR structures with deep and shallow immersion of the H0 helices22,23 involves a cooperative component due to H0-induced interactions between N-BAR proteins. EPR experiments22,23 indicate that, at low N-BAR concentrations, N-BAR proteins show shallow wedging of the H0 helices. Figure 3 predicts that H0-induced interactions between N-BAR proteins are unfavorable for the shallow immersion state of the H0 helices but can be favorable for the deep immersion state of the H0 helices22,23. We therefore speculate that, at high enough N-BAR concentrations, H0-induced N-BAR interactions may contribute to a cooperative transition of N-BAR proteins from a conformational state with shallow immersion of the H0 helices to a conformational state with deep immersion of the H0 helices13,14,22–24.
We illustrate the above physical mechanism for the concerted structural reorganization of N-BAR proteins13,14,22–24 via H0-induced N-BAR interactions by considering a simplified system consisting of a pair of diffusing, membrane-bound N-BAR proteins that interact via the H0-induced lipid bilayer deformations captured by equation (3). We thereby assume that the N-BAR concentration is low enough so that three or more N-BAR proteins are unlikely to be in close spatial proximity. Furthermore, we focus on N-BAR configurations for which the H0 helices of the two neighboring N-BAR proteins face each other, which is expected to provide a particularly favorable N-BAR configuration for a cooperative transition to the deep immersion state of the H0 helices (Figs. 3 and 4), and neglect any boundary effects due to the tips of the H0 helices. We specify the collective state of the N-BAR proteins through the variables d, s1, and s2, where s1,2 = 0,1 for the observed N-BAR conformations with shallow and deep immersion of the H0 helices22,23. The total energy of the pair of N-BAR proteins, Gpair, can be expressed as
| 4 |
where Gnon is the energy of the system in the absence of any interactions between the two N-BAR proteins, d → ∞, and Gint is the N-BAR pair interaction potential due to the H0 helices. Without loss of generality, we set Gnon (0,0) = 0 and write
| 5 |
where εd is the energy difference between the N-BAR conformations with deep and shallow immersion of the H0 helices22,23 at d → ∞. The value of the parameter εd is determined by internal conformational changes of the N-BAR proteins as well as the interactions between the lipid bilayer and the N-BAR proteins at d → ∞. As mentioned above, EPR experiments indicate that low N-BAR concentrations favor s1,2 = 022,23, suggesting that εd > 0. In the absence of detailed numerical estimates of εd, we regard εd as a free parameter. We analytically calculate Gint from equation (3) following similar steps as for Fig. 3 (see the Methods section).
From equation (4), the Boltzmann weight associated with a state (s1, s2), sampled over d, can be estimated as (see Supplementary Information Sec. S7)70
| 6 |
where c = 2/A denotes the concentration of membrane-bound N-BAR proteins, with A corresponding to the average membrane area occupied by two N-BAR proteins, rc is the long-range cutoff for pair interactions, and the Mayer-f function
| 7 |
captures contributions to the conformational statistics of N-BAR proteins due to H0-induced N-BAR interactions. Equation (6) allows calculation of the probability that the pair of N-BAR proteins is collectively in the observed conformational state with deep immersion of the H0 helices22,23:
| 8 |
To evaluate equation (8) we allowed for pair interactions up to a H0 axis-to-axis separation rc = 40 nm in equation (6), which is well beyond the range over which the H0 helices of N-BAR proteins show strong interactions (Fig. 3). For εd > 0, contributions to equation (8) due to Gnon bias the system towards N-BAR states with shallow immersion of the H0 helices. In contrast, contributions to equation (8) due to Gint tend to favor N-BAR states with deep immersion of the H0 helices22,23, with the competition between Gnon and Gint governed by c (see Fig. 6). Equation (8) thus predicts that, as the N-BAR concentration is increased to a threshold concentration, bilayer-mediated N-BAR interactions due to the H0 helices can yield a concerted structural reorganization of N-BAR proteins from the observed conformational state with shallow wedging of the H0 helices to the observed conformational state with deep wedging of the H0 helices22,23, with the latter state favoring self-assembly of supramolecular N-BAR chains5,12,26–28,33. Additional cooperative contributions to the transition energy between the N-BAR states with shallow and deep membrane immersion of the H0 helices22,23 may originate from, for instance, bilayer-mediated N-BAR interactions due to the BAR domains52–54,69.
Discussion
EPR experiments have demonstrated a conformational switch in N-BAR proteins22,23, with shallow membrane immersion of the H0 helices on vesicles but deep immersion on tubes. In these experiments, the H0 membrane immersion depth was measured with respect to the unperturbed lipid bilayer thickness. Generation of vesicles by N-BAR proteins is thought to rely on membrane-bound N-BAR proteins being oriented in a range of different directions22–24. On tubes, in contrast, N-BAR proteins have been observed to assemble into supramolecular, locally ordered tip-to-tail chains with antiparallel alignment and dimerization of the H0 helices of neighboring N-BAR proteins5,12,26–28,33, which is thought to rely on nonspecific interactions between the H0 helices of N-BAR proteins. BAR proteins lacking the H0 helices show, on tubes, supramolecular configurations distinct from those of N-BAR proteins2,5. Motivated by these experimental observations, we have developed here a coarse-grained elastic model of bilayer-mediated wedge interactions that accounts for the local thinning of the lipid bilayer induced by amphipathic protein wedges. Our model is designed to predict, based on a minimal set of assumptions about detailed system properties, how bilayer-mediated wedge interactions depend on the wedge immersion depth. We find that the observed conformational switch in N-BAR proteins from shallow to deep wedging of the H0 helices22,23 yields a corresponding switch from unfavorable to favorable bilayer-mediated N-BAR interactions due to the H0 helices. For the shallow H0 wedging observed on vesicles22,23, our model predicts repulsive interactions between the H0 helices of neighboring N-BAR proteins, thus allowing a variety of different orientations of neighboring N-BAR proteins on vesicles. In contrast, for the deep H0 wedging observed on tubes22,23, our model predicts, in agreement with experiments5,12,26–28,33, self-assembly of locally ordered tip-to-tail N-BAR chains via antiparallel alignment and dimerization of the H0 helices of neighboring N-BAR proteins.
We find here that, as the N-BAR concentration is increased to a threshold concentration, bilayer-mediated interactions between the H0 helices of N-BAR proteins can yield a concerted structural reorganization of N-BAR proteins from the observed conformational state with shallow wedging of the H0 helices to the observed conformational state with deep wedging of the H0 helices22,23. We therefore speculate that, as the N-BAR concentration is increased, H0-induced N-BAR interactions may contribute to a collective transition of N-BAR proteins from a conformational state with shallow membrane immersion of the H0 helices to a conformational state with deep membrane immersion of the H0 helices13,14,22–24. Combined with previous models of bilayer-wedge19,51,55–57 and bilayer-scaffold19–21,51–54 interactions, our model of bilayer-mediated interactions between amphipathic protein wedges provides a unifying physical picture that identifies and links key features of the observed membrane-bound molecular structures10,11,15–18,22,23 and supramolecular configurations5,12,22–24,26–28,31–33 of N-BAR proteins. We have focused here on the H0 helices of N-BAR proteins. However, our model of bilayer-mediated wedge interactions is simple enough to only rely on generic features of bilayer-wedge interactions. Our results therefore suggest that, in analogy to integral membrane proteins34–41, wedge-induced lipid bilayer thickness deformations may provide a general physical mechanism contributing to the supramolecular organization of peripheral membrane proteins with amphipathic protein wedges. For instance, consistent with the results discussed here in the context of the H0 helices of N-BAR proteins, α-synuclein helices have been observed to cluster in areas of membrane remodeling71, and it has been found72 that a threshold concentration of islet amyloid polypeptide (IAPP or amylin) helices is required to initiate membrane remodeling. Since wedging of amphipathic helices is a common motif for bilayer-protein interactions1–5, bilayer-mediated wedge interactions may contribute to the supramolecular organization of membrane proteins in a variety of different settings, and provide a fundamental design principle for membrane organization independent of any specific protein-protein interactions.
Methods
Analytic solution of bilayer-mediated wedge interactions
We analytically solved the Euler-Lagrange equations associated with equation (3) to determine the stationary lipid bilayer deformation profile associated with equation (3) (see Supplementary Information Sec. S2). For one-dimensional systems with spatial coordinate r (Fig. 2), the resulting lipid bilayer deformation profile is given by
| 9 |
| 10 |
where and the inverse square decay length
| 11 |
with the characteristic length scales and arising from the competition, in equation (3), between the leaflet bending terms and the tension and leaflet thickness deformation (Hookian spring) terms, respectively.
To determine from equations (9) and (10) the energy potential for bilayer-mediated wedge interactions we proceeded in analogy to the classic elastic model of bilayer-protein interactions for integral membrane proteins34–36,40,64–66, and fixed the coefficients Ai and Bj with i = 0, 1, 2, 3 and j = 0, 1, 2, 3 in equations (9) and (10) from the boundary conditions on h+(r) and u+(r), and their derivatives, for the lipid bilayer region separating the two protein wedges (see Supplementary Information Secs. S2 and S3): Since equation (3) is invariant under constant shifts in h+(r), we set the reference value of h+(r) equal to zero without loss of generality, and minimized equation (3) with respect to the height difference of the two wedges, which amounts to imposing zero vertical force on the protein wedges (see Supplementary Information Appendix A). Furthermore, we set u+(r) = U along the bilayer-wedge interfaces, with U ≈ 0 and U ≈ −0.9 nm for the shallow and deep H0 immersion states of N-BAR proteins22,23. Based on the helical wheel of the H0 helices of endophilin22, a computational model of bilayer-wedge interactions19,51,55,57, and previous studies of bilayer-protein interactions for integral membrane proteins36,40,64,73 we imposed slopes of h+ and u+ equal to −tan 9° and 0 along the bilayer-wedge interfaces, but our key model predictions are robust with respect to variations in these parameter values (see Supplementary Information Sec. S3). We note that, in the context of integral membrane proteins, the boundary conditions on the slope of the lipid bilayer thickness deformations at the bilayer-protein interface have been examined in some detail using MD simulations73,74, with excellent agreement between MD simulations and continuum elastic models for small (but finite) contact slopes of the bilayer thickness deformations73. We analytically calculated the wedge interaction potential used for Figs 3, 5 and 6 by transforming equation (3) with equations (9) and (10) into the form
| 12 |
where , applying Gauss’s theorem, and subtracting from equation (12) the contribution to G not due to interactions, . Detailed numerical estimates of the magnitude of bilayer-mediated wedge interactions, and the characteristic wedge separations favored by bilayer-mediated wedge interactions, may require a closer examination of the boundary conditions imposed on the slopes of u+ and h+ at the bilayer-wedge interfaces, and quantification of the relation between the measured wedge immersion depths22,23 and the wedge-induced lipid bilayer thickness deformations in the immediate vicinity of protein wedges.
Simulated annealing Monte Carlo simulations
For Fig. 4, we computed the directional N-BAR pair potentials due to H0-induced leaflet thickness deformations in two-dimensional membranes by minimizing equation (3) for h+ = 0 using finite elements as described previously40. Along the extended sides of the H0 helices we imposed a constant U ≈ −0.9 nm corresponding to the deep immersion state of the H0 helices of N-BAR proteins22,23, and gradually let U → 0 along the (rounded) wedge tips towards the centers of the wedge tips. For Fig. 4B we also used, based on previous calculations of bilayer-mediated interactions between endophilin BAR domains53, the modified Lennard-Jones pair potential
| 13 |
where r is the center-to-center distance between BAR domains, the angles θ1, 2 capture the BAR orientations with a positive modulus π rad (with the BAR domains facing each other for θ1 = θ2 = π/2), εd = 10 kBT, and rm = 10 nm. For the simulated annealing Monte Carlo simulations in Fig. 4, a single Monte Carlo step consisted, on average, of one displacement trial (δr = 0.1 nm) and one rotation trial (δθ = 1°) per N-BAR protein. The trials were accepted or rejected according to the Metropolis algorithm. In a typical run, we first used 107 Monte Carlo steps at constant T = 2Trm, where Trm = 298 K is the room temperature, and then decreased the temperature linearly to T = 0 over 5 × 106 Monte Carlo steps. (See Supplementary Information Sec. S6 for further details).
Electronic supplementary material
Acknowledgements
We thank H. Lee and P. Rangamani for helpful discussions. This work was supported by NSF award number DMR-1554716 and an Alfred P. Sloan Research Fellowship in Physics (to C.A.H.), the USC Center for High-Performance Computing, the James H. Zumberge Faculty Research and Innovation Fund at the University of Southern California, and National Institutes of Health Grants NS084345 and GM115736 (to R.L.).
Author Contributions
O.K., R.L. and C.A.H. designed the research, O.K. performed the research, O.K., R.L. and C.A.H. analysed the results, and O.K., R.L. and C.A.H. wrote the manuscript.
Data Availability Statement
All data generated or analyzed as part of this study are available through this published Article (and its Supplementary Information).
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Ralf Langen, Email: langen@usc.edu.
Christoph A. Haselwandter, Email: cah77@usc.edu
Electronic supplementary material
Supplementary information accompanies this paper at 10.1038/s41598-018-34273-2.
References
- 1.McMahon HT, Gallop JL. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature. 2005;438:590–596. doi: 10.1038/nature04396. [DOI] [PubMed] [Google Scholar]
- 2.Frost A, Unger VM, De Camilli P. The BAR domain superfamily: Membrane-molding macromolecules. Cell. 2009;137:191–196. doi: 10.1016/j.cell.2009.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Drin G, Antonny B. Amphipathic helices and membrane curvature. FEBS Lett. 2010;584:1840–1847. doi: 10.1016/j.febslet.2009.10.022. [DOI] [PubMed] [Google Scholar]
- 4.Rao Y, Haucke V. Membrane shaping by the Bin/amphiphysin/Rvs (BAR) domain protein superfamily. Cell. Mol. Life Sci. 2011;68:3983–3993. doi: 10.1007/s00018-011-0768-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mim C, Unger VM. Membrane curvature and its generation by BAR proteins. Trends Biochem. Sci. 2012;37:526–533. doi: 10.1016/j.tibs.2012.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lee E, et al. Amphiphysin 2 (Bin1) and T-tubule biogenesis in muscle. Science. 2002;297:1193–1196. doi: 10.1126/science.1071362. [DOI] [PubMed] [Google Scholar]
- 7.Milosevic I, et al. Recruitment of endophilin to clathrin-coated pit necks is required for efficient vesicle uncoating after fission. Neuron. 2011;72:587–601. doi: 10.1016/j.neuron.2011.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Boucrot E, et al. Endophilin marks and controls a clathrin-independent endocytic pathway. Nature. 2015;517:460–465. doi: 10.1038/nature14067. [DOI] [PubMed] [Google Scholar]
- 9.Renard H-F, et al. Endophilin-A2 functions in membrane scission in clathrin-independent endocytosis. Nature. 2015;517:493–496. doi: 10.1038/nature14064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Peter BJ, et al. BAR domains as sensors of membrane curvature: The amphiphysin BAR structure. Science. 2004;303:495–499. doi: 10.1126/science.1092586. [DOI] [PubMed] [Google Scholar]
- 11.Gallop JL, et al. Mechanism of endophilin N-BAR domain-mediated membrane curvature. EMBO J. 2006;25:2898–2910. doi: 10.1038/sj.emboj.7601174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mizuno N, Jao CC, Langen R, Steven AC. Multiple modes of endophilin-mediated conversion of lipid vesicles into coated tubes: Implications for synaptic endocytosis. J. Biol. Chem. 2010;285:23351–23358. doi: 10.1074/jbc.M110.143776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sorre B, et al. Nature of curvature coupling of amphiphysin with membranes depends on its bound density. Proc. Natl. Acad. Sci. USA. 2012;109:173–178. doi: 10.1073/pnas.1103594108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhu C, Das SL, Baumgart T. Nonlinear sorting, curvature generation, and crowding of endophilin N-BAR on tubular membranes. Biophys. J. 2012;102:1837–1845. doi: 10.1016/j.bpj.2012.03.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Masuda M, et al. Endophilin BAR domain drives membrane curvature by two newly identified structure-based mechanisms. EMBO J. 2006;25:2889–2897. doi: 10.1038/sj.emboj.7601176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Weissenhorn W. Crystal structure of the endophilin-A1 BAR domain. J. Mol. Biol. 2005;351:653–661. doi: 10.1016/j.jmb.2005.06.013. [DOI] [PubMed] [Google Scholar]
- 17.Jao CC, et al. Roles of amphipathic helices and the Bin/amphiphysin/Rvs (BAR) domain of endophilin in membrane curvature generation. J. Biol. Chem. 2010;285:20164–20170. doi: 10.1074/jbc.M110.127811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Qualmann B, Koch D, Kessels MM. Let’s go bananas: revisiting the endocytic BAR code. EMBO J. 2011;30:3501–3515. doi: 10.1038/emboj.2011.266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kozlov MM, et al. Mechanisms shaping cell membranes. Curr. Opin. Cell Biol. 2014;29:53–60. doi: 10.1016/j.ceb.2014.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Baumgart T, Capraro BR, Zhu C, Das SL. Thermodynamics and mechanics of membrane curvature generation and sensing by proteins and lipids. Annu. Rev. Phys. Chem. 2011;62:483. doi: 10.1146/annurev.physchem.012809.103450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Callan-Jones A, Bassereau P. Curvature-driven membrane lipid and protein distribution. Curr. Opin. Solid State Mater. Sci. 2013;17:143–150. doi: 10.1016/j.cossms.2013.08.004. [DOI] [Google Scholar]
- 22.Ambroso MR, Hegde BG, Langen R. Endophilin A1 induces different membrane shapes using a conformational switch that is regulated by phosphorylation. Proc. Natl. Acad. Sci. USA. 2014;111:6982–6987. doi: 10.1073/pnas.1402233111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Isas JM, Ambroso MR, Hegde PB, Langen J, Langen R. Tubulation by amphiphysin requires concentrationdependent switching from wedging to scaffolding. Structure. 2015;23:873–881. doi: 10.1016/j.str.2015.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gross A. Bending membranes into different shapes. Structure. 2015;23:803–804. doi: 10.1016/j.str.2015.04.012. [DOI] [PubMed] [Google Scholar]
- 25.Farsad K, et al. Generation of high curvature membranes mediated by direct endophilin bilayer interactions. J. Cell Biol. 2001;155:193–200. doi: 10.1083/jcb.200107075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fernandes F, et al. Role of Helix 0 of the N-BAR domain in membrane curvature generation. Biophys. J. 2008;94:3065–3073. doi: 10.1529/biophysj.107.113118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mim C, et al. Structural basis of membrane bending by the N-BAR protein endophilin. Cell. 2012;149:137–145. doi: 10.1016/j.cell.2012.01.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cui H, et al. Understanding the role of amphipathic helices in N-BAR domain driven membrane remodeling. Biophys. J. 2013;104:404–411. doi: 10.1016/j.bpj.2012.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Boucrot E, et al. Membrane fission is promoted by insertion of amphipathic helices and is restricted by crescent BAR domains. Cell. 2012;149:124–136. doi: 10.1016/j.cell.2012.01.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shi Z, Baumgart T. Membrane tension and peripheral protein density mediate membrane shape transitions. Nat. Commun. 2015;6:5974. doi: 10.1038/ncomms6974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Simunovic M, Srivastava A, Voth GA. Linear aggregation of proteins on the membrane as a prelude to membrane remodeling. Proc. Natl. Acad. Sci. USA. 2013;110:20396–20401. doi: 10.1073/pnas.1309819110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Simunovic M, Voth GA. Membrane tension controls the assembly of curvature-generating proteins. Nat. Commun. 2015;6:7219. doi: 10.1038/ncomms8219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Daum B, et al. Supramolecular organization of the human N-BAR domain in shaping the sarcolemma membrane. J. Struct. Biol. 2016;194:375–382. doi: 10.1016/j.jsb.2016.03.017. [DOI] [PubMed] [Google Scholar]
- 34.Dan N, Berman A, Pincus P, Safran SA. Membrane-induced interactions between inclusions. J. Phys. II. 1994;4:1713–1725. [Google Scholar]
- 35.Aranda-Espinoza H, Berman A, Dan N, Pincus P, Safran S. Interaction between inclusions embedded in membranes. Biophys. J. 1996;71:648–656. doi: 10.1016/S0006-3495(96)79265-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Phillips R, Ursell T, Wiggins P, Sens P. Emerging roles for lipids in shaping membrane-protein function. Nature. 2009;459:379–385. doi: 10.1038/nature08147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Goforth RL, et al. Hydrophobic coupling of lipid bilayer energetics to channel function. J. Gen. Physiol. 2003;121:477–493. doi: 10.1085/jgp.200308797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kaiser H-J, et al. Lateral sorting in model membranes by cholesterol-mediated hydrophobic matching. Proc. Natl. Acad. Sci. USA. 2011;108:16628–16633. doi: 10.1073/pnas.1103742108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Milovanovic D, et al. Hydrophobic mismatch sorts SNARE proteins into distinct membrane domains. Nat. Commun. 2015;6:5984. doi: 10.1038/ncomms6984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kahraman O, Koch PD, Klug WS, Haselwandter CA. Bilayer-thickness-mediated interactions between integral membrane proteins. Phys. Rev. E. 2016;93:042410. doi: 10.1103/PhysRevE.93.042410. [DOI] [PubMed] [Google Scholar]
- 41.Pollard AM, Sourjik V. Transmembrane region of bacterial chemoreceptor is capable of promoting protein clustering. J. Biol. Chem. 2018;293:2149–2158. doi: 10.1074/jbc.M117.796722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Braun AR, et al. α-Synuclein induces both positive mean curvature and negative Gaussian curvature in membranes. J. Am. Chem. Soc. 2012;134:2613–2620. doi: 10.1021/ja208316h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Braun AR, Lacy MM, Ducas VC, Rhoades E, Sachs JN. α-Synuclein-induced membrane remodeling is driven by binding affinity, partition depth, and interleaflet order asymmetry. J. Am. Chem. Soc. 2014;136:9962–9972. doi: 10.1021/ja5016958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.West A, Brummel BE, Braun AR, Rhoades E, Sachs JN. Membrane remodeling and mechanics: Experiments and simulations of α-synuclein. Biochim. Biophys. Acta Biomembr. 2016;1858:1594–1609. doi: 10.1016/j.bbamem.2016.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ludtke S, He K, Huang H. Membrane thinning caused by magainin 2. Biochemistry. 1995;34:16764–16769. doi: 10.1021/bi00051a026. [DOI] [PubMed] [Google Scholar]
- 46.Huang HW, Chen F-Y, Lee M-T. Molecular mechanism of peptide-induced pores in membranes. Phys. Rev. Lett. 2004;92:198304. doi: 10.1103/PhysRevLett.92.198304. [DOI] [PubMed] [Google Scholar]
- 47.Hristova K, et al. An amphipathic α-helix at a membrane interface: A structural study using a novel X-ray diffraction method. J. Mol. Biol. 1999;290:99–117. doi: 10.1006/jmbi.1999.2840. [DOI] [PubMed] [Google Scholar]
- 48.Perrin BS, Sodt AJ, Cotten ML, Pastor RW. The curvature induction of surface-bound antimicrobial peptides piscidin 1 and piscidin 3 varies with lipid chain length. J. Membr. Biol. 2015;248:455–467. doi: 10.1007/s00232-014-9733-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Woo SY, Lee H. Effect of lipid shape on toroidal pore formation and peptide orientation in lipid bilayers. Phys. Chem. Chem. Phys. 2017;19:21340–21349. doi: 10.1039/C7CP02708G. [DOI] [PubMed] [Google Scholar]
- 50.Woo SY, Lee H. Aggregation and insertion of melittin and its analogue MelP5 into lipid bilayers at different concentrations: effects on pore size, bilayer thickness and dynamics. Phys. Chem. Chem. Phys. 2017;19:7195–7203. doi: 10.1039/C6CP06834K. [DOI] [PubMed] [Google Scholar]
- 51.Campelo F, Fabrikant G, McMahon HT, Kozlov MM. Modeling membrane shaping by proteins: Focus on EHD2 and N-BAR domains. FEBS Lett. 2010;584:1830–1839. doi: 10.1016/j.febslet.2009.10.023. [DOI] [PubMed] [Google Scholar]
- 52.Shemesh T, et al. A model for the generation and interconversion of ER morphologies. Proc. Natl. Acad. Sci. USA. 2014;111:E5243–E5251. doi: 10.1073/pnas.1419997111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Schweitzer Y, Kozlov MM. Membrane-mediated interaction between strongly anisotropic protein scaffolds. PLoS Comput. Biol. 2015;11:e1004054–e1004054. doi: 10.1371/journal.pcbi.1004054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Noguchi H, Fournier J-B. Membrane structure formation induced by two types of banana-shaped proteins. Soft Matter. 2017;13:4099–4111. doi: 10.1039/C7SM00305F. [DOI] [PubMed] [Google Scholar]
- 55.Campelo F, McMahon HT, Kozlov MM. The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys. J. 2008;95:2325–2339. doi: 10.1529/biophysj.108.133173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zemel A, Ben-Shaul A, May S. Modulation of the spontaneous curvature and bending rigidity of lipid membranes by interfacially adsorbed amphipathic peptides. J. Phys. Chem. B. 2008;112:6988–6996. doi: 10.1021/jp711107y. [DOI] [PubMed] [Google Scholar]
- 57.Campelo F, Kozlov MM. Sensing membrane stresses by protein insertions. PLoS Comput. Biol. 2014;10:e1003556. doi: 10.1371/journal.pcbi.1003556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sodt AJ, Pastor RW. Molecular modeling of lipid membrane curvature induction by a peptide: More than simply shape. Biophys. J. 2014;106:1958–1969. doi: 10.1016/j.bpj.2014.02.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Brannigan G, Brown FLH. Contributions of Gaussian curvature and nonconstant lipid volume to protein deformation of lipid bilayers. Biophys. J. 2007;92:864–876. doi: 10.1529/biophysj.106.094953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.West B, Brown FLH, Schmid F. Membrane-protein interactions in a generic coarse-grained model for lipid bilayers. Biophys. J. 2009;96:101–115. doi: 10.1529/biophysj.108.138677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Bitbol A-F, Constantin D, Fournier J-B. Bilayer elasticity at the nanoscale: The need for new terms. PLoS ONE. 2012;7:e48306. doi: 10.1371/journal.pone.0048306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Rangamani P, et al. Small scale membrane mechanics. Biomech. Model. Mechanobiol. 2014;13:697–711. doi: 10.1007/s10237-013-0528-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Rawicz W, Olbrich KC, McIntosh T, Needham D, Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000;79:328–339. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Huang HW. Deformation free energy of bilayer membrane and its effect on gramicidin channel lifetime. Biophys. J. 1986;50:1061–1070. doi: 10.1016/S0006-3495(86)83550-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Goulian M, Bruinsma R, Pincus P. Long-range forces in heterogeneous fluid membranes. Europhys. Lett. 1993;22:145. doi: 10.1209/0295-5075/22/2/012. [DOI] [Google Scholar]
- 66.Weikl TR, Kozlov MM, Helfrich W. Interaction of conical membrane inclusions: Effect of lateral tension. Phys. Rev. E. 1998;57:6988–6995. doi: 10.1103/PhysRevE.57.6988. [DOI] [Google Scholar]
- 67.Raicu, V. & Popescu, A. Integrated Molecular and Cellular Biophysics (Springer, 2008).
- 68.Mondal S, Khelashvili G, Shan J, Andersen OS, Weinstein H. Quantitative modeling of membrane deformations by multihelical membrane proteins: Application to G-protein coupled receptors. Biophys. J. 2011;101:2092–2101. doi: 10.1016/j.bpj.2011.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Weitz S, Destainville N. Attractive asymmetric inclusions in elastic membranes under tension: cluster phases and membrane invaginations. Soft Matter. 2013;9:7804–7816. doi: 10.1039/c3sm50954k. [DOI] [Google Scholar]
- 70.Ursell T, Huang KC, Peterson E, Phillips R. Cooperative gating and spatial organization of membrane proteins through elastic interactions. PLoS Comput. Biol. 2007;3:e81. doi: 10.1371/journal.pcbi.0030081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Varkey J, et al. Membrane curvature induction and tubulation are common features of synucleins and apolipoproteins. J. Biol. Chem. 2010;285:32486–32493. doi: 10.1074/jbc.M110.139576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Kegulian NC, et al. Membrane curvature-sensing and curvature-inducing activity of Islet Amyloid Polypeptide and its implications for membrane disruption. J. Biol. Chem. 2015;290:25782–25793. doi: 10.1074/jbc.M115.659797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Argudo D, Bethel NP, Marcoline FV, Wolgemuth CW, Grabe M. New continuum approaches for determining protein-induced membrane deformations. Biophys. J. 2017;112:2159–2172. doi: 10.1016/j.bpj.2017.03.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Sodt AJ, Beaven AH, Andersen OS, Im W, Pastor RW. Gramicidin A channel formation induces local lipid redistribution II: A 3D continuum elastic model. Biophys. J. 2017;112:1198–1213. doi: 10.1016/j.bpj.2017.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data generated or analyzed as part of this study are available through this published Article (and its Supplementary Information).