Kinetic properties of persistent Na⁺ current orchestrate oscillatory bursting in respiratory neurons

Intrinsically oscillatory neurons in the pre-Bötzinger complex contribute to the rhythmic pattern of breathing. Yamanishi et al. show that the slow inactivation and slow recovery from inactivation exhibited by the persistent sodium current are important for bursting activity in these neurons.

Abstract

The rhythmic pattern of breathing depends on the pre-Bötzinger complex (preBötC) in the brainstem, a vital circuit that contains a population of neurons with intrinsic oscillatory bursting behavior. Here, we investigate the specific kinetic properties that enable voltage-gated sodium channels to establish oscillatory bursting in preBötC inspiratory neurons, which exhibit an unusually large persistent Na⁺ current (I_NaP). We first characterize the kinetics of I_NaP in neonatal rat brainstem slices in vitro, using whole-cell patch-clamp and computational modeling, and then test the contribution of I_NaP to rhythmic bursting in live neurons, using the dynamic clamp technique. We provide evidence that subthreshold activation, persistence at suprathreshold potentials, slow inactivation, and slow recovery from inactivation are kinetic features of I_NaP that regulate all aspects of intrinsic rhythmic bursting in preBötC neurons. The slow and cumulative inactivation of I_NaP during the burst active phase controls burst duration and termination, while the slow recovery from inactivation controls the duration of the interburst interval. To demonstrate this mechanism, we develop a Markov state model of I_NaP that explains a comprehensive set of voltage clamp data. By adding or subtracting a computer-generated I_NaP from a live neuron via dynamic clamp, we are able to convert nonbursters into intrinsic bursters, and vice versa. As a control, we test a model with inactivation features removed. Adding noninactivating I_NaP into nonbursters results in a pattern of random transitions between sustained firing and quiescence. The relative amplitude of I_NaP is the key factor that separates intrinsic bursters from nonbursters and can change the fraction of intrinsic bursters in the preBötC. I_NaP could thus be an important target for regulating network rhythmogenic properties.

Introduction

Membrane currents operating at voltages below the spiking threshold may be very small, but they can exert a substantial influence on neuronal activity (Vervaeke et al., 2006; Jackson and Bean, 2007; Milescu et al., 2010b). The persistent Na⁺ current (I_NaP) is a tetrodotoxin (TTX)-sensitive subthreshold current found in a wide variety of mammalian central neurons (Crill, 1996; Magistretti et al., 2006; Carter et al., 2012; Yamada-Hanff and Bean, 2013). Relative to the transient current (I_NaT) generated by all voltage-gated sodium (Nav) channels, I_NaP activates at more negative potentials and remains active even under strong depolarization (Maurice et al., 2001; Wu et al., 2005), although in some neurons it exhibits slow inactivation (Fleidervish et al., 1996; Do and Bean, 2003). These properties link I_NaP to a diversity of neuronal behaviors, including spontaneous and regular spiking, subthreshold membrane potential oscillations, and oscillatory burst firing (Taddese and Bean, 2002; Sanhueza and Bacigalupo, 2005; Wu et al., 2005; Rotstein et al., 2006; Ziskind-Conhaim et al., 2008).

The molecular identity of I_NaP is still unresolved. To our knowledge, I_NaP has not been observed without the accompanying large transient component, suggesting that it is not carried by a distinct ion channel. Instead, I_NaP is likely to be a kinetic manifestation of the molecular interactions between the Nav pore-forming α subunit and the auxiliary β subunits (Raman et al., 1997; Magistretti and Alonso, 1999; Maurice et al., 2001; Qu et al., 2001; Aman et al., 2009; Bant and Raman, 2010; Chatelier et al., 2010; Chahine and O’Leary, 2011; Lopez-Santiago et al., 2011). The persistence of I_NaP under depolarization distinguishes it from the “window” current, which is defined as the steady-state component of I_NaT, resulting from the overlap of the voltage-dependent activation and inactivation curves (Attwell et al., 1979; French et al., 1990; Magistretti and Alonso, 1999). Unlike the persistent current, the window current is assumed to vanish quickly and completely under sufficient depolarization.

A circuit that relies on I_NaP is the brainstem pre-Bötzinger complex (preBötC), a critical excitatory circuit for respiratory rhythm generation in mammals (Smith et al., 1991; Feldman and Del Negro, 2006; Richter and Smith, 2014). The preBötC contains neurons that express a characteristically large amount of I_NaP and exhibit intrinsic rhythmic bursting behavior (Del Negro et al., 2005; Koizumi and Smith, 2008). This intrinsic bursting is proposed to be essential for generating preBötC rhythmic inspiratory activity in certain conditions, such as the fetal (Pagliardini et al., 2003; Chevalier et al., 2016) and neonatal (Smith et al., 1991; Koshiya and Smith, 1999; Peña et al., 2004; Ramirez et al., 2004) preBötC, isolated in vitro and during hypoxia in the adult in vivo (Paton et al., 2006).

Despite existing evidence that strongly connects I_NaP to cellular bursting behavior, in respiratory and other central nervous system neurons (Darbon et al., 2004; Wu et al., 2005; Yue et al., 2005; Tazerart et al., 2007; Zhong et al., 2007; Ziskind-Conhaim et al., 2008), we still lack a mechanistic understanding of how I_NaP contributes to rhythmic bursting. The limited information on properties of I_NaP in preBötC neurons has been obtained from rodent neonatal neurons in brainstem slices in vitro, where patch-clamp recordings of this current have been practical (Del Negro et al., 2002; Koizumi and Smith, 2008). Previous studies have established a connection between I_NaP and cellular bursting in preBötC neurons by combining pharmacological and electrophysiological approaches, demonstrating that pharmacological agents that reduce I_NaP, such as riluzole or low-concentration TTX, abolish rhythmic bursting at cellular, as well as circuit, levels (Del Negro et al., 2002; Koizumi and Smith, 2008). However, these chemicals are not I_NaP specific and may alter the availability of the spike-generating I_NaT (Song et al., 1997; Urbani and Belluzzi, 2000; Taddese and Bean, 2002), which is obviously necessary for sustained neuronal firing during a burst. More importantly, pharmacological or genetic approaches cannot dissect out the functional I_NaP dynamics during the active and silent phases of cellular oscillatory bursting, as required to establish its mechanistic contributions. In particular, these approaches cannot establish whether the inactivation and recovery from inactivation of I_NaP play any role in bursting.

To overcome these challenges, we used the dynamic clamp (DC) technique (Sharp et al., 1993; Milescu et al., 2008, 2010b) to test the contribution of I_NaP to the rhythmic bursting of preBötC neurons in neonatal rat brainstem slice preparations in vitro. The idea is to modify the electrophysiological profile of the cell by adding or subtracting a computationally generated conductance with kinetic properties matching I_NaP. If a relatively large amount of I_NaP is the determining factor for bursting, we would expect that adding I_NaP would convert a nonburster into an intrinsic burster. Conversely, subtracting I_NaP would convert an intrinsic burster into a nonburster. Most importantly, the kinetics of the I_NaP model can be manipulated to explore the quantitative relationships between I_NaP kinetics and bursting properties.

To our knowledge, a data-derived kinetic model of I_NaP in respiratory and other neurons does not yet exist, although theoretical models have been proposed before (Butera et al., 1999a,b; Vervaeke et al., 2006). Thus, our first objective was to formulate a Markov state model that quantitatively explains all the kinetic properties of the I_NaP expressed in preBötC neurons, particularly slow inactivation. We emphasize that this model describes exclusively the I_NaP component of the total TTX-sensitive current; it does not predict the I_NaT. Through a series of voltage clamp (VC) protocols designed to isolate I_NaP from all the other currents in the cell, especially I_NaT, we found that I_NaP inactivates and recovers from inactivation very slowly, with time constants in the range of seconds. Then, we used this model in DC experiments to test whether bursting activity relies on the presence of I_NaP and whether I_NaP inactivation is necessary. To distinguish between the role of I_NaP and the potential role of calcium-related currents (Ramirez et al., 2004), all experiments were performed under bath-applied calcium channel blockers. We found that the kinetic properties of I_NaP establish all aspects of oscillatory bursting activity. Thus, I_NaP initiates and maintains the active phase of bursting because of its subthreshold voltage activation. Importantly, I_NaP terminates the burst by its slow and cumulative inactivation. Finally, I_NaP controls bursting frequency by its slow recovery from inactivation. Conceptually, these ideas have been proposed before in modeling studies (Butera et al., 1999a,b; Rybak et al., 2003, 2004), but they have not been experimentally determined and tested.

Materials and methods

Animal procedures

All animal procedures were approved by the National Institute of Neurological Disorders and Stroke of the National Institutes of Health and the University of Missouri Animal Care and Use Committees.

Medullary slice preparation

In vitro medullary slice preparations were obtained from neonatal (postnatal day 0 [P0]–P3) Sprague-Dawley male and female rats, as previously described (Koshiya and Smith, 1999; Koizumi and Smith, 2008). Briefly, the medulla was dissected in artificial cerebrospinal fluid (aCSF) containing the following (in mM): 124 NaCl, 25 NaHCO₃, 3 KCl, 1.5 CaCl₂, 1 MgSO₄, 0.5 NaH₂PO₄, and 30 d-glucose, equilibrated with 95% O₂ and 5% CO₂ (pH 7.4 ± 0.05 at room temperature). Transverse slices (300–350-µm thick) containing the preBötC and the rostral end of the hypoglossal (XII) motor nucleus, including XII nerve rootlets (Fig. 1 A), were transferred to the recording chamber and superfused with aCSF warmed to 27°C. Only one slice was obtained per animal. Bursting behavior has been observed in preBötC neurons at 3 mM extracellular K⁺ concentration ([K⁺]_o) in situ (St.-John et al., 2009). However, to enable robust rhythmic respiratory activity and minimize animal usage, we elevated [K⁺]_o to 8 mM. Although experimental conditions with higher [K⁺]_o may alter bursting properties in some types of neurons, such as hippocampal pyramidal cells (Jensen et al., 1994), the rhythmic bursting behavior of preBötC inspiratory neurons was shown to be minimally affected by changes in [K⁺]_o (Tryba et al., 2003).

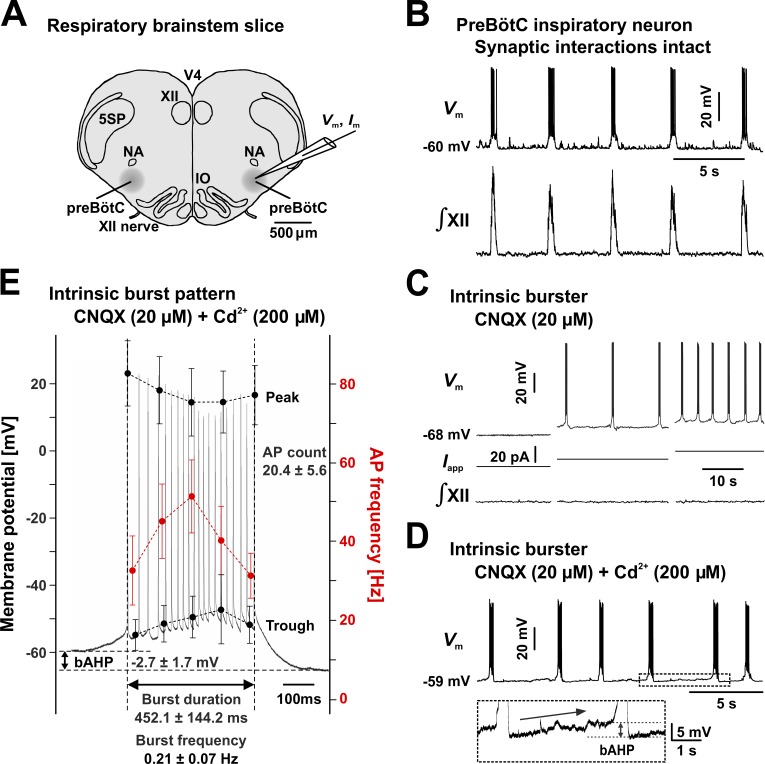
Figure 1.

Intrinsically oscillatory bursting neurons in the preBötC. (A) Schematic representation of the neonatal rat medullary transverse slice preparation (thickness: 300–350 µm), containing the inspiratory rhythm-generating circuits in the preBötC, with output to the hypoglossal motor nucleus. 5SP, spinal trigeminal nucleus; IO, inferior olivary nucleus; NA, nucleus ambiguus; V4, fourth ventricle; XII, hypoglossal motor nucleus. (B) With synaptic transmission intact, inspiratory neurons exhibit rhythmic bursting activity (upper trace, CC recording) in synchrony with inspiratory network activity (lower trace, XII motor nerve inspiratory discharge). (C) Intrinsic bursters maintain voltage-dependent rhythmic bursting activity (upper traces) when network-wide synaptic transmission is disrupted by bath-applied CNQX, which blocks non-NMDA glutamatergic receptors. No rhythmic XII nerve output can be observed (lower traces). Neuronal bursting frequency is a function of baseline membrane potential and can be modulated by injecting current (I_app, middle traces). (D) Intrinsic bursting activity is not significantly affected by bath-applied Cd²⁺, which inhibits calcium-related currents. The inset illustrates the characteristic bAHP and the slow depolarization drift (arrow). (E) Representative burst (gray trace) and statistical measures. The data points (mean and SD) were calculated at 0%, 25%, 50%, 75%, and 100% of burst time and were obtained from 19 neurons by averaging over five consecutive bursts in each neuron. All CC traces were obtained from representative neurons. AP, action potential.

Neuron identification

All patch-clamp whole-cell recordings were obtained from neurons located at depths ≥100 µm within the slice, under infrared differential interference contrast visualization or through a blind-patch approach. PreBötC neurons were identified based on their location in the slice. Respiratory neurons were confirmed based on their firing activity in phase with the hypoglossal (XII) nerve output (Fig. 1 B). Neurons were classified as intrinsic bursters if they maintained rhythmic bursting activity under bath-applied synaptic transmission blockers. For cells targeted for VC experiments, when channel blockers were added to the intracellular solution, neuronal identity was determined before gigaseal formation, in current clamp (CC) mode.

Pipette solutions

For VC, the electrodes were filled with a solution containing (in mM): 70 Cs-gluconate, 30 Na-gluconate, 10 TEA-Cl, 5 4-aminopyridine, 10 EGTA, 1 CaCl₂, 15 HEPES, 4 Mg-ATP, 0.3 Na-GTP, and 10 Na₂-phosphocreatine, pH 7.3, adjusted with CsOH (285 ± 5 mOsm/liter). Cs⁺, TEA⁺, and 4-aminopyridine minimized K⁺ currents, whereas the high Na⁺ concentration decreased the reversal potential of Na⁺ currents, reducing VC artifacts. For CC or dynamic clamp (DC), the electrodes were filled with a solution containing (in mM): 125 K-gluconate, 4 NaCl, 11 EGTA, 1 CaCl₂, 10 HEPES, 4 Mg-ATP, 0.3 Na-GTP, and 4 Na₂-phosphocreatine, pH 7.3 adjusted with KOH (285 ± 5 mOsm/liter).

Pharmacology

To block sodium currents, TTX (1 µM) was added to the superfusing aCSF. Ca²⁺-related currents, including voltage-sensitive Ca²⁺ currents and Ca²⁺-activated currents, and depolarization-evoked neurotransmitter release were minimized with bath-applied CdCl₂ (200 µM). Non-NMDA (N-methyl-D-aspartate) glutamate receptors, which mediate excitatory synaptic connections among preBötC neurons, were blocked with 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX, 20 µM; Koshiya and Smith, 1999). Each bath-applied drug was used only once in a given slice. All reagents were purchased from Sigma-Aldrich.

Electrophysiology

Recording electrodes (3–4 MΩ) were pulled from borosilicate glass (WPI) and coated with Sylgard to reduce capacitive transients, which is critical for stable operation under DC. Pipette capacitance was compensated 100% in VC and ≈70% in CC and DC. Under VC, the series resistance (R_s) was compensated ≈80% (2-µs response time) and readjusted before running a protocol. The neuronal membrane capacitance was approximated as the value necessary to compensate the slow capacitive component. In CC and DC experiments, R_s was compensated 100% and readjusted as necessary. A liquid junction potential of ≈10 mV for the K⁺-based and ≈8 mV for the Cs⁺-based solutions was corrected online. Somatic whole-cell recordings were obtained with an EPC-9 or EPC-10 patch-clamp amplifier (HEKA Electronics) controlled by Pulse 8.77 software (HEKA Electronics). VC protocols were constructed and applied with Pulse software. The membrane current was low-pass filtered at 10 kHz and digitally sampled at 50 kHz, using the amplifier’s built-in digitizer. For CC or DC recordings, the membrane voltage was sampled at 10 kHz using a PowerLab A/D converter and recorded with Chart software (AD Instruments).

VC protocols

The total TTX-sensitive Na⁺ current flowing during a burst was obtained with synthetic burst waveforms that were applied as voltage commands in VC, as shown in Fig. 2 (C and D). One waveform pattern is a construct that statistically matches the experimentally observed bursts in terms of voltage time course, spike count, and frequency (“realistic” burst waveform; Fig. 2 C, upper trace), whereas the other waveform contains a series of identical action potentials separated by a constant 20-ms interspike interval (“uniform” burst waveform; Fig. 2 D, upper trace). To characterize the kinetic properties of I_NaP, we designed VC protocols that isolate the persistent from the transient component of the TTX-sensitive Na⁺ current, based on differences in their timing and voltage dependence (Fig. 3 A–F). To better isolate the relatively small I_NaP from all other membrane currents and experimental artifacts, all protocols were constructed with P/4 leak subtraction and were repeated under bath-applied TTX (1 μM) for TTX subtraction. Neurons with evidence of poor space-clamp (unclamped action potential currents) were excluded from analysis.

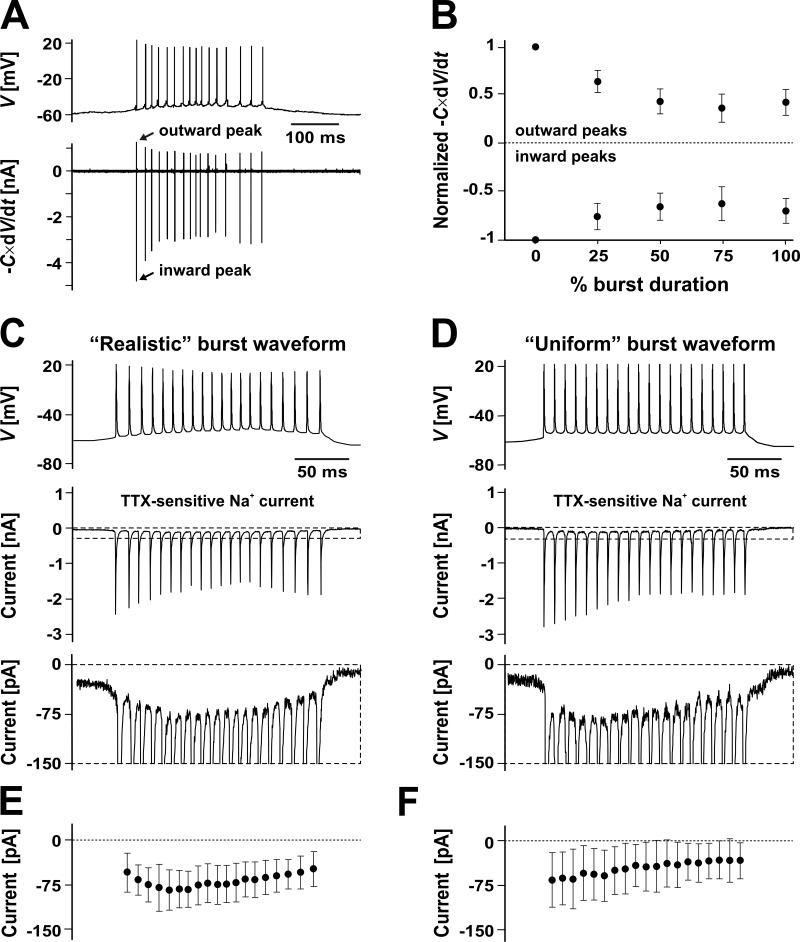
Figure 2.

Supra- and subthreshold burst currents in preBötC intrinsic bursters. (A) Representative burst waveform (upper trace, CC recording) obtained under bath-applied CNQX (20 µM) and Cd²⁺ (200 µM). The net ionic current (lower trace) was calculated as the negative time derivative of membrane potential, –C × dV/dt, where C is the estimated membrane capacitance. (B) Normalized peak inward and outward net current, as measured throughout the burst (n = 19 neurons, each point averaged over five consecutive bursts; mean and SD). (C and D) TTX-sensitive Na⁺ current evoked by synthetic burst waveforms applied as the command voltage in VC. (C) Realistic burst waveform (upper trace) statistically matching natural bursts (see Fig. 1 E and Table 2) and evoked current from a representative neuron (middle trace, with dashed line range expanded in the lower trace). (D) Same as in C, with a uniform burst waveform, with identical action potentials and constant interspike interval. (E and F) The TTX-sensitive Na⁺ current evoked by the realistic (E) and uniform (F) waveforms, calculated across the 5 ms immediately preceding each action potential (n = 4; mean and SD). Note the exponential decay in F.

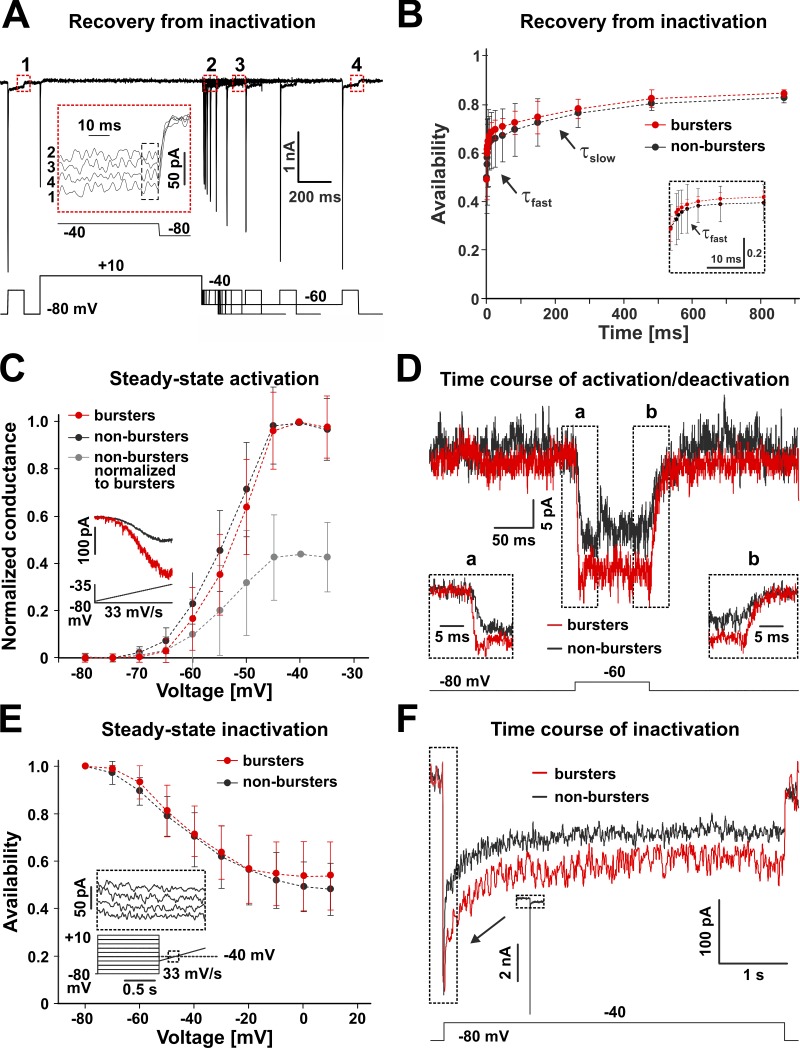
Figure 3.

Kinetic properties of I_NaP. TTX-sensitive Na⁺ currents obtained from preBötC respiratory intrinsic bursters and nonbursters, with TTX subtraction. Representative data shown. (A) VC protocol designed to isolate I_NaP and test its recovery from inactivation (example data from an intrinsic burster). (B) Biexponential recovery from inactivation. The time course is not significantly different (ANOVA, P = 0.51) between intrinsic bursters (red, n = 8) and nonbursters (n = 16). From the combined data, τ_fast = 1.4 ± 0.5 ms and τ_slow = 2.6 ± 0.4 s. (C) Steady-state activation curve (inset shows protocol and evoked current). The half-activation voltage (V_h) and slope factor (k) are not significantly different (unpaired t; V_h, P = 0.70; k, P = 0.39) between bursters (V_h = –47.7 ± 2.5 mV, k = 3.6 ± 0.6 mV; n = 8) and nonbursters (V_h = –48.4 ± 4.0 mV, k = 4.3 ± 1.6 mV; n = 16). The maximum current (I_NaP*) and conductance (G_NaP*) values are significantly different (unpaired t; P = 0.00043) between bursters (I_NaP* = 227.7 ± 54.1 pA and G_NaP* = 2.3 ± 0.5 nS) and nonbursters (I_NaP* = 106.1 ± 38.7 pA and G_NaP* = 1.1 ± 0.4 nS). (D) Time course of activation (a) and deactivation (b). The time constants of activation (τ_a) and deactivation (τ_d) are similar (unpaired t; activation, P = 0.33; deactivation, P = 0.81) between bursters (n = 4) and nonbursters (n = 7). From the combined data, τ_a = 3.4 ± 1.0 ms and τ_d = 7.9 ± 2.3 ms. (E) Steady-state inactivation curve (inset shows protocol and evoked current). The half-inactivation voltage and slope values are similar (unpaired t; V_h, P = 0.16; k, P = 0.17) between bursters (V_h = –39.1 ± 2.9 mV, k = –9.5 ± 1.2 mV; n = 4) and nonbursters (V_h = –41.8 ± 3.9 mV, k = –11.4 ± 3.1 mV; n = 8). (F) Time course of slow inactivation. The time constant of slow decay (τ_i) is similar (unpaired t; P = 0.33) between bursters (n = 5) and nonbursters (n = 9). From the combined data, τ_i = 571.0 ± 50.9 ms. Data shown in B, C, and E are mean ± SD.

I_NaP modeling

The main I_NaP model developed in this study (Model 1; Fig. 4 A) was obtained by fitting multiple VC datasets simultaneously (Fig. 4, B–E), as previously described (Milescu et al., 2010b). A second model (Model 2; Fig. 7 A) was derived by removing all inactivated states from Model 1 and adjusting the remaining rates to match a subset of VC data (Fig. 7, B and C). All rate constants were expressed as exponential functions of voltage: $k_{ij}=k_{ij}^0\times e^{k_{ij}^1\times V}$, where k_ij is the rate constant of the transition between states i and j (in ms⁻¹), $k_{ij}^0$ is a preexponential parameter equal to the rate at zero membrane potential (in ms⁻¹), $k_{ij}^1$ is an exponential parameter describing the voltage sensitivity (in mV⁻¹), and V is the voltage (in mV). In Model 1, allosteric relationships between rate constants are indicated by the a and b factors (Fig. 4 A). The kinetic parameters $k_{ij}^0$ and $k_{ij}^1$ and the allosteric factors a and b were optimized with QuB software, as previously described (Milescu et al., 2008, 2010b), enforcing microscopic reversibility and all other constraints implied by the model (Navarro et al., 2018; Salari et al., 2018). The predictions of the model, as required during the optimization process for a given set of parameters, were calculated in response to the same voltage protocols as used experimentally to record the data. The differential equations describing the time course of state occupancies were integrated using the matrix method (Milescu et al., 2008; Salari et al., 2016). The cost function was calculated as the average sum of square errors between the data and the prediction of the model. The components of the cost function were weighted so as to balance the goodness of fit between the different datasets. For this, conductance or current datasets (e.g., activation and inactivation time course) were normalized to span a range of –1 to 1 to match those datasets that express a fraction (e.g., availability or recovery) and span a 0-to-1 range. The optimization was performed with the “simplex” search engine, which was restarted several times with different initial parameter values, to avoid local minima. The optimizer was allowed to run for 300 iterations or until none of the free parameters changed more than 0.0001 between two consecutive iterations. The parameter estimates are given in Table 1. For Model 1, the following parameters were estimated directly: $k_a^0$, $k_a^1$, $k_d^0$, $k_d^1$, $k_o^0$, $k_o^1$, $k_c^0$, $k_c^1$, $k_i^0$, $k_i^1$, $k_r^0$, $k_r^1$, $k_{io}^0$, $k_{ro}^0$, $k_{is}^0$, $k_{is}^1$, $k_{rs}^0$, $k_{rs}^1$, $k_{iso}^0$, $k_{rso}^0$, a, and b. The remaining parameters were calculated as follows: $k_{io}^1=k_i^1$, $k_{ro}^1=k_r^1$, $k_{iso}^1=k_{is}^1$, $k_{rso}^1=k_{rs}^1$, $k_{oi}^0=(k_o^0+k_c^0)/[1+\left(\right(k_c^0/k_o^0)\times (k_i^0/k_r^0)\times (k_{ro}^0/k_{io}^0)\times a^3\times b^3)]$, $k_{oi}^1=k_o^1$, $k_{ci}^0=(k_o^0+k_c^0)/[1+\left(\right(k_o^0/k_c^0)\times (k_r^0/k_i^0)\times (k_{io}^0/k_{ro}^0)\times a^{-3}\times b^{-3})]$, $k_{ci}^1=k_c^1$, $k_{os}^0=(k_o^0+k_c^0)/[1+\left(\right(k_c^0/k_o^0)\times (k_{is}^0/k_{rs}^0)\times (k_{rso}^0/k_{iso}^0\left)\right)]$, $k_{os}^1=k_o^1$, $k_{\mathrm{cs}}^0=(k_{\mathrm{o}}^0+k_{\mathrm{c}}^0)/[1+\left(\right(k_{\mathrm{o}}^0/k_{\mathrm{c}}^0)\times (k_{\mathrm{rs}}^0/k_{\mathrm{is}}^0)\times (k_{\mathrm{iso}}^0/k_{\mathrm{rso}}^0\left)\right)]$, and $k_{cs}^1=k_c^1$. The calculations of $k_{oi}^0$, $k_{ci}^0$, $k_{os}^0$, and $k_{cs}^0$ not only preserve microscopic reversibility, but also ensure the same time constant for the SI₁₁–SI₁₂ and I₉–I₁₀ transitions as for C₄–O₅, further reducing the number of free parameters down to 22. To obtain the standard deviations of the estimates, which are not intrinsically computed by the simplex algorithm, we calculated a numerical approximation of the Hessian of the cost function and inverted it to produce the covariance matrix. The parameter standard deviations (Table 1) were obtained as the square root of the diagonal entries in the covariance matrix.

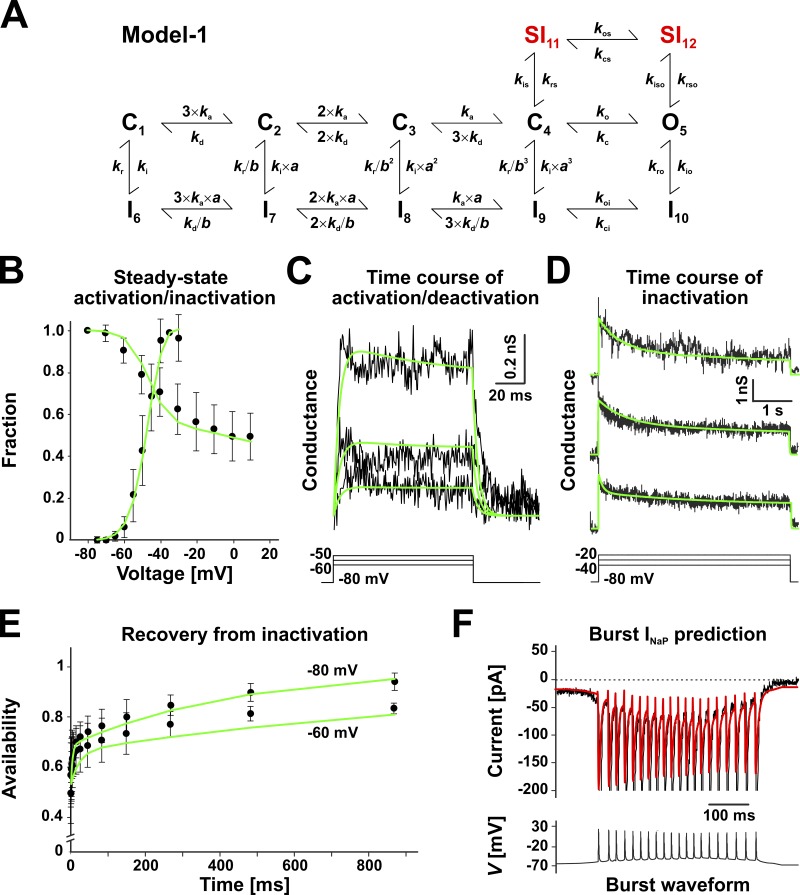
Figure 4.

A data-derived model of I_NaP (Model 1). (A) Markov state model optimized to simultaneously fit the experimental data in B–E (see Materials and methods). The closed states C₁–C₄, the open state O₅, and the inactivated states I₆–I₁₀ represent the fast activation and inactivation pathways, whereas the two inactivated states SI₁₁ and SI₁₂ create an alternative, slower inactivation pathway. The k parameters represent voltage-dependent microscopic rate constants, and a and b represent allosteric parameters. All rates are voltage dependent. (B–F) Experimental data (black traces and symbols), as described in Fig. 3 (B–E) and Fig. 2 C (F), and best-fit model predictions (green lines). The traces in C and D were obtained by converting current to conductance, assuming a reversal potential of +35 mV. In D, the initial 20 ms containing the transient were excluded from the fit. The data in F were not part of the fit, and the red waveform represents the prediction of the optimized model. The predicted current drops in amplitude during each action potential in the burst, as caused by the corresponding drop in driving force. In the experimental data, this effect is masked by the much larger I_NaT. Data shown in B and E are mean ± SD.

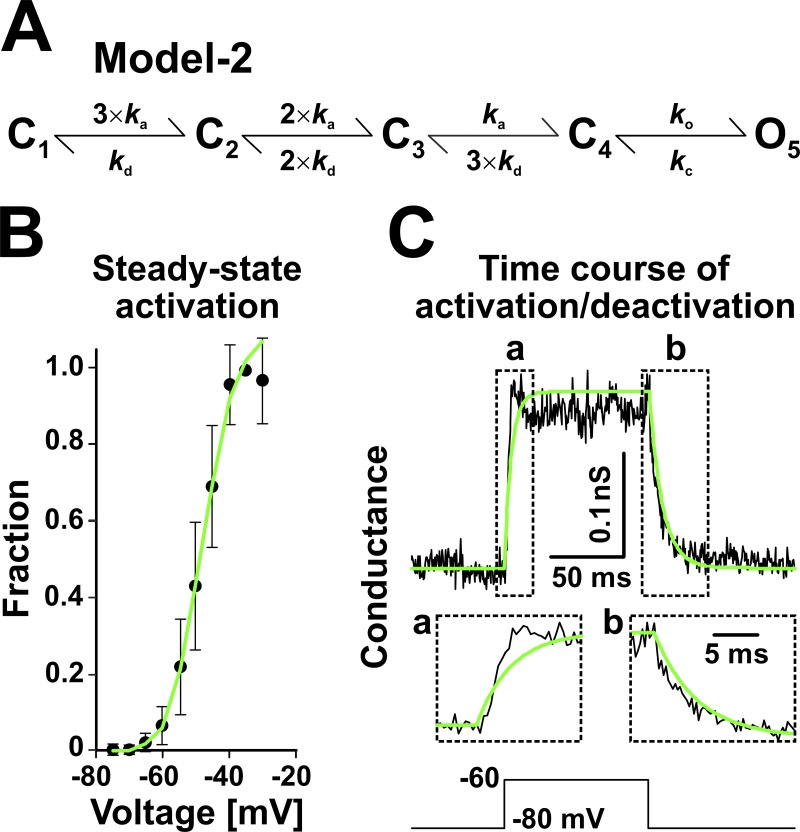
Figure 7.

A noninactivating Markov state model of I_NaP (Model 2). (A–C) Model (A) derived from Model 1, with all inactivated states removed and with the remaining parameters (see Materials and methods) adjusted to simultaneously fit the experimental data in B and C. The data (black traces and symbols) are as described in Fig. 4 (B and C), and the green lines represent Model 2 predictions. The data in B are mean ± SD.

Table 1. Model parameters.

Parameter	k0 [ms−1]	k1 [mV−1]
Model 1
ka	21.066 ± 3.341	0.025607 ± 0.003094
kd	4.9846 ± 0.7914	−0.041864 ± 0.003096
ko	79.237 ± 26.85	0.012616 ± 0.007132
kc	0.19986 ± 0.0667	−0.0042279 ± 0.006837
koi	4,059.03	0.012616
kci	75,377.9	−0.0042279
kos	14,288.7	0.012616
kcs	65,148.3	−0.0042279
ki	0.0041372 ± 0.003587	0.0081037 ± 0.02083
kr	0.025486 ± 0.006448	−0.035336 ± 0.005562
kio	0.00037617 ± 0.000664	0.0081037
kro	0.007445 ± 0.03127	−0.035336
kis	0.0102506 ± 0.004418	0.0042311 ± 0.006932
krs	3.1687 × 10−6 ± 1.455 × 10−6	−0.061102 ± 0.006231
kiso	0.00045328 ± 0.00005917	0.0042311
krso	0.00025328 ± 0.0004963	−0.061102
a	1.8728 ± 0.2528
b	7.0396 ± 0.8488
Model 2
ka	0.901	−0.079
kd	0.055	−0.167
ko	41.126	0.021
kc	0.255	0.01

The table contains the estimated parameters for Model 1 (Fig. 3 A) and Model 2 (Fig. 7 A), given as mean and SD. All rate constants have the form $k=k_{}^0\times e^{k_{}^1\times V}$. The a and b values represent allosteric factors. SD values are not given for some of the Model 1 parameters, because those parameters were not estimated but calculated (see Materials and methods). SD values are not given for Model 2, which was truncated from Model 1 and adjusted to describe only a subset of the VC data. The voltage sensitivity factors k¹ can take both positive and negative values and their SDs should be interpreted as absolute values on a scale of approximately −0.15 to +0.15 mV⁻¹, typical of voltage-gated channels. In contrast, the SDs of the pre-exponential factors k⁰ and allosteric factors a and b should be interpreted as relative to the estimated mean.

Neuronal modeling

As shown in Fig. 5, Model 1 was tested with simulations of a single-compartment preBötC neuronal model, as previously formulated (Butera et al., 1999a,b), but modified by replacing the Hodgkin–Huxley-type I_NaP model with our data-derived Markov Model 1. Besides I_NaP, the model includes a spike-generating Na⁺ current (I_NaT), a delayed-rectifier-like K⁺ current (I_DRK), and a K⁺-dominated leak current (I_Leak). To reflect more recent studies (Koizumi and Smith, 2008; Koizumi et al., 2013) and the present data, several parameters were updated as follows: membrane capacitance (C_m = 27 nS), I_NaT half-activation voltage (V_1/2 = –34.0 mV), K⁺ Nernst potential (E_K = –72 mV), I_NaT conductance (G_NaT = 25 nS), and I_DRK conductance (G_DRK = 15 nS). Numerical simulations were run with QuB software (Milescu et al., 2008), using an integration step of 20 µs.

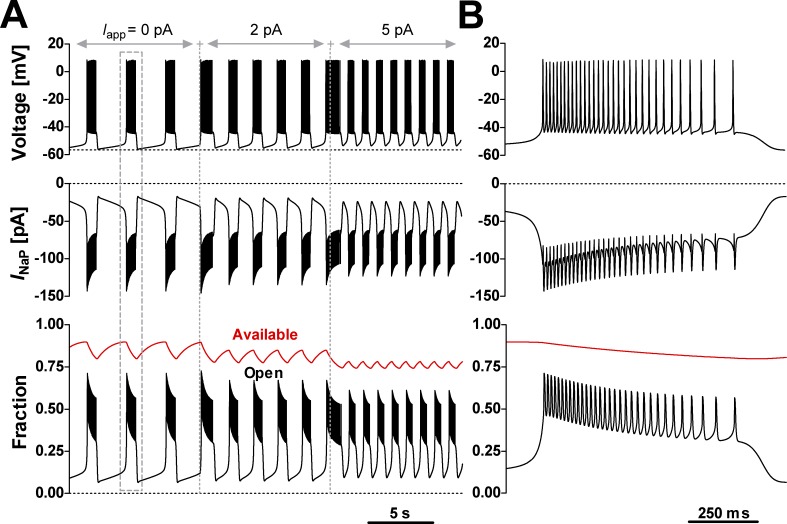
Figure 5.

I_NaP Model 1 supports voltage-dependent rhythmic bursting in computer simulations. The I_NaP model was tested in a single-compartment neuronal model that also includes spike-generating and -terminating Na⁺ and K⁺ currents, and a K⁺-dominated leak (see Materials and methods for details). A bias current (I_app) was applied to test bursting activity at different baseline voltages. (A) Time course of membrane potential (upper trace), I_NaP (middle trace), and the fractions of I_NaP channels residing in the open state (bottom graph, black trace) and available to conduct current (bottom graph, red trace). Availability was calculated as the sum occupancy of all states other than SI₁₁ and SI₁₂. (B) Expanded view of a single burst (dashed box in A). The simulations exhibit the bAHP, the depolarization drift in the interburst interval, and the voltage-dependent bursting frequency characteristic of preBötC intrinsic burster neurons (Fig. 1 D).

CC data analysis

CC recordings were analyzed to quantify cellular bursting properties (burst duration, bursting frequency, action potential count, interspike interval, and burst afterhyperpolarization [bAHP]), as summarized in Fig. 1 E. These values were calculated offline using Chart v5.0 and Igor Pro (Wavemetrics) with custom automated analysis procedures and hand checked for accuracy. A representative set of values was obtained from at least five consecutive bursts sampled from each intrinsic burster that we recorded from, examples of which are shown in Fig. 1 (C and D). Bursting frequency was calculated as the inverse of the time interval measured between two consecutive bursts, using the first action potential in the burst as the reference.

DC

To test the I_NaP Markov models in live neurons (Milescu et al., 2010b; Salari et al., 2016), we used the DC functionality in the QuB software (Milescu et al., 2008) to add or subtract a model-based I_NaP to or from nonbursters and bursters. To subtract, we set the conductance (G_NaP) to a negative value. To solve the I_NaP models in real time, we used the matrix method to integrate the differential equations and determine state probabilities (Milescu et al., 2008). Briefly, the state probability vector is updated at every time step using the equation $P_{t+dt}=P_t\times e^{Q_V\times dt}$, where Q_V is the rate matrix at the measured voltage V, t is the real time, and dt is the real time step. The quantity $e^{Q_V\times dt}$ was precalculated across a range of –80 to +40 mV every 0.5 mV and recalculated each time a kinetic parameter was changed. The refresh rate of the DC system was set to 40 kHz (dt = 25 µs), which allowed the software to simultaneously run the I_NaP Markov model, visualize the model output and data in real time, and save to disk multiple channels of data. The DC software was run under Microsoft Windows XP Pro on a dual-processor 2.8-GHz AMD Opteron computer, using a National Instruments 6052E data acquisition card and NI-DAQmx 8.1 driver, interfaced with a HEKA EPC9 or EPC10 patch-clamp amplifier.

Results

Intrinsic bursting behavior in preBötC inspiratory neurons

To understand the functional context of I_NaP, we first examined the firing properties of preBötC inspiratory neurons in medullary slice preparations obtained from neonatal rats (Fig. 1 A). In this preparation, all preBötC inspiratory neurons fire short bursts of action potentials in synchrony with inspiratory network activity, as recorded from the XII motor nerve (Fig. 1 B). However, two electrophysiologically distinct neuronal populations emerge when excitatory, non-NMDA glutamatergic synaptic interactions are blocked by bath application of CNQX (20 µM), which synaptically uncouples inspiratory neurons and disrupts network synchrony (Koshiya and Smith, 1999). Thus, some neurons (intrinsic bursters) continue to exhibit a pattern of oscillatory bursting (Fig. 1 C), whereas other neurons (nonbursters) turn quiet or fire isolated action potentials, but switch to a regimen of sustained firing when sufficiently depolarized via applied current (not depicted), as previously reported (Thoby-Brisson and Ramirez, 2001; Peña et al., 2004; Koizumi et al., 2013). The intrinsic bursters also exhibit voltage dependence. They burst with a frequency that increases monotonically with the level of depolarization (Fig. 1 C) and eventually turn to a regimen of tonic spiking under sufficiently strong depolarization (Koshiya and Smith, 1999; Del Negro et al., 2002; Koizumi et al., 2013), as originally predicted from models (Butera et al., 1999a,b).

Intrinsic bursters do not rely on Ca²⁺-related currents for bursting

We hypothesize that I_NaP plays the key role, but other currents may also give rise to bursting activity. A good candidate is the Cd²⁺-sensitive, Ca²⁺-activated, nonselective cationic current (I_CAN) that has been identified as the main burst-generating current in several mouse brainstem preparations (Thoby-Brisson and Ramirez, 2001; Peña et al., 2004; Del Negro et al., 2005; Pace et al., 2007; Zavala-Tecuapetla et al., 2008; Rubin et al., 2009). However, recent work from our group has demonstrated that TRPM4-mediated I_CAN is mostly involved in regulating burst amplitude, rather than rhythm generation (Koizumi et al., 2018). Nevertheless, to rule out the potential contribution of I_CAN to intrinsic bursting in our specific experimental preparation, we first tested whether intrinsic bursting—as identified under synaptic block with CNQX—is maintained under bath application of Cd²⁺ (200 µM), which blocks or inhibits Ca²⁺-related currents and synaptic transmission.

We found that none of the 73 intrinsic bursters identified in this study were Cd²⁺ sensitive, as they all maintained oscillatory bursting under Cd²⁺, with just minor changes in their firing characteristics (Fig. 1 D). Cd²⁺ application typically caused a small baseline membrane hyperpolarization (≤2 mV), but no significant change in burst duration and bursting frequency (not depicted), consistent with our previous observations that bursting can occur in the absence of extracellular Ca²⁺ (Del Negro et al., 2001). Interestingly, each burst ends with a small but significant (≈3 mV) bAHP, followed by a slow depolarization drift toward the next burst (Fig. 1 D), with rare isolated action potentials (not present in this example). A representative burst pattern and statistical features are shown in Fig. 1 E. Although we can conclude that in our in vitro preparation Ca²⁺-related currents do not seem to play a significant role in bursting, we performed all further experiments under bath-applied CNQX and Cd²⁺ to eliminate any potential ambiguity and focus on I_NaP.

Supra- and subthreshold burst currents

Even though a single current may be the key factor in establishing a specific pattern of firing activity (e.g., rhythmic bursting), all currents in the cell—sub- and suprathreshold—must interact appropriately to enable that behavior. To understand these interactions, we examined the dynamics of the net current, which can be obtained conveniently from the time derivative of the membrane potential, according to equation I = –C × dV/dt, where I is the total ionic current, C is the estimated membrane capacitance, and V is the membrane potential, as recorded under CC (Fig. 2 A). As a first-order approximation and considering that Ca²⁺-dependent currents were blocked, the inward phase of the net current represents the spike-generating I_NaT, and the outward phase represents the spike-terminating K⁺ currents. Within a burst, the inward and outward peak currents progressively decay at first, but then slightly recover and remain steady (Fig. 2 B). The balance between inward and outward transient currents seems to remain steady throughout the burst, suggesting that burst termination is caused neither by a cumulative inactivation of the spike-generating I_NaT nor by a progressive activation of spike-terminating outward currents.

Next, we isolated and examined the TTX-sensitive current. To obtain this current as it would actually flow during a burst, we evoked it with synthetic burst waveforms applied as the voltage command, as detailed in Materials and methods (de Hass and Vogel, 1989). First, we constructed and tested a realistic burst waveform (Fig. 2 C) that statistically resembles the natural bursts (Fig. 1 E). Under this waveform, the transient, suprathreshold Na⁺ current matches the overall trend of the inward net current (Fig. 2 A). Most importantly, this experiment uncovers a sizable Na⁺ current that flows before and after the burst, as well as in the interspike interval. Considering the voltage and timing, this current should consist mostly of I_NaP, with some possible I_NaT residual in the interspike interval. Interestingly, the amplitude of the subthreshold Na⁺ current is smaller after the burst terminates than before it starts and exhibits an overall pattern of decay within the burst (Fig. 2 E).

To more clearly examine the change in the subthreshold Na⁺ current under the repetitive firing within the burst, we constructed and tested a uniform burst waveform (Fig. 2 D). This synthetic burst contains a train of identical spikes, separated by constant 20-ms intervals, and thus is not representative of the experimentally observed bursts. However, this uniform pattern eliminates the potential confusion brought by a nonstationary driving force, emphasizing instead the kinetic effects of the current. The subthreshold Na⁺ current evoked by this burst waveform also exhibits an overall reduction in amplitude throughout the burst, but with a clearer exponential decay (Fig. 2 F). Because the driving force is now uniform, this decay in amplitude corresponds to a decay in conductance.

According to these results, both the subthreshold and the suprathreshold Na⁺ current components exhibit a progressive reduction in availability with each individual spike in the burst. However, the suprathreshold component reaches a steady level after fewer than 10 spikes (Fig. 2 D, middle trace), whereas the subthreshold Na⁺ component continues to inactivate throughout the burst (Fig. 2 C), suggesting that it may require a much longer time scale—potentially, the entire interburst interval—to recover from inactivation. This reduction in the subthreshold Na⁺ current may be responsible for the bAHP observed experimentally (Fig. 1 D). More importantly, the slow, cumulative inactivation of the subthreshold inward current may be the cause for burst termination, as it can eventually tip the balance of subthreshold currents to a point where the spike threshold cannot be reached. Furthermore, if the recovery from inactivation of the subthreshold Na⁺ current is indeed slow, it may be responsible for the long duration of the interburst interval.

I_NaP recovers slowly from inactivation

To determine the rate of I_NaP recovery from inactivation, we designed the VC pulse protocol shown in Fig. 3 A and applied it to preBötC intrinsic bursters and nonbursters. The control and test pulses (100 ms) were set at –40 mV, which we verified to be the voltage where the subthreshold Na⁺ current exhibits maximum amplitude and can be optimally detected. This voltage also elicits a large transient inward current, which could be a mixture of I_NaT and a space-clamp artifact (Milescu et al., 2010a). Thus, to better isolate the persistent component, we measured I_NaP as the average current over the last 10 ms of the control or test pulses (Fig. 3 A, inset). The control and test pulses were separated by a long (1-s) inactivating pulse at +10 mV, which we found to be long enough to induce significant, although incomplete (≈50%), I_NaP inactivation. The recovery was tested at –60 mV, which is representative for the range of membrane potentials normally experienced by preBötC cells in the interburst interval, but also at –80 mV, to characterize voltage dependence. The fraction of I_NaP recovered from inactivation was calculated as the ratio between the persistent currents evoked by a test pulse and by the control pulse (Fig. 3 B).

Interestingly, the recovery time course of I_NaP is biexponential (Fig. 3 B), with time constants separated by three orders of magnitude (milliseconds versus seconds), and with no significant difference between intrinsic bursters and nonbursters. Of the total I_NaP, the fraction that recovers slowly represents ∼20%. However, relative to the fraction that actually inactivates during the 1-s-long inactivating pulse (≈50%), the slow component is much larger (approximately half). Altogether, these results confirm our prediction that I_NaP recovers very slowly from the inactivation induced by a burst, on a time scale comparable to the interburst interval (seconds). This slow increase in a small inward current may be the factor responsible for the small depolarization drift observed between bursts (Fig. 1 D, box). Even more importantly, the rate of I_NaP recovery could control bursting frequency, because the next burst cannot be initiated and sustained until enough I_NaP becomes available.

Activation and inactivation properties of I_NaP

The rate of recovery from inactivation is clearly a critical property of I_NaP, but a quantitative understanding of I_NaP-dependent bursting requires additional information on I_NaP activation and inactivation properties. The steady-state activation curve was obtained as shown in Fig. 3 C, using a depolarizing ramp protocol (33 mV/s, from –80 to –35 mV) that is slow enough to inactivate I_NaT and leave mostly I_NaP. The current value at each voltage was first baseline-subtracted and then converted to conductance, assuming a linear current–voltage (I-V) relationship and a reversal potential of +35 mV. Then, the entire curve was normalized to the conductance value at –40 mV and fitted with a Boltzmann equation to estimate the half-activation voltage (V_h) and the slope factor (k). The results show that I_NaP starts to activate at ≈–70 mV and reaches a maximum at ≈–40 mV, with no significant difference between intrinsic bursters and nonbursters, in terms of V_h and k. However, the maximum current and conductance values are approximately twice larger in bursters. This discrepancy is likely caused by a difference in conductance density, rather than cell size, as whole-cell capacitance is not significantly different between intrinsic bursters and nonbursters (Koizumi and Smith, 2008; Koizumi et al., 2013). The activation curve clearly emphasizes the subthreshold nature of I_NaP, which is turned on at more negative membrane potentials than the typical I_NaT, by as much as 25 mV. This separation allowed us to examine the time course of I_NaP activation and deactivation at subthreshold voltages, where I_NaT is not active. As shown in Fig. 3 D, we used voltage steps (100 ms) to activate the channel at different potentials (–60 to –50 mV) and deactivate it back to –80 mV. Both activation and deactivation have a single-exponential time course, with no significant difference in time constants between intrinsic bursters and nonbursters.

The steady-state inactivation (availability) curve was obtained as shown in Fig. 3 E, using voltage steps (1 s) to inactivate the channel at different potentials (–80 to +10 mV), followed by a slow depolarizing ramp (33 mV/s) to test availability. The peak current flowing during the ramp at –40 mV was plotted as a function of step voltage, and the entire curve was normalized to the value at –80 mV and fitted with a Boltzmann equation. The results show that I_NaP starts to inactivate at ≈–70 mV and reaches a plateau at ≈+10 mV, with no significant difference between intrinsic bursters and nonbursters, in terms of V_h and k. Interestingly, approximately half the current remains noninactivated at +10 mV, in agreement with the recovery from inactivation data (Fig. 3 B). It is possible that, in a limited voltage range, some of the noninactivated fraction represents contamination with the I_NaT window current. However, we could not reliably determine this, because these neurons could not be space-clamped well enough for precise measurements of I_NaT, even with the prepulse technique (Milescu et al., 2010a).

Because I_NaP recovers very slowly from inactivation (Fig. 3 B), we examined its inactivation time course as shown in Fig. 3 F, using long voltage steps (5 s) to activate and then inactivate the channel at different potentials (–40 to –20 mV). The response to the voltage step is a large, fast transient, followed by a slow decay to a nonzero steady-state value. Starting with the transient, the decay of the current can be explained well with a sum of three exponentials. Of these, we ascribed the slowest component to I_NaP inactivation and used it for further analysis, excluding the first 20 ms that contain the fast transient. The results show that I_NaP inactivates slowly (571.0 ± 50.9 ms at –40 mV), reaching a plateau at approximately half the initial value, in agreement with the steady-state inactivation curve (Fig. 3 E), with no significant difference in the time constant of decay between intrinsic bursters and nonbursters. However, in agreement with the steady-state activation curve (Fig. 3 C), the overall I_NaP current is approximately twice larger in the intrinsic bursters. Overall, these data clearly demonstrate the persistence of I_NaP at suprathreshold potentials, where, despite inactivation, a large fraction remains active.

A data-derived model of I_NaP

Our next step was to assemble the results presented above into a kinetic model that we could then use in DC experiments to test the role of I_NaP in bursting. Our goal was to construct a model that captures only the I_NaP component of the total TTX-sensitive Na⁺ current. Consequently, this model would not have to predict the large transient component but only the subthreshold persistent current. To formulate a model, we were guided by the experimental data shown in Fig. 3, which indicate that I_NaP has voltage-dependent steady-state activation and inactivation, fast activation and deactivation kinetics, slow inactivation, and biexponential recovery from inactivation. Altogether, these kinetic properties are qualitatively similar to those exhibited by the TTX-sensitive Na⁺ current previously recorded and characterized by us in raphe serotonergic neurons (Milescu et al., 2010b), with the quantitative difference that I_NaP in preBötC neurons has slow inactivation (seconds), whereas the Na⁺ current in serotonergic neurons has fast inactivation (milliseconds). Thus, we chose the Markov state model shown in Fig. 4 A (Model 1), with the expectation that it has enough structural flexibility to explain our I_NaP data. Like our older model, Model 1 is based on a topology originally formulated for neuronal sodium channels (Kuo and Bean, 1994) and later expanded to explain resurgence (Raman and Bean, 2001) and long-term inactivation (Dover et al., 2010; Milescu et al., 2010b).

The kinetic parameters of Model 1 were optimized to fit the experimental data shown in Fig. 4 (B–E), as explained in Materials and methods. The solution is given in Table 1. The relatively low standard deviation values indicate that most of these parameters are well defined. As expected, the preexponential parameters that reflect slow transitions that are generally less well represented in the experimental data, such as k_ro, are also less well defined. The resulting model explains well a comprehensive set of data, including the incomplete steady-state inactivation and the biexponential recovery from inactivation. Importantly, the model also predicts well the subthreshold Na⁺ current evoked by the realistic burst waveform (Fig. 4 F), which was calculated but not included in the fit. Like the real Na⁺ current, the predicted current exhibits a similar reduction in amplitude throughout the burst.

Testing I_NaP Model 1 in computer simulations

Before using it in DC experiments, we first tested whether Model 1 is capable of sustaining oscillatory bursting behavior in previously developed and well-characterized single-compartment computational models of preBötC intrinsic bursters (Butera et al., 1999a,b), as described in Materials and methods. As shown by the simulations presented in Fig. 5, Model 1 is perfectly capable of generating voltage-dependent intrinsic oscillatory bursting, where burst initiation and termination can be effectively orchestrated by the voltage-dependent kinetic properties encapsulated in our I_NaP model.

At the beginning of a burst, the availability (Fig. 5 A, bottom graph, red trace) reaches a maximum value that depends on bursting frequency, which can be controlled via the applied current (I_app in Fig. 5 A, top trace). In this case, we defined “availability” as the fraction of channels that, on the burst time scale, are not “frozen” in the long-lived, slow-inactivation SI₁₁ or SI₁₂ states, and are thus available to conduct current. The availability decays throughout the burst and then recovers in the interburst interval, controlling the amount of I_NaP that can terminate a burst and initiate the next one, respectively. The decay and recovery proceed with different time constants at their respective membrane potentials, explaining the shorter bursts (less than a second) and longer interburst intervals (seconds). Overall, the simulated data match two experimentally observed key features: the bAHP and the slow depolarization drift in the interburst interval. Importantly, the simulations also confirm that bursting frequency can be tuned by shifting baseline voltage with applied current, a characteristic feature of preBötC intrinsic bursters (Fig. 1 C).

Testing I_NaP Model 1 in live neurons via DC

The previous test validates our I_NaP model in computer simulations of preBötC intrinsic bursters. Clearly, the I_NaP model establishes robust bursting in a reduced cellular model. However, the final verification is in live cells, where I_NaP must interact appropriately with a complex battery of insufficiently characterized currents, of which I_NaT is a prime example. Ideally, this verification would involve pharmacological block of I_NaP, followed by introduction of a model-based current, via DC (Milescu et al., 2010b). Because a completely specific blocker of I_NaP does not exist, we adopted a different strategy that takes advantage of the physiological differences between intrinsic bursters and nonbursters. Thus, as shown by our experiments here, I_NaP is expressed at twice greater densities in intrinsic bursters, relative to nonbursters, but its kinetic properties seem to be similar between the two subtypes (Fig. 3). Furthermore, it has been shown that the voltage-dependent bursting behavior of neonatal rat preBötC intrinsic bursters (Del Negro et al., 2002; Koizumi et al., 2013) can be abolished with pharmacological agents that, although not very specific, reduce I_NaP (Song et al., 1997; Koizumi and Smith, 2008). Therefore, one would expect that subtracting enough I_NaP from preBötC intrinsic bursters, via DC, would eliminate bursting. Conversely, adding enough I_NaP to nonbursters would instate rhythmic bursting.

First, we tested I_NaP injection with DC into nonbursters. As illustrated in Fig. 6 A, a preBötC nonburster is typically silent or fires isolated action potentials (not present in this example) but can switch to a mode of sustained firing upon sufficient depolarization (not depicted). However, with moderate levels of injected I_NaP (G_NaP = 1 nS), some clusters of action potentials and transient, small-amplitude depolarizations emerge (Fig. 6 B, top two traces). Increasing the injected G_NaP to 1.3 nS, which fully accounts for the measured difference in conductance between intrinsic bursters and nonbursters (average of 1.2 nS), instated robust oscillatory bursting in all tested neurons (n = 24; Fig. 6 B, bottom two traces). Overall, these induced bursters behave very similarly to intrinsic bursters, exhibiting the characteristic bAHP and slow depolarization drift in the interburst interval (see Fig. 1 D), as well as voltage-dependent bursting frequency under injected bias current (Fig. 6 C). No significant differences were observed between intrinsic bursters and Model 1–induced bursters in terms of bursting frequency, burst duration, and bAHP, as summarized in Table 2. However, the induced bursts exhibit significantly lower action potential count and intraburst spike intervals.

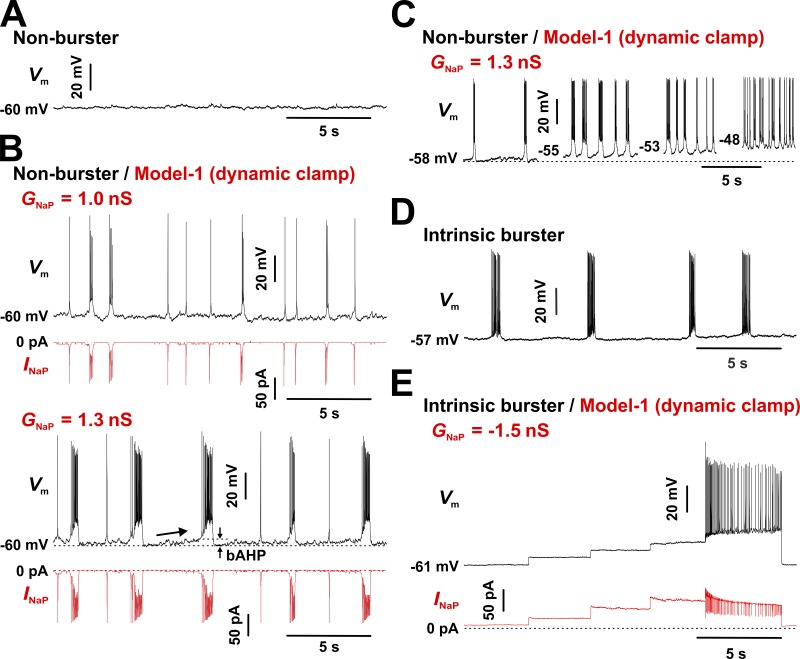
Figure 6.

Interconversion of intrinsic bursters and nonbursters by I_NaP injection via DC. I_NaP predicted by Model 1 was added to nonbursters (G_NaP > 0) or subtracted from bursters (G_NaP < 0) via DC. The recordings were obtained under bath-applied Cd²⁺ (200 µM) and CNQX (20 µM). (A) CC recording from a representative nonburster. The neuron was verified to fire repetitively when sufficiently depolarized by injecting bias current (not depicted). (B) Same cell as in A, but with I_NaP added. When sufficient I_NaP is injected (G_NaP = 1.3 nS), the neuron exhibits robust bursting, with the bAHP and the interburst depolarization drift (arrow) characteristic of intrinsic bursters (Fig. 1 D). (C) Bursting frequency depends on baseline membrane potential (changed via depolarizing bias current, not depicted), a behavior typical of intrinsic bursters. A similar outcome was observed in all tested neurons (n = 24). The statistics for measured parameters characterizing oscillatory bursting are given in Table 2. (D) CC recording from a representative intrinsic burster. The neuron was verified to have the typical voltage-dependent bursting frequency (data not shown), as illustrated in Fig. 1 D. (E) Same cell as in D, but with I_NaP subtracted. The step changes in membrane potential V_m and I_NaP reflect depolarizing bias current steps of 5–10 pA. I_NaP subtraction eliminates the ability to generate bursting activity, but the neuron can fire repetitively when sufficiently depolarized. A similar outcome was observed in all tested neurons (n = 7).

Table 2. Bursting statistics: Comparison between preBötC intrinsic bursters and Model 1-induced bursters.

Neuron type	Burst frequency (Hz)	bAHP amplitude (mV)	Burst duration (ms)	Action potential count	Spike interval (ms)
Model 1–induced bursters (n = 24)	0.22 ± 0.09	2.3 ± 0.5	516.3 ± 104.5	16.7 ± 3.7	33.6 ± 5.7
Natural bursters (n = 22)	0.21 ± 0.07	2.7 ± 1.4	452.1 ± 144.2	20.4 ± 5.6	23.7 ± 5.4
P value	0.36	0.17	0.098	0.006	0.0001

The recordings were obtained as described in Fig. 1 E (intrinsic bursters; n = 22) and Fig. 6 B (induced bursters; n = 24). The values were calculated by averaging over five consecutive bursts in each neuron. For induced bursters, the average G_NaP value that was required to induce rhythmic bursting with at least five action potentials per burst was 1.4 ± 0.7 nS (range: 0.5–2.7 nS). The data are mean ± SD.

Next, we tested I_NaP subtraction from intrinsic bursters. The maximum I_NaP conductance (G_NaP) that was subtracted was based on the measured difference in conductance between intrinsic bursters and nonbursters (see Fig. 3 C). As predicted, subtracting a Model 1–based I_NaP from preBötC intrinsic bursters via DC stopped spontaneous bursting. An example is shown in Fig. 6 (D and E), before and during I_NaP subtraction, respectively. Because the I_NaP subtraction also caused a small membrane hyperpolarization (2–3 mV), we tested whether compensating for it with a depolarizing bias current can restore bursting. As shown in Fig. 6 E, this procedure could not reinstate oscillatory bursting at any baseline voltage, in any of the intrinsic bursters tested (n = 7). However, when enough bias current was applied, the depolarization eventually induced repetitive spiking (Fig. 6 E). This result clearly demonstrates that subtracting I_NaP via DC eliminates the intrinsic ability of these neurons to generate oscillatory bursting but does not interfere with their ability to generate individual spikes.

I_NaP slow inactivation properties play a critical role in bursting

The previous results clearly demonstrate that I_NaP plays a critical role in the oscillatory bursting activity of preBötC inspiratory neurons. In a final experiment, we tested the role of slow inactivation and recovery from inactivation, which could be key properties of I_NaP that can terminate the burst, as well as control the interburst interval, as suggested by the simulation results in Fig. 5. For this, we created Model 2 (Fig. 7 A), which has the same activation pathway as Model 1 but completely lacks inactivation. Note that the I inactivated states contribute a little to slow inactivation in Model 1, and thus were removed together with the SI states. The parameters of this model were adjusted to match the steady-state activation curve (Fig. 7 B) and the time course of activation and deactivation (Fig. 7 C), which the model explains reasonably well.

Without inactivation, we would expect Model 2 to act as a nonlinear, voltage-dependent, depolarizing conductance. It should be perfectly capable of causing a neuron to switch from silence to a pattern of sustained firing riding on top of a burst-like depolarization, but once started, it should not be able to terminate it. We tested this hypothesis by injecting I_NaP into nonbursters, first with Model 1 to determine the G_NaP value necessary to establish robust induced bursting behavior, then with Model 2. Because it lacks inactivation, Model 2 has a maximum open probability ≈30% greater than that of Model 1. Therefore, to ensure similar levels of maximum injected I_NaP between the two models, G_NaP was lowered accordingly when switching to Model 2.

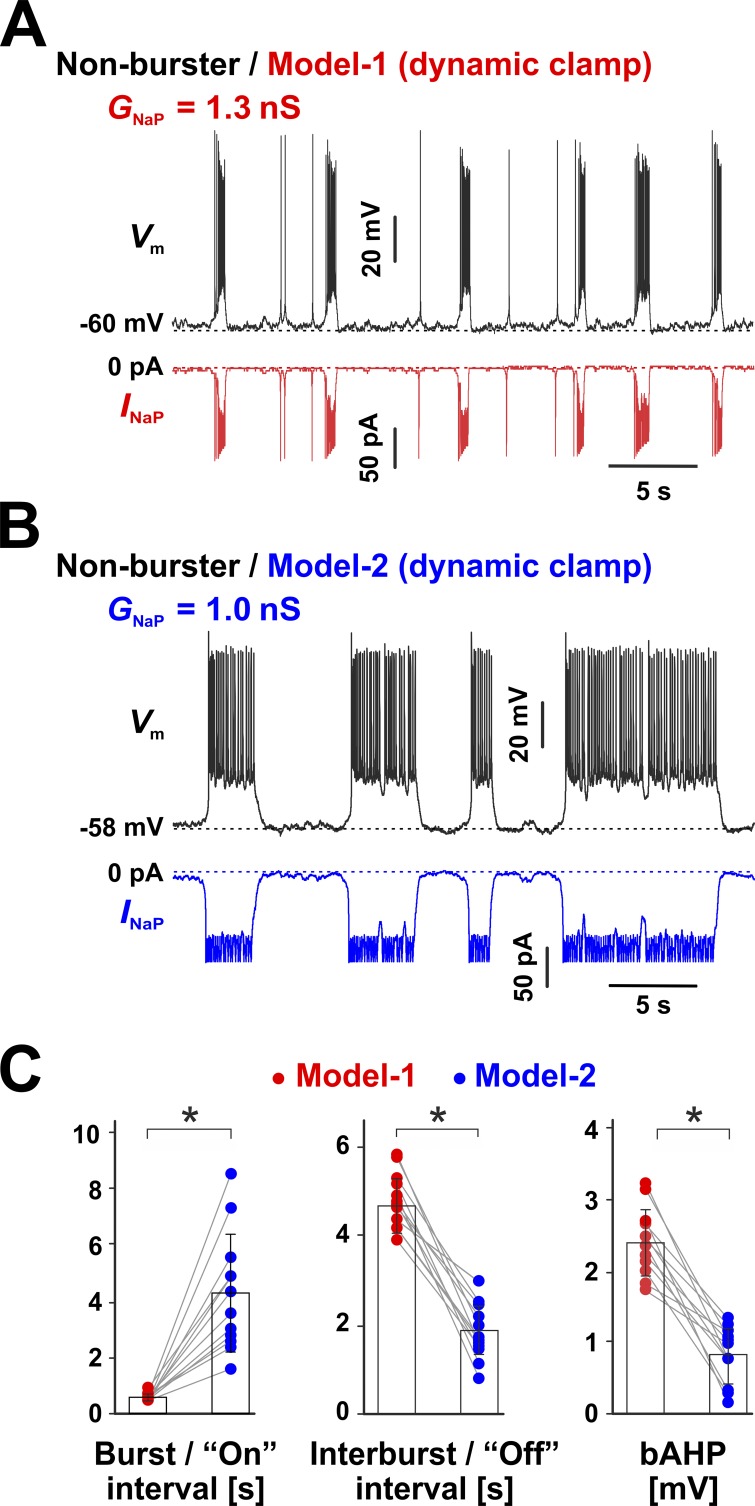
As illustrated in Fig. 8, switching from Model 1 (G_NaP = 1.3 nS) to Model 2 (G_NaP = 1.0 nS), in the same cell, marks the transition from the typical induced rhythmic bursting (Fig. 8 A) to a dramatically different firing pattern, characterized by seemingly stochastic transitions between an active phase of sustained firing and a silent phase (Fig. 8 B). As summarized in Fig. 8 C, the bursts generated with Model 1 have a reduced duration compared with the sustained firing episodes (“on” intervals) induced by Model 2, which last an order of magnitude longer and are more variable in length. In contrast, the silent phase (“off” intervals) generated by Model 2 is substantially shorter and features a reduced bAHP compared with Model 1. Overall, these results confirm our hypothesis that the slow inactivation and slow recovery from inactivation of I_NaP are the key factors that control burst termination and bursting frequency.

Figure 8.

I_NaP slow inactivation and slow recovery from inactivation are required for oscillatory bursting. (A and B) I_NaP was added to preBötC nonbursters via DC by injecting the conductance (G_NaP) predicted by Model 1 (A) or Model 2 (B). The recordings were obtained under bath-applied Cd²⁺ (200 µM) and CNQX (20 µM). (A) CC recording from a representative neuron, with I_NaP generated by Model 1. The neuron exhibits robust bursting activity, similar to intrinsic bursters. (B) Same cell as in A but with I_NaP generated by Model 2. The difference in G_NaP accounts for the difference in maximum availability between the two models. The neuron now exhibits bimodal activity, with random transitions between sustained firing and quiescence. There are no isolated action potentials during the silent phase, as observed with Model 1 (A), and the bAHP and the gradual interburst depolarization are virtually absent. (C) Statistical comparison between Model 1– and Model 2–induced firing patterns within the same cell. The “on” interval refers to the burst (514.2 ± 89.6 ms) or sustained firing (4,257.6 ± 2,109.3 ms) duration, whereas the “off” interval refers to the interburst (4,774.7 ± 618.0 ms) or quiescent (1,927.6 ± 523.2 ms) interval, for Model 1 or Model 2, respectively. The bAHP is 2.4 ± 0.5 mV for Model 1 and 0.81 ± 0.4 mV for Model 2. All three parameters are significantly different between the two models (n = 12, paired t; on interval, P = 0.00075; off interval, P = 0.00012; bAHP, P = 0.000021). The data in C are mean ± SD.

Discussion

I_NaP orchestrates rhythmic bursting

According to our results, I_NaP can regulate all essential aspects of intrinsic bursting in preBötC neurons. It does so via a simple set of kinetic properties: activation at subthreshold membrane potentials, persistence at suprathreshold potentials, and slow, voltage-dependent inactivation and recovery from inactivation (Fig. 3). Ignoring for a moment the slow inactivation and recovery, the subthreshold activation and suprathreshold persistence are two properties that effectively allow I_NaP to institute two firing modes: quiescence, when I_NaP is turned off, and sustained firing, when I_NaP is on. When I_NaP is off, the main current flowing is a K⁺-dominated leak, which holds the membrane potential at a value below the spiking threshold. When I_NaP is on, it supplies inward current that depolarizes the membrane to a value above the spiking threshold. In principle, as long as I_NaP maintains its activation state (off or on), the cell will also maintain its firing mode (quiescence or sustained firing, respectively). This scenario is captured by the experiment shown in Fig. 8, where Model 2, which lacks inactivation properties, is injected into nonbursters via DC. In this case, I_NaP is turned on and off randomly by the inevitable fluctuations in membrane potential, resulting in random transitions between quiescence and sustained firing. However, this random firing pattern should not be equated with rhythmic bursting.

To establish oscillatory bursting, an additional mechanism is required to rhythmically alternate, in a deterministic fashion, between sustained firing and quiescence. This mechanism is implemented via two key I_NaP properties: slow inactivation (Fig. 3 F) and slow recovery from inactivation (Fig. 3 B). In this context, “slow” is in reference to the burst and interburst intervals, which are both very long (0.5–5 s) relative to a single action potential (milliseconds). Interestingly, the time constant of slow inactivation is ≈600 ms, whereas the slow component of recovery has a time constant of 2.6 s, values that match the burst and the interburst intervals, respectively. Considering Model 1 (Fig. 4 A), the slow inactivation is represented by accumulation of channels into the long-lived SI₁₁ and SI₁₂ states, whereas the slow recovery corresponds to the reverse process. Importantly, this slow process is voltage dependent, favoring inactivation at the more positive membrane potentials of the burst active phase and recovery from inactivation at the more negative potentials of the interburst interval. Obviously, channels that are frozen into the SI₁₁ and SI₁₂ states cannot conduct current. Thus, the slow inactivation provides the off-switch that turns I_NaP off and terminates a burst, whereas the slow recovery from inactivation is the on-switch that initiates a burst. Both these switches are gradual, rather than instantaneous, and are on a “timer.”

During the burst, the slow inactivation caused by the overall plateau depolarization and by each action potential gradually reduces the fraction of I_NaP able to provide depolarizing current (Fig. 5). When too much I_NaP becomes unavailable, hyperpolarizing currents prevail and the burst terminates. There is now less subthreshold I_NaP available, causing a bAHP. Conversely, during the interburst interval, the slow I_NaP recovery from inactivation gradually changes the balance of net subthreshold current, creating a slow depolarization drift. When enough I_NaP has recovered, the membrane can escape the clamping effect of leak channels, and a new burst is initiated. Because these processes are voltage dependent, it is possible to have on- and off-switches with different timing characteristics, as they occur in different voltage ranges. As a first-order approximation, the time constant of slow inactivation (hundreds of milliseconds) is the parameter that controls burst duration, whereas the time constant of recovery from inactivation (seconds) controls the interburst interval. An additional control parameter is the conductance, which must be large enough to allow I_NaP to initiate and maintain a burst. However, considering that I_NaP can inactivate only down to ≈50% (Fig. 3 E), the conductance cannot be too large, otherwise the burst would not terminate and the neuron would keep firing.

I_NaP is necessary and sufficient for intrinsic bursting

Our results strongly suggest that I_NaP is necessary and sufficient to establish intrinsic rhythmic bursting activity in preBötC neurons, in neonatal rat brainstem slice preparations. We argue that I_NaP is necessary for bursting, for two simple reasons. First, the fraction of preBötC neurons that express I_NaP at lower levels do not burst intrinsically. Of course, this argument is valid only if the bursters and nonbursters differ only in their relative amount of I_NaP. We do not know if this is the case, but we do remind the reader that I_CAN, a current implicated in bursting (Thoby-Brisson and Ramirez, 2001; Peña et al., 2004; Del Negro et al., 2005; Pace et al., 2007; Rubin et al., 2009; Koizumi et al., 2018), has been silenced in our experiments (Fig. 1), together with all other Ca²⁺-related currents and synaptic transmission.

The second and stronger reason is that reducing I_NaP via DC subtraction, as shown in this study, converts intrinsic bursters into nonbursters. Certainly, the validity of this second argument is conditional on the accuracy of our I_NaP model and the subtraction technique. However, Model 1 is based on an extensive set of VC data, which it explains well, and we have shown in the past that our DC implementation is a powerful and precise tool for testing the mechanistic contribution of ion channels to neuronal firing (Milescu et al., 2008, 2010b).

We further argue that I_NaP is sufficient for rhythmic bursting because adding I_NaP to nonbursters, via DC, is enough to convert them to a firing mode of rhythmic bursting that closely resembles the activity of intrinsic bursters (Table 2). Again, this is true with synaptic transmission and Ca²⁺-related currents, including I_CAN, silenced. It is possible that the battery of ionic currents expressed in preBötC bursting neurons is specifically tuned for I_NaP-dependent bursting. However, the same is not necessarily true of nonbursters, which makes it even more remarkable that our I_NaP model cooperates so well with the other currents in these cells. Furthermore, as we show here with computer simulations (Fig. 5), adding our data-derived I_NaP model to a very simple computational neuronal model is sufficient to enable intrinsic, voltage-dependent bursting.

I_NaP kinetic model

The Markov model developed here (Model 1) explains well all the kinetic properties of I_NaP in preBötC neurons (Fig. 4), inasmuch as I_NaP could be isolated from the I_NaT and all the other currents in the cell. However, we reemphasize that this model is not meant to describe the whole kinetic mechanism of a distinct channel (Aldrich et al., 1983), but rather a subset of kinetic features of the Nav channels expressed in preBötC neurons. Nevertheless, we based Model 1 on an allosteric model previously developed for Nav channels in mammalian neurons (Kuo and Bean, 1994; Taddese and Bean, 2002), with the difference that we shortened the activation pathway and added two additional inactivated states, SI₁₁ and SI₁₂. As noted earlier, these two states are critical features that allowed us to explain the incomplete steady-state inactivation and the two components in the time course of recovery from inactivation.

Why not make a comprehensive Nav model that explains both the transient and the persistent components, and use that model in DC experiments? We initially pursued this idea but found that the preBötC cells cannot be space-clamped effectively in the brain slice preparation, even with the prepulse technique (Milescu et al., 2010a), which makes it difficult to describe with enough precision the fast, transient currents. In contrast, the much slower persistent current can be well isolated and resolved. Furthermore, having a separate model for I_NaP is actually convenient. By isolating and characterizing the persistent component, we can easily design DC experiments or simulations to test how different I_NaP properties contribute to neuronal firing, as we have done here. In contrast, a larger, more comprehensive Nav model would be more difficult to tweak, to test hypotheses.

How applicable is our model to experimental results from kinetic analyses of I_NaP in other neurons? Overall, the kinetic properties of I_NaP shown here are consistent with previous studies conducted in various types of neurons (French et al., 1990; Fleidervish et al., 1996; Kay et al., 1998; Magistretti and Alonso, 1999; Aracri et al., 2006; Magistretti et al., 2006; van Drongelen et al., 2006; Carter et al., 2012; Park et al., 2013). The rather surprising incomplete steady-state inactivation (Fig. 3 E) appears to be a consistent observation (French et al., 1990; Fleidervish et al., 1996; Kay et al., 1998; Aracri et al., 2006), although some neurons show complete I_NaP inactivation after a conditioning pulse of 10–15 s (Magistretti and Alonso, 1999; van Drongelen et al., 2006). The slow recovery from inactivation of I_NaP has also been demonstrated, using depolarizing ramp protocols (Fleidervish et al., 1996; Magistretti and Alonso, 1999; Aracri et al., 2006; Carter et al., 2012). However, we are not aware of any study that captured both the slow and the fast components of recovery from inactivation, as we have done here.

Interestingly, the biexponential recovery of I_NaP is reminiscent of the long-term inactivation (LTI) property of Nav channels, which has been described in various experiments from multiple neuronal types (Colbert et al., 1997; Jung et al., 1997; Mickus et al., 1999; Milescu et al., 2010b; Venkatesan et al., 2014) and has been explained as the open-state block caused by a regulatory factor (Goetz et al., 2009; Dover et al., 2010). LTI can be modeled well by connecting an additional inactivated state to the open state (Goldfarb et al., 2007; Dover et al., 2010; Milescu et al., 2010b), similar to what we have done here with the SI states in Model 1. Accumulation into this inactivated state is fast (milliseconds) during the brief depolarization of an action potential, whereas depletion is slow (hundreds of milliseconds) when the membrane is hyperpolarized during the interspike interval. In raphe serotonergic neurons, for example, the LTI mechanism establishes a pattern of spontaneous spiking at low frequencies (1–5 Hz), by regulating the amount of subthreshold Nav current that controls the spiking frequency (Milescu et al., 2010b). Although the preBötC bursters implement a very different firing pattern, they also rely on the slow recovery from inactivation of a subthreshold current, individually described here as I_NaP, to regulate their very slow bursting activity (0.1–0.5 Hz).

Physiological implications

The preBötC contains essential circuits for generating the normal respiratory rhythm, as well as gasping, which is a vital resuscitation mode of respiratory rhythm in response to hypoxia. These functions are blunted in vivo by targeted deletions (Gray et al., 2001; Wenninger et al., 2004; McKay and Feldman, 2008) or in vitro by pharmacological manipulation (Tryba et al., 2006) of preBötC neurons. Rhythmogenesis has been proposed to rely on both I_NaP-dependent and Ca²⁺-dependent cellular bursting mechanisms (Smith et al., 2007; Del Negro and Hayes, 2008; Rubin et al., 2009; Del Negro et al., 2010; Jasinski et al., 2013) in the isolated preBötC network in vitro, whereas in situ and in vivo studies consistently indicate that gasping relies solely on I_NaP-dependent bursting mechanisms (Aldrich et al., 1983; Ramirez et al., 2004; Paton et al., 2006; Paton and St.-John, 2007; Peña, 2008; St.-John et al., 2009). Furthermore, cellular hypoxia has been shown to augment the I_NaP expressed in preBötC neurons (Koizumi and Smith, 2008; Fu et al., 2017), as well as in other cell types (Ju et al., 1996), thus increasing the “drive” to breathe when oxygen supply is low. The dysfunction of this gasping behavior is proposed to underlie life-critical conditions such as sudden infant death syndrome (Poets et al., 1999; Leiter and Böhm, 2007).

Our study brings a better understanding of I_NaP kinetics and I_NaP-dependent bursting, which play central roles in these vital brain functions. At the molecular level, we now have a data-based, quantitative description of the kinetic properties of I_NaP, a current not only critical for respiratory-related bursting activity, but also responsible for shaping the firing patterns of many types of neurons. At the cellular level, we have advanced our understanding of the quantitative relationships between the properties of I_NaP and the mechanism of oscillatory bursting in preBötC respiratory neurons. I_NaP is ubiquitously expressed among these neurons, in both intrinsic bursters and nonbursters (Del Negro et al., 2002; Koizumi and Smith, 2008), especially within the critical excitatory glutamatergic neurons (Koizumi et al., 2013, 2016). Current models for respiratory rhythm generation incorporate I_NaP in these preBötC excitatory neurons (e.g., Butera et al., 1999a,b; Smith et al., 2007; Rubin et al., 2009; Jasinski et al., 2013; Bacak et al., 2016), where the kinetic properties of slow inactivation and slow recovery from inactivation of I_NaP have been assumed but not determined experimentally. We have quantified these properties here and thus have validated the fundamental premise that the slow inactivation and recovery from inactivation of I_NaP play a basic role in establishing oscillatory bursting.

Finally, at the network level, we have a better understanding of the molecular factors that could control the activity of circuits in the preBötC. Importantly, we show that the amount of I_NaP in bursters is about twice as large as in nonbursters, but the kinetic properties of I_NaP are similar between the two populations. Thus, if preBötC network activity is shaped by the fraction of intrinsic bursters (Purvis et al., 2007; Rybak et al., 2014), the network could be efficiently regulated via the I_NaP amplitude, which appears to be the key factor that determines the intrinsic bursting capability. Furthermore, even though nonbursters lack sufficient I_NaP to intrinsically initiate burst firing, the I_NaP inactivation and recovery properties may nonetheless influence their bursting behavior by promoting burst synchronization and termination when these cells are driven by synaptic inputs. Indeed, these cellular-level voltage-dependent properties of I_NaP are proposed to enable multiple rhythmogenic mechanisms and their dynamic features at the network level (e.g., Smith et al., 2007; Rubin et al., 2009). Accordingly, I_NaP may play yet another important role in orchestrating neuron population-level oscillatory bursting, as has been theoretically demonstrated by modeling studies (Butera et al., 1999a,b; Purvis et al., 2007; Rybak et al., 2014; Bacak et al., 2016).