Characterizing synchrony patterns across cognitive task stages of associative recognition memory

Abstract

Numerous studies seek to understand the role of oscillatory synchronization in cognition. This problem is particularly challenging in the context of complex cognitive behavior, which consists of a sequence of processing steps with uncertain duration. In this study, we analyzed oscillatory connectivity measures in time windows that previous computational models had associated with a specific sequence of processing steps in an associative memory recognition task (visual encoding, familiarity, memory retrieval, decision making, and motor response). The timing of these processing steps was estimated on a single‐trial basis with a novel hidden semi‐Markov model multivariate pattern analysis (HSMM‐MVPA) method. We show that different processing stages are associated with specific patterns of oscillatory connectivity. Visual encoding is characterized by a dense network connecting frontal, posterior, and temporal areas as well as frontal and occipital phase locking in the 4–9 Hz theta band. Familiarity is associated with frontal phase locking in the 9–14 Hz alpha band. Decision making is associated with frontal and temporo‐central interhemispheric connections in the alpha band. During decision making, a second network in the theta band that connects left‐temporal, central, and occipital areas bears similarity to the neural signature for preparing a motor response. A similar theta band network is also present during the motor response, with additionally alpha band connectivity between right‐temporal and posterior areas. This demonstrates that the processing stages discovered with the HSMM‐MVPA method are indeed linked to distinct synchronization patterns, leading to a closer understanding of the functional role of oscillations in cognition.

Introduction

Understanding the role of neural oscillations in cognition is a topic attracting growing interest. Neural oscillations are thought to provide a mechanism for the coordination and communication between different brain areas (Varela et al., 2001; Fries, 2015), which is required for controlled cognition. In addition, oscillations are thought to help to create synchronized time windows for neural computations in functionally specialized brain areas (Hanslmayr et al., 2011; Klimesch, 2012). In humans, neural oscillations can be measured non‐invasively with electroencephalography (EEG) and magnetoencephalography (MEG). EEG oscillations are mainly characterized in terms of mean power, phase locking across trials, and phase synchrony between pairs of electrodes—we will refer to the latter as connectivity in this article.

Connectivity analyses are often performed across trials on a sample‐by‐sample basis. This is problematic because across‐trials measurements (e.g., ERPs, phase locking, phase connectivity) are very sensitive to temporal jitter in the onset of the relevant cognitive events. Trials can typically only be reliably time‐locked either to the onsets of the trials or to the response to the stimulus. Consequently, examining time‐locked patterns of activity has given us valuable information about cognitive processes around the onset of a trial such as attention or visual perception (e.g., Hillyard & Anllo‐Vento, 1998), or the processes involved in generating decisions (e.g., van Vugt et al., 2014). However, the duration of cognitive processes varies between trials and subjects, which imply that cognitive processes further away from trial onset or response (e.g., memory retrieval) are harder to analyze. If it were possible to estimate the onset of such cognitive processes, we could time lock the data to these onsets and thereby minimize the impact of temporal jitter.

There have been various approaches to decompose the continuous EEG time series into a series of quasi‐stable stages. For example, Lehmann (1990) decomposes the EEG into ‘microstates’ with durations of 80 to 120 milliseconds, and some of these microstates have been linked to global mental states such as ‘abstract thought’ and ‘visual imagery’. Others have used hidden Markov models (HMMs) to identify stable states purely on the basis of the EEG signal during a resting state, not related to a specific cognitive task (Baker et al., 2014; Vidaurre et al., 2016). They showed that the different states had specific connectivity patterns and spectral content, but did not link that to any cognitive process.

Anderson et al. (2016) merged a more detailed understanding of cognitive stages, or processes, with hidden semi‐Markov models. Specifically, they proposed a method that identifies the onset of cognitive task stages. Their method combines multivariate pattern analysis with hidden semi‐Markov models (HSMM‐MVPA) to identify the onset of cognitive stages in EEG data on a trial‐by‐trial basis by looking for either positive deflection or negative deflection in the EEG signal that signify the onset of each stage. Thus, this allows for parsing each trial into time windows corresponding to specific cognitive stages (e.g., visual processing, memory retrieval). Time windows with identical cognitive stages can be time‐locked together across trials, such that temporal jitter between trials and subjects is minimized. By examining the connectivity networks in each time window, one can then link that window's cognitive operation to a pattern of synchrony, and thereby improve our understanding of the functional role of connectivity networks in cognition.

In this article, we demonstrate how the HSMM‐MVPA method can be used to relate the cognitive stages of an associative recognition memory task identified in a cognitive model of this task to distinct phase connectivity networks. Next, we introduce the HSMM‐MVPA method followed by a focused review of previous literature on connectivity networks associated with cognitive functions, and an outline of our hypothesis.

The HSMM‐MVPA method

The HSMM‐MVPA method relies on the assumption that onsets of cognitive stages produce localized phasic neuronal activity, which adds to the ongoing neural oscillations. This assumption is based on the classical theory of how EEG evoked responses are generated (Shah et al., 2004). This phasic neural activity produces a deflection in the EEG if the concentration of neural activity in a brain region is large enough to stand out from the background neural activity. This theory is often contrasted with a second theory that states that the onset of cognitive stages produce a phase reset at a certain frequency band instead of an evoked response (Başar, 1980; Makeig et al., 2002). Nevertheless, simulation studies have shown that both theories produce similar deflections in the EEG signal (Yeung et al., 2004, 2007).

Based on this idea, Anderson et al. (2016; Borst & Anderson, 2015) developed the HSMM‐MVPA method for EEG. In contrast to traditional evoked response studies, in which trials are averaged to obtain evoked brain activity, the HSMM‐MVPA method uses the topographical properties of all trials and subjects in order to estimate the parameters of a hidden process underlying all trials. This hidden process is supposed to reflect cognitive processing and is characterized as a succession of deflections in the EEG (either positive or negative), which are separated in time and spatially localized.

HSMM‐MVPA uses the expectation maximization algorithm of HSMM (Yu, 2010) to find the most likely locations and amplitudes of the deflections on each trial. The search space is constrained by a few parameters defined beforehand, such as the number of cognitive stages in a trial. In addition to estimating the underlying general process, the HSMM‐MVPA produces for each trial a probability distribution for the location of the onset of each cognitive stage.

Anderson et al. (2016) evaluated the HSMM‐MVPA method on EEG data from an associative recognition memory task, a Sternberg working memory task, as well as synthetic EEG data. Importantly, each of the HSMM‐MVPA stages was related to specific cognitive functions by means of cognitive models of the tasks for associative recognition memory (Anderson & Reder, 1999; Yonelinas, 2002; Schneider & Anderson, 2012), and for the Sternberg working memory task (Sternberg, 1966, 1969; Anderson et al., 1998; Jacobs et al., 2006). Anderson et al. (2016) observed good agreement between the number of cognitive stages in the cognitive models and the results of their respective HSMM‐MVPA analyses. In addition, the duration of the discovered cognitive stages of both tasks varied with experimental condition in the ways predicted by the cognitive models (e.g., a discovered recollection stage was longer for items that were harder to retrieve from memory according to the model).

Although the HSMM‐MVPA states were related to specific cognitive functions, the authors did not examine whether they were associated with distinct connectivity networks (of the type that was examined by Vidaurre et al., 2016). In this study, our aim was to examine whether the HSMM‐MVPA stages are associated with consistent connectivity patterns and to assess whether the observed connectivity patterns are consistent with functions ascribed to these networks in the literature.

Cognitive functions associated with specific connectivity networks

The frequency bands that are most relevant to associative recognition memory are 4–9 Hz theta and 9–14 Hz alpha oscillations. The literature on the functions of alpha and theta connectivity networks in cognition is relatively varied. Fronto‐parietal theta synchrony has been associated with learning novel finger movements (Sauseng et al., 2007), subtraction (Mizuhara & Yamaguchi, 2007), maintenance of memories (Sauseng et al., 2004; Düzel et al., 2010), as well as memory span (Kopp et al., 2006) and executive functions more generally (Sauseng et al., 2004, 2006; similar to); cf. the fronto‐parietal network in fMRI, (Cole & Schneider, 2007; Dosenbach et al., 2007; Vincent et al., 2008; Borst & Anderson, 2013).

Longer range fronto‐posterior connectivity in the theta band has been more specifically related to memory retention (Sarnthein et al., 1998; Sauseng et al., 2004), and successful memory encoding (Weiss & Rappelsberger, 2000; Summerfield & Mangels, 2005). In addition, fronto‐posterior connectivity after a person has made their response has been associated with adjusting cognitive control (Cavanagh & Frank, 2014). Fronto‐parietal–occipital connectivity has been associated with cognitive ability across participants in tasks ranging from semantic grouping to mental rotation (Anokhin et al., 1999). Connectivity of temporal regions with frontal cortex has been associated with binding information between stimulus modalities while connectivity with occipital regions has been related to maintaining relational information (Düzel et al., 2010).

The literature on the role of alpha connectivity in cognition is also quite heterogeneous. Fronto‐parietal alpha oscillations have been associated with sustained attention (Clayton et al., 2015), but also with working memory load (Hanslmayr et al., 2011) and with the recognition of words (Klimesch et al., 2010). Even longer range anterior–posterior alpha connectivity has been associated with manipulating information (Klimesch et al., 2008), dealing with conflicting information, and semantic encoding (Klimesch et al., 2008). The gradual construction of a story has also been associated with fronto‐posterior alpha connectivity, but in that case connectivity was restricted to the left hemisphere (Kujala et al., 2007). In the alpha band, interhemispheric coherence has been associated with functions such as recognition memory (Klimesch et al., 2010), and object recognition (Mima et al., 2001). When interhemispheric connectivity occurs over sensory‐motor areas, it has been well established to play a role in the successful execution of sensory‐motor tasks (Classen et al., 1998; Andres & Gerloff, 1999; Hummel & Gerloff, 2005).

From the amalgamate of findings discussed above, it is clear that a comprehensive theory of the role of oscillatory connectivity in cognition is still lacking. Previous work suggests that the associative recognition memory task consists of six cognitive stages (Borst & Anderson, 2015; Anderson et al., 2016). The first and second stages reflect visual perception and encoding the words on the screen. Our literature review suggests that this may be associated with fronto‐posterior theta connectivity (Sarnthein et al., 1998; Summerfield & Mangels, 2005). The third stage was hypothesized to be a combination of encoding the second word and assessing the familiarity of the words, and the fourth stage is associated with memory retrieval. Both stages may manifest as fronto‐posterior theta connectivity as well, although no scalp EEG studies have so far specifically focused on memory retrieval‐related connectivity to our knowledge. In the fifth task stage, the perceived information from stage two is combined with retrieved information from stage four and this drives a decision‐making process. This suggests that this stage may be associated with theta connectivity between fronto‐temporal areas (Wu et al., 2007). The last stage, stage six, is the response stage, which may be associated with interhemispheric connectivity in the alpha band over motor cortex (Classen et al., 1998; Andres & Gerloff, 1999).

Materials and methods

We examined patterns of phase connectivity, phase locking, and oscillatory power during different events on the stages indicated by the HSMM‐MVPA method of an associative recognition memory task. In this task, participants learn a set of 32 pairs of words and subsequently are asked in a testing session whether a presented pair of words is identical to one of the studied word pairs. These data were collected and first reported in a study by Borst et al. (2013).

Participants

Data from twenty subjects reported in the original study (Borst et al., 2013) were used in the current analysis. The group consisted of 11 women and 9 men, with ages ranging from 18 to 40 years and a mean age of 26 years. All subjects were right‐handed, and none of them reported a history of cognitive impairment. Written informed consent as approved by the Institutional Review Board at Carnegie Mellon University was obtained before the experiment.

Task procedure

A timeline of a trial during the testing session is shown in Fig. 1. Each trial in the test period began with a fixation cross for a random time interval between 400 and 600 msec. Next, a probe pair of words appeared on the center of the screen. Subjects were asked to press a key indicating whether they had learned the probe or not. All subjects responded with their right hand, and they were instructed to respond both quickly and accurately. An accuracy feedback indicator was shown for 1000 msec just after the subjects' responses. A blank screen followed for 500 msec, after which the next trial began. Each subject was presented with 416 trials with learned pairs of words and 416 trials with re‐paired pairs of words. Two manipulations in the original experiment—fan and word length—are irrelevant for this study, so they will be ignored. Additionally, in the original study, subjects were presented with 208 trials with new pairs of words. Trials with new pairs were not included in our analyses. We refer the reader to the original paper for further details on the experimental procedure.

Figure 1.

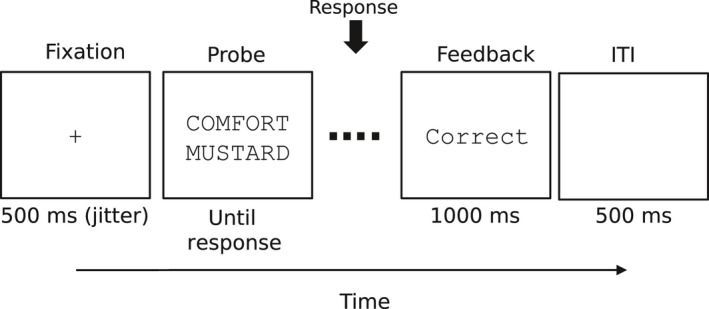
Timeline of a trial during the test phase of the associative memory recognition task. ITI stands for intertrial interval.

EEG measurements

EEG measurements took place inside an electromagnetically shielded chamber. Test trials were presented on a CRT monitor situated at 60 cm from the subjects outside of the shielded chamber. EEG data were measured from 32 Ag‐AgCl sintered electrodes (10–20 system). Reference electrodes were placed over the right and left mastoids. Bipolar montages were used to record vertical and horizontal eye movements. Scalp EEG recordings were algebraically re‐referenced to the average of both mastoid electrodes. All signals were sampled at 250 Hz with a band‐pass filter between 0.1 and 70 Hz and amplified by a Neuroscan bioamplification system (Neuroscan, Inc., Sterling, USA). Electrode impedances were kept below 5 kΩ.

EEG pre‐processing

The initial pre‐processing steps were identical to the pre‐processing carried out in Borst et al. (2013). First, visual inspection of EEG data was performed to remove artifacts. Next, EEG was decomposed into independent components with the infomax algorithm implemented in EEGLAB software (Delorme & Makeig, 2004). Independent components were visually inspected, and those components identified as blinks were removed. Subsequent pre‐processing steps were specific to our study. EEG was down sampled to 100 Hz and band‐pass filtered between 1 and 35 Hz. The band‐pass filter was designed with the default parameters in the iirfilt plug‐in for EEGLAB. The iirfilt plug‐in creates by default a causal IIR Elliptic filter. The default settings designed an order ten low‐pass filter with transition band of 1 Hz, and an order six high‐pass filter with transition band of 0.3 Hz. The amplitude ripple at passband frequencies was lower than 0.0025 dB. The amplitude at stop‐band frequencies was attenuated at least by a factor of 40 dB. The filter was passed twice in opposite directions to secure zero‐phase shift. After band‐pass filtering, linear trends were removed on a single‐trial basis by fitting a straight line and subtracting it. We down sampled the data to 100 Hz to reduce the amount of data points, so the computation of the HSMM‐MVPA was quicker. We filtered out frequencies below 1 Hz and de‐trended singles trials to fulfill the assumption of the HSMM‐MVPA that the time interval between the onsets of two consecutive cognitive stages has a mean amplitude of zero (see the next subsection for a further explanation). We observed that lower cutoff frequencies compromised this assumption and the output of the HSMM‐MVPA. After removal of artifacts and filtering, incomplete trials due to artifact rejection as well as those with amplitudes outside the range between −80 μV and +80 μV were excluded. For the segmentation of EEG into cognitive stages, trials were bounded by stimulus onset and the response. Trials with incorrect responses were removed, as well as those with responses more than three standard deviations away from the mean response time per participant and condition. Following Borst et al. (2013), any remaining trials with responses longer than 3000 msec were excluded. In total, 8.25% trials were excluded from the analysis.

For the analysis of EEG oscillations, continuous EEG data were band‐pass‐filtered in theta, alpha, and beta frequency bands (i.e., θ: 4–9 Hz, α: 9–15 Hz, and β: 15–30 Hz). The filters were designed and applied with the plug‐in iirfilt from EEGLAB with default parameters. The three filters have 1‐Hz transition band at both cutoff frequencies. The theta band filter has order of seven for the low cutoff frequency and order of nine for the high cutoff frequency. Alpha and beta band filters have order nine and ten for the low cutoff and high cutoff frequencies, respectively. These frequency‐transformed data were segmented from 300 msec before stimulus onset to the stimulus response. A baseline period before stimulus onset was added to allow us to remove background activity from task activity in subsequent processing steps. EEG processing was carried out with EEGLAB software as well as custom‐written MATLAB scripts.

Segmenting EEG into cognitive stages

The segmentation of EEG trials into cognitive stages was carried out by means of the HSMM‐MVPA method proposed by Anderson et al. (2016). Before applying HSMM‐MVPA, a principal component analysis (PCA) was performed with a unique covariance matrix on the basis of the combined data from all subjects. The covariance matrices of each trial on each subject were averaged together to compute the principal components (Cohen, 2014). Because all subjects are included in the computation of the PCA, the principal components (PCs) match across subjects and a single model for all subjects can be created. Following Anderson et al. (2016), the first ten PCs, which account for more than 95% of the variance in the data, were preserved for the HSMM‐MVPA analysis. Each of these PCs in a trial was z‐scored to ensure that each trial had a mean of zero and a variance of one.

The HSMM‐MVPA finds the most likely partition of each trial into a certain number of cognitive stages given an underlying model common to all trials. This underlying model is represented schematically in Fig. 2. In this model, each cognitive stage is assumed to start with a 50‐msec deflection either entirely positive or negative. This deflection is hypothesized by Anderson et al. (2016) to reflect a burst of phasic neural activity at the onset of a cognitive event (Shah et al., 2004), as described in the Introduction. The amplitude of the deflection is estimated by the HSMM‐MVPA. After each deflection, the neural activity is assumed to return to background oscillatory activity with zero‐mean amplitude until the next onset of a cognitive stage. The time interval between two onsets is variable. Anderson et al. (2016) assumed that this time interval can be modeled with a gamma distribution with shape parameter equal to two and free scale parameter (Fig. 2, below). The scale parameter will be estimated by the HSMM‐MVPA. In short, each cognitive stage in the model—except the first stage and the last stage—consists of a 50‐msec deflection and a zero‐mean amplitude interval whose duration is given by a gamma distribution.

Figure 2.

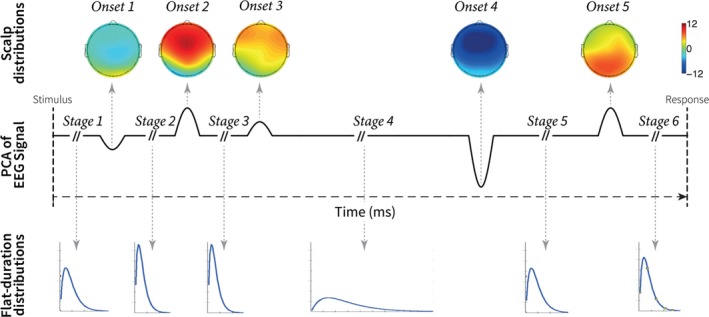
Schematic representation of the process underlying all trials estimated by the HSMM‐MVPA method. The solid black line represents the model of one principal component of one EEG trial. This model combines six stages with a mean of zero and five onsets of 50 msec long. The topographical EEG maps on the top are the amplitude of the deflections at the onsets estimated by the HSMM‐MVPA. The blue lines at the bottom represent the gamma distributions estimated by the HSMM‐MVPA. The gamma distributions determine the duration of the stages. This figure has been adapted with permission from Anderson et al. (2016). PCA stands for principal component analysis. EEG stands for electroencephalogram.

The first and the last stage are described by a slightly different model. The first stage does not include a deflection, yet its zero‐mean amplitude interval represents the time for the visual stimulus to reach cortical areas. The last stage is bound by the response to the stimulus, although the response does not necessarily represent the end of the ongoing cognitive process. We set the number of cognitive stages in the HSMM‐MVPA analysis to six; hence, there are five onsets of stages. This choice was based on computational cognitive models of the same cognitive task (Borst & Anderson, 2015; Anderson et al., 2016). In this case, the model underlying all trials is a sequence alternating zero‐mean amplitude intervals with different durations (S _i) and 50‐msec onsets (O _i) as it follows: S ₁  + O ₂  + S ₂  + O ₃  + S ₃  + O ₄  + S ₄  + O ₅  + S ₅  + O ₆  + S ₆ = Trial duration (i.e., time between stimulus onset and response). The same model of a trial is present in all PCs. The duration of each stage on a trial is the same for all PCs on the trial, but the amplitude of the deflections at the onsets may be different for each PC (Fig. 2, topology maps in top row).

HSMMs allow to model systems that have a defined set of hidden states. These systems remain in a hidden state for a certain time, and transitions between hidden states with known probabilities. The hidden states cannot be measured (hence the term ‘hidden’), however, the probability of an indirect observation given that the system is in a specific hidden state is known. When the transition probabilities and the probability of observations given certain states are unknown (like in our case), a most likely solution can be estimated from the sequence of observations with the expectation–maximization (EM) algorithm associated with HSMM (Yu, 2010). In our case, the observations are the PCs, and the model has six hidden states—the cognitive stages. The unknowns to be found are the stage durations S _i, and the amplitude of the onsets' deflection O _i. The EM algorithm estimates iteratively the gamma scale parameter for the stage durations S _i and the amplitude of the onsets' deflection O _i so as to maximize with a likelihood function the match between the PCs of all trials and the underlying model (i.e., the sequence of S _i and O _i). The intuition for this fitting process is that the EM algorithm moves the onset locations to all possible locations while estimating the onset amplitudes in a way that finds the onset locations and amplitudes that maximize the similarity with the empirical data (i.e., the PCs). We initialized the EM algorithm with uniform random onset amplitudes and gamma distributions with means equal to the longest trial. We performed 500 repetitions of the HSMM‐MVPA with different onset amplitudes to make sure that the EM algorithm did not converge to a sub‐optimal local maximum. We selected the repetition with the highest likelihood controlling that it was similar to solutions with close likelihoods. We refer the reader to the appendix of (Anderson et al., 2016) for a formal definition of the likelihood function in HSMM‐MVPA.

Localization of relevant cognitive events

The HSMM‐MVPA analysis yielded the amplitudes of the multidimensional deflections and the scale parameters of the gamma distributions reflecting the length of the stages. In addition, HSMM‐MVPA gave the probability distribution of the location of each cognitive stage onset on every trial. These probability distributions were used to estimate the expected location of each onset, as well as the center of each cognitive stage. The center of each cognitive stage was calculated as the middle point between two consecutive stage onsets, or the middle point between the boundary of a trial and its nearest stage onset. In this article, we refer to the onsets and the centers of cognitive stages as relevant ‘cognitive events’.

For the characterization of EEG oscillations associated with cognitive functions, we defined relevant cognitive events in a trial as 50‐msec windows centered on the onset of each cognitive stage, and 50‐msec windows around the center of each cognitive stage. Thus, cognitive events formed a sequence of eleven 50‐msec windows alternating the centers of cognitive stages and onsets of cognitive stages. The sequences always began and ended with the center of a cognitive stage. For simplicity, these relevant cognitive events will be abbreviated as S1 = stage one, onS2 =  onset of stage two, S2 =  stage two, etc. Figure 3 shows an example of an EEG trial with the probability distributions of the onsets of stages and the 50‐msec time windows of analysis.

Figure 3.

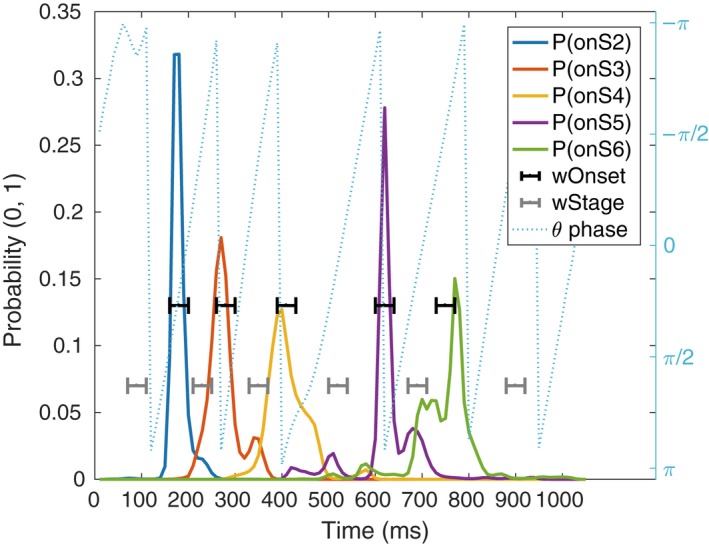
Example of one trial EEG phase (dotted, light blue), the probability distributions for the location of cognitive stages' onsets (solid lines), and the analysis windows of relevant cognitive events (brackets). The blue‐dashed line is the theta band phase during a trial in one electrode. The solid lines are the probability distributions given by the MVPA‐HSMM methods regarding the location of the onset of cognitive stages (P(onSX)). Black indicators (wOnset) show the five‐sample windows around the expected location of each onset. Similarly, gray indicators show the five‐sample windows that define the respective stages (wStage). These time windows are used to compute Power, ITPC, and dwPLI.

Given that some probability distributions of onset locations had a non‐stereotypical shape (see Figs S1 and S3 in the Supporting Information), we tried to estimate the level of uncertainty about the expected value of these probability distributions. We measured this uncertainty with two different methods. First, we used a statistical test to measure whether the probability distributions were unimodal or multimodal (Hartigan & Hartigan, 1985). The test was implemented with the R package diptest (version 0.75‐7). Second, we developed a measure of the uncertainty resulting from the probability distributions. We computed this measure of uncertainty in each probability distribution as follows (see Fig. S3 in the Supporting Information): First, we removed the onset locations (i.e., samples) with the smallest probabilities whose sum represents less than 25%. After this step, only the cores of the modes (see faded color area in Fig. S3) remain in the probability distributions. Second, the cores of the modes are normalized to have a total probability of one. Third, the cores of the modes whose area accounted for less than 25% were removed. We chose a threshold of 25% based on the exploration of multiple probability distributions. After the last step, only the cores of the most representative modes remain. Finally, we defined uncertainty as the distance between the two most extreme remaining locations (i.e., samples).

EEG oscillations

After the EEG was decomposed into theta, alpha, and beta frequency bands, the analytic signal and the phase of each frequency band were computed with the Hilbert transform. Phase was extracted with the Hilbert transform because it allowed us to precisely define the frequency of interest during band‐pass‐filtering, and its temporal resolution is the same as the EEG signal. Connectivity between pairs of electrodes across trials was assessed with the de‐biased weighted phase‐lag index (dwPLI; Vinck et al., 2011). dwPLI was chosen because it is robust against volume conductance (Cohen, 2015), and it is not biased by the number of trials. dwPLI was computed across trials for each of the five samples of a cognitive event. To obtain a robust estimate of connectivity at each relevant cognitive event, the standard deviation of the five‐dwPLI measurements in a cognitive event was subtracted from their median. This penalizes connectivity networks that are not stable along the five samples window of analysis. Robust dwPLI at each relevant cognitive event was subtracted from baseline dwPLI on each trial. Baseline dwPLI was computed as the median of the dwPLI across trials over all baseline samples.

The threshold for significant dwPLI between pairs of electrodes was determined on the basis of simulations with surrogate data. We created surrogate data representing the null hypothesis of no connectivity by making a random circular shift of the phase time series in one electrode of each pair of electrodes for each trial. Then, dwPLI was calculated in the same way as for our empirical data. The same process was repeated 200 times. The significance threshold derived from this procedure was Bonferroni‐corrected by the number of electrode pairs (i.e., 496 pairs of electrodes). dwPLI measurements from real EEG data below this 95% confidence interval were set to zero.

A global network across subjects was computed for each cognitive event. An edge between two electrodes in the global network was drawn if that edge was present in fifteen or more subjects (i.e., more than 75% of the subjects). The connectivity strength represented on each created edge was computed as the median dwPLI of the contributing subjects.

The power of each frequency band was computed as the squared modulus of the analytic signal. Power was z‐scored respect to the baseline in a single‐trial basis. Z‐scored power was first averaged across trials and then across subjects. Intertrial phase clustering (ITPC) (also known as Phase Locking Value) was calculated across trials to evaluate phase locking across trials. ITPC at cognitive events was subtracted from baseline ITPC per subject and then averaged across subjects. ITPC was considered significant if it was larger than a critical ITPC of 0.117. Critical ITPC is computed as sqrt(‐ln(p)/n) (Cohen, 2014), where n is the mean number of trials across subjects and P is a P‐value of 0.05 Bonferroni‐corrected by the number of electrodes, frequency bands, and cognitive events.

Results

Synchrony patterns were analyzed in time windows associated with cognitive events derived from the HSMM‐MVPA analysis. In total, there are eleven time windows of analysis, or cognitive events—the centers of six cognitive stages and the onset of five of these cognitive stages. According to previous works on the same task (Borst & Anderson, 2015; Borst et al., 2016), the stages should be interpreted as follows. The first two cognitive stages (i.e., S1, onS2, and S2) are associated with the visual encoding of the stimulus. The third stage is associated with a combination of encoding the second word and judging the familiarity of the encoded words. The fourth stage is the retrieval of memories. The fifth stage is the decision‐making process that determines whether the pair of words were studied together or not. Finally, in the sixth stage, a motor response is produced.

Location of the onset of cognitive stages

The first analysis step was to estimate the expected location of the onset of cognitive stages from the probability distributions given by the HSMM‐MVPA. In Fig. 4, the red dots represent the mean expected time when a cognitive stage starts (i.e., the onset) across trials and subjects. Therefore, the distance between two consecutive red dots represents the mean duration of the cognitive stage between the two onsets. The blue bars around red dots (e.g., onS1) show the standard deviation of the time when the onset of the stage occurs. Thus, the variability in stage onset is due to changes on duration of the previous stage. For example, the large standard deviation at the onset of stage five represents the variability in the duration of the stage four. The variability in duration of stage four is in agreement with the results from Anderson et al. (2016), who observed that the mean duration of the fourth stage for different manipulations differed approximately 300 ms, while the other stages varied no more than 50 ms. Similarly, the computational cognitive model of the same task implemented by Anderson et al. (2016) predicts that stage four durations are sensitive to task manipulations such as word fan and re‐pairing of word pairs. As was mentioned above, task manipulations in the original study were not studied separately in our study, so task manipulations are expressed as larger variability in stage four.

Figure 4.

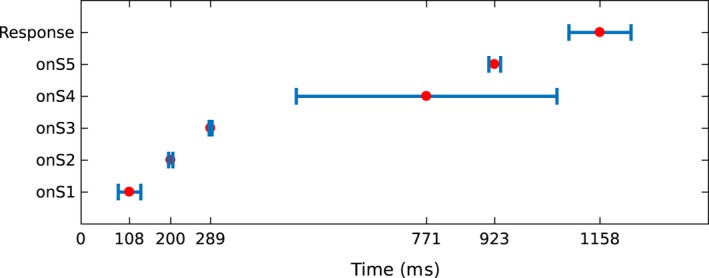
Temporal location of stage onsets in a trial. The red dot represents the mean onset location across trials and subjects. The blue bars represent the standard deviation on the location of the onset. Y‐axis labels the onset to which the red dot and standard deviation belong (onS1: onset of stage one).

Power, ITPC, and connectivity associated with cognitive stages

Next, we examined the connectivity networks in each of the cognitive stages. To do so, we used the windows defined by the HSMM‐MVPA to time lock trials and compute dwPLI, power, and ITPC. Figures 5 and 6 show the scalp profiles of grand‐averaged power, ITPC, and dwPLI. The scales are consistent across figures for each measurement. Note that the dwPLI connectivity is the same in the power and ITPC plots.

Figure 5.

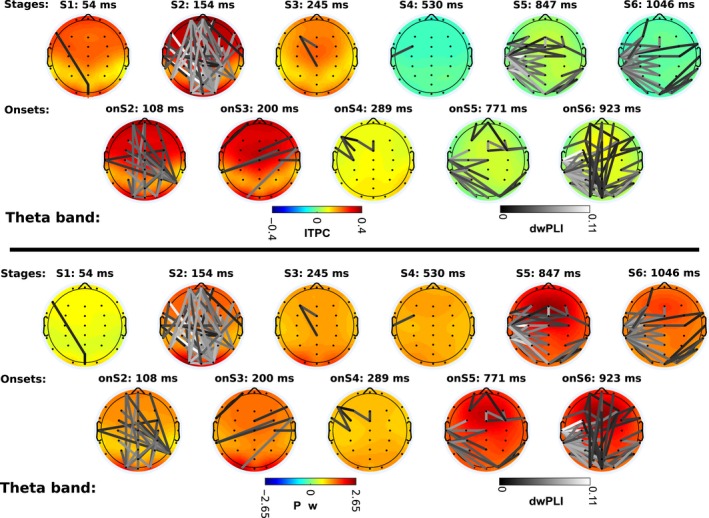
Theta band power, phase locking (ITPC: intertrial phase clustering), and phase connectivity (dwPLI: de‐biased weighted phase‐lag index). Lower panel shows the scalp profiles of grand‐averaged power across trials and subjects z‐scored respect to baseline. Upper panel shows the scalp profiles of grand‐averaged ITPC values subtracted from baseline values. dwPLI connectivity edges are superimposed on the scalp profiles on gray color scale. The color of edges depicts connectivity strength. Black color represents the lowest connectivity strength above the connectivity significance threshold; white color is the highest observed connectivity strength. dwPLI edges are the same in both panels. The mean temporal location of each scalp map is denoted on top of the map (e.g., S1: 54 ms: The stage one lays on average 54 millisecond after the onset of the trial).

Figure 6.

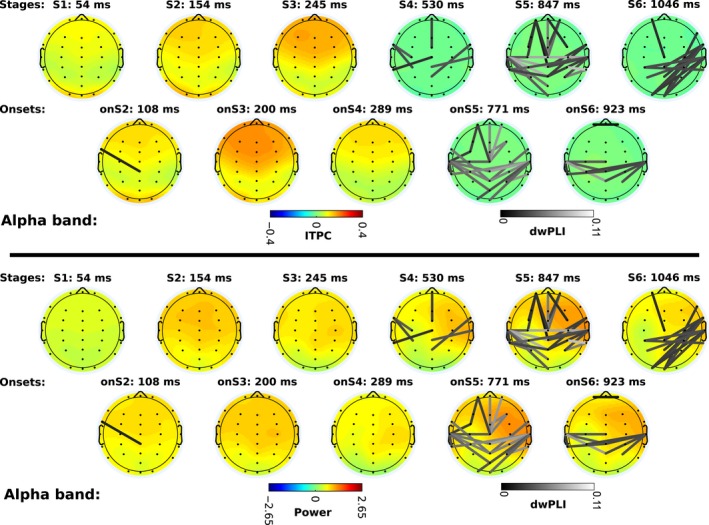
Alpha band power, phase locking (ITPC: intertrial phase clustering), and phase connectivity (dwPLI: de‐biased weighted phase‐lag index). Scalp maps and connectivity follow the same distribution as Fig. 5. To aid visual comparison, power, ITPC, and dwPLI scales are consistent in all scalps on Figs 5 and 6.

Theta band

Theta power is larger during cognitive events than at the baseline period (Fig. 6). Right after the stimuli are presented on the screen, processing of visual information starts. The first stage of visual processing shows the weakest increase in power relative to pre‐stimulus baseline. However, even though power is relatively low, ITPC is already above significance level in occipital, frontal, and central areas.

At the onset of the second stage, the encoding of visual information starts. Additionally, a connectivity network emerges connecting occipital with frontal areas and parietal with central areas. This change is accompanied by an increase in power, as well as ITPC, at occipital areas and a broad fronto‐central region. Then, during stage two (visual encoding) a dense network arises with connections between posterior, frontal, and temporal regions. ITPC and power increase again in central, pre‐frontal, and occipital regions.

At the onset of the third stage, a cognitive process of memory familiarity begins, and the previous network of visual encoding disappears (in contrast to the interpretation of Anderson et al. (2016), who assumed that stage 3 included encoding the second word). ITPC in the occipital and fronto‐central regions is reduced slightly with respect to the level of the previous event, but it is still above the critical level. Power is also reduced slightly across the whole scalp. During stage four (memory retrieval) ITPC disappears abruptly. Power is also reduced but not as abruptly as ITPC.

Theta activity remains almost unchanged until the onset of stage five (decision making), when a connectivity network emerges. This network connects occipital with left‐temporal areas, and midline electrodes with left‐temporal electrodes, as well as a small network in frontal and right‐frontal areas. Power increases globally at the onset of stage five; however, ITPC remains low over the whole scalp. During the decision‐making stage itself, connectivity between temporal and occipital areas increases further, as well as between midline electrodes and the left‐temporal region. In addition, a frontal network appears. Power increases slightly in the frontal area; however, ITPC is still low, just like at the onset of the same stage.

At the onset of the last stage, a motor response process is initiated. At this onset, the frontal network disappears, but a network between pre‐frontal and occipital areas appears. At the same time, the connections between occipital and temporal areas increase. Power remains high over the whole scalp. During the motor response stage itself, the connectivity network between pre‐frontal and occipital areas disappears. Only the connections between occipital, left‐temporal and central areas remain, while power and ITPC diminish.

In summary, two large connectivity networks appear in theta band—one fronto‐posterior network during the visual encoding, and a left‐hemisphere‐central and occipital network for the decision‐making process during which perceptual and retrieved information is integrated for the motor response. This network expands to motor response as well. ITPC is significant to the three first stages across almost the whole scalp, but it disappears in later stages. Power increases in all cognitive events with respect to baseline, with higher levels in posterior areas during visual encoding, and in frontal areas during decision making and at the onset of the motor response.

Alpha band

In the alpha band, the change of power and ITPC with respect to baseline is weaker than in the theta band. In stage one power is close to baseline levels, and ITPC increases slightly above critical ITPC. Power increases in the rest of the stages above baseline, but it does not reach a z‐score of two in any stage. ITPC increases in frontal and occipital areas during visual encoding, like in the theta band. The largest values of ITPC are observed during stage three. At the onset of the retrieval of memories (stage four) ITPC decreases, but it is still above critical ITPC; as the stage continues it decreases below critical ITPC. During the fourth stage, power in the right‐frontal area increases. The difference in power between hemispheres is maximal during the decision‐making stage (stage five).

At the onset of the decision‐making stage, the first connectivity network appears between temporal, frontal and central areas. During the stage itself more edges are incorporated to this network. At the onset of the motor response, the connections between frontal and central areas are lost, and only the network between temporal and central areas remains. During the stage of the motor response a dense network connecting the occipital, parietal, and right‐temporal areas appears.

In summary, power increases slightly with visual encoding in frontal areas and in later events it is lateralized to the right‐frontal area, although the amount of power is less than in theta band. ITPC increases with the onset of visual encoding and becomes maximal during memory retrieval in frontal areas. Connectivity networks do not emerge until the onset of decision making, at which time an interhemispheric network between predominantly temporal and parietal areas evolves along with a fronto‐central network. During motor response, a new network between right‐temporal, parietal, and occipital areas appears.

Beta band

We analyzed power, ITPC, and connectivity in the beta band in the same way as with theta and alpha bands. Beta band power fluctuations with respect to baseline were negligible in comparison with theta or alpha power fluctuations. Moreover, ITPC was non‐existent, and the same was true for connectivity (See Fig. S2 in the Supporting Information). For this reason, beta band activity is not reported here in detail. The relative absence of activity in the beta band could be related to the sensitivity of ITPC and dwPLI to time jitters across trials in combination with the short period of beta oscillations, which makes it difficult to have reliable measurements of phase. Temporal jitter issues are even more acute in the gamma frequency band, which is the reason for leaving it out of this study entirely.

Discussion

Our aim was to relate synchrony networks to different functional cognitive stages, identified by previous modeling work in an associative recognition memory task. We used the HSMM‐MVPA method to discover cognitive events on a trial‐by‐trial basis, which allowed us to find the onsets of a series of task stages. We demonstrated that particular patterns of phase locking, phase connectivity and power in the theta and alpha bands arise at each cognitive stage. The next section discusses the evolution of phase locking and phase connectivity along the cognitive stages involved in associative recognition memory—visual encoding, familiarity, memory retrieval, decision making, and motor response. It is important to note here that typically, it is assumed that even in the case of foils a memory is retrieved, which is then compared to the stimuli on the screen, and being different leads to a negative decision (recall‐to‐reject; see, e.g., Anderson & Reder, 1999; Rotello et al., 2000; Rotello & Heit, 2000; Malmberg, 2008; Schneider & Anderson, 2012). As a result, all trials in the current dataset involve the same cognitive processes, which in the case of targets leads to a positive decision and in the case of foils to a negative decision.

Functional interpretation of synchrony patterns

The analysis of EEG synchrony presented here sheds light on the dynamics of phase locking and connectivity networks and their role in cognition. Our results suggest that connectivity networks change gradually across cognitive stages, rather than sharply when a new cognitive stage starts.

Visual encoding seems to involve theta ITPC throughout all visual encoding stages including the onset of the memory retrieval. Connectivity emerges at the onset of the second visual encoding stage with long‐range frontal and posterior connections which substantially increase in number during the second stage of visual encoding. This finding is in agreement with the fronto‐posterior network observed by (Sarnthein et al., 1998) during encoding of visual information, as well as a top‐down control activation (Sauseng et al., 2006). These connections, including the occipital–temporal connections are probably related to storing the concepts related to the stimuli on the screen in a short‐term visual memory store. These networks disappear with the onset of the third stage. Anderson et al. (2016) hypothesize that the third stage is related to the visual encoding of the second word while judging the familiarity of the first word (see also Borst & Anderson, 2015; for a similar interpretation). Because the fronto‐occipital networks associated with visual encoding are present during the second stage but disappear in the third stage, our results suggest that the third stages reflect a relatively pure familiarity process that follows the encoding of both words in stage two. This is in agreement with earlier EEG correlates of the dual‐process theory of associative recognition (e.g., Rugg & Curran, 2007), and shows how these connectivity analyses improve our understanding of the discovered stages.

A slow change in connectivity networks is observed during the processes of decision making and motor response. Interestingly, the alpha and theta band show completely different topologies. On the one hand, alpha band connectivity emerges with the onset of decision making between temporal, parietal, and frontal areas. These results are in line with several previous studies. Based on a different EEG experiment, Zhang et al. (2017) hypothesized that in this stage the words that are on the screen are compared to a pair (or triplet in this experiment) retrieved from memory, word by word. Additionally, MEG data have shown that word pairs were retrieved from temporal regions and subsequently represented pre‐frontally, while the comparison itself was associated with activation in the parietal cortex (Borst et al., 2016). The process to identify pairs of words learned also seems to be in agreement with the network found by Mima et al. (2001) for object recognition. Finally, during the motor response, the interhemispheric and frontal networks are reduced to connections between the right‐temporal area with parietal and occipital areas.

On the other hand, theta band connections do not appear until the onset of the decision‐making stage. At the onset of decision making, an isolated network appears in the pre‐frontal area. This network may be related to the frontal network observed in the alpha band as well. Additionally, a network between left‐temporal, central, and occipital areas becomes visible. This network may indicate the preparation of the hand for a posterior response with the finger once the decision is taken, and perhaps a reactivation of the word pair based on the visual percepts of the words. During the stage of decision making, the pre‐frontal network disappears and more connections appear within the left hemisphere—except the pre‐frontal area—and between the occipital and the right‐temporal areas. At the onset of motor response, long‐range connections between pre‐frontal and occipital areas appear in addition to the network observed during decision making. Later, during the motor response, only the long‐range connections between frontal and posterior areas disappear. As suggested by Wu et al. (2007) the temporal–parietal networks may support the process of binding of information, while fronto‐posterior networks control the access to information in posterior areas.

In general terms, according to our review of literature on connectivity, the dense fronto‐posterior network that we observed during visual encoding may be related to top‐down control and encoding of information. The interhemispheric network and the occipito‐temporal network during decision making could be associated with the comparison of information retrieved from memory with the visual information on the screen. The long‐range connections between frontal, central, and posterior areas may indicate executive control function during the binding of information.

The HSMM‐MVPA method

We based our selection of time windows of analysis on the results of the HSMM‐MVPA method. This method assumes that at the onset of the cognitive stages there is a deflection of the EEG signal across multiple electrodes, which should also be manifest in larger power at the onset of each event relative to the period between different events. Indeed, onsets showed higher median power than stages in alpha and theta bands with a confidence interval of 95% (see Fig. S4 in the Supporting Information) Moreover, a Wilcoxon rank‐sum test indicates that these differences on power are significant (P‐value ≫ 0.01) for alpha and theta bands. In addition, the median power at onsets is higher in the theta band than in the alpha band with a 95% confidence interval and significant according to a Wilcoxon rank‐sum test. Power level can be compared across frequency bands because power was z‐scored with respect to the power at the baseline. Following the assumption made by HSMM‐MVPA, the baseline should contain only background oscillatory activity.

As the onsets are modeled as 50‐msec deflections, it would logically follow that power at the onsets in alpha band should be higher than power in theta band. Nonetheless, Anderson et al. (2016) showed on synthetic data that HSMM‐MVPA was able to recover with high accuracy onsets modeled as half‐sinus deflection lasting from 30 to 110‐msec. This means that the onsets found by HSMM‐MVPA can produce increased power in theta and alpha bands. Furthermore, we use a 50‐msec window to analyze the power. The center of this time window is estimated as the expected value of the probability distribution of the onset location. As we discussed before, the uncertainty of the HSMM‐MVPA is higher than the 50‐msec analysis window. Therefore, the peak of power at the onset might not match the center of the 50‐msec analysis window. This will introduce a bias in estimating power at the onsets—power at onsets shorter than 55‐msec (i.e., alpha band) might be underestimated because the 50‐msec analysis window captures background ongoing oscillations and not the full deflection; Onsets longer than 55‐msec (i.e., theta band) are more likely to stay within the 50‐msec window of analysis, so the power inside the window of analysis is higher.

Applying the HSMM‐MVPA to real data produced more uncertainty about the onset locations than the 140‐msec previously reported on synthetic data (Anderson et al., 2016). We tested it first by applying a test of unimodality (Hartigan & Hartigan, 1985) to the probability distributions of the onset locations. The test of unimodality reported that 66.2% of the probability distributions were not unimodal. In addition, we created a measure of uncertainty about the location of an onset (see Methods, see Fig. S3 in the Supporting Information). We concluded that 85.5% of the probability distributions (i.e., all trials times the five onsets on each trial) are within the 140‐msec uncertainty reported by Anderson et al. (2016) in synthetic data, while the remaining 14.5% of the trials present more than 140‐msec uncertainty.

Despite this uncertainty, we still observe phase connectivity and phase consistency at several cognitive events that are consistent across many subjects, suggesting that our analysis is robust enough to deal with this uncertainty. Nevertheless, uncertainty could compromise the detection of synchrony in studies with fewer trials than the current study, or in higher frequencies bands—providing a potential explanation for the lack of findings in the beta band in our study. A further argument for the robustness of this method to temporal uncertainty is the clear differences in connectivity patterns that we observed between the identified stages. As such, the current analysis lends additional credibility to the idea that the HSMM‐MVPA method identifies functionally distinct cognitive stages.

Conclusion

We have identified patterns of EEG synchrony related with specific cognitive stages in an associative recognition memory task. We have shown that combining HSMM‐MVPA with oscillatory connectivity analysis increases the capacity to characterize cognitive functions, considerably extending the applicability of this connectivity analysis. Our principled model‐based approach gives us detailed information about the cognitive operations associated with each stage, which we can then relate to the relevant connectivity pattern. This approach has shown that there is a familiarity stage between the encoding of visual information and the retrial of memories. Future studies should validate these mappings between cognitive operations and connectivity patterns in different cognitive tasks. Together, this method opens a new window to understand the dynamical interactions between brain regions in the service of complex cognitive behavior.

Conflict of interest

The authors declare no conflict of interest

Author contributions

OP involved in data analysis and wrote the article. JPB involved in support for data analysis and wrote the article. MvV involved in support for data analysis and wrote the article.

Data accessibility

No original data were reported in this article, we refer to Borst & Anderson (2015), who released the data analyzed in this article, for more information. We publish the data and the code used for this article in Figshare portal with https://doi.org/10.6084/m9.figshare.5722831.

Abbreviations

dwPLI

de‐biased weighted phase‐lag index

EEG

electroencephalogram

fMRI

functional magnetic resonance image

HMM

hidden Markov model

HSMM‐MVPA

hidden semi‐Markov model multivariate pattern analysis

ITPC

intertrial phase clustering

MEG

magnetoencephalogram

onS2

onset of stage two

onS3

onset of stage three

onS4

onset of stage four

onS5

onset of stage five

onS6

onset of stage six

PCA

principal component analysis

PC

principal component

S1

center of stage one

S2

center of stage two

S3

center of stage three

S4

center of stage four

S5

center of stage five

S6

center of stage six

Supporting information

 

Fig. S1. Example of one trial EEG phase (dotted, light blue), the probability distributions for the location of cognitive stages' onsets (solid lines), and the analysis windows of relevant cognitive events (brackets).

Fig. S2. Beta band phase locking (ITPC: inter‐trial phase clustering), and phase connectivity (dwPLI: de‐biased weighted phase‐lag index).

Fig. S3. Example of the measurement of uncertainty in stage onset locations on one trial.

Fig. S4. Box plot comparing the power in the onset (Onset) of the stages and the power in the interval between onsets or trial edges (Stage).