Dynamic Migration Modes of Collective Cells

Abstract

Collective cell migration occurs in a diversity of physiological processes such as wound healing, cancer metastasis, and embryonic morphogenesis. In the collective context, cohesive cells may move as a translational solid, swirl as a fluid, or even rotate like a disk, with scales ranging from several to dozens of cells. In this work, an active vertex model is presented to explore the regulatory roles of social interactions of neighboring cells and environmental confinements in collective cell migration in a confluent monolayer. It is found that the competition between two kinds of intercellular social interactions—local alignment and contact inhibition of locomotion—drives the cells to self-organize into various dynamic coherent structures with a spatial correlation scale. The interplay between this intrinsic length scale and the external confinement dictates the migration modes of collective cells confined in a finite space. We also show that the local alignment–contact inhibition of locomotion coordination can induce giant density fluctuations in a confluent cell monolayer without gaps, which triggers the spontaneous breaking of orientational symmetry and leads to phase separation.

Introduction

Collective cell migration occurs in diverse physiological processes ranging from wound healing to embryogenesis and is also a hallmark of pathological processes such as cancer metastasis (1, 2, 3). For example, most solid tumors feature predominantly collective invasion during metastasis, in which cancer cells invade the peritumoral stroma while maintaining cell-cell contacts (1). Early Drosophila embryos undergo extensive collective cell motions to form and shape tissues and organs, as observed in gastrulation, dorsal closure, and border cell migration (4, 5, 6). In these physiological and pathological processes, collective cells migrate with different dynamic structures, e.g., clusters, strands, and sheets.

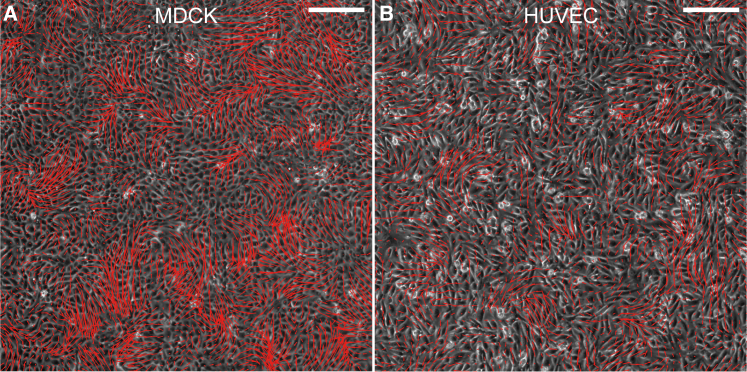
The motility of cells stems from the activity of cell protrusions (e.g., filopodia and lamellipodia), which form at the leading edge of cells, adhere to substrates and extend forward, and generate forces to propel cell migration (7). Dynamic motility enables cell assemblies to self-organize into various dynamic patterns, e.g., directed motion, swirling, and rotation (8, 9, 10, 11, 12, 13), akin to those in other biological systems such as bacterial suspensions, insect swarms, and animal groups (14, 15, 16). Among others, the swirling of collective cells, also referred to as active turbulence, has been observed in many epithelial systems, with a spatial correlation scale spanning from several to dozens of cells (8, 9, 10, 17). For instance, we observed the swirling pattern in Madin-Darby canine kidney (MDCK) cell monolayers (Fig. 1 A) and human umbilical vein endothelial cell (HUVEC) monolayers (Fig. 1 B), with spatial correlation lengths of 10–15 cells. In addition, migratory cell cohorts may interact with other nonmotile cells or surrounding confinements. These external constraints also influence the epithelial dynamics (13, 18, 19, 20, 21). For example, unconfined epithelia tend to undergo local swirling, whereas those confined in a circular domain may exhibit persistent global rotation (11, 12, 13, 19, 20). The dynamics of collective cells is not only critical for the formation of acini and ducts in glandular tissue, tissue polarity, and tubulogenesis (4, 6, 22) but also may provide a novel criterion for the diagnosis of such diseases as papillary thyroid carcinoma (23). However, it remains obscure why these mysterious, either solid- or fluid-like, coherent structures emerge and how intercellular interactions and extrinsic cues affect these migration modes.

Figure 1.

Experimentally measured velocity fields of collective cell migration in confluent monolayers. A swirling pattern was observed in (A) an MDCK cell monolayer and (B) an HUVEC monolayer. Red arrows show the velocity vectors obtained via PIV analysis. Scale bars, 200 μm. To see this figure in color, go online.

Here, we establish an active vertex model accounting for both active cell motility and intercellular social interactions to gain physical insights into the self-organized dynamic structures of collective migratory cells. In such biological systems as insects and fishes, social interactions of individuals are important for their collective behavior. Somewhat similarly, local alignment (LA) and contact inhibition of locomotion (CIL) are two key types of social interactions in many cell lines. The former tends to drive neighboring cells to move along the same direction (24, 25), whereas the latter produces a repulsive force among the cells upon contact (26, 27). From a biochemical perspective, LA is probably related to the planar cell-polarity signaling cascade (25), whereas CIL results from molecular interactions such as cadherin-mediated cell-cell adhesion (27). In this article, we use the active vertex model to decode the combined biophysical mechanisms of LA and CIL in collective cell motions. We reveal that the competition between LA and CIL can lead to rich spatiotemporal patterns with an intrinsic length scale spanning multiple cells and even induces giant density fluctuations. In addition, boundary confinements also significantly regulate the collective migratory patterns for cells in a confined regime, echoing diverse experimental observations (11, 13, 18, 19).

Materials and Methods

Experiments

MDCK strain II cells were cultured in Dulbecco’s modified Eagle’s medium supplemented with 10% fetal bovine serum (Gibco, Billings, MT), 100 μg/mL penicillin, and 100 μg/mL streptomycin. HUVECs were cultured in Dulbecco’s modified Eagle’s medium/F12 (Gibco) supplemented with 10% fetal bovine serum (Gibco), 100 μg/mL penicillin, and 100 μg/mL streptomycin. Both MDCK cells and HUVECs were maintained at 37°C in a humidified atmosphere with 5% CO₂. Confluent cell monolayers were allowed to develop on petri dishes (Falcon, Austin, TX) for enough time (typically ∼1 day) before live-cell imaging. Phase contrast images were acquired with a ×10 objective, using an Olympus IX83 inverted fluorescence microscope (Olympus, Tokyo, Japan). Two successive images of the same field were taken at a time interval of 1 min.

The velocity field in a confluent cell monolayer was computed from the phase contrast time-lapse images via particle image velocimetry (PIV). In PIV analysis, the interrogation window size was set as 48 × 48 pixels with an overlap of 50%. Outliers of the calculated velocity vectors were abolished and replaced by fitting values based on the neighboring velocity vectors. Custom-made PIV software was written in MATLAB (The MathWorks, Natick, MA).

Biophysical model

We describe a confluent epithelial monolayer as an interacting polygonal tiling of space in which each cell is modeled as a polygon with an active motile force. The potential energy of the system stems from cell area elasticity, cell contractility, and intercellular tension. It is written as (28, 29, 30, 31, 32)

$$U=\sum _J\frac{1}{2}{K}_{\text{a}}{\left(A_J-A_0\right)}^2+\sum _J\frac{1}{2}{K}_{\text{c}}{L}_J^2+\sum _{\left(i,j\right)}\Lambda l_{ij},$$ (1)

where K_a denotes the area stiffness of a cell, A₀ refers to the reference area, and A_J is the current area of the J-th cell; K_c represents the contractile modulus of a cell, and L_J is the perimeter of the J-th cell; Λ quantifies the interfacial tension between neighboring cells, and l_ij is the edge length of the cell-cell interface ij connecting vertices i and j. It is noted that the cell contractile modulus, K_c, could also be time-dependent and regulated by biochemical cues such as the ρ-ROCK signaling pathway (31, 33). For the sake of simplicity, however, we take a constant value of K_c in the following analysis.

The cellular dynamics is determined by the evolution of vertex positions, r_i(t), with i being the index of vertices. Considering the force balance at vertex i, the spatiotemporal dynamic evolution of vertices is controlled by

$$\frac{\text{d}{\mathbf{r}}_i}{\text{d}t}=\frac{1}{\gamma }{\mathbf{f}}_i^{\text{U}}+\sum _{J\in C_i}\frac{v_0{\mathbf{p}}_J}{n_J}+\sum _{J\in C_i}\frac{{\epsilon }_{\text{T}}{\mathit{\eta }}_J^{\text{T}}\left(t\right)}{n_J},$$ (2)

where γ is the friction coefficient, and ${\mathbf{f}}_i^{\text{U}}=-\partial U/\partial {\mathbf{r}}_i$ stands for the potential force acting on the vertex i; v₀ denotes the self-propelled velocity, and p_J = (cosθ_J, sinθ_J) represents the polarity vector with θ_J being its direction; ε_T is the strength of translational noises and ${\mathit{\eta }}_J^{\text{T}}\left(t\right)$ are independent unit-variance Gaussian white noise vectors; n_J refers to the number of neighboring cells of cell J, and ${\sum }_{J\in C_i}$ computes a summation over all neighboring cells C_i of vertex i.

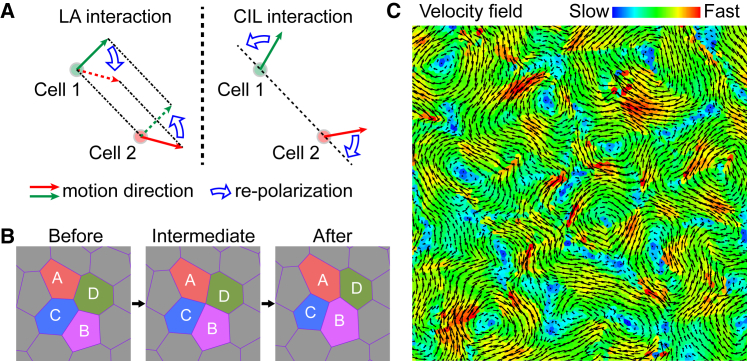
In the literature, several models have been proposed to describe cell polarity (12, 20, 24, 25, 26, 33, 34, 35, 36, 37, 38, 39, 40). For example, Koride et al. (33) considered the memory effect of cells and assumed that the cell polarity p_J depends on their movement history. We here consider the effect of two competing intercellular social interactions—LA and CIL—on cell polarity. Specifically, LA tends to align the cell polarity p_J along the motion direction of its neighbors, whereas CIL tends to orient the cell polarity p_J in the direction away from its neighbors, as illustrated in Fig. 2 A. Accordingly, the polarity direction θ_J evolves as

$$\frac{\text{d}{\theta }_J}{\text{d}t}=g_{\text{LA}}\left({\mathbf{p}}_J;{\mathbf{v}}_K\right)+g_{\text{CIL}}\left({\mathbf{p}}_J;{\mathbf{r}}_K\right)+{\epsilon }_{\text{R}}{\eta }_J^{\text{R}}\left(t\right),$$ (3)

where g_LA(p_J ; v_K) and g_CIL(p_J ; r_K) characterize the effects of LA and CIL, respectively, with r_K being the geometric center of cell K and v_K = dr_K/dt being the corresponding velocity vector; ε_R denotes the strength of rotational noise, and ${\eta }_J^{\text{R}}\left(t\right)$ are independent unit-variance Gaussian white noises. Inspired by previous studies (26, 40, 41, 42), we express g_LA(p_J ; v_K) and g_CIL(p_J ; r_K) as

$$\begin{array}{l}{g}_{\text{LA}}\left({\mathbf{p}}_J;{\mathbf{v}}_K\right)=\frac{{\mu }_{\text{a}}}{n_J}\sum _{K\in C_J}\sin \left[{\theta }_K^{\left(\text{vel}\right)}-{\theta }_J\right],\\ g_{\text{CIL}}\left({\mathbf{p}}_J;{\mathbf{r}}_K\right)=\frac{{\mu }_{\text{c}}}{n_J}\sum _{K\in C_J}\sin \left({\alpha }_{J,K}-{\theta }_J\right),\end{array}$$ (4)

where the parameters μ_a and μ_c stand for the intensities of LA and CIL, respectively; ${\theta }_K^{\left(\text{vel}\right)}=\arg \left({\mathbf{v}}_K\right)$ is the velocity direction of cell K; α_J,K = arg(r_J − r_K) denotes the argument of the direction pointing from cell K to cell J, and C_J is the collection of neighboring cells of cell J. Both LA and CIL have been reported across diverse cell lines. It has been thought that LA results from planar cell polarity associated with the dynamic cytoskeleton network (25), whereas CIL arises from cell-cell interactions such as cadherin-mediated intercellular adhesion (27). To date, however, it is still difficult to quantitatively evaluate the intensities of LA and CIL. Here, we omit the biochemical details of LA and CIL.

Figure 2.

Active vertex model accounting for intercellular social interactions. (A) A schematic of the LA and CIL interactions among cells. (B) A schematic of T1 topological transition in the active vertex model. (C) The swirling pattern obtained from our active vertex model. The black arrows denote the velocity vectors, and the color code corresponds to its magnitude. Shown here is a local window of the velocity field for a system containing N ∼ 10,000 cells (see Fig. S1 A for the global view). Parameter values: μ_a = 0.05 and μ_c = 1.0. To see this figure in color, go online.

It should be noted that although both CIL and noises tend to break the alignment of collective cell motions, their mechanisms are quite different and would lead to distinct migratory modes. For instance, at the free boundary of a cell monolayer, CIL renders boundary cells to polarize toward the free space, whereas noises favor a random cell movement without direction biases.

Equations 1, 2, 3, and 4 control the cellular motions in a confluent cell monolayer. For the sake of generality, we normalize these equations via the length scale $\ell =\sqrt{A_0}\sim 30\mathit{\mu }\text{m}$ and the timescale τ = γ/(K_aA₀) ∼ 100 s (Supporting Materials and Methods; Table 1). In our analysis, we take the dimensionless parameters as K_c = 0.02, Λ = 0.1, and v₀ = 0.1, as estimated from experiments (Table 1). μ_a and μ_c are set in the range 0.1∼1.0. To focus on the roles of LA and CIL, we ignore the noises and thus set ε_T = 0 and ε_R = 0. Besides, T1 topological transition (Fig. 2 B), which accounts for cell neighbor exchange (28, 29, 30), is involved in our simulations. We perform T1 topological transitions once any cell-cell interface is shorter than a threshold Δ_T1 (taken as 2.5Λ/(K_aA₀) here (28)) and accept it only if the potential energy of the post-transition configuration is lower than that of the pre-transition configuration (30). The key parameters and their dimensionless forms and values used in our simulations are summarized in Table 1.

Table 1.

Key Parameters Used in Our Simulations

Physical meaning	Symbol	Value	Reference	Normalization
				Formula	Value
Cell area stiffness	Ka	105–107 N ⋅ m−3	(5, 60)	ND	ND
Cell reference area	A0	900 μm2	Assumed	ND	ND
Cell contractile modulus	Kc	10−5–10−4 N ⋅ m−1	(61)	Kc/(KaA0)	0.01–0.1
Cell-cell interfacial tension	Λ	10−9–10−8 N	(62)	$\Lambda /\left(K_{\text{a}}{A}_0^{3/2}\right)$	0.01–0.1
Friction coefficient	γ	0.01–0.1 N ⋅ s ⋅ m−1	(62)	ND	ND
Length scale	$\ell$	30 μm	$\ell =\sqrt{A_0}$	ND	ND
Time scale	τ	100 s	$\tau =\gamma /\left(K_{\text{a}}{A}_0\right)$	ND	ND
Self-propelled velocity	v0	10−8 ∼ 10−7 m ⋅ s−1	(63)	$v_0\tau /\sqrt{A_0}$	0.01–0.1
LA intensity	μa	∼10−4 s−1	Assumed	μaτ	∼0.1
CIL intensity	μc	∼10−3 s−1	Assumed	μcτ	∼1.0

ND, no data.

All simulations were performed in MATLAB. The time step was set to be Δt = 0.1, and the total running step was typically N_s = 60,000. Data was collected for analysis after the system had arrived at a dynamic steady state (typically after N_d = 20,000 running steps). For statistics, 10 independent simulations were performed for each set of parameter values.

Results

Intrinsic modes and spatial correlation scale

We first explore the intrinsic modes of collective cell motions in the monolayer. To eliminate the effect of boundary constraint, we here adopt the periodic boundary conditions, with N_cell ∼ 10,000 cells in a periodic regime L × L and a fixed cell areal density ${\rho }_{\text{cell}}=N_{\text{cell}}{A}_0/L^2\equiv 1.0$. Thus, the simulated regime has a size L ∼100 times the average cell size, much larger than the spatial correlation scale of collective cell motions observed in our experiments and previously reported (∼10–20 cell size). We find that under the coordination of LA and CIL, the initially randomly polarized cells can spontaneously orchestrate into a dynamic swirling pattern (Figs. 2 C and S1 A), with the mean motion speed around 0.2v₀ ∼ 21 μm/h, in agreement with our experiments (16–22 μm/h for MDCK cell monolayers and 10–14 μm/h for HUVEC monolayers). Our simulations can capture the predominant features including migration mode and patterns of collective cell migration, as observed in our experiments on MDCK cell monolayers and HUVEC monolayers (Fig. 1) and previous experiments with other cell lines (8, 10, 18).

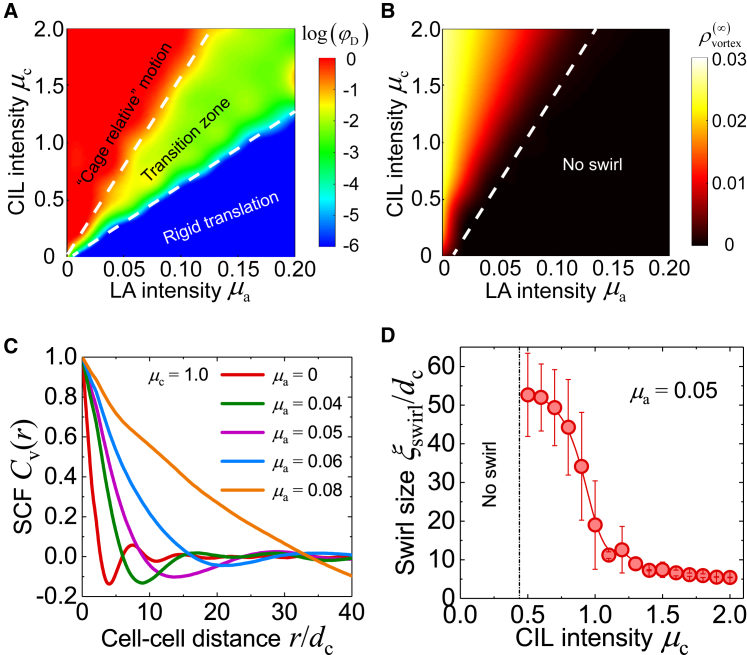
To identify how LA and CIL mediate collective cell motions, we first distinguish two typical migratory modes: 1) translational motions, in which cells in the monolayer move coherently and synchronously as a solid; and 2) “cage relative” motions, in which intercellular relative movements are dominant in the collective motions. To physically disentangle the translational and the “cage relative” motions, we examine the mean square displacement (MSD) $\langle r^2\left(\mathit{\Delta }t\right)\rangle ={\langle {\left|{\mathbf{u}}_J\left(t,\mathit{\Delta }t\right)\right|}^2\rangle }_{J,t}$ and the “cage relative” mean square displacement (CR-MSD) ${\langle r^2\left(\mathit{\Delta }t\right)\rangle }^{\text{CR}}={\langle {\left|{\mathbf{u}}_J^{\text{CR}}\left(t,\mathit{\Delta }t\right)\right|}^2\rangle }_{J,t},$ where u_J(t, Δt) = u_J(t + Δt) − u_J(t) and ${\mathbf{u}}_J^{\text{CR}}\left(t,\mathit{\Delta }t\right)={\mathbf{u}}_J\left(t,\mathit{\Delta }t\right)-{\mathbf{u}}_J^{\text{cage}}\left(t,\mathit{\Delta }t\right)$ are the total displacement and the “cage relative” displacement of cell J during the time interval t → t + Δt, respectively. Here, ${\mathbf{u}}_J^{\text{cage}}\left(t,\mathit{\Delta }t\right)$ is the displacement of the instantaneous “local cage” of cell J and is defined as ${\mathbf{u}}_J^{\text{cage}}\left(t,\mathit{\Delta }t\right)=\left(1/n_J\right){\sum }_{K\in C_J}{\mathbf{u}}_K\left(t,\mathit{\Delta }t\right)$. Based on the MSD and the CR-MSD, we introduce a dimensionless parameter ${\phi }_{\text{D}}={\lim }_{\mathit{\Delta }t\to \infty }\left[{\langle r^2\left(\mathit{\Delta }t\right)\rangle }^{\text{CR}}/\langle r^2\left(\mathit{\Delta }t\right)\rangle \right]$ to quantify the fraction of “cage relative” cellular motions. It is found that φ_D is small for strong LA and weak CIL (Fig. 3 A), exhibiting a motion mode akin to “solid-like” rigid translation (Fig. S1 B), in which the monolayer moves synchronously and directionally with few cell rearrangements, entering a “solid-like jammed” phase. For strong CIL and weak LA, φ_D is close to 1 (Fig. 3 A), which indicates that the monolayer tends to attain a fluid-like unjammed state in which the “cage relative” cellular motions are predominant (Fig. S1 C). Taken together, our results reveal that LA tends to suppress whereas CIL promotes intercellular relative motions. The trade-off between LA and CIL may determine the transition of collective cellular motion modes.

Figure 3.

Intrinsic modes and spatial correlation of collective cell migration. Phase diagrams of (A) the fraction of “cage relative” motions φ_D and (B) the intrinsic vortex density ${\rho }_{\text{vortex}}^{\left(\infty \right)}$ modulated by the intensities of LA (μ_a) and CIL (μ_c). In (A), the “cage relative” motion and rigid translation modes are defined for log(φ_D) > −1 and log(φ_D) < −5, respectively. In (B), the intrinsic vortex density ${\rho }_{\text{vortex}}^{\left(\infty \right)}$ is calculated in a system containing ∼10,000 cells. (C) The spatial correlation function (SCF) C_v(r) of cell velocity under different intensities of LA μ_a, where d_c is the mean distance between neighboring cells, is shown. (D) The swirl size ξ_swirl versus the CIL intensity μ_c is shown. Data are mean ± SD. To see this figure in color, go online.

To characterize the swirling intensity, we count the number of vortex cores N_vortex based on the angle the velocity field rotates in one loop that runs through all the instantaneous neighbors of a cell (43). The vortex density is then defined as ρ_vortex = N_vortexA₀/L². We vary the system size to examine the dependence of vortex density ρ_vortex on cell population N_cell. It is found that the vortex density ρ_vortex approaches a constant value for a sufficiently large system (Fig. S2), suggesting that an intrinsic vortex density ${\rho }_{\text{vortex}}^{\left(\infty \right)}=\underset{N_{\text{cell}}\to \infty }{\lim }\left[{\rho }_{\text{vortex}}\left(N_{\text{cell}}\right)\right]$ emerges in the confluent cell monolayer. Fig. 3 B illustrates how the intrinsic vortex density ${\rho }_{\text{vortex}}^{\left(\infty \right)}$ is regulated by LA and CIL. We find that CIL promotes the generation of swirls. In contrast, LA is found to favor directed motion rather than swirling. Because swirls can not only adjust cell orientation but also facilitate cell rearrangements, we argue that CIL should play a crucial role in collective cell planar polarization and contribute to diversifying cell-cell contacts and communications, as evidenced by mounting cell neighbor exchanges via increasing CIL (Fig. S3). Such frequent neighbor exchanges might enable cells to probe environmental cues sensitively. Besides, it has been revealed that after the epithelial-mesenchymal transition, which often occurs during tumor progression, cancer cells exhibit enhanced CIL effect due to the loss of E-cadherin and the acquisition of N-cadherin (27). Therefore, more cellular swirls will emerge in more malignant cell systems. Our findings provide theoretical foundation for the phenomenological diagnostic criterion for such cancers as papillary thyroid carcinoma through the examination of swirling intensity (23).

Both our experiments (Fig. 1) and numerical simulations (Fig. 2 C) demonstrate that the swirls in cell monolayers manifest a specified length scale, as observed in many other cell lines (10, 17). To explore this spatial scale, we calculate the spatial correlation function (SCF), $C_{\text{v}}\left(r\right)={\langle \mathit{\delta }\mathbf{v}\left(\mathbf{x}\right)\cdot \mathit{\delta }\mathbf{v}\left(\mathbf{x}+\mathbf{r}\right)\rangle }_{\mathbf{x},\phi }/{\langle \mathit{\delta }\mathbf{v}\left(\mathbf{x}\right)\cdot \mathit{\delta }\mathbf{v}\left(\mathbf{x}\right)\rangle }_{\mathbf{x}}$ of cell velocity, where $\mathit{\delta }\mathbf{v}\left(\mathbf{x}\right)=\mathbf{v}\left(\mathbf{x}\right)-\overline{\mathbf{v}}$ is the velocity fluctuation field, with $\overline{\mathbf{v}}$ being the spatial mean velocity vector; ${\langle \cdot \rangle }_{\mathbf{x},\phi }$ computes an average over the spatial field x and all directions φ = arg(r). The length scale of swirls (effective diameter), ξ_swirl, can be obtained by seeking the minimum of C_v(r) (8).

We first examine the SCF C_v(r) versus cell-cell distance r upon varying the intensity of LA (Fig. 3 C). It is seen that if there exists CIL interaction alone (μ_a = 0), C_v(r) exhibits a minimum at ∼4 cells, meaning that the typical size of swirls caused by CIL alone is approximately ξ_swirl ∼ 4 cell length. Increasing the LA intensity μ_a will enlarge the size of swirls, as indicated by the right-shifting position of the minimum of C_v(r) (Fig. 3 C). The swirling dynamics will be suppressed if LA is sufficiently strong (e.g., μ_a = 0.08). Moreover, we find that CIL tends to reduce the swirl size (Fig. 3 D), which can be attributed to its potential of promoting neighbor exchanges (Fig. S3). Overall, the LA-CIL regulated swirl size (diameter) ranges from ∼4 cells to several dozens of cells, in agreement with our experiments (10–15 cells) as well as previously reported results (10–20 cells). It is known that a larger size of cell cluster undergoing collective migration benefits efficiently transporting cells or molecules to distant location. However, a smaller scale of swirling allows more frequent exchanges of cell neighbors, enhancing biogenic mixing. Therefore, the coordination between LA and CIL may yield an optimal size of swirls, which may enable rapid molecular or cell transport and adequate biomixing. Experimentally quantifying these in the future would be very useful.

Migratory modes of collective cells in confined space

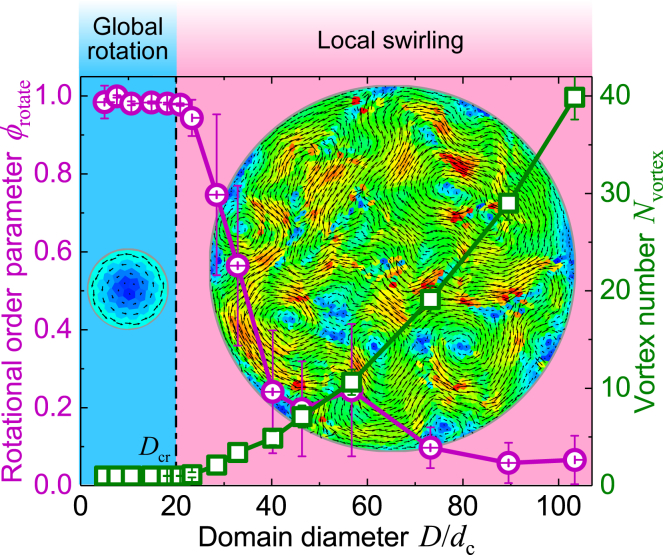
The in vivo migration of collective cells often confronts geometric confinements. In vitro experiments have revealed that boundary confinements could affect the migratory mode of collective cells confined in a finite space (13, 18, 19). To elucidate the influence of geometric confinements on the collective cell dynamics, we next consider cells confined in a circular domain of diameter D. The cell density is fixed as ρ_cell = 1, and the boundary vertices are allowed to slide along the perimeter freely. Besides, we take μ_a = 0.05 and μ_c = 1, which results in an intrinsic swirl size of ∼19 cells.

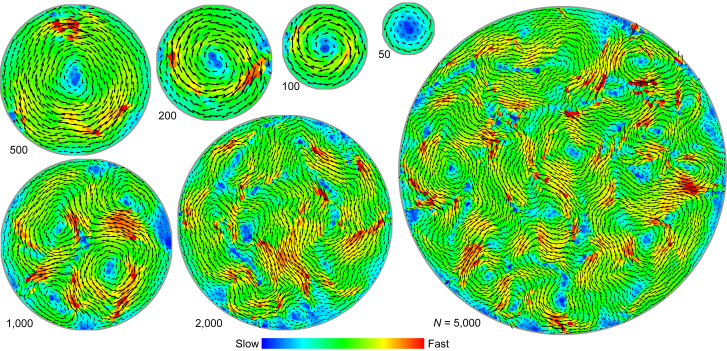
Our simulations show that the cells confined in a small domain will self-organize into a persistent global rotation pattern, whereas those in a large domain will orchestrate into a dynamic swirling pattern (Fig. 4). We further use the rotational order parameter ${\varphi }_{\text{rotate}}={\langle \left|\left(1/N\right)\sum _J{\hat{\mathbf{v}}}_J\cdot {\mathbf{e}}_{\phi J}\right|\rangle }_t$ to quantify such mode transition, where ${\hat{\mathbf{v}}}_J={\mathbf{v}}_J/\left|{\mathbf{v}}_J\right|$ is the instantaneous motion direction of cell J and e_φJ the circumferential direction. There exists a critical diameter D_cr below which ϕ_rotate remains ∼1 and N_vortex = 1 (Fig. 5). Increasing D beyond D_cr leads to a sharp decrease in ϕ_rotate and a dramatic increase in N_vortex, indicating the breakdown of the persistent global rotation mode (Fig. 5). Here, the critical diameter of the confinement, D_cr ∼ 20 cell-length, is determined by taking ϕ_rotate = 0.95, below which the system switches to a dynamic swirling mode. Notably, D_cr is very close to the intrinsic swirl size (ξ_swirl ∼ 19 cell length) in a cell monolayer without geometric constraints.

Figure 4.

Patterns of collective cell migration confined in circular domain with different diameters. In different domains, cell population N is varied but cell density ρ_cell = 1 is kept constant. The arrows denote velocity vectors of cells, and the color code indicates magnitude of cell velocity. Parameter values: μ_a = 0.05 and μ_c = 1.0. To see this figure in color, go online.

Figure 5.

Motion modes of collective cells confined in a circular domain. The rotational order parameter ϕ_rotate and the vortex number N_vortex vary with the diameter D. Data are mean ± SD. The inset images show the velocity field of two typical modes: global rotation and local swirling. Parameter values: μ_a = 0.05 and μ_c = 1.0. To see this figure in color, go online.

These results suggest that when collective cells are confined in a finite space, the length scale of the confinement also influences their self-organized patterns. The competition between the intrinsic and extrinsic scales leads to the migration pattern transition. Our prediction is consistent with relevant experiments (19).

Density fluctuations in confluent cell monolayers

Giant density (or number) fluctuations, which are a hallmark of the inhomogeneous spatial distribution of individual components, have been recognized as a powerful indicator of mesoscopic scale fluctuations in both active particulate systems (44, 45) and biological systems (10, 16, 46, 47, 48). In these systems, populations spontaneously form scattered, closely packed clusters with high local density. Those clusters are mobile and often leave empty space or gaps in regions they just pass, inducing low density therein. Consequently, migratory clusters often engender giant density fluctuations. In our system, however, all cells are mechanically linked to their neighbors in the gap-free monolayer. We wonder whether giant density fluctuations may be triggered and modulated by intercellular social interactions in a confluent cell sheet.

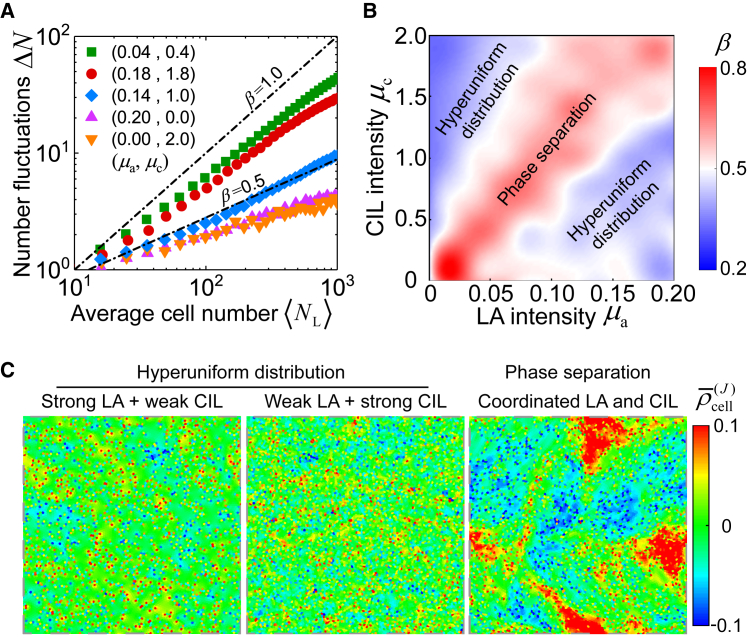
To quantify the density fluctuations in a cell monolayer, we calculate the number fluctuations $\mathit{\Delta }N=\sqrt{\langle {\left(N_{\text{L}}-\langle N_{\text{L}}\rangle \right)}^2\rangle }$ of cells in a square subregion of linear size L, containing an average number of cells, $\langle N_{\text{L}}\rangle$. It is observed that the number fluctuations scales as $\mathit{\Delta }N\sim {\langle N_{\text{L}}\rangle }^{\beta }$ (Fig. 6 A). The scaling exponent β characterizes the dynamics of number fluctuations: β = 1/2 corresponds to a thermodynamic equilibrium, whereas β < 1/2 and β > 1/2 denote suppressed and enhanced density fluctuations, respectively. According to the scaling exponent β, we establish a phase diagram to illustrate the effects of LA and CIL (Fig. 6 B). It shows that if either LA or CIL is strong alone, the system exhibits suppressed density fluctuations, resulting in a hyperuniform distribution of cells in which the characteristic size of cells across the whole monolayer is uniform. Surprisingly, the coordination between LA and CIL can result in giant density fluctuations with β>1/2, leading to phase separation. The density fluctuations can be intuitively reflected by the local cell density field ${\overline{\rho }}_{\text{cell}}^{\left(J\right)}={\rho }_{\text{cell}}^{\left(J\right)}-{\langle {\rho }_{\text{cell}}^{\left(J\right)}\rangle }_J$ with ${\rho }_{\text{cell}}^{\left(J\right)}=A_0/A_J$ (Fig. 6 C). If either LA or CIL is strong alone, the local cell density field exhibits a uniform spatial distribution. When LA and CIL are appropriately coordinated, however, giant density fluctuations may emerge, and the spatial cell density exhibits a strong heterogeneity in which large or small cells gather and move as a group, breaking the orientational symmetry of collective migration. Such density heterogeneity may also engender heterogeneous mechanical properties in epithelial tissues. We reveal that under the interplay of LA and CIL, the scaling exponent β can be as high as 0.8, comparable to those emerging in other biological systems such as bacterial suspensions (46), fibroblast cells (47), and neural progenitor cells (48).

Figure 6.

Density fluctuations in a confluent cell monolayer tailored by intercellular social interactions. (A) Number fluctuations ΔN versus average number $\langle N_{\text{L}}\rangle$ of cells in a subregion of size L under different intensities of LA and CIL. (B) A phase diagram of the scaling exponent β of number fluctuations is shown. (C) The local cell density field for hyperuniform distribution of cells (left and middle) and phase separation pattern (right). The color denotes the local cell density field ${\overline{\rho }}_{\text{cell}}^{\left(J\right)}$. From left to right, parameter values are taken as (μ_a, μ_c) = (0.2, 0.1), (0.01, 2.0), and (0.12, 1.4). To see this figure in color, go online.

Discussion

We have established an active vertex model to investigate collective dynamics of cell migration in confluent monolayers. We show that the cell-level LA-CIL coordination can engender the tissue-level migration modes and dynamic structures, which are further modulated by environmental confinements. These modes and structures are not only essential for cell-cell communication, molecular transport, and environmental probing in cell monolayers but may also provide possible means of diagnosis for some carcinoma. Although much effort has been directed toward collective cell migration (2, 3, 8, 9, 10, 12, 13, 17, 18, 20, 25, 26, 31, 34, 35, 36, 37, 40, 49, 50, 51, 52, 53, 54), our theoretical model uniquely identifies how the coordination of cellular-level social interactions sculpts morphodynamics at the tissue scale.

In the literature, several models have also been proposed to investigate collective cell migration. Some models considered cell polarity to be self-renewal, in which cell reorientation was treated as either a pure diffusive process (34) or a memory process in which cells adapted to the previous motion (12, 33, 35, 36, 37, 38), or a mechanical process in which cells adjusted along the long axis of cell shape to obtain plithotaxis (25). In addition, some studies attributed cell polarity to the effect of intercellular social interactions including alignment and repulsion. For example, the LA effect was introduced to examine flocking transition in cell collectives (24, 25, 39). The CIL effect was taken into account to decode chemotaxis or cell colony dynamics (20, 26, 40). However, most of these previous studies considered only one kind of intercellular social interaction. In general, both LA and CIL effects function in cell polarity. In this work, we integrate LA and CIL into an active vertex model to scrutinize collective cell dynamics. We show that the trade-off between the two kinds of intercellular interactions dictates the emergence of dynamic coherent structures, spatial scales, and phase separation in cell monolayers.

Mechanical cues, e.g., intercellular adhesion (18, 55) and substrate stiffness (8, 50), have been revealed to regulate collective cell migration via affecting cell polarity or cell-cell communication. Recent studies demonstrated that geometric constraints also dictate collective cell migration in a confined space, engendering persistent angular rotations or dynamic swirls (11, 12, 13). In this study, we argue that the coordinated cell rotation and swirling in a circular domain can be ascribed to the competition between the social-interaction-induced intrinsic length scale and the external scale of geometric confinement. We believe this argument could provide novel insights into constrained collective cell dynamics. The scale-competition mechanism also helps us understand collective cell motion in other confined spaces such as channels (18) and cylinders (52). For instance, previous experiments showed that the modes of epithelial flow confined in a long channel can be tailored by its width: collectively directed migration generally occurs in narrow channels, whereas wide channels favor local swirling of cells (18). Such a mode transition can be readily interpreted by the scale competition mechanism proposed here. An open question is how topology and anisotropy of confinement mediate collective cell dynamics.

Giant density fluctuations, usually recognized as a prominent feature of nonequilibrium dynamics, have been investigated extensively in active particle systems. Recently, it was reported that giant density fluctuations also emerge in biological systems. For instance, it has been experimentally measured and theoretically predicted that bacterial suspensions (16, 46) and cell monolayers (10, 40, 47, 48) can self-organize into a phase-separated state featuring giant density fluctuations. In our work, we find that social interactions among cell collectives tailor the density fluctuations in a coherent cell monolayer and can even generate giant density fluctuations. Moreover, such giant density fluctuations are not restricted to emerging in the highly ordered state of collective motions but take place in a state with the motion order in a rather broad range (Fig. S4). This is quite different from active particle systems (14), revealing a distinct dynamic feature for coherent cell systems.

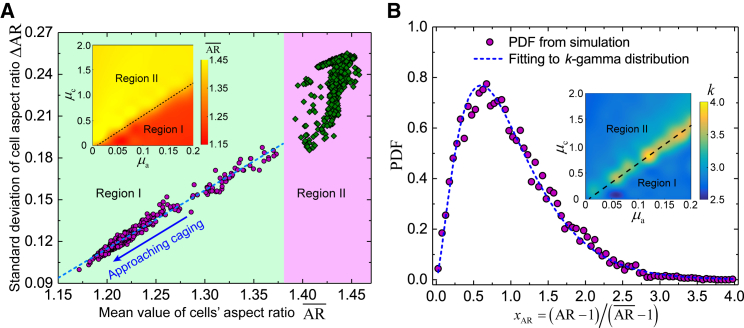
Epithelial morphogenesis is always accompanied by cell shape variation, as observed during wound healing and cancer metastasis (1, 2). Very recently, it has been revealed that the variation and distribution of cell shapes collapse to potentially universal laws across diverse epithelial systems as the jamming transition of cell collectives is approached (56). Specifically, across diverse epithelial systems, there exists a potentially universal linear relationship between the mean and the variation of cells’ aspect ratio, and moreover the distribution of cells’ aspect ratio collapses to a family of k-γ distributions. We wonder whether and how the social interactions among cells affect cell shape variation and distribution in an epithelial-like monolayer. Our simulations show that under the social interactions among cells—LA and CIL—the relationship between the variation and the mean of cells’ aspect ratio remains linear as the monolayer approaches caging (i.e., active jamming) (Fig. 7 A). However, this relationship deviates from a linear one when the CIL interaction is relatively strong (Fig. 7 A), presumably due to the frequent “cage relative” cell movements in such situation. Nevertheless, under the regulation of LA and CIL, the probability density functions (PDFs) of cell aspect ratio still collapse into a family of PDFs (Fig. 7 B). Such PDFs can be well fitted by the k-γ distribution f_Γ(x;k) = k^kx^{k − 1}e^−kx/Γ(k) with Γ(.) the Legendre γ function and k the shape parameter that characterizes the shape of the k-γ distribution. It is found that the shape parameter k mainly locates in the range 2.5–3.0 (Fig. 7 B), in agreement with experimental measurements (2–2.5) (56). These findings deepen our understanding of the cell shape variation in epithelial tissues away from jamming transition.

Figure 7.

Features of cell shape regulated by intercellular social interactions. (A) A scatter diagram of the mean value $\overline{\text{AR}}$ and the standard deviation ΔAR of cell aspect ratio upon changing the intensities of LA and CIL. Here, the aspect ratio of a polygonal cell is defined as $\text{AR}=\sqrt{I_1/I_2}$, with I₁ and I₂ (I₁ > I₂) being the principal centroidal moments of inertia of the polygonal cell. The purple circular dots in region I are obtained from simulations in the case of relatively strong LA, and the green rhombic dots in region II are obtained from simulations in the case of relatively strong CIL (see the inset). The blue dashed line corresponds to a linear fitting of the data set ($\overline{\text{AR}}$, ΔAR) in region I (the purple circular dots), with the fitting equation $\mathit{\Delta }\text{AR}=0.419\overline{\text{AR}}-0.388$ and the corresponding correlation coefficient R² = 0.9765. The inset shows a phase diagram of the mean cell aspect ratio $\overline{\text{AR}}$ regulated by LA and CIL. (B) The probability density functions (PDFs) of cell shape collapse into a family of PDFs upon varying the intensities of LA and CIL. Typical PDF of the rescaled cell aspect ratio $x_{\text{AR}}=\left(\text{AR}-1\right)/\left(\overline{\text{AR}}-1\right)$. The dashed curve corresponds to the fitting to k-γ distribution via maximal likelihood estimation. The inset shows a phase diagram of the shape parameter k tailored by LA and CIL. The definition of regions I and II are consistent with (A). To see this figure in color, go online.

In our study, we do not involve the detailed biochemical signaling pathways. Recent work on Drosophila amnioserosa and MDCK monolayers identified the critical role of intracellular contraction and polarity in epithelial morphogenesis (31, 57). In fact, cell contractility as well as cell polarity is related to the complicated intracellular signaling pathways and transmembrane transport of signaling molecules (58, 59). In addition, the collective migration of cells is also affected by stiffness, topology, and curvature of the underlying substrate (3, 8, 50, 51, 52). These issues merit further investigation to develop refined theories toward addressing the intricate cell dynamics.

Author Contributions

B.L. and X.-Q.F. designed research. S.-Z.L., S.Y., G.-K.X., B.L., and X.-Q.F. performed research. S.-Z.L., B.L., and X.-Q.F. analyzed data. S.-Z.L., B.L., G.-K.X., and X.-Q.F. wrote the manuscript.

Editor: Sean Sun.