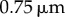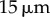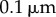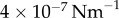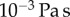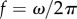Abstract
Despite evidence for a hydrodynamic origin of flagellar synchronization between different eukaryotic cells, recent experiments have shown that in single multi-flagellated organisms, coordination hinges instead on direct basal body connections. The mechanism by which these connections lead to coordination, however, is currently not understood. Here, we focus on the model biflagellate Chlamydomonas reinhardtii, and propose a minimal model for the synchronization of its two flagella as a result of both hydrodynamic and direct mechanical coupling. A spectrum of different types of coordination can be selected, depending on small changes in the stiffness of intracellular couplings. These include prolonged in-phase and anti-phase synchronization, as well as a range of multi-stable states induced by spontaneous symmetry breaking of the system. Linking synchrony to intracellular stiffness could lead to the use of flagellar dynamics as a probe for the mechanical state of the cell.
Keywords: flagella, oscillators, microhydrodynamics, synchronization, cytoskeleton, Chlamydomonas reinhardtii, cilia
1. Introduction
Cilia and flagella are structurally identical, whip-like cellular organelles employed by most eukaryotes for tasks ranging from sensing and locomotion of single cells [1], to directing embryonic development [2] and driving cerebrospinal fluid flow [3] in animals. Originally observed in 1677 by the Dutch pioneer Antonie van Leeuwenhoek, groups of motile cilia and flagella have a seemingly spontaneous tendency to coordinate their beating motion and generate large-scale patterns known as metachronal waves [4]. Coordination has often been proposed to provide an evolutionary advantage by improving transport and feeding efficiency [5–10], although estimates of the magnitude of this effect are notoriously difficult. Despite the uncertainty on its biological role, however, the universality of flagellar coordination is an empirical fact, and it suggests the existence of a correspondingly general mechanism for synchronization. Mechanical forces, transmitted either by the surrounding fluid or internally through the cells, have often been proposed as responsible for this coordination [11–15]. Understanding how synchronization emerges could therefore highlight novel and potentially subtle roles played by physical forces in cell biology. Here, we develop a minimal model that links small changes in the mechanical properties of cells with the dynamics of their protruding flagella. In turn, this approach could lead to coordination being used as a probe to measure the internal mechanical state of a cell.
Reports of coordinated motion in nearby swimming sperm [16,17] hint at the importance of hydrodynamic coupling. Hydrodynamic-led coordination of self-sustained oscillators, mimicking the active motion of cilia and flagella [18,19], has been extensively investigated theoretically [12,20–22], numerically [23–25], and experimentally with colloidal rotors [26,27] and rowers [28,29]. Despite the peculiar constraints of low-Reynolds number hydrodynamics, these studies suggest that hydrodynamic interactions can lead to ciliary coordination when coupled to either a phase-dependent driving force [12,21], or axonemal elasticity [30]. Indeed, hydrodynamic-mediated synchronization has been confirmed experimentally between pairs of eukaryotic flagella from different somatic cells from the green alga Volvox carteri [14].
Inter-cellular coordination of flagella, however, does not necessarily imply intracellular coordination, and therefore it is not a priori clear whether hydrodynamic coupling is also responsible for the synchronization observed in individual multi-flagellated cells. Experimental studies of flagellar coordination within a single cell have focused mainly on the biflagellate green alga Chlamydomonas reinhardtii (CR) [31,32], whose flagella are usually locked in a characteristic in-phase breaststroke motion. Early studies of flagellar coordination in CR [33–35] were recently refined [11,36] and extended [37] using microfluidic devices and high-speed imaging of flagella [38]. These pointed at a fundamentally hydrodynamic origin for the observed synchronization, either through direct coupling or via a mechanism based on cell-body rocking [13]. However, a series of elegant novel experiments in CR and other flagellates challenged this view convincingly, showing instead that coordination requires the intracellular striated fibres that join flagellar basal bodies [39,40]. For the CR mutant vfl3, with impaired mechanical coupling and a variable number of flagella, synchronization is completely disrupted [39] except for sporadic periods of synchrony in cells with two close flagella oriented in the same direction (see fig. S1 in [40]). Even though the precise mechanism by which direct connections affect flagellar coordination remains to be clarified [15], the spontaneous transitions between extended in-phase (IP) and anti-phase (AP) beating in the CR mutant ptx1 [41] already suggest that multiple synchronization states should be achievable through changes in the fibres’ mechanical properties within the physiological range.
Here we propose a minimal model for flagellar dynamics for CR which can sustain both stable IP and stable AP states even in the absence of hydrodynamic coupling. Within this framework, the phase dynamics are determined principally by the mechanical state of the basal body fibres [42], with both types of coordination possible within a physiological range of fibre stiffnesses [43]. The inclusion of hydrodynamic coupling leads to the emergence of a region in parameter space where non-trivial states can emerge as a result of spontaneous symmetry breaking through pitchfork bifurcations of limit cycles.
2. Minimal model and leading order dynamics
Figure 1a summarizes our minimal model of flagella coupled through hydrodynamic and basal body interactions. Following previous theoretical work [20,44], and experimental measurements of flagellar flow fields and waveform elasticity [14], the two flagella of Chlamydomonas are represented here by two spheres of radius a, immersed in a three-dimensional fluid of viscosity μ, and driven around circular orbits of radii 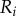 (
(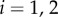 ) by constant tangential driving forces
) by constant tangential driving forces 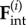 . Springs of stiffness λ resist radial excursions from the equilibrium length R0; and the magnitude of the internal driving forces
. Springs of stiffness λ resist radial excursions from the equilibrium length R0; and the magnitude of the internal driving forces 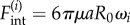 guarantees that, when isolated, the ith oscillator will rotate at the intrinsic angular speed
guarantees that, when isolated, the ith oscillator will rotate at the intrinsic angular speed 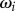 . The orbits are centred along the x-axis, a distance l apart, and lie along the xy plane. Polar and radial coordinates
. The orbits are centred along the x-axis, a distance l apart, and lie along the xy plane. Polar and radial coordinates 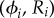 define the oscillators’ instantaneous positions around the centres of their respective orbits. We will refer to
define the oscillators’ instantaneous positions around the centres of their respective orbits. We will refer to 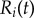 as the external rotor radii.
as the external rotor radii.
Figure 1.
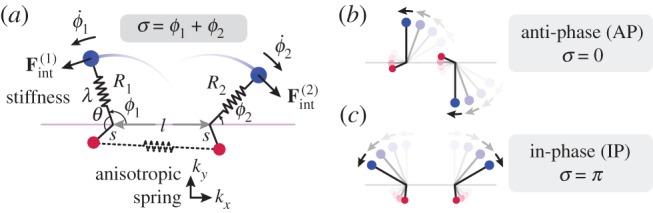
Physical configuration. (a) Two external rotors (blue), moving in the fluid, mimic the beating motion of flagellar filaments. Internal rotors (red) represent the flagellar basal bodies and are coupled through an anisotropic spring. (b) Anti-phase (AP) and (c) in-phase (IP) states. (Online version in colour.)
Both hydrodynamic and direct elastic interactions couple these minimal cilia. Hydrodynamic coupling is mediated by the fluid disturbance generated by each sphere’s motion, modelled here as the flow from a point force. These interactions affect the instantaneous angular speeds 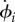 both directly, through a hydrodynamic torque, and indirectly by modifying the orbits’ radii. For counter-rotating oscillators like those describing Chlamydomonas flagella, the resulting effective coupling will promote AP synchronization [15,41,44,45] (figure 1b). In addition to external flagellar interactions, considerable evidence [39,40] suggests that flagellar dynamics are strongly influenced by direct intracellular mechanical coupling, through striated fibres joining the basal bodies [33,46] that can lead the system to IP synchrony (figure 1c). Intracellular connections are modelled here by introducing, for each oscillator, an auxiliary arm of fixed length
both directly, through a hydrodynamic torque, and indirectly by modifying the orbits’ radii. For counter-rotating oscillators like those describing Chlamydomonas flagella, the resulting effective coupling will promote AP synchronization [15,41,44,45] (figure 1b). In addition to external flagellar interactions, considerable evidence [39,40] suggests that flagellar dynamics are strongly influenced by direct intracellular mechanical coupling, through striated fibres joining the basal bodies [33,46] that can lead the system to IP synchrony (figure 1c). Intracellular connections are modelled here by introducing, for each oscillator, an auxiliary arm of fixed length 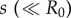 at an angle θ ahead of the rotating sphere. The endpoints of these arms (red spheres in figure 1a) are coupled via an anisotropic elastic medium acting as elastic springs of stiffnesses
at an angle θ ahead of the rotating sphere. The endpoints of these arms (red spheres in figure 1a) are coupled via an anisotropic elastic medium acting as elastic springs of stiffnesses 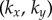 and equilibrium lengths
and equilibrium lengths 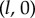 in the x and y directions, respectively. This is intended to represent the intrinsically anisotropic structure of the fibre bundles connecting the basal bodies [42]. The equations of motion, derived in electronic supplementary material, S1, follow from the requirement of zero net force and torque on each oscillator, and in the limit
in the x and y directions, respectively. This is intended to represent the intrinsically anisotropic structure of the fibre bundles connecting the basal bodies [42]. The equations of motion, derived in electronic supplementary material, S1, follow from the requirement of zero net force and torque on each oscillator, and in the limit 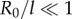 can be approximated as (see electronic supplementary material, S1)
can be approximated as (see electronic supplementary material, S1)
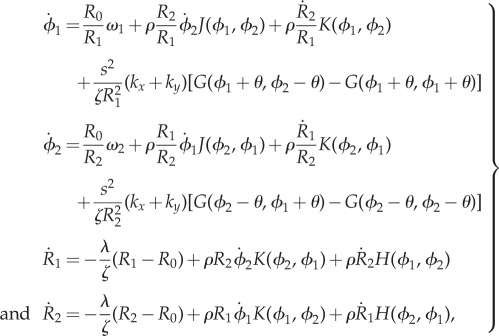 |
2.1 |
where 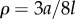 (
(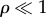 as
as 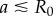 );
); 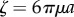 is the viscous drag coefficient of the rotating sphere; and
is the viscous drag coefficient of the rotating sphere; and
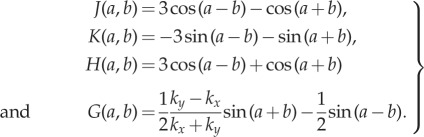 |
2.2 |
In order to model the configuration typical of Chlamydomonas, we will focus here on identical but counter-rotating oscillators, 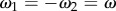 . Parameter values are given in table 1 unless otherwise specified.
. Parameter values are given in table 1 unless otherwise specified.
Table 1.
Minimal model parameters used throughout, unless stated otherwise.
3. Fibres-only coupling
Despite the apparent simplicity, this minimal system displays rich dynamics, and it is therefore convenient to analyse its behaviour following steps of increasing complexity. Let us begin by considering the case in which hydrodynamic coupling is completely neglected. The hydrodynamic drag is still necessary for each model cilium (through 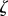 ) in order to balance the driving force, but there is no direct hydrodynamic coupling between the spheres. In this case,
) in order to balance the driving force, but there is no direct hydrodynamic coupling between the spheres. In this case, 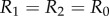 , and recasting the angular dynamics in terms of phase sum and difference
, and recasting the angular dynamics in terms of phase sum and difference 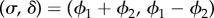 , we obtain
, we obtain
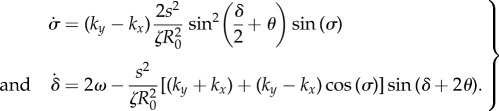 |
3.1 |
Requiring that the maximal torque exerted on each oscillator by the internal springs is always smaller than that from the driving force (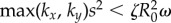 ) guarantees that the cilia will always be beating (
) guarantees that the cilia will always be beating (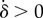 ), and defines a physiologically plausible range for k’s, which in our case is
), and defines a physiologically plausible range for k’s, which in our case is 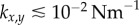 . At the same time, unless
. At the same time, unless 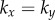 , the system will monotonically converge to either IP (
, the system will monotonically converge to either IP ( ) or AP (
) or AP (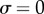 ) synchrony, depending on whether ky is larger or smaller than
) synchrony, depending on whether ky is larger or smaller than 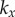 . Figure 2a–c shows the convergence to either state, for a set of initial conditions and increasing internal stiffnesses. When
. Figure 2a–c shows the convergence to either state, for a set of initial conditions and increasing internal stiffnesses. When 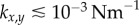 , the phase difference evolves much faster than the sum, and
, the phase difference evolves much faster than the sum, and  follows the approximate dynamics
follows the approximate dynamics
| 3.2 |
as shown in figure 2d. The instantaneous and average phase speed profile can be solved analytically (see electronic supplementary material, S3). In the case of 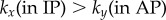 , the model predicts a lower average phase speed in IP than in AP which is in qualitative agreement with experimental observations [41]. Recent studies argue that hydrodynamics plays a negligible role in flagellar synchronization for single cells [39,40]. Without hydrodynamics, our model predicts that the effective interflagellar coupling should be given by
, the model predicts a lower average phase speed in IP than in AP which is in qualitative agreement with experimental observations [41]. Recent studies argue that hydrodynamics plays a negligible role in flagellar synchronization for single cells [39,40]. Without hydrodynamics, our model predicts that the effective interflagellar coupling should be given by 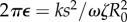 . Using the known value for Chlamydomonas,
. Using the known value for Chlamydomonas, 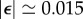 [11,41], we obtain
[11,41], we obtain 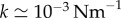 . The Young’s modulus for the bundle of striated fibres can then be estimated as
. The Young’s modulus for the bundle of striated fibres can then be estimated as 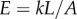 , where L and A are the length and cross-sectional area of the bundle, respectively. Taking
, where L and A are the length and cross-sectional area of the bundle, respectively. Taking 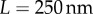 and
and 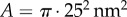 results in the value
results in the value 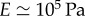 [42,47]. This is a biologically plausible estimate, midway between the elastic modulus of relaxed skeletal muscle (
[42,47]. This is a biologically plausible estimate, midway between the elastic modulus of relaxed skeletal muscle (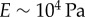 ) and elastin (
) and elastin (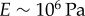 ) [43].
) [43].
Figure 2.
Synchronization dynamics for pairs of model cilia in the absence of hydrodynamic interactions. Phase sum, 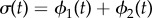 , for (a)
, for (a) 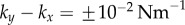 , (b)
, (b) 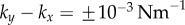 and (c)
and (c) 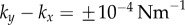 . In each case (starting with
. In each case (starting with 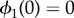 ), IP (blue) and AP (red) synchronized states are obtained for
), IP (blue) and AP (red) synchronized states are obtained for 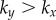 and
and 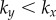 , respectively, over a timescale inversely proportional to
, respectively, over a timescale inversely proportional to 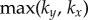 . (d) Values of
. (d) Values of 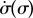 measured from numerical simulations (circles) compare favourably with equation (3.2) for sufficiently soft internal springs. Other model parameters as given in table 1. (Online version in colour.)
measured from numerical simulations (circles) compare favourably with equation (3.2) for sufficiently soft internal springs. Other model parameters as given in table 1. (Online version in colour.)
4. Stiff flagella hydrodynamics
We begin now to include the effect of hydrodynamic interactions under the assumption of artificially stiff flagella, implemented in this section by increasing the radial spring stiffness to 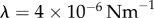 (10× the value in table 1). Increasing λ reduces the typical response time of the radial coordinate (
(10× the value in table 1). Increasing λ reduces the typical response time of the radial coordinate (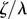 ) and, when this is much smaller than the angular timescale (
) and, when this is much smaller than the angular timescale (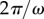 ), it allows us to simplify the dynamics by assuming an instantaneous radial response [44]. Then, to first order in the small parameter ρ, equations (2.1) imply that
), it allows us to simplify the dynamics by assuming an instantaneous radial response [44]. Then, to first order in the small parameter ρ, equations (2.1) imply that  will obey
will obey
| 4.1 |
once the dynamics have been averaged over the fast variable 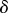 . The coefficient of
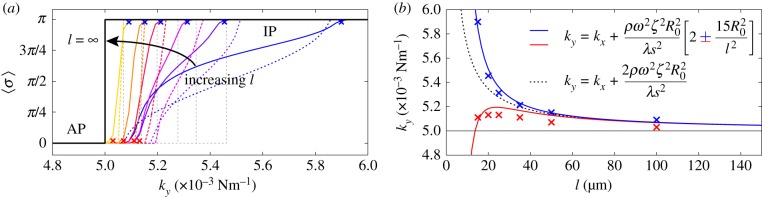
. The coefficient of 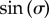 above provides an intuitive understanding of the roles of basal body coupling and elasto-hydrodynamic interactions in determining the synchronization state of the system, which is useful as a general rule of thumb to assess the relative importance of these phenomena even beyond the ‘stiff flagella’ case. Within this approximation, hydrodynamics appears to simply shift the location of the transition between AP and IP states, determined by the steady state time average
above provides an intuitive understanding of the roles of basal body coupling and elasto-hydrodynamic interactions in determining the synchronization state of the system, which is useful as a general rule of thumb to assess the relative importance of these phenomena even beyond the ‘stiff flagella’ case. Within this approximation, hydrodynamics appears to simply shift the location of the transition between AP and IP states, determined by the steady state time average 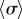 , from
, from 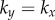 to
to 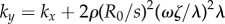 . This is indeed confirmed by simulations of the full system for large l (see figure 4b).
. This is indeed confirmed by simulations of the full system for large l (see figure 4b).
Figure 4.
Transitions between synchronization states mediated by basal body coupling. Radial dynamics are again fast compared to phase dynamics (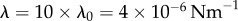 ). (a) Steady state
). (a) Steady state 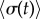 as a function of ky for various ciliary spacings (
as a function of ky for various ciliary spacings (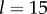 , 20, 25, 35, 50,
, 20, 25, 35, 50, 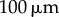 ). Numerical solutions (smooth, coloured) are shown alongside analytical predictions to leading order (dashed, black) and second order in
). Numerical solutions (smooth, coloured) are shown alongside analytical predictions to leading order (dashed, black) and second order in 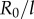 (dashed, coloured). The transition zone boundaries are quantified by
(dashed, coloured). The transition zone boundaries are quantified by 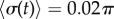 (red crosses) and
(red crosses) and 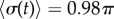 (blue crosses), respectively. (b) These are shown as a function of l, together with leading order (black) and second order in
(blue crosses), respectively. (b) These are shown as a function of l, together with leading order (black) and second order in 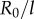 (coloured) analytical predictions. (Online version in colour.)
(coloured) analytical predictions. (Online version in colour.)
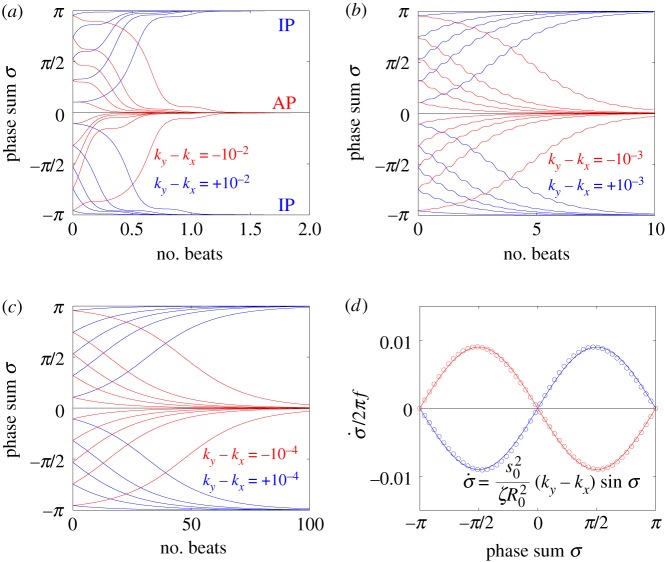
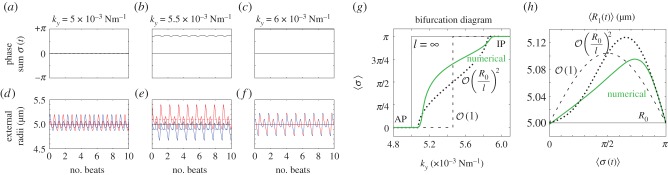
A closer inspection, however, reveals more intriguing dynamics which become particularly evident for small interflagellar separations. Figure 3a–c shows the steady state dynamics of σ for 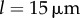 , as ky is swept across the transition. Between AP and IP coordination (figure 3a,c) there is a distinct region of ky values for which the system synchronizes in a non-trivial intermediate state (figure 3b). This is accompanied by a permanent difference in the average values of the oscillators’ radii (figure 3e), with the asymmetry depending on which of the equally probable signs of
, as ky is swept across the transition. Between AP and IP coordination (figure 3a,c) there is a distinct region of ky values for which the system synchronizes in a non-trivial intermediate state (figure 3b). This is accompanied by a permanent difference in the average values of the oscillators’ radii (figure 3e), with the asymmetry depending on which of the equally probable signs of 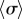 is chosen by the system. Figure 3g shows the full positive branch of
is chosen by the system. Figure 3g shows the full positive branch of 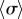 as ky is swept between AP and IP values (simulations: green solid line). This can be compared to the leading order behaviour with and without hydrodynamics (black dashed and solid lines); and the one predicted by refining equation (4.1) to next-to-leading order in
as ky is swept between AP and IP values (simulations: green solid line). This can be compared to the leading order behaviour with and without hydrodynamics (black dashed and solid lines); and the one predicted by refining equation (4.1) to next-to-leading order in 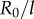 (black dotted line; see electronic supplementary material, S2)
(black dotted line; see electronic supplementary material, S2)
| 4.2 |
The semi-quantitative agreement between the simulated and predicted dependence of the steady state 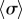 extends also to the ky-dependence of the time-averaged radii (figure 3h), which follows in the same approximation
extends also to the ky-dependence of the time-averaged radii (figure 3h), which follows in the same approximation
| 4.3 |
Figure 3.
Steady state solutions when radial dynamics are fast compared to the phase dynamics. This is achieved by setting 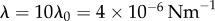 . In each simulation
. In each simulation 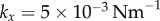 . Other parameters are shown in table 1. (a–c) Phase sum
. Other parameters are shown in table 1. (a–c) Phase sum 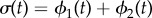 and (d–f) external rotor radii
and (d–f) external rotor radii 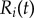 are shown as functions of time for various values of ky. (g) The mean value of phase sum
are shown as functions of time for various values of ky. (g) The mean value of phase sum 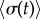 and (h) external rotor radius
and (h) external rotor radius 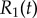 are computed from numerical solutions (green) and compared with analytical predictions of equation (4.1) (dashed) and equations (4.2), (4.3) (dotted). (Online version in colour.)
are computed from numerical solutions (green) and compared with analytical predictions of equation (4.1) (dashed) and equations (4.2), (4.3) (dotted). (Online version in colour.)
Figure 4a shows that the agreement extends across the full range of separations 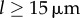 , with particularly accurate estimates for the values of ky marking the beginning and end of the transition (figure 4b). These results suggest that the simple expression in equation (4.2) captures the essential features of the dynamics and can therefore be used to analyse the nature of the transition. For small deviations
, with particularly accurate estimates for the values of ky marking the beginning and end of the transition (figure 4b). These results suggest that the simple expression in equation (4.2) captures the essential features of the dynamics and can therefore be used to analyse the nature of the transition. For small deviations 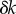 in ky around the transition from AP, equation (4.2) can be approximated as
in ky around the transition from AP, equation (4.2) can be approximated as
| 4.4 |
which therefore suggests that the emergence of non-trivial coordination follows a supercritical pitchfork bifurcation [48]. A similar argument leads to an equivalent conclusion for the bifurcation from IP as ky is decreased. AP and IP domains are therefore bounded by a pitchfork bifurcation of limit cycles.
Within the intermediate regime, the system becomes naturally bistable through a spontaneous symmetry breaking from a state where both oscillators follow the same limit cycle to one where they sustain a stable difference in their average oscillation amplitudes (see figure 3e). Transitions between homogeneous and inhomogeneous oscillation states, and bistability, have only recently been discovered in pairs of coupled limit cycle oscillators, also as a consequence of non-equilibrium symmetry breaking pitchfork bifurcations [49,50]. Here, we discover their emergence in a simple model of hydrodynamic- and basal body-coupled flagella. Intermediate equilibrium states appear when the internal elastic interaction promoting IP coordination is approximately compensated by the leading order hydrodynamic coupling favouring AP, amplifying the importance of higher-order hydrodynamic effects. In this parameter range, the oscillators are able to sustain a stable difference in their average amplitude (external rotor radii). Interestingly, the permanent difference in the average radii of the two oscillators after the bifurcation could be easily interpreted by an observer as a difference in intrinsic frequency (since 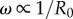 ). The rotors would then appear intrinsically different despite in fact being identical. Eventually, a sufficient increase of the internal stiffness can overcome the antagonistic effect of hydrodynamic interactions at any given separation l, and drive the system to a stable IP state.
). The rotors would then appear intrinsically different despite in fact being identical. Eventually, a sufficient increase of the internal stiffness can overcome the antagonistic effect of hydrodynamic interactions at any given separation l, and drive the system to a stable IP state.
5. The full model
We conclude by looking at the full system with realistic parameters throughout (see table 1). In this case, radial and phase dynamics have comparable timescales (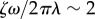 ) and the radii cannot be considered as approximately slaved to the phases anymore. Together with the sizeable radial deformations (
) and the radii cannot be considered as approximately slaved to the phases anymore. Together with the sizeable radial deformations (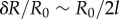 here and
here and 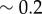 for Chlamydomonas-like
for Chlamydomonas-like 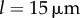 ) this results in a complex interplay between radial and phase variables and implies the need to consider the full system of governing equations (see electronic supplementary material, S1). These will be explored here through numerical simulations only.
) this results in a complex interplay between radial and phase variables and implies the need to consider the full system of governing equations (see electronic supplementary material, S1). These will be explored here through numerical simulations only.
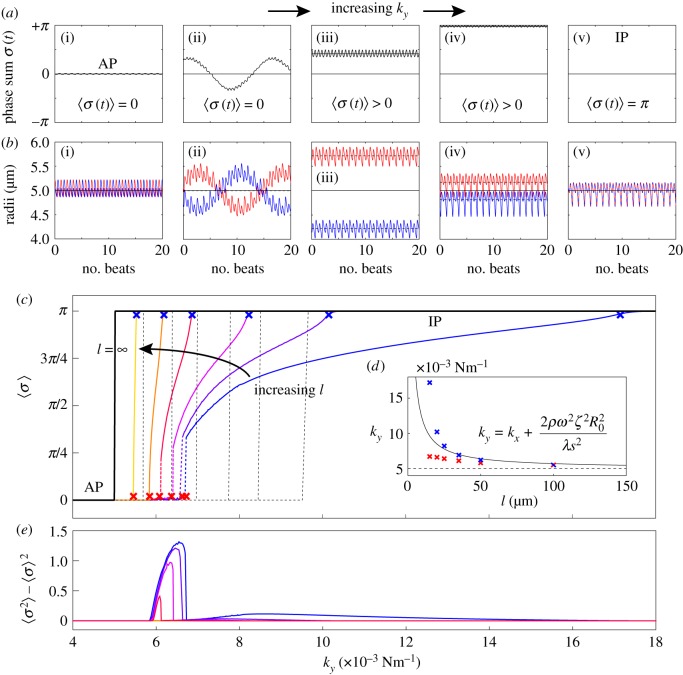
Figure 5a,b shows a representative set of curves for a ky sweep with 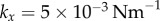 and
and 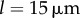 . Electronic supplementary material movies 1–5 show the dynamics for (i)–(v) respectively. Similarly to the case of stiffer flagella, low and high values of ky correspond, respectively, to AP (i) and IP (v) synchronization, and in each of these states the oscillators follow the same dynamics as one another. The average phase speed, however, is observed to be lower in IP than in AP (a difference of
. Electronic supplementary material movies 1–5 show the dynamics for (i)–(v) respectively. Similarly to the case of stiffer flagella, low and high values of ky correspond, respectively, to AP (i) and IP (v) synchronization, and in each of these states the oscillators follow the same dynamics as one another. The average phase speed, however, is observed to be lower in IP than in AP (a difference of 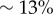 between
between 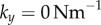 and
and 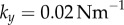 ), in qualitative agreement with experimental observations of CR mutants [41] (see electronic supplementary material, S3). In between, there is a range of ky values for which the system synchronizes around intermediate values of
), in qualitative agreement with experimental observations of CR mutants [41] (see electronic supplementary material, S3). In between, there is a range of ky values for which the system synchronizes around intermediate values of 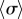 , with the two oscillators following again different limit cycles (iii,iv). A new state, however, appears as ky approaches the symmetry breaking transition from the AP side (ii). Despite corresponding formally to AP (
, with the two oscillators following again different limit cycles (iii,iv). A new state, however, appears as ky approaches the symmetry breaking transition from the AP side (ii). Despite corresponding formally to AP (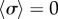 ), the system displays symmetric excursions in the relative phase difference which are long lived and not much smaller than π. In this state, the oscillators spend most of their time at values of σ far from 0, and the null average is only guaranteed by the symmetry of the dynamics. Although the system oscillates here by about
), the system displays symmetric excursions in the relative phase difference which are long lived and not much smaller than π. In this state, the oscillators spend most of their time at values of σ far from 0, and the null average is only guaranteed by the symmetry of the dynamics. Although the system oscillates here by about 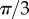 , amplitudes
, amplitudes 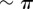 can be easily obtained just by increasing a (electronic supplementary material, figure S2). In this condition, the system will not appear synchronized in AP at all, but will rather be continuously alternating between IP at π and IP at
can be easily obtained just by increasing a (electronic supplementary material, figure S2). In this condition, the system will not appear synchronized in AP at all, but will rather be continuously alternating between IP at π and IP at 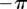 . Figure 5c,e shows that this situation is typical for all of the separations displaying a discontinuous, rather than continuous, transition out of the AP state (here all
. Figure 5c,e shows that this situation is typical for all of the separations displaying a discontinuous, rather than continuous, transition out of the AP state (here all 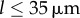 ). In the IP case, instead, the transition maintains its continuous nature throughout, and in fact the bifurcation point is still well predicted by the first order expression from equation (4.1) (see inset).
). In the IP case, instead, the transition maintains its continuous nature throughout, and in fact the bifurcation point is still well predicted by the first order expression from equation (4.1) (see inset).
Figure 5.
Basal body coupling and hydrodynamic interactions. (a) Steady state phase sum 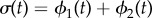 and (b) external radii
and (b) external radii 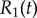 and
and 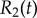 . Results are shown for
. Results are shown for 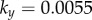 , 0.006, 0.007, 0.017,
, 0.006, 0.007, 0.017, 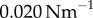 with
with 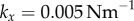 and
and 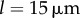 . For intermediate values of ky, the external rotors display a permanent difference in their average radii despite being identical. Electronic supplementary material movies 1–5 show the dynamics for (i)–(v), respectively. (c) Value of
. For intermediate values of ky, the external rotors display a permanent difference in their average radii despite being identical. Electronic supplementary material movies 1–5 show the dynamics for (i)–(v), respectively. (c) Value of 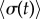 as a function of ky for various values of l (results shown for
as a function of ky for various values of l (results shown for 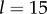 , 20, 25, 35, 50,
, 20, 25, 35, 50, 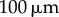 ). The transition zone boundaries are quantified by
). The transition zone boundaries are quantified by 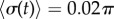 (red crosses) and
(red crosses) and 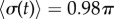 (blue crosses) respectively; dashed black lines show far-field analytical predictions to leading order (from equation (4.1)). (d) Measured boundaries compared with leading order far-field analytical results. (e) The variance of the time-dependent phase sum,
(blue crosses) respectively; dashed black lines show far-field analytical predictions to leading order (from equation (4.1)). (d) Measured boundaries compared with leading order far-field analytical results. (e) The variance of the time-dependent phase sum, 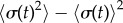 , for given values of ky and l, reveals large excursions in the phase sum prior to the bifurcation (see (a(ii)) for the raw time-dependent signal). (Online version in colour.)
, for given values of ky and l, reveals large excursions in the phase sum prior to the bifurcation (see (a(ii)) for the raw time-dependent signal). (Online version in colour.)
From the AP side, discontinuous transitions are always preceded by a region of ky values where the system displays large excursions in σ, which act as a predictor of the impending discontinuity [51]. Figure 5e shows the variance, 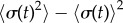 , of the time-dependent signal,
, of the time-dependent signal, 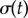 , averaged over 7 s (
, averaged over 7 s (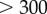 beats). The large excursions evident in figure 5a(ii) manifest in the peak of figure 5e.
beats). The large excursions evident in figure 5a(ii) manifest in the peak of figure 5e.
The presence of the discontinuity in 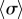 and the preceding large fluctuations depend on both the separation l and kx, as shown in figure 6 for a
and the preceding large fluctuations depend on both the separation l and kx, as shown in figure 6 for a 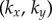 parameter sweep. For the realistic interflagellar separation (
parameter sweep. For the realistic interflagellar separation (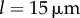 ), figure 6a shows that the region of discontinuous transition out of AP, marked by the large standard deviation of
), figure 6a shows that the region of discontinuous transition out of AP, marked by the large standard deviation of 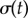 , exists only for
, exists only for 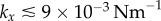 . Above this value, the bifurcation changes its nature and becomes continuous but sharp. At the slightly larger separation of
. Above this value, the bifurcation changes its nature and becomes continuous but sharp. At the slightly larger separation of 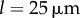 , the width of the extended transition zone observed previously for
, the width of the extended transition zone observed previously for 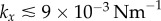 is reduced (see figures 6b, 5c). Further increasing the separation to
is reduced (see figures 6b, 5c). Further increasing the separation to 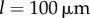 reduces hydrodynamic forces by an order of magnitude compared to the
reduces hydrodynamic forces by an order of magnitude compared to the 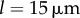 case, and for all the kx values explored, the system follows a sharp continuous transition from AP to IP as ky is increased.
case, and for all the kx values explored, the system follows a sharp continuous transition from AP to IP as ky is increased.
Figure 6.
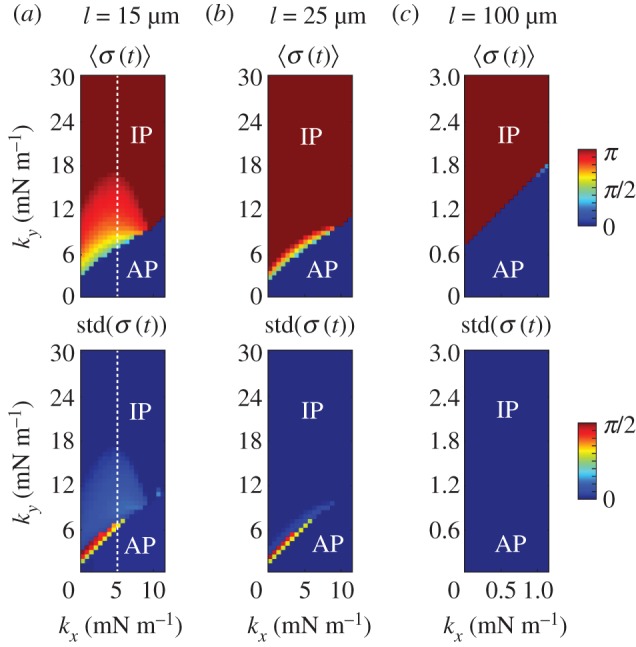
The transition between AP and IP states is mediated by internal spring constants. Mean and standard deviation of  as functions of kx and ky for external rotor separations (a)
as functions of kx and ky for external rotor separations (a) 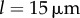 , (b)
, (b) 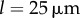 , and (c)
, and (c) 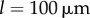 . White dotted lines correspond to the blue bifurcation plot in figure 5c. For small kx, the system is capable of supporting intermediate phase-locked states, with
. White dotted lines correspond to the blue bifurcation plot in figure 5c. For small kx, the system is capable of supporting intermediate phase-locked states, with 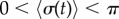 . However, for larger kx, an abrupt transition between AP and IP occurs. (Online version in colour.)
. However, for larger kx, an abrupt transition between AP and IP occurs. (Online version in colour.)
Although exploring in detail the nature of these bifurcations is beyond the scope of the present work, clear similarities with the case of stiff flagella suggest strongly that the qualitative nature of the continuous transition is the same in the two cases. We expect therefore the continuous transitions to be supercritical pitchfork bifurcations of limit cycles, inducing the observed symmetry breaking in the system (figure 5a(iii–iv)). For 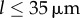 , the emergence of a discontinuity in
, the emergence of a discontinuity in 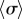 implies that decreasing kx can change the nature of the transition. Looking closely at the discontinuous case, we find that there is an extended region of overlap between the
implies that decreasing kx can change the nature of the transition. Looking closely at the discontinuous case, we find that there is an extended region of overlap between the 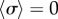 and the intermediate
and the intermediate 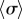 branches (see electronic supplementary material, S5). This is typical of a catastrophe-like transition which, given the
branches (see electronic supplementary material, S5). This is typical of a catastrophe-like transition which, given the 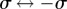 symmetry of the system, is likely to be a subcritical pitchfork bifurcation.
symmetry of the system, is likely to be a subcritical pitchfork bifurcation.
Coexistence of three different states, all of which are locally stable for the dynamics, means that the system displays multi-stability: presence of noise might then induce the system to jump between these locally stable states and therefore alternate between periods of AP synchronization an other non-trivial types of coordination, with transitions dictated by escape rate arguments [52–54].
6. Conclusion
While mechanisms for hydrodynamic-led synchronization of cilia and flagella have been extensively studied [12,14,20,21,23–27,55], the impact of direct intracellular connections on flagellar dynamics is only starting to be recognized [15,39,40]. Here we have extended a simple and popular minimal model for the hydrodynamically interacting flagella pair of Chlamydomonas to account for intracellular mechanical coupling. The clearly anisotropic ultrastructure of striated fibres [42] is mirrored in the use of a non-isotropic elastic interaction between the oscillators (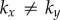 ) and results in a phase–phase coupling that can promote by itself either IP or AP synchronization, within a biologically plausible range of Young’s moduli. Transitions would then result simply through changes in the relative magnitude of kx and ky. Given that intracellular calcium can control the contraction of striated fibres in Chlamydomonas [56], we hypothesize that the transitions in coordination observed experimentally could be the result of localized apical variations in cytoplasmic
) and results in a phase–phase coupling that can promote by itself either IP or AP synchronization, within a biologically plausible range of Young’s moduli. Transitions would then result simply through changes in the relative magnitude of kx and ky. Given that intracellular calcium can control the contraction of striated fibres in Chlamydomonas [56], we hypothesize that the transitions in coordination observed experimentally could be the result of localized apical variations in cytoplasmic 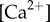 [57–59]. Natural extensions of this model to amplitude–phase coupling do not influence the leading order coordination dynamics (see electronic supplementary material, S1, for brief discussion) and have been omitted here. IP coordination has recently been proposed to result from a different nonlinear interplay between hydrodynamic and intracellular mechanical coupling [15], with AP due to either one of them operating in isolation. However, several experimental observations, from the absence of phase-locking in mutants lacking striated fibres [39,40], to the complex synchronization observed in multi-flagellated algae [40], suggest that hydrodynamics plays in fact only a minimal role in this system. The model introduced here can sustain both AP and IP states without the need for external coupling, through a mechanism potentially under the direct control of the cell. Unequal tightening of the different fibres joining the basal bodies of cells with more than two flagella could then lead to the complex synchronization patterns observed experimentally [40]. Yet, subtle hydrodynamic effects can exist and need to be investigated through dedicated experiments blocking fluid-mediated coupling between flagella. These are currently underway.
[57–59]. Natural extensions of this model to amplitude–phase coupling do not influence the leading order coordination dynamics (see electronic supplementary material, S1, for brief discussion) and have been omitted here. IP coordination has recently been proposed to result from a different nonlinear interplay between hydrodynamic and intracellular mechanical coupling [15], with AP due to either one of them operating in isolation. However, several experimental observations, from the absence of phase-locking in mutants lacking striated fibres [39,40], to the complex synchronization observed in multi-flagellated algae [40], suggest that hydrodynamics plays in fact only a minimal role in this system. The model introduced here can sustain both AP and IP states without the need for external coupling, through a mechanism potentially under the direct control of the cell. Unequal tightening of the different fibres joining the basal bodies of cells with more than two flagella could then lead to the complex synchronization patterns observed experimentally [40]. Yet, subtle hydrodynamic effects can exist and need to be investigated through dedicated experiments blocking fluid-mediated coupling between flagella. These are currently underway.
With coordination of cilia and flagella within single cells being sensitive to the direct intracellular coupling between the filaments, we believe that better understanding its emergence will eventually enable synchronization to be used as a new and sensitive probe for the intracellular mechanical state of a cell.
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Acknowledgements
M.P. gratefully acknowledges the hospitality of the School of Mathematics and Statistics from The University of Melbourne, where part of this work was done.
Data accessibility
Additional data are included in the electronic supplementary material.
Authors' contributions
M.P. and D.R.B. designed the research; M.P., D.R.B., and R.C. developed the initial model; D.R.B. and Y.L. developed the full model and performed the simulations; M.P., D.R.B. and Y.L. analysed the data and wrote the manuscript.
Competing interests
We declare we have no competing interests.
Funding
This work was supported by: a Discovery Early Career Researcher Award (DECRA) from the Australian Research Council (D.R.B.); The University of Melbourne through an Albert Shimmins International Fellowship (M.P. and D.R.B.), and a Mathematics Vacation Scholarship (Y.L.).
References
- 1.Gray J, Hancock GJ. 1955. The propulsion of sea-urchin spermatozoa. J. Exp. Biol. 32, 802–814. [Google Scholar]
- 2.Nonaka S, Shiratori H, Saijoh Y, Hamada H. 2002. Determination of left–right patterning of the mouse embryo by artificial nodal flow. Nature 418, 96–99. ( 10.1038/nature00849) [DOI] [PubMed] [Google Scholar]
- 3.Hagenlocher C, Walentek P, Müller C, Thumberger T, Feistel K. 2013. Ciliogenesis and cerebrospinal fluid flow in the developing Xenopus brain are regulated by foxj1. Cilia 2, 12 ( 10.1186/2046-2530-2-12) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Knight-Jones EW. 1954. Relations between metachronism and the direction of ciliary beat in metazoa. Q. J. Microsc. Sci. 95, 503–521. [Google Scholar]
- 5.Gueron S, Levit-Gurevich K. 1999. Energetic considerations of ciliary beating and the advantage of metachronal coordination. Proc. Natl Acad. Sci. USA 96, 12 240–12 245. ( 10.1073/pnas.96.22.12240) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tam D, Hosoi AE. 2011. Optimal feeding and swimming gaits of biflagellated organisms. Proc. Natl Acad. Sci. USA 108, 1001–1006. ( 10.1073/pnas.1011185108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Taylor GI. 1951. Analysis of the swimming of microscopic organisms. Proc. R. Soc. Lond. A 209, 447–461. ( 10.1098/rspa.1951.0218) [DOI] [Google Scholar]
- 8.Mettot C, Lauga E. 2011. Energetics of synchronized states in three-dimensional beating flagella. Phys. Rev. E 84, 061905 ( 10.1103/PhysRevE.84.061905) [DOI] [PubMed] [Google Scholar]
- 9.Michelin S, Lauga E. 2010. Efficiency optimization and symmetry-breaking in a model of ciliary locomotion. Phys. Fluids 22, 111901 ( 10.1063/1.3507951) [DOI] [Google Scholar]
- 10.Ding Y, Nawroth JC, McFall-Ngai MJ, Kanso E. 2014. Mixing and transport by ciliary carpets: a numerical study. J. Fluid Mech. 743, 124–140. ( 10.1017/jfm.2014.36) [DOI] [Google Scholar]
- 11.Goldstein RE, Polin M, Tuval I. 2009. Noise and synchronization in pairs of beating eukaryotic flagella. Phys. Rev. Lett. 103, 168103 ( 10.1103/PhysRevLett.103.168103) [DOI] [PubMed] [Google Scholar]
- 12.Uchida N, Golestanian R. 2011. Generic conditions for hydrodynamic synchronization. Phys. Rev. Lett. 106, 058104 ( 10.1103/PhysRevLett.106.058104) [DOI] [PubMed] [Google Scholar]
- 13.Geyer VF, Jülicher F, Howard J, Friedrich BM. 2013. Cell-body rocking is a dominant mechanism for flagellar synchronization in a swimming alga. Proc. Natl Acad. Sci. USA 110, 18 058–18 063. ( 10.1073/pnas.1300895110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Brumley DR, Wan KY, Polin M, Goldstein RE. 2014. Flagellar synchronization through direct hydrodynamic interactions. eLife 3, e02750 ( 10.7554/eLife.02750) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Klindt GS, Ruloff C, Wagner C, Friedrich BM. 2017. In-phase and anti-phase flagellar synchronization by waveform compliance and basal coupling. New J. Phys. 19, 113052 ( 10.1088/1367-2630/aa9031) [DOI] [Google Scholar]
- 16.Rothschild V. 1949. Measurement of sperm activity before artificial insemination. Nature 163, 358–359. ( 10.1038/163358a0) [DOI] [PubMed] [Google Scholar]
- 17.Riedel IH, Kruse K, Howard J. 2005. A self-organized vortex array of hydrodynamically entrained sperm cells. Science 309, 300–303. ( 10.1126/science.1110329) [DOI] [PubMed] [Google Scholar]
- 18.Bruot N, Cicuta P. 2016. Realizing the physics of motile cilia synchronization with driven colloids. Annu. Rev. Condens. Matter Phys. 7, 323–348. ( 10.1146/annurev-conmatphys-031115-011451) [DOI] [Google Scholar]
- 19.Brumley DR, Rusconi R, Son K, Stocker R. 2015. Flagella, flexibility and flow: physical processes in microbial ecology. Eur. Phys. J. Special Topics 224, 3119–3140. ( 10.1140/epjst/e2015-50138-9) [DOI] [Google Scholar]
- 20.Vilfan A, Jülicher F. 2006. Hydrodynamic flow patterns and synchronization of beating cilia. Phys. Rev. Lett. 96, 058102 ( 10.1103/PhysRevLett.96.058102) [DOI] [PubMed] [Google Scholar]
- 21.Uchida N, Golestanian R. 2012. Hydrodynamic synchronization between objects with cyclic rigid trajectories. Eur. Phys. J. E 35, 135 ( 10.1140/epje/i2012-12135-5) [DOI] [PubMed] [Google Scholar]
- 22.Brumley DR, Polin M, Pedley TJ, Goldstein RE. 2012. Hydrodynamic synchronization and metachronal waves on the surface of the colonial alga Volvox carteri. Phys. Rev. Lett. 109, 268102 ( 10.1103/PhysRevLett.109.268102) [DOI] [PubMed] [Google Scholar]
- 23.Lagomarsino MC, Jona P, Bassetti B. 2003. Metachronal waves for deterministic switching two-state oscillators with hydrodynamic interaction. Phys. Rev. E 68, 021908 ( 10.1103/PhysRevE.68.021908) [DOI] [PubMed] [Google Scholar]
- 24.Lenz P, Ryskin A. 2006. Collective effects in ciliar arrays. Phys. Biol. 3, 285–294. ( 10.1088/1478-3975/3/4/006) [DOI] [PubMed] [Google Scholar]
- 25.Wollin C, Stark H. 2011. Metachronal waves in a chain of rowers with hydrodynamic interactions. Eur. Phys. J. E 34, 42 ( 10.1140/epje/i2011-11042-7) [DOI] [PubMed] [Google Scholar]
- 26.Brumley DR, Bruot N, Kotar J, Goldstein RE, Cicuta P, Polin M. 2016. Long-range interactions, wobbles, and phase defects in chains of model cilia. Phys. Rev. Fluids 1, 081201(R) ( 10.1103/PhysRevFluids.1.081201) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kotar J, Leoni M, Bassetti B, Lagomarsino MC, Cicuta P. 2010. Hydrodynamic synchronization of colloidal oscillators. Proc. Natl Acad. Sci. USA 107, 7669–7673. ( 10.1073/pnas.0912455107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Di Leonardo R, Búzás A, Kelemen L, Vizsnyiczai G, Oroszi L, Ormos P. 2012. Hydrodynamic synchronization of light driven microrotors. Phys. Rev. Lett. 109, 034104 ( 10.1103/PhysRevLett.109.034104) [DOI] [PubMed] [Google Scholar]
- 29.Uchida N, Golestanian R. 2010. Synchronization and collective dynamics in a carpet of microfluidic rotors. Phys. Rev. Lett. 104, 178103 ( 10.1103/PhysRevLett.104.178103) [DOI] [PubMed] [Google Scholar]
- 30.Kotar J, Debono L, Bruot N, Box S, Phillips D, Simpson S, Hanna S, Cicuta P. 2013. Optimal hydrodynamic synchronization of colloidal rotors. Phys. Rev. Lett. 111, 228103 ( 10.1103/PhysRevLett.111.228103) [DOI] [PubMed] [Google Scholar]
- 31.Jeanneret R, Contino M, Polin M. 2016. A brief introduction to the model microswimmer Chlamydomonas reinhardtii. Eur Phys. J. Special Topics 225, 2141–2156. ( 10.1140/epjst/e2016-60065-3) [DOI] [Google Scholar]
- 32.Goldstein RE. 2015. Green algae as model organisms for biological fluid dynamics. Annu. Rev. Fluid Mech. 47, 343–375. ( 10.1146/annurev-fluid-010313-141426) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ringo DL. 1967. Flagellar motion and fine structure of the flagellar apparatus in Chlamydomonas. J. Cell Biol. 33, 543–571. ( 10.1083/jcb.33.3.543) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rüffer U, Nultsch W. 1998. Flagellar coordination in Chlamydomonas cells held on micropipettes. Cell Motil. Cytoskeleton 41, 297–307. ( 10.1002/(SICI)1097-0169(1998)41:4%3C297::AID-CM3%3E3.0.CO;2-Y) [DOI] [PubMed] [Google Scholar]
- 35.Rüffer U, Nultsch W. 1987. Comparison of the beating of cis- and trans-flagella of Chlamydomonas cells held on micropipettes. Cell Motil. Cytoskeleton 7, 87–93. ( 10.1002/cm.970070111) [DOI] [PubMed] [Google Scholar]
- 36.Polin M, Tuval I, Drescher K, Gollub JP, Goldstein RE. 2009. Chlamydomonas swims with two ‘gears’ in a eukaryotic version of run-and-tumble locomotion. Science 325, 487–490. ( 10.1126/science.1172667) [DOI] [PubMed] [Google Scholar]
- 37.Goldstein RE, Polin M, Tuval I. 2011. Emergence of synchronized beating during the regrowth of eukaryotic flagella. Phys. Rev. Lett. 107, 148103 ( 10.1103/PhysRevLett.107.148103) [DOI] [PubMed] [Google Scholar]
- 38.Son K, Brumley DR, Stocker R. 2015. Live from under the lens: exploring microbial motility with dynamic imaging and microfluidics. Nat. Rev. Microbiol. 13, 761–775. ( 10.1038/nrmicro3567) [DOI] [PubMed] [Google Scholar]
- 39.Quaranta G, Aubin-Tam M-E, Tam D. 2015. Hydrodynamics versus intracellular coupling in the synchronization of eukaryotic flagella. Phys. Rev. Lett. 115, 238101 ( 10.1103/PhysRevLett.115.238101) [DOI] [PubMed] [Google Scholar]
- 40.Wan KY, Goldstein RE. 2016. Coordinated beating of algal flagella is mediated by basal coupling. Proc. Natl Acad. Sci. USA 113, E2784–E2793. ( 10.1073/pnas.1518527113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Leptos KC, Wan KY, Polin M, Tuval I, Pesci AI, Goldstein RE. 2013. Antiphase synchronization in a flagellar-dominance mutant of Chlamydomonas. Phys. Rev. Lett. 111, 158101 ( 10.1103/PhysRevLett.111.158101) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wright RL, Chojnacki B, Jarvik JW. 1983. Abnormal basal-body number, location, and orientation in a striated fiber-defective mutant of Chlamydomonas reinhardtii. J. Cell Biol. 96, 1697–1707. ( 10.1083/jcb.96.6.1697) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kamm R, Grodzinsky A. 2015. Molecular, cellular, and tissue biomechanics. MIT OpenCourseWare. Cambridge, MA: Massachusetts Institute of Technology. [Google Scholar]
- 44.Niedermayer T, Eckhardt B, Lenz P. 2008. Synchronization, phase locking, and metachronal wave formation in ciliary chains. Chaos 18, 037128 ( 10.1063/1.2956984) [DOI] [PubMed] [Google Scholar]
- 45.Rüffer U, Nultsch W. 1997. Flagellar photoresponses of ptx1, a nonphototactic mutant of Chlamydomonas. Cell Motil. Cytoskeleton 37, 111–119. ( 10.1002/(SICI)1097-0169(1997)37:2%3C111::AID-CM3%3E3.0.CO;2-B) [DOI] [PubMed] [Google Scholar]
- 46.Inouye I. 1993. Flagella and flagellar apparatuses of algae. In Ultrastructure of microalgae (ed. T Berner), pp. 99–133. Boca Raton, FL: CRC Press.
- 47.Landau LD, Lifshitz EM. 1986. Course of theoretical physics. In Theory of elasticity, 3rd edn, vol. 7. Oxford, UK: Butterworth-Heinemann.
- 48.Strogatz SH. 1994. Nonlinear dynamics and chaos. Cambridge, MA: Perseus Books Publishing, LLC. [Google Scholar]
- 49.Röhm A, Lüdge K, Schneider I. 2018. Bistability in two simple symmetrically coupled oscillators with symmetry-broken amplitude- and phase-locking. Chaos 28, 063114 ( 10.1063/1.5018262) [DOI] [PubMed] [Google Scholar]
- 50.Banerjee T, Biswas D, Ghosh D, Bandyopadhyay B, Kurths J. 2018. Transition from homogeneous to inhomogeneous limit cycles: effect of local filtering in coupled oscillators. Phys. Rev. E 97, 042218 ( 10.1103/PhysRevE.97.042218) [DOI] [PubMed] [Google Scholar]
- 51.Scheffer M. et al. 2009. Early-warning signals for critical transitions. Nature 461, 53–59. ( 10.1038/nature08227) [DOI] [PubMed] [Google Scholar]
- 52.Thompson JMT, Sieber J. 2011. Predicting climate tipping as a noisy bifurcation: a review. Int. J. Bifurcation Chaos 21, 399–423. ( 10.1142/S0218127411028519) [DOI] [Google Scholar]
- 53.Miller NJ, Shaw SW. 2012. Escape statistics for parameter sweeps through bifurcations. Phys. Rev. E 85, 046202 ( 10.1103/PhysRevE.85.046202) [DOI] [PubMed] [Google Scholar]
- 54.Herbert C, Bouchet F. 2017. Predictability of escape for a stochastic saddle-node bifurcation: when rare events are typical. Phys. Rev. E 96, 030201(R) ( 10.1103/PhysRevE.96.030201) [DOI] [PubMed] [Google Scholar]
- 55.Elgeti J, Gompper G. 2013. Emergence of metachronal waves in cilia arrays. Proc. Natl Acad. Sci. USA 110, 4470–4475. ( 10.1073/pnas.1218869110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Harris EH, Stern DB, Witman GB. 2009. The chlamydomonas sourcebook, vol. 1 San Diego, CA: Elsevier. [Google Scholar]
- 57.Collingridge P, Brownlee C, Wheeler GL. 2013. Compartmentalized calcium signaling in cilia regulates intraflagellar transport. Curr. Biol. 23, 2311–2318. ( 10.1016/j.cub.2013.09.059) [DOI] [PubMed] [Google Scholar]
- 58.Wheeler GL, Joint I, Brownlee C. 2008. Rapid spatiotemporal patterning of cytosolic Ca2+ underlies flagellar excision in Chlamydomonas reinhardtii. Plant J. 53, 401–413. ( 10.1111/j.1365-313X.2007.03349.x) [DOI] [PubMed] [Google Scholar]
- 59.Wheeler GL, Brownlee C. 2008. Ca2+ signalling in plants and green algae—changing channels. Trends Plant Sci. 13, 506–514. ( 10.1016/j.tplants.2008.06.004) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Additional data are included in the electronic supplementary material.