Structural Determination of Antioxidant and Anticancer Flavonoid Rutin in Solution through DFT Calculations of ¹H NMR Chemical Shifts

Abstract

As the knowledge of the predominant molecular structure of antioxidant and anticancer flavonoid rutin in solution is very important for understanding the mechanism of action, a quantum chemical investigation of plausible rutin structures including solvent effects is of relevance. In this work, DFT calculations were performed to find possible minimum energy structures for the rutin molecule. ¹H NMR chemical shift DFT calculations were carried out in DMSO solution using the polarizable continuum model (PCM) to simulate the solvent effect. Analysis of the experimental and theoretical ¹H NMR chemical shift profiles offers a powerful fingerprint criterion to determine the predominant molecular structure in solution. Therefore, our aim is to find the best match between experimental (in DMSO‐d) and theoretical (PCM–DMSO) ¹H NMR spectrum profiles. Among 34 optimized structures located on the potential energy surface, we found that structure 32, with a B‐ring deviated 30° from a planar configuration (geometry usually assumed for polyphenols), showed an almost perfect agreement with experimental the ¹H NMR pattern when compared to the corresponding fully optimized planar geometry. This structure is also predicted as the global minimum based on room‐temperature Gibbs free energy calculations in solution and, therefore, should be experimentally observed. This is new and valuable structural information regarding structure–activity relationship studies, and such information is hard to obtain by experimentalists without the aid of the X‐ray diffraction technique.

1. Introduction

Flavonoids belong to a large subclass of natural polyphenols with relatively low molar mass, which can be found in vegetables, fruits, and tea leaves.1, 2, 3, 4, 5 The occurrence of these compounds in fruits, for example, depends on several factors that may affect their biosynthesis, such as ambient temperature, incident light intensity, local latitude, and forms of cultivation.6 According to the literature, flavonoids have antitumor,7, 8, 9, 10 antimicrobial,11 antioxidant12, 13, 14, 15 and anti‐inflammatory16 activities. However, it is proven that most of the biological properties of these polyphenols are associated with its high antioxidant potential.13, 15 One of the mechanisms of antioxidant action is related to chelation of transition metals in low oxidation state (Zn²⁺, Fe²⁺ and Cu²⁺, for example), reducing the concentration of these ions in specific parts of the human body. These metals can participate in oxidation reactions involving reactive oxygen species (such as H₂O₂), producing a free radical (Fenton reaction).14, 17 The release of these free radicals may be greater in hydrogen peroxide accumulation sites in the human body, for example, in dopaminergic neurons of nerve tissue.

The base nucleus of the flavonoids (the benzopyrone group) may present several functional groups that give rise to the classes of flavonoids, making this family of compounds one of the most complex in the area of natural products. The rutin (Scheme 1), belonging to the flavonols class, contains two hydroxyls in A‐ring (positions 5 and 7), and two other hydroxyl substituents on B‐ring (positions 3′ and 4′). These characteristics confer to the rutin molecule a high ability to act as a ligand in coordination compounds, with two chelating sites, named site I (C4O and C5O) and site II (C4′O and C5′O or catechol moiety). It can be found in the literature, synthesis and characterization of rutin complexes with Zn^II,8 Cu^II,18 Fe^II,19 Sn^II,16 Al^III[17] and other metal ions, revealing coordination compounds with various ligand–metal stoichiometries (1:1, 1:2, 2:1) and spatial conformations. According to Ikeda et al.,8 the formation of coordination compounds with rutin greatly increases the antioxidant power and consequently other properties (especially antitumor activity), with the rutin‐zinc(II) complexes showing significant higher antioxidant activity, and no toxicity against normal cells of rat organ and potential cytotoxicity against the cancer cells.

Scheme 1.

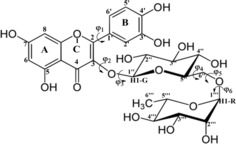
Rutin: Numbering scheme and dihedral angle (φ_i) definition.

The literature9 reports that the planarity of the C ring significantly increases the antioxidant activity of the flavonoid molecules and this property may be related to other stereochemical characteristics. This shows the importance of understanding the chemical structure of polyphenols and recipient species (such as genes and proteins, for example) in the elucidation of the antitumor action of flavonoids. QSAR (Quantitative Structure‐Activity Relationship) studies, in which it is possible to quantify a biological property varying some structural characteristic (functional group and molecular geometry, for example), were used by Farkas et al.15 to analyze the antioxidant activities of dozens of flavonoids that have different functional groups and substituents. Atrahimovich et al.20 used the same type of study to investigate 12 flavonoid molecules, and in one of the proposed mechanisms it was established that ring A contributes significantly to the hydrophobic interaction of flavonoid with intracellular proteins and enzymes. Therefore, the conformation of flavonoids is another decisive factor in the understanding of their antioxidant activity and consequently other biological properties.

Crystallographic analysis by X‐ray diffraction is an important tool for obtaining structural data of solid phase flavonoids.19 Another useful technique in the structural description of organic molecules is nuclear magnetic resonance spectroscopy (NMR). Detailed analysis of NMR chemical shifts may provide specific information regarding molecular structure.21, 22, 23 Molecular modeling associated with density functional theory (DFT) has been widely employed by our group24, 25, 26, 27, 28, 29, 30, 31 in studies at the molecular level of the action mechanism of potential drugs candidates for the treatment of cancer and other diseases. De Souza et al.30 used B3LYP/6‐31G(d,p) calculations of ¹H NMR chemical shifts for the flavonoids catechin, quercetin and kaempferol to evaluate the conformation adopted by these molecules in solution. The authors showed that rotation of B‐ring, causing a deviation of the planar configuration of the flavonoid molecule, is necessary to reproduce the experimental ¹H NMR spectrum in solution. These new structural data for flavonoids may be relevant in theoretical studies of the formation of metal complexes and antitumor action of these compounds. Recently, our group reported a DFT conformational analysis study31 involving thermodynamics and spectroscopic characterization of twenty structures of zinc(II) complexes formed by the flavonoid kaempferol in solution. We have shown that theoretical calculations of IR and UV/Vis absorption bands are able to indicate the preferred site for the coordination of the metal by the kaempferol ligand. In addition, the ¹H NMR results showed that the ligand does not assume a planar conformation in solution after the formation of the complexes, as reported by recent experimental work. Therefore, we believe that the combination of theoretical and experimental NMR spectra can be a good procedure to determine the conformation of free flavonoids and flavonoid‐metal coordination compounds in solution, which is a hard task for experimentalists. It is worth to mention the work addressing the complete prediction of NMR spectra of complex organic molecules trough DFT calculations reported by Bagno et al.32 Comparisons between theoretical and experimental ¹H NMR and ¹³C NMR chemical shift data for a series of complex organic molecules, naturally occurring, carried out using various functionals led to the conclusion that a considerable degree of accuracy can be attained by DFT NMR calculations. According to the authors the origin of observed discrepancies from experimental data can be attributed to incomplete modeling of conformational and specific solvent effects.

To clarify the mechanism of rutin adsorption on functionalized resins, Ye et al.33 through DFT studies, observed that the most stable form of the adsorbed rutin molecule is that in which the molecule has a hydrogen bond between carbonyl and the hydroxyl C5OH groups (see Scheme 1) and with the carboxyl group of the resins. Thus, inter and intramolecular interactions strongly influence the molecular geometry of the rutin molecule. Payán‐Gómez et al.34 carried out a theoretical study of the structural, physicochemical and spectroscopic properties of the rutin molecule and revealed another type of intramolecular hydrogen bond between the C4′OH and C3′OH hydroxyls, which in turn interact with a hydroxyl of the glycolic group (C2′′′OH, see Scheme 1). According to the authors, such interactions may be related to greater solubility of the rutin in water and in alcoholic solvents (such as, methanol and ethanol), as confirmed by calculation of solvation energies.

In the light of previous reported studies, and due to the variety of conformations and their dependent chemical and biological properties, a systematic and detailed structural investigation of flavonoids is very much welcome. Therefore, in this work we carried out a reasonable search for possible minimum energy structures on the potential energy surface (PES) for the rutin molecule employing the DFT methodology.35 Then, the optimized structures were used to perform a thermodynamic analysis using standard statistical thermodynamics formalism36 and calculation of ¹H NMR spectra in DMSO solution using the polarizable continuum model (PCM)37 to simulate the solvent effect. Our extensive DFT gas phase conformational analysis of rutin produced 34 unique optimized structures. Through comparisons with experimental ¹H NMR spectrum in DMSO‐d solution we were able to elucidate the preferred conformation of rutin molecule in solution (with the aid of DFT PCM‐DMSO NMR calculations), which exhibits the best match with observed ¹H NMR profile in solution. Difficulties naturally arise for experimental structural determination, and theoretical investigation, due to the high flexibility of the molecule with six distinct inter‐ring torsion angles (see Scheme 1) what open the possibility of many conformations for this polyphenol.

Computational Details

The initial step in the conformational analysis procedure for rutin molecule, which has a high degree of flexibility (see Scheme 1), was a rigid scan calculation (starting from a random optimized structure) varying each of the six torsion angles indicated in Scheme 1 from 0° to 360° in step size of 10°, to sample the likely local minima on the potential energy curve (PEC), using the hybrid B3LYP functional38, 39 and 6‐31G(d,p) basis set.40 The 14 equilibrium structures located on the PEC, varying the torsion angles (φ₁, φ₂, φ₃, φ₄, φ₅ and φ₆) independently with the CH₃‐C5′′′ group in axial position (see Scheme 1), are indicated in Figure 1 (named with odd labels: M1, M3, …, M27). There are 14 equivalent minima with the CH₃‐C5′′′ group in equatorial position (named with even labels: M2, M4, …, M28). These initial 28 geometries were fully optimized at the B3LYP/6‐31G(d,p) level of theory, followed by harmonic frequency calculations characterizing them as a true minimum on the PES. The optimized torsion angles for eight unique molecular structures (CH₃‐C5′′′ group axial) found after full geometry optimization are given in Table 1 (named 1, 5, 11, 15, 17, 21, 23 and 27), along with relative energy and Gibbs free energy (ΔG) values, gas phase and PCM‐H₂O values. To further extend the conformational search a combination of the six optimized torsion angles (φ_i) was used to generate new inputs for geometry re‐optimization leading to the location of additional three distinct lower energy equilibrium structures with the CH₃‐C5′′′ group in axial position, named 29, 31 and 33 (with corresponding equatorial forms: 30, 32, 34). These results are given in the second part of Table 1, showing that structure 33 is the lowest energy minimum. There are eleven equivalent structures but with the CH₃‐C5′′′ group in equatorial position all having lower energy than axial forms (2, 6, 12, 16, 18, 22, 24, 28, 30, 32 and 34), with structure 34 being the global minimum among all thirty‐four optimized rutin structures. The torsion angles and energy data for all 34 structures are given as Supporting Information (Table S1). To improve the description of conformer relative energies, the M062x functional based on the meta‐GGA‐approximation, developed by Zhao and Truhlar,41 was also used in single‐point calculations at the B3LYP/6‐31G(d,p) optimized structures. This DFT functional was reported to perform well for the prediction of general trends in the conformer relative energies and locating the global minimum conformer, being adequate in situations where dispersion interactions is relevant to the conformer energetics.42 In addition, we also used the B97D functional due to Grimme and co‐workers43 which includes dispersion contribution. Since intramolecular H‐bond interactions may play a role for rutin molecule the use of these improved functionals seems appropriated.

Figure 1.

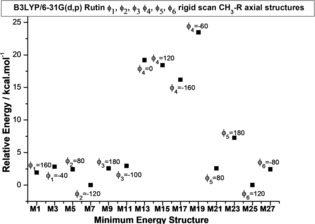
Rutin local minima calculated through B3LYP/6‐31G(d,p) rigid scan jobs (varying dihedral angles φ₁, φ₂, φ₃, φ₄, φ₅ and φ₆ as indicated), with the CH₃–C5′′′ group in the axial position. The local minima (M_i) structures are indicated. There are 14 equivalent minima with the CH₃–C5′′′ group in the equatorial position (named: M2, M4, M6, M8, M10, M12, M14, M16, M18, M20, M22, M24, M26, M28).

Table 1.

B3LYP/6‐31G(d,p) fully optimized dihedral angles (φ₁ to φ₆ in degrees) and relative energies (ΔE _rel and ΔG _rel, in kcal mol⁻¹) for eight possible distinct configurations of the sugar moieties in the rutin molecule, with the CH₃–C5′′′ group in axial position, located on the PES. There are eight equivalent structures but with the CH₃–C5′′′ group in equatorial position having lower energy than axial forms (2, 6, 12, 16, 18, 22, 24 and 28). In the second part of the Table fully optimized geometries using as input combinations of φ_i's optimized torsion angles from structures 1 to 27 are given. There are three equivalent structures but with the CH₃–C5′′′ group in equatorial position having lower energy than axial forms (30, 32 and 34).

Rutin	Rotating	Optimized dihedral angles [°]						ΔE rel [a,c] [kcal mol−1]		ΔG rel [b]
molecule	dihedral angle [°]	φ1	φ 2	φ 3	φ 4	φ 5	φ 6	Vacuum	PCM (H2O)	PCM (H2O)
Fully optimized geometries using minimum energy input structures from the rigid 1D scan (Figure 1)
1	φ1: M1‐axial	162.3	−80.2	176.3	−169.3	−68.8	−44.3	19.7	17.6	15.9
5 [d]	φ2: M3‐axial	160.4	124.4	134.2	−169.2	−68.9	−43.3	13.5	13	11.6
11 [d]	φ3: M6‐axial	154.6	−97.2	−64.0	−170.0	−68.0	−46.4	14.9	15.8	14.1
15 [e]	φ4: M8‐axial	156.0	−75.5	170.7	68.9	−83.3	−35.7	14.6	15.2	16.7
17 [d]	φ4: M9‐axial	161.7	−79.7	175.0	−72.4	−102.9	−25.4	19.3	15.9	14.5
21 [f]	φ5: M11‐axial	162.2	−80.8	175.3	173.3	157.3	−83.6	14.1	10.8	9.6
23	φ5: M12‐axial	162.8	−81.0	176.1	162.7	−165.9	−59.9	20	16.8	13.9
27 [e]	φ6: M14‐axial	164.5	−85.1	177.1	116.2	−77.8	−156.6	16.4	17.3	15.3
Geometries optimized using input combinations of φ1, φ2, φ3, φ4, φ5 and φ6 from structures 1 to 27
29g	E‐ax (φ5: M11‐eq)	−145.4	106.8	−86.7	−170.0	−100.6	177.4	16.1	14.6	11.9
31g	E‐ax (φ5: M11‐eq)	−174.5	114.2	138.2	−168.7	−98.4	177.9	7.7	6.4	5.4
33g	H‐ax (φ5: M11‐eq)	−171.6	109.1	138.9	−60.9	−125.5	−168.8	0	0	0

[a] The PCM‐water relative energy values are evaluated as single‐point calculations using gas phase optimized geometries. [b] ΔG _rel (kcal mol⁻¹) in PCM‐water are evaluated with gas phase thermal corrections (p=1 atm., T=298.15 K). [c] The corresponding PCM‐DMSO relative energies are very similar to PCM–water values (the same energetic trend). [d] Unique spatial arrangement: 5/6; 11/12; 17/18 (axial and equivalent equatorial forms are separated by slash). [e] Group 2 structures (15/16=19/20; 27/28). [f] Group 1 structures (1/2=3/4=7/8=9/10=13/14=25/26; 21/22; 23/24). [g] Unique structures obtained through re‐optimization combining different dihedral angles: 29/30, 31/32, 33/34.

Having established that there are thirty four possible conformations for rutin molecule, the Gauge‐Independent Atomic Orbital (GIAO) method implemented by Wolinski et al.44 was used for calculation of ¹H magnetic shielding constants (σ), with chemical shifts (δ), obtained on a δ‐scale relative to the TMS, taken as reference, at the B3LYP/6‐31G(d,p) level including solvent effect using the PCM model37 and DMSO solvent (dielectric constant, ϵ=46.826), through single point calculation on optimized structures in the vacuum. In our previous work on NMR spectra of l‐quebrachitol molecule22 we also performed geometry optimization considering the solvent effect using the PCM model. The deviation between PCM single point and PCM fully optimized structure ¹H NMR chemical shift values was insignificant. Therefore, in this work we carried out geometry optimization calculations in the vacuum. All calculations were performed with the Gaussian 09 package.45

2. Results and Discussion

B3LYP/6‐31G(d,p) optimized torsion angles φ_i (°) for 14 distinct configurations of rutin molecule with CH₃‐R in axial position (see Scheme 1), using as input initial guess structures obtained from rigid scan, are given in Figure 2. There are corresponding 14 conformers with the CH₃–R in equatorial position (see Scheme 1). The following structures are equivalent: 1=3=7=9=13=25; 15=19. These eight unique configurations are highlighted in bold, with the torsion angles circled: 1, 5, 11, 15, 17, 21, 23 and 27. B3LYP/6‐31G(d,p) fully optimized structures showing the possible distinct configurations of sugar moieties (highlighted in tube modes) for rutin molecule (CH₃–C5′′′ group axial indicated) are shown in Figures 3 a–h. The equivalent structures with the CH₃–C5′′′ group in equatorial position are indicated in parenthesis (even labels). Intra‐molecular sugar‐sugar H‐bonds are indicated by dotted line. Additional three optimized unique structures obtained from combinations of six φ_i dihedral angles from structures 1 to 28 are shown in Figure 3 j–l (there are three equivalent equatorial structures, named with even labels). The eleven different spatial arrangements of sugar moieties shown in Figure 3 sampled the plausible conformations of the rutin molecule that may exist in the gas phase.

Figure 2.

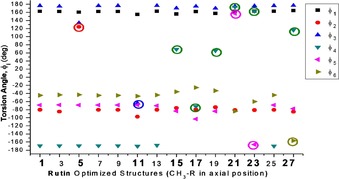
B3LYP/6‐31G(d,p) optimized torsion angles φ_i (°) for 14 distinct configurations of rutin molecule with CH₃–R in the axial position (see Scheme 1), using as input initial guess structures obtained from rigid scan (Figure 1). The unique configurations are highlighted in bold and the angles circled.

Figure 3.

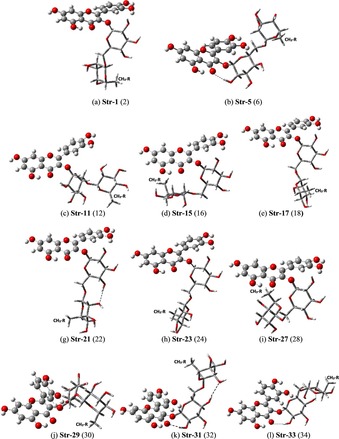
B3LYP/6‐31G(d,p) fully optimized structures showing the 11 possible distinct configurations of sugar moieties (highlighted in tube modes) for rutin molecule (CH₃–C5′′′ group axial indicated). The equivalent structures with the CH₃–C5′′′ group in the equatorial position are indicated in parenthesis. Intra‐molecular sugar–sugar H bonds are indicated by dotted line.

Experimental (in [D6]DMSO)46 and B3LYP/6‐31G(d,p)‐PCM‐DMSO ¹H NMR spectra for twelve selected distinct optimized spatial arrangements out of 34 local minima located on the PES for the rutin molecule are shown in Figure 4. The φ₁ and φ₂ inter‐ring torsion angles (°) are also given (the non‐rotated angles are indicated by the label OPT). R and G represent signals from rhamnose and glucose moieties, respectively, and CH₃R the methyl (C6′′′) hydrogen signals. The H2′′–H5′′ (G) and H2′′′–H5′′′ (R) C−H protons are grouped together and underlined. In a previous experimental study for rutin47 ¹H NMR chemical shift data for H2′′–H5′′ and H2′′′–H5′′′ protons were not provided. In Ref. 46 Napolitano et al reported complete assignments for all C−H protons, which was used as a reference experimental source of information on ¹H NMR chemical shift for rutin molecule in DMSO solution.

Figure 4.

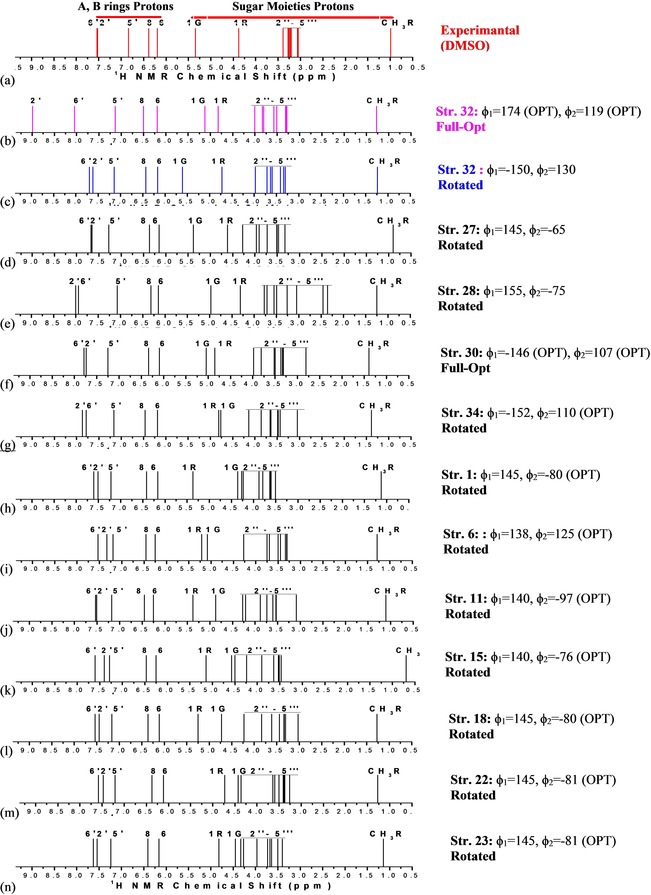
Experimental (in [D6]DMSO) from Ref. 46 (a) and B3LYP/6‐31G(d,p) PCM–DMSO ¹H NMR spectra for the 12 selected B‐ring rotated distinct optimized spatial arrangements out of 34 local minima located on the PES for the rutin molecule (c–n). B3LYP spectrum for the fully optimized planar structure 32 is shown for comparison (b). The φ₁ and φ₂ inter‐ring torsion angles (°) are also given.

With exception of fully optimized structure 30, where the B‐ring is not coplanar with A and C rings (φ₁=−146°), φ₁ and/or φ₂ torsion angles were rotated to reach better agreement with experimental chemical shift data for H2′ and H6′ protons. ¹H NMR spectra for non‐rotated (almost planar) structure 32 is also given for reason of comparison (Figure 4 b) revealing that protons H2′ and H6′ are misplaced leading to a wrong NMR profile compared to experiment. All fully optimized rutin structure (except for structure 30) exhibit the same wrong ¹H NMR profile for A–B ring protons (See Figures S1 and S2, Supporting Information). By comparing Figure 4 b (fully optimized structure) and Figure 4 c (rotated structure), the non‐coplanarity of the A and B rings in DMSO solution is promptly seen, which is new and relevant information, regarding structure–activity relationship studies. A nice agreement with experiment for sugar moieties ¹H NMR profile is strong evidence that a given rotated rutin conformation should be present in the experimental sample used in the NMR experiment. The relative position of 1G and 1R protons (see Scheme 1) can be used to rule out some conformers. It can be seen from Figure 4 c–n that the structures 1, 6, 11, 15, 18, 22 and 23 can be discarded. Structure 34, which is the global minimum on the B3LYP/6‐31G(d,p) rutin PES (in the vacuum), shows the wrong position of 1G and 1R protons signals. Visual comparison between experimental and theoretical line spectra for the remaining structures reveals that conformations 32 and 27 are the preferred ones, having the best fit with ¹H NMR chemical shift experimental data for all protons (A–B rings, 1G, 1R and sugar moieties) and following very closely the experimental pattern.

The agreement with experimental ¹H NMR signals for rutin lateral chain protons could be improved using explicit solvent molecules as reported in Ref. 27 for l‐quebrachitol, where 50 water molecules surrounded the solute embedded in a continuum model (PCM). Such approach involves a high computational demand and according to the results from Ref. 27 is not strictly necessary. It was found that the PCM model provides a very reasonable account of the solvent effect on the calculation of NMR spectra for organic molecules. The fine adjustment in the DFT ¹H NMR spectrum provided by the inclusion of explicit solvent molecules would not change significantly the NMR profile and so the same conclusion regarding the conformational preference in solution should be obtained.

Besides visual comparison of NMR spectra, analysis of statistical parameters is also relevant when theoretical and experimental data are confronted. Figure 5 reports ¹H NMR chemical shift relative deviation (in ppm) from experimental data regarding A and B rings protons for fully optimized almost planar (Figure 5 a) and rotated rutin structures (Figure 5 b). Corresponding sugar moieties protons values for rotated structures are shown in Figure 5 c. Average deviation (AVE), mean absolute error (MAE), root mean square deviation (RMSD) and root mean square error (RMS) with respect to experimental data for selected rotated rutin structures are given in Figure 5 d. The best fit with experimental data, structure 32, is highlighted. All statistical indices (AVE, MAE, RMSD and RMS) for structure 27 are substantially higher than structure 32, what leaves it as the preferred rutin structure in DMSO solution based on visual comparisons of experimental and theoretical ¹H NMR spectra and statistical indices values. Very recently, Rzepa et al.48 reported a convenient method for evaluation of ¹¹B chemical shifts, regarding the identification and characterization of reaction intermediates in organic synthesis and reactions of organoboron compounds, highlighting the relevance and wide applicability of DFT calculations of NMR chemical shifts. A regression analysis for ¹¹B NMR shifts was used to select an adequate procedure, using standard quantum chemical approach, yielding theoretical predictions of enough accuracy (1–2 ppm) that can be useful to determine the likely structures in boron‐mediated chemical reactions. B3LYP/6‐31G(d,p) linear regression data (¹H NMR chemical shifts) for rutin molecule are reported in Table 2 (PCM–DMSO results). While all four statistical indices values reported in Figure 5 d pointed out unambiguously to structure 32 as the preferred one based on analysis of ¹H NMR spectra, the regression analysis date given in Table 2 opens a possibility of structure 30 (and 27) based on the regression slope and regression intercept results, using both basis sets. However, the adjusted R‐squared (adj‐R²) data predict structure 32 as the most likely to be found in DMSO solution (exhibiting the smallest residual sum of squares), in agreement with the AVE, MAE, RMSD and RMS results reported in Figure 5 d. In the light of this analysis it seems to us that the adj‐R ² linear regression parameter is more adequate in conformational studies than regression slope and regression intercept theoretical data, which however predict structure 32 as having the smallest standard error values, in accordance with the analysis of ¹H NMR profile and data from Figure 5 d. A comparison of linear regression data (adj‐R ²) between rotated and fully optimized (almost planar) structures are given in Figure S3 showing poor results for the non‐rotated structures corroborating the analysis of ¹H NMR profile and statistical indices.

Figure 5.

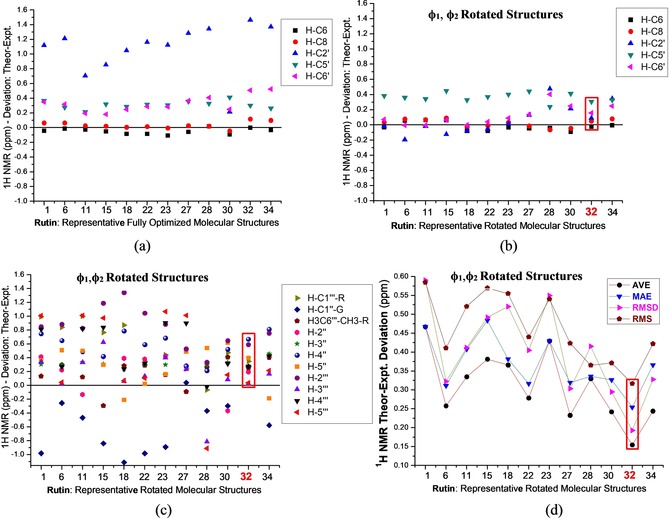
B3LYP/6‐31G(d,p) PCM–DMSO ¹H NMR chemical shift relative deviation from experimental data for A–B ring protons of a planar rutin molecule (a), rotated structures (b), and corresponding values for sugar moieties protons (c). AVE, MAE, RMSD and RMS with respect to experimental data for rotated rutin structures (d). All values are given in ppm. The best fit to experimental NMR data is highlighted.

Table 2.

B3LYP‐PCM‐DMSO ¹H NMR chemical shifts (in ppm) regression analysis for rutin molecule.

Rutin	B3LYP/6‐31G(d,p)‐PCM‐DMSO
strs.	Regression slope[a]	Regression intercept[a]	Adjusted R 2 (adj‐R2)[b]
27	0.952(±.041)	0.515(±0.198)	0.973(±1.342)
28	1.033(±0.058)	−0.096(±0.281)	0.954(±2.698)
30	0.959(±0.040)	0.408(±0.195)	0.974(±1.295)
32	0.960(±0.025)	0.427(±0.122)	0.990(±0.506)
34	0.948(±0.044)	0.499(±0.214)	0.968(±1.565)

[a] Standard error values are given in parenthesis. [b] Residual sum of squares values are given in parenthesis.

B3LYP/6‐31G(d,p) optimized structures (φ₁, φ₂ rotated) for relevant sugar moieties conformations of rutin in DMSO solution are shown in Figure 6 (right side), along with B3LYP/6‐31G(d,p)‐PCM‐DMSO relative energies (ΔE _rel), and room temperature enthalpy (ΔH _rel) and Gibbs free energy (ΔG _rel) corrected values (in kcal mol⁻¹) (square boxes on the right side). The occurrence of H‐bonds (shown as dotted lines in Figure 6) are responsible for the lower ΔE _rel and ΔH _rel values for structures 32 and 34, making them predominant on energetic basis. The enhanced thermodynamic stability of rotated rutin conformation 32, reflected by the lowest ΔG _rel value (−1.0 kcal mol⁻¹), is governed by entropy contribution (TΔS), making it the global minimum structure based on Gibbs free energy calculations in DMSO solution. Structure 34 with two intramolecular H bonds adding extra stability on an energetic bases, however, is not entropically favored. B3LYP/6‐31G(d,p) Mulliken atomic charges (see Scheme 1) of the preferred structures of the rutin molecule are shown in Table S2 (Supporting Information). Note that all hydrogen and oxygen atoms are positive and negative, respectively. Except for structures 27, 28 and 30 (Figure 6), the hydroxyl group (C2“ atom–sugar moiety) of structures 32 and 34 form long‐distance hydrogen bonds with the carbonyl group (C ring). The rotation of B ring of rutin molecule does not cause a significant variation in the Mulliken charge values of the atoms involved in this interaction (see values highlighted in Table S2), as well as all other atoms in each structure. Thus, the intramolecular interactions are unaffected due to the rotation of the B ring of rutin molecule, ensuring greater thermodynamic stability of structures 32 and 34. The graphs in Figures S4.1 to S4.5 (Supporting Information) clearly show that the Mulliken charge calculated for the five geometries shown in Figure 6 show slight changes if we compare the optimized and rotated structures. Gandhi et al.49 carried out a theoretical‐experimental study of the synthesis, structural and electronic properties of the 2‐Chloro‐4‐(4‐fluoro‐phenyl)‐6‐isopropyl‐pyrimidine‐5‐carboxylic acid methyl ester compound. The authors showed through Mullikan charge distribution that the neutral chlorine atom does not participate in intermolecular interactions between the molecular units of the compound unit cell, whereas the fluorine atom participates in C–F–π‐type interactions. Table S3 (Supporting Information) shows an attempt to assign the main IR stretching C−H and O−H of the A and rings. Our results show that the rotation of B ring in the most relevant structures 27 and 32 does not cause a significant shift of the calculated frequencies, as well as insignificant intensity variations. The IR spectra simulations shown in Figure S5 (Supporting Information) for rutin structures 27, 28, 30 and 32 revealed that it is not possible to distinguish the planar and rotated rutin structures for any of the geometries shown in Figure 6, different from the ¹H NMR analysis. This result was also observed for the structural analysis of Zn^II‐kaempferol complexes recently published by our group.31

Figure 6.

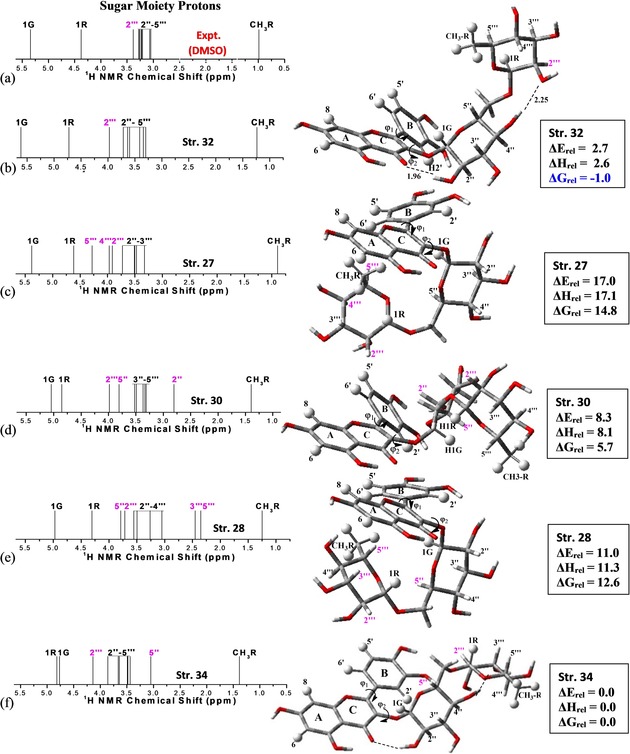
B3LYP/6‐31G(d,p) optimized structures (φ₁ and φ₂ rotated) for the preferred sugar moieties conformations of rutin in DMSO solution, along with B3LYP/6‐31G(d,p) relative energy values (in kcal mol⁻¹). Experimental (in [D6]DMSO) from Ref. 46 (a) and B3LYP/6‐31G(d,p)‐PCM‐DMSO (b–f) ¹H NMR spectra are also shown. The hydrogen atoms showing larger deviations are highlighted in pink color.

Experimental (in [D6]DMSO) (Figure 6 a) and B3LYP/6‐31G(d,p) PCM–DMSO ¹H NMR spectra expanded for sugar moieties protons are shown in Figure 6 b–f. The hydrogen atoms showing larger chemical shift deviations are highlighted in pink color. In this zoomed Figure it can be clearly visualized that for structure 32 only the 2′′′ proton signal (less shielded) is shifted to low‐field regions in agreement with the experimental chemical shift pattern, with the other 2′′‐ 5′′′ protons following closely the experimental profile. For structure 27 the 4′′′ and 5′′′ protons signals are significantly deviated from the experimental trend (Figure 6 c) shifting approximately 1 ppm for low‐field regions. For structure 30 the 2′′ (strongly shielded by π network of the B‐ring) and 5′′ (less shielded) protons are dislocated to high‐field and low‐field regions, respectively, from the experimental pattern. The same happened with 3′′′, 5′′′ (strongly shielded by π network of the A‐ring) and 5′′ (less shielded) protons for structure 28, as well as for 1G and 1R protons (most shielded) and 5′′ (less shielded) proton for structure 34. Therefore, only structure 32 provided a correct match between theoretical and experimental NMR profile in DMSO solution being the most probable candidate structure for rutin in solution both from spectroscopic and thermodynamics point of view.

To assess the accuracy of our results the basis set was improved to a triple‐zeta quality (6–311+G(2d,p))40 and the M062x41 and B97D43 functionals were used; the last one including empirical dispersion energy correction designed to describe adequately vdW interactions. Energy results for rutin rotated structures are given as Supporting Information (Table S4). The specific torsion angle used as variable to generate the 1D rigid scan curve (Figure 1), from where the respective initial geometry was obtained and then submit to full geometry optimization, is quoted in the second column of Table S4. ΔH _rel and ΔG _rel values for five selected structures, 27, 28, 30, 32 and 34, are summarized in Figure 7. ΔE _rel and ΔH _rel results pointed out to structure 34 (Figure 6 f) as global minimum, with conformer 32 (Figure 6 b) being around 3 kcal mol⁻¹ energetically higher. However, ΔG _rel data in DMSO solution (PCM results), which is a criterion of spontaneity, predict structure 32 as the most favorable in agreement with the ¹H NMR analysis, using both B3LYP and M062x functionals. Improving the basis set to a triple‐zeta quality increases the relative stability of conformer 32 to a ΔG _rel value of −2.7 and −1.4 kcal mol⁻¹, respectively, for B3LYP and M062x functionals. The B97D functional tend to favor structure 28 (Figure 6 e), maybe due to the presence of weak intramolecular interactions contemplated by the dispersion term embedded in this functional, but not structure 27 which is very similar to structure 28 except for the CH₃–C5′′′ group in axial position. However, the entropy contribution smooths out this tendency of B97D functional.

Figure 7.

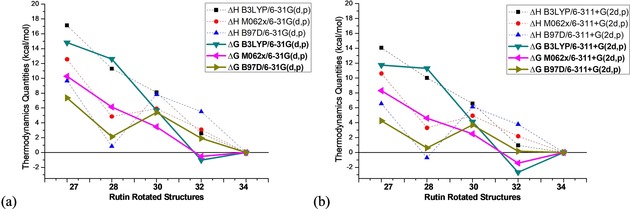
B3LYP, M062x and B97D PCM‐DMSO relative room temperature enthalpy (ΔH _rel) and Gibbs free energy (ΔG _rel) for five selected B3lYP/6‐31G(d,p) rotated rutin structures, showing reasonable agreement with experimental ¹H NMR profile, using two basis sets, 6‐31G(d,p) and 6–311+G(2d,p). All values in units of kcal mol⁻¹.

The rotated structures (except for structure 32) are not true minima on the B3LYP PES exhibiting one or two small imaginary frequency values. A procedure used previously50 ignoring two lowest frequency modes in the evaluation of the vibrational partition function (having the right balance of imaginary frequencies) was employed here which enabled the calculation of ΔG _rel involving structure having different number of imaginary frequencies (0, 1, 2). B3LYP, M062x and B97D gas phase and PCM‐DMSO ΔE _rel and ΔG _rel values for fully optimized rutin structures are given in Figure S6 (Supporting Information). In addition, structure 28, where weak intramolecular interactions may be present, is considerably stabilized at the M062x/6‐31G(d,p) and B97D/6‐31G(d,p) levels of calculation as compared to the B3LYP, maybe because description of dispersion contribution is not contemplated by the hybrid functional.

B3LYP, M062x and B97D ¹H NMR chemical shift results are grouped in Figure S7 (Supporting Information). Similar ¹H NMR patterns are predicted by the B3LYP functional with both basis sets (6‐31G(d,p) and 6–311+G(2d,p)), validating out spectroscopic analysis using the B3LYP/6‐31G(d,p) level of calculation. There is an overall good agreement between B3LYP and M062x spectra, with essentially the same NMR profile being predicted. The B97D functional tend to shift the sugar moieties 1G,1R, H2′′‐H5′′′ signals to higher values, but keeping almost the same pattern. At this point it seems to us that both B3LYP and M062x functionals are adequate for the calculation of NMR spectra, however, an extensive analysis using various functional would be required to reach a definitive conclusion, what is beyond the scope of this work. Corresponding B3LYP, M062x and B97D ¹H NMR spectra for fully optimized structures are reported in Figure S8, showing the same behavior. In addition, the MAE and RMSD values reported in Figure S9 with 6‐31G(d,p) and 6–311+G(2d,p) basis sets using the three functionals exhibit almost the same trend, with the B97D results showing sizeable deviation in accordance with the previous analysis. The RMSD profiles reported in Figure S9 show an excellent accordance for B3LYP, M062x and B97D functionals using the 6–311+G(2d,p) basis set. The B3LYP functional was found to yield smaller values for the statistical parameters than M062x and B97D, indicating that is very adequate for the calculation of ¹H NMR chemical shifts related to conformational analysis, using a modest 6‐31G(d,p) basis set, which is computationally viable for the study of large molecules. A comparison among B3LYP, M062x and B97D regression analysis data, using 6‐31G(d,p) and 6–311+G(2d,p) basis sets are given as Supporting Information (Figure S10 and Table S5). The B3LYP/6‐31G(d,p) values (highlighted in Figure S10) show good agreement with the corresponding values evaluated with the larger 6–311+G(2d,p) basis set. Essentially the same trend is predicted for the three functionals when the 6–311+G(2d,p) basis set is used. Therefore, it appears to us that the use of another DFT functional for the calculation of NMR spectra is not strictly necessary.

It is important to recognize that Boltzmann distribution of representative rutin conformations should play a role. Using standard thermodynamic equations, the conformation population in DMSO solution can be evaluated from calculated ΔG _rel values (Table S4). Using B3LYP/6–311+G(2d,p) and M062x/6–311+G(2d,p) relative Gibbs free energy values (PCM‐DMSO) the following populations are obtained: Pop‐32=91–92 %, Pop‐34=1–9 %, Pop‐30 <0.1 %. Therefore, only structure 32 and 34 should be consider on thermodynamics basis. Depending on the basis set and functional used the population of conformation 32 can vary, but contributing in average more than 90 % to the conformational mixture and so, should play the major role to the ¹H NMR profile observed experimentally, which is in nice agreement with the results of theoretical spectroscopic analysis.

Analysis of experimental and theoretical ¹H NMR chemical shift profile is a powerful fingerprint criterion to determine the predominant molecular structure in solution, due to the high sensibility of the NMR signals to the changes in the chemical environment. We believe that the thirty‐four distinct rutin configurations sampled in this work are representative of the possible molecular structures that can be present in the experimental sample handled in the NMR experiment in solution, and that the B‐ring rotated structure 32 should be predominant in DMSO and water solution.

3. Conclusions

Conformational analysis is of fundamental importance in structure–activity relationship studies. In this work, we aimed to determine the preferred molecular structure of flavonoid rutin in DMSO solution combining experimental ¹H NMR chemical shifts with theoretical DFT calculations. The high sensibility of ¹H NMR chemical shifts to local chemical environment gives a motivation to use the best match between experimental and theoretical NMR spectra as a sound criterion to select the preferred conformation in solution. We believe this can be a useful strategy once structural determination in solution is hard to be accomplished by experimentalists without the aid of X‐ray diffraction technique. Experimental determination of molecular structure in solution through direct NMR analysis is not trivial, since no detailed structural information is available from NMR chemical shift experimental data.

The reported NMR theoretical results strongly indicate that there is no coplanarity of the A, B and C rings of polyphenol rutin in DMSO (and water) solution, which is theoretically predicted in the gas phase. Rotation of inter‐ring dihedral angle (φ₁) leads to a deviation from the planarity of the A and B rings, and this is necessary to reach an agreement with experimental ¹H NMR data in DMSO solution. This is a new and relevant information, regarding structure–activity relationship studies. To the best of our knowledge this is the first time that a detailed conformational analysis of polyphenol rutin is reported using the match between experimental and theoretical ¹H NMR spectra (instead of the common relative energy criterion) as a procedure to elucidate the molecular structure of the flavonoid in solution.

Our extensive conformational search using B3LYP/6‐31G(d,p) gas phase calculations yielded 34 distinct equilibrium structures on the PES for rutin molecule, characterized as true minima through harmonic frequency analysis. NMR calculations were performed for all optimized structures with DMSO (and water) solvent effects included using the PCM model. Comparison with experimental spectrum (in [D6]DMSO) enabled us to unambiguously assign structure named 32 (with the B‐ring deviated in 30° from a planar configuration) as the most probable to be present in the experimental sample handled in the NMR experiment, exhibiting the best match with experimental ¹H NMR profile. Room temperature Gibbs free energy calculations in solution (DFT PCM‐DMSO) showed that this structure is the preferred one (global minimum), with enhanced thermodynamic stability (more than 2 kcal mol⁻¹) of rutin rotated conformation 32 being governed by entropy contribution (TΔS).

To assess the accuracy of our results the basis set was improved to a triple‐zeta quality (6–311+G(2d,p)). B3LYP PCM‐DMSO room temperature relative ΔG calculations in solution (employing the 6‐31G(d,p) and 6–311+G(2d,p) basis sets) also corroborate the NMR analysis, predicting structure 32 as the preferred one among thirty‐four possible rutin conformers. In addition, B3LYP ¹H NMR spectra calculated with both basis sets are essentially the same. Therefore, this rutin conformation should be experimentally observed in solution, or make the major contribution among the various plausible structures for such a flexible molecule, and must be considered in further studies focusing on the interaction of rutin with biological targets.

Regarding the level of quantum chemical theory utilized in this work, three different DFT functionals (B3LYP, M062x and B97D) were used for the calculation of ¹H NMR chemical shifts and relative ΔG values in DMSO solution (PCM model), using optimized B3LYP/6‐31G(d,p) geometries and harmonic frequencies. The B3LYP and M062x functionals agree very well for evaluation of ¹H NMR spectrum profile and relative ΔG values using the 6‐31G(d,p) and 6–311+G(2d,p) basis sets. Sizeable deviations were observed for the B97D functional which tend to dislocate the sugar moieties proton ¹H NMR signals toward higher values. This functional also tends to favor energetically structure 28, where weak intramolecular interactions may be present, as compared to the B3LYP, maybe because of dispersion contribution embedded in the B97D functional. Among four statistical indices the RMSD produced essentially the same pattern for all three functionals, indicating structure 32 as the preferred one in DMSO solution (and aqueous media), and it seems more adequate to analyze ¹H NMR data. Our results provide convincing evidence that the B3LYP/6‐31G(dip) level is enough for analysis of ¹H NMR spectra and relative energies of flavonoids.

In conclusion, we show in this work that that DFT optimized molecular geometries in the vacuum can deviate substantially from the molecular structure present in solution, where solute‐solute and solute‐solvent interactions play an important role and such effects are difficult to be included in quantum mechanical geometry optimization procedure. Once a reasonable sample of the possible molecular conformations have been carried out, using for example classical simulation methods such as Monte Carlo, if necessary, followed by DFT geometry optimization calculations, we have shown that adjusting fully optimized inter‐ring torsion angles, to reproduce the experimental ¹H NMR spectrum recorded in solution can be an efficient and computationally viable strategy to locate the observed molecular structure in solution, with NMR chemical shift pattern acting as a fingerprint criterion to select the correct molecular structure.

Please note: Minor changes have been made to this manuscript since original publication

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

L. A. De Souza, H. C. Da Silva, W. B. De Almeida, ChemistryOpen 2018, 7, 902.