Abstract
Various kinds of flexibility have been observed in metal–organic frameworks, which may originate from the topology of the material or the presence of flexible ligands. The construction of free energy profiles describing the full dynamical behavior along the phase transition path is challenging since it is not trivial to identify collective variables able to identify all metastable states along the reaction path. In this work, a systematic three-step protocol to uniquely identify the dominant order parameters for structural transformations in flexible metal–organic frameworks and subsequently construct accurate free energy profiles is presented. Methodologically, this protocol is rooted in the time-structure based independent component analysis (tICA), a well-established statistical modeling technique embedded in the Markov state model methodology and often employed to study protein folding, that allows for the identification of the slowest order parameters characterizing the structural transformation. To ensure an unbiased and systematic identification of these order parameters, the tICA decomposition is performed based on information from a prior replica exchange (RE) simulation, as this technique enhances the sampling along all degrees of freedom of the system simultaneously. From this simulation, the tICA procedure extracts the order parameters—often structural parameters—that characterize the slowest transformations in the material. Subsequently, these order parameters are adopted in traditional enhanced sampling methods such as umbrella sampling, thermodynamic integration, and variationally enhanced sampling to construct accurate free energy profiles capturing the flexibility in these nanoporous materials. In this work, the applicability of this tICA-RE protocol is demonstrated by determining the slowest order parameters in both MIL-53(Al) and CAU-13, which exhibit a strongly different type of flexibility. The obtained free energy profiles as a function of this extracted order parameter are furthermore compared to the profiles obtained when adopting less-suited collective variables, indicating the importance of systematically selecting the relevant order parameters to construct accurate free energy profiles for flexible metal–organic frameworks, which is in correspondence with experimental findings. The method succeeds in mapping the full free energy surface in terms of appropriate collective variables for MOFs exhibiting linker flexibility. For CAU-13, we show the decreased stability of the closed pore phase by systematically adding adsorbed xylene molecules in the framework.
1. Introduction
Only a few materials have received as much attention as potential candidates for future applications as metal–organic frameworks (MOFs).1−5 This class of porous, crystalline materials has intrigued the scientific community due to their large internal surface areas, a result of their scaffold-like network composed of metal–oxide moieties that are interconnected through organic ligands.6−8 This ordered nanoporosity makes MOFs very promising for applications such as controlled drug release,9,10 heterogeneous catalysis,11,12 gas storage, and separation.13 An increasingly important subclass of these framework materials exhibits intriguing structural flexibility.14,15 These so-called soft porous crystals (SPCs) or flexible MOFs undergo structural transformations upon external stimuli such as temperature, pressure, and guest adsorption, while retaining their crystallinity.16,17 As a result, flexible MOFs may be exploited for a variety of industrial applications,18 including nanosensors15 and dampeners.19
The study of flexibility has been the topic of various experimental and theoretical studies.14 Flexibility may refer to various types of structural changes such as ligand flipping, pore gate opening, breathing, etc. Following the classification of Kitagawa and Kazuhiro for 3D materials, three types of framework flexibility are distinguished: (i) intrinsic topological flexibility, (ii) intrinsic linker flexibility, and (iii) displacive transformations of interpenetrated structures.20 For materials exhibiting topological flexibility accompanied by substantial changes of the volume during the phase transformation we have recently developed a method to determine the thermodynamic potential for systems characterized by the temperature, volume, and number of particles from a theoretical point of view. Pressure versus volume profiles are constructed which by means of thermodynamic integration yield the Helmholtz free energy of the system.21 In the work of Vanduyfhuys et al., it is shown that the thermodynamic potential allows for the unique identification of the conditions under which a material breathes.17 The extension of the protocol toward materials exhibiting more complex forms of flexibility such as intrinsic linker flexibility is so far unclear as the volume is not necessarily a good order parameter or collective variable, i.e. able to correctly capture all states of the material during the phase transformation. Examples of such materials are gate opening MOFs such as ZIF-822 and linker flexible MOFs such as CAU-13.23
For some of these materials computational studies have been performed, but those were mainly concentrated on the behavior of the material near the respective metastable phases. While most of the existing studies have predicted the (bi)stability of flexible MOFs by means of static structure optimizations with DFT methods including dispersion,24−26 complemented in some cases with additional tensorial analysis for the derivation of the elastic properties of the material,25 also a limited number of high-pressure ab initio molecular dynamics (AIMD) simulations have been performed. We refer in particular to the work of Ortiz et al. where AIMD calculations at high pressure succeeded in predicting two phases of CAU-13 and NOTT-300, whose flexibility has not yet been demonstrated experimentally at that time.26 Anyway, all studies done so far were focused on the behavior of the material around the metastable equilibria. The dynamical behavior of the structural transformation connecting these metastable phases and reflecting the flexibility of these materials has not yet been investigated, and thus a microscopic understanding of the observed flexibility of most of the materials is still missing. One of the main reasons of this shortcoming is that framework flexibility exists in diverse ways and that no strict protocol has been fixed for the assignment of the optimal collective variables able to correctly capture the dynamical progress of these materials going from one phase to another. The terminology collective variables, order parameters, and reaction coordinates are often used interchangeably. To avoid any confusion, we define a collective variable as any function of the internal coordinates, an order parameter as a special collective variable which is able to distinguish between various stable states, and a reaction coordinate as a special order parameter able to describe the dynamical progress along the phase transformation. These definitions are adopted from the work of Peters.27 In this work, we present a protocol to construct free energy profiles along appropriate collective variables for materials exhibiting either topological or intrinsic linker flexibility. Free energy profiles constructed along these collective variables give direct insight regarding the relative stability of the multiple (meta)stable geometrical conformations.
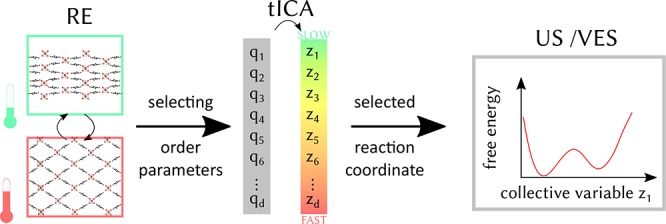
Although the different metastable states of MOFs exhibiting intrinsic linker flexibility are also often characterized by a significant volume difference, the volume is not systematically a good descriptor of the phase transformation. We need reaction coordinates able to describe the slow mode involving the structural change of the material. Once they are determined they are used in dedicated free energy estimation methods to accurately compute the free energy profile. To achieve this goal we have set up a protocol based on the time-lagged or time-structure-based independent component analysis (tICA),28 which finds its roots in signal processing and was demonstrated to be an excellent dimension reduction method for the construction of Markov state models (MSM) for protein folding.29−31 The method can best be understood as a generalization of the principal component analysis, as it solves a generalized eigenvalue problem with the instantaneous and time-lagged correlation matrices of the input coordinates. The tICA method linearly transforms an initially chosen set of order parameters, e.g. distances, bend angles, and dihedral angles, into collective coordinates sorted by “slowness”. To gather input for the tICA technique, we use the replica exchange (RE) molecular dynamics method which enhances sampling along all degrees of freedom. This allows for the generation of input data that take into account all relevant structural changes of the material. Once the dominant order parameter has been determined via this tICA-RE procedure, it can act as a collective variable for various free energy estimation methods that enhance sampling along this specific variable to obtain an accurate free energy profile.32 In this work, three different free energy estimation methods are compared to explore the phase space along the previously identified collective variable: thermodynamic integration (TI),33 umbrella sampling (US),34 and variationally enhanced sampling (VES).35
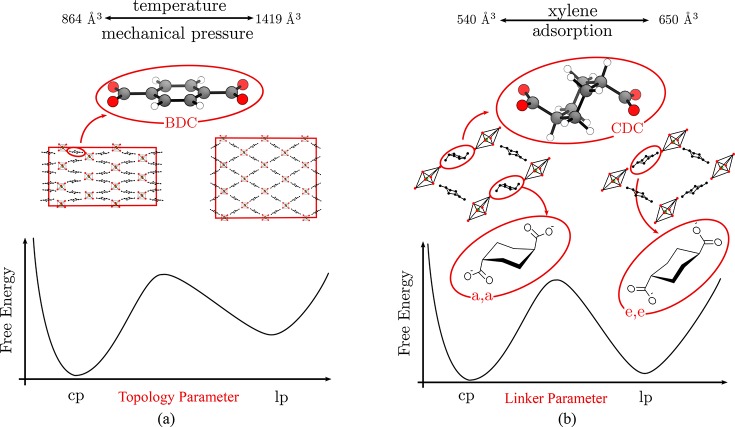
The protocol is applied and verified on two materials namely, MIL-53(Al) and CAU-13, which exhibit two different types of flexibility corresponding to topological and linker flexibility. For MIL-53(Al), a plethora of theoretical studies already appeared, and thus the material is an ideal test case to benchmark the method with respect to earlier approaches. MIL-53(Al) is composed of inorganic [Al(OH)]∞ chains connected by benzenedicarboxylate (BDC) linkers, forming one-dimensional channels and exhibiting a typical winerack topology.36 The material may become flexible under the influence of temperature,37 pressure,19 and guest adsorption.38 For the aluminum variant studied here, a transition between a large pore (lp) and closed pore (cp) phase of the empty framework may be induced under the influence of both temperature and pressure (see Figure 1). CAU-13 also exhibits the typical winerack topology of MIL-53(Al), but the BDC ligands of MIL-53(Al) are substituted by trans-cyclohexanedicarboxylate (CDC) linkers.39 Experimentally, flexibility in CAU-13 is induced under the influence of xylene adsorption (see Figure 1). More in particular, Niekiel et al. related the flexibility of CAU-13, which corresponds with a volume increase of 25%, with the deformation of the CDC linker between the a,a- and e,e-configuration.23 A similar transition is observed due to the adsorption of certain pyrazines.40 Herein, we adopt the terminology closed pore (cp) and large pore (lp) state for those two configurations of CAU-13, respectively. The main driver for the observed flexibility is a ring flip of the substituted CDC linker from its a,a-configuration to its e,e-configuration. The ring flip of an isolated cyclohexane molecule is a well understood process in stereochemistry.41 In order to allow a comparison with free energy profiles obtained further in this paper, Figure 2 shows the commonly used free energy diagram for the conformational inversion of cyclohexane. A substantial volume change in CAU-13 was observed upon the phase transformation, but it is a priori unclear whether the volume is a good collective variable to describe the full free energy profile along the transformation. To the best of our knowledge free energy profiles in terms of appropriate collective variables which may serve as reaction coordinates for the phase transformation have not yet been constructed for materials exhibiting intrinsic linker flexibility.
Figure 1.
An example of (a) intrinsic topological flexibility in MIL-53(Al) and (b) intrinsic linker flexibility in CAU-13 is shown in the left and right parts of the figure, respectively. The particular linker type which is the main difference between both structures is highlighted in the figure. In both cases, the hypothetical free energy profile reveals two (meta)stable phases as a function of an order parameter that governs the transition between a close pore (cp) and a large pore (lp) phase: either a topology parameter (MIL-53) or a linker parameter (CAU-13).
Figure 2.
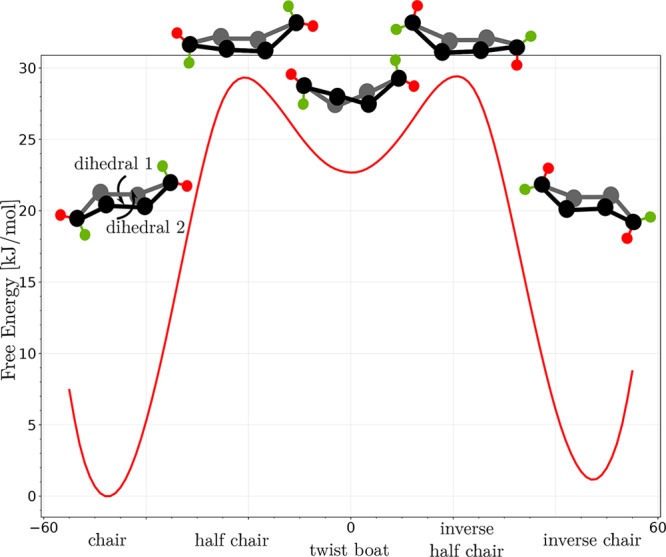
Free energy profile of the ring inversion of the cyclohexane molecule at 300 K obtained using VES and based on a force field generated with QuickFF.42 Schematic representation of the various configurations, with carbon atoms in black and hydrogen atoms in red and green. Due to the ring flip, the red atom transforms from an equatorial position toward an axial position. The employed collective variable corresponds to the average of two dihedral angles which stem from two different sets of four carbon atoms shown in the figure. Its value varies from −60° (chair) to +60° (inverse chair).
This paper is organized as follows. The next section describes briefly the theoretical background on the methods employed in this work. In the third section, computational details are provided. In the fourth section, the tICA-RE protocol is applied to the two aforementioned materials. Subsequently, free energy profiles are constructed with the help of enhanced sampling MD techniques and further discussed in terms of their flexibility behavior.
2. Methodology: Order Parameters and Enhanced Sampling Methods
2.1. Time-Structure Based Independent Component Analysis (tICA)
The time-structure based independent component analysis (tICA) is a well-established statistical modeling technique incorporated into Markov state models that aims to reduce the dimensionality of the problem under study. It is frequently applied in the field of biomolecules and protein folding.43 tICA can be understood as a dimension reduction method comparable to the principal component analysis (PCA) method. In PCA, the observed dynamics is projected on those components which correspond to the motions with the largest amplitudes. Similarly, tICA reduces the dimensionality of the system while minimizing the loss of kinetic information by identifying the slowest motions in the system. As a result, tICA provides an excellent procedure to identify the most optimal order parameter indicating the progress of the slow transitions, as demonstrated independently by three groups.29−31
The tICA method starts by gathering MD data
of a chosen set of d order parameters q = {qi(x)}(i=1,...,d). These order parameters
span a subset of the full phase space Ω and represent geometrical
properties such as distances, bending angles, and dihedral angles.
It is important to start from collective variables which are able
to distinguish between the various states and thus may be identified
as order parameters. The MD data should contain relevant information
on the important transitions, and in this sense, replica exchange
(RE) is ideally suited to gather data as it enhances all degrees of
freedom and will also sample the less probable regions of the phase
space.44 The MD trajectories of these order
parameters are then used to construct the time-lagged covariance matrix  . In tICA, one searches for a linear transformation
matrix U transforming q to a new set of
collective variables z = Uq that are uncorrelated
and describe in descending order the slowest motions of the system.
By imposing the autocovariances Cz(τ) to be maximum at a fixed lag time τ with the constraint
that Cz(0) is the unity matrix,
one can show that this constrained optimization problem leads to a
generalized eigenvalue equation UiTCqUj = λiδij, as outlined in more detail in the SI and ref (30). The
eigenvalue λi is a measure for the
relaxation of the motion, i.e. λi = e–τ/ti. The largest eigenvalue, λ1, is unity, and
the first and largest time scale is thus t1 = ∞, describing the steady-state of the system. The other
time scales are finite and are ordered with decreasing magnitude and
therefore decreasing eigenvalues. Of great importance for our protocol
is the tIC eigenvector belonging to the largest eigenvalue λ1: z1 = ∑i=1dU1iqi. The largest amplitudes U1i in this linear combination denote the most dominant
slow order parameters qi, describing the
structural transition of the material.
. In tICA, one searches for a linear transformation
matrix U transforming q to a new set of
collective variables z = Uq that are uncorrelated
and describe in descending order the slowest motions of the system.
By imposing the autocovariances Cz(τ) to be maximum at a fixed lag time τ with the constraint
that Cz(0) is the unity matrix,
one can show that this constrained optimization problem leads to a
generalized eigenvalue equation UiTCqUj = λiδij, as outlined in more detail in the SI and ref (30). The
eigenvalue λi is a measure for the
relaxation of the motion, i.e. λi = e–τ/ti. The largest eigenvalue, λ1, is unity, and
the first and largest time scale is thus t1 = ∞, describing the steady-state of the system. The other
time scales are finite and are ordered with decreasing magnitude and
therefore decreasing eigenvalues. Of great importance for our protocol
is the tIC eigenvector belonging to the largest eigenvalue λ1: z1 = ∑i=1dU1iqi. The largest amplitudes U1i in this linear combination denote the most dominant
slow order parameters qi, describing the
structural transition of the material.
Hence, we aim to combine RE simulations and the tICA method to identify the relevant order parameters in the structural transformation of MOFs. RE data is ideally suited since transitions in RE simulations take place without any prior bias on the important coordinates of the system. Based on the tICA method, the slowest mode can be identified. Order parameters contributing the most to the slow mode can serve as collective variables in enhanced sampling simulations. More information on the tICA method can be found in Section II of the Supporting Information.
2.2. Proposing Suitable Collective Variables or Order Parameters as Input for the tICA Protocol
As outlined in the previous section, the tICA method relies on input data of a set of order parameters generated from enhanced molecular dynamics simulations. Indeed most phase transformations are activated processes, and MD input data need to be generated with the introduction of enhanced sampling techniques to also sample less probable regions of the phase space. A suitable collective variable or a linear combination of multiple collective variables is necessary to describe the phase transformation. The tICA protocol offers the most appropriate collective variable(s) to describe the structural transformation. It can be a single collective or a linear combination of collective variables, which have been used as input in the tICA protocol. The finally selected collective variable(s) should satisfy some criteria in the sense that their values clearly distinguish the various (meta)stable and transition states. In this sense, they may be identified as good order parameters. Furthermore, they need to describe the dynamical progress along the reaction path on the multidimensional phase space and thus may act as a suitable reaction coordinate of the rare event.45,46 In the case of a one-dimensional collective variable it should monotonically increase or decrease as one moves from one (meta)stable state to the next. In MOFs with a flexible topology the framework is often characterized by large changes in volume, and it is expected that the unit cell volume would represent a dominant order parameter. However, this result should also follow from the tICA-RE analysis.
The bistable behavior of MIL-53(Al) is clearly demonstrated experimentally and computationally with unit cell volumes which differ significantly.21,32,47 In this material the volume was already identified as a perfect collective variable and thus reaction coordinate in recent studies employing advanced sampling methods.17,21,32 However, this does not exclude the existence of other suitable collective variable(s) to be used in free energy estimation methods such as internal angles, dihedrals, or distances. In materials with a linker flexibility it is not a priori clear whether the volume is a good collective variable. For CAU-13, the phase transition is characterized experimentally by an increase of the unit cell volume and ring inversion of the organic ligands.23 The tICA-RE protocol should allow for the identification of the appropriate collective variables.
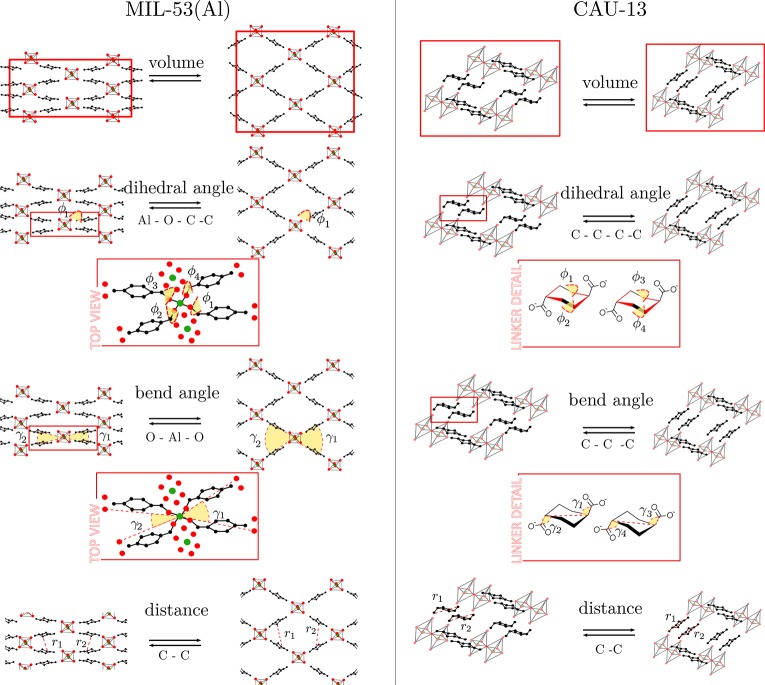
For both materials under investigation, a variety of possible order parameters to study the phase transformations may be proposed. The most straightforward ones are displayed in Figure 3. For MIL-53(Al) they comprise—besides the unit cell volume—the dihedral angles ϕ1, ϕ2, ϕ3, and ϕ4 associated with the kneecap motion of the BDC linker,48 interdiagonal bending angles γ1 and γ2 associated with the pore opening, and distances r1 and r2 measuring the pore opening. For the CDC linker in CAU-13, we propose the bending angles γ1, γ2, γ3, and γ4, the dihedral angles ϕ1, ϕ2, ϕ3, and ϕ4 characterizing the ring flip in CDC linkers, and the distances measuring the linker length. In Table 1 their specific values at the cp and lp structures are tabulated. Consequently, an initial set of d order parameters {qi(x)}(i=1,...,d) is constructed and submitted to the tICA procedure to extract the most dominant collective variable.
Figure 3.
Potential order parameters or collective variables that can be employed to study the flexibility in MIL-53(Al) (left) and CAU-13 (right). For MIL-53(Al), the dihedral angle associated with the knee-cap motion, the bend angle of the linkers, the interlinker distances, and the volume are considered as possible order parameters. For CAU-13, our model contains four CDC linkers of which two are flexible and give rise to four bending angles, γ1,2,3,4, and four dihedral angles, ϕ1,2,3,4, corresponding to the flexible nature of both flexible CDC linkers. In addition, the distances between the carboxylate carbons and the volume are also tested as potential order parameters.
Table 1. Structural Parameters of and Energy Difference between the Different Metastable Phases of MIL-53(Al) and CAU-13 As Obtained from Periodic Force Field Optimizations at 0 Ka.
| MIL-53(Al) |
CAU-13 |
|||
|---|---|---|---|---|
| cp | lp | cp | lp | |
| ΔElp–cp [kJ/mol] | 42.50 | 1.0 | ||
| volume [Å3] | 792 | 1462 | 568 | 677 |
| a, b, c [Å] | 19.52, 13.03, 6.28 | 16.79, 13.18, 13.20 | 13.72, 10.26, 8.85 | 12.98, 11.09, 12.29 |
| α, β, γ [°] | 91, 89, 97 | 89, 89, 89 | 111, 100, 90 | 120, 115, 85 |
| r1 [Å] | 4.3 | 8.7 | 4.9 | 5.9 |
| γ1 [°] | 24 | 87 | 108 | 155 |
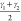 , , 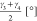
|
108, 108 | 155, 155 | ||
| ϕ1 [°] | 114 | 164 | –57 | 55 |
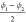 , , 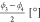
|
–57, −57 | 55, 55 | ||
2.3. Enhanced Sampling and Free Energy Methods
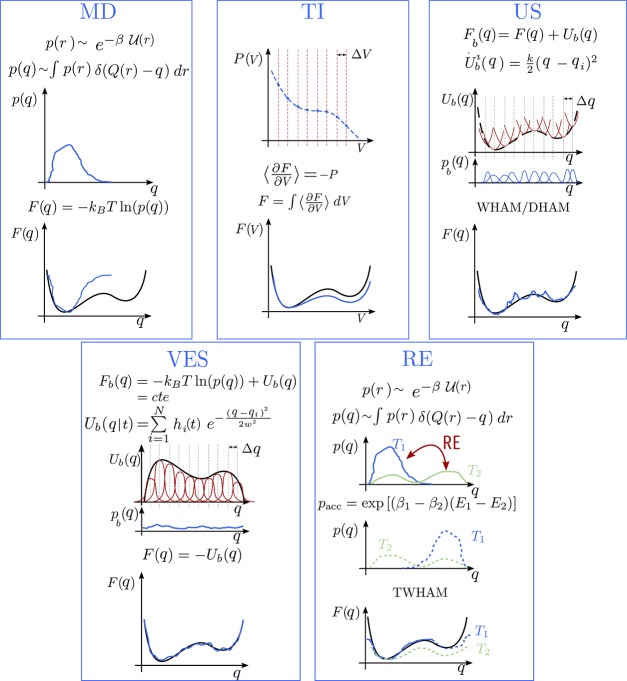
Once the appropriate collective variable is selected using the tICA-RE method, free energy profiles in terms of this variable may be constructed. As framework flexibility is usually associated with large barriers, enhanced sampling MD techniques are necessary. The various methods used in this work are schematically shown in Figure 4, and more information on the underlying theory of the free energy methods can be found in Section I of the Supporting Information. A distinction is made between two categories of enhanced sampling techniques, contrasting those techniques that enhance the sampling of all degrees of freedom,44,49−51 such as the RE method mentioned above, to those that enhance the sampling only along the direction of a set of collective variables.33−35,52−54 In the literature, a plethora of enhanced sampling techniques have been proposed. An extensive overview is given in some recent reviews.55,56
Figure 4.
Schematic representation of the free energy methods considered in this work. Each panel represents a different free energy method. Within each panel, the top figure shows the simulation result, and the bottom figure concerns the estimated free energy profile. The color coding is black for the unknown free energy, blue for the simulation results and the estimated free energy, and red for the sampling methods. An extended scope on the theory of the different free energy methods can be found in Section I of the Supporting Information.
In the first category of enhanced sampling methods, we only consider replica exchange (RE),44 a method in which the evolution of the system is simulated by means of several parallel MD simulations performed at different temperatures. Due to the increased kinetic energy related with the higher temperature simulations, higher energy barriers can be overcome, and therefore larger portions of the phase space are sampled. By exchanging high- and low-temperature replicas, the sampled configuration space might be extended also for the lower-temperature simulations. To govern the replica exchange step, a Metropolis-Hastings acceptance rule needs to be obeyed. The combination of thermostated MD simulations with Monte Carlo exchange steps yields canonically distributed samples of the phase space. Subsequently, the probability distribution function and the corresponding free energy profile as a function of any collective variable can be estimated using a histogram procedure or a more statistical optimal analysis method.57−59 Herein, we opt to use the temperature weighted histogram analysis method (TWHAM).57 To apply RE for nanoporous materials, the different MD simulations are performed in the (N, P, σa = 0, T) ensemble. This ensemble controls both the hydrostatic pressure P and anisotropic stress σa, allowing the volume V and unit cell shape h0 to fluctuate. For more information on the notation of the various ensembles, we refer to ref (21).
In the second category of enhanced sampling methods, thermodynamic integration (TI),33 umbrella sampling (US),34 and variationally enhanced sampling (VES)35 are considered. The particular selection of methods is motivated by the accurate free energy profiles extracted with these methods in our previous work.32 Up to now, the majority of free energy profiles that aimed to predict framework flexibility is constructed with the aid of TI and using the volume as a collective variable.17,21,32,47,60−62 Afterward the free energy can be determined by integration of the negative hydrostatic pressure. In this work, a free energy profile is obtained in terms of a more general collective variable q by performing a series of molecular dynamics simulations in the (N, P, σa = 0, T) ensemble for various values of q. More information on how to extract the free energy profile may be found in Section I of the Supporting Information. Rather than constraining the collective variable, US restrains it by means of a harmonic bias potential. In essence, a series of molecular dynamics simulations are performed where an external potential is added to the potential energy surface to sample efficiently a certain range of the collective variable. Afterward, to reconnect the information on the various independent simulations, algorithms such as the weighted histogram analysis method (WHAM)63 or dynamic histogram analysis method (DHAM)64 can be used. Finally, VES is related to metadynamics (MTD), in which a changing bias potential aids to explore all relevant regions of the phase space.35,54 In MTD, the bias potential is updated in such a fashion that already visited collective variable states experience an increased bias potential. To this end, Gaussian contributions with a preset height and width are added to the bias potential. The location of the deposited Gaussian contributions depends on the average of the collective variable value since the last update of the bias potential. In VES, a similar bias potential is constructed by optimizing the height of the different Gaussian contributions, which are located at predefined values of the collective variable. To this end, a functional of this bias potential is minimized, which is equivalent to reducing the Kullback–Leibler divergence between the sampled distribution and a uniform target distribution. The latter targets the sampling of a specific region of the phase space. Minimization of the functional is executed with the aid of a stochastic optimization algorithm. For a thorough comparison of the various free energy methods applied to the breathing behavior of MIL-53(Al), we refer the reader to ref (32).
3. Computational Details
All molecular simulations are performed using the in-house MD engine Yaff65 in either the (N, V, σa = 0, T) ensemble or the (N, P, σa = 0, T) ensemble. The notation for the thermodynamic ensembles was introduced in the work of Rogge et al. and corresponds to simulations where the volume or the pressure is controlled while the unit cell shape is allowed to fluctuate.21 This is achieved by bifurcating the isotropic pressure P and the anisotropic stress σa, on the one hand, and the cell shape h0 and the unit cell volume V, on the other hand. The temperature and pressure are controlled using the Nosé–Hoover chain thermostat with three beads and a time constant of 100 fs and the Martyna-Tuckerman-Tobias-Klein barostat with a time constant of 1 ps.66−68 Where applicable, the temperature and isotropic pressure are controlled at 300 K and 0 MPa, respectively. For the RE simulations, the temperature and pressure depend on the specific application.
Atomic interactions are modeled with the aid of force fields for both MIL-53(Al) and CAU-13. Force fields are derived from ab initio data following the QuickFF protocol42,69 and complemented with MBIS charges and MM3 parameters to model nonbounding interactions.70,71 Furthermore, simulations are performed with p-xylene loaded into the pores of CAU-13. To this end, a force field for xylene is constructed with QuickFF again complemented with MBIS charges and MM3 parameters. Both MIL-53(Al) and CAU-13 are modeled using a supercell obtained by doubling the unit cell along the metal-oxide chain, yielding a total of 152 and 100 atoms for MIL-53(Al) and CAU-13, respectively. The electrostatic interactions are computed using an Ewald summation with a real-space cutoff of 15 Å, a splitting parameter of 0.213 Å–1, and a reciprocal space cutoff of 0.320 Å–1. For the van der Waals interactions, a smooth cutoff at 15 Å is applied. In Table 1, an overview of the electronic energy difference between the two metastable states of MIL-53(Al) and CAU-13 as obtained from the force fields is provided. Moreover, the values of all order parameters which have been proposed, for the optimized minima in both materials, are also provided in Table 1.
The MD simulations in this work are performed using the velocity Verlet integration scheme with a time step of 0.5 fs. Simulations performed in the frame of TI and US have a simulation time amounting to minimally 125 ps, while for VES and RE simulations of 1 ns are performed. The larger simulation time for VES and RE is motivated by the fact that only one single simulation is performed in this technique, whereas multiple simulations need to be performed for TI and US. For the final free energy profile in RE, we perform over 50 independent RE simulations to deal with the large imprecision associated with this method.72 Moreover, an equilibration time of 5.0 ps is respected for each of those simulations.
For the RE simulations, the different replicas are simulated at different temperatures, herein defined by an arithmetic sequence Ti = Ti–1 + 2i, and at constant pressure (−60 MPa for MIL-53(Al), 0 MPa for CAU-13). For MIL-53(Al), 20 replicas are considered, and the reference temperature T0 is 200 K, resulting in the temperature sequence 200, 202, 206, 212, ..., 542, and 580 K. For CAU-13, 40 replicas are considered, and the reference temperature T0 is 300 K, resulting in the different replicas being simulated at the following temperatures: 300, 302, 306, 312, ..., 1782, and 1860 K. For both CAU-13 and MIL-53(Al), RE simulations are performed in the (N, P, σa = 0, T) ensemble. A high swapping frequency, i.e. every 5 fs, is maintained to boost the RE efficiency.73,74 To analyze the obtained data from the RE simulations, we employ the temperature weighted histogram analysis method (TWHAM),57 and tICA is performed with the MSMbuilder tool.75
For MIL-53(Al), free energy profiles are constructed using the volume as the collective variable. Within the TI methodology, 165 simulations are performed in the (N, V, σa = 0, T) ensemble. All simulations differ in unit cell volume, which is uniformly distributed over the entire volume range, i.e. from 725 Å3 to 1545 Å3 with a step size of 5 Å3. In the umbrella sampling (US) method, 165 simulations are run in the (N, P, σa = 0, T) ensemble. For each US simulation, a static bias potential is added that forces enhanced sampling in the phase space around a different reference volume. The harmonic constant of the umbrella potential amounts to 300 K kB/1000 Å6. In VES, the Gaussian functions are placed 50 Å3 apart and have a width of 50 Å3 and a height that is updated every 8 ps employing a stochastic update algorithm with an update parameter of 1 kJ/mol. For a description of the parameters of the enhanced sampling schemes and a rationalization of the chosen values, we refer to Section I of the Supporting Information and our earlier work in which a large variety of advanced MD simulations have been tested for their ability to construct free energy profiles for MOFs.32
For CAU-13,
four sets of collective variables were proposed in Figure 3 to characterize
the linker flexibility of the material. First, the unit cell volume
is considered as a collective variable. To this end, 100 simulations
are performed in the (N, V, σa = 0, T) ensemble in the context of TI. All simulations differ in unit cell
volume, which is uniformly distributed over the entire volume range
from 500 Å3 to 750 Å3 with a step
size of 2.5 Å3. A second set of collective variables
is given by the average bending angles of the carbon atoms in the
CDC linker, 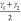 and
and 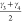 (see Figure 3), forming a two-dimensional
collective variable. To
cover the entire phase transformation in CAU-13, we adopt a range
of 100° to 170° for the bending angles. In US, we consider
a total of 35 × 35 = 1225 umbrella simulations with a harmonic
potential added to the potential energy surface as a function of the
average bending angle with a force constant of 2.5 kJ/mol/deg2. Each of these 1225 US windows belongs to a specific value
for the two bending angles ranging from 100° to 170° with
a stepsize of 2°. For VES, one long simulation is performed in
the (N, P, σa = 0, T) ensemble. The bias
potential is constructed on-the-fly, by updating the height of the
Gaussian contributions. These Gaussian contributions have a width
of 5° and are placed 5° apart from 100° to 170°
for both collective variables. The height of the Gaussian contributions
is updated every 0.5 ps with an update parameter of 0.5 kJ/mol. A
third and final set of collective variables employed in an enhanced
sampling setup to study the linker flexibility in CAU-13 is a linear
combination of the dihedral angles
(see Figure 3), forming a two-dimensional
collective variable. To
cover the entire phase transformation in CAU-13, we adopt a range
of 100° to 170° for the bending angles. In US, we consider
a total of 35 × 35 = 1225 umbrella simulations with a harmonic
potential added to the potential energy surface as a function of the
average bending angle with a force constant of 2.5 kJ/mol/deg2. Each of these 1225 US windows belongs to a specific value
for the two bending angles ranging from 100° to 170° with
a stepsize of 2°. For VES, one long simulation is performed in
the (N, P, σa = 0, T) ensemble. The bias
potential is constructed on-the-fly, by updating the height of the
Gaussian contributions. These Gaussian contributions have a width
of 5° and are placed 5° apart from 100° to 170°
for both collective variables. The height of the Gaussian contributions
is updated every 0.5 ps with an update parameter of 0.5 kJ/mol. A
third and final set of collective variables employed in an enhanced
sampling setup to study the linker flexibility in CAU-13 is a linear
combination of the dihedral angles 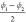 and
and 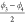 . As was the
case for the bending angles,
we employ both US and VES to construct a two-dimensional free energy
surface in terms of the dihedral angles. The combined dihedrals vary
between −60° and 60°. For US, harmonic bias potentials,
with again a force constant of 2.5 kJ/mol/deg2, are placed
4° apart, amounting to a total of (31 × 31 =) 961 simulations.
For VES, the Gaussian contributions have a width of 5° and are
placed 2° apart. An update time of 0.5 ps is respected, and the
update parameter of 0.5 kJ/mol is retained. To construct free energy
profiles for CAU-13 loaded with a varying number of xylene molecules,
VES simulations are performed with similar settings.
. As was the
case for the bending angles,
we employ both US and VES to construct a two-dimensional free energy
surface in terms of the dihedral angles. The combined dihedrals vary
between −60° and 60°. For US, harmonic bias potentials,
with again a force constant of 2.5 kJ/mol/deg2, are placed
4° apart, amounting to a total of (31 × 31 =) 961 simulations.
For VES, the Gaussian contributions have a width of 5° and are
placed 2° apart. An update time of 0.5 ps is respected, and the
update parameter of 0.5 kJ/mol is retained. To construct free energy
profiles for CAU-13 loaded with a varying number of xylene molecules,
VES simulations are performed with similar settings.
4. Results and Discussion
4.1. tICA-RE Protocol for Collective Variable Selection
The tICA-RE protocol, outlined in subsection 2.1, will be now applied in some specific cases to describe the phase transformations between the metastable phases in MIL-53(Al) and CAU-13. In a first step, a RE simulation has been performed, which enhances the sampling of all degrees of freedom. Subsequently, trajectories of this RE method were analyzed to identify the suitable collective variables. The values of all possible order parameters, corresponding to the structure of the metastable phases in the two materials, are listed in Table 1. The decomposition of the first time-structure based independent component (tIC) eigenvector for both MIL-53 and CAU-13 is displayed in Figure 5 visualizing the most prominent contributions. They are identified as the slowest varying collective variables and potential suitable reaction coordinates to describe correctly the flexible behavior of the two materials.
Figure 5.
tICA analysis of the RE simulations for (a) MIL-53(Al) and (b) CAU-13. Amplitudes of the most important contributions in the first tIC eigenvector are displayed. For MIL-53(Al), the volume (blue) turns out to be a dominant order parameter, while in CAU-13, the dihedral angles (orange) are the rate limiting order parameters.
For MIL-53(Al), the tICA-RE result clearly reveals the volume as the order parameter corresponding to the largest amplitude in the slowest mode. This observation is in line with prior results from the literature, in which accurate free energy profiles for MIL-53(Al) were already constructed employing the unit cell volume as collective variable. The tICA-RE protocol also reveals two other components with non-negligible amplitudes. These components are related to topological quantities defining the ring opening, like the interdiagonal bending angle γ1 and the linker length r1, as visualized in Figure 3.
In contrast to the topological flexibility
in MIL-53(Al), for which
the volume arises as a natural collective variable, several order
parameters can be envisioned to study the breathing behavior of CAU-13,
associated with linker flexibility, as indicated in Figure 3. Niekiel et al. reported a
unit cell volume increase of approximately 25%, associated with the
elongation of the unit cell parameter. Moreover, experiments reveal
that the phase transition is accompanied by an inversion of the CDC
linker, which can be described by various collective variables. The
order parameters which best describe the transition dynamics are related
to the largest amplitudes in the tICA spectrum (see Figure 5b). Remarkably, the unit cell
volume contribution to the slowest eigenmode is negligibly small.
This is a surprising result and highlights the added value of the
tICA method to determine good reaction coordinates. The dihedral angles
ϕ1, ϕ2, ϕ3, and
ϕ4 turn out to be the slowest varying order parameters
in our parameter set. Based on their amplitude in the slowest mode,
we suggest to consider 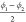 and
and 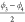 as collective
variables to be applied in
enhanced sampling simulations. Their values vary from approximately
−60° for the a,a-configuration to ca. 60° for
the e,e-configuration. If both collective variables change from
−60° toward 60°, then the structure transforms from
the cp to the lp phase. At this moment it is interesting to remark
the resemblance with the typical dihedral angles observed in the ring
flip of the cyclohexane molecule (Figure 2).
as collective
variables to be applied in
enhanced sampling simulations. Their values vary from approximately
−60° for the a,a-configuration to ca. 60° for
the e,e-configuration. If both collective variables change from
−60° toward 60°, then the structure transforms from
the cp to the lp phase. At this moment it is interesting to remark
the resemblance with the typical dihedral angles observed in the ring
flip of the cyclohexane molecule (Figure 2).
4.2. Free Energy Profiles as a Function of the Identified Collective Variables
4.2.1. MIL-53(Al)
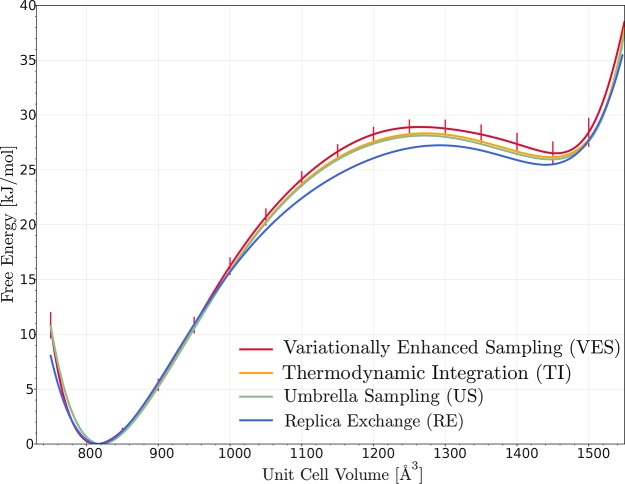
To study the suitability of the slowest order parameters resulting from the tICA method, free energy profiles will be extracted using various enhanced sampling MD techniques. In the literature, many studies have already been devoted to the reproduction of the free energy profile of MIL-53,17,21,32,60,76 such that this material can be used as a proof of concept for the suggested methodology. Profiles have been constructed using various enhanced MD techniques among which are TI, MTD, US, and VES. The free energy profiles were derived by employing the unit cell volume as the collective variable. Based on the first tICA mode, the volume indeed seems to be an optimal collective variable to study the breathing behavior of MIL-53(Al) (see Figure 5a). The resulting free energy profiles as a function of the unit cell volume are shown in Figure 6. The various methods clearly give a unified picture of the topological flexibility of MIL-53(Al). These free energy profiles clearly predict the bistable behavior of the material as observed experimentally. Deviations with regard to the experimental relative stability can be attributed to the force field description of the potential energy surface and more in particular to the nonbonding terms.24
Figure 6.
MIL-53(Al) free energy profile as a function of the unit cell volume, as obtained by using different free energy estimation methods.
Herewith we want to stress that RE, without any prior knowledge about the thermodynamic conditions in which the phase transition takes place, has its limitations. As mentioned in the Computational Details (Section 3), RE simulations are performed in the (N, P, σa = 0, T) ensemble in which the pressure is controlled. For MIL-53(Al) only 20 replicas are considered in a relatively small temperature range 200–580 K, which could not be enlarged due to the thermal instability of the material. By applying the RE method at a fixed pressure of 0 MPa, transitions from the cp to the lp phase should overcome high free energy differences of approximately 25 kJ/mol (see Figure 6), and exchange of replicas within this limited temperature range turns out to be insufficient to allow for a sufficient sampling of the lp and transition region. However, using prior knowledge on the lp-to-cp and cp-to-lp transition pressures, 29.6 MPa and −182 MPa,21 the transition can be facilitated. Performing the RE simulations at a fixed pressure of −60 MPa instead of 0 MPa increases the relative stability of the lp state with respect to the cp state, facilitating the cp-to-lp transition and significantly improving the sampling of the relevant regions during the RE simulations.
To extract the free energy profile (at 0 MPa) from these simulations at P0 = −60 MPa, we subtract the P0V term from the obtained thermodynamic potential. The resulting free energy profile in terms of unit cell volume at 290 K is shown in Figure 6. Obviously, the RE result now approaches the other enhanced sampling predictions as it should.
In conclusion, the here proposed tICA-RE procedure is shown to correctly identify the volume as the appropriate collective variable to study the topological flexibility of MIL-53(Al). Using this collective variable, TI, US, and VES perform exceptionally well to predict both (meta)stable phases of MIL-53(Al). For RE, however, prior knowledge of the transition pressures is required to accurately predict the bistable behavior of MIL-53(Al).
4.2.2. CAU-13
A more stringent test and real challenge for the tICA-RE protocol is the identification of appropriate collective variables for CAU-13. Intuitively, the unit cell volume can be regarded as a good order parameter for the phase transformation, as the volumes associated with the metastable lp and cp phases of CAU-13 are sufficiently distinct (568 Å3 versus 677 Å3). However, the tICA-RE protocol visualized in Figure 5b assigns an almost negligible amplitude to the volume, predicting that the volume would not be a good collective variable. To test the validity of the volume as a collective variable, we first constructed the free energy profile as a function of the volume using TI. In frameworks showing a topology flexibility as MIL-53(Al), TI has demonstrated to be one of the most appropriate methods to construct the free energy profile.17,21,32,60−62 The TI result for CAU-13 is displayed in Figure 7a (yellow curve) and clearly fails in reproducing the bistability. Only one stable minimum around 625 Å3 is found, which does not match the experimental observation of either of the two stable phases, i.e. cp or lp which are also indicated in Figure 7a. The prediction of tICA-RE that the volume is not suited as a reaction coordinate seems to hold based on this first test.
Figure 7.
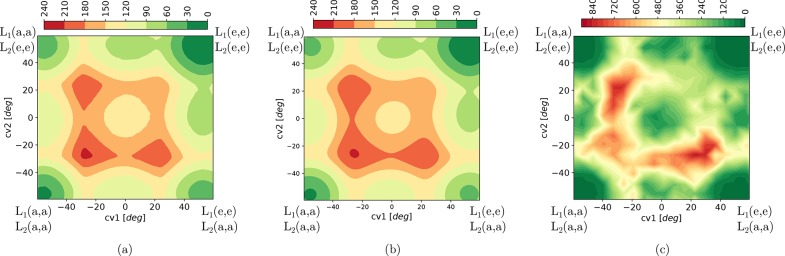
Free energy profile corresponding to the flexible behavior of CAU-13 at 300 K obtained with various enhanced sampling methods and as a function of three different collective variables: (a) the unit cell volume, (b) the dihedral angles ϕi, and (c) the bending angles γi. The profiles shown in panes (b) and (c) are obtained by a projection of a 2D free energy surface. A distinction is made between the techniques enhancing along those collective variables (TI, US, and VES) and enhancing all degrees of freedom (RE). Based on the transformation outlined in eq 1, free energy profiles as a function of the unit cell volume and bending angles can be constructed starting from the free energy profile for the dihedral angles. These transformed profiles, US(T) and VES(T), are indicated with dotted lines.
Based on the tICA-RE
analysis, other collective variables can be
suggested which should perform better than the volume, i.e. the bending
and dihedral angles. Rather than biasing each bending angle or dihedral
angle separately, a linear combination of those angles, based on the
tICA amplitudes, is preferred. The following linear combinations are
considered: 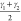 and
and 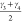 which are based
on the bending angles of
the linker and
which are based
on the bending angles of
the linker and 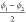 and
and  which are based
on the dihedral angles
in the cyclohexane linkers of the CDC structure, as schematically
indicated in Figure 3. While the bending angles of the linker,
which are based
on the dihedral angles
in the cyclohexane linkers of the CDC structure, as schematically
indicated in Figure 3. While the bending angles of the linker, 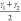 and
and  , already give
a larger contribution to
the slowest tIC eigenvector than the volume, the dihedral angles
, already give
a larger contribution to
the slowest tIC eigenvector than the volume, the dihedral angles 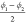 and
and  of the CDC
rings are clearly identified
as the dominant collective variables in the transition between the
cp and lp state of CAU-13. The pair of angles
of the CDC
rings are clearly identified
as the dominant collective variables in the transition between the
cp and lp state of CAU-13. The pair of angles 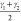 and
and 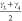 or
or 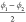 and
and 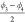 specify the
position and orientation of
the two CDC linkers lying on the origin of the flexibility in
CAU-13. To get thorough insight into the full phase space in terms
of these two collective variables, a two-dimensional free energy surface
is constructed using US and VES simulations (Figure 8). Afterward one-dimensional profiles may
be obtained by projecting these two-dimensional surfaces onto a one-dimensional
coordinate.
specify the
position and orientation of
the two CDC linkers lying on the origin of the flexibility in
CAU-13. To get thorough insight into the full phase space in terms
of these two collective variables, a two-dimensional free energy surface
is constructed using US and VES simulations (Figure 8). Afterward one-dimensional profiles may
be obtained by projecting these two-dimensional surfaces onto a one-dimensional
coordinate.
Figure 8.
Two-dimensional free energy surface of CAU-13 at 300 K as a function
of the collective variables, 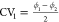 and
and 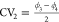 , proposed in this work obtained with three
different free energy methods: (a) US, (b) VES, and (c) RE.
, proposed in this work obtained with three
different free energy methods: (a) US, (b) VES, and (c) RE.
Figure 8 displays
the two-dimensional free energy surface as a function of two collective
variables 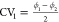 and
and 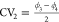 which were identified by the tICA-RE procedure
to act as the dominant. The contour plots of Figures 8(a) and 8(b) resulting
from US and VES are very similar, and the small differences which
are hardly observable are due to the finite sampling. Stable configurations
or local minima are located at CV1 = CV2 = −57°,
corresponding to the cp phase, where all linkers are in the a,a-configuration,
and CV1 = CV2 = +55°, corresponding to
the lp phase, where all linkers are in the e,e-configuration. In a
concerted transition where the two CDC linkers transform simultaneously
from an axial a,a-conformation (cp) to an elongated e,e-conformation
(lp), the reaction path would have to cross from the bottom left to
the top right of the contour plots in Figure 8 and needs to overcome free energy barriers
of the order 150–240 kJ/mol. A more favorable transition path
between the cp and lp states is given by a two-step process where
the two linkers undergo their conformational changes in a subsequent
way. Along this path—which will be further discussed later
in this section—smaller barriers of the order of 100 kJ/mol
are observed, and several other metastable states are present. A projection
of the free energy surface onto the average value
which were identified by the tICA-RE procedure
to act as the dominant. The contour plots of Figures 8(a) and 8(b) resulting
from US and VES are very similar, and the small differences which
are hardly observable are due to the finite sampling. Stable configurations
or local minima are located at CV1 = CV2 = −57°,
corresponding to the cp phase, where all linkers are in the a,a-configuration,
and CV1 = CV2 = +55°, corresponding to
the lp phase, where all linkers are in the e,e-configuration. In a
concerted transition where the two CDC linkers transform simultaneously
from an axial a,a-conformation (cp) to an elongated e,e-conformation
(lp), the reaction path would have to cross from the bottom left to
the top right of the contour plots in Figure 8 and needs to overcome free energy barriers
of the order 150–240 kJ/mol. A more favorable transition path
between the cp and lp states is given by a two-step process where
the two linkers undergo their conformational changes in a subsequent
way. Along this path—which will be further discussed later
in this section—smaller barriers of the order of 100 kJ/mol
are observed, and several other metastable states are present. A projection
of the free energy surface onto the average value 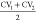 is shown in Figure 7b. The profiles resulting from
VES and US
are nearly identical.
is shown in Figure 7b. The profiles resulting from
VES and US
are nearly identical.
A similar procedure as for the dihedrals has been performed for the bending angles which were identified as less suitable order parameters from the tICA analysis. The two-dimensional free energy surfaces are displayed in Figure SI2 of the Supporting Information. The one-dimensional projection for the US and VES methods are reported in Figure 7c. In contrast to the previous case with the dihedrals as collective variables, the profiles obtained with US and VES drastically differ from each other. The various minima are approximately located at the same position, but relative stabilities of the cp, lp, and an intermediate state differ substantially. It is important to remark that this diffuse picture is neither related to the simulation time nor to imprecise results but is only due to the particular choice of the collective variable. To further stress this point, the evolution of the free energy profile with increasing time is included in Section V of the Supporting Information.
To investigate to which extent the replica exchange method itself is able to generate free energy profiles in terms of appropriate collective variables we now focus on the free energy profiles directly obtained from the replica exchange (RE) simulations. As discussed earlier, RE allows for the construction of free energy profiles as a function of any collective variable, since all degrees of freedom are sampled. Hence, based on the RE data, free energy profiles for CAU-13 can be constructed directly as a function of the volume, bend angles, and dihedral angles (see Figure 7). For CAU-13, the RE free energy profile as a function of the unit cell volume is depicted in Figure 7a and shows two shallow minima occurring around 600 Å3 and 700 Å3, which qualitatively correspond with the two stable states at 0 K (see Table 1). The agreement with the profile obtained by directly sampling volume states in TI is inadequate. This is another indication of the less appropriate choice of the volume as collective variable. The unit cell volume is not able to distinguish between the various stable states (see Section V of the Supporting Information).
Subsequently, we constructed
a two-dimensional free energy surface
spanned by the two collective variables 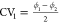 and
and 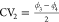 using RE (displayed in Figure 8c). Qualitatively, the free
energy surface resembles a great deal the US and VES surfaces displayed
in Figure 8a and Figure 8b. The (meta)states
are localized at the same position on the surface. However, significantly
larger free energy barriers are observed in RE simulation, with respect
to US and VES simulations. This is best visualized when projecting
the surface onto one dimension with
using RE (displayed in Figure 8c). Qualitatively, the free
energy surface resembles a great deal the US and VES surfaces displayed
in Figure 8a and Figure 8b. The (meta)states
are localized at the same position on the surface. However, significantly
larger free energy barriers are observed in RE simulation, with respect
to US and VES simulations. This is best visualized when projecting
the surface onto one dimension with 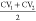 as parameter (Figure 7b). Positions of maxima and
minima of the
various curves are correctly reproduced; only the heights of the barriers
are overestimated. It indicates that the region of the phase space
around the transition state(s) is insufficiently sampled in RE. With
a sufficiently large simulation time one could expect that the RE
surface would show the same patterns as the US and VES surfaces. In
RE all degrees of freedom are sampled, there is no preferential order
parameter, and only when performing simulations for extremely long
simulation times, one could expect a more realistic sampling of that
specific region around the transition state. The probability of visiting
that specific region of the phase space directly affects the height
of the barrier but not the position. Hence, RE simulation data are
suitable as input for the tICA method giving a correct prediction
of the slowest modes but less suited to obtain precise free energy
surfaces in terms of appropriate collective variables.
as parameter (Figure 7b). Positions of maxima and
minima of the
various curves are correctly reproduced; only the heights of the barriers
are overestimated. It indicates that the region of the phase space
around the transition state(s) is insufficiently sampled in RE. With
a sufficiently large simulation time one could expect that the RE
surface would show the same patterns as the US and VES surfaces. In
RE all degrees of freedom are sampled, there is no preferential order
parameter, and only when performing simulations for extremely long
simulation times, one could expect a more realistic sampling of that
specific region around the transition state. The probability of visiting
that specific region of the phase space directly affects the height
of the barrier but not the position. Hence, RE simulation data are
suitable as input for the tICA method giving a correct prediction
of the slowest modes but less suited to obtain precise free energy
surfaces in terms of appropriate collective variables.
As a further test for the proper selection of collective variables, one can also derive, based on the knowledge of the free energy profile in terms of a first collective variable q1, a free energy profile as a function of another collective variable q2 by means of the following transformation:
| 1 |
Here, p(q2|q1) is the conditional probability of the collective variable q2 in terms of the collective variable q1, and c represents the appropriate normalization factor. The proof of this transformation is based on statistical mechanics and can be found in Section III of the Supporting Information. The precision of the free energy profile obtained with this approach is largely dependent on the conditional probability p(q2|q1) of the collective variable q2 in terms of q1 and requires sufficient sampling of the q2 coordinate for each relevant value of q1. Starting from the profiles as a function of the dihedrals (ϕi), derived profiles can be constructed by means of the transformation of eq 1 in terms of the bending angles. Those transformed profiles are presented by the dotted curves labeled US(T) and VES(T) in Figures 7a and 7c. It is important to note that any projection leads to a loss of information and hence that reasonable transformations of energy profiles can only be expected starting from an accurate energy profile F(q1) along an appropriate set of collective variables.
We observe that the free energy profile VES(T), obtained after transformation of a profile extracted from VES simulations along the dominant dihedral pathway, approaches the RE result. Similarly, a qualitative agreement regarding the relative stability of the (meta)stable states is obtained for the transformed profiles along the bending angles US(T) and VES(T) and the RE profile. Such an agreement is by far not found if bending angles are considered as collective variables (Figure 7c). Introducing bias potentials in the direction of this reaction coordinate, we obtain VES and US predictions for the free energy profiles in a direct way, but they are drastically different as already reported. On the contrary the projected VES(T) and US(T) results originating from Figure 7b are much more consistent and support our conclusion that the bending angles are failing in describing the structural transition, while the dihedrals angles act as optimal collective variables.
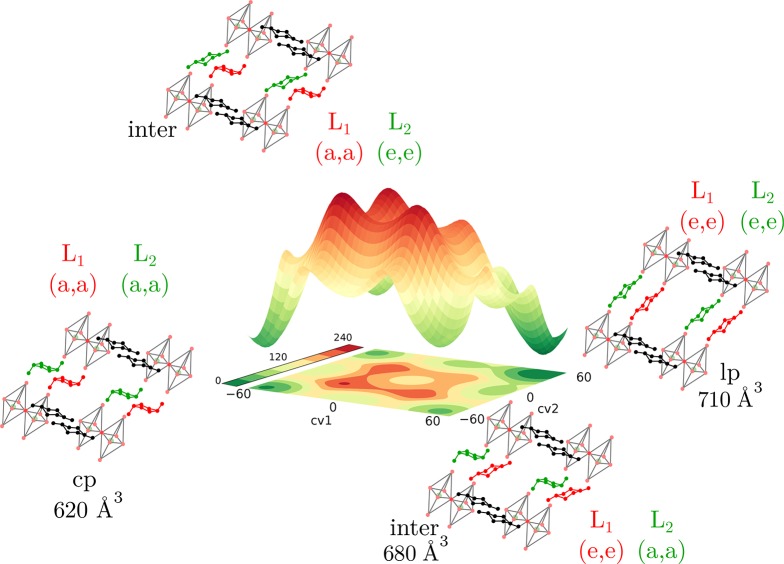
Summarizing, all simulations and collective variable transformations indicate that the dihedrals corresponding to the ring flip of the CDC linker are indeed the most appropriate set of collective variables to describe the linker flexibility in CAU-13 as predicted by our tICA-RE protocol. The most accurate free energy profile is then obtained by US or VES as displayed in Figure 8 by a two-dimensional landscape with the dihedrals of the two CDC linkers as collective variables. This profile gives an accurate description of the breathing behavior of CAU-13 at 300 K. The most favorable transition path from cp to lp is given by a two-step process. To describe the transition from the cp to lp state, the nomenclature of the cyclohexane state can be employed (see Figure 2). In the first step, the first CDC linker (L1) undergoes a transition from chair conformation (cp) (CV1 = CV2 = −60°) toward inverse chair conformation (CV1 = 60°, CV2 = −60°) (see Figure 9). This path crosses some intermediate states: a half chair conformation (CV1 = −30°, CV2 = −60°), a twisted boat (CV1 = 0°, CV2 = −60°), and again a half chair conformation (CV1 = 30°, CV2 = −60°). In the second step the second CDC linker (L2) undergoes a similar transformation from a chair toward an inversed chair configuration, and both linkers are in an elongated e,e-conformation (lp). A similar path can be followed in which the second CDC linker undergoes a ring flip before the first linker flips. Comparing the free energy profile with the textbook example of the isolated cyclohexane molecule (see Figure 2) clearly indicates the influence of the framework which is manifested by two observations. First, the free energy barrier for a CDC linker to undergo a ring flip is much higher than the barrier for cyclohexane. Second, the ring flip of one CDC linker is not symmetric, i.e. the inverse chair configuration is not as stable as the chair configuration. The resulting free energy surface, depicted in Figure 9, indicates substantial free energy barriers even when a subsequent transition of the linkers is followed. To study the influence of guest molecules on the barriers a similar analysis is performed with adsorbed xylene molecules.
Figure 9.
Free energy surface (in kJ/mol and obtained with VES) of CAU-13 at 300 K as a function of the proposed collective variables corresponding to the ring inversion in CAU-13. Schematic representation of one of the folding pathways of CAU-13 of our simulation cell and the periodic extension.
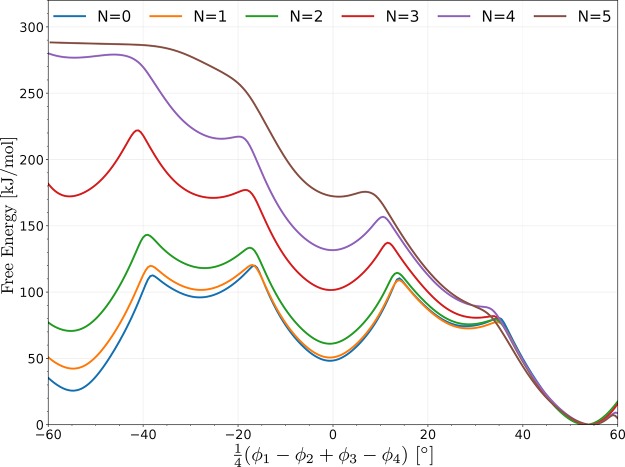
4.3. CAU-13 with Adsorbed Xylene Molecules
The stepwise transition between different states in CAU-13 is remarkable. Rather than a global breathing behavior, such as the proposed layer-by-layer transitions in MIL-53(Al),77 each linker can transform individually. In the experimental work of Niekiel et al.,23 CAU-13 undergoes a transition from the cp to the lp state under the influence of xylene adsorption. This flexible behavior is characterized by a volume change of approximately 25%, and the CDC linkers deform from an a,a-configuration to an e,e-configuration. Based on the free energy surface displayed in Figure 9, CAU-13 is able to occur in the cp, lp, or intermediate states if no xylene molecules are present. However, the barriers for the transformation are relatively high which suggests that the phase transformation will not occur spontaneously. Furthermore, and contrary to topological flexible MOFs, pressure does not trigger changes in the relative stability of the various phases of CAU-13. To investigate the influence of guest molecules on the free energy profiles we performed a series of VES simulations with a systematically higher loading of xylene molecules. The resulting free energy profiles are shown in Figure 10. The cp state becomes less stable with increasing xylene loading. For a loading lower than four xylene molecules in our simulation cell, the cp minimum is still present, and thus we expect the cp structure to be retained when initially starting from this phase. However, the cp minimum disappears from a loading of four xylene molecules in our simulation cell, forcing the system to transform toward the lp phase. Experimentally, the cp to lp transition also takes place when four xylene molecules are adsorbed in CAU-13.23 Hence, despite the use of force fields, which approximate the true potential energy surface, we are able to match experimental observations. This is an additional proof that the collective variables predicted within the tICA-RE protocol allow for an accurate construction of the free energy surface. To the best of our knowledge a free energy profile with adsorbed guest molecules in terms of an appropriate reaction coordinate was not yet constructed for frameworks exhibiting linker flexibility.
Figure 10.
Projection of the free energy surface (obtained with VES) of CAU-13 at 300 K for various loadings of xylene molecules.
5. Conclusions
This work offers an efficient protocol to identify the most appropriate collective variables that can be employed in enhanced sampling MD techniques to construct accurate free energy profiles for MOFs that contain various types of flexibility. The tICA-RE protocol proposed here consists of a three-step procedure. In a first step, replica exchange (RE) simulations are performed to gather sufficient molecular dynamics data on the transitions between the various stable states of the MOF, taking into account that in RE all degrees of freedom are sampled. Subsequently, slow order parameters are identified by means of the time-structure based independent component analysis (tICA) method. A decomposition of the first tIC eigenvector, corresponding with the slowest mode of the system, discloses the dominant order parameters in the transition covering the structural transformation. In the third and final step, accurate free energy profiles can be constructed by means of enhanced sampling MD simulations targeting the sampling of these slow modes. Based on this three-step tICA-RE procedure to construct accurate free energy profiles for breathing MOFs, we were able to elucidate on the breathing behavior of both MIL-53(Al) and CAU-13 with different types of flexibility.
The case of the topologically flexible MIL-53(Al) has already been studied in the literature, and in this case the unit cell volume largely contributes to the slowest independent component. However, while most phase transformations in MOFs are accompanied by a significant volume change, this work shows that the volume does not always represent an appropriate reaction coordinate to map the full dynamical behavior of the phase transformation. This is the case for CAU-13 whose flexibility is associated with a flexible linker. In this case, a combination of internal dihedral angles formed by the subsequent carbon atoms in the CDC ring was identified as the slowest order parameter. The reliability of this collective variable is not surprising when comparing the behavior of the CDC linkers in the lattice to ring flips in cyclohexane molecules. We explicitly showed that use of the unit cell volume as a collective variable for enhanced sampling simulations in CAU-13 yields an inaccurate free energy profile as it was not able to distinguish between the cp and lp states. The case study on CAU-13 clearly supports the merits of the tICA-RE protocol as it provides evidence for the selection of appropriate collective variables to construct the free energy profile associated with the flexible behavior. By constructing two-dimensional profiles in terms of the internal dihedral angles in the linkers, we could show that the transformation from the cp to lp phase follows a stepwise behavior with several intermediate states on the reaction path. Furthermore, we have extended the analysis toward frameworks loaded with xylene molecules. We could show, based on the constructed free energy surfaces, the decreased stability of the cp and intermediate states with increased xylene loading favoring the lp state. The latter observation is in line with experimental input.
In conclusion, we have presented a protocol which allows the construction of free energy surfaces for various kinds of flexibility in MOFs. Whereas free energy profiles constructed in the literature were mainly based on the volume as a collective variable, this protocol can also be used for MOFs with linker flexibility where the volume is not a good reaction coordinate.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b00725.
Theoretical details on the various free energy methods derived from basic statistical mechanics, tICA method and free energy transformations, two-dimensional free energy surfaces in terms of the bending angles of the CDC linkers in CAU-13, further analysis of the inadequate collective variables in CAU-13 (PDF)
The authors acknowledge the Fund for Scientific Research – Flanders (FWO), the Research Board of Ghent University (BOF), and BELSPO in the frame of IAP/7/05 for financial support. R.D. and V.V.S. acknowledge funding from the European Union’s Horizon 2020 research and innovation programme (consolidator ERC grant agreement no. 647755 DYNPOR (20152020)). The computational resources and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by the Research Foundation - Flanders (FWO) and the Flemish Government – department EWI.
The authors declare no competing financial interest.
Supplementary Material
References
- Czaja A. U.; Trukhan N.; Müller U. Industrial applications of metal–organic frameworks. Chem. Soc. Rev. 2009, 38, 1284–1293. 10.1039/b804680h. [DOI] [PubMed] [Google Scholar]
- Furukawa H.; Cordova K. E.; O’Keeffe M.; Yaghi O. M. The Chemistry and Applications of Metal-Organic Frameworks. Science 2013, 341, 1230444. 10.1126/science.1230444. [DOI] [PubMed] [Google Scholar]
- Yi F.-Y.; Chen D.; Wu M.-K.; Han L.; Jiang H.-L. Chemical Sensors Based on Metal–Organic Frameworks. ChemPlusChem 2016, 81, 675–690. 10.1002/cplu.201600137. [DOI] [PubMed] [Google Scholar]
- Pettinari C.; Marchetti F.; Mosca N.; Tosi G.; Drozdov A. Application of Metalorganic Frameworks. Polym. Int. 2017, 66, 731–744. 10.1002/pi.5315. [DOI] [Google Scholar]
- Kang Z.; Fan L.; Sun D. Recent Advances and Challenges of Metal–Organic Framework Membranes for Gas Separation. J. Mater. Chem. A 2017, 5, 10073–10091. 10.1039/C7TA01142C. [DOI] [Google Scholar]
- Li H.; Eddaoudi M.; O’Keeffe M.; Yaghi O. M. Design and Synthesis of an Exceptionally Stable and Highly Porous Metal-Organic Framework. Nature 1999, 402, 276–279. 10.1038/46248. [DOI] [Google Scholar]
- Férey G. Microporous Solids: From Organically Templated Inorganic Skeletons to Hybrid Frameworks···Ecumenism in Chemistry. Chem. Mater. 2001, 13, 3084–3098. 10.1021/cm011070n. [DOI] [Google Scholar]
- Kitagawa S.; Kitaura R.; Noro S.-i. Functional Porous Coordination Polymers. Angew. Chem., Int. Ed. 2004, 43, 2334–2375. 10.1002/anie.200300610. [DOI] [PubMed] [Google Scholar]
- Horcajada P.; Chalati T.; Serre C.; Gillet B.; Sebrie C.; Baati T.; Eubank J. F.; Heurtaux D.; Clayette P.; Kreuz C.; Chang J.-S.; Hwang Y. K.; Marsaud V.; Bories P.-N.; Cynober L.; Gil S.; Férey G.; Couvreur P.; Gref R. Porous metal–organic-framework nanoscale carriers as a potential platform for drug delivery and imaging. Nat. Mater. 2010, 9, 172–178. 10.1038/nmat2608. [DOI] [PubMed] [Google Scholar]
- Horcajada P.; Gref R.; Baati T.; Allan P. K.; Maurin G.; Couvreur P.; Férey G.; Morris R. E.; Serre C. Metal–Organic Frameworks in Biomedicine. Chem. Rev. 2012, 112, 1232–1268. 10.1021/cr200256v. [DOI] [PubMed] [Google Scholar]
- Gascon J.; Corma A.; Kapteijn F.; Llabrés i Xamena F. X. Metal Organic Framework Catalysis: Quo vadis?. ACS Catal. 2014, 4, 361–378. 10.1021/cs400959k. [DOI] [Google Scholar]
- Rogge S. M. J.; Bavykina A.; Hajek J.; Garcia H.; Olivos-Suarez A. I.; Sepúlveda-Escribano A.; Vimont A.; Clet G.; Bazin P.; Kapteijn F.; Daturi M.; Ramos-Fernandez E. V.; Llabrés i Xamena F. X.; Van Speybroeck V.; Gascon J. Metal-Organic and Covalent Organic Frameworks As Single-Site Catalysts. Chem. Soc. Rev. 2017, 46, 3134–3184. 10.1039/C7CS00033B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J.-R.; Kuppler R. J.; Zhou H.-C.; Musselman I. H.; Kang Y. S.; Kim S.-J.; Kim Y.; Jegal J.; Morsi B. I.; Schroeder K. T.; Vos D. E. D.; Sakata M.; Takata M. Selective Gas Adsorption and Separation in Metal-Organic Frameworks. Chem. Soc. Rev. 2009, 38, 1477–1504. 10.1039/b802426j. [DOI] [PubMed] [Google Scholar]
- Schneemann A.; Bon V.; Schwedler I.; Senkovska I.; Kaskel S.; Fischer R. A. Flexible Metal-Organic Frameworks. Chem. Soc. Rev. 2014, 43, 6062–6096. 10.1039/C4CS00101J. [DOI] [PubMed] [Google Scholar]
- Férey G.; Serre C. Large Breathing Effects in Three-Dimensional Porous Hybrid Matter: Facts, Analyses, Rules and Consequences. Chem. Soc. Rev. 2009, 38, 1380–1399. 10.1039/b804302g. [DOI] [PubMed] [Google Scholar]
- Coudert F.-X. Responsive Metal-Organic Frameworks and Framework Materials: Under Pressure, Taking the Heat, in the Spotlight, with Friends. Chem. Mater. 2015, 27, 1905–1916. 10.1021/acs.chemmater.5b00046. [DOI] [Google Scholar]
- Vanduyfhuys L.; Rogge S. M. J.; Wieme J.; Vandenbrande S.; Maurin G.; Waro- quier M.; Van Speybroeck V. Thermodynamic insight into stimuli-responsive behaviour of soft porous crystals. Nat. Commun. 2018, 9, 204. 10.1038/s41467-017-02666-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang Z.; Yang D.-H.; Xu J.; Hu T.-L.; Bu X.-H. Flexible metal–organic frameworks: recent advances and potential applications. Adv. Mater. 2015, 27, 5432–5441. 10.1002/adma.201501523. [DOI] [PubMed] [Google Scholar]
- Yot P. G.; Boudene Z.; Macia J.; Granier D.; Vanduyfhuys L.; Verstraelen T.; Van Speybroeck V.; Devic T.; Serre C.; Férey G.; Stock N.; Maurin G. Metal-Organic Frameworks As Potential Shock Absorbers: The Case of the Highly Flexible MIL-53(Al). Chem. Commun. 2014, 50, 9462–9464. 10.1039/C4CC03853C. [DOI] [PubMed] [Google Scholar]
- Kitagawa S.; Uemura K. Dynamic porous properties of coordination polymers inspired by hydrogen bonds. Chem. Soc. Rev. 2005, 34, 109–119. 10.1039/b313997m. [DOI] [PubMed] [Google Scholar]
- Rogge S. M. J.; Vanduyfhuys L.; Ghysels A.; Waroquier M.; Verstraelen T.; Maurin G.; Van Speybroeck V. A Comparison of Barostats for the Mechanical Characterization of Metal-Organic Frameworks. J. Chem. Theory Comput. 2015, 11, 5583–5597. 10.1021/acs.jctc.5b00748. [DOI] [PubMed] [Google Scholar]
- Fairen-Jimenez D.; Moggach S.; Wharmby M.; Wright P.; Parsons S.; Düren T. Opening the gate: framework flexibility in ZIF-8 explored by experiments and simulations. J. Am. Chem. Soc. 2011, 133, 8900–8902. 10.1021/ja202154j. [DOI] [PubMed] [Google Scholar]
- Niekiel F.; Lannoeye J.; Reinsch H.; Munn A. S.; Heerwig A.; Zizak I.; Kaskel S.; Walton R. I.; De Vos D.; Llewellyn P.; Lieb A.; Guillaume M.; Stock N. Conformation-controlled sorption properties and breathing of the aliphatic Al-MOF [Al (OH)(CDC)]. Inorg. Chem. 2014, 53, 4610–4620. 10.1021/ic500288w. [DOI] [PubMed] [Google Scholar]
- Walker A. M.; Civalleri B.; Slater B.; Mellot-Draznieks C.; Corà F.; Zicovich-Wilson C. M.; Román-Pérez G.; Soler J. M.; Gale J. D. Flexibility in a Metal-Organic Framework Material Controlled by Weak Dispersion Forces: The Bistability of MIL-53(Al). Angew. Chem., Int. Ed. 2010, 49, 7501–7503. 10.1002/anie.201002413. [DOI] [PubMed] [Google Scholar]
- Ortiz A. U.; Boutin A.; Fuchs A. H.; Coudert F.-X. Anisotropic Elastic Properties of Flexible Metal-Organic Frameworks: How Soft Are Soft Porous Crystals?. Phys. Rev. Lett. 2012, 109, 195502. 10.1103/PhysRevLett.109.195502. [DOI] [PubMed] [Google Scholar]
- Ortiz A. U.; Boutin A.; Coudert F.-X. Prediction of Flexibility of Metal-Organic Frameworks CAU-13 and NOTT-300 by First Principles Molecular Simulations. Chem. Commun. 2014, 50, 5867–5870. 10.1039/c4cc00734d. [DOI] [PubMed] [Google Scholar]
- Peters B.Reaction rate theory and rare events; Elsevier: 2017. [Google Scholar]
- Molgedey L.; Schuster H. G. Separation of a mixture of independent signals using time delayed correlations. Phys. Rev. Lett. 1994, 72, 3634. 10.1103/PhysRevLett.72.3634. [DOI] [PubMed] [Google Scholar]
- Naritomi Y.; Fuchigami S. Slow dynamics in protein fluctuations revealed by time-structure based independent component analysis: the case of domain motions. J. Chem. Phys. 2011, 134, 065101. 10.1063/1.3554380. [DOI] [PubMed] [Google Scholar]
- Pérez-Hernández G.; Paul F.; Giorgino T.; De Fabritiis G.; Noé F. Identification of slow molecular order parameters for Markov model construction. J. Chem. Phys. 2013, 139, 015102. 10.1063/1.4811489. [DOI] [PubMed] [Google Scholar]
- Schwantes C. R.; Pande V. S. Improvements in Markov state model construction reveal many non-native interactions in the folding of NTL9. J. Chem. Theory Comput. 2013, 9, 2000–2009. 10.1021/ct300878a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demuynck R.; Rogge S. M. J.; Vanduyfhuys L.; Wieme J.; Waroquier M.; Van Speybroeck V. Efficient Construction of Free Energy Profiles of Breathing Metal–Organic Frameworks Using Advanced Molecular Dynamics Simulations. J. Chem. Theory Comput. 2017, 13, 5861–5873. 10.1021/acs.jctc.7b01014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkwood J. G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. 10.1063/1.1749657. [DOI] [Google Scholar]
- Torrie G.; Valleau J. Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella Sampling. J. Comput. Phys. 1977, 23, 187–199. 10.1016/0021-9991(77)90121-8. [DOI] [Google Scholar]
- Valsson O.; Parrinello M. Variational Approach to Enhanced Sampling and Free Energy Calculations. Phys. Rev. Lett. 2014, 113, 090601. 10.1103/PhysRevLett.113.090601. [DOI] [PubMed] [Google Scholar]
- Loiseau T.; Serre C.; Huguenard C.; Fink G.; Taulelle F.; Henry M.; Bataille T.; Férey G. A Rationale for the Large Breathing of the Porous Aluminum Terephthalate (MIL-53) upon Hydration. Chem. - Eur. J. 2004, 10, 1373–1382. 10.1002/chem.200305413. [DOI] [PubMed] [Google Scholar]
- Liu Y.; Her J.-H.; Dailly A.; Ramirez-Cuesta A. J.; Neumann D. A.; Brown C. M. Reversible Structural Transition in MIL-53 with Large Temperature Hysteresis. J. Am. Chem. Soc. 2008, 130, 11813–118138. 10.1021/ja803669w. [DOI] [PubMed] [Google Scholar]
- Boutin A.; Springuel-Huet M.-A.; Nossov A.; Gédéon A.; Loiseau T.; Volkringer C.; Férey G.; Coudert F.-X.; Fuchs A. H. Breathing Transitions in MIL-53(Al) Metal-Organic Framework upon Xenon Adsorption. Angew. Chem., Int. Ed. 2009, 48, 8314–8317. 10.1002/anie.200903153. [DOI] [PubMed] [Google Scholar]
- Niekiel F.; Ackermann M.; Guerrier P.; Rothkirch A.; Stock N. Aluminum-1,4-cyclohexanedicarboxylates: High-Throughput and Temperature-Dependent in Situ EDXRD Studies. Inorg. Chem. 2013, 52, 8699–8705. 10.1021/ic400825b. [DOI] [PubMed] [Google Scholar]
- Reinsch H.; Benecke J.; Etter M.; Heidenreich N.; Stock N. Combined in-and ex situ studies of pyrazine adsorption into the aliphatic MOF Al-CAU-13: structures, dynamics and correlations. Dalton Trans. 2017, 46, 1397–1405. 10.1039/C6DT03998G. [DOI] [PubMed] [Google Scholar]
- Leventis N.; Hanna S. B.; Sotiriou-Leventis C. A three-dimensional energy surface for the conformational inversion of cyclohexane. J. Chem. Educ. 1997, 74, 813. 10.1021/ed074p813. [DOI] [Google Scholar]
- Vanduyfhuys L.; Vandenbrande S.; Wieme J.; Waroquier M.; Verstraelen T.; Van Speybroeck V. Extension of the QuickFF force field protocol for an improved accuracy of structural, vibrational, mechanical and thermal properties of metal–organic frameworks. J. Comput. Chem. 2018, 39, 999–1011. 10.1002/jcc.25173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shukla D.; Hernandez C. X.; Weber J. K.; Pande V. S. Markov state models provide insights into dynamic modulation of protein function. Acc. Chem. Res. 2015, 48, 414–422. 10.1021/ar5002999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugita Y.; Okamoto Y. Replica-Exchange Molecular Dynamics Method for Protein Folding. Chem. Phys. Lett. 1999, 314, 141–151. 10.1016/S0009-2614(99)01123-9. [DOI] [Google Scholar]
- Peters B. Reaction Coordinates and Mechanistic Hypothesis Tests. Annu. Rev. Phys. Chem. 2016, 67, 669–690. 10.1146/annurev-physchem-040215-112215. [DOI] [PubMed] [Google Scholar]
- Rohrdanz M. A.; Zheng W.; Clementi C. Discovering Mountain Passes Via Torch-light: Methods for the Definition of Reaction Coordinates and Pathways in Complex Macromolecular Reactions. Annu. Rev. Phys. Chem. 2013, 64, 295–316. 10.1146/annurev-physchem-040412-110006. [DOI] [PubMed] [Google Scholar]
- Rogge S. M. J.; Caroes S.; Demuynck R.; Waroquier M.; Van Speybroeck V.; Ghysels A. The Importance of Cell Shape Sampling To Accurately Predict Flexibility in MetalOrganic Frameworks. J. Chem. Theory Comput. 2018, 14, 1186–1197. 10.1021/acs.jctc.7b01134. [DOI] [PubMed] [Google Scholar]
- Serre C.; Bourrelly S.; Vimont A.; Ramsahye N.; Maurin G.; Llewellyn P.; Daturi M.; Filinchuk Y.; Leynaud O.; Barnes P.; F́erey G. An Explanation for the Very Large Breathing Effect of a Metal–Organic Framework During CO2 Adsorption. Adv. Mater. 2007, 19, 2246–2251. 10.1002/adma.200602645. [DOI] [Google Scholar]
- Swendsen R. H.; Wang J.-S. Replica Monte Carlo Simulation of Spin-Glasses. Phys. Rev. Lett. 1986, 57, 2607–2609. 10.1103/PhysRevLett.57.2607. [DOI] [PubMed] [Google Scholar]
- Marinari E.; Parisi G. Simulated Tempering: A New Monte Carlo Scheme. EPL 1992, 19, 451. 10.1209/0295-5075/19/6/002. [DOI] [Google Scholar]
- Hansmann U. H. E. Parallel Tempering Algorithm for Conformational Studies of Biological Molecules. Chem. Phys. Lett. 1997, 281, 140–150. 10.1016/S0009-2614(97)01198-6. [DOI] [Google Scholar]
- Patey G. N.; Valleau J. P. A Monte Carlo Method for Obtaining the Interionic Potential of Mean Force in Ionic Solution. J. Chem. Phys. 1975, 63, 2334–2339. 10.1063/1.431685. [DOI] [Google Scholar]
- Zwanzig R. W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. 10.1063/1.1740409. [DOI] [Google Scholar]
- Laio A.; Parrinello M. Escaping Free-Energy Minima. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 12562–12566. 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen N.; van Gunsteren W. F. Practical Aspects of Free-Energy Calculations: A Review. J. Chem. Theory Comput. 2014, 10, 2632–2647. 10.1021/ct500161f. [DOI] [PubMed] [Google Scholar]
- Pietrucci F. Strategies for the Exploration of Free Energy Landscapes: Unity in Diversity and Challenges Ahead. Rev. Phys. 2017, 2, 32–45. 10.1016/j.revip.2017.05.001. [DOI] [Google Scholar]
- Gallicchio E.; Andrec M.; Felts A. K.; Levy R. M. Temperature weighted histogram analysis method, replica exchange, and transition paths. J. Phys. Chem. B 2005, 109, 6722–6731. 10.1021/jp045294f. [DOI] [PubMed] [Google Scholar]
- Shirts M. R.; Chodera J. D. Statistically Optimal Analysis of Samples from Multiple Equilibrium States. J. Chem. Phys. 2008, 129, 124105. 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H.; Paul F.; Wehmeyer C.; Noé F. Multiensemble Markov models of molecular thermodynamics and kinetics. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, E3221–E3230. 10.1073/pnas.1525092113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wieme J.; Vanduyfhuys L.; Rogge S. M. J.; Waroquier M.; Van Speybroeck V. Exploring the Flexibility of MIL-47(V)-Type Materials Using Force Field Molecular Dynamics Simulations. J. Phys. Chem. C 2016, 120, 14934–14947. 10.1021/acs.jpcc.6b04422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans J. D.; Bocquet L.; Coudert F.-X. Origins of Negative Gas Adsorption. Chem. 2016, 1, 873–886. 10.1016/j.chempr.2016.11.004. [DOI] [Google Scholar]
- Rogge S. M. J.; Waroquier M.; Van Speybroeck V. Reliably Modeling the Mechanical Stability of Rigid and Flexible Metal–Organic Frameworks. Acc. Chem. Res. 2018, 51, 138–148. 10.1021/acs.accounts.7b00404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S.; Rosenberg J. M.; Bouzida D.; Swendsen R. H.; Kollman P. A. The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. the Method. J. Comput. Chem. 1992, 13, 1011–1021. 10.1002/jcc.540130812. [DOI] [Google Scholar]
- Rosta E.; Hummer G. Free Energies from Dynamic Weighted Histogram Analysis Using Unbiased Markov State Model. J. Chem. Theory Comput. 2015, 11, 276–285. 10.1021/ct500719p. [DOI] [PubMed] [Google Scholar]
- Verstraelen T.; Vanduyfhuys L.; Vandenbrande S.; Rogge S. M. J.. Yaff, Yet Another Force Field. http://molmod.ugent.be/software/ (accessed Oct 24, 2018).
- Hoover W. G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A 1985, 31, 1695–1697. 10.1103/PhysRevA.31.1695. [DOI] [PubMed] [Google Scholar]
- Martyna G. J.; Tobias D. J.; Klein M. L. Constant Pressure Molecular Dynamics Algorithms. J. Chem. Phys. 1994, 101, 4177. 10.1063/1.467468. [DOI] [Google Scholar]
- Martyna G. J.; Tuckerman M. E.; Tobias D. J.; Klein M. Explicit Reversible Integrators for Extended Systems Dynamics. Mol. Phys. 1996, 87, 1117–1157. 10.1080/00268979600100761. [DOI] [Google Scholar]
- Vanduyfhuys L.; Verstraelen T.; Vandichel M.; Waroquier M.; Van Speybroeck V. Ab Initio Parametrized Force Field for the Flexible Metal-Organic Framework MIL-53(Al). J. Chem. Theory Comput. 2012, 8, 3217–3231. 10.1021/ct300172m. [DOI] [PubMed] [Google Scholar]
- Allinger N. L.; Yuh Y. H.; Lii J. H. Molecular Mechanics. the MM3 Force Field for Hydrocarbons. 1. J. Am. Chem. Soc. 1989, 111, 8551–8566. 10.1021/ja00205a001. [DOI] [Google Scholar]
- Verstraelen T.; Vandenbrande S.; Heidar-Zadeh F.; Vanduyfhuys L.; Van Speybroeck V.; Waroquier M.; Ayers P. W. Minimal Basis Iterative Stockholder: Atoms in Molecules for Force-Field Development. J. Chem. Theory Comput. 2016, 12, 3894–3912. 10.1021/acs.jctc.6b00456. [DOI] [PubMed] [Google Scholar]
- Zhang B. W.; Dai W.; Gallicchio E.; He P.; Xia J.; Tan Z.; Levy R. M. Simulating replica exchange: Markov state models, proposal schemes, and the infinite swapping limit. J. Phys. Chem. B 2016, 120, 8289–8301. 10.1021/acs.jpcb.6b02015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sindhikara D.; Meng Y.; Roitberg A. E. Exchange frequency in replica exchange molecular dynamics. J. Chem. Phys. 2008, 128, 024103. 10.1063/1.2816560. [DOI] [PubMed] [Google Scholar]
- Rosta E.; Hummer G. Error and efficiency of replica exchange molecular dynamics simulations. J. Chem. Phys. 2009, 131, 165102. 10.1063/1.3249608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrigan M. P.; Sultan M. M.; Hernández C. X.; Husic B. E.; Eastman P.; Schwantes C. R.; Beauchamp K. A.; McGibbon R. T.; Pande V. S. MSMBuilder: statistical models for biomolecular dynamics. Biophys. J. 2017, 112, 10–15. 10.1016/j.bpj.2016.10.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cockayne E. Thermodynamics of the Flexible Metal-Organic Framework Material MIL-53(Cr) from First-Principles. J. Phys. Chem. C 2017, 121, 4312–4317. 10.1021/acs.jpcc.6b11692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Triguero C.; Coudert F.-X.; Boutin A.; Fuchs A. H.; Neimark A. V. Mechanism of Breathing Transitions in Metal-Organic Frameworks. J. Phys. Chem. Lett. 2011, 2, 2033–2037. 10.1021/jz2008769. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.