Modelling the coefficient of thermal expansion in graphite crystals: implications of lattice strain due to irradiation and pressure

Abstract

Theoretical models for the coefficient of thermal expansion (CTE) first proposed in the 1970s are expanded upon, allowing them, for the first time, to be implemented over a wide temperature range. The models are of interest because they predict the effects of the changes in the crystal lattice spacing and crystallite modulus on the CTE. Hence, they can in turn be used to investigate the influence of pressure and irradiation on the CTE. To date, typographical and mathematical errors and incomplete or conflicting assumptions between the various papers had made the complex mathematical formulations difficult, if not impossible, to follow and apply. This paper has two main aims: firstly to revisit and review the CTE models, correcting the errors and compiling and updating various input data, secondly to use the revised models to investigate the effect of loading and irradiation on the CTE. In particular, the models have been applied to data for natural and highly orientated pyrolytic graphite and compared with experimental data, giving an insight into the influence of temperature, loading and irradiation on both single crystal and polycrystalline graphite. The findings lend credence to postulated microstructural mechanisms attributed to the in-reactor behaviour of nuclear graphite, which finds a wide use in predictive multiscale modelling.

1. Introduction

Significant property and dimensional changes are exhibited by polycrystalline graphite subjected to fast neutron irradiation [1] and high pressure [2]. Of particular interest are the changes to the coefficient of thermal expansion (CTE). It is postulated that changes to the CTE in polycrystalline graphite under loading and irradiation are related to a combination of changes to: the crystallites, the porosity, the crystal orientation, the microstructural stiffness or more likely a combination of these factors [3,4]. To separate out these effects, it is therefore important to understand and define the possible contribution that crystal CTE changes have on the bulk CTE. To this end, Kelly [5] derived several theoretical models capable of predicting the CTE of a graphite crystal as a function of temperature and crystal lattice spacing [6–13]. Unfortunately, to date, these theoretical models have not been widely taken up as typographical errors and incomplete or conflicting assumptions between the various papers make the complex mathematical formulations difficult, if not impossible, to follow and apply.

This paper revisits and reviews these CTE models, correcting the errors as well as compiling and updating various model input data. The models are used to investigate the effect of loading and irradiation on the CTE, and are compared with available experimental data. In particular, the models have been applied to data for natural and highly orientated pyrolytic graphite and compared with experimental data, giving an insight into the influence of temperature, loading and irradiation on both single crystal and polycrystalline graphite.

2. Development of a graphite semi-continuum coefficient of thermal expansion model

The relationship between crystal strains e_ij and crystal stresses τ_ij are defined by the Cartesian co-ordinate system, given in figure 1a, with the z-axis parallel to the hexagonal axis of the crystal c-axis as follows:

$$\left(\begin{array}{c}{e}_{xx}\\ e_{yy}\\ e_{zz}\\ e_{zx}\\ e_{zy}\\ e_{xy}\end{array}\right)=\left(\begin{array}{cccccc}{S}_{11}& S_{12}& S_{13}& 0& 0& 0\\ S_{12}& S_{11}& S_{13}& 0& 0& 0\\ S_{13}& S_{13}& S_{33}& 0& 0& 0\\ 0& 0& 0& S_{44}& 0& 0\\ 0& 0& 0& 0& S_{44}& 0\\ 0& 0& 0& 0& 0& \frac{S_{11}-S_{12}}{2}\end{array}\right)\left(\begin{array}{c}{\tau }_{xx}\\ {\tau }_{yy}\\ {\tau }_{zz}\\ {\tau }_{zx}\\ {\tau }_{zy}\\ {\tau }_{xy}\end{array}\right).$$ 2.1

The stresses τ_ij are defined as the force acting on unit area parallel to the ith direction, the normal to the unit area being in the jth direction. The matrix elements, S_ij, are the elastic compliance constants. This matrix can be inverted to obtain the elastic stiffness constants, C_ij, as given below:

$$\left(\begin{array}{c}{\tau }_{xx}\\ {\tau }_{yy}\\ {\tau }_{zz}\\ {\tau }_{zx}\\ {\tau }_{zy}\\ {\tau }_{xy}\end{array}\right)=\left(\begin{array}{cccccc}{C}_{11}& C_{12}& C_{13}& 0& 0& 0\\ C_{12}& C_{11}& C_{13}& 0& 0& 0\\ C_{13}& C_{13}& C_{33}& 0& 0& 0\\ 0& 0& 0& C_{44}& 0& 0\\ 0& 0& 0& 0& C_{44}& 0\\ 0& 0& 0& 0& 0& \frac{C_{11}-C_{12}}{2}\end{array}\right)\left(\begin{array}{c}{e}_{xx}\\ e_{yy}\\ e_{zz}\\ e_{zx}\\ e_{zy}\\ e_{xy}\end{array}\right).$$ 2.2

The relationships between the compliance and stiffness constants are:

$$\begin{array}{rl}{S}_{11}& =\frac{C_{11}{C}_{33}-C_{13}^2}{(C_{11}-C_{12})X},\\ S_{33}& =\frac{C_{11}+C_{12}}{X},\\ S_{13}& =-\frac{C_{13}}{X},\\ S_{12}& =\frac{C_{13}^2-C_{12}{C}_{33}}{(C_{11}-C_{12})X},\\ S_{44}& =\frac{1}{C_{44}},\\ S_{66}& =\frac{2}{C_{11}-C_{12}},\end{array}$$

where

$$X=C_{33}(C_{11}+C_{12})-2C_{13}^2.$$ 2.3

Figure 1.

(a) Neighbouring basal layers of graphite; coloured atoms emphasize the offset between ABAB basal planes. (b) Graphite crystal lattice and first Brillouin zone, a = 0.246 nm, d = 0.335 nm [14,15]; the ‘equivalent cylinder’ is shown dashed. (Online version in colour.)

The stiffness constants for a graphite crystal are given in table 1 of appendix A; these were obtained using Born's long-wave method [14] and local density approximation (LDA) [15]. Owing to the crystal structure in which atoms within layers are held together by strong covalent bonding, whereas bonding between layers is via weak van der Waals bonds, the values of the stiffness constants perpendicular, C₃₃, and parallel, C₁₁, to the basal planes are different by orders of magnitude. The shear components C₄₄ and C₆₆ = (C₁₁ − C₁₂)/2 are also small.

Table 1.

Crystal elastic stiffness and compliance constants for graphite.

stiffness constants [14,15]	GPa	compliance constants (calculated from stiffness constants)	10−12 (Pa)−1
C11	1060	S11	0.97
C33	36.5	S33	27.47
C12	180	S12	-0.17
C13	7.9	S13	-0.18
C44	5.05	S44	198
C66	440	S66	2.27

The most thermodynamically stable form of graphite crystal is the ABAB hexagonal stacking, giving a theoretical density of 2.266 × 10³ kg m⁻³. The lattice a-spacing is 0.1415 nm and the c-spacing is 0.335 nm—calculated using LDA [15]; the lattice d-spacing is half that of the c-spacing.

The development of a semi-continuum model is based on the consideration of the free energy, F, in a unit cube of graphite crystallites in a thermally dilated state, assuming that there are no shear strains as follows:

$$\begin{array}{rl}F& =U_0+\frac{1}{2}(e_{xx}^2+e_{yy}^2)C_{11}+\frac{1}{2}{C}_{33}{e}_{zz}^2+C_{12}{e}_{xx}{e}_{yy}+C_{13}{e}_{zz}(e_{xx}+e_{yy})\\ & +kT{\iiint }_{BZ}\sum _p\ln [1-\exp (-\frac{h{v}_p}{kT})]{\mathrm{d}}^3\sigma ,\end{array}$$ 2.4

where the first term, U₀, is the energy/unit volume at absolute zero temperature in the unrestrained state; the next four terms are the elastic strain energy density; and the last term is the thermal energy density of the first Brillouin zone, where

• v_p is the frequency of the pth vibrational mode (Hz),

• k is Boltzmann's constant (1.38064852 × 10⁻²³ J K⁻¹),

• h is Planck's constant (6.626070040 × 10⁻³⁴ J s⁻¹), and

• T is the absolute temperature (K).

The integral is over the first Brillouin zone of the graphite crystal structure [16,17], i.e. the reciprocal lattice space between two adjacent basal planes; see figure 1b. Note that there must be a whole number of waves, denoted by the wavenumber, in the x and y planes. Therefore, the wavenumber z varies from ±1/2d =  ± 1.49 × 10⁹ m⁻¹. To simplify the integration, the hexagonal prismatic Brillouin zone has been approximated as a cylinder with an equivalent radius, defined as:

$${\sigma }_m=\frac{1}{\pi a}\sqrt{\frac{2\pi }{\sqrt{3}}}.$$ 2.5

We use the short-hand notation d³σ≡dσ_xdσ_ydσ_z.

The integral will be performed in cylindrical co-ordinates (σ_a, ϕ, σ_z) with σ_a defined as ${\sigma }_a=\sqrt{{\sigma }_x^2+{\sigma }_y^2}$, tranforming to cylindrical co-ordinates and assuming cylindrical symmetry leads to d³σ = 2πσ_adσ_adσ_z.

It should be noted that previous authors [9] did not include the integral over the Brillouin zone at this stage of the derivation. In this paper, we explicitly separate the summation over frequencies from the summation over modes (integration over the first Brillouin zone) for clarity. This also removes confusion about the dimensionality of the different terms in equation (2.4).

The principal graphite crystallite coefficients of thermal expansion required are given by the differentials

$$\begin{array}{rl}{\alpha }_c& =\frac{\mathrm{\partial }{e}_{zz}}{\mathrm{\partial }T}\\ \mathrm{and}{\alpha }_a& =\frac{\mathrm{\partial }{e}_{xx}}{\mathrm{\partial }T}=\frac{\mathrm{\partial }{e}_{yy}}{\mathrm{\partial }T}.\end{array}\}$$ 2.6

At equilibrium, the free energy, F, given by equation (2.4) is a minimum with respect to the strains. Thus, noting that v_p is a function of strain, differentiating equation (2.4) with respect to e_zz and e_xx and equating each to zero leads to

$$\begin{array}{rl}& e_{xx}^2\frac{\mathrm{\partial }{C}_{11}}{\mathrm{\partial }{e}_{zz}}+C_{33}{e}_{zz}+\frac{1}{2}{e}_{zz}^2\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}+e_{xx}^2\frac{\mathrm{\partial }{C}_{12}}{\mathrm{\partial }{e}_{zz}}+2e_{xx}{C}_{13}+2e_{zz}{e}_{xx}\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}\\ & -{\iiint }_{BZ}\sum _p\frac{h{v}_p}{\exp (h{v}_p/kT)-1}{[{\gamma }_p]}_{zz}\hspace{0.17em}{d}^3\sigma =0\\ \mathrm{and}& e_{xx}^2\frac{\mathrm{\partial }{C}_{11}}{\mathrm{\partial }{e}_{xx}}+(C_{11}+C_{12})e_{xx}+\frac{1}{2}{e}_{zz}^2\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{xx}}+e_{xx}^2\frac{\mathrm{\partial }{C}_{12}}{\mathrm{\partial }{e}_{xx}}+e_{zz}{C}_{13}+2e_{zz}{e}_{xx}\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{xx}}\\ & -{\iiint }_{BZ}\sum _p\frac{h{v}_p}{\exp (h{v}_p/kT)-1}{[{\gamma }_p]}_{xx}\hspace{0.17em}{d}^3\sigma =0,\end{array}\}$$ 2.7

where [γ_p]_ii≡ − (1/v_p)(∂v_p/∂e_ii), which are the mode Grüneisen [18] parameters describing the frequency shifts due to strain which have previously been referred to as the anharmonic terms. In addition, the equations have been simplified by using the fact that, due to symmetry, the strains in the crystal basal planes are equal, i.e. e_xx = e_yy.

It will be shown analytically later that the derivatives of the elastic constants are of greater magnitude than the elastic constants themselves; however, the elastic strains are very small, and so terms that are higher order in the elastic strains can be neglected. Thus, equation (2.7) can be simplified to

$$\begin{array}{rl}& C_{33}{e}_{zz}+2e_{xx}{C}_{13}-{\iiint }_{BZ}\sum _p\frac{h{v}_p}{\exp (h{v}_p/kT)-1}{[{\gamma }_p]}_{zz}\hspace{0.17em}{d}^3\sigma =0\\ \mathrm{and}& (C_{11}+C_{12})e_{xx}+e_{zz}{C}_{13}-{\iiint }_{BZ}\sum _p\frac{h{v}_p}{\exp (h{v}_p/kT)-1}{[{\gamma }_p]}_{xx}{d}^3\sigma =0.\end{array}\}$$ 2.8

Previously, the assumption was made that the higher order strain terms given above are negligible, although this is not discussed in [9].

Equations (2.8) can be solved for e_xx and e_yy and then differentiated with respect to temperature to give the principal crystal CTE as

$$\begin{array}{rl}\frac{\mathrm{\partial }{e}_{zz}}{\mathrm{\partial }T}& ={\alpha }_c=\left(\frac{C_{11}+C_{12}}{C_{33}(C_{11}+C_{12})-2C_{13}^2}\right){\iiint }_{BZ}\sum _{p}k{\left(\frac{h{v}_p}{kT}\right)}^2\frac{\exp (h{v}_p/kT){[{\gamma }_p]}_{zz}}{{\{\exp (h{v}_p/kT)-1\}}^2}{d}^3\sigma \\ & -\left(\frac{2C_{13}}{C_{33}(C_{11}+C_{12})-2C_{13}^2}\right){\iiint }_{BZ}\sum _{p}k{\left(\frac{h{v}_p}{kT}\right)}^2\frac{\exp (h{v}_p/kT){[{\gamma }_p]}_{xx}}{{\{\exp (h{v}_p/kT)-1\}}^2}{d}^3\sigma \end{array}$$ 2.9

and

$$\begin{array}{rl}\frac{\mathrm{\partial }{e}_{xx}}{\mathrm{\partial }T}& ={\alpha }_a=\left(\frac{C_{33}}{C_{33}(C_{11}+C_{12})-2C_{13}^2}\right){\iiint }_{BZ}\sum _{p}k{\left(\frac{h{v}_p}{kT}\right)}^2\frac{\exp (h{v}_p/kT){[{\gamma }_p]}_{xx}}{{\{\exp (h{v}_p/kT)-1\}}^2}{d}^3\sigma \\ & -\left(\frac{C_{13}}{C_{33}(C_{11}+C_{12})-2C_{13}^2}\right){\iiint }_{BZ}\sum _{p}k{\left(\frac{h{v}_p}{kT}\right)}^2\frac{\exp (h{v}_p/kT){[{\gamma }_p]}_{zz}}{{\{\exp (h{v}_p/kT)-1\}}^2}{d}^3\sigma .\end{array}$$ 2.10

The elastic stiffness constants, C_ij, can be related to the elastic compliance constants, S_ij, by equations (2.3), thus equations (2.9) and (2.10) become

$$\begin{array}{rl}{\alpha }_c& =S_{33}{\iiint }_{BZ}\sum _{p}k{\left(\frac{h{v}_p}{kT}\right)}^2\frac{\exp (h{v}_p/kT){[{\gamma }_p]}_{zz}}{{\{\exp (h{v}_p/kT)-1\}}^2}{d}^3\sigma \\ & +2S_{13}{\iiint }_{BZ}\sum _{p}k{\left(\frac{h{v}_p}{kT}\right)}^2\frac{\exp (h{v}_p/kT){[{\gamma }_p]}_{xx}}{{\{\exp (h{v}_p/kT)-1\}}^2}{d}^3\sigma \end{array}$$ 2.11

and

$$\begin{array}{rl}{\alpha }_a& =(S_{11}+S_{12}){\iiint }_{BZ}\sum _{p}k{\left(\frac{h{v}_p}{kT}\right)}^2\frac{\exp (h{v}_p/kT){[{\gamma }_p]}_{xx}}{{\{\exp (h{v}_p/kT)-1\}}^2}{d}^3\sigma \\ & +S_{13}{\iiint }_{BZ}\sum _{p}k{\left(\frac{h{v}_p}{kT}\right)}^2\frac{\exp (h{v}_p/kT){[{\gamma }_p]}_{zz}}{{\{\exp (h{v}_p/kT)-1\}}^2}{d}^3\sigma .\end{array}$$ 2.12

A model for the frequencies of crystallite vibration modes, v_p, is provided by Komatsu & Nagamiya [19,20], as described in the next section.

3. Graphite vibration model

To solve for α_c and α_a, we require the frequency of the vibrational modes in the longitudinal, transverse and out-of-plane principal directions and also the anharmonic modes — themselves functions of the principal vibrational frequencies. Below, we summarize the Komatsu [20] model for calculating the principal frequencies; this assumes that the graphite crystallites can be modelled as elastic extensional vibrations in a series of n thin plates [21,22]. The present authors modify Komatsu's notation [20] to match the rest of this paper. The equations for the elastic extensional vibrations in a series of n thin plates are

$$\begin{array}{rl}\frac{{\mathrm{\partial }}^2{u}_n}{\mathrm{\partial }{t}^2}& =\frac{1}{\rho (1-{\nu }^2)}\{C_{11}\frac{{\mathrm{\partial }}^2{u}_n}{\mathrm{\partial }{x}^2}+\frac{C_{11}-C_{12}}{2}(1-\nu )\frac{{\mathrm{\partial }}^2{u}_n}{\mathrm{\partial }{y}^2}+\frac{C_{11}-C_{12}}{2}(1-\nu )\frac{{\mathrm{\partial }}^2{v}_n}{\mathrm{\partial }x\mathrm{\partial }y}\},\\ \frac{{\mathrm{\partial }}^2{v}_n}{\mathrm{\partial }{t}^2}& =\frac{1}{\rho (1-{\nu }^2)}\{C_{11}\frac{{\mathrm{\partial }}^2{v}_n}{\mathrm{\partial }{y}^2}+\frac{C_{11}-C_{12}}{2}(1-\nu )\frac{{\mathrm{\partial }}^2{v}_n}{\mathrm{\partial }{x}^2}+\frac{C_{11}-C_{12}}{2}(1-\nu )\frac{{\mathrm{\partial }}^2{u}_n}{\mathrm{\partial }x\mathrm{\partial }y}\}\\ \mathrm{and}\frac{{\mathrm{\partial }}^2{w}_n}{\mathrm{\partial }{t}^2}& =-{\delta }^2[\frac{{\mathrm{\partial }}^4{w}_n}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^4{w}_n}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^4{w}_n}{\mathrm{\partial }{y}^4}]+\frac{C_{33}}{\rho d^2}(w_{n+1}+w_{n-1}-2w_n),\end{array}\}$$ 3.1

where u_n, v_n, w_n are the displacements at a lattice layer point (x, y) in the x-, y- and z-axis directions, differentiated with respect to time, t; ν is Poisson's ratio, ρ is the density and d is the graphite interlayer spacing; δ is related to the bending modulus of a plate. Kelly & Walker [9] give a value of δ = 6.11 × 10⁻⁷ m² s⁻¹. In the third equation of (3.1), the second term on the r.h.s. accounts for the interaction between neighbouring plates.

Komatsu [20] modified equations (3.1) to account for shear stress, obtaining the following terms:

$$\begin{array}{rl}\frac{{\mathrm{\partial }}^2{u}_n}{\mathrm{\partial }{t}^2}& =\frac{1}{\rho (1-{\nu }^2)}\{C_{11}\frac{{\mathrm{\partial }}^2{u}_n}{\mathrm{\partial }{x}^2}+\frac{C_{11}-C_{12}}{2}(1-\nu )\frac{{\mathrm{\partial }}^2{u}_n}{\mathrm{\partial }{y}^2}+\frac{C_{11}-C_{12}}{2}(1-\nu )\frac{{\mathrm{\partial }}^2{v}_n}{\mathrm{\partial }x\mathrm{\partial }y}\}\\ & +\frac{C_{44}}{\rho d^2}(u_{n+1}+u_{n-1}-2u_n)+\frac{C_{44}}{2\rho d}(\frac{\mathrm{\partial }{w}_{n+1}}{\mathrm{\partial }x}-\frac{\mathrm{\partial }{w}_{n-1}}{\mathrm{\partial }x}),\\ \frac{{\mathrm{\partial }}^2{v}_n}{\mathrm{\partial }{t}^2}& =\frac{1}{\rho (1-{\nu }^2)}\{C_{11}\frac{{\mathrm{\partial }}^2{v}_n}{\mathrm{\partial }{y}^2}+\frac{C_{11}-C_{12}}{2}(1-\nu )\frac{{\mathrm{\partial }}^2{v}_n}{\mathrm{\partial }{x}^2}+\frac{C_{11}-C_{12}}{2}(1-\nu )\frac{{\mathrm{\partial }}^2{u}_n}{\mathrm{\partial }x\mathrm{\partial }y}\}\\ & +\frac{C_{44}}{\rho d^2}(v_{n+1}+v_{n-1}-2v_n)+\frac{C_{44}}{2\rho d}(\frac{\mathrm{\partial }{w}_{n+1}}{\mathrm{\partial }y}-\frac{\mathrm{\partial }{w}_{n-1}}{\mathrm{\partial }y})\\ \mathrm{and}\frac{{\mathrm{\partial }}^2{w}_n}{\mathrm{\partial }{t}^2}& =-{\delta }^2[\frac{{\mathrm{\partial }}^4{w}_n}{\mathrm{\partial }{x}^4}+2\frac{{\mathrm{\partial }}^4{w}_n}{\mathrm{\partial }{x}^2\mathrm{\partial }{y}^2}+\frac{{\mathrm{\partial }}^4{w}_n}{\mathrm{\partial }{y}^4}]+\frac{C_{33}}{\rho d^2}(w_{n+1}+w_{n-1}-2w_n)\\ & +\frac{C_{44}}{\rho }(\frac{{\mathrm{\partial }}^2{w}_n}{\mathrm{\partial }{x}^2}+\frac{{\mathrm{\partial }}^2{w}_n}{\mathrm{\partial }{y}^2})+\frac{C_{44}}{2\rho d}(\frac{\mathrm{\partial }{u}_{n+1}}{\mathrm{\partial }x}-\frac{\mathrm{\partial }{u}_{n-1}}{\mathrm{\partial }x}+\frac{\mathrm{\partial }{v}_{n+1}}{\mathrm{\partial }y}-\frac{\mathrm{\partial }{v}_{n-1}}{\mathrm{\partial }y}).\end{array}\}$$ 3.2

The longitudinal (transverse) velocity is defined as the square root of the pre-factor in front of the x (y) second derivative term in the u_n displacement equation. Assuming that Poisson's ratio is zero, the velocity of the longitudinal wave, V_L, can be simplified to

$$V_{\mathrm{L}}=\sqrt{\frac{C_{11}}{\rho }}.$$ 3.3

Similarly, the velocity of the transverse wave V_T is given by

$$V_{\mathrm{T}}=\sqrt{\frac{C_{11}-C_{12}}{2\rho }}.$$ 3.4

Equations (3.2) are solved using the conventional substitution in reciprocal space, i.e. in the first Brilliouin zone

$$\begin{array}{rl}{u}_n& =U\exp \{2\pi \mathrm{i}({\sigma }_{x}x+{\sigma }_{y}y+{\sigma }_{z}nd-v_{U}t)\},\\ v_n& =V\exp \{2\pi \mathrm{i}({\sigma }_{x}x+{\sigma }_{y}y+{\sigma }_{z}nd-v_{V}t)\}\\ \mathrm{and}{w}_n& =W\exp \{2\pi \mathrm{i}({\sigma }_{x}x+{\sigma }_{y}y+{\sigma }_{z}nd-v_{W}t)\},\end{array}\}$$ 3.5

where σ_x, σ_y and σ_z are the wavenumbers as discussed previously and v_U, v_V and v_W are frequencies of the vibrational mode. Komatsu [20] solved for the principal vibrational modes, v_p, which are linear superpositions of v_U, v_V and v_W, leading to

$$\begin{array}{rl}{v}_1& =\sqrt{\frac{C_{11}{\sigma }_a^2}{\rho }+\frac{C_{44}}{\rho {\pi }^2{d}^2}{\sin }^2(\pi {\sigma }_{z}d)},\\ v_2& =\sqrt{\frac{(C_{11}-C_{12}){\sigma }_a^2}{2\rho }+\frac{C_{44}}{\rho {\pi }^2{d}^2}{\sin }^2(\pi {\sigma }_{z}d)}\\ \mathrm{and}{v}_3& =\sqrt{4{\pi }^2{\delta }^2{\sigma }_a^4+\frac{C_{33}}{\rho {\pi }^2{d}^2}{\sin }^2(\pi d{\sigma }_z)+\frac{C_{44}{\sigma }_a^2}{\rho }},\end{array}\}$$ 3.6

where again σ²_a = σ²_x + σ²_y. It should be noted that, in the derivation, Komatsu [20] assumes that τ = C₄₄/ρ is small and therefore cross terms with τ as a pre-factor are ignored.

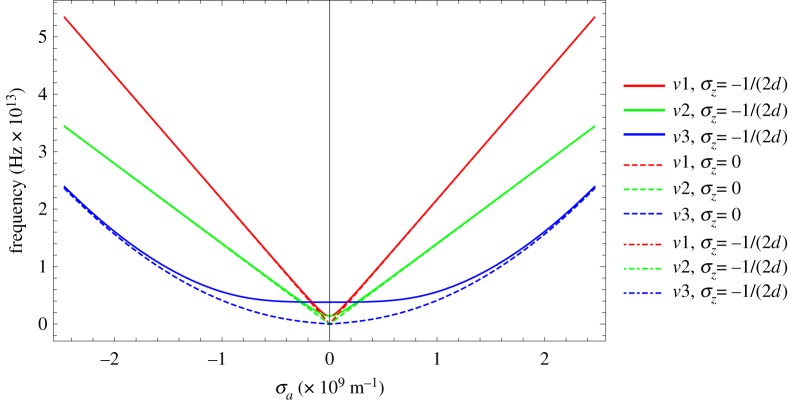
The three vibration modes given in equations (3.6) are insensitive to σ_z. For illustration, three of the vibration modes are plotted in figure 2 over the first Brillouin zone for different values of σ_z.

Figure 2.

Examples of vibration modes plotted over the first Brillouin zone (frequency ν_i versus Brillouin radius σ_a). Note for each vibration mode the curves overlap except for v₃, where the difference is small. (Online version in colour.)

Equations (3.6) are the equations for lattice vibration used previously [9]. The anharmonic functions for the longitudinal, transverse and out-of-plane principal modes are as follows:

$$\begin{array}{rl}{[{\gamma }_1]}_{ii}& =-\frac{1}{v_1}\frac{\mathrm{\partial }{v}_1}{\mathrm{\partial }{e}_{ii}}=-\frac{1}{2}{[\frac{C_{11}{\sigma }_a^2}{\rho }+\frac{C_{44}}{\rho {\pi }^2{d}^2}{\sin }^2(\pi {\sigma }_{z}d)]}^{-1}\\ & \times \{\frac{{\sigma }_a^2}{\rho }\frac{\mathrm{\partial }{C}_{11}}{\mathrm{\partial }{e}_{ii}}+\frac{{\sin }^2(\pi {\sigma }_{z}d)}{\rho {\pi }^2{d}^2}\frac{\mathrm{\partial }{C}_{44}}{\mathrm{\partial }{e}_{ii}}\},\\ {[{\gamma }_2]}_{ii}& =-\frac{1}{v_2}\frac{\mathrm{\partial }{v}_2}{\mathrm{\partial }{e}_{ii}}=-\frac{1}{2}{[\frac{(C_{11}-C_{12}){\sigma }_a^2}{2\rho }+\frac{C_{44}}{\rho {\pi }^2{d}^2}{\sin }^2(\pi {\sigma }_{z}d)]}^{-1}\\ & \times \{\frac{{\sigma }_a^2}{2\rho }\frac{\mathrm{\partial }(C_{11}-C_{12})}{\mathrm{\partial }{e}_{ii}}+\frac{{\sin }^2(\pi {\sigma }_{z}d)}{\rho {\pi }^2{d}^2}\frac{\mathrm{\partial }{C}_{44}}{\mathrm{\partial }{e}_{ii}}\}\\ \mathrm{and}{[{\gamma }_3]}_{ii}& =-\frac{1}{v_3}\frac{\mathrm{\partial }{v}_3}{\mathrm{\partial }{e}_{ii}}=-\frac{1}{2}{[4{\pi }^2{\delta }^2{\sigma }_a^4+\frac{C_{33}}{\rho {\pi }^2{d}^2}{\sin }^2(\pi d{\sigma }_z)+\frac{C_{44}{\sigma }_a^2}{\rho }]}^{-1}\\ & \times \{8{\pi }^2\delta {\sigma }_a^4\frac{\mathrm{\partial }\delta }{\mathrm{\partial }{e}_{ii}}+\frac{{\sin }^2(\pi d{\sigma }_z)}{\rho {\pi }^2{d}^2}\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{ii}}+\frac{{\sigma }_a^2}{\rho }\frac{\mathrm{\partial }{C}_{44}}{\mathrm{\partial }{e}_{ii}}\}.\end{array}\}$$ 3.7

To evaluate these, the differentials of the elastic constants ∂C_ij/∂e_kk and ∂δ/∂e_ii are required with respect to the strain in the longitudinal and transverse in-plane x-axis and the out-of-plane z-axis. The values used in our simulations are given in table 2 (appendix A). In this paper, only the anharmonic functions [γ₃]_zz, in their full form, are used in the derived expressions for α_c. The in-plane [γ₁]_xx and [γ₂]_xx anharmonics are simplified in the case of α_a, and in effect can be regarded as constants.

Table 2.

Estimated values of derivatives required to evaluate the anharmonic functions.

differential	value	reference
$\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}$	−6 × 1011 N m−2	[7]
	−5.5 × 1011 N m−2	[55]
$\frac{\mathrm{\partial }{C}_{44}}{\mathrm{\partial }{e}_{zz}}$	−3.55 × 1010 N m−2	[9]
	−10 × 1010 N m−2	[9]
	−8.1 × 1010 N m−2	[8]
	−4.05 × 1010 N m−2	[7]
	−2.4 × 1010 N m−2	[55]
$\frac{\mathrm{\partial }\delta }{\mathrm{\partial }{e}_{zz}}$	−1.4 × 10−7 m2 s−1	[9,56]
$\frac{1}{C_{11}}\frac{\mathrm{\partial }{C}_{11}}{\mathrm{\partial }{e}_{xx}}$	−8.2	[6]
$\frac{1}{(C_{11}\hspace{0.17em}-\hspace{0.17em}{C}_{12})}\frac{\mathrm{\partial }(C_{11}\hspace{0.17em}-\hspace{0.17em}{C}_{12})}{\mathrm{\partial }{e}_{xx}}$	−8.2	[6]
$\frac{1}{\delta }\frac{\mathrm{\partial }\delta }{\mathrm{\partial }{e}_{xx}}$	8.2	[6]

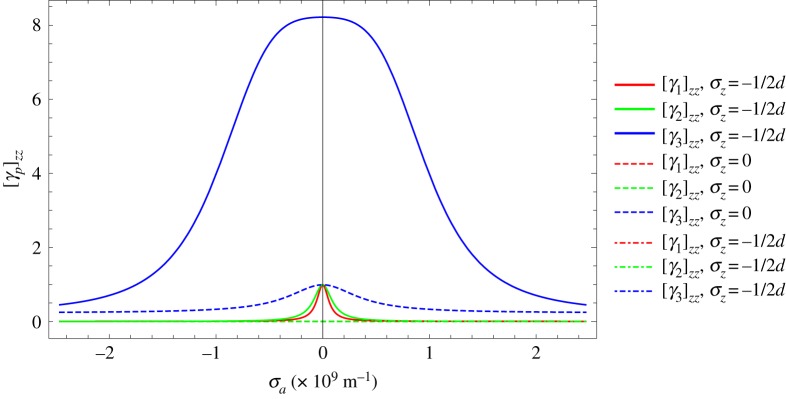
The anharmonic functions [γ_p]_zz are plotted as a function of σ_a for different values of σ_z in figure 3.

Figure 3.

Anharmonic functions [γ_p]_zz versus Brillouin radius σ_a for different values of σ_z. Note the largest contribution to CTE is from [γ₃]_zz for σ_z = ± 1/2d, the centre-top and centre-bottom of the Brillouin zone, with the smallest contribution when σ_z = 0. (Online version in colour.)

The differentials of the anharmonic functions with respect to e_xx are discussed later with reference to the derivation of α_a.

4. Coefficient of thermal expansion perpendicular to the basal plane—α_c

Having obtained expressions for the orthogonal vibrations and anharmonic modes, expressions for the CTE can be derived using the semi-continuum model over a range of temperatures to compare the model with experimental data. Firstly, we consider the thermal expansion coefficient perpendicular to the basal plane.

It can be seen from table 1 (appendix A) that S₁₃ is two orders of magnitude smaller than S₃₃, thus equation (2.11) simplifies to

$${\alpha }_c=S_{33}{\iiint }_{BZ}\sum _{p}k{\left(\frac{h{v}_p}{kT}\right)}^2\frac{\exp (h{v}_p/kT){[{\gamma }_p]}_{zz}}{{\{\exp (h{v}_p/kT)-1\}}^2}{d}^3\sigma .$$ 4.1

There are three possible vibration modes to consider when calculating α_c: in-plane longitudinal mode, in-plane transverse mode and out-of-plane mode. Previously it has been argued that only the out-of-plane mode is significant. Unfortunately, the reasoning behind this assumption in [9] is unclear and there appear to be mistakes in the references and supporting data. However, due to the large difference in stiffness between the in-plane C₁₁ (1060 GPa) and the out-of-plane C₃₃ (36.5 GPa) it is not unreasonable to assume that the out-of-plane strain e_zz would have less influence on the values of C₁₁ and C₁₂ than it would have on C₃₃. This assumption appears to be justified by the implementation of the theory as demonstrated below. The final step is to perform the integral over a cylinder of equivalent volume to the true Brillouin zone,

$$\begin{array}{rl}{\alpha }_c& =-\pi S_{33}k{\left(\frac{h}{kT}\right)}^2{\int }_0^{{\sigma }_m}{\int }_{-1/2d}^{1/2d}\\ & \times \frac{{\sigma }_a\{8{\pi }^2\delta {\sigma }_a^4(\mathrm{\partial }\delta /\mathrm{\partial }{e}_{zz})+({\sin }^2(\pi d{\sigma }_z)/\rho {\pi }^2{d}^2)(\mathrm{\partial }{C}_{33}/\mathrm{\partial }{e}_{zz})+({\sigma }_a^2/\rho )(\mathrm{\partial }{C}_{44}/\mathrm{\partial }{e}_{zz})\}}{{\{\exp (h/kT\sqrt{4{\pi }^2{\delta }^2{\sigma }_a^4+(C_{33}/\rho {\pi }^2{d}^2){\sin }^2(\pi d{\sigma }_z)+C_{44}{\sigma }_a^2/\rho })-1\}}^2}\\ & \times \exp \left(\frac{h}{kT}\sqrt{4{\pi }^2{\delta }^2{\sigma }_a^4+\frac{C_{33}}{\rho {\pi }^2{d}^2}{\sin }^2(\pi d{\sigma }_z)+\frac{C_{44}{\sigma }_a^2}{\rho }}\right)\mathrm{d}{\sigma }_z\hspace{0.17em}\mathrm{d}{\sigma }_a.\end{array}$$ 4.2

Data giving the changes in graphite crystal CTE as a function of temperature can be obtained by direct thermal expansion measurements or via changes to lattice spacing using X-ray diffraction (XRD). Measurements have been obtained using either naturally occurring graphite crystals or highly oriented pyrolytic graphite (HOPG). The quality of these measurements depends on the graphitic perfection of the sample used, which is usually defined using a p-factor [23,24]; p-factors range from zero to unity, representing the degree of cryptographic order. Measurements made on various graphitic structures with p-factors between 0 and 0.7, including irradiated graphite by Steward et al. [25,26], show that curves of changed interlayer d-spacing versus temperature are parallel to one another between ∼0 and ∼2600 K, indicating that the thermal expansion coefficients, which are related to the slopes of these curves, are unaffected by significant disorder of the graphite lattice. This observation agrees with the estimates of change in CTE due to strain and irradiation discussed later in this paper.

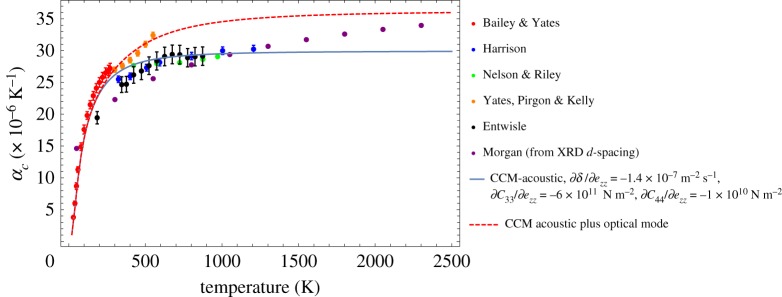
Morgan [27] presents a comprehensive set of XRD measurements giving changes to α_a and α_c taken from Kellett & Richards [28], Nelson & Riley [29], Yang [30], Kellett et al. [31] and Baskin & Meyer [32].

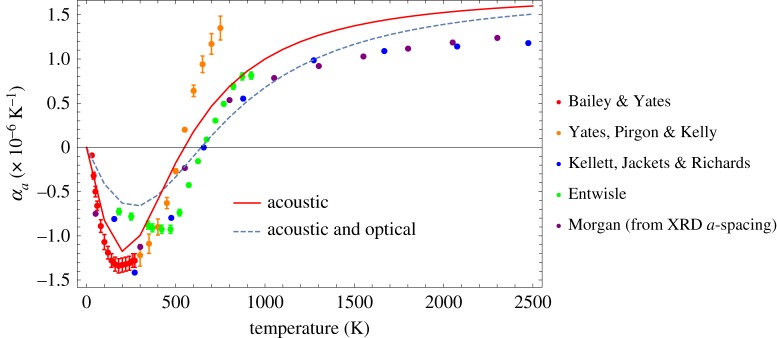
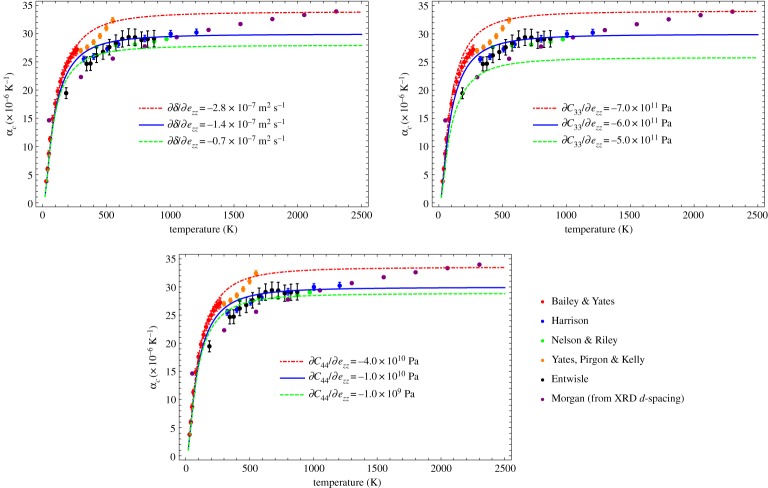
Kelly [33] also presents a dataset of crystal CTE measurements, but there is confusion with regard to the source of some of the data. Figure 4 brings together various datasets for α_c from Entwisle [34], Bailey & Yates [35], Yates et al. [36], Harrison [37], Nelson & Riley [29] and Morgan [27]. Where the measurement error on data are available error bars are given; most of the data originates from XRD data on graphitic materials with a p-factor of 0.2. The prediction of α_c using equation (4.2) is also included. While equation (4.2) fits well at low values to medium values of temperature, it does not appear to capture the measured CTE increase at higher temperatures. Also plotted is an attempt to include the contribution to the CTE of the optical modes of the system. It is possible to make the simplifying assumption [6] that extending the upper integration limit to $\sqrt{2}{\sigma }_m$ has the effect of including contributions from both the in-plane acoustic and the higher frequency optical mode. It is difficult to say with current experimental data whether the inclusion of optical modes produces a better fit.

Figure 4.

Comparison of fit of the theoretical, semi-continuum model with experimental data; see [27,29,34–37]. (Online version in colour.)

The behaviour of the thermal expansion coefficient can be understood in the high and low temperature limits by examining the leading order behaviour for hv₃≫kT and hv₃≪kT.

For low temperatures, hv₃≫kT, the leading order behaviour is

$$\begin{array}{rl}{\alpha }_c& \approx -\pi S_{33}k{\left(\frac{h}{kT}\right)}^2{\int }_0^{{\sigma }_m}{\int }_{-1/2d}^{1/2d}{\sigma }_a\{8{\pi }^2\delta {\sigma }_a^4\frac{\mathrm{\partial }\delta }{\mathrm{\partial }{e}_{zz}}+\frac{{\sin }^2(\pi d{\sigma }_z)}{\rho {\pi }^2{d}^2}\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}+\frac{{\sigma }_a^2}{\rho }\frac{\mathrm{\partial }{C}_{44}}{\mathrm{\partial }{e}_{zz}}\}\\ & \times \exp (-\frac{h}{kT}\sqrt{4{\pi }^2{\delta }^2{\sigma }_a^4+\frac{C_{33}}{\rho {\pi }^2{d}^2}{\sin }^2(\pi d{\sigma }_z)+\frac{C_{44}{\sigma }_a^2}{\rho }})\mathrm{d}{\sigma }_z\hspace{0.17em}\mathrm{d}{\sigma }_a.\end{array}$$ 4.3

For high temperatures, hv₃≪kT, the leading order behaviour is

$$\begin{array}{rl}{\alpha }_c& \approx -\pi S_{33}k{\int }_0^{{\sigma }_m}{\int }_{-1/2d}^{1/2d}{\sigma }_a\{8{\pi }^2\delta {\sigma }_a^4\frac{\mathrm{\partial }\delta }{\mathrm{\partial }{e}_{zz}}+\frac{{\sin }^2(\pi d{\sigma }_z)}{\rho {\pi }^2{d}^2}\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}+\frac{{\sigma }_a^2}{\rho }\frac{\mathrm{\partial }{C}_{44}}{\mathrm{\partial }{e}_{zz}}\}\\ & \times \left(4{\pi }^2{\delta }^2{\sigma }_a^4+\frac{C_{33}}{\rho {\pi }^2{d}^2}{\sin }^2(\pi d{\sigma }_z)+\frac{C_{44}{\sigma }_a^2}{\rho }\right)\mathrm{d}{\sigma }_z\hspace{0.17em}\mathrm{d}{\sigma }_a.\end{array}$$ 4.4

We see that as the temperature tends to zero the thermal expansion coefficient exponentially approaches zero, whereas at high temperatures the thermal expansion coefficient loses all temperature dependence and becomes simply a constant.

The sensitivities of the predictions of equation (4.2) to the differentials with respect to strain of δ, C₃₃ and C₄₄ are given in appendix B. Doubling ∂δ/∂e_zz has a significant effect on the prediction but the effect of halving the value is much less, i.e. the influence is nonlinear. Changing ∂C₃₃/∂e_zz by ±1 × 10¹¹ Pa (a few per cent) increases/decreases the prediction by the same amount, whereas increasing the value of ∂C₄₄/∂e_zz by a factor of 4 increases the prediction significantly; however, reducing it by a factor 10 makes only a small difference, i.e. again the influence is nonlinear.

5. Coefficient of thermal expansion parallel to the basal plane—α_a

The CTE, α_a, is based on equation (2.12). As before, in deriving an expression for the CTE perpendicular to the basal plane, the second term in equation (2.12) can be ignored by reasoning that S₁₃ is relatively small, thereby making this term insignificant. Thus, the thermal strains within the basal planes are assumed to be independent of those between layers.

Thus equation (2.12) becomes

$${\alpha }_a=(S_{11}+S_{12}){\iiint }_{BZ}\sum _{p}k{\left(\frac{h{v}_p}{kT}\right)}^2\frac{\exp (h{v}_p/kT){[{\gamma }_p]}_{xx}}{{\{\exp (h{v}_p/kT)-1\}}^2}{d}^3\sigma .$$ 5.1

Noting that the first terms inside the square brackets for the three vibrational modes given in equations (3.6) are dominant, it was therefore assumed that the other terms could be ignored. This assumption greatly simplifies the mathematics. The vibrational mode terms given by equations (3.6) become

$$\begin{array}{rl}{v}_1& =\sqrt{\frac{C_{11}}{\rho }}{\sigma }_a,\\ v_2& =\sqrt{\frac{(C_{11}-C_{12})}{2\rho }}{\sigma }_a\\ \mathrm{and}{v}_3& =2\pi \delta {\sigma }_a^2.\end{array}\}$$ 5.2

The anharmonic terms can then be easily calculated for the three modes, giving

$$\begin{array}{rl}\hspace{0.17em}{[{\gamma }_1]}_{xx}& =-\frac{1}{v_1}\frac{\mathrm{\partial }{v}_1}{\mathrm{\partial }{e}_{xx}}=-\frac{1}{2C_{11}}\frac{\mathrm{\partial }{C}_{11}}{\mathrm{\partial }{e}_{xx}},\\ {[{\gamma }_2]}_{xx}& =-\frac{1}{v_2}\frac{\mathrm{\partial }{v}_2}{\mathrm{\partial }{e}_{xx}}=-\frac{1}{2(C_{11}-C_{12})}\frac{\mathrm{\partial }(C_{11}-C_{12})}{\mathrm{\partial }{e}_{xx}}\\ \mathrm{and}{[{\gamma }_3]}_{xx}& =-\frac{1}{v_3}\frac{\mathrm{\partial }{v}_3}{\mathrm{\partial }{e}_{xx}}=-\frac{1}{\delta }\frac{\mathrm{\partial }\delta }{\mathrm{\partial }{e}_{xx}}.\end{array}\}$$ 5.3

The integral on the right-hand side of equation (5.1) is accomplished using various substitutions, defining Debye characteristic temperatures for the longitudinal, transverse and out-of-plane directions, θ_L, θ_T and θ_o, as

$$\begin{array}{rl}\frac{{\theta }_L}{T}& =x_L=\frac{h}{kT}\sqrt{\frac{C_{11}}{\rho }}{\sigma }_m=\frac{2562}{T},\\ \frac{{\theta }_T}{T}& =x_T=\frac{h}{kT}\sqrt{\frac{(C_{11}-C_{12})}{2\rho }}{\sigma }_m=\frac{1650}{T}\\ \mathrm{and}\frac{{\theta }_o}{T}& =x_o=\frac{h}{kT}2\pi \delta {\sigma }_m^2=\frac{1120}{T}.\end{array}\}$$ 5.4

Treating each term individually we have that

$${\alpha }_a={\alpha }_{a_1}+{\alpha }_{a_2}+{\alpha }_{a_3},$$ 5.5

with the in-plane longitudinal modes

$${\alpha }_{a_1}=(S_{11}+S_{12})k{\left(\frac{h}{kT}\right)}^{2}2\pi {\int }_{-1/2d}^{1/2d}d{\sigma }_z{\int }_0^{{\sigma }_m}(-\frac{{\sigma }_a^3}{2\rho }\hspace{0.17em}\frac{\mathrm{\partial }{C}_{11}}{\mathrm{\partial }{e}_{xx}}\hspace{0.17em}\frac{\exp (h/kT\sqrt{(C_{11}/\rho )}{\sigma }_a)}{{\{\exp (h/kT\sqrt{C_{11}/\rho }{\sigma }_a)-1\}}^2})\mathrm{d}{\sigma }_a,$$ 5.6

giving

$${\alpha }_{a_1}=-\frac{\pi \rho k(S_{11}+S_{12})}{C_{11}d}{\left[\frac{kT}{h}\right]}^2\left\{\left(\frac{1}{C_{11}}\right)\frac{\mathrm{\partial }{C}_{11}}{\mathrm{\partial }{e}_{xx}}\right\}{J}_3\left(\frac{{\theta }_L}{T}\right).$$ 5.7

The expression for the in-plane transverse modes, α_a2, is identical to the expression for α_a1, with C₁₁ replaced with $C_{66}=\frac{1}{2}(C_{11}-C_{12})$,

$${\alpha }_{a_2}=-\frac{\pi \rho k(S_{11}+S_{12})}{C_{66}d}{\left[\frac{kT}{h}\right]}^2\left\{\left(\frac{1}{C_{66}}\right)\frac{\mathrm{\partial }{C}_{66}}{\mathrm{\partial }{e}_{xx}}\right\}{J}_3\left(\frac{{\theta }_T}{T}\right).$$ 5.8

For the out-of-plane transverse modes, we have

$${\alpha }_{a_3}=(S_{11}+S_{12})k{\left(\frac{h}{kT}\right)}^{2}2\pi {\int }_{-1/2d}^{1/2d}d{\sigma }_z{\int }_0^{{\sigma }_m}(-4{\pi }^2\delta {\sigma }_a^5\frac{\mathrm{\partial }\delta }{\mathrm{\partial }{e}_{xx}}\frac{\exp (2\pi h\delta {\sigma }_a^2/kT)}{{\{\exp (2\pi h\delta {\sigma }_a^2/kT)-1\}}^2})\mathrm{d}{\sigma }_a,$$ 5.9

giving

$${\alpha }_{a_3}=-\frac{k(S_{11}+S_{12})}{2d\delta }\left[\frac{kT}{h}\right]\left\{\left(\frac{1}{\delta }\right)\frac{\mathrm{\partial }\delta }{\mathrm{\partial }{e}_{xx}}\right\}{J}_2\left(\frac{{\theta }_o}{T}\right),$$ 5.10

where J₃(θ_L/T), J₃(θ_T/T) and J₂(θ_o/T) are Debye integrals of order 3 and 2 which can be solved numerically as

$$J_n(x_i)={\int }_0^{x_i}\frac{t^n{e}^t}{{(e^t-1)}^2}\hspace{0.17em}\mathrm{d}t.$$ 5.11

It is possible to make the simplifying assumption [6] that including contributions from both the in-plane acoustic and the higher frequency optical mode can be made by extending the upper integral limit as follows:

$$\begin{array}{rl}{\theta }_M& =\sqrt{2}{\theta }_L=3623,\\ {\theta }_Q& =\sqrt{2}{\theta }_T=2334\\ \mathrm{and}{\theta }_N& =2{\theta }_o=2238.\end{array}\}$$ 5.12

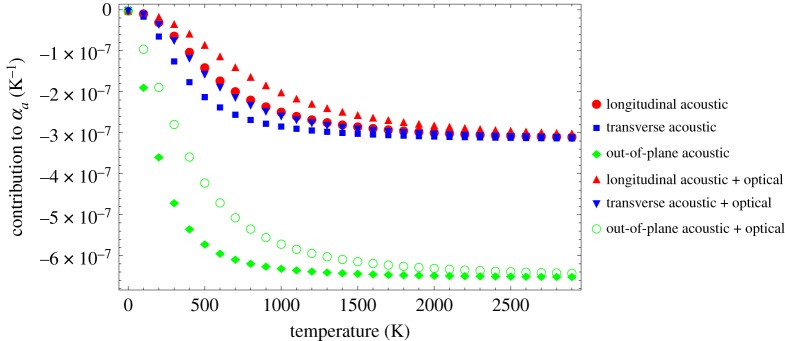
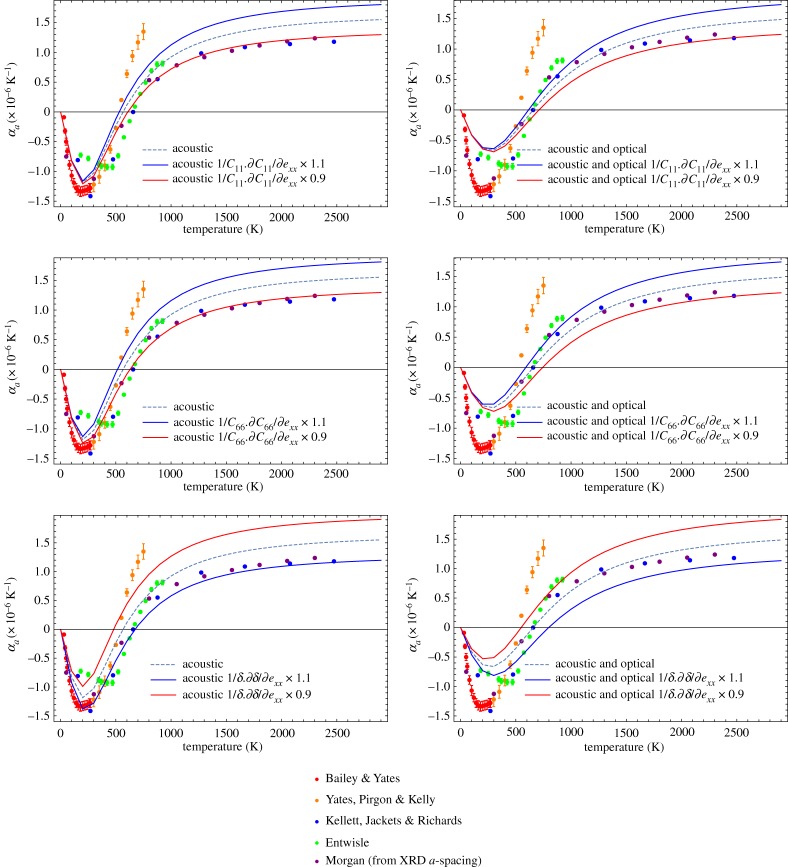
The square root arises from the particular wavenumber–frequency relationships for the in-plane mode. The contributions that each of equations (5.7), (5.8) and (5.10) makes to the total CTE, assuming that C₁₁⁻¹∂C₁₁/∂e_xx = C₆₆⁻¹∂C₆₆/∂e_xx = δ⁻¹∂δ/∂e_xx = 1, are given in figure 5. Solutions are included for acoustic (θ_L, θ_T, θ_o) and acoustic plus optical (θ_M, θ_Q, θ_N) modes.

Figure 5.

Contribution of each of the terms in equations (5.7), (5.8) and (5.10) to α_a. (Online version in colour.)

The resultant curves are slightly different from those previously published [6], which may be related to some errors in the previous equations. Generally, the contributions to α_a from the longitudinal and transverse modes are similar in magnitude, while the magnitude of the out-of-plane mode is larger, as would be expected. In all cases, the acoustic plus optical is smaller in magnitude in the lower to mid-temperature range (between 0 and ∼1500 K) than for the acoustic alone. This effect is larger in the case of the out-of-plane mode. These differences indicate that combining the optical and acoustic modes results in less excitation in the lower to mid-temperature ranges. Above ∼1500 K, the contributions from the two cases converge. This has implications for the prediction of the basal plane CTE α_a as discussed and shown in figure 6.

Figure 6.

Predictions of the basal plane coefficient of thermal expansion α_a compared with experimental data; see references [27,31,34–36]. (Online version in colour.)

Kelly [6] derived values for terms C₁₁⁻¹∂C₁₁/∂e_xx, C₆₆⁻¹∂C₆₆/∂e_xx and δ⁻¹∂δ/∂e_xx based on assuming a Morse potential and ‘scientific judgement’ on coefficients as −8.2, −8.2 and 8.2, respectively; however, his calculations are not outlined in any great detail. In addition, there are typing errors and omissions in the version of equations (5.7), (5.8) and (5.10) given in [6]. In this paper, to obtain a reasonable fit by eye, it was found necessary to use values of −8.2, −8.2 and 5.47, respectively. Data from various references for α_a, as discussed in §4 of this paper, are given in figure 6 along with the prediction of α_a obtained using equation (5.5).

Applying these values and summing the three expressions as equation (5.5), the following comparisons with experimental data are obtained.

The fit to the data in figure 6 is very similar to that given by Kelly [6], although there is significant scatter in the data; a much better experimental dataset would be required to justify further optimization of equation (5.5). The initial negative CTE at low temperatures arises from the interaction of the out-of-plane anharmonic modes with the two in-plane modes, whereas at temperatures above about 300 K the in-plane modes start to dominate and α_a becomes positive around 675 K. With reference to figure 5, making the approximation of ignoring the optical contribution gives a better fit to the data at low to mid-temperature ranges (between 0 and 1500 K) and makes little contribution to the higher temperatures, above 1500 K.

6. Graphite crystal CTE model—Lennard-Jones approach to deriving a relationship for α_c

(a). The relationship between lattice d-spacing and temperature

To develop the methodology further, a relationship between lattice d-spacing and temperature is required. This is obtained using fits to experimental data obtained from Nelson & Riley [29],

$$d=\frac{1}{2}(0.66915+18.7\times {10}^{-6}(T+273)+1.263\times {10}^{-9}{(T+273)}^2),$$ 6.1

Matuyama [38]

$$d=0.33525+8.241\times {10}^{-6}(T+273)+1.03\times {10}^{-9}{(T+273)}^2$$ 6.2

and Walker et al. [39]

$$d=0.3358+9.52\times {10}^{-6}(T+273).$$ 6.3

Taking the simple mean of the above fits gives

$$d=0.3328+8.63\times {10}^{-6}T+5.538\times {10}^{-10}{T}^2.$$ 6.4

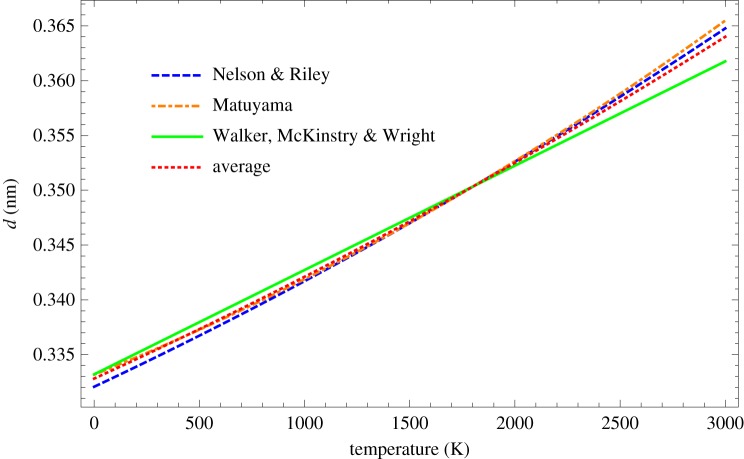
These fits are shown in figure 7. The average fit implies that the d-spacing at absolute zero and room temperature has values of 0.3328 nm and 0.3354 nm, respectively, compared with the usually accepted value of 0.335 nm at ambient room temperature [14,15]. It is of course possible to determine an equilibrium value of d from a calculation of the thermodynamically stable crystal structure. We, however, decided to take an average from experimental data because, as will become apparent later on, this lattice spacing temperature dependence is crucial for better matching to experimental data at high temperatures.

Figure 7.

Fits to experimental data of lattice d-spacing as a function of temperature [29,33,38,39]. (Online version in colour.)

(b). Lennard-Jones approach to deriving a relationship for α_c

This approach is outlined in references [10–12] and starts with the Lennard-Jones-type relationship for the potential energy between two atoms separated by distance d₀,

$$E^{\prime }=-A\{\frac{1}{r^6}-\frac{1}{2}\frac{r_0^6}{r^{12}}\},$$ 6.5

where r is the atomic separation, A = 2.43 × 10⁻⁷⁸ Jm⁶ and r₀ is a constant.

An approximation is required in which the carbon atoms are assumed to be distributed with uniform density within a set of basal planes. This is achieved by integrating equation (6.5) over the graphite crystal lattice to give the equivalent energy per unit volume of the lattice. Following a methodology suggested by Crowell [40] gives

$$E=-2\pi \sigma A{N}_0{\int }_0^{\mathrm{\infty }}\frac{x}{{(d^2+x^2)}^3}\hspace{0.17em}\mathrm{d}x+\pi \sigma A{N}_0{r}_0^6{\int }_0^{\mathrm{\infty }}\frac{x}{{(d^2+x^2)}^6}\hspace{0.17em}\mathrm{d}x,$$ 6.6

where σ = 1/q (q = 2.62 × 10⁻²⁰ m² is the area per atom in a basal layer [8]) and N₀ = ^ρN_a/_M = 1.13 × 10²⁹ atoms m⁻³ is the number of atoms per unit volume (graphite crystal density ρ_c = 2.26 g cm⁻³, Avogadro's number N_a = 6.022 × 10²³ atoms or molecules per gram-mole, the molecular weight of carbon M = 12.01 atomic mass units). The radial distance in the basal planes is given by x.

Solving equation (6.6) gives

$$E=\frac{\pi \sigma A{N}_0}{2d^4}[\frac{1}{5}{\left(\frac{r_0}{d}\right)}^6-1].$$ 6.7

The equilibrium spacing, d₀, is given by ∂E/∂d = 0, which leads to

$$r_0^6=2d_0^6.$$ 6.8

The elastic modulus for a lattice spacing, d, perpendicular to the basal plane is given by the second derivative of equation (6.7) with respect to strain between the basal planes, i.e.

$$C_{33}(d)=\frac{{\mathrm{\partial }}^{2}E}{\mathrm{\partial }{e}_{zz}^2}=d^2\left(\frac{{\mathrm{\partial }}^{2}E}{\mathrm{\partial }{d}^2}\right)=\frac{\pi \sigma A{N}_0}{2d^4}[22{\left(\frac{r_0}{d}\right)}^6-20],$$ 6.9

which gives an equilibrium value of

$$C_{33}(d_0)=\frac{12\pi \sigma A{N}_0}{d_0^4}.$$ 6.10

Another important function is the derivative of the elastic modulus with respect to strain,

$$\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}=d^3\frac{{\mathrm{\partial }}^{3}E}{\mathrm{\partial }{d}^3}=\frac{\pi \sigma A{N}_0}{d^4}[60-132{\left(\frac{r_0}{d}\right)}^6],$$ 6.11

with an equilibrium value of

$${\left(\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}\right)}_{d_0}=-\frac{204\pi \sigma A{N}_0}{d_0^4}=-17C_{33}(d_0).$$ 6.12

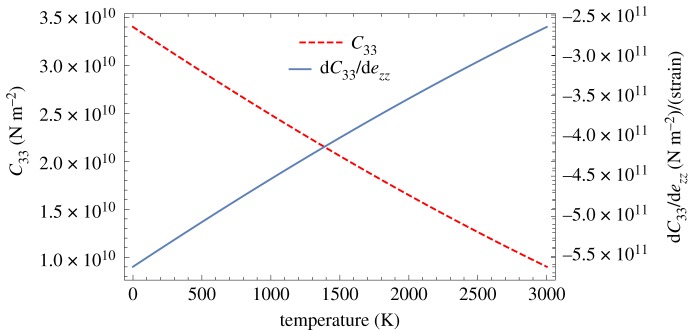
Using the average relationship between temperature and lattice spacing d, given by equation (6.4), the relationships given by equations (6.9) and (6.11) are shown in figure 8. Thus we obtain room temperature values for C₃₃ and ∂C₃₃/∂e_zz of 31.25 GPa and −531.7 GPa, respectively, which are slightly lower than the accepted value of 36.5 GPa [15] for C₃₃ and −600.0 GPa for ∂C₃₃/∂e_zz used by Kelly & Walker [9].

Figure 8.

Modulus perpendicular to the basal plane, C₃₃, and its derivative, ∂C₃₃/∂e_zz, as a function of temperature. (Online version in colour.)

If the crystal lattice is expanded from d₀ to some other spacing d, equation (6.7) becomes

$$E=\frac{C_{33}(d_0)}{24}[\frac{2}{5}{\left(\frac{d_0}{d}\right)}^{10}-{\left(\frac{d_0}{d}\right)}^4].$$ 6.13

Thus, equation (2.4) can be modified to

$$F=U_0+\frac{C_{33}(d_0)}{24}[\frac{2}{5}{\left(\frac{d_0}{d}\right)}^{10}-{\left(\frac{d_0}{d}\right)}^4]+kT{\iiint }_{BZ}\sum _p\ln [1-\exp (-\frac{h{v}_p}{kT})]d^3\sigma .$$ 6.14

Minimizing equation (6.14) gives

$$\frac{\mathrm{\partial }F}{\mathrm{\partial }d}=\frac{C_{33}(d_0)}{6}[-\frac{d_0^{10}}{d^{11}}+\frac{d_0^4}{d^5}]-\frac{1}{d}{\iiint }_{BZ}\sum _p\frac{h{v}_p}{\exp (h{v}_p/kT)-1}{[{\gamma }_p]}_{zz}{d}^3\sigma =0.$$ 6.15

Noting that α_c = (1/d)(∂d/∂T) and pre-multiplying by d before differentiating equation (6.15) with respect to T gives

$$\frac{C_{33}(d_0)}{6}[10{\left(\frac{d_0}{d}\right)}^{10}-4{\left(\frac{d_0}{d}\right)}^4]{\alpha }_c={\iiint }_{BZ}\sum _{p}k{\left(\frac{h{v}_p}{kT}\right)}^2\frac{\exp (h{v}_p/kT){[{\gamma }_p]}_{zz}}{{\{\exp (h{v}_p/kT)-1\}}^2}{d}^3\sigma .$$ 6.16

As previously discussed, in the case of deriving α_c only the out-of-plane mode v₃ is required. It can also be argued [12] that the only significant term in the vibrational mode is the first one, whereas the only significant term in the anharmonic term is the second one. This was justified by stating that previous numerical modelling showed this to be true for the first model [11], meaning it is reasonable that this would still hold true in this new approach. It should be noted that this approximation cannot hold to zero wavenumber, as will be shown later. Applying this reasoning, equations (3.6) and (3.7) simplify to

$$\begin{array}{rl}{v}_3& =2\pi \delta {\sigma }_a^2\\ \mathrm{and}{[{\gamma }_3]}_{zz}& =-\frac{{\sin }^2(\pi d_0{\sigma }_z)}{8\rho {\pi }^4{\delta }^2{d}_0^2{\sigma }_a^4}\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}.\end{array}\}$$ 6.17

This simplifies equation (6.16) upon rearranging to

$${\alpha }_c=-\frac{6}{C_{33}(d_0)}\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}{[10{\left(\frac{d_0}{d}\right)}^{10}-4{\left(\frac{d_0}{d}\right)}^4]}^{-1}\frac{h}{8\rho {\pi }^2\delta d_0^3}\frac{1}{T}{\int }_0^{x_m}\frac{\exp (x)}{{(\exp (x)-1)}^2}\mathrm{d}x,$$ 6.18

with an upper integration limit defined as

$$x_m=\frac{{\theta }_o}{T}=\frac{2\pi h\delta {\sigma }_m^2}{kT}=\frac{1120}{T}.$$ 6.19

The version of equation (6.18) derived [12] mistakenly has a denominator of 4 instead of 8; however, this mistake is compensated for by an error in the lower integration limit as discussed below. The integral in equation (6.18) does not converge for small values of x—the neglected frequency terms in the approximation (equation (6.17)) are important in the small wavenumber regime—it is therefore necessary to define a lower limit. It was originally assumed [11] that the smallest value of σ_a at which the out-of-plane vibrations can be regarded as purely two dimensional is at the point where the first term starts to become significant and equal to the second term, leading to

$$\frac{C_{33}(d_0)}{\rho d_0^2{\pi }^2}=4{\pi }^2{\delta }^2{\sigma }_o^4,$$

giving

$${\sigma }_o^2=\frac{1}{2{\pi }^2{d}_0\delta }\sqrt{\frac{C_{33}(d_0)}{\rho }}$$

and

$$x_o=\frac{{\theta }^{\prime }}{T}=\frac{2\pi h\delta {\sigma }_o^2}{kT}=\frac{169.61}{T}.$$ 6.20

However, this lower limit underestimates the value of the Debye integral derived using the full expressions for the out-of-plane vibration and its anharmonic by a factor of approximately 2. A lower limit of x_o ≈ 0.083x_m, θ′ ≈ 93 K is required to give a good fit to available data. A smaller limit will overestimate the Debye integral whereas a higher limit will underestimate the Debye integral.

Equation (6.11) can be written in terms of equilibrium values as

$$\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}=-\frac{1}{34}{\left(\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}\right)}_{d_0}[10{\left(\frac{d_0}{d}\right)}^4-44{\left(\frac{d_0}{d}\right)}^{10}].$$ 6.21

Equation (6.18) can now be solved to give

$$\begin{array}{r}{\alpha }_c=\frac{1}{C_{33}(d_0)}{\left(\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}\right)}_{d_0}\left(\frac{6}{34}\right)\frac{[10-44{(d_0/d)}^6]}{[10{(d_0/d)}^6-4]}\frac{h}{8\rho {\pi }^2\delta d_0^3}\frac{1}{T}\left\{\frac{\exp ({\theta }_o/T)-\exp ({\theta }^{\prime }/T)}{[1-\exp ({\theta }_o/T)][1-\exp ({\theta }^{\prime }/T)]}\right\},\end{array}$$ 6.22

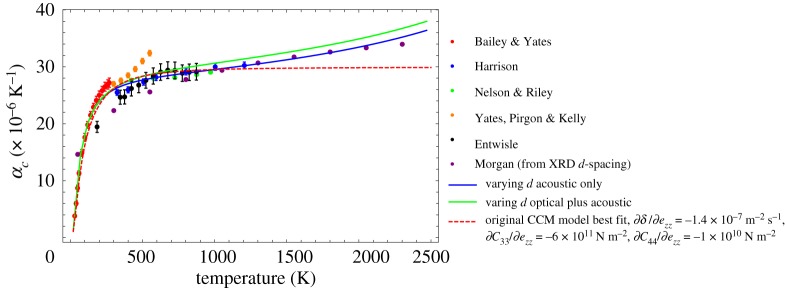
which is plotted in figure 9 along with the previous model given by equation (4.2) for reference. As before an attempt to include optical modes is included [6], by taking an upper limit of 2θ_o.

Figure 9.

Prediction of α_c taking account of the change in d-spacing with increasing temperature, compared with experimental data [27,29,34–37] and previous model (equation (4.2)). (Online version in colour.)

We can again examine the behaviour of the thermal expansion coefficient in the high and low temperature limits by examining the leading order behaviour for θ′, θ₀≫T and θ′, θ₀≪T. It is important to remember that θ_o > θ′.

For low temperatures, θ′, θ₀≫T, the leading order behaviour is

$${\alpha }_c=\frac{1}{C_{33}(d_0)}{\left(\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}\right)}_{d_0}\left(\frac{6}{34}\right)\frac{[10-44{(d_0/d)}^6]}{[10{(d_0/d)}^6-4]}\frac{h}{8\rho {\pi }^2\delta d_0^3}\frac{1}{T}\left\{\exp (-\frac{{\theta }^{\prime }}{T})-\exp (-\frac{{\theta }_o}{T})\right\}.$$ 6.23

For high temperatures, θ′, θ₀≪T, the leading order behaviour is

$${\alpha }_c=\frac{1}{C_{33}(d_0)}{\left(\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}\right)}_{d_0}\left(\frac{6}{34}\right)\frac{[10-44{(d_0/d)}^6]}{[10{(d_0/d)}^6-4]}\frac{h}{8\rho {\pi }^2\delta d_0^3}\left(\frac{{\theta }_o-{\theta }^{\prime }}{{\theta }_o{\theta }^{\prime }}\right).$$ 6.24

We again see that, as the temperature tends to zero, the thermal expansion coefficient exponentially approaches zero. However, at high temperatures, the thermal expansion coefficient only has temperature dependence through the change in lattice spacing, d, with temperature. This temperature dependence is responsible for the up-turn of the CTE at high temperatures, which appears to be in good agreement with the data. Without it, the CTE would level off at high temperatures just like the original continuum coefficient of thermal expansion model.

Equations (5.5), (4.2) and (6.22) give methods of estimating crystal α_a and α_c, respectively, from first principles without resorting to atomistic modelling. Furthermore, they allow for sensitivity studies to be performed to determine the influence of crystal strain, modulus, temperature, etc. on CTE. The sensitivity of this simplified methodology is mainly dependent on the ratio C⁻¹₃₃(d₀)(∂C₃₃/∂e_zz)_d0, which is (from equation (6.12)) equal to −17. Kelly & Duff [8] calculated this ratio using a slightly different methodology based on the work of Agranovich & Semenov [41] and Girifalco & Lad [42] to be −7.27 × 10¹¹/38.6 × 10⁹ =  − 18.8 and −6.04 × 10¹¹/36.5 × 10⁹ =  − 16.5, respectively. Thus, the first ratio of 18.8 would overpredict α_c by 10% and the second ratio would underpredict by 3%.

7. Influence of loading polycrystalline graphite on individual crystal thermal expansion

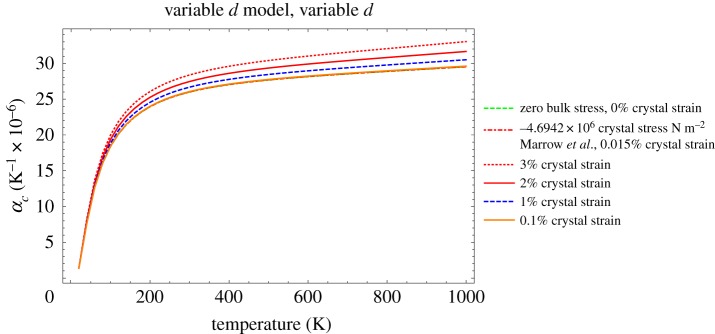
It has been observed that both mechanical applied loading of unirradiated polycrystalline graphite [2] and irradiation creep strain [43] can induce a significant change in bulk CTE, with tensile strains reducing CTE and compressive strains increasing CTE. The equation for α_c derived above can be used to investigate the effect of pressure on the thermal expansion coefficients of graphite crystals [7], assuming a change in interlayer spacing. More recently, Marrow et al. [44] measured the change in lattice d-spacing with loading using neutron diffraction and synchrotron XRD. Taking the room temperature lattice d-spacing from [44] to be 0.3353 nm implies a maximum strain of ∼0.015% associated with a bulk stain of 3000 μϵ. Assuming a Young's modulus of 11.9 GPa [44], this implies a bulk stress loading of 35 MPa, which is a similar order to that given in [2].

Modifying equation (6.22) to be a function of strain gives

$$\begin{array}{rl}{\alpha }_c& =\frac{1}{C_{33}(d_0)}{\left(\frac{\mathrm{\partial }{C}_{33}}{\mathrm{\partial }{e}_{zz}}\right)}_{d_0}\left(\frac{6}{34}\right)\frac{[10-44{(1/{ϵ}_{PT})}^6]}{[10(1/{ϵ}_{PT})6-4]}\frac{h}{8\rho {\pi }^2\delta d_0^3}\frac{1}{T}\\ & \times \left\{\frac{\exp ({\theta }_o/T)-\exp ({\theta }^{\prime }/T)}{[1-\exp ({\theta }_o/T)][1-\exp ({\theta }^{\prime }/T)]}\right\},\end{array}$$ 7.1

where

$${ϵ}_{PT}=ϵ(T)+ϵ(P),$$ 7.2

ϵ(T) is the lattice thermal strain, which can be calculated using equation (6.4), and ϵ(P) is the lattice strain due to bulk loading. Predictions of α_c are plotted in figure 10 over the range 20 to 1000 K.

Figure 10.

Prediction of α_c, taking account of the change in d-spacing, with increasing temperature and differing amounts of crystal strain, note that the 0%, 0.015% (measured by Marrow et al. [44]) and 0.1% curves overlie each other. (Online version in colour.)

From these calculations, it is clear that the change in crystal strain measured by Marrow et al. [44] is unlikely to account for the change in bulk CTE due to loading. It is also clear that crystal strains greater than approximately 1% are required to lead to significant changes in α_c. Thus for practical purposes such strains are unlikely to be generated by bulk loading. However, they could result from fast neutron irradiation as discussed below.

8. Influence of irradiation on α_a and α_c

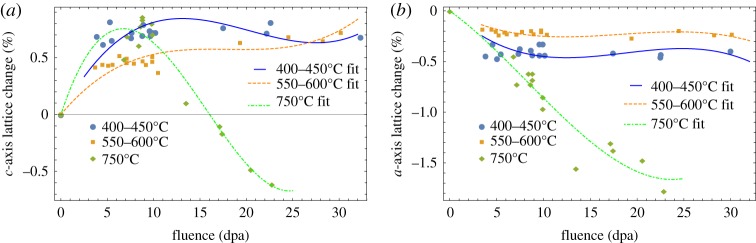
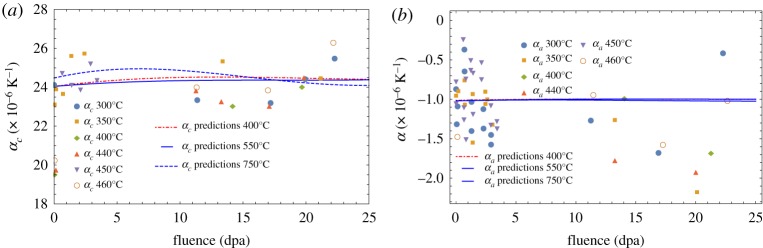
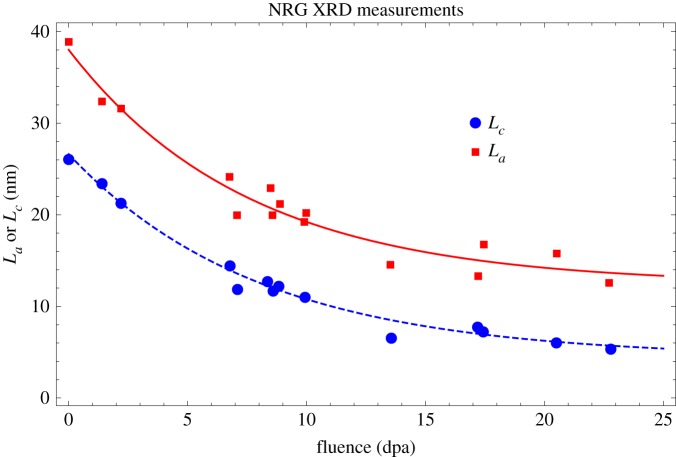
Small changes, less than a maximum of 2% at an irradiation fluence of 25 dpa, in lattice spacing due to fast neutron irradiation measured using XRD have been reported by the United Kingdom Atomic Energy Authority (UKAEA) [45–47] and more recently by the Nuclear Research Group (NRG) in Petten, The Netherlands [48]; see figure 11. These data have been used here in equations (5.5) and (7.1) to predict the change in CTE in the a- and c-directions as a function of fast neutron fluence and are compared with measurement of the thermal expansion measured on HOPG irradiated between 300°C and 650°C in figure 12. Although there is significant scatter in the measured data the predictions uphold the assumption of invariance in graphite crystal CTE for all practical purposes. However, data on irradiated polycrystalline graphite show a significant reduction in CTE with increasing fast neutron fluence. Possible reasons for this behaviour are discussed in §9.

Figure 11.

Irradiation-induced changes to the lattice c-spacing (a) and a-spacing (b), reported by the various authors from the UKAEA [45–47] and from NRG in Petten [48]. (Online version in colour.)

Figure 12.

Thermal expansion coefficients both perpendicular (a) and parallel (b) to the basal plane measured on irradiated HOPG [1] and predictions using the NRG XRD data and equations (7.1) (a) and (5.5) (b). (Online version in colour.)

9. Irradiation-induced changes to bulk polycrystalline CTE—application and some observations

To determine the bulk CTE, one can consider a simple Reuss model [49], in which all the crystals are arranged in series. For isotropic graphite, this gives a linear CTE of

$${\alpha }_{\mathrm{bulk}}=\frac{1}{3}({\alpha }_c+2{\alpha }_a).$$ 9.1

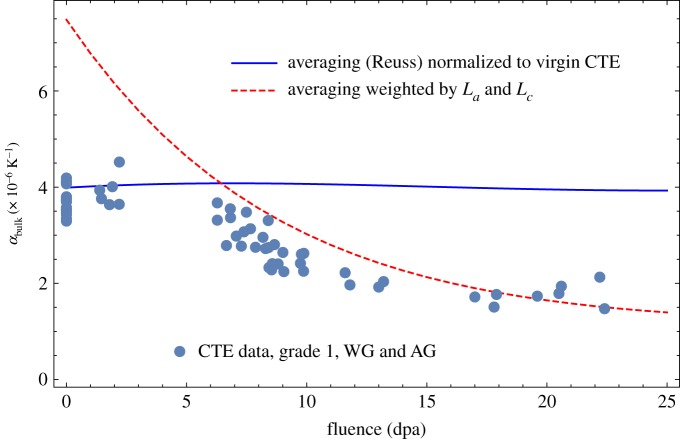
If all the crystallites in nuclear graphite were randomly distributed with no porosity, this would imply an unirradiated CTE of ∼8 × 10⁻⁶ K⁻¹. However, there is porosity particularly perpendicular to the crystal c-axis, which reduces the influence of the crystal c-axis expansion, reducing the overall bulk CTE. The expansion in the c-direction is said to fill this accommodation porosity without increasing the specimen length in that direction. Thus, using the predictions of crystal CTE in equation (9.2) and normalizing the results to the virgin value a prediction of irradiated bulk CTE is compared with the measured data for well-graphitized, medium-grained nuclear graphite grade 1 in figure 13.

Figure 13.

Predictions of bulk CTE compared with experimental data [48] for grade 1 graphite. (Online version in colour.)

While this does predict some reduction in CTE with increasing fluence as observed in all medium-grained graphite, the reduction is small compared with the experimental observations. The Reuss approximation effectively assumes that the phases are infinite in one direction or are at least continuously connected in one direction. However, analysis of the XRD peak broadening, based on the Scherrer equation [50], showed that the crystal size L_a and L_c both decreased with increasing irradiation, appearing to start to saturate at higher fluence [48,51]; this is shown in figure 14. This may suggest that the Reuss approximation breaks down in much the same way as it does in composite mechanics with discontinuous reinforcements [52–54].

Figure 14.

Grade 1 graphite irradiated at 750°C, change in crystal size L_a and L_c [48,51]. (Online version in colour.)

Assuming that the reduction in crystallite size increases porosity these data can be used to try and account for the increase in porosity by weighting equation (9.1) as follows:

$${\alpha }_{\mathrm{bulk}}=\frac{1}{3}({\alpha }_c\frac{L_c}{L_c(0)}+2{\alpha }_a\frac{L_a}{L_a(0)}),$$ 9.2

where L_c(0) and L_a(0) are the unirradiated values of L_c and L_a.

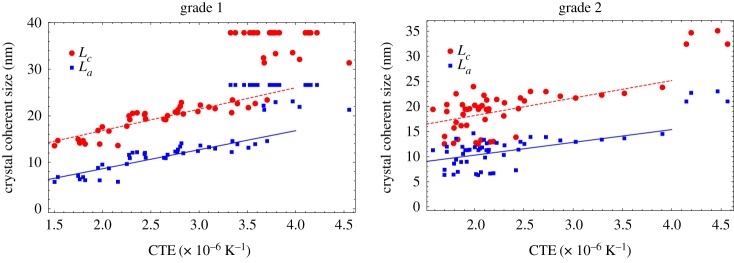
Figure 13 suggests a combination of the two models is required to fit the data, above and below about 5 dpa. Below 5 dpa bulk CTE is largely invariant to fast neutron fluence, whereas above 5 dpa CTE falls with increasing fluence. Figure 15 shows the crystal coherent scattering domain size data [48,51] against irradiated CTE for EU medium-grained nuclear graphite grade 1 and grade 2, clearly showing a correlation between CTE and large coherence crystal size. These comparisons suggest that the reason for the fall in CTE above 5 dpa is caused by irradiation-induced changes in crystal perfection, leading to disruption of the crystal lattice, and resulting in a smaller scattering length.

Figure 15.

Measurements of crystal coherent scattering domain size against irradiated CTE for grade 1 and grade 2 graphite [48,51]. (Online version in colour.)

10. Conclusion

• —Theoretical models for the prediction of the CTE in graphite crystals and HOPG proposed in the 1970s and 1980s have been revisited. Numerous errors have been corrected and equations reformulated where necessary.
• —Using more recent input data, the equations have then been applied to the prediction of graphite crystal CTE both parallel and perpendicular to the hexagonal basal planes as a function of temperature, from absolute zero to 3000 K. The results are shown to give an excellent fit to experimental data.
• —The theoretical equations have been reformulated to give the change in CTE as a function of strain. Recent neutron and XRD experiments measuring changes to lattice spacing under load have demonstrated that, in bulk graphite, crystal CTE is unlikely to be modified under load. This implies that changes in bulk graphite CTE observed in loaded graphite are most likely to be due to changes in microstructural perfection and orientation.
• —The equations have then been applied to the prediction of crystal CTE subject to fast neutron irradiation showing that above 300°C the crystal CTE is largely invariant of fluence. This confirms experimental observations obtained on irradiated HOPG.
• —The use of averaging techniques (Reuss) to predict irradiated induced bulk CTE in polycrystalline graphite is shown to give poor results. However, the fall in CTE at moderate to high irradiation fluence is shown to be proportional to the crystal coherent scattering domain size. This may imply that changes to irradiated CTE may be driven by the formation of nano-cracks or that there exists a length below which the Reuss approximation is invalid. This would also imply that irradiation-induced dimensional changes and modulus changes are driven by larger microstructural features.

Appendix A. Tables of data

See tables 1 and 2.

Appendix B. Sensitivity studies

See figures 16 and 17.

Figure 16.

Sensitivity of α_c to ∂C₃₃/∂e_zz, ∂C₄₄/∂e_zz and ∂δ/∂e_zz [27,29,34–37].

Figure 17.

Sensitivity of α_a to simplified anharmonics C₁₁⁻¹∂C₁₁/∂e_xx, C₆₆⁻¹∂C₆₆/∂e_xx and δ⁻¹∂δ/∂e_xx [27,31,34–36].

Data accessibility

This article does not contain any additional data.

Author's contributions

A.M. interpreted and devised the mathematical models. The numerical calculations and comparisons were performed by B.M., who also wrote the majority of the paper. B.M. and P.M. interpreted the results and drew the conclusions. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by Innovate UK grant no. TS/K004638/1.