Mitochondrial Diagnostics: A Multiplexed Assay Platform for Comprehensive Assessment of Mitochondrial Energy Fluxes

SUMMARY

Chronic metabolic diseases have been linked to molecular signatures of mitochondrial dysfunction. Nonetheless, molecular remodeling of the transcriptome, proteome, and/or metabolome does not necessarily translate to functional consequences that confer physiologic phenotypes. The work here aims to bridge the gap between molecular and functional phenomics by developing and validating a multiplexed assay platform for comprehensive assessment of mitochondrial energy transduction. The diagnostic power of the platform stems from a modified version of the creatine kinase energetic clamp technique, performed in parallel with multiplexed analyses of dehydrogenase activities and ATP synthesis rates. Together, these assays provide diagnostic coverage of the mitochondrial network at a level approaching that gained by molecular “-omics” technologies. Application of the platform to a comparison of skeletal muscle versus heart mitochondria reveals mechanistic insights into tissue-specific distinctions in energy transfer efficiency. This platform opens exciting opportunities to unravel the connection between mitochondrial bioenergetics and human disease.

In Brief

Fisher-Wellman et al. develop and validate a multiplexed assay platform that permits deep and comprehensive phenotyping of mitochondrial bioenergetics under conditions that model in vivo fluctuations in energy supply and demand. The report provides a blueprint for building this platform and a workflow for executing and interpreting the assays.

Graphical Abstract

INTRODUCTION

Mitochondria are the principal site of energy conversion in mammalian systems and primarily responsible for establishing the free energy of ATP hydrolysis (ΔG_ATP) through the process of oxidative phosphorylation (OXPHOS). Defects in oxidative metabolism represent a common manifestation of aging and age-related metabolic disorders such as obesity, diabetes, heart disease, and cancer (Gonzalez Herrera et al., 2015; Muoio and Neufer, 2012; Sun et al., 2016). The strong association between mitochondrial metabolism and pathophysiological phenotypes has also emerged as a prominent theme among studies that have deployed discovery technologies, such as genomics, proteomics, and metabolomics, to identify molecular signatures prognostic of disease risk (Davies et al., 2016; Koves et al., 2008; Overmyer et al., 2015; Williams et al., 2016). Together, these findings provide traction for theories implicating mitochondrial dysfunction as a cornerstone of metabolic disease and have sparked intense interest in drug development strategies targeting mitochondrial health.

Implicit in this field of study is the idea that complex disease traits arise from metabolic flux limitations or perturbations imposed by the sum of all aberrant changes in the quantity and quality of mitochondrial proteins. In most cases, pathological remodeling of these organelles involves multiple enzyme complexes, at multiple steps, along multiple oxidative pathways that act cooperatively to transduce the energy in carbon fuels to a more biologically accessible form of currency (i.e., ΔG_ATP). Importantly, molecular remodeling at the level of the transcriptome, proteome, and/or metabolome does not necessarily translate to functional consequences that confer physiologic phenotypes. Thus, progress toward deciphering the precise role of the mitochondria in disease etiology requires tools and methods that can capture changes in metabolic and respiratory flux in intact mitochondria working to regenerate ATP in the context of a physiologically relevant energy charge. To this end, we have developed a multiplexed platform for interrogating respiratory fluxes under multiple substrate and energetic conditions. The goal of the project was to bridge the gap between molecular and functional phenomics by developing a suite of assays that permit modeling of in vivo mitochondrial energy transduction in a comprehensive manner. Application of these assays to a functional comparison between mouse skeletal muscle versus the heart revealed several profound distinctions in energy transduction efficiency between the mitochondrial pools resident in these two tissues. Herein, we provide a blueprint for building this platform and a workflow for executing and interpreting the assays.

RESULTS

Working Model of Mitochondrial Energy Transduction

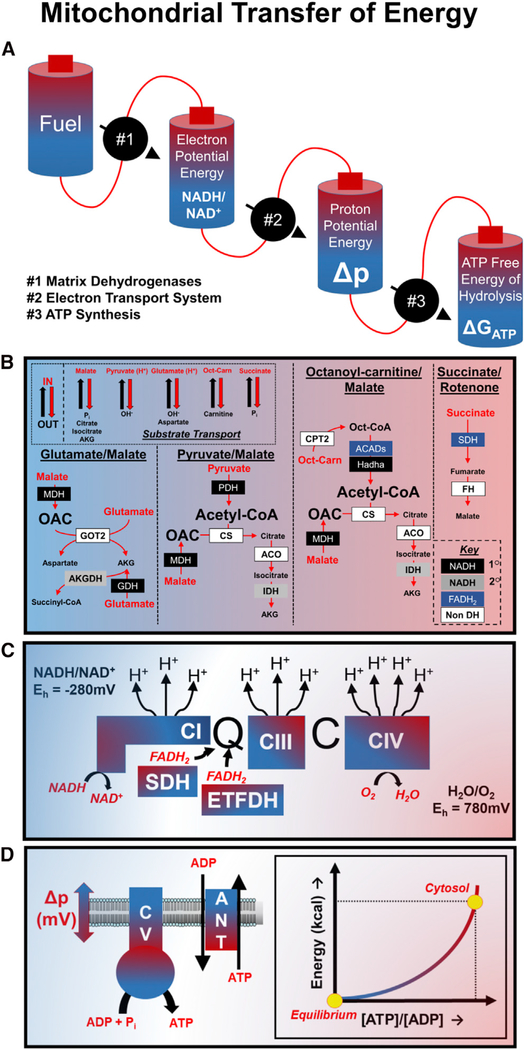
Before discussing the design and implementation of the mitochondrial diagnostics platform, it is important to review several fundamental bioenergetics principles that formed the framework for this project. First, experiments tasked with providing insights into mitochondrial metabolism must consider the basic mechanisms by which biological energy transduction proceeds, as well as caveats of studying bioenergetics using a cell-free, in vitro system. These considerations are modeled in Figure 1A, which depicts mitochondrial energy transduction as a series of inter-connected energy cells (i.e., batteries) that power a sequential set of energy transformation steps. Inherent to this model is the critical concept that the energy potential (i.e., “charge”) of any one cell is constrained by the maximal charge of the preceding battery. The charging and discharging of each battery are regulated by three distinct flux control nodes that act as power generators to collectively convert the chemical energy in electron-rich carbon substrates (“Fuel”) to ATP free energy (ΔG_ATP). In intact cells, substrate availability can exert substantial control over respiratory kinetics and thermodynamics. By contrast, flux control at this step is eliminated when isolated mitochondria are provided with saturating substrate concentrations. Thus, the first control node under evaluation in our experimental system (node 1) is the power generator defined as the “Matrix Dehydrogenases” (Figure 1B). This node encompasses substrate uptake across the mitochondrial inner membrane via a collection of proteins that mediate electroneutral or electrogenic ion transfer, as well as catabolism by multiple dehydrogenase enzymes that remove hydrogens while transferring electrons from specific carbon substrates to nicotinamide adenine dinucleotide (NAD⁺) and/or protein-bound flavin adenine dinucleotide (FAD). The resulting production of NADH and FADH₂ provides reducing power that drives the electron transport system (ETS). Simply stated, the “Matrix Dehydrogenases” transfer the charge available in the “Fuel” cell into “Electron Potential Energy,” thus establishing the energetic driving force for the subsequent transfer step. The efficiency of energy transfer at node 1 can be assessed experimentally via the fluorescent measurement of the NADH/NAD⁺ and/or FADH₂/FAD⁺ redox couples (Koretsky and Balaban, 1987). Importantly, the specific subset of dehydrogenases engaged by these assays depends on the substrates provided. It should be noted that the common practice of adding high concentrations of malate (>2 mM) to respiring mitochondria is intended to (1) promote efflux and depletion of matrix tricarboxylic acid (TCA) cycle intermediates via malate exchange with citrate, isocitrate, and alpha-ketoglutarate, which prevents enzyme product inhibition; and (2) eliminate succinate dehydrogenase (SDH) flux via malate-fumarate equilibration, which results in feedback inhibition of the enzyme. Alternatively, dehydrogenase flux can be limited exclusively to SDH by adding succinate as the substrate in combination with inorganic phosphate, which promotes malate-phosphate exchange, along with rotenone, an inhibitor of complex I that causes hyper-reduction of the NADH/NAD⁺ couple and feedback inhibition of malate dehydrogenase (MDH). Thus, these strategies are designed to isolate fluxes through specific dehydrogenases and/or enzyme complexes.

Figure 1. Mitochondrial Energy Transfer.

(A–D) Simplified model (A) and detailed depictions (B–D) of mitochondrial energy transfer and the corresponding control nodes. (B) Upper left box shows several common mechanisms of metabolite exchange in the inner mitochondrial membrane. “IN” and “OUT” refer to substrate uptake into, or export from the matrix, respectively. The enzymes (color-filled boxes) activated under each substrate condition are depicted within distinct segments. Black filled, primary (1°) NAD-linked dehydrogenase; gray filled, secondary (2°) NAD-linked dehydrogenases; blue filled, FAD-linked dehydrogenases; white filled, nondehydrogenase enzymes. (C) The difference in redox potentials between NADH/NAD⁺ and H₂O/O₂ (780 mV - (-280 mV) = 1,060 mV) provides energy for pumping of protons from the matrix to the inner-membrane space during the process of electron transport. (D) depicts the increase in ATP free energy as the ATP:ADP ratio is displaced from equilibrium during the process of mitochondrial energy transfer.

Node 2 (“Electron Transport System”; Figure 1C) represents the ETS generator, which transfers electron potential energy in the form of NADH/NAD⁺ and FADH₂/FAD⁺ to the electrochemical proton gradient known as the protonmotive force (Δp; “Proton Potential Energy” cell). This process consists of a series of oxidoreductase reactions in which electrons flow down an energy gradient as they transfer by default to redox cofactors with sequentially more positive reduction potentials, each residing within a multi-subunit protein complex embedded in the inner mitochondrial membrane. Molecular oxygen serves as the final electron acceptor, resulting in the formation of a water molecule. The exothermic transfer of electrons to oxygen drives the pumping of protons from the matrix to the inner membrane space at three locations (CI, CIII, and CIV), in turn establishing Δp. The electrical component of this potential can be assessed using a variety of fluorescent cationic compounds (Scaduto and Grotyohann, 1999), or via tetraphenylphosphonium (TPP) in conjunction with a TPP-selective electrode (Palmeira and Rolo, 2012). In node 3 (“ATP Synthesis”; Figure 1D), the energy available in Δp drives the generation and transport of ATP, as the proton current traverses the inner mitochondrial membrane via the ATP synthase complex (CV) and the adenine nucleotide translocase (ANT). Under most circumstances, proton flux is tightly coupled to OXPHOS, which is a demand-driven process regulated by the rate of cellular ATP turnover and the subsequent availability of ADP. An acute increase in ATP hydrolysis leads to a transient fall in cellular energy charge, which in turn promotes proton flux and ATP resynthesis. However, it is important to consider that Δp can also be dissipated by proton leak and/or consumed by processes such as metabolite or ion transport (e.g., Ca²⁺ uptake) (Figure S1). Thus, a drop in Δp due either to elevated demands for ATP regeneration or proton leak will result in a partial loss of ATP free energy, triggering increased electron transport and proton pumping in effort to defend and recharge ΔG_ATP. The net flux of the proton current is reflected by the rate at which oxygen is reduced at CIV, measured as the rate of mitochondrial oxygen consumption (JO₂), which therefore serves as the experimental measurement of node 3.

In sum, mitochondria serve two primary functions: (1) ATP resynthesis, and (2) displacement of the ATP/ADP ratio far from equilibrium, by about 10 orders of magnitude. This means that mitochondria are typically pumping ATP into a sea of ATP, “up an energetic hill.” The extent to which the ATP generator at node 3 can displace the extra-mitochondrial ATP/ADP ratio away from equilibrium dictates the free energy of ATP hydrolysis (ΔG_ATP), which in turn determines the power available for cellular work. The energy available to displace ATP/ADP depends entirely on the potential energy harnessed in the steady-state Δp, which in turn draws its charge from the steady-state redox potential that is maintained by the dehydrogenase enzymes and regulated by enzyme activities and fuel availability. As such, a decline in capacity and/or efficiency within any of the power-generating control nodes will by default impact the energy charge and discharge of all batteries, ultimately leading to a loss in ATP free energy and ensuing biological consequences. Thus, given the interconnectivity of the foregoing energy transduction circuit, attempts to identify potential lesions in oxidative metabolism would greatly benefit from comprehensive information that enables one to diagnose shifts in flux control at each of the three nodes during mitochondrial respiration occurring under near-physiologic energetic conditions. In other words, the conventional approach of measuring JO₂ alone in the context of unlimited ADP availability (i.e., ATP/ADP ratio approaching equilibrium) severely limits the diagnostic utility of that assay.

The Creatine Kinase Clamp Technique and the Assessment of OXPHOS Conductance

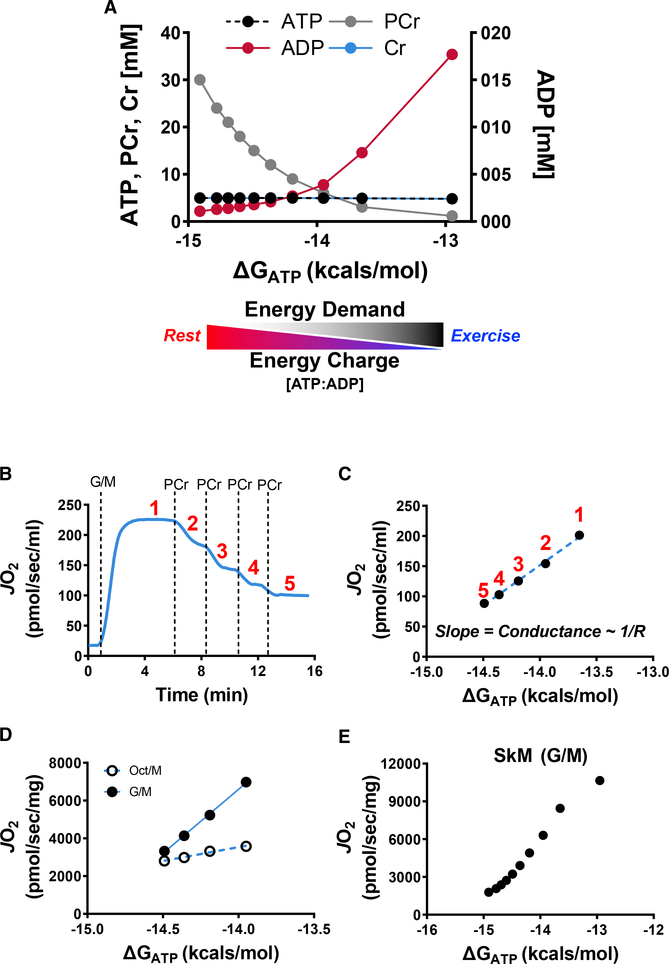
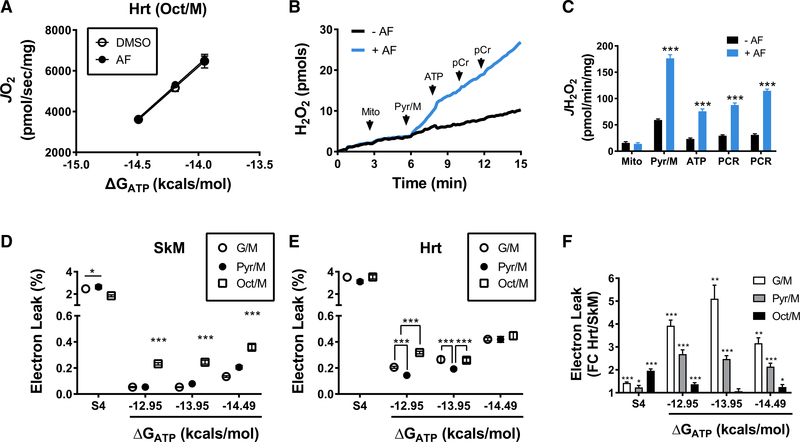
Conventional respirometry assays measure JO2 in response to an ADP bolus or an ADP clamp. In these assays, the ATP/ADP ratio is essentially at or near equilibrium, which means the mitochondria are operating under conditions that are physiologically irrelevant. The approach described here was designed to interrogate a multitude of mitochondrial fluxes under more physiologically meaningful conditions using a population of mitochondria isolated from a single mouse. The diagnostic power of the platform stems from the application of a modified version of the creatine kinase (CK) energetic clamp (Glancy et al., 2008, 2013; Messer et al., 2004; Willis et al., 2016). This technique leverages the enzymatic activity of CK, which couples the interconversion of ATP and ADP to that of phosphocreatine (PCr) and free creatine, to titrate the extra-mitochondrial ATP/ADP ratio. Importantly, the CK clamp permits assessment of respiratory control across a range of ATP free-energy states (expressed herein in kilocalories per mole and estimated per details in STAR Methods), effectively modeling in vivo flux demands for ATP regeneration. An increase in ATP energy charge (ATP/ADP ratio) mimics a decrease in demand and vice versa. A simple analogy is that the transition from high to low ATP/ADP ratio mimics the transition between rest and exercise; thus, the assay serves as an in vitro stress test. Figure 2A depicts the concentrations of the primary clamp components (ADP, ATP, Cr, PCr) across a span of ATP free energies, which are varied via the sequential addition of PCr from a starting concentration of 1 mM to a final concentration of 30 mM. Consistent with the study by Glancy et al. (2013), exposure of energized mitochondria to increasing ATP free energies (i.e., more negative ΔG_ATP values corresponding to an increased ATP/ADP ratio) progressively diminished respiratory flux (Figure 2B). This is because a fall in demand facilitates recharging of the Δp battery, and consequently, proton pumping at CIV is met with increasing backpressure. Plotting mitochondrial JO₂ as a function of ΔG_ATP permits a calculation of conductance (the reciprocal of resistance) throughout the entire OXPHOS pathway, according to the equation I = V/R (Figure 2C), wherein current (I) corresponds to the proton current (experimentally represented via JO₂) and voltage (V) is represented by ΔG_ATP (Willis et al., 2016). The slope of the inverse relationship between JO₂ and ΔG_ATP reflects relative flux resistance (R) within the entire mitochondrial OXPHOS energy transduction pathway, such that the steeper slope observed in skeletal muscle mitochondria energized by glutamate/malate (G/M) as compared to octanoylcarnitine/malate (Oct/M) (Figure 2D) indicates lower resistance and greater conductance (sensitivity) in the context of the respective substrate conditions (Glancy et al., 2013). These results are interpreted as indication of a respiratory flux limitation, and thus decreased responsiveness to energy challenge, when Oct/M is provided as substrate. In others words, muscle mitochondria are better capable of responding to an energy deficit when provided with glutamate as opposed to fatty acid substrate. It should be noted that the relationship between JO₂ and ΔG_ATP loses linearity at either extreme of oxygen flux (Figure 2E), further underscoring the caveats of interpretations based on state 3 respiration kinetics.

Figure 2. Assessment of Mitochondrial Respiratory Conductance via the CK Clamp.

(A) Changes in ADP, ATP, creatine (Cr), and phosphocreatine (PCr) and the estimated free energy of ATP hydrolysis (ΔG_ATP) during a typical CK clamp experiment. The transition from a high to low energy charge, and thus low to high energy demand, mimics the transition from rest to exercise.

(B–D) Representative JO₂ trace (B) and linear relationship between JO₂ and ΔG_ATP during a PCr titration experiment in skeletal muscle mitochondria energized with G/M (C) or G/M versus Oct/M (D).

(E) Representative PCr titration experiments in skeletal muscle mitochondria demonstrating the linear range of the relationship between JO2 and

ΔG_ATP.

Multiplexed Assessment of Mitochondrial ΔΨ and NAD(P)H/NAD(P)⁺ Redox State across Increasing ATP Free Energies

A central bioenergetics tenet relevant to the goals of this project is that shifts in JO₂ and respiratory responsiveness are difficult to interpret without corresponding information on the energy charge of the redox and Δp batteries. Accordingly, the platform we developed incorporates concurrent assessments of mitochondrial membrane potential (ΔΨ) and the NAD(P)H/NAD(P)⁺ redox state. Mitochondrial ΔΨ was assessed using the fluorescent cationic dye tetramethylrhodamine methyl ester (TMRM), which was selected because this fluorophore is amenable to a multiplexed assay platform. Here, TMRM emission spectra at 590 nm following excitation at both 551 and 552 nm were used to estimate ΔΨ by converting the 572/551 ratio to millivolts, based on a KCl calibration curve performed in the presence of valinomycin (Krumschnabel et al., 2014). Next, the NAD(P)H/ NAD(P)⁺redox state, expressed as a percentage of complete reduction, was obtained by a second fluorometric reading based on NAD(P)H auto-fluorescence, in which emission intensity at 450 nm is recorded following excitation at 340 nm. These fluorometric assays were performed with a QuantaMaster Spectrofluorometer (QM-400; Horiba Scientific) equipped with a temperature-controlled four-position multi-sample turret, which permits processing of four samples per experiment. Simultaneous fluorescent measurements (Ex/ Em; 340/450, 551/590, 572/590) alongside parallel respirometry experiments using multiple O2K instruments permitted multiplexed assessment of respiratory conductance and associated steady-state energetic potentials (i.e., ΔΨ and NAD(P)H/ NAD(P)⁺) under various substrate combinations. Further details pertaining to optimization and validation of these assays are provided in STAR Methods and Figure S2.

Validating the Diagnostic Utility of the CK Clamp Technique Using Respiratory Inhibitors

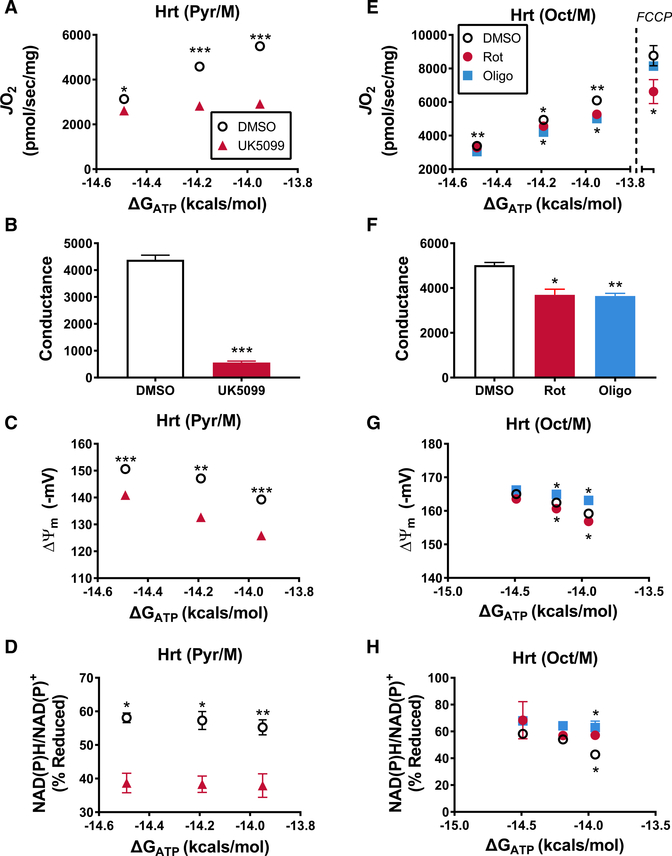
In theory, parallel measurements of JO₂, ΔΨ, and the NAD(P)H/ NAD(P)⁺ redox state should permit both the detection and generalized localization of relative shifts in respiratory conductance. To directly test this concept, experiments were conducted in isolated heart mitochondria in the presence and absence of three distinct respiratory inhibitors that act specifically at each of the three nodes (Figures 1B–1D). Each inhibitor was applied at a sub-saturating dose in the presence of increasing ATP free energies to simulate submaximal respiratory resistance (flux limitation). The pyruvate carrier inhibitor, UK5099, was used to induce resistance at control node 1 (“Dehydrogenases”) by restricting substrate supply to the pyruvate dehydrogenase (PDH) complex (Bricker et al., 2012). Application of resistance at this node should limit the steady-state reduction potential generated by PDH (i.e., NAD(P)H/NAD(P)⁺ redox state), therefore impairing all subsequent energy transfer steps. The substrate combination of pyruvate and malate was utilized for these experiments to activate the PDH complex. Consistent with the predicted outcome, addition of UK5099 imposed respiratory resistance compared to DMSO-treated mitochondria (Figures 3A and 3B), while also causing a relative depolarization of the ΔΨ (Figure 3C) and a decrease in NAD(P)H/NAD(P)⁺ (Figure 3D) reduction potential. Thus, the observed respiratory phenotype fit perfectly with that expected by a flux limitation at node 1.

Figure 3. Respiratory Conductance Workflow Localizes Distinct Sites of Resistance Imposed by Specific Inhibitors.

(A–H) Relationship between mitochondrial oxygen consumption (JO₂) and ATP free energy (ΔG_ATP) in heart mitochondria energized with either Pyr/Mal (A–D) or Oct/M (E–H) performed in the presence of DMSO and (A–D) UK5099 or (E–H) oligomycin and rotenone. In (E), the JO₂ rates depicted to the right of the dashed line, at ΔG_ATP = 0, represent maximal, uncoupled JO₂ induced via addition of 1 mM FCCP. (B and F) Slope of the relationships between JO₂ and ΔG_ATP depicted in (A) and (B), respectively. (C and G) Mitochondrial Δ and (D and H) NAD(P)H/NAD(P)⁺ redox state measured under identical conditions to those displayed in (A) and (E). Data are mean ± SEM. Differences between DMSO and each inhibitor (UK5099, Rot, Oligo) were analyzed by paired t tests. *p < 0.05, **p < 0.001, and ***p < 0.0001. (E, G, and H) The asterisks (*) above the data points correspond to the DMSO versus Oligo comparison, while those below correspond to DMSO versus Rot. n = 3–4/ group, where n represents 3–4 biological replicates (i.e., mitochondrial preparations).

We next used rotenone and oligomycin to simulate resistance within nodes 2 (“Electron Transport System”) and 3 (“ATP Synthesis”), respectively. Rotenone inhibits electron entry into the ETS at the level of CI. Submaximal flux resistance at this stage should impair energy transfer efficiency at all points downstream of CI, while also imposing a bottleneck that results in the buildup of free energy in the form of redox potential. Thus, in experimental terms, rotenone would be expected to decrease both JO₂ and respiratory conductance due to relative depolarization of ΔΨ, while causing a hyperreduction in the NAD(P)H/NAD(P)⁺ redox state. This scenario was indeed evident in isolated heart mitochondria energized with Oct/M and treated with 9 nM rotenone (Figures 3E–3H; DMSO versus Rot). In contrast to rotenone, oligomycin inhibits CV, where it restricts the transfer of energetic potential between the Δp and ΔG_ATP. As such, this agent would also be predicted to lower both JO₂ and respiratory conductance, but with the bottleneck now occurring further downstream, a buildup of free energy should be observed at all preceding sites of the energy transduction pathway. Consistent with this notion, exposure of isolated heart mitochondria to 15 nM oligomycin led to a ~30% drop in respiratory conductance, combined with a relative hyper-polarization of the ΔΨ and hyper-reduction of the NAD(P)H/NAD(P)⁺ redox state (Figures 3E–3H; DMSO versus Oligo). Addition of the uncoupling agent, carbonyl cyanide 4-(trifluoromethoxy)phenylhydrazone (FCCP) (1μM), at the end of the respirometry experiments rescued absolute rates of JO₂ in oligomycin, but not the rotenone-treated mitochondria (Figure 3E; rates to the right of the dotted line). This is because uncoupling eliminates flux control imposed by the ATP synthesis node (CV and/or ANT) and amplifies flux resistance at the ETS node. In sum, rotenone and oligomycin led to indistinguishable phenotypes at the level of respiratory conductance and NAD(P)H/NAD(P)⁺ reduction potential; however, the effects of the drugs diverged at the level of the ΔΨ, in a manner consistent with the known molecular target of each agent. Taken together, these data validate the diagnostic power of the assay platform and highlight its ability to identify and localize respiratory resistance to one of three energy transfer control nodes within the entire OXPHOS pathway.

Application of the Respiratory Diagnostics Platform Reveals Tissue-Specific Conductance Phenotypes and Dehydrogenase Limitations in Skeletal Muscle and Heart Mitochondria

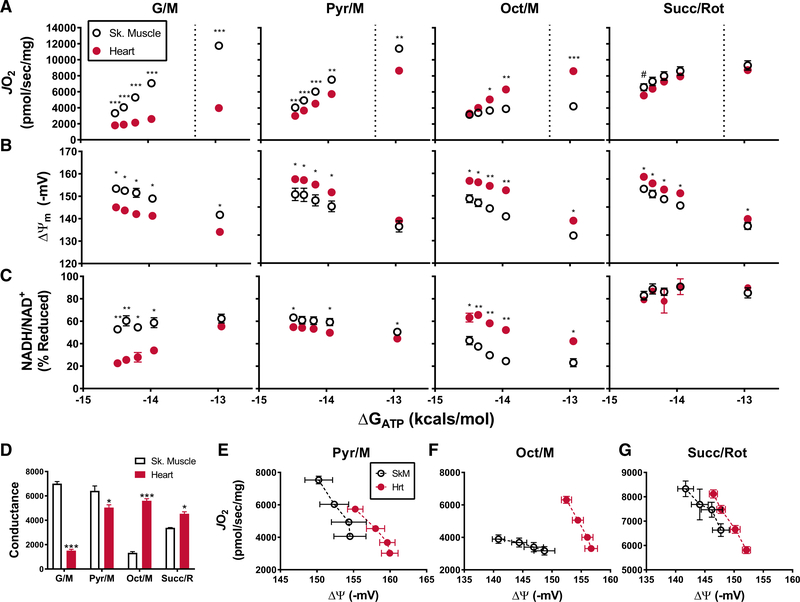
The assay platform was subsequently deployed to investigate energy transfer in mitochondrial populations derived from mouse skeletal muscle as compared to heart. Notably, mitochondrial content, as determined by the expression of CIII, CIV, and CV (Larsen et al., 2012), were not different between skeletal muscle and heart mitochondrial preparations when normalized to total protein (Figures S4A and S4B). The substrate combinations employed for these assays included G/M, pyruvate/malate (Py/M), Oct/M, and succinate/rotenone (Succ/R), each of which engage a distinct set of dehydrogenase enzymes (Figure 1B). In the presence of G/M and Pyr/M, both of which are NAD-linked substrate combinations, absolute rates of JO₂ as well as calculated conductance measurements (Figures 4A and 4D; G/M and Pyr/M) were as much as 4-fold greater in mitochondria from skeletal muscle as compared to heart, a distinction that was particularly pronounced in the context of G/M. By contrast, upon exposure to Oct/M, both JO₂ and respiratory conductance (Figures 4A and 4D; Oct/M) were substantially lower in mitochondria derived from skeletal muscle versus heart. Interestingly, the presence of Succ/Rot produced similar maximal JO₂ in skeletal muscle and heart mitochondria (Figure 4A; Succ/Rot), but respiratory conductance was greater in the latter group (Figure 4D; Succ/Rot).

Figure 4. Respiratory Control in Mitochondria Isolated from Heart Compared to Skeletal Muscle.

(A–C) Changes in mitochondrial (A) JO₂, (B) Δ Ψ, and (C) NAD(P)H/NAD(P)⁺ redox state as a function of ATP free energy (ΔG_ATP) and substrate: G/M, Pyr/M, Oct/M, and Succ/Rot.

(D) The linear range of JO₂, located to the left of the dashed line in (A), was used to calculate the corresponding slopes.

(E–G) Relationship between mitochondrial JO₂ and Δ in the presence of (E) Pyr/M, (F) Oct/M, and (G) Succ/Rot. Data are mean ± SEM. Tissue-specific differences in mitochondrial phenotypes were analyzed by Student’s t test. *p < 0.05, **p < 0.001, and ***p < 0.0001. n = 4–7 individual mice/group.

To localize the site of the substrate-specific flux limitations detected by the foregoing conductance assays, measurements of ΔΨ (Figure 4B) and NAD(P)H/NAD(P)⁺ redox status (Figure 4C) were performed simultaneously using the same two populations of mitochondria. For each of the substrate conditions tested, the mitochondrial pool that produced a more robust conductance plot also produced a more polarized ΔΨ and a more reduced NAD(P)H/NAD(P)⁺ redox state. These results align with the respiratory phenotype observed in the presence versus absence of the pyruvate carrier inhibitor, UK5099 (Figure 3), and thus points to substrate delivery and/or dehydrogenase activity (node 1) as the primary node that explains the phenotypic distinctions between muscle and heart mitochondria. For example, the low respiratory conductance observed in heart mitochondria supplied with G/M appeared to stem from insufficient substrate flux through the enzymes that use those substrates to generate electron potential energy (Figure 1B), thereby resulting in a lower NAD(P)H/NAD(P)⁺ redox state. Likewise, the same was true of skeletal muscle mitochondria when Oct/M served as the substrate.

Adaptations in Energy Transfer Efficiency within Heart Mitochondria Maximize ΔG_ATP across Physiological Flux Demands

The lower respiratory conductance observed in heart as compared to muscle mitochondria fueled by Pyr/M (Figures 4B and 4D; Pyr/M) was accompanied by a relative hyper-polarization of ΔΨ (Figure 4B; Pyr/M) and a slight hypo-reduction of NAD(P)H/NAD(P)⁺ redox state (Figure 4C; Pyr/M). Lower respiratory conductance combined with heightened energetic potential within the Δp could indicate increased resistance in the ATP synthesis control node, as demonstrated by the experiments with low-dose oligomycin (Figure 3). However, unlike that observed with oligomycin, hyper-polarization of ΔΨ in heart mitochondria energized with Pyr/M was accompanied by a relative decrease in electron potential energy (i.e., lower NAD(P)H/NAD(P)⁺ redox), a combination that instead implies enhanced energy transfer efficiency (i.e., thermodynamics). Likewise, plotting JO₂ against ΔΨ for high flux substrate combinations revealed a pronounced rightward shift in the curves corresponding to heart mitochondria (Figures 4E–4G), such that any given JO₂ corresponded with a more negative ΔΨ, consistent with increased OXPHOS efficiency. The hyper-polarized phenotype of heart mitochondria was also apparent in Percoll-purified preparations (Figures S4F and S4G). This relationship is of particular importance because, in vivo, the energy available in the ΔΨ determines the magnitude to which the mitochondria can displace the ATP/ADP ratio from equilibrium, which in turn drives ΔG_ATP. Accordingly, our findings suggest that heart mitochondria maintain a greater (i.e., more negative) ΔG_ATP for a given oxygen flux. It must be noted, however, that in these in vitro assays, ΔG_ATP is held constant (clamped) by large excesses of CK and a defined creatine/ adenylate pool, which together confer unlimited capacitance to compensate for potential deficits in the rate of mitochondrial ATP regeneration. For this reason, in the context of our assay, the precise contributions of JO₂ and CK flux to ΔG_ATP are unknown, and therefore we are unable to discriminate between changes in energy transfer efficiency (i.e., more negative Δp for a given JO₂) and/or flux resistance at the level of ATP synthesis and transport, without additional diagnostics (addressed below).

Mitochondrial JH₂O₂ Emission Is Greater in Heart Than Skeletal Muscle and Increases across a Physiologic Span of ATP Free Energies in Both Tissues

Alterations in respiratory conductance that promote hyperreduction of the NAD(P)H/AD(P)⁺ redox state might favor electron leak (Quinlan et al., 2012). Because electron leak and oxidative stress have been implicated as culprits in numerous pathologies (Kanaan and Harper, 2017), we sought to add further value to our mitochondrial diagnostics platform by incorporating measures of JH₂O₂ emission as a function of ATP free energy. The rate of electron leak can be determined in isolated mitochondrial by measuring the rate of H₂O₂ emission using the Amplex Ultra Red/Horseradish Peroxidase system (Fisher-Wellman et al., 2013a). Accurate quantification of H₂O₂ using this system requires that all substrates/chemicals employed in the protocol be evaluated for potential interference with resorufin fluorescence (Fisher-Wellman et al., 2013a). To this end, H₂O₂ standard curves were generated in the presence of each inhibitor/ATP/ PCr combination necessary for the CK clamp technique (Figure S3A). Slopes calculated from the linear regression of resorufin fluorescence intensity versus H₂O₂ (in picomoles) were unaffected by auranofin (0.1 μM) and ATP (5 mM), either alone or in combination, but were depressed with the additional inclusion of PCr (6 mM) (Figure S3B). To control for this effect, quantification of H₂O₂ within a given experiment was performed using standard curves unique to each of the substrate/PCr combinations tested. Another important consideration for these assays is that the observed H₂O₂ emission rates represent the balance between ROS generation and scavenging. To gain a better approximation of absolute H₂O₂ production rates, the protocol developed includes auranofin, which inhibits thioredoxin reductase-mediated scavenging of H₂O₂ in the mitochondrial matrix (Fisher-Wellman et al., 2013a; Munro et al., 2016). Importantly, the concentration of auranofin used in these assays did not affect respiratory conductance (Figure 5A), but as expected, its presence increased JH₂O₂ emission (Figures 5B and 5C). In these experiments, mitochondria isolated from skeletal muscle were energized with Pyr/M under state 4 conditions (nonphosphorylating), and then exposed to increasing ATP free energies by the addition of PCr. Consistent with previous reports, JH₂O₂ emission was greatest during state 4 respiration, and markedly diminished upon exposure to low ATP free energy (i.e., near-maximal JO₂). Subsequent additions of PCr, resulting in a more physiologic energy charge (ΔG_ATP), progressively increased JH₂O₂ (Figures 5B and 5C).

Figure 5. Thioredoxin Reductase Inhibition Reveals Stepwise Increases in Electron Leak during Transition from High to Low Energetic Demands.

(A) Relationship between mitochondrial oxygen consumption and ATP free energy (ΔG_ATP) in heart mitochondria (0.1 mg/mL) energized with Oct/M performed in the presence of DMSO or auranofin (AF) (0.1 mM).

(B) Representative trace showing H₂O₂ emission from skeletal muscle mitochondria energized with Pyr/M under increasing ATP free energies performed in the absence (AF) or presence (+AF) of AF.

(C) Quantification of the data depicted in (B).

(D and E) Electron leak, expressed as a percentage of total flux (JH₂O₂/JO₂ = % Electron Leak), measured in isolated mitochondria prepared from (D) skeletal muscle or (E) heart. Mitochondria were energized with G/M, Pyr/M, or Oct/M and assayed under near-state 4 conditions followed by exposure to ATP free energies of 12.95, 13.95, and 14.49 kcal/mol corresponding to PCr concentrations of 1, 6, and 15 mM.

(F) Difference in absolute JH₂O₂ emitting potential between skeletal muscle and heart for each experimental condition expressed as linear fold chance (FC) (Hrt/SkM). Data are mean ± SEM.

Differences between groups were analyzed by Student’s t tests in (C) and (F), and one-way ANOVA with Tukey’s multiple comparison in (D) and (E). *p < 0.05, **p < 0.001, and ***p < 0.0001. n = 4–7/group, where n represents 4–7 biological replicates (i.e., mitochondrial preparations).

To determine tissue-specific differences in the relationship between electron leak and ΔG_ATP, both JO₂ and JH₂O₂ emission were measured under identical conditions using the CK clamp technique applied to isolated mitochondria from skeletal muscle and heart energized with G/M, Pyr/M, and Oct/M. Because JH₂O₂ increases as a function of total electron flux, rates of electron leak were expressed as a percent of oxygen flux (JH₂O₂/JO₂) (Figures 5D and 5E). This experiment revealed near stepwise increases in electron leak in both skeletal muscle (Figure 5D) and heart (Figure 5E) mitochondria, particularly for the NAD-linked substrate combinations (G/M and Pyr/M). Interestingly, although not apparent under state 4 conditions, relative rates of fatty acid (Oct/M)-supported electron leak were higher than all other substrate combinations at each ΔG_ATP in skeletal muscle, and for the lowest (i.e., least negative) ΔG_ATP in heart mitochondria (Figures 5D and 5E). Absolute rates of electron leak were higher in heart compared to skeletal muscle mitochondria for all conditions assessed, with the exception of Oct/M at a ΔG_ATP of 13.95 (kcal/mol) (Figure 5F). These results are consistent with the finding that heart mitochondria generate a greater ΔΨ for any given rate of oxygen flux (Figures 4E–4G), and provide evidence that rates of ROS emission under physiological conditions are sensitive to shifts in substrate supply and energy demand.

Comprehensive Assessment of Mitochondrial Energy Transfer and Enzymatic Fluxes Provide Mechanistic Insights into Tissue-Specific Differences in Respiratory Conductance

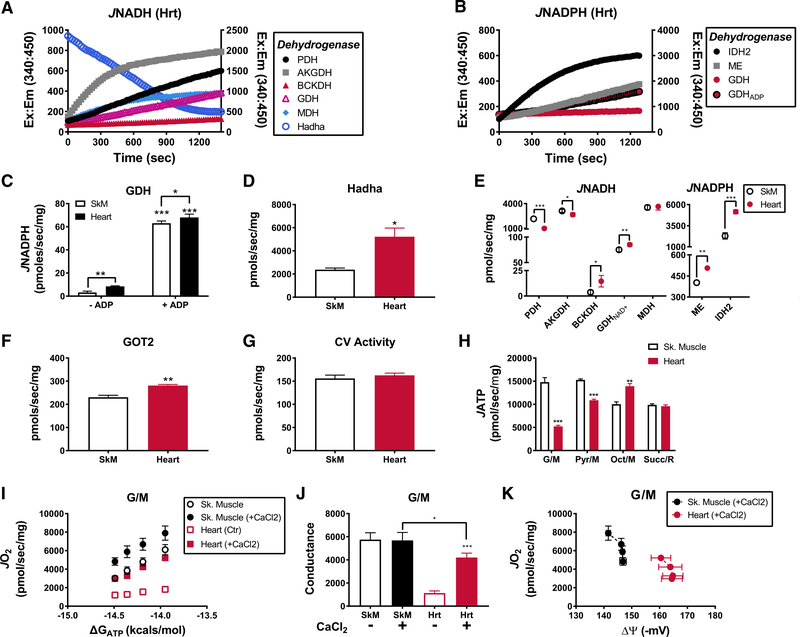
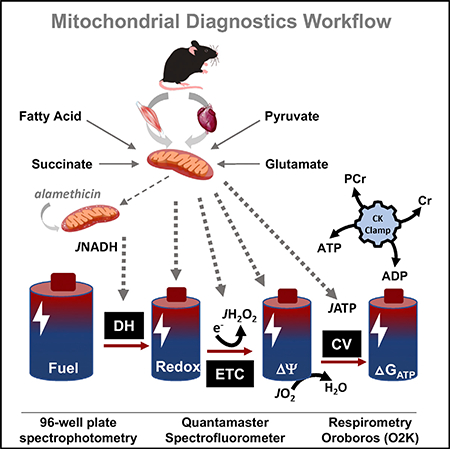
The final arm of this platform involves real-time assessment of multiple enzyme activities using alamethicin-permeabilized mitochondria, along with substrate-specific rates of ATP synthesis measured in intact mitochondria, assayed together in a single 96-well plate. These assays employ spectrofluorometric (excitation/emission, 340/450 nm) measures of NADH or NADPH kinetics to evaluate maximal activities of several NAD-linked dehydrogenases; including, the pyruvate (PDH), alphaketoglutarate (AKGDH), and branched-chain keto acid (BCKDH) dehydrogenase complexes, glutamate dehydrogenase (GDH), MDH, and hydroxyacyl-CoA dehydrogenase (HADHA), all of which were measured in the forward direction (NADH production [JNADH]), with the exception of HADHA activity (assessed via NADH degradation) (Figure 6A; representative traces). NADP-linked enzyme activities (JNADPH) included isocitrate dehydrogenase (IDH2), malic enzyme (ME), and GDH (Figure 6B; representative traces). Consistent with previous studies in liver mitochondria (Godinot and Gautheron, 1971; Ronchi et al., 2016), we found that GDH can generate NADPH in both skeletal muscle and heart mitochondria when ADP is provided (Figure 6C). As expected, HADHA activity was 2-fold greater in heart compared to skeletal muscle mitochondria (Figure 6D). Likewise, JNADH from GDH and the BCKDH complex were also elevated in heart mitochondria (Figure 6E). By contrast, JNADH from PDH and AKGDH complexes were lower in heart mitochondria (Figure 6E), whereas MDH activity was similar between tissues (Figure 6E). The activities of all NADPH-producing enzymes were greater in heart compared to skeletal muscle mitochondria (Figure 6E; JNADPH). Given that JNADPH determines H₂O₂-scavenging capacity within the matrix (Cortassa et al., 2014), high activity of cardiac NADP-linked dehydrogenases might confer protection against the relatively greater peroxide burden imposed by the heart mitochondrial program (Figure 5F).

Figure 6. Comprehensive Assessment of Dehydrogenase Activities and ATP Synthase.

(A) Representative traces depicting NADH auto-fluorescence during JNADH assays of various dehydrogenase enzymes. Hadha activity is assessed via NADH oxidation and thus plotted on the right y axis. Mitochondrial concentrations were aΔΨ usted to obtain linearity over time: MDH (0.005 mg/mL), PDH, AKGDH, and Hadha (0.025 mg/mL), GDH (0.15 mg/mL), and BCKDH (0.3 mg/mL).

(B) Representative traces depicting NADPH auto-fluorescence during JNADPH assays of various dehydrogenases. NADPH production from GDH was assessed in the absence (GDH) and presence (GDP_ADP) of ADP (2 mM). IDH2 is plotted on the right y axis. Mitochondrial concentrations were as follows: IDH2, ME (0.025 mg/mL), GDH (0.15 mg/mL).

(C) JNADPH from GDH in both skeletal muscle and heart mitochondria recorded in the absence and presence of ADP (2 mM).

(D) HADHA activity in isolated mitochondria prepared from skeletal muscle and heart.

(E) Rates of NADH and NADPH production from all dehydrogenases studies in skeletal muscle and heart mitochondria.

(F) GOT2 activity in mitochondrial lysates from skeletal muscle and heart.

(G) CV activity in mitochondrial lysates prepared from skeletal muscle and heart.

(H) Quantified rates of ATP synthesis (JATP) from skeletal muscle and heart mitochondria energized with G/M, Pyr/M, Oct/M, and Succ/R assayed in the context of a hexokinase ADP (0.2 mM) clamp.

(I) Relationship between mitochondrial JO₂ versus ATP free energies (ΔG_ATP) in mitochondria energized with G/M in the absence and presence of 0.6 mM CaCl₂ (free Ca⁺~500 nM).

(J) Calculated slopes from the data depicted in (I).

(K) Mitochondria JO₂ plotted against Δ in the presence of G/M and CaCl₂. Data are mean ± SEM. Differences between tissues were analyzed by Student’s t tests. *p < 0.05, **p < 0.001, and ***p < 0.0001. n = 3–7 individual mice/group.

Integration of the NAD-linked enzyme activity results (Figure 6E) and the respiratory conductance phenotypes (Figure 4) revealed strong agreement across substrate conditions, with the notable exception of G/M. Thus, the low G/M-supported conductance in heart mitochondria was not explained by a corresponding decline in a relevant dehydrogenase activity. Although we did observe a slight decrease in AKGDH activity in heart mitochondria, respiratory conductance in the presence of AKG alone was similar between tissues (Figures S4C and S4D). Moreover, the primary dehydrogenases activated in the presence of G/M are MDH and GDH, because high malate concentrations tend to deplete matrix AKG via metabolite exchange (Figure 1B). Under these conditions, maximal MDH flux depends on the rate at which glutamate oxaloacetate transaminase (GOT2) can remove oxaloacetate. However, GOT2 activity was actually ~15% higher in heart compared to skeletal muscle mitochondria (Figure 6F). In aggregate, these discordant results prompted us to consider limitations in substrate delivery imposed at the level of glutamate/aspartate exchange. This process is carried out via the aspartate/glutamate carriers (AGC), aralar (SLC25A12) and citrin (SLC25A13), which are known to be differentially expressed in these two tissues and differentially sensitive to and activated by extra-mitochondrial calcium (Contreras et al., 2007; Palmieri et al., 2001). We therefore examined G/M-supported respiratory conductance in absence and presence of 0.6 mM CaCl₂ (free calcium ~500 nM in the presence of 1 mM EGTA). Strikingly, addition of calcium increased G/M-supported conductance nearly 4-fold in heart mitochondria, while having little impact in skeletal muscle (Figures 6I and 6J). The presence of calcium also normalized NAD(P)H/ NAD(P)⁺ redox between the two pools of mitochondria (Figure S4E) and led to a relative hyper-polarization of ΔΨ in the heart (Figure 6K). Plotting JO₂ against ΔΨ once again revealed a rightward shift in heart mitochondria (Figure 6K), identical to that seen with the other substrate combinations and consistent with heightened OXPHOS efficiency in the heart.

Last, we sought to determine whether the rightward shift in the relationship between JO₂ and Δ in heart mitochondria (Figures 4E–4G) might reflect increased resistance within the ATP synthesis control node, and/or heightened OXPHOS efficiency. To account for the former, the assay platform incorporates multiple assessments of ATP synthase activity and flux (JATP). The activity of ATP synthase was assayed in mitochondrial lysates in the reverse direction (i.e., ATP hydrolysis) in the absence or presence of oligomycin, which permits subtraction of ATPase activity not requiring the ATP synthase complex (Figure S5A). Maximal activity of the ATP synthase complex was similar between skeletal muscle and heart mitochondria (Figure 6G). Assessment of JATP in intact mitochondria (Figure 6H), which depends on maximal rates of energy transfer through nodes 1–3, revealed substrate-dependent differences between skeletal muscle and heart that closely matched the maximal dehydrogenase fluxes. Interestingly, maximal JATP was similar between the skeletal muscle and heart (Figure 6H; compare Sk. Muscle G/M and Pyr/M to Heart Oct/M). Taken together, these findings offer no evidence that resistance at node 3 is dissimilar between the two mitochondrial populations, suggesting that the rightward shift in ΔΨ at any given JO₂, observed in heart mitochondria under all substrate combinations, reflects increased OXPHOS efficiency that appears to be independent of differences in proton leak (Figures S5D and S5E).

DISCUSSION

While the advent of “-omics” technologies has spawned an extraordinary new era of discovery science, challenges and limitations pertaining to data interpretation are increasingly recognized as a potential pitfall and source of misinformation. Inarguably, unbiased analyses of SNPs, transcripts, proteins, post-translational modifications, and metabolites offer great potential to identify molecular signatures of health and disease, but the biological relevance and clinical implications of those signatures cannot be clearly understood without similarly comprehensive approaches for phenotyping of cellular and/or organelle function. To address this important methodological gap, we developed a mitochondrial diagnostics platform for deep phenotyping of respiratory fluxes and function at a level that is highly complementary to most molecular -omics tools. The assay platform can be integrated with other high-throughput technologies to facilitate functional phenomics of the same pool of mitochondria or tissue specimens used for unbiased molecular analyses, greatly enhancing the interpretive power of the science. Using the specified instrumentation and workflow, the entire collection of assays described herein can be performed in isolated mitochondria from a single mouse, and expanded to accommodate approximately four mice per day, depending on logistical constraints. Assuming a mitochondrial yield of >1.5 mg/tissue, the final mitochondrial pellet can be subdivided into 2× aliquots dedicated to functional (~1 mg) and other molecular analyses (~0.5 mg). Comprehensive mitochondrial flux assessments can then be informed by concurrent molecular phenomics assays, and vice versa, to produce high-confidence candidate targets for follow-up investigation.

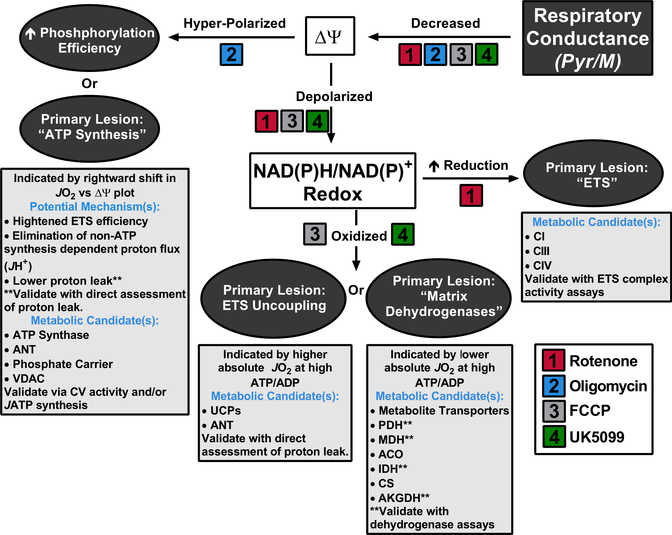
As with other biological and physiological outcomes measures, capturing dynamic respiratory responses to energy challenge can be much more revealing than a static snapshot. Thus, the key element of the platform described here is a CK energetic clamp technique that enables a highly tractable in vitro system for assessing respiratory sensitivity and resistance to dynamic energetic conditions. Importantly, we have adapted the CK assay as originally described (Glancy et al., 2013; Messer et al., 2004) to optimize the buffer conditions (Figure S1) and accommodate high-throughput analysis, which permits multiplexing of substrate conditions. The workflow developed includes measurements of respiratory conductance, Δ Ψ, NAD(P)H/NAD(P)⁺ redox, and JH₂O₂ emission across a physiologic span of ATP free energies, combined with parallel assessments of multiple dehydrogenase activities and ATP synthetic capacity, all performed in real time. The comprehensive nature of the platform not only allows for an estimation of relative conductance throughout the respiratory system but also pinpoints potential sites of flux resistance within the three major control nodes. To aid data interpretation, we provide a diagnostics tree (Figure 7) that predicts likely sites of differential regulation based on the collective respiratory phenotypes of two discordant mitochondrial populations.

Figure 7. Mitochondrial Diagnostics Tree.

Diagram summarizing how this functional assay platform can be used to diagnose distinct sites of resistance within the mitochondrial energy transduction pathway. Primary respiratory phenotypes are depicted in the gray-filled ovals. Listed below each phenotype are candidate sites of regulation and potential strategies for validation, assuming Pyr/M was the substrate. Expected diagnostic results for several common respiratory inhibitors are listed.

To demonstrate the diagnostic utility of the assay platform, we sought to characterize and decipher functional distinctions between mitochondria resident in mouse skeletal muscle tissue as compared to those derived from the heart. The results revealed insights into the unique programming and/or organization of these two mitochondrial populations. Interestingly, OXPHOS conductance in heart mitochondria was higher in the presence of FAD-linked substrates (Oct/M and Succ/R), but surprisingly lower in the presence of NAD-linked fuels (Pyr/M and G/M). The contrast between the two populations of mitochondria was most remarkable when respiration was supported by either G/M or Oct/M, both which produced a ~4-fold tissue-specific difference in conductance, but in opposite directions, with the heart strongly preferring Oct/M. In these experiments, a fall in conductance was universally associated with less polarized Δ and less reduced NAD(P)H/NAD(P)⁺ redox, thereby revealing lower steady-state free energies generated by nodes 1 and 2. As depicted by the diagnostic tree diagram (Figure 7), the phenotype of “Decreased” Respiratory Conductance → “Depolarized” ΔΨ → “Oxidized” NAD(P)H/NAD(P)⁺ redox state, predicts OXPHOS resistance at control node 1 (“Matrix Dehydrogenases”). This interpretation was subsequently validated for the fatty-acid substrate combination by the dehydrogenase assay module (Figure 6D).

Whereas mouse heart mitochondria are known to have high capacity to oxidize fatty acids (Fisher-Wellman et al., 2013b), the dramatic fall in respiratory conductance when the fuel source switched to G/M was unanticipated. In sum, the findings suggested that G/M-supported flux in mitochondria from mouse heart was limited by resistance at node 1. Because comprehensive assessment of enzyme activities linked to glutamate flux failed to identify an enzymatic explanation for the dramatic differences in G/M-supported respiratory conductance, we reasoned that this phenotype might be driven by differences in metabolite transport. Indeed, subsequent experiments revealed that G/M-supported conductance in heart mitochondria is highly dependent on extra-mitochondrial calcium. Given that previous studies have shown that aspartate/glutamate transport in heart mitochondria is activated by calcium (Contreras et al., 2007), we surmise that the G/M-supported respiratory phenotypes observed herein are mediated by tissue-specific expression and/or regulation of the two distinct isoforms of the AGC. Because the AGC is a key component of the malate-aspartate shuttle, which transfers redox equivalents from the cytoplasm to the mitochondrial matrix, these findings raise intriguing possibilities regarding the potential role of this carrier in the setting of heart failure and other pathologies linked to impaired calcium signaling (Carley et al., 2014; Finkel et al., 2015).

Irrespective of substrate conditions, maximal respiratory conductance was ~10% lower in mitochondria from heart (max conductance with Oct/M) compared to skeletal muscle (max conductance with Pyr/M or G/M). Similarly, maximal flux measurements of the most robust NAD-linked dehydrogenases (AKGDH and PDH) were also ~10%–50% lower in heart mitochondria. Thus, skeletal muscle mitochondria have superior OXPHOS flux capacity and sensitivity, driven primarily by more robust dehydrogenase enzyme kinetics, and therefore appear better poised to respond to a sudden and dramatic discharge of ΔG_ATP during the transition from rest to intense exercise. Measurements of maximal JO₂ and/or JATP in isolation might lead one to conclude that heart mitochondria are surprisingly inferior. However, when results from the entire assay platform are synthesized, new insights emerge. For example, although maximal JO₂ was lower in heart compared to skeletal muscle mitochondria, when assayed under more physiologically relevant energetic states (greater ATP free energy), heart mitochondria were able to maintain a greater (more negative) steady-state Δ for any given rate of JO₂, as compared to skeletal muscle mitochondria working against the same energy charge and fueled by the same carbon substrates. Here, it is important to underscore that, in vivo, the capacity of the oxidative system to maintain or “recharge” the ΔG_ATP battery during elevated work rates is determined largely by the Δp charge (the exception being a state of CV/ANT inhibition). Thus, whereas JO₂ provides a measure of energy demand, Δp (or Δ ) is a better indicator of ΔG_ATP. A drop in steady-state Δp lowers the driving force to displace the ATP/ADP ratio from equilibrium, thus diminishing ΔG_ATP and weakening the energy released by hydrolysis of each ATP molecule, which in turn threatens metabolic and functional homeostasis. By contrast, maintenance of a higher Δ for any given JO₂ and JATP equates to an elevated driving force to maintain ΔG_ATP, and thus increased aerobic power to sustain energetic stability in the face of a high work rate. When taken together, our results suggest that heart mitochondria are uniquely programmed to defend ΔG_ATP across a physiologic span of energetic demands, which appears attributable to some combination of heightened efficacy of energy transfer within the ETS and/or differences in CV/ANT-independent consumption of the proton current. These findings strongly agree with the known ability of healthy working hearts to maintain steady-state concentrations of adenylates (e.g., ATP, ADP) and NADH/NAD⁺ redox charge across a span of increasing workloads (Balaban et al., 1986; Heineman and Balaban, 1990). Increased OXPHOS efficiency could prove advantageous in mouse cardiac tissue, which maintains a resting heart rate of ~500—600 beats/min and therefore must defend the ATP free energy charge within a narrow range of consistently high metabolic demands. The biological trade-off for increased efficiency appears to be a relatively lower OXPHOS elasticity along with heighted electron leak, as demonstrated herein by the elevated JH₂O₂ emitting potential observed in heart versus muscle mitochondria. In the context of a healthy heart, such trade-offs might be counterbalanced by increased JNADPH flux, which is expected to mitigate potential toxicities imposed by a heavy peroxide load. By contrast, when confronted with pathophysiological insults such as ischemia-reperfusion, the phenotype of heart mitochondria might present unique vulnerabilities to oxidative stress.

In sum, this work provides a manual for building and operating a diagnostics tool kit designed to facilitate deep phenotyping of mitochondrial energy transduction and respiratory function. Application of this platform to a comparison of mitochondrial populations derived from skeletal muscle and heart uncovered discordant respiratory phenotypes mediated by each of the three regulatory nodes highlighted in Figure 1, which in turn provided provocative insights into the link between tissue-specific mitochondrial programming and function. The suite of assays described here is meant to serve as a base platform, upon which new modules can be added and/or tailored to expand coverage and/or meet specific research needs. Inclusion of additional substrate combinations that broaden the scope of the metabolic network engaged by respiring mitochondria would surely strengthen the diagnostics value of the platform. When combined with other “shotgun” -omics technologies, this respiratory phenomics workflow now presents exciting opportunities for discovering novel biology and disentangling mechanisms of pathophysiology and disease.

STAR ★ METHODS

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Total Rodent OXPHOS WB Antibody Cocktail	Abcam	Cat# ab110413; RRID: AB_2629281
Chemicals, Peptides, and Recombinant Proteins
Tris salt of phosphocreatine	Millipore Sigma	Cat# P1937
		CAS# 108321–17-1
Tris salt of ATP	Millipore Sigma	Cat# A9062
		CAS# 102047–34-7
Potassium pyruvate	Combi-Blocks	Cat# QA-1116
		CAS# 4151–33-1
Potassium NADP+	Ark-Pharm, Inc	Cat# AK671068
Creatine kinase from rabbit muscle	Millipore Sigma	Cat# 10736988001
Percoll solution	Millipore Sigma	Cat# P1937
		CAS#108321–17-1
Amplex Ultra Red Reagent (AUR)	ThermoFisher Scientific	Cat# A36006
CelLytic M	Millipore Sigma	Cat# C2978
Tetramethylrhodamine methyl ester (TMRM)	ThermoFisher Scientific	Cat# T668
Phosphoenoyl-pyruvate	Millipore Sigma	Cat# 10108294001;
		CAS# 4265–07-0
UK5099	Millipore Sigma	Cat# PZ0160;
		CAS# 56396–35-1
Auranofin	Millipore Sigma	Cat# A6733;
P1,P5-Di(adenosine-5ʹ)pentaphosphate	Millipore Sigma	Cat# D6392;
		CAS# 75522–97-3
Oligomycin	Millipore Sigma	Cat# 75351
		CAS# 579–13-5
Rotenone	Millipore Sigma	Cat# R8875
		CAS# 83–79-4
Potassium cyanide	Millipore Sigma	Cat# 60178
		CAS# 151–50-8
Carbonyl cyanide 4-(trifluoromethoxy)phenylhydrazone (FCCP)	Millipore Sigma	Cat# C2920
		CAS# 370–86-5
Peroxidase from horseradish (HRP)	Millipore Sigma	Cat# P8375
		CAS# 9003–99-0
Superoxide dismutase (SOD)	Millipore Sigma	Cat# S9697
		CAS# 9054–89-1
Glucose-6-phosphate Dehydrogenase (G6PDH)	Millipore Sigma	Cat# G6378
		CAS# 9001–40-5
Malate dehydrogenase (MDH)	Millipore Sigma	Cat# 442610-M
		CAS# 9001–64-3
Pyruvate Kinase/Lactic Dehydrogenase enzymes from rabbit muscle	Millipore Sigma	Cat# P0294
Hexokinase	Millipore Sigma	Cat# H4502
		CAS# 9002–07-7
Trypsin from porcine pancreas (Trypsin)	Millipore Sigma	Cat# T4799
		CAS# 9001–51-8
Creatine Monohydrate	Millipore Sigma	Cat# C3630
		CAS# 6020–87-7
Octanoyl-L-carnitine	Millipore Sigma	Cat# 50892
		CAS# 25243–95-2
Malic acid (Malate)	Millipore Sigma	Cat# M1000
		CAS# 97–67-6
Glutamic acid (Glutamate)	Millipore Sigma	Cat# G1501
		CAS# 6382–01-0
Succinic acid (Succinate)	Millipore Sigma	Cat# S3674
		CAS# 110–15-6
α-ketoglutaric acid (AKG)	Millipore Sigma	Cat# K1750
		CAS# 328–50-7
3-Methyl-2-oxopentanoic acid (α -keto-β-methylvalerate)	Millipore Sigma	Cat#198978;
		CAS#3715–31-9
Isocitrate	Millipore Sigma	Cat#58790;
		CAS#20226–99-7
Adenosine diphosphate (ADP)	Millipore Sigma	Cat# A5285
		CAS# 72696–48-1
Tetraphenylphosphonium (TPP+)	Millipore Sigma	Cat# 218790
		CAS# 2001–45-8
NADH	Millipore Sigma	Cat# N4505
		CAS# 104809–32-7
Nicotinamide adenine dinucleotide (NAD+)	Millipore Sigma	Cat# N1636
		CAS# 53–84-9
L-Aspartic acid (Aspartate)	Millipore Sigma	Cat# A9256
		CAS# 56–84-8
Acetoacetyl-CoA	Millipore Sigma	Cat# A1625
		CAS# 1420–36-6
Coenzyme A	Millipore Sigma	Cat# C3019
		CAS# 18439–24-2
Thiamine pyrophosphate	Millipore Sigma	Cat# C8754
		CAS# 154–87-0
Pyridoxal 5′-phosphate	Millipore Sigma	Cat# P9255
		CAS# 853645–22-4
Experimental Models: Organisms/Strains
C56BL/6NJ mice	The Jackson Laboratory	Stock #005304
Software and Algorithms
Jupyter notebook containing the aΔΨ ustment calculations interspersed with procedural descriptions needed to calculate ΔGATP.	N/A	https://github.com/dmpio/bioenergeticcalculators/blob/master/jupyter_notebook/creatine-kinase-clamp.ipynb
Web-based ΔGATP calculator	N/A	https://dmpio.github.io/bioenergeticcalculators/ck_clamp/
Other
Ultracentrifuge tubes for mitochondrial percoll purifications	Beckman Coulter	Cat# 344061
Swinging bucket ultracentrifuge rotor for mitochondrial percoll purifications – Surespin 630 with tube adapters	ThermoFisher Scientific	Cat# 79363
QuantaMaster Spectrofluorometer	Horiba Scientific	Cat# QM-400

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Deborah Muoio (debbie.muoio@duke.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All animal studies were approved by the Duke University Institutional Animal Care and Use Committee. Male C57BL/6NJ (Stock #005304)mice were purchased from Jackson Laboratory as littermates at 8 weeks of age. All experiments were carried out on mice between the ages of 8–12 weeks. All mice were housed in a temperature (22C) and light controlled (12 hour light/12 hour dark) room and given free access to food and water. Unless otherwise stated, mice were fasted 1 hour, anesthetized with Nembutal (intraperitoneal injection; 40mg/kg), and the following tissues were removed for mitochondrial isolation and subsequent functional analysis: skeletal muscle (gastrocnemius, plantaris, soleus, quadriceps) and heart (complete left and right ventricles).

METHOD DETAILS

Chemical & Reagents

Unless otherwise stated, all chemicals were purchased from Sigma-Aldrich. Tris salts of phosphocreatine (P1937) and ATP (A9062) were purchased from Sigma-Aldrich. Potassium pyruvate was purchased from Combi-Blocks (QA-1116). Potassium NADP⁺ was purchased from Ark-Pharm (AK671068). Amplex Ultra Red (A36006), and Tetramethylrhodamine methyl ester (TMRM; T668) were purchased from Thermo Fisher Scientific. Creatine kinase (CK-RO) from rabbit muscle was purchased from Roche Life Science.

Mitochondrial Isolation

Differential centrifugation was employed to prepare isolated mitochondria from skeletal muscle and heart. The following buffers were utilized for all isolations: Buffer A – (phosphate buffered saline (pH = 7.4), supplemented with EDTA (10mM); Buffer B – MOPS (50mM; pH = 7.1), KCl (100mM), EGTA (1mM), MgSO4 (5mM); Buffer C – Buffer B, supplemented with bovine serum albumin (BSA; 2g/L). Skeletal muscle and heart were excised and immediately placed in ice-cold Buffer A. All tissues were minced and subjected to a 5-minute incubation on ice in Buffer A, supplemented with 0.025% trypsin. Following trypsin incubation, skeletal muscle and heart suspensions were centrifuged at 200 X g for 5-minutes at 4°C to remove trypsin. Tissue pellets were resuspended in Buffer C and then homogenized via a Teflon pestle and boroscilicate glass vessel. Tissue homogenates were centrifuged at 500 × g for 10-minutes at 4°C. Supernatant from each tissue was then filtered through thin layers of gauze and subjected to an additional centrifugation at 10,000 × G for 10-minutes at 4°C. Mitochondrial pellets were washed in 1.4ml of Buffer B, transferred to microcentrifuge tubes and centrifuged at 10,000 × g for 10-minutes at 4°C. Buffer B was aspirated from each tube and final mitochondrial pellets were suspended in 100–200 μL of Buffer B. Protein content was determined via the Pierce BCA protein assay. Functional assays involving isolated mitochondria were carried out in the following buffers; Buffer D – Potassium-MES (105mM; pH = 7.2), KCl (30mM), KH₂PO₄ (10mM), MgCl₂ (5mM), EGTA (1mM), BSA (2.5g/L); Buffer E – HEPES (20mM; pH = 8.0), KCl (100mM), KH₂PO₄ (2.5mM), MgCl₂ (2.5mM), Glycerol (1%).

Mitochondrial purification with Percoll

Mitochondrial Percoll purification was carried out as previously described (Glancy and Balaban, 2011; Graham, 2001), with some modifications. Mitochondrial pellets (~5mgs) were resuspended in 1ml of sucrose wash buffer (250mM sucrose, 10mM HEPES (pH = 7.2), 0.1% BSA). A 30% percoll solution was prepared by mixing sucrose wash buffer with Percoll solution (Sigma: P4937) and aΔΨ usting the pH to 7.2. Self-generating percoll gradients were prepared by adding 15ml of the 30% Percoll solution to ultracentrifuge tubes (Beckman: #344061) and then layering the mitochondrial suspensions atop using a plastic transfer pipette. Samples were centrifuged in a swinging bucket ultracentrifuge rotor (ThermoFisher Scientific Cat #79363) at 22,700 RPM for 20 minutes at 4°C. This process yielded two distinct bands containing a top unpurified fraction and a bottom purified mitochondrial fraction. Purified mitochondria were extracted using a plastic transfer pipette and immediately washed in 40ml of sucrose wash buffer. Following centrifugation at 10,000 × g for 10-minutes at 4°C, mitochondrial pellets were washed once more in Buffer B prior to final resuspension in Buffer. Protein content was determined using the Pierce BCA assay.

Preparation of mouse mitochondrial pellets for western blotting

Flash frozen isolated mitochondrial pellets from each tissue were thawed on ice and homogenized in CelLytic M (Sigma-Aldrich) supplemented with protease inhibitor cocktail using a motor-drive Potter-Elvehjem tissue grinder. Samples were centrifuged at 14,000 × g for 10 min at 4°C and the supernatant saved and frozen at 80°C until later analysis. Protein concentration was determined via the Pierce BCA assay and the samples were diluted in CelLytic M. Forty micrograms of protein sample were combined with 5× loading buffer and resolved by SDS-PAGE, transferred to nitrocellulose, blocked for ~1 hr in 5% Milk prepared with TBS followed by western blotting with specific antibodies. Antibodies employed herein were: OXPHOS cocktail (Abcam: #ab110413).

Mitochondrial Respiratory Control

High-resolution O₂ consumption measurements were conducted using the Oroboros Oxygraph-2K (Oroboros Instruments). All experiments were carried out at 37°C in a 2ml reaction volume. Steady-state oxygen consumption rates (JO₂) ranging from near resting up to ~95% of maximal were sequentially determined within individual experiments using a modified version of the creatine energetic clamp technique (Glancy et al., 2013; Messer et al., 2004). In this assay, the free energy of ATP hydrolysis (ΔG’_ATP) can be calculated based on known amounts of creatine (Cr), phosphocreatine (PCr) and ATP in combination with excess amounts of creatine kinase (CK) and the equilibrium constant for the CK reaction (i.e., K_CK). Calculation of DG’_ATP was performed according to the following formula:

$$\Delta G_{ATP}^{\prime }=\Delta G_{ATP}^{\prime }+RT\ln \frac{[Cr]\left[P_i\right]}{[PCr]\left[K{\prime }_{CK}\right]}$$

where ΔG’°_ATP is the standard apparent transformed Gibbs energy (under a specified pH, ionic strength, free magnesium and pressure), R is the gas constant (8.3145 J/kmol) and T is temperature in kelvin (310.15). Given that experiments were performed via sequential additions phosphocreatine, both the ΔG’°_ATP and K’_CK were determined at each titration step based on the changes in buffer ionic strength and free magnesium, as previously described (Golding et al., 1995; Teague et al., 1996). For complete details regarding the calculation of ΔG’_ATP at each titration point see the “ADDITIONAL RESOURCES” section below.

Buffer for all assays was Buffer D, supplemented with ATP (5mM), creatine (Cr; 5mM), phosphocreatine (PCr; 1mM) and creatine kinase (CK; 20U/ml). To begin, isolated mitochondria (0.025mg/ml) were added to assay buffer, followed by the addition of respiratory substrates. The following substrate conditions were tested: [Octanoyl-carnitine/Malate – (Oct/M; 0.2/2.5mM), Glutamate/Malate – (G/M; 10/2.5mM), Pyruvate/Malate – (Pyr/M; 5/2.5mM), Succinate/Rotenone – (Succ/R; 10/0.005mM)]. Following substrate additions, sequential additions of PCr to 3, 6, 9,12, 15, 18, 21, 24, 30mM were performed to gradually reduce JO₂ back toward baseline. For experiments in which a state 4 (i.e., non-phosphorylating) respiration rate were determined, ATP was omitted from the initial buffer and added after the addition of respiratory substrates. Plotting the calculated ΔG’_ATP against the corresponding JO₂ reveals a linear force-flow relationship, the slope of which represents the conductance/elasticity of the entire respiratory system under specified substrate constraints.

Importantly, the foregoing working model of respiratory conductance assumes that the ATP synthetic complexes (ATP synthase (CV) and the adenine nucleotide translocase; ANT) are the sole resistors through which the proton current flows (Glancy et al., 2013), which also implies that buffer components other than carbon substrates do not impact JO₂ in a CV-independent manner. Contrary to this assumption, preliminary experiments revealed that the presence of Na⁺ ions (supplied via NaCl) resulted in a ~25% increase in maximal ADP-stimulated JO₂ in skeletal muscle mitochondria (Figures S1A and S1B). Given that this increase in JO₂ was not met by a comparable increase in maximal JATP synthesis (Figure S1C), it was hypothesized that the presence of Na⁺ ions activated a futile pathway of oxygen consumption. The most commonly available commercial sources of phosphocreatine and ATP are di-sodium salts. We further hypothesized that the use of these salts in the assessment of mitochondrial respiratory conductance might violate the critical assumption detailed above, thereby precluding accurate determination of OXPHOS conductance. To test this hypothesis, force-flow experiments were performed in isolated mitochondria from both skeletal muscle and heart mitochondria, energized with G/M (Figure S1D) and Oct/M (Figure S1E), respectively. For these experiments, the CK clamp was established using ATP and phosphocreatine supplied as either di-sodium or di-tris salts. Once again, absolute rates of JO₂ were higher in the presence of sodium compared to tris salts (Figures S1D and S1E); however, the slopes of the relationship between JO₂ and ΔG_ATP were greater in the presence of tris compared to sodium-salts in both tissues (Figure S1F). These findings strongly suggest that the heightened JO₂ observed in the presence of Na⁺ ions does not contribute to ATP synthesis.

With respect to the source of the increase in JO₂ in the presence of Na⁺, the mechanism likely arises from the activation of Ca²⁺/3Na⁺ exchange at the inner mitochondrial, which along with concurrent Na⁺/H⁺ exchange promotes matrix Ca²⁺ depletion in a process driven by the Δp (Territo et al., 2001). Activation of this cycling pathway would increase respiratory flux without providing any additional ATP flux and as such could explain the lower respiratory conductance observed in the presence of Na⁺ salts. Additionally, the impact of matrix calcium depletion must also be considered. Although most well-known for its role in activating several matrix dehydrogenases (PDH, AKDH and IDH) (McCormack and Denton, 1980), free calcium in the matrix has recently been demonstrated to enhance electron conductance within the ETS and promote the increased activity of the ATP synthase complex (Glancy et al., 2013). Thus, impairments in ETS efficiency and ATP synthase capacity could also account for the lower respiratory conductance observed in the presence Na⁺ compared to Tris-salts. In addition, Na⁺-dependent oxygen flux could arise secondary to the use of trypsin/EDTA in the mitochondrial preparation, as removal of Mg²⁺ can impact membrane integrity [2] and proteolysis of the mitochondrial calcium uniporter has recently been shown induce leak conductance [3,4]. To directly test this, phosphocreatine titration experiments employing either Na⁺ or Tris⁺ salts were repeated in isolated mitochondrial prepared from heart tissues without the use of trypsin or EDTA. Similar to that seen in the previous experiments (Figures S1D–S1F), the presence of Na⁺ increased absolute JO₂ at each ATP free energy and tended to lower respiratory conductance compared to the use of Tris⁺ salts (Figures S1G and S1H). Regardless of the mechanism and in order to satisfy the critical assumption of the CK energetic clamp detailed above, sodium-salts were avoided for all experiments.

Assay Rationale

Traditional respirometry involves the assessment of mitochondrial JO₂ capacity via the addition of ADP, either in bolus amounts (e.g., no ADP “state 4” versus 5mM ADP “state 3”) or in submaximal clamped titrations (e.g., hexokinase ADP clamp technique). In either case, respiratory flux is stimulated exclusively via ADP. Such conditions differ dramatically from those present in vivo whereby mitochondrial flux rates respond to alterations in the free energy of ATP hydrolysis (ΔG’_ATP), which itself exists as the “back-pressure” in living systems preventing unabated metabolic flux. A total collapse in ΔG’_ATP (i.e., excess amounts of ADP) would eliminate the ability of ATP to carry out cellular work and as such would exist only in non-living systems. The creatine kinase clamp technique bypasses the need for bolus ADP to stimulate respiration and in turn does so via manipulation of the extra-mitochondrial ATP/ADP ratio and, thus, free energy of ATP hydrolysis. This system better mimics physiologic constraints and allows for an estimation of respiratory conductance/elasticity throughout the OXPHOS system based on a linear force:flow relationship (e.g., Ohm’s Law; I = V/R). In this equation, current (i.e., flow; I) is respiratory flux, net driving force (V) is the difference between two free energies (i.e., DG’_ATP) and conductance is the reciprocal of resistance (R). By plotting mitochondrial JO₂ against the ΔG’_ATP the resulting slope represents the conductance and/or elasticity of the respiratory system under defined substrate conditions. A change in respiratory conductance implies that resistance has either been increased (depressed slope) or decreased (increased slope) at some point or points within the OXPHOS system. The general source of resistance can then be interrogated by measuring the mitochondrial membrane potential and NAD(P)H/NAD(P)+ redox state under identical conditions. For example, a decrease in respiratory conductance (i.e., depressed slope) in the presence of no change or hyperpolarization of the mitochondrial membrane potential suggests that the source of resistance driving the change in respiratory conductance likely exists within the ATP synthesis step. Likewise, a decrease in respiratory conductance (i.e., depressed slope) in the presence of a depolarized mitochondrial membrane potential suggests that the source of resistance lies within the proton pumps of the electron transport system (e.g., CI, CIII, CIV) and/or the dehydrogenase enzymes responsible for generating the reducing charge. In the latter scenario, the contribution of the dehydrogenases can be accounted for by assessing the NAD(P)H/NAD(P)+ redox state (no change or hyper-reduction suggest the proton pumps are the source of resistance, whereas an oxidation of the redox state suggests the dehydrogenase are impaired). In essence, by assessing mitochondrial JO₂, membrane potential (Δ ) and NAD(P)H/NAD(P)+ redox state in parallel under defined energetic demands, it becomes possible to determine global alterations in OXPHOS conductance/elasticity and subsequently assign the location of the source of altered conductance into one of three control nodes [e.g., 1) Matrix Dehydrogenases, 2) Electron Transport System and 3) ATP synthesis].

Mitochondrial membrane potential (Δ ) and NAD(P)H/NAD(P)⁺ Redox

Fluorescent determination of Δ and NAD(P)H/NAD(P)⁺ were carried out simultaneously via a QuantaMaster Spectrofluorometer (QM-400; Horiba Scientific). Determination of Δ via TMRM was done as described previously (Scaduto and Grotyohann, 1999), taking the fluorescence ratio of the following excitation/emission parameters [Ex/Em, (572/590)/(551/590)]. The concentration of TMRM employed in our assays did not affect respiratory conductance (Figure S2A). Consistent with previous reports (Scaduto and Grotyohann, 1999), TMRM uptake into energized mitochondria resulted in fluorescent quenching and shifts in the excitation and emission spectra (Figure S2B). Comparing the excitation spectra obtained in the presence and absence of FCCP, a respiratory uncoupler that depolarizes ΔΨ, revealed maximal differences at wavelengths of 551 and 572 nm (Figure S2C). These values were subsequently utilized as parallel excitation wavelengths, with emission recorded at 590 nm. Figure S1D depicts changes in TMRM emission intensities, following excitation at both 551 and 572 nm during a typical CK clamp assay. In this experiment, de-energized heart mitochondria were assessed in the presence of minimal ATP free energy (13.6 kcals/mol), followed by the addition of respiratory substrates (Oct/M). Once mitochondria were energized with Oct/M, mitochondrial Δ became hyperpolarized (i.e., more negative), reflected by a decrease in TMRM emission intensity after excitation at 551 nm. Sequential increases in ATP free energy via PCr additions further polarized the ΔΨ, which was then depolarized at the completion of the experiment via addition of the complex IV inhibitor, cyanide. Plotting the ratio of the emission intensities recorded following excitation at both 551 and 572 nm increased the magnitude of changes in TMRM fluorescence above a single excitation/emission protocol (i.e., using 551/590 or 572/590 and was thus utilized for all experiments moving forward (Figure S2E). The 572/551 ratio was then converted to millivolts via a KCl standard curve performed in the presence of valinomycin as described by (Krumschnabel et al., 2014). In this protocol, isolated mitochondria energized with Succ/Rot were incubated in a potassium-free buffer in the presence of valinomycin, a potassiumspecific ionophore. Assuming a matrix potassium concentration of 120 mM, Δ can be reasonably estimated by applying the Nernst equation and buffer ion concentrations resulting from sequential additions of KCl (Krumschnabel et al., 2014). Figure S2F depicts the 572/551 ratio over time as Δ was varied from ~155mV to ~102mV via increasing concentrations of KCl. This protocol allowed for an approximation of Δ via the generation of a calibration curve in which the 572/551 ratio was plotted against the calculated ΔΨ at each titration step (Figure S2G). While the KCl titration experiments in the presence of valinomycin allow for mitochondrial Δ quantification, it should be noted that the resulting absolute voltages should be regarded as approximations. Such calculations are of course only as accurate as the inherent assumptions, which for TMRM based ΔΨ -quantification include: 1) equal mitochondrial protein content between groups and 2) a matrix potassium concentration of 120mM. To validate this approach, TMRM-based ΔΨ -quantification was compared against parallel assessment of Δ using a tetraphenylphosphonium (TPP⁺) selective electrode performed with isolated skeletal muscle mitochondria energized with Pyr/M (Figures S2H–S2J). Although the two methods resulted in slight differences in absolute mV calculations (Figure S2I), the change in voltage across the assays were identical (~10 mVs; Figure S2J).

NAD(P)H excitation/emission parameters were 340/450. All experiments were carried out at 37°C in a 0.2ml reaction volume. Buffer for all assays was Buffer D, supplemented with creatine (Cr; 5mM), phosphocreatine (PCr; 1mM), creatine kinase (CK; 20U/ml) and TMRM (0.2 μM). To begin, isolated mitochondria (0.1mg/ml) were added to the assay buffer, followed by the addition of respiratory substrates (Oct/M, G/M, Pyr/M, Succ/R), ATP (5mM), and then sequential PCr additions to a final of 3, 6, 9,12, 15, 18, 21, 24, 30mM. Following the final PCr addition, cyanide (4mM) was added to induce a state of 100% reduction within the NAD(P)H/NAD(P)⁺ couple. The fluorescence (Ex/Em, 340/450) signal recorded in the presence of mitochondria alone without respiratory substrates was used as the 0% reduction state for the NAD(P)H/NAD(P)⁺ couple. NAD(P)H/NAD(P)⁺ during the entire experiment was expressed as a percentage reduction according to the following formula: % Reduction = (F-F_0%)/(F_100%-F_0%)*100.

Assay Rationale

In this assay, mitochondrial membrane potential is assessed using the cationic fluorophore TMRM. The positive charge carried by TMRM allows it to equilibrate with the negative membrane potential generated across the inner mitochondrial membrane in energized mitochondria according to the Nernst equation. Accumulation of TMRM within energized mitochondria results in fluorescence quenching, as well as spectral shift of ~20nM. This spectral shift is utilized to approximate mitochondrial membrane potential. Specifically, TMRM is excited at both 572nM and 551nM (emission settings are 590nM) and the ratio of 572:590/551:590 is then converted to a mV value using a standard curve assay protocol (see below). The use of the 572:590/551:590 ratio increases the dynamic range of the assay and allows for more accurate quantification/comparison between experiments. The standard curve protocol involves measuring the TMRM fluorescence ratio under defined membrane potentials. Membrane potential is determined by incubating isolated mitochondria in a buffer devoid of potassium and then subsequently titrating in KCl in the presence of valinomycin (40ng/ml), which is a highly selective ionophore specific for potassium. The matrix potassium concentration for these assays is assumed to be 120mM. Since valinomycin allows for any added KCl in the buffer to equilibrate with the matrix potassium, a membrane potential (expressed in mV) can be reasonably calculated according to the Nernst equation (mV = (RT/zF*ln[K⁺_buffer]/[K⁺_matrix]). As mentioned, the mitochondrial isolation buffer for these standard curve assays contains no potassium (250mM Sucrose, 20mM HEPES, 0.5mM EGTA, pH = 7.2). The assay buffer also contains no potassium (250mM sucrose, 10mM HEPES, 0.2mM EGTA, 2mM NaH2PO4, 1mM MgCl2, 10mM Na-succinate, pH = 7.1). The decision to use TMRM as our experimental tool for assessing Δ was chosen based on its ability to be easily incorporated into multiplexed platforms and its relative ease of use for non-mitochondrial scientists with respect to a TPP⁺ electrode. Although determination of ΔΨ with TPP⁺ in conjunction with a TPP-selective electrode provides for highly accurate ΔΨ quantification, the temporal restriction imposed by the necessary probe cleaning and calibration procedures required before, as well as between each experimental run limits its amenability to high throughput platforms.

Mitochondrial membrane potential (Δ ) using a TPP⁺ selective electrode

Membrane potential was measured using the OROBOROS Oxygraph-2k (Oroboros Instruments) combined with electrodes sensitive to TPP⁺ and oxygen at 37°C in a 2 mL volume, as previously described (Gilliam et al., 2013). All experiments were run in Buffer D containing 20U/ml CK, 5 mM creatine, 5mM Na-ATP, 1mM Na-phosphocreatine, 5mM Na-pyruvate, 2.5mM malate and 1.1 μM TPP⁺. During the protocol the TPP⁺ electrode was calibrated by a 6-point titration (1.1–1.35 μM TPP⁺) for quantifying the concentration of TPP⁺. Isolated skeletal muscle mitochondria (0.075mg/ml) were added and ρG_ATP was manipulated by Na-phosphocreatine titration from a starting concentration of 1mM to 6, 9 and 15mM. The calculation of Δ is based on the Nernst equation with internal/ external binding correction factors and estimates of mitochondrial volume. The Oroboros TPP⁺-Δ calculation template (http://wiki. oroboros.at/index.php/OROBOROS_INSTRUMENTS) was used with the following equation:

$$\Delta \psi =\frac{RT}{zF}\cdot \ln \left(\frac{\frac{n_{add}}{C_{ext,free}}-V_{ext}-K_o^{\prime }\cdot P_{mt}}{V_{mt}(spec)\cdot P_{mt}+K_i^{\prime }\cdot P_{mt}}\right)$$

Variables and constants of the equation include: n_add = total amount of ions added to the system; c_ext,free = free concentration of TPP⁺ outside mitochondria; V_ext = volume of the external solution outside mitochondria; V_mt = volume of the mitochondrial matrix (1 μl/mg) (Labajova et al., 2006); K_i’ = internal partition coefficient of TPP⁺(11 μl/mg) (Labajova et al., 2006); K_o’ = external partition coefficient of TPP⁺(11 μl/mg) (Labajova et al., 2006); P_mt = total mitochondria protein.

Low-Dose Inhibitor Experiments

In an effort to test the ability of the respiratory conductance assay workflow to localize the source of respiratory resistance to each of the 3 control nodes listed previously, experiments were conducted using sub-maximal concentrations of the respiratory inhibitors rotenone (9nM), oligomycin (15nM) and UK5099 (100nM). These inhibitors impact Complex I, Complex V and the pyruvate carrier specifically and thus should localize resistance to the following control nodes: 1) Substrate delivery and dehydrogenase activity (UK5099), 2) Electron transport (Rotenone) and 3) ATP synthesis (Oligomycin). Concentrations of each drug were selected following pilot experiments designed to identify the concentrations required to induce a submaximal drop in respiratory conductance. Slight modifications to the protocol detailed above were required in order to account for the fact that the impact of each drug on respiratory conductance was found to be highly dependent on the mitochondrial concentration.

UK5099

Reaction master mixes of 2.5ml of Buffer D, supplemented with 5mM creatine, 5mM ATP, 6mM PCr and 20U/ml CK were prepared. TMRM (0.2 μM), mitochondria (0.1mg/ml) and UK5099 or DMSO were then added to these master mixes and subsequently added to respective chambers of the O2K. After an initial ~5 minute temperature equilibration period, 200 μL was removed from each chamber and placed in 0.5ml cuvette. Chamber stoppers were then added to the O2K and respiration was assessed as described above. Cuvettes were placed inside the QuantaMaster Spectrofluorometer (Horiba Scientific) and Δ and NAD(P)H/NAD(P)⁺ redox assessments were carried out as detailed above. Additions during the assay were Pyr/Mal (1mM/2.5mM), 3mM PCR (total = 9mM) and 6mM PCR (total = 15mM), followed by CN (4mM). UK5099 was made up in DMSO as a 160μM stock.

Rotenone/Oligomycin

Reaction master mixes of 2.5ml of Buffer D, supplemented with 5mM creatine, 5mM ATP, 6mM PCr and 20U/ml CK were prepared. TMRM (0.2uM), mitochondria (0.1mg/ml) and Rotenone (9nM), Oligomycin (15nM) or DMSO were then added to these master mixes and subsequently added to respective chambers of the O2K. After an initial ~5 minute temperature equilibration period, 200uL was removed from each chamber and placed in a cuvette. Chamber stoppers were then added to the O2K and respiration was assessed as described above. Cuvettes were placed inside the QuantaMaster Spectrofluorometer (Horiba Scientific) and Δ and NAD(P)H/ NAD(P)⁺ redox assessments were carried out as detailed above. Additions during the assay were Oct/M (0.2mM/2.5mM), 3mM PCR (total = 9mM) and 6mM PCR (total = 15mM), followed by CN (4mM). Rotenone and oligomycin were prepared in DMSO as 30mM stocks.

Mitochondrial JH₂O₂ Emission

Mitochondrial H₂O₂ emission was measured fluorometrically via the Amplex Ultra Red (AUR)/horseradish peroxidase (HRP) detection system (Ex:Em 565:600) as described previously (Fisher-Wellman et al., 2013a), with slight modifications. Fluorescence was monitored via a QuantaMaster Spectrofluorometer (Horiba Scientific). For each experiment, resorufin fluorescence was converted to pmoles H₂O₂ via an H₂O₂ standard curve generated under identical substrate conditions as employed for each protocol. All experiments were carried out at 37°C in a 0.2ml reaction volume. Buffer for all assays was Buffer D, supplemented with creatine (Cr; 5mM), phosphocreatine (PCr; 1mM), creatine kinase (CK; 20U/ml), AUR (10 μM), HRP (1U/ml) and superoxide dismutase (20U/ml). To begin, isolated mitochondria (0.1mg/ml) were added to assay buffer, followed by the addition of respiratory substrates (Oct/M, G/M, Pyr/M), auranofin (0.1 μM), ATP (5mM), and then sequential PCr additions to a final of 6, and 15mM. The percentage of electron leak is calculated by dividing the rate of H₂O₂ production by the corresponding O₂ consumption rate measured under identical conditions and expressed as a percentage (% Leak = JH₂O₂/JO₂*100). Of note, the JH₂O₂ rates used in the calculation were generated in the presence of auranofin; however, the corresponding JO₂ assays did not contain auranofin, as the inhibitor was found to not impact respiratory conductance.

Assay Rationale

During the process of OXPHOS, a small percentage of electrons are prematurely leaked to O₂, thus yielding the superoxide radical (O₂-,•). The majority of superoxide produced is rapidly converted to H₂O₂ via superoxide dismutase (SOD) located in the matrix (mg-SOD) or inner-mitochondrial membrane (Cu/Zn-SOD). This assay measures the rate of H₂O₂ appearance in the buffer as it diffuses from the point of origin within the electron transport system and/or matrix across the mitochondrial membranes. Amplex Ultra Red reacts with the H₂O₂ in the presence of horse radish peroxidase to generate the fluorescence compound resorufin. Excess SOD is included in the assay buffer to ensure that any superoxide diffusing from the mitochondria is rapidly converted to H₂O₂. A portion of the H₂O₂ generated within the matrix is buffered by the endogenous antioxidant buffering networks (e.g., thioredoxin reductase system, glutathione reductase system), thus in the absence of any inhibitors of these buffering systems, the measured rate of H₂O₂ emission represents the net H₂O₂ (H₂O₂ produced – H₂O₂ buffered = H₂O₂ emitted). The principle buffering system in skeletal muscle and heart mitochondria is the thioredoxin system (Fisher-Wellman et al., 2015), thus inclusion of the thioredoxin reductase inhibitor auranofin in the assay provides a more accurate approximation of the total H₂O₂ produced under any respiratory substrate condition. A variety of chemicals can interfere with resorufin fluorescence and thus H₂O₂ standard curves must be run under all specified substrate/inhibitor conditions in order to achieve accurate quantitation of H₂O₂.

JATP Synthesis

Rates of ATP synthesis were determined as described previously (Lark et al., 2016) with slight modifications. Buffer for the assay was Buffer D, supplemented with glucose (5mM), hexokinase (1U/ml), glucose-6-phosphate dehydrogenase (G6PDH; 2U/ml), NADP⁺ (2mM) and ADP (0.2mM). Assay buffer (200 μL) was loaded into individual wells of a 96-well plate, followed by isolated mitochondria (2 μg/well). The assay was initiated with the addition of respiratory substrates following a ~5 minute pre-incubation at 37°C in the absence of substrates to deplete endogenous metabolites. In the assay, NADPH and ATP are produced in a 1:1 stoichiometry and thus JATP was determined via monitoring the NADPH auto-fluorescence (Ex:Em 340/450) signal. Fluorescence values were converted to pmoles of ATP via an ATP standard curve. The following substrate conditions were tested in parallel for each assay [Oct/M; 0.2/2.5mM, G/M; 10/2.5mM, Pyr/M; 5/2.5mM, Succ/R; 10/0.005mM]. Pilot experiments were performed to assess ATP production from the other known mitochondrial ATP generating enzyme adenylate kinase (mAK). These assays were performed in the presence and absence of the mAK inhibitor P1,P5-Di(adenosine-5^ʹ)pentaphosphate (AP5A; 0.2mM) (Kurebayashi et al., 1980). Under the assay conditions utilized herein, AP5A was found to exert no impact on mitochondrial JATP and thus was excluded (Figures S5B and S5C).

Assay Rationale

In this assay, the rate of mitochondrial ATP synthesis (JATP) is assessed via tracking the fluorescence signal generated by NADPH as it is produced via G6PDH. In short, upon addition of ADP to energized mitochondria (i.e., mitochondria with saturating carbon substrates), this ADP is converted to ATP via ATP synthase and then exported back into the buffer via the adenine nucleotide translocase (ANT). Once in the buffer, the newly synthesized ATP is converted back to ADP via hexokinase (glucose + ATP > glucose-6-phosphate + ADP). Through an enzyme-coupled mechanism, the G6P along with NADP⁺ (present in the buffer) is then converted to 6-phospho-D-glucono-1,5-lactone and NADPH via G6PDH. In this assay system, ATP and NAPDH are produced at 1:1 stoichiometry, thus the rate of NADPH generation serves as a measure of mitochondrial ATP synthesis.

JNADH and JNADPH Production

Rates of NADH and NADPH production were determined as described previously (Fisher-Wellman et al., 2013a) with slight modifications. Buffer for the assays was Buffer D, supplemented with alamethicin (0.03mg/ml), rotenone (0.005mM) and NAD⁺ (2mM) or NADP⁺ (2mM). For experiments designed to assess JNADH from the pyruvate dehydrogenase complex (PDH), the alpha-ketoglutarate dehydrogenase complex (AKGDH) and the branched-chain keto-acid dehydrogenase complex (BCKDH) the followed cofactors were included in the assay: coenzyme A (0.1mM) and thiamine pyrophosphate (0.3mM). Rates of NADPH production from glutamate dehydrogenase (GDH) were determined in the absence and presence of ADP (5mM). Assay buffer (200 μL) was loaded into individual wells of a 96-well plate, followed by isolated mitochondria (2–60 μg/well). The assay was initiated with the addition of enzymatic substrates. In the assay, NADH and NADPH were determined via auto-fluorescence (Ex:Em 340/450). Fluorescence values were converted to pmoles of NADH or NADPH via an NADH/NADPH standard curve. The following substrates were tested in parallel for each assay [pyruvate (5mM), alpha ketoglutarate (10mM), α-keto-β-methylvalerate (5mM), glutamate (10mM), malate (5mM), isocitrate (5mM)].

Assay Rationale

In this assay, the activity of soluble matrix dehydrogenase enzymes are assessed in isolated mitochondria following chemical permeabilization of the inner mitochondrial membrane with the pore-forming peptide alamethicin. Permeabilization with alamethicin is required to allow for specific enzyme cofactors (e.g., CoA, thiamine pyrophosphate, NAD⁺, NADP⁺) to traverse the mitochondrial inner-membrane and activate matrix dehydrogenases. Once inside the matrix, NAD⁺ and NADP⁺ are converted to NADH and NADPH, which then diffuse back out into the buffer and are measured via fluorescence. The rate of NADH/NADPH appearance in the buffer indicates dehydrogenase activity. Specific dehydrogenases are targeted via the addition of specific carbon substrates and cofactors (e.g., pyruvate along with CoA, thiamine pyrophosphate and NAD⁺ activates the pyruvate dehydrogenase complex while malate along with NADP⁺ activates malic enzyme).

CV Activity Assay

CV activity was assessed as described previously (Barrientos et al., 2009) with slight modifications. Mitochondrial lysates for the assay were prepared via dilution of the final isolated mitochondrial suspensions in CelLytic M (Sigma-Aldrich; C2978) at a protein concentration of 2mg/ml. Buffer for the assay was Buffer E, supplemented with lactate dehydrogenase/pyruvate kinase (10U/ml), phosphoenoyl-pyruvate (5mM), rotenone (0.005mM) and NADH (0.2mM). Assay buffer (200 μL) was loaded into individual wells of a 96-well plate, followed by mitochondrial lysate (2 μg/well). Assays were done in the absence and presence of oligomycin (0.005mM) in order to calculate the oligomycin-sensitive rates of ATP hydrolysis. The assay was initiated with the addition of ATP (5mM). In the assay, NADH oxidation and ATP hydrolysis occur at a 1:1 stoichiometry and thus CV activity (pmoles of ATP/sec/mg) was determined via tracking the degradation in the NADH auto-fluorescence (Ex:Em 376/450) signal upon ATP addition. Fluorescence values were converted to pmoles of NADH via an NADH standard curve.

Assay Rationale

In this assay, the activity of mitochondrial ATP synthase is assessed in the forward direction (i.e., ATP hydrolysis) via an enzymecoupled mechanism. To begin, isolated mitochondria are first solubilized in a non-denaturing, low-percentage detergent buffer (CelLytic M), which serves to liberate intact ATP synthase from the inner mitochondrial membrane. Alamethicin-permeabilized mitochondria can also be used for this assay, but in our hands the dynamic range of the assay is improved upon the use of CelLytic M. This likely stems from the greater stability of NADH at alkaline pH (e.g., pH = 8.0), compared to the pH of the alamethicin-permeabilization buffer (pH = 7.1). Upon addition of ATP, ATP synthase hydrolyzes the ATP to ADP, which is then converted back to ATP via pyruvate kinase (ADP + phosphoenoyl-pyruvate > ATP + pyruvate). The pyruvate is then converted to lactate in the presence of NADH (present in the buffer at 0.2mM), thus generating NAD⁺. ATP hydrolysis and NADH oxidation occur at 1:1 stoichiometry, thus the rate of disappearance of NADH (assessed via fluorescence) serves as an indicator of ATP synthase activity. To control for ATP hydrolysis by enzyme systems other than ATP synthase, the assay is performed in the absence and presence of ATP synthase inhibitor oligomycin. The rate of NADH disappearance measured in the presence of oligomycin is subtracted from the rate of NADH disappearance measured in the absence of the inhibitor and thus the final rate represents ATP synthase-dependent activity only.

Hydroxyacyl-CoA Dehydrogenase Activity

Mitochondrial lysates for the assay were prepared via dilution of the final isolated mitochondrial suspensions in CelLytic M at a protein concentration of 2mg/ml. Buffer for the assay was Buffer E, supplemented with rotenone (0.005mM) and NADH (0.2mM). Assay buffer (200 μL) was loaded into individual wells of a 96-well plate, followed by mitochondrial lysate (5 mg/well). The assay was initiated with the addition of acetoacetyl-CoA (0.2mM). The activity of hydroxyacyl-CoA dehydrogenase was determined via tracking the degradation in the NADH auto-fluorescence (Ex:Em 340/450) signal upon acetoacetyl-CoA addition. Fluorescence values were converted to pmoles of NADH via an NADH standard curve.

Assay Rationale

Hydroxyacyl-CoA dehydrogenase (Hadha) is the primary NAD⁺-linked dehydrogenase within the beta-oxidation pathway. In this assay, the activity of Hadha is assessed in the reverse direction by tracking the rate of NADH disappearance upon oxidation of acetoacetyl-CoA. To begin, isolated mitochondria are first solubilized in a non-denaturing, low-percentage detergent buffer (CelLytic M), which serves to solubilize the mitochondria outer and inner membrane and allow access to Hadha. Alamethicin-permeabilized mitochondria can also be used for this assay, but in our hands the dynamic range of the assay is improved upon the use of CelLytic M.

GOT2 Activity

Mitochondrial lysates for the assay were prepared via dilution of the final isolated mitochondrial suspensions in CelLytic M at a protein concentration of 2mg/ml. Buffer for the assay was Buffer E, supplemented with aspartate (200mM), pyridoxal 5^ʹ-phosphate (0.1mM), malate dehydrogenase (2U/ml), rotenone (0.005mM) and NADH (0.2mM). Assay buffer (200 μL) was loaded into individual wells of a 96-well plate, followed by mitochondrial lysate (10 μg/well). The assay was initiated with the addition of AKG (12mM). The activity of GOT2 was determined via tracking the degradation in the NADH auto-fluorescence (Ex:Em 340/450) signal upon AKG addition (Siest et al., 1975). Fluorescence values were converted to pmoles of NADH via an NADH standard curve.

Assay Rationale

GOT2 catalyzes a transamination reaction whereby aspartate and AKG are converted to glutamate and oxaloacetate. In this assay, GOT2 present in the mitochondrial lysate generates glutamate and oxaloacetate from aspartate and AKG present in the buffer. Excess malate dehydrogenase also present in the assay buffer converts the oxaloacetate into malate at the expense of NADH oxidation.

Proton Leak Kinetics

Mitochondrial proton leak was assessed in Buffer D, supplemented with oligomycin (0.005mM) and TMRM (0.2 μM). Reaction master mixes of 2.5ml of the experimental buffer were prepared which contained mitochondria (0.1mg/ml) and added to respective chambers of the O2K. After an initial ~5 minute temperature equilibration period, 200 μL was removed from each chamber and placed in 0.5ml cuvette. Chamber stoppers were then added to the O2K and respiration was assessed. Cuvettes were placed inside the QuantaMaster Spectrofluorometer (Horiba Scientific) and Δ assessments were carried out as detailed above. Additions during the assay were Pyr/M (1mM/2.5mM) and sequential additions of UK5099 (2, 4, 6, 8 μM).

Assay Rationale

The assay allows for proton leak (i.e., respiration in the presence of the ATP synthase inhibitor oligomycin) and ΔΨ to be assessed over time as leak rates are sequentially aΔΨ usted by the pyruvate carrier inhibitor, similar to that described previously for Succ/R substrate conditions (Affourtit et al., 2012). Plotting JO₂ against Δ during the assay allows for the determination of maximal proton leak (i.e., JO₂ in the absence of UK5099), as well as the leak rates at the highest common membrane potential. Because proton leak is determined primarily by ΔΨ, the latter measurement normalizes proton leak to ΔΨ and as such allows for a direct comparison of proton leak potential (Divakaruni and Brand, 2011).

Free Magnesium Quantification

Fluorescent determination of free magnesium concentration was performed in a QuantaMaster Spectrofluorometer (Horiba Scientific). The assay buffer was Buffer D, supplemented with creatine (Cr; 5mM), phosphocreatine (PCr; 1μM), creatine kinase (CK; 20U/ml), and 1mM Magnesium Green (ThermoFisher Scientific M3733). The fluorescent signal (Ex:Em 475:530 nm) was converted to free magnesium concentration by the following equation:

$$\left[M{g}^{2+}\right]=K_d\frac{F-F_{min}}{F_{max}-F}-0.055mM$$

where F_min and F_max represent the signal with saturating concentrations of EDTA or MgCl₂, respectively. The dissociation constant, K_d, is 1mM (Chinopoulos et al., 2009). This measurement was performed following the addition of ATP (5 mM) and sequential PCr additions to a final concentration of 3, 6, 9,12, 15, 18, 21, 24, 30mM. The concentrations of free magnesium were used in calculating the ΔG’_ATP over the CK clamp.

Experimental Logistics and Practical Considerations

Although the current data were generated using mitochondria derived from mouse muscle and cardiac tissues, the entire suite of assays should be easily adaptable for studies using other tissues that are enriched in mitochondria, such as brain, liver and brown adipose tissue. For tissues with lower mitochondrial content (e.g., white adipose tissue, smooth muscle, pancreas, ext.), pooling of several rodents might be necessary in order to acquire sufficient material for the entire collection of assays. Assuming the incorporation of 4 unique substrate combinations, the minimum mitochondrial requirements to perform the entire battery of assays in the screening platform is 0.44mgs (O2K experiments ~0.05mg/substrate condition; ΔΨ /NAD(P)H/NAD(P)⁺ experiments ~0.02mg/substrate condition; Electron Leak experiments ~0.02mg/substrate condition; JATP synthesis ~0.005mg/substrate conditions; Enzyme activity assays ~0.005mg/assay).

Moreover, we believe the platform can also be adapted for application to permeabilized cell systems. Efforts to optimize the platform for new applications must consider several critical factors, including: a) tissue and cell type-specific differences in matrix dehydrogenase profiles, b) prioritization of substrate conditions when mitochondrial yield is limiting, and c) purity of tissue-specific mitochondrial isolations and potential need for sucrose- or Percoll-based purification protocols (Glancy and Balaban, 2011; Graham, 2001). To this point, it is noteworthy that the simple isolation protocol (without a sucrose-based buffer) used in the current work was sufficient to produce fractions with similar amounts of mitochondrial protein between tissues (Figures S4A and S4B). However, additional mitochondrial purification may be required for tissue types in which cytosolic, ER and/or lipid contamination within the mitochondrial fraction is more problematic. These considerations could become more important in studies where proteomics analyses are desired (Glancy and Balaban, 2011). Finally, the substrate conditions employed herein were selected to cover the primary metabolic pathways operating in muscle mitochondria, as evidenced by the dehydrogenase profiles of the tissues. That said, mitochondria from different tissues possess distinct dehydrogenase profiles, thus initial pilot studies may be required in order to determine the most relevant substrate combinations for assessing any specific mitochondrial population.

QUANTIFICATION AND STATISTICAL ANALYSIS

Data are presented as mean ± SEM. Differences between groups were analyzed by Student’s t tests or among groups using one-way ANOVA with Tukey’s multiple comparison tests. The level of significance was set at p < 0.05. Figures were generated using GraphPad Prism (Version 7.0). Statistical details of each experiment are located in the figure legends. Unless otherwise stated, the number of mice per experiment is represented by “N.”

ADDITIONAL RESOURCES

Ionic strength, pH, free magnesium, temperature, and pressure affect the apparent equilibrium constants of biochemical reactions. At each step of the CK clamp, ionic strength and free magnesium are altered. Therefore, accurate bioenergetic quantification requires the creatine kinase and ATP hydrolysis equilibrium constants be adjusted (Golding et al., 1995; Teague et al., 1996). Implementing this calculation proved tedious and prompted the development of a simplified web resource. First, a Jupyter notebook containing the aΔΨ ustment calculations interspersed with procedural descriptions is provided. The calculations are rendered in the Python programming language and intended to serve as an instructional overview. The second component is a web-based calculator that performs the bioenergetic aΔΨ ustments for user-specified conditions. The source code for this calculator is publicly available from the resource link.

Highlights.

• Bridging the gap between molecular and functional mitochondrial phenomics

• An assay platform for diagnosing perturbations in mitochondrial energy transduction

• Use of the creatine kinase energetic clamp technique to model in vivo bioenergetics

• Insights into tissue-specific distinctions in energy transfer efficiency