Disentangling transcription factor binding site complexity

Abstract

The binding motifs of many transcription factors (TFs) comprise a higher degree of complexity than a single position weight matrix model permits. Additional complexity is typically taken into account either as intra-motif dependencies via more sophisticated probabilistic models or as heterogeneities via multiple weight matrices. However, both orthogonal approaches have limitations when learning from in vivo data where binding sites of other factors in close proximity can interfere with motif discovery for the protein of interest. In this work, we demonstrate how intra-motif complexity can, purely by analyzing the statistical properties of a given set of TF-binding sites, be distinguished from complexity arising from an intermix with motifs of co-binding TFs or other artifacts. In addition, we study the related question whether intra-motif complexity is represented more effectively by dependencies, heterogeneities or variants in between. Benchmarks demonstrate the effectiveness of both methods for their respective tasks and applications on motif discovery output from recent tools detect and correct many undesirable artifacts. These results further suggest that the prevalence of intra-motif dependencies may have been overestimated in previous studies on in vivo data and should thus be reassessed.

INTRODUCTION

The interaction between DNA and transcription factors (TFs) is one of the cornerstones of gene regulation. Binding of TFs to DNA can be either indirect, mediated by other TFs or it can be a direct contact of a TF to specific DNA elements called TF-binding sites (TFBS).

The standard model for describing the properties of binding sites for a particular TF, i.e. its sequence motif, is the position weight matrix (PWM) model (1,2), which allows an intuitive visualization as a sequence logo (3). While it has widely replaced earlier consensus-based approaches due to a higher flexibility in handling mismatches, its complete independence assumptions among nucleotides appear rather extreme, once one has chosen a probabilistic modeling approach.

The development of more complex alternatives has been a research topic in computational biology for decades (4–8). Progress in devising appropriate motif models and learning algorithms has been accompanied with a lively discussion concerning the prevalence of more complex features and their usefulness for TF-binding prediction (9–11).

The rise of high-throughput technologies for measuring protein–DNA interaction has spawned a renewed interest in that topic in recent years. Chromatin-immunoprecipitation followed by high-throughput sequencing (ChIP-seq) (12) allows a high-resolution quantification of the in vivo binding affinity of a TF to genomic regions, so the resulting data are of particular interest for learning accurate motif models. Multiple recent studies have shown that models that take into account intra-motif dependencies can be learned effectively within de novo motif discovery from ChIP-seq data and that they improve genome-wide prediction accuracy in relation to a PWM for many, albeit not all, TFs (13–19).

An orthogonal approach to model TFBS complexity assumes multiple PWM models (20–22). Here, intra-motif complexity is expressed as heterogeneities as opposed to dependencies, although both representations take into account similar features. For instance, the complexity of the CTCF sequence motif has been described by both intra-motif dependencies (23) and heterogeneities (20).

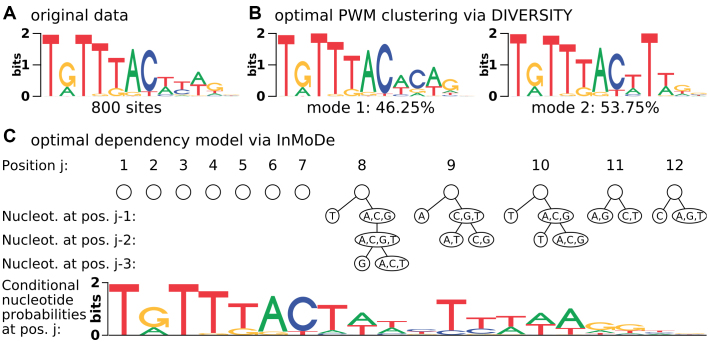
Figure 1 illustrates how intra-motif complexity can be explained from different points of view: once through a mixture of two PWMs learned by DIVERSITY (22), and once through a dependency model learned by InMoDe (24). Both tools employ a model selection step for finding either the optimal number of PWMs or the optimal dependency structure. However, to date there has been no attempt to perform a model selection across both representations, so it is yet unclear whether heterogeneities or dependencies are the more appropriate view on TFBS complexity.

Figure 1.

Intra-motif complexity can be explained by both heterogeneities and dependencies. (A) Sequence logo of Foxa2 from the JASPAR data base. (B) Two-component PWM mixture model learned by DIVERSITY from the underlying 800 binding sites. (C) Dependency model learned by InMoDe from the same data.

Irrespective of the chosen representation, reasons for observed intra-motif complexity can be manifold. For instance, DNA shape effects (25,26), optional contact of zinc fingers (27) or variable-length spacers (28) have been observed, and all can be associated with TFBS complexity beyond what can be represented with a single PWM.

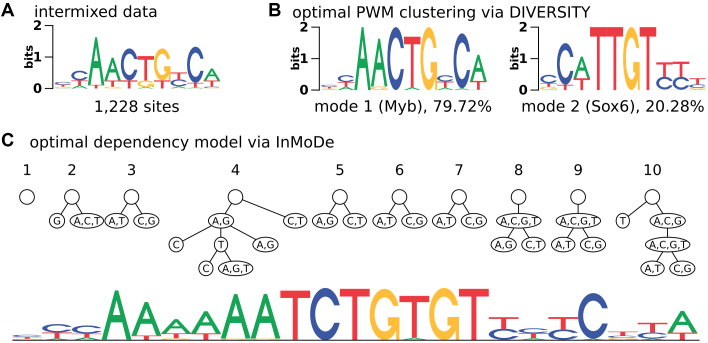
Another reason for complexity may arise when the data, a model is derived from, contain binding sites of multiple TFs. Figure 2 illustrates such a situation using a minimal example of artificially intermixed binding sites of Sox6 and Myb. The sequence logo of the intermixture (Figure 2A) is not overly informative, but learning a mixture model recovers the original sequence motifs (Figure 2B). However, a dependency model can also be used to describe this ‘inter-motif heterogeneity’ by modeling the two motifs through very different conditional probability distributions (Figure 2C).

Figure 2.

Complexity caused by intermixing binding sites from different TFs (inter-motif heterogeneity). (A) Sequence logo of data set with binding sites of Sox6 and Myb intermixed. (B) Original sequence motifs, seamlessly recovered by DIVERSITY. (C) Dependency model learned by InMoDe. Labels at y-axis are here omitted due to space constraints (see Figure 1C).

One possible source of intermixtures is ChIP-seq data, which contain not only binding sites of the TF of interest, but also enriched motifs of non-targeted TFs (29). Attempting to learn dependency models from ChIP-seq data via de novo motif discovery with the aim of inferring dependencies along the lines of Figure 1 can easily combine binding motifs of different TFs into one model (16,17). This effect is even more pronounced for TFs that do not bind directly to DNA (30), where ChIP-seq peaks may thus not contain a single dominating motif (31). Under these circumstances, dependency models may still perform well in e.g. genome-wide prediction of approximate binding locations (16,17), as they aggregate any over-represented or discriminating features of ChIP-seq-positive regions. But whether such models are an appropriate representation of the binding specificity of the TF(s) of interest remains questionable.

One might argue that for these reasons the view through heterogeneities is to be preferred, as PWMs that represent binding sites of different TFs are clearly separated. But since there is no semantic attached to the learned PWMs, it remains unclear whether they represent indeed co-occurring binding sites of different TFs or actually encode intra-motif heterogeneities. In the latter case, it is also unclear whether mixtures of PWMs are, in comparison to dependency models, an effective representation of intra-motif complexity.

We thus face a dilemma: on the one hand, learning a complex dependency model from in vivo data of TF–DNA interaction may erroneously combine sequence motifs of different TFs into one motif. On the other hand, by learning multiple PWMs we cannot distinguish intra-motif from inter-motif heterogeneity. In both cases, careful inspection and manual annotation of the discovered motifs are needed, which may be especially difficult when the found motifs are not known in the literature.

In this article, we study this problem of computationally disentangling TFBS complexity, not only concerning statistical efficiency, but also with respect to the underlying semantics. For this purpose, we propose the tool Disentangler, which consists of two methods that can be applied either independently or within a joint pipeline.

Intermixture detection (IMD) determines whether inter-motif heterogeneity (Figure 2) occurs in a given TFBS data set and clusters the binding sites accordingly. The key idea is to exploit the empirical observation that inter-motif heterogeneities are typically stronger than intra-motif heterogeneities for defining an intermixture measure that quantifies inter-motif heterogeneity.

Motif complexity analysis (MCA) determines whether intra-motif complexity (Figure 1) for a particular TF is modeled more effectively by heterogeneities, dependencies or a combination thereof. Here, the key idea is that dependency or heterogeneity can both model intra-motif complexity, but they may require a very different number of parameters to take into account the same features. We employ model selection principles for defining an intra-motif complexity measure that allows to choose a model optimally represents a data set, and to quantify differences to possible alternatives. Additionally, this measure can be used to quantify the strength of effectively representable intra-motif complexity and to compare different data sets accordingly.

In the case studies, we evaluate the effectiveness and limitations of both methods for their respective tasks based on benchmark data from JASPAR (26) and GTRD (32). For demonstrating practical use, we then apply recent de novo motif discovery tools (16,18,22,24) on ENCODE ChIP-seq data (33) and analyze the output in terms of predicted binding sites with Disentangler. We find that learning dependencies during motif discovery indeed overestimates intra-motif complexity, but also observe that the underlying reasons are more complex than the simple example in Figure 2 suggests. Different intermixture types can be identified and be explained by different biological and computational origins. We also find that the orthogonal approach of estimating an optimal number of PWM-based motifs from ChIP-seq data may underestimate intra-motif complexity.

MATERIALS AND METHODS

First, we summarize the models and learning algorithm that this work is based on and refer to Supplementary Section S1 for technical details. Afterward, we describe how these concepts are used in IMD and MCA, the two main components of Disentangler. Finally, we specify the data used in the case studies.

Models and learning

A TFBS data set D  consists of N sequences of fixed length L over the alphabet 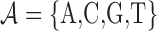. They are assumed to be pre-aligned in the same strand orientation without containing gaps or ambiguous nucleotides.

A mixture model allows the sequences in D  to be of different types, i.e to follow the distribution of one out of K component models. We model the missing knowledge which component each sequence is associated with as a latent variable vector 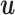of length N; each element assumes a value from 1 to K. Mixture models also include non-mixtures as a special case with K = 1. We consider three different types of mixture components, which substantially differ in their expressiveness and learning complexity.

First, we use the standard choice of a PWM model (1), where learning solely consists of estimating its position-specific marginal probability parameters.

Second, we take into account proximal dependency by an dth-order inhomogeneous Markov model, equipped with a Parsimonious Context Tree (PCT) (34) at each position. This model is the core of the InMoDe tools (24), examples are shown in Figures 1C and 2C. For this model, learning additionally requires selecting PCTs at each position based on the data for which we employ a sophisticated dynamic programming algorithm (35).

Third, we model distal dependency through a Bayesian network (36) with indegree limit d, equipped with a PCT for each conditional distribution, hereby assuming that parent variables are ordered according to their position in the sequence. This model generalizes variable-order Bayesian networks (7), which use traditional context trees (37) instead of PCTs. It is the most expressive but also computationally most demanding alternative. Learning additionally requires selecting the optimal network structure based on learned PCTs, for which we use Edmonds’ algorithm for d = 1 (38) and dynamic programming (39) otherwise.

Given a mixture model with up to K_max components of possible variable structure, we need to simultaneously learn both the optimal number of mixture components 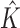and the optimal structures within each component. For this task, we use the factorized asymptotic Bayesian (FAB) inference (40), which assumes a variational distribution 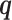over the latent variables 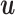so that structure and parameter learning becomes tractable given 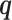. This algorithm starts with a random initialization and then iteratively updates the set of model parameters Θ and 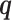. This approach is very similar to the expectation–maximization algorithm (41), which it contains as special case when all components have a fixed model structure. FAB inference monotonically increases the score

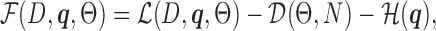(1)

which consists of three conceptually different terms. 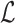is a weighted log-likelihood that measures the fit of the model to the data under latent variable distribution 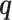. 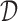is a penalty term for the number of model parameters in Θ in relation to the sample size N, with more parameters yielding a higher penalty. 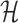is the entropy of 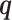and penalizes the flexibility arising from fitting the latent variables of the mixture model. In the special case of a K = 1, 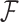reduces to the Bayesian Information Criterion score (42). Otherwise it is a lower bound to the Factorized Information Criterion (FIC), which is itself an approximation of the marginal likelihood of the entire mixture model (40). As such, it allows a comparison of single models of high complexity, mixtures of low complexity models and variants in between.

Intermixture detection (IMD)

Every TFBS data set D can be formally viewed as an intermixture of M ≥ 1 data sets D₁, …, D_M, where M = 1 represents the special case that D is intermixture-free. Using this formalism, we call M the intermixture number of D, which is typically unknown. The computational problem is to give an estimate 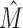of M based on the statistical properties of D and to cluster the data set into 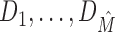accordingly.

To solve this problem, we employ a recursive approach that decides in every step whether a data set is intermixture-free (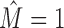) or not. In a single step, we learn a mixture of up to two PWM models from D using the FAB inference described above. If the resulting score of a two-component mixture model (Equation 1) is not greater than the score of a single PWM model learned on D, we set 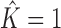. Otherwise 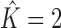, which means that a mixture two PWM models represent the data more effectively than a single PWM model. But that alone is not sufficient to decide upon presence or absence of intermixture of binding sites from two TFs yet.

To make this decision, we quantify the difference among the nucleotide distribution at the ℓth positions of the two learned PWMs P₁ and P₂ by the Jenson–Shannon divergence (43), defined by

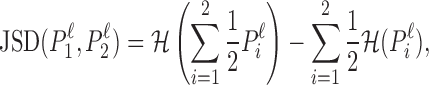(2)

where 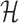denotes the entropy in bits. Next, we compute an weighted average over the L positions in the sequence, where the weight 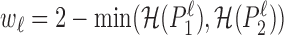is the maximum of the stack-height in the sequence logo of both PWMs at position ℓ. The purpose of the weighting is to ensure that adding entirely uninformative positions to the flanks of the binding sites preserves the average divergence among positions that are informative in at least one component. We then define the intermixture measure

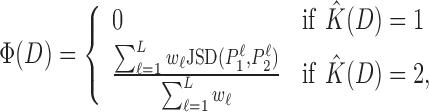(3)

which assumes values in (0,1). If Φ(D) ≤ T, we consider the two PWMs similar enough to represent binding sites of a single TF, so we call T the intermixture threshold. If not, we cluster all sequences in D according to their log-probability scores given P₁ and P₂ into new data sets D₁ and D₂ and discard D. We then recursively repeat the entire procedure above for D₁ and D₂.

IMD terminates when for all data sets Φ(D) ≤ T. The estimate of the intermixture number is then given by the number of created data sets, i.e. .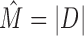

Motif complexity analysis (MCA)

Given a data set D of aligned binding sites, the purpose of MCA  is to find an optimal representation, i.e. to select a model among candidates that take into account dependencies and/or heterogeneities.

Here, we select among mixtures of PWM models, mixtures of up to dth order proximal dependency models and mixtures of up to dth order distal dependency models, always including the special case of K_max = 1, and denote the set of all tested model classes by 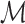. In all practical studies within the present work, 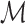comprises the 17 model combinations displayed in Table 1. The software is not limited to these candidates, but does allow higher K_max and d, constrained only by available time and memory budget. Comparing entirely different types of generative models, such as undirected graphical models or local structures other than PCTs, is at least in principle possible with the present methodology.

Table 1.

Dependency models and mixtures thereof that are used in MCA

Dependency	Order	K max = 1	2	3	4	5
None (PWM)	–
Proximal	1
Proximal	2
Proximal	3
Distal	1
Distal	2
Distal	3

For each model 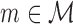, we run the FAB inference for maximizing the score of Equation (1). It finds only a local optimum of the target function, so multiple restarts with different initializations are required for approximating the global optimum. We use a global time limit of 3 h for each model, which ensures that all non-mixture models can be optimized exactly. We terminate a single restart of a mixture model when either the difference in the target function is smaller than 10⁻⁶ or the elapsed time amounts more than 1 h so that at least three restarts are executed within the global time limit. We denote the optimal score obtained for model 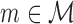on a data set D within the time limit by FIC_m(D).

Since the absolute scores depend on the number of data points and sequence length, we evaluate the improvement in percentage with respect to the baseline of a PWM model. For each type of model, 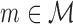we compute for a data set D the quantity

(4)

which we dub intra-motif complexity measure. Finally, we select the model 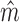as the 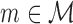that maximizes Δ_m(D) as optimal model for data set D. Since the effects of sample size and sequence length cancel out by taking the ratio of FIC scores, Δ_m(D) is comparable not only among different models in 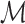, but also among different data sets. It thus quantifies the amount of intra-motif complexity in a data set. We consider 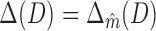as intra-motif complexity of D, and denote it simply by Δ if D is clear from context.

Data extraction

In the case studies, we use three types of data, each for a particular purpose. Here, we give a description in brief, more details are provided in Supplementary Section S3.

JASPAR aligned binding sites

As ground truth for non-intermixed TFBS, we pick all data sets from the JASPAR 2016 release (44) that have actual sequence data, as opposed to sole weight matrices, available. From each data set, we extract the alignment proposed by the database, which is indicated by upper-case letters in the sequence files. We further process the data for removing artifacts. Afterward, we discard all data sets that contain <100 sequences and finally retain 158 data sets.

GTRD metaclusters

We use ChIP-seq metaclusters for human and mouse from GTRD (32) as validation data for motif models derived from JASPAR binding sites. Metaclusters aggregate multiple ChIP-seq experiments and evaluation pipelines, yielding a unique data set for each TF, which is identified by its TFclass (45) ID. We associate TFclass IDs with JASPAR IDs according to the TF name or variants thereof. For each match, we extract the sequences for the metacluster from the human/mouse genome and treat them as positive data set. For each positive data set, we generate control data by learning a second-order homogeneous Markov chain and sampling 100 000 sequences of length 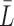from it, where 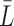is the mean sequence length in the positive data set.

ENCODE ChIP-seq data

For motif discovery studies, we use all data sets in the Uniform TFBS track of the ENCODE project (33) as input data. The data sets differ in TF (antibody), cell line, treatment or producing lab, but have been processed with a uniform pipeline, yielding a ranked peak list with corresponding enrichment scores. For each data set, we pick the top 5000 peaks and extract, for each peak, a 500-bp sequence fragment (250-bp upstream/downstream from the peak center) the human genome, version hg19. Construction of negative data follows the same procedure as for GTRD.

RESULTS

This section comprises two sets of case studies. First, benchmark studies systematically evaluate the performance of both subtools of Disentangler based on pre-aligned TFBS from different sources and ChIP-seq metaclusters from GTRD. Second, application examples demonstrate how Disentangler can be used in practice to process and refine output from de novo motif discovery.

Benchmark studies

As a pilot study, we consider the simple task of finding the optimal number of PWMs for each of the 158 JASPAR data sets. We compare the FIC-based learning approach of Disentangler with two other tools that can be used to solve this task, namely DIVERSITY (22) and NPLB (46); see Supplementary Section S2 for details about all tools used in the case studies. Results (Supplementary Section S4.1) show that for the majority of data sets all three methods predict more than one PWM to be optimal. This observation implies that selecting the optimal number of PWM models alone cannot accurately detect inter-motif heterogeneity (Figure 2), as it cannot distinguish it from intra-motif complexity (Figure 1).

Quality of intermixture measure

We use the 158 JASPAR data sets and consider them to be ground truth for the positive class (single TF, no intermixture). In order to obtain data for a negative class, i.e. intermixed sites of two binding factors, we use the 47 data sets with L = 15 and construct all possible 1081 pairwise intermixtures.

For each data set, we perform one iteration of IMD for computing the intermixture measure (Equation 3). We plot histograms of all obtained values for both classes, normalized to enable a direct comparison despite the different class sizes, in Figure 3A. The overlap among both histograms occurs only in the tails of both distributions, suggesting a promising classification potential of the intermixture measure.

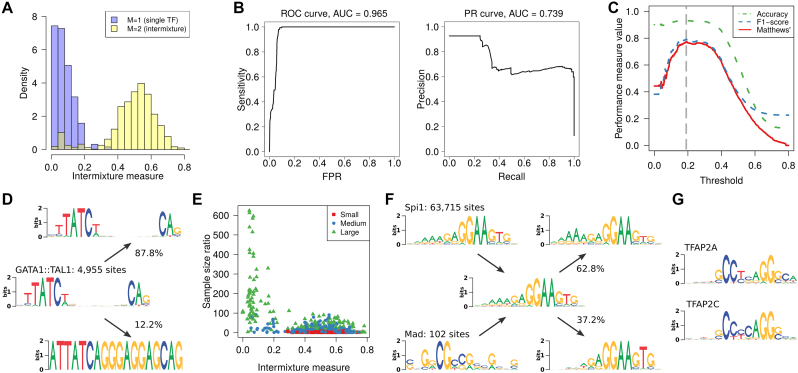
Figure 3.

Intermixture detection as binary classification. The task is to distinguish data sets containing binding sites of a single TF (M = 1) from those where binding sites of two TFs are intermixed (M = 2). (A) Histograms of intermixture measure for both classes normalized by the number of members of each class. (B) Classification performance with varying intermixture threshold according to ROC and PR curves. (C) Different aggregating performance measures as function of the intermixture threshold. The optimal threshold is marked by vertical dashed line. (D) Example of a data set that IMD classifies as intermixture, where the second component is a binding site that occurs within a transposable element and has thus been massively amplified in the genome. (E) Dependence of the intermixture measure on the disparity of the sample sizes of the intermixed data sets. The legend indicates the total sample size, distinguishing between small (N < 1000), medium and large (N > 10 000). (F) Example where the sample size disparity is so high that the sequence logo of the intermixture is virtually identical to that the larger data set (Spi1). De-mixing then reveals only heterogeneities with the Spi1 motif instead of recovering the two ground-truth PWMs. (G) Examples for data sets that are so similar that inter-motif heterogeneity appears as intra-motif heterogeneity.

For quantifying this potential, we next vary intermixture threshold T, calculate the resulting Receiver Operating Characteristic (ROC) curve and Precision Recall (PR) curve (47) using PRROC (48) and display the results in Figure 3B. The area under the ROC curve amounts 0.965, the area under the PR curve 0.739, which shows that the intermixture measure enables a satisfying classification.

For assessing the classification performance for a particular T, we use Matthews’ correlation coefficient (49) due to the imbalance among the class sizes in the present study, but also compute F1-score and accuracy for comparison (Figure 3C). All three performance measures report T = 0.19 to be optimal, and for all of them the performance varies only slightly in the interval (0.15, 0.30). This coincides with the separation among the histograms in Figure 3C, so choosing T is robust.

Reasons for misclassification

With T = 0.19 we correctly classify 154 of 158 data sets as intermixture-free, yielding a true positive rate (TPR) of 97.5%. For GATA1::TAL1, we obtain Φ = 0.331, which is the highest value in the positive class and thus justifies inspection in detail (Figure 3D).

We find that the first mixture component, representing 87.8% of the sequences in the original data set, resembles the original PWM. The remaining 12.2% sequences follow a very different distribution with almost completely conserved nucleotides at all positions, which extends beyond the motif boundaries in the sequences, from which the 18-mer was extracted. Running RepeatMasker (http://www.repeatmasker.org) on the entire 118-bp long sequences available in JASPAR classifies 99.97% of them as long terminal repeat (ERV class II). One binding site for GATA1::TAL1 appears to be massively amplified in the genome due to location within a transposable element, a mechanism that is known, e.g. for E2F in plants (50).

In the negative class, intermixture is ground truth by construction. Yet, 77 of 1081 data sets yield Φ ≤ 0.19, amounting to a false positive rate (FPR) of ∼7.1%. There are at least two causes, which may also intertwine.

First, the data sets with vary in size by several orders of magnitude from as little as 10² up to nearly 10⁶. As a consequence, some intermixtures have a large imbalance among the number of binding sites from each ground-truth data set. All intermixtures with a sample size disparity of more than 100:1 yield Φ < 0.1 (Figure 3E), so contamination below 1% frequency cannot be reliably detected by IMD. We illustrate the reason for misclassification in Figure 3F using the most imbalanced example of intermixing Spi1 (63 715 sequences) with Mad (102 sequences). The statistics of the intermixture is dominated by Spi1, and de-mixing yields rather heterogeneities among these sites instead of discovering the few intermixed Mad sequences.

Second, there are a few intermixtures in which both original PWMs are very similar, as illustrated in Figure 3G by the example of TFAP2A and TFAP2C (Φ = 0.032). However, since both TFs belong to the AP-2 family, of which all members contain a conserved helix-span-helix DNA binding domain, they may actually recognize the same motif (51).

Arbitrary intermixture number

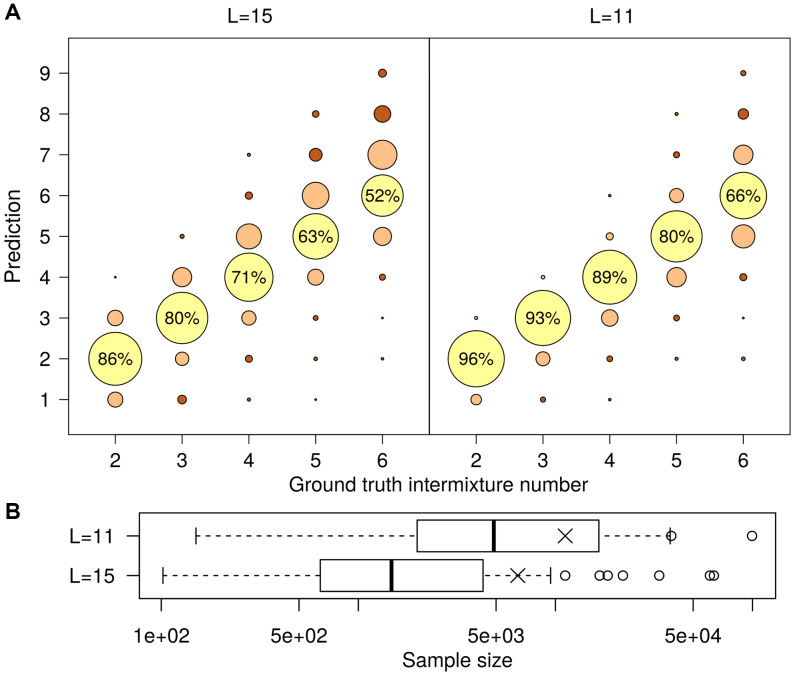
For ground truth M > 2, systematically studying all possible intermixtures becomes intractable due to the sheer number of combinations. We thus employ a sampling-based approach by randomly picking M data sets out of a pool of candidates. The pool comprises once 47 data sets with L = 15 and once 48 data sets with L = 11 and we use the ground-truth intermixture numbers M ∈ (2, 3, 4, 5, 6). For each L and M, we repeat the procedure R = 1000 times, so the total number of constructed data sets amounts 10⁴. For each constructed data set, we run IMD using T = 0.19 until termination and compare the predicted intermixture number 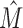with the ground truth M (Figure 4).

Figure 4.

Benchmark for fully recursive IMD using artificial intermixtures constructed by randomly sampling from one out of two data set pools that differ in sequence length. (A) Predicted intermixture numbers in relation to ground truth. Area of circles corresponds to fraction of predictions. Numbers show the percentage of entirely correct predictions. (B) Sample size distribution for data set pools, the intermixtures are constructed from. Symbol × indicates the mean. The L = 11 pool contains larger data sets on average, which partially explains the better performance of IMD.

IMD finds the correct intermixture number in the majority of cases. The error rate gradually increases with ground truth intermixture number, since intermixing more data sets increases the probability of a data set pair with either a high sample size disparity or a very similar binding motif. However, predictions that deviate from the ground truth by more than one are rare. IMD performs for the L = 11 pool even better than for L = 15, which can be explained by a larger average sample size (Figure 4). Larger samples are generally an advantage in statistical learning, but here they also entail less extreme sample size disparities.

Distribution of intra-motif complexity

For benchmarking MCA, we first compute Δ_m(D) of Equation (4), where D varies over the 158 JASPAR data sets and model m varies among the alternatives in Table 1, and show the resulting distribution in Supplementary Section S4.2.

Mixtures of PWM models are a poor representation of intra-motif complexity on average, albeit there are cases, such as motifs with a conserved core of three nucleotides or more, where they outperform proximal dependence. Distal dependency captures the same features often in a more effective way and increases, compared to proximal dependence, intra-motif complexity by ∼33% on average.

One data set in detail

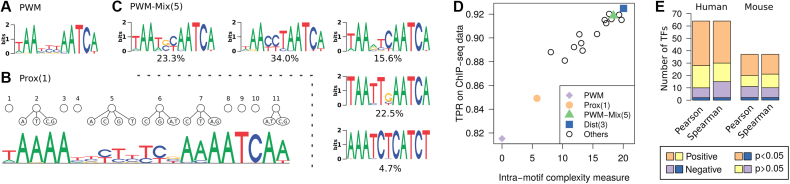
The TF with the highest intra-motif complexity for the optimal model is DUX4, which is known to bind variations of a tandem TAAT consensus, with TAATCTAATCA yielding the highest affinity (52). Its JASPAR-extracted binding sites contain three highly conserved nucleotides at positions 3, 8 and 9 (Figure 5A), so only the remaining eight positions are relevant from statistical point of view. First-order proximal dependency (Figure 5B) cannot model any correlations across these conserved positions, so it yields only Δ_m = 5.77. In contrast, third-order distal dependency (visualization in Supplementary Section S4.3) achieves Δ_m = 20.05. For DUX4, a five-component mixture model (Figure 5C) is, in contrast to the general trend, a competitive alternative with Δ_m = 18.39. Since the number of low-conserved sequence positions is fairly small, even a few PWMs can express most of the intra-motif complexity.

Figure 5.

Complexity analysis using the example of DUX4. (A) PWM model. (B) First-order proximal dependency model. (C) Five-component PWM mixture model. (D) Complexity measure of all learned models in relation to the TPR on ChIP-seq data (with FPR = 0.01). (E) Correlation of intra-motif complexity measure with classification on independent ChIP-seq metaclusters from GTRD for all data sets for human and mouse.

Next, we investigate the capability of the different learned DUX4 models to predict in vivo binding by classifying 39 554 sequences in the corresponding GTRD data set as bound by the TF or not. To this end, we compute binding site probabilities in the control data in order to choose a classification threshold that yields one false positive per 100 sequences. We predict binding sites in the sequences in the positive data set and consider a sequence as bound when it contains at least one hit. Figure 5D shows a scatter plot of the classification performance in terms of the TPR against the intra-motif complexity measure. The correlation among both quantities (Pearson r = 0.961, Spearman ρ = 0.939) is surprisingly high, given that the two types of data are based on different experiments and processing pipelines.

Large-scale benchmark

We now repeat this analysis with all data sets from human and mouse that have an associated data set in GTRD (Figure 5E) and observe a positive correlation between intra-motif complexity and sensitivity in the majority of cases. Non-significance occurs for data sets where differences among models according to MCA  are small. Significantly negative correlation may indicate disagreement of the two data sources with respect to the binding motif or overfitting effects. Overall, the intra-motif complexity measure is a good, albeit not perfect, indicator for the capability of different motif models to predict TF binding to DNA in vivo.

Different ground truth data

For further validation, we repeat the benchmarks with binding extracted from the SwissRegulon database (53) as ground truth (Supplementary Section S4.4). The performance of IMD for recognizing arbitrary intermixture numbers is widely identical to that observed in Figure 4, which underpins that T = 0.19 is indeed a robust choice. In contrast to JASPAR data, data sets extracted from SwissRegulon contain much less intra-motif dependencies on average, which makes the MCA benchmark less informative due to a high number of insignificant correlations.

Stability of optimal solutions

The studies from the previous sections benchmark the performance of IMD and MCA across a large number of data sets. To study the stability of the solutions for individual cases, we employ a bootstrapping approach for some key data sets and find that both methods are generally stable across resamples (Supplementary Section S4.8).

Application examples

We next study the practical application of Disentangler for processing and refining de novo motif discovery output obtained from different tools that model either dependencies or heterogeneities explicitly.

Intermixtures produced by motif discovery

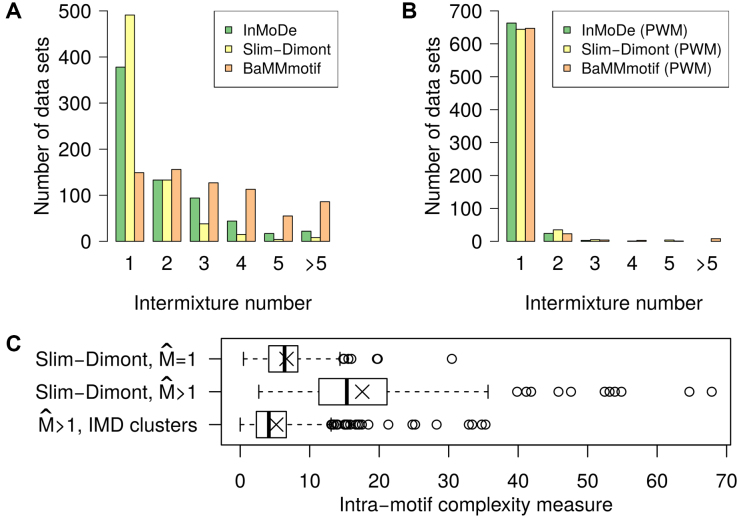
We perform de novo motif discovery in 690 ENCODE ChIP-seq data sets with three recent tools that focus on learning intra-motif dependencies, namely InMoDe (24), Slim-Dimont (16) and BaMM-motif (18), which output not only the learned motif, but also the underlying binding sites (Supplementary Section S2). For each tool we run motif discovery twice, once with default parameters, which takes into account intra-motif dependencies, and once with constraining the motif model to a PWM. After extracting the binding sites for each learned primary motif, we apply IMD for computing the intermixture number, and summarize the results in Figure 6.

Figure 6.

Intermixture detection on binding sites predicted by de novo motif discovery with various tools (legend). (A) Motif discovery taking into account intra-motif dependencies. (B) Motif discovery based on the PWM model. (C) Intra-motif complexity measure for Slim-Dimont predicted binding sites. Symbol × indicates the mean. Top and middle distribution correspond to intermixture-free and intermixed data sets, respectively. The bottom distribution represents data sets that are obtained as output from IMD for data sets classified as intermixture.

When taking into account intra-motif dependencies during motif discovery, all three tools make predictions that show intermixture, albeit the magnitude differs among them considerably. Using a PWM as motif model avoids this almost entirely, which demonstrates that learning dependencies within de novo motif discovery is indeed a source of intermixtures.

For further analysis, we now focus on the intermixed data sets produced by Slim-Dimont, since it is the most conservative tool, yielding only 30% intermixtures. For all predicted sets of binding sites, we perform MCA and plot the distribution of the intra-motif complexity measure, hereby distinguishing intermixed from intermixture-free cases (Figure 6C). For 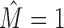the distribution is in the range of that on JASPAR data sets (cf. Supplementary Section S4.2), whereas data sets that are classified as intermixed show a much higher intra-motif complexity.

Running MCA on the clusters produced by IMD for the data sets with 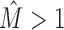, we find that the resulting intra-motif complexity is now substantially reduced, the distribution resembles the 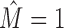group. MCA thus provides quantitative evidence that modeling dependencies during motif discovery can overestimate intra-motif complexity considerably and that IMD can be used to effectively recover from artifacts.

Different intermixture types

The sequence logos for all 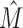clusters for each of the 171 data sets with 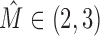are given in Supplementary Section S4.5. We observe that intermixtures are of different types that can be explained by different biological and/or computational origins (Figure 7).

Figure 7.

Different types of intermixtures: (A) Clearly distinguishable motifs of two different TFs. (B) Primary motif intermixed with seemingly nonfunctional sequences. (C) Elongated motif as part of transposable element. In each panel, the leftmost sequence logo shows the prediction by Slim-Dimont, whereas the other two sequence logos correspond to the IMD-clusters. Φ and Δ show intermixture measure and intra-motif complexity measure of the data sets.

For c-fos, the intermixture consists of binding sites of two substantially different motifs that are easily recognized as such (Figure 7A). The first cluster follows the motif of NF-Y and the second cluster that of AP-1. Both motifs are known to be enriched in c-fos target regions (54). Such typical intermixtures that resemble the toy example of Figure 2 amount ∼50% of all cases with 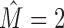. Another example is ELK1, which shows an intermixture with SRF that can be explained by direct interaction of both TFs (55). A third example is CHD2, which is assumed not to bind directly to DNA (56). Here, we find almost equally many binding sites that either follow either the NF-Y motif or the TCTCGCGAGA consensus (57).

In ∼10 cases, the primary motif of interest is intermixed with sequences that appear to be non-functional background. One example is SRF (Figure 7B), where ∼75.8% of binding sites correspond to the MADS-box CC(A/T)₆GG motif (58). The remaining 24.2% strongly deviate from it, without resembling a binding motif of a different TF. Low-affinity binding of SRF to these sequences cannot be excluded entirely by in silico analysis, but it seems more likely that this intermixture is a computational artifact.

Figure 7C visually resembles Figure 3D, and for TFIIIC the origin is similar indeed. The 15-bp consensus sequence of the second component occurs as exact match in 279 of 1858 original ChIP-seq positive sequences. However, not a single match remains after applying RepeatMasker to these sequences, which classifies 37.8% of them as interspersed repeat, the vast majority (26.87%) as SINEs of the Alu-type. Binding of TFIIIC to SINEs is known and associated with function (59), so the second component cannot be treated as artifact. However, the amplification of a particular k-mer through transposable elements affects the intra-motif complexity considerably.

Intermixtures are not only of these three types, but there are some additional variants, such as intermixed reverse complementary sequences or gapped motifs (Supplementary Section S4.6). Moreover, all intermixture types discussed so far pertain to cases with estimated intermixture numbe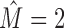r . For 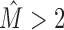, we often observe a combination of different types, such as two conserved motifs according to type A that are additionally intermixed with background sequences according to type B.

Intermixtures in different cell lines

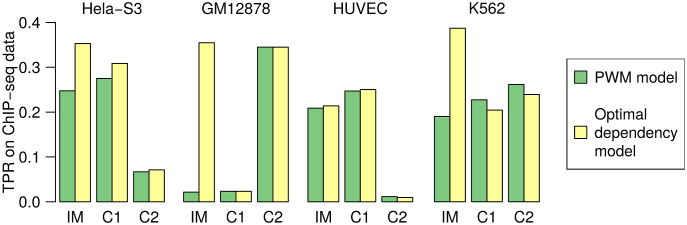
The sequence logos in Figure 7A represent three sets of binding sites: one intermixture obtained as output from applying Slim-Dimont on c-fos ChIP-seq data, and two clusters of binding sites produced by applying IMD to the first set of sites. For each of these three data sets, we next compare the predictive performance on the top-5000 peaks within different cell lines, once based on a PWM model and once based on an optimal dependency model according to MCA. The performance measure is, in analogy to the MCA-benchmark, the TPR under an FPR of 0.01 on control data. The results are shown in Figure 8.

Figure 8.

Predictive performance of models learned from intermixture (IM) and both IMD clusters for c-fos (Figure 7A) on four cell lines.

For Hela-S3 the perceived gain by taking into account intra-motif dependencies is high, whereas it is substantially reduced when evaluating both clusters individually. Since this is the cell line where the intermixture originates from, this observation confirms expectations. In other cell lines, such as K562, the difference can be even more pronounced, but its magnitude also depends depends on the distribution of hits for the two separate motifs. For GM12878, the top-5000 peaks contain very little hits of the TGACTCA-motif (cluster 1), which dominates the mononucleotide statistics of the intermixture, leading to a massive improvement in TPR via the dependency model. For HUVEC the top-5000 peaks contain almost no CCAAT, so the intermixture predicts in vivo binding with less accuracy than the first cluster alone.

Heterogeneities or dependencies?

In a final study, we apply Disentangler to motif discovery output that consists of multiple PWMs and the corresponding binding sites. Here, we do not expect intermixtures, but that the number of motifs may be overestimated at the expense of intra-motif complexity.

To test this hypothesis, we use DIVERSITY (22) to predict the optimal number and width of modes (PWM models) de novo from ENCODE ChIP-seq data. We here focus on data sets for CTCF and YY1, which did not show any intermixture in the previous study and can thus be expected to contain one primary motif. This section summarizes the key findings, whereas Supplementary Section S4.7 contains all results in detail.

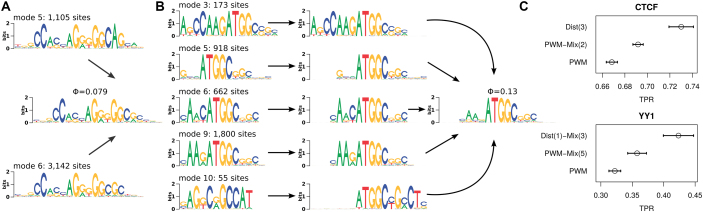
For CTCF, nine PWMs are optimal according to DIVERSITY, but seven of them are minor motifs of low frequency. More than 85% of all sequences correspond to either mode 5 or mode 6 (Figure 9A), which are both a variant of the known CTCF motif (60). Since both PWMs are here present in the same shift and strand orientation, we simply merge the underlying binding sites and apply IMD, obtaining the verdict that all binding sites are bound by the same TF (Φ = 0.079). MCA selects third-order distal dependency as best motif representation (Δ_m = 4.47), whereas the two-component PWM mixture receives only Δ_m = 1.67. To validate this model selection and to measure possible overfitting effects, we evaluate the predictive performance of in vivo binding on 52 different cell lines (Figure 9C), and find that the distal dependency model performs indeed substantially better on average, albeit at the price of a higher variance.

Figure 9.

Disentangler applied on output from DIVERSITY. (A) Two dominating PWM-based CTCF motifs found by DIVERSITY are classified by IMD as single motif. (B) For YY1, DIVERSITY predicts five PWM motifs that all contain an ATGGC/GCCAT consensus. The underlying binding sites can be merged only after correcting for different shifts and strand orientation. They are then classified by IMD as belonging to a single motif. (C) Prediction performance on ENCODE ChIP-seq data from different cell lines. The performance measure is the true positive rate, i.e. fraction of top-5000 ChIP-seq positive sequences with at least one hit, under a false positive rate of 0.01 on control data. Both plots compare the optimal models according to MCA (top), optimal number of PWM mixture model according to DIVERSITY (middle), and baseline PWM model (bottom).

For YY1, the application of Disentangler is a bit less straightforward. Here, ten PWMs are optimal according to DIVERSITY, and five of them contain the ATGGC consensus sequence that is typical for the YY1 motif (61). To further complicate matters, these five PWMs are of different length, shift and strand orientation. Hence, we first put all five motifs (and the corresponding binding sites) in the same shift and strand orientation using the ATGGC consensus as common anchor point, and pad empty left and right flanks with ambiguous nucleotides (Figure 9B). Merging the five data sets and applying IMD predicts also in this case that all binding sites are recognized by the same TF (Φ = 0.13). According MCA,  a three-component mixture of first-order distal dependence models is optimal (Δ_m = 3.04) for the merged data set, whereas a five-component PWM mixture yields Δ_m = 2.76. The predictive performance of in vivo binding (Figure 9C) confirms this assessment.

Learning multiple PWMs from ChIP-seq data by methods such as DIVERSITY has the undeniable advantage that complexity is taken into account without producing intermixtures, i.e. unrealistic models of direct TF–DNA interaction. The results from this section demonstrate that this comes at the cost of a possibly poor representation of intra-motif complexity. Disentangler can substantially improve on that by identifying PWMs that represent variants of the same motif and subsequently finding a motif representation better than a PWM–mixture.

DISCUSSION

This work was primarily motivated by the observation that two recent orthogonal approaches for de novo motif discovery from ChIP-seq data can both produce unwanted artifacts, which originate from their model assumptions. Learning complex motif models by taking into account intra-motif dependencies is prone to combining the binding preferences of multiple TFs into one motif. Learning multiple PWM models avoids this problem but it may yield a suboptimal representation of intra-motif complexity.

To address these issues, we propose Disentangler, a method for analyzing aligned TFBS with two different subtools: IMD checks whether a set of binding sites is an intermixture of binding sites from multiple TFs and clusters the sequences accordingly. MCA decides whether the intra-motif complexity is better explained by proximal dependencies, distal dependencies, mixtures of PWMs or variants in between. While both subtools can be used independently, one obvious pipeline first runs IMD on a set of TFBS, and subsequently applies MCA on every obtained cluster. This pipeline essentially returns a hierarchical view on TFBS complexity, where the first layer represents inter-motif and the second layer intra-motif complexity.

Benchmark studies with TFBS data sets from JASPAR and further validation with data from SwissRegulon demonstrate that IMD is capable of distinguishing these data sets from artificially constructed intermixtures with high accuracy. This may appear surprising at first glance, as it implies that intra-motif heterogeneities are generally weaker than inter-motif heterogeneities. One may speculate that this is not a mere coincidence, but a rather biophysical necessity for retaining a sufficiently high specificity of TF binding.

Although Disentangler as a whole is not a traditional motif discovery tool, IMD does operate de novo in the sense that it does not require lookup in databases for literature motifs or entirely different types of experimental data to decide upon intermixture. As a consequence, IMD can not only detect binding sites from different TFs, but also atypical intermixtures of various types.

One noteworthy type comprises binding sites that were massively amplified as part of transposable elements. While such sites can remain functional (50), it is not obvious whether they should be used for learning a motif model. This decision may depend on the notion of sequence motif, for which at least two interpretations are possible. It can be viewed as a distribution over the occurrence frequency of its functional binding sites in the genome. From such a perspective, often implicitly taken by motif discovery algorithms, it is correct to include these k-mers with the given frequency. But a sequence motif can also be viewed to represent the binding affinity of the TF of interest, an interpretation closer to what is measured by in vitro experiments (62). Since occurrence frequency does not necessarily correlate with binding affinity, downweighting or entirely excluding such k-mers appears to be correct.

MCA quantifies the performance of a motif model by computing an intra-motif complexity measure based on aligned TFBS. While the performance of different models is partially data set specific, a few general conclusions can be drawn. Mixtures of PWMs are insufficient to represent TFBS complexity in the general case, but also proximal dependency is not sufficient, as it cannot take into account correlations among distant nucleotides by definition.

The best representation is given by distal dependency models, but not without cost. Finding a globally optimal model structure beyond order one is time consuming, so higher order distal dependency is hard to learn within an iterative motif discovery algorithm. In addition, visualization of the learned model is more complicated than in the case of a PWM–mixture with only a handful of components. Provided a direct visualization of the learned model is of importance, it boils down to a trade-off between higher statistical efficiency and easier human perception. While MCA allows to quantify the former, the latter is an intrinsically subjective matter.

Disentangler can be used to refine predictions from complex motif discovery algorithms that either learn dependencies among nucleotides or learn multiple PWMs. However, processing output of the former is technically simpler as it requires only a single run of the pipeline. For the latter, candidate PWMs and the corresponding sets of binding sites must be manually selected and aligned before IMD can be applied. If a fully automatic approach is desired, all possible pairs of PWMs, and for each of them all combinations of shifts and strand orientation need to be tested. From this perspective, it is thus less cumbersome to perform initial motif discovery with a dependency model rather than searching for many PWMs.

The performance of motif models has often been assessed by their capability of in vivo prediction of TF binding (16,23), but this evaluation method may be flawed. This is admittedly a philosophical question and related to the precise definition of the term ‘transcription factor binding site’. Often it refers to the k-mer that matches the sequence motif and that is found at the exact location of direct protein–DNA interaction. However, sometimes it can also refer to approximate binding location up to a certain resolution (63), a notion more in line with a wet-lab experiment. When performing motif discovery on ChIP-seq data, we essentially learn a model that is meant to contain information about the former but use data that is based on the latter. While that alone is not critical yet, a disturbing problem arises from the use of an evaluation method that is also based on the second notion. Since both are influenced by the intermixture problem, errors during learning are not punished but rather rewarded by the evaluation method.

As a consequence, the prevalence intra-motif complexity has—at least to some degree—been overestimated in previous studies and should be reassessed. Devising a better evaluation method for motif models that avoids aforementioned problem is certainly a challenging topic for future research. In the meantime, Disentangler can be used to inspect motif discovery output before the performance of the learned model is assessed. Another obvious alternative is to augment existing motif discovery algorithms with an internal intermixture detection step that is called at certain iteration steps during the search. It hardly constitutes additional computational burden, since IMD is a fast procedure that requires only seconds to minutes rather than hours in the typical case.

DATA AVAILABILITY

Disentangler is implemented in Java using the open source library Jstacs (64). Supplementary Section S5 contains a brief description of features and user interfaces. Runnable .jar-files, source code, and further documentation are available from http://www.jstacs.de/index.php/Disentangler.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Academy of Finland [276864] “Supple Exponential Algorithms”. Funding for open access charge: Project funds.

Conflict of interest statement. None declared.