COUPLING TOXICOKINETIC-TOXICODYNAMIC (TK-TD) AND POPULATION MODELS FOR ASSESSING AQUATIC ECOLOGICAL RISKS TO TIME-VARYING PESTICIDE EXPOSURES

Abstract

Population modeling evaluations of pesticide exposure time series were compared to aspects of a currently used risk assessment process. The US Environmental Protection Agency’s Office of Pesticide Programs models daily aquatic pesticide exposure values for 30 years in its risk assessments, but does not routinely make full use of the information in those time series. We used mysid shrimp Americamysis bahia toxicity and demographic data to demonstrate the value of a toxicokinetic-toxicodynamic model coupled with a series of matrix population models in risk assessment refinements. This species is a small epibenthic marine crustacean routinely used in regulatory toxicity tests. We demonstrate how the model coupling can refine current risk assessments using only existing standard regulatory toxicity test results. Several exposure scenarios (each with the same initial risk characterization as determined by a more traditional organismal-based approach) were created within which population modeling documented different risks than assessments based on the traditional approach. We also present different acute and chronic toxicity data scenarios where TK-TD coupled with population modeling can distinguish different responses; responses that tradition risk evaluations are not designed to detect. Our results reinforce the benefits of this type of modeling in risk evaluations, especially related to time-varying exposure concentrations.

INTRODUCTION

Most determinations of acceptable toxicant concentrations to aquatic organisms are still based on a combination of single species, organismal-level standardized laboratory tests conducted using constant exposure concentrations (e.g., Stephan et al. 1985; CCME 1991). The need for this type of testing will likely never go away; however, real world toxicity exposures are rarely constant— even for short durations. This is particularly true for pesticides because they are applied on a periodic schedule. In recognition of this, mechanistic effect models are receiving increasing attention, especially as they relate to risk assessment of pesticides. Many of these incorporate some aspect of toxicokinetics (TK) and toxicodynamics (TD) at either the organismal or population level (Hommen et al. 2016). Toxicokinetics describes the accumulation of a toxicant from the surrounding medium or food and the subsequent metabolism or elimination of the absorbed material. The balance of these two processes determines the time course of the internal concentration. Toxicodynamics describes the effect of this internal concentration on the organism—either lethal or sublethal. In the simplest application of TK-TD the effect is directly proportional the internal concentration.

There is a rich history of TK and TD modeling within the toxicity testing research community with attempts to address extrapolation from relatively simple laboratory exposure scenarios to time-varying exposures that might be more likely in the field. Through some straightforward mathematics, internal toxicant concentrations can be calculated (TK), and an organism’s response to that internal concentration can be estimated (TD). This approach provides more realistic assessments of time-varying toxicant concentrations than are achieved assuming constant exposure concentrations. Most of the earliest applications of the technique addressed survival in laboratory exposures in which the toxicant concentrations declined appreciably over the duration of the test (e.g., Southworth et al. 1978; Kooijman 1981; Widianarko and Van Straalen 1996). Among the earliest applications, Mancini (1983) used the technique to evaluate both declining and increasing concentrations with time. Others have followed, applying TK-TD methods to the evaluation of a variety of time-varying concentration scenarios (e.g., Péry et al. 2001; Ashauer et al. 2007).

Most applications of TK modeling make the simplifying assumption that an organism is a onecompartment model (i.e., the whole-body concentration represents the target concentration), and assume uptake and elimination kinetics are first order. Modifications to these efforts include expanding on TD through incorporating damage and recovery rates within the organisms. Instead of assuming instantaneous damage and instantaneous recovery, these models include response kinetics for translating internal concentration into damage, as well as recovery rate for the repair of damage (Lee et al. 2002; Ashauer et al. 2007). This added feature explains effects which continue after exposure has ended (e.g., Ashauer, et al. 2010). The enhancement, however, comes with additional data requirements to estimate damage and recovery kinetics—often requiring measured internal concentrations (Jager et al. 2011), which are generally not available in standard regulatory test procedures. One potential objection for using toxicokinetics is the perceived need for internal concentration measurements. This objection, however, is overcome by using a scaled internal concentration. The concept of rescaling the internal concentration was used by Kooijman (1981) and Mancini (1983). The former scaled the internal concentration by dividing by the bioconcentration factor (which can be estimated by the ratio of the uptake rate constant to the elimination rate constant), and this is how rescaling is often done now (Péry et al. 2001; Jager et al. 2011; Ashauer et al. 2013). Mancini (1983), however, scaled by only dividing by the uptake rate constant. Either technique permits TK-TD modeling without the need to measure internal concentrations or to estimate the uptake rate constant, since a time course of survival or other effects can be related to the scaled internal concentration.

Linking TK-TD to population models is a useful way to incorporate variations in life history strategies into the risk evaluation of time varying exposure concentrations. This has often been accomplished through either individual-based models or matrix models (Billoir et al. 2007; Gabsi et al. 2014; Galic et al. 2014; Liu et al. 2014; Dohmen et al. 2016; Ducrot et al. 2016). However, despite this and despite the routine use of population models in ecology, conservation biology and natural resource management, their application in environmental risk assessment is extremely limited (Schmolke et al. 2010, Galic et al. 2014; Hommen et al. 2016). Although guidance for the use of a TK-TD population model (based on dynamic energy budget—DEB— theory) has been included in the European Union’s (EU) risk-assessment guidance for the evaluation of ecotoxicological data (OECD 2006), its use, or any other population model, in formal risk assessments is uncommon (Forbes et al. 2009; Ducrot et al., 2016; Raimondo et al. 2018). The approach to using DEB in population-level risk assessments is one of the more sophisticated modeling efforts. However, standard toxicity tests will rarely if ever have enough data to justify the complexity, thus, simplifications are frequently used (Jager et al. 2104, and references therein).

Toxicokinetic-toxicodynamic models are one of the most suitable methods to incorporate realistic exposure patterns into effects (Ducrot et al. 2016). Coupling TK-TD and population models also integrates several organismal effects (e.g., survival and reproduction) into a unified risk evaluation (population growth, recovery rate, etc.). In addition, population models address the influence of life history differences among species such as the timing of reproduction relative to exposure in their response to a specific exposure scenario (e.g., Etterson and Bennett 2013). Most population models provide insight that cannot be otherwise achieved with traditional risk assessments (Schmolke et al. 2010). With all the potential advantages of modeling, especially TK-TD linked modeling, it seems counterintuitive why they are not considered more in risk evaluations (Raimondo et al. 2018). Just the opposite is true for chemical fate and exposure models. These are routinely used in pesticide risk evaluations in the EU (FOCUS 2001) and the U.S. (Pesticide in Water Calculator, see methods for citation link). Despite the acceptance and use of exposure models, there remain obstacles facing the adoption of population effect models in ecological risk assessment—not the least of which is convincing risk assessors and other stakeholders that effects models can result in more accurate and realistic risk characterizations (Forbes et al. 2009). Current risk assessment relies heavily on exposure model predictions compared to empirical toxicity test results and assumes the latter are not amenable to predictive modeling such as TK-TD. The work we present herein not only reinforces the benefit of TK-TD models, but also demonstrates this using standard regulatory toxicity data.

We have developed a coupled TK-TD population modeling platform that can be used with existing data on exposure and effects. To demonstrate its utility in risk assessment, we have contrasted its results with those of “traditional” risk assessment methods which use empirical measures of effects and deterministic and probabilistic measures of exposure. We used mysid shrimp Americamysis bahia toxicity and demographic data to demonstrate the value of a TK-TD model coupled with a series of matrix population models in risk assessment refinements. The mysid shrimp is a small marine epibenthic crustacean, and a standard marine invertebrate toxicity test species. We are not promoting our mysid model as the only, or necessarily the best way to accomplish this risk refinement. Although, we do provide a novel way to incorporate sublethal effects into TK-TD models when restricted to standard toxicity data. Our paper only shows the value for risk to a single test species. It does not address other aspects of pesticide risk evaluation—such as species sensitivity distributions, joint probability curves, etc.

MATERIALS AND METHODS

The Office of Pesticides Programs has specific test guidelines for acute and chronic tests for the mysid shrimp Americamysis bahia (OCSPP 850.1035 and OPPTS 850.1350, respectively, https://www.epa.gov/test-guidelines-pesticides-and-toxic-substances). To demonstrate the utility of TK-modeling under the current regulatory framework, parameter estimation for TK-TD modeling was restricted to data typically expected from these standard toxicity tests.

Exposure modeling

For assessing pesticide risks to aquatic organisms, the USEPA’s Office of Pesticide Programs (OPP) models pesticide spray drift, runoff and erosion into a hypothetical agricultural pond with specific water body and watershed characteristics. Numerous scenarios represent different crop, regional, climate, watershed and agronomic specification across the United States. These scenarios are intended to capture agronomic and regional factors that influence the delivery of pesticides to surface waters (e.g., precipitation patterns, soil characteristics, pesticide application timing). With each of these agricultural scenarios, the Pesticide in Water Calculator (PWC, https://www.epa.gov/pesticide-science-and-assessing-pesticide-risks/models-pesticide-riskassessment) simulates daily concentrations for 30-year exposure distributions for surface water, sediment and interstitial (pore) water. Because the PWC output depends in part on soil properties, soil and crop management practices and weather data, different regions of the country and different crop types will have different aquatic exposure time series for equivalent applications of the same pesticide.

The three 30-year time series for our comparisons were based on one of OPP’s modeled aquatic endosulfan exposures (USEPA 2010). The exposure calculations for endosulfan were calculated using USEPA’s PRZM/EXAMS models—these have now been replaced by the Pesticide in Water Calculator referenced above. Endosulfan is an organochloride insecticide and acaricide whose use in the United States was cancelled in 2010, with a phase-out period lasting through 2016 (https://archive.epa.gov/pesticides/reregistration/web/html/endosulfan-agreement.html). The selected water concentration series was used to create two additional series by multiplying almost all the daily values by either 0.5 (low) or 1.5 (high). As explained below, OPP’s initial deterministic risk assessment is based on an evaluation of the 30 annual maximum values (we did not adjust the daily values associated with these annual maxima). We created the “low” and “high” time-series in such a way to maintain these 30 annual maxima—thus guaranteeing that the deterministic risk evaluation would be identical for each of the three exposure time series. These time series are presented in Thursby (2016).

Risk analyses

Three common types of risk analyses were used for calculating the toxicity effects of the different exposure time series—deterministic, probabilistic, and population-level methods. The deterministic approach is currently the first tier of an assessment within an OPP regulatory risk determination. In this approach, the daily average time series data are used for comparison against acute toxicity data, or, are converted to either a 21-d running average (for evaluating chronic exposure to invertebrates) or a 60-d running average (for evaluating chronic exposure to fish or aquatic phase amphibians). These running averages are part of an existing regulatory program which made science policy decisions to represent chronic exposure as either 21-d or 60d running averages. Once a time series is selected—and the running averages calculated—the maximum value for each year is recorded. An estimated environmental concentration (EEC) is determined for each time series as the 90^th percentile of the 30 ranked values of annual maxima and is subsequently used to calculate a risk quotient (RQ), which is the EEC divided by a toxicity value of interest. Chronic data for the marine invertebrate mysid shrimp Americamysis bahia were used, thus 21-d running averages of each time series exposure data were calculated for the deterministic comparisons. The chronic endpoint for A. bahia is 0.27 ug/L, based on the geometric mean of five values for the 28-d No Observable Adverse Effect Concentration (NOAEC) for endosulfan (McKenny 1982). Use of NOAECs is criticized by some; however, we apply it here because it is the chronic value used in the calculation of RQ values for the registration of pesticides in the US. The probabilistic approach also used the 21-d running average data, but included all the exposure data, not just the annual maxima, as cumulative distributions. The same mysid chronic endpoint was used as in the deterministic approach, except this approach calculates the probability that the exposure data exceeds that endpoint using counts of how many concentration values in each time series are greater than the endpoint value (28-d NOAEC). The third risk analysis approach used TK-TD modeling coupled with matrix population models. The details are described in the following sections. What is worth noting here relative to the deterministic and probabilistic approaches, however, is that the population modeling approach used the daily exposure values rather than the 21-d running averages.

Toxicological factors

Toxicokinetics using scaled internal concentration.

We used Mancini’s (1983) method for estimating the scaled internal concentration—although this author did not use the phrase. Equation (1) is the commonly used differential equation for a one-compartment model to estimate the rate of toxicant change in an organism’s internal concentration.

$$\frac{d{Q}_{(t)}}{dt}=k_i{C}_w-k_e{Q}_{(t)}$$ (1)

Where

• Q_(t) = concentration of toxicant inside organism at time t (μg/g);

• C_w = concentration of toxicant in external medium (e.g., water—μg/L);

• k_i = uptake into organism rate constant (L/g·t);

• k_e = elimination rate constant (1/t);

• t = time.

Simply put, the amount by which the internal concentration increases in each time interval is equal to a constant proportion of the external concentration minus an elimination rate that is proportional to the current internal concentration. The elimination rate does not distinguish between actual excretion or any of several potential internal detoxification processes. The solution to this differential equation is:

$$Q_{(t)}=\frac{k_i}{k_e}{C}_w\left[1-e^{-k_e\cdot t}\right]$$ (2)

The internal concentration is then scaled by dividing both sides by k_i, which is usually not known directly nor can it be easily calculated indirectly from standard toxicity test data.

$$\frac{Q_{(t)}}{k_i}=\frac{C_w\left[1-e^{-k_e\cdot t}\right]}{k_e}$$ (3)

The scaled internal concentration is now a function of the external water concentration—which can be measured or modeled—and the elimination rate constant. The elimination rate parameter can be estimated from standard acute test data by plotting the LC50 vs time (Verhaar et al. 1999; Lee et al. 2002).

$$LC{50}_t=\frac{LC{50}_{\infty }}{1-e^{-k_{e}t}}$$ (4)

Toxicodynamics for survival.

Survival probability is treated as proportional to the scaled internal concentration (Bedaux and Kooijman 1994) and can be calculated once the killing rate (k_kill, defined below) is estimated. This survival probability is in addition to natural background survival. In other words, the probabilities of surviving from one age group to the next in the control are multiplied by S(t) calculated below. The killing rate constant is initially derived from standard toxicity data (usually acute data) by fitting a survival probability equation to time-todeath data for a given external concentration (see equation B-13 in Thursby 2016). Using the Widianarko and Van Straalen (1996) proportionality constant’s relationship to the Bedaux and Kooijman (1994) killing rate we can derive the hazard function.

$$h(t)=k_{kill}\cdot k_e\cdot \left[\frac{Q_{(t)}}{k_i}-\frac{Q_{NEC}}{k_i}\right]$$ (5)

Where:

• h(t) = hazard function—the probability of dying at time t given the individual has survived to time t (Lee and Wang 2003),

• Q_NEC/k_i = the scaled no effect internal concentration—determined during the calibration step, see below, and k_kill = killing rate (L/μg·t).

Survival is a function of the cumulative hazard function over a given time interval (Lee and Wang 2003).

$$S(t)=\exp \left(-\underset{0}{\overset{t}{\int }}h(x)dx)\right)$$ (6)

Because our time interval is daily (t = 1), Equation (6) simplifies to:

$$S(t)=\exp \left(-k_{kill}\cdot k_e\cdot \left[\frac{Q_{(t)}}{k_i}-\frac{Q_{NEC}}{k_i}\right]\right)$$ (7)

Equation (7) converts a 30-year daily time series into a 30-year series of daily survival rates. Note, the model was set so that S(t) defaults to 1.0 when Q_(t)/k_i < Q_NEC/k_i.

Toxicodynamics for reproduction.

Reproductive effects cannot usually be handled in the same manner as survival. Simple toxicodynamics for sublethal effects are not easily calibrated and generally require more data than provided by traditional test protocols (Ashauer and Brown 2013, Martin et al. 2013). Standard tests often do not have sufficient time series data for reproductive output to estimate directly the kinetic coefficient for reproduction (i.e., analogous to the survival killing rate). To compensate for this the reproductive effects rate (k_R) was calculated by multiplying k_kill by a reproduction adjustment factor (RAF)—which assumes a constant relationship between survival and reproduction kinetic rates (k_R = k_kill·RAF). A RAF value of zero means there is no direct effect of the toxicant on reproduction. Values greater than zero indicate some degree of direct effect on reproduction, and the greater the value the greater the effect relative to survival. The most readily available reproduction data usually will be chronic end-of-test effects information. For the model used herein, the ratio of chronic reproduction (28d EC50) to chronic survival effect (28-d LC50) to was used as a starting value which was further adjusted during the calibration procedure described below. While not ideal, this is the best that can be done with the available standard mysid toxicity data. The equation for reproduction proportional effects is:

$$R(t)=\exp \left(-k_R\cdot k_e\cdot \left[\frac{Q_{(t)}}{k_i}-\frac{Q^{*}{}_{NEC}}{k_i}\right]\right)$$ (8)

Where Q*_NEC/k_i is the scaled internal no effect concentration for reproduction, which is estimated independently from the NEC for survival (see calibration section below).

Matrix population model

Our population approach builds upon a matrix population model previously developed for the marine invertebrate Americamysis bahia (Thursby 2009). The approach was patterned after periodic matrix models (Caswell 2001), creating 52 sub-matrices to represent weekly population activity. Unlike true periodic matrix models, the sub-matrices were not multiplied together to create a single annual matrix. This adaptation of the model retains the basic structure of the original matrix model—subpopulation groups were age classes with a one-week time step (Thursby 2009). All age classes (ranging from 1 to 13 weeks) were assigned the same sensitivity, differing only in the length of time exposed. The earlier model is density independent, stochastic, and assumes constant exposure concentrations. The current model is density dependent and deterministic and allows variable exposure concentrations. The density dependent factor was calculated based on Leslie (1948) and required specification of a carrying capacity. Because the maximum size of field populations for mysids is not easily known, 100 was chosen as the maximum—100%, so the carrying capacity is a relative number. For specifics on the density dependence equation see Thursby (2016).

Each sub-matrix represented the population’s status for a given week within the year, and therefore integrated a different past exposure. Each age class within a sub-matrix maintained a separate record of its past exposure. For example, age classes 1 and 2 integrated exposure from the previous 7 and 14 days, respectively. The model endpoint was the proportion of weeks within the 30-year time series where the model population declined to or below a given threshold based on weekly counts of total population size. The decline was measured against a control response using a time series without exposure. The survival and fecundity rates for each weekly submatrix were modified based on the daily S(t) and R(t) time series; however, the sub-matrix timestep was one week. To compensate, the minimum survival for each week was used for that week’s matrix adjustments. For reproduction, the R(t) value for the last day of each week was used. The modeling result was a time series showing the weekly change in population size as a percentage of the control response. The response was quantified by counting the number of times the weekly population size fell below a given threshold—expressed as a fraction of the total number of weeks in 30 years (1,560 weeks).

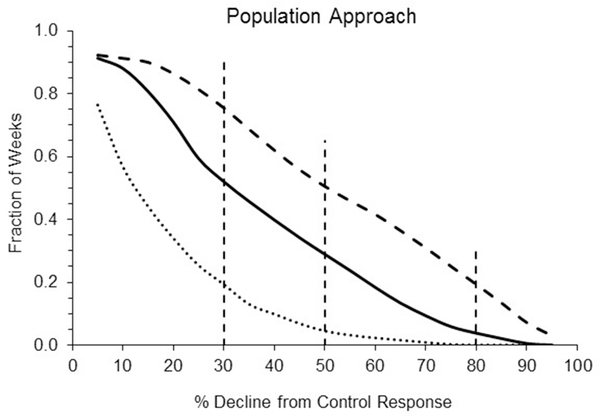
The risk of a population falling below a threshold is obviously a function of a specified threshold (the closer the threshold to the control, the greater the potential for observing that change). Using a range of percentage declines from the control, risk curves were constructed, in which a range of population thresholds (i.e., 5 to 95% in 5% steps) were used and the area under such curves was considered proportional to the total risk (Burgman et al. 1993). As a comparison, we included the World Conservation Union thresholds for vulnerable (30% decline), endangered (50% decline) and critically endangered (80% decline).

Model calibration.

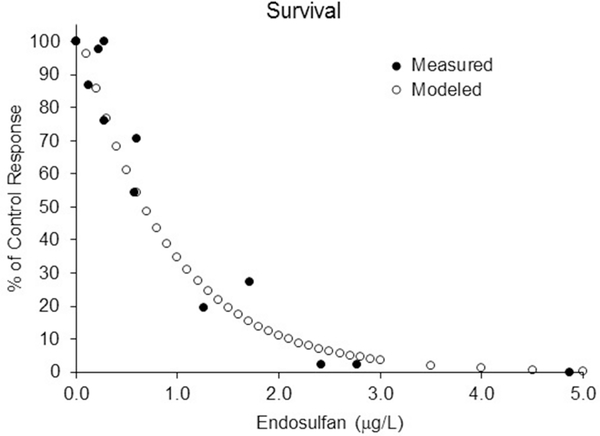
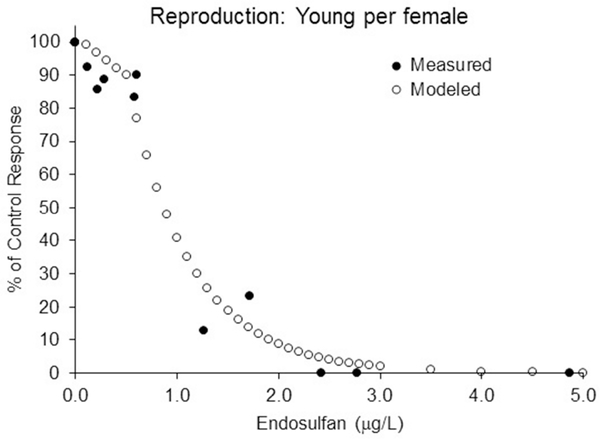
The toxicological data for the model runs were based on endosulfan acute and chronic interlaboratory comparisons (Schimmel 1981 and McKenney 1982). For calibration purposes, the model was run using constant concentrations covering the range of measured values within the available 28-d chronic tests (McKenny 1982). A special, four-week, density independent version of the model was used for calibration. Chronic toxicity tests were assumed to have sufficient feeding rates and low enough population density to make density dependent factors irrelevant. As with the standard chronic toxicity test, the model runs began with all 100 individuals assigned to the youngest age class (corresponding to 100%). Calibration runs only tracked this initial cohort through each additional week as a measure of survival. The initial estimate of the survival kinetic parameter (killing rate) was adjusted to achieve the best fit to the endosulfan chronic data. In addition, a threshold parameter was added to the Thursby (2016) model allowing the incorporation of a no-effect lower limit for the scaled internal concentration. The final kinetic killing rate used in all the 30-year model runs was 0.30, and the scaled internal no effect threshold concentration (Q_NEC/k_i) was set to 0.25. The modeled values for survival for A. mysis match well the measured survival data endosulfan in a 28-d standard chronic test (Figure 1). Similarly, the reproduction adjustment factor (RAF, which creates the reproduction kinetic rate) and the reproduction-scaled internal no-effect concentration were manipulated to achieve a reasonable fit to the measured reproduction data (Figure 2). The RAF for this fit was 4.5 and the reproduction threshold (Q*_NEC/k_i) was 2.00.

Figure 1.

Comparison of modeled survival output with data from a 28-d laboratory chronic test using Americamysis bahia. Solid markers are the measured survival data from the endosulfan chronic test. Open markers are the modeled output—k_e = 0.25, k_kill = 0.30, and scaled internal no effect concentration (Q_NEC/k_i) = 0.25.

Figure 2.

Comparison of modeled reproduction (based on number of young per female) output with the data from a 28-d laboratory chronic test using Americamysis bahia. Solid markers are the measured reproduction data from the endosulfan chronic test. Open markers are the modeled output. Survival kinetic parameters as in Figure 1, in addition, RAF = 4.5 and scaled internal no reproduction effect (Q*_NEC/k_i) was 2.00. The discontinuity around 0.5 μ/L is because the population reproduction is a function of both survival and maternity rate. At the lowest concentrations there is no direct effect on reproduction, but there is an indirect effect due to female mortality.

Toxicity scenarios

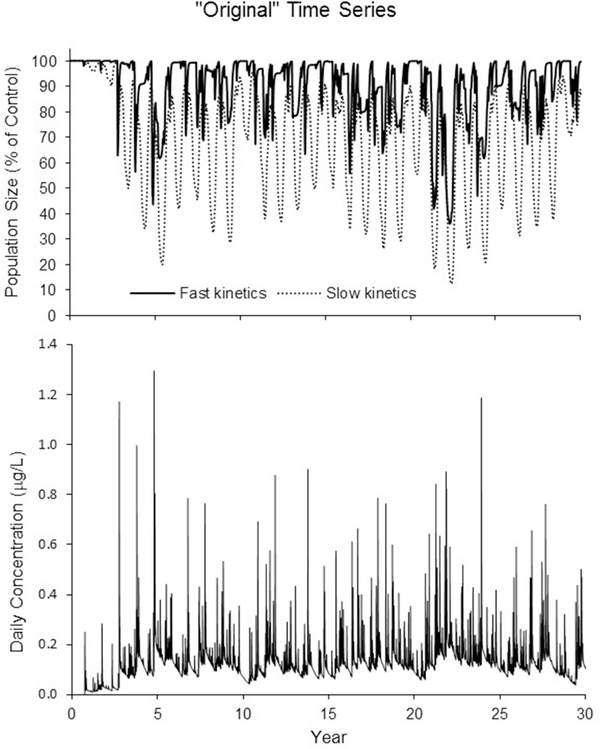
The population model was used to compare not only the different exposure time series, but also to evaluate the effect of changes in kinetic rates, as well as the relative sensitivity of survival and reproduction, on risk estimations using the same time series. The kinetic parameters for each of these are listed in Table 1. Two different species exposed to the same toxicant could have similar 96 hr LC50 values, but significantly different LC50 values at other time intervals. Using the standard deterministic or probabilistic risk analysis approaches, two similar 96 hr LC50 values would result in the same estimation of acute risk for a given exposure time series. However, LC50 values can change substantially with length of exposure in standard tests, even beyond the usual 96 hr test limit. It also is not unusual for the 24 hr LC50 result to be similar to the 96 hr value. These two scenarios were created using k_e values of 0.025 and 1.25 d⁻¹ (“slow” and “fast” kinetics, respectively). The 96 hr LC50 was 1.3 μg/L and the 24 hr values were 5.01 and 1.81 μg/L, respectively.

Table 1.

TK-TD kinetic parameters for the various modeling scenarios^a

		Acute Kineticsb		Chronic Sensitivity
Model Parameters	Standard Run	Slow	Fast	Survival = Reproduction	Survival < Reproduction
ke	0.25	0.025	1.25	0.25	0.25
kkill	0.30	0.30	0.30	0.30	0.10
RAF	4.5	4.5	4.5	4.5	13.5
kR	1.35	1.35	1.35	1.35	1.35

^aParameters for the standard run are those based on the mysid acute and chronic endosulfan tests. The acute kinetics and chronic sensitivity parameters deviated from these values to make the toxicity scenario comparisons. bSlow: 24 hr LC50 value greater than 96 hr value. Fast: 24 hr LC50 value approximately equal to 96 hr value.

^bSlow: 24 hr LC50 value greater than 96 hr value. Fast: 24 hr LC50 value approximately equal to 96 hr value.

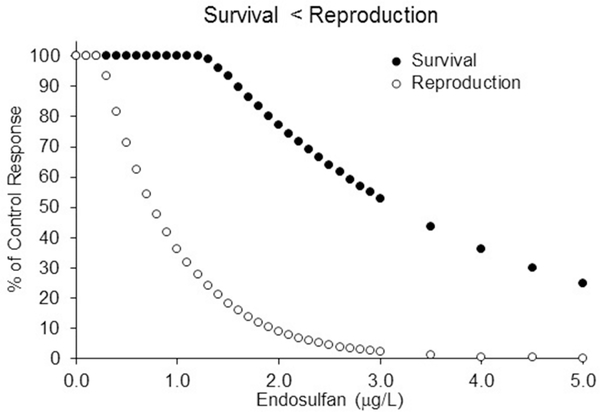
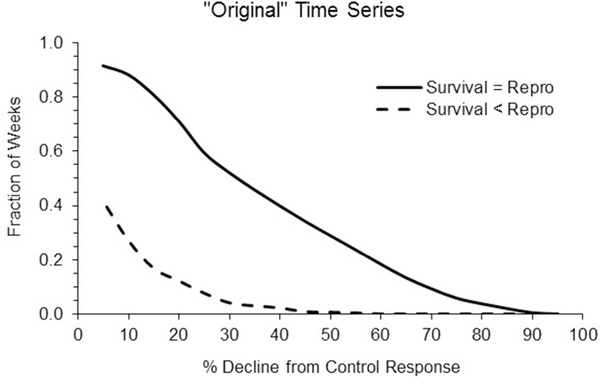
The population model was also used to address the relative toxicological sensitivity of survival compared to reproduction. In one scenario, survival and reproduction had similar dose response curves (Figures 1 and 2). This was based on the actual endosulfan mysid chronic test data. In the other scenario, survival was assumed to be insensitive relative to reproduction (Figure 3). Toxicity data were selected so that both scenarios had similar NOAEC values (based on reproduction), and therefore both would have similar traditional deterministic and probabilistic evaluations of chronic risk. In the special model run where survival was artificially set to be significantly less sensitive to endosulfan than reproduction, the RAF was changed to 13.5, and the thresholds for survival and reproduction were 5 and 1, respectively. In addition, k_kill was changed to 0.10 to keep k_R at 1.35 (the same value used in the other scenario).

Figure 3.

Hypothetical 28-d dose responses for survival and reproduction where survival is less sensitive to endosulfan than reproduction. Model parameters were k_e = 0.25, k_kill = 0.10, RAF = 13.5, and no effect concentrations for survival and reproduction were 5 and 1 respectively.

RESULTS

Deterministic

All three 30-year exposure series have the same annual maxima for the 21-d running average concentrations (Table 2), and thus the same 90^th percentile value (0.772 ug/L). For this example, the mysid endosulfan chronic NOAEC is 0.27 ug/L (McKenny 1982) making the RQ for mysids 2.86. By design, this estimated risk was the same for all three time series.

Table 2.

Annual maximum daily concentration values based on 21-d running averages^a

Year	Maximum (ug/L)	Year	Maximum (ug/L)
1	0.147	16	0.462
2	0.185	17	0.572
3	0.754	18	0.691
4	0.759	19	0.631
5	1.135	20	0.377
6	0.468	21	0.478
7	0.585	22	0.971
8	0.724	23	0.598
9	0.532	24	0.890
10	0.402	25	0.419
11	0.531	26	0.468
12	0.623	27	0.561
13	0.453	28	0.625
14	0.663	29	0.324
15	0.522	30	0.575

^aThe 90^th percentile is between the 3^rd (year 24) and 4^th (year 4) highest values.

Probabilistic

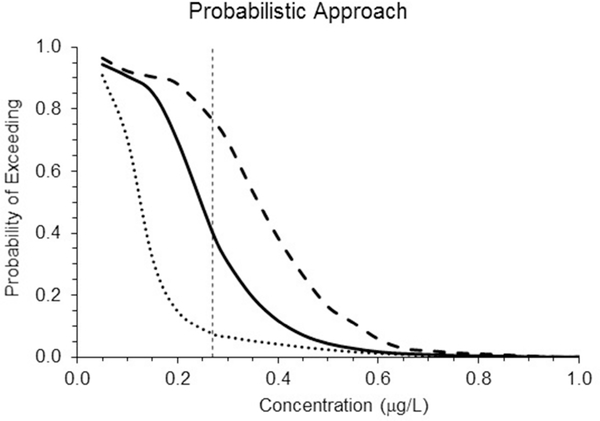
The cumulative distributions of the three endosulfan concentration exposure series are shown in Figure 4. Although the deterministic approach shows the same risk analysis for each of the three exposure scenarios, the probabilistic approach clearly shows differences among the three. The probabilities of exceeding the chronic value for mysids (0.27 ug/L) are 8, 40 and 76%, for the x0.5, original and x1.5 series, respectively.

Figure 4.

Probability of exceeding a given concentration within the 21-d running averages of the exposure data. The center solid line is for the “original” time series, the lower dotted line for the “x0.5” data, and the upper dashed line for “x1.5”. The vertical dashed line is the NOAEC chronic value for mysids exposed to endosulfan (0.27 μg/L).

Population modeling

Predicted mysid population declines for the three 30-year endosulfan exposures are shown in Figure 5. As an example, a 10% decline means that the threshold for counting was 90% of the control, and this occurred in approximately half of the weekly counts for the “x0.5” exposure time series. The areas under the curves are 14% for x0.5-time series, 35% for original time series and 52% for the x1.5-time series. The greater the area under a curve, the greater the overall probability of effect. Summary statistics using the IUCN thresholds for vulnerable, endangered and critically endangered populations are listed in Table 3. Note that the vulnerable category values are similar to those from the probabilistic approach, but this is likely coincidence.

Figure 5.

Summary of the chance of a given % decline in mysid population size relative to the control response for each of the three exposures. The x-axis represents the estimated decline in the mysid population relative to the control. The y-axis is the fraction of weeks within the time series where a given decline (or greater) was present. The center solid line is for the “original” time series, the lower dotted line for the “x0.5” data, and the upper dashed line for “x1.5”. Vertical dashed lines represent % declines corresponding to IUCN categories of vulnerable (30%), endangered (50%) and critically endangered (80%).

Table 3.

Summary statistics using the IUCN thresholds for Figure 5

		Probability of falling below cut off (%)
IUCN Thresholds	Cut off, % decline from control	x0.5	Original	x1.5
Vulnerable	30	19	52	75
Endangered	50	4	29	51
Critically Endangered	80	0	4	19

Acute scenarios.

The population modeling results from the comparison with different acute toxicity kinetics are plotted in Figure 6—the acute dose responses for both model runs had the same 96 hr LC50, but significantly different LC50 vs time scenarios. Only the data from the “original” exposure time series (Figure 6, bottom) are displayed. However, the results for the other two exposure time series were similar. The modeled population responded quicker when the 24 hr LC50 value was closer to the 96 hr LC50 value, but displayed a larger decline when the 24 hr value was greater than the 96 hr value.

Figure 6.

Time series for population size relative to the control response showing two LC50 kinetic scenarios (top)—elimination kinetic constants were 0.025 d⁻¹ (dashed line, 24 hr LC50 greater than 96 hr value) and 1.25 d⁻¹ (solid line, 24 hr LC50 approximately equal to 96 hr value). For comparison, the daily concentration time series is shown (bottom).

Chronic scenarios.

The modeling outputs for two different survival-reproduction toxicity scenarios are plotted in Figure 7. The NOAEC for each was similar and based on reproduction. Only the results for model runs using the original time series are shown, but as with the acute scenarios the relative results for the other two exposure time series were similar.

Figure 7.

Summary of the chance of % decline in population size relative to the control for the original exposure time series. The data represent two different chronic test data scenarios. For the Survival = Repro scenario the dose response data for reproduction and survival were similar (see Figures 1 and 2). For the Survival < Repro model run survival was set to be less sensitive than reproduction, while keeping the reproduction doseresponse like that in the other run (see Figure 3). The area under the Survival = Repro curves is 35% and the area under the Survival < Repro is 5%.

DISCUSSION

We successfully coupled toxicokinetic-toxicodynamic and matrix population models for risk evaluations of 30-year exposure time series. Most significantly, we demonstrated how this coupling can refine current risk assessments by using only results from standard toxicity test data. Ecological risk assessments for pesticides in the United States involve a complex exposure characterization and effects assessment, which are then combined into a final risk characterization. The effect and risk characterizations are applied to a broad range of freshwater, marine and terrestrial organisms, as well as to both acute and chronic effects scenarios. We restricted our evaluation to the marine invertebrate, Americamysis bahia, however, there is no reason this approach cannot be accomplished for any of the standard species used in pesticide risk assessments. Clearly, we are not the first to recognize and promote the value of population modeling in moving beyond the current standard use of single species toxicity tests based on the response of individuals (see reviews in Forbes et al. 2008 and Forbes et al. 2016), or the use of standard toxicity data (Ashauer et al. 2013). In the past, however, most of the emphasis on this value focuses on the ability of population models to merge lethal and sublethal endpoints into a single endpoint (e.g., population growth rate, or population recovery rate), as well as on the ability of TK-TD models to integrate time-varying exposure series. These are certainly very valuable attributes; however, population models still are rarely used in regulatory risk decisions (Raimondo et al. 2018). Regulatory programs still primarily rely on empirical toxicity data as the evaluation of choice. Modeled output for exposure is readily accepted—for the evaluation of exposure scenarios that are difficult if not impossible to evaluate empirically. Why not the same acceptability for effects predictions?

One reason could be the perception that population models are too complex to adequately derive the variety of needed parameters. As one paper expressed it, some of the more sophisticated effects models are “data hungry” (Jager et al 2014). This is not a good reason to avoid effects models altogether while we wait on test guidelines to catch up to model data needs. We have added to the growing number of analyses showing the ease and utility of TK-TD/population models. We have done this by emphasizing the use of data already submitted during the registration process for pesticides. These data were used in comparisons among population modeling results and more “traditional” risk assessments.

In our initial comparisons, risk characterization began with a simple deterministic approach whereby risk quotients (RQ) were calculated by dividing estimated environmental concentrations by the mysid’s chronic value. Because the three 30-year time series were created to contain the same annual maxima, they all had the same RQ—2.86. This value was compared against an established level of concern (LOC) for chronic risk to aquatic animals (see Chapter 5 in USEPA 2010). The RQ exceeded the LOC value of 1, therefore there is the potential for chronic risk to marine invertebrates. However, this first tier approach could make no distinction in terms of risk among the three very different time series. The more inclusive probabilistic approach creates an obvious distinction among the three exposure time series. The probabilistic approach, however, cannot distinguish among a variety of potential toxicological or exposure scenarios. These include fast versus slow acute kinetics, potential differences in survival versus reproduction effects, and distinguishing differences caused by the timing of a spike in exposure concentration. For this latter case, the probabilistic approach only displays how many times within 30 years that a give concentration occurs. It cannot, for example, even distinguish between an impactful concentration occurring 30 times within a single year and the same concentration only occurring once a year for 30 years. Because TK-TD modeling can track time-varying concentrations, population modeling which includes TK-TD can easily distinguish between these.

Where the utility of population models was best demonstrated, and perhaps will best demonstrate their usefulness in the refinement of risk assessments, was to distinguish between difference in toxicological scenarios. We chose comparisons using plausible differences in toxicity situations that traditional assessments are not designed to detect. Yet with some simple refinements this need not be the case. One of these scenarios focused on TK-TD differences with otherwise similar standard acute toxicity data summaries (i.e., similar 96 hr LC50 values). While the k_e value for an individual species/toxicant combination is generally assumed to be constant, k_e values can vary substantially among species (Rubach et al. 2010). The effects on population size are not always intuitive. The more similar a 24hr LC50 is to a 96 hr LC50 the quicker a species internal concentration responds to a change in the environmental concentration for a given 96 hr LC50—fast kinetics. One might be tempted to assume that this would mean greater potential mortality, thus a greater effect on the number of individuals in the population. The greater the k_e value, the faster the kinetics, also means the quicker the internal concentration declines when the environmental concentration declines. When the acute kinetics are such that the 24 hr value is significantly greater than the 96 hr value, a peak in exposure may pass before the full potential mortality is realized. However, this also means the internal concentration may not decline quickly when a peak occurs, thus allowing continual increase in the internal concentration—and greater overall mortality. In the example we present, the case with the lower 24 hr LC50 is less detrimental to the population growth. Coupling TK-TD and population models gives a refinement that aids in distinguishing among exposure time series. It is worth noting that the distinction revealed with these differences in k_e values was within the same 30-year time series. The traditional risk evaluation would have assigned the same risk under both conditions (because the 96 hr LC50s were the same).

Being able to accommodate differences in toxicokinetics is only one value demonstrated by our evaluations. Linking population modeling with TK-TD adds an additional refinement that cannot be accomplished with traditional risk assessments. While the probabilistic approach also used all the exposure data, and clearly differentiated among the three different 30-year time series, it is not designed to distinguish between the toxicity scenarios we presented. It is easy to envision a set of chronic toxicity data within which reproduction is significantly impaired, yet survival is little effected—as well as a data set within which reproduction and survival have similar concentration responses. We present a compelling argument for the utility of coupled TK-TD and population models in distinguishing between these two data situations. The way we set up these two situations, the chronic values (based on the NOAEC for reproduction) were the same—therefore the expected chronic risk based on traditional assessments of a given time series would be the same. However, the model runs where both survival and reproduction had similar dose responses to endosulfan had a higher probability of decline than those model runs where reproduction is essentially the only effected parameter. This is consistent with earlier assertions that reproduction generally has a lower elasticity than other life cycle traits, especially among small invertebrates (Forbes et al. 2010). We also tested the scenario where survival was the basis for the NOAEC and reproduction had similar sensitivity as survival or no effects at all (results not shown). The results of these two scenarios were not very different, largely because the matrix reproduction parameter was a function of both survival and maternity rate (see Caswell 2001, equation 2.34). So even though we could eliminate toxic effects on the number of offspring per female, the model still shows a reproductive effect because of effects on female survival rate.

Including a TK-TD/population model is not a cure-all for risk characterizations. We can calculate an effect relative to a control response and provide an estimate of the probability of decline below a threshold. A challenge with this approach is the selection of a population threshold. One solution is to use thresholds that have already been established. For example, the World Conservation Union (IUCN 2012) defines a population as vulnerable if a 30% decline is observed over a specified amount of time or number of generations. A population is endangered if there is a 50% decline, and critically endangered if an 80% decline is observed. While the IUCN uses different data than those calculated herein, their thresholds present a useful starting point for establishing biologically significant thresholds. The issue of “what is ‘biologically significant’ is a major problem in conservation biology and does not seem to have easy solutions” and it is more a policy decision which should be agreed upon by consensus (Reed and Blaustein 1997).

An alternate approach to summarizing population model results, that solves the problem of what threshold to select, is to use a series of thresholds. This approach calculates the area under a curve that plots probability of decline against a full range of thresholds. This is analogous to population viability risk curves, where the area under the curves represents the change in the expected minimum population size (Burgman et al. 1993). Our population data are not the same as those used in the quasi-extinction definition of risk in Burgman, et al. (1993). The concept, however, of relating total risk to the area under the curve is similar. The decision of what constitutes a biologically significant probability of risk still looms. Establishing an acceptable change in area under the “risk curve” still requires consensus, and is still a science-policy decision. We may be better able to understand and feel more comfortable defending a population modeling endpoint compared to the probability of a chronic value being below exposure data; however, we cannot eliminate the need for judgement.

Coupled TK-TD/population models are a convenient mathematical method to integrate multiple sources of effects (e.g., effects on survival and reproduction) into a single endpoint. We must keep in mind that applying population modeling for interpreting a time series of exposure does not automatically mean greater sensitivity of a species to that time series relative to the single endpoint (e.g., RQ approach). It just gives us greater ability to explain and characterize risk according to time-varying exposures. When examining only organism-level data, large effects on the demographic rates (e.g., survival or reproduction) do not necessarily translate into large population growth rate (Caswell 1996). In other words, a compound cannot be assumed to cause the same degree of effect on population growth rate as it does on survival or reproduction. This phenomenon is true for a variety of exposure scenarios with A. bahia (Raimondo and McKenney 2006; and Grear 2016). Similarly, nematode reproduction is more sensitive to cadmium than juvenile period (duration as juvenile); however, change in juvenile period has a greater effect on population fitness than does effects on reproduction (Kammenga et al. 1996). Clearly, species that have different life history strategies can respond differently to a stressor producing responses of similar type and magnitude at the individual level (Stark et al. 2004; Baveco et al. 2014).

Population models hold great promise for integrating exposure, toxicity and life history information into meaningful measures of risk. The value added from population modeling is the ability to distinguish among risks due to differences in toxicity kinetics, as well as differences in patterns of exposure time series. The acute and chronic scenarios we presented clearly indicate the potential for enhancing risk assessments through coupling TK-TD and population modeling—without requiring new toxicity test guidelines. Several circumstances can occur wherein population modeling results in different risk conclusions than do assessments based on more traditional endpoints such as LC50s, NOAECs and RQs. Population modeling provides a more complete assessment of the potential risk of a time-varying exposure. In the future, with wider acceptance of TK-TD and population modeling in the regulatory arena, standard regulatory toxicity test procedures may change to reflect the need for better derivation of model parameters. In the meantime, we have shown that existing toxicity data requirements are effective in the application of simple population models. We stress that our purpose was not to promote a definitive model, but rather to quantify the ability of these types of models to distinguish among various exposure time series, as well as among different toxicological features. We presented output for the same time series wherein very different risk conclusions can result from choice of determinate, probabilistic or population modeling approaches. Population models clearly refine the evaluation of toxicant exposure time series, and can be a significant part of a tiered assessment approach. However, such models do not have to be relegated to later tiers. Population modeling can be incorporated into the first levels of risk evaluation using existing required toxicity data. If an initial population modeling effort using minimal toxicity data demonstrates the potential for a significant risk, higher tiered efforts can require more complex toxicity testing, yet still use the same modeling approach. We demonstrated a way for regulatory programs to incorporate TK-TD and population models using existing data until improvements are made to modeling and test guidelines.

Next steps

It is tempting to make a list of ways within which existing population models or standard toxicity tests could be improved to meet regulatory needs. These might include refinements for the inclusion of sublethal effects in TK-TD models, or changes to toxicity test guidelines to accommodate modeling needs. These latter needs could include measured internal concentrations to estimate recovery kinetic parameters (Jager et al 2011), or post exposure monitoring within existing test protocols to evaluate carryover effects (Ashauer, et al. 2010; Galic et al. 2014). Additional work comparing the outputs among models of different complexities would be useful (e.g., Baveco et al. 2014), as well as guidance on when different levels of complexity are justified. Models and test guidelines can always be refined; however, until some sort of effects modeling is deemed acceptable (i.e., required) in formal risk assessments, all the refinement in the world will not matter. Hunka et al. (2013) provide an interesting analysis of stakeholders’ perspectives on applications of ecological modeling to pesticide risk assessments. The authors list a variety of obstacles to the acceptability of population models for regulatory use. It is interesting that most obstacles appear to have less to do with the above refinements, and more about communication between model makers and model users (i.e, risk managers). Raimondo et al. (2018) confirm that the issue of lack of population model use is less about scientific limitations and more about proper guidance on model selection in output interpretation, that is, communication.