Role of income mobility for the measurement of inequality in life expectancy

Significance Statement

People in the bottom of the income distribution live shorter lives than those in the top. This is an important dimension of inequality in society. We demonstrate how forces of income mobility are important for conclusions about inequality in life expectancy. Some people escape poverty, and many people at the top of the distribution only have high incomes temporarily. Those moving out of an income class have very different mortality patterns than those staying. We provide a method that incorporates income mobility in calculations of life-expectancy inequality. The good news is that the degree of inequality in life expectancy is only half as big once accounting for income mobility. The bad news is that inequality continues to rise.

Abstract

This work proposes a method to compute the income gradient in period life expectancy that accounts for income mobility. Using income and mortality records of the Danish population over the period 1980–2013, we validate the method and provide estimates of the income gradient. The period life expectancy of individuals at a certain age, and belonging to a certain income class, is normally computed by using the mortality of older cohorts in the same income class. This approach does not take into account that a substantial fraction of the population moves away from their original income class, which leads to an upward bias in the estimation of the income gradient in life expectancy. For 40-y-olds in the bottom 5% of the income distribution, the risk of dying before age 60 is overestimated by 25%. For the top 5% income class, the risk of dying is underestimated by 20%. By incorporating a classic approach from the social mobility literature, we provide a method that predicts income mobility and future mortality simultaneously. With this method, the association between income and life expectancy is lower throughout the income distribution. Without accounting for income mobility, the estimated difference in life expectancy between persons in percentiles 20 and 80 in the income distribution is 4.6 y for males and 4.1 y for females, while it is only half as big when accounting for mobility. The estimated rise in life-expectancy inequality over time is also halved when accounting for income mobility.

Life expectancy is strongly associated with income across societies and within societies (1–8). The relationship between income class and life expectancy within a society is important for evaluating equity and assessing the costs and benefits of public health and social security policies (9–14). It is well established that mortality is decreasing in income across individuals, and this relationship is used to estimate the association between income and life expectancy (6–8, 10, 15). An impressive recent study (7) provides nonparametric estimates of the association between income class and period life expectancy using tax return data for the US population and shows that those in the top of the income distribution at age 40 can expect to live nearly 15 y longer than those in the bottom of the distribution.

The calculation of period life expectancy for a given age group in a given year uses life tables with information about mortality of older cohorts to estimate future mortality. In an unchanging society, in which mortality rates are constant, period life expectancy will equal the observed average life length. Period life expectancy is, therefore, a useful summary measure of cross-sectional mortality rates in a given year and is often used to study trends in mortality (16).

When segregating period life expectancy by income class, the mortality of older cohorts in the same income class is used to estimate future mortality. This approach assumes that individuals stay in the same income classes over time, which is in contrast to evidence in economics and sociology documenting significant income mobility (17). As a consequence, estimates of period life expectancy of the different income classes will in general not be equal to the observed average life length, even when considering an unchanging society in which mortality and mobility rates are constant. Some of the individuals originally in the top of the income distribution within their cohort will move down in the distribution, while individuals in the bottom of the distribution will tend to move up. Therefore, the method assigns too-high future mortality rates to low-income classes and too-low rates to high-income classes. This creates an upward bias in the estimation of the income gradient in period life expectancy (18).

To see the potential quantitative importance, consider the extreme case of perfect mobility, where income in 1 y is uncorrelated with income in preceding years. In this case, life expectancy of individuals alive 1 y from now is independent of their current income class, even when mortality rates vary strongly with income at each age. Estimates not accounting for income mobility would then point to a large income gradient in period life expectancy for these individuals, although the true gradient is zero.

Table 1 uses our data to illustrate the actual degree of income mobility in society and its importance for predicting future mortality of different income classes. Among 40-y-old males belonging to the bottom 5% of the income distribution, nearly half of those alive at age 50 (45% to be exact) have moved up in the income distribution (labeled movers), while the remaining half have stayed in the bottom part of the distribution (labeled stayers). Similarly, among individuals in the top 5% of the distribution, about half are movers, moving down in the income distribution, while the other half are stayers. This mobility across income classes is important for predictions of future mortality. During the subsequent 10 y, from age 50 to 60, we find that 29% of the stayers in the bottom part of the distribution die, but only 13.5% of the movers die. We observe the reverse pattern in the top of the distribution, where 3.5% of the stayers die, while 5% of the movers die. This example illustrates the potential for more accurate predictions of future mortality and life expectancy by income groups if it is possible to account for mobility across income classes.

Table 1.

Income mobility and mortality by income class

	Income class
	Bottom 5%		Top 5%
Outcome	Movers	Stayers	Movers	Stayers
Share of income class, %*	45	55	53	47
10-y mortality, %†	13.4	29.0	4.9	3.5

The sample includes 40-y-old males in the bottom 5% or top 5% income class and surviving until age 50.

^*The share of stayers (same income class at age 50) and movers (another income class at age 50).

^†Mortality from age 50–60 of the different groups.

Size of Income Gradient in Life Expectancy When Accounting for Income Mobility

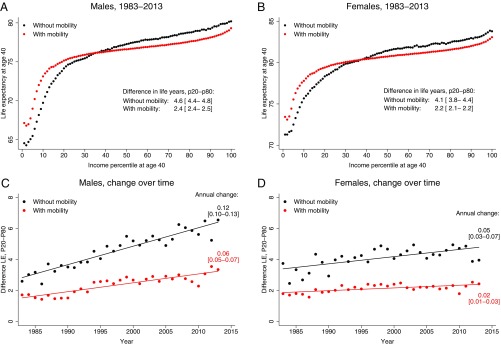
We incorporate a classic model of social mobility to account for movements across income classes in the measurement of the income gradient in period life expectancy. The approach is described below, and details about how to apply the method to data are provided in SI Appendix, SI Text. Fig. 1 displays the main results of applying the method to the data for the Danish population. Because we use population data, the average life expectancy in Fig. 1 matches official statistics from Statistics Denmark. Fig. 1 A and B display nonparametric evidence of the association between income class at age 40 and period life expectancy for males and females, respectively. The individuals are divided into 100 socioeconomic groups according to their percentile rank in the household income distribution at age 40. The black dots plot period life expectancy by income class when ignoring income mobility. The red dots account for income mobility. Fig. 1 A and B show the relationship estimated on pooled data for the period 1983–2013. When ignoring mobility, individuals in the top percentiles of the income distribution at age 40 can expect to live $\sim$15 y longer than those in the bottom of the distribution, which resembles recent evidence for the United States (7). The steep income gradient at the bottom of the distribution reflects the presence of disability benefit recipients (SI Appendix, SI Text). If we focus on individuals in the middle part of the distribution, from percentile 20 to 80, then the relationship is almost linear, with a slope of 0.070 for males and 0.063 for females. Hence, moving up 10 percentiles in the income distribution increases life expectancy by 8.4 mo for males and 7.6 mo for females.

Fig. 1.

Association between income class at age 40 and period life expectancy when not accounting for income mobility (black dots) and when accounting for income mobility (red dots). Income class is measured by the percentile rank in the income distribution of the individuals. The 95% confidence intervals are reported in brackets. (A and B) The relationship estimated by using pooled data for the 30-y observation period for males (A) and females (B). (C and D) The differences in life expectancy between percentiles 20 and 80 for each year during the 30-y period for males (C) and females (D).

When accounting for income mobility, life expectancy is about the same at percentiles 35–40, but substantially lower at higher percentiles and higher at lower percentiles. For example, the life expectancy of males at the 80th percentile is 77.6 y instead of 78.8 y, while at the 20th percentile, it is 75.2 y instead of 74.2 y. The difference between the 20th and 80th percentiles of 4.6 y for males and 4.1 y for females is only half as large for both genders after accounting for mobility.

Fig. 1 C and D display the difference in life expectancy between percentiles 20 and 80 over the 30-y period available in the data. The graphs reveal increasing inequality in life expectancy over time for both males and females, which is in line with other recent studies (7, 10, 12–14, 19). However, the change over time is less dramatic when accounting for income mobility. For males, the difference in life expectancy increases from $\sim$2.5 y at the beginning of the period to $\sim$6.5 y at the end of the period when not accounting for mobility. This increase of 4 y reduces to <2 y when we account for mobility.

The change over time in the mobility-corrected gradient could, in principle, be caused by changes in the degree of income mobility. However, in SI Appendix, SI Text, we show that income mobility is very stable over time and that the increasing income gradient in life expectancy is driven entirely by a rising income gradient in mortality. A change in the income gradient in mortality simply has half as much pass-through on the income gradient in life expectancy when accounting for the movements of people between income classes.

Method to Account for Income Mobility

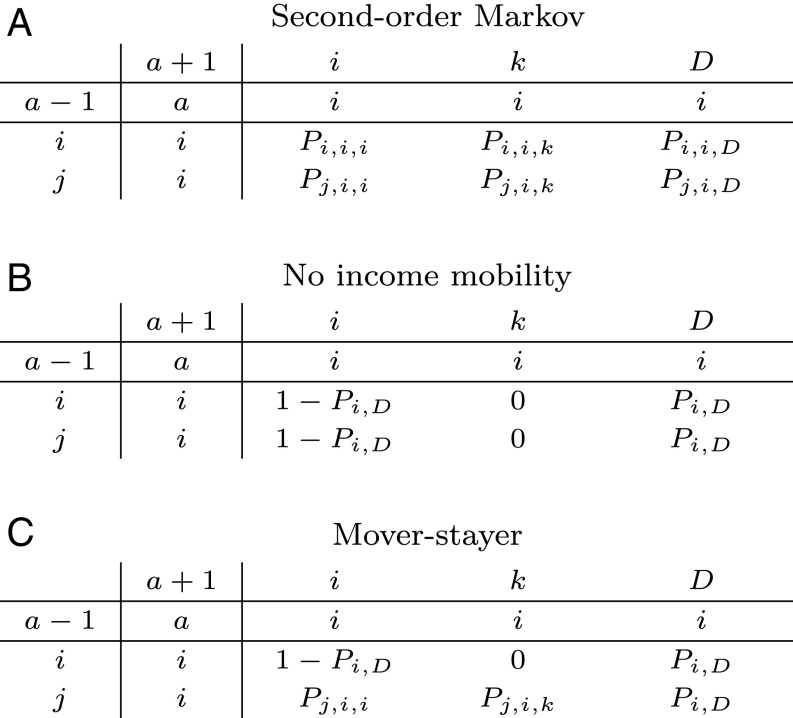
Changes in socioeconomic status over time are often described by transition matrices (17). Fig. 2 illustrates three versions of a transition matrix $T_a^{a+1}$ describing the likelihood of individuals moving from one state at age $a$ to another state at $a+1$ conditional on being in certain states at ages $a$ and $a-1$. The state space consists of the different income classes and an absorbing state, $D$, capturing death. Hence, the number of rows and columns in the matrix depends on the number of income classes in the empirical application (e.g., the 100 classes in Fig. 1). To focus on the key mechanisms, Fig. 2 shows only a segment of the matrix. $P_{j,i,k}$ and $P_{j,i,D}$ in matrix $A$ (Fig. 2A) denote the probabilities that an individual in the income classes $j$ and $i$ at ages $a-1$ and $a$ moves to income class $k$ or the death state, $D$, at age $a+1$.

Fig. 2.

Illustration of transition matrices for different models of social mobility.

Under the (Markov) assumption that the transition probabilities are homogenous across individuals, the transition probabilities $P_{j,i,k}$ and $P_{j,i,D}$ can be estimated by calculating the share of individuals with a given income history $\left(j,i\right)$ transitioning to income class $k$ and death state $D$ in the data.

To predict the future mobility and mortality of individuals at the initial age $â$ (40 y in our analysis), we start by creating a distribution matrix $K_{â}$, which represents the initial distribution of individuals over the states at ages $â-1$ and $â$. We then multiply this distribution matrix by the transition matrix, $T_{â}^{â+1}$, and thereby obtain a new distribution matrix, $K_{â+1}=K_{â}\cdot T_{â}^{â+1}$, giving the unconditional bivariate distribution of individuals across income classes and death at ages $â$ and $â+1$. By continuing this multiplication, we may use transition matrices to obtain a distribution matrix, $K_{â+t}$, for any given age, $â+t$, and, therefore, a prediction of both mobility and mortality at all ages. From the mortality rates, it is then straightforward to derive survival curves, which we use to compute period life expectancy conditional on initial income classes.

It is well known that standard Markov models are not good at predicting income mobility (20, 21). For example, the second-order Markov model, illustrated in matrix $A$, overestimates the degree of mobility across income classes. Nonetheless, using first- or second-order Markov models provides better predictions of future mortality by income class than assuming no mobility (results are in SI Appendix, SI Text). Our preferred specification is a mover–stayer model (22–24), which produces accurate predictions of both income mobility and future mortality using the same data. This model is illustrated in matrix C in Fig. 2C and is a hybrid of the second-order Markov model illustrated in matrix A (Fig. 2A) and the standard model without income mobility illustrated in matrix B (Fig. 2B). In the standard model, mortality rates depend on social class $i$. However, if an individual survives from $a$ to $a+1$, then the individual is assumed to stay in the same income class $i$, and, therefore, the probability of moving from group $i$ to group $k$ is zero in matrix B.

The mover–stayer model divides individuals at a given age $a$ into “movers” and “stayers.” A stayer is an individual who stayed in the same socioeconomic class from $a-1$ to $a$, while a mover is an individual who moved income class from $a-1$ to $a$. Stayers are simply assumed to stay in the same income class at $a+1$ if they survive, corresponding to the case of no mobility (the first rows are identical in matrices B and C). Movers may move into all socioeconomic classes at age $a+1$, and the transition probabilities are estimated in the same way as in the second-order Markov model. After having estimated transition matrix C for each age group, the procedures to obtain survival curves and life expectancies are the same as described above for the second-order Markov model. The details are described in SI Appendix, SI Text, and Stata code to apply the method is included in SI Appendix.

Validating the Methods

The availability of individual-level information about income and mortality over three decades allows us test the methods and the importance of accounting for income mobility. For this purpose, we follow cohorts of males males aged 40 in 1983–1993 over a 20-y period from age 40 to 60 and compare the predictions of mortality for an income class to the historically observed actual mortality rates. Even without income mobility, these historical mortality rates measured across time for a given cohort, as used in cohort life expectancy, may differ from mortality rates measured across cohorts for a given time, as used in period life expectancy (16). To eliminate this discrepancy in the validation exercise, we base the prediction of future mortality for the 40-y-olds on the observed mortality rates by income and time of their own cohort. For example, in the no-income-mobility model, the predicted future mortality of individuals who are in a certain income class at age 40 uses the mortality of individuals from their own cohort who are in this income class later in life. If the assumption of no income mobility is correct, such that individuals’ income class is the same at age 40 and later in life, then predicted and actual mortality rates would be identical.

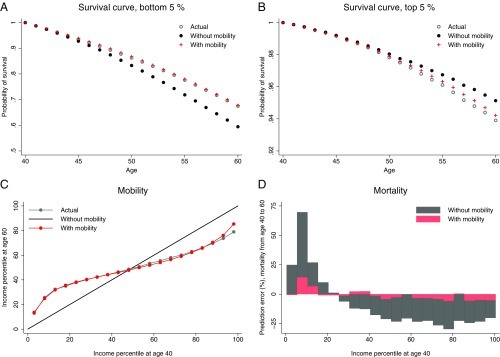
Fig. 3 A and B show the actual survival curves of individuals who belong to the bottom 5% and the top 5% of the income distribution at age 40 (open circles). We compare these survival curves to the predictions assuming no income mobility (filled circles) and when accounting for income mobility (red plusses). The graph shows that the prediction error becomes larger when moving forward in time—this is particularly the case when assuming no income mobility. For 40-y-olds in the bottom 5% of the income distribution, the risk of dying before age 60 is estimated to be 40% when not accounting for income mobility, while, in reality, only 32% of the group died, which is an overestimation of 25%. The estimation error amounts to <1% when accounting for mobility. For a person in the top 5% income class, the risk of dying is predicted to be 5% without accounting for mobility, while in reality 6.1% of the group died, corresponding to an underestimation of 20%. This estimation error is only 5% when accounting for mobility.

Fig. 3.

Illustration of the ability of the methods to predict income mobility and future mortality by income class for males. (A) Actual survival curves of persons in the bottom 5% of the income distribution at age 40 and the predictions based on whether income mobility is accounted for or not. (B) Similar survival curves displayed for the top 5% income class. (C) Actual and predicted income class at age 60 conditional on income class at age 40. (D) Percentage error in the prediction of mortality from age 40 to 60 by income class.

Fig. 3C evaluates how well the method accounts for income mobility. It displays the predicted average position in the income distribution at age 60, as well as the actual position, against the position in the income distribution at age 40 for individuals who survive until age 60. The assumption of no mobility across income classes corresponds to the 45-degree line. Perfect mobility would correspond to a predicted average percentile rank of 50, independent of initial income class. Fig. 3C shows that individuals initially positioned above the average in the distribution tend to move downward over time, while individuals below average tend to move upward, corresponding to statistical mean reversion. Individuals in percentile 20 at age 40 will, on average, end up in percentile 35 at age 60, while individuals in percentile 80 at age 40, on average, end up in percentile 65. Hence, at age 60, these individuals are halfway to the average income rank of 50, implying that the level of mobility in the data are halfway between no income mobility and perfect income mobility. As is apparent from Fig. 3C, the predicted average income class at age 60 of the mover–stayer model is quite close to the actual income class. The largest prediction error is in the top of the distribution, but the error is small compared with assuming no mobility.

Fig. 3D shows the percentage error in the prediction of the death rate from age 40 to 60 across the different income classes. Fig. 3D reveals a systematic bias when not accounting for income mobility and mirrors the systematic error in the survival curves in Fig. 3 A and B. The predicted probability of dying is up to 70% higher than the actual death rates in the bottom part of the distribution. The prediction errors are also large in the upper half of the distribution, where predicted death rates are $\sim$25% lower than actual death rates for each income group. For all income classes, mortality is much better predicted by accounting for income mobility in the measurement, and for most income classes, the prediction error is very small in this case.

The validation exercise is based on in-sample predictions. We reach the same conclusions if we split our panel dataset into two equally sized random samples: one sample to estimate the model parameters and one sample to test predictions of mobility and mortality (results are provided in SI Appendix, SI Text).

Inequality in Life Expectancy at Older Ages

Our main analysis focuses on inequality in life expectancy at age 40. Validation exercises in SI Appendix, SI Text show that the mover–stayer model also accurately predicts future mobility and mortality by income class at older ages. Table 2 presents estimates of the inequality in period life expectancy at ages 40, 50, 60, 70, and 80 with and without accounting for income mobility. The difference in life expectancy between percentiles 20 and 80 is lower at older ages. Without income mobility, the difference is 4.6 y at age 40; 3 y at age 60; and 0.9 y at age 80. When accounting for income mobility, the inequality in life expectancy is half as big at age 40, two-thirds as big at age 60, and identical at age 80. Thus, income mobility is less important for the measurement of inequality in life expectancy at older ages, but for individuals surviving this long, the remaining inequality in life expectancy is also much smaller.

Table 2.

Inequality in period life expectancy at older ages

Method	Difference in life expectancy p20–p80 at age:
	40	50	60	70	80
Without income mobility	4.6	3.9	3.0	2.1	0.9
With income mobility	2.4	2.5	2.0	1.9	0.9

p20, percentile 20; p80, percentile 80.

Concluding Remarks

In the empirical application, accounting for income mobility halves the income gradient in life expectancy as well as the change over time in the gradient. In the following, we report a number of additional results supporting our approach (details are provided in SI Appendix, SI Text). First, we address whether it is possible to obtain more precise estimates using other approaches. For example, we analyze alternative ways to account for income mobility in the estimation of the income gradient. These alternatives, without being exhaustive, also yield a smaller income gradient compared with the assumption of no mobility. They are also better at predicting mobility and mortality in the validation test, but are outperformed by the mover–stayer model. Another alternative approach is to maintain the assumption of no mobility across income classes, but divide people into these classes based on average income over several years. This improves the performance of the no-mobility model slightly, but it requires more data and remains strictly dominated by the mover–stayer model of social mobility.

Second, we apply our method to other environments. Our main results are based on full population data for Denmark. We show, using standard survey data on household income for the United States, that the mover–stayer model also predicts income mobility in the United States well. By combining this result with recent empirical evidence for the United States on the association between income classes (income percentiles as in our study) and period life expectancy, we provide suggestive evidence that the association for the United States would also be more than halved when accounting for income mobility compared with assuming no mobility.

Third, we show that the incorporation of income mobility into the measurement of inequality in life expectancy also works well with 5, 10, or 20 income groups instead of 100 income percentiles.

Fourth, socioeconomic status is commonly measured by income. Another simple cardinal measure commonly used is length of education (25). This measure is independent of social mobility, but a well-known drawback is that it is difficult to make education groups that are comparable across cohorts, which is needed to get accurate estimates of the association between education and period life expectancy (13). Furthermore, we show that, even within education groups, income class is a strong predictor of life expectancy and that these education-specific income gradients are also halved when incorporating income mobility.

Data and Methods

The empirical analyses are based on population-wide Danish administrative data provided by Statistics Denmark and are known to be of high quality (26). Here, we describe the data sources and how access to the data is obtained. The project was carried out under Agreement 2015-54-0993 between The Danish Data Protection Agency and Statistics Denmark. The project was approved by Statistics Denmark and has Project no. 704838. There is no Danish institutional review board for studies based on standard register data at Statistics Denmark. The analyses were conducted on a secure server hosted by Statistics Denmark and owned by the Department of Economics, University of Copenhagen. All empirical analyses were carried out with the software STATA (Version 14) using the secure internet interface of Statistics Denmark. Project 704838 has its own directory where data and programs are stored. Individual-level information from the administrative registers is confidential according to the Danish Administrative Procedures (Section 27) and the Danish Criminal Code (Section 152), implying that the data used for the analysis cannot be made publicly available. However, independent researchers who receive approval by a Danish university, business school, or research institute can apply for access to Statistics Denmark. They can use the program code included in SI Appendix, also stored on the server, to reproduce all of the results reported in the paper and in SI Appendix, SI Text. We will assist in any way we can with this procedure. The data for the main analysis were created by linking individual-level information from the population registers BEF and FAIN, the death registers DODSAARS and DODSAASG, and the income register IND using the Danish personal identifier (called the CPR number in Danish). Additional information about the empirical methodology and the full set of results are provided in SI Appendix, SI Text.