Significance
The jamming transition is a key property of granular materials, including sand and dense suspensions. In the generic situation of nonspherical particles, its scaling properties are not completely understood. Previous empirical and theoretical work in ellipsoids and spherocylinders indicates that both structural and vibrational properties are fundamentally affected by shape. Here we explain these observations using a combination of marginal stability arguments and the replica method. We unravel a universality class for particles with internal degrees of freedom and derive how the structure of packings and their vibrations scale as the particles evolve toward spheres.
Keywords: jamming, glass, marginal stability, nonspherical particles
Abstract
Amorphous packings of nonspherical particles such as ellipsoids and spherocylinders are known to be hypostatic: The number of mechanical contacts between particles is smaller than the number of degrees of freedom, thus violating Maxwell’s mechanical stability criterion. In this work, we propose a general theory of hypostatic amorphous packings and the associated jamming transition. First, we show that many systems fall into a same universality class. As an example, we explicitly map ellipsoids into a system of “breathing” particles. We show by using a marginal stability argument that in both cases jammed packings are hypostatic and that the critical exponents related to the contact number and the vibrational density of states are the same. Furthermore, we introduce a generalized perceptron model which can be solved analytically by the replica method. The analytical solution predicts critical exponents in the same hypostatic jamming universality class. Our analysis further reveals that the force and gap distributions of hypostatic jamming do not show power-law behavior, in marked contrast to the isostatic jamming of spherical particles. Finally, we confirm our theoretical predictions by numerical simulations.
Upon compression, an athermal system consisting of purely repulsive particles suddenly acquires finite rigidity at a certain jamming transition density at which constituent particles start to touch each other, producing a finite mechanical pressure (1–3). The jamming transition is observed in a wide variety of physical, engineering, and biological systems such as metallic balls (4), foams (5, 6), colloids (7), polymers (8), candies (9), dices (10), and tissues (11). In the past decade, a lot of progress has been made in understanding the jamming transition of spherical and frictionless particles with repulsive interactions. Key findings involve (i) the power-law behaviors of the elastic modulus and contact number as a function of the proximity to (6, 12, 13), (ii) the emergence of excess soft modes in the vibrational density of states (6), and (iii) the power-law divergence of the gap distribution function and power-law tail of the force distribution function at (6, 14–16). Those phenomena can be understood in terms of a marginal stability principle (17, 18): The system lies close to a mechanical instability. More precisely, at , the contact number per particle is (4, 6), which barely satisfies Maxwell’s mechanical stability condition (19). Accepting marginal stability as a basic principle, one can successfully predict the critical exponents of soft spheres (17, 18) and derive a scaling relation between critical exponents of hard spheres (20–23). The importance of marginal stability is also highlighted by exact calculations for hard spheres in the large-dimension limit (15) and in a perceptron model of the jamming transition (24–26). These first-principle calculations prove that a full replica symmetric breaking (RSB) phase transition occurs ahead of the jamming transition. In the full RSB phase, the eigenvalue distribution function is gapless, and thus the system is indeed marginally stable (24). This approach provides exact results for the critical exponents, which agree well with the numerical results (15), once localized excitation modes are carefully separated (16, 22).
However, a system of spherical particles is an idealized model and, in reality, constituent particles are, in general, nonspherical. In this case, one should specify the direction of each particle in addition to the particle position. The effects of those extra degrees of freedom have been investigated in detail in the case of ellipsoids (2, 3, 9, 27–32). Notably, the contact number at the jamming point continuously increases from the isostatic value of spheres, as , where denotes the deviation from the perfectly spherical shape. The system is thus hypostatic: The contact number is lower than what is expected by the naive Maxwell’s stability condition, which would predict where is the number of rotational degrees of freedom per particle (9, 28, 29). As a consequence of hypostaticity, has anomalous zero modes at , which are referred to as “quartic modes” because they are stabilized by quartic terms of the potential energy (29–32). Hypostatic packings are also obtained for spherocylinders (33–37), superballs (38), superellipsoids (39), other convex-shaped particles (40), and even deformable polygons (41). Compared with spherical particles, the theoretical understanding of the jamming transition of nonspherical particles is still in its infancy (29, 42). In particular, the physical mechanism that induces a scaling behavior such as is unclear.
In this work, we propose a theoretical framework to describe the universality class of hypostatic jamming. As a first example of universality, we map ellipsoids into a model of “breathing” spherical particles (BP), recently introduced in ref. 43. Based on the mapping, we show that the two models indeed have the same critical exponents by using a marginal stability argument. Next, we propose a generalization of the random perceptron model that mimics the BP and can be solved analytically using the replica method. We confirm that this model is in the same universality class of ellipsoids, BP, and other nonspherical particles that display hypostatic jamming. This analysis further predicts the scaling behavior of and near the jamming point. Interestingly, we find that these functions do not show a power-law behavior even at the jamming point, in marked contrast to the jamming of spherical particles. Also the simplicity of the model allows us to derive an analytical expression of the density of states , which exhibits the very same scaling behavior as that of ellipsoids and BP. Finally, we confirm our predictions by numerical simulations of the BP model.
BP Model
The BP model (43) was originally introduced to understand the physics of the swap Monte Carlo algorithm (44), but here we focus on its relation with the jamming of ellipsoids. The model consists of spherical particles with positions in dimensions and radius , interacting via the potential energy
| [1] |
where, defining as the Heaviside theta function,
| [2] |
is the standard harmonic repulsive interaction potential of spherical particles such as bubbles and colloids (5), and the distribution of , which can fluctuate around a reference value , is controlled by the chemical potential term
| [3] |
Here, is determined by imposing that the dimensionless SD is constant, with . Note that (corresponding to ) gives back the usual spherical particles (5) and that the full distribution of radii, , can generically change even if is kept fixed. Upon approaching jamming, where the adimensional pressure (in units of ) vanishes, it is found that and remains constant (43).
Because the BP model has translational degrees of freedom and radial degrees of freedom, the naive Maxwell stability condition requires in the thermodynamic limit (19, 45). However, a marginal stability argument and numerical simulations prove that the contact number at the jamming point increases continuously as (43) and the system is hypostatic for sufficiently small ; i.e., the number of constraints is smaller than that required by Maxwell’s stability condition. This is very similar to ellipsoids and motivates us to conjecture that the two models could belong to the same universality class. In the following, we show that this expectation is indeed true: Hypostatic packings of the BP and ellipsoids are stabilized by a common mechanism and have the same critical exponents.
Mapping from Ellipsoids to BP
We now construct a mapping from a system of ellipsoids to the spherical BP model introduced above. Ellipsoids are described by their position and by unit vectors along their principal axis, and for concreteness we model them by the Gay–Berne potential (31, 46)
| [4] |
where the gap function is defined as
| [5] |
Here, is the unit vector connecting the th and th particles, is the length of the principal axis, and , where denotes the aspect ratio. Because we are interested in the nearly spherical case, we expand the pair potential in small as
| [6] |
where and denotes the term that we do not need to write explicitly. Substituting this in Eq. 4 and keeping terms up to , we obtain , where
| [7] |
The stiffness matrix is , where . Note that near the jamming point, behaves as , which is the same scaling of the stiffness of the BP model, Eq. 3. Hence, if we identify with , in the vicinity of jamming the potential for ellipsoids can be analyzed essentially in the same way as in the BP model (43), as we discuss next.
Marginal Stability
The distinctive feature of both BP and ellipsoids is that the total potential, and thus the Hessian matrix, can be split into two parts: one having finite stiffness and the second one having vanishing stiffness by dimensional arguments. The zero modes of the first term are stabilized by the second one, as recognized in refs. 29 and 32. We now provide additional insight on this structure by generalizing a marginal stability argument discussed for the BP in ref. 43. At jamming, and because . The constraints coming from , one per mechanical contact, stabilize the same number of vibrational modes. Because the system is hypostatic, there remain zero-frequency modes, where and is the number of extra degrees of freedom per particle; i.e., for the BP and for ellipsoids. Above jamming, where , the zero modes are stabilized by the “soft” constraint coming from whose characteristic stiffness is , where is the stiffness associated to . Hence, the energy scale of these modes remains well separated from that of the other modes, and we can restrict to the -dimensional subspace of the soft modes. In this space, we have degrees of freedom, and provides constraints; hence the number of degrees of freedom is less than the number of constraints. When , a variational argument developed in refs. 17 and 47 describes the low-frequency spectrum. It shows that the soft modes are shifted above a characteristic frequency , which is reduced by by the so-called prestress terms, resulting in , where and are unknown constants. Assuming that the system is marginally stable, , results in (43)
| [8] |
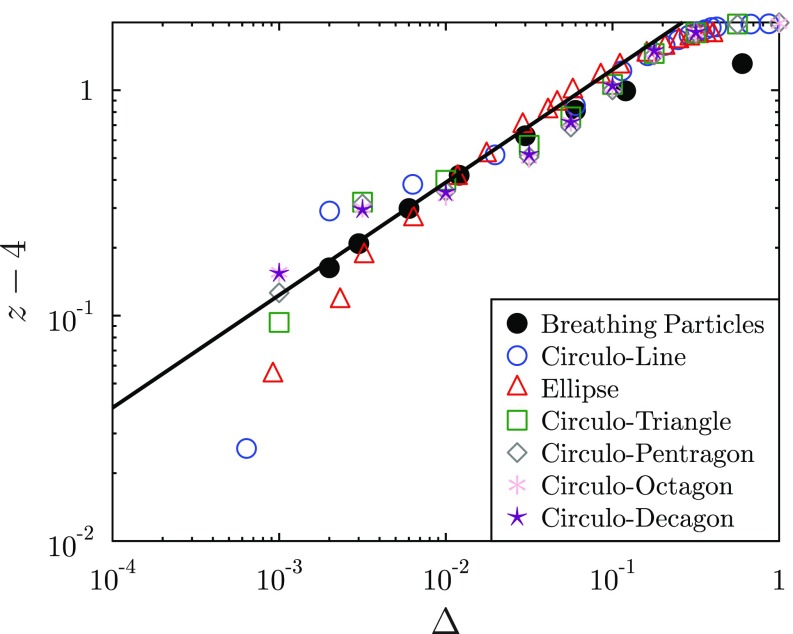
This explains the universal square-root singularity of the contact number observed in ellipsoids, BP, and several other models (9, 29, 43), as illustrated in Fig. 1. Eq. 8 holds when , because in the argument we assumed to be close to jamming () at fixed . On the contrary, when , the contact number should have the same scaling of spherical particles:
| [9] |
Eqs. 8 and 9 imply that and have the same scaling dimension and the following scaling holds:
| [10] |
In the limit, Eq. 10 reduces to Eq. 9, which requires and for . In the limit, we should recover Eq. 8, which requires for . For the BP, Eq. 10 is confirmed by numerical simulations (43). Assuming that is a regular function around , one can expand it as and obtains
| [11] |
where . This is compatible with previous numerical results of ellipsoids, where (48). We can also study the response to shear deformation, which mainly excites the zero modes (30). Applying the argument in ref. 18 to the zero modes and using Eq. 8, the shear modulus behaves as , in perfect agreement with the numerical result (30).
Fig. 1.
Universal scaling of the contact number. Symbols denote the numerical result, while the solid line denotes the theoretical prediction . Data for nonspherical particles are reproduced from ref. 40, and from the sphericity , we defined , which recovers the correct scaling relation between the sphericity and aspect ratio of ellipses for small . We set to collapse all data. Data for the BP correspond to a pressure .
Vibrational Spectrum
The marginal stability argument suggests that soft vibrational modes can be found in the frequency range , with due to marginal stability and , while the remaining modes have finite frequency at jamming. We now refine the argument to discuss in more detail the vibrational density of states . It is convenient to define the Hessian matrix of the BP model, with , as the second derivative of the interaction potential w.r.t. and , in such a way that it has a similar scaling to the one of ellipsoids, where is mapped onto the angular degrees of freedom .
Then, near jamming can be separated into the following three regions: (i) The lowest band corresponds to the zero modes stabilized by . Their typical frequency is . The remaining modes can be split into two bands: (ii) an intermediate band corresponding to the extra (rotational or radial) degrees of freedom , with typical frequency , and (iii) the highest band corresponding to the translational degrees of freedom. For , the additional degrees of freedom do not strongly affect these modes, and one can apply the standard variational argument of spherical particles (17, 47), which predicts that their typical frequency is . The resulting differs significantly from that of isostatic packings of spherical particles, which displays a single translational band.
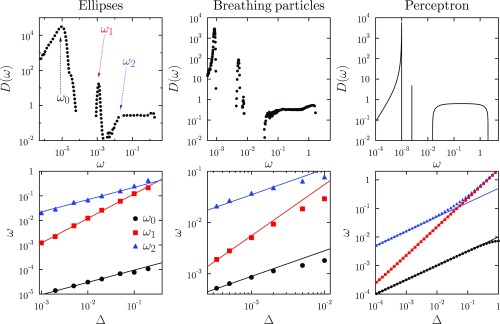
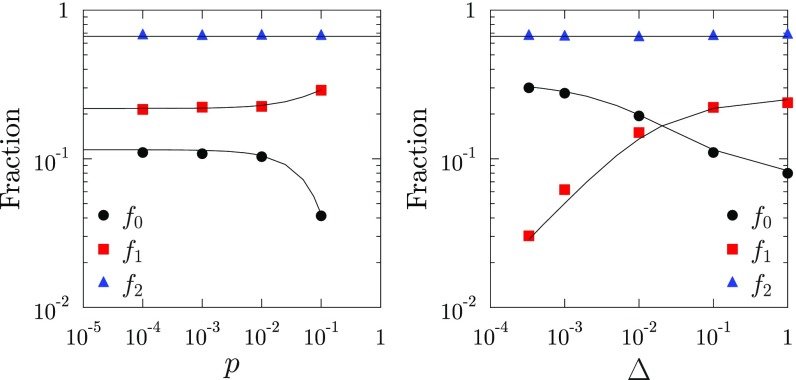
Numerical results for of ellipsoids from ref. 30 and of the BP from ref. 43 and analytical results for the perceptron model introduced below are reported in Fig. 2. Details about the simulations of the BP are explained in ref. 43; here we show data for particles, averaged over at least 1,000 samples for each state point. As predicted by our theory, consists of three separated bands with characteristic peak frequencies . Their scaling with , also reported in Fig. 2 at fixed , follows the theoretical predictions , , and . We also find that for small , while do not change much with , which is again consistent with the theory. Finally, in Fig. 3 we report the fraction of modes in each band for the BP, which also follow the theoretical prediction as a function of and .
Fig. 2.
Universality of the density of states. (Top) Density of states for ellipses, BP, and the perceptron. (Bottom) Evolution with of the characteristic frequencies at . Solid lines denote the theoretical predictions, , , and , respectively. Data of ellipses are reproduced from ref. 32.
Fig. 3.
Weights of the density of states. Shown is the fraction of modes in the three bands of given in Fig. 2, plotted as functions of at fixed (Left) and at fixed (Right) for BP (with and ). The theoretical predictions , , and are plotted as solid lines, inferred from the measured .
Mean-Field Model
The universality class of isostatic jamming is well understood: It can be described analytically by particles in (15) or, equivalently, by the perceptron model (24–26). Both models reproduce the critical exponents of isostatic jamming in all dimensions , leading to the conjecture that its lower critical dimension is (49).
We now introduce a mean-field model which describes the universality class of hypostatic jamming in the BP, ellipsoids, and many other models of nonspherical particles. The model, which is a generalization of the perceptron, can be solved analytically and, as we show, the solution reproduces all of the critical exponents of hypostatic jamming. It consists of one tracer particle with coordinate on the surface of the -dimensional hypersphere of radius and obstacles of coordinates and “size” . The interaction potential between the tracer particle and the obstacles is
| [12] |
where and the gap variable is defined as
| [13] |
The are frozen variables, and each of their components follows independently a normal distribution of zero mean and unit variance. The dynamical variables are and the , whose variance is controlled by the chemical potential . We fix the value of so that . In the limit, the system reduces to the standard perceptron model investigated in ref. 26, while for the play the same role as the particle sizes in the BP model.
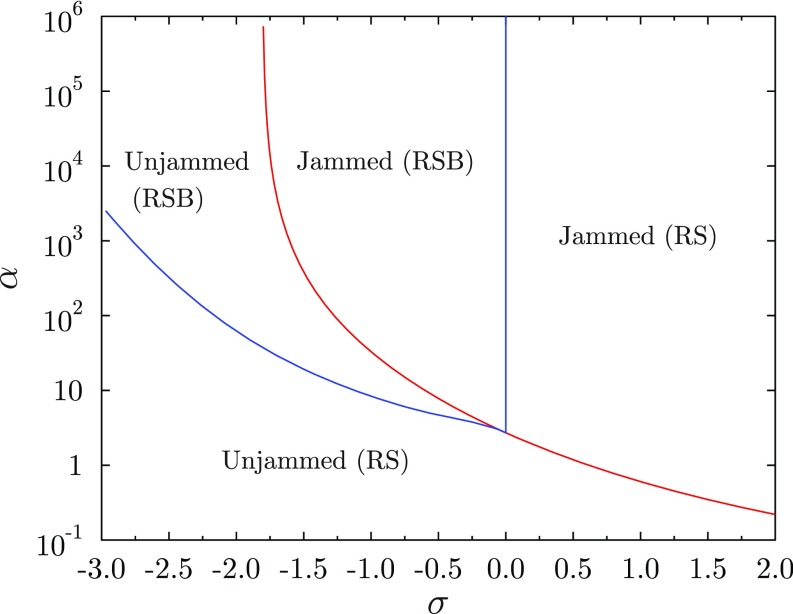
Because the model can be solved by the same procedure as that of the standard perceptron model, here we give just a brief sketch of our calculation. The free energy of the model at temperature can be calculated by the replica method, , where and the overbar denotes the averaging over the quenched randomness . Here we are interested in the athermal limit . Using the saddle-point method, the free energy can be expressed as a function of the overlap , where and denote the positions of the tracer particles of the th and th replicas, respectively. In the limit, is parameterized by a continuous variable , . The function plays the role of the order parameter and characterizes the hierarchical structure of the metastable states (50). We first calculate the phase diagram assuming a constant , which is the so-called replica symmetric (RS) ansatz that describes an energy landscape with a single minimum. The result for is shown in Fig. 4. The control parameters are the obstacle density and size . If is small, the tracer particle can easily find islands of configurations that satisfy all of the constraints : The total potential energy and the pressure vanish and the system is unjammed. The overlap measures the typical distance between two zero-energy configurations. Upon increasing , increases and eventually reaches at , which is the jamming transition point (Fig. 4). Naturally, due to the additional degrees of freedom when , we have for equal . For , the RS ansatz is stable for all values of and it describes the jamming transition. For instead, the jamming line is surrounded by a RSB region where the RS ansatz is unstable. The jamming transition should thus be described by the RSB ansatz where is not constant, corresponding to a rough energy landscape. The qualitative behavior of the phase diagram is independent of ; in particular, the jamming line for is always surrounded by a RSB region.
Fig. 4.
The phase diagram of the perceptron model for . The red line denotes the jamming point. The blue lines denote the RSB instability. The jamming line in the nonconvex region () is surrounded by the RSB lines.
An important observable to characterize jamming is the gap distribution that also gives the contact number . At jamming, counts the gaps that are exactly equal to zero. For comparison with numerical results, we introduce the positive gap distribution and the force distribution , where (corresponding to negative gaps), both normalized to 1. For the standard perceptron model with and , jamming is isostatic with (26), and both and exhibit a power-law behavior (24–26). In the jammed phase and , the system is described by a “regular” full RSB solution where for , and and are regular and finite functions. The prefactor is predominantly controlled by the contact number and diverges at isostaticity when (26) and the regular solution breaks down. At , the model is described by the “jamming” solution where , , and , with critical exponents , , and (15, 24–26). Near , the regular solution should connect to the jamming solution. This matching argument leads to , which is the same scaling behavior as that of spherical particles (6).
The situation is completely different if . One can show that the contact number at jamming is , meaning that the regular solution persists even at . Consequently, and are finite and regular functions at jamming, and the square-root behavior of the contact number is replaced by . At , the regular solution should connect to the jamming solution in the limit of . Using the form of the scaling solution derived for in ref. 26 and , this matching argument leads to the scaling behavior of and at :
| [14] |
| [15] |
with new critical exponents and and a universal scaling function . The scaling analysis also leads to and , consistent with the marginal stability argument, Eqs. 8 and 11.
The simplicity of the model allows us to derive the analytical form of the density of states . As before, we define the Hessian matrix as the second derivatives of the interaction potential , Eq. 12, w.r.t. and . Using the Edwards–Jones formula for the eigenvalue density (51, 52), the density of states can be expressed analytically in closed form as a function of , , and . These quantities should be obtained by solving numerically the full RSB equations but for simplicity, because here we are interested only in the scaling properties of , to obtain Fig. 2 we used arbitrary functions , , and which are compatible with the analytical scaling derived from the full RSB equation. We find that displays three separate bands (Fig. 2). As in the standard perceptron (24), marginal stability in the full RSB phase implies that the lowest band starts from and for small , . The lowest band terminates at near which exhibits a sharp peak. At a delta peak is found, while the highest band starts from . The qualitative behavior of and the scaling of , , and are the same as those of all of the models displaying hypostatic jamming, such as ellipsoids (31, 32) and BP (43). This confirms that the generalized perceptron can reproduce analytically all of the critical properties of the hypostatic jamming transition.
As a final check of universality, we test the prediction for the dependence of the gap distribution function at the jamming point, Eq. 14. In Fig. 5, we show numerical results (obtained as in ref. 43) for of the BP model at , a value small enough to observe the critical behavior. Here, as usual for particle systems, is normalized by for larger . When , exhibits a power-law divergence, , where , consistent with previous numerical observation (6, 14, 15). For finite , on the contrary, the divergence of is cut off (Fig. 5), consistent with the theoretical prediction of Eq. 14.
Fig. 5.
Gap distribution of BP near the jamming point, . (Left) Symbols denote the numerical result, while the solid line denotes the theoretical prediction, . (Right) Scaling plot of the same data according to Eq. 14.
Conclusions
Using a marginal stability argument, we derived the scaling behavior of the contact number and the density of states of ellipsoids and breathing particles. Our theory predicts that the scaling behaviors of the two models are identical, which we confirmed numerically. Many other models of nonspherical particles display the same jamming criticality (40), which defines another universality class of hypostatic jamming. We introduced an analytically solvable model which allows us to derive analytically the critical exponents associated to this universality class.
One of the most surprising outputs of our theory is the universality of the density of states (Fig. 2). This might be relevant for some colloidal experiments where the constituents are nonspherical (53), in which the vibrational modes could be experimentally extracted from the fluctuations of positions (54, 55). Another relevant question is how nonspherical particles would flow under shear (30). The divergence of the viscosity at jamming is related to the low eigenvalues of (56), which suggests that the shear flow of nonspherical particles should be quite different from that of spherical particles, in agreement with recent experiments (57).
Acknowledgments
We thank B. Chakraborty, A. Ikeda, J. Kurchan, S. Nagel, and S. Franz for interesting discussions. We thank the authors of refs. 40 and 32 for sharing their data used in Figs. 1 and 2, respectively. This project received funding from the European Research Council under the European Union’s Horizon 2020 Research and Innovation program (Grant 723955-GlassUniversality). This work was supported by Grants 689 454953 (to M.W.) and 454955 (to F.Z.) from the Simons Foundation and by a public grant from the “Laboratoire d’Excellence Physics Atoms Light Mater” (LabEx PALM) overseen by the French National Research Agency (ANR) as part of the “Investissements d’Avenir” program (reference no. ANR-10-LABX-0039-PALM; to P.U.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Liu AJ, Nagel SR, van Saarloos W, Wyart M. In: The Jamming Scenario: An Introduction and Outlook. Berthier L, Biroli G, Bouchaud J, Cipeletti L, van Saarloos W, editors. Oxford Univ Press; Oxford: 2010. [Google Scholar]
- 2.Van Hecke M. Jamming of soft particles: Geometry, mechanics, scaling and isostaticity. J Phys Condens Matter. 2009;22:033101. doi: 10.1088/0953-8984/22/3/033101. [DOI] [PubMed] [Google Scholar]
- 3.Torquato S, Stillinger FH. Jammed hard-particle packings: From Kepler to Bernal and beyond. Rev Mod Phys. 2010;82:2633–2672. [Google Scholar]
- 4.Bernal J, Mason J. Packing of spheres: Co-ordination of randomly packed spheres. Nature. 1960;188:910–911. [Google Scholar]
- 5.Durian DJ. Foam mechanics at the bubble scale. Phys Rev Lett. 1995;75:4780–4783. doi: 10.1103/PhysRevLett.75.4780. [DOI] [PubMed] [Google Scholar]
- 6.O’Hern CS, Silbert LE, Liu AJ, Nagel SR. Jamming at zero temperature and zero applied stress: The epitome of disorder. Phys Rev E. 2003;68:011306. doi: 10.1103/PhysRevE.68.011306. [DOI] [PubMed] [Google Scholar]
- 7.Zhang Z, et al. Thermal vestige of the zero-temperature jamming transition. Nature. 2009;459:230–233. doi: 10.1038/nature07998. [DOI] [PubMed] [Google Scholar]
- 8.Karayiannis NC, Foteinopoulou K, Laso M. The structure of random packings of freely jointed chains of tangent hard spheres. J Chem Phys. 2009;130:164908. doi: 10.1063/1.3117903. [DOI] [PubMed] [Google Scholar]
- 9.Donev A, et al. Improving the density of jammed disordered packings using ellipsoids. Science. 2004;303:990–993. doi: 10.1126/science.1093010. [DOI] [PubMed] [Google Scholar]
- 10.Jaoshvili A, Esakia A, Porrati M, Chaikin PM. Experiments on the random packing of tetrahedral dice. Phys Rev Lett. 2010;104:185501. doi: 10.1103/PhysRevLett.104.185501. [DOI] [PubMed] [Google Scholar]
- 11.Bi D, Lopez J, Schwarz J, Manning ML. A density-independent rigidity transition in biological tissues. Nat Phys. 2015;11:1074–1079. [Google Scholar]
- 12.O’Hern CS, Langer SA, Liu AJ, Nagel SR. Random packings of frictionless particles. Phys Rev Lett. 2002;88:075507. doi: 10.1103/PhysRevLett.88.075507. [DOI] [PubMed] [Google Scholar]
- 13.Ellenbroek WG, Somfai E, van Hecke M, van Saarloos W. Critical scaling in linear response of frictionless granular packings near jamming. Phys Rev Lett. 2006;97:258001. doi: 10.1103/PhysRevLett.97.258001. [DOI] [PubMed] [Google Scholar]
- 14.Donev A, Torquato S, Stillinger FH. Pair correlation function characteristics of nearly jammed disordered and ordered hard-sphere packings. Phys Rev E. 2005;71:011105. doi: 10.1103/PhysRevE.71.011105. [DOI] [PubMed] [Google Scholar]
- 15.Charbonneau P, Kurchan J, Parisi G, Urbani P, Zamponi F. Fractal free energy landscapes in structural glasses. Nat Commun. 2014;5:3725. doi: 10.1038/ncomms4725. [DOI] [PubMed] [Google Scholar]
- 16.Charbonneau P, Corwin EI, Parisi G, Zamponi F. Jamming criticality revealed by removing localized buckling excitations. Phys Rev Lett. 2015;114:125504. doi: 10.1103/PhysRevLett.114.125504. [DOI] [PubMed] [Google Scholar]
- 17.Wyart M, Silbert LE, Nagel SR, Witten TA. Effects of compression on the vibrational modes of marginally jammed solids. Phys Rev E. 2005;72:051306. doi: 10.1103/PhysRevE.72.051306. [DOI] [PubMed] [Google Scholar]
- 18.Wyart M. On the rigidity of amorphous solids. Ann Phys Fr. 2006;30:3. [Google Scholar]
- 19.Maxwell JC. L. on the calculation of the equilibrium and stiffness of frames. Lond Edinb Dublin Philos Mag J Sci. 1864;27:294–299. [Google Scholar]
- 20.Brito C, Wyart M. On the rigidity of a hard-sphere glass near random close packing. Europhys Lett. 2006;76:149–155. [Google Scholar]
- 21.Wyart M. Marginal stability constrain force and pair distributions at random close packing. Phys Rev Lett. 2012;109:125502. doi: 10.1103/PhysRevLett.109.125502. [DOI] [PubMed] [Google Scholar]
- 22.Lerner E, Düring G, Wyart M. Low-energy non-linear excitations in sphere packings. Soft Matter. 2013;9:8252–8263. [Google Scholar]
- 23.DeGiuli E, Lerner E, Brito C, Wyart M. Force distribution affects vibrational properties in hard-sphere glasses. Proc Natl Acad Sci USA. 2014;111:17054–17059. doi: 10.1073/pnas.1415298111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Franz S, Parisi G, Urbani P, Zamponi F. Universal spectrum of normal modes in low-temperature glasses. Proc Natl Acad Sci USA. 2015;112:14539–14544. doi: 10.1073/pnas.1511134112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Franz S, Parisi G. The simplest model of jamming. J Phys A Math Theor. 2016;49:145001. [Google Scholar]
- 26.Franz S, Parisi G, Sevelev M, Urbani P, Zamponi F. Universality of the SAT-UNSAT (jamming) threshold in non-convex continuous constraint satisfaction problems. SciPost Phys. 2017;2:019. [Google Scholar]
- 27.Man W, et al. Experiments on random packings of ellipsoids. Phys Rev Lett. 2005;94:198001. doi: 10.1103/PhysRevLett.94.198001. [DOI] [PubMed] [Google Scholar]
- 28.Delaney G, Weaire D, Hutzler S, Murphy S. Random packing of elliptical disks. Philos Mag Lett. 2005;85:89–96. [Google Scholar]
- 29.Donev A, Connelly R, Stillinger FH, Torquato S. Underconstrained jammed packings of nonspherical hard particles: Ellipses and ellipsoids. Phys Rev E. 2007;75:051304. doi: 10.1103/PhysRevE.75.051304. [DOI] [PubMed] [Google Scholar]
- 30.Mailman M, Schreck CF, O’Hern CS, Chakraborty B. Jamming in systems composed of frictionless ellipse-shaped particles. Phys Rev Lett. 2009;102:255501. doi: 10.1103/PhysRevLett.102.255501. [DOI] [PubMed] [Google Scholar]
- 31.Zeravcic Z, Xu N, Liu A, Nagel S, van Saarloos W. Excitations of ellipsoid packings near jamming. Europhys Lett. 2009;87:26001. [Google Scholar]
- 32.Schreck CF, Mailman M, Chakraborty B, O’Hern CS. Constraints and vibrations in static packings of ellipsoidal particles. Phys Rev E. 2012;85:061305. doi: 10.1103/PhysRevE.85.061305. [DOI] [PubMed] [Google Scholar]
- 33.Williams SR, Philipse AP. Random packings of spheres and spherocylinders simulated by mechanical contraction. Phys Rev E. 2003;67:051301. doi: 10.1103/PhysRevE.67.051301. [DOI] [PubMed] [Google Scholar]
- 34.Blouwolff J, Fraden S. The coordination number of granular cylinders. Europhys Lett. 2006;76:1095–1101. [Google Scholar]
- 35.Wouterse A, Williams SR, Philipse AP. Effect of particle shape on the density and microstructure of random packings. J Phys Condens Matter. 2007;19:406215. doi: 10.1088/0953-8984/19/40/406215. [DOI] [PubMed] [Google Scholar]
- 36.Wouterse A, Luding S, Philipse A. On contact numbers in random rod packings. Granular Matter. 2009;11:169–177. [Google Scholar]
- 37.Marschall T, Teitel S. Compression-driven jamming of athermal frictionless spherocylinders in two dimensions. Phys Rev E. 2018;97:012905. doi: 10.1103/PhysRevE.97.012905. [DOI] [PubMed] [Google Scholar]
- 38.Jiao Y, Stillinger FH, Torquato S. Distinctive features arising in maximally random jammed packings of superballs. Phys Rev E. 2010;81:041304. doi: 10.1103/PhysRevE.81.041304. [DOI] [PubMed] [Google Scholar]
- 39.Delaney GW, Cleary PW. The packing properties of superellipsoids. Europhys Lett. 2010;89:34002. [Google Scholar]
- 40.VanderWerf K, Jin W, Shattuck MD, O’Hern CS. Hypostatic jammed packings of frictionless nonspherical particles. Phys Rev E. 2018;97:012909. doi: 10.1103/PhysRevE.97.012909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Boromand A, Signoriello A, Ye F, O’Hern CS, Shattuk M. 2018. Jamming of deformable polygons. arXiv:1801.06150. Preprint, posted January 18, 2018.
- 42.Baule A, Mari R, Bo L, Portal L, Makse HA. Mean-field theory of random close packings of axisymmetric particles. Nat Commun. 2013;4:2194. doi: 10.1038/ncomms3194. [DOI] [PubMed] [Google Scholar]
- 43.Brito C, Lerner E, Wyart M. Theory for swap acceleration near the glass and jamming transitions for continuously polydisperse particles. Phys Rev X. 2018;8:031050. [Google Scholar]
- 44.Ninarello A, Berthier L, Coslovich D. Models and algorithms for the next generation of glass transition studies. Phys Rev X. 2017;7:021039. [Google Scholar]
- 45.Alexander S. Amorphous solids: Their structure, lattice dynamics and elasticity. Phys Rep. 1998;296:65–236. [Google Scholar]
- 46.Gay J, Berne B. Modification of the overlap potential to mimic a linear site–site potential. J Chem Phys. 1981;74:3316–3319. [Google Scholar]
- 47.Yan L, DeGiuli E, Wyart M. On variational arguments for vibrational modes near jamming. Europhys Lett. 2016;114:26003. [Google Scholar]
- 48.Schreck CF, Xu N, O’Hern CS. A comparison of jamming behavior in systems composed of dimer-and ellipse-shaped particles. Soft Matter. 2010;6:2960–2969. [Google Scholar]
- 49.Goodrich CP, Liu AJ, Nagel SR. Finite-size scaling at the jamming transition. Phys Rev Lett. 2012;109:095704. doi: 10.1103/PhysRevLett.109.095704. [DOI] [PubMed] [Google Scholar]
- 50.Mézard M, Parisi G, Virasoro M. Spin Glass Theory and Beyond: An Introduction to the Replica Method and Its Applications. Vol 9 World Scientific; Singapore: 1987. [Google Scholar]
- 51.Edwards SF, Jones RC. The eigenvalue spectrum of a large symmetric random matrix. J Phys A Math Gen. 1976;9:1595–1603. [Google Scholar]
- 52.Livan G, Novaes M, Vivo P. 2018. Introduction to Random Matrices: Theory and Practice. SpringerBriefs in Mathematical Physics (Springer, Cham, Switzerland)
- 53.Kim JW, Larsen RJ, Weitz DA. Synthesis of nonspherical colloidal particles with anisotropic properties. J Am Chem Soc. 2006;128:14374–14377. doi: 10.1021/ja065032m. [DOI] [PubMed] [Google Scholar]
- 54.Chen K, et al. Low-frequency vibrations of soft colloidal glasses. Phys Rev Lett. 2010;105:025501. doi: 10.1103/PhysRevLett.105.025501. [DOI] [PubMed] [Google Scholar]
- 55.Ghosh A, Chikkadi VK, Schall P, Kurchan J, Bonn D. Density of states of colloidal glasses. Phys Rev Lett. 2010;104:248305. doi: 10.1103/PhysRevLett.104.248305. [DOI] [PubMed] [Google Scholar]
- 56.Lerner E, Düring G, Wyart M. A unified framework for non-Brownian suspension flows and soft amorphous solids. Proc Natl Acad Sci USA. 2012;109:4798–4803. doi: 10.1073/pnas.1120215109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Tapia F, Shaikh S, Butler JE, Pouliquen O, Guazzelli E. Rheology of concentrated suspensions of non-colloidal rigid fibres. J Fluid Mech. 2017;827:718–740. [Google Scholar]