Predicting Pressure Injury in Critical Care Patients: A Machine-Learning Model

Abstract

Background

Hospital-acquired pressure injuries are a serious problem among critical care patients. Some can be prevented by using measures such as specialty beds, which are not feasible for every patient because of costs. However, decisions about which patient would benefit most from a specialty bed are difficult because results of existing tools to determine risk for pressure injury indicate that most critical care patients are at high risk.

Objective

To develop a model for predicting development of pressure injuries among surgical critical care patients.

Methods

Data from electronic health records were divided into training (67%) and testing (33%) data sets, and a model was developed by using a random forest algorithm via the R package “randomforest.”

Results

Among a sample of 6376 patients, hospital-acquired pressure injuries of stage 1 or greater (outcome variable 1) developed in 516 patients (8.1%) and injuries of stage 2 or greater (outcome variable 2) developed in 257 (4.0%). Random forest models were developed to predict stage 1 and greater and stage 2 and greater injuries by using the testing set to evaluate classifier performance. The area under the receiver operating characteristic curve for both models was 0.79.

Conclusion

This machine-learning approach differs from other available models because it does not require clinicians to input information into a tool (eg, the Braden Scale). Rather, it uses information readily available in electronic health records. Next steps include testing in an independent sample and then calibration to optimize specificity. (American Journal of Critical Care. 2018; 27:461–468)

Hospital-acquired pressure injuries (HAPIs) occur among 3% to 24% of critical care patients in the United States, and patients with these injuries have longer stays, increased costs, and more human suffering than do patients without such injuries.^1,2 Although pressure injuries are common, some can be prevented by using measures such as specialty beds, which are not feasible for every patient because of the costs.³ In addition, recognizing patients at highest risk for a HAPI is important because clinicians can then conduct thorough skin assessments to identify pressure injuries at the earliest, reversible stage.⁴

Recommended standards of practice include assessing each patient’s risk for pressure injury at admission and with any change in the patient’s clinical status.⁵ Unfortunately, identification of high-risk patients in the inten sive care unit (ICU) is difficult because currently available risk-assessment tools have high sensitivity but low specificity in critical care patients and tend to indicate that most patients are at high risk.⁶

Machine learning can effectively and efficiently use large amounts of data from the electronic health record to predict development of pressure injuries.

Machine learning is a type of artificial intelligence that can be used to build predictive models, but it is rarely used in research on pressure injuries.⁷ Raju et al⁷ advocated for a machine-learning approach to build a useful model for predicting pressure injuries because machine-learning techniques can effectively and efficiently use large amounts of clinical data that are routinely collected in electronic health records (EHRs). Raju et al specifically recommended a type of machine learning called random forest, a method that uses an ensemble decision tree, in which random subsets are drawn from the data with replacement. The advantages of a random-forest approach are that all of the data can be used for training and validation while avoiding the decision-tree tendency to overfit the model and that the approach is relatively powerful when multicollinearity occurs and when data are missing.^8,9 The purpose of our study was to use a big-data/machine-learning approach to develop a model for predicting pressure injuries among critical care patients.

Methods

Data Preprocessing

The institutional review board at the University of Utah Hospital, Salt Lake City, Utah, approved the study. A biomedical informatics team assisted us in our data discovery process. We queried an enterprise data warehouse for EHR data consistent with our sampling criteria and variables of interest. We used an iterative approach to refine our query via validation procedures and review by domain experts, data stewards, and the biomedical informatics team. We validated the data extracted from the EHRs by manually comparing the values and date/time stamps found in the extracted data with those displayed in the the clinicians’ view of the electronic health record for 30 randomly selected cases, including 15 with pressure injury and 15 without such injury. On implementing the fully developed query for all manually validated cases, we found consistent values and date/time stamps (within 10 minutes) for all 30 cases (100% agreement). We cleaned individual variables by using Stata 13 software (StataCorp LLC) and then compiled the analysis data set by using SAS, version 9.4, software (SAS Institute Inc).

Sample

The sample consisted of data on patients admitted to the adult surgical or surgical cardiovascular ICU at University of Utah Hospital, an academic medical center with a level I trauma center, either directly or after an acute care stay between September 1, 2008, and May 1, 2013, who met inclusion criteria. We included patients younger than 18 years who were admitted to the adult ICU in an effort to include all patients admitted to the adult surgical or adult surgical cardiovascular ICU. In an effort to avoid misattribution of community-acquired pressure injuries as HAPIs, we excluded data on patients who had a pressure injury at the time of admission to the ICU and patients in whom a pressure injury developed within 24 hours of ICU admission. Among patients with more than 1 hospitalization during the study period, we included data from the first hospitalization only.

Treatment protocols for all patients included targeted interventions based on parameters of the Braden Scale (eg, use of moisture-wicking pads and barrier creams for patients with moist skin). In addition, the standard of care in the ICUs was turning and repositioning at least every 2 hours for patients who were unable to turn themselves.

Measures

Variables were selected on the basis of a combination of input from clinicians and relevant publications. The predictor variables selected are detailed in Tables 1 and 2. Data on vital signs were obtained from electronic monitors (oxygen saturation by pulse oximetry and blood pressure) and, because of concern about spurious values that occur sporadically with continuous monitoring, were included only if the low value was evident 3 or more times in a row. The outcome variables were HAPIs classified as stage 1 to 4, deep-tissue injury, or unstageable and HAPIs classified as stage 2 to 4, deep-tissue injury, or unstageable. We included stage 1 injuries in our first outcome variable because pressure injuries at the earliest stage are reversible, and therefore early recognition of this stage is ideal.⁴ We excluded stage 1 injuries from the second outcome variable because of concern that nurses might misidentify transient redness as a stage 1 injury.¹⁰

Table 1.

Predictor variables: number and percentage

Measure: variable	No. (%) of patients
Delirium: Confusion assessment method
Delirious	491 (7.7)
Not delirious	2347 (36.8)
Unable to assess	125 (2.0)
Missing	3413 (53.5)
Hypotension: mean arterial pressure <60 mm Hg
Not hypotensive	4186 (65.7)
Hypotensive	2184 (34.3)
Missing	6 (0.1)
Level of consciousness: Glasgow Coma Scale (lowest score)
3	861 (13.5)
4	15 (0.2)
5	27 (0.4)
6	86 (1.3)
7	111 (1.7)
8	111 (1.7)
9	98 (1.5)
10	305 (4.8)
11	150 (2.4)
12	19 (0.3)
13	84 (1.3)
14	317 (5.0)
15	813 (12.8)
Missing	3379 (53.0)
Oxygenation: oxygen saturation <90% by pulse oximetry
Altered oxygenation	964 (15.1)
Oxygenation not altered	5405 (84.8)
Missing	7 (0.1)
Sedation: Riker sedation and agitation score (lowest score)
1	686 (10.8)
2	441 (6.9)
3	504 (7.9)
4	1342 (21.0)
5	6 (0.1)
Missing	3397 (53.3)
Severity of illness: American Society of Anesthesiologists severity-of-illness score (maximum score)
1, Healthy person	43 (0.7)
2, Mild systemic disease	241 (3.8)
3, Severe systemic disease	958 (15.0)
4, Severe systemic disease that is a constant threat to life	673 (10.6)
5, Moribund	69 (1.1)
6, Brain dead	10 (0.2)
Missing	4382 (68.7)
Temperature: fever >38°C
Fever	767 (12.0)
No fever	5595 (87.8)
Missing	7 (0.1)
Vasopressor medication received (any dose/duration)
Dopamine	257 (4.0)
Epinephrine	73 (1.1)
Norepinephrine	695 (10.9)
Vasopresssin	10 (0.2)
Phenylephrine	23 (0.4)

Table 2.

Predictor variables: minimum-maximum, mean, and standard deviation

Variable	Minimum-maximum	Minimum-maximum Mean	SD
Body mass index at admissiona	12.19–149.11	29.16	9.6
Laboratory value
Albumin, minimum, mg/dL	0.80–5.70	3.54	0.81
Creatinine, maximum, mg/dL	0.31–52.7	1.70	2.06
Glucose, maximum, mg/dL	52–1915	178.17	81.3
Hemoglobin, minimum, g/dL	3.10–18.6	9.6	2.36
Lactate, maximum, mg/dL	0.30–29	2.02	2.24
Prealbumin, minimum, mg/dL	3.0–40.1	13.4	6.9
Surgical time, min	0–366	287.24	234.64

SI conversion factors: to convert creatinine to μmol/L, multiply by 88.4; to convert glucose to mmol/L, multiply by 0.0555; to convert lactate to mmol/L, multiply by 0.111.

^aCalculated as weight in kilograms divided by height in meters squared. Data for 1423 patients (22.3%) were missing.

Analysis

Random Forest.

The random forest algorithm is derived from the classification tree, in which a training set of data is successively split into partitions, or nodes, so that ultimately a previously unseen record can be accurately assigned to a class¹¹ (in this study, development of a HAPI or no HAPI). Advantages of decision trees include ease of use and interpretation, resistance to outliers (ie, the statistics do not change, or change a tiny amount, when outliers are added to the mix), the ability to work efficiently with a large number of predictor variables, and built-in mechanisms for handling missing data by using correlated variables.^7,11 In the decision-tree approach, the best-fitting variable is used at each node, and therefore the resulting model fits nearly perfectly (a situation that is problematic, because the model is overfitted).⁷

The random forest approach retains the advantages of a classification tree but addresses the problem of overfit via bootstrap aggregation, also known as bagging.¹¹ Bagging refers to the collection of many random subsamples of data with replacement, so that for each sample (bootstrap) taken, samples that were not included will be left behind. A new decision tree is developed (or trained) on each sample. Instead of using the best-fitting variable in the data set at each node, a number equal to the square root of the number of features are selected at random, and the node is split by using the best fit out of that group.¹² The random forest approach generates many individual decision trees, and ultimately each tree gets 1 vote for the class (in this study, yes or no for pressure injury). Although the approach does not provide an effect size for each variable, as in hypothesis-based research, output does include the importance of each variable in rank order. The importance of a variable may be due to complex interactions with other variables rather than to a direct, causal relationship.¹²

The random forest model uses bootstrap aggregation, which is collection of many random subsamples with replacement.

Data Processing.

We used R, version 3.3.2, via the RStudio interface, version 1.0.136,¹³ to analyze all data. (The complete procedure is described in the Supplement—available online only at www.ajcconline.org). First, we examined relationships among the available predictor variables and identified (through QR decomposition of the matrix of predictors) a potential linear combination of variables that kept the variable matrix from being of full rank. After identifying the variable vasopressin infusion as the problem, we removed vasopressor infusion and the set of predictors was restored to full rank. Next, we looked for patterns of missingness and determined that the data were not missing completely at random by applying the “missing completely at random” test of Little¹⁴ within the R package BaylorEdPsych (P < .001). Because data were not missing completely at random, we used multiple imputation (using the R package Amelia),¹⁵ an approach that imputes missing values while allowing for a degree of uncertainty; for example, a multiple imputation algorithm may code missing sex as “80% likely to be male” instead of simply “male.”¹⁶

Model Creation.

We divided our data into training (67%) and testing (33%) data sets by using the R package caTools¹⁷ and developed a random forest algorithm via the R package randomForest¹⁸ on the training data set for each of the 2 outcome variables (HAPIs ≥ stage 2 and HAPIs ≥ stage 1). We used the training data set to develop the random forest model, and then we tested the model’s performance with the testing (or held out) data set.

We determined that 4 was the best number of features to be used for each tree (where M = total number of features and m = best number of features for each tree, $\text{m}=\sqrt{\text{M}}$ or $4.47=\sqrt{20}$ [rounded to 4]). We determined that the optimal number of iterations (or trees in the forest) was 500, because after that value, the estimated “out-of-bag” error rate was sufficiently stabilized. We included all of the predictor variables except vasopressin and sampled participants with replacement. We set the cutoff value at 0.5 so that each tree “voted” and a simple majority won. After building the model with the training set, we applied the algorithm to the data in the testing data set. Next, we used the R package randomForest¹⁸ to rank importance of each variable; we then constructed visual representations of relationships between variables to assess directionality. Finally, we used the R package ROCR¹⁹ to assess receiver operating characteristic curves (ROC curves) and the area under the curve for each of our models by using the testing data set.

Results

Sample

The query produced 7218 records. We omitted 841 records because of incomplete patient identification (eg, a date instead of an identification number or single-digit numbers). The final sample therefore consisted of the records of 6376 patients admitted to the adult surgical or cardiothoracic ICU. The mean age was 54 (SD, 19) years. The sample consisted of 2403 women (37.7%) and 3924 men (61.5%); sex data were missing for 49 patients (0.8%). The majority of the sample was white (n = 4838, 75.9%). The mean length of stay was 10 days (SD, 12 days; range, 1–229 days).

Predictor and Outcome Variables

Pressure injuries of stage 2 or greater developed in 257 patients (4.0%). Injuries of stage 1 or greater developed in 516 patients (8.1%); among these, 259 patients had injuries of stage 1, and 257 had injuries of stage 2 or greater). Frequency data for predictor variables are presented in Tables 1 and 2.

Predictive Model: Stage 1 and Greater Pressure Injuries

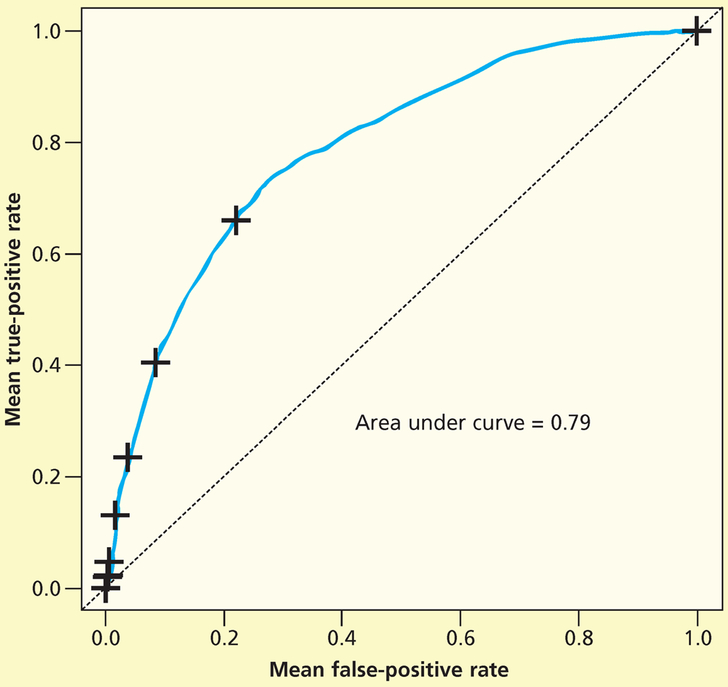
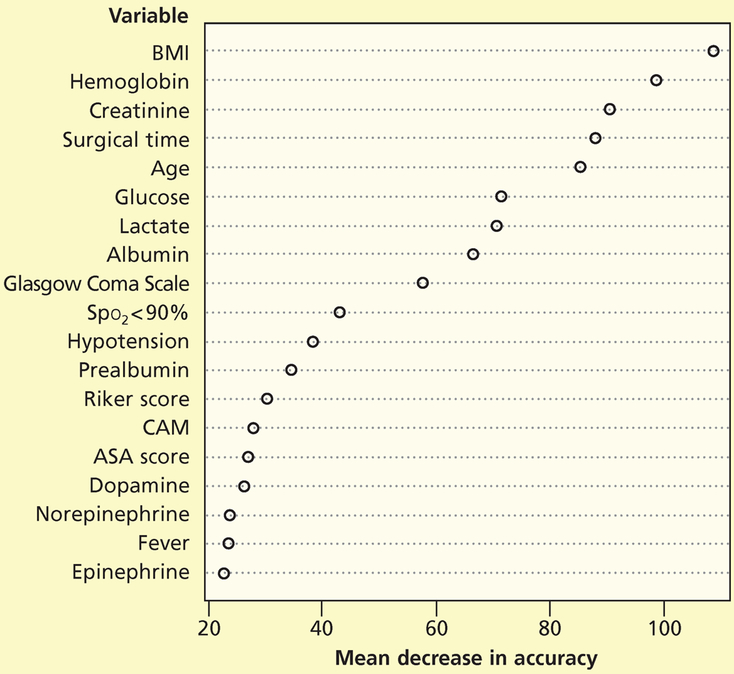
We developed a random forest to predict development of stage 1 and greater pressure injuries among critical care patients in the training data set and then applied the model to the test data set. We used the testing data set to fit the ROC curve. The area under the curve was 0.79 (Figure 1). Figure 2 shows the mean decrease in accuracy for each variable; although some variables were clearly more important than others according to the mean decrease in accuracy, all variables were included and were assessed in the model. The mean decrease in accuracy is measured by removing the association between a predictor variable and the outcome variable and determining the resulting increase in error. The mean decrease in accuracy does not describe discrete values, so we also constructed visual representations to assess directionality.

Figure 1.

Receiver operating characteristic curve for stage 1 pressure injury random forest (PI-1 RF) classifier (test data).

Figure 2.

Importance of variables for pressure injuries of stage 1 or greater.

Abbreviations: ASA score, American Society of Anesthesiologists physical status classification system; BMI, body mass index (calculated as weight in kilograms divided by height in meters squared); CAM, Confusion Assessment Method; Spo₂, oxygen saturation by pulse oximetry.

Predictive Model: Stage 2 and Greater Pressure Injuries

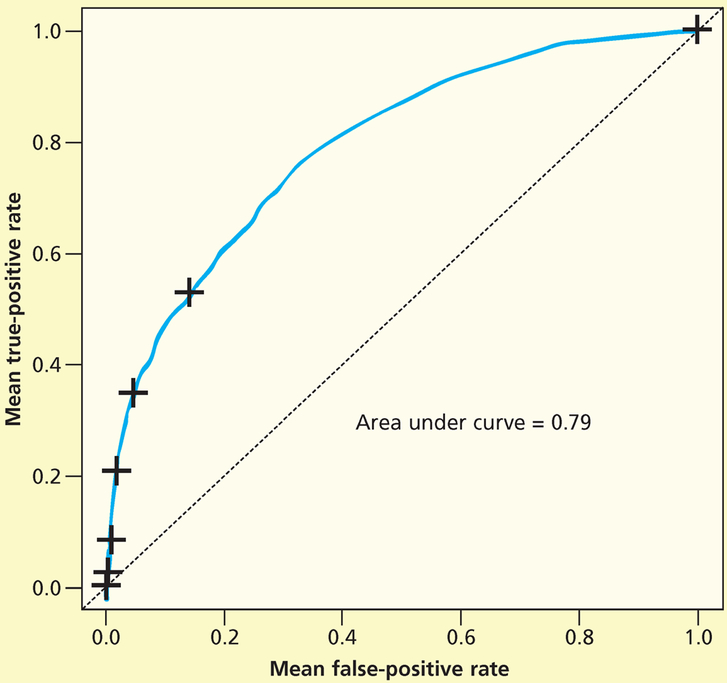
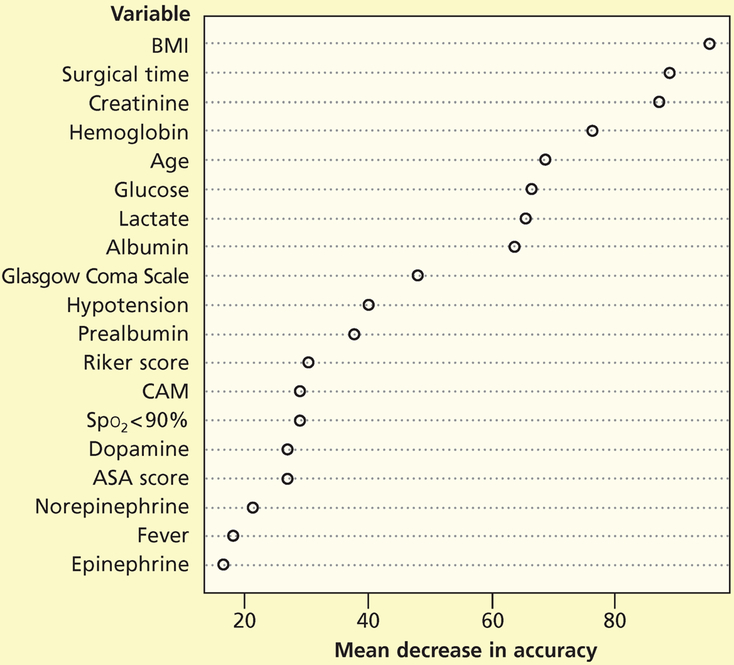
Next, we repeated the random forest analysis for stage 2 and greater pressure injuries. We used the testing data set to fit the ROC curve. The area under the curve was 0.79 (Figure 3). Figure 4 shows the mean decrease in accuracy for each variable.

Figure 3.

Receiver operating characteristic curve for stage 2 pressure injury random forest (PI-2 RF) classifier (test data).

Figure 4.

Importance of variables for pressure injuries of stage 2 or greater.

Abbreviations: ASA score, American Society of Anesthesiologists physical status classification system; BMI, body mass index (calculated as weight in kilograms divided by height in meters squared); CAM, Confusion Assessment Method; Spo₂, oxygen saturation by pulse oximetry.

Limitations

We were unable to access some variables in the EHRs that may be important for development of pressure injuries. Specifically, we were unable to obtain nursing skin assessments (general skin condition, edema, moisture) and treatment-related data (surfaces and repositioning schedules).

Although we used our testing (held out) data set to test our model, validation with an unrelated clinical sample, such as data on patients from a different hospital system, is still needed. When the model is used with a different clinical sample, most likely calibration will be required because of population-related differences (eg, patients in our level I trauma center are generally younger than patients in a surgical critical care unit at a non-trauma center).

Discussion

So far as we know, our study is the only one in which machine learning was used to predict development of pressure injuries among critical care patients. We applied the random forest technique, which is a particularly efficient use of large data sets because bootstrap replicates are used to train each classifier.⁷ Random forest is also advantageous because it is powerful when data are missing, a common problem in clinical data obtained from EHRs.^8,9 In addition, random forest is relatively unaffected by moderate correlations among variables, an important characteristic because correlations among clinical variables are common in health research, and excising correlated variables can result in data destruction that introduces bias.²⁰

One way to consider our model’s performance is to place our results alongside the Braden Scale. The Braden Scale is the most commonly used tool in North America for predicting risk for pressure injury and measures cumulative risk for pressure injuries via 7 categories: sensory perception, activity, mobility, moisture, nutrition, and friction/shear. Total scores range from 9 (very high risk) to 23 (very low risk).²¹ Our model’s relatively strong performance (area under the ROC curve = 0.79 vs 0.68 for the Braden Scale²²) suggests the model would be a useful way to differentiate among critical care patients in order to apply preventive measures that are not feasible for every patient because of cost, such as specialty beds.

The 5 variables deemed most important on the basis of the mean decrease in accuracy for stage 1 and greater pressure injuries were, in descending order, body mass index (calculated as weight in kilograms divided by height in meters squared), hemoglobin level, creatinine level, time required for surgery, and age. For stage 2 and greater pressure injuries, the 5 variables deemed most important were body mass index, time required for surgery, creatinine level, hemoglobin level, and age. The mean decrease in accuracy is calculated by removing a variable from the analysis and then assessing the decrease in the model’s performance, and is therefore a reflection of complex relationships among variables rather than the direct result of any single variable. Even so, our results are interesting, particularly related to time required for surgery, because surgical time has not been well studied as a potential contributor to risk for pressure injury among critical care patients.²³

The variables deemed not important according to the mean decrease in accuracy are also informative. Perfusion is theoretically a key concept in development of pressure injuries because skin cannot survive without delivery of oxygen-rich blood.⁵ In our analysis, variables related to perfusion, including vasopressor infusions, oxygenation, and hypo-tension, were not identified as important according to the mean decrease in accuracy, although those variables were important risk factors in other studies.²² However, we used a single-measure approach: Possibly, variables related to perfusion are better delineated by using a longitudinal approach, which would indicate the dynamic effects of an unstable hemodynamic status. Future researchers may consider a survival random forest approach, which would take into account repeated measures related to perfusion.

Our model’s performance was nearly identical for the stage 1 and greater outcome variable and the stage 2 and greater outcome variable, and both models had similar variables in terms of mean decrease in accuracy for each outcome. Although some studies exclude stage 1 pressure injuries from analysis, our findings lend support to the clinical relevance of stage 1 pressure injuries because of the similar etiologies in terms of predictor variables.

Conclusions

We developed a model to predict risk for pressure injuries among critical care patients by using a machine-learning, random forest approach. Our model relies on information that is readily available in EHRs and therefore does not require clinicians to enter values into a tool such as the Braden Scale. The next step will be using the model with an independent sample. At that point, calibration may be required to optimize specificity so that the model can used to identify patients who would benefit most from interventions such as specialty beds or continuous bedside pressure mapping that are not financially feasible for every patient. Finally, our finding that time required for surgery was an important variable in the analysis warrants further investigation.