Towards a quantitative understanding of cell identity

Abstract

Cells have traditionally been characterized using expression levels of a few proteins that are thought to specify phenotype. This requires a priori selection of proteins, which can introduce descriptor bias, and neglects the wealth of additional molecular information nested within each cell in a population, which often makes these sparse descriptors qualitative. Recently, more unbiased and quantitative cell characterization has been made possible by new high-throughput, information-dense experimental approaches and data-driven computational methods. This review discusses such quantitative descriptors in the context of three central concepts of cell identity: definition, creation, and stability. Collectively, these concepts are essential for constructing quantitative phenotypic landscapes, which will enhance our understanding of cell biology and facilitate cell engineering for research and clinical applications.

Understanding cell identity

All cells in a given organism have the same basic chemical composition and metabolic activity necessary for life. What, then, makes one cell type different from another? Historically, cells were simply catalogued by their location in the body, such as heart cells or liver cells. It was also observed that cells within the same organ could exhibit very different morphologies: a star-shaped astrocyte looks different from a neuron with long axons and dendrites. Conversely, cells in different organs were found to have similar functions; for example, collagen-producing fibroblasts are found in the heart, liver, and other connective tissue. Thus, a combination of location, appearance, and functionality was used to define a cell. During this same period, the first continuous immortal cell line was derived, isolated, and expanded from a single cervical cancer cell taken from Henrietta Lacks [1,2]. The advent of such immortal cell lines has played an instrumental role in further refining our understanding of cell identity by enabling on-demand expansion and characterization of clonal cell populations. Despite tremendous progress over the past few decades, cell identity has often been based on a small number of biomarkers and some functionality testing. In the last several years, a rapidly expanding toolbox of high-throughput, single-cell experimental methods and data-driven modeling (see Glossary) approaches is ushering in a new era of quantitative cellular analysis that can be applied to more rigorously define a cell’s phenotype, track its creation, and describe its stability. In this review, we describe recent efforts to quantify cell identity based upon a cell’s epigenome, transcriptome, proteome, and morphology. Our focus is on phenotypic landscapes associated with normal cells, so here we do not explicitly consider genetic mutations and corresponding genomic models.

Defining cell identity

To isolate a specific cell type from a heterogeneous population, a small number of biomarkers (typically, 2–4) are fluorescently labeled and the desired subpopulation is recovered by fluorescence-activated cell sorting, enabling further characterization by bulk methods such as reverse transcription/polymerase chain reaction. However, the chosen biomarker signature may be insufficient to accurately identify the cells of interest [3–6]. For example, the role of CD4⁺ FOXP3⁺ T cells in tumors used to be controversial, but can now be explained by adding a sub-classification based on FOXP3 expression. CD4+ FOXP3^+,high cells contribute to tumor progression whereas CD4+ FOXP3^+,low cells suppress tumor growth [5,6]. This further suggests that a simple binary classification of markers such as FOXP3⁺ and FOXP3⁻ is not sufficient to describe cell identity.

With the rapid advancement of cell engineering and conversion techniques – including directed differentiation, reprogramming, and transdifferentiation – it is also important to establish more stringent definitional standards to ensure the quality of engineered cells. For example, one group found that by knocking down RE1 silencing transcription factor (REST), human embryonic stem cells (hESCs) still express all of the traditional pluripotency biomarkers OCT4, NANOG, and SOX2, but also exhibit higher survival rates in long-term cell culture. However, these REST-knockdown cells are functionally different from hESCs as they have an acquired bias toward mesendoderm differentiation and higher genetic instability compared to unmodified cells, thus limiting their use as true hESC replacements [7].

By increasing the number of relevant biomarkers in the molecular signature of a cell, a definition of cell identity with this signature becomes more systematic, unbiased, and reliable. Furthermore, resolving the signatures of subpopulations – down to individual cells – ensures that any heterogeneities in specific biomarkers are explicitly observed and not averaged out in bulk measurements. Of course, making thousands of measurements per cell in thousands of single cells generates datasets that are difficult if not impossible to interpret by eye; fortunately, data-driven models can be used to not only make sense of the data but to also generate more quantitative definitions of cell identity (Table 1). This has been a burgeoning field in the past several years, with researchers applying new experimental and computational tools to provide unprecedented resolution into a cell’s epigenome, transcriptome, and proteome.

Table 1. Algorithms used to quantify cell identities.

Algorithm	Data input	Molecular identifiers	Basis for selection of molecular identifiersa	Quantification	Single-cell source	Dimension reduction	Example application
CellNet, 2014 [20]	RNA-seq data	Key gene regulatory networks from database	Specificity, regulatory influence	Similarity in the gene regulatory network expression distribution	Mouse, human	N/A	Identification of transcription factors for transdifferentiation; quantification of cell identity score
Mogrify, 2016 [25]	Cell types	Differentially expressed genes; core transcription factors from database	Abundance, specificity, regulatory influence	Scores of key transcription factors	Mouse, human	N/A (MDS used in later steps for landscape construction)	Identification of transcription factors for transdifferentiation; prediction of transdifferentiation potential of a cell type
sci-MET, 2018 [17]	Single-cell bisulfite sequencing data	Top 1000 variable methylation regulatory loci from database	Variance	Correlation in DNA methylation pattern between sample data and database	Human	NMF followed by t-SNE	Prediction of cell identity

Abbreviations: multidimensional scaling (MDS), non-negative matrix factorization (NMF), t-distributed stochastic neighbor embedding (t-SNE)

^aAlthough abundance is not always explicitly mentioned as a selection criterion, it is an implicit criterion for all algorithms due to sensitivity limits in experimental measurements.

Epigenomic signatures

The epigenome of a cell directs the regulatory gene expression pattern by modulating the conformation and accessibility of chromatin. Most research linking the cell’s epigenome to its identity is either specific to a certain cell type [8] or a specific form of epigenetic modification [9–11]. This is because there are multiple forms of epigeneti6c changes including histone modifications, DNA methylation, and RNA-based chromatin modification including those controlled by small non-coding microRNAs [12]. Moreover, there are a number of technology platforms for examining epigenetic modifications, and epigenomic models typically focus on data collected from the same experimental platform to ensure comparability. There are some major public epigenome databases compiled from experimentally compatible data, including the Roadmap Epigenomics Consortium [13] and the ENCODE project [14] that contain cell-specific profiles for histone modification patterns, DNA methylation, and DNA accessibility. The FANTOM5 project also published several epigenomic studies, including a human atlas for promoters [15] and enhancers [16].

In a recent study, an algorithm called single-cell combinatorial indexing for methylation analysis (sci-MET) has been developed [17] to characterize cell types from single-cell methylome data using two epigenome databases as references [13,14]. First, sci-MET clusters methylome data using non-negative matrix factorization (NMF) (see Text Box 1) followed by t-distributed stochastic neighbor embedding (t-SNE) (see Text Box 1). Then, it compares the pattern of each cluster to the public DNA methylation database for the 1,000 most variable sites in the sample data using Pearson correlation. The algorithm correctly identified HEK293 cells, GM128778 cells, and primary human fibroblasts from a cell mixture [17].

Diffusion maps (nonlinear dimension reduction)

Diffusion maps reorganize data based on its underlying structure, creating a low-dimensional space in which the Euclidean distance between points is similar to the diffusion distance in the high-dimensional space. The algorithm first determines a kernel function (usually the normal distribution function) and a kernel matrix. It then normalizes the rows of the kernel matrix to obtain a diffusion matrix. The dimension reduction is achieved by only considering the orthogonal eigenvectors of the diffusion space. It then calculates the eigenvector of the diffusion matrix and maps to the low-dimensional diffusion space using 2 or 3 dominant eigenvectors. Diffusion maps have performed well in reproducing the structure of cluster relationships and relative spatial locations, but are not suitable for the identification of rare subpopulation of cells [69,70].

Independent component analysis (ICA; linear dimension reduction)

ICA is a linear transformation that aims to identify maximally independent sources that can reconstitute variables of the original system. This method works best when it is known that the dataset is composed of information from separate sources that do not interfere with each other, but is less commonly used in applications of cell identity.

k-means clustering (clustering)

k-means clustering is an unsupervised clustering algorithm. The algorithm first determines the number of groups and randomly selects center points. Then, the distances between each data point and the center points are calculated, and each data point is assigned to the closest center point. Based on the newly formed groups, the algorithm recalculates the mean of all the points in the group. These steps are repeated until the group centers do not change significantly between iterations.

k-medoids clustering (clustering)

The k-medoids algorithm is an unsupervised clustering algorithm that is similar to k-means clustering. The main difference between the two methods is that k-medoids clustering chooses data points as centers. This algorithm is more robust to noise and outliers because it aims to minimize the sum of general pairwise dissimilarities between data points instead of a sum of squared Euclidean distances.

k-nearest neighbors (KNN; classification)

The KNN algorithm is a supervised classification algorithm. KNN stores all available data points and classifies new data points based on a similarity measure, which is usually a distance function in cell identity applications. One data point is classified by a majority vote of its neighbors, i.e. the data point is assigned to the class most common among its k-nearest neighbors.

Linear discriminant analysis (LDA; linear dimension reduction)

LDA aims to maximize the separability among groups. Its primary latent variable accounts for the most variation among categories. This method requires a priori knowledge of the number of groups, and it can then determine which factors most contributed to the separation of the groups.

Multidimensional scaling (MDS; linear dimension reduction)

MDS measures the pairwise distances among all data points and then clusters them based on minimizing the linear distances. This method is similar to principal component analysis (see below), but MDS is more flexible in determining the distances, which can be computed using Euclidean distances, log fold changes, or other methods.

Non-negative matrix factorization (NMF; linear dimension reduction)

Non-negative matrix factorization is an unsupervised data decomposition technique that shows good performance in multivariate data. A high-dimensional matrix is decomposed into two lower dimensional matrices, with the constraint that all three matrices have no negative elements. This non-negativity and lower dimensionality makes the resulting two output matrices easier to inspect [71].

Principal component analysis (PCA; linear dimension reduction)

PCA is a dimension reduction method based on correlation among samples. The dataset is projected to a low-dimensional space with latent variables that capture the maximal variance. In the high-dimensional space, the latent variable that explains the most variation is defined as the first principal component (PC), the one that explains the second-most is the second PC, and so on. The advantage of PCA is that the key genes that contribute to a given PC are directly identifiable. However, this method may perform poorly for nonlinear datasets. For example, for high-dimensional transcriptome datasets, the first two or three PCs may not capture most of the variance, so PCA does not present an accurate picture of the data structure in low-dimensional space in this case.

t-distributed stochastic neighbor embedding (t-SNE; nonlinear dimension reduction)

In t-SNE, data points that are close in their original high-dimensional space preserve their proximity in the reduced two- or three-dimensional space. The algorithm first constructs a matrix based on normalized distance for an element and its neighboring elements. Then it randomly projects all data points into a low-dimensional space and calculates a new distance matrix. It moves data points around until the new distance matrix converges to the original distance matrix in the high-dimensional space. Thus, this method is good for conservation of high-dimensional data structure. However, t-SNE does not provide explicit information about the contribution of each component and the visualization in low-dimensional space changes every time the algorithm is applied.

Another group used the assay for transposase-accessible chromatin using sequencing (ATAC-seq) for single-cell analysis [18]. Since accessibility is associated with specific trans-factors, the group established trans-factor variability patterns for eight different cell types based on single-cell ATAC-seq data. The study showed that scATAC-seq can be used for identification of subgroups in cell mixtures. For example, regions associated with the pluripotent genes Nanog and Sox are most variable in mouse stem cells, so these cells may therefore be identified using this approach [18].

Most epigenomic studies examine expression patterns but do not investigate the structure of the underlying gene regulatory network that is determined by epigenetic regulation and modulates cell identity. This more mechanistic insight requires accurate prior knowledge of the cell type of interest. Moreover, epigenomic studies are often compared with parallel transcriptomic studies. One reason for this is that epigenomic information is a more indirect link to cell functionality compared to proteomic and transcriptomic information. Another reason is that databases for epigenomic features are smaller and less standardized than those for transcriptomic and proteomic features. Most single-cell transcriptomic studies use Illumina sequencing or standardized microarray platforms. However, there are many techniques available for global methylation analysis, including bisulfite sequencing, luminometric methylation assay (LUMA), and high performance liquid chromatography (HPLC) [19], and the data from these different methods cannot be directly compared because they have different sensitivities and specificities. Standardization of epigenetic analytical techniques should enable more robust characterization of epigenomic signatures and cell identities.

Transcriptomic signatures

In contrast to epigenomic approaches, transcriptome-based methods for cell identity modeling are more prevalent and better developed. Various quantitative criteria for cell identity have been developed, including regulatory network similarity, transcriptome uniformity, and transcriptome stability [20–22]. For example, the CellNet group built an algorithm that identifies the similarity in the key gene regulatory networks (GRNs) between engineered cells and target cells [20]. They constructed cell-specific and tissue-specific GRNs based on correlation significance between transcriptional regulators and target genes. They were then able to assign a classification score to the cells based on the expression level of the genes in the GRN. The CellNet algorithm was tested and verified using various cell type data from human and mouse. Moreover, it provides information on what genes (e.g., transcription factors) could be modified to drive engineered cells towards a target cell type of interest. Some of these suggestions were experimentally verified, such as transdifferentiation of B cells to macrophages, and fibroblasts to hepatocyte-like cells [23]. Like sci-MET, CellNet examines the similarity between the test data and data from a known cell type. However, the two algorithms differ in their objects of comparison: CellNet compares the expression of key interconnected genes within functional regulatory networks in established cell lines, whereas sci-MET compares the most variant epigenetic positions in the test sample independent of regulatory properties or cell type. CellNet can perform more robustly when the unknown sample is very heterogeneous because the top variant genes may not always be sufficient to uniquely quantify cell identity. However, both algorithms require prior knowledge of the purified cell populations and the technology platform that was used to obtain the data [20].

Proteomic signatures

Compared to epigenomic and transcriptomic approaches, proteins are most directly related to cellular function, and thus, identity. Many well-established cell conversion protocols are based on manipulation of the expression levels of key transcription factors (TFs). However, proteomic data are typically sparser and harder to measure compared to transcriptomic data, because each protein requires its own antibody for specific detection (and antibody quality can vary greatly) whereas all mRNA can be collectively recovered via the common poly-A tail and processed in bulk for high-throughput sequencing. Therefore, researchers have made efforts to link the transcriptome to the proteome by quantifying the conversion factors between mRNA abundance and protein abundance for individual genes [24] or by mapping the entire transcriptomic profile to the proteomic profile [22,25]. If high-content proteomic data are successfully obtained, it is possible to quantify cell identity in a similar fashion to that used with transcriptomic data. One group devised an algorithm that selects core regulatory TFs based on high protein expression and specificity from a pool of 503 TFs. For a given cell type, they assigned a specificity score to each of the highly expressed TFs and selected the top ones as the specificity pools for that particular cell [26]. Similar to CellNet, this approach was also able to predict TF profiles for transdifferentiation, which was experimentally verified from induced retinal pigment epithelium cells. However, it did not generate a cell identity score; rather, it quantified the expression of these key TFs using an entropy-based measure of Jensen-Shannon divergence to determine if the TF is uniquely expressed in a certain cell type. Interestingly, the researchers cross-checked their TFs with epigenomic and transcriptomic data, and found that the TFs corresponded to sites such as super-enhancers and regulatory genes related to the specific cell identity of interest [26].

The algorithm Mogrify is also a TF-based network tool focused on predicting the key factors responsible for transdifferentiation. However, Mogrify starts with the transcriptomic profile and maps gene expression to TF abundance. Mogrify also adds an additional standard for TF selection, known as the regulatory influence. The regulatory influence of each TF in a given cell type is determined by the specificity of the TF to the target cell and the directness of regulation [25]. Compared to the core TF identification method described above, Mogrify is more comprehensive since it uses the entire transcriptomic profile instead of a pre-selected pool of TFs.

In addition to TFs, secreted factors, or the secretome, are important indicators of cell identity. In one study on macrophages, the single-cell secretion levels of 42 proteins under untreated and lipopolysaccharide (LPS)-treated conditions were examined using microchambers [27]. To characterize cell populations, they used a method called viSNE, which is a practical and fast implementation of the t-SNE algorithm for large datasets. It expands the computational limit of t-SNE through random sampling of the dataset and each cell is then positioned on a two-dimensional plot based on high-dimensional data [28]. The researchers were able to identify multiple subpopulations of macrophages with different levels of LPS activation and a distinct macrophage inhibitory factor (MIF)-positive subpopulation that consistently potentiates the activation of LPS-induced cytokine function.

Physical signatures

A complementary approach to the development of quantitative chemical descriptors of cell identity is the advancement of quantitative physical descriptors. An early example of such software is CellProfiler, which determines and standardizes the shape of cells from original images. It then measures features for each identified cell or subcellular compartment, including area, shape, intensity, and texture/smoothness [29]. Another group developed a method that uses pattern recognition and classification to quantify the cellular localization patterns of four proteins [30]. In an organismal context, a method was developed to convert confocal images of Caenorhabditis elegans into a data table with quantified expression of fluorescence reporters with single-cell resolution. Using knowledge of cell number, morphology of cell nuclei, and relative cellular positions, they were able to obtain the expression profiles of 93 genes in 363 specific cells [31]. More advanced software, such as CellProfiler Analyst 2.0 [32], can handle high-throughput, high-content imaging data and utilizes multiple machine learning algorithms to quantify cell phenotypes. A notable recent paper developed a method known as iterative indirect immunofluorescence imaging (4i) to achieve high-throughput imaging of more than 40 protein features across length scales spanning millimeters to nanometers [33]. This multi-scale imaging approach not only identified protein localization within subcellular compartments, but also contextualized these observations within complex multicellular environments, enabling spatial identification of cell phenotypes within a tissue architecture.

Creating cell identity

The process of cell conversion – the transformation of a cell from one phenotype to another – involves time-dependent changes in the biochemical signature of the cell along the transformation pathway. Quantifying this trajectory provides a more accurate and comprehensive understanding of the creation of cell identity. To do this, models can be constructed that capture the dynamical changes in the molecular components that underlie cellular decision making. Depending on the a priori knowledge of the cell conversion process and the goal of the study, the form of the model can differ, as can the manner in which it describes cell trajectories.

Mechanistic models

When the network of key regulatory proteins (e.g., transcription factors) that drives a conversion process is already well characterized, mechanistic modeling – generally using ordinary differential equations (ODEs) – can be employed to study network dynamics and examine the trajectories of individual species in the network (Figure 1A). For example, one group used mutual inhibition between GATA1 and PU.1 to simulate bifurcations in the lineage commitment of bipotent progenitor cells [34]. Another group recently identified a similar mutual inhibition/self-activation model for Th1 and Th2 to generate multistability for hybrid T helper cells [35]. An additional group used mechanistic modeling of the erythropoietin receptor (EpoR)/GATA1 network topology, which demonstrates robust bistability [36,37], to explain their experimental observations that expression levels of EpoR and GATA1 modulate the velocity along the erythrocyte commitment trajectory (Figure 1B–D) [38,39]. In these examples, only two key lineage-specifying proteins are explicitly modeled, but the network interactions are nonlinear, so the resulting trajectories exhibit rich, often multistable, dynamics. Similar mathematical models focus on other complex regulatory relationships, such as the asymmetric cell fate models used for T cell differentiation that suggest memory T cells and effector T cells can arise from the same precursor cell upon antigen activation [40], connected positive and negative regulation of pluripotency genes in inner cell mass [41], and extrinsic cross-antagonism autoregulation [42]. Such minimal models can be visualized using a phase portrait, in which the x- and y-axes typically represent two key regulatory genes, and velocity vectors on this phase plane describe the trajectories or ‘flow’ in the system.

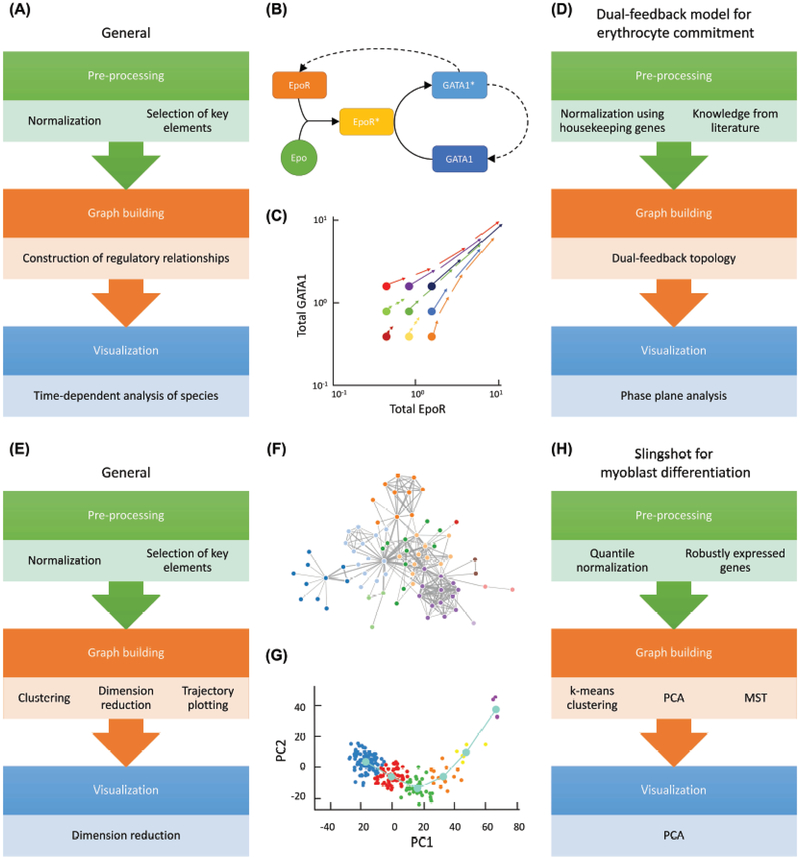
Figure 1. Construction of temporal cell trajectories using mechanistic and data-driven models.

(A) Flowchart for construction of mechanistic models of a cellular process.

(B) Example of erythroid lineage-commitment model with two non-cooperative positive feedback loops from active transcription factor GATA1*, creating more of its inactive self (GATA1) and more erythropoietin receptor (EpoR). The solid arrows represent binding/activation steps and the dashed arrows represent upregulation via protein synthesis. This network creates bistability with respect to erythropoietin (Epo) concentration, enabling robust binary decision making.

(C) A phase plane showing the trajectories of nine cells, each with different initial concentrations of GATA1 and EpoR. Cells with sufficiently high concentrations of GATA1 and/or EpoR can differentiate along the shown trajectories to a committed state in the top right corner; by contrast, cells with sub-threshold levels of these critical factors peter out and are unable to commit.

(D) The specific application of part A to the erythroid lineage-commitment model in parts B and C.

(E) Flowchart for construction of data-driven models of a cellular process. The pre-processing step is sometimes incorporated in the algorithm; if not, the data should be normalized and filtered as appropriate for the specific data and application. During graphing, clustering is an optional step. Some models perform dimension reduction before trajectory plotting, while others perform these two steps simultaneously. The sub-steps listed under each category are not necessarily in sequential order; the actual order is determined by the specific algorithm (see Table 2).

(F) A data-driven model typically uses a large dataset to construct an interaction network that is implicated in cell conversion, but the linkages and network structure are generally based on correlation, not biological mechanism.

(G) A trajectory of differentiating human skeletal muscle myoblasts generated using Slingshot. The dimension reduction method used is principal component analysis (PCA) and the axis are the primary principal component (PC1) and secondary principal component (PC2).

(H) The specific application of part E to myoblast differentiation using Slingshot. The data are visualized in two dimensions using k-means clustering and PCA, and the trajectory is overlaid on these data (light blue line in part G) using a minimum spanning tree (MST).

When there are many elements in the system, the ODEs used in mechanistic models can require significant computing power. One way to reduce this computational cost is to bin the expression of each gene into a small number of discrete states so that, in contrast to allowing a continuous spectrum of gene expression levels, far fewer calculations have to be performed [43,44]. In a stem cell model that takes into consideration nine gene nodes, the gene expression profile was reduced to a binary on-or-off system to deduce the reprogramming path from somatic cells to stem cells. This simulation of binary gene expression states necessitated some loss of information but still provided useful insights into the interaction effects of key regulatory genes [43].

Data-driven models

To analyze the dynamics of cell conversion using high-content data such as whole transcriptomes, data-driven models offer ways to condense the input data in a quantitative manner (Figure 1E). Unlike mechanistic models, the biological relationships among elements are either not explicitly taken into consideration or are highly simplified (Figure 1F). Algorithms such as Monocle [45] and StemID [46] do not identify explicit mechanistic interactions between individual genes or proteins, but rather examine overall patterns of gene expression in each cell. CellRouter [47] and SLICE [48] do consider the network of signaling and regulatory elements, but do not incorporate mechanistic mathematical relationships to describe network interactions. Most algorithms select key elements based on abundance, variance, or regulatory significance before data processing. An example of a data-driven trajectory model, application of the algorithm Slingshot to myoblast differentiation, is depicted in Figure 1G,H [49,50]. A more comprehensive listing and description of trajectory models is given in Table 2.

Table 2. Algorithms used to plot cell conversion trajectories.

Algorithm	Required inputa (optional in parentheses)	Dimension reduction (D)	Trajectory plotting (T)	Cell Clustering (C)	Order	Example application	Properties	Assumptions / requirementsb
Monocle, 2014 [45]	Branches	ICA	Weighted complete graph, MST	No	D,T	scRNA-seq datasets for human myoblast differentiation	Robust to changes in subpopulation structure, subsampling. Resolves cellular transitions during differentiation through temporal profiling of the entire transcriptome without a priori knowledge of marker genes.	Continuous transcriptome path. Known number of branches.
SCUBA, 2014 [72]	(Time course, marker genes)	k-means clustering	Gap statistic, penalized likelihood function, cusp bifurcation theory	k-means clustering	DC (simultaneous), T	RT-PCR and scRNA-seq datasets for early mouse embryo development	Robust to experimental platform differences. Uses temporal information.	Continuous transcriptome path. One or two branches.
Wanderlust, 2014 [73]	Starting cells	KNN graph	Sets of random reference points (waypoints) and determines the position of each cell by weighted shortest-path distance	No	D,T	sc-mass cytometry data for human naïve B cell differentiation	Robust to technical and biological noise.	Continuous transcriptome path. Non-branching trajectory. Known starting point of development.
Waterfall, 2015 [74]	None	PCA	k-means clustering, MST	Unsupervised hierarchical clustering	C,D,T	scRNA-seq datasets for adult neurogenesis in mouse hippocampus	Does not need temporal information or a priori knowledge of marker genes. Applicable for diverse single-cell multi-dimensional datasets, including RNA-seq and mass cytometry.	Continuous transcriptome path.
destiny, 2016 [52]	None	KNN graph	Diffusion maps	No	D,T	scRNA-seq datasets for mouse embryonic fibroblast reprogramming; qRT-PCR data for mouse embryonic cell development; sc-mass cytometry for mouse induced pluripotent stem cell reprogramming	Robust to biological noise and variation in sample density.	Continuous transcriptome path.
DPT, 2016 [53]	(Marker genes)	Diffusion maps	Diffusion maps, branching identification by comparing two independent diffusion pseudo-time (DPT) orderings over cells, metastable state identification	No	DT (simultaneous)	scRNA-seq datasets for mouse blood cell development	Robust to parameter choice. Does not need temporal information, a priori knowledge of marker genes, or starting and end cell identities.	Continuous and smooth transcriptome path.
SLICE, 2016 [48]	(Cell grouping, marker genes)	PCA	Linear Prize-Collecting Steiner Tree (LPCST) problem, MST, shortest-path approach, principal curve based approach	Partitioning around medoids (PAM) / complete weighted graph	D,C,T	scRNA-seq datasets for differentiation of mouse lung alveolar type	Robust to parameter choice. Does not need temporal information, a priori knowledge of marker genes, or starting and end cell identities.	Continuous transcriptome path. Cells with higher pluripotent potential are hypothesized to express genes with more diverse and heterogeneous functions.
SLICER, 2016 [75]	None	KNN graph, locally linear embedding (LLE)	Geodesic entropy	No	D,T	scRNA-seq datasets for mouse lung and neural cells	Robust to biological noise and presence of irrelevant elements (genes). Detects non-tree-like loop structures in development path. Does not need temporal information or a priori knowledge of marker genes.	Continuous transcriptome path.
TSCAN, 2016 [61]	None	PCA / ICA	MST	Hierarchical clustering	D,C,T	scRNA-seq datasets for human skeletal muscle myoblast differentiation	Graphical user interface. Direct comparison with other algorithms.	Continuous transcriptome path. Known number of cell clusters.
Wishbone, 2016 [76]	Starting and ending cells, (marker genes)	Diffusion maps	KNN graph, waypoint sparse approximation	No	D,T	sc-mass cytometry data and scRNA-seq data for human myeloid differentiation	Robust to parameter choice. Good branching point detection in bifurcating systems.	Continuous transcriptome path. One or two branches.
Monocle 2, 2017 [60]	(Number of cell fates)	PCA / t-SNE / diffusion maps	Reversed graph embedding (RGE)	k-means clustering	D,C,T	scRNA-seq data for human myoblast differentiation	Robust to biological noise. Does not need a priori knowledge of genes that characterize the biological process or the number of branch points in the trajectory.	Continuous transcriptome path.
scTDA, 2017 [54]	(Time course)	MDS, top 5000 variant genes	Single-cell topological data analysis (scTDA)	Single-linkage clustering	D,C,T	scRNA-seq data for mouse motor neuron differentiation	Detects transient cellular populations and their transcriptional repertoires. Detects non-tree-like loop structures in development path. Identifies cell-cycle-related features from loop structures in the trajectory.	Continuous transcriptome path.
CellRouter, 2018 [47]	(Marker genes)	t-SNE / diffusion maps	Flow network	KNN graph	D,C,T	scRNA-seq data for human neutrophil differentiation	Robust to subpopulation structure, subsampling, and choice of dimension reduction techniques.	A continuum of phenotypically distinct subpopulations. State transitions are continuous with molecular hallmarks activated or silenced in a progressive manner.
Slingshot, 2018 [50]	(Starting and ending cells)	PCA / ICA / diffusion maps	MST	k-means clustering / Gaussian mixture modeling	D,C,T	scRNA-seq data for olfactory stem cell niche	Robust to subsampling and cluster assignments. Flexibility in upstream analysis, including choice of dimension reduction and clustering algorithms. Identification of multiple cell fates.	Continuous transcriptome path.

Abbreviations: independent component analysis (ICA), minimum spanning tree (MST), k-nearest neighbors (KNN), principal component analysis (PCA), t-distributed stochastic neighbor embedding (t-SNE), multidimensional scaling (MDS)

^aThese are in addition to required gene and/or protein expression data.

^bAlthough not always explicitly mentioned as a criterion, a continuous transcriptome path is an implicit assumption for all algorithms.

Most trajectory models use gene expression data from scRNA-seq or protein expression data from single-cell mass cytometry (CyTOF). Some algorithms, such as Monocle 2, include a normalization option in the software package. In other algorithms, pre-processing of datasets is required; for example, in TSCAN, raw scRNA-seq data must be normalized to fragments per kilobase million (FPKM) or transcripts per kilobase million (TPM).

For large datasets, the dimensions of these datasets need to be reduced to enable graph building and more compact visualization (Figure 1E). Linear dimension reduction techniques, such as principal component analysis (PCA), independent component analysis (ICA), and multidimensional scaling (MDS) (see Text Box 1), perform a linear transformation on the expression data matrix, so that the first two dimensions of the resultant matrix often capture many of the features of the whole dataset. Non-linear dimension reduction methods, such as t-SNE and diffusion maps (see Text Box 1), normally calculate the distances between data points and plot the trajectory in high-dimensional space, and then project the geometry to low-dimensional space, thus preserving more of the high-dimensional structure of the dataset.

Another recent approach, called potential of heat-diffusion for affinity-based transition embedding (PHATE), was specifically developed for dimension reduction of high-content biological datasets [51]. The algorithm transforms each input cell into a probability distribution of affinities based on similarity to its neighbors. These local affinities are then propagated through the data by diffusion, which provides global, denoised structural information. The resultant diffusion-based informational distances are embedded in MDS for visualization and further analysis. PHATE has been used in several applications, including identification of distinct groupings of skin, oral, and fecal samples in human microbiome data.

In complex systems that consider thousands of factors, it is common for trajectory models to use time or pseudo-time to represent the cell conversion path [45,52–54]. Assuming cell conversion is a continuous and unsynchronized process, Monocle is an algorithm that plots this trajectory by arranging individual cells by transcriptional similarity rather than collection time. First, it employs independent component analysis (ICA) to reduce the data to two dimensions; then it uses the minimum spanning tree (MST) approach to find the longest distance between cells, assigning cells that are not on the longest trajectory to branches of the main trajectory [45]. Using single-cell RNA-seq data of differentiating human myoblasts at several time points, Monocle was able to reconstruct bifurcating cell fate trajectories within the population by assigning a pseudo-time to each cell on the plot.

Although Monocle is a pioneering approach in the reconstruction of pseudo-time trajectories, it has some limitations, such as the ability to identify alternative cell conversion paths in some applications. This issue was improved in the algorithm StemID, in which cells were first grouped using k-medoids clustering (see Text Box 1) to determine the number of cell types, and then considered possible links between the different cell clusters to deduce that the most enriched and densely covered link was the conversion trajectory of interest. Using this method, the researchers were able to find transdifferentiation paths in intestinal cells that were not identified in Monocle [46].

Compared to StemID, another cell atlas model uses a similar but more complex approach [55]. This method first employs KNN clustering and pseudo-temporal ordering of transcriptome data using a newly developed algorithm called partition-based graph abstraction (PAGA) [56], and then determines a pluripotency score for each cell cluster. The approach also uses an RNA velocity algorithm called velocyto [57] to consolidate the directionality of cell development. The velocyto algorithm can extrapolate the gene expression profile from the rate of change of mRNA expression (i.e., mRNA velocity), which is calculated from the balance between production (of spliced mRNA from unspliced mRNA) and degradation. Combining PAGA, velocyto, and marker gene expression analysis for cell type identification, the researchers mapped out the cell atlas and complete lineage tree of a whole organism, the planarian Schmidtea mediterranea.

Lineage construction is widely used in developmental biology. However, in contrast to applications in planarians, which are regenerative and contain both adult cells and neoblasts, single-cell sequencing of most animal tissues only provides a snapshot of a certain developmental stage. Recently, a group used CRISPR/Cas9-induced genetic scars together with a computational method known as lineage tracing by nuclease-activated editing of ubiquitous sequences (LINNAEUS), to plot lineage trees for zebrafish larvae and adults [58]. The experimental design was based on the knowledge that when there is no template for homologous repair, Cas9 produces random mutations, or scars, at the target sites. The researchers introduced random scars on a large number of cells at the early stage of development such that the scars were propagated in daughter cells via recombination [58]. At later time points, they obtained single-cell transcriptome data and reconstructed the lineage tree based on scar analysis [58]. They first clustered cells using t-SNE and identified cell types by biomarkers. In their scar network analysis, two scars are considered connected nodes if they are both seen in the same cell; across all of the cells, this results in a scar network, with each scar having different levels of connectivity. The scar with the highest degree of connectivity is from the common ancestor of all analyzed cells and therefore the earliest progenitor along the developmental trajectory. The second earliest scar is identified using the same algorithm but with the first scar removed, enabling identification of the next set of cells in the developmental hierarchy. Repeating this process results in reconstruction of the full developmental lineage.

For a given application, different trajectory plotting models can each offer unique advantages, which arise from the sequence of how the different steps are performed. For example, models such as diffusion pseudo-time (DPT) do not perform dimension reduction before lineage construction, better conserving the high-dimensional data structure. The DPT model showed better robustness across multiple datasets compared to Monocle [45] and Wishbone, which is another trajectory plotting algorithm that uses diffusion maps and KNN graphs (see Text Box 1) [53]. On the other hand, for algorithms that perform clustering before plotting lineage trees such as StemID, they show good ability to identify rare sub-populations because there is less data loss in sub-population identification [46]. For trajectories generated in computational methods such as Waterfall, TSCAN, and Slingshot, adding a clustering step before trajectory plotting greatly improved the computational speed without losing accuracy [59]. Slingshot, which was shown to work well among all types of trajectories [59], first uses cluster-based MST to identify the global structure of the trajectory and then fits smooth curves to the general structure, with a pseudo-time assigned to each cell [50]. The sequence of the model-building steps for a number of algorithms is provided in Table 2.

Trajectory plotting models may have other algorithm-specific advantages. For example, single-cell topological data analysis (scTDA) can be used to study time-dependent transcriptome profiles [54]. It first clusters the data in high-dimensional space; then, it assigns a node to each cluster, with clusters that share cells connected by an edge. Nodes that are connected in the low-dimensional representation lie near each other in the original high-dimensional expression space. Using temporal input information, this algorithm is able to identify the most pluripotent state without prior knowledge of the least differentiated state. Compared with parallel analyses of the same data using principal component analysis (PCA), t-SNE, or Monocle, scTDA had superior ability to identify the continuous chronological structure of motor neuron differentiation using simulated data [54]. Another method for trajectory plotting is CellRouter, which employs unique techniques in clustering (KNN graph) and lineage determination (graph theory) to reinforce the connections among cells that show phenotypic likeness and to identify the data structure in high-dimensional space. The algorithm does not make any assumptions about branching and it provides information on transient states during cell conversion [47].

The available computational tools are also rapidly evolving. For example, the researchers who developed Monocle recently published Monocle 2, which no longer assumes previous knowledge of cell-fate branches. Instead, Monocle 2 uses a machine learning technique called reversed graph embedding (RGE) to produce the geometry of high-dimensional data in a low-dimensional space without making any assumptions about branch number [60]. Another improvement is in the accessibility of complex algorithms to non-specialists; for example, TSCAN offers a graphical user interface to facilitate pseudo-time reconstruction [61]. These models typically take the gene expression data of multiple single cells as input, and they output the pseudo-time of each cell, assigning each cell to a defined position along the cell conversion trajectory.

Another type of algorithm that uses single-cell network entropy to construct differentiation trajectories models is known as single cell lineage inference using cell expression similarity and entropy (SLICE) [48]. In SLICE, the algorithm first calculates single-cell entropy based on expression of functional gene clusters and then it groups cells based on similarity of these entropy scores. It next identifies stable states by finding cells with local minima in entropy. The cell differentiation paths are reconstructed by following decreasing entropy towards the stable cell states [48]. For example, using a cross-sectional single-cell dataset from mouse lung at a single time point (E16.5), SLICE identified different cell clusters, found the stable states of each cluster, and reconstructed a two-branch cell pathway. The algorithm identified the types of cells in the dataset using known information about mouse lung cells and then determined the position of these cell types along the differentiation trajectory.

Characterizing stability of cell identity

Compared to the two-dimensional trajectory models (as described above), three-dimensional landscape models present a more holistic view of cell phenotype because they additionally include information about cell stability. The most famous qualitative representation of this information in developmental biology is Waddington’s epigenetic landscape [62]. This landscape depicts a marble as a progenitor cell rolling down a slope, with bifurcating ridges representing lineage commitments and the lowest positions on the slope representing final cell states. More recent quantitative landscape models (Table 3) are based on the combination of one-dimensional cell stability (or potential) quantification and two-dimensional trajectory models, with the z-axis representing cell stability, and the x-y plane a representation of the trajectory model (Figure 2). Cell stability/potential is related to the capability of a cell to become other cell types; cells with low stability have a high potential (high z-value) and thus more easily ‘roll down’ the landscape to more stable/lower potential cell states.

Table 3. Algorithms used to quantify and plot cell potential landscapes.

Algorithm	Data input	Z-axis quantification	Z-axis	X-Y plane	Example application
Banerji et al., 2013 [22]	scRNA-seq data	Network entropy z = SR= −∑(π*p*ln(p))	Measure for pluripotent potential, which is based on the functional pathway promiscuity, defined as the weighted sum of entropy for all pathway proteins, π*p*ln(p)	t-SNE	Prediction that a human embryonic stem cell population contains a small fraction of cells of lower potency that are primed for differentiation
Fard et al., 2016 [44]	Gene expression data	Hopfield energy z = E = −½HWHT	Measure of pluripotent potential, determined by the updated energy state, which is calculated based on weighted (Wi) interactions between each node (Hi) and its connected neighbors	PCA	Description of stem cell differentiation
Grün et al. (StemID), 2016 [46]	scRNA-seq data	Transcriptome entropy z = S = l*E	Measure for pluripotent potential, determined by number of possible fates (l) and uniformity of gene expression (E)	t-SNE	Description of differentiation lineages of hematopoietic stem cells in the bone marrow
Rackham et al. (Mogrify), 2016 [25]	Microarray data	Conversion potential z = (AUC of the cumulative coverage for the top eight transcription factors) / (maximum possible AUC to retrieve a value between 0 and 1 for each ontology as the height)	Measure for how likely a cell type is to be a good starting cell source	MDS	Description of human cell types in terms of naturally occurring states and the transitions among them

Abbreviations: t-distributed stochastic neighbor embedding (t-SNE), principal component analysis (PCA), area under the curve (AUC), multidimensional scaling (MDS)

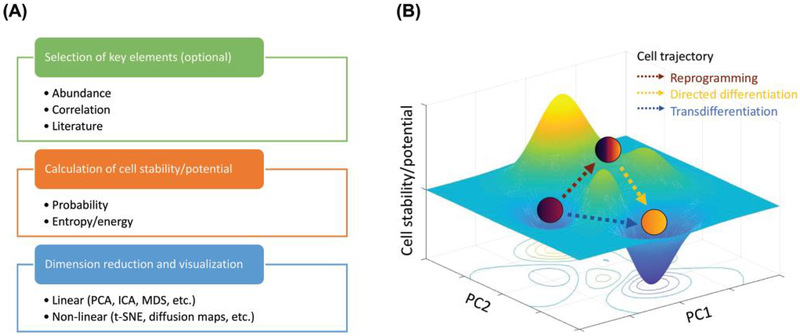
Figure 2. Steps for generating a landscape model.

(A) The selection of key elements is an optional step that is commonly used to save computational power and reduce noise. The z-axis, which is the cell stability or potential, is the key calculation that distinguishes different models (see Table 3). For dimension reduction, principal component analysis (PCA), independent component analysis (ICA) and multidimensional scaling (MDS) are commonly used linear methods while t-distributed stochastic neighbor embedding (t-SNE) and diffusion maps are popular non-linear methods.

(B) In this depiction of a cell phenotype landscape, the z-axis represents cell stability or potential (see Table 3). A lower z-value corresponds to greater stability, with local minima representing stable (or metastable) states. The x-y plane represents cell identity, as quantified by algorithms based on epigenomic, transcriptomic, and/or proteomic profiles (see Table 1), and changes in position along the landscape are quantified by trajectory models (see Table 2).

Probabilistic landscapes

Probabilistic landscape models, which are based purely on statistics and do not make any assumptions about biological mechanism, are widely used for descriptions of cell development. The cell potential is calculated from the probabilities of appearance of certain states; differentiated, stable cells are seen as attractor states that have lower z-values [63]. To calculate this potential value, significant genes are selected based on their expression levels and extent of change during the process. These significant genes are reduced to two dimensions using algorithms such as PCA and the cell potential is calculated as a function of the probability of appearance. Although different networks or dimension-reduction methods may be applied, the landscapes in these models are compiled based on the probability of the cell state, with the cell potential represented by the negative natural logarithm of the probability [64–66]. For example, one group constructed a stem cell regulatory network, comprised of 52 genes, to generate a landscape plot that has two local minima, with the higher local minimum representing the pluripotent cell state and the lower local minimum representing the differentiated cell state [65].

Entropic/energetic landscapes

There are also entropy- or energy-based models for constructing landscapes. In the entropy models, the z-axis is often informational entropy which is not a direct measure of cell stability but rather a representation of pluripotency potential (i.e., the ability of the cell to differentiate to other cell identities). In contrast to probability models, these models are usually based on biological properties or assumptions that are specific to stem cells.

Entropy can also be a measure of pathway promiscuity [21]. In this context, it is assumed that pluripotent cells have access to more signaling pathways than differentiated cells, which express only a restricted set of functional pathways. The transcriptome data maps genes to proteins, and then protein-protein interaction networks are used to calculate the possible pathways for each individual signaling protein. Using this method, pluripotent stem cells and cancer cells were observed to have higher entropies compared to those from a set of miscellaneous differentiated cells [21].

The SLICE model mentioned earlier is also based on a similar assumption of functional activation promiscuity in pluripotent cells, which are postulated to have more evenly distributed activation across functional classes of genes [48]. Unlike the network entropy model, SLICE eliminates mapping of the transcriptome to the proteome to analyze the functional pathways. Instead, it clusters genes according to their functional similarity using Gene Ontology annotation. It then analyzes the associations between gene clusters and gene expression profiles based on cell-specific posterior probability distributions. This probability is equivalent to the single-cell entropy. Using SLICE with scRNA-seq data, the group successfully predicted the entropic states of differentiating human skeletal muscle myoblasts, enabling reconstruction of an entropic landscape for this process.

In StemID, entropy is defined with respect to the uniformity of gene expression in the transcriptome. The method assumes that stem cells have more noisy expression of mRNA, which should lead to more branches on the lineage tree. The entropy of the cell is calculated as the sum of the normalized entropy of each protein. Cell potential is calculated as the number of possible lineage trajectory branches multiplied by this transcriptome entropy. This model was validated in several biological contexts, including hematopoietic cells and pancreas cells [46].

An energy-based landscape model computes its x-y plane in a manner similar to such entropy models, but differs in its calculation of the z-axis. This axis, an energy, is computed based on the idea that a GRN is less interconnected in differentiated cells, so there is a higher co-variation of gene expression, resulting in a lower energy state [44]. A neural network model known as a Hopfield network is used to calculate the energy of each cell state [44]. In this approach, each gene becomes a node in the network and has a starting value determined by normalized expression data. The link between two nodes is assigned a weight, calculated as a Pearson correlation. The expression value of each node is discretized to the values −1, 0, or 1. The sign of each expression value is then constantly updated, based on the expression of all neighboring nodes and the correlations with each neighbor. Energies are calculated based on the extent of agreement or disagreement between nodes, and the corresponding landscape is generated using the first two principal components in PCA as the x- and y-axes. The use of such discretized models, in general, showed robustness towards noise and perturbations [67]. The Hopfield network has been applied to study the differentiation of hESCs into mature cells and the differentiation of THP1 monocytes into macrophages using microarray expression data. The transient states along the differentiation pathways were found to have higher energies, enabling identification of upregulated or downregulated genes in these specific higher-energy states.

Concluding remarks

The development of advanced cell conversion techniques, including directed differentiation, reprogramming, and transdifferentiation, necessitate more quantitative descriptions and understanding of cell identity: what identity means, how it is created, and how stable it is. Additionally, the ability to now study many cell conversion processes with single-cell resolution has resulted in large and rich experimental datasets. The convergence of these experimental advances has resulted in complementary computational methods that can take these high-content, high-resolution datasets as inputs and produce quantitative outputs that enhance our descriptions of cell identity, cell trajectories, and cell stability.

We can see several trends in the development of these computational techniques. First, dimension reduction is no longer restricted to linear methods; nonlinear methods such as t-SNE and diffusion maps have seen considerable success in more recent models. These nonlinear methods normally supersede linear methods in retention of high-dimensional data structure. Among the nonlinear methods, the main differences lie in how distances between data points are calculated and mapped to a lower-dimensional space.

Second, there are fewer restrictions on the input data. Datasets can now have unknown subpopulations, unknown starting and ending points, and little-to-no temporal information. There are also algorithms that split up the tasks for lineage determination and landscape construction, allowing researchers to choose the dimension reduction methods or visualizations that are best for a particular application. For example, Netland allows users to choose between deterministic (ODE-based), stochastic, and probabilistic landscapes based on the complexity of the input data [68].

Third, there is less loss of information in more recent models. There are two steps at which loss of information can occur: the selection of key regulatory networks and dimension reduction of the dataset. Deterministic ODE-based models typically incorporate GRNs that are selected based on prior knowledge, variation, correlation, and/or abundance; however, supervised selection of regulatory genes can introduce bias and it is not realistic to experimentally obtain all of the parameters required for simulation. By contrast, probabilistic, entropy, and energy models can circumvent these bias and parameter problems, as they can agnostically select key regulatory elements and generate simplified interaction networks among them. More recent data-driven models have also begun to address the loss of information associated with dimension reduction; for example, scTDA and DPT determine the lineage structure or landscape topology in high-dimensional space and then apply dimension reduction at a later step for distance calculation and data visualization.

Looking forward, this nascent field could benefit from standardization of computational methods. Although efforts have been made to make these algorithms accessible to the broader cell biology community, it is sometimes difficult to determine what information is required and what assumptions are implicit, thus confounding interpretation of the results. Additionally, while several methods make efforts to demonstrate robustness of their approach, the nature of this robustness can be highly varied (e.g., differences in sample size, parameter variation, or missing data).

Additionally, the development of new models (and parallel experimental approaches) will continue to push the field rapidly forward. For example, the quantification of cell identity based on epigenomic signature is in its early stages and can be improved by considering the interconnectivity among epigenetic sites. There are currently models that relate epigenetic profiles to transcriptomic data, map transcriptomic data to proteomic data, and link morphological properties to transcriptomic data; however, there are currently no methods that integrate all of the quantitative descriptors of cell identity into a holistic computational framework. Advances towards this goal will allow more robust cross-validation of a cell’s chemical and physical properties, which should further enhance our quantitative understanding of cell identity (see ‘Outstanding Questions’).

Outstanding questions.

To what extent are quantitative single-cell epigenomic, transcriptomic, and proteomic analyses distinct or redundant? Can these methods be used to cross-validate measurements of gene expression?

Can methods be developed to reduce technical bias against low-expressing but potentially important genes?

Can model standards be developed to enhance clarity of required inputs, underlying assumptions, and cross-platform comparisons?

Can single-cell molecular measurements be integrated with single-cell imaging data to link chemical and physical signatures of cell identity?

Highlights.

• High-throughput, single-cell experimental methods enable high-content epigenomic, transcriptomic, and proteomic signatures of cell identity

• Data-driven modeling approaches facilitate analysis of high-content datasets and more quantitative descriptors of cell identity

• Integration of experimental and modeling approaches further enables tracking trajectories for creating a cell identity and assessing its stability

• Model-guided understanding of cell identity, conversion trajectories, and stability facilitates construction of quantitative phenotypic landscapes

Glossary

Data-driven modeling

Mathematical approaches to quantitatively characterize a system (e.g., a cell) by changes in the structure of measured system variables, rather than by prior mechanistic knowledge about these variables.

Directed differentiation

The process of guiding pluripotent cells towards a specific differentiated state.

Dimension reduction

The process of condensing high-dimensional data into a smaller number of components. This is often applied to cellular transcriptomes or proteomes to enable visualization of cell identities, trajectories, or landscapes in two or three dimensions.

High-dimensional space

A description of state in which each variable (e.g., gene) represents a single dimension. Such descriptors are not readily intuited, so they are often compacted into a smaller number of high-content dimensions that can be easily visualized (see Dimension reduction).

Mechanistic modeling

Mathematical approaches to quantitatively characterize a system (e.g., a cell) using prior knowledge of the system variables, their interactions, and their modes of action.

Multistability

The potential for a system (e.g., a cell) to adopt more than one stable state for a given set of conditions (bistability corresponds to two stable states, tristability to three, etc.). The specific stable state that is actually attained is dictated by the history of the system.

Phase portrait

A commonly used graphical method to analyze dynamics of mechanistic models formulated with differential equations. The time derivatives of species in the model represent their velocities, which can be used to visualize their trajectories in the phase plane.

Reprogramming (or dedifferentiation)

The process of reverting a differentiated cell to a pluripotent state.

Stability

A measure of how likely a system (e.g., a cell) will remain in its current state. This quantity is often the z-axis in cell phenotypic landscapes.

Transdifferentiation

The process of converting one mature cell type directly into another, without backtracking to a progenitor state.

Waddington’s epigenetic landscape

A commonly used metaphor in developmental biology, depicted as a slope with valleys and ridges that dictate what paths a progenitor cell traverses in reaching mature cell fates.