Transcriptome Deconvolution of Heterogeneous Tumor Samples with Immune Infiltration

Summary

Transcriptome deconvolution in cancer and other heterogeneous tissues remains challenging. Available methods lack the ability to estimate both component-specific proportions and expression profiles for individual samples. We present DeMixT, a new tool to deconvolve high-dimensional data from mixtures of more than two components. DeMixT implements an iterated conditional mode algorithm and a novel gene-set-based component merging approach to improve accuracy. In a series of experimental validation studies and application to TCGA data, DeMixT showed high accuracy. Improved deconvolution is an important step toward linking tumor transcriptomic data with clinical outcomes. An R package, scripts, and data are available: https://github.com/wwylab/DeMixTallmaterials.

Graphical Abstract

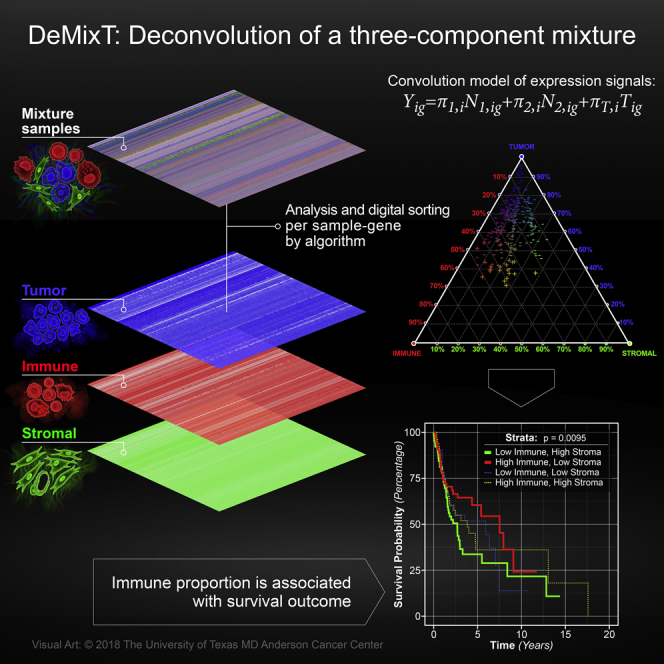
Highlights

• •A new tool DeMixT for efficient and accurate transcriptome deconvolution
• •Individual-level gene expression deconvolution of three components in cancer samples
• •Accurate estimation of both component-specific proportions and expression profiles
• •New insight in head and neck cancer prognosis and immune infiltration

Computational Bioinformatics; Cancer; Transcriptomics

Introduction

Heterogeneity of malignant tumor cells adds confounding complexity to cancer treatment. The evaluation of individual components of tumor samples is complicated by the tumor-stroma-immune interaction. Anatomical studies of the tumor-immune cell contexture have demonstrated that it primarily consists of a tumor core, lymphocytes, and the tumor microenvironment (Pages et al., 2009, Fridman et al., 2012). Further research supports the association of infiltrating immune cells with clinical outcomes for individuals with ovarian cancer, colorectal cancer, and follicular lymphoma (Dave et al., 2004, Galon et al., 2006, Zhang et al., 2003). The use of experimental approaches such as laser-capture microdissection (LCM) and cell sorting is limited by the associated expense and time. Therefore, understanding the heterogeneity of tumor tissue motivates a computational approach to integrate the estimation of type-specific expression profiles for tumor cells, immune cells, and the tumor microenvironment. Most commonly available deconvolution methods assume that malignant tumor tissue consists of two distinct components, epithelium-derived tumor cells and surrounding stromal cells (Ahn et al., 2013, Gong and Szustakowski, 2013). Other deconvolution methods for more than two compartments require knowledge of cell-type-specific gene lists (Liebner et al., 2014), i.e., reference genes, with some of these methods applied to estimate subtype proportions within immune cells (Li et al., 2016a, Li et al., 2016b, Newman et al., 2015). Therefore, there is still a need for methods that can jointly estimate the proportions and compartment-specific gene expression for more than two compartments in each tumor sample.

The existing method, ISOpure (Quon et al., 2013), may address this important problem. However, ISOpure assumes a linear mixture of raw expression data and represents noncancerous profiles in the mixed tissue samples by a convex combination of all the available profiles from reference samples. A drawback of this modeling approach is that the variance for noncancerous profiles is not compartment specific; therefore (1) the variances that are needed for estimating sample- and compartment-specific expressions cannot be estimated and (2) not accounting for sample variances can result in large bias in the estimated mixing proportions and mean expressions. As we aim to address the need for both gene-specific variance parameters and two unknown mixing proportions per sample in the three-component scenario, our previous heuristic search algorithm developed for two components (Ahn et al., 2013) is inadequate for the computation.

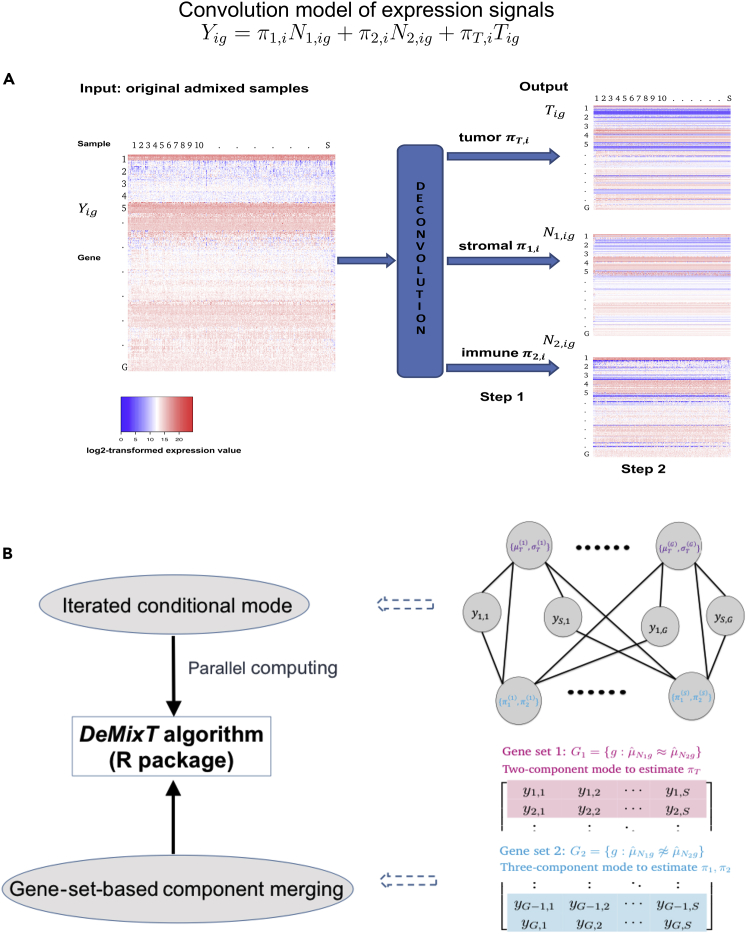
We have developed a new computational tool, DeMixT, to accurately and efficiently estimate the desired high-dimensional parameters in a linear additive model that accounts for variance in the gene expression levels in each compartment (Figure 1A). The corresponding R package and data for DeMixT is freely available for downloading at https://github.com/wwylab/DeMixTallmaterials.

Figure 1.

The Model and Algorithm of DeMixT

(A) DeMixT performs three-component deconvolution to output tissue-specific proportions and isolated expression matrices of tumor (T-component), stromal (N₁-component), and immune cells (N₂-component). Heatmaps of expression levels correspond to the original admixed samples, the deconvolved tumor component, stromal component, and immune component.

(B) DeMixT-based parameter estimation is achieved by using the iterated conditional modes (ICM) algorithm and a gene-set-based component merging (GSCM) approach. The top graph describes the conditional dependence between the unknown parameters, which can be assigned to two groups: genome-wise parameters (top row, red superscript) and sample-wise parameters (bottom row, blue superscript). They are connected by edges, which suggest conditional dependence. The unconnected nodes on the top row are independent of each other when conditional on those on the bottom row, and vice versa. Because of conditional independence, we implemented parallel computing to substantially increase computational efficiency. The bottom graph illustrates the GSCM approach, which first runs a two-component deconvolution on gene set G₁ (red), where ${\hat{\mu }}_{N_{1}g}\approx {\hat{\mu }}_{N_{2}g}$ to estimate π_T, and then runs a three-component deconvolution on gene set G₂ (blue), where ${\hat{\mu }}_{N_{1g}}$ ≉ ${\hat{\mu }}_{N_{2g}}$ and π_T is given by the prior step, to estimate π₁ and π₂.

Results

The DeMixT Model and Algorithm

Here, we summarize our convolution model as follows (Figure 1A; see further details in Transparent Methods). The observed signal Y_ig is written as Y_ig = π_1,iN_1,ig+π_2,iN_2,ig+(1−π_1,i−π_2,i)T_ig for each gene g and each sample i, where Y_ig is the expression for the observed mixed tumor samples and N_1,ig, N_2,ig, and T_ig represent unobserved raw expression values from the constituents. We assume that N_1,ig, N_2,ig, and T_ig each follow a log₂-normal distribution with compartment-specific means and variances (Ahn et al., 2013, Löonnstedt and Speed, 2002). The N₁-component and the N₂-component are the first two components, the distributions of which need to be estimated from available reference samples, and π_1,i and π_2,i are the corresponding proportions for sample i. The last component is the T-component, the distribution of which is unknown. In practice, the T-component can be any of the following three cell types: tumor, stromal, or immune cells. For inference, we calculate the full likelihood and search for parameter values that maximize the likelihood. Our previously developed heuristic search algorithm (Ahn et al., 2013) for a two-component model is inadequate for a three-component model, which is exponentially more complex: (1) there are two degrees of freedom in the mixing proportions, which is unidentifiable in a large set of genes that are not differentially expressed between any two components, and (2) in each iteration in the parameter search, we need to perform tedious numerical double integrations to calculate the full likelihood. The DeMixT algorithm introduce two new elements that help ensure estimation accuracy and efficiency (Figure 1B). We first apply an optimization approach, iterated conditional modes (ICM) (Besag, 1986), which cyclically maximizes the probability of each set of variables conditional on the rest, for which we have observed rapid convergence (Besag, 1986) to a local maximum (see the pseudo-code in Figure S1). The ICM framework further enables parallel computing, which helps compensate for the expensive computing time used in the repeated numerical double integrations. However, this is not sufficient for accurate parameter estimation. We observed that including genes that are not differentially expressed between the N₁ and N₂ components in the three-component deconvolution can introduce large biases in the estimated π₁ and π₂ (Figure S2), whereas the π_T estimation is little affected. We therefore introduce a novel gene-set-based component merging (GSCM) approach (Figure 1B). Here, we first select gene set 1, where μ_N1g≈μ_N2g, and run the two-component model to estimate π_T,i. Then we select gene set 2, where μ_N1g≉μ_N2g, and run the three-component model with fixed π_T from the above-mentioned equation, to estimate {π_1,i,π_2,i}. Our goal is to avoid searching in the relatively flat regions of the full likelihood (model unidentifiable, Figure S3) and focus on regions where the likelihood tends to be convex. Using this approach, we not only improve the estimation accuracy but also further reduce the computing time, as only a small part of the entire parameter space needs to be searched.

Validation Using Data with Known Truth

We validated DeMixT in two datasets with known truth in proportions and mean expressions: a publicly available microarray dataset (Shen-Orr et al., 2010) generated using mixed RNAs from rat brain, liver, and lung tissues in varying proportions and an RNA sequencing (RNA-seq) dataset generated using mixed RNAs from three cell lines, lung adenocarcinoma (H1092), cancer-associated fibroblasts (CAFs), and tumor infiltrating lymphocytes (TILs).

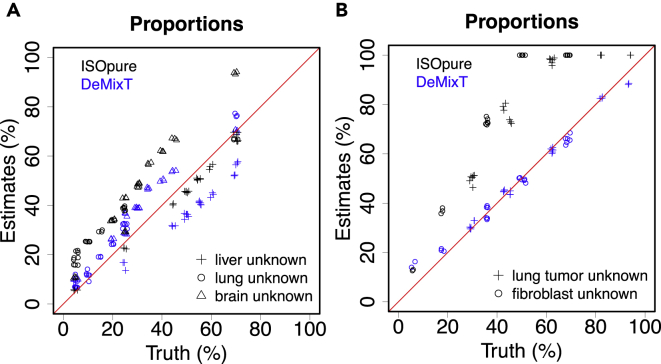
We used GEO: GSE19830 (Shen-Orr et al., 2010) as our first dataset for benchmarking. This microarray experiment was designed for the expression profiling of samples from Rattus norvegicus with the Affymetrix Rat Genome 230 2.0 Array, including 30 mixed samples of liver, brain, and lung tissues in 10 different mixing proportions with three replicates (Table S1). To run DeMixT, we used the samples with 100% purity to generate the respective reference profiles for the N₁-component, N₂-component, and T-component. We ran the deconvolution for the 30 mixed samples under three scenarios, respectively, assuming the liver, brain, and lung tissues to be the unknown T-component tissue. To generate the second dataset in RNA-seq, we performed a mixing experiment, in which we mixed mRNAs from three cell lines, lung adenocarcinoma in humans (H1092), CAFs, and TILs, at different proportions to generate 32 samples, including 9 samples that correspond to three repeats of a pure cell-line sample for the three cell lines (Table S2). The RNA amount of each tissue in the mixture samples was calculated on the basis of real RNA concentrations tested in the biologist's laboratory. We assessed our deconvolution approach through a number of statistics, e.g., concordance correlation coefficients (CCCs) (Lawrence and Lin, 1989), root mean square errors, and a summary statistic for measuring the reproducibility of the estimated π across scenarios when a different component is unknown (see Transparent Methods). We showed that DeMixT performed well and outperformed ISOpure in terms of accuracy and reproducibility (Figures 2A and 2B; see Transparent Methods for further details, Figures S4–S7, Tables S3–S7).

Figure 2.

Validation Results using Microarray and RNA-seq Data from Tissue and Cell-Line Mixture Experiments

(A) Scatterplot of estimated tissue proportions versus the truth when liver (plus), brain (triangle), or lung (circle) tissue is assumed to be the unknown tissue in the microarray experiments mixing the three; estimates from ISOpure are also presented.

(B) Scatterplot of estimated tissue proportions versus the truth when either lung tumor (plus) or fibroblast (circle) cell lines are assumed to be the unknown tissue in the RNA-seq experiments mixing lung tumor, fibroblast, and lymphocyte cell lines.

See also Figures S4 and S6 and Tables S3–S7.

Validation Using LCM Data

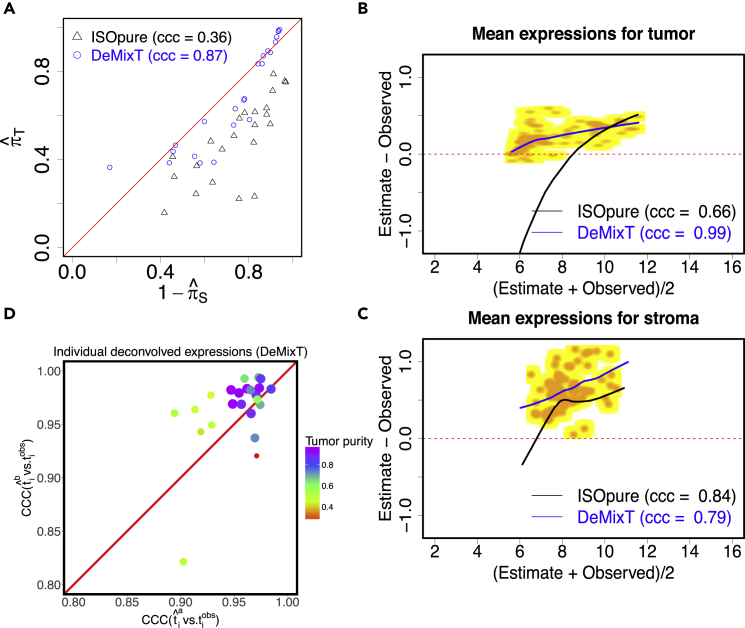
We then applied DeMixT to a “gold standard” validation dataset from real tumor tissue that has known proportions, mean expressions, and individual component-specific expressions. This dataset (GEO: GSE97284) was generated at Dana Farber Cancer Institute through Laser capture microdissection (LCM) experiments on tumor samples from patients with prostate cancer. It consists of 25 samples of isolated tumor tissues, 25 samples of isolated stromal tissues, and 23 admixture samples (Tyekucheva et al., 2017b). LCM was performed on formalin-fixed paraffin embedded (FFPE) tissue samples from 23 patients with prostate cancer, and microarray gene expression data were generated using the derived and the matching dissected stromal and tumor tissues (GEO: GSE97284 [Tyekucheva et al., 2017a]). Owing to the low quality of the FFPE samples, we selected a subset of probes (see Transparent Methods) and ran DeMixT under a two-component mode. DeMixT obtained concordant estimates of the tumor proportions when the proportion of the stromal component was unknown and when the proportion of tumor tissue was unknown (CCC = 0.87) (Figure 3A). DeMixT also tended to provide accurate component-specific mean expression levels (Figures 3B, 3C, and S8) and yielded standard deviation estimates that are close to those from the dissected tumor samples (Figure S9). As a result, the DeMixT individually deconvolved expressions achieved high CCCs (mean = 0.96) for the tumor component (Figures 3D and S10). The expressions for the stromal component were more variable than those for a common gene expression dataset, hence both DeMixT and ISOpure gave slightly biased estimates of the means and standard deviations.

Figure 3.

Analyses of Real Data Using DeMixT through Validation Using LCM Data in Prostate Cancer

(A) Scatterplot of estimated tumor proportions versus 1- estimated stromal proportions; estimates from DeMixT (blue) are compared with those from ISOpure (black).

(B) Smoothed scatter MA plots between observed and deconvolved mean expression values at the log2 scale from DeMixT for the tumor component (yellow for low values and orange for high values). The lowest smoothed curves for DeMixT are shown in blue and those for ISOpure in black. (C) Smoothed scatter MA plots between observed and deconvolved mean expression values at the Log2 scale from DeMixT for the stromal component.

(D) Scatterplot of concordance correlation coefficient (CCC) between individual deconvolved expression profiles for the tumor component (${\hat{t}}_i$) and observed values ($t_i^{obs}$) for 23 LCM matching prostate cancer samples. Superscript a: stromal component is represented by reference samples; b: tumor component is represented by reference samples. Color gradient and size of each point corresponds to the estimated tumor proportion.

Application to the Cancer Genome Atlas Head and Neck Squamous Cell Carcinoma Data

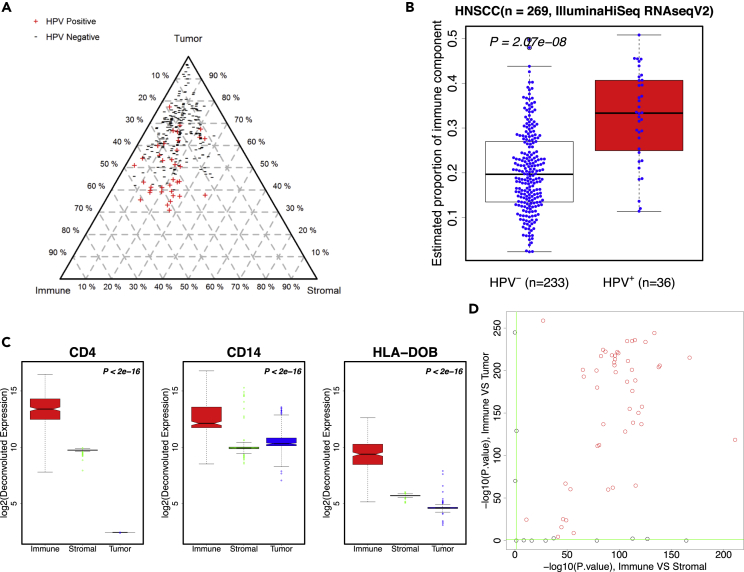
A recent study of head and neck squamous cell carcinoma (HNSCC) showed that the infiltration of immune cells, both lymphocytes and myelocytes, is positively associated with viral infection in virus-associated tumors (Li et al., 2016a, Li et al., 2016b). We downloaded HNSCC RNA-seq data from The Cancer Genome Atlas (TCGA) data portal (Cancer Genome Atlas Network, 2015) and ran DeMixT for deconvolution. We normalized the expression data with the total count method and filtered out genes with zero count in any sample. There was a total of 44 normal tissue and 269 tumor samples in the HNSCC dataset. We collected the information of human papillomavirus (HPV) infection status for the HNSCC samples. Samples were classified as HPV-positive (HPV+) using an empiric definition of the detection of >1,000 mapped RNA-seq reads, primarily aligning to viral genes E6 and E7, which resulted in 36 HPV+ samples (Cancer Genome Atlas Network, 2015). Since only reference samples for the stromal component are available from TCGA (i.e., 44 normal samples and 269 tumor samples), we devised an analytic pipeline for DeMixT to run successfully on the HNSCC samples (for details, see Transparent Methods and Figure S11). In brief, we first used data from the HPV+ tumors to derive reference samples for the immune component and then ran the three-component DeMixT on the entire dataset to estimate the proportions for both HPV-negative (HPV-) and HPV+ samples. For all tumor samples, we obtained the immune (mean = 0.22, standard deviation = 0.10), the tumor (mean = 0.64, standard deviation = 0.13), and the stromal proportions (mean = 0.14, standard deviation = 0.07; see Figure 4A). The distribution of stromal proportions seems independent, whereas the tumor and immune proportions are inversely correlated. As expected, HPV+ tumor samples had significantly higher immune proportions than those that tested as HPV- (Li et al., 2016a, Li et al., 2016b, Fakhry et al., 2008) (p value = 2 × 10⁻⁸; Figures 4A, 4B, and S12). To further evaluate the performance of our deconvolved expression levels, we performed differential expression tests for immune versus stromal tissue and immune versus tumor tissue, respectively, on 63 infiltrating immune cell-related genes (CD and HLA genes). For example, Figure 4C illustrates that the deconvolved expressions were much higher in the immune component than in the other two components for three important immune marker genes, CD4, CD14, and HLA-DOB. What we observed with the purified expression levels of these genes is as expected. Overall, 51 of 63 genes were significantly more highly expressed in the immune component than in the other two components (adjusted p values are listed in Data S1; also see Figure 4D). In addition, we divided the patient samples into four groups based on their estimated immune and stromal proportions, using simply the median values as cutoffs. The corresponding four groups of patient samples are significantly different in terms of overall survival outcomes. The Cox proportional hazards regression coefficient of the high-immune-low-stroma group versus the low-immune-high-stroma group is −0.66 with the Wald test (p value = 0.001). As expected, the high-immune-low-stroma group of patients have the best prognosis as compared with the other groups. In comparison, we performed the same survival analysis on patients who are categorized by dichotomizing the immune and stromal scores of ESTIMATE (Yoshihara et al., 2013), also in four groups. Although the ESTIMATE-defined high-immune-low-stroma group remains on top of all four survival curves, we did not observe a statistically significant difference between these groups. Therefore, DeMixT-based immune and stroma proportions is more useful in categorizing patients with different prognosis outcomes (Figure S13).

Figure 4.

Analyses of Real Data Using DeMixT through Application to TCGA RNA-seq Data in HNSCC

(A) A triangle plot of estimated proportions (%) of the tumor component (top), the immune component (bottom left), and the stromal component (bottom right) in the HNSCC data. Points closer to a component's vertex suggests higher proportion for the corresponding component, whose quantity equals the distance between the side opposite the vertex and a parallel line (illustrated as dashed gray lines for the multiples of 10th percentile) that a point is sitting on. The “+” and “−” signs correspond to the infectious status of HPVs.

(B) Boxplots of estimated immune proportions for HNSCC samples in the test set display differences between HPV+ (red) and HPV− (white) samples.

(C) Boxplots of log2-transformed deconvolved expression profiles for three important immune genes (CD4, CD14, HLA-DOB) in the test set of HNSCC samples. Red: immune component; green: stromal component; blue: tumor component. P values of differential tests are at the top right corner for each gene: the first p value is for immune versus stromal component; second p value is for immune versus tumor component.

(D) Scatterplot of negative log-transformed p values for comparing deconvolved expression profiles between immune component and the other two components of 63 immune cell-related genes. The x axis: immune component versus stromal component; y axis: immune component versus tumor component. Genes in red are significant in both comparisons. Green horizontal and vertical lines: cutoff value for statistical significance.

Discussion

We present a novel statistical method and software, DeMixT (R package at https://github.com/wwylab/DeMixTallmaterials), for dissecting a mixture of tumor, stromal, and immune cells based on the gene expression levels and providing an accurate solution. Our method allows us to simultaneously estimate both cell-type-specific proportions and reconstitute patient-specific gene expression levels with little prior information. Distinct from the input data of most other deconvolution methods such as CIBERSORT and ESTIMATE, our input data consist of gene expression levels from (1) observed mixtures of tumor samples and (2) a set of reference samples from p-1 compartments (where p is the total number of compartments). Our different model assumptions and goal for individual-level deconvolved expression levels have brought unique analytical challenges that are not relevant for deconvolution methods aforementioned, which use input from all p compartments and are regression based. Our output data provide the mixing proportions, the means and variances of expression levels for genes in each compartment, as well as the expression levels for each gene in each compartment and each sample. The full gene-compartment sample-specific output allows for the application of all pipelines previously developed for downstream analyses, such as clustering and feature selection methods in cancer biomarker studies, which are still applicable to the deconvolved gene expressions. We achieved this output by modeling compartment-specific variance and addressing the associated inferential challenges. Our model assumes a linear mixture of data before a log2-transformation (Ahn et al., 2013, Löonnstedt and Speed, 2002), thereby introducing nonlinear associations into the log-space of the data. Beyond extending the DeMix model (Ahn et al., 2013) from two-component to three-component deconvolution, DeMixT also proposes new features as summarized below, resulting in an overall better performance (Figure S14). DeMixT addresses transcriptome deconvolution in two steps. In the first step, rather than using a heuristic search as before, we now estimate the mixing proportions and the gene-specific distribution parameters for each compartment using an ICM method (Besag, 1986), which can quickly converge and is guaranteed to find a local maximum. We have further proposed a novel GSCM approach and integrated it with ICM for three-component deconvolution, to substantially improve model identifiability and computational efficiency. In the second step, we reconstitute the expression profiles for each sample and each gene in each compartment based on the parameter estimates from the first step. The success of the second step relies largely on the success of the first. We have overcome the otherwise significant computational burden for searching the high-dimensional parameter space and numerical double integration, owing to our explicit modeling of variance through parallel computing and gene-set-based component merging. On a PC with a 3.07-GHz Intel Xeon processor with 20 parallel threads, DeMixT takes 14 min to complete the full three-component deconvolution task of a dataset consisting of 50 samples and 500 genes (see Table S8). Our new design makes it possible to first select a subset of genes for accurate and efficient proportion estimation and then estimate gene expression for any gene set or for the whole transcriptome. This overcomes the deficiency of most existing deconvolution tools that enforce using the same set of genes in the estimations of both proportions and gene expression levels. Our method can be applied to other data types that are generated from mixed materials.

We have used a series of experimental datasets to validate the performance of DeMixT. These datasets were generated from a mixture of normal tissues, a mixture of human cell lines, and LCM of FFPE tumor samples. DeMixT succeeded in recapitulating the truth in all datasets. When compared with ISOpure, DeMixT gave more accurate estimations of proportions in all datasets. DeMixT more explicitly accounts for sample variances, an assumption that adheres more closely to the real biological samples. Even for the in vitro dataset of admixed rat tissues, which generated only technical replicates that had very small variances so that assuming no variance becomes reasonable, we showed that the estimation of gene expression by DeMixT is still comparable with the estimation by ISOpure. On the dataset of mixed human cell lines, DeMixT performed as well as CIBERSORT (in estimating the tumor and the fibroblast components), a popular method for estimating only the proportions of cell types in complex tissues (Figure S6), even though DeMixT used reference profiles from one less component than CIBERSORT. We further demonstrated tumor-stroma-immune deconvolution by DeMixT using TCGA HNSCC data. We were able to correlate our immune proportion estimates with the available HPV infection status in HNSCC, as is consistent with previous observations that a high level of immune infiltration appears with viral infection in cancer (Li et al., 2016a, Li et al., 2016b). For this dataset, DeMixT is the first to provide a triangular view of tumor-stroma-immune proportions (Figure 4A), the interesting dynamics of which may shed new light on predicting the prognosis of HNSCC.

Here, we discuss four major factors that would potentially impact the performance of deconvolution, regardless of the model and method used. (1) The number and diversity of tumor samples and reference profiles. Some cancer types, such as breast cancer, are more heterogeneous within the tumor component than others. Some cancer types show more genomic rearrangements and copy number changes, which impact transcriptomic activities, whereas others, such as prostate cancer, are less often so. There exist large variations in the availability of the number and type of reference profiles across cancer types. We recently applied DeMixT to the datasets from the TCGA PanCanAtlas project across 16 cancer types. Among them, we used RNA-seq data generated from the corresponding normal tissues for 15 cancer types, with the sample size for normal samples ranging from 10 to 98. With the remaining cancer types in TCGA, there are <10 normal samples available, for which we have not run DeMixT, except for one cancer type (pancreatic cancer, PAAD). In PAAD, we used tumor samples that had been determined to have very low tumor content as the reference profiles (n = 7). In both scenarios of normal controls, we obtained reasonable results, based on which we performed clustering analysis, pathway analysis, and variable selection for gene sets associated with survival outcomes. Our analyses suggested that the estimated mixing proportions and individual expression levels are useful to identify biological signals that were previously diluted in the mixed measures (unpublished results). Generally, our model assumptions will be mildly violated in most studies (e.g., in the TCGA datasets) and strongly violated in some studies. Assuming there is a reasonable level of homogeneity within a component, increasing the sample size will increase the reliability of parameter estimations (i.e., ${\hat{\mu }}_{N_{1g}}$, ${\hat{\mu }}_{N_{2g}}$; ${\hat{\sigma }}_{N_{1g}}$, ${\hat{\sigma }}_{N_{2g}}$). (2) The platforms used to profile gene expression. We observed good performances of DeMixT on data generated from real tumor samples using both Affymetrix microarray and Illumina RNA sequencing platforms. Testing DeMixT on other platforms should involve a first step of checking whether the linearity combination of the log-normal distributions still holds. (3) The tissues from which the various input profiles were derived. We found that expression measurements from FFPE samples are much noisier than those from fresh-frozen samples, and in the analysis of the LCM data, had to devise a more stringent filtering criteria on the set of genes to be used for deconvolution. (4) The genes selected for the sequential steps of the DeMixT algorithm. In a two-component setting, we observed that both variances and mean differences in the expression levels between the two components for each gene can affect how accurately the mixing proportions are estimated, whereas not all genes are needed for the proportion estimation. We therefore proposed to select genes that have moderate variances and large differences between the two components to estimate proportions. In a three-component setting, using the GSCM approach to reduce to a pseudo-two-component problem allowed us to apply a similar strategy. The GSCM approach is general in sequentially merging components through gene selections and can be extended to deconvolution problems with more than three components but will incur high computational cost. Currently, our gene selection and GSCM strategy follow the principle of focusing on a subspace of the high-dimensional parameters for model identifiability but are heuristic and may need adaptation across datasets. We observed the performance of GSCM is robust to the number of genes selected within the range of hundreds. Future work includes systematically evaluating the impact of each set of high-dimensional parameters on the full likelihood underlying our convolution model and search for a unified gene selection method for the deconvolution of datasets that range over a wide spectrum of biological phenomena. Future work also includes development of a numerical measure of confidence to filter out potentially unreliable expression estimates.

Reference gene-based deconvolution is popular for estimating immune subtypes within immune cells (Liebner et al., 2014, Newman et al., 2015). Our method does not require reference genes, which we consider as difficult to obtain for the tumor component; however, DeMixT can take reference genes when available. With the reference sample approach, we assume that the first p-1 compartments in the observed mixture are similar to those in reference samples, whereas the remaining compartment is unknown and so may end up capturing most of the heterogeneity. The reference samples can be derived from historical patient data or from the corresponding healthy tissues, such as data from GTEx (Lonsdale et al., 2013) (e.g., RNA-seq data from sun-exposed skin as reference samples for melanoma, unpublished results). Furthermore, each of the three components may contain more than one type of cell, in particular, the immune component. It was reported that, although the immune cell subtypes are heterogeneous, their relative proportions within the immune component are consistent across patient samples (Gentles et al., 2015), which supports our approach that models the pooled immune cell population using one distribution. Estimating low proportions is more prone to biases in methods without reference genes than those with reference genes, as observed in our cell-line mixed RNA-seq dataset in which the immune cell component is consistently low. However, it occurred only in this artificially mixed dataset, whereas in real data, such as the HNSCC dataset, there are samples presenting a high level of immune infiltration, thus improving the accuracy for all parameter estimations, including those in samples presenting a low level of immune infiltration. In future work, we will consider expanding to a hierarchical model for immune subpopulations that will include dynamic immune components. For optimized performance of DeMixT, the data analysis should be linked with cancer-specific biological knowledge.

Limitations of the Study

Here we are focused on resolving statistical challenges in a new concept of jointly estimating component-specific proportions and distributions of gene expression, as well as individual gene expression levels in a mixture of three components. Our approach has been comprehensively benchmarked using multiple datasets. However, DeMixT needs further studies to improve its utility in real cancer data, including (1) a unified gene selection method that automatically detects, in a high-dimensional likelihood space, the most identifiable region for parameter estimation; (2) a numerical measure of confidence to filter out potentially unreliable expression estimates; (3) extension to a hierarchical model to accommodate multiple immune cell subtypes; (4) cancer-specific data analyses to further understand and remedy for the potential impact of available normal tissues as input reference profiles.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: November 30, 2018

Supplemental Information

Document S1. Transparent Methods, Figures S1–S15, and Tables S1–S9

Data S1. A Summary Table of p-Values for 63 Selected CDs, and HLA Immune Genes

P-values are calculated for differential test (Benjamini-Hochberg correction) of deconvolved expression for immune component versus stromal component, and immune component versus tumor component, respectively, related to Figure 4.