The effects of nonignorable missing data on label-free mass spectrometry proteomics experiments

Abstract

An idealized version of a label-free discovery mass spectrometry proteomics experiment would provide absolute abundance measurements for a whole proteome, across varying conditions. Unfortunately, this ideal is not realized. Measurements are made on peptides requiring an inferential step to obtain protein level estimates. The inference is complicated by experimental factors that necessitate relative abundance estimation and result in widespread non-ignorable missing data. Relative abundance on the log scale takes the form of parameter contrasts. In a complete-case analysis, contrast estimates may be biased by missing data and a substantial amount of useful information will often go unused.

To avoid problems with missing data, many analysts have turned to single imputation solutions. Unfortunately, these methods often create further difficulties by hiding inestimable contrasts, preventing the recovery of interblock information and failing to account for imputation uncertainty. To mitigate many of the problems caused by missing values, we propose the use of a Bayesian selection model. Our model is tested on simulated data, real data with simulated missing values, and on a ground truth dilution experiment where all of the true relative changes are known. The analysis suggests that our model, compared with various imputation strategies and complete-case analyses, can increase accuracy and provide substantial improvements to interval coverage.

1. Introduction

Label-free mass spectrometry proteomics experiments provide quintessential applications for the field of missing data statistics. The sources of missing data are rooted in known technological and scientific processes and the proportion of missing values will often exceed 50% of a dataset (Karpievitch et al., 2009). Consequently, well-informed missing data models can be used to substantially impact the final results of an analysis. However, straightforward applications of missing data techniques are complicated by the unusual nature of proteomics data. In the experiments we explore, all of the parameters of interest are contrasts. Understanding how missing data affects these contrasts has profound implications for informing data analysis techniques and interpreting the results. Modeling a missing data mechanism allows us to avoid numerous pitfalls associated with complete-case analyses and imputation based methods while utilizing information in the data that would otherwise not contribute to estimation. Specifically, we create a selection model which is informed by all the observed and missing values within each protein, along with an overall estimated relationship between outcomes and the probability of missingness. An R package for the implementation of the selection model can be installed from www.github.com/ColtoCaro/missMS.

At the highest level, proteomics is the large scale study of the structure and function of proteins. The properties and methods discussed in this paper pertain to a set of experiments called data-dependent, label-free, bottom-up, discovery proteomics (Chen and Yates, 2007). This paper does not apply to methods using isobaric tags (Ross et al., 2004; Thompson et al., 2003), top-down proteomics (Catherman, Skinner and Kelleher, 2014), data-independent analysis (Röst et al., 2014) or targeted proteomics (Liebler and Zimmerman, 2013). Furthermore, our discussion is limited to a single step in a complicated workflow, where peptide level measurements are used to make protein level inferences. The full workflow for a proteomics experiment goes far beyond this, with software packages typically performing analyte identification, quality control, false discovery rate filtration and many other essential informatics tasks. These aspects of the experimental workflow are outside of the scope of this paper, but their importance cannot be overstated.

If the rest of the workflow has not been done well, then no statistical modeling will ever make up for the loss in quality. However, we will demonstrate that the choice of statistical methodology alone can profoundly alter the final results of a discovery mass spectrometry experiment. The challenges to statistical inference posed by missing data are substantial and progress can only be made by isolating one problem at a time. With this goal in mind we will explore the challenges of estimating relative protein abundance without regard to the prerequisite steps in the overall workflow. Consequently, the dangers and advances discussed in this paper can be applied to any workflow capable of exporting peptide level intensities prior to protein level estimation.

In Section 2, we will discuss the pertinent experimental details that motivate our data generating model, with a special focus on sources of missing data and the necessity of relative quantification. In Section 3, we discuss various methods that have been proposed for handling missing data in proteomics experiments. We then define our selection model and discuss a general framework for protein estimation. In Section 4, we analyze simulated data, real data with simulated missing values and finally a ground truth dataset with known relative changes that we created with a series of dilution experiments. The first two analyses are designed to demonstrate the basic relationships between missing data and contrast estimation in the simplest possible setting. We show that our missing data model can improve accuracy and that non-ignorable missingness can cause a divergence between methods that would otherwise provide identical results. This divergence has important implications for how the results of a study are summarized and used in downstream analyses. The analysis of the ground truth dilution experiment presents more complicated patterns of missing data and shows the advantages of our selection model in terms of accuracy and interval coverage. Section 5 contains a discussion of our findings and highlights areas for future research.

2. Pertinent Experimental Details

The label-free quantification (LFQ) experiments described in this paper are referred to as bottom-up proteomic methods because inference about relative protein abundance is made from measurements on protein fragments called peptides. A typical bottom-up proteomic workflow involves the extraction of proteins from cells, tissues or biological secretions, followed by proteolysis which cleaves proteins into peptides. Typically cleaving proteins into peptides is achieved by adding a protease (usually trypsin) that breaks the peptide bond after lysine and arginine amino acid residues. After this digestion, peptides from the sample are separated according to each peptide's hydrophobicity, where the more hydrophobic peptides will be the last to elute. This process is referred to as liquid chromatography. As they elute, peptides are ionized into the gas phase and enter a mass spectrometer, where the number of ions corresponding to each mass is measured. How exactly the measurement is made depends on the specific technology. Two commonly used types of mass spectrometers are time of flight and Orbitrap® instruments. All of the data generated in this paper were analyzed with Orbitrap® mass spectrometers. Regardless of the specific technology, the process of separating ions and measuring their masses happens continuously as analytes elute.

Peptides with the largest signals (relative to whatever else is simultaneously processed) will be selected for fragmentation and a second mass measurement (MS2) which will be used to sequence the peptide. The process of selecting peptides for a second mass measurement, based on the relative magnitude of the counts, is called data-dependent analysis (DDA). In an iTRAQ or TMT experiment quantification also takes place during or after MS2, which has important consequences for the missing data mechanism and places these technologies beyond the scope of this paper. Each identified peptide may be associated with many ion counts measured through time. The term, peptide intensity, refers to a summary of these measurements which is usually computed as either an area under an interpolated curve or as the maximum observed measurement (Cox and Mann, 2008). A more comprehensive description of the LFQ workflow can be found in Sandin et al. (2011). In this manuscript, we will focus on only the experimental details which motivate our statistical model.

2.1. Relative abundance

Advances in mass spectrometry technology have provided us with a tremendous ability to manipulate ions. Consequently, ionization of peptide molecules is an indispensable aspect of a mass spectrometry based proteomics experiment. Critically, not all of the peptides from the sample will successfully ionize and enter the mass spectrometer. Certain peptides tend to ionize more efficiently, while others will not ionize at all. The probability that a given peptide molecule will ionize can be referred to as ionization efficiency.

Ionization efficiency is a function of the chemical structure of a peptide and other properties of the solution at the time of ionization. For example, the presence of other co-eluting peptides, sometimes referred to as matrix interferences, or changes in the salinity of the solution could alter ionization efficiency. Schliekelman and Liu (2014) found that competition for charge between background peptides may actually be a more important factor than abundance in determining if a peptide will be detected. Regardless of which factors are most important, ionization efficiency can cause the proportion of peptides that enter into the mass spectrometer to be drastically altered. Consequently, intensities are not a monotone increasing function of concentration.

One peptide might be far more abundant than another in a given sample but a lower ionization efficiency could reverse the relationship for peptide intensities. The observed intensities represent the abundance of a peptide found in the sample multiplied by the proportion of those molecules that are successfully measured by the mass spectrometer. Fortunately, if the proportion parameter, p, is considered to be a property of the individual peptide, it will cancel out when put into a ratio with the same peptide from another sample. This relationship is outlined in Table 1. In theory the assumption of equivalent ionization efficiencies for each peptide is sound, since the determining factors should be equivalent from run-to-run. Of course, in practice this may not be true. Unexpected changes in electrospray voltage or flow rate could lead to slightly different probabilities from run-to-run. One of the motivations for multiplexing with isobaric tags (Thompson et al., 2003) is that such variations will affect all of the experimental conditions in the same way since they are measured concurrently. Thus, peptide by run interactions can be used as a blocking variable. However, in a label free experiment, condition and run are usually confounded, leaving little choice but to allow run-to-run variations to increase to the overall experimental error.

Table 1.

This table shows the relationship between relative protein abundance and the intensities of a peptide belonging to that protein. p is the probability that the peptide ionizes and enters into the mass spectrometer. pW and pZ represent the expected intensities from samples A and B, respectively.

	Protein Abundance	Peptide Abundance	Ion Abundance
Sample A	X	W	pW
Sample B	Y	Z	pZ
Ratio	$\frac{X}{Y}=\mu$	$\frac{W}{Z}=\frac{X}{Y}=\mu$	$\frac{\mathit{\text{pW}}}{\mathit{\text{pZ}}}=\mu$

Ionization efficiency explains why proteomics experiments are often referred to as relative quantification experiments. When modeling the data from a log-normal distribution, parameter ratios take the form of contrasts on the log scale. The contrasts give us information on the relative abundance that existed in the original sample, whereas estimates of parameters that describe the average log intensity for a protein are confounded by variations in the ionization efficiency. This distinction becomes especially important when considering the impact of missing data.

2.2. Intensity-Dependent Missingness

Unlike microarray experiments in which missing values often comprise about 1-11% of the data (de Brevern, Hazout and Malpertuy, 2004), proteomics datasets almost always have a much higher percentage of missing data. A multitude of sources create this missing data problem. When combined, the missing data mechanisms yield data where both missing at random (MAR) and non-ignorable missing values, are found throughout the entire range of intensities. We say that a missing value is non-ignorable when the probability that the random variable will be unobserved is dependent on the underlying value. In contrast, MAR peptides are missing for reasons entirely unrelated to their intensities. In this section we will explain some of the primary sources of both MAR and non-ignorable missingness.

2.2.1. Detection Limit

Mass spectrometers have both theoretical and practical limits of detection (LOD). The theoretical LOD is the minimum number of ions a given instrument can capture while still producing an ion current with adequate signal enhancement. Although any peptide exceeding this number of ions could theoretically be detected by the mass spectrometer, every sample contains a considerable amount of noise. This noise results in a practical detection limit, whereby the software fails to distinguish peptide peaks from background noise. How exactly the processing software delivers signal intensities depends on both the type of mass spectrometer and even the instrument vendor. For this reason, sample-related factors that either result in a higher practical detection limit or a decreased intensity due to the nature of the sample can result in missing values. As discussed previously, a major driver in this setting is the peptide ionization efficiency. If the ionization efficiency is low then the intensity will be low and may fall below the detection limit. This is a form of non-ignorable missingness where the probability of a missing value is directly related to the magnitude of the intensity.

2.2.2. Data-Dependent Tandem Mass Spectrometry

Sequence identification occurs by selecting a peptide peak from the first scan (MS1) in a mass spectrometer and then mass analyzing the fragments of the ions that generated the MS1 peak. Many methods utilize data dependent analysis (DDA) whereby peptides are selected for MS2 according to the rank order of their signal intensities during a brief window of time. In a DDA analysis, peptides that are not identified will usually result in missing values. Thus, even above the practical LOD, an intensity dependent process can result in non-ignorable missing values. Consequently, in DDA experiments we need to consider two sources of non-ignorable missingness, one which occurs below a random detection limit and another above.

2.2.3. Sources of random missingness

A peptide might appear in one sample and not in another simply because it was misidentified. Identification algorithms are designed to minimize this problem, but false identifications will still be present in every dataset. A similar problem comes from shared peptides; i.e., peptides that are properly identified but that could belong to more than one protein. Many software programs assign shared peptides to the candidate protein highest number of other identified peptides Cox and Mann (2008), however more conservative approaches could treat peptides with no unique labels as missing. Missingness of this sort would be due to the sequence mapping and not the magnitude of the outcome. It is also possible that due to interfering ions, a particular peptide will simply fail to be identified with any certainty, resulting in more missing values. It is probably safe to classify missingness caused by classification errors as MAR since the mechanisms are independent of the intensities.

The MAR distinction is important because ignoring MAR values will not result in biased estimates. However, since MAR values can occur throughout the whole range of intensity values, the problem of determining which peptides are MAR is likely intractable. In the next section, we present a way to incorporate a missing data mechanism without attempting to decipher the exact source of missing data for each peptide.

3. Methods

3.1. The mean model

We first need discuss the mean model for a complete case analysis. For the rest of this paper we assume that intensities have undergone a log base 2 transformation so that additive models are appropriate, and the ratios of interest are contrasts.

A common experimental design might include factors for protein, peptide within protein, sample and run. Protein parameters might represent unique protein identifications nested within conditions, biological replicates or even groups of proteins that researchers expect to share a parameter. Similarly, the condition parameters might represent disease states, time courses or just biological replication. The exact design of the experiment is not relevant for the purposes of this paper.

Let the jth peptide j(i) = 1,…, J_i, be nested within the ith protein, i = 1,…, I, in condition k, k = 1,…, K and replicate l, l(k) = 1,…, L_k. Then for a given peptide the number of molecules in a sample should depend on the sample, the peptide and possibly some systematic experimental deviations in the form of a run effect. The mean model for peptide abundance, a_ijkl, is given by

$$E(a_{ijkl})={\beta }_0+{\alpha }_i+{\beta }_{j(i)}+{\gamma }_k+{\delta }_{l(k)}+{\eta }_{\mathit{\text{ik}}}.$$

Where, the difference in protein abundance across conditions, η_ik, would typically be the parameter of interest. Systematic variations in conditions, γ_k and replicates δ_l(k) are usually considered to be artifacts since the experiments are built on the assumption that overall protein abundance will be the same from run-to-run. Note that this is more than a theoretical assumption. Multiple steps in the experimental procedure, prior to mass analysis, repeatedly alter sample concentration to ensure that an equal amount of total protein is contained in each sample.

Unfortunately, we never directly observe the peptide abundance that was in the solution. So the model for a_ijkl is purely theoretical. When considering a model for the observed intensities, y_ijkl, we must first consider a model for the probability that a peptide will ionize and enter a mass spectrometer π_ijkl. This unobserved probability can be conceptualized with a slightly different framework.

$${\pi }_{ijkl}={\beta }_0^{\ast }+{\beta }_{j(i)}^{\ast }+{\delta }_{l(k)}^{\ast }$$

where the sum of parameters is constrained between 0 and 1.

Notice that we have not included an interaction term for peptide level ionization effects. Such an interaction could be used to model peptides sticking to an elution column or run-to-run variations in ionization efficiency, labeling efficiency, peptide digestion, spray instability and over-labeling. Unfortunately, in a label-free experiment, a peptide-by-run interaction results in a saturated model. Attempting to estimate anything else, including the contrasts of interest, will result in identifiability problems. Accordingly, great care must be taken to minimize the run-to-run variation experimentally.

Having decided on appropriate models for abundance and ionization we can describe the model for the observed intensities with the sum

$$E(y_{ijkl})=({\beta }_0+{\beta }_0^{\ast })+{\alpha }_i+({\beta }_{j(i)}+{\beta }_{j(i)}^{\ast })+{\gamma }_k+({\delta }_{l(k)}+{\delta }_{l(k)}^{\ast })+{\eta }_{\mathit{\text{ik}}}.$$

Notice that in this model, though many parameters can only be interpreted as a combination of ionization and abundance effects, the contrast between two samples k and k′ with all other factors fixed, (γ_k+η_ik–γ_k′–η_ik′), only contains parameters from the abundance model. Thus, even though we only make observations on the number of ions that enter a mass spectrometer, estimating contrasts still provides a way to make inference on the original sample.

A potential alteration to this model may be needed for researchers working with large population level studies who need to differentiate between biological and technical replicates. One way to achieve this would be to completely nest biological replicates within a protein, and technical replicates within each biological replicate. The parameter of interest, at the population level, could then be defined as a hierarchical mean parameter for the contrasts shared by all of the biological replicates, e.g. if q(i), q = 1,…, Q indexes biological replicates, then letting the contrast parameter η_qk ∼ N(μ_i, τ) would make μ_i be the parameter of interest in the population level study. This example highlights an important and unusual aspect of proteomics experiments; statistical inference is required just to figure out what was in a single sample. Simultaneously making inference to both protein levels within individual samples, and population level parameters, would require complex models like the one just suggested. However, exploring the properties of such models goes beyond the scope of this paper where we aim to study the effects of missing data on even the simplest of models.

We now define the notation used in this paper for an arbitrary design matrix X_n×p, parameter vector θ, of length p and outcome vector y, of length n. The mean model can be described as E(y) = X_θ. We use the matrix subscripts to denote submatrices such that X_[.,i] denotes the ith column of X and θ_[j] denotes the jth entry of θ. Negative indices imply a vector component, matrix column or row has been removed. For the Bayesian formulation we assume that y|θ ∼ N(Xθ, σ²I_n×n), where I_n×n is an identity matrix. Further, let the ith entry of θ, ${\theta }_i~N({\beta }_i,{\tau }_i^2)$, and for all i ≠ j, θ_i ⊥θ_j. The hyperparameters β_i, ${\tau }_i^2$, σ² could be treated as random variables or they could be fixed real numbers. Later in this paper we will assign non-informative distributions to the hyperparameters. However the use of informative priors might be a desirable alternative, as researchers often have a very good idea of the range of values their experiments will produce.

3.2. Modeling Missingness

Many efforts have been made to correct for missing data biases in proteomics experiments. However, the vast majority of solutions involve using single imputations. By default, MSstats (Clough et al., 2012) uses an imputation from an accelerated failure time (AFT) model which is similar to the approach proposed by Tekwe, Carroll and Dabney (2012). Inferno by Taverner et al. (2012) allows for K-Nearest Neighbors (KNN) imputation (Troyanskaya et al., 2001) and in previous versions allowed for imputation from a mixture model proposed by Karpievitch et al. (2009). Many more single imputation methods have been evaluated in review papers by Lazar et al. (2016) and Webb-Robertson et al. (2015), including simple imputations of column means and column minimums as well as an imputation based on the singular value decomposition originally proposed for microarray data (Owen and Perry, 2009).

A few imputations operate on the protein level including an algorithm in the popular Perseus software package (Keilhauer, Hein and Mann, 2015) and another based on a survival model Tekwe, Carroll and Dabney (2012). Since these imputations occur after protein estimation has occurred they do not address the problems discussed in this manuscript and will not be discussed further.

Lazar et al. (2016) reported that missing not at random (MNAR) imputation methods were problematic since the range of imputed values is not representative of the true range of missing values. These MNAR imputations along with the the AFT model assume that every missing value falls below or at some lower limit of detection. As discussed in Section 2.2, MAR values can occur throughout the entire range of values. Thus, imputing below a detection limit may inappropriately take values that should be MAR above the estimated detection limit and forces them to be too small. Webb-Robertson et al. (2015) evaluated many different single imputation methods in regards to accuracy and downstream effects on classification problems. They found that no one method was superior and in certain situations not using any imputations improved performance. Consequently, they recommended only using imputation when absolutely necessary. We largely share their concerns, but believe that the dangers of single imputation methods go further still.

Imputing from an inappropriate model may bias point estimates, but a larger problem is poor estimation of experimental error. As explained by Little and Rubin (1987, ch. 4.4) standard errors are systematically underestimated when nothing is done to account for imputation uncertainty. Karpievitch, Dabney and Smith (2012) sought to resolve the underestimated variance through a post-estimation adjustment of p-values. Whether or not this effort succeeds, it only aims to correct p-values, and does not address concerns regarding point and interval estimation. Furthermore, though not accounting for imputation uncertainty may underestimate error on average, for any given protein, which will often have only a small number observations, the results are unpredictable. The error may be too small or, as we will show, it may be far too large as a result of imputing values far away from where the true values would have been.

Problems with single imputations are amplified in the field of proteomics due to the nature of a relative quantification experiment. Since the parameters of interest are contrasts, imputations might hide the fact that certain contrasts are inestimable. Furthermore, even if the contrast is estimable, it might only be estimable through the recovery of interblock information (Scheffé, 1999, pp. 170-178). In the absence of missing data, most estimation techniques will rely solely on intrablock contrasts. Consequently, an imputation may result in the failure to recover interblock information precisely when it is most needed. For these reasons we will attempt to model missing data without using any imputations.

One missing data solution that does not use single imputations is the mixture model proposed by Karpievitch et al. (2009), which proposes a maximum likelihood based approach. They explicitly model a combination of censored values below a peptide-specific detection limit and a missing at random mechanism above this detection limit. This does not exactly meet our requirement for allowing non-ignorable missingness throughout the whole range of values, but it is a very interesting idea and might serve as a useful approximation. Unfortunately, their algorithm relies on the existence of fixed effects estimates as initial conditions. This works well for the authors because they employ a filtering algorithm that removes proteins with either low information content or that contain any inestimable contrasts. While this almost certainly leads to a more reliable final set of inferences, the amount of discarded data could be substantial, potentially resulting in lost discoveries that would have been detected by simpler methods.

To escape the dangers of single imputations while attempting to utilize the entirety of a collected dataset, we model the probability of missingness in the form of a selection model (Little and Rubin, 1987, ch. 15). In a selection model, the likelihood is parametrized in terms of the probability of a missing value conditional on the outcome. We refer to this as the selection model for proteomics (SMP).

Let I() be an indicator function, and let R_i = I(y_i is observed), where y_i is the ith response, so that R_i = 1 when the ith outcome is observed and R_i = 0 when the value is missing. We assume (R_i|y_i) ∼ Bernoulli(Φ(a+by_i)) where a and b are real valued parameters and Φ() is the cumulative distribution function of a N(0,1) random variable. We use R to denote the vector of all R_i values for i = 1, …, n.

This missing data mechanism, combined with the mean model from the previous section defines the data generating model. An advantage of this missing data mechanism is that full conditionals, for use in a Gibbs Sampler, are straightforward to derive. Two non-standard relationships are required: the distribution of a missing value, y, given everything else f_(y|θ,R,a,b) , and the distribution of θ_i given everything else, f_{(θi|Y,θ[−i],R)} .

Derivations (shown in the Supplementary Text (O'Brien et al., 2018a)) reveal that if the mth data point, y_m, is missing then the full conditional has an Extended Skew Normal distribution (Azzalini and Capitanio, 2014).

$$f_{(y_m|\theta ,\mathbf{R},a,b)}(x)=\frac{\varphi \left(\frac{x-{\mu }_x}{\sigma }\right)\mathrm{\Phi }(-a-\mathit{\text{bx}})}{\sigma \mathrm{\Phi }(\omega )}$$

where

$${\mu }_x={(\mathbf{X}\theta )}_{[m]},\omega =\frac{-a-b{\mu }_x}{\sqrt{1+{(\sigma b)}^2}}.$$

We also find that

$$({\theta }_{\mathbf{i}}|\mathbf{y},{\theta }_{[-\mathbf{i}]},\mathbf{R})~N(\frac{{\beta }_i{\sigma }^2+{\tau }_i^2{\sum }_j^J(y_i-(\mathbf{X}\theta ){\ast }_{[j]})}{{\sigma }^2+{\tau }_i^{2}I},\frac{{\sigma }^2{\tau }_i^2}{{\sigma }^2+{\tau }_i^{2}J}),$$

where (Xθ)* is the product of the matrix X without the ith column, with the vector θ without the ith component. The indices j,…, J represent the row indices for which X_[.,i] = 1. In other words, j,…, J represent the data points that depend on θ_i.

It should be noted that this model is similar to one proposed for iTRAQ data by Luo et al. (2009), where the probability of a missing value is modeled with a logistic regression. However, iTRAQ and other types of isobaric tag data, are fundamentally different from LFQ data. With isobaric labeling, ions from all of the conditions contribute to the MS1 signal. Consequently, the missing data mechanism should not be a function of a single intensity, rather it would be a function of the ion count from all conditions combined. This is a very difficult problem since changes to any one of the conditions could have resulted in a smaller sum. Further complicating the situation, the sum of observed intensities in an isobaric tag experiment will not actually add up to the corresponding observed MS1 signal. This is in part because the observed signals are constrained, resulting in a type of compositional data (O'Brien et al., 2018b). Consequently, the reasoning that motivated the SMP model is not valid when considering data from an isobaric tag proteomics experiment.

4. Results

To test model performance we analyze simulated data, real data with simulated missing values, and a new ground truth dataset with known relative abundances. The first two analyses are designed to elucidate the important relationship between missing values and relative abundance estimates in the simplest possible setting. The ground truth experiment is used to highlight more complex missing data patterns and to evaluate model performance in terms of accuracy and interval coverage without resorting to any simulations.

We first explore the relationship between missing data and contrasts taken within peptide blocks. We will show that missing data can result in a substantial divergence between contrast estimates from models that would otherwise yield equivalent results. As explained in Section 2, the parameters of interest should be the contrasts between conditions. The danger we wish to emphasize is that researchers might plot or report estimates of non-relative parameters without realizing that these results are not equivalent to what would be obtained if contrasts were estimated directly. Scientifically it should be clear that ionization efficiency prevents the estimation of absolute abundance. Yet, in a statistical model a protein term exists and it is difficult to see why some sort of quasi-absolute abundance should not be estimated directly.

This notion of quasi-absolute abundance is similar to the a number of published methods including a linear model based protein quantification proposed by Clough et al. (2012), iBAQ which is computed as the average protein intensity adjusted for the theoretical number of peptides that could be observed (Fabre et al., 2014), and QRollup which estimates proteins using the average of the upper 66% of peptides within a protein (Polpitiya et al., 2008). Clough et al. (2012) are careful to explain that their protein quantification estimates differ from absolute abundance estimates, because they should not be used to make any comparisons between different proteins. They also observe that their protein quantification will differ from relative quantification when missing data is present, and suggest that the relative estimates will be more accurate. It is this relationship between relative abundance estimates and missing data that we wish to explore by analyzing the simplest possible LFQ proteomics experiment: the comparison of proteomes between just two conditions where the contrast is estimable given the observed data alone.

4.1. Two-sample model

Data was simulated from the SMP model where the design matrix contains factors for protein within sample and peptide within protein. Details of the simulation, including the full specification of the SMP model, are provided in the Supplementary Text (O'Brien et al., 2018a). We examine accuracy in terms of root mean squared error (RMSE) of the posterior means from the SMP model along with estimates from five other methods for relative protein estimation: a two-way ANOVA (twoway), a one-way ANOVA (oneway), a mixed model (MM), the two-way ANOVA after imputing column minimums (cMin), and the two-way ANOVA after imputing column means (cMean). Details of model implementation are provided in the Supplementary Text(O'Brien et al., 2018a). Notice that in the absence of missing data contrast estimates from the mixed model and the one-way and two-way ANOVA's would all be equivalent.

When simulating missing values, not all protein contrasts will be estimable. For the rest of this paper we will refer to proteins as either estimable or inestimable based on whether or not the contrasts would be estimable in the complete case two-way ANOVA model. This terminology will be used even in conjunction with Bayesian models for which estimability is not relevant. In a two-sample fixed effects model that includes peptide blocks, for a protein contrast to be estimable, at least one peptide must be observed in both samples. In larger datasets, the distinction becomes more complicated. An algorithm for determining which model parameters are estimable is detailed in the Supplementary Text(O'Brien et al., 2018a). For the simulation we examine estimates from only estimable contrasts so that comparisons are being made on equivalent sets of simulated proteins.

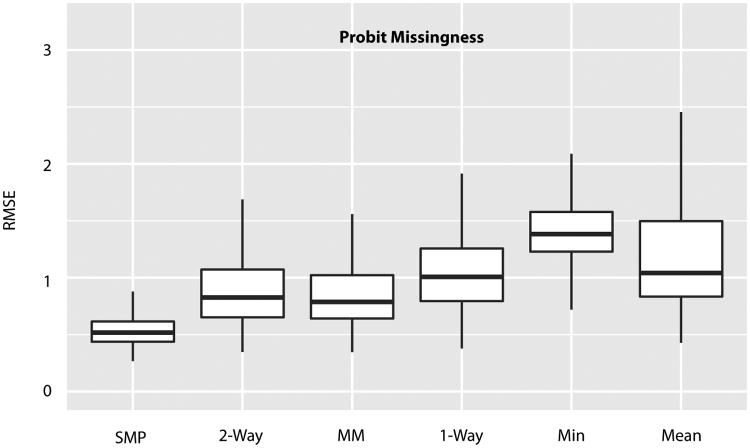
The results in Figure 1 show that the SMP model does appear to provide an increase in accuracy, the column based imputation methods appear to be purely detrimental and there is a clear divergence in performance between the one- and two-way ANOVAs. The contrast in a one-way ANOVA is essentially just the average intensity in one condition minus the average from the other. While in the two-way ANOVA, when a peptide is observed in one sample but not in the other, the observed peptide contributes nothing to the contrast estimate. Consequently, the divergence between the one- and two-way ANOVA's demonstrates why it is ill advised to estimate non-relative protein effects. When dealing with non-ignorable missing data, the contrast between protein averages is not the same as the direct estimate of a protein contrast.

Fig 1.

Root mean squared error (RMSE) of log base 2 fold-changes from 500 simulated data sets where missing values were simulated from a probit missing data mechanism. Only estimable contrasts are included in this plot.

Two obvious weaknesses to this study are that the simulation is unfairly biased towards the SMP model, and that there are more intelligent ways to perform an imputation. The former concern will be addressed by repeating the simulations with two distinct missing data mechanisms, analyzing real data with simulated missing values, and finally testing performance on a dilution experiment with known true ratios. The latter concern will be addressed only with the dilution experiment as better imputation methods often rely on an abundance of samples in order to identify patterns in the data. Two samples provide very little information to rely upon for imputation, hence the use of simple column summary statistics.

Simulation results from data generated with different missing data mechanisms (one using a quadratic logit probability model and another using a combination of random detection limits and a missing completely at random mechanism) can be found in the Supplementary Text(O'Brien et al., 2018a). Interestingly, these analyses provide very similar results in terms of accuracy. In all cases, SMP provides a substantial improvement, there is a noticeable divergence between the ANOVA's and the imputations always perform poorly.

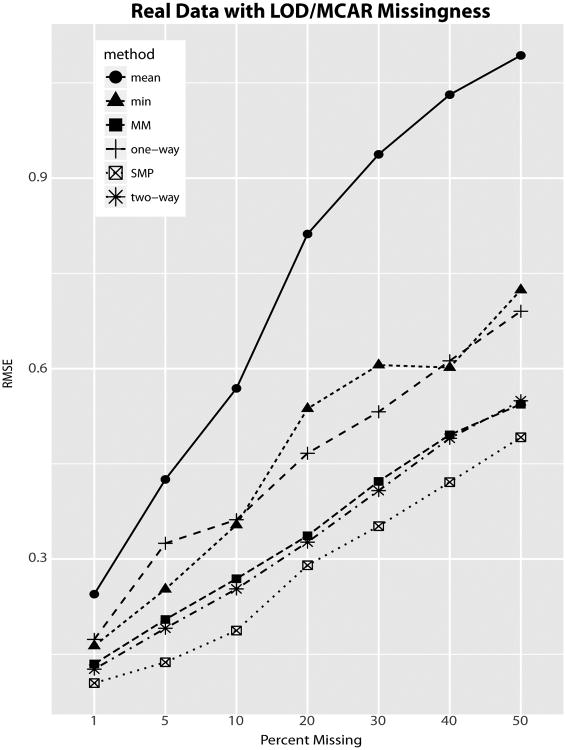
To further validate these results we analyze data obtained from two breast cancer tumor tissues (Basal and Luminal A). The data, described in the Supplementary Text (O'Brien et al., 2018a), can be found in the Supplementary Tables. The problem with using real data to evaluate methodologies is that we never know the true values. However, we can still use the data to to analyze the effects of non-ignorable missingness on contrast estimation. To this end, we reduced the cancer data to only peptides that were observed in both conditions. We then simulated missing values with a combination of MAR and random limits of detection. By increasing the mean of the random detection limits and the percentage of random missingness, details in the Supplementary Text(O'Brien et al., 2018a), we generated 7 data sets with approximately 1, 5, 10, 20, 30, 40 and 50 percent missing values. Each dataset was analyzed with the six methods and root mean squared error was computed by using estimates from the two-way ANOVA computed on the complete data as the truth. Divergence from these baseline results are shown in Figure 2.

Fig 2.

Root mean squared error (RMSE) of log base 2 fold-changes with varying amounts of simulated data. The cancer data was reduced to remove all missing values. Missing data was then simulated and the estimates on the complete data were treated as the true values for computing RMSE. Only contrasts estimable at all levels of missingness are included in the analysis.

These results provide further support for the three lessons from the simulation studies. Once again the SMP provided a substantial improvement to accuracy and both the mixed model and the two-way ANOVA steadily outperformed the one-way ANOVA and the two imputation methods.

While these studies offer simplicity and a clear demonstration of the divergence between methods, a larger dataset is necessary to show the full complexity of missing data patterns and the effects of different methodologies on both point and interval estimation.

4.2. Accuracy and Coverage

The assessment of accuracy in a mass spectrometry experiment is a difficult task because we rarely know what proteins will be observed, let alone their true values. Nevertheless, many datasets that include known relative abundances of proteins can be found on websites such as http://compms.org/resources/reference-data. We expect the effects of missing data to be the strongest for label-free experiments that utilize DDA. Unfortunately, we were able to find only one benchmark dataset generated with this technology and it contains only six proteins with known abundance ratios (Mueller et al., 2007). For this reason we conducted our own dilution experiment. Using 3 different human cell lines analyzed at 4 different dilution levels (1:4:16:100), with either one or two technical replicates, we generated LFQ DDA data with known relative abundances. Details of the dilution experiment and models used for analysis can be found in the supplement(O'Brien et al., 2018a).

Having established a ground truth dataset, we compare seven estimation strategies in terms of accuracy and coverage. The SMP model is compared against the two-way ANOVA, the mixed model and four different imputation strategies. Now that we have more data we can utilize more advanced imputation techniques. In addition to the column minimum imputation from the previous section, we also add a KNN imputation, an SVD imputation, and the imputation of the minimum observed intensity for each peptide sequence (pMin). Of critical importance, we no longer confine our analysis to parameters that are estimable. The distinction between estimable and non-estimable parameters proves to be very important as some methods do not adequately capture the error associated with estimation in these particularly difficult situations. Consequently, reference selection also becomes highly important as the reference choice will determine what comparisons are estimable and in a complete case analysis it will determine which data points end up being used in estimation.

The results presented in Table 2 show convincingly that the effects of missing data can be profound. This analysis provides further support for the lessons from the simulation analyses and the cancer data. SMP once again provides the best accuracy and the imputation methods continue to hurt performance relative to complete case analyses. Regarding the inestimable contrasts, SMP still provides the most accurate estimates and the cMin and pMin imputations outperform both SVD and KNN.

Table 2. Root Mean Squared Error from the Dilution Experiment.

Accuracy of different missing data methods found in our dilution experiment. The square root of the mean of squared errors, across all proteins, of log base 2 fold changes are presented for seven different methods of analysis. Results are shown separately for proteins with estimable and inestimable relative abundance contrasts.

	SVD	KNN	pMin	cMin	SMP	MM	2-Way
Estimable	1.72	2.28	1.43	2.08	0.94	1.13	1.19
Inestimable	4.39	5.48	3.51	3.48	3.30	NA	NA

Just as important as our ability to accurately estimate relative abundance is the ability to estimate the associated error. To this end we examine the frequency in which 95% confidence and credible intervals contain the true values. The results are shown in Table 3. Interestingly, the best coverage comes from the cMin imputation for both estimable and inestimable parameters, while the second best performance comes from the SMP model. The other imputation methods yield comparable coverage numbers to the complete case analyses for estimable contrasts but completely fail to compensate for the imputation uncertainty when the contrasts are inestimable. This finding strongly highlights the risk of allowing imputations to hide an inestimable contrast, as many of these cases could end up creating false positive discoveries.

Table 3. Interval Coverage from the Dilution Experiment.

Interval coverage from different missing data methods found in our dilution experiment. Only proteins that have intervals from all methods are included, i.e. proteins with only a single peptide have been removed. Results are shown separately for proteins with estimable and inestimable contrast parameters.

	SVD	KNN	pMin	cMin	SMP	MM	2-Way
Estimable	0.66	0.66	0.76	0.85	0.82	0.61	0.71
Inestimable	0.14	0.25	0.24	0.79	0.65	NA	NA

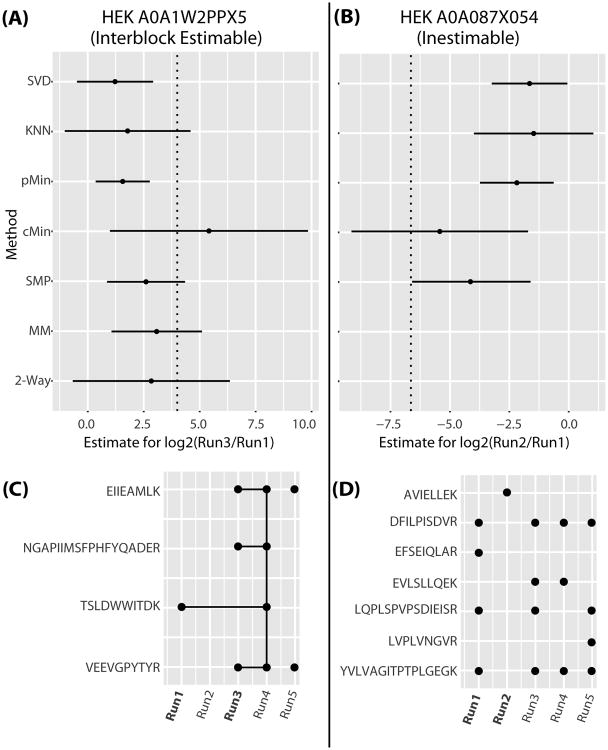
To better visualize the performance of different algorithms, Figure 3 highlights two interesting proteins from this study. The contrast between condition 1 and 3 for protein A0A1W2PPX5, from the HEK cell line can be estimated, in a complete case analysis, only through the recovery of interblock information (shown in part A). The path to estimability is shown by the connecting lines in part C). In part B, we show the contrast between conditions 1 and 2 for protein A0A087X054, also from the HEK cell line, is inestimable in the two way ANOVA (however none of the conditions is completely missing as shown in part D).

Fig 3.

Two examples of how different techniques handle missing data. (A, B) Point estimates and 95% intervals for seven different methods for relative abundance estimates between Run1 and Run 3 in C) and Run1 and Run2 in D). The true values are shown with vertical dashed lines. (C, D) Observed peptides are shown with solid dots and the connecting line shows a path to estimability.

Figure 3 reveals why the cMin method had the best coverage: the intervals are substantially larger. This shows that in general, it is not always true that imputations will artificially decrease error estimation. The cMin method always imputes very small values which works decently well in a dataset dominated by large changes, but it also tends to drastically increase the error estimate.

We also see in Figure 3 (A) that the SVD, KNN and pMin estimates are a bit shifted to the left of the SMP, MM and 2-way estimates. The former methods all rely solely on intrablock estimates while the latter are informed by interblock information. In Figure 3 (B) we can see that the SVD, KNN and pMin imputations did not impute values that brought the estimate near to the true values. The SMP estimate came close and the interval is far removed from zero suggesting that SMP would have been useful here to detect an interesting change even though the parameter was not estimable. cMin also would have achieved this goal, but it does so with a rather high increase to the error estimation. Notice further that only the error from the SMP model changes dramatically from the estimable to the inestimable scenario (as it should).

Many software packages have various safeguards to remove proteins with severe missing data problems. However, while these criteria will mitigate the problems, they are not sufficient to prevent imputations from hiding inestimable contrasts. Furthermore, these results shows that removing inestimable contrasts from the dataset may not be desirable. Our predictions for inestimable contrasts have more error than the estimable ones, but there seems to be little reason to discard this information so long as the increased error is properly taken in account.

5. Discussion

The combination of non-ignorable missingness and relative abundance estimation complicates the analysis of label-free discovery proteomics experiments. Complete case analyses may yield biased results and often result in discarding, or simply not making use of, large amounts of data. Single imputation solutions create a whole new set of problems by failing to account for imputation uncertainty, masking inestimable contrasts and preventing the recovery of interblock information.

Label-free data sets will commonly be missing upwards of 50% of the peptide level data. Some efforts have been made to alleviate the missing data problem by matching peptides across runs so that intensities can be obtained in the absence of an identification (Cox et al., 2014). However, this approach does not solve the missing data problem. A recent paper that used a peptide matching algorithm, provides a dataset where 56.5% of the peptide level data is still missing even after the matching (Sacco et al., 2016). Nonetheless, the concept of matching between runs does introduce a new source of information not utilized in our analysis. Attempting to incorporate information from the matching into the missing data modeling would be a very promising direction for future research.

Another common approach to dealing with missing values is to avoid making inference on proteins that fail to meet some threshold percentage of observed values. This approach is prudent and has served the field well. However, a necessary consequence of this decision is that large amounts of valuable data will essentially be discarded. We contend that all of the data can be used, so long as efforts are made to properly adjust for the uncertainty caused by missing values. Even keeping track of which parameters are estimable and which are not, would be a great improvement.

Based on the experimental process, we know that the probability a peptide will be missing should be a monotone increasing function of the underlying intensity. This means that the missing values contain valuable information about relative abundance. If dozens of peptide replicates appear with high intensities in one condition, but the values are almost all missing in another, this is highly suggestive of a large relative abundance. In a complete case analysis this change may not be estimable and neither the missing data pattern or peptides observed in only one condition would ever be put to use. By estimating a missing data mechanism, our selection model improves contrast prediction by incorporating this otherwise lost information.

The selection model approach relies heavily on model assumptions (the form of the missing data mechanism, distributional assumptions, shared variance components, etc.). However, with non-ignorable missing data, this is always the case. Even using a complete case analysis assumes (falsely) that the missing values are missing at random. The analysis presented on a ground truth data set is especially useful because it suggests that our selection model improves performance despite any deficiencies in the model assumptions. Relative to complete case analyses, we were able to increase overall accuracy, expand the depth of discovery, and greatly improve on interval coverage.

We hope that our model will be a useful framework for future research. Better models may be developed, but they should all take into account the main lessons of this paper: the parameters of interest are relative abundance estimates which take the form of contrasts; single imputations greatly simplify data analysis, but they do so at a severe cost to performance; relative to a complete case analysis, modeling a missing data mechanism can provide gains to accuracy, depth of discovery and interval coverage.

Supplementary Material

Supplemental Text

Supplementary Text (doi: 10.1214/00-AOASXXXXSUPP; .pdf). Additional text containing proofs, simulation details, algorithmic and experimental procedures.

W2W16 Tables (doi: 10.1215/00-AOASXXXXSUPP; .xlsx). Data tables and results pertaining to the two sample breast cancer data.

Dilution Tables part 1 (doi: 10.1217/00-AOASXXXXSUPP; .xlsx). Data tables and results pertaining to the ground truth dilution experiment.

Dilution Tables part 2 (doi: 10.1218/00-AOASXXXXSUPP; .xlsx). Data tables and results pertaining to the ground truth dilution experiment.

Dilution Tables part 3 (doi: 10.1317/00-AOASXXXXSUPP; .xlsx). Data tables and results pertaining to the ground truth dilution experiment.