A NEURAL POPULATION MECHANISM FOR RAPID LEARNING

SUMMARY

Long-term learning of language, mathematics, and motor skills likely requires cortical plasticity, but behavior often requires much faster changes, sometimes even after single errors. Here, we propose one neural mechanism to rapidly develop new motor output without altering the functional connectivity within or between cortical areas. We tested cortico-cortical models relating the activity of hundreds of neurons in the premotor (PMd) and primary motor (M1) cortices throughout adaptation to reaching movement perturbations. We found a signature of learning in the “output-null” subspace of PMd with respect to M1 reflecting the ability of premotor cortex to alter preparatory activity without directly influencing M1. The output-null subspace planning activity evolved with adaptation, yet the “output-potent” mapping that captures information sent to M1 was preserved. Our results illustrate a population-level cortical mechanism to 18 progressively adjust the output from one brain area to its downstream structures that could be exploited for rapid behavioral adaptation.

Graphical abstract

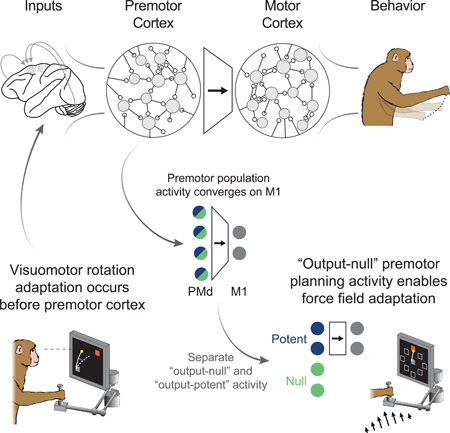
eTOC

Behavioral adaptation occurs rapidly, even after single errors. Perich et al., propose that the premotor cortex can exploit an “output-null” subspace to learn to adjust its output to downstream regions in response to behavioral errors.

INTRODUCTION

A fundamental question in neuroscience is how the coordinated activity of interconnected neurons gives rise to behavior, and how these neurons adapt their output rapidly and flexibly during learning to adapt behavior. There is evidence that learning extended over days to weeks is associated with persistent synaptic changes in the cortex (Kleim et al., 2004). Yet, behavior can also be adapted much more rapidly: motor errors can be corrected on a trial-by-trial basis (Thoroughman and Shadmehr, 2000), and sensory associations can be learned even following a single exposure (Bailey and Chen, 1988). Furthermore, in the motor system there appear to be constraints on the types of motor learning that can occur rapidly. In a brain-computer interface experiment, monkeys had difficulty learning to control a computer cursor when a novel control decoder required that they alter the natural covariation among the recorded neurons (Sadtler et al., 2014). There is evidence that such covariance structure relates to synaptic connectivity (Okun et al., 2015), which may not be readily modified on short time scales (i.e., seconds to minutes) (Bailey and Chen, 1983, 1988). Together, these observations suggest that changes in motor cortical structural connectivity may not be the primary mechanism governing changes in neural activity during short-term behavioral adaptation.

To achieve skilled movements, internal cortical computations needed to achieve the motor action must be combined with sensory input and transformed into a plan executed by the motor cortices (Kalaska et al., 1997). Behavioral adaptation can thus be achieved by adapting this association between sensory input and the motor plan, defined here as the neural activity necessary to move the limb to achieve the desired goal. Such adaptation likely involves interactions between the cortex and subcortical structures such as the cerebellum (Wolpert et al., 1998). Within the cortex, the dorsal premotor (PMd) area is ideally situated to perform the re-association required for short-term learning. PMd is intimately involved in movement planning (Cisek and Kalaska, 2005) and has diverse inputs from areas such as the cerebellum (Dum and Strick, 2003), a major center for error-based learning. PMd also shares strong connectivity with the primary motor cortex (M1) (Dum and Strick, 2002), the main cortical output to the spinal cord (Rathelot and Strick, 2009). Despite the behavioral observations during BCI learning described above, and the apparent association between the neural covariance structure and synaptic connectivity, we cannot rule out the possibility that fast connectivity changes between PMd and M1 could underlie the adapted behavior. However, an alternative possibility is that short-term motor adaptation is driven by changes in planning-related computations within PMd that are subsequently sent through a stable functional mapping to M1, without any changes in neural covariance and perhaps even synaptic connectivity. At present, such a mechanism has not been described.

Recent work studying population activity during motor planning provides a possible explanation (Elsayed et al., 2016; Kaufman et al., 2014). Using dimensionality reduction methods, the activity of hundreds of motor cortical neurons can be represented in a reduced-dimensional “neural manifold” that reflects the covariance across the neuronal population (Gallego et al., 2017). Activity within the neural manifold can be separated into subspaces that are “output-potent” or “output-null” with respect to downstream activity (Elsayed et al., 2016; Kaufman et al., 2014). Intuitively, the outputpotent subspace captures activity that functionally maps onto downstream activity, while the output-null subspace captures patterns of population activity that can be modulated without directly affecting the downstream target. In the case of movement execution, previous work has shown that muscle activity can be viewed as a weighted sum of motor cortical activity: this direct mapping is output-potent. Since more neurons exist than muscles, many patterns of neural activity could produce the same muscle activity. Changes in activity that keep this fixed motor output are output-null.

Intriguingly, during movement preparation, most motor cortical population activity is confined to the null subspace (Kaufman et al., 2014). Adopting the language of dynamical systems, this activity seemingly converges during the instructed-delay period toward an “attractor” state, a point in the neural state space to which the activity naturally settles. This state ultimately sets the initial conditions necessary to initiate a particular movement (Churchland et al., 2012; Elsayed et al., 2016); indeed, proximity to this attractor state is correlated with reaction time (Churchland et al., 2006). In our experiment, we applied this framework to study PMd and M1 activity during short-term motor learning. Our results illustrate a novel mechanism within PMd by which the brain rapidly adapts behavior by exploiting the output-null subspace to develop altered planning activity. This change in planning activity could be thought of as the equivalent of modifying the attractor state to produce the desired action (Remington et al., 2018). Ultimately, the adapted initial conditions for that action would be carried to M1 for execution via a fixed output-potent mapping.

Possible mechanisms underlying adaptive neural activity changes in PMd and M1

In our experiment, we recorded simultaneously from electrode arrays implanted in both M1 and PMd as macaque monkeys learned to make accurate reaching movements that were perturbed either by “curl field” (CF) forces applied to the hand (Li et al., 2001; Perich and Miller, 2017), or by a rotation of the visual feedback (VR) (Krakauer et al., 2005). We developed an analytical approach based on functional connectivity to understand adaptation-related changes in the activity of M1 and PMd, and distinguish the role of the output-null and output-potent subspaces within PMd throughout this adaptation process. We trained computational cortico-cortical models (Figure 1), i.e., models that predict the spiking of single M1 and PMd neurons based on the activity the remaining neural population, both local (same brain area) and distant (different brain area). These models provide a statistical description of the functional connectivity governing the interactions of these cortical areas. We trained the models during periods of stable behavior, and then tested their ability to predict neural spiking throughout short-term trial-by-trial motor adaptation to explore three fundamental questions: 1) does the functional connectivity within M1 and PMd change during adaptation? 2) does the functional connectivity between the PMd output-potent activity and M1 change? 3) can evolving output-null planning activity in PMd explain behavioral adaptation? Any model that fails to predict neural spiking consistently from the population activity throughout adaptation provides evidence that the particular modeled functional connectivity has changed. Within this framework, we can make four specific hypotheses that could explain the adaptive changes in M1 activity (Figure 1). Note that these four possibilities are not mutually exclusive.

Figure 1. Possible mechanisms of motor cortical activity changes underlying behavioral adaptation.

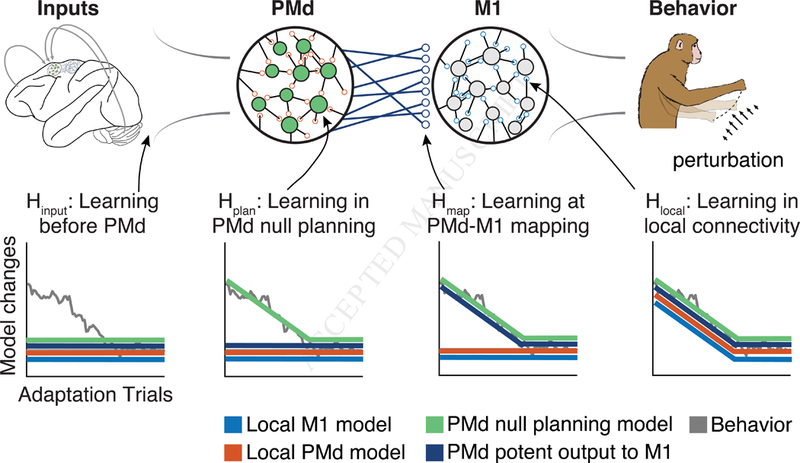
Hypotheses that could explain the changes in M1 spiking observed during adaptation. We assume a simplified hierarchical model where M1 responds to inputs from PMd, and its outputs drive the adapted behavior. We consider four models describing the functional connectivity within M1 (blue), functional connectivity within PMd (orange), the functional connectivity between the outputs of PMd and the M1 neurons (dark blue), or how the local PMd activity relates to M1 (green). Our experiment studies the generalization of such models during adaptation. Each inset plot shows the timecourse of changes in the behavior (gray line) and the predicted change in modeled connectivity (colored lines). We then identified four hypotheses that could explain the change in firing rates of M1: 1) the local functional connectivity could change, causing all four models to change as behavior adapts (H_local); 2) learning could arise from changes in planningrelated computations in PMd that are sent to M1 (H_plan). Here, the PMd outputs should predict changes in M1 (dark blue); 3) the mapping between PMd and M1 could change (H_map), which would not impact the within-area models (blue and orange) but would prevent the PMd to M1 models from generalizing; 4) learning could occur independently of M1 and PMd at the inputs to these areas (H_input), which would not require a change in any of the models describing this circuit.

H_local: The functional connectivity locally within a population of neurons (either M1 or PMd) can change, preventing the corresponding local models from generalizing throughout learning (H_local in Figure 1). One possible cause of such a functional change would be a change in synaptic connectivity within the network of neurons.

H_plan: Changes in activity within the output-null subspace allow PMd to generate new motor plans to compensate for the perturbation, which are ultimately sent through an unchanged mapping captured by the output-potent subspace. Here, models based on the output-potent activity should predict M1 spiking throughout adaptation, but the output-null activity would not (H_plan). To achieve this, synaptic connectivity could remain unchanged, while instead, PMd directly modifies the motor plan by adjusting its population activity, perhaps through interactions with other areas associated with learning, such as the cerebellum. Importantly, the local models will continue to predict spiking within each area accurately throughout this process.

H_map: A change in the mapping between PMd and M1 will not impact the ability of the local models to predict neural spiking within either PMd or M1, but will prevent both output-potent and output-null PMd activity from predicting spiking in M1 (H_map). This could be caused by a change in the synaptic connectivity between PMd neurons and their M1 targets.

H_input: Lastly, we consider the case that adaptation occurs upstream of PMd, and that the observed activity changes in M1 and PMd are solely in response to altered input from a third brain area, such as parietal cortex. In this case, all models should predict neural spiking throughout adaptation (H_input).

In the following analyses, we used these cortico-cortical models to explore each of the hypotheses describing shortterm adaptation to CF and VR perturbations. We first show that functional connectivity between neurons within each area were preserved throughout adaptation to the CF and VR perturbations. We then present evidence that planning activity within the output-null subspace of PMd plays a direct and unique role in enabling rapid adaptation to the curl field, but not the VR. These results suggest that the CF-related adaptation corresponds to changes in output-null planning activity within PMd, as described by H_plan above, while VR adaptation would be mediated by inputs from other brain areas (H_input).

RESULTS

Curl field adaptation involves widespread, complex changes in firing rate across the motor cortices

We performed experiments to study the functional connectivity relating distinct motor and premotor cortical populations during motor learning, and whether output-potent and output-null activity in premotor cortex enables adapted motor planning. We trained two rhesus macaque monkeys to perform an instructed-delay center-out reaching task (Figure 2A) and implanted 96-channel recording arrays in M1 and PMd (Figure 2B). Each experimental session consisted of three behavioral epochs, each beginning with reaches with no perturbation (Baseline epoch) before the monkeys were exposed to a perturbation: either the CF (Force epoch), or the VR (Rotation epoch) in the rotation experiments. The CF altered movement dynamics and required the monkeys to adapt to a new mapping between muscle activity and movement direction (Cherian et al., 2013; Thoroughman and Shadmehr, 1999) in order to make straight reaches. The VR preserved the natural movement dynamics, but offset the visual cursor feedback by a static 30º rotation about the center of the screen. In the following analyses, we focus exclusively on short-term learning occurring within a single day. We first consider the CF experiments. Within each session, the monkeys exhibited large errors upon exposure to the CF, which were gradually reduced until behavior stabilized (Figures 2C,D). Further evidence of adaptation was revealed by behavioral after-effects (mirror image errors) that occurred upon return to normal reaching during the Washout epoch (Figure 2D). We studied the neural activity recorded from the M1 and PMd populations after first computing a smooth firing rate on each trial (see Methods). During Baseline reaching, M1 and PMd neurons exhibited diverse firing rate patterns; a small number of examples are shown in Figures S1 and S2B. At the end of the Force epoch, the firing rate patterns of most neurons had changed in complex ways to enable the adapted movements (Figure S1, S2A,B). Similar changes in firing rate have been previously described in the motor cortex during CF adaptation, along with corresponding changes in the spatial tuning for reach direction of single neurons (Li et al., 2001; Perich and Miller, 2017). In this study, we explore several competing hypotheses, described above. Each of these proposes a distinct mechanism that can explain the diverse adaptation-related changes in single neuron firing and corresponding changes in directional tuning that have been observed within M1 and PMd (Li et al., 2001; Perich and Miller, 2017; Xiao et al., 2006).

Figure 2. Curl field task.

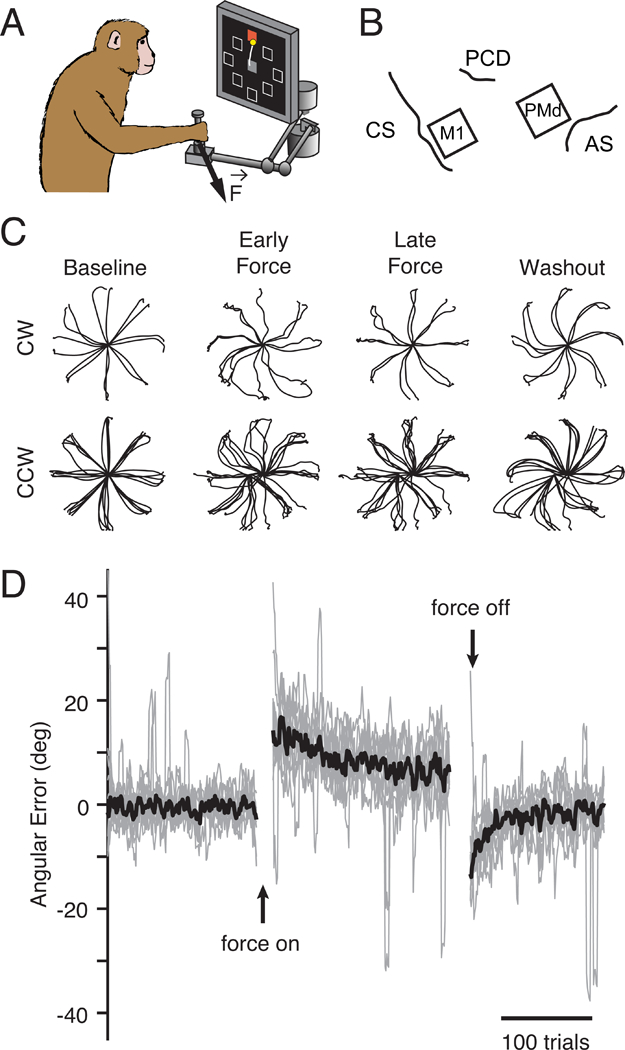
a) Monkeys performed a standard center-out task with a variable instructed delay period following cue presentation. b) We recorded from populations of neurons in M1 and PMd using implanted electrode arrays (CS: central sulcus, PCD: precentral dimple, AS: arcuate sulcus). c) Position traces for the first reach to each target (8cm distance) from two sessions with a clockwise CF (top row) and five sessions with a counter-clockwise CF (bottom row). Sessions from both monkeys are included. d) Error in the takeoff angle for all sessions (light gray lines), with the median across sessions shown in black. Gray traces were smoothed with a 4-trial moving average to reduce noise while preserving the time course of adaptation.

Models to study adaptation-related changes in the functional connectivity within or between cortical populations

We designed an analysis to test the above hypotheses using Linear-Nonlinear Poisson Generalized Linear Models (GLMs). The GLMs predicted the spiking of individual neurons using the activity of the neural population as inputs (Figure 3A; see Methods) (Pillow et al., 2008; Truccolo et al., 2010), thereby providing a quantitative means to study changes in the interactions between a single neuron and its neighbors in M1 or PMd. Once trained, these models can be used to predict neural spiking during behavioral adaptation even on single trials. This feature allowed us to test the extent to which each model could generalize throughout trial-by-trial changes in behavior, in particular in the beginning of the Force epoch before behavior plateaued. We assessed model performance using a relative pseudo-R² (rpR²) metric, which quantified the improvement in performance due to the neural covariates above that of the reach kinematic covariates alone (Figure S5A; Methods). Including kinematic covariates helped to account for the linear shared variability related to the executed movement, while leaving the unique contributions of individual neurons. We separated the adaptation epochs (Force or Rotation) into two sets of trials: training trials taken from the end of the epoch when the behavioral adaptation had stabilized, and testing trials taken from the beginning of adaptation. To address the hypotheses described above (Figure 1), we asked whether the models could consistently predict neural activity throughout this early block of testing trials when behavior was rapidly changing, i.e., whether performance was as accurate for the testing trials as for the training trials (Figure S5D). Failure to generalize would indicate that the functional connectivity was altered, perhaps to drive the changing behavior, while consistently high performance would suggest that no functional connectivity change had occurred.

Figure 3. Predicting neural spiking with GLMs.

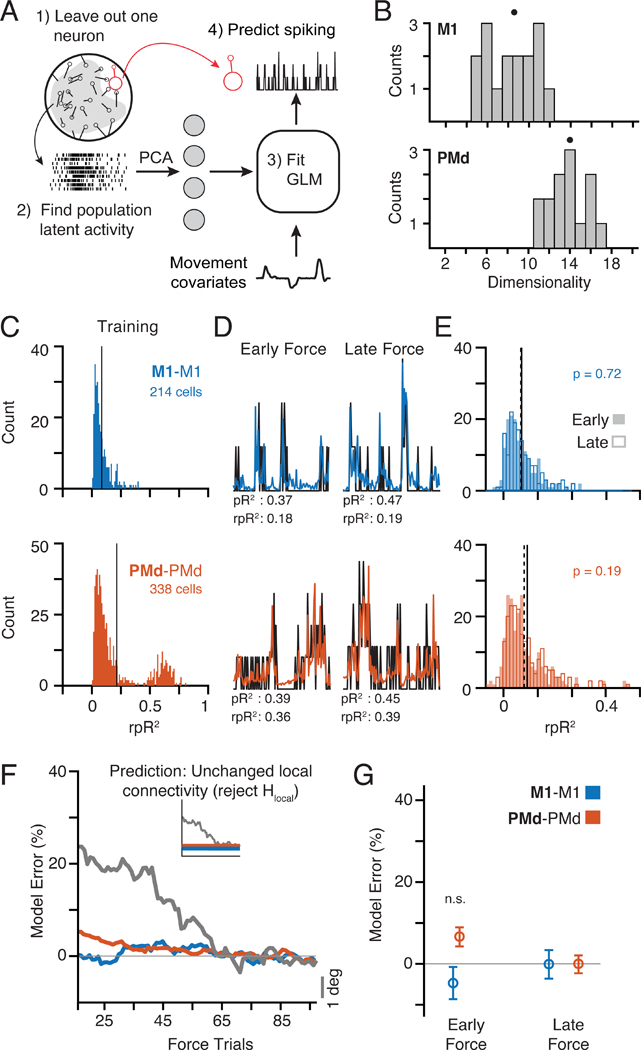
a) We trained GLMs using movement kinematics as well as the latent activity of the population of neurons within an area to predict the spiking of a single left-out neuron (see Methods). b) Histogram of dimensionality estimates for M1 (top) and PMd (bottom) manifolds across all sessions from both monkeys. Dots above each distribution indicate the median. PMd activity was consistently higher-dimensional than M1. c) We trained GLMs (M1-M1, blue, and PMd-PMd, orange) using data from the end of Force after behavior had stabilized and tested them for generalization throughout the initial phase of adaptation, beginning at the first CF trial (Early) and tested once behavior plateaued (Late). The left histograms show the distribution of rpR² for all neurons (pooled across nine sessions) with significant GLM fits (Figure S5; see Methods) based on a cross-validation procedure in the training data from the end of Force. d) Spiking for representative neurons (black) and model predictions (colors) during three Early ((highest behavioral error) and Late (lowest error) adaptation trials. e) Histograms of rpR² values for predictions in the Early and Late blocks. We compared Early (hollow bars; mean: dashed line) and Late (filled bars; mean: solid line) Force trials. M1-M1 and PMd-PMd had similar distributions during Early and Late. f) Time course of model performance changes. Predictions were made for individual trials, and then smoothed with a 30-trial window (see Methods). The horizontal axis labels represent the center-point of this window. Plotted data indicate the mean across all neurons. Trial-to-trial behavioral error processed with the same methods is overlaid in gray and scaled vertically for comparison (gray scale bar on left). The inset replicates our hypothesis prediction from Figure 1. g) Percent error in model performance during the Early and Late adaptation trials as in Panels D and E. No effects were significant (two-sample t-test). See also Figures S1-S7.

Using single-trial neural spiking data, we computed the low-dimensional latent activity in PMd and M1 (Gallego et al., 2017) and used the latent activity as input to the models. We used principal component analysis (PCA), a common dimensionality reduction technique. This approach implicitly assumes that the neural population covariance matrix (i.e., the neural manifold) is unchanged throughout each experimental session. To confirm this, we compared the covariance between each unit before, during, and after learning (see Methods), and observed that it remained constant throughout the entire experiment (Figure S2; for a representative session: Pearson’s correlation with Baseline values r ≥ 0.85 for M1 and r ≥ 0.93 for PMd). Across all sessions, the differences in covariance strongly resembled those obtained from random subsamples of Baseline data for which the covariance structure should be unchanged (Figure S3A). These results show that although neurons in M1 and PMd change their activity to compensate for the curl field, the underlying population covariance (which defines the neural manifold) remains unchanged.

In order to determine an appropriate number of principal components to use as model inputs, we estimated the dimensionality of the manifold that captured the neural population activity (see Methods). In brief, the dimensionality was defined as the number of principal components whose explained variance exceeded a threshold determined by the variability across trials (Machens et al., 2010). In all sessions, the PMd manifold contained more dimensions than did the M1 manifold (Figure 3B; M1 median, 8.5; PMd median, 14). This difference between areas was robust to the number of recorded neurons (Figure S4D). We assume that the neural activity occupies linear manifolds and that the activity within PMd is somehow related to activity in M1. Thus, the higher dimensionality of PMd necessarily leads to the existence of both output-potent and output-null subspaces in PMd activity with respect to the M1 latent activity (Kaufman et al., 2014), as hypothesized above. In later analyses focusing on activity in these subspaces, we sought to constrain the output-potent and output-null subspaces to have equal dimensionality. Thus, for M1 we used the first eight components and twice that value (16) for PMd. Our results were qualitatively unchanged within a reasonable range of dimensionality (see Figure S7).

Curl field adaptation is not associated with changes in functional connectivity within M1 or PMd

First, we used GLMs to assess whether curl field adaptation was associated with functional connectivity changes within local neural populations (H_local above, Figure 1). To study the functional connectivity within the M1 and PMd populations, we trained two models: M1-M1 predicted single M1 neurons from the M1 population activity and PMd-PMd predicted PMd neurons from the PMd population. To quantify the model accuracy, we calculated rpR² for each GLM in the “Early” and “Late” blocks of our testing trials taken from the beginning of the Force epoch. We defined the “model error” to be the change in rpR2 normalized by its cross-validated performance on the training data (see Methods). We tested whether predictions in the Early block were significantly worse than the Late block, an indication that the models failed to generalize. We set a significance threshold of p = 0.01 for all statistical comparisons of GLM performance. Note that if adaptation affects the accuracy of the models, the highest model error is expected to be in the Early block since it is the furthest removed from the training trials and has the largest behavioral error. We found that both within-area models (M1-M1, PMd-PMd) generalized well, predicting the adaptation-related changes in single-neuron spiking nearly equally well in both blocks (Figure 3E,F; Figure S6 shows individual monkeys; Figure S7A). As a qualitative test of the relation between the behavioral and neural changes during adaptation, we smoothed the rpR² of single-trial GLM predictions and compared their time course to that of the changing behavioral error (Figure 3F; Figure S6 shows individual monkeys). Neither model changed significantly, in contrast with the clear behavioral adaptation (Figure 3G). Based on the good generalization of the GLMs during learning and the unchanging covariance structure (Figures S2, S3), learning is unlikely to arise from changes in the connectivity within M1 or PMd (Figure 1).

Output-potent activity in PMd consistently predicts M1 neurons throughout curl field adaptation

We next trained models to test whether curl field adaptation corresponded to a change in the output-potent mapping that captures putative outputs from PMd to M1 (H_map above; Figure 1), or in the output-null computations performed by the PMd population and that seem to capture computations related to movement preparation (Elsayed et al., 2016; Kaufman et al., 2014) (H_plan). We identified the output-null and output-potent activity of PMd, defined as the projections of the PMd latent activity into the respective subspaces (see Methods), and used this activity as the inputs for two additional GLMs: Null-M1 and Pot-M1 (Figure 4B). Importantly, we computed the output-null and output-potent subspaces during Baseline, to avoid any possible bias resulting from adaptation-related changes in neural activity during the Force epoch. If the mapping between PMd and M1 changes (H_map), Pot-M1 will fail to predict M1 spiking during adaptation. Alternatively, if there is a change in the output-null computations reflecting an altered motor plan (H_plan), then Pot-M1, but not Null-M1, will accurately predict M1 spiking during adaptation.

Figure 4. Predicting M1 spiking from PMd output-potent and output-null subspaces.

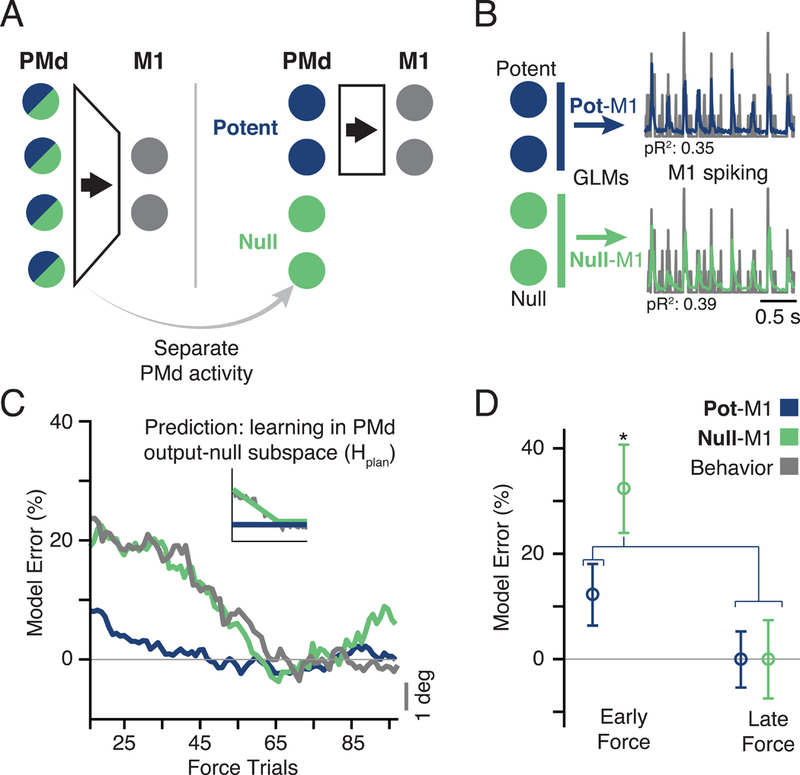
a) Hierarchical schematic of motor planning in PMd and M1. The PMd population activity is higher-dimensional, giving extra degrees of freedom at the input to M1 (Figure 3B). We devised an analysis to separate the putative PMd outputs to M1 from the other functions of the population. The former comprises the output-potent subspace, while the latter reside in the output-null subspace. b) The output-potent and output-null activity of PMd were used as the inputs to a GLM model to predict M1 spiking. c) The time course of model performance for Pot-M1 and Null-M1 for all sessions. Plots formatted as in Figure 3F. Gray line is the same behavioral error plotted in Figure 3F. Interestingly, the Null-M1 error alone paralleled the time course of behavior. d) The bar plot compares model error performance during early and late trials with outputpotent (Pot-M1) and output-null (Null-M1) activity. The performance of Null-M1 was significantly decreased during adaptation (asterisk indicates significant difference at p < 0.01, two-sample t-test). See also Figures S5–7.

Both models had similar accuracy when evaluated within the end-of-Force training trials using ten-fold crossvalidation (Figure S5E; see Methods). We then tested the generalization of these same models during learning. Here, the time-courses of the prediction accuracy from the output-potent and output-null activity were quite different from each other (Figure 4C). The Pot-M1 model generalized well throughout learning, making accurate predictions in Early Force as well as Late Force (Figure 4E, blue), despite the concurrent behavioral changes. However, the Null-M1 model generalized significantly worse in the Early block than in the Late block (Figure 4E, green), and changed with a time-course similar to that of behavioral adaptation (Figure 4C). Therefore, curl field motor adaptation is accompanied by changes in the outputnull subspace activity of PMd, while the output-potent mapping between M1 and PMd is unchanged (H_plan in Figure 1). This shows that the output-null subspace of PMd plays a distinct role in CF adaptation, yet the output to M1 via the output-potent space retains a fixed mapping.

We performed several controls to validate these results. To show that the difference between the models could not be trivially explained by our choice of dimensionality, we varied the number of principal component inputs across a broad range and observed similar results (Figure S7E). We also developed an additional model, PC-M1, which used all principal components from PMd as inputs. Since PC-M1 contained all of the output-potent and output-null subspace activity, we expected that, similarly to Null-M1, it would fail to generalize during adaptation. Indeed, its accuracy changed progressively during adaptation (Figure S6, pink), with a time-course very much like that of behavior. Moreover, if our results capture fundamental aspects of the population activity, they should be robust to the particular dimensionality reduction technique used. We thus replicated these main results using Factor Analysis, another common method for dimensionality reduction of neural data, instead of PCA (Cunningham and Yu, 2014) (Figure S7F). As a final control, we repeated the GLM analyses using the spiking activity of all single neurons in M1 or PMd as inputs, as opposed to the lower-dimensional latent activity (Figure S7C,D). Since the latent activity captured the dominant patterns of the single neuron spiking across the population, we expected to find similar results. Indeed, the local models (M1sn-M1, PMdsnPMd) generalized well throughout adaptation, while the between area model (PMdsn-M1) did not, similarly to the full PMd population activity model (PC-M1 in Figure S6).

An important hallmark of motor adaptation is the behavior during Washout: brief mirror-image aftereffects of the errors are seen early in adaptation (Shadmehr and Mussa-Ivaldi, 1994). If the inaccurate Null-M1 predictions were a consequence of motor adaptation, we hypothesized that we should see a similar signature of de-adaptation in the Null-M1 models as behavior returns to normal in Washout. To test this hypothesis, we trained GLMs using Baseline data and predicted the early Washout trials – conditions which, although separated widely in time, had the same dynamic environment but a very different state of adaptation. We found that Null-M1 generalized poorly in the earliest trials, then rapidly improved with de-adaptation as output-null activity began to return to Baseline. There was no such effect for the Pot-M1 model, which accurately predicted both early and late Washout trials (Figure 5). As was the case for behavioral adaptation, the stability of Pot-M1, and the corresponding change in Null-M1, match H_plan in Figure 1. Therefore, we conclude that there exists a direct mapping between PMd and M1 that persists unchanged throughout short-term motor adaptation to a curl field, while the evolving output-null activity within PMd changes in a way that drives behavioral adaptation.

Figure 5. GLM performance during de-adaptation in Washout.

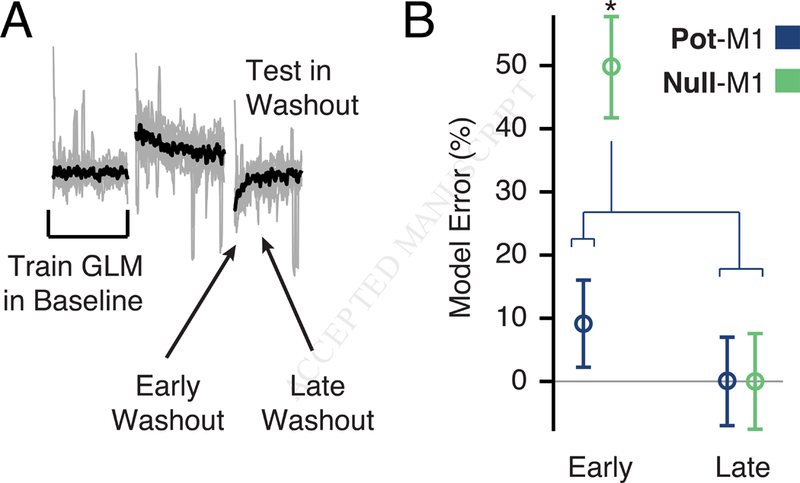
a) We asked whether de-adaptation following the removal of the CF triggered a return to the Baseline Null-M1 model. We trained GLMs using Baseline trials and asked how well they generalized in Washout. b) We found that for Null-M1 only, performance was worse in the first eight trials compared to eight trials taken later in Washout. This result supports the idea that the Baseline model was restored in the later trials. Asterisks indicate significant differences at p < 0.01 (twosample t-test). See also Figure S7.

Evolving changes in PMd output-null planning activity lead to adapted motor output

We next investigated the nature of the activity changes in the output-null and output-potent PMd subspaces during CF adaptation. In order to visualize these changes, we plotted activity in the single leading axis of the output-potent and output-null subspaces for movements to a single target during a Baseline reach (black) and throughout adaptation (red-toorange shades; Figure 6A). During behavioral adaptation, output-potent and output-null activity both progressively deviated from that of baseline. In this simple example, activity preferentially changed along the output-null axis prior to the go cue, then it began to modulate in the output-potent axis during the subsequent movement. Based on the preceding results, we speculate that the changes in output-null activity reflect the computations necessary to formulate a new motor plan, a plan that ultimately influences activity in M1. Given this interpretation, one prediction is that the output-null activity should precede the output-potent activity to which it is linked (Elsayed et al., 2016). We estimated the lag between the output-null and output-potent activity by computing their canonical correlations at varying time shifts (see Methods). We identified the shift at which the correlation was maximum and found that output-null activity did consistently precede output-potent activity (Figure 6B,C), during both Baseline and at the end of Force, when behavior was fully adapted.

Figure 6. Output-potent and output-null activity during CF adaptation.

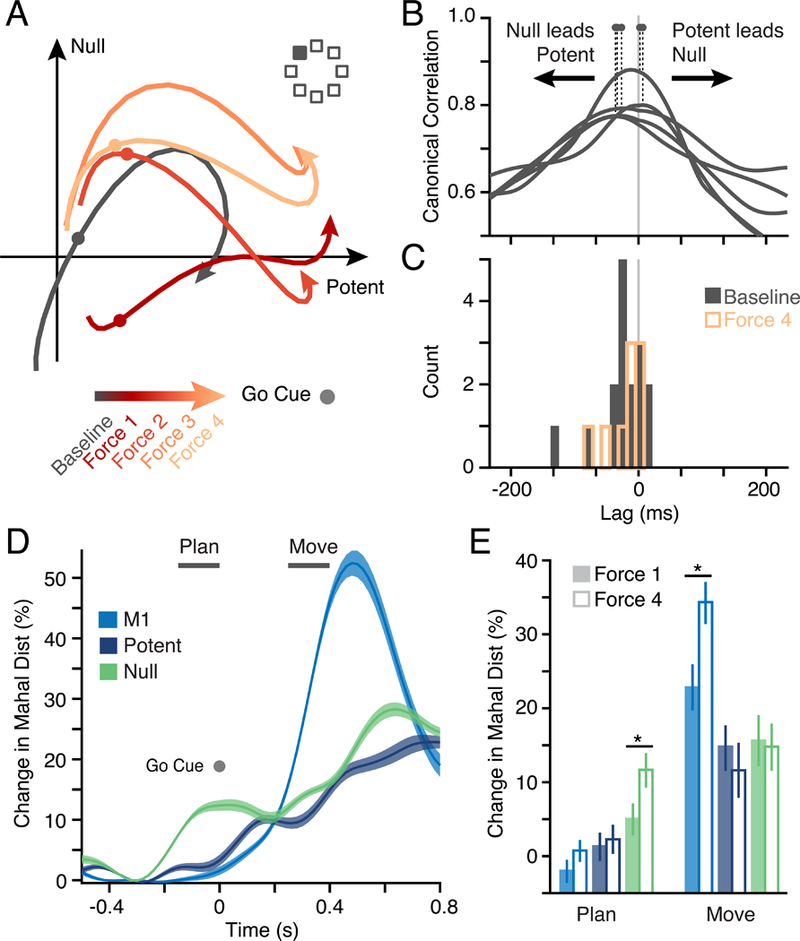
a) Examples of PMd subspace activity during one CF adaptation session for a single reach direction (filled square) averaged in four blocks of trials. Activity within both null and potent subspaces changed with adaptation. b) We used Canonical Correlation Analysis (CCA; see Methods) to compare the output-null and output-potent activity at different time shifts to identify their relative lag. The first canonical correlation value is shown for five example sessions. Dots indicate the lag with peak correlation. A peak left of zero indicates that output-null leads output-potent activity. d) Peak lag across Baseline for all 16 CF and VR sessions (black histogram). Output-null activity preceded output-potent by 35 ms on average, and the distribution was significantly negative (t-test; p = 0.02). The distribution obtained from the end of the Force period for the CF sessions (9 sessions) is overlaid in red. d) Analysis of neural state shows a progressive change in activity in both subspaces during adaptation. We computed a normalized Mahalanobis distance across all trials in a time window aligned on the go cue, which represents the separation of the instantaneous neural state from that of the Baseline. The plot shows the mean and s.e.m. across all CF sessions in Late adaptation for both M1 and the two PMd subspaces. e) A comparison of average change in relevant windows for planning and movement (indicated by horizontal bars in Panel D) in the Early (solid bars) and Late (hollow bars) phase of the Force epoch. Asterisks indicate significance at p < 0.05. Changes in planning activity predominantly occurred in the output-null subspace.

To better understand how the evolving activity in M1 and PMd leads to the adapted behavior, we studied the changes in output-potent, output-null, and M1 activity throughout planning and movement in the Force trials. On each learning trial, we computed the Mahalanobis distance in the low-dimensional neural manifold between the neural activity in Force and Baseline at each time point, after alignment on the go cue (Figure 6D; see Methods). We normalized this distance within each session such that it could be compared across days and monkeys. Changes in preparatory activity were largely confined to the output-null subspace. Furthermore, the amount of this altered preparatory activity increased significantly between Early and Late adaptation (Figure 6E, green). Since the increased distance was observed well before the onset of movement, these changes are suggestive of an adapting motor plan, as predicted by hypothesis H_plan. This observation, coupled with the GLM results, provides evidence that the changes in output-null activity may be causally related to the formation and subsequent execution of an adapted motor plan.

PMd to M1 mapping is unchanged throughout adaptation to a visuomotor rotation

In an important parallel experiment, we asked whether changes between PMd and M1 are a necessary consequence of adapted behavior, or indicative of a specialized role for PMd in the CF task. The same monkeys also learned to reach in the presence of a 30 deg visuomotor rotation (VR), a static rotation of the reach-related visual feedback (Figure 7A). Considerable evidence suggests that the brain areas involved in adapting to the VR differ from those required for CF (Diedrichsen et al., 2005; Krakauer et al., 1999; Tanaka et al., 2009), and include the parietal cortex, upstream of PMd. If the change in Null-M1 mapping during CF adaptation represents updated motor planning within PMd, we hypothesized that VR adaptation might not result in a similar change. Instead, VR adaptation should be mediated by processes occurring before the inputs to M1 and PMd (H_input in Figure 1).

Figure 7. Adaptation during a visuomotor rotation task.

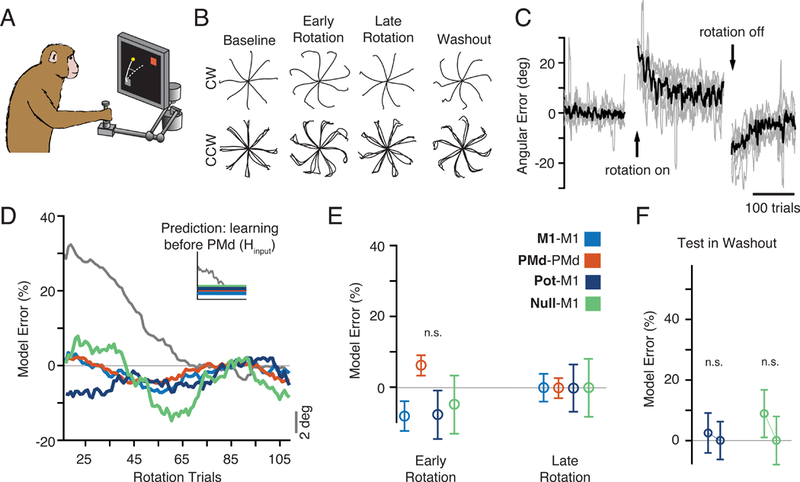
a)The same monkeys also adapted to a 30º visuomotor rotation (VR). b) c) Behavioral adaptation traces, plotted as in Panel B of Figure 2, for the VR sessions (one clockwise and four counter-clockwise). c) Same as Figure 2C but for the VR sessions, showing behavioral errors similar to those of the CF condition. d) The time course of model prediction error during rotation adaptation. Inset: we hypothesized that compensation for the altered feedback of the VR involved brain structures upstream of PMd. In this case, all three of the GLM models should generalize. As predicted, all GLM models, including Null-M1 generalized well to both Early and Late Rotation trials, despite clear behavioral adaptation (gray). e) Same format as Figure 3G. There were no significant changes throughout adaptation (all p > 0.01, two-sample t-test). f) Washout model performance for the VR task. Methods and data are as presented in Figure 5. We observed no change in performance during de-adaptation. See also Figure S7.

In many respects, adaptation during the CF and VR sessions was quite similar. Behavioral errors were similar in magnitude and time course (Figure 7B,C), with large initial errors in the Rotation epoch, and strong after-effects in Washout. Single neurons also changed their firing in complex ways (Figure S1B), and the altered activity was observed during pre-movement planning. Additionally, changes in neural activity preserved the population covariance structure (Figure S2B). However, all GLM models, including Null-M1, accurately generalized throughout Rotation (Figure 7D,E). Furthermore, we did not see any effect of de-adaptation in the neural predictions during Washout, despite the presence of behavioral after-effects (Figure 7F). Thus, there were no changes in the relationships between the PMd output-null activity and M1, despite behavioral adaptation and diverse changes in single-neuron activity. This result highlights a fundamental difference in the neural adaptation to these two perturbations, and supports the view that VR adaptation occurs upstream of PMd (Tanaka et al., 2009). It also strengthens our conclusions about the CF task: the poor generalization of the Null-M1 GLM is not a necessary consequence of changing behavior, but rather captures a previously undescribed mechanism by which the premotor cortex can drive rapid sensorimotor adaptation by exploiting the population-wide output-null subspace.

DISCUSSION

We have reported an experiment designed to help understand how the motor cortex can rapidly adapt behavior. We analyzed the functional connectivity between local and distant neural populations in M1 and PMd during two common motor adaptation tasks, and studied PMd activity in output-potent and output-null subspaces. We focused exclusively on short-term adaptation achieved within a single day of learning. Our analyses revealed several intriguing results: 1) during both adaptation tasks, we saw no change in the local functional connectivity or neural covariance within M1 and PMd; 2) the estimated dimensionality of PMd activity was larger than that of M1, suggesting the existence of output-null and output-potent subspaces; 3) PMd output-potent activity had a consistent relationship with M1 throughout adaptation in both tasks; 4) the relationship between PMd output-null activity and neurons in M1 changed with behavioral adaptation and subsequent de-adaptation in Washout for the curl field task (Figures 4,5,S6), but not visuomotor rotation (Figure 7); 5) pre-movement activity within PMd appears to reflect motor planning within the output-null subspace that evolves gradually during CF adaptation (Figure 6).

This study was enabled by the large neural populations recorded simultaneously from two distinct regions of the motor cortices. These analyses would not have been possible with sequential single-neuron recordings, as they are dependent on the precise interactions between neurons on single trials of behavioral adaptation. Nor could the conclusions have been reached by other means, such as through studying the activity of each neuron individually. First, the neural manifold, as well as the output-potent and output-null subspaces, capture population-wide features, and cannot be estimated using single neurons. Second, our GLM models study the instantaneous interactions between large numbers of cortical neurons.

Our results are inconsistent with the idea that altered connectivity is a necessary mechanism for short-term motor learning. Instead, they show that within the constrained, low-dimensional manifold (Sadtler et al., 2014), the cortex can exploit output-null activity to change behavioral output rapidly on a trial-by-trial basis while maintaining an unchanged output-potent projection to downstream structures. This illustrates a powerful mechanism that could underlie a variety of rapid learning processes throughout the brain.

The link between output-potent and output-null activity

The relation between the output-null and output-potent subspaces in movement execution and motor learning is an intriguing area of inquiry. Two recent studies using natural reaching movements and a BCI paradigm, respectively, suggest that the appropriate neural state must be established within the cortical output-null subspace to initiate outputpotent activity and subsequent motor output (Kaufman et al., 2014; Stavisky et al., 2017a). In our CF experiment, we observed progressive adaptation-related changes in the output-null activity (Figure 4) and corresponding changes during the more rapid de-adaptation process in Washout (Figure 5). Critically, changes in the output-null activity were observed during the planning period, well before movement (Figure 6). While we also observed changes in output-potent activity, the output-null activity led the output-potent activity during the planning period (Figure 6D,E). What, then, is the cause of this altered planning activity within PMd during CF adaptation? During movement, the altered sensory feedback from the induced errors could explain some of these changes, but they cannot account for the adjustment of preparatory activity well before movement onset. More plausibly, the PMd output-null activity could serve to adjust an inverse model of the dynamics needed to drive the limb (Wolpert et al., 1995), or change the inputs to such an inverse model, while the outputpotent activity of PMd recruits M1 to generate the adapted behavior.

Together with evidence from prior studies implicating output-null activity in motor preparation (Elsayed et al., 2016; Kaufman et al., 2014), our results strongly suggest that the evolving activity within the output-null subspace of PMd serves to set this preparatory state within PMd prior to movement initiation. One possible interpretation is that during movement preparation, an attractor-like state within PMd is altered, thereby establishing new initial conditions for the execution of an adapted movement by M1 (Remington et al., 2018). Generally, the output-potent and output-null activity evolves independently during movement preparation and execution. Yet, at the transition between movement planning and initiation, the output-null and output-potent subspaces are thought to be transiently coupled, such that the state in the output-null subspace initiates the cortical dynamics necessary to cause the desired motor output (Elsayed et al., 2016; Kaufman et al., 2014, 2016). The nature of this transition, including the underlying mechanism and its timing, are the subject of ongoing experimental and modeling efforts. Kaufman et al. propose that the transition could be driven by influence from a third area, perhaps a higher cortical area or the basal ganglia (Kaufman et al., 2016). In our experiments, the altered state in the output-null subspace is used to initiate a new, adapted movement. Importantly, this process could be accomplished without changing either the functional connectivity within either area, or the output-potent mapping from PMd to M1.

Interpreting changes in output-null activity

We divided the neural manifold spanning the activity within PMd into output-null and output-potent subspaces relative to the latent activity of M1. Critically, we computed the subspaces using data from the Baseline epoch, i.e., independently of the CF trials used for the subsequent GLM analyses. By definition, the output-null activity is orthogonal to that of the output-potent activity and M1 latent activity. An obvious question then, is how it is possible to use GLMs to predict the activity of M1 neurons from output-null activity in PMd? Although the output-potent and output-null subspace activity reside in orthogonal axes, the activity along any two of these axes can be linearly related during behavior since they are constructed from different weighted combinations of the common set of PMd latent activity. This explains why both output-null and output-potent activity can be used to predict M1 spiking in the GLMs. Yet, during CF learning the precise relationship between output-null activity and M1 appears to evolve with adaptation (Figure 4C), while outputpotent activity maintains the same relation with M1 spiking throughout the entire adaptation period. What is the correct way to interpret these activity changes? Adaptation could result in a change in either the orientation of these subspaces within the higher-dimensional PMd manifold, the trajectory of PMd neural activity within the fixed subspaces, or both (Figure S3C illustrates these distinctions). The similarity of the neural covariance structure (Figure S2, S3), as well as the consistent generalization of the PMd-PMd model, is evidence that the orientation of the M1 and PMd manifolds did not change during adaptation. As a consequence, it is unlikely that the orientation of the output-null and output-potent subspaces within PMd changed, in particular because the subspaces identified using Baseline data could be applied throughout adaptation. Instead, activity within these fixed subspaces must have changed as the monkeys learned, causing the change between the output-null activity and M1 while conserving the connectivity within both areas.

Testing the limits of the relations inferred from GLMs

While it is tempting to infer detailed cortical circuitry from the statistical structure in the neural population activity, it is dangerous to do so. This is especially true given the dependence of these models on relatively low-frequency coherence between neurons, rather than fast spike-to-spike interactions. The simple neural covariance approach (Figures S2,S3) is particularly far from cortical circuitry, as it is driven to a great extent by the common input received by all the recorded neurons (Stevenson et al., 2008). Furthermore, because many trials of data are necessary to estimate the covariance structure accurately, such covariance approaches are ill-suited to study trial-by-trial adaptive changes. Our GLMs are instead able to predict spiking activity on single trials. Furthermore, the GLMs can make a better estimate of the direct statistical dependencies, which we interpret as functional connectivity, between groups of neurons by discounting some of the common input that drives their activity. To achieve this, other studies have incorporated a wide variety of covariates, such as spiking history, the activity of neighboring neurons, expected reward, or kinematics (Lawlor et al., 2018; Pillow et al., 2008). We included additional kinematic covariates as inputs to the models to account for the shared inputs to the neurons (see Methods) (Glaser et al., 2016, 2018; Lawlor et al., 2018; Pillow et al., 2008; Ramkumar et al., 2016), though our results were not qualitatively dependent on the precise set of signals used. Note that our use of kinematic signals in the model does not assume a direct link between neural activity and movement kinematics. Rather, it is an attempt to discount influences in common input across a large number of neurons, which would otherwise obscure subtler, unique influences. Here, this approach revealed a differential effect of adaptation on the functional connectivity between M1 and the outputnull and output-potent subspaces of PMd. Importantly, all models received the same set of behavioral kinematic inputs. Thus, the poor generalization of Null-M1 in the CF task cannot be trivially explained by the fact that behavior was changing during the learning process; if this were true we should have observed the same results in the VR task.

Visuomotor rotation and curl field likely employ distinct adaptive processes

The visuomotor rotation experiments provide an intriguing counterpoint to curl field results. Adaptation to the VR is believed to involve neural processes that are independent from those of force field adaptation (Krakauer et al., 1999; Mathis et al., 2017). Previous evidence from modeling studies has led to the proposition that VR adaptation involves changes in functional connectivity between parietal cortex and motor and premotor cortices (Tanaka et al., 2009). Consistent with that proposal, despite the dramatic changes in PMd and M1 activity during VR adaptation (Figures S1,S2B), all GLM models generalized well: there were no changes in PMd to M1 functional connectivity throughout adaptation (Fig. 6), and we did not observe the effect of de-adaptation in the Washout Null-M1 GLM mapping (Figure 7F). We interpret this result to mean that VR adaptation occurs upstream of the inputs to PMd, although the current experiment cannot show this directly. This experiment also serves as an important control for our main result in the CF task, because a motor adaptation process with very similar magnitude of error and time course of adaptation yielded a very different result.

Recent work has shown that such changes in neural preparatory state in M1 can account for adaptation to a visuomotor perturbation (_S1_Reference52,Stavisky et al., 2017b), and in fact can provide a transfer of learning from a brain-computer interface task to a reaching task (Vyas et al., 2018). Our results support a similar model of how preparatory activity could influence subsequent dynamics to drive adaptation. However, they also suggest that these changes in M1 dynamical state can be driven by different sources depending on the task: in the case of the CF, inputs from PMd, and in the VR, upstream from PMd. An interesting future experiment would be to repeat the GLM modeling analysis using simultaneous recordings from parietal cortex and PMd during VR adaptation (Tanaka et al., 2009). In this case, we would hypothesize to see evolving output-null subspace activity in parietal cortex similar to that observed in PMd during the CF task. Such activity would serve to initialize the downstream preparatory dynamics necessary to initiate the adapted movement.

Relation between short- and long-term learning

Long-term learning is known to alter connectivity in the motor cortex, resulting in increased horizontal connections (Rioult-Pedotti et al., 1998) and synaptogenesis (Kleim et al., 2004). Many have proposed that the brain also uses similar plastic mechanisms to adapt behavior on shorter timescales (Classen et al., 1998; Li et al., 2001). However, any such changes of behaviorally-relevant magnitude would very likely have impaired the predictions of the Pot-M1, M1-M1, or PMd-PMd GLM models (Ahissar et al., 1992; Gerhard et al., 2013). Hence our results suggest that such connectivity changes within PMd or M1 likely play at most a minimal role during rapid trial-by-trial adaptation.

Our lab has previously found that the relation between evolving M1 activity and the dynamics of the motor output remains unchanged during CF adaptation (Cherian et al., 2013), with no evidence that adaptive changes in spatial tuning have a time course like that of behavioral adaptation (Perich and Miller, 2017). Therefore, we hypothesized that CF adaptation must be mediated by changes in recruitment of M1 by upstream areas, including PMd. Our new results illustrate how this can occur: in the short-term, PMd could exploit its output-null subspace to formulate new motor plans reflecting the modified task demands of the CF, which are sent to M1 through a fixed output-potent mapping. We speculate that this mechanism may be analogous to that proposed for working memory (Machens et al., 2010). In the seconds to minutes time range, distributed, reverberant population activity (involving PMd and presumably other areas, including the cerebellum) can hold a memory of the recent motor output. Its combination with an error signal could be used to modify the activity of a future trial in a manner to reduce error. This short term “memory” of the motor plan may be refreshed and further modified on each trial, until the behavior is adapted. This mechanism could be implemented within the null space, so that adjusting the plan does not directly impact the motor output to M1 until it is time to move.

However, if short-term CF adaptation occurs without connectivity changes in the cerebral cortex, how can we account for the performance improvements that are maintained across sessions (Huang et al., 2011; Krakauer and Shadmehr, 2006)? Recent psychophysical work has argued that the “savings” earned across subsequent days of practice could be of a fundamentally different origin than that of single-day, short-term learning (Haith et al., 2015; Huberdeau et al., 2015). How could such motor recall be enabled? The cerebellum has long been implicated in a variety of supervised, error-driven motor-learning problems, including both the CF and VR paradigms explored in this study (Diedrichsen et al., 2005; Galea et al., 2011; Izawa et al., 2012). Importantly, the cerebellum is thought to be a site at which inverse internal models of limb dynamics may be learned (Imamizu et al., 2000; Wolpert et al., 1998). Furthermore, plastic adaptive processes occur at multiple sites in the cerebellum and over several time scales (Yang and Lisberger, 2013; Zheng and Raman, 2010). Perhaps its extensive interconnections with PMd (Dum and Strick, 2003) allow new motor plans developed during force field adaptation to drive an evolving cerebellar internal model (Thoroughman and Shadmehr, 2000; Wolpert et al., 1998). Other evidence suggests that while these internal models may depend on the cerebellum for their modification, they may actually be located elsewhere (Shadmehr and Holcomb, 1997). In this case, such connectivity changes might eventually emerge within PMd and even M1 to support the long-term refinement and rapid recall of skills.

Wherever their ultimate location, we envision a mechanism whereby the tentative plans progressively developed in something resembling a “neural scratch pad” of cortical output-null subspaces, ultimately become consolidated in neural structural changes. Analogous population latent activity has been described in prefrontal cortex for decision-making (Mante et al., 2013), working memory (Machens et al., 2010), and rule-learning (Durstewitz et al., 2010), in the motor cortex for movement planning (Dekleva et al., 2018) and execution (Gallego et al., 2018), and in the parietal cortex for navigation (Harvey et al., 2012) among others. These widespread observations suggest a general mechanism by which the brain may leverage output-null subspaces of cortical activity for rapid learning without the need to engage potentially slow processes to alter the cortical circuitry.

STAR METHODS

Contact for reagent and resource sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Dr. Lee E. Miller (lm@northwestern.edu).

Experimental model and subject details

Non-human primates

All procedures involving animals in this study were performed in accordance with the ethical standards of the Northwestern University Institutional Animal Care and Use Committee and are consistent with Federal guidelines. The experiments were performed using two monkeys (male, mucaca mulatta; Monkey C: 11.7 kg, Monkey M: 10.5 kg). The subjects were fed a standard laboratory animal diet with a supplement of fresh fruits and vegetables. Whenever possible, the animals were pair-housed, and were always provided with frequent access to a variety of types of enrichment.

Method details

Behavioral task

Two monkeys were seated in a primate chair and made reaching movements with a custom 2-D planar manipulandum to control a cursor displayed on a computer screen. We recorded the position of the handle at a sampling frequency of 1kHz using encoders. The monkeys performed a standard center-out reaching task with eight outer targets evenly distributed around a circle at a radius of 8 cm. All targets were 2cm squares. The behavioral task was run using custom code interfacing with Simulink (The Mathworks, Inc). The first three sessions with Monkey C used a radius of 6 cm. However, we observed no qualitative different in the behavioral or neural results for the shorter reach distance, and all sessions were thus treated equally. Each trial began when the monkey moved to the center target. After a variable hold period (0.5 – 1.5 s), one of the eight outer targets appeared. The monkey had a variable instructed delay period (0.5 – 1.5 s) which allowed us to study neural activity during explicit movement planning and preparation, in addition to movement execution. The monkeys then received an auditory go cue, and the center target disappeared. The monkeys had one second to reach the target, and were required to hold there for 0.5 s.

In the curl field (CF) task, two motors applied torques to the elbow and shoulder joints of the manipulandum in order to achieve the desired endpoint force. The magnitude and direction of the force depended on the velocity of hand movement according to Equation 1, where $\overrightarrow{F}$ is the endpoint force, $\dot{p}$is the derivative of the hand position $\overrightarrow{p}$, θ_c is the angle of curl field application (85°), and k is a constant, set to 0.15 N·s/cm:

$$\overrightarrow{F}=\left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]=k\left[\begin{array}{cc}\cos {\theta }_c& -\sin {\theta }_c\\ \sin {\theta }_c& \cos {\theta }_c\end{array}\right]\left[\begin{array}{c}{\dot{p}}_x\\ {\dot{p}}_y\end{array}\right]$$ 1

In the visuomotor rotation (VR) task, hand position p was rotated by θ_r (here, chosen to be 30°) to provide altered visual cursor feedback $\overrightarrow{C}$ on the screen. The rotation was position-dependent so that the cursor would return to the center target with the return reach:

$$\overrightarrow{C}=\left[\begin{array}{c}{C}_x\\ C_y\end{array}\right]=\left[\begin{array}{cc}\cos {\theta }_r& -\sin {\theta }_r\\ \sin {\theta }_r& \cos {\theta }_r\end{array}\right]\left[\begin{array}{c}{p}_x\\ p_y\end{array}\right]$$ 2

Both the CF and VR perturbations were imposed continuously throughout the block of adaptation trials, including the return to center and outer target hold periods.

Each session was of variable length since we allowed the monkeys to reach as long as possible to ensure that behavior had sufficient time to stabilize, and to allow for large testing and training sets for the GLMs. For the CF sessions, the monkeys performed a set of unperturbed trials in the Baseline epoch (range across sessions: 170 – 225 rewards) followed by a Force epoch with the CF perturbations (201 – 337 rewards). The session concluded with a Washout epoch, in which the perturbation was removed and the monkeys readapted to making normal reaches (153 – 404 rewards). The curl field was applied in both clockwise (CW) and counter-clockwise (CCW) directions in separate sessions, though we saw no qualitative difference between the sessions. Monkey C had three CW sessions and two CCW sessions, while Monkey M had four CCW sessions. For the VR sessions, the monkeys performed 154 – 217 successful trials in Baseline, 219 – 316 during Rotation (either CW or CCW), and then 162 – 348 in Washout. Monkey C performed two CW VR sessions and two CCW sessions, while monkey M performed three CCW sessions. There is considerable evidence that learning can be consolidated, resulting in savings across sessions (Huang et al., 2011). In this study, we minimized the effect of savings to focus on single-session adaptation in the following ways. The monkeys: 1) received different perturbations day-to-day, as we alternated between CF and VR sessions, 2) received opposing directions of the perturbation on subsequent days, and 3) often had multiple days between successive perturbation exposures.

Behavioral adaptation analysis

For a quantitative summary of behavioral adaptation, we used the errors in the angle of the initial hand trajectory. We measured the angular deviation of the hand from the true target direction measured 150 ms after movement onset. To account for the slightly curved reaches made by the monkeys, we found the difference on each trial from the average deviation for that target in Baseline trials. Sessions with the CW and CCW perturbations were similar except for the sign of the effects. Thus, for the behavioral adaptation time course data such as that presented in Figure 2D, we pooled all perturbation directions together and flipped the sign of the CW errors.

Neural recordings

After extensive training in the unperturbed center-out reaching task, we surgically implanted chronic multi-electrode arrays (Blackrock Microsystems, Salt Lake City, UT) in M1 and PMd. From each array, we recorded 96 channels of neural activity using a Blackrock Cerebus system (Blackrock Microsystems, Salt Lake City, UT). The snippet data was manually processed offline using spike sorting software to identify single neurons (Offline Sorter v3, Plexon, Inc, Dallas, TX). We sorted data from all three task epochs (Baseline, Force or Rotation, and Washout) simultaneously to ensure we reliably identified the same neurons throughout each session. With such array recordings, there is a small possibility that duplicate neurons can appear on different channels as a result of electrode shunting, which would influence our GLM models by providing perfectly correlated inputs for these cells. While such duplicate channels are often easily identifiable during recording, we took two precautionary steps to ensure our data included only independent channels. First, we used the electrode crosstalk utility in the Blackrock Cerebus system to identify and disable any potential candidates with high crosstalk. Second, offline we computed the percent of coincident spikes between any two channels, and compared this percentage against an empirical probability distribution from all sessions of data. We excluded any cells whose coincidence was above a 95% probability threshold (in practice, this was approximately 15–20% coincidence, which excluded no more than one or two low-firing cells per session).

Across all sessions, we isolated between 137 – 256 PMd and 55 – 93 M1 neurons for Monkey C, and 66 – 121 PMd and 26 – 51 M1 neurons for Monkey M. For the neural covariance analysis, we excluded cells with trial-averaged firing rates of less than 1 Hz. Our GLM models were by necessity poorly fit for neurons with low firing rates. Thus, for the GLM analyses, we only considered neurons with a trial-averaged mean firing rate greater than 5 Hz. Pooled across all monkeys and CF and VR sessions, this gave a population of 918 M1 and 2221 PMd neurons. Given the chronic nature of these recordings, it is certain that some individual neurons appeared in multiple sessions. However, our analyses primarily focus on the population-level relationships which we found to be robust to changes in the exact cells recorded, so we do not expect our results to biased by partial resampling.

Single neuron covariance

For each trial, we considered all time points between target presentation and successful target acquisition. We binned the neural spiking activity in 10ms bins. We divided each session into five blocks of trials: two from the Baseline, two from Force, and then one from the Washout epochs. In each block, we averaged across trials for each target direction. We then computed the covariance between the spiking activity of all pairs of simultaneously recorded neurons.

Next, we sought to summarize the similarity of this covariance within each block to the Baseline condition to look for learning-related changes. For each pair of neurons, we compared the covariance in the Force and Washout blocks to the Baseline covariance. Across the recorded population on each session, we computed the Pearson’s correlation value to quantify the similarity in the covariance. We also created a reference distribution using correlations within the Baseline epoch to assess the ceiling for this metric when the covariance structure should not have changed. We randomly subsampled the Baseline trials and compared the correlations between each set. We repeated this procedure 100 times for each of the 9 CF and 7 VR sessions. The white distributions in Figure S3 show the correlations for these Baseline trials. For the heat maps shown in Figure S2, we used a simple hierarchical clustering algorithm to sort the neurons in the Baseline condition. To enhance this clustering and visualization, we normalized each row to range from −1 to 1. The same sort order was used in the heat map for each block as a means of visually assessing the consistency in the correlation structure.

Dimensionality reduction

We counted spikes in 50 ms bins and square root transformed the raw counts to stabilize the variance (Cunningham and Yu, 2014). We then convolved the spike train of each neuron for each trial with a non-causal Gaussian kernel of width 100 ms to compute a smooth firing rate. We used Principal Component Analysis (PCA) to reduce the smoothed firing rates of the neurons in each session to a small number of components for M1 and PMd separately(Cunningham and Yu, 2014). PCA finds the dominant covariation patterns in the population and provides a set of orthogonal basis vectors that capture the population variance. We call these covariance patterns “latent activity.” Importantly, this latent activity reflected the firing of nearly all individual neurons. For the control in Figure S7F, we repeated our analysis using Factor Analysis (factoran in Matlab, The Mathworks Inc) instead of PCA to achieve the dimensionality reduction. We assumed the same dimensionalities for M1 and PMd that we used for the PCA analysis (8 and 16, respectively).

For the output-null and output-potent subspace analysis described below, we needed to select dimensionalities for M1 and PMd. We adapted a method developed by (Machens et al., 2010) to estimate the dimensionality of our recorded populations. In brief, PCA provides an orthogonal basis set (the principal axes) with the same dimensionality as the neural input. However, the variance captured by many of the higher dimensions (with the smallest eigenvalues) is typically quite small. We estimated the noise in the neural activity patterns using the trial-to-trial variation in the activity of each neuron. We subtracted the activity of each neuron between random pairs of trials for each reach direction. This gave an estimate of the variation in spiking of each neuron (trial-to-trial noise) across targets. We then ran PCA on the neural “noise” provided by this difference for all targets. We repeated this 1000 times, giving a distribution of eigenvalues for each of these noise dimensions. We used the 99% limit of these distributions to estimate the amount of noise variance explained for each dimension. This allowed us to put a threshold on the amount of variance that could be explained by noise. The dimensionality was thus defined by the number of dimensions needed to explain 95% of the remaining variance (Figure 2B shows all sessions for M1 and PMd). Importantly, the dimensionality we estimated was robust to the number of recorded neurons since it reflected population-level patterns. We performed a control where we repeated the above analysis with random subsamples of neurons, taking fixed and equal numbers of neurons from the M1 or PMd populations for a session (Figure S4D) and observed no change in the estimated dimensionality.

Output-potent and output-null subspaces

Using the above method, we estimated the dimensionality of the M1 and PMd populations on each session. Since we consistently identified a larger dimensionality for PMd than M1, there existed a “null subspace” in PMd, which encompassed PMd activity with no net effect on M1 (Kaufman et al., 2014). To identify the geometry of the output-null and output-potent subspaces, we constructed multi-input multi-output (MIMO) linear models W relating the N dimensions of PMd latent activity to the R dimensions of M1 latent activity (with N > R):

$$\text{M = W P}$$ 3

where M is an R x t matrix whose rows contain the R dimensions of M1 latent activity, and P is an N x t whose rows contain the N dimensions of PMd latent activity; each column of both matrices contains the activity at time t. The matrix W, which contains the linear model that maps the PMd latent activity onto the M1 latent activity, has dimensions R x N.

We then performed a singular value decomposition (SVD) of the matrix W:

$$W=US{V}^T$$ 4

SVD decomposes the rectangular matrix W into a set of orthonormal basis vectors that allows us to define the output-null and output-potent subspaces. For our purposes, the vectors making up matrix V^T define the output-potent and output-null subspaces, with the first N rows corresponding to the output-potent subspace, and the remaining R - N rows defining the output-null subspace (Equation 5):

$$V=\left[\begin{array}{ccc}{v}_{11}& \cdots & v_{10}\\ ⋮& \ddots & ⋮\\ v_{N1}& \cdots & v_{NO}\end{array}\right]$$ 5

We used only trials from the Baseline period of each session to find the axes for PCA, as well as the output-null and output-potent subspaces. The Baseline trials were independent of the CF/VR trials used for both testing and training the GLM models, ensuring that we did not bias our results to find any specific solutions. This is potentially quite important, as it eliminates the possibility that the output-null and output-potent subspaces simply reflect activity patterns developed during adaptation. In practice, we obtained nearly identical results if we used all of the data, or data only from the CF/VR trials to compute the output-potent and output-null subspaces, indicating that they did not change throughout the session.

It is also important to note that the output-null and output-potent subspaces, as with the PCA axes, typically comprised population-wide activity patterns, rather than sub-groups of neurons. To show this, we defined an index quantifying whether a cell was more strongly weighted towards the output-potent or output-null dimensions. When projected into the output-potent and output-null subspaces, the firing rate of each individual cell is multiplied by weights defined in the PCA matrix as well as the matrix defining the output-null and output-potent subspaces (V in Equation 5). We thus multiplied these two matrices to get an effective weighting of each cell onto the axes of the output-potent and output-null subspaces. We then computed an index defined as the difference between the magnitude of the output-potent and output-null weights (summed across all dimensions) divided by the total weights. Thus, a value of −1 indicates that the neuron contributed only to output-null dimensions, +1 indicates the neuron contributed only to output-potent dimensions, and values near zero indicate the cell has no preference. The resulting distribution, centered on zero, is plotted in Figure S4C. We generated a control distribution by randomly shuffling the weights across neurons and repeating the comparison thousands of times.

Quantifying changes in neural state space activity

To compare the dynamics of activity changes in the output-potent and output-null subspaces during CF learning, we computed the Mahalanobis distance of the activity in state space during learning. Mahalanobis distance is analogous to Euclidean distance but incorporates the variance along each of the dimensions. We aligned each trial on the time of go cue presentation. We then computed the low-dimensional activity of M1 and PMd for all Baseline and Force trials in 20ms bins and computed the distance in state space at each time point between that force trial and all Baseline reaches to the same target direction. In order to compare across monkeys and sessions, we normalized the distance at each time point by subtracting the value at a reference point and normalizing by the max distance observed throughout the adaptation period. We performed this procedure to study latent activity within the M1 manifold, as well as activity within the output-potent and output-null subspaces of PMd. We compared two blocks of trials from within the Force epoch: Early adaptation included the first trials where behavior was changing, and Late adaptation contained the last trials, when behavior had reached a plateau.

Calculating the lag between output-null and output-potent activity

We used Canonical Correlation Analysis (CCA) to compare the activity in the output-potent and output-null subspaces of PMd. In brief, CCA finds linear transformations that when applied to two sets of latent activity maximize their pairwise correlation. Thus, it provides a principled measure of the similarity of signals in the output-potent and output-null subspaces. We used CCA to estimate the delay between the output-null and output-potent activity during Baseline trials within a motor planning window of duration 700 ms following target presentation. We shifted the outputpotent activity relative to the output-null activity by a series of lags (−350 to 350 ms in 10ms steps) and performed CCA at each lag. We identified the lag that maximized the correlation between the set of activity. We repeated this analysis using a block of trials from the end of Force to determine if the lags changed as a consequence of learning (Fig. 6d).

Generalized Linear Models

In our analyses, we used GLMs to predict the spiking activity of single neurons based on the activity of the remaining population, as well as kinematic signals. We trained Poisson Generalized Linear Models (GLMs) to predict the spiking activity of individual neurons on a single-trial basis (Truccolo et al., 2010). GLMs extend Gaussian multilinear regression approaches to the Poisson statistics of neural spiking. We took weighted linear combinations of the desired covariates, x_i, such as population spiking:

$${\displaystyle \sum _i{\theta }_i}{x}_i=X\Theta$$ 6

where X and θ are matrices containing all x_i and θ_i, respectively. The weighted covariates were passed through an exponential inverse link function. The exponential provides a non-negative conditional intensity function; $\lambda$, analogous to the firing rate of the predicted neuron:

$$\lambda |X,\Theta =\exp (X\Theta )$$ 7

The number of observed spikes, n, in any given time bin is assumed to a Poisson process with an instantaneous firing rate mean of;;λ:

$$n|\lambda ~Poisson(\lambda \cdot \text{d}t)$$ 8

Covariate inputs to the GLMs

We binned the neural spikes at 50ms intervals and downsampled the continuous kinematic signals to 20 Hz to match the binned spikes and dimensionality-reduced latent activity. We shifted the kinematic signals backwards in time by three bins (150 ms) to account for transmission delays between cortical activity and the motor output. The range of delays can be quite broad, so we convolved the kinematic signals with raised cosine basis functions centered at 0 ms and 100 ms, adapting the method of Pillow et al., where bases further back in history become wider (Pillow et al., 2008). By including these convolved signals as inputs to our GLM models, we allowed the neurons to have more flexible temporal relationships with the kinematics. Note that all GLM models in the main text included the same convolved endpoint position, velocity, and acceleration signals as covariates. For Figure S7C,D, we performed a control in which we repeated the GLM models for the CF task using only the velocity inputs.

We trained two types of models: the Basic models included only kinematic covariates, while the Full models included both the kinematic covariates and the spiking activity of the neural populations (Figure S5A). For the GLM analysis with neural population latent activity as inputs, we selected a dimensionality for M1 and chose the PMd dimensionality to be twice this value. This decision was to control for the number of inputs to the GLM when analyzing the output-null and output-potent subspace activity. For the PMd-M1 model, we identified the low-dimensional latent activity in PMd (see above) and used these as inputs to the GLM. For M1-M1 and PMd-PMd, we left out the single predicted neuron and computed the latent activity using the remaining neurons in that brain area. We then used these signals to predict the activity of the left-out neuron. For Pot-M1 and Null-M1, we projected the time-varying PMd latent activity onto the axes for the output-potent and output-null subspace, respectively (see above). We then used these timevarying signals as inputs to GLMs to predict the spiking of M1 neurons. For the GLMs with single neuron inputs, we trained three different types of Full models. M1sn-M1 models predicted the spiking activity of each M1 neuron from the activity of all other M1 neurons recorded on the same session, PMdsn-PMd models predicted the spiking of each PMd neuron from all other PMd neurons, and PMdsn-M1 models predicted M1 neurons using the activity of all PMd cells. Since PCA captures population-wide covariance patterns, we expected that this approach would provide nearly identical results to the single neuron models, and it was included primarily as a control.

Training the GLMs

We trained the models using the last 50% of Force or Rotation when behavior was most stable, including only trials in which the monkeys reached successfully to the outer target (reward trials) (Figure S5D). This allowed us to test the generalization of the GLMs between late and early adaptation trials. For the CF, it was important to both train and test the GLMs using trials from the Force epoch to avoid extrapolating between the Baseline and CF conditions: when we imposed the CF, it changed the relationship between the kinematics and dynamics of limb movement. Thus, if we trained the GLM on Baseline trials, the altered relationship between kinematics and neural activity during CF trials (Cherian et al., 2013) would lead to poor GLM generalization for all models. By both training and testing within the Force epoch, we avoided the problem of extrapolating to new dynamics conditions. Although the VR sessions did not have this problem, we adopted this same approach for the sake of consistency. We performed an additional analysis to look for deadaptation effects in Washout (Figures 5,7F). The procedures were similar for this analysis, though we trained the GLMs using Baseline data and then tested using trials from early Washout.

We trained the models using a maximum likelihood method (glmfit in Matlab, The Mathworks Inc). In the case of our full population spiking models, we had dozens to hundreds of covariate inputs for a single predicted output. Although we had very large numbers of training datapoints (typically on the order of 10,000 samples), there is the possibility our models were impaired by overfitting. We guarded against overfitting using ten-fold cross-validation of our training dataset. We also repeated our analyses using Lasso GLM for regularization and observed nearly identical results (data not shown). We thus chose to use the non-regularized GLM for simplicity and to reduce the computational load, since it did not impact our results.

Evaluating GLM performance

We evaluated GLM performance using a particular formulation of the pseudo-R² (pR²). The pR² is analogous to the R² commonly used in model-fitting with Gaussian statistics, but it is generalized to incorporate the approximate Poisson statistics of the neural spiking data:

$${\text{pR}}^2=1-\frac{\log L(n)-\log L(\widehat{\lambda })}{\log L(n)-\log L(\overline{n})}$$ 9

The pR² finds the difference in log-likelihood between the observed spiking data (n) and the model predictions ($\widehat{\lambda }$). This value is compared against the difference in log-likelihood for the mean of the dataset ($\overline{n}$). We used the Likelihood (L) for Poisson data according to

$$L={\displaystyle {\prod }_{t=1}^{T}Poisson\left(n_t|{\lambda }_t\right)}={\displaystyle {\prod }_{t=1}^T\frac{{\lambda }_t^{n_t}\exp \left(-{\lambda }_t\right)}{n_t!}}$$ 10

And thus, the log-likelihood (log L) across all time bins (t) of a given spike train is:

$$\log L={\displaystyle {\sum }_{t=1}^T\left(n_t\log {\lambda }_t-{\lambda }_t-\log n_t!\right)}$$ 11

Although the upper bound for pR² is one, poor model fits can be less than zero. A pR² of one indicates a perfect model fit, a value of zero indicates that the model prediction performs as well as finding the mean of the data, while values less than zero indicate that the model performed worse than merely fitting the mean. pR² values are smaller in magnitude than those typically found with the Gaussian R². When evaluating GLM fits on a block of data, we used a bootstrapping procedure to resample the data with 1,000 iterations to obtain 95% confidence bounds on the pR² value. We considered a model fit to be significant if this bootstrapped confidence interval was above zero, indicating that the model helped to explain the spiking activity.

For many analyses, we used the relative pseudo-R² (rpR²), which directly compares two separate GLM models. While pR² compared the log-likelihood of the model predictions to the mean of the data, the rpR² compares the predictions of a Full model to a Basic model with fewer covariates (Heinzl and Mittlböck, 2003).

$$rpR{}^2(\text{ Basic, Full })=1-\frac{\log L(n)-\log L\left({\tilde{\lambda }}_F\right)}{\log L(n)-\log L\left({\tilde{\lambda }}_B\right)}$$ 12

Here,${\widehat{\lambda }}_F$, the Full model prediction, which includes both the kinematics and the population spiking, is compared to${\widehat{\lambda }}_B$, the prediction of the Basic model, which includes only kinematics. This metric thus quantifies the improvement in performance afforded by the additional neuronal inputs. Positive values indicate that the Full model performed better than the Basic model, while negative values indicate that predictions were better with kinematics alone. As with the pR², we obtained confidence bounds with a bootstrapping procedure and assessed significance by determining if the lower bound was above zero. This indicated that the addition of population spiking added information over the kinematics alone, and thus could be capturing statistical dependencies between the population and the predicted cell.

For the time course of GLM model performance plots, such as Figure 3F, we predicted neural spiking on individual trials. However, single-trial predictions could be quite noisy, particularly for neurons with relatively low firing rates. For example, if a cell fired very few spikes on a particular trial, the pR² may be quite low, even though the model otherwise performed quite well when viewed across all trials. To remove some of this variability for purposes of visualization, we smoothed the trial-to-trial predictions for each neuron (together with the overlaid behavior) with a moving average. We chose a window of 30 trials, though we observed similar (but noisier) traces even down to window sizes of 5–10 trials. Since there were rapid behavioral improvements in the early trials, we padded the beginning of the block of trials with NaNs, each of a length of half of the window size. This helped to prevent averaging out the changing behavioral effects, with the tradeoff of increased noise. In practice, the appearance of the figures was similar without this padding.

Selecting cells with significant GLM predictions

For most of our analyses, we studied cells that were well-predicted by our GLMs. We determined this by two main criteria using ten-fold cross-validation on the training data. First, we required that the Basic pR² was significantly above zero. This reduced the pool of candidate cells to 522 of 918 (57%) in M1 and 612 of 2221 (28%) in PMd, but was necessary so that the rpR² would be well defined. Qualitatively, we obtained similar results when we relaxed this criterion to include more cells. We also required that the rpR² was significantly above zero. We only included cells that were significantly above zero for all ten of the folds for both pR² and rpR². This conservative method ensured that we only studied cells that were reliably predicted.

Calculating GLM error

To compare performance of the different GLM models, we first defined a fixed reference point of eight consecutive trials in Late adaptation, which was close to (but independent from) the trials from the second half of adaptation that we used to train the GLMs (around 70 trials from the start). On each trial, we computed the difference in rpR² relative to this Late adaptation performance. To account for inherent differences in performance of the models, we normalized this difference by the rpR² computed from the cross validated training set. Thus, the model error metric represents the % change in performance from Late to Early adaptation. Note that as constructed, the model error is necessarily zero in Late adaptation (such as when plotted in Figure 3G). This metric provides a compact way to compare whether the models performed worse during Early adaptation compared to Late adaptation. For the Washout predictions, the rate of deadaptation was faster than adaptation in either Force or Rotation. Thus, the blocks of trials that we selected for the Early and Late reference when testing the GLMs in Washout were closer to each other in time than the blocks we used for the Force or Rotation epochs.

Controls for the output-potent and output-null subspaces

For the PMd output-potent and output-null subspaces, we ensured our results did not depend on the particular dimensionality chosen. We repeated the full GLM analysis selecting different M1 dimensionalities ranging from 5 to 20. We enforced that PMd always had twice the number of dimensions of M1 to control for the number of inputs to the GLM models. We then trained the GLM models using the methods described above and computed the model error for each dimensionality (shown in Figure S7E).

Quantification and statistical analysis

For the GLM models, we assessed the significance of model fits empirically using a bootstrapping procedure on cross-validated data as described above. Additionally, we used two-sample statistical tests to compare the distributions of pR² changes in Early and Late adaptation. For Figures 3E and S5F, which did not satisfy criteria for normality, we used a Kolmogorov-Smirnov test of the rpR² values. For the Model Error comparisons, which summarized differences in the metric, we used a t-test of the normalized change in rpR². All tests were two-sided.

Data and Software Availability

Custom code was used to process the neural and kinematic data in preparation for analysis. This code may be shared upon reasonable request. The neural covariance, PCA, and Factor Analysis were performed using the Matlab functions “cov”, “pca”, and “factoran”, respectively. The GLMs were fit using the glmfit routine in Matlab. Lastly, the Mahalonibis distance analysis for Figure 6 was computed using “mahal” in Matlab. All statistical tests were also performed within Matlab. Data and neural recordings supporting the findings of this study may be shared upon reasonable request.

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Models: Organisms/Strains
Macaca mulatta	Pacific Resources Ltd/Rhenos LLC or Alpha Genesis	N/A
Software and Algorithms
MATLAB	The Mathworks, Inc	https://www.mathwor ks.com/products/matlab.html
Simulink Realtime	The Mathworks, Inc	https://www.mathworks.com/products/sim ulink-real-time.html
Other
Cerebus neural data acquisition system	Blackrock Microsystems, Inc	http://blackrockmicro.com/neuroscienceresearchproducts/neuraldata-acquisitionsystems/cerebusdaq-system/
Utah microelectrode arrays	Blackrock Microsystems, Inc	http://blackrockmicro.com/electrodetypes/utah-array/

Highlights.

• Macaque monkeys rapidly adapted to reaching movement perturbations

• Functional connectivity within motor and premotor cortex was unchanged

• The “output-null” activity within PMd held a signature of force-field learning

• There was no corresponding change accompanying visuomotor rotation learning