Significance
The reciprocal evolution of interacting species, or coevolution, generates impressive adaptations in pairs of species across geographic regions. However, we currently do not understand how coevolution shapes adaptations in large groups of species that interact not just locally but also across ecosystems. We use a mathematical model of coevolution and network tools to show that gene flow resulting from movement of individuals among populations may favor, rather than swamp, reciprocal adaptation in mutualisms, especially in large and heterogeneous networks typical of pollination and seed dispersal interactions. Our results suggest that the disruption of gene flow, fueled by human activities, may undermine long-term adaptation in mutualistic assemblages, with severe consequences for the functioning of ecological systems.
Keywords: coadaptation, ecological networks, gene flow, mutualism, trait matching
Abstract
Ecological interactions shape adaptations through coevolution not only between pairs of species but also through entire multispecies assemblages. Local coevolution can then be further altered through spatial processes that have been formally partitioned in the geographic mosaic theory of coevolution. A major current challenge is to understand the spatial patterns of coadaptation that emerge across ecosystems through the interplay between gene flow and selection in networks of interacting species. Here, we combine a coevolutionary model, network theory, and empirical information on species interactions to investigate how gene flow and geographical variation in selection affect trait patterns in mutualistic networks. We show that gene flow has the surprising effect of favoring trait matching, especially among generalist species in species-rich networks typical of pollination and seed dispersal interactions. Using an analytical approximation of our model, we demonstrate that gene flow promotes trait matching by making the adaptive landscapes of different species more similar to each other. We use this result to show that the progressive loss of gene flow associated with habitat fragmentation may undermine coadaptation in mutualisms. Our results therefore provide predictions of how spatial processes shape the evolution of species-rich interactions and how the widespread fragmentation of natural landscapes may modify the coevolutionary process.
Ecological interactions are a fundamental component of biodiversity (1). Phenotypic traits of many species have evolved through selection imposed by ecological interactions, such as toxins in prey and resistance to toxins in their predators (2) or floral tubes of plants and mouthparts of their pollinators (3). These examples show how reciprocal selection shapes coadaptation in pairs or small groups of interacting species. However, small groups of species rarely interact in isolation. Species are usually embedded in networks containing dozens or even hundreds of interacting species (4, 5). Understanding how patterns of coadaptation arise and favor species persistence in large assemblages of interacting species is currently a major challenge requiring approaches at the interface of ecology, evolution, and network science (6–8).
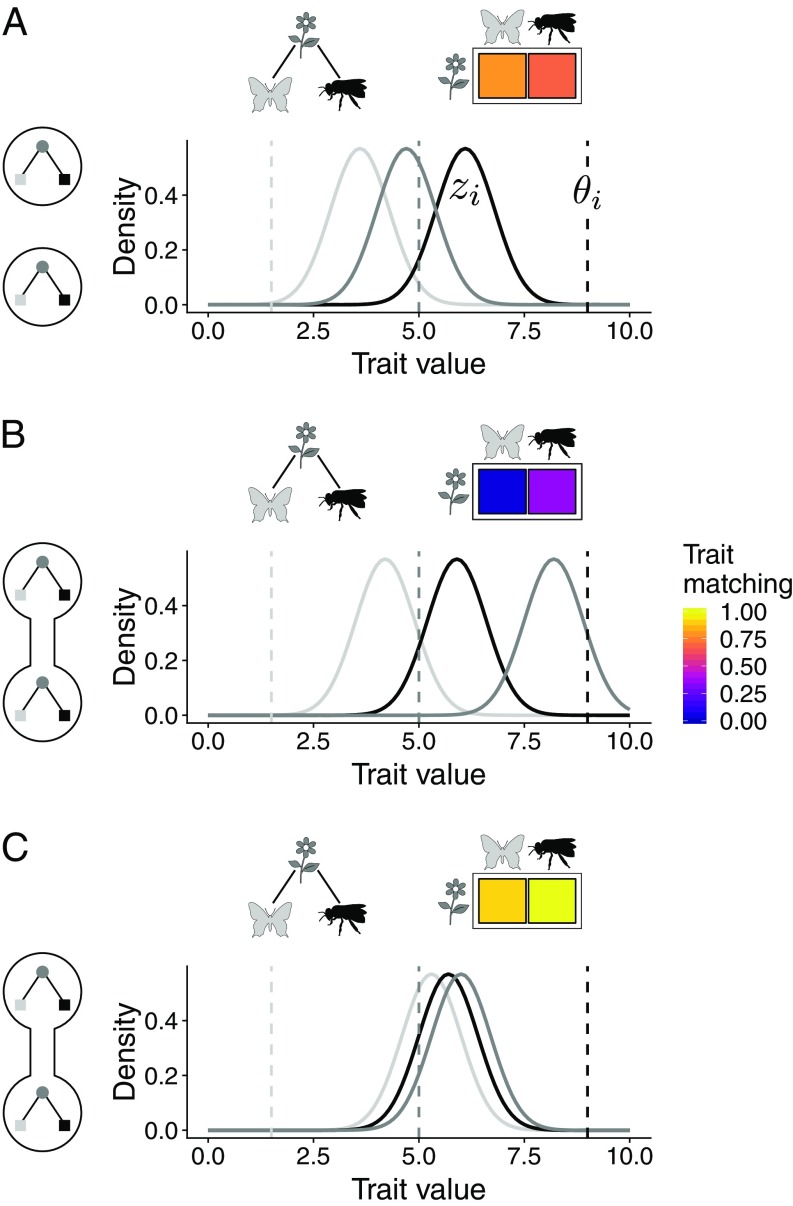
For mutualisms, previous studies have explored how coevolution may affect network architecture—that is, the pattern of interactions among species—and, in turn, how such architecture may drive coevolution. The role of coevolution in shaping the organization of links of empirical networks is still uncertain (9–12). Nevertheless, it is known that network architecture varies with fundamental aspects of the natural history of interactions, potentially leading to distinct coevolutionary dynamics (7, 13). For example, multiple-partner mutualisms, in which an individual interacts with several individuals throughout its life, such as pollination or seed dispersal by animals, typically form species-rich and nested networks (14, 15). Theoretical evidence suggests that coevolution in multiple-partner mutualisms operates in part through indirect evolutionary effects—that is, evolutionary outcomes caused by species that are not linked as interacting partners (7), favoring similarity in traits at the community level (i.e., trait convergence) (16, 17). In contrast, intimate mutualisms, in which an individual completes at least a life stage on a single host, such as protection of host plants by ants or protection of anemonefishes by host anemones, generate species-poor and modular networks (18, 19). Coevolution in intimate mutualisms is expected to exhibit frequent and reciprocal effects between species that interact directly (13), leading to the tight trait matching observed in many intimate interactions (20). Thus, studies of coevolution in mutualistic networks have shown how adaptive landscapes may be modified by the underlying network structure, molding trait patterns (Fig. 1A).
Fig. 1.
Potential effects of gene flow on trait evolution in mutualistic networks. In this example, there are two sites in which the same two pollinator species interact with the same plant species. Each curve represents a trait distribution with mean of one population in one of the sites (light gray and black: pollinator species; dark gray: plant species). Dashed lines indicate the trait values favored by the local environment (). (A) In the absence of gene flow across sites, trait matching (colors in the interaction matrix) evolves because mutualistic interactions modify local adaptive landscapes. (B and C) Gene flow across sites with distinct selection regimes may shift species traits, further altering adaptive landscapes and trait patterns in two possible ways. (B) First, gene flow may induce trait mismatching. (C) Second, gene flow may strengthen the coadaptation pattern previously observed for the isolated assemblage.
Coevolution in multispecific interactions, however, is a geographic process, as the assembly of interaction networks and the ongoing coevolution in these networks may vary across space (1). In pairs or small groups of species, theoretical and empirical work on the geographic mosaic of coevolution have shown that patterns of adaptation vary widely across geographic regions depending on the distribution of local selection regimes (2, 21–23). In addition, the connection of different populations via gene flow as well as other genetic and genomic processes may remix trait distributions across the landscape, promoting or inhibiting the evolution of local coadaptation (24–27). Although gene flow may strengthen local adaptation by increasing the genetic variation available to selection in some systems (28), this mechanism alone is unlikely in coevolving systems, in which gains in genetic variation would not compensate the deviations from local adaptation (21).
Despite the importance of gene flow and geographical variation in selection in interactions involving few species, we currently lack a framework to understand how these processes shape trait evolution in species-rich metacommunities (29, 30). In spatial metanetworks (31), the interplay between gene flow, geographical variation in selection, and both direct and indirect coevolutionary effects may reshape local adaptive landscapes with important consequences for trait evolution (Fig. 1 B and C).
Here, we combine a mathematical model of coevolution, network theory, and empirical data on species interactions to develop a framework that merges the geographic mosaic of coevolution with coevolutionary networks. We use this framework to investigate how the interplay between gene flow, geographical variation in selection, and network structure may affect the emergence of coadaptation in mutualisms. Through numerical simulations parameterized by 72 empirical networks, we show that gene flow increases trait matching between mutualistic partners, especially in species-rich, nested networks. Additional simulations using an analytical approximation of our model show that the progressive loss of gene flow due to habitat fragmentation could undermine coadaptations by altering species adaptive landscapes.
Results
Gene Flow, Geographical Variation in Selection, and the Evolution of Trait Patterns.
We first explored the emergence of trait matching in a single site using a previously developed model (7) that describes the evolution of a single trait shaped by mutualistic interactions among populations of different species (Materials and Methods). In this model, the mean trait value of each species () evolves toward a fixed environmental optimum () in the absence of mutualism. Mutualistic selection modifies this simple adaptive landscape by favoring trait matching among mutualistic partners (Fig. 1A). We performed numerical simulations of this model parameterized by the structure of 72 empirical mutualistic networks (SI Appendix, Table S1). We found that increasing mutualistic selection () leads to stronger reciprocal selection and to higher trait matching (SI Appendix, Fig. S1). As a consequence, networks in which is high and there is strong reciprocal selection (hereafter hotspots) favor higher levels of trait matching than networks in which is low and there is weak reciprocal selection (hereafter coldspots).
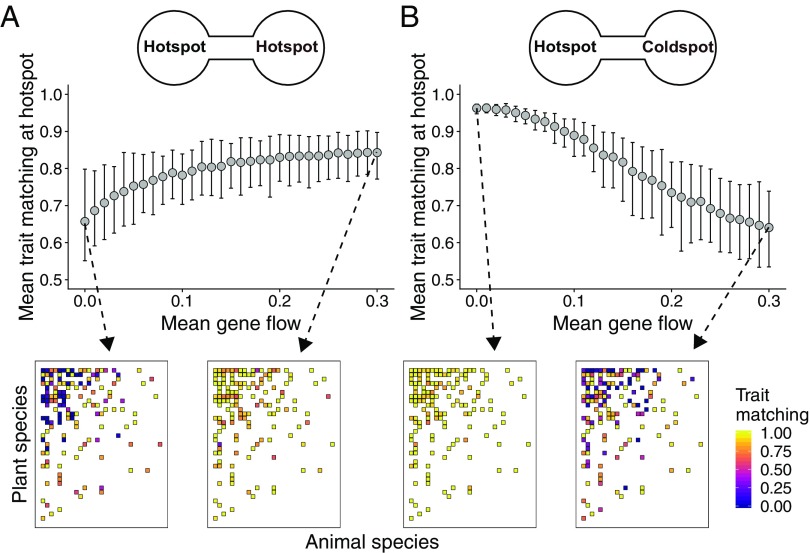
We next extended the coevolutionary model to two sites to explore how gene flow and geographical variation in mutualistic selection affect trait evolution (Materials and Methods). We performed simulations parameterized by our 72 empirical networks, assuming that the same network occurs at both sites. We found that gene flow () can either enhance or reduce trait matching, depending on mutualistic selection. For the majority of combinations of mutualistic selection, including two hotspots (), gene flow favors the emergence of trait matching (Fig. 2A and SI Appendix, Fig. S2). This surprising effect occurs because gene flow cancels out local conflicting selective pressures and allows trait matching to evolve, especially in pairs of generalist species (i.e., species with many interactions; Fig. 2A and SI Appendix, Fig. S3). This effect of gene flow results both from the uncoupling of species traits from their environmental optima and from the geographical homogenization of traits (SI Appendix, Fig. S4).
Fig. 2.
Effects of gene flow on the evolution of trait matching in mutualistic networks. (A and B) Each point is the mean trait matching at equilibrium at the hotspot () for 100 simulations parameterized with a seed dispersal network (network 64 in SI Appendix, Table S1), and bars show the 95% confidence interval. (A) When mutualistic selection is high at both sites (), gene flow favors trait matching at each hotspot. (B) When mutualistic selection is high at only one site (, ), gene flow reduces trait matching at the hotspot. Changes in mean trait matching (A and B) are a consequence of changes in the matching among generalist species, as shown in the interaction matrices (colors depict equilibrium pairwise trait matching for one simulation with the indicated value of gene flow). Sample distributions and values for simulation parameters: , , , , , , and .
Importantly, gene flow promotes trait matching especially when environmental optima (, ) are not correlated across sites, meaning that the selection regime of each species varies geographically as a selection mosaic (SI Appendix, Fig. S5). For a few combinations of mutualistic selection, such as a hotspot and a coldspot (, ), gene flow disrupts trait matching at the hotspot (Fig. 2B and SI Appendix, Fig. S2). In this case, populations at the coldspot are trapped into their environmental optima, and gene flow inhibits the evolution of trait matching at the hotspot. Sensitivity analyses showed that these results hold for many different parameter values (SI Appendix, Table S2 and Fig. S5), for a scenario in which gene flow is greater in generalist than in specialist species (SI Appendix, Fig. S6), and for a scenario in which species composition and network structure vary across sites (SI Appendix, Fig. S7).
We then obtained analytical equilibrium expressions to understand how coevolution shapes trait patterns (SI Appendix). With a single site, the trait values at equilibrium (vector ) are connected to species environmental optima (vector ) through a matrix () that contains direct and indirect coevolutionary effects: (7). Row of T represents how other species directly or indirectly affect the adaptive landscape of species . By measuring the correlation among rows of T, we showed that similar mutualistic adaptive landscapes among species favor trait matching and trait convergence (SI Appendix). Moreover, we found that increasing mutualistic selection leads to greater similarity of adaptive landscapes and higher trait matching, because indirect effects become stronger when mutualistic selection is higher (SI Appendix, Figs. S8 and S9). With two sites, the matrix T combines direct and indirect coevolutionary effects within and between sites. We found that increasing gene flow contributes to the similarity of adaptive landscapes, fueling trait matching in both mutualistic assemblages (SI Appendix, Figs. S10 and S11A). It does so by expanding the indirect effects of mutualistic selection across sites. In contrast, gene flow between a hotspot and a coldspot has an opposite effect and decreases trait matching (SI Appendix, Fig. S11B).
Network Structure and the Evolution of Trait Patterns.
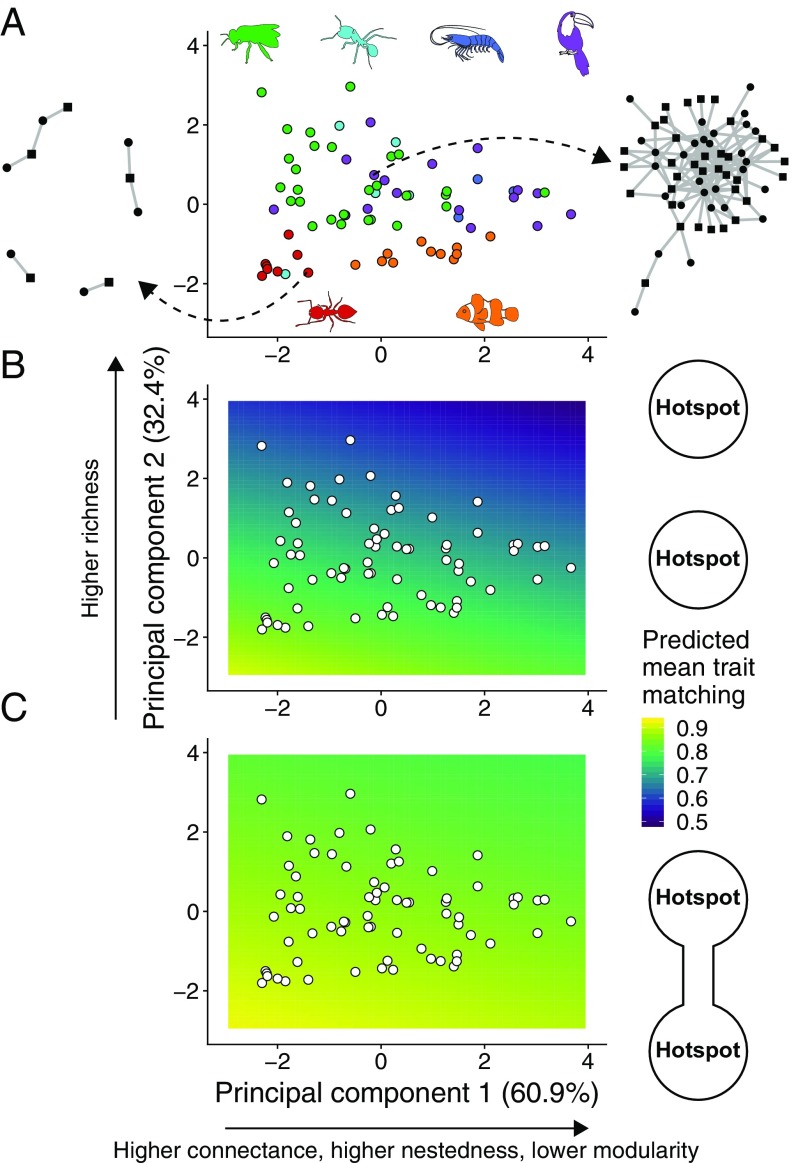
Our next step was to investigate how network structure influences coevolution and mediates the effects of gene flow. We characterized the structure of our 72 empirical networks using four metrics: species richness, connectance, nestedness, and modularity (Materials and Methods). We performed a Principal Component Analysis (PCA) of these metrics to obtain two variables ( and ) that describe the range of variation in network structure in our empirical dataset (Fig. 3A and SI Appendix, Table S1).
Fig. 3.
Network structure, gene flow, and the emergence of trait matching in mutualistic networks. (A) and of a PCA using four network structure metrics measured for our 72 empirical networks. accounted for 60.9% of all variation and was strongly correlated with connectance (0.56), nestedness (0.58), and modularity (−0.56). accounted for 32.4% of all variation and was strongly correlated with species richness (0.81). Network structure was highly variable, as illustrated by an ants–myrmecophytes (Left, network 14 in SI Appendix, Table S1) and a seed dispersal (Right, network 64 in SI Appendix, Table S1) network. Types of mutualism: green, pollination; cyan, ants–nectary-bearing plants; dark blue, marine cleaning; purple, seed dispersal; red, ants–myrmecophytes; orange, anemones–anemonefishes. (B and C) Predicted mean trait matching at the hotspot () for a linear model with and as explanatory variables and trait matching from simulations as the response variable (white points are the networks in A). (B) Species-poor, modular networks favored the emergence of trait matching in isolated hotspots (, , n = 100 simulations per network). (C) The effect of network structure is reduced when the two hotspots are connected by gene flow, and species-rich, nested networks may also favor high trait matching (, , n = 100 simulations per network). Simulation parameters as in Fig. 2.
In the absence of gene flow, species-poor, modular networks typical of intimate mutualisms favored the evolution of higher levels of trait matching than species-rich, nested networks typical of multiple-partner mutualisms (Fig. 3B, multiple linear regression: ). When gene flow is present, however, network structure has a weaker effect on the emergence of trait matching, allowing multiple-partner mutualisms to attain levels of trait matching almost as high as the ones observed for intimate mutualisms (Fig. 3C, ). This result occurs because networks of multiple-partner mutualisms contain a core of interacting generalists and the effect of gene flow on trait matching is stronger for pairs of generalist species than for other pairs of species (SI Appendix, Fig. S3). Our simulations using other combinations of mutualistic selection (, ) support the interpretation that gene flow has a stronger effect on multiple-partner mutualisms (SI Appendix, Fig. S2).
Disruption of Gene Flow and Its Consequences for Coevolution.
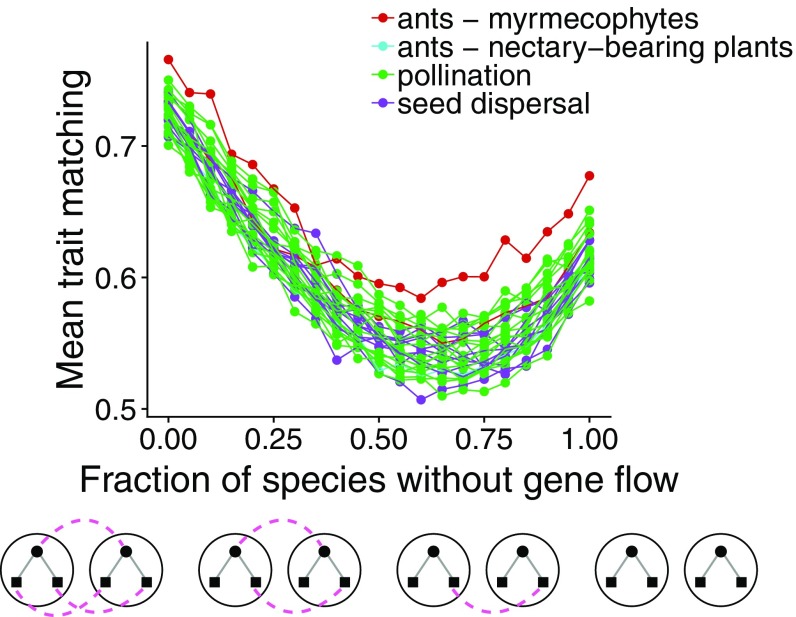
Having shown that gene flow may favor the emergence of coadaptation in mutualistic networks, we next considered the consequences of the disruption of gene flow to trait evolution. To do so, we simulated a progressive loss of gene flow in two initially connected mutualistic assemblages and computed equilibrium trait values using our analytical approximation (Materials and Methods). We used empirical information on ecological dependencies between mutualistic partners (i.e., weights in adjacency matrices; SI Appendix, Table S1) of 29 networks in our dataset to parameterize the evolutionary effects () of the matrix . By removing gene flow from an increasing fraction of species, we altered the direct and indirect coevolutionary effects within and between networks present in .
We found that the ongoing disruption of gene flow causes trait matching to decrease, but extreme loss of gene flow may recover some level of trait matching (Fig. 4and SI Appendix, Fig. S12). Further analysis revealed that the lowest values of trait matching in these simulations occur when gene flow is highly variable across species in the network (SI Appendix, Fig. S13).
Fig. 4.
Disruption of gene flow and its consequences for trait matching in mutualistic networks. Trait matching decreases as gene flow is progressively lost in mutualistic networks but increases slightly with an extreme loss of gene flow. Initially, all species in the network have a high value of gene flow (), and species randomly lose gene flow until all species lack gene flow (). Each point is the mean equilibrium trait matching at site () calculated with our analytical equilibrium expression using 10 different environmental optimum () samples in each of 10 distinct simulations. Lines connect points from the same network, and different colors indicate different types of mutualism. Sample distributions and values for simulation parameters: , , , , and .
Discussion
The geographical and multispecific complexity of coevolution poses a challenge to our understanding of the evolution of interacting species. In this study, we tackled this challenge by taking a first step in merging the geographic mosaic theory of coevolution with the recent approach of coevolutionary networks. Our framework combines a coevolutionary model and network theory to evaluate how gene flow, hotspots, and coldspots shape trait matching in multiple-partner and intimate mutualisms. Our findings reveal three main ways in which gene flow may be a fundamental process catalyzing the evolution of coadaptation in species-rich systems across simple landscapes.
First, gene flow may promote trait matching among mutualists within large networks. Previous results have shown that gene flow is capable of promoting adaptive evolution in natural populations by increasing local genetic variation (28) or when individuals disperse to specific habitats (32). Here, we reveal an additional mechanism for how gene flow may contribute to adaptation. When two mutualistic assemblages are connected by gene flow, the effects of environmental selection are canceled out, allowing mutualistic selection to drive trait evolution. As a consequence, gene flow makes the adaptive landscape of different species more similar to each other, erasing the conflicting selective pressures on highly interacting species and allowing trait matching and trait convergence to emerge. This result may provide a mechanism for one of the most challenging problems in coevolution, which is how local adaptation scales up to generate trait patterns in interacting species across broad geographical areas. We also found that gene flow may reduce trait matching for some specific scenarios, such as when a hotspot is linked to a coldspot. Therefore, specific combinations of gene flow and geographical variation in selection may generate trait mismatching in interacting species (2, 21). By analyzing pairs of interacting species, we showed that the observed changes in coadaptation patterns are mainly driven by species with a high number of interactions, such as generalist bees in pollination networks (33). This result, combined with our simulations incorporating simple spatial turnover in species composition, allows us to hypothesize that the observed effects of gene flow and geographical variation in selection should hold whenever generalist species are consistently present across local interaction networks. Our conclusions, however, may not hold for more complex landscapes, in which spatial heterogeneity may lead to unanticipated evolutionary dynamics.
Second, we show that network architecture mediates the effects of gene flow and geographical variation in selection on the evolution of trait patterns. The study of coadaptation in mutualistic systems has often focused on specialized interactions, such as the protection of host plants by their sheltered ant colonies (20, 34). In small networks of specialized species, coevolution should operate through frequent reciprocal changes between interacting species, generating impressive matching between morphological or physiological traits (20, 23, 34). However, in networks with dozens of interacting partners, coevolution may proceed through indirect effects (7), potentially driving community-level trait patterns such as trait convergence in assemblages of mimetic species (35) or fruiting plants (16). Because our results indicate that gene flow favors coadaptation mainly among generalist species, the effect of gene flow is greater in species-rich, nested networks than in species-poor, modular networks. Thus, networks of intimate mutualisms such as protective ants and their host myrmecophytes may favor tight trait matching between interacting partners irrespective of how well-connected populations are across a landscape. In contrast, the emergence of strong trait matching in multiple-partner mutualisms such as pollination may be contingent upon gene flow between populations.
Third, the trait patterns observed in species-rich mutualisms may be fragile in the face of processes leading to the disruption of gene flow, such as habitat fragmentation. Habitat fragmentation is one of the most widespread environmental impacts of human activities (36). Because habitat fragmentation may disrupt gene flow, genetic variability may wane in isolated populations, with severe consequences for the persistence of such populations (37). Our results suggest an additional effect of the gradual disruption of gene flow: the loss of coadaptation in mutualistic systems. This loss of coadaptation could, in turn, erode the potential robustness of coevolved interaction networks to human disturbance (8). We hypothesize, therefore, that habitat fragmentation may cause species-rich mutualisms to lose their ecological effects over time, with severe consequences for ecosystem services such as crop pollination and regeneration of plant populations (38).
Materials and Methods
Single-Site Coevolutionary Model.
We first used a single-site coevolutionary model to explore the emergence of trait patterns (7) (SI Appendix). This model is based on a selection gradient that connects trait evolution with the mean fitness consequences of mutualisms. In this model, populations of distinct species interact mutualistically at a given site, and the mean value of a single trait of each population () evolves in discrete time. Trait mediates mutualistic interactions (e.g., flower tube length, pollinator mouthpart length) and affects the fitness consequences of the mutualism (mutualistic selection) as well as other fitness components, such as abiotic factors (environmental selection). The trait evolution of species is described as follows:
| [1] |
where is proportional to the slope of the selection gradient and to the additive genetic variance of the trait, represents the evolutionary effect of species on species , and is the trait value favored by the environment. We assumed that mutualistic selection is mediated by trait matching and, therefore, the trait value of species favored by selection imposed by species is . The evolutionary effects are defined as a function of trait matching as:
| [2] |
where measures the relative importance of all mutualistic interactions , is an element of A—the binary adjacency matrix of a given mutualistic network—and is the level of trait matching between and . We defined trait matching as , in which controls the sensitivity of to differences between traits. If species and do not interact in the mutualistic network, then and is an evolutionary forbidden link. In contrast, if and are mutualistic partners, then and changes through time according to trait matching.
Two-Site Coevolutionary Model.
We extended the single-site coevolutionary model to a scenario with two mutualistic assemblages connected by gene flow (SI Appendix), which is consistent with the concept of a spatial metanetwork (31). We assumed that, at each generation, a fraction of the individuals of species migrate from site to site and from site to site (). Thus, a fraction of all individuals in both populations remains at its own site. The mean trait value of species at site changes according to the following equation:
| [3] |
where . The term and the equation for the evolutionary change in are obtained by interchanging subscripts and in and in Eq. 3. Importantly, model parameters (, , ), species richness (), and interaction networks () can all vary across sites, which allowed us to explore how geographical variation in these components affects trait evolution (SI Appendix).
Simulations of the Coevolutionary Models.
We performed numerical simulations of the coevolutionary models to investigate how mutualistic selection (, ) and gene flow () influence the emergence of trait matching (SI Appendix). First, we explored how mutualistic selection affects reciprocal selection and trait matching in an isolated site by performing simulations of the single-site model (Eq. 1), using different values of the mean mutualistic selection in the network (). Then, we focused on how the mean value of gene flow in the network (), which we varied from 0 to 0.3, affects the evolution of trait matching in two connected hotspots () in which reciprocal selection among species was strong and in a hotspot connected to a coldspot (, ) in which reciprocal selection was weak. For each combination of , , and , we performed 100 simulations of the two-site model (Eq. 3) per empirical mutualistic network in our dataset (n = 72 networks, SI Appendix, Table S1). In all simulations with the same empirical network, we parameterized the term by setting when species and interacted in the network and otherwise. All other parameters (, , , , ) and initial trait values were sampled at the beginning of each simulation from statistical distributions (SI Appendix, Table S2). In each simulation, we recorded trait values through time and computed trait matching for pairs of species as well as the mean value across all interacting species at both sites. The equilibrium values of trait matching and were calculated when species traits at both sites achieved asymptotic values, defined as and . In addition to performing simulations, we obtained analytical approximations of the coevolutionary models (Eqs. 1 and 3) to understand how trait patterns emerge in mutualistic networks (SI Appendix). All of the codes and empirical datasets required to reproduce our results are available at https://github.com/wgar84/spatial_coevo_mutnet.
Empirical Dataset.
Our dataset consisted of 72 empirical networks of both terrestrial and marine mutualisms (SI Appendix, Table S1). We chose these networks because they spanned diverse natural history attributes and network structures. Our dataset included six types of mutualism that can be divided into two broad categories: first, multiple-partner mutualisms in which individuals may interact with dozens or hundreds of different partners over a lifetime and form species-rich, nested networks—(i) ants that protect plants with extrafloral nectaries (n = 5 networks), (ii) animals that pollinate flowering plants (n = 28), (iii) fruit-eating vertebrates that disperse the seeds of plants with fleshy fruits (n = 17), and (iv) fishes and shrimps that clean client fishes (n = 3); second, intimate mutualisms in which individuals create sustained interactions and form species-poor, modular networks: (v) anemones that protect anemonefishes (n = 11) and (vi) ants that protect their host plants, the myrmecophytes (n = 8).
Network Structure.
We quantified four widely used metrics to characterize the arrangement of interactions in our networks: (i) species richness, (ii) connectance, (iii) nestedness, and (iv) modularity (SI Appendix). We used only information on the presence and absence of interactions (i.e., 1 and 0) to quantify these metrics. Species richness () is the total number of species in the network. Connectance () is the proportion of all possible interactions that are in fact realized (14). Nestedness measures how much the interactions of species with low degree values are proper subsets of the interactions of species with higher degree values (15). We quantified nestedness using the metric (39). Finally, modularity measures how much the network is partitioned into groups of species with many interactions within groups and few interactions among different groups (33). We computed modularity using a simulated annealing algorithm to optimize the value of a bipartite version of the metric (40). Because network structure metrics are often highly correlated among each other, we used PCA to describe how the values of our four metrics covary across networks. We used the first and second principal components ( and ) to describe the variation in network structure of our dataset and to explore how network structure affects the emergence of trait patterns.
Disruption of Gene Flow and Its Consequences for Coevolution.
We used our analytical approximation of the coevolutionary model to simulate the progressive loss of gene flow in two initially connected mutualistic assemblages (SI Appendix). We began each simulation by building a matrix with and a high value of gene flow (). We used the ecological dependencies between interacting species (i.e., weights in adjacency matrices; SI Appendix, Table S1) available for 29 networks in our dataset as proxies for the evolutionary effects () in . Then, we perturbed by randomly removing gene flow from an increasing proportion of species (i.e., of species without gene flow). The simulation ended when all species had lost gene flow (). After each perturbation of matrix , we sampled 10 different vectors using a statistical distribution and used our analytical equilibrium expression to calculate trait values () and trait matching (). We performed simulations for many different combinations of , , and (SI Appendix).
Supplementary Material
Acknowledgments
We thank P. I. Prado, R. Vicente, R. Cogni, G. Marroig, C. Reigada, P. Jordano, M. M. Pires, F. M. D. Marquitti, M. Galetti, and members of the P.R.G. laboratory for suggestions and discussions regarding this work. We also thank the researchers that kindly provided their empirical datasets. Icons are under public domain except for flower (Ab-dul Wahhab), anemonefish (parkjisun), toucan (Sma-rtez), and shrimp (Jerey Qua). L.P.M. was supported by Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) Grant 2015/12956-7. P.R.G. was supported by FAPESP Grants 2016/20739-9 and 2017/08406-7 and Conselho Nacional de Desenvolvimento Científico e Tecnológico.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: All of the codes and empirical datasets required to reproduce our results are available at https://github.com/wgar84/spatial_coevo_mutnet.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1809088115/-/DCSupplemental.
References
- 1.Thompson JN. The Geographic Mosaic of Coevolution. Univ of Chicago Press; Chicago: 2005. [Google Scholar]
- 2.Hanifin CT, Brodie ED, Brodie ED. Phenotypic mismatches reveal escape from arms-race coevolution. PLoS Biol. 2008;6:0471–0482. doi: 10.1371/journal.pbio.0060060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pauw A, Stofberg J, Waterman RJ. Flies and flowers in Darwin’s race. Evolution. 2009;63:268–279. doi: 10.1111/j.1558-5646.2008.00547.x. [DOI] [PubMed] [Google Scholar]
- 4.McCann KS. Food Webs. Princeton Univ Press; Princeton: 2011. [Google Scholar]
- 5.Bascompte J, Jordano P. Mutualistic Networks. Princeton Univ Press; Princeton: 2014. [Google Scholar]
- 6.Andreazzi CS, Thompson JN, Guimarães PR., Jr. Network structure and selection asymmetry drive coevolution in species-rich antagonistic interactions. Am Nat. 2017;190:99–115. doi: 10.1086/692110. [DOI] [PubMed] [Google Scholar]
- 7.Guimarães PR, Pires MM, Jordano P, Bascompte J, Thompson JN. Indirect effects drive coevolution in mutualistic networks. Nature. 2017;550:511–514. doi: 10.1038/nature24273. [DOI] [PubMed] [Google Scholar]
- 8.Nuismer SL, Week B, Aizen MA. Coevolution slows the disassembly of mutualistic networks. Am Nat. 2018;192:490–502. doi: 10.1086/699218. [DOI] [PubMed] [Google Scholar]
- 9.Nuismer SL, Jordano P, Bascompte J. Coevolution and the architecture of mutualistic networks. Evolution. 2013;67:338–354. doi: 10.1111/j.1558-5646.2012.01801.x. [DOI] [PubMed] [Google Scholar]
- 10.Hui C, Minoarivelo HO, Landi P. Modelling coevolution in ecological networks with adaptive dynamics. Math Meth Appl Sci 2017 [Google Scholar]
- 11.Ponisio LC, M’Gonigle LK. Coevolution leaves a weak signal on ecological networks. Ecosphere. 2017;8:e01798. [Google Scholar]
- 12.Valverde S, et al. The architecture of mutualistic networks as an evolutionary spandrel. Nat Ecol Evol. 2018;2:94–99. doi: 10.1038/s41559-017-0383-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Guimarães PR, et al. Interaction intimacy affects structure and coevolutionary dynamics in mutualistic networks. Curr Biol. 2007;17:1797–1803. doi: 10.1016/j.cub.2007.09.059. [DOI] [PubMed] [Google Scholar]
- 14.Jordano P. Patterns of mutualistic interactions in pollination and seed dispersal: Connectance, dependence asymmetries, and coevolution. Am Nat. 1987;129:657–677. [Google Scholar]
- 15.Bascompte J, Jordano P, Melián CJ, Olesen JM. The nested assembly of plant–animal mutualistic networks. Proc Natl Acad Sci USA. 2003;100:9383–9387. doi: 10.1073/pnas.1633576100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lomascolo SB, Levey DJ, Kimball RT, Bolker BM, Alborn HT. Dispersers shape fruit diversity in Ficus (Moraceae) Proc Natl Acad Sci USA. 2010;107:14668–14672. doi: 10.1073/pnas.1008773107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Guimarães PR, Jordano P, Thompson JN. Evolution and coevolution in mutualistic networks. Ecol Lett. 2011;14:877–885. doi: 10.1111/j.1461-0248.2011.01649.x. [DOI] [PubMed] [Google Scholar]
- 18.Fonseca CR, Ganade G. Asymmetries, compartments and null interactions in an Amazonian ant-plant community. J Anim Ecol. 1996;65:339–347. [Google Scholar]
- 19.Ricciardi F, Boyer M, Ollerton J. Assemblage and interaction structure of the anemonefish-anemone mutualism across the Manado region of Sulawesi, Indonesia. Environ Biol Fishes. 2010;87:333–347. [Google Scholar]
- 20.Orona-Tamayo D, et al. Exclusive rewards in mutualisms: Ant proteases and plant protease inhibitors create a lock-key system to protect Acacia food bodies from exploitation. Mol Ecol. 2013;22:4087–4100. doi: 10.1111/mec.12320. [DOI] [PubMed] [Google Scholar]
- 21.Gomulkiewicz R, Thompson JN, Holt RD, Nuismer SL, Hochberg ME. Hot spots, cold spots, and the geographic mosaic theory of coevolution. Am Nat. 2000;156:156–174. doi: 10.1086/303382. [DOI] [PubMed] [Google Scholar]
- 22.Kalske A, Leimu R, Scheepens JF, Mutikainen P. Spatiotemporal variation in local adaptation of a specialist insect herbivore to its long-lived host plant. Evolution. 2016;70:2110–2122. doi: 10.1111/evo.13013. [DOI] [PubMed] [Google Scholar]
- 23.Thompson JN, Schwind C, Friberg M. Diversification of trait combinations in coevolving plant and insect lineages. Am Nat. 2017;190:171–184. doi: 10.1086/692164. [DOI] [PubMed] [Google Scholar]
- 24.Vogwill T, Fenton A, Buckling A, Hochberg ME, Brockhurst MA. Source populations act as coevolutionary pacemakers in experimental selection mosaics containing hotspots and coldspots. Am Nat. 2009;173:E171–E176. doi: 10.1086/597374. [DOI] [PubMed] [Google Scholar]
- 25.Toju H, Ueno S, Taniguchi F, Sota T. Metapopulation structure of a seed-predator weevil and its host plant in arms race coevolution. Evolution. 2011;65:1707–1722. doi: 10.1111/j.1558-5646.2011.01243.x. [DOI] [PubMed] [Google Scholar]
- 26.Yoder JB, et al. Effects of gene flow on phenotype matching between two varieties of Joshua tree (Yucca brevifolia; Agavaceae) and their pollinators. J Evol Biol. 2013;26:1220–1233. doi: 10.1111/jeb.12134. [DOI] [PubMed] [Google Scholar]
- 27.Lion S, Gandon S. Evolution of spatially structured host-parasite interactions. J Evol Biol. 2015;28:10–28. doi: 10.1111/jeb.12551. [DOI] [PubMed] [Google Scholar]
- 28.Fitzpatrick SW, Gerberich JC, Kronenberger JA, Angeloni LM, Funk WC. Locally adapted traits maintained in the face of high gene flow. Ecol Lett. 2015;18:37–43. doi: 10.1111/ele.12388. [DOI] [PubMed] [Google Scholar]
- 29.Urban MC, et al. The evolutionary ecology of metacommunities. Trends Ecol Evol. 2008;23:311–317. doi: 10.1016/j.tree.2008.02.007. [DOI] [PubMed] [Google Scholar]
- 30.Toju H, et al. Species-rich networks and eco-evolutionary synthesis at the metacommunity level. Nat Ecol Evol. 2017;1:0024. doi: 10.1038/s41559-016-0024. [DOI] [PubMed] [Google Scholar]
- 31.Emer C, et al. Seed-dispersal interactions in fragmented landscapes—A metanetwork approach. Ecol Lett. 2018;21:484–493. doi: 10.1111/ele.12909. [DOI] [PubMed] [Google Scholar]
- 32.Jacob S, et al. Gene flow favours local adaptation under habitat choice in ciliate microcosms. Nat Ecol Evol. 2017;1:1407–1409. doi: 10.1038/s41559-017-0269-5. [DOI] [PubMed] [Google Scholar]
- 33.Olesen JM, Bascompte J, Dupont YL, Jordano P. The modularity of pollination networks. Proc Natl Acad Sci USA. 2007;104:19891–19896. doi: 10.1073/pnas.0706375104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Brouat C, Garcia N, Andary C, McKey D. Plant lock and ant key: Pairwise coevolution of an exclusion filter in an ant-plant mutualism. Proc Biol Sci B. 2001;268:2131–2141. doi: 10.1098/rspb.2001.1763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Elias M, Gompert Z, Jiggins C, Willmott K. Mutualistic interactions drive ecological niche convergence in a diverse butterfly community. PLoS Biol. 2008;6:2642–2649. doi: 10.1371/journal.pbio.0060300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Haddad NM, et al. Habitat fragmentation and its lasting impact on earth’s ecosystems. Sci Adv. 2015;1:e1500052. doi: 10.1126/sciadv.1500052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Aguilar R, Quesada M, Ashworth L, Herrerias-Diego Y, Lobo J. Genetic consequences of habitat fragmentation in plant populations: Susceptible signals in plant traits and methodological approaches. Mol Ecol. 2008;17:5177–5188. doi: 10.1111/j.1365-294X.2008.03971.x. [DOI] [PubMed] [Google Scholar]
- 38.Schleuning M, Fründ J, García D. Predicting ecosystem functions from biodiversity and mutualistic networks: An extension of trait-based concepts to plant-animal interactions. Ecography. 2015;38:380–392. [Google Scholar]
- 39.Almeida-Neto M, Guimarães P, Guimarães PR, Loyola RD, Ulrich W. A consistent metric for nestedness analysis in ecological systems: Reconciling concept and measurement. Oikos. 2008;117:1227–1239. [Google Scholar]
- 40.Marquitti FMD, Guimarães PR, Pires MM, Bittencourt LF. MODULAR: Software for the autonomous computation of modularity in large network sets. Ecography. 2014;37:221–224. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.